Some Classical Inequalities Associated with Generic Identity and Applications

Abstract

In this paper, we derive a new generic equality for the first-order differentiable functions. Through the utilization of the general identity and convex functions, we produce a family of upper bounds for numerous integral inequalities like Ostrowski’s inequality, trapezoidal inequality, midpoint inequality, Simpson’s inequality, Newton-type inequalities, and several two-point open trapezoidal inequalities. Also, we provide the numerical and visual explanation of our principal findings. Later, we provide some novel applications to the theory of means, special functions, error bounds of composite quadrature schemes, and parametric iterative schemes to find the roots of linear functions. Also, we attain several already known and new bounds for different values of $\gamma$ and parameter $\xi$.

1. Introduction

Among all of the fundamental functions in mathematical analysis, convexity-preserving functions exhibit numerous fascinating geometrical and analytical properties. They play a vital role in various scientific domains, including optimization, topology, functional analysis, economics, neural networking, and differential equations. However, its impact on the development of integral inequalities is unparalleled, as it provides a straightforward approach for estimating various mathematical quantities, making it particularly useful for error estimations in the form of inequalities. The theory of inequalities is extensively studied from multiple perspectives, including fractional calculus, quantum calculus, interval analysis, and functions of bounded variation. Many well-known results in inequalities are directly or indirectly linked to convex functions. Dynamic and error inequalities, such as the Hermite–Hadamard inequality, Jensen’s inequality, Jensen–Mercer inequality, Hardy inequality, Ostrowski’s inequality, and Simpson’s inequality, have been examined via convex functions. The error analysis of the quadrature rule is investigated for various purposes, often with the aim of determining tight bounds or upper bounds. One key research problem is how to find the error term for certain functions that are not sufficiently differentiable. For instance, deriving error terms for Newton–Cotes formulas when only first-order differentiable functions are available presents a challenge. To address this, several approaches have been developed using integrable kernels and other mathematical tools such as functions of bounded variation, Lipschitz continuous functions, generalized variation, Montgomery identity, and Taylor series. In 1998, Dragomir and Agarwal [1] introduced a systematic approach for developing upper bounds for the trapezoidal rule using first-order differentiable identity and convex functions. Following this approach, numerous inequalities have been explored for convex functions and their generalizations. For more details, see references [2,3,4].

Here, we revisit the famous Ostrowski’s inequality, which is explored as follows: Let $\mathcal{S}:[a,\omega ]\to \mathbb{R}$ be a differentiable function and ${\mathcal{S}}^{\prime }\in Ł(a,\omega )$. If $\left|{\mathcal{S}}^{\prime }\right|\le M$, then

$$\begin{array}{c}\hfill \left|\mathcal{S}\left(\gamma \right)-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\le M(\omega -a)\left[{\displaystyle \frac{1}{4}}+{\displaystyle \frac{{\left(\gamma -\frac{a+\omega }{2}\right)}^2}{{(\omega -a)}^2}}\right].\end{array}$$

This inequality predicts the error estimates of one one-point rule and mid-point rule. Furthermore, it has a significant impact on probability theory, special functions, and numerical analysis as well. It is investigated from approaches involving bounded variation, Lipschitzian, convex, and n times differentiable functions in the frame of classical calculus, fractional calculus, and time scale calculus.

Bohner and Matthews [5] examined the Ostrwoski-like inequalities via time scale concepts. In [6], the author formulated some versions of Ostrowski’s inequalities through the mean value theorem. In 2002, Anastassiou [7] analyzed the novel Ostrowski-type inequalities and Montgomery identities for nth-order differentiable functions. For detailed information, see [8,9,10].

First, we recollect the error inequality of Simpson’s rule, which is stated as:

If $\mathcal{S}:[a,\omega ]\to \mathbb{R}$ is four times continuously differentiable on $(a,\omega )$

$$\begin{array}{c}\hfill \left|\right|{\mathcal{S}}^{\left(4\right)}{\left|\right|}_{\infty }={sup}_{\gamma \in (a,\omega )}\left|{\mathcal{S}}^{\left(4\right)}\left(\gamma \right)\right|<\infty ,\end{array}$$

then

$$\begin{array}{c}\hfill \left|{\displaystyle \frac{1}{6}}\left[\mathcal{S}\left(a\right)+4\mathcal{S}\left({\displaystyle \frac{a+\omega }{2}}\right)+\mathcal{S}\left(\omega \right)\right]-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(\gamma \right)\mathrm{d}\gamma \right|\le {\displaystyle \frac{1}{2880}}\left|\right|{\mathcal{S}}^{\left(4\right)}{\left|\right|}_{\infty }{(\omega -a)}^4.\end{array}$$

Also, we recover the error inequality of the Simpson, s${\displaystyle \frac{3}{8}}$, or Newton inequality.

If $\mathcal{S}:[a,\omega ]\to \mathbb{R}$ is four times continuously differentiable on $(a,\omega )$

$$\begin{array}{c}\hfill \left|\right|{\mathcal{S}}^{\left(4\right)}{\left|\right|}_{\infty }={sup}_{\gamma \in (a,\omega )}\left|{\mathcal{S}}^{\left(4\right)}\right|<\infty ,\end{array}$$

then

$$\begin{array}{c}\hfill \left|{\displaystyle \frac{1}{8}}\left[\mathcal{S}\left(a\right)+3\mathcal{S}\left({\displaystyle \frac{2a+\omega }{3}}\right)+3\mathcal{S}\left({\displaystyle \frac{a+2\omega }{3}}\right)+\mathcal{S}\left(\omega \right)\right]-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(\gamma \right)\mathrm{d}\gamma \right|\le {\displaystyle \frac{1}{6480}}\left|\right|{\mathcal{S}}^{\left(4\right)}{\left|\right|}_{\infty }{(\omega -a)}^4.\end{array}$$

These inequalities are explored through various approaches to find more accurate and refined bounds. In 1998, Dragomir et al. [11] initiated a new way of thinking about these inequalities for first-order differentiable functions to determine upper bounds. Following this, Liu [12] developed Simpson-like inequalities for nth order differentiable functions to generalize previous results. In 2009, Alomari et al. [13] discussed Simpson-type inequalities via generalized convex functions. Sarikaya et al. [14] derived several new estimates of Simpson’s inequality through differentiable s-convex functions. For more information, see [15,16]. In [17], the authors introduced a new technique to investigate various inequalities by generalized kernels based on parameters. In 2000, Hanna et al. [18] constructed the two-dimensional Ostrowski’s inequality over the rectangular domain. In [19], Alomari and Dragomir unified the error inequalities of two-, three-, and four-point quadrature rules via a new generic kernel involving three parameters. In 2022, Iftikhar et al. [20] established a fresh two-dimensional lemma and computed new coordinated Newton-like inequalities associated with convex functions. In [21], the authors utilized quantum calculus to evaluate both kinds of Simpson’s inequality. Moreover, in [22], Butt and colleagues proved the majorized Simpson- and Newton-type inequalities with applications. In 2023, Meftah [23] studied Maclaurin-like inequalities incorporated with convex functions in the setting of multiplicative calculus. In 2023, Peng and Du [24] constructed some multiplicative analogues of Maclaurin’s inequality involving a p class of functions. Furthermore, In the same year, Hezenci [25] studied the conformable fraction analogues of corrected Euler–Maclaurin-like inequalities through convexity. In 2013, Alomari [26] for the first time estimated the bounds for Milne’s quadrature rule by lowering the derivative and using convex functions. Budak et al. [27] established the fractional counterparts of Milne’s schemes via convex functions. Bin-Mohsin et al. [28] utilized the Mercer approach and quantum calculus to derive the bounds for Milne’s inequality. In [29], Tseng et al. computed the Bullen-type inequalities by taking into account Lipschitzian function and presented some applications. In [30], Cakmak developed Bullen-type inequalities by making use of conformable fractional operators. The conformable operators satisfy several properties that other operators do not satisfy. In [31], Du and Cao established the fractional general family of Bullen’s inequality with implications. Cortez et al. [32] investigated the Bullen–Mercer-type inequalities and explored their efficacy by presenting novel applications to the iterative method. In 2012, Xi and Qi [33] investigated a unified governing equation for first-order differentiable function and deduced several new and interesting inequalities. Nwaeze and Tameru [34] investigated the blended form of inequalities through $\eta$-quasi convexity in the quantum setting. For further details, see [35,36,37].

This paper will establish a new general class of error bounds incorporated with convex functions. To achieve our goal, we distribute our study into four major parts: We initiate our study by revisiting the essential facts and previous work to discuss the problem’s background. In the next section, we build a new parametric equality, which plays a vital role in the further proceedings. Due to the generic nature of this identity, several new and known identities can be achieved to deduce bounds for numerical quadrature strategies. Then, we will construct unified bounds of error inequalities by considering the key auxiliary result, well-known inequalities, and convexity of first-order differentiable functions. Also, we will deliver several new and known consequences of the primary findings. Next, we will present numerous graphical visualisations of the main results. Finally, we will deliver the implementations of primary findings in terms of numerical integration, modified Bessel functions, theory of means, and novel iterative scheme as well as its convergence analysis.

2. Main Results

In the subsequent part, we derive the new unified error boundaries of both open and closed Newton–Cotes integration schemes through convex functions. Here, $L[a,\omega ]$ represents the space of all integral functions.

2.1. Auxiliary Result

We now prove a new unified identity for first-order differentiable functions depending on parameter $\xi$.

Lemma 1.

Let $\mathcal{S}:[a,\omega ]\to \mathbb{R}$ be a differentiable function and ${\mathcal{S}}^{\prime }\in Ł[a,\omega ]$; then

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\xi \left(\mathcal{S}\right(a)+\mathcal{S}(\omega \left)\right)}{2}}+{\displaystyle \frac{(1-\xi )\left(\mathcal{S}\right(a+\omega -\gamma )+\mathcal{S}(\gamma \left)\right)}{2}}-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\hfill \\ \hfill & =(\omega -a)\left[{\int }_0^{{\displaystyle \frac{\gamma -a}{\omega -a}}}\left(⋎-{\displaystyle \frac{\xi }{2}}\right){\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\mathrm{d}⋎+{\int }_{{\displaystyle \frac{\gamma -a}{\omega -a}}}^{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}\left(⋎-{\displaystyle \frac{1}{2}}\right){\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\mathrm{d}⋎\right.\hfill \\ \hfill & \left.+{\int }_{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}^1\left(⋎-1+{\displaystyle \frac{\xi }{2}}\right){\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\mathrm{d}⋎\right],\hfill \end{array}$$

(1)

where $\gamma \in [a,\omega ]$ and $\xi \in [0,1]$, satisfying the condition $a+\xi {\displaystyle \frac{\omega -a}{2}}\le \gamma \le {\displaystyle \frac{a+\omega }{2}}$.

Proof. 

From the right-hand side of (1), we have

$$\begin{array}{cc}\hfill I& =(\omega -a)\left[{\int }_0^{{\displaystyle \frac{\gamma -a}{\omega -a}}}\left(⋎-{\displaystyle \frac{\xi }{2}}\right){\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\mathrm{d}⋎+{\int }_{{\displaystyle \frac{\gamma -a}{\omega -a}}}^{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}\left(⋎-{\displaystyle \frac{1}{2}}\right){\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\mathrm{d}⋎\right.\hfill \\ \hfill & \left.+{\int }_{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}^1\left(⋎-1+{\displaystyle \frac{\xi }{2}}\right){\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\mathrm{d}⋎\right]\hfill \\ \hfill & =\left[I_1+I_2+I_3\right],\hfill \end{array}$$

(2)

where

$$\begin{array}{cc}\hfill I_1& =(\omega -a){\int }_0^{{\displaystyle \frac{\gamma -a}{\omega -a}}}\left(⋎-{\displaystyle \frac{\xi }{2}}\right){\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\mathrm{d}⋎\hfill \\ \hfill & ={\displaystyle \frac{2(\gamma -a)-\xi (\omega -a)}{2(\omega -a)}}\mathcal{S}\left(\gamma \right)+{\displaystyle \frac{\xi }{2}}\mathcal{S}\left(a\right)-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\gamma }\mathcal{S}\left(u\right)\mathrm{d}u.\hfill \end{array}$$

Also,

$$\begin{array}{cc}\hfill I_2& =(\omega -a){\int }_{{\displaystyle \frac{\gamma -a}{\omega -a}}}^{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}\left(⋎-{\displaystyle \frac{1}{2}}\right){\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\mathrm{d}⋎\hfill \\ \hfill & =\left({\displaystyle \frac{\omega -\gamma }{\omega -a}}-{\displaystyle \frac{1}{2}}\right)\mathcal{S}(a+\omega -\gamma )+{\displaystyle \frac{(\omega -a)-2(\gamma -a)}{2(\omega -a)}}\mathcal{S}\left(\gamma \right)-{\displaystyle \frac{1}{\omega -a}}{\int }_{\gamma }^{a+\omega -\gamma }\mathcal{S}\left(u\right)\mathrm{d}u.\hfill \end{array}$$

And

$$\begin{array}{cc}\hfill I_3& =(\omega -a){\int }_{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}^1\left(⋎-1+{\displaystyle \frac{\xi }{2}}\right){\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\mathrm{d}⋎\hfill \\ \hfill & ={\displaystyle \frac{\xi }{2}}\mathcal{S}\left(\omega \right)-\left({\displaystyle \frac{\omega -\gamma }{\omega -a}}-1+{\displaystyle \frac{\xi }{2}}\right)\mathcal{S}(a+\omega -\gamma )-{\displaystyle \frac{1}{\omega -a}}{\int }_{a+\omega -\gamma }^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u.\hfill \end{array}$$

Adding $I_1,I_2$, and $I_3$, we achieve our desired result. □

Now, we report some novel consequences of Lemma 1:

• Choosing $\xi =0$ in (1), we obtain

  $$\begin{array}{cc}\hfill & {\displaystyle \frac{\mathcal{S}(a+\omega -\gamma )+\mathcal{S}\left(\gamma \right)}{2}}-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\hfill \\ \hfill & =(\omega -a)\left[{\int }_0^{{\displaystyle \frac{\gamma -a}{\omega -a}}}⋎{\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\mathrm{d}⋎+{\int }_{{\displaystyle \frac{\gamma -a}{\omega -a}}}^{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}\left(⋎-{\displaystyle \frac{1}{2}}\right){\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\mathrm{d}⋎\right.\hfill \\ \hfill & \left.+{\int }_{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}^1(⋎-1){\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\mathrm{d}⋎\right].\hfill \end{array}$$
• Choosing $\xi =0$ and $\gamma ={\displaystyle \frac{a+\omega }{2}}$ in (1), it coincides with the result of [38],

  $$\begin{array}{cc}\hfill & \mathcal{S}\left({\displaystyle \frac{a+\omega }{2}}\right)-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\hfill \\ \hfill & =(\omega -a)\left[{\int }_0^{{\displaystyle \frac{1}{3}}}⋎{\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\mathrm{d}⋎+{\int }_{{\displaystyle \frac{1}{2}}}^1(⋎-1){\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\mathrm{d}⋎\right].\hfill \end{array}$$
• Choosing $\xi =0$ and $\gamma ={\displaystyle \frac{2a+\omega }{3}}$ in (1),

  $$\begin{array}{cc}\hfill & {\displaystyle \frac{\mathcal{S}\left(\frac{2a+\omega }{3}\right)+\mathcal{S}\left(\frac{a+2\omega }{3}\right)}{2}}-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\hfill \\ \hfill & =(\omega -a)\left[{\int }_0^{{\displaystyle \frac{1}{3}}}⋎{\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\mathrm{d}⋎+{\int }_{{\displaystyle \frac{1}{3}}}^{{\displaystyle \frac{2}{3}}}\left(⋎-{\displaystyle \frac{1}{2}}\right){\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\mathrm{d}⋎\right.\hfill \\ \hfill & \left.+{\int }_{{\displaystyle \frac{1}{2}}}^1(⋎-1){\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\mathrm{d}⋎\right].\hfill \end{array}$$
• Choosing $\xi =0$ and $\gamma ={\displaystyle \frac{3a+\omega }{4}}$ in (1),

  $$\begin{array}{cc}\hfill & {\displaystyle \frac{\mathcal{S}\left(\frac{3a+\omega }{4}\right)+\mathcal{S}\left(\frac{a+3\omega }{4}\right)}{2}}-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\hfill \\ \hfill & =(\omega -a)\left[{\int }_0^{{\displaystyle \frac{1}{4}}}⋎{\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\mathrm{d}⋎+{\int }_{{\displaystyle \frac{1}{4}}}^{{\displaystyle \frac{3}{4}}}\left(⋎-{\displaystyle \frac{1}{2}}\right){\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\mathrm{d}⋎\right.\hfill \\ \hfill & \left.+{\int }_{{\displaystyle \frac{3}{4}}}^1(⋎-1){\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\mathrm{d}⋎\right].\hfill \end{array}$$
• Choosing $\xi =0$ and $\gamma ={\displaystyle \frac{4a+\omega }{5}}$ in (1),

  $$\begin{array}{cc}\hfill & {\displaystyle \frac{\mathcal{S}\left(\frac{4a+\omega }{5}\right)+\mathcal{S}\left(\frac{a+4\omega }{5}\right)}{2}}-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\hfill \\ \hfill & =(\omega -a)\left[{\int }_0^{{\displaystyle \frac{1}{5}}}⋎{\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\mathrm{d}⋎+{\int }_{{\displaystyle \frac{1}{5}}}^{{\displaystyle \frac{4}{5}}}\left(⋎-{\displaystyle \frac{1}{2}}\right){\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\mathrm{d}⋎\right.\hfill \\ \hfill & \left.+{\int }_{{\displaystyle \frac{4}{5}}}^1(⋎-1){\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\mathrm{d}⋎\right].\hfill \end{array}$$
• Choosing $\xi =1$ and $\gamma ={\displaystyle \frac{a+\omega }{2}}$, we then obtain the trapezium equation established in [1].
• Choosing $\xi ={\displaystyle \frac{1}{3}}$ and $\gamma ={\displaystyle \frac{a+\omega }{2}}$ in (1), we then obtain the Simpson’s equality established in [13].
• Choosing $\xi ={\displaystyle \frac{1}{4}}$ and $\gamma ={\displaystyle \frac{2a+\omega }{3}}$ in (1), we then obtain the Newton’s equality established in [39].

2.2. Bounds for Several Error Inequalities Involving Convex Functions

Theorem 1.

Presume that all conditions of Lemma 1 are fulfilled. If $|{\mathcal{S}}^{\prime }|$ is a convex function, then

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\xi \left(\mathcal{S}\right(a)+\mathcal{S}(\omega \left)\right)}{2}}+{\displaystyle \frac{(1-\xi )\left(\mathcal{S}\right(a+\omega -\gamma )+\mathcal{S}(\gamma \left)\right)}{2}}-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\hfill \\ \hfill & \le (\omega -a)\left[\left(E_1+E_2+E_3\right)|{\mathcal{S}}^{\prime }\left(a\right)|+\left(E_4+E_5+E_6\right)\left|{\mathcal{S}}^{\prime }\left(\omega \right)\right|\right],\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill E_1& ={\int }_0^{{\displaystyle \frac{\gamma -a}{\omega -a}}}\left|⋎-{\displaystyle \frac{\xi }{2}}\right|(1-⋎)\mathrm{d}⋎={\displaystyle \frac{6{\xi }^2-6\xi -{\xi }^3}{24}}+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{\gamma -a}{\omega -a}}\right)}^2-{\displaystyle \frac{1}{3}}{\left({\displaystyle \frac{\gamma -a}{\omega -a}}\right)}^3+{\displaystyle \frac{\xi }{4}}{\left({\displaystyle \frac{\omega -\gamma }{\omega -a}}\right)}^2.\hfill \\ \hfill E_2& ={\int }_{{\displaystyle \frac{\gamma -a}{\omega -a}}}^{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}\left|⋎-{\displaystyle \frac{1}{2}}\right|(1-⋎)\mathrm{d}⋎=-{\displaystyle \frac{7}{24}}+{\displaystyle \frac{3}{4}}\left({\displaystyle \frac{{(\gamma -a)}^2+{(\omega -\gamma )}^2}{{(\omega -a)}^2}}\right)-{\displaystyle \frac{1}{3}}\left({\displaystyle \frac{{(\omega -\gamma )}^3+{(\gamma -a)}^3}{{(\omega -a)}^3}}\right).\hfill \\ \hfill E_3& ={\int }_{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}^1\left|⋎-1+{\displaystyle \frac{\xi }{2}}\right|(1-⋎)\mathrm{d}⋎\hfill \\ \hfill & ={\displaystyle \frac{\left(1-\frac{\xi }{2}\right)}{2}}{\left({\displaystyle \frac{\gamma -a}{\omega -a}}\right)}^2-{\displaystyle \frac{\left(1-\frac{\xi }{2}\right){\xi }^2}{4}}+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{\omega -\gamma }{\omega -a}}\right)}^2-{\left(1-{\displaystyle \frac{\xi }{2}}\right)}^2+{\displaystyle \frac{2}{3}}{\left(1-{\displaystyle \frac{\xi }{2}}\right)}^3-{\displaystyle \frac{1}{3}}{\left({\displaystyle \frac{\omega -\gamma }{\omega -a}}\right)}^3+{\displaystyle \frac{1}{6}}.\hfill \\ \hfill E_4& ={\int }_0^{{\displaystyle \frac{\gamma -a}{\omega -a}}}\left|⋎-{\displaystyle \frac{\xi }{2}}\right|⋎\mathrm{d}⋎={\displaystyle \frac{{\xi }^3}{24}}+{\displaystyle \frac{1}{3}}{\left({\displaystyle \frac{\gamma -a}{\omega -a}}\right)}^3-{\displaystyle \frac{\xi }{4}}{\left({\displaystyle \frac{\gamma -a}{\omega -a}}\right)}^2.\hfill \\ \hfill E_5& ={\int }_{{\displaystyle \frac{\gamma -a}{\omega -a}}}^{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}\left|⋎-{\displaystyle \frac{1}{2}}\right|⋎\mathrm{d}⋎={\displaystyle \frac{1}{24}}-{\displaystyle \frac{1}{4}}\left({\displaystyle \frac{{(\gamma -a)}^2+{(\omega -\gamma )}^2}{{(\omega -a)}^2}}\right)+{\displaystyle \frac{1}{3}}\left({\displaystyle \frac{{(\omega -\gamma )}^3+{(\gamma -a)}^3}{{(\omega -a)}^3}}\right).\hfill \\ \hfill E_6& ={\int }_{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}^1\left|⋎-1+{\displaystyle \frac{\xi }{2}}\right|⋎\mathrm{d}⋎\hfill \\ \hfill & ={\left(1-{\displaystyle \frac{\xi }{2}}\right)}^3-{\displaystyle \frac{2}{3}}{\left(1-{\displaystyle \frac{\xi }{2}}\right)}^3-{\displaystyle \frac{\left(1-\frac{\xi }{2}\right)}{2}}{\left({\displaystyle \frac{\omega -\gamma }{\omega -a}}\right)}^2+{\displaystyle \frac{1}{3}}{\left({\displaystyle \frac{\omega -\gamma }{\omega -a}}\right)}^3+{\displaystyle \frac{1}{3}}-{\displaystyle \frac{\left(1-\frac{\xi }{2}\right)}{2}}.\hfill \end{array}$$

Proof. 

Through Lemma 1 and implementing the convexity of $|{\mathcal{S}}^{\prime }|$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\xi \left(\mathcal{S}\right(a)+\mathcal{S}(\omega \left)\right)}{2}}+{\displaystyle \frac{(1-\xi )\left(\mathcal{S}\right(a+\omega -\gamma )+\mathcal{S}(\gamma \left)\right)}{2}}-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\hfill \\ \hfill & \le (\omega -a)\left[{\int }_0^{{\displaystyle \frac{\gamma -a}{\omega -a}}}\left|⋎-{\displaystyle \frac{\xi }{2}}\right||{\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )|\mathrm{d}⋎+{\int }_{{\displaystyle \frac{\gamma -a}{\omega -a}}}^{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}\left|⋎-{\displaystyle \frac{1}{2}}\right|\left|{\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\right|\mathrm{d}⋎\right.\hfill \\ \hfill & \left.+{\int }_{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}^1\left|⋎-1+{\displaystyle \frac{\xi }{2}}\right|\left|{\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\right|\mathrm{d}⋎\right]\hfill \\ \hfill & \le (\omega -a)\left[{\int }_0^{{\displaystyle \frac{\gamma -a}{\omega -a}}}\left|⋎-{\displaystyle \frac{\xi }{2}}\right|\left[(1-⋎)\right|{\mathcal{S}}^{\prime }\left(a\right)|+⋎|{\mathcal{S}}^{\prime }\left(\omega \right)\left|\right]\mathrm{d}⋎+{\int }_{{\displaystyle \frac{\gamma -a}{\omega -a}}}^{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}\left|⋎-{\displaystyle \frac{1}{2}}\right|\left[(1-⋎)\right|{\mathcal{S}}^{\prime }\left(a\right)|+⋎|{\mathcal{S}}^{\prime }\left(\omega \right)\left|\right]\mathrm{d}⋎\right.\hfill \\ \hfill & \left.+{\int }_{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}^1\left|⋎-1+{\displaystyle \frac{\xi }{2}}\right|\left[(1-⋎)\right|{\mathcal{S}}^{\prime }\left(a\right)|+⋎|{\mathcal{S}}^{\prime }\left(\omega \right)\left|\right]\mathrm{d}⋎\right]\hfill \\ \hfill & =(\omega -a)\left[\left({\int }_0^{{\displaystyle \frac{\gamma -a}{\omega -a}}}\left|⋎-{\displaystyle \frac{\xi }{2}}\right|(1-⋎)\mathrm{d}⋎+{\int }_{{\displaystyle \frac{\gamma -a}{\omega -a}}}^{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}\left|⋎-{\displaystyle \frac{1}{2}}\right|(1-⋎)\mathrm{d}⋎+{\int }_{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}^1\left|⋎-1+{\displaystyle \frac{\xi }{2}}\right|(1-⋎)\mathrm{d}⋎\right)\left|{\mathcal{S}}^{\prime }\left(a\right)\right|\right.\hfill \\ \hfill & \left.+\left({\int }_0^{{\displaystyle \frac{\gamma -a}{\omega -a}}}\left|⋎-{\displaystyle \frac{\xi }{2}}\right|⋎\mathrm{d}⋎+{\int }_{{\displaystyle \frac{\gamma -a}{\omega -a}}}^{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}\left|⋎-{\displaystyle \frac{1}{2}}\right|⋎\mathrm{d}⋎+{\int }_{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}^1\left|⋎-1+{\displaystyle \frac{\xi }{2}}\right|⋎\mathrm{d}⋎\right)\left|{\mathcal{S}}^{\prime }\left(\omega \right)\right|\right].\hfill \end{array}$$

Some simple computations yield the required result. □

Now, we discuss some consequences of Theorem 1.

Corollary 1

([38]). By selecting $\xi =0$ and $\gamma ={\displaystyle \frac{a+\omega }{2}}$, we have

$$\begin{array}{c}\hfill \left|\mathcal{S}\left({\displaystyle \frac{a+\omega }{2}}\right)-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\le {\displaystyle \frac{(\omega -a)}{8}}\left[\right|{\mathcal{S}}^{\prime }\left(a\right)|+|{\mathcal{S}}^{\prime }\left(\omega \right)\left|\right].\end{array}$$

Corollary 2.

By selecting $\xi =0$ and $\gamma ={\displaystyle \frac{2a+\omega }{3}}$, we have

$$\begin{array}{c}\hfill \left|{\displaystyle \frac{\mathcal{S}\left(\frac{2a+\omega }{3}\right)+\mathcal{S}\left(\frac{a+2\omega }{3}\right)}{2}}-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\le {\displaystyle \frac{5(\omega -a)}{72}}\left[\right|{\mathcal{S}}^{\prime }\left(a\right)|+|{\mathcal{S}}^{\prime }\left(\omega \right)\left|\right].\end{array}$$

Corollary 3.

By selecting $\xi =0$ and $\gamma ={\displaystyle \frac{3a+\omega }{4}}$, we have

$$\begin{array}{c}\hfill {\displaystyle \frac{\mathcal{S}\left(\frac{3a+\omega }{4}\right)+\mathcal{S}\left(\frac{a+3\omega }{4}\right)}{2}}-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\le {\displaystyle \frac{(\omega -a)}{16}}\left[\right|{\mathcal{S}}^{\prime }\left(a\right)|+|{\mathcal{S}}^{\prime }\left(\omega \right)\left|\right].\end{array}$$

Corollary 4.

By selecting $\xi =1$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathcal{S}\left(a\right)+\mathcal{S}\left(\omega \right)}{2}}-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\hfill \\ \hfill & \le (\omega -a)\left[\left(E_1^{*}+E_2+E_3^{*}\right)|{\mathcal{S}}^{\prime }\left(a\right)|\left(E_4^{*}+E_5+E_6^{*}\right)\left|{\mathcal{S}}^{\prime }\left(\omega \right)\right|\right],\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill E_1^{*}& ={\displaystyle \frac{-1}{24}}+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{\gamma -a}{\omega -a}}\right)}^2-{\displaystyle \frac{1}{3}}{\left({\displaystyle \frac{\gamma -a}{\omega -a}}\right)}^3+{\displaystyle \frac{1}{4}}{\left({\displaystyle \frac{\omega -\gamma }{\omega -a}}\right)}^2\hfill \\ \hfill E_3^{*}& ={\displaystyle \frac{-1}{8}}+{\displaystyle \frac{1}{4}}{\left({\displaystyle \frac{\gamma -a}{\omega -a}}\right)}^2+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{\omega -\gamma }{\omega -a}}\right)}^2-{\displaystyle \frac{1}{3}}{\left({\displaystyle \frac{\omega -\gamma }{\omega -a}}\right)}^3\hfill \\ \hfill E_4^{*}& ={\displaystyle \frac{1}{24}}+{\displaystyle \frac{1}{3}}{\left({\displaystyle \frac{\gamma -a}{\omega -a}}\right)}^3-{\displaystyle \frac{1}{4}}{\left({\displaystyle \frac{\gamma -a}{\omega -a}}\right)}^2\hfill \\ \hfill E_6^{*}& ={\displaystyle \frac{1}{8}}-{\displaystyle \frac{1}{4}}{\left({\displaystyle \frac{\omega -\gamma }{\omega -a}}\right)}^2+{\displaystyle \frac{1}{3}}{\left({\displaystyle \frac{\omega -\gamma }{\omega -a}}\right)}^3,\hfill \end{array}$$

and $E_2$ and $E_5$ are defined in Theorem 1.

Corollary 5.

By selecting $\xi =1$ and $\gamma ={\displaystyle \frac{a+\omega }{2}}$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathcal{S}\left(a\right)+\mathcal{S}\left(\omega \right)}{2}}-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\le {\displaystyle \frac{(\omega -a)}{8}}\left[|{\mathcal{S}}^{\prime }\left(a\right)|+|{\mathcal{S}}^{\prime }\left(\omega \right)|\right].\hfill \end{array}$$

Corollary 6.

By selecting $\xi =1$ and $\gamma ={\displaystyle \frac{2a+\omega }{3}}$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathcal{S}\left(a\right)+\mathcal{S}\left(\omega \right)}{2}}-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\le {\displaystyle \frac{(\omega -a)}{72}}\left[5|{\mathcal{S}}^{\prime }\left(a\right)|+11|{\mathcal{S}}^{\prime }\left(\omega \right)|\right].\hfill \end{array}$$

Corollary 7.

By selecting $\xi ={\displaystyle \frac{1}{3}}$ and $\gamma ={\displaystyle \frac{a+\omega }{2}}$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{1}{6}}\left[\mathcal{S}\left(a\right)+4\mathcal{S}\left({\displaystyle \frac{a+\omega }{2}}\right)+\mathcal{S}\left(\omega \right)\right]-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\le {\displaystyle \frac{5(\omega -a)}{72}}\left[|{\mathcal{S}}^{\prime }\left(a\right)|+|{\mathcal{S}}^{\prime }\left(\omega \right)|\right].\hfill \end{array}$$

Corollary 8.

By selecting $\xi ={\displaystyle \frac{1}{2}}$ and $\gamma ={\displaystyle \frac{a+\omega }{2}}$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{1}{2}}\left[{\displaystyle \frac{\mathcal{S}\left(a\right)+\mathcal{S}\left(\omega \right)}{2}}+\mathcal{S}\left({\displaystyle \frac{a+\omega }{2}}\right)\right]-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\le {\displaystyle \frac{(\omega -a)}{16}}\left[|{\mathcal{S}}^{\prime }\left(a\right)|+|{\mathcal{S}}^{\prime }\left(\omega \right)|\right].\hfill \end{array}$$

Corollary 9.

By selecting $\xi ={\displaystyle \frac{1}{4}}$ and $\gamma ={\displaystyle \frac{2a+\omega }{3}}$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{1}{8}}\left[\mathcal{S}\left(a\right)+3\mathcal{S}\left({\displaystyle \frac{2a+\omega }{3}}\right)+3\mathcal{S}\left({\displaystyle \frac{a+2\omega }{3}}\right)+\mathcal{S}\left(\omega \right)\right]-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\le {\displaystyle \frac{(\omega -a)}{576}}\left[13|{\mathcal{S}}^{\prime }\left(a\right)|+25|{\mathcal{S}}^{\prime }\left(\omega \right)|\right].\hfill \end{array}$$

Theorem 2.

Presume that all conditions of Lemma 1 are fulfilled. If $|{\mathcal{S}}^{\prime }{|}^q$ is a convex function, then

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\xi \left(\mathcal{S}\right(a)+\mathcal{S}(\omega \left)\right)}{2}}+{\displaystyle \frac{(1-\xi )\left(\mathcal{S}\right(a+\omega -\gamma )+\mathcal{S}(\gamma \left)\right)}{2}}-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\hfill \\ \hfill & \le (\omega -a)\left[E_7^{1-{\displaystyle \frac{1}{q}}}{\left(E_1|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+E_4{\left|{\mathcal{S}}^{\prime }\left(\omega \right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}+E_8^{1-{\displaystyle \frac{1}{q}}}{\left(E_2|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+E_5{\left|{\mathcal{S}}^{\prime }\left(\omega \right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & \left.+{\left(E_9\right)}^{1-{\displaystyle \frac{1}{q}}}{\left(E_3|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+E_6{\left|{\mathcal{S}}^{\prime }\left(\omega \right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\right],\hfill \end{array}$$

where ($E_1$–$E_6$) are proved in Theorem 1 and

$$\begin{array}{cc}\hfill E_7& ={\int }_0^{{\displaystyle \frac{\gamma -a}{\omega -a}}}\left|⋎-{\displaystyle \frac{\xi }{2}}\right|\mathrm{d}⋎={\displaystyle \frac{{\xi }^2}{4}}+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{\gamma -a}{\omega -a}}\right)}^2-{\displaystyle \frac{\xi }{2}}\left({\displaystyle \frac{\gamma -a}{\omega -a}}\right)\hfill \\ \hfill E_8& ={\int }_{{\displaystyle \frac{\gamma -a}{\omega -a}}}^{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}\left|⋎-{\displaystyle \frac{1}{2}}\right|\mathrm{d}⋎=-{\displaystyle \frac{1}{4}}+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{\gamma -a}{\omega -a}}\right)}^2+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{\omega -\gamma }{\omega -a}}\right)}^2\hfill \\ \hfill E_9& ={\int }_{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}^1\left|⋎-1+{\displaystyle \frac{\xi }{2}}\right|\mathrm{d}⋎={\displaystyle \frac{{\left(1-\frac{\xi }{2}-\frac{\omega -\gamma }{\omega -a}\right)}^2}{2}}+{\displaystyle \frac{{\xi }^2}{8}}.\hfill \end{array}$$

Proof. 

Through Lemma 1, using power mean inequality and implementing the convexity of $|{\mathcal{S}}^{\prime }|$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\xi \left(\mathcal{S}\right(a)+\mathcal{S}(\omega \left)\right)}{2}}+{\displaystyle \frac{(1-\xi )\left(\mathcal{S}\right(a+\omega -\gamma )+\mathcal{S}(\gamma \left)\right)}{2}}-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\hfill \\ \hfill & \le (\omega -a)\left[{\int }_0^{{\displaystyle \frac{\gamma -a}{\omega -a}}}\left|⋎-{\displaystyle \frac{\xi }{2}}\right||{\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )|\mathrm{d}⋎+{\int }_{{\displaystyle \frac{\gamma -a}{\omega -a}}}^{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}\left|⋎-{\displaystyle \frac{1}{2}}\right|\left|{\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\right|\mathrm{d}⋎\right.\hfill \\ \hfill & \left.+{\int }_{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}^1\left|⋎-1+{\displaystyle \frac{\xi }{2}}\right|\left|{\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\right|\mathrm{d}⋎\right]\hfill \\ \hfill & \le (\omega -a)\left[{\left({\int }_0^{{\displaystyle \frac{\gamma -a}{\omega -a}}}\left|⋎-{\displaystyle \frac{\xi }{2}}\right|\mathrm{d}⋎\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\int }_0^{{\displaystyle \frac{\gamma -a}{\omega -a}}}\left|⋎-{\displaystyle \frac{\xi }{2}}\right|{\left|{\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\right|}^q\mathrm{d}⋎\right)}^{{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & +{\left({\int }_{{\displaystyle \frac{\gamma -a}{\omega -a}}}^{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}\left|⋎-{\displaystyle \frac{1}{2}}\right|\mathrm{d}⋎\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\int }_{{\displaystyle \frac{\gamma -a}{\omega -a}}}^{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}\left|⋎-{\displaystyle \frac{1}{2}}\right|{\left|{\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\right|}^q\mathrm{d}⋎\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & \left.+{\left({\int }_{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}^1\left|⋎-1+{\displaystyle \frac{\xi }{2}}\right|\mathrm{d}⋎\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\int }_{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}^1\left|⋎-1+{\displaystyle \frac{\xi }{2}}\right|{\left|{\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\right|}^q\mathrm{d}⋎\right)}^{{\displaystyle \frac{1}{q}}}\right]\hfill \\ \hfill & \le (\omega -a)\left[E_7^{1-{\displaystyle \frac{1}{q}}}{\left({\int }_0^{{\displaystyle \frac{\gamma -a}{\omega -a}}}\left|⋎-{\displaystyle \frac{\xi }{2}}\right|\left[(1-⋎)\right|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+⋎|{\mathcal{S}}^{\prime }\left(\omega \right){|}^q]\mathrm{d}⋎\right)}^{{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & +E_8^{1-{\displaystyle \frac{1}{q}}}{\left({\int }_{{\displaystyle \frac{\gamma -a}{\omega -a}}}^{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}\left|⋎-{\displaystyle \frac{1}{2}}\right|\left[(1-⋎)\right|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+⋎|{\mathcal{S}}^{\prime }\left(\omega \right){|}^q]\mathrm{d}⋎\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & \left.+{\left(E_9\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\int }_{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}^1\left|⋎-1+{\displaystyle \frac{\xi }{2}}\right|\left[(1-⋎)\right|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+⋎|{\mathcal{S}}^{\prime }\left(\omega \right){|}^q]\mathrm{d}⋎\right)}^{{\displaystyle \frac{1}{q}}}\right].\hfill \end{array}$$

Some simple computations determine the required result. □

Now we discuss some consequences of Theorem 2.

Corollary 10

([38]). By selecting $\xi =0$ and $\gamma ={\displaystyle \frac{a+\omega }{2}}$, we have

$$\begin{array}{cc}\hfill & \left|\mathcal{S}\left({\displaystyle \frac{a+\omega }{2}}\right)-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\hfill \\ \hfill & \le (\omega -a){\left({\displaystyle \frac{1}{8}}\right)}^{1-{\displaystyle \frac{1}{q}}}\left[{\left({\displaystyle \frac{3|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{8}}\right)}^{{\displaystyle \frac{1}{q}}}+{\left({\displaystyle \frac{|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+3{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{8}}\right)}^{{\displaystyle \frac{1}{q}}}\right].\hfill \end{array}$$

Corollary 11.

By selecting $\xi =0$ and $\gamma ={\displaystyle \frac{2a+\omega }{3}}$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathcal{S}\left(\frac{2a+\omega }{3}\right)+\mathcal{S}\left(\frac{a+2\omega }{3}\right)}{2}}-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\hfill \\ \hfill & \le (\omega -a)\left[{\left({\displaystyle \frac{1}{18}}\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\displaystyle \frac{7|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+2{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{162}}\right)}^{{\displaystyle \frac{1}{q}}}+{\left({\displaystyle \frac{1}{36}}\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\displaystyle \frac{|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{72}}\right)}^{{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & \left.+{\left({\displaystyle \frac{1}{18}}\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\displaystyle \frac{2|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+7{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{162}}\right)}^{{\displaystyle \frac{1}{q}}}\right].\hfill \end{array}$$

Corollary 12.

By selecting $\xi =0$ and $\gamma ={\displaystyle \frac{3a+\omega }{4}}$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathcal{S}\left(\frac{3a+\omega }{4}\right)+\mathcal{S}\left(\frac{a+3\omega }{4}\right)}{2}}-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\hfill \\ \hfill & \le (\omega -a)\left[{\left({\displaystyle \frac{1}{32}}\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\displaystyle \frac{5|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{192}}\right)}^{{\displaystyle \frac{1}{q}}}+{\left({\displaystyle \frac{1}{16}}\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\displaystyle \frac{|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{32}}\right)}^{{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & \left.+{\left({\displaystyle \frac{1}{32}}\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\displaystyle \frac{|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+5{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{192}}\right)}^{{\displaystyle \frac{1}{q}}}\right].\hfill \end{array}$$

Corollary 13.

By selecting $\xi =1$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathcal{S}\left(a\right)+\mathcal{S}\left(\omega \right)}{2}}-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\hfill \\ \hfill & \le (\omega -a)\left[{\left(E_7^{*}\right)}^{1-{\displaystyle \frac{1}{q}}}{\left(E_1^{*}|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+E_4^{*}{\left|{\mathcal{S}}^{\prime }\left(\omega \right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}+E_8^{1-{\displaystyle \frac{1}{q}}}{\left(E_2|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+E_5{\left|{\mathcal{S}}^{\prime }\left(\omega \right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & \left.+{\left(E_9^{*}\right)}^{1-{\displaystyle \frac{1}{q}}}{\left(E_3^{*}|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+E_6^{*}{\left|{\mathcal{S}}^{\prime }\left(\omega \right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\right],\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill E_7^{*}& ={\displaystyle \frac{1}{4}}+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{\gamma -a}{\omega -a}}\right)}^2-{\displaystyle \frac{1}{2}}\left({\displaystyle \frac{\gamma -1}{\omega -a}}\right)\hfill \\ \hfill E_8& =-{\displaystyle \frac{1}{4}}+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{\gamma -a}{\omega -a}}\right)}^2+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{\omega -\gamma }{\omega -a}}\right)}^2\hfill \\ \hfill E_9^{*}& ={\displaystyle \frac{1}{8}}+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{\omega -\gamma }{\omega -a}}\right)}^2,\hfill \end{array}$$

where $E_1^{*},E_3^{*},E_4^{*}$, and $E_6^{*}$ are defined in Corollary 36, and $E_2$ and $E_5$ are defined in Theorem 1.

Corollary 14.

By selecting $\xi =1$ and $\gamma ={\displaystyle \frac{a+\omega }{2}}$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathcal{S}\left(a\right)+\mathcal{S}\left(\omega \right)}{2}}-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\hfill \\ \hfill & \le (\omega -a){\left({\displaystyle \frac{1}{8}}\right)}^{1-{\displaystyle \frac{1}{q}}}\left[{\left({\displaystyle \frac{5|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{48}}\right)}^{{\displaystyle \frac{1}{q}}}+{\left({\displaystyle \frac{|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+5{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{48}}\right)}^{{\displaystyle \frac{1}{q}}}\right].\hfill \end{array}$$

Corollary 15.

By selecting $\xi =1$ and $\gamma ={\displaystyle \frac{2a+\omega }{3}}$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathcal{S}\left(a\right)+\mathcal{S}\left(\omega \right)}{2}}-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\hfill \\ \hfill & \le (\omega -a)\left[{\left({\displaystyle \frac{5}{36}}\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\displaystyle \frac{19|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+17{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{648}}\right)}^{{\displaystyle \frac{1}{q}}}+{\left({\displaystyle \frac{1}{36}}\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\displaystyle \frac{|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{72}}\right)}^{{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & \left.+{\left({\displaystyle \frac{5}{36}}\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\displaystyle \frac{17|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+73{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{648}}\right)}^{{\displaystyle \frac{1}{q}}}\right].\hfill \end{array}$$

Corollary 16.

By selecting $\xi ={\displaystyle \frac{1}{3}}$ and $\gamma ={\displaystyle \frac{a+\omega }{2}}$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{1}{2}}\left[{\displaystyle \frac{\mathcal{S}\left(a\right)+\mathcal{S}\left(\omega \right)}{2}}+\mathcal{S}\left({\displaystyle \frac{a+\omega }{2}}\right)\right]-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\hfill \\ \hfill & \le (\omega -a){\left({\displaystyle \frac{5}{72}}\right)}^{1-{\displaystyle \frac{1}{q}}}\left[{\left({\displaystyle \frac{61|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+29{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{1296}}\right)}^{{\displaystyle \frac{1}{q}}}+{\left({\displaystyle \frac{29|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+61{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{1296}}\right)}^{{\displaystyle \frac{1}{q}}}\right].\hfill \end{array}$$

Corollary 17.

By selecting $\xi ={\displaystyle \frac{1}{2}}$ and $\gamma ={\displaystyle \frac{a+\omega }{2}}$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{1}{2}}\left[{\displaystyle \frac{\mathcal{S}\left(a\right)+\mathcal{S}\left(\omega \right)}{2}}+\mathcal{S}\left({\displaystyle \frac{a+\omega }{2}}\right)\right]-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\hfill \\ \hfill & \le (\omega -a){\left({\displaystyle \frac{1}{16}}\right)}^{1-{\displaystyle \frac{1}{q}}}\left[{\left({\displaystyle \frac{3|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{64}}\right)}^{{\displaystyle \frac{1}{q}}}+{\left({\displaystyle \frac{|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+3{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{64}}\right)}^{{\displaystyle \frac{1}{q}}}\right].\hfill \end{array}$$

Corollary 18.

By selecting $\xi ={\displaystyle \frac{1}{4}}$ and $\gamma ={\displaystyle \frac{2a+\omega }{3}}$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{1}{8}}\left[\mathcal{S}\left(a\right)+3\mathcal{S}\left({\displaystyle \frac{2a+\omega }{3}}\right)+3\mathcal{S}\left({\displaystyle \frac{a+2\omega }{3}}\right)+\mathcal{S}\left(\omega \right)\right]-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\hfill \\ \hfill & \le (\omega -a)\left[{\left({\displaystyle \frac{17}{576}}\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\displaystyle \frac{109|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+251{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{41472}}\right)}^{{\displaystyle \frac{1}{q}}}+{\left({\displaystyle \frac{1}{36}}\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\displaystyle \frac{|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{72}}\right)}^{{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & \left.+{\left({\displaystyle \frac{17}{576}}\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\displaystyle \frac{251|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+973{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{41472}}\right)}^{{\displaystyle \frac{1}{q}}}\right].\hfill \end{array}$$

Theorem 3.

Presume that all conditions of Lemma 1 are fulfilled. If $|{\mathcal{S}}^{\prime }{|}^q$ is a convex function, then

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\xi \left(\mathcal{S}\right(a)+\mathcal{S}(\omega \left)\right)}{2}}+{\displaystyle \frac{(1-\xi )\left(\mathcal{S}\right(a+\omega -\gamma )+\mathcal{S}(\gamma \left)\right)}{2}}-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\hfill \\ \hfill & \le (\omega -a)\left[C_1^{{\displaystyle \frac{1}{p}}}{\left(\left({\displaystyle \frac{{(\omega -a)}^2-{(\omega -\gamma )}^2}{2{(\omega -a)}^2}}\right)|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{\gamma -a}{\omega -a}}\right)}^2{\left|{\mathcal{S}}^{\prime }\left(\omega \right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & +C_2^{{\displaystyle \frac{1}{p}}}{\left(\left({\displaystyle \frac{{(\omega -\gamma )}^2-{(\gamma -a)}^2}{2{(\omega -a)}^2}}\right)\left[\right|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+|{\mathcal{S}}^{\prime }\left(\omega \right){|}^q]\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & \left.+C_3^{{\displaystyle \frac{1}{p}}}{\left({\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{\gamma -a}{\omega -a}}\right)}^2|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+{\displaystyle \frac{1}{2}}\left({\displaystyle \frac{{(\omega -a)}^2-{(\omega -\gamma )}^2}{{(\omega -a)}^2}}\right){\left|{\mathcal{S}}^{\prime }\left(\omega \right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\right],\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill C_1& ={\int }_0^{{\displaystyle \frac{\gamma -a}{\omega -a}}}{\left|⋎-{\displaystyle \frac{\xi }{2}}\right|}^p\mathrm{d}⋎={\displaystyle \frac{{\left(\frac{\xi }{2}\right)}^{p+1}+{\left(\frac{\gamma -a}{\omega -a}-\frac{\xi }{2}\right)}^{p+1}}{1+p}}\hfill \\ \hfill C_2& ={\int }_{{\displaystyle \frac{\gamma -a}{\omega -a}}}^{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}{\left|⋎-{\displaystyle \frac{1}{2}}\right|}^p\mathrm{d}⋎={\displaystyle \frac{{\left(\frac{1}{2}-\frac{\gamma -a}{\omega -a}\right)}^{p+1}+{\left(\frac{\omega -\gamma }{\omega -a}-\frac{1}{2}\right)}^{p+1}}{1+p}}\hfill \\ \hfill C_3& ={\int }_{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}^1{\left|⋎-1+{\displaystyle \frac{\xi }{2}}\right|}^p\mathrm{d}⋎={\displaystyle \frac{{\left(\frac{\xi }{2}\right)}^{p+1}+{\left(1-\frac{\xi }{2}-\frac{\omega -\gamma }{\omega -a}\right)}^{p+1}}{1+p}}.\hfill \end{array}$$

Proof. 

Through Lemma 1, using Hölder’s inequality and implementing the convexity of $|{\mathcal{S}}^{\prime }{|}^q$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\xi \left(\mathcal{S}\right(a)+\mathcal{S}(\omega \left)\right)}{2}}+{\displaystyle \frac{(1-\xi )\left(\mathcal{S}\right(a+\omega -\gamma )+\mathcal{S}(\gamma \left)\right)}{2}}-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\hfill \\ \hfill & \le (\omega -a)\left[{\int }_0^{{\displaystyle \frac{\gamma -a}{\omega -a}}}\left|⋎-{\displaystyle \frac{\xi }{2}}\right||{\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )|\mathrm{d}⋎+{\int }_{{\displaystyle \frac{\gamma -a}{\omega -a}}}^{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}\left|⋎-{\displaystyle \frac{1}{2}}\right|\left|{\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\right|\mathrm{d}⋎\right.\hfill \\ \hfill & \left.+{\int }_{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}^1\left|⋎-1+{\displaystyle \frac{\xi }{2}}\right|\left|{\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\right|\mathrm{d}⋎\right]\hfill \\ \hfill & \le (\omega -a)\left[{\left({\int }_0^{{\displaystyle \frac{\gamma -a}{\omega -a}}}{\left|⋎-{\displaystyle \frac{\xi }{2}}\right|}^p\mathrm{d}⋎\right)}^{{\displaystyle \frac{1}{p}}}{\left({\int }_0^{{\displaystyle \frac{\gamma -a}{\omega -a}}}{\left|{\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\right|}^q\mathrm{d}⋎\right)}^{{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & +{\left({\int }_{{\displaystyle \frac{\gamma -a}{\omega -a}}}^{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}{\left|⋎-{\displaystyle \frac{1}{2}}\right|}^p\mathrm{d}⋎\right)}^{{\displaystyle \frac{1}{p}}}{\left({\int }_{{\displaystyle \frac{\gamma -a}{\omega -a}}}^{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}{\left|{\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\right|}^q\mathrm{d}⋎\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & \left.+{\left({\int }_{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}^1{\left|⋎-1+{\displaystyle \frac{\xi }{2}}\right|}^p\mathrm{d}⋎\right)}^{{\displaystyle \frac{1}{p}}}{\left({\int }_{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}^1{\left|{\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\right|}^q\mathrm{d}⋎\right)}^{{\displaystyle \frac{1}{q}}}\right]\hfill \\ \hfill & \le (\omega -a)\left[{\left({\int }_0^{{\displaystyle \frac{\gamma -a}{\omega -a}}}{\left|⋎-{\displaystyle \frac{\xi }{2}}\right|}^p\mathrm{d}⋎\right)}^{{\displaystyle \frac{1}{p}}}{\left({\int }_0^{{\displaystyle \frac{\gamma -a}{\omega -a}}}\left[(1-⋎)\right|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+{⋎\left|\mathcal{S}\left(\omega \right)\right|}^q]\mathrm{d}⋎\right)}^{{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & +{\left({\int }_{{\displaystyle \frac{\gamma -a}{\omega -a}}}^{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}{\left|⋎-{\displaystyle \frac{1}{2}}\right|}^p\mathrm{d}⋎\right)}^{{\displaystyle \frac{1}{p}}}{\left({\int }_{{\displaystyle \frac{\gamma -a}{\omega -a}}}^{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}\left[(1-⋎)\right|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+{⋎\left|\mathcal{S}\left(\omega \right)\right|}^q]\mathrm{d}⋎\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & \left.+{\left({\int }_{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}^1{\left|⋎-1+{\displaystyle \frac{\xi }{2}}\right|}^p\mathrm{d}⋎\right)}^{{\displaystyle \frac{1}{p}}}{\left({\int }_{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}^1\left[(1-⋎)\right|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+{⋎\left|\mathcal{S}\left(\omega \right)\right|}^q]\mathrm{d}⋎\right)}^{{\displaystyle \frac{1}{q}}}\right].\hfill \end{array}$$

Some simple computations provide the required result. □

Now, we discuss some consequences of Theorem 3.

Corollary 19

([38]). By selecting $\xi =0$ and $\gamma ={\displaystyle \frac{a+\omega }{2}}$, we have

$$\begin{array}{cc}\hfill & \left|\mathcal{S}\left({\displaystyle \frac{a+\omega }{2}}\right)-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\hfill \\ \hfill & \le (\omega -a){\left({\displaystyle \frac{1}{2^{1+p}(1+p)}}\right)}^{{\displaystyle \frac{1}{p}}}\left[{\left({\displaystyle \frac{3|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{8}}\right)}^{{\displaystyle \frac{1}{q}}}+{\left({\displaystyle \frac{|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+3{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{8}}\right)}^{{\displaystyle \frac{1}{q}}}\right].\hfill \end{array}$$

Corollary 20.

By selecting $\xi =0$ and $\gamma ={\displaystyle \frac{2a+\omega }{3}}$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathcal{S}\left(\frac{2a+\omega }{3}\right)+\mathcal{S}\left(\frac{a+2\omega }{3}\right)}{2}}-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\hfill \\ \hfill & \le (\omega -a)\left[{\left({\displaystyle \frac{1}{3^{1+p}(1+p)}}\right)}^{{\displaystyle \frac{1}{p}}}{\left({\displaystyle \frac{5|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{18}}\right)}^{{\displaystyle \frac{1}{q}}}+{\left({\displaystyle \frac{1}{2\left(3^{1+p}\right)(1+p)}}\right)}^{{\displaystyle \frac{1}{p}}}{\left({\displaystyle \frac{|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{6}}\right)}^{{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & \left.+{\left({\displaystyle \frac{1}{3^{1+p}(1+p)}}\right)}^{{\displaystyle \frac{1}{p}}}{\left({\displaystyle \frac{|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+5{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{18}}\right)}^{{\displaystyle \frac{1}{q}}}\right].\hfill \end{array}$$

Corollary 21.

By selecting $\xi =0$ and $\gamma ={\displaystyle \frac{3a+\omega }{4}}$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathcal{S}\left(\frac{3a+\omega }{4}\right)+\mathcal{S}\left(\frac{a+3\omega }{4}\right)}{2}}-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\hfill \\ \hfill & \le (\omega -a)\left[{\left({\displaystyle \frac{1}{4^{1+p}(1+p)}}\right)}^{{\displaystyle \frac{1}{p}}}{\left({\displaystyle \frac{7|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{32}}\right)}^{{\displaystyle \frac{1}{q}}}+{\left({\displaystyle \frac{1}{2^{1+2p}(1+p)}}\right)}^{{\displaystyle \frac{1}{p}}}{\left({\displaystyle \frac{|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{4}}\right)}^{{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & \left.+{\left({\displaystyle \frac{1}{4^{1+p}(1+p)}}\right)}^{{\displaystyle \frac{1}{p}}}{\left({\displaystyle \frac{|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+7{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{32}}\right)}^{{\displaystyle \frac{1}{q}}}\right].\hfill \end{array}$$

Corollary 22.

By selecting $\xi =1$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathcal{S}\left(a\right)+\mathcal{S}\left(\omega \right)}{2}}-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\hfill \\ \hfill & \le (\omega -a)\left[{\left(C_1^{*}\right)}^{{\displaystyle \frac{1}{p}}}{\left(\left({\displaystyle \frac{{(\omega -a)}^2-{(\omega -\gamma )}^2}{2{(\omega -a)}^2}}\right)|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{\gamma -a}{\omega -a}}\right)}^2{\left|{\mathcal{S}}^{\prime }\left(\omega \right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & +C_2^{{\displaystyle \frac{1}{p}}}{\left(\left({\displaystyle \frac{{(\omega -\gamma )}^2-{(\gamma -a)}^2}{2{(\omega -a)}^2}}\right)\left[\right|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+|{\mathcal{S}}^{\prime }\left(\omega \right){|}^q]\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & \left.+{\left(C_3^{*}\right)}^{{\displaystyle \frac{1}{p}}}{\left({\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{\gamma -a}{\omega -a}}\right)}^2|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+{\displaystyle \frac{1}{2}}\left({\displaystyle \frac{{(\omega -a)}^2-{(\omega -\gamma )}^2}{{(\omega -a)}^2}}\right){\left|{\mathcal{S}}^{\prime }\left(\omega \right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\right],\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill C_1^{*}& ={\displaystyle \frac{{\left(\frac{1}{2}\right)}^{p+1}+{\left(\frac{\gamma -a}{\omega -a}-\frac{1}{2}\right)}^{p+1}}{1+p}}\hfill \\ \hfill C_2& ={\displaystyle \frac{{\left(\frac{1}{2}-\frac{\gamma -a}{\omega -a}\right)}^{p+1}+{\left(\frac{\omega -\gamma }{\omega -a}-\frac{1}{2}\right)}^{p+1}}{1+p}}\hfill \\ \hfill C_3^{*}& ={\displaystyle \frac{{\left(\frac{1}{2}\right)}^{p+1}+{\left(\frac{1}{2}-\frac{\omega -\gamma }{\omega -a}\right)}^{p+1}}{1+p}}.\hfill \end{array}$$

Corollary 23.

By selecting $\xi =1$ and $\gamma ={\displaystyle \frac{a+\omega }{2}}$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathcal{S}\left(a\right)+\mathcal{S}\left(\omega \right)}{2}}-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\hfill \\ \hfill & \le (\omega -a){\left({\displaystyle \frac{1}{2^{1+p}(1+p)}}\right)}^{{\displaystyle \frac{1}{p}}}\left[{\left({\displaystyle \frac{3|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{8}}\right)}^{{\displaystyle \frac{1}{q}}}+{\left({\displaystyle \frac{|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+3{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{8}}\right)}^{{\displaystyle \frac{1}{q}}}\right].\hfill \end{array}$$

Corollary 24.

By selecting $\xi =1$ and $\gamma ={\displaystyle \frac{2a+\omega }{3}}$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathcal{S}\left(a\right)+\mathcal{S}\left(\omega \right)}{2}}-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\hfill \\ \hfill & \le (\omega -a)\left[{\left({\displaystyle \frac{{\left(\frac{-1}{6}\right)}^{1+p}+2^{-1-p}}{1+p}}\right)}^{{\displaystyle \frac{1}{p}}}{\left({\displaystyle \frac{5|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{18}}\right)}^{{\displaystyle \frac{1}{q}}}+{\left({\displaystyle \frac{1}{2^p{3}^{1+p}(1+p)}}\right)}^{{\displaystyle \frac{1}{p}}}{\left({\displaystyle \frac{|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{6}}\right)}^{{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & \left.+{\left({\displaystyle \frac{{\left(\frac{-1}{6}\right)}^{1+p}+2^{-1-p}}{1+p}}\right)}^{{\displaystyle \frac{1}{p}}}{\left({\displaystyle \frac{|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+5{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{18}}\right)}^{{\displaystyle \frac{1}{q}}}\right].\hfill \end{array}$$

Corollary 25.

By selecting $\xi ={\displaystyle \frac{1}{3}}$ and $\gamma ={\displaystyle \frac{a+\omega }{2}}$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{1}{2}}\left[{\displaystyle \frac{\mathcal{S}\left(a\right)+\mathcal{S}\left(\omega \right)}{2}}+\mathcal{S}\left({\displaystyle \frac{a+\omega }{2}}\right)\right]-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\hfill \\ \hfill & \le (\omega -a){\left({\displaystyle \frac{6^{-1-p}(1+2^{1+p})}{1+p}}\right)}^{{\displaystyle \frac{1}{p}}}\left[{\left({\displaystyle \frac{3|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{18}}\right)}^{{\displaystyle \frac{1}{q}}}+{\left({\displaystyle \frac{|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+3{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{18}}\right)}^{{\displaystyle \frac{1}{q}}}\right].\hfill \end{array}$$

Corollary 26.

By selecting $\xi ={\displaystyle \frac{1}{2}}$ and $\gamma ={\displaystyle \frac{a+\omega }{2}}$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{1}{2}}\left[{\displaystyle \frac{\mathcal{S}\left(a\right)+\mathcal{S}\left(\omega \right)}{2}}+\mathcal{S}\left({\displaystyle \frac{a+\omega }{2}}\right)\right]-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\hfill \\ \hfill & \le (\omega -a){\left({\displaystyle \frac{1}{2^{1+p}(1+p)}}\right)}^{{\displaystyle \frac{1}{p}}}\left[{\left({\displaystyle \frac{3|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{8}}\right)}^{{\displaystyle \frac{1}{q}}}+{\left({\displaystyle \frac{|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+3{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{8}}\right)}^{{\displaystyle \frac{1}{q}}}\right].\hfill \end{array}$$

Corollary 27.

By selecting $\xi ={\displaystyle \frac{1}{4}}$ and $\gamma ={\displaystyle \frac{2a+\omega }{3}}$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{1}{8}}\left[\mathcal{S}\left(a\right)+3\mathcal{S}\left({\displaystyle \frac{2a+\omega }{3}}\right)+3\mathcal{S}\left({\displaystyle \frac{a+2\omega }{3}}\right)+\mathcal{S}\left(\omega \right)\right]-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\hfill \\ \hfill & \le (\omega -a)\left[{\left({\displaystyle \frac{{\left(\frac{5}{24}\right)}^{1+p}+8^{-1-p}}{1+p}}\right)}^{{\displaystyle \frac{1}{p}}}{\left({\displaystyle \frac{5|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{18}}\right)}^{{\displaystyle \frac{1}{q}}}+{\left({\displaystyle \frac{1}{2^p{3}^{1+p}(1+p)}}\right)}^{{\displaystyle \frac{1}{p}}}{\left({\displaystyle \frac{|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{6}}\right)}^{{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & \left.+{\left({\displaystyle \frac{{\left(\frac{5}{24}\right)}^{1+p}+2^{-1-p}}{1+p}}\right)}^{{\displaystyle \frac{1}{p}}}{\left({\displaystyle \frac{|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+5{|{\mathcal{S}}^{\prime }\left(\omega \right)|}^q}{18}}\right)}^{{\displaystyle \frac{1}{q}}}\right].\hfill \end{array}$$

Theorem 4.

Presume that all conditions of Lemma 1 are fulfilled. If $|{\mathcal{S}}^{\prime }{|}^q$ is a convex function, then

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\xi \left(\mathcal{S}\right(a)+\mathcal{S}(\omega \left)\right)}{2}}+{\displaystyle \frac{(1-\xi )\left(\mathcal{S}\right(a+\omega -\gamma )+\mathcal{S}(\gamma \left)\right)}{2}}-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\hfill \\ \hfill & \le (\omega -a)\left[{\displaystyle \frac{C_1+C_2+C_3}{p}}+{\displaystyle \frac{|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+{\left|{\mathcal{S}}^{\prime }\left(\omega \right)\right|}^q}{2q}}\right],\hfill \end{array}$$

where $C_1,C_2$, and $C_3$ are obtained in Theorem 3.

Proof. 

Through Lemma 1, using Young’s inequality and implementing the convexity of $|{\mathcal{S}}^{\prime }{|}^q$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\xi \left(\mathcal{S}\right(a)+\mathcal{S}(\omega \left)\right)}{2}}+{\displaystyle \frac{(1-\xi )\left(\mathcal{S}\right(a+\omega -\gamma )+\mathcal{S}(\gamma \left)\right)}{2}}-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\hfill \\ \hfill & \le (\omega -a)\left[{\int }_0^{{\displaystyle \frac{\gamma -a}{\omega -a}}}\left|⋎-{\displaystyle \frac{\xi }{2}}\right||{\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )|\mathrm{d}⋎+{\int }_{{\displaystyle \frac{\gamma -a}{\omega -a}}}^{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}\left|⋎-{\displaystyle \frac{1}{2}}\right|\left|{\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\right|\mathrm{d}⋎\right.\hfill \\ \hfill & \left.+{\int }_{{\displaystyle \frac{\omega -\gamma }{\omega -a}}}^1\left|⋎-1+{\displaystyle \frac{\xi }{2}}\right|\left|{\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\right|\mathrm{d}⋎\right]\hfill \\ \hfill & \le (\omega -a)\left[{\displaystyle \frac{{\int }_0^{\frac{\gamma -a}{\omega -a}}{\left|⋎-\frac{\xi }{2}\right|}^p\mathrm{d}⋎}{p}}+{\displaystyle \frac{{\int }_0^{\frac{\gamma -a}{\omega -a}}{\left|{\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\right|}^q\mathrm{d}⋎}{q}}\right.\hfill \\ \hfill & +{\displaystyle \frac{{\int }_{\frac{\gamma -a}{\omega -a}}^{\frac{\omega -\gamma }{\omega -a}}{\left|⋎-\frac{1}{2}\right|}^p\mathrm{d}⋎}{p}}+{\displaystyle \frac{{\int }_{\frac{\gamma -a}{\omega -a}}^{\frac{\omega -\gamma }{\omega -a}}{\left|{\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\right|}^q\mathrm{d}⋎}{q}}\hfill \\ \hfill & \left.+{\displaystyle \frac{{\int }_{\frac{\omega -\gamma }{\omega -a}}^1{\left|⋎-1+\frac{\xi }{2}\right|}^p\mathrm{d}⋎}{p}}+{\displaystyle \frac{{\int }_{\frac{\omega -\gamma }{\omega -a}}^1{\left|{\mathcal{S}}^{\prime }((1-⋎)a+⋎\omega )\right|}^q\mathrm{d}⋎}{q}}\right]\hfill \\ \hfill & \le (\omega -a)\left[{\displaystyle \frac{{\int }_0^{\frac{\gamma -a}{\omega -a}}{\left|⋎-\frac{\xi }{2}\right|}^p\mathrm{d}⋎}{p}}+{\displaystyle \frac{{\int }_0^{\frac{\gamma -a}{\omega -a}}\left[(1-⋎)\right|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+⋎|{\mathcal{S}}^{\prime }\left(\omega \right){|}^q]\mathrm{d}⋎}{q}}\right.\hfill \\ \hfill & +{\displaystyle \frac{{\int }_{\frac{\gamma -a}{\omega -a}}^{\frac{\omega -\gamma }{\omega -a}}{\left|⋎-\frac{1}{2}\right|}^p\mathrm{d}⋎}{p}}+{\displaystyle \frac{{\int }_{\frac{\gamma -a}{\omega -a}}^{\frac{\omega -\gamma }{\omega -a}}\left[(1-⋎)\right|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+⋎|{\mathcal{S}}^{\prime }\left(\omega \right){|}^q]\mathrm{d}⋎}{q}}\hfill \\ \hfill & \left.+{\displaystyle \frac{{\int }_{\frac{\omega -\gamma }{\omega -a}}^1{\left|⋎-1+\frac{\xi }{2}\right|}^p\mathrm{d}⋎}{p}}+{\displaystyle \frac{{\int }_{\frac{\omega -\gamma }{\omega -a}}^1\left[(1-⋎)\right|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+⋎|{\mathcal{S}}^{\prime }\left(\omega \right){|}^q]\mathrm{d}⋎}{q}}\right].\hfill \end{array}$$

Some simple computations provide the required result. □

Now, we discuss some consequences of Theorem 4.

Corollary 28.

By selecting $\xi =0$ and $\gamma ={\displaystyle \frac{a+\omega }{2}}$, we have

$$\begin{array}{cc}\hfill & \left|\mathcal{S}\left({\displaystyle \frac{a+\omega }{2}}\right)-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\hfill \\ \hfill & \le (\omega -a)\left({\displaystyle \frac{1}{2^{p}p(1+p)}}\right)\left[{\displaystyle \frac{|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+{\left|{\mathcal{S}}^{\prime }\left(\omega \right)\right|}^q}{2q}}\right].\hfill \end{array}$$

Corollary 29.

By selecting $\xi =1$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathcal{S}\left(a\right)+\mathcal{S}\left(\omega \right)}{2}}-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\hfill \\ \hfill & \le (\omega -a)\left[{\displaystyle \frac{(C_1^{*}+C_2+C_3^{*})}{p}}+{\displaystyle \frac{|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+{\left|{\mathcal{S}}^{\prime }\left(\omega \right)\right|}^q}{2q}}\right],\hfill \end{array}$$

where $C_1^{*},C_2^{*}$, and $C_3^{*}$ are defined in Corollary 22.

Corollary 30.

By selecting $\xi ={\displaystyle \frac{1}{3}}$ and $\gamma ={\displaystyle \frac{a+\omega }{2}}$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{1}{2}}\left[{\displaystyle \frac{\mathcal{S}\left(a\right)+\mathcal{S}\left(\omega \right)}{2}}+\mathcal{S}\left({\displaystyle \frac{a+\omega }{2}}\right)\right]-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\hfill \\ \hfill & \le (\omega -a)\left[{\displaystyle \frac{1+2^{1+p}}{2^p{3}^{1+p}p(1+p)}}+{\displaystyle \frac{|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+{\left|{\mathcal{S}}^{\prime }\left(\omega \right)\right|}^q}{2q}}\right].\hfill \end{array}$$

Corollary 31.

By selecting $\xi ={\displaystyle \frac{1}{2}}$ and $\gamma ={\displaystyle \frac{a+\omega }{2}}$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{1}{2}}\left[{\displaystyle \frac{\mathcal{S}\left(a\right)+\mathcal{S}\left(\omega \right)}{2}}+\mathcal{S}\left({\displaystyle \frac{a+\omega }{2}}\right)\right]-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\hfill \\ \hfill & \le (\omega -a)\left[{\displaystyle \frac{1}{4^{p}p(1+p)}}+{\displaystyle \frac{|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+{\left|{\mathcal{S}}^{\prime }\left(\omega \right)\right|}^q}{2q}}\right].\hfill \end{array}$$

Corollary 32.

By selecting $\xi ={\displaystyle \frac{1}{4}}$ and $\gamma ={\displaystyle \frac{2a+\omega }{3}}$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{1}{8}}\left[\mathcal{S}\left(a\right)+3\mathcal{S}\left({\displaystyle \frac{2a+\omega }{3}}\right)+3\mathcal{S}\left({\displaystyle \frac{a+2\omega }{3}}\right)+\mathcal{S}\left(\omega \right)\right]-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\hfill \\ \hfill & \le (\omega -a)\left[{\displaystyle \frac{\left(3^{p+1}+4^{p+1}+5^{p+1}\right)}{2^{-3p-2}{3}^{1+p}p(p+1)}}++{\displaystyle \frac{|{\mathcal{S}}^{\prime }{\left(a\right)|}^q+{\left|{\mathcal{S}}^{\prime }\left(\omega \right)\right|}^q}{2q}}\right].\hfill \end{array}$$

Theorem 5.

Presume that all conditions of Lemma 1 are fulfilled. If $|{\mathcal{S}}^{\prime }|$ is a convex function and $|{\mathcal{S}}^{\prime }|\le M$ such that $M>0$, then

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\xi \left(\mathcal{S}\right(a)+\mathcal{S}(\omega \left)\right)}{2}}+{\displaystyle \frac{(1-\xi )\left(\mathcal{S}\right(a+\omega -\gamma )+\mathcal{S}(\gamma \left)\right)}{2}}-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\hfill \\ \hfill & \le M(\omega -a)\left[{\displaystyle \frac{3{\xi }^2}{8}}-{\displaystyle \frac{1}{4}}+{\left({\displaystyle \frac{\gamma -a}{\omega -a}}\right)}^2+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{\omega -\gamma }{\omega -a}}\right)}^2-{\displaystyle \frac{\xi }{2}}\left({\displaystyle \frac{\gamma -a}{\omega -a}}\right)+{\displaystyle \frac{1}{2}}{\left(1-{\displaystyle \frac{\xi }{2}}-{\displaystyle \frac{\omega -\gamma }{\omega -a}}\right)}^2\right].\hfill \end{array}$$

Proof. 

The proof is contained for curious readers. □

Now, we discuss some consequences of Theorem 5.

Corollary 33.

By selecting $\xi =0$ and $\gamma ={\displaystyle \frac{a+\omega }{2}}$, we have

$$\begin{array}{c}\hfill \left|\mathcal{S}\left({\displaystyle \frac{a+\omega }{2}}\right)-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\le {\displaystyle \frac{M(\omega -a)}{4}}.\end{array}$$

Corollary 34.

By selecting $\xi =0$ and $\gamma ={\displaystyle \frac{2a+\omega }{3}}$, we have

$$\begin{array}{c}\hfill \left|{\displaystyle \frac{\mathcal{S}\left(\frac{2a+\omega }{3}\right)+\mathcal{S}\left(\frac{a+2\omega }{3}\right)}{2}}-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\le {\displaystyle \frac{5M(\omega -a)}{36}}.\end{array}$$

Corollary 35.

By selecting $\xi =0$ and $\gamma ={\displaystyle \frac{3a+\omega }{4}}$, we have

$$\begin{array}{c}\hfill {\displaystyle \frac{\mathcal{S}\left(\frac{3a+\omega }{4}\right)+\mathcal{S}\left(\frac{a+3\omega }{4}\right)}{2}}-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\le {\displaystyle \frac{M(\omega -a)}{8}}.\end{array}$$

Corollary 36.

By selecting $\xi =1$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathcal{S}\left(a\right)+\mathcal{S}\left(\omega \right)}{2}}-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\hfill \\ \hfill & \le M(\omega -a)\left[{\displaystyle \frac{1}{8}}+{\left({\displaystyle \frac{\gamma -a}{\omega -a}}\right)}^2+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{\omega -\gamma }{\omega -a}}\right)}^2-{\displaystyle \frac{1}{2}}\left({\displaystyle \frac{\gamma -a}{\omega -a}}\right)+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{\omega -\gamma }{\omega -a}}\right)}^2\right].\hfill \end{array}$$

Corollary 37.

By selecting $\xi =1$ and $\gamma ={\displaystyle \frac{a+\omega }{2}}$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathcal{S}\left(a\right)+\mathcal{S}\left(\omega \right)}{2}}-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\le {\displaystyle \frac{M(\omega -a)}{4}}.\hfill \end{array}$$

Corollary 38.

By selecting $\xi =1$ and $\gamma ={\displaystyle \frac{2a+\omega }{3}}$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\mathcal{S}\left(a\right)+\mathcal{S}\left(\omega \right)}{2}}-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\le {\displaystyle \frac{11M(\omega -a)}{36}}.\hfill \end{array}$$

Corollary 39.

By selecting $\xi ={\displaystyle \frac{1}{3}}$ and $\gamma ={\displaystyle \frac{a+\omega }{2}}$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{1}{6}}\left[\mathcal{S}\left(a\right)+4\mathcal{S}\left({\displaystyle \frac{a+\omega }{2}}\right)+\mathcal{S}\left(\omega \right)\right]-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\le {\displaystyle \frac{5M(\omega -a)}{36}}.\hfill \end{array}$$

Corollary 40.

By selecting $\xi ={\displaystyle \frac{1}{2}}$ and $\gamma ={\displaystyle \frac{a+\omega }{2}}$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{1}{2}}\left[{\displaystyle \frac{\mathcal{S}\left(a\right)+\mathcal{S}\left(\omega \right)}{2}}+\mathcal{S}\left({\displaystyle \frac{a+\omega }{2}}\right)\right]-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\le {\displaystyle \frac{M(\omega -a)}{8}}.\hfill \end{array}$$

Corollary 41.

By selecting $\xi ={\displaystyle \frac{1}{4}}$ and $\gamma ={\displaystyle \frac{2a+\omega }{3}}$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{1}{8}}\left[\mathcal{S}\left(a\right)+3\mathcal{S}\left({\displaystyle \frac{2a+\omega }{3}}\right)+3\mathcal{S}\left({\displaystyle \frac{a+2\omega }{3}}\right)+\mathcal{S}\left(\omega \right)\right]-{\displaystyle \frac{1}{\omega -a}}{\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u\right|\le {\displaystyle \frac{25M(\omega -a)}{288}}.\hfill \end{array}$$

Remark 1.

By different choices of ξ and corresponding γ in Theorems 1–5, we can generate several novel error boundaries for Newton–Cotes schemes.

3. Visual Analysis

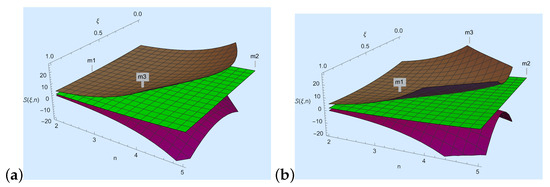
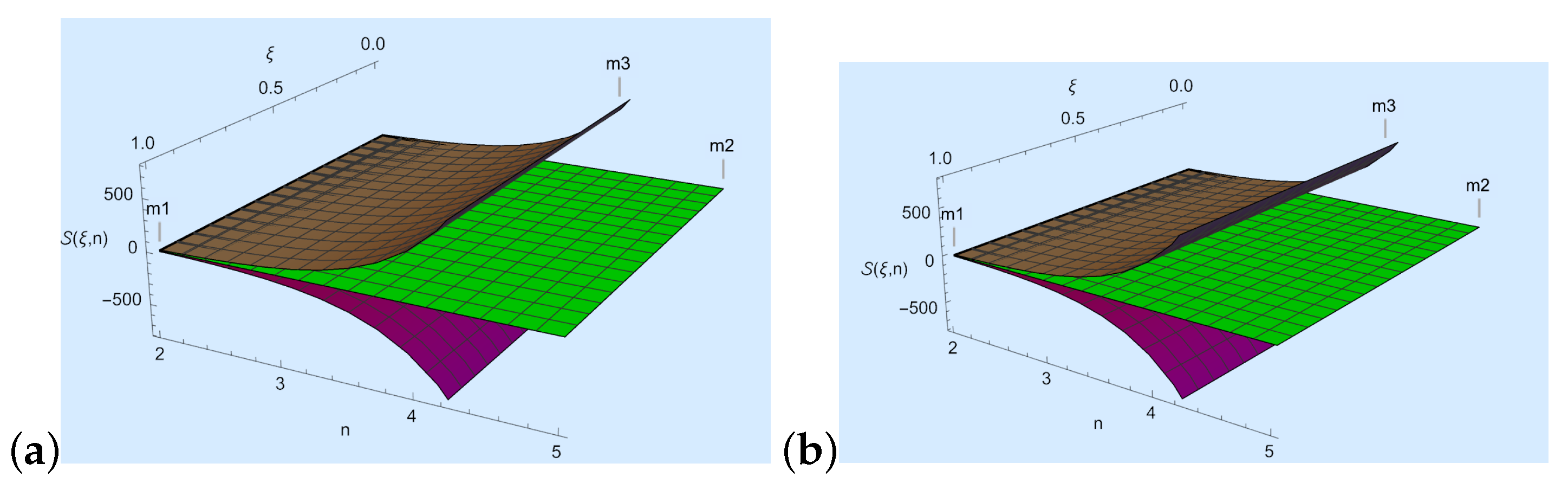
In the current portion of the study, we showcase the correctness of our primary findings aided with convex functions. First, we discuss Theorem 1.

• We take $\mathcal{S}\left(\gamma \right)={\gamma }^{n}n\ge 2$, $a=0$, $\omega =2$, and $\gamma ={\displaystyle \frac{a+\omega }{2}}$ in Theorem 1; then, $m_1\le m_2\le m_3$, where

  $$\begin{array}{c}\hfill m_1=-2^{n}n\left[{\displaystyle \frac{1}{24}}\left({\xi }^3+10\right)+{\displaystyle \frac{1}{3}}{\left(1-{\displaystyle \frac{\xi }{2}}\right)}^3-{\displaystyle \frac{5}{8}}\left(1-{\displaystyle \frac{\xi }{2}}\right)-{\displaystyle \frac{\xi }{16}}\right]+2^{n-1}\xi +(1-\xi ).\end{array}$$

  $$\begin{array}{c}\hfill m_2={\displaystyle \frac{2^n}{n+1}}.\end{array}$$

  $$\begin{array}{c}\hfill m_3=2^{n}n\left[{\displaystyle \frac{1}{24}}\left({\xi }^3+10\right)+{\displaystyle \frac{1}{3}}{\left(1-{\displaystyle \frac{\xi }{2}}\right)}^3-{\displaystyle \frac{5}{8}}\left(1-{\displaystyle \frac{\xi }{2}}\right)-{\displaystyle \frac{\xi }{16}}\right]+2^{n-1}\xi +(1-\xi ).\end{array}$$
• We take $\mathcal{S}\left(\gamma \right)={\gamma }^{n}n\ge 2$, $a=0$, $\omega =2$, and $\gamma ={\displaystyle \frac{2a+\omega }{3}}$ in Theorem 1; then, $m_1\le m_2\le m_3$, where

  $$\begin{array}{c}\hfill m_1=-2^{n}n\left({\displaystyle \frac{1}{72}}\left(3{\xi }^3-2\xi \right)+{\displaystyle \frac{1}{3}}{\left(1-{\displaystyle \frac{\xi }{2}}\right)}^3-{\displaystyle \frac{13}{18}}\left(1-{\displaystyle \frac{\xi }{2}}\right)+{\displaystyle \frac{4}{9}}\right)+{\displaystyle \frac{1}{2}}\left({\left({\displaystyle \frac{2}{3}}\right)}^n+{\left({\displaystyle \frac{4}{3}}\right)}^n\right)(1-\xi )+2^{n-1}\xi .\end{array}$$

  $$\begin{array}{c}\hfill m_2={\displaystyle \frac{2^n}{n+1}}.\end{array}$$

  $$\begin{array}{c}\hfill m_3=2^{n}n\left({\displaystyle \frac{1}{72}}\left(3{\xi }^3-2\xi \right)+{\displaystyle \frac{1}{3}}{\left(1-{\displaystyle \frac{\xi }{2}}\right)}^3-{\displaystyle \frac{13}{18}}\left(1-{\displaystyle \frac{\xi }{2}}\right)+{\displaystyle \frac{4}{9}}\right)+{\displaystyle \frac{1}{2}}\left({\left({\displaystyle \frac{2}{3}}\right)}^n+{\left({\displaystyle \frac{4}{3}}\right)}^n\right)(1-\xi )+2^{n-1}\xi .\end{array}$$

• For Figure 1a, we choose $\xi$ and n to develop a visual explanation of Theorem 1 at $\gamma ={\displaystyle \frac{a+\omega }{2}}$.
  

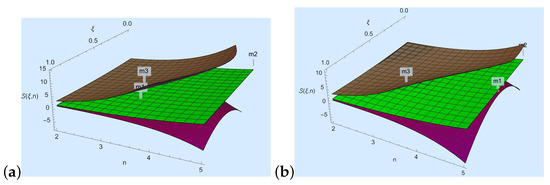  Figure 1. Here, the purple, green, and brown colors represent $m_1,m_2$, and $m_3$, respectively.
• For Figure 1b, we choose $\xi$ and n to a develop visual explanation of Theorem 1 at $\gamma ={\displaystyle \frac{2a+\omega }{3}}$.

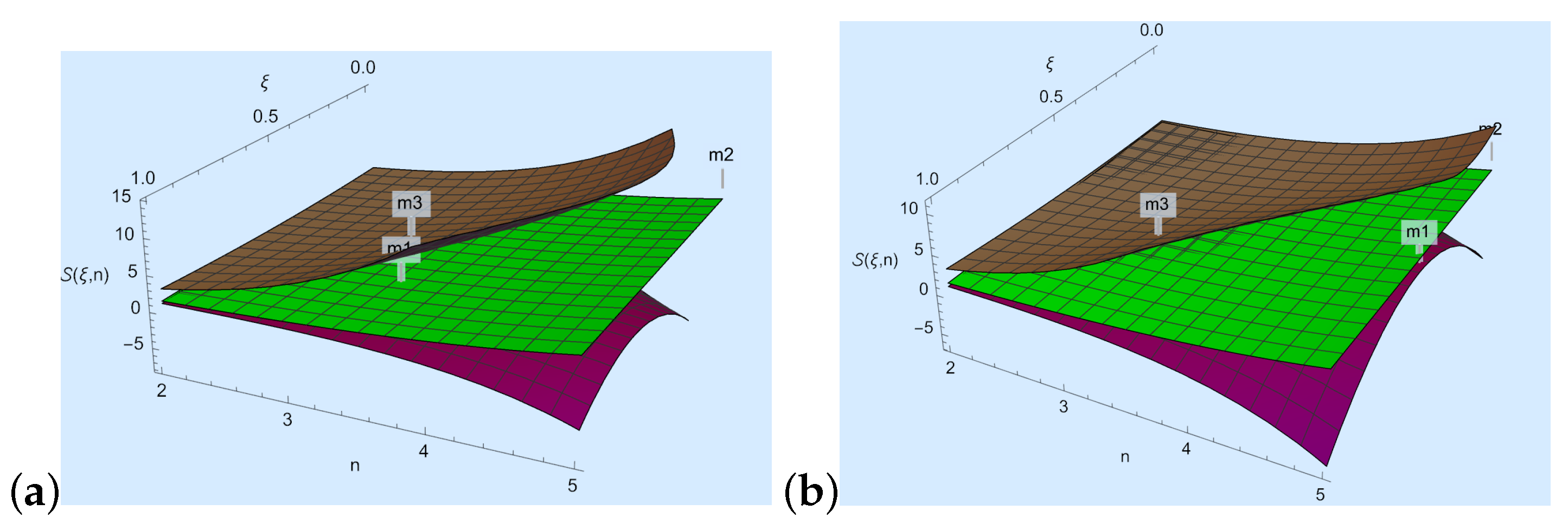
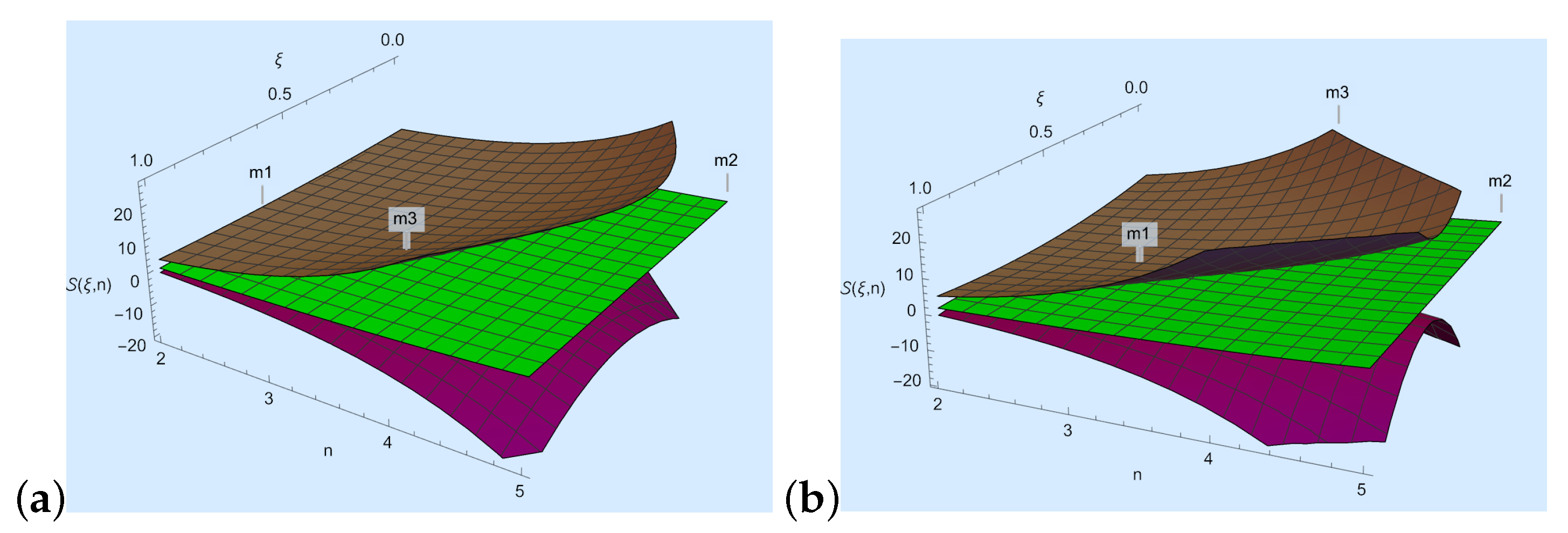
Now, we discuss Theorem 2.

• We take $\mathcal{S}\left(\gamma \right)={\gamma }^{n}n\ge 2$, $a=0$, $\omega =2$, and $\gamma ={\displaystyle \frac{a+\omega }{2}}$ in Theorem 2; then, $m_1\le m_2\le m_3$, where

  $$\begin{array}{cc}\hfill m_1& =-2^{n}n\left[\sqrt{{\displaystyle \frac{1}{8}}\left({\xi }^2+{(1-\xi )}^2\right)}\sqrt{{\displaystyle \frac{1}{3}}{\left(1-{\displaystyle \frac{\xi }{2}}\right)}^3-{\displaystyle \frac{5}{8}}\left(1-{\displaystyle \frac{\xi }{2}}\right)+{\displaystyle \frac{9}{24}}}\right.\hfill \\ \hfill & \left.+\sqrt{{\displaystyle \frac{1}{4}}\left({\xi }^2-\xi \right)+{\displaystyle \frac{1}{8}}}\sqrt{{\displaystyle \frac{1}{24}}\left({\xi }^3+1\right)-{\displaystyle \frac{\xi }{16}}}\right]+2^{n-1}\xi +(1-\xi ).\hfill \end{array}$$

  $$\begin{array}{c}\hfill m_2={\displaystyle \frac{2^n}{n+1}}.\end{array}$$

  $$\begin{array}{cc}\hfill m_3& =2^{n}n\left[\sqrt{{\displaystyle \frac{1}{8}}\left({\xi }^2+{(1-\xi )}^2\right)}\sqrt{{\displaystyle \frac{1}{3}}{\left(1-{\displaystyle \frac{\xi }{2}}\right)}^3-{\displaystyle \frac{5}{8}}\left(1-{\displaystyle \frac{\xi }{2}}\right)+{\displaystyle \frac{9}{24}}}\right.\hfill \\ \hfill & \left.+\sqrt{{\displaystyle \frac{1}{4}}\left({\xi }^2-\xi \right)+{\displaystyle \frac{1}{8}}}\sqrt{{\displaystyle \frac{1}{24}}\left({\xi }^3+1\right)-{\displaystyle \frac{\xi }{16}}}\right]+2^{n-1}\xi +(1-\xi ).\hfill \end{array}$$
• We take $\mathcal{S}\left(\gamma \right)={\gamma }^{n}n\ge 2$, $a=0$, $\omega =2$, and $\gamma ={\displaystyle \frac{2a+\omega }{3}}$ in Theorem 2; then, $m_1\le m_2\le m_3$, where

$$\begin{array}{cc}\hfill m_1& =-2^{n}n\left(\sqrt{{\displaystyle \frac{{\xi }^2}{8}}+{\displaystyle \frac{1}{72}}{(2-3\xi )}^2}\sqrt{{\displaystyle \frac{1}{3}}{\left(1-{\displaystyle \frac{\xi }{2}}\right)}^3-{\displaystyle \frac{13}{18}}\left(1-{\displaystyle \frac{\xi }{2}}\right)+{\displaystyle \frac{35}{81}}}\right.\hfill \\ \hfill & \left.+\sqrt{{\displaystyle \frac{1}{12}}\left(3{\xi }^2-2\xi \right)+{\displaystyle \frac{1}{18}}}\sqrt{{\displaystyle \frac{{\xi }^3}{24}}-{\displaystyle \frac{\xi }{36}}+{\displaystyle \frac{1}{81}}}+{\displaystyle \frac{\sqrt{2}}{72}}\right)+{\displaystyle \frac{1}{2}}\left({\left({\displaystyle \frac{2}{3}}\right)}^n+{\left({\displaystyle \frac{4}{3}}\right)}^n\right)(1-\xi )+2^{n-1}\xi .\hfill \end{array}$$

$$\begin{array}{c}\hfill m_2={\displaystyle \frac{2^n}{n+1}}.\end{array}$$

$$\begin{array}{cc}\hfill m_3=& 2^{n}n\left(\sqrt{{\displaystyle \frac{{\xi }^2}{8}}+{\displaystyle \frac{1}{72}}{(2-3\xi )}^2}\sqrt{{\displaystyle \frac{1}{3}}{\left(1-{\displaystyle \frac{\xi }{2}}\right)}^3-{\displaystyle \frac{13}{18}}\left(1-{\displaystyle \frac{\xi }{2}}\right)+{\displaystyle \frac{35}{81}}}\right.\hfill \\ \hfill & \left.+\sqrt{{\displaystyle \frac{1}{12}}\left(3{\xi }^2-2\xi \right)+{\displaystyle \frac{1}{18}}}\sqrt{{\displaystyle \frac{{\xi }^3}{24}}-{\displaystyle \frac{\xi }{36}}+{\displaystyle \frac{1}{81}}}+{\displaystyle \frac{\sqrt{2}}{72}}\right)+{\displaystyle \frac{1}{2}}\left({\left({\displaystyle \frac{2}{3}}\right)}^n+{\left({\displaystyle \frac{4}{3}}\right)}^n\right)(1-\xi )+2^{n-1}\xi .\hfill \end{array}$$

• For Figure 2a, we choose $\xi$ and n to develop a visual explanation of Theorem 2 at $\gamma ={\displaystyle \frac{a+\omega }{2}}$.
  

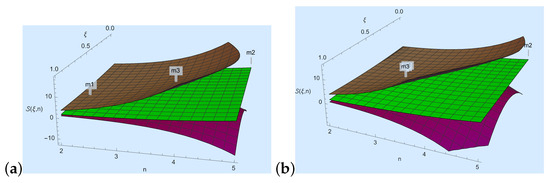  Figure 2. Here, the purple, green and brown colors represent $m_1,m_2$, and $m_3$, respectively.
• For Figure 2b, we choose $\xi$ and n to develop a visual explanation of Theorem 2 at $\gamma ={\displaystyle \frac{2a+\omega }{3}}$.

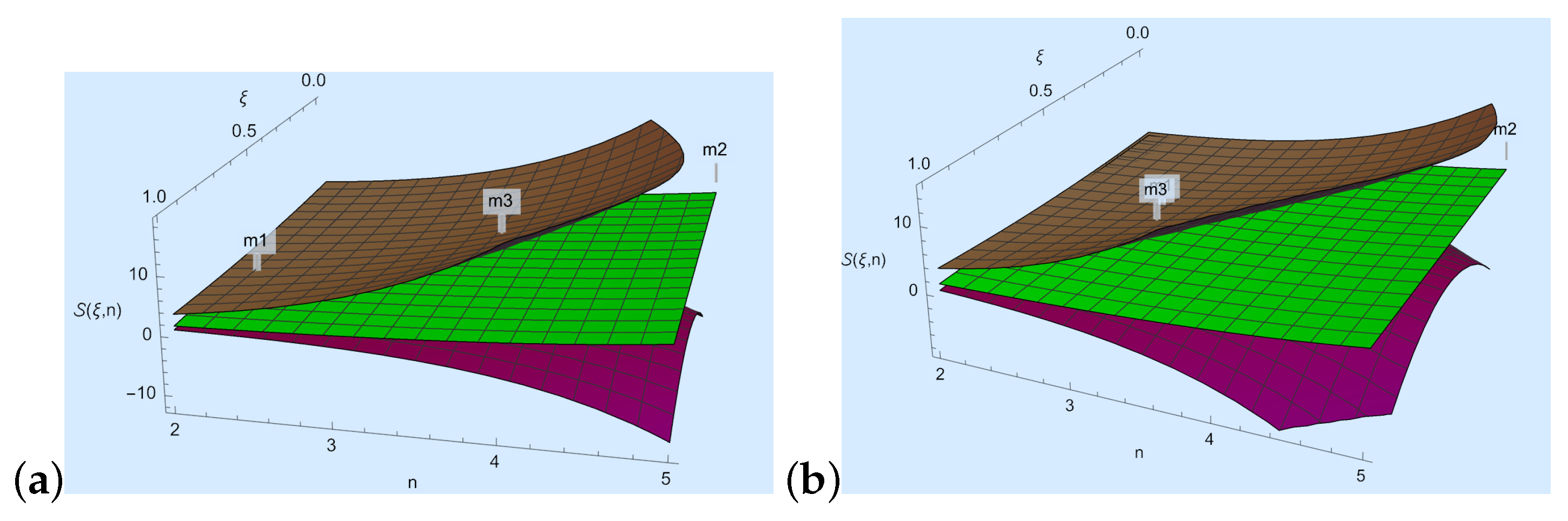
Now, we discuss Theorem 3.

• We take $\mathcal{S}\left(\gamma \right)={\gamma }^{n}n\ge 2$, $a=0$, $\omega =2$, $\gamma ={\displaystyle \frac{a+\omega }{2}}$, and $p=q=2$ in Theorem 3; then, $m_1\le m_2\le m_3$, where

  $$\begin{array}{cc}\hfill m_1& =-n{2}^n\left(\left(\sqrt{{\displaystyle \frac{1}{8}}}+\sqrt{{\displaystyle \frac{3}{8}}}\right)\sqrt{{\displaystyle \frac{1}{24}}\left({\xi }^3+{(1-\xi )}^3\right)}\right)+2^{n-1}\xi +(1-\xi ).\hfill \end{array}$$

  $$\begin{array}{c}\hfill m_2={\displaystyle \frac{2^n}{n+1}}.\end{array}$$

  $$\begin{array}{cc}\hfill m_3& =n{2}^n\left(\left(\sqrt{{\displaystyle \frac{1}{8}}}+\sqrt{{\displaystyle \frac{3}{8}}}\right)\sqrt{{\displaystyle \frac{1}{24}}\left({\xi }^3+{(1-\xi )}^3\right)}\right)+2^{n-1}\xi +(1-\xi ).\hfill \end{array}$$
• We take $\mathcal{S}\left(\gamma \right)={\gamma }^{n}n\ge 2$, $a=0$, $\omega =2$, $\gamma ={\displaystyle \frac{2a+\omega }{3}}$, and $p=q=2$ in Theorem 3; then, $m_1\le m_2\le m_3$, where

  $$\begin{array}{cc}\hfill m_1& =-2^{n}n\left(\left(\sqrt{{\displaystyle \frac{1}{18}}}+\sqrt{{\displaystyle \frac{5}{18}}}\right)\sqrt{{\displaystyle \frac{{\xi }^3}{24}}+{\displaystyle \frac{1}{648}}{(2-3\xi )}^3}+{\displaystyle \frac{\sqrt{6}}{108}}\right)+{\displaystyle \frac{1}{2}}\left({\left({\displaystyle \frac{2}{3}}\right)}^n+{\left({\displaystyle \frac{4}{3}}\right)}^n\right)(1-\xi )+2^{n-1}\xi .\hfill \end{array}$$

  $$\begin{array}{c}\hfill m_2={\displaystyle \frac{2^n}{n+1}}.\end{array}$$

  $$\begin{array}{cc}\hfill m_3=& 2^{n}n\left(\left(\sqrt{{\displaystyle \frac{1}{18}}}+\sqrt{{\displaystyle \frac{5}{18}}}\right)\sqrt{{\displaystyle \frac{{\xi }^3}{24}}+{\displaystyle \frac{1}{648}}{(2-3\xi )}^3}+{\displaystyle \frac{\sqrt{6}}{108}}\right)+{\displaystyle \frac{1}{2}}\left({\left({\displaystyle \frac{2}{3}}\right)}^n+{\left({\displaystyle \frac{4}{3}}\right)}^n\right)(1-\xi )+2^{n-1}\xi .\hfill \end{array}$$

• For Figure 3a, we choose $\xi$ and n to develop a visual explanation of Theorem 3 at $\gamma ={\displaystyle \frac{a+\omega }{2}}$.
  

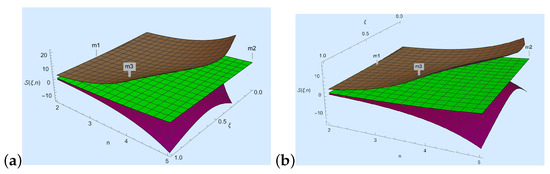  Figure 3. Here the purple, green, and brown colors represent $m_1,m_2$, and $m_3$, respectively.
• For Figure 3b, we choose $\xi$ and n to develop a visual explanation of Theorem 3 at $\gamma ={\displaystyle \frac{2a+\omega }{3}}$.

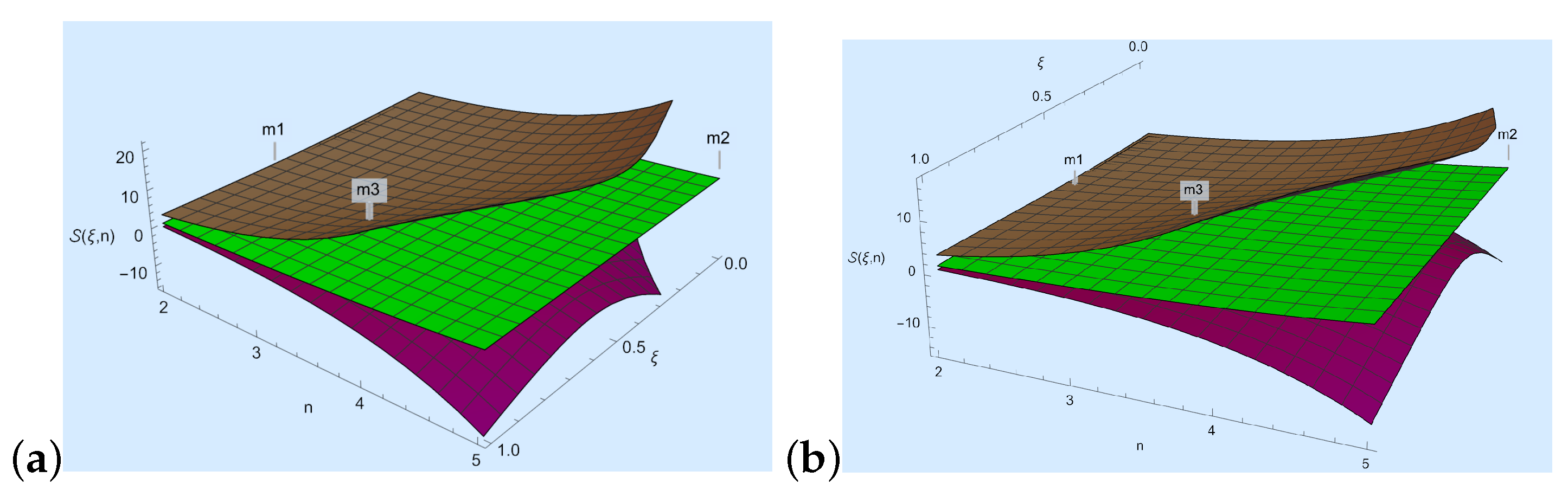
Now, we discuss Theorem 4.

• We take $\mathcal{S}\left(\gamma \right)={\gamma }^{n}n\ge 2$, $a=0$, $\omega =2$, $\gamma ={\displaystyle \frac{a+\omega }{2}}$, and $p=q=2$ in Theorem 4; then, $m_1\le m_2\le m_3$, where

  $$\begin{array}{cc}\hfill m_1& =2^{n-1}\xi -{\displaystyle \frac{1}{2}}{\left(n{2}^{n-1}\right)}^2-{\displaystyle \frac{1}{12}}\left({\xi }^3+{(1-\xi )}^3\right)+(1-\xi ).\hfill \end{array}$$

  $$\begin{array}{c}\hfill m_2={\displaystyle \frac{2^n}{n+1}}.\end{array}$$

  $$\begin{array}{cc}\hfill m_3& =2^{n-1}\xi +{\displaystyle \frac{1}{2}}{\left(n{2}^{n-1}\right)}^2+{\displaystyle \frac{1}{12}}\left({\xi }^3+{(1-\xi )}^3\right)+(1-\xi ).\hfill \end{array}$$
• We take $\mathcal{S}\left(\gamma \right)={\gamma }^{n}n\ge 2$, $a=0$, $\omega =2$, $\gamma ={\displaystyle \frac{2a+\omega }{3}}$ and $p=q=2$ in Theorem 4, then $m_1\le m_2\le m_3$, where

  $$\begin{array}{cc}\hfill m_1& ={\displaystyle \frac{1}{2}}\left({\left({\displaystyle \frac{2}{3}}\right)}^n+{\left({\displaystyle \frac{4}{3}}\right)}^n\right)(1-\xi )+2^{n-1}\xi -{\displaystyle \frac{1}{2}}{\left(n{2}^{n-1}\right)}^2-{\displaystyle \frac{1}{324}}\left(27{\xi }^3+{(2-3\xi )}^3+1\right).\hfill \end{array}$$

  $$\begin{array}{c}\hfill m_2={\displaystyle \frac{2^n}{n+1}}.\end{array}$$

  $$\begin{array}{cc}\hfill m_3=& {\displaystyle \frac{1}{2}}\left({\left({\displaystyle \frac{2}{3}}\right)}^n+{\left({\displaystyle \frac{4}{3}}\right)}^n\right)(1-\xi )+2^{n-1}\xi +{\displaystyle \frac{1}{2}}{\left(n{2}^{n-1}\right)}^2+{\displaystyle \frac{1}{324}}\left(27{\xi }^3+{(2-3\xi )}^3+1\right).\hfill \end{array}$$

• For Figure 4a, we choose $\xi$ and n to develop a visual explanation of Theorem 4 at $\gamma ={\displaystyle \frac{a+\omega }{2}}$.
  

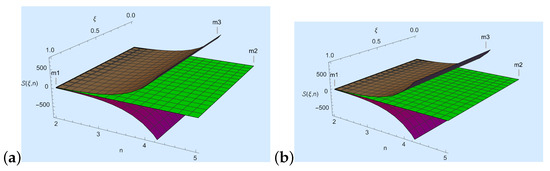  Figure 4. Here, the purple, green, and brown colors represent $m_1,m_2$, and $m_3$, respectively.
• For Figure 4b, we choose $\xi$ and n to develop a visual explanation of Theorem 4 at $\gamma ={\displaystyle \frac{2a+\omega }{3}}$.

Now, we discuss Theorem 5.

• We take $\mathcal{S}\left(\gamma \right)={\gamma }^{n}n\ge 2$, $a=0$, $\omega =2$, $\gamma ={\displaystyle \frac{a+\omega }{2}}$, and $p=q=2$ in Theorem 4; then, $m_1\le m_2\le m_3$, where

  $$\begin{array}{cc}\hfill m_1& =-{\displaystyle \frac{n{2}^n}{8}}\left(3{\xi }^2+{(1-\xi )}^2-2\xi +1\right)+2^{n-1}\xi +(1-\xi ).\hfill \end{array}$$

  $$\begin{array}{c}\hfill m_2={\displaystyle \frac{2^n}{n+1}}.\end{array}$$

  $$\begin{array}{cc}\hfill m_3& ={\displaystyle \frac{n{2}^n}{8}}\left(3{\xi }^2+{(1-\xi )}^2-2\xi +1\right)+2^{n-1}\xi +(1-\xi ).\hfill \end{array}$$
• We take $\mathcal{S}\left(\gamma \right)={\gamma }^{n}n\ge 2$, $a=0$, $\omega =2$, $\gamma ={\displaystyle \frac{2a+\omega }{3}}$, and $p=q=2$ in Theorem 5; then, $m_1\le m_2\le m_3$, where

  $$\begin{array}{cc}\hfill m_1& =-n{2}^n\left({\displaystyle \frac{1}{8}}\left(3{\xi }^2+{(2-3\xi )}^2\right)-{\displaystyle \frac{\xi }{4}}+{\displaystyle \frac{1}{12}}\right)+{\displaystyle \frac{1}{2}}\left({\left({\displaystyle \frac{2}{3}}\right)}^n+{\left({\displaystyle \frac{4}{3}}\right)}^n\right)(1-\xi )+2^{n-1}\xi .\hfill \end{array}$$

  $$\begin{array}{c}\hfill m_2={\displaystyle \frac{2^n}{n+1}}.\end{array}$$

  $$\begin{array}{cc}\hfill m_3=& 2^{n}n\left({\displaystyle \frac{1}{8}}\left(3{\xi }^2+{(2-3\xi )}^2\right)-{\displaystyle \frac{\xi }{4}}+{\displaystyle \frac{1}{12}}\right)+{\displaystyle \frac{1}{2}}\left({\left({\displaystyle \frac{2}{3}}\right)}^n+{\left({\displaystyle \frac{4}{3}}\right)}^n\right)(1-\xi )+2^{n-1}\xi .\hfill \end{array}$$

• For Figure 5a, we choose $\xi$ and n to develop a visual explanation of Theorem 5 at $\gamma ={\displaystyle \frac{a+\omega }{2}}$.
  

  Figure 5. Here, the purple, green, and brown colors represent $m_1,m_2$, and $m_3$, respectively.
• For Figure 5b, we choose $\xi$ and n to develop a visual explanation of Theorem 5 at $\gamma ={\displaystyle \frac{2a+\omega }{3}}$.

4. Applications

Finally, we address some novel applications of our produced results to the theory of means, error inequalities of composite quadrature rules, special functions, and generalized iterative schemes.

4.1. Error Boundaries of Composite Newton–Cotes Schemes

Let $\Delta :a={\gamma }_0<{\varrho }_1<{\varrho }_2<\dots <{\varrho }_i<{\varrho }_{i+1}<\dots {\varrho }_n=\omega$ be a partition of $[a,\omega ]$ and $h_i={\varrho }_{i+1}-{\varrho }_i,i=0,1,2,\dots n-1$; then, using the unified composite Newton–Cotes formula,

$$\begin{array}{c}\hfill {⋎}_n(\Delta ,\mathcal{S})=\sum _{i=0}^{n-1}{\displaystyle \frac{h_i}{2}}\left[\xi \left\{\mathcal{S}\left({\varrho }_i\right)+\mathcal{S}\left({\varrho }_{i+1}\right)\right\}+(1-\xi )\left\{\mathcal{S}({\varrho }_i+{\varrho }_{i+1}-{\mathcal{O}}_i)+\mathcal{S}\left({\mathcal{O}}_i\right)\right\}\right],\end{array}$$

satisfying the conditions ${\varrho }_i+{\displaystyle \frac{\xi h_i}{2}}\le {\mathcal{O}}_i\le {\displaystyle \frac{{\varrho }_i+{\varrho }_{i+1}}{2}}$. Also,

$$\begin{array}{c}\hfill {⋎}_n(\Delta ,\mathcal{S})+{\mathcal{R}}_n(\Delta ,\mathcal{S})={\int }_a^{\omega }\mathcal{S}\left(u\right)\mathrm{d}u.\end{array}$$

Proposition 1.

From Theorem 1, we have

$$\begin{array}{c}\hfill \left|{\mathcal{R}}_n(\Delta ,\mathcal{S})\right|\le \sum _{i=0}^{n-1}{h}_i^2\left[\left(E_{10}+E_{11}+E_{12}\right)|{\mathcal{S}}^{\prime }\left({\varrho }_i\right)|+\left(E_{13}+E_{14}+E_{15}\right)\left|{\mathcal{S}}^{\prime }\left({\varrho }_{i+1}\right)\right|\right],\end{array}$$

where

$$\begin{array}{cc}\hfill & E_{10}={\displaystyle \frac{6{\xi }^2-6\xi -{\xi }^3}{24}}+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{{\mathcal{O}}_i-{\varrho }_i}{{\varrho }_{i+1}-{\varrho }_i}}\right)}^2-{\displaystyle \frac{1}{3}}{\left({\displaystyle \frac{{\mathcal{O}}_i-{\varrho }_i}{{\varrho }_{i+1}-{\varrho }_i}}\right)}^3+{\displaystyle \frac{\xi }{4}}{\left({\displaystyle \frac{{\varrho }_{i+1}-{\mathcal{O}}_i}{{\varrho }_{i+1}-{\varrho }_i}}\right)}^2.\hfill \end{array}$$

$$\begin{array}{cc}\hfill & E_{11}=-{\displaystyle \frac{7}{24}}+{\displaystyle \frac{3}{4}}\left({\displaystyle \frac{{({\mathcal{O}}_i-{\varrho }_i)}^2+{({\varrho }_{i+1}-{\mathcal{O}}_i)}^2}{{({\varrho }_{i+1}-{\varrho }_i)}^2}}\right)-{\displaystyle \frac{1}{3}}\left({\displaystyle \frac{{({\varrho }_{i+1}-{\mathcal{O}}_i)}^3+{({\mathcal{O}}_i-{\varrho }_i)}^3}{{({\varrho }_{i+1}-{\varrho }_i)}^3}}\right).\hfill \end{array}$$

$$\begin{array}{cc}\hfill E_{12}& ={\displaystyle \frac{\left(1-\frac{\xi }{2}\right)}{2}}{\left({\displaystyle \frac{{\mathcal{O}}_i-{\varrho }_i}{{\varrho }_{i+1}-{\varrho }_i}}\right)}^2-{\displaystyle \frac{\left(1-\frac{\xi }{2}\right){\xi }^2}{4}}+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{{\varrho }_{i+1}-{\mathcal{O}}_i}{{\varrho }_{i+1}-{\varrho }_i}}\right)}^2-{\left(1-{\displaystyle \frac{\xi }{2}}\right)}^2+{\displaystyle \frac{2}{3}}{\left(1-{\displaystyle \frac{\xi }{2}}\right)}^3-{\displaystyle \frac{1}{3}}{\left({\displaystyle \frac{{\varrho }_{i+1}-{\mathcal{O}}_i}{{\varrho }_{i+1}-{\varrho }_i}}\right)}^3+{\displaystyle \frac{1}{6}}.\hfill \end{array}$$

$$\begin{array}{cc}\hfill & E_{13}={\displaystyle \frac{{\xi }^3}{24}}+{\displaystyle \frac{1}{3}}{\left({\displaystyle \frac{{\mathcal{O}}_i-{\varrho }_i}{{\varrho }_{i+1}-{\varrho }_i}}\right)}^3-{\displaystyle \frac{\xi }{4}}{\left({\displaystyle \frac{{\mathcal{O}}_i-{\varrho }_i}{{\varrho }_{i+1}-{\varrho }_i}}\right)}^2.\hfill \end{array}$$

$$\begin{array}{cc}\hfill & E_{14}={\displaystyle \frac{1}{24}}-{\displaystyle \frac{1}{4}}\left({\displaystyle \frac{{({\mathcal{O}}_i-{\varrho }_i)}^2+{({\varrho }_{i+1}-{\mathcal{O}}_i)}^2}{{({\varrho }_{i+1}-{\varrho }_i)}^2}}\right)+{\displaystyle \frac{1}{3}}\left({\displaystyle \frac{{({\varrho }_{i+1}-{\mathcal{O}}_i)}^3+{({\mathcal{O}}_i-{\varrho }_i)}^3}{{({\varrho }_{i+1}-{\varrho }_i)}^3}}\right).\hfill \end{array}$$

$$\begin{array}{cc}\hfill E_{15}& ={\left(1-{\displaystyle \frac{\xi }{2}}\right)}^3-{\displaystyle \frac{2}{3}}{\left(1-{\displaystyle \frac{\xi }{2}}\right)}^3-{\displaystyle \frac{\left(1-\frac{\xi }{2}\right)}{2}}{\left({\displaystyle \frac{{\varrho }_{i+1}-{\mathcal{O}}_i}{{\varrho }_{i+1}-{\varrho }_i}}\right)}^2+{\displaystyle \frac{1}{3}}{\left({\displaystyle \frac{{\varrho }_{i+1}-{\mathcal{O}}_i}{{\varrho }_{i+1}-{\varrho }_i}}\right)}^3+{\displaystyle \frac{1}{3}}-{\displaystyle \frac{\left(1-\frac{\xi }{2}\right)}{2}}.\hfill \end{array}$$

Proof. 

Employ Theorem 1 on $[{\varrho }_i,{\varrho }_{i+1}]$ such that ${\mathcal{O}}_i\in [{\varrho }_i,{\varrho }_{i+1}]$ and take the sum from $i=0$ to $n-1$. □

Proposition 2.

From Theorem 1, we have

$$\begin{array}{c}\hfill \left|{\mathcal{R}}_n(\Delta ,\mathcal{S})\right|\le M\sum _{i=0}^{n-1}{h}_i^2\left[{\displaystyle \frac{3{\xi }^2}{8}}-{\displaystyle \frac{1}{4}}+{\left({\displaystyle \frac{{\mathcal{O}}_i-{\varrho }_i}{{\varrho }_{i+1}-{\varrho }_i}}\right)}^2+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{{\varrho }_{i+1}-{\mathcal{O}}_i}{{\varrho }_{i+1}-{\varrho }_i}}\right)}^2-{\displaystyle \frac{\xi }{2}}\left({\displaystyle \frac{{\mathcal{O}}_i-{\varrho }_i}{{\varrho }_{i+1}-{\varrho }_i}}\right)+{\displaystyle \frac{1}{2}}{\left(1-{\displaystyle \frac{\xi }{2}}-{\displaystyle \frac{{\varrho }_{i+1}-{\mathcal{O}}_i}{{\varrho }_{i+1}-{\varrho }_i}}\right)}^2\right].\end{array}$$

Proof. 

Employ Theorem 4 on $[{\varrho }_i,{\varrho }_{i+1}]$ such that ${\mathcal{O}}_i\in [{\varrho }_i,{\varrho }_{i+1}]$, and then take the sum from $i=0$ to $n-1$. □

Remark 2.

For different choices of ξ and ${\mathcal{O}}_i$, we can obtain various known and new error inequalities for composite closed- and open-type Newton–Cotes formulas. For example, by choosing $\xi =0$ and ${\mathcal{O}}_i={\displaystyle \frac{{\varrho }_i+{\varrho }_{i+1}}{2}},{\displaystyle \frac{2{\varrho }_i+{\varrho }_{i+1}}{3}},{\displaystyle \frac{3{\varrho }_i+{\varrho }_{i+1}}{4}},\dots$, we obtain the error estimate of the midpoint inequality and open trapezoidal-type inequalities, respectively. Furthermore, for $\xi ={\displaystyle \frac{1}{3}},{\displaystyle \frac{1}{4}},{\displaystyle \frac{1}{2}}$ and ${\mathcal{O}}_i={\displaystyle \frac{{\varrho }_i+{\varrho }_{i+1}}{2}},{\displaystyle \frac{2{\varrho }_i+{\varrho }_{i+1}}{3}},{\displaystyle \frac{{\varrho }_i+{\varrho }_{i+1}}{2}}$, we acquire the error bound of the composite Simpson’s inequality, Newton-type inequality, and Bullen’s inequality, respectively.

4.2. Applications for the Linear Combination of Means

In the subsequent part, we explore the impact of our study on the theory of means. To accomplish our goal, first we recapture the well-known binary means of positive real numbers.

• $A(a,\omega )={\displaystyle \frac{a+\omega }{2}}.$
• $H(a,\omega )={\displaystyle \frac{2ab}{a+\omega }}.$
• $Ł(a,\omega )={\displaystyle \frac{\omega -a}{ln\left(\omega \right)-ln\left(a\right)}}$.
• ${Ł}_n(a,\omega )={\left[{\displaystyle \frac{{\omega }^{n+1}-a^{n+1}}{(\omega -a)(n+1)}}\right]}^{{\displaystyle \frac{1}{n}}},n\in \mathbb{Z}-\{0,-1\}.$

Proposition 3.

From Theorem 3, we have

$$\begin{array}{cc}\hfill & \left|\xi A(a^n,{\omega }^n)+(1-\xi )A({(a+\omega -\gamma )}^n,{\gamma }^n)-{Ł}_n^n(a,\omega )\right|\hfill \\ \hfill & \le (\omega -a)\left[C_1^{{\displaystyle \frac{1}{p}}}{\left(\left({\displaystyle \frac{{(\omega -a)}^2-{(\omega -\gamma )}^2}{2{(\omega -a)}^2}}\right){|n{a}^{n-1}|}^q+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{\gamma -a}{\omega -a}}\right)}^2{\left|n{b}^{n-1}\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & +C_2^{{\displaystyle \frac{1}{p}}}{\left(2A\left(\right|n{a}^{n-1}|q,|n{b}^{n-1}{|}^q)\left({\displaystyle \frac{{(\omega -\gamma )}^2-{(\gamma -a)}^2}{2{(\omega -a)}^2}}\right)\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & \left.+C_3^{{\displaystyle \frac{1}{p}}}{\left({\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{\gamma -a}{\omega -a}}\right)}^2{|n{a}^{n-1}|}^q+{\displaystyle \frac{1}{2}}\left({\displaystyle \frac{{(\omega -a)}^2-{(\omega -\gamma )}^2}{{(\omega -a)}^2}}\right){\left|n{b}^{n-1}\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\right].\hfill \end{array}$$

Also

$$\begin{array}{cc}\hfill & \left|\xi H^{-1}(a,\omega )+(1-\xi )H^{-1}(a+\omega -\gamma ,\gamma )-{Ł}^{-1}(a,\omega )\right|\hfill \\ \hfill & \le (\omega -a)\left[C_1^{{\displaystyle \frac{1}{p}}}{\left({\displaystyle \frac{{(\omega -a)}^2-{(\omega -\gamma )}^2}{2a^{2q}{(\omega -a)}^2}}+{\displaystyle \frac{1}{2{\omega }^{2q}}}{\left({\displaystyle \frac{\gamma -a}{\omega -a}}\right)}^2\right)}^{{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & +C_2^{{\displaystyle \frac{1}{p}}}{\left(2H^{-1}(a^{2q},{\omega }^{2q})\left({\displaystyle \frac{{(\omega -\gamma )}^2-{(\gamma -a)}^2}{2{(\omega -a)}^2}}\right)\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & \left.+C_3^{{\displaystyle \frac{1}{p}}}{\left({\displaystyle \frac{1}{2a^{2q}}}{\left({\displaystyle \frac{\gamma -a}{\omega -a}}\right)}^2+{\displaystyle \frac{1}{2{\omega }^{2q}}}\left({\displaystyle \frac{{(\omega -a)}^2-{(\omega -\gamma )}^2}{{(\omega -a)}^2}}\right)\right)}^{{\displaystyle \frac{1}{q}}}\right],\hfill \end{array}$$

where $C_1,C_2$, and $C_3$ are defined in Theorem 3.

Proof. 

Applying the convex function $\mathcal{S}\left(\gamma \right)={\gamma }^n,n\ge 2$, and $\mathcal{S}\left(\gamma \right)={\displaystyle \frac{1}{\gamma }}$ on Theorem 3, we achieve our desired relations. □

Proposition 4.

From Theorem 4, we have

$$\begin{array}{cc}\hfill & \left|\xi A(a^n,{\omega }^n)+(1-\xi )A({(a+\omega -\gamma )}^n,{\gamma }^n)-{Ł}_n^n(a,\omega )\right|\hfill \\ \hfill & \le (\omega -a)\left[{\displaystyle \frac{C_1+C_2+C_3}{p}}+{\displaystyle \frac{A\left(\right|n{a}^{n-1}|q,|n{b}^{n-1}{|}^q)}{q}}\right].\hfill \end{array}$$

Also

$$\begin{array}{cc}\hfill & \left|\xi H^{-1}(a,\omega )+(1-\xi )H^{-1}(a+\omega -\gamma ,\gamma )-{Ł}^{-1}(a,\omega )\right|\hfill \\ \hfill & \le (\omega -a)\left[{\displaystyle \frac{C_1+C_2+C_3}{p}}+{\displaystyle \frac{H^{-1}(a^{2q},{\omega }^{2q})}{q}}\right],\hfill \end{array}$$

where $C_1,C_2$, and $C_3$ are defined in Theorem 3.

Proof. 

Applying the convex function $\mathcal{S}\left(\gamma \right)={\gamma }^n,n\ge 2$, and $\mathcal{S}\left(\gamma \right)={\displaystyle \frac{1}{\gamma }}$ on Theorem 4, we achieve our desired relations. □

4.3. Application for Special Functions

Let ${\psi }_{\delta }:\mathbb{R}\to (0,1]$ be defined by

$$\begin{array}{c}\hfill {\psi }_{\delta }\left(v\right)=2^{\delta }\mathsf{\Gamma }(1+\delta )v^{-{\varkappa }_3}{I}_p\left(v\right),\end{array}$$

For this, we retrospect the representation of modified Bessel functions, which is given as detailed in [40]:

$$\begin{array}{c}\hfill {\psi }_{\delta }\left(v\right)=\sum _{u\ge 0}{\displaystyle \frac{{\left(\frac{v}{2}\right)}^{\delta +2u}}{u!\mathsf{\Gamma }(\delta +u+1)}}.\end{array}$$

The first and nth-order derivative formula’s ${\psi }_{\delta }\left(v\right)$, which are given as detailed in [41]:

$$\begin{array}{ccc}\hfill & {\psi }_{\delta }^{\prime }\left(v\right)={\displaystyle \frac{v}{2(1+\delta )}}{\psi }_{\delta +1}\left(v\right),\hfill & \hfill {\displaystyle \frac{{\partial }^n{\psi }_{\delta }}{{\partial }^{n}v}}=2^{n-2\delta }\sqrt{\pi }{v}^{\delta -n}\mathsf{\Gamma }{(1+\delta )}_2{F}_3\left({\displaystyle \frac{1+\delta }{2}},{\displaystyle \frac{2+\delta }{2}};{\displaystyle \frac{1+\delta -n}{2}},{\displaystyle \frac{2+\delta -n}{2}},1+\delta ;{\displaystyle \frac{v^2}{4}}\right),\end{array}$$

where${ }_2{F}_3(.,.,.)$ is a hypergeometric function, and its integral and summation representation are given as:

$$\begin{array}{c}\hfill { }_2{F}_3\left({\displaystyle \frac{1+\delta }{2}},{\displaystyle \frac{2+\delta }{2}};{\displaystyle \frac{1+\delta -n}{2}},{\displaystyle \frac{2+\delta -n}{2}},(1+\delta );{\displaystyle \frac{v^2}{4}}\right)=\sum _{k=0}^{\infty }{\displaystyle \frac{{\left(\frac{1+\delta }{2}\right)}_k{\left(\frac{2+\delta }{2}\right)}_k{v}^{2k}}{{\left(\frac{1+\delta -n}{2}\right)}_k{\left(\frac{2+\delta -n}{2}\right)}_k{(1+\delta )}_k{4}^{k}k!}}.\end{array}$$

Proposition 5.

For any $[a,\omega ]\in \mathbb{R}$ and $\delta \ge 1$, then

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{\xi \left(a{\psi }_{\delta +1}\left(a\right)+\omega {\psi }_{\delta +1}\left(\omega \right)\right)+(1-\xi )\left((a+\omega -\gamma ){\psi }_{\delta +1}(a+\omega -\gamma )+\gamma {\psi }_{\delta +1}\left(\gamma \right)\right)}{4(1+\delta )}}-{\displaystyle \frac{{\psi }_{\delta }\left(\omega \right)-{\psi }_{\delta }\left(a\right)}{\omega -a}}\right|\hfill \\ \hfill & \le (\omega -a)2^{1-2\delta }\sqrt{\pi }\mathsf{\Gamma }(1+\delta )\left[\left(E_1+E_2+E_3\right){a^{\delta -1}}_2{F}_3\left({\displaystyle \frac{1+\delta }{2}},{\displaystyle \frac{2+\delta }{2}};{\displaystyle \frac{\delta }{2}},{\displaystyle \frac{1+\delta }{2}},(1+\delta );{\displaystyle \frac{a^2}{4}}\right)\right.\hfill \\ \hfill & \left.+{\left(E_4+E_5+E_6\right)}_2{F}_3\left({\displaystyle \frac{1+\delta }{2}},{\displaystyle \frac{2+\delta }{2}};{\displaystyle \frac{\delta }{2}},{\displaystyle \frac{1+\delta }{2}},(1+\delta );{\displaystyle \frac{a^2}{4}}\right)\right],\hfill \end{array}$$

where ($E_1$–$E_6$) are defined in Theorem 1.

Proof. 

To attain the final outcome, we implement $\mathcal{S}\left(\gamma \right)={\psi }_{\delta }^{\prime }\left(\gamma \right)$ in Theorem 1. □

4.4. Family of Iterative Methods to Find the Roots of Non-Linear Equations

Now, we provide another significant implication of the proposed results to evaluate the roots of non-linear equations.

Consider

$$\begin{array}{c}\hfill \mathcal{S}\left(\gamma \right)=0.\end{array}$$

(3)

It is a very interesting research topic in the realm of numerical analysis to derive the roots of non-linear equations. In the following context, various approaches have been deployed to construct new methodologies like quadrature formulae, interpolating polynomials, Taylor’s series, and decomposition procedures. Methods like Newton’s, Halley’s, and Householder’s are the best classical methods, which still served as a base point for further proceedings. Now, we construct a novel family of iterative methods by using the general error bounds obtained in Theorem 5.

Proposition 6.

For any $[\varkappa ,{\varkappa }_3]\subset \mathbb{R}$ such that $\mathcal{S}\left(\gamma \right)=0$ is a non-linear equation, then

$$\begin{array}{c}\hfill {\gamma }_{n+1}={\gamma }_n-{\displaystyle \frac{2\mathcal{S}\left({\gamma }_n\right)}{\xi \left({\mathcal{S}}^{\prime }\left({\gamma }_n\right)+{\mathcal{S}}^{\prime }\left({\gamma }_n\right)\right)+(1-\xi )\left({\mathcal{S}}^{\prime }\left(\frac{4{\gamma }_n+{\gamma }_n}{5}\right)+{\mathcal{S}}^{\prime }\left(\frac{{\gamma }_n+4{\gamma }_n}{5}\right)\right)}},\end{array}$$

(4)

where

$$\begin{array}{c}\hfill {\gamma }_n={\gamma }_n-{\displaystyle \frac{\mathcal{S}\left({\gamma }_n\right)}{{\mathcal{S}}^{\prime }\left({\gamma }_n\right)}}.\end{array}$$

Remark 3.

• By taking $\xi =0$ in Proposition 6, we then have the following iterative scheme

  $$\begin{array}{c}\hfill {\gamma }_{n+1}={\gamma }_n-{\displaystyle \frac{2\mathcal{S}\left({\gamma }_n\right)}{{\mathcal{S}}^{\prime }\left(\frac{4{\gamma }_n+{\gamma }_n}{5}\right)+{\mathcal{S}}^{\prime }\left(\frac{{\gamma }_n+4{\gamma }_n}{5}\right)}},\end{array}$$

  where ${\gamma }_n$ is already defined in Proposition 6.
• By taking $\xi =1$ in Proposition 6, we then have the following iterative scheme

  $$\begin{array}{c}\hfill {\gamma }_{n+1}={\gamma }_n-{\displaystyle \frac{2\mathcal{S}\left({\gamma }_n\right)}{{\mathcal{S}}^{\prime }\left({\gamma }_n\right)+{\mathcal{S}}^{\prime }\left({\gamma }_n\right)}},\end{array}$$

  where ${\gamma }_n$ is already defined in Proposition 6.
• By taking $\xi ={\displaystyle \frac{1}{3}}$ in Proposition 6, we then have the following iterative scheme

  $$\begin{array}{c}\hfill {\gamma }_{n+1}={\gamma }_n-{\displaystyle \frac{6\mathcal{S}\left({\gamma }_n\right)}{{\mathcal{S}}^{\prime }\left({\gamma }_n\right)+{\mathcal{S}}^{\prime }\left({\gamma }_n\right)+2\left({\mathcal{S}}^{\prime }\left(\frac{4{\gamma }_n+{\gamma }_n}{5}\right)+{\mathcal{S}}^{\prime }\left(\frac{{\gamma }_n+4{\gamma }_n}{5}\right)\right)}},\end{array}$$

  where ${\gamma }_n$ is already defined in Proposition 6.
• By taking $\xi ={\displaystyle \frac{1}{2}}$ in Proposition 6, we then have the following iterative scheme

  $$\begin{array}{c}\hfill {\gamma }_{n+1}={\gamma }_n-{\displaystyle \frac{4\mathcal{S}\left({\gamma }_n\right)}{{\mathcal{S}}^{\prime }\left({\gamma }_n\right)+{\mathcal{S}}^{\prime }\left({\gamma }_n\right)+{\mathcal{S}}^{\prime }\left(\frac{4{\gamma }_n+{\gamma }_n}{5}\right)+{\mathcal{S}}^{\prime }\left(\frac{{\gamma }_n+4{\gamma }_n}{5}\right)}},\end{array}$$

  where ${\gamma }_n$ is already defined in Proposition 6.
• By taking $\xi ={\displaystyle \frac{1}{5}}$ in Proposition 6, we have the following iterative scheme

  $$\begin{array}{c}\hfill {\gamma }_{n+1}={\gamma }_n-{\displaystyle \frac{10\mathcal{S}\left({\gamma }_n\right)}{{\mathcal{S}}^{\prime }\left({\gamma }_n\right)+{\mathcal{S}}^{\prime }\left({\gamma }_n\right)+4\left({\mathcal{S}}^{\prime }\left(\frac{4{\gamma }_n+{\gamma }_n}{5}\right)+{\mathcal{S}}^{\prime }\left(\frac{{\gamma }_n+4{\gamma }_n}{5}\right)\right)}},\end{array}$$

  where ${\gamma }_n$ is already defined in Proposition 6.
• By taking $\xi ={\displaystyle \frac{2}{3}}$ in Proposition 6, we then have the following iterative scheme

  $$\begin{array}{c}\hfill {\gamma }_{n+1}={\gamma }_n-{\displaystyle \frac{6\mathcal{S}\left({\gamma }_n\right)}{2\left({\mathcal{S}}^{\prime }\left({\gamma }_n\right)+{\mathcal{S}}^{\prime }\left({\gamma }_n\right)\right)+{\mathcal{S}}^{\prime }\left(\frac{4{\gamma }_n+{\gamma }_n}{5}\right)+{\mathcal{S}}^{\prime }\left(\frac{{\gamma }_n+4{\gamma }_n}{5}\right)}},\end{array}$$

  where ${\gamma }_n$ is already defined in Proposition 6.
• It is worth noting that for different choices of γ and ξ in Theorem 5, we can generate a family of iterative methods, as well as by making use of another method in place of Newton’s method as corrector methods.

Now, we investigate the convergence analysis of (4).

Theorem 6.

Let $r\in I$ be a simple zero of sufficiently differentiable function $\mathcal{S}$ on $I^{\circ }$. If ${\gamma }_{\circ }$ is sufficiently close to r, then Equation (4) has a third order of convergence for any $\xi \in [0,1]$.

Proof. 

Let r be a zero of differentiable $\mathcal{S}$; by expanding $\mathcal{S}\left({\gamma }_n\right)$ and ${\mathcal{S}}^{\prime }\left({\gamma }_n\right)$ about r, we have

$$\begin{array}{c}\hfill \mathcal{S}\left({\gamma }_n\right)={\mathcal{S}}^{\prime }\left(r\right)[e_n+c_2{e}_n^2+c_3{e}_n^3+c_4{e}_n^4+\dots ].\end{array}$$

(5)

Also,

$$\begin{array}{c}\hfill {\mathcal{S}}^{\prime }\left({\gamma }_n\right)={\mathcal{S}}^{\prime }\left(r\right)[1+2c_2{e}_n+3c_3{e}_n^2+4c_4{e}_n^3+5c_4{e}_n^4+\dots ],\end{array}$$

(6)

where $c_k={\displaystyle \frac{1}{k!}}{\displaystyle \frac{{\mathcal{S}}^k\left(r\right)}{{\mathcal{S}}^{\prime }\left(r\right)}},k=1,2,3,\dots$, where $e_n={\gamma }_n-r$. Now, from (5) and (6), we have

$$\begin{array}{c}\hfill {\gamma }_n={\gamma }_n-{\displaystyle \frac{\mathcal{S}\left({\gamma }_n\right)}{{\mathcal{S}}^{\prime }\left({\gamma }_n\right)}}=[r+c_2{e}_n^2+2(c_3-c_2^2)e_n^3+(-7c_2{c}_3+4c_2^3+3c_4)e_n^4+\dots ].\end{array}$$

(7)

This implies

$$\begin{array}{c}\hfill \mathcal{S}\left({\gamma }_n\right)={\mathcal{S}}^{\prime }\left(r\right)[c_2{e}_n^2+2(c_3-c_2^2)e_n^3+(-7c_2{c}_3+5c_2^3+3c_4)e_n^4+\dots ],\end{array}$$

(8)

and

$$\begin{array}{c}\hfill {\mathcal{S}}^{\prime }\left({\gamma }_n\right)={\mathcal{S}}^{\prime }\left(r\right)[1+2c_2{e}_n^2+4(c_2{c}_3-c_2^3)e_n^3+(-11c_2^2{c}_3+8c_2^4+6c_2{c}_4)e_n^4+\dots ].\end{array}$$

(9)

Also

$$\begin{array}{c}\hfill {\mathcal{S}}^{\prime }\left({\displaystyle \frac{4{\gamma }_n+{\gamma }_n}{5}}\right)={\mathcal{S}}^{\prime }\left(r\right)[c_1+{\displaystyle \frac{8}{5}}{c}_1{c}_2{e}_n+c_1\left({\displaystyle \frac{48}{25}}{c}_3+{\displaystyle \frac{c_2^2}{5}}\right)e_n^2+c_1\left({\displaystyle \frac{256}{125}}{c}_4+{\displaystyle \frac{24}{25}}{c}_2{c}_3+2c_2\left(-{\displaystyle \frac{2c_2^2}{5}}+{\displaystyle \frac{2c_3}{5}}\right)\right)e_n^3+\dots ],\end{array}$$

(10)

and

$$\begin{array}{c}\hfill {\mathcal{S}}^{\prime }\left({\displaystyle \frac{{\gamma }_n+4{\gamma }_n}{5}}\right)={\mathcal{S}}^{\prime }\left(r\right)[c_1+{\displaystyle \frac{2}{5}}{c}_1{c}_2{e}_n+c_1\left({\displaystyle \frac{2}{25}}{c}_3+{\displaystyle \frac{8c_2^2}{5}}\right)e_n^2+c_1\left({\displaystyle \frac{4c_4}{125}}+{\displaystyle \frac{24}{25}}{c}_2{c}_3+2c_2\left(-{\displaystyle \frac{8c_2^2}{5}}+{\displaystyle \frac{8c_3}{5}}\right)\right)e_n^3+\dots ].\end{array}$$

(11)

By using (7)–(11), we achieve

$$\begin{array}{c}\hfill {\gamma }_{n+1}=\left({\displaystyle \frac{(24\xi +1)c_3}{50}}+c_2^2\right)e_n^3+O\left(e_n^4\right).\end{array}$$

Hence, the result is acquired. □

4.5. Examples and Visual Analysis of Equation (4)

Initially, we explore some physical examples in light of Equation (4).

• In our first example, we consider the problem related to the plug flow of Casson fluids of blood in the rheology and fractional non-linear equations model [42]. The fall in flow rate can be estimated through the following equation

  $$\varphi \left(\gamma \right)=1-{\displaystyle \frac{16}{7}}\sqrt{\gamma }+{\displaystyle \frac{4}{3}}\gamma -{\displaystyle \frac{1}{21}}{\gamma }^4-G,$$

  here, we choose $G=0.4$, and by selecting the initial guess of ${\gamma }_0=0.1$, Equation (4) with $\xi ={\displaystyle \frac{1}{5}}$ results in the required root $\gamma =0.1046986515365482281163926975$ in the third iteration.
• Now, we consider the problem related to permeability in Biogels [42]. The dependence of pressure and velocity is demonstrated by the following equation:

  $$\varphi \left(\gamma \right)={\Re }_e{\gamma }^3-20\kappa {(1-\gamma )}^2,$$

  where ${\Re }_e={10}^{-8}$, $\kappa =0.3655$, and ${\gamma }_0=2$ as the initial guess. Then, Equation (4) with $\xi ={\displaystyle \frac{1}{5}}$ predicts the desired solution $\gamma =1.000037003578296426668052574$ in 13 iterations.

To showcase the efficiency of our proposed scheme, we offer the comparative study with classical methods such as Newton’s method (NM) [43], Abbasbandy’s method (AM) [44], Halley’s method (HM) [43], and Chun’s method (CM) [45]. To proceed further, we consider the following non-linear equations:

• $\varphi \left(\gamma \right)={\gamma }^3+4{\gamma }^2-15$,
• $\varphi \left(\gamma \right)=x{e}^{{\gamma }^2}-{sin}^2\gamma +3cos\gamma +5$,
• $\varphi \left(\gamma \right)=10\gamma e^{-{\gamma }^2}-1$,
• $\varphi \left(\gamma \right)=e^{-\gamma }+cos\gamma$.

We fix the tolerance of $ϵ={10}^{-15}$ and

• $|{\gamma }_{n+1}-{\gamma }_n|<ϵ$,
• $\left|\varphi \right({\gamma }_{n+1}\left)\right|<ϵ$.

The numerical results were performed on an Intel(R) Core(TM) i5 processor with 1.60 GHz and 16 GB of RAM. Maple 2018 was considered for coding, while the visual display was processed by Matlab 2021.

After performing the numerical tests on the software, we present tabular as well as visual illustrations of Equation (4) for the above-mentioned examples.

Methods	${\gamma }_0$	IT	${\gamma }_n$	$\mathcal{S}\left({\gamma }_n\right)$	$\delta$
$NM$	2	5	$1.6319808055660635175$	0	$4.77035\times {10}^{-14}$
$AM$	2	4	$1.6319808055660635175$	0	0
$HM$	2	4	$1.6319808055660635175$	0	0
$CM$	2	4	$1.6319808055660635175$	0	0
$ALG$	2	4	$1.6319808055660635175$	0	0

Methods	${\gamma }_0$	IT	${\gamma }_n$	$\varphi \left({\gamma }_n\right)$	$\delta$
$NM$	$-1$	6	$-1.2076478271309189270$	$4.0\times {10}^{-19}$	$7.58\times {10}^{-17}$
$AM$	$-1$	5	$-1.2076478271309189270$	$4.0\times {10}^{-19}$	0
$HM$	$-1$	4	$-1.2076478271309189270$	$4.0\times {10}^{-19}$	0
$CM$	$-1$	5	$-1.2076478271309189270$	$4.0\times {10}^{-19}$	0
$ALG$	$-1$	5	$-1.2076478271309189270$	$4.0\times {10}^{-19}$	0

Methods	${\gamma }_0$	IT	${\gamma }_n$	$\varphi \left({\gamma }_n\right)$	$\delta$
$NM$	$1.8$	5	$1.6796306104284499407$	$-9\times {10}^{-20}$	$4.7395\times {10}^{-15}$
$AM$	$1.8$	4	$1.6796306104284499407$	$-9\times {10}^{-20}$	$1.0\times {10}^{-19}$
$HM$	$1.8$	4	$1.6796306104284499407$	$-9\times {10}^{-20}$	0
$CM$	$1.8$	4	$1.6796306104284499407$	$2.0\times {10}^{-19}$	0
$ALG$	$1.8$	4	$1.6796306104284499407$	$-9\times {10}^{-20}$	0

Methods	${\gamma }_0$	IT	${\gamma }_n$	$\varphi \left({\gamma }_n\right)$	$\delta$
$NM$	2	4	$1.7461395304080124177$	$6.0\times {10}^{-20}$	$1.611907606\times {10}^{-19}$
$AM$	2	4	$1.7461395304080124177$	$-6\times {10}^{-20}$	$1.0\times {10}^{-19}$
$HM$	2	4	$1.7461395304080124176$	$6.0\times {10}^{-20}$	$1.0\times {10}^{-19}$
$CM$	2	3	$1.7461395304080124177$	$-6\times {10}^{-20}$	$4.63\times {10}^{-17}$
$ALG$	2	4	$1.7461395304080124177$	$-6\times {10}^{-20}$	$1\times {10}^{-19}$

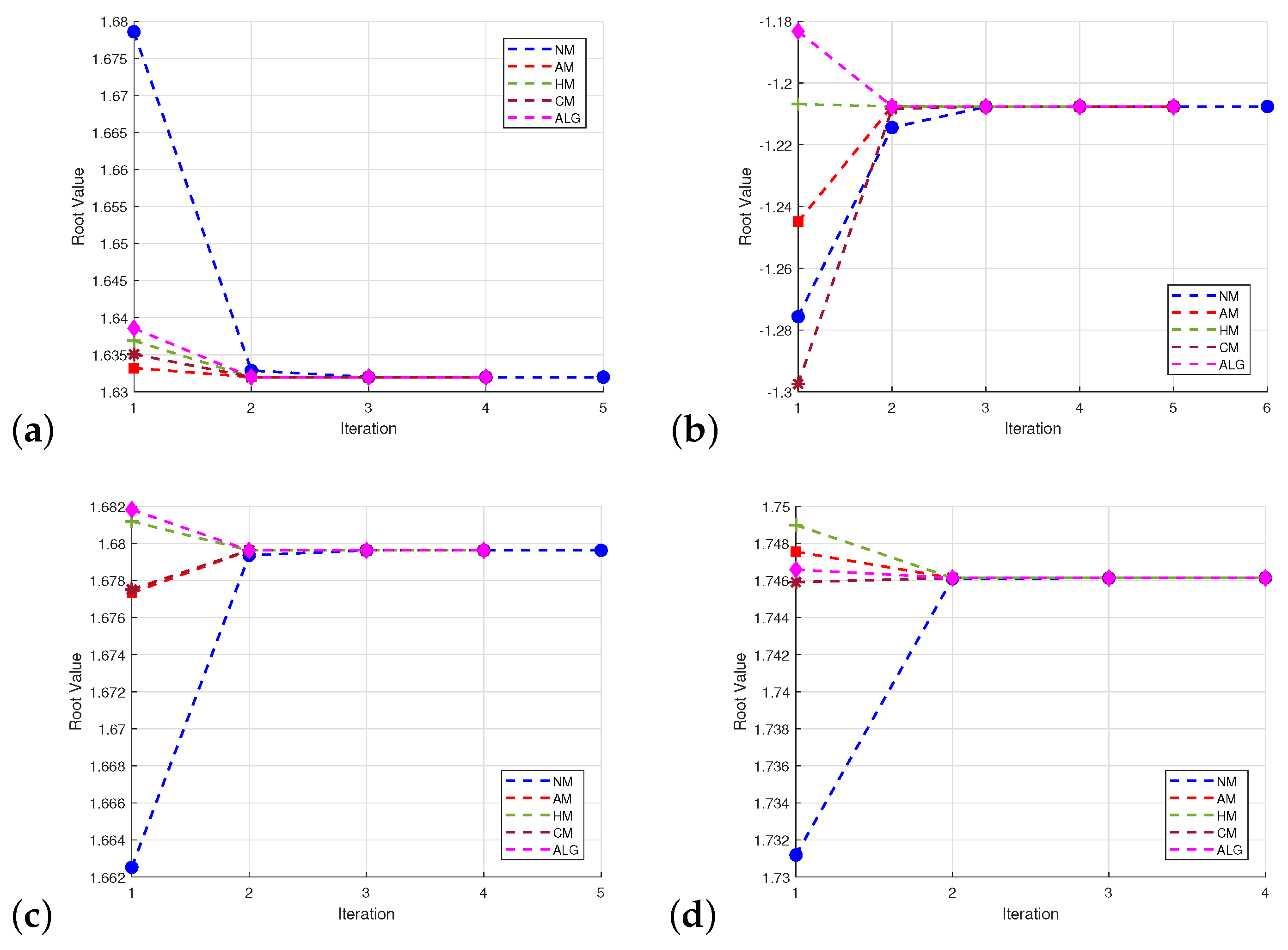
• Figure 6a describe the comparative study of our proposed Algorithm with classical schemes with respect to number of iterations and root values for $\varphi \left(\gamma \right)={\gamma }^3+4{\gamma }^2-15$.
  

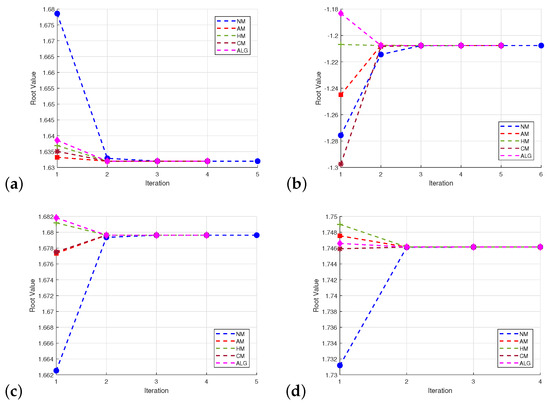  Figure 6. Graphical visuals of nonlinear equations.
• Figure 6b describe the comparative study of our proposed Algorithm with classical schemes with respect to number of iterations and root values for $\varphi \left(\gamma \right)=x{e}^{{\gamma }^2}-{sin}^2\gamma +3cos\gamma +5$.
• Figure 6c describe the comparative study of our proposed Algorithm with classical schemes with respect to number of iterations and root values for $\varphi \left(\gamma \right)=10\gamma e^{-{\gamma }^2}-1$.
• Figure 6d describe the comparative study of our proposed Algorithm with classical schemes with respect to number of iterations and root values for $\varphi \left(\gamma \right)=e^{-\gamma }+cos\gamma$.

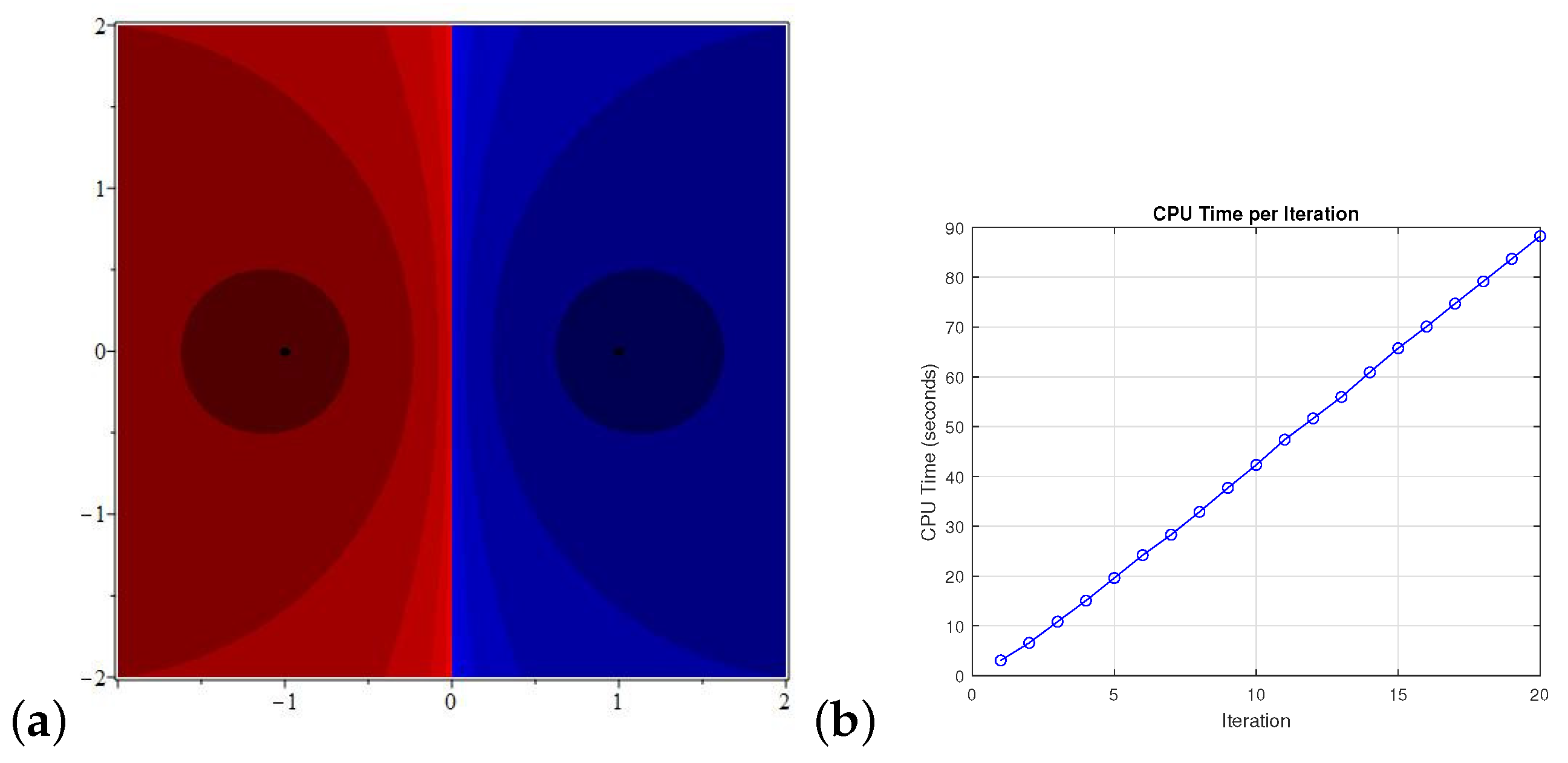
4.6. Basin of Attraction

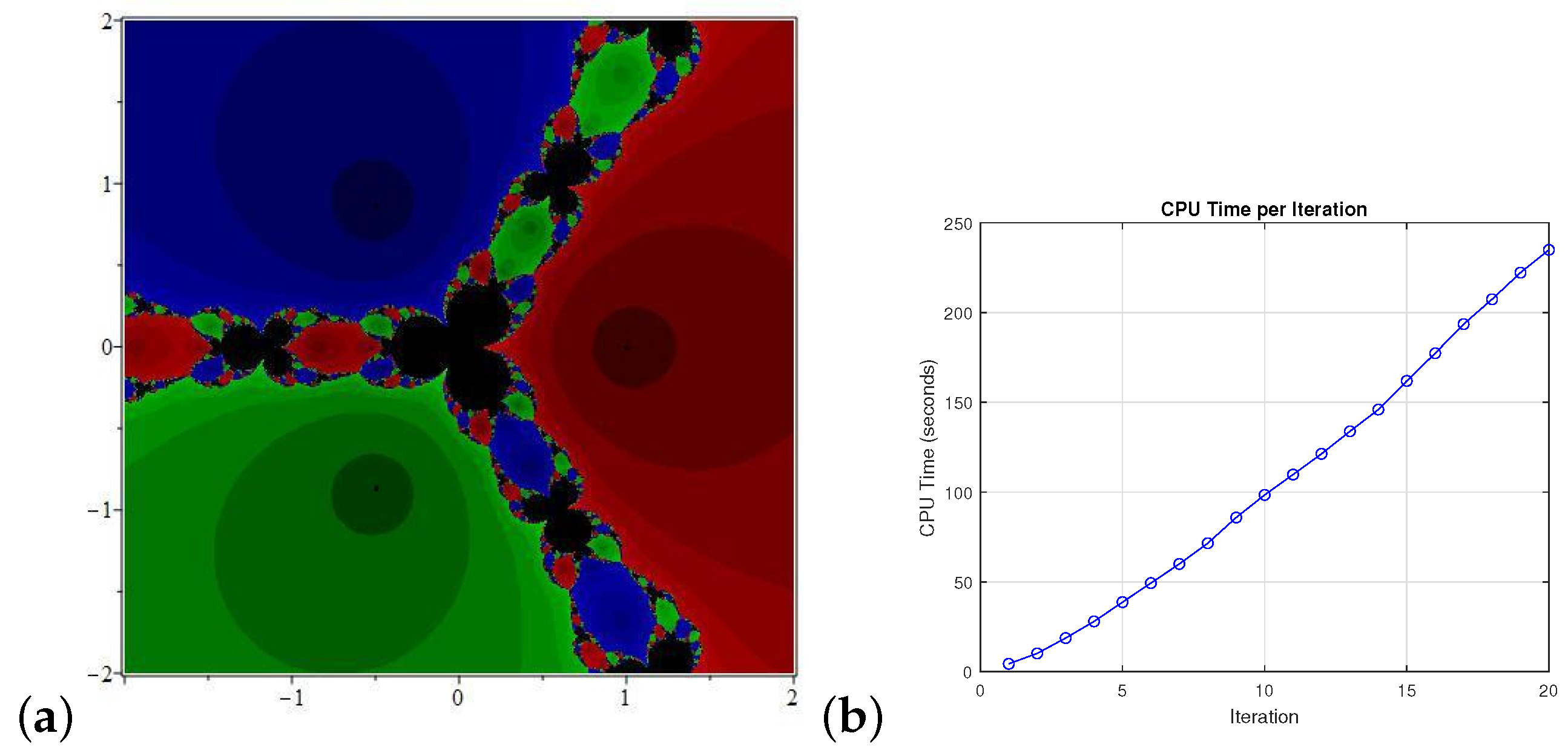
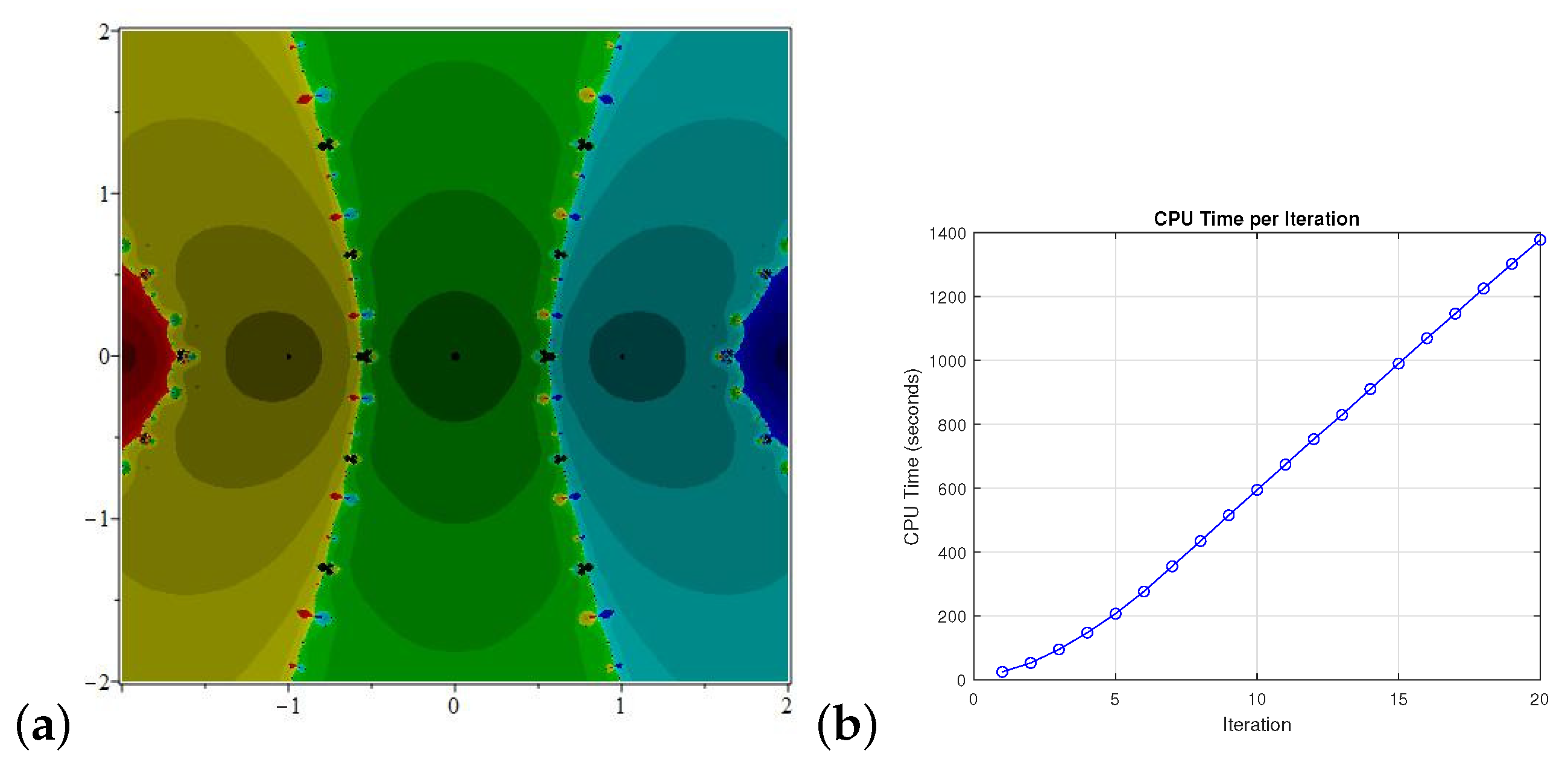
Here, we briefly describe Equation (4) through the basin of attraction and some illustrations corresponding to CPU time to generate the basin of attractions (Figure 7, Figure 8 and Figure 9). We deploy our proposed Algorithm on $[-2,2]\times [-2,2]$ with a $500\times 500$ points grid by fixing the tolerance $\left|\mathcal{S}\right({\gamma }_n\left)\right|<1\times {10}^{-10}$, and the maximum number of iterations is 20. For this purpose, we consider the extensively known problem $\mathcal{S}\left(\gamma \right)={\gamma }^n-1,n\in \mathbb{N}$. We take only $n=2,3$.

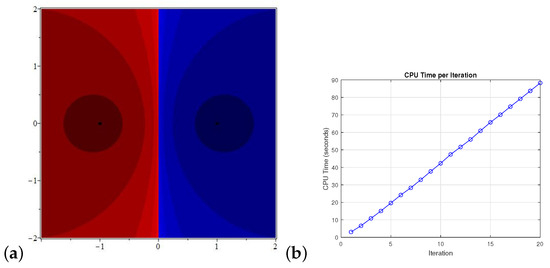
Figure 7. (a) is the basin of attraction for ${\gamma }^2-1$ and (b) illustrates the CPU time to produce the basin of attraction.

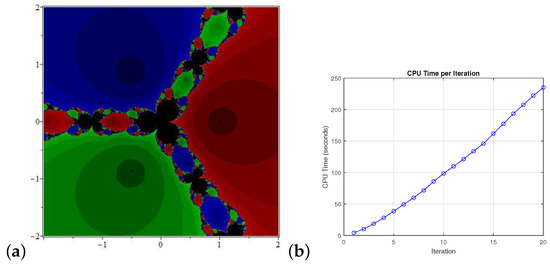
Figure 8. (a) is the basin of attraction for ${\gamma }^3-1$ and (b) illustrates the CPU time to produce the basin of attraction.

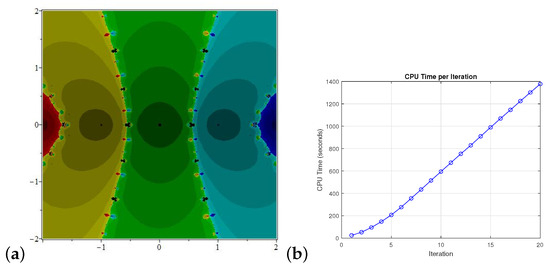
Figure 9. (a) is the basin of attraction for ${\gamma }^5-5{\gamma }^3+4\gamma$ and (b) illustrates the CPU time to produce the basin of attraction.

5. Conclusions

In recent years, multiple approaches such as fractional calculus, quantum calculus, different generalizations of convexity, and majorization theory have been deployed to establish the error inequalities of numerical quadrature schemes. In this article, we have derived the parametric integral inequalities via convex functions. The benefit of our study is that we can generate a blend of integral inequalities by choosing the different values of $\xi$ and $\gamma$. It is evident that our results reduce to Ostrowski’s, midpoint, trapezoidal, Simpson’s, Newton’s, Bullen’s, and other two-point open integral inequalities for certain values of parameters. To ensure the correctness of our findings, we have presented various graphical visuals. Furthermore, to enhance the significance of results, we have reported an abundant amount of applications to linear combinations of means, composite quadrature formulas, modified Bessel functions, and novel parametric iterative schemes having cubic order of convergence. Also, we have investigated the iterative scheme through physical examples. Most importantly, the results obtained in this article are beneficial to compute the bounds of several other special functions, such as gamma function, beta function, and hypergeometric functions. In the future, we will try to extend the idea for non-convex functions, quantum and symmetric calculus, fractional calculus, and fuzzy valued functions as well. By employing a similar procedure, we investigate two-dimensional unified inequalities and their applications. One of the important research questions is to unify Milne’s and Maclaurin’s and correct Euler-type inequalities by developing a new identity. We hope this will be an effective contribution to the literature and will pave a new way of thinking.