Fox’s H-Functions: A Gentle Introduction to Astrophysical Thermonuclear Functions
Abstract
1. Fox’s -Functions
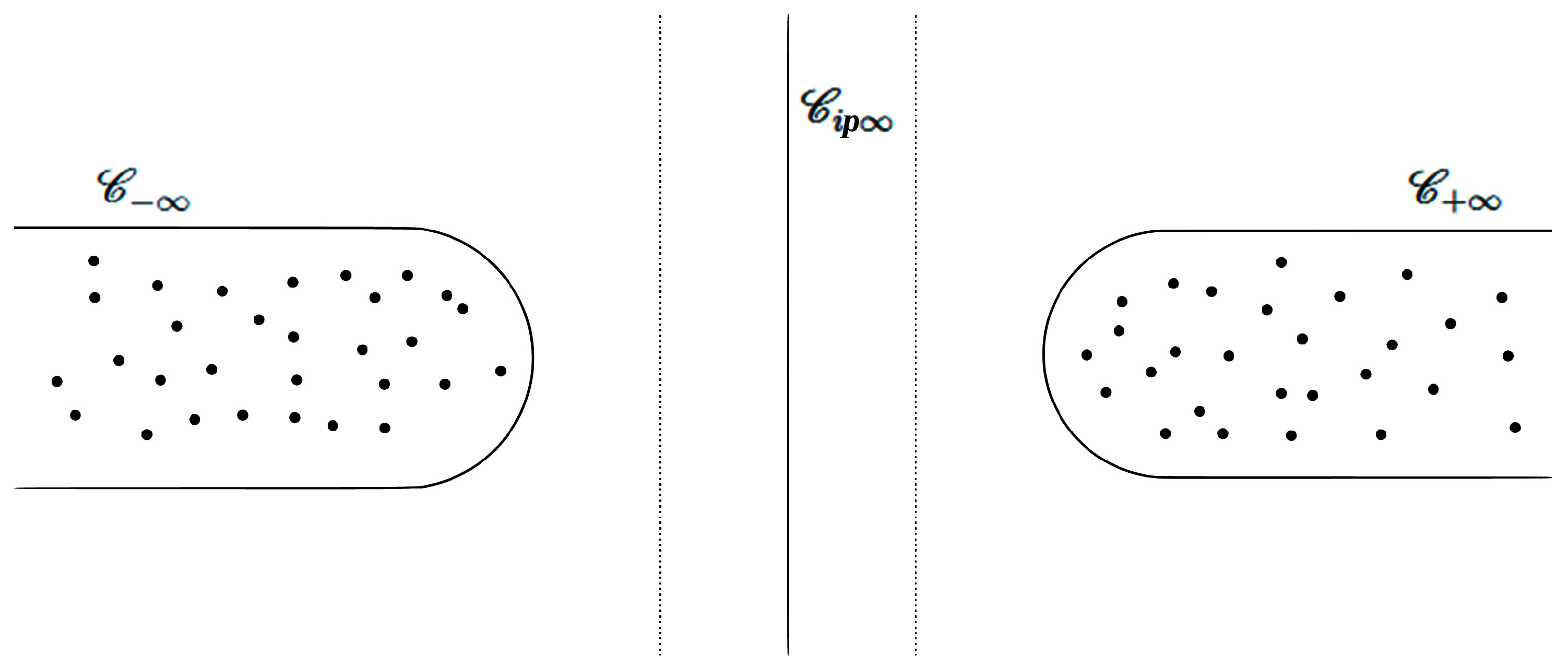
2. Thermonuclear Reactions
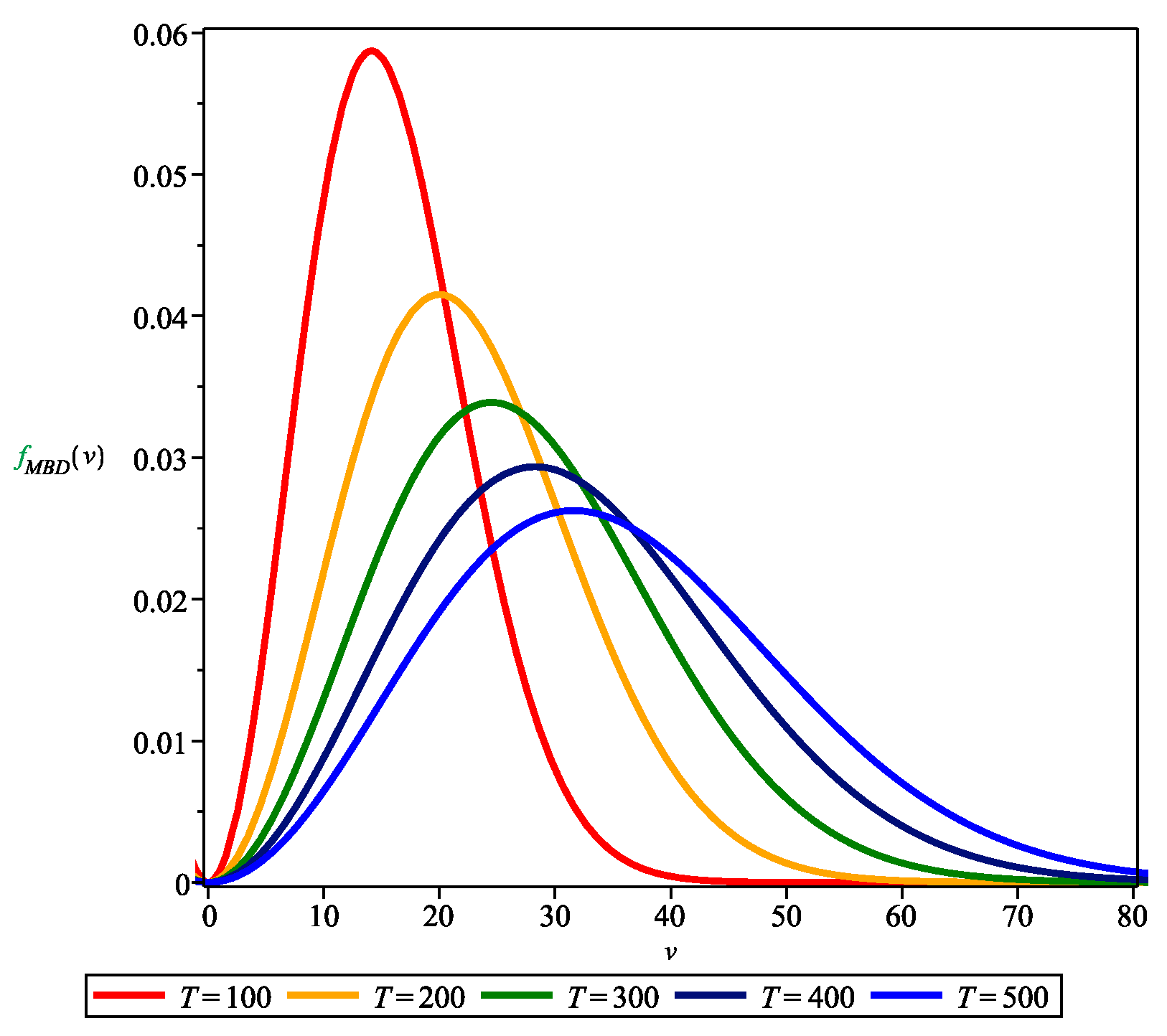
3. Maxwell–Boltzmann Case
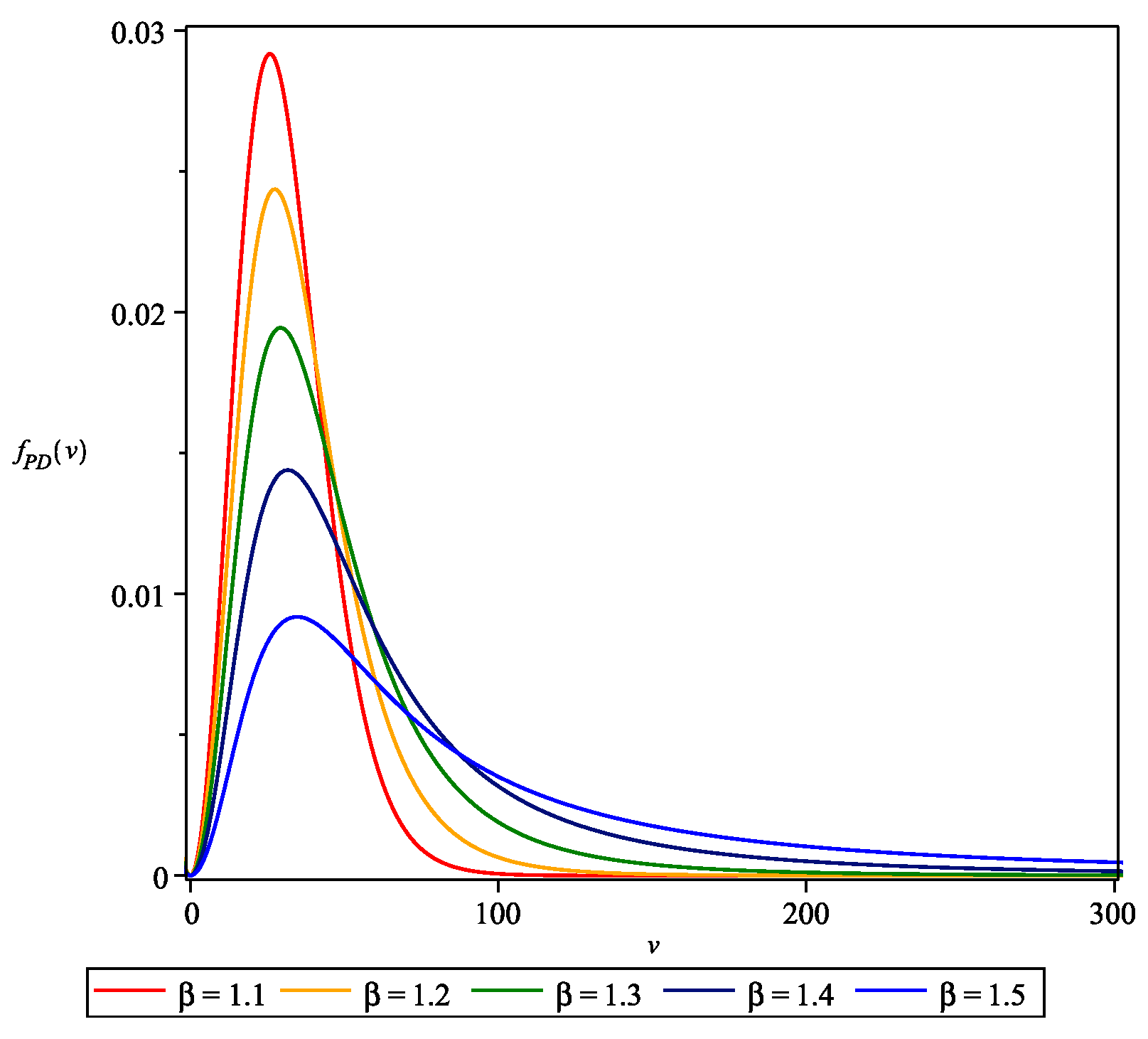
4. Pathway Case
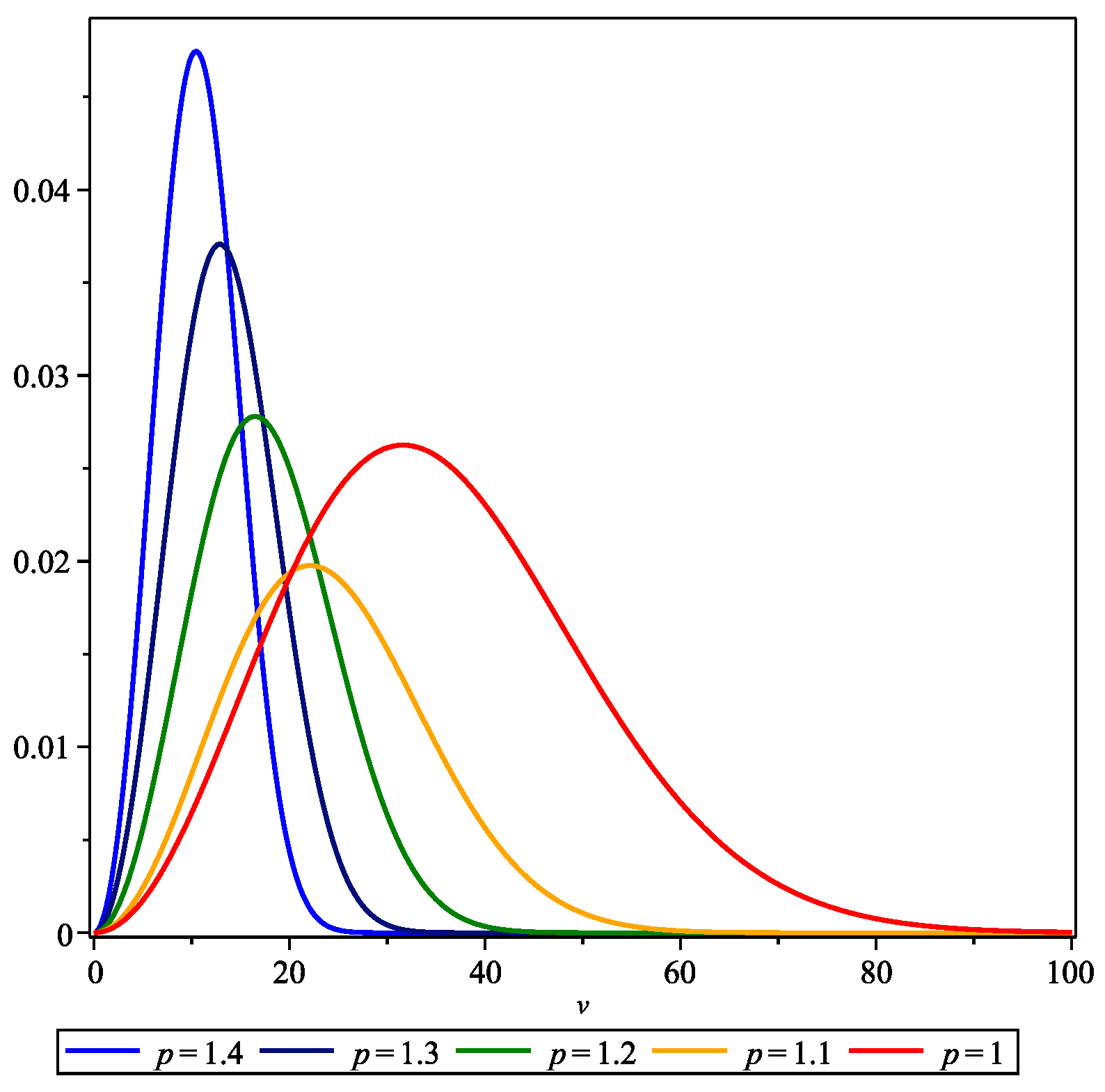
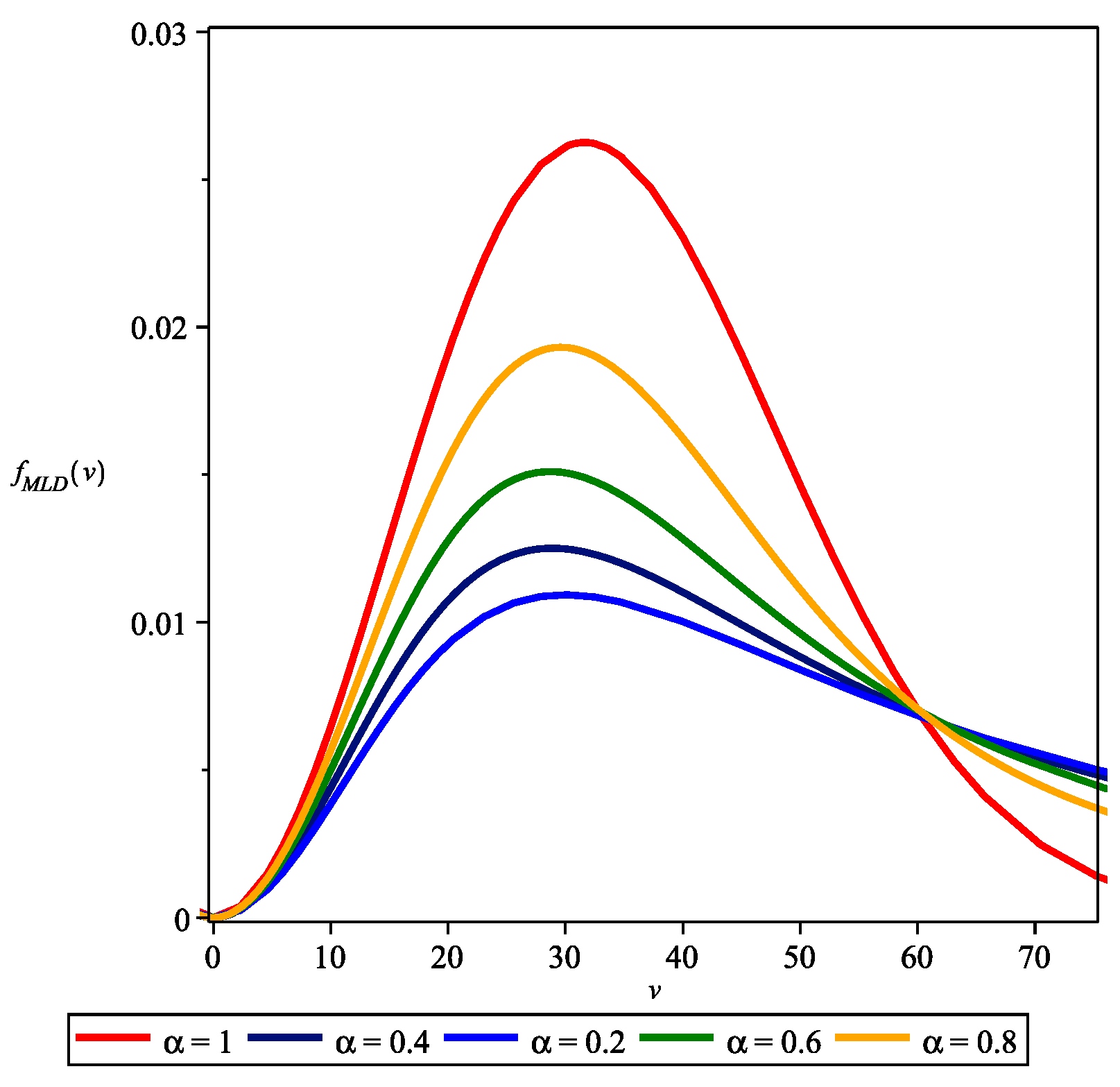
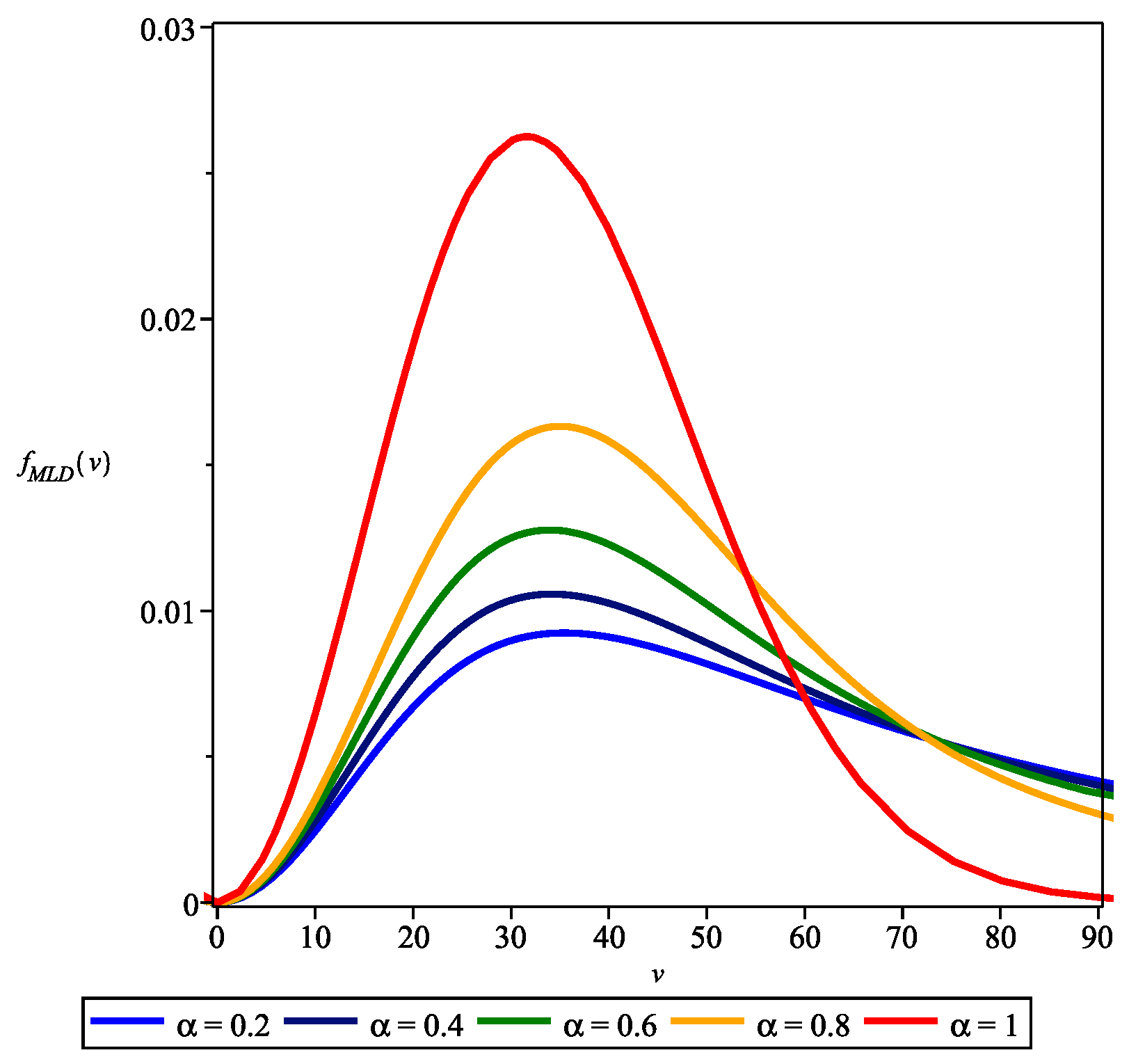
5. Mittag-Leffler Case
6. Interpretations and Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Meijer, C. Über Whittakersche bezw. Besselsche Funktionen und deren Produkten. Nieuw Arch. Wisk. 1936, 18, 10–39. [Google Scholar]
- Fox, C. The G and H-functions as symmetrical Fourier kernels. Trans. Am. Math. Soc. 1961, 98, 395–429. [Google Scholar]
- Mathai, A.M.; Saxena, R.K.; Haubold, H.J. The H-Function: Theory and Applications; Springer: New York, NY, USA, 2010. [Google Scholar]
- Kilbas, A.A.; Saigo, M. On the H-function. J. Appl. Math. Stoch. Anal. 1999, 12, 191–204. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Saigo, M. H-Transforms: Theory and Application; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Prudnikov, A.P.; Brychkov, Y.A.; Marichev, O.I. Integrals and Series; Gordon and Breach: New York, NY, USA, 1990; Volume 3. [Google Scholar]
- Buschman, R.G. H-function of two variables. Indian J. Math. 1978, 20, 105–116. [Google Scholar]
- Inayat-Hussain, A.A. New properties of hypergeometric series derivable from Feynman integrals: II. A generalization of the H-function. J. Phys. A Math. Gen. 1987, 20, 4119–4128. [Google Scholar] [CrossRef]
- Saxena, R.K.; Pogány, T.K. On fractional integration formulae for Aleph functions. Appl. Math. Comput. 2011, 218, 985–990. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Saxena, R.K.; Parmar, R.K. Some Families of the Incomplete H-Functions and the Incomplete -Functions and Associated Integral Transforms and Operators of Fractional Calculus with Applications. Russ. J. Math. Phys. 2018, 25, 116–138. [Google Scholar] [CrossRef]
- Shen, Y.P.; Guo, B.; Liu, W.P. Alpha-cluster transfer reactions: A tool for understanding stellar helium burning. Prog. Part. Nucl. Phys. 2021, 119, 103857. [Google Scholar] [CrossRef]
- Haubold, H.J.; Kumar, D. Extension of thermonuclear functions through the pathway model including Maxwell-Boltzmann and Tsallis’ distributions. Astropart. Phys. 2008, 29, 70–76. [Google Scholar] [CrossRef]
- Haubold, H.J.; Kabeer, A.A.; Kumar, D. Analytic forms of thermonuclear functions. Physica A 2023, 630, 129249. [Google Scholar] [CrossRef]
- Mathai, A.M. A pathway to matrix-variate gamma and normal densities. Linear Algebra Its Appl. 2005, 396, 317–328. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann–Gibbs statistics. J. Stat. Phys. 1998, 52, 479–487. [Google Scholar] [CrossRef]
- Agahi, H.; Alipour, M. Mittag-Leffler-Gaussian distribution: Theory and application to real data. Math. Comput. Simul. 2019, 156, 227–235. [Google Scholar] [CrossRef]
- Gorenflo, R.; Kilbas, A.A.; Mainardi, F.; Rogosin, S.V. Mittag-Leffler Functions, Related Topics and Applications, 2nd ed.; Springer Monographs in Mathematics; Springer: Berlin, Germany, 2020. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haubold, H.J.; Kumar, D.; Kabeer, A.A. Fox’s H-Functions: A Gentle Introduction to Astrophysical Thermonuclear Functions. Axioms 2024, 13, 532. https://doi.org/10.3390/axioms13080532
Haubold HJ, Kumar D, Kabeer AA. Fox’s H-Functions: A Gentle Introduction to Astrophysical Thermonuclear Functions. Axioms. 2024; 13(8):532. https://doi.org/10.3390/axioms13080532
Chicago/Turabian StyleHaubold, Hans J., Dilip Kumar, and Ashik A. Kabeer. 2024. "Fox’s H-Functions: A Gentle Introduction to Astrophysical Thermonuclear Functions" Axioms 13, no. 8: 532. https://doi.org/10.3390/axioms13080532
APA StyleHaubold, H. J., Kumar, D., & Kabeer, A. A. (2024). Fox’s H-Functions: A Gentle Introduction to Astrophysical Thermonuclear Functions. Axioms, 13(8), 532. https://doi.org/10.3390/axioms13080532






