Quasi-Configurations Derived by Special Arrangements of Lines

Abstract

A quasi-configuration is a point–line incidence structure in which each point is incident with at least three lines and each line is incident with at least three points. We investigate derived quasi-configurations that arise both by duality and intersecting lines of three special arrangements of lines. Sets with few intersection numbers are provided.

1. Introduction

In finite geometry, the concepts of points and lines are translated from the continuous to the discrete world. A natural way to make this explicit is by starting with a geometry over the complex field ℂ and replacing the field ℂ by a finite field, 𝔽_q, of order q, where q is a power of a prime number, thus obtaining a discrete object. The axiomatic approach to geometry contributes to this point of view, allowing geometries consisting only of a finite number of objects that have many applications in coding theory, data storage, or cryptography. Recall that a point–line incidence structure is a triple (P,L,I), where P is a set of points and L is a set of lines, together with a point–line incidence relation I ⊆ P × L, where two points of P can be incident with at most one line of L, and two lines of L can be incident with at most one point of P. Throughout the paper, we only consider connected incidence structures, where any two elements of P∪L are connected via a path of incident elements.

One of the main problems in the theory of point–line incidence structures is to clarify the existence of regular ones, i.e., in which any line contains the same number of points, and any point is contained in the same number of lines. A (v_r,b_k)-configuration is a point–line incidence structure (P,L) where the size of P is v, the size of L is b, each point of P is contained in r lines of L and each line of L contains k points of P. In such a configuration, we have that vr = bk. If the number of points is equal to the number of lines, we call it a symmetric (n_k) configuration.

A point–line incidence structure (P,L,I) is said to be a quasi-configuration of type $\left(\left(p_{r_1}^1\right)\left(p_{r_2}^2\right)\dots \left(p_{r_{m\left(P\right)}}^{m\left(P\right)}\right),\left(n_{k_1}^1\right)\left(n_{k_2}^2\right)\dots \left(n_{k_{m\left(L\right)}}^{m\left(L\right)}\right)\right)$ if P is a disjoint union of subsets P_i of cardinality pⁱ with i = 1, 2, …, m(P), and L is a disjoint union of subsets L_j of cardinality n_j with j = 1, 2, …, m(L), such that each point in P_i is incident with r_i lines, and each line in L_j is incident with k_j points. Quasi-configurations were introduced in [1] and used as building blocks for larger point–line incidence structures, see also [2]. Note that a quasi-configuration with m(P) = m(L) = 1 is a configuration, and if all the parameters are the same for points and lines we say that it is a symmetric quasi-configuration of type $\left(\left(n_{k_1}^1\right)\left(n_{k_2}^2\right)\dots \left(n_{k_{m\left(L\right)}}^{m\left(L\right)}\right)\right)$. Let 𝔽 denote a field and consider the projective plane ℙ² over 𝔽. Let d ≥ 3 be an integer. An arrangement of d lines A is a set of d lines {L₁, L₂, …, L_d} in ℙ², such that $\bigcap _{i=1}^d{L}_i=\varnothing$. For i ≥ 2, an i-point is a point in A which belongs to exact i lines in A. We denote the number of i-points by t_i. In characteristic zero, apart from pencil of three or more lines, only three types of complex line arrangements with t₂ = 0 are currently known: Ceva, Klein, and Wiman arrangements.

2. Materials and Methods

A finite projective plane is a symmetric configuration, such that two points are contained in exactly one line, two lines meet in exactly one point, and there are four points, three by three not collinear. Finite projective planes are constructed using homogeneous coordinates with entries from a finite field 𝔽_q. There are also planes not derived from finite fields, but they are beyond the scope of this research. We will study quasi-configurations which arise both by duality and intersecting lines of these special arrangements of lines, by replacing the field of complex numbers ℂ by the smallest finite field 𝔽_q containing them. The idea is that if an arrangement of lines is special, then its derived quasi-configuration is also special. A k-set K in a finite projective plane is a set of k points. A k-set K is said to be symmetric if the number v_i(P) of i-secant lines, through a point P of K is the same for any point P. A k-set K is said to be a blocking set if K meets every line. It is minimal if it properly contains no blocking sets. A k-set K is said to be of type (m₁, m₂, …, m_s) if any line has exactly m points in common with K with m∈{m₁, m₂, …, m_s} and every value occurs. The integers m₁, m₂, …, m_s are called intersection numbers. Sets with few intersection numbers define projective linear codes with few weights that are useful in authentication codes, secret sharing schemes, and data storage systems. The paper falls into three sections. In the first, we will prove that, in characteristic 2, the Ceva (3) configuration closes, from the incidence point of view, in a projective plane of order four, and this, to our knowledge, seems to be novel. In the second section, we will show that, in characteristic 7, the Klein quasi-configuration is the set of the internal points of a conic of PG (2,7). Unfortunately, this representation is well known, see [3] (p. 7511), [4] (p. 342), and [5] (p. 121), but we provide direct proof arising from the Singer construction of the quasi-configuration. In the third section, we will prove that, in PG (2,19), the Wiman configuration gives rise to a symmetric minimal blocking 45-set of type (1,3,4,5), which, to our knowledge, seems to be novel.

3. Ceva Arrangements of Lines

Ceva(n) arrangements of lines are defined by the set of zeros of linear factor of the polynomial (xⁿ − yⁿ)(xⁿ − zⁿ)(yⁿ − zⁿ), see [6]. This polynomial splits over a field 𝔽 containing a primitive root $\omega$ of unity of degree n, into the linear factors x − ω^ky, x − ω^kz, y − ω^kz, k = 0, 1, …, n − 1. Since dual Ceva (1) is a set of three collinear points and dual Ceva (2) is a complete quadrangle, suppose that the characteristic of the field 𝔽 is not three, and consider Ceva (3). The arrangement consists of the nine lines: x − y = 0, x − ωy = 0, x − ω²y = 0, x − z = 0, x − ω²z = 0, x − ωz = 0, y − z = 0, y − ωz = 0, y − ω²z = 0. Dually, we get a set of nine points:

A: = (0,1,−1), B: = (0,1,−ω), C: = (0,1,−ω²);
P: = (1,0,−1), Q: = (1,0,−ω²), R: = (1,0,−ω);
X: = (1,−1,0), Y: = (1,−ω,0), Z: = (1,−ω²,0).

A direct check shows that the nine points of the above point matrix are contained in the twelve lines, three by three, that are rows, columns, and determinantal products. Thus, we get the matrix of the twelve lines:

ABC: x = 0, PQR: y = 0, XYZ: z = 0;
APX: x + y + z = 0, BQY: x + ω²y + ωz = 0, CRZ: x + ωy + ω²z = 0;
AQZ: x + ωy + ωz = 0, BRX: x + y + ω²z = 0, CPY: x + ω²y + z = 0;
CQX: x + y + ωz = 0, ARY: x + ω²y + ω²z = 0, BPZ: x + ωy + z = 0;

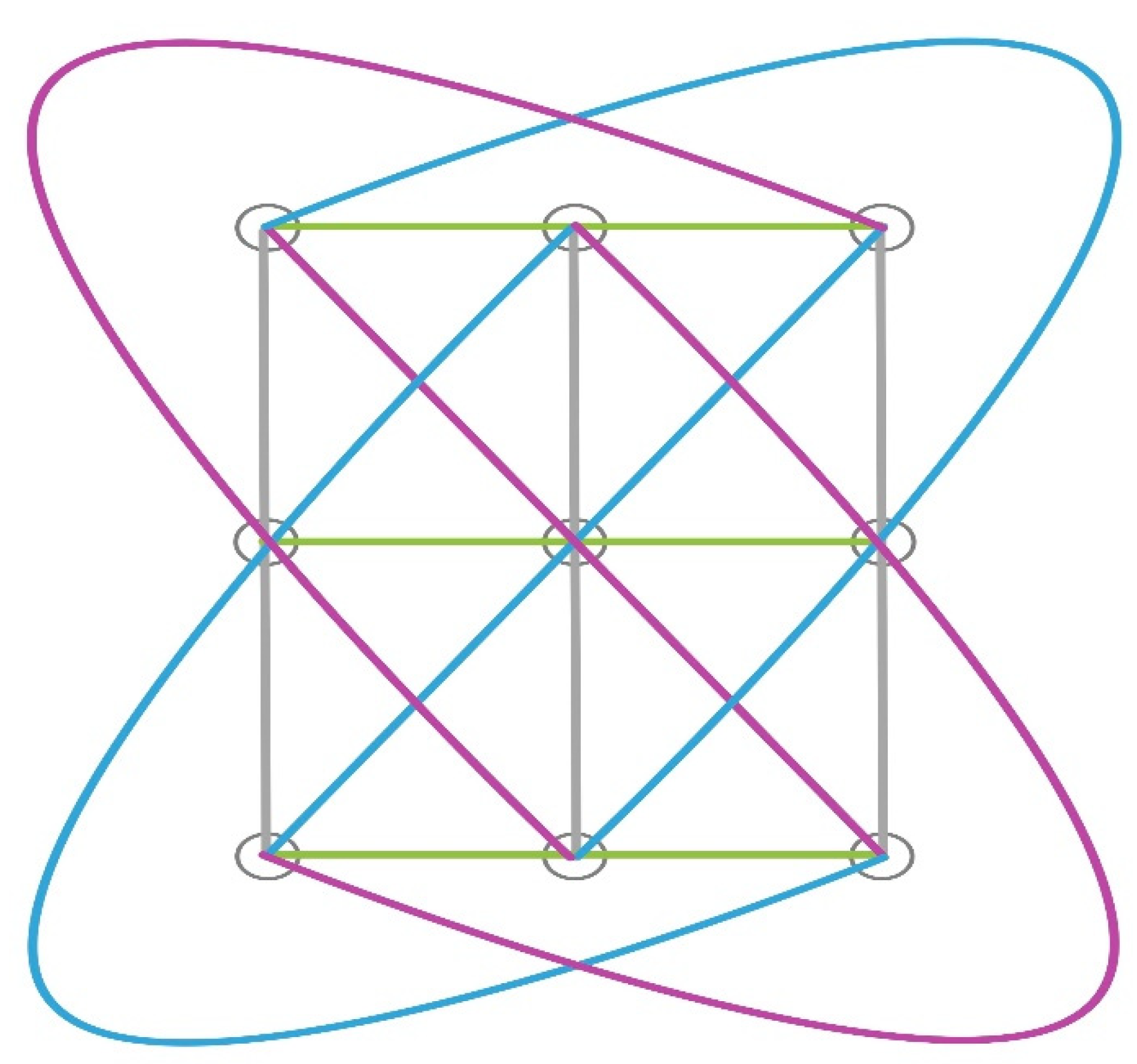
i.e., the Hesse (9₄,12₃) configuration as in Figure 1.

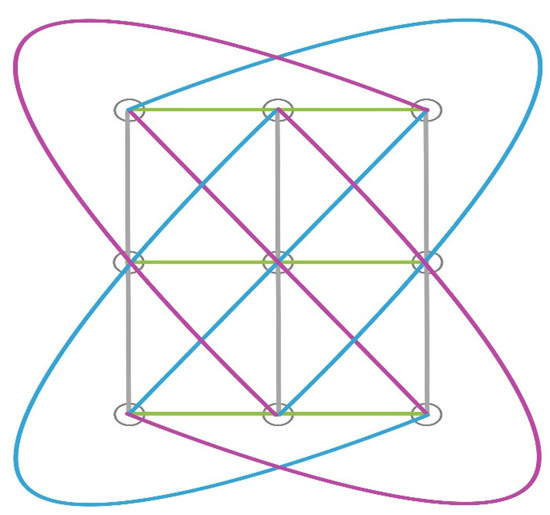
Figure 1. The Hesse (9₄,12₃) configuration.

Since the characteristic of the field 𝔽 is not three, then each triple of parallel lines forms a different triangle, i.e., each row of the above line matrix is a triangle whose vertices are written in the rows of the matrix below:

D: = (0,0,1), E: = (1,0,0), F: = (0,1,0);
G: = (1,ω,ω²), H: = (1,ω²,ω), I: = (1,1,1);
L: = (1,ω,1), M: = (1,1,ω), N: = (1,ω²,ω²);
U: = (1,ω,ω), T: = (1,ω²,1), S: = (1,1,ω²).

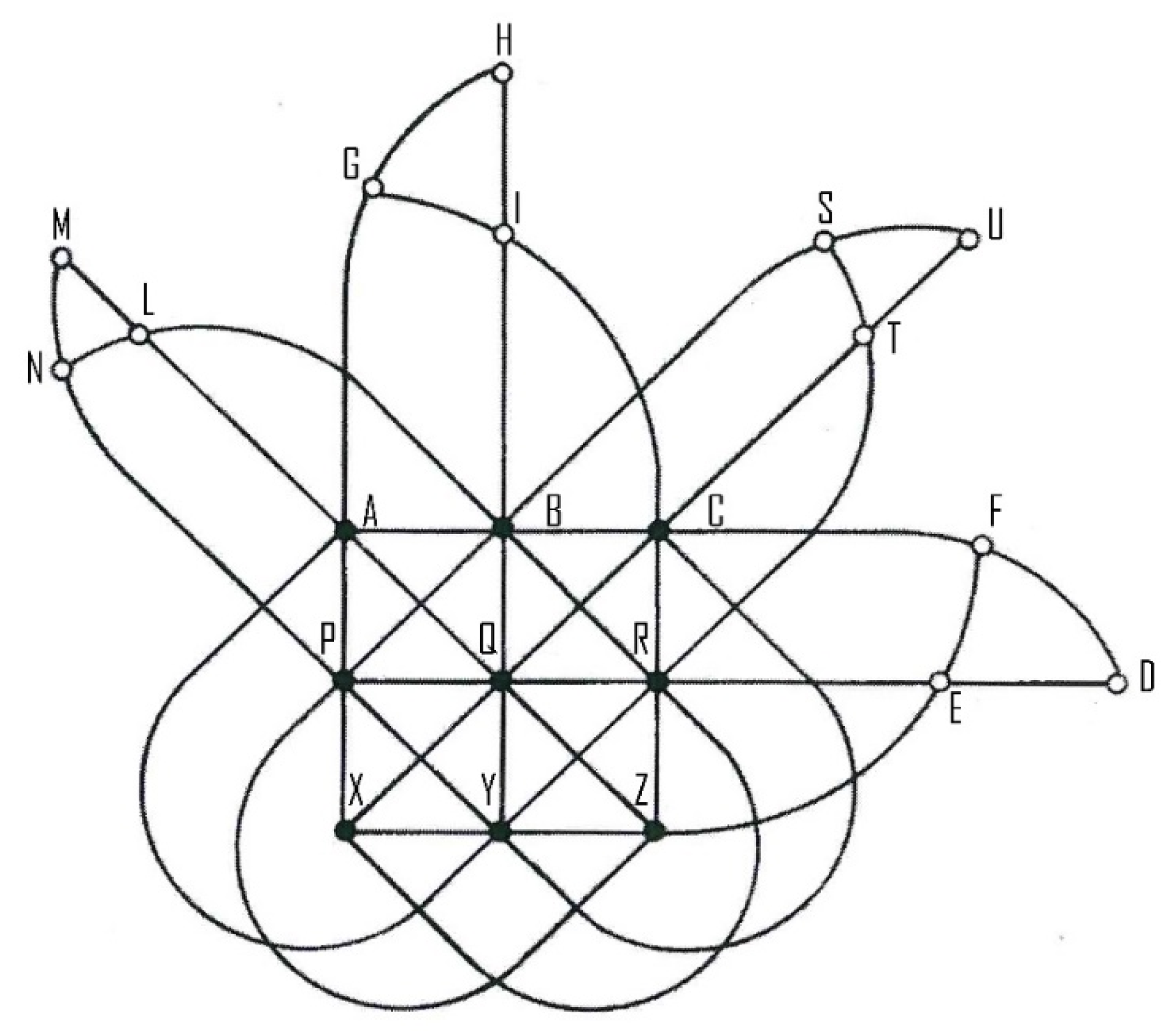
The points and their alignments are shown in Figure 2.

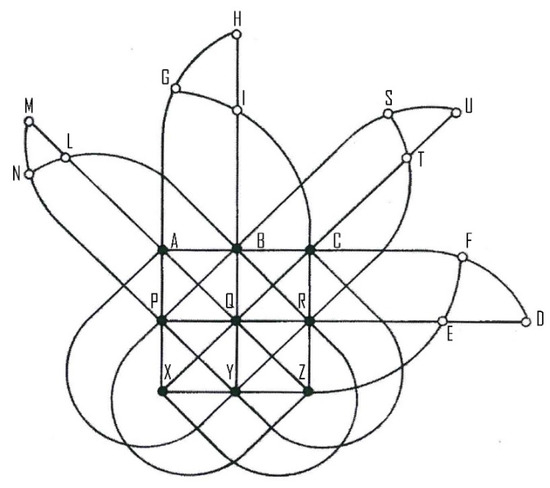
Figure 2. The Hesse (9₄,12₃) configuration with the 12 intersection points of the parallel lines.

A direct check shows that these twelve points are contained, four by four, in the nine lines of the Ceva arrangement:

DGLU: x − ω²y = 0, DIMS: x − y = 0, DHNT: x − ωy = 0;
EGMT: y − ω²z = 0, EHSL: y − ωz = 0, EINU: y − z = 0;
FGNS: x − z = 0, FHMU: x − ω²z = 0, FILT: x − ωz = 0.

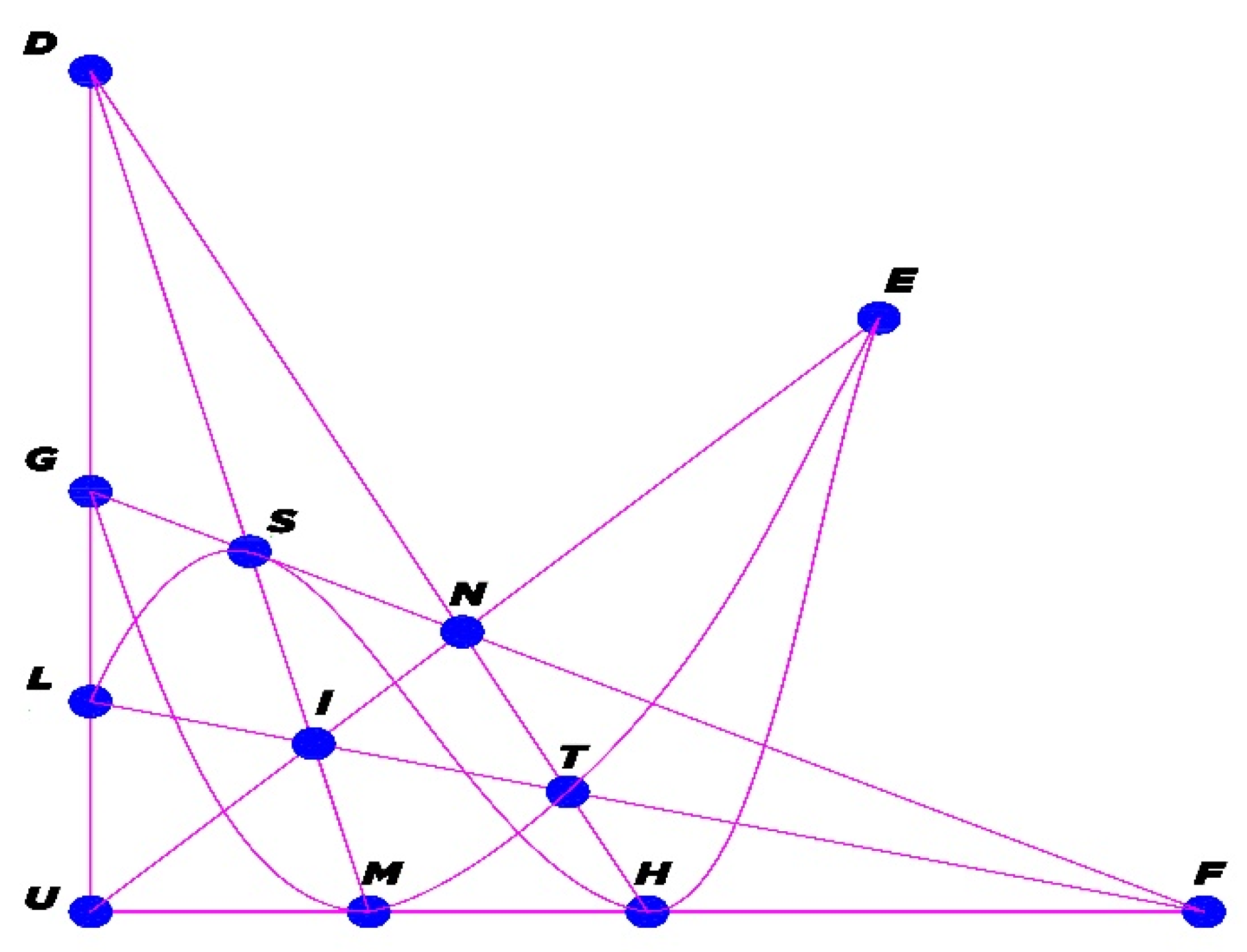
The 12 intersection points of the parallel lines and their alignments are shown in Figure 3.

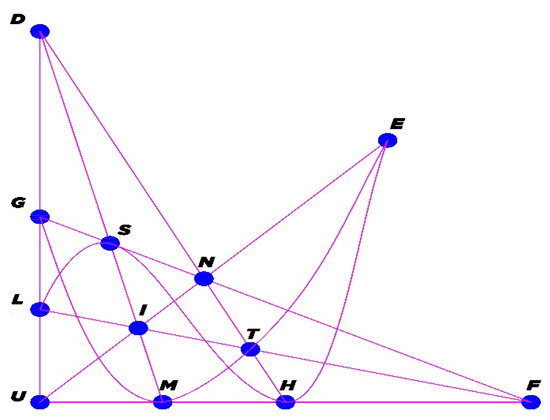
Figure 3. The 12 intersection points of the parallel lines are contained in the nine lines of the Ceva arrangement.

In a direct check, if the characteristic of the field 𝔽 is two, then we have that

X∈DIMS, Y∈DGLU, Z∈DHNT,
A∈EINU, B∈EGMT, C∈EHSL,
P∈FILT, Q∈FGNS, R∈FHMU,

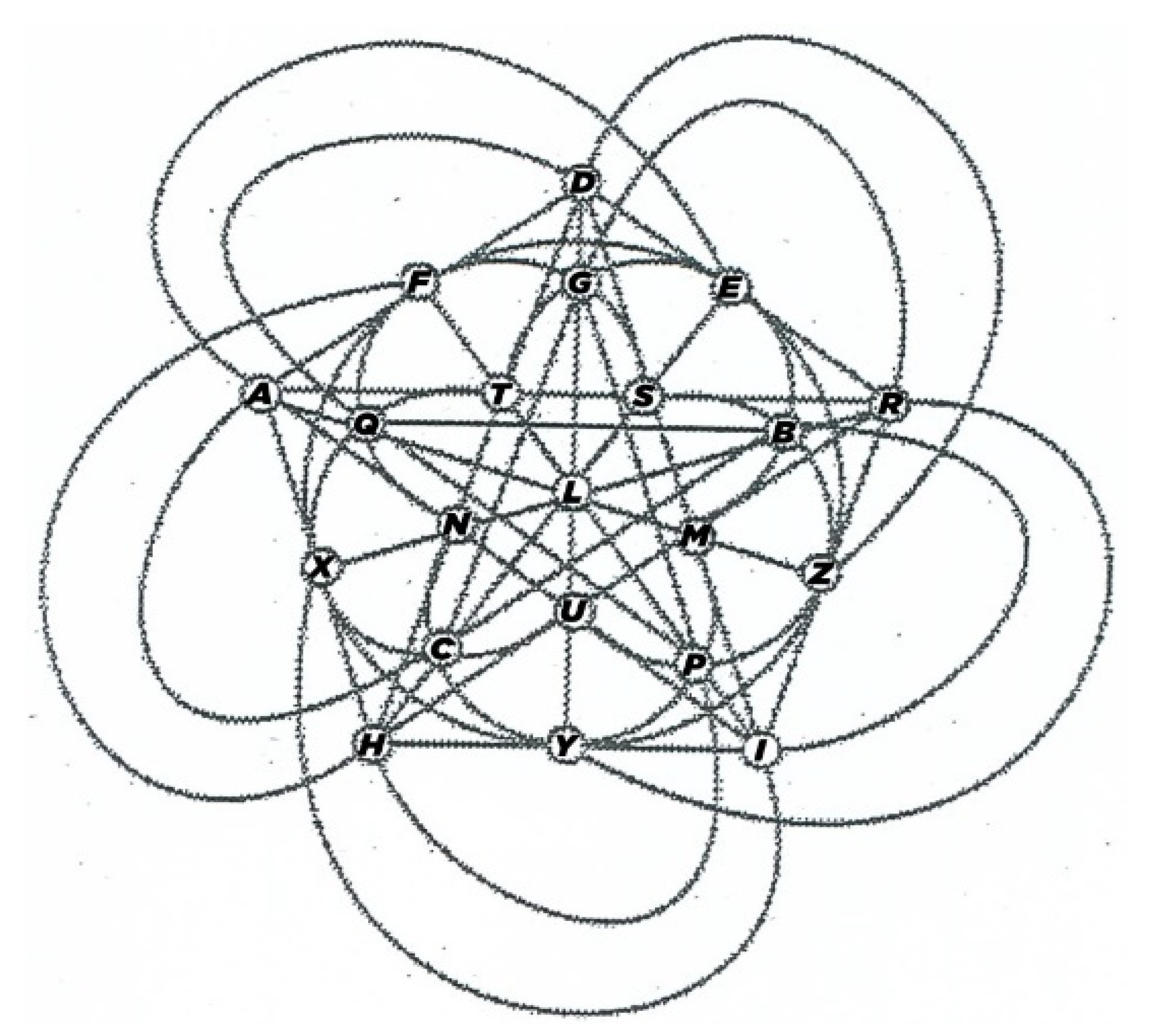
and we get a symmetric (21₅) configuration, i.e., a projective plane of order four, as shown in Figure 4.

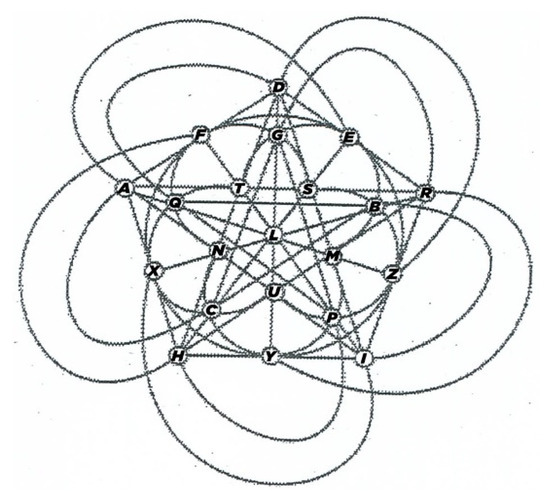
Figure 4. The projective plane of order four.

In a direct check, if the characteristic of the field 𝔽 is two, then the Ceva (3) configuration closes, from incidence point of view, in a projective plane of order four, and this, to our knowledge, seems to be novel.

If the characteristic of the field 𝔽 is not two, then we get either, without considering two lines, a symmetric $\left(\left(9_4^1\right)\left({12}_5^2\right)\right)$ quasi-configuration or a 21-set of type (0,1,2,4,5).

4. Klein Arrangement of Lines

The Klein arrangement of lines naturally arises from the subgroup PSL (2,7), the finite simple group of order 168, which is the automorphism group of the Klein quartic curve x³y + y³z + z³y = 0 of ℙ², see [7,8]. It contains 21 involutions, each leaving a line fixed. The arrangement of these 21 lines is called the Klein arrangement. Let 𝔽 be a field containing a root $\omega$ of x² + x + 2. The Klein arrangement consists of the 21 lines:

x = 0, y + z = 0, ωx + y − z = 0, ωx − y + z = 0, −y + z = 0, x + ωy − z = 0, ωx − y − z = 0,
−x + y + ωz = 0, ωx + y + z = 0, −x + ωy + z = 0, −x − y + ωz = 0, x + z = 0, −x + ωy − z = 0, x + ωy + z = 0,
−x + z = 0, x − y + ωz = 0, x + y + ωz = 0, z = 0, −x + y = 0, x + y = 0, y = 0.

Dually, we get a set of 21 points:

P₁: = (1,0,0), P₂: = (0,1,1), P₃: = (1,ω⁻¹,−ω⁻¹), P₄: = (1,−ω⁻¹,ω⁻¹), P₅: = (0,1,−1), P₆: = (1,ω,−1), P₇: = (1,−ω⁻¹,−ω⁻¹),
P₈: = (1,−1,−ω), P₉: = (1,ω⁻¹,ω⁻¹), P₁₀: = (1,−ω,−1), P₁₁: = (1,1,−ω), P₁₂: = (1,0,1), P₁₃: = (1,−ω,1), P₁₄: = (1,ω,1),
P₁₅: = (1,0,−1), P₁₆: = (1,−1,ω), P₁₇: = (1,1,ω), P₁₈: = (0,0,1), P₁₉: = (1,−1,0), P₂₀: = (1,1,0), P₂₁: = (0,1,0).

A direct check shows either that the 21 points of the above point matrix are contained four by four in the 21 lines,

P₂P₅P₁₈P₂₁ x = 0, P₁P₁₂P₁₅P₁₈ y = 0, P₁P₁₉P₂₀P₂₁ z = 0, P₁P₃P₄P₅ y + z = 0, P₁₂P₁₃P₁₄P₂₁ x − z = 0,
P₁₁P₁₇P₁₈P₂₀ x − y = 0, P₆P₁₀P₁₅P₂₁ x + z = 0, P₁P₂P₇P₉ y − z = 0, P₈P₁₆P₁₈P₁₉ x + y = 0,
P₃P₁₀P₁₁P₁₂ x − (ω + 1)y − z = 0, P₄P₁₄P₁₅P₁₆ x + (ω + 1)y + z = 0, P₉P₁₃P₁₅P₁₇ x − (ω + 1)y + z = 0,
P₇P₁₀P₁₆P₂₀ x − y + (ω + 1)z = 0, P₂P₄P₆P₁₁ (ω + 1)x − y + z = 0, P₅P₇P₁₁P₁₄ (ω + 1)x − y − z = 0,
P₅P₈ P₉P₁₀ (ω + 1)x + y + z = 0, P₃P₆P₁₇P₁₉ x + y + (ω + 1)z = 0, P₂P₃P₁₃P₁₆ (ω + 1)x + y − z = 0,
P₆P₇P₈P₁₂ x + (ω + 1)y − z = 0, P₄P₈P₁₃P₂₀ x − y − (ω + 1)z = 0, P₉P₁₁P₁₄P₁₉ x + y − (ω + 1)z = 0,

or that the 21 points of the above point matrix are contained three by three in the 28 lines,

P₁P₆P₁₃ y + ωz = 0, P₁P₁₀P₁₄ y − ωz = 0, P₆P₁₄P₁₈ ωx − y = 0, P₁P₈P₁₇ ωy − z = 0, P₂P₈P₁₄ (−ω + 1)x + y − z = 0,
P₃P₁₄P₂₀ x − y + (ω − 1)z = 0, P₃P₈P₁₅ x + (−ω + 1)y + z = 0, P₁₀P₁₃P₁₈ ωx + y = 0, P₃P₉P₁₈ x − ωy = 0,
P₆P₉P₂₀ x − y + (−ω + 1)z = 0, P₇P₁₃P₁₉ x + y + (ω − 1)z = 0, P₃P₇P₂₁ x + ωz = 0, P₄P₇P₁₈ x + ωy = 0, P₂P₁₅P₂₀ x − y + z = 0,
P₇P₁₁P₁₅ x + (ω − 1)y + z = 0, P₁P₁₁P₁₆ ωy + z = 0, P₅P₁₁P₁₃ (ω − 1)x + y + z = 0, P₈P₁₁P₂₁ ωx + z = 0, P₂P₁₂P₁₉ x + y − z = 0,
P₅P₁₅P₁₉ x + y + z = 0, P₄P₉P₂₁ x − ωz = 0, P₄P₁₀P₁₉ x + y + (−ω + 1)z = 0, P₂P₁₀P₁₇ (ω − 1)x + y − z = 0,
P₉P₁₂P₁₆ x + (−ω + 1)y − z = 0, P₄P₁₂P₁₇ x + (ω − 1)y − z = 0, P₅P₆P₁₆ (ω − 1)x − y − z = 0, P₅P₁₂P₂₀ x − y − z = 0,
P₁₆P₁₇P₂₁ ωx − z = 0.

Thus, we get a ((21₈),$\left({28}_3^1\right)\left({21}_4^2\right)$) quasi-configuration.

Since 7 is the smallest order, with characteristic different from 2, of a finite field, which contains a root of x² + x + 2, such that ℙ² contains at least 21 points, let us consider the field 𝔽₇. In 𝔽₇, 3 is a root of x² + x + 2. In order to write the cyclic structure of ℙ²: = PG (2,7), let ω be a primitive element of 𝔽₇³ over 𝔽₇ and let $f\left(x\right)=a_0+a_{1}x+a_2{x}^2+x^3$ be its minimal polynomial over 𝔽₇. The companion matrix $C\left(f\right)$ of f is given by $C\left(f\right)=\left(\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ {-a}_0& {-a}_1& {-a}_2\end{array}\right)$ and it induces a Singer cycle γ of PG(2,7), cf. [9]. Let us consider a primitive polynomial with minimal weight, i.e., the minimal number of non-zero coefficients, among all primitives of that degree over 𝔽₇, f(x) = x³ + 3x + 2, cf. [10]. The companion matrix C(f) is $\left(\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 5& 4& 0\end{array}\right)$. Let us consider the point ${\omega }^0=\left(\begin{array}{c}{x}_0\\ x_1\\ x_2\end{array}\right)=\left(\begin{array}{c}1\\ 0\\ 0\end{array}\right)$. We get:

$$\begin{gathered} {\omega }^2=C(f{)}^2{\omega }^0=C(f){\omega }^1=\left(\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 5& 4& 0\end{array}\right)\left(\begin{array}{c}0\\ 0\\ 1\end{array}\right)=\left(\begin{array}{c}0\\ 1\\ 0\end{array}\right),{\omega }^3=C(f{)}^3{\omega }^0=C(f){\omega }^2=\left(\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 5& 4& 0\end{array}\right)\left(\begin{array}{c}0\\ 1\\ 0\end{array}\right)=\left(\begin{array}{c}1\\ 0\\ 4\end{array}\right), \\ {\omega }^4=C(f{)}^4{\omega }^0=C(f){\omega }^3=\left(\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 5& 4& 0\end{array}\right)\left(\begin{array}{c}1\\ 0\\ 4\end{array}\right)=\left(\begin{array}{c}0\\ 4\\ 5\end{array}\right)=4\left(\begin{array}{c}0\\ 1\\ 3\end{array}\right)=\left(\begin{array}{c}0\\ 1\\ 3\end{array}\right), \\ {\omega }^5=C(f{)}^4{\omega }^0=C(f){\omega }^4=\left(\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 5& 4& 0\end{array}\right)\left(\begin{array}{c}0\\ 1\\ 3\end{array}\right)=\left(\begin{array}{c}1\\ 3\\ 4\end{array}\right), \end{gathered}$$

by continuing in this way, we obtain the cyclic structure of PG (2,7) as shown in Table 1.

Table 1. The cyclic structure of the points of PG (2,7).

ω0 = (1,0,0)
ω1 = (0,0,1)	ω2 = (0,1,0)	ω3 = (1,0,4)	ω4 = (0,1,3)	ω5 = (1,3,4)	ω6 = (1,6,1)	ω7 = (1,6,6)	ω8 = (1,1,6)
ω9 = (1,6,2)	ω10 = (1,5,6)	ω11 = (1,4,5)	ω12 = (1,3,0)	ω13 = (1,0,1)	ω14 = (0,1,5)	ω15 = (1,5,4)	ω16 = (1,5,5)
ω17 = (1,1,5)	ω18 = (1,5,2)	ω19 = (1,6,5)	ω20 = (1,2,6)	ω21 = (1,3,3)	ω22 = (1,1,1)	ω23 = (1,1,2)	ω24 = (1,2,2)
ω25 = (1,1,3)	ω26 = (1,3,2)	ω27 = (1,3,1)	ω28 = (1,5,1)	ω29 = (1,3,5)	ω30 = (1,4,1)	ω31 = (1,2,0)	ω32 = (1,0,3)
ω33 = (0,1,4)	ω34 = (1,4,4)	ω35 = (1,1,0)	ω36 = (1,0,2)	ω37 = (0,1,6)	ω38 = (1,6,4)	ω39 = (1,3,6)	ω40 = (1,2,1)
ω41 = (1,4,3)	ω42 = (1,6,0)	ω43 = (1,0,6)	ω44 = (0,1,2)	ω45 = (1,2,4)	ω46 = (1,2,3)	ω47 = (1,5,3)	ω48 = (1,2,5)
ω49 = (1,6,3)	ω50 = (1,4,6)	ω51 = (1,5,0)	ω52 = (1,0,5)	ω53 = (0,1,1)	ω54 = (1,1,4)	ω55 = (1,4,2)	ω56 = (1,4,0)

Let us denote the points represented by ωⁱ simply by i. Thus, the Singer group is isomorphic to the additive group Z₅₇, the integers modulo 57. The sets of 21 points are:

P₁ = (1,0,0) = 0, P₂ = (0,1,1) = 53, P₃ = (1,5,2) = 18, P₄ = (1,2,5) = 48, P₅ = (0,1,6) = 37, P₆ = (1,3,6) = 39,
P₇ = (1,2,2) = 24, P₈ = (1,6,4) = 38, P₉ = (1,5,5) = 16, P₁₀ = (1,4,6) = 50, P₁₁ = (1,1,4) = 54, P₁₂ = (1,0,1) = 13,
P₁₃ = (1,4,1) = 30, P₁₄ = (1,3,1) = 27, P₁₅ = (1,0,6) = 43, P₁₆ = (1,6,3) = 49, P₁₇ = (1,1,3) = 25, P₁₈ = (0,0,1) = 1,
P₁₉ = (1,6,0) = 42, P₂₀ = (1,1,0) = 35, P₂₁ = (0,1,0) = 2,

Now, select any line, for example, we choose the line ℓ₀: = x₁ = 0, which contains the 8-set of points written in Table 2.

Table 2. The starting line.

ℓ0

0

1

3

13

32

36

43

52

The remaining lines of the plane are found by adding 1 to each point of the preceding line beginning with ℓ₀ and using addition modulo 57. For the convenience of the reader, we represent the projective plane of order 7 as a set of four orthogonal arrays of the affine plane of order 7, with the intersection point of the elements of each parallel class indicated to the right of the row array and at the bottom of the column array.

Let us color the points of the 21-set green and the others red.

{0,1,2,13,16,18,24,25,27,30,35,37,38,39,42,43,48,49,50,53,54},

{3,4,5,6,7,8,9,10,11,12,14,15,17,19,20,21,22,23,26,28,29,31,32,33,34,36,40,41,44,45,46,47,51,52,55,56}.

The alignments of the Singer representation, written in Table 3, show that the Klein ($\left({21}_7^1\right)$,$\left({28}_3^1\right)\left({21}_4^2\right)$) quasi-configuration embedded in PG (2,7) is a symmetric 21-set of type (0,3,4), which are, by the result in [11], the internal points of a conic, see also [12,13,14].

Table 3. The projective plane PG (2,7) in which the points of the 21-set are colored green and its complementary set colored red.

5	12	21	26	27	29	39	1	2	5	15	34	38	45	54	3
6	42	7	38	9	49	19		6	46	55	35	39	16	4
8	35	22	25	17	54	23		22	42	48	47	33	26	50
18	51	16	28	15	10	47		28	23	7	29	41	14	31
37	2	53	4	14	33	44		27	10	25	37	24	56	19
41	56	34	11	50	55	30		30	53	12	20	17	49	18
48	31	24	20	46	40	45		40	11	44	9	51	8	21
0								13
33	35	45	11	7	18	27	32	48	49	51	4	23	27	34	43
34	10	6	31	17	26	44		2	50	7	10	20	8	39
46	21	25	49	47	2	41		11	24	54	12	6	47	14
8	30	29	15	4	24	42		16	5	30	9	33	31	25
12	38	50	37	40	23	16		19	35	26	41	15	53	40
19	14	51	22	5	55	20		17	28	37	45	21	55	42
28	48	53	39	56	9	54		29	44	46	22	56	38	18
36								52

5. Wiman Arrangement of Lines

Let 𝔽 be a field containing a root of x⁴ – x² + 4 and sufficiently large such that the resulting 201 points are different. The Wiman arrangement of lines consists of 45 lines of ℙ², with 36 quintuple points, 45 quadruple points, and 120 triple points, see [3,15,16] for a detailed description of the group action giving rise to it.

Since 19 is the smallest order, with characteristic different from 2, of a finite field, such that ℙ² contains at least 201 points, let us consider the field 𝔽₁₉. In 𝔽₁₉, 3 is a root of x⁴ − x² + 4. The dual of the Wiman arrangement of lines consists of the 45 points, see [16]:

P₁: = (0,1,0), P₂: = (1,16,15), P₃: = (0,0,1), P₄: = (1,3,15), P₅: = (1,14,6), P₆: = (1,5,6), P₇: = (1,9,5), P₈: = (1,10,5),
P₉: = (1,3,4), P₁₀: = (1,14,13), P₁₁: = (1,5,4), P₁₂: = (1,12,18), P₁₃: = (1,9,14), P₁₄: = (1,15,2), P₁₅: = (1,15,17),
P₁₆: = (1,16,4), P₁₇: = (1,5,13), P₁₈: = (1,14,4), P₁₉: = (1,7,18), P₂₀: = (1,10,14), P₂₁: = (1,4,2), P₂₂: = (1,4,17),
P₂₃: = (1,1,12), P₂₄: = (1,14,15), P₂₅: = (1,5,15), P₂₆: = (1,12,1), P₂₇: = (1,11,0), P₂₈: = (1,8,8), P₂₉: = (1,7,1),
P₃₀: = (1,10,17), P₃₁: = (1,18,12), P₃₂: = (1,8,0), P₃₃: = (1,11,8), P₃₄: = (1,9,17), P₃₅: = (1,0,7), P₃₆: = (1,0,0),
P₃₇: = (1,10,2), P₃₈: = (0,1,11), P₃₉: = (1,8,11), P₄₀: = (1,11,11), P₄₁: = (1,9,2), P₄₂: = (0,1,8), P₄₃: = (1,18,7),
P₄₄: = (1,0,12), P₄₅: = (1,1,7).

In order to write the cyclic structure of PG (2,19), let ω be a primitive element of GF (19³) over GF (19) and let $f\left(x\right)=a_0+a_{1}x+a_2{x}^2+x^3$ be its minimal polynomial over GF (19). The companion matrix $C\left(f\right)$ of f is given by

$$C\left(f\right)=\left(\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ {-a}_0& {-a}_1& {-a}_2\end{array}\right)$$

and it induces a Singer cycle γ of PG (2,19), cf. [9]. Let us consider a primitive polynomial with minimal weight, i.e., the minimal number of non-zero coefficients, among all primitives of that degree over GF (19), f(x) = 17 + 15x² + x³, cf. [10]. The companion matrix C(f) is $\left(\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 2& 0& 4\end{array}\right)$.

Let us consider the point ${\omega }^0=\left(\begin{array}{ccc}{x}_0& x_1& x_2\end{array}\right)=\left(\begin{array}{ccc}1& 0& 0\end{array}\right)$. We get:

$$\begin{gathered} {\omega }^1={\omega }^{0}C(f)=\left(\begin{array}{ccc}1& 0& 0\end{array}\right)\left(\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 2& 0& 4\end{array}\right)=\left(\begin{array}{ccc}0& 1& 0\end{array}\right). \\ {\omega }^2={\omega }^{0}C(f{)}^2={\mathsf{\omega }}^{1}C(f)=\left(\begin{array}{ccc}0& 1& 0\end{array}\right)\left(\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 2& 0& 4\end{array}\right)=\left(\begin{array}{ccc}0& 0& 1\end{array}\right). \\ {\omega }^3={\omega }^{0}C(f{)}^3={\mathsf{\omega }}^{2}C(f)=\left(\begin{array}{ccc}0& 0& 1\end{array}\right)\left(\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 2& 0& 4\end{array}\right)=\left(\begin{array}{ccc}2& 0& 4\end{array}\right)=2\left(\begin{array}{ccc}1& 0& 2\end{array}\right)=\left(\begin{array}{ccc}1& 0& 2\end{array}\right), \end{gathered}$$

by continuing in this way, we obtain the cyclic structure of PG (2,19) as shown in Table 4.

Table 4. The cyclic structure of the points of PG (2,19).

ω0 = (1,0,0)			ω1 = (0,1,0)			ω2 = (0,0,1)
ω3 = (1,0,2)	ω4 = (1,5,2)	ω5 = (1,5,8)	ω6 = (1,6,13)	ω7 = (1,11,11)	ω8 = (1,13,12)	ω9 = (1,4,16)	ω10 = (1,3,14)	ω11 = (1,17,15)
ω12 = (1,7,7)	ω13 = (1,15,12)	ω14 = (1,4,5)	ω15 = (1,2,10)	ω16 = (1,1,4)	ω17 = (1,12,14)	ω18 = (1,17,16)	ω19 = (1,3,15)	ω20 = (1,7,4)
ω21 = (1,12,10)	ω22 = (1,1,14)	ω23 = (1,17,0)	ω24 = (0,1,17)	ω25 = (1,0,16)	ω26 = (1,3,2)	ω27 = (1,5,18)	ω28 = (1,14,15)	ω29 = (1,7,5)
ω30 = (1,2,16)	ω31 = (1,3,8)	ω32 = (1,6,1)	ω33 = (1,10,5)	ω34 = (1,2,3)	ω35 = (1,16,15)	ω36 = (1,7,0)	ω37 = (0,1,7)	ω38 = (1,0,17)
ω39 = (1,14,2)	ω40 = (1,5,15)	ω41 = (1,7,18)	ω42 = (1,9,8)	ω43 = (1,6,18)	ω44 = (1,9,18)	ω45 = (1,9,7)	ω46 = (1,15,4)	ω47 = (1,12,11)
ω48 = (1,13,6)	ω49 = (1,8,11)	ω50 = (1,13,11)	ω51 = (1,13,0)	ω52 = (0,1,13)	ω53 = (1,0,13)	ω54 = (1,11,2)	ω55 = (1,5,0)	ω56 = (0,1,5)
ω57 = (1,0,4)	ω58 = (1,12,2)	ω59 = (1,5,5)	ω60 = (1,2,12)	ω61 = (1,4,10)	ω62 = (1,1,6)	ω63 = (1,8,10)	ω64 = (1,1,10)	ω65 = (1,1,3)
ω66 = (1,16,18)	ω67 = (1,9,13)	ω68 = (1,11,6)	ω69 = (1,8,14)	ω70 = (1,17,5)	ω71 = (1,2,17)	ω72 = (1,14,11)	ω73 = (1,13,13)	ω74 = (1,11,12)
ω75 = (1,4,8)	ω76 = (1,6,7)	ω77 = (1,15,16)	ω78 = (1,3,9)	ω79 = (1,18,18)	ω80 = (1,9,12)	ω81 = (1,4,0)	ω82 = (0,1,4)	ω83 = (1,0,14)
ω84 = (1,17,2)	ω85 = (1,15,11)	ω86 = (1,13,10)	ω87 = (1,1,15)	ω88 = (1,7,9)	ω89 = (1,18,14)	ω90 = (1,17,4)	ω91 = (1,12,16)	ω92 = (1,3,0)
ω93 = (0,1,3)	ω94 = (1,0,18)	ω95 = (1,9,2)	ω96 = (1,5,9)	ω97 = (1,18,16)	ω98 = (1,3,18)	ω99 = (1,9,10)	ω100 = (1,1,11)	ω101 = (1,13,15)
ω102 = (1,7,17)	ω103 = (1,14,5)	ω104 = (1,2,11)	ω105 = (1,13,11)	ω106 = (1,18,8)	ω107 = (1,6,15)	ω108 = (1,7,6)	ω109 = (1,8,1)	ω110 = (1,10,6)
ω111 = (1,8,6)	ω112 = (1,8,9)	ω113 = (1,18,14)	ω114 = (1,11,10)	ω115 = (1,1,13)	ω116 = (1,11,13)	ω117 = (1,11,9)	ω118 = (1,18,10)	ω119 = (1,1,1)
ω120 = (1,10,12)	ω121 = (1,4,4)	ω122 = (1,12,12)	ω123 = (1,4,12)	ω124 = (1,4,18)	ω125 = (1,9,0)	ω126 = (0,1,9)	ω127 = (1,0,1)	ω128 = (1,10,2)
ω129 = (1,5,14)	ω130 = (1,17,11)	ω131 = (1,13,14)	ω132 = (1,17,14)	ω133 = (1,17,6)	ω134 = (1,8,5)	ω135 = (1,2,18)	ω136 = (1,9,1)	ω137 = (1,10,16)
ω138 = (1,3,13)	ω139 = (1,11,16)	ω140 = (1,3,16)	ω141 = (1,3,11)	ω142 = (1,13,3)	ω143 = (1,16,1)	ω144 = (1,10,10)	ω145 = (1,1,12)	ω146 = (1,4,6)
ω147 = (1,8,15)	ω148 = (1,7,1)	ω149 = (1,10,15)	ω150 = (1,7,15)	ω151 = (1,7,13)	ω152 = (1,11,3)	ω153 = (1,16,7)	ω154 = (1,15,14)	ω155 = (1,17,10)
ω156 = (1,1,0)	ω157 = (0,1,1)	ω158 = (1,0,12)	ω159 = (1,4,2)	ω160 = (1,5,3)	ω161 = (1,16,6)	ω162 = (1,8,16)	ω163 = (1,3,7)	ω164 = (1,15,9)
ω165 = (1,18,6)	ω166 = (1,8,13)	ω167 = (1,11,14)	ω168 = (1,17,18)	ω169 = (1,9,3)	ω170 = (1,16,13)	ω171 = (1,11,7)	ω172 = (1,15,15)	ω173 = (1,7,12)
ω174 = (1,4,11)	ω175 = (1,13,16)	ω176 = (1,3,3)	ω177 = (1,16,12)	ω178 = (1,4,9)	ω179 = (1,18,17)	ω180 = (1,14,17)	ω181 = (1,15,3)	ω182 = (1,16,14)
ω183 = (1,17,8)	ω184 = (1,6,9)	ω185 = (1,18,15)	ω186 = (1,7,14)	ω187 = (1,17,7)	ω188 = (1,15,10)	ω189 = (1,1,17)	ω190 = (1,14,16)	ω191 = (1,3,6)
ω192 = (1,8,7)	ω193 = (1,15,8)	ω194 = (1,6,16)	ω195 = (1,3,1)	ω196 = (1,10,13)	ω197 = (1,11,17)	ω198 = (1,14,4)	ω199 = (1,12,18)	ω200 = (1,9,15)
ω201 = (1,7,8)	ω202 = (1,6,6)	ω203 = (1,8,12)	ω204 = (1,4,15)	ω205 = (1,7,11)	ω206 = (1,13,17)	ω207 = (1,14,13)	ω208 = (1,11,4)	ω209 = (1,12,1)
ω210 = (1,10,8)	ω211 = (1,6,5)	ω212 = (1,2,14)	ω213 = (1,17,17)	ω214 = (1,14,12)	ω215 = (1,4,1)	ω216 = (1,10,4)	ω217 = (1,12,8)	ω218 = (1,6,17)
ω219 = (1,14,10)	ω220 = (1,1,16)	ω221 = (1,3,5)	ω222 = (1,2,8)	ω223 = (1,6,14)	ω224 = (1,17,9)	ω225 = (1,18,4)	ω226 = (1,12,9)	ω227 = (1,18,9)
ω228 = (1,18,3)	ω229 = (1,16,5)	ω230 = (1,2,15)	ω231 = (1,7,16)	ω232 = (1,3,4)	ω233 = (1,12,0)	ω234 = (0,1,12)	ω235 = (1,0,6)	ω236 = (1,8,2)
ω237 = (1,5,4)	ω238 = (1,12,5)	ω239 = (1,2,7)	ω240 = (1,15,13)	ω241 = (1,11,15)	ω242 = (1,7,3)	ω243 = (1,16,0)	ω244 = (0,1,16)	ω245 = (1,0,5)
ω246 = (1,2,2)	ω247 = (1,5,12)	ω248 = (1,4,3)	ω249 = (1,16,9)	ω250 = (1,18,5)	ω251 = (1,2,0)	ω252 = (0,1,2)	ω253 = (1,0,7)	ω254 = (1,15,2)
ω255 = (1,5,1)	ω256 = (1,10,14)	ω257 = (1,17,1)	ω258 = (1,10,1)	ω259 = (1,10,7)	ω260 = (1,15,0)	ω261 = (0,1,15)	ω262 = (1,0,9)	ω263 = (1,18,2)
ω264 = (1,5,16)	ω265 = (1,3,17)	ω266 = (1,14,6)	ω267 = (1,8,0)	ω268 = (0,1,8)	ω269 = (1,0,8)	ω270 = (1,6,2)	ω271 = (1,5,13)	ω272 = (1,11,0)
ω273 = (0,1,11)	ω274 = (1,0,15)	ω275 = (1,7,2)	ω276 = (1,5,18)	ω277 = (1,9,9)	ω278 = (1,18,12)	ω279 = (1,4,17)	ω280 = (1,14,1)	ω281 = (1,10,9)
ω282 = (1,18,11)	ω283 = (1,13,8)	ω284 = (1,6,4)	ω285 = (1,12,17)	ω286 = (1,14,18)	ω287 = (1,9,14)	ω288 = (1,17,3)	ω289 = (1,16,8)	ω290 = (1,6,3)
ω291 = (1,16,3)	ω292 = (1,16,11)	ω293 = (1,13,1)	ω294 = (1,10,18)	ω295 = (1,9,16)	ω296 = (1,3,10)	ω297 = (1,1,5)	ω298 = (1,2,4)	ω299 = (1,12,7)
ω300 = (1,15,11)	ω301 = (1,13,7)	ω302 = (1,15,7)	ω303 = (1,15,18)	ω304 = (1,9,4)	ω305 = (1,12,15)	ω306 = (1,7,10)	ω307 = (1,1,9)	ω308 = (1,18,1)
ω309 = (1,10,11)	ω310 = (1,13,18)	ω311 = (1,9,5)	ω312 = (1,2,1)	ω313 = (1,10,3)	ω314 = (1,16,10)	ω315 = (1,1,18)	ω316 = (1,9,11)	ω317 = (1,13,5)
ω318 = (1,2,9)	ω319 = (1,18,0)	ω320 = (0,1,18)	ω321 = (1,0,11)	ω322 = (1,13,2)	ω323 = (1,5,10)	ω324 = (1,1,7)	ω325 = (1,15,17)	ω326 = (1,14,3)
ω327 = (1,16,17)	ω328 = (1,14,17)	ω329 = (1,14,8)	ω330 = (1,6,10)	ω331 = (1,1,8)	ω332 = (1,6,8)	ω333 = (1,6,0)	ω334 = (0,1,6)	ω335 = (1,0,10)
ω336 = (1,1,2)	ω337 = (1,5,7)	ω338 = (1,15,1)	ω339 = (1,10,0)	ω340 = (0,1,10)	ω341 = (1,0,3)	ω342 = (1,16,2)	ω343 = (1,5,6)	ω344 = (1,8,4)
ω345 = (1,12,3)	ω346 = (1,16,4)	ω347 = (1,12,4)	ω348 = (1,12,13)	ω349 = (1,11,1)	ω350 = (1,10,17)	ω351 = (1,14,9)	ω352 = (1,18,7)	ω353 = (1,15,6)
ω354 = (1,8,8)	ω355 = (1,6,12)	ω356 = (1,4,7)	ω357 = (1,15,5)	ω358 = (1,2,13)	ω359 = (1,11,5)	ω360 = (1,2,5)	ω361 = (1,2,6)	ω362 = (1,8,18)
ω363 = (1,9,17)	ω364 = (1,14,14)	ω365 = (1,17,12)	ω366 = (1,4,13)	ω367 = (1,11,8)	ω368 = (1,6,11)	ω369 = (1,13,4)	ω370 = (1,12,6)	ω371 = (1,8,3)
ω372 = (1,16,16)	ω373 = (1,3,12)	ω374 = (1,4,14)	ω375 = (1,17,3)	ω376 = (1,11,18)	ω377 = (1,9,6)	ω378 = (1,8,17)	ω379 = (1,14,0)	ω380 = (0,1,14)

Let us denote the points represented by ωⁱ simply by i. Thus, the Singer group is isomorphic to the additive group Z₃₈₁, the integers modulo 381.

P₁: = (0,1,0) = 1, P₂: = (1,16,15) = 35, P₃: = (0,0,1) = 2, P₄: = (1,3,15) = 19, P₅: = (1,14,6) = 266, P₆: = (1,5,6) = 343,
P₇: = (1,9,5) = 311, P₈: = (1,10,5) = 33, P₉: = (1,3,4) = 232, P₁₀: = (1,14,13) = 207, P₁₁: = (1,5,4) = 237,
P₁₂: = (1,12,18) = 199, P₁₃: = (1,9,14) = 287, P₁₄: = (1,15,2) = 254, P₁₅: = (1,15,17) = 325, P₁₆: = (1,16,4) = 346,
P₁₇: = (1,5,13) = 271, P₁₈: = (1,14,4) = 198, P₁₉: = (1,7,18) = 41, P₂₀: = (1,10,14) = 256, P₂₁: = (1,4,2) = 159,
P₂₂: = (1,4,17) = 279, P₂₃: = (1,1,12) = 145, P₂₄: = (1,14,15) = 28, P₂₅: = (1,5,15) = 40, P₂₆: = (1,12,1) = 209,
P₂₇: = (1,11,0) = 272, P₂₈: = (1,8,8) = 354, P₂₉: = (1,7,1) = 148, P₃₀: = (1,10,17) = 350,
P₃₁: = (1,18,12) = 278, P₃₂: = (1,8,0) = 267, P₃₃: = (1,11,8) = 367, P₃₄: = (1,9,17) = 363,
P₃₅: = (1,0,7) = 253, P₃₆: = (1,0,0) = 0, P₃₇: = (1,10,2) = 128, P₃₈: = (0,1,11) = 273,
P₃₉: = (1,8,11) = 49, P₄₀: = (1,11,11) = 7, P₄₁: = (1,9,2) = 95, P₄₂: = (0,1,8) = 268,
P₄₃: = (1,18,7) = 352, P₄₄: = (1,0,12) = 158, P₄₅: = (1,1,7) = 324.

Now, select any line as the line at infinity, for example, we choose the line ℓ_∞:= x₀ = 0. The remaining lines of the plane are found by adding 1 to each point of the preceding line beginning with ℓ_∞ as ℓ₀ and using addition modulo 381. Table 5 shows that the above 45 points are contained in 36 5-lines, 45 4-lines and 120 3-lines.

Table 5. The cyclic structure of the lines of PG (2,19) in which the points of the 45-set are colored red.

ℓ0	1	2	24	37	52	56	82	93	126	157	234	244	252	261	268	273	320	334	340	380
ℓ1	0	2	3	25	38	53	57	83	94	127	158	235	245	253	262	269	274	321	335	341
ℓ2	1	3	4	26	39	54	58	84	95	128	159	236	246	254	263	270	275	322	336	342
ℓ3	2	4	5	27	40	55	59	85	96	129	160	237	247	255	264	271	276	323	337	343
ℓ4	3	5	6	28	41	56	60	86	97	130	161	238	248	256	265	272	277	324	338	344
ℓ5	4	6	7	29	42	57	61	87	98	131	162	239	249	257	266	273	278	325	339	345
ℓ6	5	7	8	30	43	58	62	88	99	132	163	240	250	258	267	274	279	326	340	346
ℓ7	6	8	9	31	44	59	63	89	100	133	164	241	251	259	268	275	280	327	341	347
ℓ8	7	9	10	32	45	60	64	90	101	134	165	242	252	260	269	276	281	328	342	348
ℓ9	8	10	11	33	46	61	65	91	102	135	166	243	253	261	270	277	282	329	343	349
ℓ10	9	11	12	34	47	62	66	92	103	136	167	244	254	262	271	278	283	330	344	350
ℓ11	10	12	13	35	48	63	67	93	104	137	168	245	255	263	272	279	284	331	345	351
ℓ12	11	13	14	36	49	64	68	94	105	138	169	246	256	264	273	280	285	332	346	352
ℓ13	12	14	15	37	50	65	69	95	106	139	170	247	257	265	274	281	286	333	347	353
ℓ14	13	15	16	38	51	66	70	96	107	140	171	248	258	266	275	282	287	334	348	354
ℓ15	14	16	17	39	52	67	71	97	108	141	172	249	259	267	276	283	288	335	349	355
ℓ16	15	17	18	40	53	68	72	98	109	142	173	250	260	268	277	284	289	336	350	356
ℓ17	16	18	19	41	54	69	73	99	110	143	174	251	261	269	278	285	290	337	351	357
ℓ18	17	19	20	42	55	70	74	100	111	144	175	252	262	270	279	286	291	338	352	358
ℓ19	18	20	21	43	56	71	75	101	112	145	176	253	263	271	280	287	292	339	353	359
ℓ20	19	21	22	44	57	72	76	102	113	146	177	254	264	272	281	288	293	340	354	360
ℓ21	20	22	23	45	58	73	77	103	114	147	178	255	265	273	282	289	294	341	355	361
ℓ22	21	23	24	46	59	74	78	104	115	148	179	256	266	274	283	290	295	342	356	362
ℓ23	22	24	25	47	60	75	79	105	116	149	180	257	267	275	284	291	296	343	357	363
ℓ24	23	25	26	48	61	76	80	106	117	150	181	258	268	276	285	292	297	344	358	364
ℓ25	24	26	27	49	62	77	81	107	118	151	182	259	269	277	286	293	298	345	359	365
ℓ26	25	27	28	50	63	78	82	108	119	152	183	260	270	278	287	294	299	346	360	366
ℓ27	26	28	29	51	64	79	83	109	120	153	184	261	271	279	288	295	300	347	361	367
ℓ28	27	29	30	52	65	80	84	110	121	154	185	262	272	280	289	296	301	348	362	368
ℓ29	28	30	31	53	66	81	85	111	122	155	186	263	273	281	290	297	302	349	363	369
ℓ30	29	31	32	54	67	82	86	112	123	156	187	264	274	282	291	298	303	350	364	370
ℓ31	30	32	33	55	68	83	87	113	124	157	188	265	275	283	292	299	304	351	365	371
ℓ32	31	33	34	56	69	84	88	114	125	158	189	266	276	284	293	300	305	352	366	372
ℓ33	32	34	35	57	70	85	89	115	126	159	190	267	277	285	294	301	306	353	367	373
ℓ34	33	35	36	58	71	86	90	116	127	160	191	268	278	286	295	302	307	354	368	374
ℓ35	34	36	37	59	72	87	91	117	128	161	192	269	279	287	296	303	308	355	369	375
ℓ36	35	37	38	60	73	88	92	118	129	162	193	270	280	288	297	304	309	356	370	376
ℓ37	36	38	39	61	74	89	93	119	130	163	194	271	281	289	298	305	310	357	371	377
ℓ38	37	39	40	62	75	90	94	120	131	164	195	272	282	290	299	306	311	358	372	378
ℓ39	38	40	41	63	76	91	95	121	132	165	196	273	283	291	300	307	312	359	373	379
ℓ40	39	41	42	64	77	92	96	122	133	166	197	274	284	292	301	308	313	360	374	380
ℓ41	0	40	42	43	65	78	93	97	123	134	167	198	275	285	293	302	309	314	361	375
ℓ42	1	41	43	44	66	79	94	98	124	135	168	199	276	286	294	303	310	315	362	376
ℓ43	2	42	44	45	67	80	95	99	125	136	169	200	277	287	295	304	311	316	363	377
ℓ44	3	43	45	46	68	81	96	100	126	137	170	201	278	288	296	305	312	317	364	378
ℓ45	4	44	46	47	69	82	97	101	127	138	171	202	279	289	297	306	313	318	365	379
ℓ46	5	45	47	48	70	83	98	102	128	139	172	203	280	290	298	307	314	319	366	380
ℓ47	0	6	46	48	49	71	84	99	103	129	140	173	204	281	291	299	308	315	320	367
ℓ48	1	7	47	49	50	72	85	100	104	130	141	174	205	282	292	300	309	316	321	368
ℓ49	2	8	48	50	51	73	86	101	105	131	142	175	206	283	293	301	310	317	322	369
ℓ50	3	9	49	51	52	74	87	102	106	132	143	176	207	284	294	302	311	318	323	370
ℓ51	4	10	50	52	53	75	88	103	107	133	144	177	208	285	295	303	312	319	324	371
ℓ52	5	11	51	53	54	76	89	104	108	134	145	178	209	286	296	304	313	320	325	372
ℓ53	6	12	52	54	55	77	90	105	109	135	146	179	210	287	297	305	314	321	326	373
ℓ54	7	13	53	55	56	78	91	106	110	136	147	180	211	288	298	306	315	322	327	374
ℓ55	8	14	54	56	57	79	92	107	111	137	148	181	212	289	299	307	316	323	328	375
ℓ56	9	15	55	57	58	80	93	108	112	138	149	182	213	290	300	308	317	324	329	376
ℓ57	10	16	56	58	59	81	94	109	113	139	150	183	214	291	301	309	318	325	330	377
ℓ58	11	17	57	59	60	82	95	110	114	140	151	184	215	292	302	310	319	326	331	378
ℓ59	12	18	58	60	61	83	96	111	115	141	152	185	216	293	303	311	320	327	332	379
ℓ60	13	19	59	61	62	84	97	112	116	142	153	186	217	294	304	312	321	328	333	380
ℓ61	0	14	20	60	62	63	85	98	113	117	143	154	187	218	295	305	313	322	329	334
ℓ62	1	15	21	61	63	64	86	99	114	118	144	155	188	219	296	306	314	323	330	335
ℓ63	2	16	22	62	64	65	87	100	115	119	145	156	189	220	297	307	315	324	331	336
ℓ64	3	17	23	63	65	66	88	101	116	120	146	157	190	221	298	308	316	325	332	337
ℓ65	4	18	24	64	66	67	89	102	117	121	147	158	191	222	299	309	317	326	333	338
ℓ66	5	19	25	65	67	68	90	103	118	122	148	159	192	223	300	310	318	327	334	339
ℓ67	6	20	26	66	68	69	91	104	119	123	149	160	193	224	301	311	319	328	335	340
ℓ68	7	21	27	67	69	70	92	105	120	124	150	161	194	225	302	312	320	329	336	341
ℓ69	8	22	28	68	70	71	93	106	121	125	151	162	195	226	303	313	321	330	337	342
ℓ70	9	23	29	69	71	72	94	107	122	126	152	163	196	227	304	314	322	331	338	343
ℓ71	10	24	30	70	72	73	95	108	123	127	153	164	197	228	305	315	323	332	339	344
ℓ72	11	25	31	71	73	74	96	109	124	128	154	165	198	229	306	316	324	333	340	345
ℓ73	12	26	32	72	74	75	97	110	125	129	155	166	199	230	307	317	325	334	341	346
ℓ74	13	27	33	73	75	76	98	111	126	130	156	167	200	231	308	318	326	335	342	347
ℓ75	14	28	34	74	76	77	99	112	127	131	157	168	201	232	309	319	327	336	343	348
ℓ76	15	29	35	75	77	78	100	113	128	132	158	169	202	233	310	320	328	337	344	349
ℓ77	16	30	36	76	78	79	101	114	129	133	159	170	203	234	311	321	329	338	345	350
ℓ78	17	31	37	77	79	80	102	115	130	134	160	171	204	235	312	322	330	339	346	351
ℓ79	18	32	38	78	80	81	103	116	131	135	161	172	205	236	313	323	331	340	347	352
ℓ80	19	33	39	79	81	82	104	117	132	136	162	173	206	237	314	324	332	341	348	353
ℓ81	20	34	40	80	82	83	105	118	133	137	163	174	207	238	315	325	333	342	349	354
ℓ82	21	35	41	81	83	84	106	119	134	138	164	175	208	239	316	326	334	343	350	355
ℓ83	22	36	42	82	84	85	107	120	135	139	165	176	209	240	317	327	335	344	351	356
ℓ84	23	37	43	83	85	86	108	121	136	140	166	177	210	241	318	328	336	345	352	357
ℓ85	24	38	44	84	86	87	109	122	137	141	167	178	211	242	319	329	337	346	353	358
ℓ86	25	39	45	85	87	88	110	123	138	142	168	179	212	243	320	330	338	347	354	359
ℓ87	26	40	46	86	88	89	111	124	139	143	169	180	213	244	321	331	339	348	355	360
ℓ88	27	41	47	87	89	90	112	125	140	144	170	181	214	245	322	332	340	349	356	361
ℓ89	28	42	48	88	90	91	113	126	141	145	171	182	215	246	323	333	341	350	357	362
ℓ90	29	43	49	89	91	92	114	127	142	146	172	183	216	247	324	334	342	351	358	363
ℓ91	30	44	50	90	92	93	115	128	143	147	173	184	217	248	325	335	343	352	359	364
ℓ92	31	45	51	91	93	94	116	129	144	148	174	185	218	249	326	336	344	353	360	365
ℓ93	32	46	52	92	94	95	117	130	145	149	175	186	219	250	327	337	345	354	361	366
ℓ94	33	47	53	93	95	96	118	131	146	150	176	187	220	251	328	338	346	355	362	367
ℓ95	34	48	54	94	96	97	119	132	147	151	177	188	221	252	329	339	347	356	363	368
ℓ96	35	49	55	95	97	98	120	133	148	152	178	189	222	253	330	340	348	357	364	369
ℓ97	36	50	56	96	98	99	121	134	149	153	179	190	223	254	331	341	349	358	365	370
ℓ98	37	51	57	97	99	100	122	135	150	154	180	191	224	255	332	342	350	359	366	371
ℓ99	38	52	58	98	100	101	123	136	151	155	181	192	225	256	333	343	351	360	367	372
ℓ100	39	53	59	99	101	102	124	137	152	156	182	193	226	257	334	344	352	361	368	373
ℓ101	40	54	60	100	102	103	125	138	153	157	183	194	227	258	335	345	353	362	369	374
ℓ102	41	55	61	101	103	104	126	139	154	158	184	195	228	259	336	346	354	363	370	375
ℓ103	42	56	62	102	104	105	127	140	155	159	185	196	229	260	337	347	355	364	371	376
ℓ104	43	57	63	103	105	106	128	141	156	160	186	197	230	261	338	348	356	365	372	377
ℓ105	44	58	64	104	106	107	129	142	157	161	187	198	231	262	339	349	357	366	373	378
ℓ106	45	59	65	105	107	108	130	143	158	162	188	199	232	263	340	350	358	367	374	379
ℓ107	46	60	66	106	108	109	131	144	159	163	189	200	233	264	341	351	359	368	375	380
ℓ108	0	47	61	67	107	109	110	132	145	160	164	190	201	234	265	342	352	360	369	376
ℓ109	1	48	62	68	108	110	111	133	146	161	165	191	202	235	266	343	353	361	370	377
ℓ110	2	49	63	69	109	111	112	134	147	162	166	192	203	236	267	344	354	362	371	378
ℓ111	3	50	64	70	110	112	113	135	148	163	167	193	204	237	268	345	355	363	372	379
ℓ112	4	51	65	71	111	113	114	136	149	164	168	194	205	238	269	346	356	364	373	380
ℓ113	0	5	52	66	72	112	114	115	137	150	165	169	195	206	239	270	347	357	365	374
ℓ114	1	6	53	67	73	113	115	116	138	151	166	170	196	207	240	271	348	358	366	375
ℓ115	2	7	54	68	74	114	116	117	139	152	167	171	197	208	241	272	349	359	367	376
ℓ116	3	8	55	69	75	115	117	118	140	153	168	172	198	209	242	273	350	360	368	377
ℓ117	4	9	56	70	76	116	118	119	141	154	169	173	199	210	243	274	351	361	369	378
ℓ118	5	10	57	71	77	117	119	120	142	155	170	174	200	211	244	275	352	362	370	379
ℓ119	6	11	58	72	78	118	120	121	143	156	171	175	201	212	245	276	353	363	371	380
ℓ120	0	7	12	59	73	79	119	121	122	144	157	172	176	202	213	246	277	354	364	372
ℓ121	1	8	13	60	74	80	120	122	123	145	158	173	177	203	214	247	278	355	365	373
ℓ122	2	9	14	61	75	81	121	123	124	146	159	174	178	204	215	248	279	356	366	374
ℓ123	3	10	15	62	76	82	122	124	125	147	160	175	179	205	216	249	280	357	367	375
ℓ124	4	11	16	63	77	83	123	125	126	148	161	176	180	206	217	250	281	358	368	376
ℓ125	5	12	17	64	78	84	124	126	127	149	162	177	181	207	218	251	282	359	369	377
ℓ126	6	13	18	65	79	85	125	127	128	150	163	178	182	208	219	252	283	360	370	378
ℓ127	7	14	19	66	80	86	126	128	129	151	164	179	183	209	220	253	284	361	371	379
ℓ128	8	15	20	67	81	87	127	129	130	152	165	180	184	210	221	254	285	362	372	380
ℓ129	0	9	16	21	68	82	88	128	130	131	153	166	181	185	211	222	255	286	363	373
ℓ130	1	10	17	22	69	83	89	129	131	132	154	167	182	186	212	223	256	287	364	374
ℓ131	2	11	18	23	70	84	90	130	132	133	155	168	183	187	213	224	257	288	365	375
ℓ132	3	12	19	24	71	85	91	131	133	134	156	169	184	188	214	225	258	289	366	376
ℓ133	4	13	20	25	72	86	92	132	134	135	157	170	185	189	215	226	259	290	367	377
ℓ134	5	14	21	26	73	87	93	133	135	136	158	171	186	190	216	227	260	291	368	378
ℓ135	6	15	22	27	74	88	94	134	136	137	159	172	187	191	217	228	261	292	369	379
ℓ136	7	16	23	28	75	89	95	135	137	138	160	173	188	192	218	229	262	293	370	380
ℓ137	0	8	17	24	29	76	90	96	136	138	139	161	174	189	193	219	230	263	294	371
ℓ138	1	9	18	25	30	77	91	97	137	139	140	162	175	190	194	220	231	264	295	372
ℓ139	2	10	19	26	31	78	92	98	138	140	141	163	176	191	195	221	232	265	296	373
ℓ140	3	11	20	27	32	79	93	99	139	141	142	164	177	192	196	222	233	266	297	374
ℓ141	4	12	21	28	33	80	94	100	140	142	143	165	178	193	197	223	234	267	298	375
ℓ142	5	13	22	29	34	81	95	101	141	143	144	166	179	194	198	224	235	268	299	376
ℓ143	6	14	23	30	35	82	96	102	142	144	145	167	180	195	199	225	236	269	300	377
ℓ144	7	15	24	31	36	83	97	103	143	145	146	168	181	196	200	226	237	270	301	378
ℓ145	8	16	25	32	37	84	98	104	144	146	147	169	182	197	201	227	238	271	302	379
ℓ146	9	17	26	33	38	85	99	105	145	147	148	170	183	198	202	228	239	272	303	380
ℓ147	0	10	18	27	34	39	86	100	106	146	148	149	171	184	199	203	229	240	273	304
ℓ148	1	11	19	28	35	40	87	101	107	147	149	150	172	185	200	204	230	241	274	305
ℓ149	2	12	20	29	36	41	88	102	108	148	150	151	173	186	201	205	231	242	275	306
ℓ150	3	13	21	30	37	42	89	103	109	149	151	152	174	187	202	206	232	243	276	307
ℓ151	4	14	22	31	38	43	90	104	110	150	152	153	175	188	203	207	233	244	277	308
ℓ152	5	15	23	32	39	44	91	105	111	151	153	154	176	189	204	208	234	245	278	309
ℓ153	6	16	24	33	40	45	92	106	112	152	154	155	177	190	205	209	235	246	279	310
ℓ154	7	17	25	34	41	46	93	107	113	153	155	156	178	191	206	210	236	247	280	311
ℓ155	8	18	26	35	42	47	94	108	114	154	156	157	179	192	207	211	237	248	281	312
ℓ156	9	19	27	36	43	48	95	109	115	155	157	158	180	193	208	212	238	249	282	313
ℓ157	10	20	28	37	44	49	96	110	116	156	158	159	181	194	209	213	239	250	283	314
ℓ158	11	21	29	38	45	50	97	111	117	157	159	160	182	195	210	214	240	251	284	315
ℓ159	12	22	30	39	46	51	98	112	118	158	160	161	183	196	211	215	241	252	285	316
ℓ160	13	23	31	40	47	52	99	113	119	159	161	162	184	197	212	216	242	253	286	317
ℓ161	14	24	32	41	48	53	100	114	120	160	162	163	185	198	213	217	243	254	287	318
ℓ162	15	25	33	42	49	54	101	115	121	161	163	164	186	199	214	218	244	255	288	319
ℓ163	16	26	34	43	50	55	102	116	122	162	164	165	187	200	215	219	245	256	289	320
ℓ164	17	27	35	44	51	56	103	117	123	163	165	166	188	201	216	220	246	257	290	321
ℓ165	18	28	36	45	52	57	104	118	124	164	166	167	189	202	217	221	247	258	291	322
ℓ166	19	29	37	46	53	58	105	119	125	165	167	168	190	203	218	222	248	259	292	323
ℓ167	20	30	38	47	54	59	106	120	126	166	168	169	191	204	219	223	249	260	293	324
ℓ168	21	31	39	48	55	60	107	121	127	167	169	170	192	205	220	224	250	261	294	325
ℓ169	22	32	40	49	56	61	108	122	128	168	170	171	193	206	221	225	251	262	295	326
ℓ170	23	33	41	50	57	62	109	123	129	169	171	172	194	207	222	226	252	263	296	327
ℓ171	24	34	42	51	58	63	110	124	130	170	172	173	195	208	223	227	253	264	297	328
ℓ172	25	35	43	52	59	64	111	125	131	171	173	174	196	209	224	228	254	265	298	329
ℓ173	26	36	44	53	60	65	112	126	132	172	174	175	197	210	225	229	255	266	299	330
ℓ174	27	37	45	54	61	66	113	127	133	173	175	176	198	211	226	230	256	267	300	331
ℓ175	28	38	46	55	62	67	114	128	134	174	176	177	199	212	227	231	257	268	301	332
ℓ176	29	39	47	56	63	68	115	129	135	175	177	178	200	213	228	232	258	269	302	333
ℓ177	30	40	48	57	64	69	116	130	136	176	178	179	201	214	229	233	259	270	303	334
ℓ178	31	41	49	58	65	70	117	131	137	177	179	180	202	215	230	234	260	271	304	335
ℓ179	32	42	50	59	66	71	118	132	138	178	180	181	203	216	231	235	261	272	305	336
ℓ180	33	43	51	60	67	72	119	133	139	179	181	182	204	217	232	236	262	273	306	337
ℓ181	34	44	52	61	68	73	120	134	140	180	182	183	205	218	233	237	263	274	307	338
ℓ182	35	45	53	62	69	74	121	135	141	181	183	184	206	219	234	238	264	275	308	339
ℓ183	36	46	54	63	70	75	122	136	142	182	184	185	207	220	235	239	265	276	309	340
ℓ184	37	47	55	64	71	76	123	137	143	183	185	186	208	221	236	240	266	277	310	341
ℓ185	38	48	56	65	72	77	124	138	144	184	186	187	209	222	237	241	267	278	311	342
ℓ186	39	49	57	66	73	78	125	139	145	185	187	188	210	223	238	242	268	279	312	343
ℓ187	40	50	58	67	74	79	126	140	146	186	188	189	211	224	239	243	269	280	313	344
ℓ188	41	51	59	68	75	80	127	141	147	187	189	190	212	225	240	244	270	281	314	345
ℓ189	42	52	60	69	76	81	128	142	148	188	190	191	213	226	241	245	271	282	315	346
ℓ190	43	53	61	70	77	82	129	143	149	189	191	192	214	227	242	246	272	283	316	347
ℓ191	44	54	62	71	78	83	130	144	150	190	192	193	215	228	243	247	273	284	317	348
ℓ192	45	55	63	72	79	84	131	145	151	191	193	194	216	229	244	248	274	285	318	349
ℓ193	46	56	64	73	80	85	132	146	152	192	194	195	217	230	245	249	275	286	319	350
ℓ194	47	57	65	74	81	86	133	147	153	193	195	196	218	231	246	250	276	287	320	351
ℓ195	48	58	66	75	82	87	134	148	154	194	196	197	219	232	247	251	277	288	321	352
ℓ196	49	59	67	76	83	88	135	149	155	195	197	198	220	233	248	252	278	289	322	353
ℓ197	50	60	68	77	84	89	136	150	156	196	198	199	221	234	249	253	279	290	323	354
ℓ198	51	61	69	78	85	90	137	151	157	197	199	200	222	235	250	254	280	291	324	355
ℓ199	52	62	70	79	86	91	138	152	158	198	200	201	223	236	251	255	281	292	325	356
ℓ200	53	63	71	80	87	92	139	153	159	199	201	202	224	237	252	256	282	293	326	357
ℓ201	54	64	72	81	88	93	140	154	160	200	202	203	225	238	253	257	283	294	327	358
ℓ202	55	65	73	82	89	94	141	155	161	201	203	204	226	239	254	258	284	295	328	359
ℓ203	56	66	74	83	90	95	142	156	162	202	204	205	227	240	255	259	285	296	329	360
ℓ204	57	67	75	84	91	96	143	157	163	203	205	206	228	241	256	260	286	297	330	361
ℓ205	58	68	76	85	92	97	144	158	164	204	206	207	229	242	257	261	287	298	331	362
ℓ206	59	69	77	86	93	98	145	159	165	205	207	208	230	243	258	262	288	299	332	363
ℓ207	60	70	78	87	94	99	146	160	166	206	208	209	231	244	259	263	289	300	333	364
ℓ208	61	71	79	88	95	100	147	161	167	207	209	210	232	245	260	264	290	301	334	365
ℓ209	62	72	80	89	96	101	148	162	168	208	210	211	233	246	261	265	291	302	335	366
ℓ210	63	73	81	90	97	102	149	163	169	209	211	212	234	247	262	266	292	303	336	367
ℓ211	64	74	82	91	98	103	150	164	170	210	212	213	235	248	263	267	293	304	337	368
ℓ212	65	75	83	92	99	104	151	165	171	211	213	214	236	249	264	268	294	305	338	369
ℓ213	66	76	84	93	100	105	152	166	172	212	214	215	237	250	265	269	295	306	339	370
ℓ214	67	77	85	94	101	106	153	167	173	213	215	216	238	251	266	270	296	307	340	371
ℓ215	68	78	86	95	102	107	154	168	174	214	216	217	239	252	267	271	297	308	341	372
ℓ216	69	79	87	96	103	108	155	169	175	215	217	218	240	253	268	272	298	309	342	373
ℓ217	70	80	88	97	104	109	156	170	176	216	218	219	241	254	269	273	299	310	343	374
ℓ218	71	81	89	98	105	110	157	171	177	217	219	220	242	255	270	274	300	311	344	375
ℓ219	72	82	90	99	106	111	158	172	178	218	220	221	243	256	271	275	301	312	345	376
ℓ220	73	83	91	100	107	112	159	173	179	219	221	222	244	257	272	276	302	313	346	377
ℓ221	74	84	92	101	108	113	160	174	180	220	222	223	245	258	273	277	303	314	347	378
ℓ222	75	85	93	102	109	114	161	175	181	221	223	224	246	259	274	278	304	315	348	379
ℓ223	76	86	94	103	110	115	162	176	182	222	224	225	247	260	275	279	305	316	349	380
ℓ224	0	77	87	95	104	111	116	163	177	183	223	225	226	248	261	276	280	306	317	350
ℓ225	1	78	88	96	105	112	117	164	178	184	224	226	227	249	262	277	281	307	318	351
ℓ226	2	79	89	97	106	113	118	165	179	185	225	227	228	250	263	278	282	308	319	352
ℓ227	3	80	90	98	107	114	119	166	180	186	226	228	229	251	264	279	283	309	320	353
ℓ228	4	81	91	99	108	115	120	167	181	187	227	229	230	252	265	280	284	310	321	354
ℓ229	5	82	92	100	109	116	121	168	182	188	228	230	231	253	266	281	285	311	322	355
ℓ230	6	83	93	101	110	117	122	169	183	189	229	231	232	254	267	282	286	312	323	356
ℓ231	7	84	94	102	111	118	123	170	184	190	230	232	233	255	268	283	287	313	324	357
ℓ232	8	85	95	103	112	119	124	171	185	191	231	233	234	256	269	284	288	314	325	358
ℓ233	9	86	96	104	113	120	125	172	186	192	232	234	235	257	270	285	289	315	326	359
ℓ234	10	87	97	105	114	121	126	173	187	193	233	235	236	258	271	286	290	316	327	360
ℓ235	11	88	98	106	115	122	127	174	188	194	234	236	237	259	272	287	291	317	328	361
ℓ236	12	89	99	107	116	123	128	175	189	195	235	237	238	260	273	288	292	318	329	362
ℓ237	13	90	100	108	117	124	129	176	190	196	236	238	239	261	274	289	293	319	330	363
ℓ238	14	91	101	109	118	125	130	177	191	197	237	239	240	262	275	290	294	320	331	364
ℓ239	15	92	102	110	119	126	131	178	192	198	238	240	241	263	276	291	295	321	332	365
ℓ240	16	93	103	111	120	127	132	179	193	199	239	241	242	264	277	292	296	322	333	366
ℓ241	17	94	104	112	121	128	133	180	194	200	240	242	243	265	278	293	297	323	334	367
ℓ242	18	95	105	113	122	129	134	181	195	201	241	243	244	266	279	294	298	324	335	368
ℓ243	19	96	106	114	123	130	135	182	196	202	242	244	245	267	280	295	299	325	336	369
ℓ244	20	97	107	115	124	131	136	183	197	203	243	245	246	268	281	296	300	326	337	370
ℓ245	21	98	108	116	125	132	137	184	198	204	244	246	247	269	282	297	301	327	338	371
ℓ246	22	99	109	117	126	133	138	185	199	205	245	247	248	270	283	298	302	328	339	372
ℓ247	23	100	110	118	127	134	139	186	200	206	246	248	249	271	284	299	303	329	340	373
ℓ248	24	101	111	119	128	135	140	187	201	207	247	249	250	272	285	300	304	330	341	374
ℓ249	25	102	112	120	129	136	141	188	202	208	248	250	251	273	286	301	305	331	342	375
ℓ250	26	103	113	121	130	137	142	189	203	209	249	251	252	274	287	302	306	332	343	376
ℓ251	27	104	114	122	131	138	143	190	204	210	250	252	253	275	288	303	307	333	344	377
ℓ252	28	105	115	123	132	139	144	191	205	211	251	253	254	276	289	304	308	334	345	378
ℓ253	29	106	116	124	133	140	145	192	206	212	252	254	255	277	290	305	309	335	346	379
ℓ254	30	107	117	125	134	141	146	193	207	213	253	255	256	278	291	306	310	336	347	380
ℓ255	0	31	108	118	126	135	142	147	194	208	214	254	256	257	279	292	307	311	337	348
ℓ256	1	32	109	119	127	136	143	148	195	209	215	255	257	258	280	293	308	312	338	349
ℓ257	2	33	110	120	128	137	144	149	196	210	216	256	258	259	281	294	309	313	339	350
ℓ258	3	34	111	121	129	138	145	150	197	211	217	257	259	260	282	295	310	314	340	351
ℓ259	4	35	112	122	130	139	146	151	198	212	218	258	260	261	283	296	311	315	341	352
ℓ260	5	36	113	123	131	140	147	152	199	213	219	259	261	262	284	297	312	316	342	353
ℓ261	6	37	114	124	132	141	148	153	200	214	220	260	262	263	285	298	313	317	343	354
ℓ262	7	38	115	125	133	142	149	154	201	215	221	261	263	264	286	299	314	318	344	355
ℓ263	8	39	116	126	134	143	150	155	202	216	222	262	264	265	287	300	315	319	345	356
ℓ264	9	40	117	127	135	144	151	156	203	217	223	263	265	266	288	301	316	320	346	357
ℓ265	10	41	118	128	136	145	152	157	204	218	224	264	266	267	289	302	317	321	347	358
ℓ266	11	42	119	129	137	146	153	158	205	219	225	265	267	268	290	303	318	322	348	359
ℓ267	12	43	120	130	138	147	154	159	206	220	226	266	268	269	291	304	319	323	349	360
ℓ268	13	44	121	131	139	148	155	160	207	221	227	267	269	270	292	305	320	324	350	361
ℓ269	14	45	122	132	140	149	156	161	208	222	228	268	270	271	293	306	321	325	351	362
ℓ270	15	46	123	133	141	150	157	162	209	223	229	269	271	272	294	307	322	326	352	363
ℓ271	16	47	124	134	142	151	158	163	210	224	230	270	272	273	295	308	323	327	353	364
ℓ272	17	48	125	135	143	152	159	164	211	225	231	271	273	274	296	309	324	328	354	365
ℓ273	18	49	126	136	144	153	160	165	212	226	232	272	274	275	297	310	325	329	355	366
ℓ274	19	50	127	137	145	154	161	166	213	227	233	273	275	276	298	311	326	330	356	367
ℓ275	20	51	128	138	146	155	162	167	214	228	234	274	276	277	299	312	327	331	357	368
ℓ276	21	52	129	139	147	156	163	168	215	229	235	275	277	278	300	313	328	332	358	369
ℓ277	22	53	130	140	148	157	164	169	216	230	236	276	278	279	301	314	329	333	359	370
ℓ278	23	54	131	141	149	158	165	170	217	231	237	277	279	280	302	315	330	334	360	371
ℓ279	24	55	132	142	150	159	166	171	218	232	238	278	280	281	303	316	331	335	361	372
ℓ280	25	56	133	143	151	160	167	172	219	233	239	279	281	282	304	317	332	336	362	373
ℓ281	26	57	134	144	152	161	168	173	220	234	240	280	282	283	305	318	333	337	363	374
ℓ282	27	58	135	145	153	162	169	174	221	235	241	281	283	284	306	319	334	338	364	375
ℓ283	28	59	136	146	154	163	170	175	222	236	242	282	284	285	307	320	335	339	365	376
ℓ284	29	60	137	147	155	164	171	176	223	237	243	283	285	286	308	321	336	340	366	377
ℓ285	30	61	138	148	156	165	172	177	224	238	244	284	286	287	309	322	337	341	367	378
ℓ286	31	62	139	149	157	166	173	178	225	239	245	285	287	288	310	323	338	342	368	379
ℓ287	32	63	140	150	158	167	174	179	226	240	246	286	288	289	311	324	339	343	369	380
ℓ288	0	33	64	141	151	159	168	175	180	227	241	247	287	289	290	312	325	340	344	370
ℓ289	1	34	65	142	152	160	169	176	181	228	242	248	288	290	291	313	326	341	345	371
ℓ290	2	35	66	143	153	161	170	177	182	229	243	249	289	291	292	314	327	342	346	372
ℓ291	3	36	67	144	154	162	171	178	183	230	244	250	290	292	293	315	328	343	347	373
ℓ292	4	37	68	145	155	163	172	179	184	231	245	251	291	293	294	316	329	344	348	374
ℓ293	5	38	69	146	156	164	173	180	185	232	246	252	292	294	295	317	330	345	349	375
ℓ294	6	39	70	147	157	165	174	181	186	233	247	253	293	295	296	318	331	346	350	376
ℓ295	7	40	71	148	158	166	175	182	187	234	248	254	294	296	297	319	332	347	351	377
ℓ296	8	41	72	149	159	167	176	183	188	235	249	255	295	297	298	320	333	348	352	378
ℓ297	9	42	73	150	160	168	177	184	189	236	250	256	296	298	299	321	334	349	353	379
ℓ298	10	43	74	151	161	169	178	185	190	237	251	257	297	299	300	322	335	350	354	380
ℓ299	0	11	44	75	152	162	170	179	186	191	238	252	258	298	300	301	323	336	351	355
ℓ300	1	12	45	76	153	163	171	180	187	192	239	253	259	299	301	302	324	337	352	356
ℓ301	2	13	46	77	154	164	172	181	188	193	240	254	260	300	302	303	325	338	353	357
ℓ302	3	14	47	78	155	165	173	182	189	194	241	255	261	301	303	304	326	339	354	358
ℓ303	4	15	48	79	156	166	174	183	190	195	242	256	262	302	304	305	327	340	355	359
ℓ304	5	16	49	80	157	167	175	184	191	196	243	257	263	303	305	306	328	341	356	360
ℓ305	6	17	50	81	158	168	176	185	192	197	244	258	264	304	306	307	329	342	357	361
ℓ306	7	18	51	82	159	169	177	186	193	198	245	259	265	305	307	308	330	343	358	362
ℓ307	8	19	52	83	160	170	178	187	194	199	246	260	266	306	308	309	331	344	359	363
ℓ308	9	20	53	84	161	171	179	188	195	200	247	261	267	307	309	310	332	345	360	364
ℓ309	10	21	54	85	162	172	180	189	196	201	248	262	268	308	310	311	333	346	361	365
ℓ310	11	22	55	86	163	173	181	190	197	202	249	263	269	309	311	312	334	347	362	366
ℓ311	12	23	56	87	164	174	182	191	198	203	250	264	270	310	312	313	335	348	363	367
ℓ312	13	24	57	88	165	175	183	192	199	204	251	265	271	311	313	314	336	349	364	368
ℓ313	14	25	58	89	166	176	184	193	200	205	252	266	272	312	314	315	337	350	365	369
ℓ314	15	26	59	90	167	177	185	194	201	206	253	267	273	313	315	316	338	351	366	370
ℓ315	16	27	60	91	168	178	186	195	202	207	254	268	274	314	316	317	339	352	367	371
ℓ316	17	28	61	92	169	179	187	196	203	208	255	269	275	315	317	318	340	353	368	372
ℓ317	18	29	62	93	170	180	188	197	204	209	256	270	276	316	318	319	341	354	369	373
ℓ318	19	30	63	94	171	181	189	198	205	210	257	271	277	317	319	320	342	355	370	374
ℓ319	20	31	64	95	172	182	190	199	206	211	258	272	278	318	320	321	343	356	371	375
ℓ320	21	32	65	96	173	183	191	200	207	212	259	273	279	319	321	322	344	357	372	376
ℓ321	22	33	66	97	174	184	192	201	208	213	260	274	280	320	322	323	345	358	373	377
ℓ322	23	34	67	98	175	185	193	202	209	214	261	275	281	321	323	324	346	359	374	378
ℓ323	24	35	68	99	176	186	194	203	210	215	262	276	282	322	324	325	347	360	375	379
ℓ324	25	36	69	100	177	187	195	204	211	216	263	277	283	323	325	326	348	361	376	380
ℓ325	0	26	37	70	101	178	188	196	205	212	217	264	278	284	324	326	327	349	362	377
ℓ326	1	27	38	71	102	179	189	197	206	213	218	265	279	285	325	327	328	350	363	378
ℓ327	2	28	39	72	103	180	190	198	207	214	219	266	280	286	326	328	329	351	364	379
ℓ328	3	29	40	73	104	181	191	199	208	215	220	267	281	287	327	329	330	352	365	380
ℓ329	0	4	30	41	74	105	182	192	200	209	216	221	268	282	288	328	330	331	353	366
ℓ330	1	5	31	42	75	106	183	193	201	210	217	222	269	283	289	329	331	332	354	367
ℓ331	2	6	32	43	76	107	184	194	202	211	218	223	270	284	290	330	332	333	355	368
ℓ332	3	7	33	44	77	108	185	195	203	212	219	224	271	285	291	331	333	334	356	369
ℓ333	4	8	34	45	78	109	186	196	204	213	220	225	272	286	292	332	334	335	357	370
ℓ334	5	9	35	46	79	110	187	197	205	214	221	226	273	287	293	333	335	336	358	371
ℓ335	6	10	36	47	80	111	188	198	206	215	222	227	274	288	294	334	336	337	359	372
ℓ336	7	11	37	48	81	112	189	199	207	216	223	228	275	289	295	335	337	338	360	373
ℓ337	8	12	38	49	82	113	190	200	208	217	224	229	276	290	296	336	338	339	361	374
ℓ338	9	13	39	50	83	114	191	201	209	218	225	230	277	291	297	337	339	340	362	375
ℓ339	10	14	40	51	84	115	192	202	210	219	226	231	278	292	298	338	340	341	363	376
ℓ340	11	15	41	52	85	116	193	203	211	220	227	232	279	293	299	339	341	342	364	377
ℓ341	12	16	42	53	86	117	194	204	212	221	228	233	280	294	300	340	342	343	365	378
ℓ342	13	17	43	54	87	118	195	205	213	222	229	234	281	295	301	341	343	344	366	379
ℓ343	14	18	44	55	88	119	196	206	214	223	230	235	282	296	302	342	344	345	367	380
ℓ344	0	15	19	45	56	89	120	197	207	215	224	231	236	283	297	303	343	345	346	368
ℓ345	1	16	20	46	57	90	121	198	208	216	225	232	237	284	298	304	344	346	347	369
ℓ346	2	17	21	47	58	91	122	199	209	217	226	233	238	285	299	305	345	347	348	370
ℓ347	3	18	22	48	59	92	123	200	210	218	227	234	239	286	300	306	346	348	349	371
ℓ348	4	19	23	49	60	93	124	201	211	219	228	235	240	287	301	307	347	349	350	372
ℓ349	5	20	24	50	61	94	125	202	212	220	229	236	241	288	302	308	348	350	351	373
ℓ350	6	21	25	51	62	95	126	203	213	221	230	237	242	289	303	309	349	351	352	374
ℓ351	7	22	26	52	63	96	127	204	214	222	231	238	243	290	304	310	350	352	353	375
ℓ352	8	23	27	53	64	97	128	205	215	223	232	239	244	291	305	311	351	353	354	376
ℓ353	9	24	28	54	65	98	129	206	216	224	233	240	245	292	306	312	352	354	355	377
ℓ354	10	25	29	55	66	99	130	207	217	225	234	241	246	293	307	313	353	355	356	378
ℓ355	11	26	30	56	67	100	131	208	218	226	235	242	247	294	308	314	354	356	357	379
ℓ356	12	27	31	57	68	101	132	209	219	227	236	243	248	295	309	315	355	357	358	380
ℓ357	0	13	28	32	58	69	102	133	210	220	228	237	244	249	296	310	316	356	358	359
ℓ358	1	14	29	33	59	70	103	134	211	221	229	238	245	250	297	311	317	357	359	360
ℓ359	2	15	30	34	60	71	104	135	212	222	230	239	246	251	298	312	318	358	360	361
ℓ360	3	16	31	35	61	72	105	136	213	223	231	240	247	252	299	313	319	359	361	362
ℓ361	4	17	32	36	62	73	106	137	214	224	232	241	248	253	300	314	320	360	362	363
ℓ362	5	18	33	37	63	74	107	138	215	225	233	242	249	254	301	315	321	361	363	364
ℓ363	6	19	34	38	64	75	108	139	216	226	234	243	250	255	302	316	322	362	364	365
ℓ364	7	20	35	39	65	76	109	140	217	227	235	244	251	256	303	317	323	363	365	366
ℓ365	8	21	36	40	66	77	110	141	218	228	236	245	252	257	304	318	324	364	366	367
ℓ366	9	22	37	41	67	78	111	142	219	229	237	246	253	258	305	319	325	365	367	368
ℓ367	10	23	38	42	68	79	112	143	220	230	238	247	254	259	306	320	326	366	368	369
ℓ368	11	24	39	43	69	80	113	144	221	231	239	248	255	260	307	321	327	367	369	370
ℓ369	12	25	40	44	70	81	114	145	222	232	240	249	256	261	308	322	328	368	370	371
ℓ370	13	26	41	45	71	82	115	146	223	233	241	250	257	262	309	323	329	369	371	372
ℓ371	14	27	42	46	72	83	116	147	224	234	242	251	258	263	310	324	330	370	372	373
ℓ372	15	28	43	47	73	84	117	148	225	235	243	252	259	264	311	325	331	371	373	374
ℓ373	16	29	44	48	74	85	118	149	226	236	244	253	260	265	312	326	332	372	374	375
ℓ374	17	30	45	49	75	86	119	150	227	237	245	254	261	266	313	327	333	373	375	376
ℓ375	18	31	46	50	76	87	120	151	228	238	246	255	262	267	314	328	334	374	376	377
ℓ376	19	32	47	51	77	88	121	152	229	239	247	256	263	268	315	329	335	375	377	378
ℓ377	20	33	48	52	78	89	122	153	230	240	248	257	264	269	316	330	336	376	378	379
ℓ378	21	34	49	53	79	90	123	154	231	241	249	258	265	270	317	331	337	377	379	380
ℓ379	0	22	35	50	54	80	91	124	155	232	242	250	259	266	271	318	332	338	378	380
ℓ380	0	1	23	36	51	55	81	92	125	156	233	243	251	260	267	272	319	333	339	379

Thus, we get a ($\left({45}_{16}^1\right)$,$\left({120}_3^1\right)\left({45}_4^2\right)\left({36}_5^3\right)$) quasi-configuration embedded in PG (2,19), which is a symmetric minimal blocking 45-set of type (1,3,4,5), which, to our knowledge, seems to be novel.

6. Conclusions

Sets with few intersection numbers are connected with many theoretical and applied areas, such as coding theory, strongly regular graphs, association schemes, optimal multiple coverings, and secret sharing, cf. [17]. In this paper, sets with few intersection numbers are provided by quasi-configurations derived by special arrangements of lines.