Jordan-Type Inequalities and Stratification

Abstract

In this paper, two double Jordan-type inequalities are introduced that generalize some previously established inequalities. As a result, some new upper and lower bounds and approximations of the sinc function are obtained. This extension of Jordan’s inequality is enabled by considering the corresponding inequalities through the concept of stratified families of functions. Based on this approach, some optimal approximations of the sinc function are derived by determining the corresponding minimax approximants.

1. Introduction

The function:

$$\mathrm{sinc}x=\left\{\begin{array}{cc}{\displaystyle \frac{sinx}{x}},& x\ne 0\\ 1,& x=0\end{array}\right.$$

has numerous applications in mathematics. The basic approximation of the $\mathrm{sinc}x$ function is given by the well-known Jordan’s inequality:

Theorem 1

([1]). For $x\in \left(0,{\displaystyle \frac{\pi }{2}}\right]$, it holds that

$${\displaystyle \frac{2}{\pi }}\le {\displaystyle \frac{sinx}{x}}<1.$$

(1)

Since then, many authors have worked on extensions and improvements of Jordan’s inequality [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22]. In [7], F. Qi, D.-W. Niu and B.-N. Guo conducted elaborate research, thus summarizing previously discovered improvements and applications of Jordan’s inequality, along with related problems. Motivated by some of the following results, this paper provides an additional contribution to this topic.

F. Qi and B.-N. Guo, in the paper [2], provided an enhancement of Jordan’s inequality through the following assertion:

Theorem 2.

Let $x\in \left(0,{\displaystyle \frac{\pi }{2}}\right]$. Then, it holds that

$${\displaystyle \frac{2}{\pi }}+{\displaystyle \frac{2}{{\pi }^2}}\left(\pi -2x\right)\ge {\displaystyle \frac{sinx}{x}}\ge {\displaystyle \frac{2}{\pi }}+{\displaystyle \frac{\pi -2}{{\pi }^2}}\left(\pi -2x\right).$$

(2)

F. Qi then, in the paper [3], provided further improvement of Jordan’s inequality through the following assertion:

Theorem 3.

Let $x\in \left(0,{\displaystyle \frac{\pi }{2}}\right]$. Then, it holds that

$${\displaystyle \frac{2}{\pi }}+{\displaystyle \frac{1}{{\pi }^3}}\left({\pi }^2-4x^2\right)\le {\displaystyle \frac{sinx}{x}}\le {\displaystyle \frac{2}{\pi }}+{\displaystyle \frac{\pi -2}{{\pi }^3}}\left({\pi }^2-4x^2\right).$$

(3)

In the paper [4], K. Deng contributed to improvements of Jordan’s inequality by proving the following:

Theorem 4.

Let $x\in \left(0,{\displaystyle \frac{\pi }{2}}\right]$. Then, it holds that

$${\displaystyle \frac{2}{\pi }}+{\displaystyle \frac{2}{3{\pi }^4}}\left({\pi }^3-8x^3\right)\le {\displaystyle \frac{sinx}{x}}\le {\displaystyle \frac{2}{\pi }}+{\displaystyle \frac{\pi -2}{{\pi }^4}}\left({\pi }^3-8x^3\right).$$

(4)

Based on the inequality (3), W. D. Jiang and H. Yun provided further extension of Jordan’s inequality in their paper [5] through the following theorem:

Theorem 5.

Let $x\in \left(0,{\displaystyle \frac{\pi }{2}}\right]$. Then, it holds that

$${\displaystyle \frac{2}{\pi }}+{\displaystyle \frac{1}{2{\pi }^5}}\left({\pi }^4-16x^4\right)\le {\displaystyle \frac{sinx}{x}}\le {\displaystyle \frac{2}{\pi }}+{\displaystyle \frac{\pi -2}{{\pi }^5}}\left({\pi }^4-16x^4\right).$$

(5)

Shortly afterwards, in the paper [6], J.-L. Li and Y.-L. Li provided a more general statement that encompasses the previous inequalities, (2)–(5), thereby introducing an entire family of inequalities. Namely, the following theorem holds:

Theorem 6.

Let $x\in \left(0,{\displaystyle \frac{\pi }{2}}\right]$. Then, it holds that

$$\begin{array}{c}{\displaystyle \frac{2}{\pi }}+{\displaystyle \frac{2}{{\pi }^2}}\left(\pi -2x\right)\ge {\displaystyle \frac{sinx}{x}}\ge {\displaystyle \frac{2}{\pi }}+{\displaystyle \frac{\pi -2}{{\pi }^2}}\left(\pi -2x\right)\end{array}$$

(6)

$$\begin{array}{c}{\displaystyle \frac{2}{\pi }}+{\displaystyle \frac{2}{n{\pi }^{n+1}}}\left({\pi }^n-{\left(2x\right)}^n\right)\le {\displaystyle \frac{sinx}{x}}\le {\displaystyle \frac{2}{\pi }}+{\displaystyle \frac{\pi -2}{{\pi }^{n+1}}}\left({\pi }^n-{\left(2x\right)}^n\right)\left(\mathit{for} n\in N,n\ge 2\right).\end{array}$$

(7)

Inspired by Theorems 2–6, in this paper, based on the concept of the stratification of corresponding families of functions from the paper [23], we introduce a new extension of Jordan’s inequality. Namely, by applying stratification, it is possible to extend the inequality (7) so that the parameter n can be a positive real number. The extension of inequalities for real parameters has recently been the subject of various studies [24,25,26,27]; see also [28,29,30,31]. Additionally, we provide the best constants for this type of Jordan’s inequality, as well as an analysis of the upper and lower bounds and minimax approximations of the $\mathrm{sinc}x$ function based on the inequalities (2)–(5), as well as on the newly obtained inequalities.

2. Preliminaries

Recently, in the paper [23], the authors considered families of functions ${\phi }_p\left(x\right)$, where $x\in (a,b)\subseteq R^{+}$ and $p\in R^{+}$, which are monotonic with respect to the parameter p. In that paper, such families of functions are referred to as stratified families of functions with respect to the parameter p. If, for each $x\in (a,b)$, it holds that

$$\left(\forall p_1,p_2\in R^{+}\right)p_1<p_2⟺{\phi }_{p_1}\left(x\right)<{\phi }_{p_2}\left(x\right),$$

then the family of functions ${\phi }_p\left(x\right)$ is increasingly stratified with respect to the parameter p. If, for each $x\in (a,b)$, it holds that

$$\left(\forall p_1,p_2\in R^{+}\right)p_1<p_2⟺{\phi }_{p_1}\left(x\right)>{\phi }_{p_2}\left(x\right),$$

then the family of functions ${\phi }_p\left(x\right)$ is decreasingly stratified with respect to the parameter p.

If it is possible to determine a value of the parameter $p=p_0\in R^{+}$ for which the infimum of the error

$$d_0=d\left(p_0\right)=\underset{x\in (a,b)}{sup}\left|{\phi }_{p_0}\left(x\right)\right|$$

is attained, then the function ${\phi }_{p_0}\left(x\right)$ is the minimax approximant of the family of functions ${\phi }_p\left(x\right)$ on the interval $(a,b)$. Based on the stratifiedness, the parameter value $p=p_0$ is unique.

In this paper, we consider the inequalities (2)–(7) by introducing the corresponding stratified families of functions. When proving inequalities, we will utilize L’Hôpital’s rule for monotonicity, as well as the method for proving MTP (Mixed Trigonometric Polynomial) inequalities described in the paper [32].

L’Hôpital’s rule for monotonicity was described by the author I. Pinelis in the paper [33]; see also [34]. In this paper, we use the following formulation:

Lemma 1.

(Monotone form of L’Hôpital’s rule). Let f and g be continuous functions that are differentiable on $(a,b)$. Suppose $f(a+)=g(a+)=0$ or $f(b-)=g(b-)=0$, and assume that $g^{\prime }\left(x\right)\ne 0$ for all $x\in (a,b)$. If $f^{\prime }/g^{\prime }$ is an increasing (decreasing) function on $(a,b)$, then so is $f/g$.

The method to prove inequalities of the form $f\left(x\right)>0$ on the interval $(a,b)\subseteq R$, where $f\left(x\right)$ is an MTP function, as outlined in [32], is based on determining a downward polynomial approximation $P\left(x\right)$ with respect to the observed function $f\left(x\right)$. In [32], the determination of a polynomial $P\left(x\right)$ as a polynomial with rational coefficients is considered. If there exists a polynomial $P\left(x\right)$ such that $f\left(x\right)>P\left(x\right)$ and $P\left(x\right)>0$ on the interval $(a,b)$, then $f\left(x\right)>0$ holds on the interval $(a,b)$. The polynomial $P\left(x\right)>0$ is determined as a polynomial with rational coefficients and is examined on the interval $(a,b)$ with rational endpoints. Then, the proof of the inequality $P\left(x\right)>0$ is an algorithmically decidable problem based on Sturm’s theorem; see Theorem 4.2 in [35]. In this paper, the application of Sturm’s theorem will not be necessary for proving polynomial inequalities.

3. Main Results

In this section, several statements are presented and proven, with a special emphasis on the connection between Jordan’s inequality and stratification. Particularly, for each family of functions induced by the aforementioned inequality (7), the best approximations derived from the minimax approximants are identified in Statements 1 and 2.

Lemma 2.

The two-parameter family of functions

$${\phi }_{p,q}\left(x\right)={\displaystyle \frac{sinx}{x}}-{\displaystyle \frac{2}{\pi }}-p\left({\pi }^q-{\left(2x\right)}^q\right)$$

is individually decreasingly stratified both with respect to the parameter $p\in R^{+}$ and with respect to the parameter $q\in R^{+}$ on the interval $(0,\pi /2)$.

Proof. 

For the first derivative of ${\phi }_{p,q}\left(x\right)$ with respect to p, it holds that

$${\displaystyle \frac{\partial {\phi }_{p,q}\left(x\right)}{\partial p}}={\left(2x\right)}^q-{\pi }^q<0$$

for $x\in (0,\pi /2)$ and $q\in R^{+}$. For the first derivative of ${\phi }_{p,q}\left(x\right)$ with respect to q, it holds that

$${\displaystyle \frac{\partial {\phi }_{p,q}\left(x\right)}{\partial q}}=p\left({\left(2x\right)}^{q}ln\left(2x\right)-{\pi }^{q}ln\left(\pi \right)\right)<0$$

for $x\in (0,\pi /2)$ and $p,q\in R^{+}$. □

Based on the inequality (7), we introduce the following stratified families of functions in the auxiliary statement:

Lemma 3.

Let

$$A\left(q\right)={\displaystyle \frac{\pi -2}{{\pi }^{q+1}}}andB\left(q\right)={\displaystyle \frac{2}{q{\pi }^{q+1}}}.$$

Then, it holds:

• (i) The family of functions

  $${\phi }_{A\left(q\right),q}\left(x\right)={\displaystyle \frac{sinx}{x}}-{\displaystyle \frac{2}{\pi }}-A\left(q\right)\left({\pi }^q-{\left(2x\right)}^q\right)$$

  (8)

  is decreasingly stratified with respect to the parameter $q\in R^{+}$ on the interval $(0,\pi /2)$.
• (ii) The family of functions

  $${\phi }_{B\left(q\right),q}\left(x\right)={\displaystyle \frac{sinx}{x}}-{\displaystyle \frac{2}{\pi }}-B\left(q\right)\left({\pi }^q-{\left(2x\right)}^q\right)$$

  (9)

  is increasingly stratified with respect to the parameter $q\in R^{+}$ on the interval $(0,\pi /2)$.

Proof. 

(i) Since $A\left(q\right)={\displaystyle \frac{\pi -2}{{\pi }^{q+1}}}$, we obtain the one-parameter family of functions:

$${\phi }_{A\left(q\right),q}\left(x\right)={\displaystyle \frac{sinx}{x}}-1+{\left({\displaystyle \frac{2x}{\pi }}\right)}^q\left(1-{\displaystyle \frac{2}{\pi }}\right).$$

(10)

The first derivative of ${\phi }_{A\left(q\right),q}\left(x\right)$ with respect to q is

$${\displaystyle \frac{\partial {\phi }_{A\left(q\right),q}\left(x\right)}{\partial q}}=\left(1-{\displaystyle \frac{2}{\pi }}\right){\left({\displaystyle \frac{2x}{\pi }}\right)}^{q}ln{\displaystyle \frac{2x}{\pi }}.$$

It is evident that

$${\displaystyle \frac{\partial {\phi }_{A\left(q\right),q}\left(x\right)}{\partial q}}<0$$

on the interval $(0,\pi /2)$ for $q\in R^{+}$, which concludes the proof.

• (ii) Since $B\left(q\right)={\displaystyle \frac{2}{q{\pi }^{q+1}}}$, we obtain the one-parameter family of functions:

$${\phi }_{B\left(q\right),q}\left(x\right)={\displaystyle \frac{sinx}{x}}-{\displaystyle \frac{2}{\pi }}-{\displaystyle \frac{2}{q\pi }}+{\displaystyle \frac{2^{q+1}{x}^q}{q{\pi }^{q+1}}}.$$

(11)

The first derivative of ${\phi }_{B\left(q\right),q}\left(x\right)$ with respect to parameter q is

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial {\phi }_{B\left(q\right),q}\left(x\right)}{\partial q}}& =& {\displaystyle \frac{2}{q^2\pi }}+{\displaystyle \frac{2^{q+1}{x}^q\left(qln2+qlnx-qln\pi -1\right)}{q^2{\pi }^{q+1}}}\hfill \\ \hfill & =& {\displaystyle \frac{2}{q^2\pi }}{\left({\displaystyle \frac{2x}{\pi }}\right)}^q\left(ln{\left({\displaystyle \frac{2x}{\pi }}\right)}^q+{\left({\displaystyle \frac{\pi }{2x}}\right)}^q-1\right).\hfill \end{array}$$

Let $t={\left({\displaystyle \frac{2x}{\pi }}\right)}^q$. We now form the following function:

$$g\left(t\right)=ln\left(t\right)+{\displaystyle \frac{1}{t}}-1:(0,1)\to R.$$

Since ${\displaystyle \frac{dg\left(t\right)}{dt}}={\displaystyle \frac{1}{t}}-{\displaystyle \frac{1}{t^2}}<0$ for $t\in (0,1)$, the function $g\left(t\right)$ is decreasing on the interval $(0,1)$. Considering that $g\left(t\right)$ is a decreasing function and that $g\left(1\right)=0$, we conclude that

$$g\left(t\right)>0$$

for $t\in (0,1)$. Thus, it follows that

$${\displaystyle \frac{\partial {\phi }_{B\left(q\right),q}\left(x\right)}{\partial q}}>0$$

on the interval $(0,\pi /2)$ because $g\left(t\right)>0$ on $(0,1)$. This finishes the proof. □

Statement 1.

Let

$$q_1={\displaystyle \frac{2}{\pi -2}}=1.75193\dots and{q}_2=2.$$

Then, it holds:

• (i) If $q\in \left(0,q_1\right]$, then the lower bounds of the function ${\displaystyle \frac{sinx}{x}}$ are given by

$$x\in \left(0,{\displaystyle \frac{\pi }{2}}\right)⟹{\displaystyle \frac{sinx}{x}}>{\displaystyle \frac{2}{\pi }}+A\left(q_1\right)\left({\pi }^{q_1}-{\left(2x\right)}^{q_1}\right)\ge {\displaystyle \frac{2}{\pi }}+A\left(q\right)\left({\pi }^q-{\left(2x\right)}^q\right)$$

and the constant $q_1$ is the best possible.

• (ii) If $q\in (q_1,q_2)$, then the equality

$${\phi }_{A\left(q\right),q}\left(x\right)={\displaystyle \frac{sinx}{x}}-{\displaystyle \frac{2}{\pi }}-A\left(q\right)\left({\pi }^q-{\left(2x\right)}^q\right)=0$$

has a unique solution $x_0^{\left(q\right)}$, and it holds that

$$x\in \left(0,x_0^{\left(q\right)}\right)⟹{\displaystyle \frac{sinx}{x}}>{\displaystyle \frac{2}{\pi }}+A\left(q\right)\left({\pi }^q-{\left(2x\right)}^q\right)$$

and

$$x\in \left(x_0^{\left(q\right)},{\displaystyle \frac{\pi }{2}}\right)⟹{\displaystyle \frac{sinx}{x}}<{\displaystyle \frac{2}{\pi }}+A\left(q\right)\left({\pi }^q-{\left(2x\right)}^q\right).$$

• (iii) If $q\in \left[q_2,+\infty \right)$, then the upper bounds of the function ${\displaystyle \frac{sinx}{x}}$ are given by

$$x\in \left(0,{\displaystyle \frac{\pi }{2}}\right)⟹{\displaystyle \frac{sinx}{x}}<{\displaystyle \frac{2}{\pi }}+A\left(q_2\right)\left({\pi }^{q_2}-{\left(2x\right)}^{q_2}\right)\le {\displaystyle \frac{2}{\pi }}+A\left(q\right)\left({\pi }^q-{\left(2x\right)}^q\right)$$

and the constant $q_2$ is the best possible.

• (iv) Each function from the family ${\phi }_{A\left(q\right),q}\left(x\right)$, for $q\in (q_1,q_2)$, has exactly one maximum and exactly one minimum at certain points $m_1^{\left(q\right)},m_2^{\left(q\right)}\in (0,\pi /2)$, respectively, on the interval $(0,\pi /2)$. Additionally, it holds that $m_1^{\left(q\right)}<m_2^{\left(q\right)}$. The function ${\phi }_{A\left(q\right),q}\left(x\right)$, for $q=q_1$, has exactly one maximum on $(0,\pi /2)$, and for $q=q_2$ has exactly one minimum on $(0,\pi /2)$.
• (v) The equality

$$\left|{\phi }_{A\left(q\right),q}\left(m_1^{\left(q\right)}\right)\right|=\left|{\phi }_{A\left(q\right),q}\left(m_2^{\left(q\right)}\right)\right|$$

has the solution $q=q_0$ for the parameter $q\in (q_1,q_2)$, which is numerically determined as

$$q_0=1.84823\dots .$$

For value

$$d_0=\left|{\phi }_{A\left(q_0\right),q_0}\left(m_1^{\left(q_0\right)}\right)\right|=\left|{\phi }_{A\left(q_0\right),q_0}\left(m_2^{\left(q_0\right)}\right)\right|=0.0026604\dots ,$$

it holds that

$$d_0=\underset{q\in (0,\infty )}{inf}\underset{x\in (0,\pi /2)}{sup}\left|{\phi }_{A\left(q\right),q}\left(x\right)\right|.$$

Hence, the minimax approximant of the family of functions ${\phi }_{A\left(q\right),q}\left(x\right)$ is

$${\phi }_{A\left(q_0\right),q_0}\left(x\right)={\displaystyle \frac{sinx}{x}}-{\displaystyle \frac{2}{\pi }}-A\left(q_0\right)\left({\pi }^{q_0}-{\left(2x\right)}^{q_0}\right),$$

which determines the corresponding (minimax) approximation

$${\displaystyle \frac{sinx}{x}}\approx {\displaystyle \frac{2}{\pi }}+0.043803\dots \left({\pi }^{1.84823\dots }-{\left(2x\right)}^{1.84823\dots }\right).$$

(12)

Proof. 

(i) Let us notice that the assertion is equivalent to ${\phi }_{A\left(q\right),q}\left(x\right)>0$ for $q\le {\displaystyle \frac{2}{\pi -2}}$ and $x\in (0,\pi /2)$. Based on (10), it holds that

$${\phi }_{A\left(q\right),q}\left(x\right)=0⟺q=g\left(x\right)={\displaystyle \frac{ln{\displaystyle \frac{x(\pi -2)}{\pi (x-sinx)}}}{ln{\displaystyle \frac{\pi }{2x}}}}.$$

(13)

We first prove that the function $g\left(x\right)$ is monotonic on the interval $(0,\pi /2)$ using L’Hôpital’s rule for monotonicity (Lemma 1). Let us form the functions $f_1\left(x\right)=ln{\displaystyle \frac{x(\pi -2)}{\pi (x-sinx)}}$ and $f_2\left(x\right)=ln{\displaystyle \frac{\pi }{2x}}$ on $(0,\pi /2)$. Note that $f_1(\pi /2-)=0$ and $f_2(\pi /2-)=0$. It holds that

$${\displaystyle \frac{f_1^{\prime }\left(x\right)}{f_2^{\prime }\left(x\right)}}={\displaystyle \frac{-xcosx+sinx}{x-sinx}}.$$

We now examine the monotonicity of the function $h\left(x\right)={\displaystyle \frac{-xcosx+sinx}{x-sinx}}$ on the interval $(0,\pi /2)$. The first derivative of the function $h\left(x\right)$ is

$$h^{\prime }\left(x\right)={\displaystyle \frac{xcosx+cosxsinx+x^{2}sinx-sinx-x}{{(x-sinx)}^2}}.$$

To examine the sign of the function $h^{\prime }\left(x\right)$, let us examine the sign of the MTP function

$$h_1\left(x\right)=xcosx+cosxsinx+x^{2}sinx-sinx-x=xcosx+{\displaystyle \frac{1}{2}}sin2x+x^{2}sinx-sinx-x$$

on the interval $(0,\pi /2)$.

We prove that $h_1\left(x\right)<0$ using the method from the paper [32]. If we approximate the functions $cosx$ and $sin2x$ using Maclaurin polynomials of degrees 4 and 9, respectively, and approximate the function $sinx$ using the Maclaurin polynomial of degree 5 in the addend $x^{2}sinx$ and using the Maclaurin polynomial of degree 7 in the addend $-sinx$, then the function $h_1\left(x\right)$ has the upward polynomial approximation

$$P_1\left(x\right)={\displaystyle \frac{2}{2835}}{x}^9-{\displaystyle \frac{1}{240}}{x}^7$$

on the interval $(0,\pi /2)$. It is evident that $P_1\left(x\right)<0$ on the interval $(0,\pi /2)$. Thus,

$$h_1\left(x\right)<0$$

on the observed interval. From here, we conclude that

$$h^{\prime }\left(x\right)<0$$

on the interval $(0,\pi /2)$. Thus, $h\left(x\right)={\displaystyle \frac{f_1^{\prime }\left(x\right)}{f_2^{\prime }\left(x\right)}}$ is a decreasing function on the interval $(0,\pi /2)$. Furthermore, since $f_1(\pi /2-)=0$ and $f_2(\pi /2-)=0$, based on L’Hôpital’s rule for monotonicity, it follows that $g\left(x\right)={\displaystyle \frac{f_1\left(x\right)}{f_2\left(x\right)}}$ is also a decreasing function on the interval $(0,\pi /2)$.

By applying L’Hôpital’s rule, it can be shown that

$${\displaystyle \underset{x\to \frac{\pi }{2}-}{lim}g\left(x\right)={\displaystyle \frac{2}{\pi -2}}.}$$

Considering that $g\left(x\right)$ is a decreasing function on the interval $(0,\pi /2)$, we conclude that the function ${\phi }_{A\left(q\right),q}\left(x\right)$, for $q=q_1={\displaystyle \frac{2}{\pi -2}}$, does not have a root on the observed interval. Since ${\displaystyle {\phi }_{A\left(q_1\right),q_1}(\pi /4)={\displaystyle \frac{2^{\frac{-2}{\pi -2}}(\pi -2)-\pi +2\sqrt{2}}{\pi }}=0.0082048\dots >0}$, we conclude that

$${\phi }_{A\left(q_1\right),q_1}\left(x\right)>0$$

for $x\in (0,\pi /2)$. Additionally, based on the stratification (Lemma 3), it holds that

$${\phi }_{A\left(q\right),q}\left(x\right)>{\phi }_{A\left(q_1\right),q_1}\left(x\right)>0$$

for $q<{\displaystyle \frac{2}{\pi -2}}$ on the interval $(0,\pi /2)$.

• (ii) It is easily seen that ${\displaystyle \underset{x\to 0+}{lim}{\phi }_{A\left(q\right),q}\left(x\right)=0}$ and ${\displaystyle \underset{x\to \pi /2-}{lim}{\phi }_{A\left(q\right),q}\left(x\right)=0}$. In part $\left(iv\right)$ of this proof, it will be shown that each function ${\phi }_{A\left(q\right),q}\left(x\right)$, for $q\in (q_1,q_2)$, has exactly one maximum and exactly one minimum on the interval $(0,\pi /2)$, respectively. Hence, the stated inequalities follow.
• (iii) The assertion is equivalent to ${\phi }_{A\left(q\right),q}\left(x\right)<0$ for $q\ge 2$ and $x\in (0,\pi /2)$. Continuing from part $\left(i\right)$ of this proof, using multiple applications of L’Hôpital’s rule, it can be shown that

$${\displaystyle \underset{x\to 0+}{lim}g\left(x\right)=2.}$$

Considering that $g\left(x\right)$ is a decreasing function on the interval $(0,\pi /2)$, we conclude that the function ${\phi }_{A\left(q\right),q}\left(x\right)$, for $q=q_2=2$, does not have a root on the observed interval. Since ${\phi }_{A\left(q_2\right),q_2}(\pi /4)={\displaystyle \frac{8\sqrt{2}-2-3\pi }{4\pi }}=-0.0088386\dots <0$, it holds that

$${\phi }_{A\left(q_2\right),q_2}\left(x\right)<0$$

for $x\in (0,\pi /2)$. Additionally, based on the stratification (Lemma 3), it holds that

$${\phi }_{A\left(q\right),q}\left(x\right)<{\phi }_{A\left(q_2\right),q_2}\left(x\right)<0$$

for $q>2$ on the interval $(0,\pi /2)$.

• (iv) Let us examine the monotonicity of functions from the family ${\phi }_{A\left(q\right),q}\left(x\right)$ for $q\in (q_1,q_2)$ on $(0,\pi /2)$. The fourth derivative of ${\phi }_{A\left(q\right),q}\left(x\right)$ with respect to x is

$${\displaystyle \frac{{\partial }^4{\phi }_{A\left(q\right),q}\left(x\right)}{\partial x^4}}={\displaystyle \frac{x^{q+1}{f}_4\left(q\right)+h_4\left(x\right)}{x^5}},$$

where

$$f_4\left(q\right)={\pi }^{-q-1}{2}^{q}q(q-1)(q-2)(q-3)(\pi -2)$$

and

$$h_4\left(x\right)=4x\left(x^2-6\right)cosx+\left(x^4-12x^2+24\right)sinx.$$

Moreover, the function $h_4\left(x\right)$ is defined at both endpoints of the interval $(0,\pi /2)$, which we will use in the subsequent proof. The first derivative of the function $h_4\left(x\right)$ with respect to x is

$$h_4^{\prime }\left(x\right)=x^{4}cosx>0$$

for $x\in (0,\pi /2)$. Therefore, the function $h_4\left(x\right)$ is increasing on the interval $(0,\pi /2)$. Since $h_4\left(0\right)=0$, it holds that

$$h_4\left(x\right)>0$$

on the interval $(0,\pi /2)$. It is evident that

$$f_4\left(q\right)>0$$

for $q\in (q_1,q_2)$. Hence, we have

$${\displaystyle \frac{{\partial }^4{\phi }_{A\left(q\right),q}\left(x\right)}{\partial x^4}}>0$$

(14)

on $(0,\pi /2)$ for $q\in (q_1,q_2)$. Consequently, each function ${\displaystyle \frac{{\partial }^3{\phi }_{A\left(q\right),q}\left(x\right)}{\partial x^3}}$, for $q\in (q_1,q_2)$, is increasing on $(0,\pi /2)$. The third derivative of ${\phi }_{A\left(q\right),q}\left(x\right)$ with respect to x is

$${\displaystyle \frac{{\partial }^3{\phi }_{A\left(q\right),q}\left(x\right)}{\partial x^3}}={\displaystyle \frac{x^{q+1}{f}_3\left(q\right)+h_3\left(x\right)}{x^4}},$$

where

$$f_3\left(q\right)={\pi }^{-q-1}{2}^{q}q(q-1)(q-2)(\pi -2)\mathrm{and}{h}_3\left(x\right)=\left(-x^3+6x\right)cosx+\left(3x^2-6\right)sinx.$$

It is evident that $f_3\left(q\right)<0$ for $q\in (q_1,q_2)$. It holds that

$${\displaystyle \underset{x\to 0+}{lim}{\displaystyle \frac{f_3\left(q\right)}{x^{3-q}}}=-\infty \left(\mathrm{for} q\in (q_1,q_2)\right)\mathrm{and}\underset{x\to 0+}{lim}{\displaystyle \frac{h_3\left(x\right)}{x^4}}=\underset{x\to 0+}{lim}{\displaystyle \frac{h_3^{\prime }\left(x\right)}{{\left(x^4\right)}^{\prime }}}=\underset{x\to 0+}{lim}{\displaystyle \frac{x^{3}sinx}{4x^3}}=0.}$$

Hence, we have

$${\displaystyle \underset{x\to 0+}{lim}{\displaystyle \frac{{\partial }^3{\phi }_{A\left(q\right),q}\left(x\right)}{\partial x^3}}=-\infty }$$

(15)

for $q\in (q_1,q_2)$. It holds that

$${\displaystyle \underset{x\to \frac{\pi }{2}-}{lim}{\displaystyle \frac{{\partial }^3{\phi }_{A\left(q\right),q}\left(x\right)}{\partial x^3}}={\displaystyle \frac{(8\pi -16)q^3+(48-24\pi )q^2+(16\pi -32)q+12{\pi }^2-96}{{\pi }^4}}:=k_3\left(q\right).}$$

Since $k_3^{\prime }\left(q\right)={\displaystyle \frac{8}{{\pi }^4}}(3q^2-6q+2)(\pi -2)>0$ for $q\in (q_1,q_2)$, it follows that $k_3\left(q\right)$ is an increasing function for $q\in (q_1,q_2)$. Considering that $k_3\left(q\right)$ is an increasing function and that $k_3\left(q_1\right)={\displaystyle \frac{12{\pi }^3-48{\pi }^2-16\pi +160}{{\pi }^3{(\pi -2)}^2}}=0.19968\dots >0$, it can be concluded that

$${\displaystyle \underset{x\to \frac{\pi }{2}-}{lim}{\displaystyle \frac{{\partial }^3{\phi }_{A\left(q\right),q}\left(x\right)}{\partial x^3}}>0}$$

(16)

for $q\in (q_1,q_2)$. Based on (14)–(16), each function ${\displaystyle \frac{{\partial }^2{\phi }_{A\left(q\right),q}\left(x\right)}{\partial x^2}}$, for $q\in (q_1,q_2)$, has exactly one minimum on $(0,\pi /2)$. The second derivative of ${\phi }_{A\left(q\right),q}\left(x\right)$ with respect to x is

$${\displaystyle \frac{{\partial }^2{\phi }_{A\left(q\right),q}\left(x\right)}{\partial x^2}}={\displaystyle \frac{x^{q+1}{f}_2\left(q\right)+h_2\left(x\right)}{x^3}},$$

where

$$f_2\left(q\right)={\pi }^{-q-1}{2}^{q}q(q-1)(\pi -2)\mathrm{and}{h}_2\left(x\right)=-2xcosx-\left(x^2-2\right)sinx.$$

It is evident that $f_2\left(q\right)>0$ for $q\in (q_1,q_2)$. It holds that

$${\displaystyle \underset{x\to 0+}{lim}{\displaystyle \frac{f_2\left(q\right)}{x^{2-q}}}=+\infty \left(\mathrm{for} q\in (q_1,q_2)\right)\mathrm{and}\underset{x\to 0+}{lim}{\displaystyle \frac{h_2\left(x\right)}{x^3}}=\underset{x\to 0+}{lim}{\displaystyle \frac{h_2^{\prime }\left(x\right)}{{\left(x^3\right)}^{\prime }}}=\underset{x\to 0+}{lim}{\displaystyle \frac{-x^{2}cosx}{3x^2}}=-{\displaystyle \frac{1}{3}}.}$$

Hence, we have

$${\displaystyle \underset{x\to 0+}{lim}{\displaystyle \frac{{\partial }^2{\phi }_{A\left(q\right),q}\left(x\right)}{\partial x^2}}=+\infty }$$

(17)

for $q\in (q_1,q_2)$. It holds that

$${\displaystyle \underset{x\to \frac{\pi }{2}-}{lim}{\displaystyle \frac{{\partial }^2{\phi }_{A\left(q\right),q}\left(x\right)}{\partial x^2}}={\displaystyle \frac{(4\pi -8)q^2+(-4\pi +8)q-2{\pi }^2+16}{{\pi }^3}}:=k_2\left(q\right).}$$

Since $k_2^{\prime }\left(q\right)={\displaystyle \frac{4}{{\pi }^3}}(2q-1)(\pi -2)>0$ for $q\in (q_1,q_2)$, it follows that $k_2\left(q\right)$ is an increasing function for $q\in (q_1,q_2)$. Considering that $k_2\left(q\right)$ is an increasing function and that $k_2\left(q_1\right)={\displaystyle \frac{-2{\pi }^2+4\pi +8}{{\pi }^2(\pi -2)}}=0.073414\dots >0$, it can be concluded that

$${\displaystyle \underset{x\to \frac{\pi }{2}-}{lim}{\displaystyle \frac{{\partial }^2{\phi }_{A\left(q\right),q}\left(x\right)}{\partial x^2}}>0}$$

(18)

for $q\in (q_1,q_2)$. We have proven that each function ${\displaystyle \frac{{\partial }^2{\phi }_{A\left(q\right),q}\left(x\right)}{\partial x^2}}$, for $q\in (q_1,q_2)$, has exactly one minimum on $(0,\pi /2)$. Therefore, based on (17) and (18), for functions ${\displaystyle \frac{\partial {\phi }_{A\left(q\right),q}\left(x\right)}{\partial x}}$, for $q\in (q_1,q_2)$, there are two possibilities: either they are increasing, or they have exactly one maximum and exactly one minimum on $(0,\pi /2)$, respectively. We will prove that

$$(\ast )\underset{x\to 0+}{lim}{\displaystyle \frac{\partial {\phi }_{A\left(q\right),q}\left(x\right)}{\partial x}}=0,\underset{x\to \frac{\pi }{2}-}{lim}{\displaystyle \frac{\partial {\phi }_{A\left(q\right),q}\left(x\right)}{\partial x}}>0\mathrm{and}\left({\displaystyle \frac{\partial {\phi }_{A\left(q\right),q}}{\partial x}}\right)\left(x\right){|}_{\begin{array}{c}x=\frac{\pi }{4}\end{array}}<0$$

for $q\in (q_1,q_2)$; thus, it will be clear that each function ${\displaystyle \frac{\partial {\phi }_{A\left(q\right),q}\left(x\right)}{\partial x}}$, for $q\in (q_1,q_2)$, has exactly one maximum and exactly one minimum on $(0,\pi /2)$, respectively. The first derivative of ${\phi }_{A\left(q\right),q}\left(x\right)$ with respect to x is

$${\displaystyle \frac{\partial {\phi }_{A\left(q\right),q}\left(x\right)}{\partial x}}={\displaystyle \frac{x^{q+1}{f}_1\left(q\right)+h_1\left(x\right)}{x^2}},$$

where

$$f_1\left(q\right)={\pi }^{-q-1}{2}^{q}q(\pi -2)\mathrm{and}{h}_1\left(x\right)=xcosx-sinx.$$

It holds that

$${\displaystyle \underset{x\to 0+}{lim}{\displaystyle \frac{f_1\left(q\right)}{x^{1-q}}}=0\left(\mathrm{for} q\in (q_1,q_2)\right)\mathrm{and}\underset{x\to 0+}{lim}{\displaystyle \frac{h_1\left(x\right)}{x^2}}=0.}$$

Hence, we have

$${\displaystyle \underset{x\to 0+}{lim}{\displaystyle \frac{\partial {\phi }_{A\left(q\right),q}\left(x\right)}{\partial x}}=0}$$

(19)

for $q\in (q_1,q_2)$. It is easily seen that

$${\displaystyle \underset{x\to \frac{\pi }{2}-}{lim}{\displaystyle \frac{\partial {\phi }_{A\left(q\right),q}\left(x\right)}{\partial x}}={\displaystyle \frac{2\left(q\right(\pi -2)-2)}{{\pi }^2}}>0}$$

(20)

for $q\in (q_1,q_2)$. We now examine the sign of the functions ${\phi }_{A\left(q\right),q}\left(x\right)$, for $q\in (q_1,q_2)$, at the point $x=\pi /4$. It holds that

$$\left({\displaystyle \frac{\partial {\phi }_{A\left(q\right),q}}{\partial x}}\right)\left(x\right){|}_{\begin{array}{c}x=\frac{\pi }{4}\end{array}}={\displaystyle \frac{2^{-q}q(4\pi -8)+2\sqrt{2}(\pi -4)}{{\pi }^2}}:=k_1\left(q\right).$$

Since $k_1^{\prime }\left(q\right)={\displaystyle \frac{-42^{-q}(\pi -2)(qln2-1)}{{\pi }^2}}<0$ for $q\in (q_1,q_2)$, it follows that $k_1\left(q\right)$ is a decreasing function. Considering that $k_1\left(q\right)$ is a decreasing function and that $k_1\left(q_1\right)={\displaystyle \frac{2^{\frac{3\pi -8}{\pi -2}}\pi -2^{\frac{4\pi -10}{\pi -2}}+(2{\pi }^2-12\pi +16)\sqrt{2}}{(\pi -2){\pi }^2}}=-0.0053418\dots <0$, it can be concluded that

$$\left({\displaystyle \frac{\partial {\phi }_{A\left(q\right),q}}{\partial x}}\right)\left(x\right){|}_{\begin{array}{c}x=\frac{\pi }{4}\end{array}}<0$$

(21)

for $q\in (q_1,q_2)$. Hence, each function ${\displaystyle \frac{\partial {\phi }_{A\left(q\right),q}\left(x\right)}{\partial x}}$, for $q\in (q_1,q_2)$, has exactly one maximum and exactly one minimum on $(0,\pi /2)$, respectively. Note that $(\ast )$ is a substitution for the conjunction (19)–(21). Additionally, based on the monotonicity of the functions ${\displaystyle \frac{\partial {\phi }_{A\left(q\right),q}\left(x\right)}{\partial x}}$ for $q\in (q_1,q_2)$ and $(\ast )$, we can conclude that each function ${\phi }_{A\left(q\right),q}\left(x\right)$, for $q\in (q_1,q_2)$, has exactly one maximum and exactly one minimum on $(0,\pi /2)$, respectively.

• By analyzing the monotonicity of the functions ${\displaystyle \frac{{\partial }^4{\phi }_{A\left(q\right),q}\left(x\right)}{\partial x^4}}$, ${\displaystyle \frac{{\partial }^3{\phi }_{A\left(q\right),q}\left(x\right)}{\partial x^3}}$, ${\displaystyle \frac{{\partial }^2{\phi }_{A\left(q\right),q}\left(x\right)}{\partial x^2}}$, ${\displaystyle \frac{\partial {\phi }_{A\left(q\right),q}\left(x\right)}{\partial x}}$, and ${\phi }_{A\left(q\right),q}\left(x\right)$ for $q=q_1$ and for $q=q_2$, in a similar manner, it can be concluded that the function ${\phi }_{A\left(q\right),q}\left(x\right)$, for $q=q_1$, has exactly one maximum on $(0,\pi /2)$, while the function ${\phi }_{A\left(q\right),q}\left(x\right)$, for $q=q_2$, has exactly one minimum on $(0,\pi /2)$.
• $\left(v\right)$ Note that the infimum of the error $d\left(q\right)={sup}_{x\in (0,\pi /2)}\left|{\phi }_{A\left(q\right),q}\left(x\right)\right|$, for $q\in (q_1,q_2)$, exists and is attained when

$$\left|{\phi }_{A\left(q\right),q}\left(m_1^{\left(q\right)}\right)\right|=\left|{\phi }_{A\left(q\right),q}\left(m_2^{\left(q\right)}\right)\right|.$$

(22)

The Equation (22) can be numerically solved using the computer algebra system Maple, thus yielding the value of the parameter $q=q_0$, which is numerically determined as

$$q_0=1.84823\dots ,$$

which determines the minimax approximant ${\phi }_{A\left(q_0\right),q_0}\left(x\right)$ of the family of functions ${\phi }_{A\left(q\right),q}\left(x\right)$. □

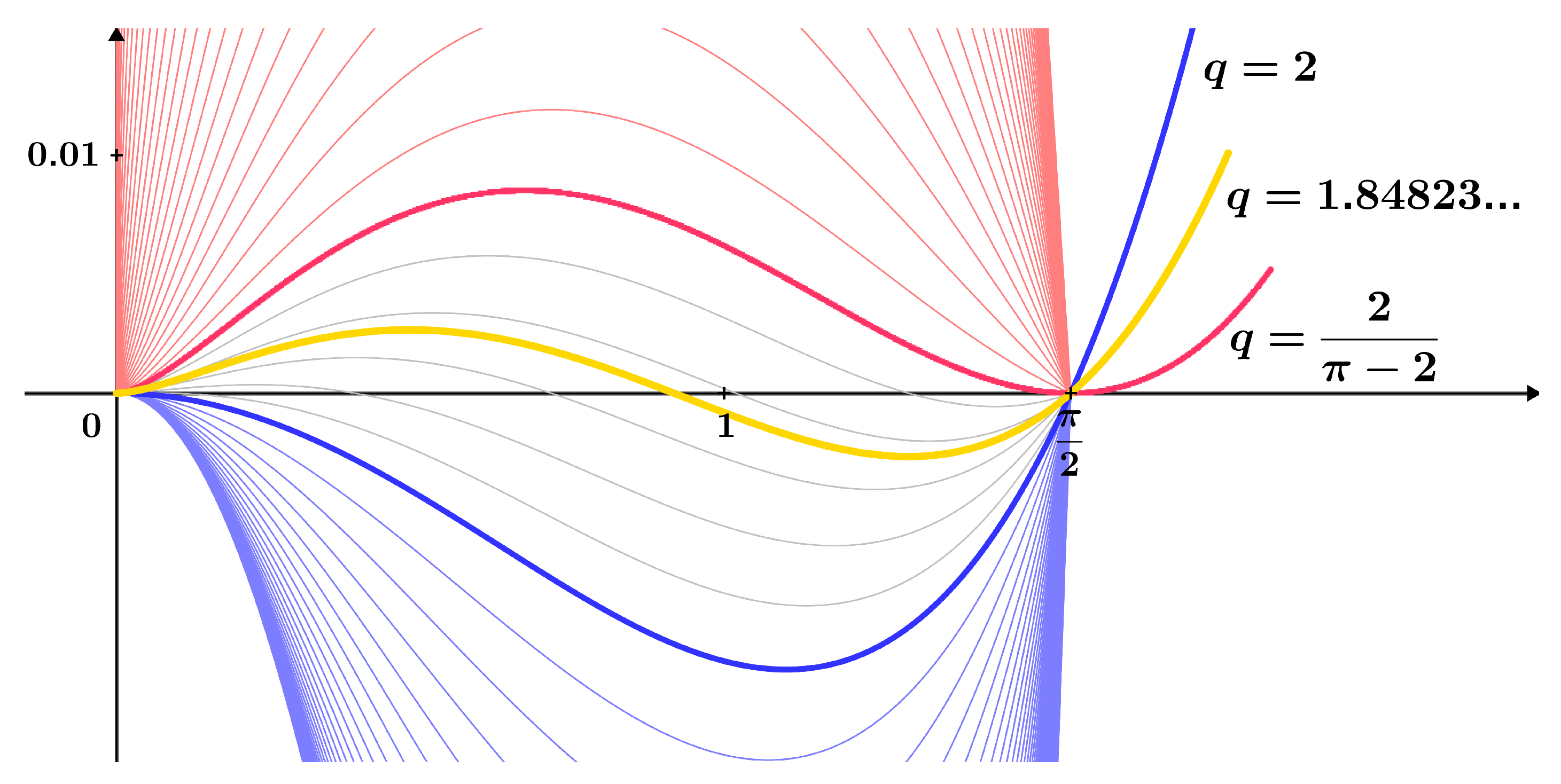
Figure 1 illustrates the stratified family of functions ${\phi }_{A\left(q\right),q}$; see $\left(8\right)$. Cases for all values of the parameter $q\in R^{+}$ are shown, with a special emphasis on the cases with constants obtained in Statement 1.

Figure 1. Stratified family of functions ${\phi }_{A\left(q\right),q}$; see $\left(8\right)$.

Statement 2.

Let

$$q_1={\displaystyle \frac{{\pi }^2}{4}}-1=1.46740\dots and{q}_2={\displaystyle \frac{2}{\pi -2}}=1.75193\dots .$$

Then, it holds:

• (i) If $q\in \left(0,q_1\right]$, then the upper bounds of the function ${\displaystyle \frac{sinx}{x}}$ are given by

  $$x\in \left(0,{\displaystyle \frac{\pi }{2}}\right)⟹{\displaystyle \frac{sinx}{x}}<{\displaystyle \frac{2}{\pi }}+B\left(q_1\right)\left({\pi }^{q_1}-{\left(2x\right)}^{q_1}\right)\le {\displaystyle \frac{2}{\pi }}+B\left(q\right)\left({\pi }^q-{\left(2x\right)}^q\right)$$

  and the constant $q_1$ is the best possible.
• (ii) If $q\in (q_1,q_2)$, then the equality

$${\phi }_{B\left(q\right),q}\left(x\right)={\displaystyle \frac{sinx}{x}}-{\displaystyle \frac{2}{\pi }}-B\left(q\right)\left({\pi }^q-{\left(2x\right)}^q\right)=0$$

has a unique solution $x_0^{\left(q\right)}$, and it holds that

$$x\in \left(0,x_0^{\left(q\right)}\right)⟹{\displaystyle \frac{sinx}{x}}<{\displaystyle \frac{2}{\pi }}+B\left(q\right)\left({\pi }^q-{\left(2x\right)}^q\right)$$

and

$$x\in \left(x_0^{\left(q\right)},{\displaystyle \frac{\pi }{2}}\right)⟹{\displaystyle \frac{sinx}{x}}>{\displaystyle \frac{2}{\pi }}+B\left(q\right)\left({\pi }^q-{\left(2x\right)}^q\right).$$

• (iii) If $q\in \left[q_2,+\infty \right)$, then the lower bounds of the function ${\displaystyle \frac{sinx}{x}}$ are given by

$$x\in \left(0,{\displaystyle \frac{\pi }{2}}\right)⟹{\displaystyle \frac{sinx}{x}}>{\displaystyle \frac{2}{\pi }}+B\left(q_2\right)\left({\pi }^{q_2}-{\left(2x\right)}^{q_2}\right)\ge {\displaystyle \frac{2}{\pi }}+B\left(q\right)\left({\pi }^q-{\left(2x\right)}^q\right)$$

and the constant $q_2$ is the best possible.

• (iv) Each function from the family ${\phi }_{B\left(q\right),q}\left(x\right)$, for $q\in (q_1,q_2]$, has exactly one maximum at a point $m^{\left(q\right)}\in (0,\pi /2)$ on the interval $(0,\pi /2)$.
• (v) The equality

$$\left|{\phi }_{B\left(q\right),q}\left(0+\right)\right|=\left|{\phi }_{B\left(q\right),q}\left(m^{\left(q\right)}\right)\right|$$

has the solution $q=q_0$ for the parameter $q\in (q_1,q_2)$, which is numerically determined as

$$q_0=1.72287\dots .$$

For value

$$d_0=\left|{\phi }_{B\left(q_0\right),q_0}\left(0+\right)\right|=\left|{\phi }_{B\left(q_0\right),q_0}\left(m^{\left(q_0\right)}\right)\right|=0.0061296\dots ,$$

it holds that

$$d_0=\underset{q\in (0,\infty )}{inf}\underset{x\in (0,\pi /2)}{sup}\left|{\phi }_{B\left(q\right),q}\left(x\right)\right|.$$

Hence, the minimax approximant of the family of functions ${\phi }_{B\left(q\right),q}\left(x\right)$ is

$${\phi }_{B\left(q_0\right),q_0}\left(x\right)={\displaystyle \frac{sinx}{x}}-{\displaystyle \frac{2}{\pi }}-B\left(q_0\right)\left({\pi }^{q_0}-{\left(2x\right)}^{q_0}\right),$$

which determines the corresponding (minimax) approximation

$${\displaystyle \frac{sinx}{x}}\approx {\displaystyle \frac{2}{\pi }}+0.051415\dots \left({\pi }^{1.72287\dots }-{\left(2x\right)}^{1.72287\dots }\right).$$

(23)

Proof. 

$\left(i\right)$ Let us notice that the assertion is equivalent to ${\phi }_{B\left(q\right),q}\left(x\right)<0$ for $q\le {\displaystyle \frac{{\pi }^2}{4}}-1$ and $x\in (0,\pi /2)$. We begin by proving that ${\phi }_{B\left(q\right),q}\left(x\right)$ is a monotonic function on the interval $(0,\pi /2)$ for $q={\displaystyle \frac{{\pi }^2}{4}}-1$. Through elementary transformations, based on (11), it can be shown that the following equivalence holds:

$$\begin{array}{cc}& {\displaystyle \frac{\partial {\phi }_{B\left(q\right),q}\left(x\right)}{\partial x}}={\displaystyle \frac{xcosx-sinx+{\left({\displaystyle \frac{2x}{\pi }}\right)}^{q+1}}{x^2}}=0\\ ⟺& q=g\left(x\right)={\displaystyle \frac{ln{\displaystyle \frac{2x}{\pi (-xcosx+sinx)}}}{ln{\displaystyle \frac{\pi }{2x}}}}.\end{array}$$

(24)

It is necessary to prove that $g\left(x\right)\ne {\displaystyle \frac{{\pi }^2}{4}}-1$ for every $x\in (0,\pi /2)$ in order for the function ${\phi }_{B\left(q\right),q}\left(x\right)$ to be monotonic on the interval $(0,\pi /2)$ for $q={\displaystyle \frac{{\pi }^2}{4}}-1$. We first prove that the function $g\left(x\right)$ is monotonic on the interval $(0,\pi /2)$ by applying L’Hôpital’s rule for monotonicity (Lemma 1). Let us form the functions $f_1\left(x\right)=ln{\displaystyle \frac{2x}{\pi (-xcosx+sinx)}}$ and $f_2\left(x\right)=ln{\displaystyle \frac{\pi }{2x}}$ on $(0,\pi /2)$. Note that $f_1(\pi /2-)=0$ and $f_2(\pi /2-)=0$. It holds that

$${\displaystyle \frac{f_1^{\prime }\left(x\right)}{f_2^{\prime }\left(x\right)}}={\displaystyle \frac{xcosx+x^{2}sinx-sinx}{-xcosx+sinx}}.$$

We now examine the monotonicity of the function $h\left(x\right)={\displaystyle \frac{xcosx+x^{2}sinx-sinx}{-xcosx+sinx}}$ on the interval $(0,\pi /2)$. The first derivative of the function $h\left(x\right)$ is

$$h^{\prime }\left(x\right)={\displaystyle \frac{-x(xcosxsinx-2{sin}^{2}x+x^2)}{{(-xcosx+sinx)}^2}}.$$

Let us examine the sign of the MTP function

$$h_1\left(x\right)=xcosxsinx-2{sin}^{2}x+x^2=cos2x+{\displaystyle \frac{1}{2}}xsin2x+x^2-1$$

on the interval $(0,\pi /2)$. If we approximate the functions $cos2x$ and $sin2x$ using Maclaurin polynomials of degrees 6 and 7, respectively, then the function $h_1\left(x\right)$ has the downward polynomial approximation

$$P_1\left(x\right)=-{\displaystyle \frac{4}{315}}{x}^8+{\displaystyle \frac{2}{45}}{x}^6$$

on the interval $(0,\pi /2)$. It is evident that $P_1\left(x\right)>0$ on the interval $(0,\pi /2)$. Thus,

$$h_1\left(x\right)>0$$

on the observed interval. From here, we conclude that

$$h^{\prime }\left(x\right)<0$$

on the observed interval. Thus, $h\left(x\right)={\displaystyle \frac{f_1^{\prime }\left(x\right)}{f_2^{\prime }\left(x\right)}}$ is a decreasing function on the interval $(0,\pi /2)$. Furthermore, since $f_1(\pi /2-)=0$ and $f_2(\pi /2-)=0$, based on L’Hôpital’s rule for monotonicity, it follows that $g\left(x\right)={\displaystyle \frac{f_1\left(x\right)}{f_2\left(x\right)}}$ is also a decreasing function on the interval $(0,\pi /2)$. By applying L’Hôpital’s rule, it can be shown that

$${\displaystyle \underset{x\to \frac{\pi }{2}-}{lim}g\left(x\right)={\displaystyle \frac{{\pi }^2}{4}}-1.}$$

Hence, $g\left(x\right)>{\displaystyle \frac{{\pi }^2}{4}}-1$ on the interval $(0,\pi /2)$. Thus, the function ${\phi }_{B\left(q\right),q}\left(x\right)$, for $q=q_1={\displaystyle \frac{{\pi }^2}{4}}-1$, is monotonic on the interval $(0,\pi /2)$. It holds that ${\displaystyle \underset{x\to 0+}{lim}{\phi }_{B\left(q_1\right),q_1}\left(x\right)={\displaystyle \frac{{\pi }^2-2\pi -4}{{\pi }^2-4}}=-0.070461\dots <0}$ and ${\displaystyle \underset{x\to \pi /2-}{lim}{\phi }_{B\left(q_1\right),q_1}\left(x\right)=0}$. Therefore, ${\phi }_{B\left(q_1\right),q_1}\left(x\right)$ is an increasing function and negative on $(0,\pi /2)$. Considering that ${\phi }_{B\left(q_1\right),q_1}\left(x\right)<0$, based on the stratification (Lemma 3), it holds that

$${\phi }_{B\left(q\right),q}\left(x\right)<{\phi }_{B\left(q_1\right),q_1}\left(x\right)<0$$

for $q<{\displaystyle \frac{{\pi }^2}{4}}-1$ on the interval $(0,\pi /2)$.

• (ii) Continuing from the previous part of the proof, $\left(i\right)$, using multiple applications of L’Hôpital’s rule, it can be shown that

$${\displaystyle \underset{x\to 0+}{lim}g\left(x\right)=2.}$$

The function $g\left(x\right)$ from (24) determines the values of the parameter q for which the family of functions ${\phi }_{B\left(q\right),q}\left(x\right)$ have extremes or inflection points on the interval $(0,\pi /2)$. Considering that the function $g\left(x\right)$ is monotonic on $(0,\pi /2)$ and that ${\displaystyle \underset{x\to 0+}{lim}g\left(x\right)=2}$ and ${\displaystyle \underset{x\to \pi /2-}{lim}g\left(x\right)={\displaystyle \frac{{\pi }^2}{4}}-1=q_1}$, every function from the family ${\phi }_{B\left(q\right),q}\left(x\right)$ has either exactly one extremum or exactly one inflection point on the interval $(0,\pi /2)$ for $q\in \left({\displaystyle \frac{{\pi }^2}{4}}-1,2\right)$ and therefore for $q\in (q_1,q_2]$, where $q_2={\displaystyle \frac{2}{\pi -2}}$, since $q_2<2$. Let us prove that each function ${\phi }_{B\left(q\right),q}\left(x\right)$, for $q\in (q_1,q_2)$, has exactly one maximum on the interval $(0,\pi /2)$ by proving that all these functions are negative in the right neighborhood of zero and positive and decreasing in the left neighborhood of $\pi /2$.

It holds that

$${\displaystyle \underset{x\to 0+}{lim}{\phi }_{B\left(q\right),q}\left(x\right)={\displaystyle \frac{(\pi -2)q-2}{\pi q}}.}$$

Therefore, there exists a right neighborhood of zero such that

$${\phi }_{B\left(q\right),q}\left(x\right)<0$$

(25)

for $q\in (q_1,q_2)$. The Taylor expansion of the family of functions ${\phi }_{B\left(q\right),q}\left(x\right)$ around $\pi /2$ is

$${\phi }_{B\left(q\right),q}\left(x\right)={\displaystyle \frac{4q-{\pi }^2+4}{{\pi }^3}}{\left(x-{\displaystyle \frac{\pi }{2}}\right)}^2+O\left({\left(x-{\displaystyle \frac{\pi }{2}}\right)}^3\right).$$

Therefore, there exists a left neighborhood of $\pi /2$ such that

$${\phi }_{B\left(q\right),q}\left(x\right)>0\mathrm{and}{\displaystyle \frac{\partial {\phi }_{B\left(q\right),q}\left(x\right)}{\partial x}}<0$$

(26)

for $q\in (q_1,q_2)$. Based on (25) and (26), the functions ${\phi }_{B\left(q\right),q}\left(x\right)$, for $q\in (q_1,q_2)$, have exactly one maximum on the interval $(0,\pi /2)$, and the stated inequalities follow.

• (iii) The assertion is equivalent to ${\phi }_{B\left(q\right),q}\left(x\right)>0$ for $q\ge {\displaystyle \frac{2}{\pi -2}}$ and $x\in (0,\pi /2)$. Let us notice that $A\left(q\right)=B\left(q\right)$ for $q={\displaystyle \frac{2}{\pi -2}}$, where $A\left(q\right)={\displaystyle \frac{\pi -2}{{\pi }^{q+1}}}$. In Statement 1, it has already been proven that ${\phi }_{A\left(q\right),q}\left(x\right)={\phi }_{B\left(q\right),q}\left(x\right)>0$ for $q=q_2={\displaystyle \frac{2}{\pi -2}}$ on the interval $(0,\pi /2)$. Given that the family of functions ${\phi }_{B\left(q\right),q}\left(x\right)$ is increasingly stratified with respect to the parameter q based on Lemma 3, for $q>{\displaystyle \frac{2}{\pi -2}}$, it will also hold that

$${\phi }_{B\left(q\right),q}\left(x\right)>{\phi }_{B\left(q_2\right),q_2}\left(x\right)>0$$

on the interval $(0,\pi /2)$.

• (iv) It has been established in part $\left(ii\right)$ of the proof for $q\in (q_1,q_2)$. Similarly, the proof holds for $q=q_2$.
• (v) Note that the infimum of the error $d\left(q\right)={sup}_{x\in (0,\pi /2)}\left|{\phi }_{B\left(q\right),q}\left(x\right)\right|$, for $q\in (q_1,q_2)$, exists and is attained when

$$\left|{\phi }_{B\left(q\right),q}\left(0+\right)\right|=\left|{\phi }_{B\left(q\right),q}\left(m^{\left(q\right)}\right)\right|.$$

(27)

Equation (27) can be numerically solved using the computer algebra system Maple, thus yielding the value of the parameter $q=q_0$, which is numerically determined as

$$q_0=1.72287\dots ,$$

which determines the minimax approximant ${\phi }_{B\left(q_0\right),q_0}\left(x\right)$ of the family of functions ${\phi }_{B\left(q\right),q}\left(x\right)$. □

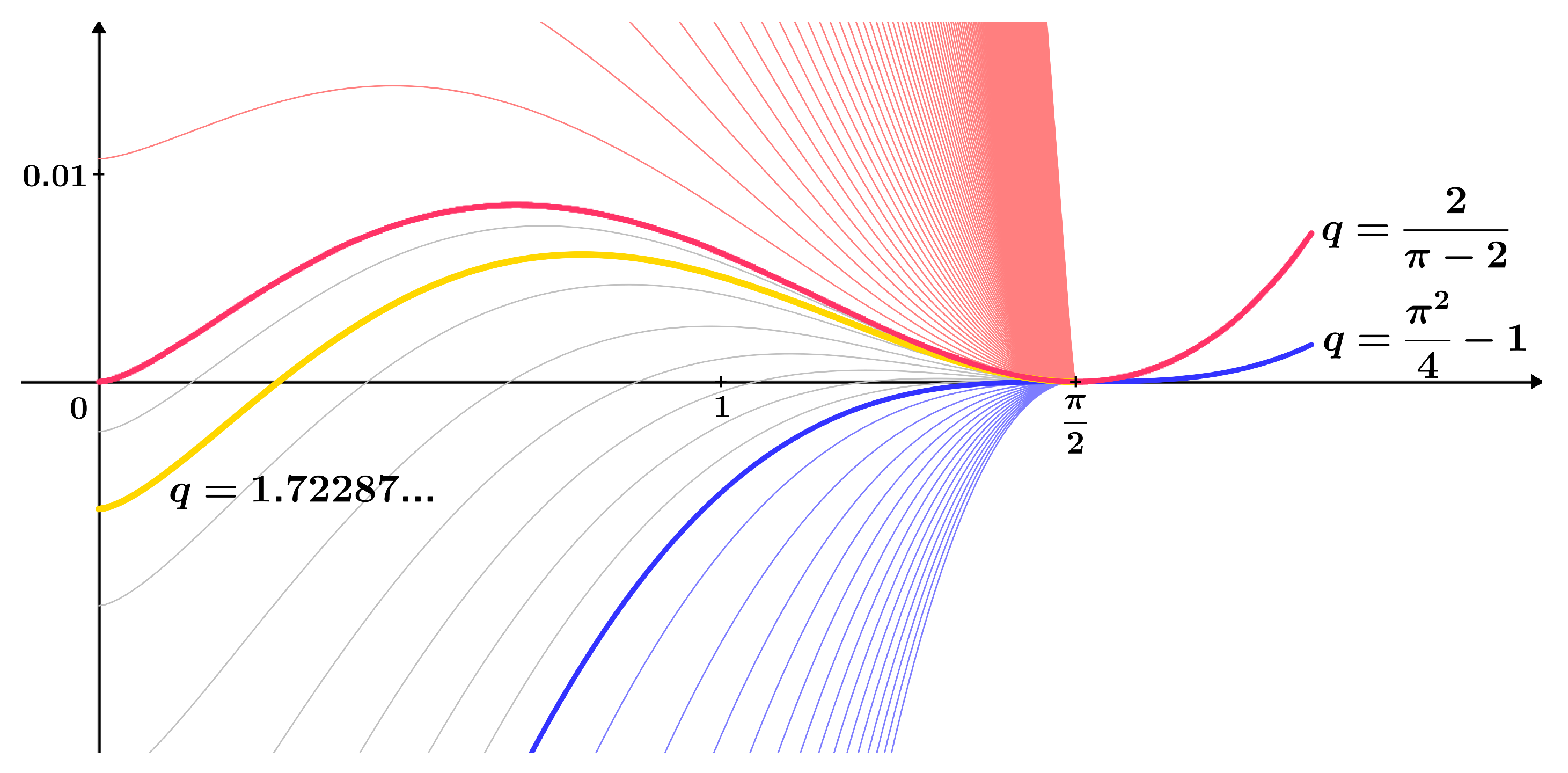
Figure 2 illustrates the stratified family of functions ${\phi }_{B\left(q\right),q}$; see $\left(9\right)$. Cases for all values of the parameter $q\in R^{+}$ are shown, with a special emphasis on the cases with constants obtained in Statement 2.

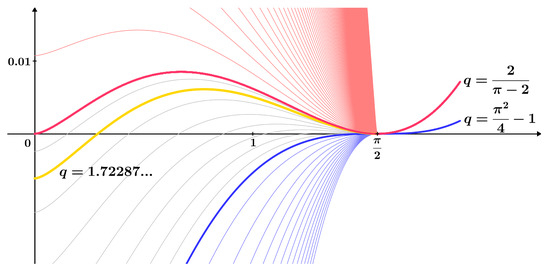
Figure 2. Stratified family of functions ${\phi }_{B\left(q\right),q}$; see $\left(9\right)$.

In the style of writing Theorem 6, based on Statements 1 and 2, we present the following assertion:

Statement 3.

Let $x\in \left(0,{\displaystyle \frac{\pi }{2}}\right]$. Then, we have the following:

• (i) For $q_1\in \left(0,{\displaystyle \frac{{\pi }^2}{4}}-1\right]=\left(0,1.46740\dots \right]$ and $q_2\in \left(0,{\displaystyle \frac{2}{\pi -2}}\right]=\left(0,1.75193\dots \right]$, it holds that

$${\displaystyle \frac{2}{\pi }}+{\displaystyle \frac{2}{q_1{\pi }^{q_1+1}}}\left({\pi }^{q_1}-{\left(2x\right)}^{q_1}\right)\ge {\displaystyle \frac{sinx}{x}}\ge {\displaystyle \frac{2}{\pi }}+{\displaystyle \frac{\pi -2}{{\pi }^{q_2+1}}}\left({\pi }^{q_2}-{\left(2x\right)}^{q_2}\right).$$

(28)

• (ii) For $q_1\in \left[{\displaystyle \frac{2}{\pi -2}},+\infty \right)=\left[1.75193\dots ,+\infty \right)$ and $q_2\in \left[2,+\infty \right)$, it holds that

$${\displaystyle \frac{2}{\pi }}+{\displaystyle \frac{2}{q_1{\pi }^{q_1+1}}}\left({\pi }^{q_1}-{\left(2x\right)}^{q_1}\right)\le {\displaystyle \frac{sinx}{x}}\le {\displaystyle \frac{2}{\pi }}+{\displaystyle \frac{\pi -2}{{\pi }^{q_2+1}}}\left({\pi }^{q_2}-{\left(2x\right)}^{q_2}\right).$$

(29)

Remark 1.

The equalities in (28) and (29) clearly hold for $x=\pi /2$.

Remark 2.

Note that the inequalities (28) and (29) reduce to inequalities (6) and (7), respectively, when $q_1,q_2\in N$.

4. Applications

In this section, we present two applications. The first application is about the improvements and expansions of Theorems 2–5. The second application refers to obtaining some approximations of the $\mathrm{sinc}$ function based on some upper and lower bounds of this function and minimax approximants of the corresponding families of functions.

4.1. Improvements of Theorems 2–5

In order to obtain a generalization of all inequalities from Theorems 3–6 for the stratified family of functions ${\phi }_{p,q}\left(x\right)$ from Lemma 2, we considered the values of the parameter $p=A\left(q\right)={\displaystyle \frac{\pi -2}{{\pi }^{q+1}}}$ and $p=B\left(q\right)={\displaystyle \frac{2}{q{\pi }^{q+1}}}$ as functions depending on the parameter q. It is possible to consider the family of functions ${\phi }_{p,q}\left(x\right)$ from Lemma 2 by fixing either parameter p or q to some real value. For the cases $q=1$, $q=2$, $q=3$, and $q=4$, by applying Statements 1 and 2, improvements and extensions of Theorems 2–5, respectively, can be obtained, as will be shown in the following. Particularly, for each family of functions induced by the considered inequalities, the best approximations derived from the minimax approximants are identified in Statements 4–7.

In order to improve and extend Theorem 2, we consider the family of functions ${\phi }_{p,q}\left(x\right)$ for the case $q=1$. The family of functions ${\phi }_{p,1}\left(x\right)$ reduces to

$${\phi }_{p,1}\left(x\right)={\displaystyle \frac{sinx}{x}}-{\displaystyle \frac{2}{\pi }}-p(\pi -2x)$$

(30)

and is decreasingly stratified with respect to the parameter $p\in R^{+}$ on the interval $(0,\pi /2)$, as proven in Lemma 2. For this family, the following statement holds:

Statement 4.

Let

$$p_1={\displaystyle \frac{\pi -2}{{\pi }^2}}=0.11566\dots and{p}_2={\displaystyle \frac{2}{{\pi }^2}}=0.20264\dots .$$

Then, it holds:

• (i) If $p\in (0,p_1]$, then

$$x\in \left(0,{\displaystyle \frac{\pi }{2}}\right)⟹{\displaystyle \frac{sinx}{x}}>{\displaystyle \frac{2}{\pi }}+p_1(\pi -2x)\ge {\displaystyle \frac{2}{\pi }}+p(\pi -2x).$$

• (ii) If $p\in (p_1,p_2)$, then the equality

$${\phi }_{p,1}\left(x\right)={\displaystyle \frac{sinx}{x}}-{\displaystyle \frac{2}{\pi }}-p(\pi -2x)=0$$

has a unique solution $x_0^{\left(p\right)}$, and it holds that

$$x\in \left(0,x_0^{\left(p\right)}\right)⟹{\displaystyle \frac{sinx}{x}}<{\displaystyle \frac{2}{\pi }}+p(\pi -2x)$$

and

$$x\in \left(x_0^{\left(p\right)},{\displaystyle \frac{\pi }{2}}\right)⟹{\displaystyle \frac{sinx}{x}}>{\displaystyle \frac{2}{\pi }}+p(\pi -2x).$$

• (iii) If $p\in [p_2,+\infty )$, then

$$x\in \left(0,{\displaystyle \frac{\pi }{2}}\right)⟹{\displaystyle \frac{sinx}{x}}<{\displaystyle \frac{2}{\pi }}+p_2(\pi -2x)\le {\displaystyle \frac{2}{\pi }}+p(\pi -2x).$$

• (iv) Each function from the family ${\phi }_{p,1}\left(x\right)$, for $p\in (p_1,p_2]$, has exactly one maximum at a point $m^{\left(p\right)}\in (0,\pi /2)$ on the interval $(0,\pi /2)$.
• (v) The equality

$$\left|{\phi }_{p,1}\left(0+\right)\right|=\left|{\phi }_{p,1}\left(m^{\left(p\right)}\right)\right|$$

has the solution $p=p_0$ for the parameter $p\in (p_1,p_2)$, which is numerically determined as

$$p_0=0.13323\dots .$$

For value

$$d_0=\left|{\phi }_{p_0,1}\left(0+\right)\right|=\left|{\phi }_{p_0,1}\left(m^{\left(p_0\right)}\right)\right|=0.055187\dots ,$$

it holds that

$$d_0=\underset{p\in (0,\infty )}{inf}\underset{x\in (0,\pi /2)}{sup}\left|{\phi }_{p,1}\left(x\right)\right|.$$

Hence, the minimax approximant of the family of functions ${\phi }_{p,1}\left(x\right)$ is

$${\phi }_{p_0,1}\left(x\right)={\displaystyle \frac{sinx}{x}}-{\displaystyle \frac{2}{\pi }}-p_0(\pi -2x),$$

which determines the corresponding (minimax) approximation

$${\displaystyle \frac{sinx}{x}}\approx {\displaystyle \frac{2}{\pi }}+0.13323\dots (\pi -2x).$$

(31)

Proof. 

(i) The claim follows directly from Statement 1 and based on the stratification. Namely, for $q=1$, it holds that $A\left(q\right)={\displaystyle \frac{\pi -2}{{\pi }^{q+1}}}=p_1$.

• (ii) Let us examine the monotonicity of functions ${\phi }_{p,1}\left(x\right)$ for $p\in (p_1,p_2)$ on the interval $(0,\pi /2)$ in a similar manner as in the proof of Statement 1. The second derivative of ${\phi }_{p,1}\left(x\right)$ with respect to x is

$${\displaystyle \frac{{\partial }^2{\phi }_{p,1}\left(x\right)}{\partial x^2}}={\displaystyle \frac{f\left(x\right)}{x^3}},$$

where the function $f\left(x\right)$ is an MTP function given by

$$f\left(x\right)=-2xcosx-x^{2}sinx+2sinx.$$

Let us note that

$$f^{\prime }\left(x\right)=-x^{2}cosx<0$$

on the interval $(0,\pi /2)$. Thus, the function $f\left(x\right)$ is decreasing on the observed interval. Considering that $f\left(x\right)$ is a decreasing function on the interval $(0,\pi /2)$ and that $f(0+)=0$, it follows that

$$f\left(x\right)<0$$

for $x\in (0,\pi /2)$. Hence,

$${\displaystyle \frac{{\partial }^2{\phi }_{p,1}\left(x\right)}{\partial x^2}}<0$$

(32)

for $x\in (0,\pi /2)$.

The Taylor expansion of the family of functions ${\phi }_{p,1}\left(x\right)$ around zero is

$${\phi }_{p,1}\left(x\right)=\left(1-{\displaystyle \frac{2}{\pi }}-p\pi \right)+2px+O\left(x^2\right).$$

Therefore, there exists a right neighborhood of zero such that

$${\phi }_{p,1}\left(x\right)<0\mathrm{and}{\displaystyle \frac{\partial {\phi }_{p,1}\left(x\right)}{\partial x}}>0$$

(33)

for $p\in (p_1,p_2)$. The Taylor expansion of the family of functions ${\phi }_{p,1}\left(x\right)$ around $\pi /2$ is

$${\phi }_{p,1}\left(x\right)=\left(-{\displaystyle \frac{4}{{\pi }^2}}+2p\right)\left(x-{\displaystyle \frac{\pi }{2}}\right)+O\left({\left(x-{\displaystyle \frac{\pi }{2}}\right)}^2\right).$$

Therefore, there exists a left neighborhood of $\pi /2$ such that

$${\phi }_{p,1}\left(x\right)>0\mathrm{and}{\displaystyle \frac{\partial {\phi }_{p,1}\left(x\right)}{\partial x}}<0$$

(34)

for $p\in (p_1,p_2)$.

By analyzing the monotonicity of the functions ${\displaystyle \frac{{\partial }^2{\phi }_{p,1}\left(x\right)}{\partial x^2}}$, ${\displaystyle \frac{\partial {\phi }_{p,1}\left(x\right)}{\partial x}}$, and ${\phi }_{p,1}\left(x\right)$ for $p\in (p_1,p_2)$ on the interval $(0,\pi /2)$, in a similar manner as in the proof of Statement 1 and based on (32)–(34), it can be concluded that each function ${\phi }_{p,1}\left(x\right)$, for $p\in (p_1,p_2)$, has exactly one maximum on the interval $(0,\pi /2)$. From ${\displaystyle \underset{x\to 0+}{lim}{\phi }_{p,1}\left(x\right)<0}$ and ${\displaystyle \underset{x\to \pi /2-}{lim}{\phi }_{p,1}\left(x\right)>0}$, for $p\in (p_1,p_2)$, the corresponding inequalities follow.

• (iii) The claim follows directly from Statement 2 and based on the stratification. Namely, for $q=1$, it holds that $B\left(q\right)={\displaystyle \frac{2}{q{\pi }^{q+1}}}=p_2$.
• (iv) It has been proven within proof $\left(ii\right)$.
• (v) Note that the infimum of the error $d\left(p\right)={sup}_{x\in (0,\pi /2)}\left|{\phi }_{p,1}\left(x\right)\right|$, for $p\in (p_1,p_2)$, exists and is attained when

$$\left|{\phi }_{p,1}\left(0+\right)\right|=\left|{\phi }_{p,1}\left(m^{\left(p\right)}\right)\right|.$$

(35)

Equation (35) can be numerically solved using the computer algebra system Maple, thus yielding the value of the parameter $p=p_0$, which is numerically determined as

$$p_0=0.13323\dots ,$$

which determines the minimax approximant ${\phi }_{p_0,1}\left(x\right)$ of the family of functions ${\phi }_{p,1}\left(x\right)$. □

In order to improve and extend Theorem 3, we consider the family of functions ${\phi }_{p,q}\left(x\right)$ for the case $q=2$. The family of functions ${\phi }_{p,2}\left(x\right)$ reduces to

$${\phi }_{p,2}\left(x\right)={\displaystyle \frac{sinx}{x}}-{\displaystyle \frac{2}{\pi }}-p\left({\pi }^2-4x^2\right)$$

(36)

and is decreasingly stratified with respect to the parameter $p\in R^{+}$ on the interval $(0,\pi /2)$, as proven in Lemma 2. For this family, the following statement holds:

Statement 5.

Let

$$p_1={\displaystyle \frac{1}{{\pi }^3}}=0.032251\dots and{p}_2={\displaystyle \frac{\pi -2}{{\pi }^3}}=0.036818\dots .$$

Then, it holds:

• (i) If $p\in (0,p_1]$, then

$$x\in \left(0,{\displaystyle \frac{\pi }{2}}\right)⟹{\displaystyle \frac{sinx}{x}}>{\displaystyle \frac{2}{\pi }}+p_1\left({\pi }^2-4x^2\right)\ge {\displaystyle \frac{2}{\pi }}+p\left({\pi }^2-4x^2\right).$$

• (ii) If $p\in (p_1,p_2)$, then the equality

$${\phi }_{p,2}\left(x\right)={\displaystyle \frac{sinx}{x}}-{\displaystyle \frac{2}{\pi }}-p\left({\pi }^2-4x^2\right)=0$$

has a unique solution $x_0^{\left(p\right)}$, and it holds that

$$x\in \left(0,x_0^{\left(p\right)}\right)⟹{\displaystyle \frac{sinx}{x}}>{\displaystyle \frac{2}{\pi }}+p\left({\pi }^2-4x^2\right)$$

and

$$x\in \left(x_0^{\left(p\right)},{\displaystyle \frac{\pi }{2}}\right)⟹{\displaystyle \frac{sinx}{x}}<{\displaystyle \frac{2}{\pi }}+p\left({\pi }^2-4x^2\right).$$

• (iii) If $p\in [p_2,+\infty )$, then

$$x\in \left(0,{\displaystyle \frac{\pi }{2}}\right)⟹{\displaystyle \frac{sinx}{x}}<{\displaystyle \frac{2}{\pi }}+p_2\left({\pi }^2-4x^2\right)\le {\displaystyle \frac{2}{\pi }}+p\left({\pi }^2-4x^2\right).$$

• (iv) Each function from the family ${\phi }_{p,2}\left(x\right)$, for $p\in (p_1,p_2]$, has exactly one minimum at a point $m^{\left(p\right)}\in (0,\pi /2)$ on the interval $(0,\pi /2)$.
• (v) The equality

$$\left|{\phi }_{p,2}\left(0+\right)\right|=\left|{\phi }_{p,2}\left(m^{\left(p\right)}\right)\right|$$

has the solution $p=p_0$ for the parameter $p\in (p_1,p_2)$, which is numerically determined as

$$p_0=0.036014\dots .$$

For value

$$d_0=\left|{\phi }_{p_0,2}\left(0+\right)\right|=\left|{\phi }_{p_0,2}\left(m^{\left(p_0\right)}\right)\right|=0.0079283\dots ,$$

it holds that

$$d_0=\underset{p\in (0,\infty )}{inf}\underset{x\in (0,\pi /2)}{sup}\left|{\phi }_{p,2}\left(x\right)\right|.$$

Hence, the minimax approximant of the family of functions ${\phi }_{p,2}\left(x\right)$ is

$${\phi }_{p_0,2}\left(x\right)={\displaystyle \frac{sinx}{x}}-{\displaystyle \frac{2}{\pi }}-p_0\left({\pi }^2-4x^2\right),$$

which determines the corresponding (minimax) approximation

$${\displaystyle \frac{sinx}{x}}\approx {\displaystyle \frac{2}{\pi }}+0.036014\dots \left({\pi }^2-4x^2\right).$$

(37)

Proof. 

$\left(i\right)$ The claim follows directly from Statement 2 and based on the stratification. Namely, for $q=2$, it holds that $B\left(q\right)={\displaystyle \frac{2}{q{\pi }^{q+1}}}=p_1$.

• (ii) Let us examine the monotonicity of functions ${\phi }_{p,2}\left(x\right)$ for $p\in (p_1,p_2)$ on the interval $(0,\pi /2)$ in a similar manner as in the proof of Statement 1. The third derivative of ${\phi }_{p,2}\left(x\right)$ with respect to x is

$${\displaystyle \frac{{\partial }^3{\phi }_{p,2}\left(x\right)}{\partial x^3}}={\displaystyle \frac{f\left(x\right)}{x^4}},$$

where the function $f\left(x\right)$ is an MTP function given by

$$f\left(x\right)=-x^{3}cosx+6xcosx+3x^{2}sinx-6sinx.$$

Let us note that

$$f^{\prime }\left(x\right)=x^{3}sinx>0$$

on the interval $(0,\pi /2)$. Thus, the function $f\left(x\right)$ is increasing on the observed interval. Considering that $f\left(x\right)$ is an increasing function on the interval $(0,\pi /2)$ and that $f(0+)=0$, it follows that

$$f\left(x\right)>0$$

for $x\in (0,\pi /2)$. Hence,

$${\displaystyle \frac{{\partial }^3{\phi }_{p,2}\left(x\right)}{\partial x^3}}>0$$

(38)

for $x\in (0,\pi /2)$.

The Taylor expansion of the family of functions ${\phi }_{p,2}\left(x\right)$ around zero is

$${\phi }_{p,2}\left(x\right)=\left(1-{\displaystyle \frac{2}{\pi }}-p{\pi }^2\right)+\left(-{\displaystyle \frac{1}{6}}+4p\right)x^2+O\left(x^4\right).$$

Therefore, there exists a right neighborhood of zero such that

$${\phi }_{p,2}\left(x\right)>0,{\displaystyle \frac{\partial {\phi }_{p,2}\left(x\right)}{\partial x}}<0\mathrm{and}{\displaystyle \frac{{\partial }^2{\phi }_{p,2}\left(x\right)}{\partial x^2}}<0$$

(39)

for $p\in (p_1,p_2)$. The Taylor expansion of the family of functions ${\phi }_{p,2}\left(x\right)$ around $\pi /2$ is

$${\phi }_{p,2}\left(x\right)=\left(-{\displaystyle \frac{4}{{\pi }^2}}+4\pi p\right)\left(x-{\displaystyle \frac{\pi }{2}}\right)+\left({\displaystyle \frac{8}{{\pi }^3}}-{\displaystyle \frac{1}{\pi }}+4p\right){\left(x-{\displaystyle \frac{\pi }{2}}\right)}^2+O\left({\left(x-{\displaystyle \frac{\pi }{2}}\right)}^3\right).$$

Therefore, there exists a left neighborhood of $\pi /2$ such that

$${\phi }_{p,2}\left(x\right)<0,{\displaystyle \frac{\partial {\phi }_{p,2}\left(x\right)}{\partial x}}>0\mathrm{and}{\displaystyle \frac{{\partial }^2{\phi }_{p,2}\left(x\right)}{\partial x^2}}>0$$

(40)

for $p\in (p_1,p_2)$.

By analyzing the monotonicity of the functions ${\displaystyle \frac{{\partial }^3{\phi }_{p,2}\left(x\right)}{\partial x^3}}$, ${\displaystyle \frac{{\partial }^2{\phi }_{p,2}\left(x\right)}{\partial x^2}}$, ${\displaystyle \frac{\partial {\phi }_{p,2}\left(x\right)}{\partial x}}$, and ${\phi }_{p,2}\left(x\right)$ for $p\in (p_1,p_2)$ on the interval $(0,\pi /2)$, in a similar manner as in the proof of Statement 1 and based on (38)–(40), it can be concluded that each function ${\phi }_{p,2}\left(x\right)$, for $p\in (p_1,p_2)$, has exactly one minimum on the interval $(0,\pi /2)$. From ${\displaystyle \underset{x\to 0+}{lim}{\phi }_{p,2}\left(x\right)>0}$ and ${\displaystyle \underset{x\to \pi /2-}{lim}{\phi }_{p,2}\left(x\right)<0}$, for $p\in (p_1,p_2)$, the corresponding inequalities follow.

• (iii) The claim follows directly from Statement 1 and based on the stratification. Namely, for $q=2$, it holds that $A\left(q\right)={\displaystyle \frac{\pi -2}{{\pi }^{q+1}}}=p_2$.
• (iv) It has been proven within proof $\left(ii\right)$.
• (v) Note that the infimum of the error $d\left(p\right)={sup}_{x\in (0,\pi /2)}\left|{\phi }_{p,2}\left(x\right)\right|$, for $p\in (p_1,p_2)$, exists and is attained when

$$\left|{\phi }_{p,2}\left(0+\right)\right|=\left|{\phi }_{p,2}\left(m^{\left(p\right)}\right)\right|.$$

(41)

Equation (41) can be numerically solved using the computer algebra system Maple, thus yielding the value of the parameter $p=p_0$, which is numerically determined as

$$p_0=0.036014\dots ,$$

which determines the minimax approximant ${\phi }_{p_0,2}\left(x\right)$ of the family of functions ${\phi }_{p,2}\left(x\right)$. □

In order to improve and extend Theorem 4, we consider the family of functions ${\phi }_{p,q}\left(x\right)$ for the case $q=3$. The family of functions ${\phi }_{p,3}\left(x\right)$ reduces to

$${\phi }_{p,3}\left(x\right)={\displaystyle \frac{sinx}{x}}-{\displaystyle \frac{2}{\pi }}-p\left({\pi }^3-8x^3\right)$$

(42)

and is decreasingly stratified with respect to the parameter $p\in R^{+}$ on the interval $(0,\pi /2)$, as proven in Lemma 2. For this family, the following statement holds:

Statement 6.

Let

$$p_1={\displaystyle \frac{2}{3{\pi }^4}}=0.0068439\dots and{p}_2={\displaystyle \frac{\pi -2}{{\pi }^4}}=0.011719\dots .$$

Then, it holds:

• (i) If $p\in (0,p_1]$, then

$$x\in \left(0,{\displaystyle \frac{\pi }{2}}\right)⟹{\displaystyle \frac{sinx}{x}}>{\displaystyle \frac{2}{\pi }}+p_1\left({\pi }^3-8x^3\right)\ge {\displaystyle \frac{2}{\pi }}+p\left({\pi }^3-8x^3\right).$$

• (ii) If $p\in (p_1,p_2)$, then the equality

$${\phi }_{p,3}\left(x\right)={\displaystyle \frac{sinx}{x}}-{\displaystyle \frac{2}{\pi }}-p\left({\pi }^3-8x^3\right)=0$$

has a unique solution $x_0^{\left(p\right)}$, and it holds that

$$x\in \left(0,x_0^{\left(p\right)}\right)⟹{\displaystyle \frac{sinx}{x}}>{\displaystyle \frac{2}{\pi }}+p\left({\pi }^3-8x^3\right)$$

and

$$x\in \left(x_0^{\left(p\right)},{\displaystyle \frac{\pi }{2}}\right)⟹{\displaystyle \frac{sinx}{x}}<{\displaystyle \frac{2}{\pi }}+p\left({\pi }^3-8x^3\right).$$

• (iii) If $p\in [p_2,+\infty )$, then

$$x\in \left(0,{\displaystyle \frac{\pi }{2}}\right)⟹{\displaystyle \frac{sinx}{x}}<{\displaystyle \frac{2}{\pi }}+p_2\left({\pi }^3-8x^3\right)\le {\displaystyle \frac{2}{\pi }}+p\left({\pi }^3-8x^3\right).$$

• (iv) Each function from the family ${\phi }_{p,3}\left(x\right)$, for $p\in (p_1,p_2]$, has exactly one minimum at a point $m^{\left(p\right)}\in (0,\pi /2)$ on the interval $(0,\pi /2)$.
• (v) The equality

$$\left|{\phi }_{p,3}\left(0+\right)\right|=\left|{\phi }_{p,3}\left(m^{\left(p\right)}\right)\right|$$

has the solution $p=p_0$ for the parameter $p\in (p_1,p_2)$, which is numerically determined as

$$p_0=0.010441\dots .$$

For value

$$d_0=\left|{\phi }_{p_0,3}\left(0+\right)\right|=\left|{\phi }_{p_0,3}\left(m^{\left(p_0\right)}\right)\right|=0.039635\dots ,$$

it holds that

$$d_0=\underset{p\in (0,\infty )}{inf}\underset{x\in (0,\pi /2)}{sup}\left|{\phi }_{p,3}\left(x\right)\right|.$$

Hence, the minimax approximant of the family of functions ${\phi }_{p,3}\left(x\right)$ is

$${\phi }_{p_0,3}\left(x\right)={\displaystyle \frac{sinx}{x}}-{\displaystyle \frac{2}{\pi }}-p_0\left({\pi }^3-8x^3\right),$$

which determines the corresponding (minimax) approximation

$${\displaystyle \frac{sinx}{x}}\approx {\displaystyle \frac{2}{\pi }}+0.010441\dots \left({\pi }^3-8x^3\right).$$

(43)

Proof. 

It is analogous to the proof of Statement 5. □

In order to improve and extend Theorem 5, we consider the family of functions ${\phi }_{p,q}\left(x\right)$ for the case $q=4$. The family of functions ${\phi }_{p,4}\left(x\right)$ reduces to

$${\phi }_{p,4}\left(x\right)={\displaystyle \frac{sinx}{x}}-{\displaystyle \frac{2}{\pi }}-p\left({\pi }^4-16x^4\right)$$

(44)

and is decreasingly stratified with respect to the parameter $p\in R^{+}$ on the interval $(0,\pi /2)$, as proven in Lemma 2. For this family, the following statement holds:

Statement 7.

Let

$$p_1={\displaystyle \frac{1}{2{\pi }^5}}=0.0016338\dots and{p}_2={\displaystyle \frac{\pi -2}{{\pi }^5}}=0.0037304\dots .$$

Then, it holds:

• (i) If $p\in (0,p_1]$, then

$$x\in \left(0,{\displaystyle \frac{\pi }{2}}\right)⟹{\displaystyle \frac{sinx}{x}}>{\displaystyle \frac{2}{\pi }}+p_1\left({\pi }^4-16x^4\right)\ge {\displaystyle \frac{2}{\pi }}+p\left({\pi }^4-16x^4\right).$$

• (ii) If $p\in (p_1,p_2)$, then the equality

$${\phi }_{p,4}\left(x\right)={\displaystyle \frac{sinx}{x}}-{\displaystyle \frac{2}{\pi }}-p\left({\pi }^4-16x^4\right)=0$$

has a unique solution $x_0^{\left(p\right)}$, and it holds that

$$x\in \left(0,x_0^{\left(p\right)}\right)⟹{\displaystyle \frac{sinx}{x}}>{\displaystyle \frac{2}{\pi }}+p\left({\pi }^4-16x^4\right)$$

and

$$x\in \left(x_0^{\left(p\right)},{\displaystyle \frac{\pi }{2}}\right)⟹{\displaystyle \frac{sinx}{x}}<{\displaystyle \frac{2}{\pi }}+p\left({\pi }^4-16x^4\right).$$

• (iii) If $p\in [p_2,+\infty )$, then

$$x\in \left(0,{\displaystyle \frac{\pi }{2}}\right)⟹{\displaystyle \frac{sinx}{x}}<{\displaystyle \frac{2}{\pi }}+p_2\left({\pi }^4-16x^4\right)\le {\displaystyle \frac{2}{\pi }}+p\left({\pi }^4-16x^4\right).$$

• (iv) Each function from the family ${\phi }_{p,4}\left(x\right)$, for $p\in (p_1,p_2]$, has exactly one minimum at a point $m^{\left(p\right)}\in (0,\pi /2)$ on the interval $(0,\pi /2)$.
• (v) The equality

$$\left|{\phi }_{p,4}\left(0+\right)\right|=\left|{\phi }_{p,4}\left(m^{\left(p\right)}\right)\right|$$

has the solution $p=p_0$ for the parameter $p\in (p_1,p_2)$, which is numerically determined as

$$p_0=0.0031146\dots .$$

For value

$$d_0=\left|{\phi }_{p_0,4}\left(0+\right)\right|=\left|{\phi }_{p_0,4}\left(m^{\left(p_0\right)}\right)\right|=0.059981\dots ,$$

it holds that

$$d_0=\underset{p\in (0,\infty )}{inf}\underset{x\in (0,\pi /2)}{sup}\left|{\phi }_{p,4}\left(x\right)\right|.$$

Hence, the minimax approximant of the family of functions ${\phi }_{p,4}\left(x\right)$ is

$${\phi }_{p_0,4}\left(x\right)={\displaystyle \frac{sinx}{x}}-{\displaystyle \frac{2}{\pi }}-p_0\left({\pi }^4-16x^4\right),$$

which determines the corresponding (minimax) approximation

$${\displaystyle \frac{sinx}{x}}\approx {\displaystyle \frac{2}{\pi }}+0.0031146\left({\pi }^4-16x^4\right).$$

(45)

Proof. 

It is analogous to the proof of Statement 5. □

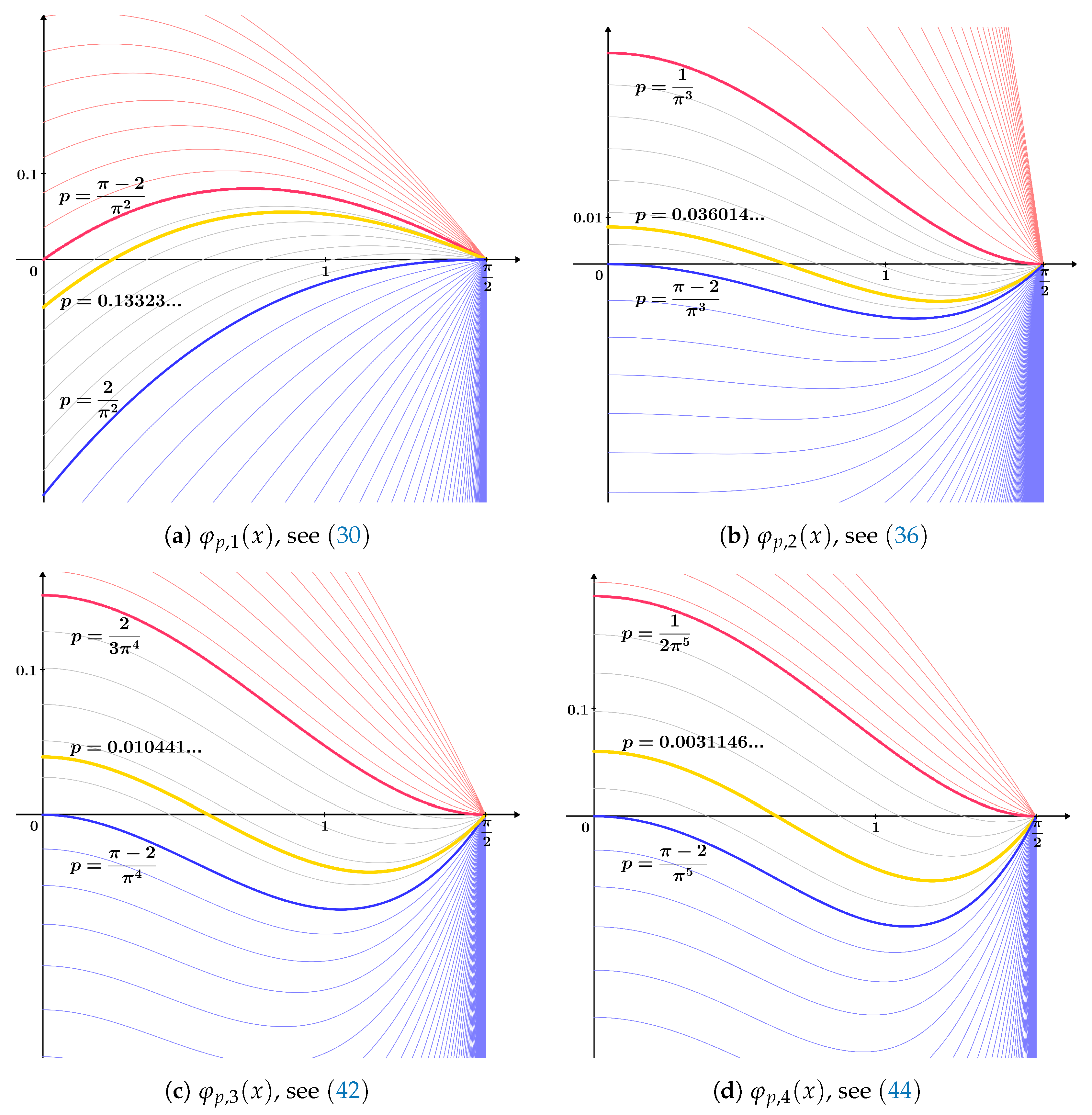
Figure 3 illustrates the stratified families of functions ${\phi }_{p,1}\left(x\right)$, ${\phi }_{p,2}\left(x\right)$, ${\phi }_{p,3}\left(x\right)$, and ${\phi }_{p,4}\left(x\right)$; see $\left(30\right)$, $\left(36\right)$, $\left(42\right)$ and $\left(44\right)$, respectively. For each family, cases for all values of the parameter $p\in R^{+}$ are shown. Particularly, cases with constants obtained in Statements 4–7, some of which are also obtained in Theorems 2–5, are singled out.

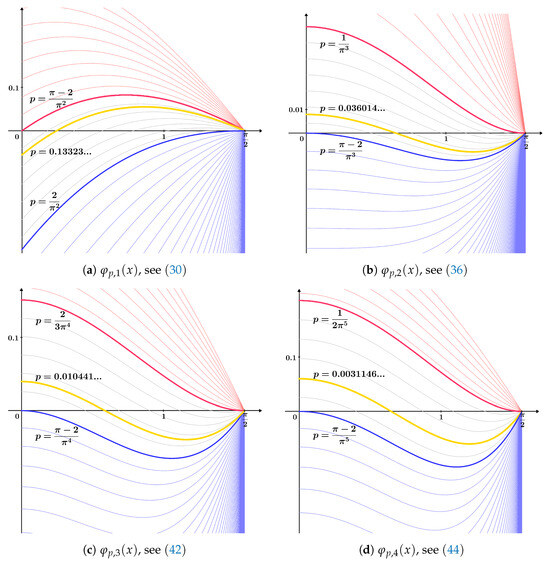
Figure 3. Stratified families of functions (a) ${\phi }_{p,1}\left(x\right)$, (b) ${\phi }_{p,2}\left(x\right)$, (c) ${\phi }_{p,3}\left(x\right)$, and (d) ${\phi }_{p,4}\left(x\right)$.

4.2. Approximations of the $Sinc$ Function

In this subsection, we provide some approximations of the $\mathrm{sinc}$ function and analyze the maximum approximation errors. The previously obtained upper and lower bounds of the $\mathrm{sinc}$ function can be used to derive some approximations of this function. Furthermore, more optimal approximations can be obtained through the corresponding minimax approximants.

In Table 1, we present some upper bounds of the $\mathrm{sinc}$ function derived from Theorems 2–5, that is, Statements 4–7 and Statements 1 and 2. It is noteworthy that the upper bound from Theorem 3 (the best upper bound from Statement 5) is identical to the best upper bound from Statement 1.

Table 1. Upper bounds of the $\mathrm{sinc}x$ function on the interval $(0,\pi /2)$.

Upper Bound of the $\mathbf{Sinc}\mathit{x}$ Function on the Interval $(\mathbf{0},\mathit{\pi }/\mathbf{2})$	Maximum Deviation from the $\mathbf{Sinc}\mathit{x}$ Function on the Interval $(\mathbf{0},\mathit{\pi }/\mathbf{2})$
${\displaystyle \frac{sinx}{x}}<{\displaystyle \frac{2}{\pi }}+{\displaystyle \frac{2}{{\pi }^2}}\left(\pi -2x\right)$	${\displaystyle \frac{\pi -4}{\pi }}=0.27323\dots$
${\displaystyle \frac{sinx}{x}}<{\displaystyle \frac{2}{\pi }}+{\displaystyle \frac{\pi -2}{{\pi }^3}}\left({\pi }^2-4x^2\right)$	$0.011612\dots$
${\displaystyle \frac{sinx}{x}}<{\displaystyle \frac{2}{\pi }}+{\displaystyle \frac{\pi -2}{{\pi }^4}}\left({\pi }^3-8x^3\right)$	$0.065358\dots$
${\displaystyle \frac{sinx}{x}}<{\displaystyle \frac{2}{\pi }}+{\displaystyle \frac{\pi -2}{{\pi }^5}}\left({\pi }^4-16x^4\right)$	$0.10245\dots$
${\displaystyle \frac{sinx}{x}}<{\displaystyle \frac{2}{\pi }}+{\displaystyle \frac{2}{\left(\frac{{\pi }^2}{4}-1\right){\pi }^{\frac{{\pi }^2}{4}}}}\left({\pi }^{\frac{{\pi }^2}{4}-1}-{\left(2x\right)}^{\frac{{\pi }^2}{4}-1}\right)$	${\displaystyle \frac{-{\pi }^2+2\pi +4}{{\pi }^2-4}}=0.070461\dots$

In Table 2, we present some lower bounds of the $\mathrm{sinc}$ function derived from Theorems 2–5, that is, Statements 4–7 and Statements 1 and 2. It is noteworthy that the best lower bound from Statement 1 is identical to the best lower bound from Statement 2.

Table 2. Lower bounds of the $\mathrm{sinc}x$ function on the interval $(0,\pi /2)$.

Lower Bound of the $\mathbf{Sinc}\mathit{x}$ Function on the Interval $(\mathbf{0},\mathit{\pi }/\mathbf{2})$	Maximum Deviation from the $\mathbf{Sinc}\mathit{x}$ Function on the Interval $(\mathbf{0},\mathit{\pi }/\mathbf{2})$
${\displaystyle \frac{2}{\pi }}+{\displaystyle \frac{\pi -2}{{\pi }^2}}\left(\pi -2x\right)<{\displaystyle \frac{sinx}{x}}$	$0.082395\dots$
${\displaystyle \frac{2}{\pi }}+{\displaystyle \frac{1}{{\pi }^3}}\left({\pi }^2-4x^2\right)<{\displaystyle \frac{sinx}{x}}$	${\displaystyle \frac{\pi -3}{\pi }}=0.045070\dots$
${\displaystyle \frac{2}{\pi }}+{\displaystyle \frac{2}{3{\pi }^4}}\left({\pi }^3-8x^3\right)<{\displaystyle \frac{sinx}{x}}$	${\displaystyle \frac{3\pi -8}{3\pi }}=0.15117\dots$
${\displaystyle \frac{2}{\pi }}+{\displaystyle \frac{1}{2{\pi }^5}}\left({\pi }^4-16x^4\right)<{\displaystyle \frac{sinx}{x}}$	${\displaystyle \frac{2\pi -5}{2\pi }}=0.20422\dots$
${\displaystyle \frac{2}{\pi }}+{\displaystyle \frac{\pi -2}{{\pi }^{\frac{2}{\pi -2}+1}}}\left({\pi }^{\frac{2}{\pi -2}}-{\left(2x\right)}^{\frac{2}{\pi -2}}\right)<{\displaystyle \frac{sinx}{x}}$	$0.0085153\dots$

In Table 3, we present some minimax approximations of the $\mathrm{sinc}$ function derived from the minimax approximants of the families ${\phi }_{p,1}\left(x\right)$, ${\phi }_{p,2}\left(x\right)$, ${\phi }_{p,3}\left(x\right)$, ${\phi }_{p,4}\left(x\right)$, ${\phi }_{A\left(q\right),q}\left(x\right)$, and ${\phi }_{B\left(q\right),q}\left(x\right)$, respectively. These families are considered in Statements 4, 5, 6, and 7 with the aim of improving Theorems 2, 3, 4, and 5, respectively, and in Statements 1 and 2.

Table 3. Minimax approximations of the $\mathrm{sinc}x$ function on the interval $(0,\pi /2)$.

Minimax Approximation of the $\mathbf{Sinc}\mathit{x}$ Function on the Interval $(\mathbf{0},\mathit{\pi }/\mathbf{2})$	Maximum Deviation from the $\mathbf{Sinc}\mathit{x}$ Function on the Interval $(\mathbf{0},\mathit{\pi }/\mathbf{2})$
${\displaystyle \frac{sinx}{x}}\approx {\displaystyle \frac{2}{\pi }}+0.13323\dots \left(\pi -2x\right)$	$0.055187\dots$
${\displaystyle \frac{sinx}{x}}\approx {\displaystyle \frac{2}{\pi }}+0.036014\dots \left({\pi }^2-4x^2\right)$	$0.0079283\dots$
${\displaystyle \frac{sinx}{x}}\approx {\displaystyle \frac{2}{\pi }}+0.010441\dots \left({\pi }^3-8x^3\right)$	$0.039635\dots$
${\displaystyle \frac{sinx}{x}}\approx {\displaystyle \frac{2}{\pi }}+0.0031146\dots \left({\pi }^4-16x^4\right)$	$0.059981\dots$
${\displaystyle \frac{sinx}{x}}\approx {\displaystyle \frac{2}{\pi }}+0.043803\dots \left({\pi }^{1.84823\dots }-{\left(2x\right)}^{1.84823\dots }\right)$	$0.0026604\dots$
${\displaystyle \frac{sinx}{x}}\approx {\displaystyle \frac{2}{\pi }}+0.051415\dots \left({\pi }^{1.72287\dots }-{\left(2x\right)}^{1.72287\dots }\right)$	$0.0061296\dots$

5. Conclusions

In this paper, two double Jordan-type inequalities have been obtained, thereby encompassing the inequalities established in papers [2,3,4,5,6]. These inequalities were explored in the context of stratified families of functions, which is a concept introduced in recent research [23]. The introduction of stratified families of functions enables the derivation of known results for specific parameter choices, including the analysis of parameter values previously unknown in the Theory of Analytic Inequalities. Furthermore, we identify parameter values within each examined family of functions for which the function, as a member of that family, exhibits some optimal properties (minimax approximant). Based on these minimax approximants and functions representing the upper and lower bounds of the $\mathrm{sinc}$ function, we provided some approximations of the $\mathrm{sinc}$ function. Additionally, we analyzed the errors associated with all mentioned approximations.

It is crucial to emphasize that the minimax approximant of the stratified family of functions is the function for which the minimal error in approximations is obtained within the given family of functions. Therefore, identifying those parameter values is significant in the Approximation Theory.

By considering the stratified family of functions individually with respect to two parameters, we were able to analyze Jordan-type inequalities in a unified manner, thereby resulting in both previously established and novel findings. Future research endeavors will focus on extending this approach even further.