Ratio-Type Estimator for Estimating the Neutrosophic Population Mean in Simple Random Sampling under Intuitionistic Fuzzy Cost Function

Abstract

Survey sampling has a wide range of applications in biomedical, meteorological, stock exchange, marketing, and agricultural research based on data collected through sample surveys or experimentation. The collected set of information may have a fuzzy nature, be indeterminate, and be summarized by a fuzzy number rather than a crisp value. The neutrosophic statistics, a generalization of fuzzy statistics and classical statistics, deals with the data that have some degree of indeterminacy, imprecision, and fuzziness. In this article, we introduce a fuzzy decision-making approach for deciding a sample size under a fuzzy measurement cost modeled by an intuitionistic fuzzy cost function. Our research introduces neutrosophic ratio-type estimators for estimating the population mean of the neutrosophic study variable $Y_N\in [Y_L,Y_U]$ utilizing all the indeterminate values of the neutrosophic auxiliary variable $X_N\in [X_L,X_U]$ rather than only the extreme values $X_L$ and $X_U$. Three simulation studies are carried out to explain the proposed methods of parameter estimation, sample size determination, and efficiency comparison. The results reveal that the proposed neutrosophic class of estimators produces more accurate and precise estimates of the neutrosophic population mean than the existing neutrosophic estimators in simple random sampling, which is the ultimate goal of inferential statistics.

1. Introduction

Survey sampling is the most practical and cost-effective approach for collecting data for research or estimating population means for making decisions. The validity and practicality of these judgments are dependent on the accuracy and precision of estimates, which are significantly affected by two important decisions made during the planning stage of a simple random sampling scheme. The first is determining a sample size under cost constraints, and the second is selecting an efficient estimator of the population mean. Refs. [1,2,3] explained the utilization of a survey budget to the per-unit measurement cost and modeled it as a classical linear cost function of sample size. Many researchers like [4,5,6,7,8,9,10,11,12], etc., used different transformation techniques to develop efficient ratio-type estimators of the population mean by utilizing auxiliary information. These classical ratio-type estimators produce a crisp value as an estimate of the population mean in a deterministic sampling environment

However, different types of uncertainties exist in the real world, in science, and in everyday life due to variation, incomplete information, fuzziness, imprecision, and indeterminacy. The classical sampling theory is unable to deal with the determination of sample size and the estimation of parameters of interest under these nonrandom uncertainties. Many theories have been developed to model these uncertainties in real-life problems. Refs. [13,14,15] developed the fuzzy sets theory to deal with decision-making problems under fuzzy uncertainty. Ref. [16] discussed the uncertainty modeling and sensitivity analysis of the different techniques of survey sampling. Refs. [17,18] proposed fuzzy assessment methods to aggregate the fuzzy responses. Ref. [19] provided a comparative survey of fuzzy data set measures of central tendency and examined the robustness of fuzzy sample statistics. Ref. [20] developed the sampling framework to classify and model the random and nonrandom uncertainties that affect the public strategy for making decisions about environmental changes. Ref. [21] suggested the fuzzy importance of sampling methods for estimating the possibility of failure by increasing the efficiency of classical fuzzy simulation. Ref. [22] presented the notion of random sampling with fuzzy replacement, with the fuzzification parameter taking a value in the range [0, 1].

But in many studies, the information collected through survey sampling or experimentation can be expressed in the interval form rather than as a single value due to impression and indeterminacy. For example, the daily temperature of a city, the daily share price of a company, the daily blood pressure of a person, the daily cholesterol level of a person, etc., are presented in an interval linked with a linguistic fuzzy variable. The indeterminate collected information can be summarized as a neutrosophic number. In 2013, Samarandache introduced the statistical methods to be used for finding descriptive neutrosophic measures such as the mean, variance, coefficient of skewness, coefficient of kurtosis, etc., to determine the relationship between two neutrosophic variables; connected probability logic with neutrosophic logic; and introduced the concepts of neutrosophic probability theory [23,24]. The neutrosophic statistics summarized the data that have some degree of uncertainty due to fuzziness, imprecision, and indeterminacy. The neutrosophic estimation methods are equivalent to the classical methods if this degree of uncertainty is zero. Ref. [24] proposed a sample neutrosophic estimator for the neutrosophic population mean in simple random sampling. Ref. [25] developed a new sampling strategy for considering neutrosophic process loss. Ref. [26] proposed neutrosophic ratio and exponential ratio estimators for the estimation of the neutrosophic population mean in simple random sampling under the given sample size. Ref. [27] suggested the neutrosophic exponential-type estimator of the population mean in simple random sampling. Ref. [28] suggested neutrosophic estimators for the estimation of a finite neutrosophic population mean using underrank set sampling and compared the efficiency of the proposed estimators using solar energy data. Ref. [27] proposed the neutrosophic exponential-type estimator for estimating the population mean. Ref. [29] suggested the robust neutrosophic ratio estimator for estimating the average stock prices of pharmaceutical companies. Ref. [30] proposed a ratio and an exponential-type estimator to estimate the imprecise population parameter and compared the efficiency of the proposed estimator with that of existing neutrosophic estimators. Ref. [31] proposed robust Hartley–Ross-type estimators for estimating the population mean of sensitive and non-sensitive variables under simple random sampling.

1.1. Research Gap

All the existing neutrosophic estimators are based on the extreme values of the neutrosophic study variable and the neutrosophic auxiliary variable. These neutrosophic estimators always produce biased and imprecise estimates, which lead to misleading inferences about unknown parameters of the neutrosophic variable of interest. Moreover, the accuracy and precision of the estimate are directly proportional to the sample size that is determined under the given budget of the survey. The classical linear cost function in survey sampling relies on an estimate of the per-unit measurement cost that occurred in a pilot survey but does not take into account expert knowledge, the historical survey cost, the inflation factor, or fuzzy uncertainty in the per-unit measurement cost.

1.2. Scope of the Study

Fuzzy sampling theory has the flexibility of modeling the cost of a sample survey, the decision of sample size, and the estimation of the parameters of interest in a nonrandom, uncertain environment. These uncertainties are studied in the domains of fuzzy set theory and neutrosophic theory. This study has two main objectives, given as follows:

• To decide the sample size under a nonrandom, uncertain measurement cost.
• To propose a more efficient neutrosophic estimator for estimating the population mean of the neutrosophic study variable, utilizing all indeterminate values of the neutrosophic auxiliary variable.

This article presents fresh research on the estimation of the mean utilizing all values of the neutrosophic auxiliary variable rather than extreme indeterminate points. The fuzzy decision-making approach for deciding the per-unit measurement cost, considering the expert opinion, the cost incurred in pilot surveys, prior surveys, and fuzzy uncertainty is suggested. In this approach, the utilization of the survey budget is modeled as an intuitionistic fuzzy cost function, taking into account the per-unit measurement cost as an intuitionistic fuzzy number and suggesting the sample size estimation procedure. We propose the neutrosophic ratio class of estimator, the neutrosophic exponential class of estimator, and the neutrosophic ratio–exponential class of estimator, which utilizes all indeterminate values by introducing the function of the neutrosophic auxiliary variable. The intuitionistic fuzzy cost function and procedure for determining the sample size are explained in Section 2. Section 3 includes the theoretical formulation and mathematical properties of the proposed neutrosophic estimators. The mathematical expression for a theoretical efficiency comparison with existing neutrosophic ratio-type estimators and the criteria for an empirical efficiency comparison are given in Section 4. To explain the numerical computations and efficiency comparisons, a simulation study is presented in Section 5. The discussion and conclusion are presented in Section 6 and Section 7, respectively.

2. Intuitionistic Fuzzy Cost Function

Resource constraints (cost, trained staff, time, etc.) are the main reasons for conducting a study based on data collected through survey sampling instead of a census. The determination of sample size is an important part of planning survey sampling as well as estimation procedures. The required precision and available resources are key parameters for deciding the sample size. Considering the fixed cost $c_0$, per-unit measurement cost c, and budget available for survey B, the sample size n under the classical linear cost function in simple random sampling is defined as

$$c_0+cn=B$$

$$\Rightarrow n=\frac{B-c_0}{c}$$

As we know, the accuracy of an estimate is directly proportional to the sample size n. But $n\propto (B-c_0)$ and $n\propto \frac{1}{c}$. The decision on per-unit measurement cost c is based on its values from previous surveys, pilot surveys, estimated costs, etc. Mathematically, the cost c is selected from the universal set of costs D:

$$D=\left\{a_1,a_2,\dots ,a_i,\dots ,a_o\right\}.$$

The classical or crisp value of $\mathit{c}\in D$ is defined by the characteristic function:

$${\varphi }_D\left(c\right)=\left\{\begin{array}{c}1\mathrm{if}c=a_i\hfill \\ 0\mathrm{otherwise}.\hfill \end{array}\right.$$

The selected value of c by this indicator function, used in the classical linear cost function, may be either true or false, i.e., ${\varphi }_D\left(c\right)=\left\{0,1\right\}$. But in this time of rapidly changing inflation, it is a difficult decision to select a sharply defined value of c and ignore the expert’s judgment. The decision-maker is facing uncertainty in selecting the true single value of c from set D. The intuitionistic fuzzy decision-making approach has the adaptability and flexibility to include a subset of set D in a decision on the per-unit measurement cost. This approach covers fuzzy uncertainty and expert knowledge and is a generalization of the classical approach. Under this approach, the per-unit measurement cost is determined by mapping c in the interval $\left[0,1\right]$ rather than being bound to the bi-valued set $\left\{0,1\right\}$. The intuitionistic fuzzy set (IFS) of the measurement unit cost ${\tilde{c}}^i$ is defined as a triplet:

$${\tilde{c}}^i=\left\{\left(a_i,{\mu }_{\tilde{c}}^i\left(a_i\right),{\nu }_{\tilde{c}}^i\left(a_i\right)\right):a_i\in \mathit{D}\right\}$$

where ${\mu }_{\tilde{c}}^i\left(a_i\right)$ is the degree of expert satisfaction regarding the cost $a_i$ to set ${\tilde{c}}^i$ and ${\nu }_{\tilde{c}}^i\left(a_i\right)$ is the degree of expert dissatisfaction regarding the cost $a_i$ to set $\tilde{c}$ such that ${\mu }_{\tilde{c}}^i\left(a_i\right)+{\nu }_{\tilde{c}}^i\left(a_i\right)=1$. The intuitionistic fuzzy measurement cost set ${\tilde{c}}^i$ is called the intuitionistic fuzzy number if ${\tilde{c}}^i$ satisfies the normality, convexity, and continuity condition of IFS. The intuitionistic fuzzy cost function in simple random sampling is defined as follows:

$$c_0+{\tilde{c}}^{i}n=B$$

(1)

Let ${\tilde{c}}^i=(a_1,a_2,a_3)$ be the linear triangular intuitionistic fuzzy cost and be defined by ${\mu }_{{\tilde{c}}^i}\left(c\right):R^{+}\to [0.5,1]$, ${\nu }_{{\tilde{c}}^i}\left(c\right):R^{+}\to [0.5,1]$ given as follows:

$${\mu }_{{\tilde{c}}^i}\left(c\right)=\left\{\begin{array}{l}{\mu }_l=\frac{c-a_1}{a_2-a_1},a_1<c<a_2\hfill \\ 1,c=a_2\\ {\mu }_u=\frac{a_3-c}{a_3-a_2},a_2<c\le a_3\\ 0,\mathrm{otherwise}.\end{array}\right.$$

$${\nu }_{{\tilde{c}}^i}\left(c\right)=\left\{\begin{array}{l}{\nu }_l=\frac{a_2-c}{a_2-a_1},a_1<c<a_2\hfill \\ 0,c=a_2\\ {\nu }_u=\frac{c-a_2}{a_3-a_2},a_2<c\le a_3\\ 0,\mathrm{otherwise}.\end{array}\right.$$

where ${\mu }_l:R^{+}\to [0.5,1]$, ${\mu }_u:R^{+}\to [0.5,1]$, ${\nu }_l:R^{+}\to [0.5,1]$, and ${\nu }_u:R^{+}\to [0.5,1]$. Let ${\mu }_l^{-1}:[0.5,1]\to R^{+}$, ${\mu }_u^{-1}:[0.5,1]\to R^{+}$, ${\nu }_l^{-1}:[0.5,1]\to R^{+}$, and ${\nu }_u^{-1}:[0.5,1]\to R^{+}$ be the inverse functions of ${\mu }_l,{\mu }_u,{\nu }_l$, and ${\nu }_u$, respectively. Let ${\mu }_{{\tilde{c}}^i}^{-1}(z):[0.5,1]\to R^{+}$ and ${\nu }_{{\tilde{c}}^i}^{-1}(z):[0.5,1]\to R^{+}$ be the inverse functions of ${\mu }_{{\tilde{c}}^i}(c)$ and ${\nu }_{{\tilde{c}}^i}(c)$, respectively, defined as

$${\mu }_{{\tilde{c}}^i}^{-1}\left(z\right)=\left\{\begin{array}{c}{\mu }_l^{-1}=a_1+z(a_2-a_1),0.5\le z\le 1\hfill \\ {\mu }_u^{-1}=a_3+z(a_2-a_3),0.5\le z\le 1\end{array}\right.$$

$${\nu }_{{\tilde{c}}^i}^{-1}\left(z\right)=\left\{\begin{array}{c}{\nu }_l^{-1}=a_2+z(a_1-a_2),0.5\le z\le 1\hfill \\ {\nu }_u^{-1}=a_2+z(a_3-a_2),0.5\le z\le 1\end{array}\right.$$

Now, the centriod point $\left(A\right({\tilde{c}}^i),Z({\tilde{c}}^i\left)\right)$ of the triangular intuitionistic fuzzy cost ${\tilde{c}}^i$ is calculated as follows:

$$A_{\mu }\left({\tilde{c}}^i\right)=\frac{{\int }_{a_1}^{a_2}c{\mu }_{l}dc+{\int }_{a_2}^{a_3}c{\mu }_{u}dc}{{\int }_{a_1}^{a_2}{\mu }_{l}dc+{\int }_{a_2}^{a_3}{\mu }_{u}dc}$$

$$A_{\mu }\left({\tilde{c}}^i\right)=\frac{{\int }_{a_1}^{a_2}\frac{c^2-a_{1}c}{a_2-a_1}dc+{\int }_{a_2}^{a_3}\frac{a_{3}c-c^c}{a_3-a_2}dc}{{\int }_{a_1}^{a_2}\frac{c-a_1}{a_2-a_1}dc+{\int }_{a_2}^{a_3}\frac{a_3-c}{a_3-a_2}dc}$$

$$A_{\mu }\left({\tilde{c}}^i\right)=\frac{a_1+a_2+a_3}{3}$$

(2)

$$A_{\nu }\left({\tilde{c}}^i\right)=\frac{{\int }_{a_1}^{a_2}c{\nu }_{l}dc+{\int }_{a_2}^{a_3}c{\nu }_{u}dc}{{\int }_{a_1}^{a_2}{\nu }_{l}dc+{\int }_{a_2}^{a_3}{\nu }_{u}dc}$$

$$A_{\nu }\left({\tilde{c}}^i\right)=\frac{{\int }_{a_1}^{a_2}\frac{a_{2}c-c^2}{a_2-a_1}dc+{\int }_{a_2}^{a_3}\frac{c^2-a_{2}c}{a_3-a_2}dc}{{\int }_{a_1}^{a_2}\frac{a_2-c}{a_2-a_1}dc+{\int }_{a_2}^{a_3}\frac{c-a_2}{a_3-a_2}dc}$$

$$A_{\nu }\left({\tilde{c}}^i\right)=\frac{2a_1-a_2+2a_3}{3}$$

(3)

$$Z_{\mu }\left({\tilde{c}}^i\right)=\frac{{\int }_{0.5}^{1}z{\mu }_u^{-1}dz-{\int }_{0.5}^{1}z{\mu }_l^{-1}dz}{{\int }_{0.5}^1{\mu }_u^{-1}dz-{\int }_{0.5}^1{\mu }_l^{-1}dz}$$

$$Z_{\mu }\left({\tilde{c}}^i\right)=\frac{{\int }_{0.5}^1(a_{3}z+(a_2-a_3)z^2)dz-{\int }_{0.5}^1(a_{1}z+(a_2-a_1)z^2)dz}{{\int }_{0.5}^1(a_3+(a_2-a_3)z)dz-{\int }_{0.5}^1(a_1+(a_2-a_1)z)dz}$$

$$Z_{\mu }\left({\tilde{c}}^i\right)=\frac{2}{3}$$

(4)

$$Z_{\nu }\left({\tilde{c}}^i\right)=\frac{{\int }_{0.5}^{1}z{\nu }_u^{-1}dz-{\int }_{0.5}^{1}z{\nu }_l^{-1}dz}{{\int }_{0.5}^1{\nu }_u^{-1}dz-{\int }_{0.5}^1{\nu }_l^{-1}dz}$$

$$Z_{\nu }\left({\tilde{c}}^i\right)=\frac{{\int }_{0.5}^1(a_{2}z+(a_3-a_2)z^2)dz-{\int }_{0.5}^1(a_{2}z+(a_1-a_2)z^2)dz}{{\int }_{0.5}^1(a_2+(a_3-a_2)z)dz-{\int }_{0.5}^1(a_2+(a_1-a_2)z)dz}$$

$$Z_{\nu }\left({\tilde{c}}^i\right)=\frac{7}{9}$$

(5)

The rank function $d\left({\tilde{c}}^i\right)$ for the single crisp value of the TrIF cost ${\tilde{c}}^i$ is defined as

$$d\left({\tilde{c}}^i\right)=\sqrt{\frac{1}{2}\left[{\left(A_{\mu }\left({\tilde{c}}^i\right)-Z_{\mu }\left({\tilde{c}}^i\right)\right)}^2+{\left(A_{\nu }\left({\tilde{c}}^i\right)-Z_{\nu }\left({\tilde{c}}^i\right)\right)}^2\right]}$$

$$d\left({\tilde{c}}^i\right)=\sqrt{\frac{1}{2}\left[{\left(\frac{a_1+a_2+a_3}{3}-\frac{2}{3}\right)}^2+{\left(\frac{2a_1-a_2+2a_3}{3}-\frac{7}{9}\right)}^2\right]}$$

(6)

The fuzzy cost functions given in Equation (1) are written in crisp form as

$$c_o+d\left({\tilde{c}}^i\right)n=B$$

(7)

$$\Rightarrow n=\frac{B-c_0}{d\left({\tilde{c}}^i\right)}$$

(8)

3. Neutrosophic Estimators of Population Mean

The neutrosophic population consists of data that have some degree of indeterminacy and imprecision and is presented in interval form rather than as an information object summarized by a precise value. The classical estimator can be transformed into a neutrosophic form that depends on the extreme points in the neutrosophic data set. The neutrosophic estimator provides a nonrandom interval value as an estimate of an imprecise parameter of interest. Let Y be the determinate part and $I_Y$ be the indeterminate part of a quantitative neutrosophic study variable $Y_N$ which can be written as $Y_N=Y+I_Y$ or more precisely presented in interval form as $Y_N\in [Y_L,Y_U]$. Let X be the determinate part and $I_X$ be the indeterminate part of a quantitative neutrosophic auxiliary variable $X_N$ which can be written as $X_N=X+I_X$ or more precisely presented in interval form as $X_N\in [X_L,X_U]$. Let $y_{Ni}\in [y_{Li},y_{Ui}]$ and $x_{Ni}\in [x_{Li},x_{Ui}]$ be the neutrosophic values of $Y_N$ and $X_N$ observed from the $i^{th}$ unit of a population containing M units. Let ${\overline{y}}_N\in [{\overline{y}}_L,{\overline{y}}_U]$ be the sample mean and ${\overline{Y}}_N\in [{\overline{Y}}_L,{\overline{Y}}_U]$ be the population mean of $Y_N$. Let ${\overline{x}}_N\in [{\overline{x}}_L,{\overline{x}}_U]$ be the sample mean and ${\overline{X}}_N\in [{\overline{X}}_L,{\overline{X}}_U]$ be the population mean of $X_N$. Let $S_{YN}^2\in [S_{YL}^2,S_{YU}^2]$ and $S_{XN}^2\in [S_{XL}^2,S_{XU}^2]$ be the neutrosophic population variances, and let $C_{Y_N}\in [C_{Y_L},C_{Y_U}]$ and $C_{X_N}\in [C_{X_L},C_{X_U}]$, respectively, be the neutrosophic population coefficients of variation of $Y_N$ and $X_N$. Let ${\beta }_{1\left(X_N\right)}\in [{\beta }_{1\left(X_L\right)},{\beta }_{1\left(X_U\right)}]$ be the coefficient of skewness and ${\beta }_{2\left(X_N\right)}\in [{\beta }_{2\left(X_L\right)},{\beta }_{2\left(X_U\right)}]$ the coefficient of kurtosis of the neutrosophic auxiliary variable. Let ${\rho }_{Y_N{X}_N}\in [{\rho }_{Y_L{X}_L},{\rho }_{Y_U{X}_U}]$ be the neutrosophic population population correlation coefficient.

3.1. Existing Neutrosophic Estimators

Ref. [26] proposed the neutrosophic ratio estimators for the estimation of the neutrosophic population mean given in (9), (11), (13), and (15) below.

$${\overline{y}}_{NR}=\frac{{\overline{y}}_N}{{\overline{x}}_N}{\overline{X}}_N,$$

(9)

$${\overline{y}}_{NR}\in \left[{\overline{y}}_{LR},{\overline{y}}_{UR}\right].$$

The bias and mean square error of ${\overline{y}}_{NR}$ are defined as

$$Bias\left({\overline{y}}_{NR}\right)={\lambda }_N{\overline{Y}}_N\left(C_{x_N}^2-C_{y_N}{C}_{x_N}{\rho }_{x_N{y}_N}\right)$$

where ${\lambda }_N=\frac{M_N-n_N}{M_N{n}_N}$, ${\lambda }_N\in [{\lambda }_L,{\lambda }_U].$

$$Bias\left({\overline{y}}_{NR}\right)\in \left[Bias\left({\overline{y}}_{LR}\right),Bias\left({\overline{y}}_{UR}\right)\right].$$

$$MSE\left({\overline{y}}_{NR}\right)={\lambda }_N{\overline{Y}}_N^2\left(C_{y_N}^2+C_{x_N}^2-2C_{y_N}{C}_{x_N}{\rho }_{x_N{y}_N}\right),$$

(10)

$$MSE\left({\overline{y}}_{NR}\right)\in [MSE\left({\overline{y}}_{LR}\right),MSE\left({\overline{y}}_{UR}\right).$$

$${\overline{y}}_{SDrN}={\overline{y}}_N\frac{{\overline{X}}_N+C_{xN}}{{\overline{x}}_N+C_{xN}},$$

(11)

$${\overline{y}}_{SDrN}\in [{\overline{y}}_{SDrL},{\overline{y}}_{SDrU}].$$

The bias and MSE of ${\overline{y}}_{SDrN}$ are given as

$$Bias\left({\overline{y}}_{SDrN}\right)={\lambda }_N{\overline{Y}}_N\left({\theta }_{Nr1}^2{C}_{x_N}^2-{\theta }_{Nr1}{C}_{y_N}{C}_{x_N}{\rho }_{x_N{y}_N}\right),$$

where

$${\theta }_{Nr1}=\frac{{\overline{X}}_N}{{\overline{X}}_N+C_{xN}},{\theta }_{Nr1}\in \left[{\theta }_{Lr1},{\theta }_{Ur1}\right],$$

$$Bias\left({\overline{y}}_{SDrN}\right)\in \left[Bias\left({\overline{y}}_{SDrL}\right),Bias\left({\overline{y}}_{SDrU}\right)\right].$$

$$MSE\left({\overline{y}}_{SDrN}\right)={\lambda }_N{\overline{Y}}_N^2\left(C_{y_N}^2+{\theta }_{Nr1}^2{C}_{x_N}^2-2{\theta }_{Nr1}{C}_{y_N}{C}_{x_N}{\rho }_{x_N{y}_N}\right),$$

(12)

$$MSE\left({\overline{y}}_{SDrN}\right)\in \left[MSE\left({\overline{y}}_{SDrL}\right),MSE\left({\overline{y}}_{SDrU}\right)\right].$$

$${\overline{y}}_{SKrN}={\overline{y}}_N\frac{{\overline{X}}_N+{\beta }_{2\left(X_N\right)}}{{\overline{x}}_N+{\beta }_{2\left(X_N\right)}}$$

(13)

$${\overline{y}}_{SKrN}\in [{\overline{y}}_{SKrL},{\overline{y}}_{SKrU}].$$

The bias and MSE of ${\overline{y}}_{SKrN}$ are given as:

$$Bias\left({\overline{y}}_{SKrN}\right)={\lambda }_N{\overline{Y}}_N\left({\theta }_{Nr2}^2{C}_{x_N}^2-{\theta }_{Nr2}{C}_{y_N}{C}_{x_N}{\rho }_{x_N{y}_N}\right),$$

where

$${\theta }_{Nr2}=\frac{{\overline{X}}_N}{{\overline{X}}_N+{\beta }_{2\left(X_N\right)}},{\theta }_{Nr2}\in \left[{\theta }_{Lr2},{\theta }_{Ur2}\right],$$

$$Bias\left({\overline{y}}_{SKrN}\right)\in \left[Bias\left({\overline{y}}_{SKrL}\right),Bias\left({\overline{y}}_{SKrU}\right)\right].$$

$$MSE\left({\overline{y}}_{SKrN}\right)={\lambda }_N{\overline{Y}}_N^2\left(C_{y_N}^2+{\theta }_{Nr2}^2{C}_{x_N}^2-2{\theta }_{Nr2}{C}_{y_N}{C}_{x_N}{\rho }_{x_N{y}_N}\right),$$

(14)

$$MSE\left({\overline{y}}_{SKrN}\right)\in \left[MSE\left({\overline{y}}_{SKrL}\right),MSE\left({\overline{y}}_{SKrU}\right)\right].$$

$${\overline{y}}_{USrN}={\overline{y}}_N\frac{{\overline{X}}_N{\beta }_{2\left(X_N\right)}+C_{xN}}{{\overline{x}}_N{\beta }_{2\left(X_N\right)}+C_{xN}},$$

(15)

$${\overline{y}}_{USrN}\in [{\overline{y}}_{USrL},{\overline{y}}_{USrU}].$$

The bias and MSE of ${\overline{y}}_{USrN}$ are given as

$$Bias\left({\overline{y}}_{USrN}\right)={\lambda }_N{\overline{Y}}_N\left({\theta }_{Nr3}^2{C}_{x_N}^2-{\theta }_{Nr3}{C}_{y_N}{C}_{x_N}{\rho }_{x_N{y}_N}\right),$$

where

$${\theta }_{Nr3}=\frac{{\overline{X}}_N{\beta }_{2\left(X_N\right)}}{{\overline{X}}_N{\beta }_{2\left(X_N\right)}+C_{xN}},{\theta }_{Nr3}\in \left[{\theta }_{Lr3},{\theta }_{Ur3}\right],$$

$$Bias\left({\overline{y}}_{USrN}\right)\in \left[Bias\left({\overline{y}}_{USrL}\right),Bias\left({\overline{y}}_{USrU}\right)\right].$$

$$MSE\left({\overline{y}}_{USrN}\right)={\lambda }_N{\overline{Y}}_N^2\left(C_{y_N}^2+{\theta }_{Nr3}^2{C}_{x_N}^2-2{\theta }_{Nr3}{C}_{y_N}{C}_{x_N}{\rho }_{x_N{y}_N}\right),$$

(16)

$$MSE\left({\overline{y}}_{USrN}\right)\in \left[MSE\left({\overline{y}}_{USrL}\right),MSE\left({\overline{y}}_{USrU}\right)\right].$$

Ref. [26] proposed the neutrosophic exponential estimators for the estimation of the neutrosophic population mean, given in (17) and (19) below:

$${\overline{y}}_{BTrN}={\overline{y}}_{N}exp\left(\frac{{\overline{X}}_N-{\overline{x}}_N}{{\overline{X}}_N+{\overline{x}}_N}\right),$$

(17)

$${\overline{y}}_{BTrN}\in \left[{\overline{y}}_{BTrL},{\overline{y}}_{BTrN}\right].$$

The bias and MSE of ${\overline{y}}_{BTrN}$ are given as

$$Bias\left({\overline{y}}_{BTrN}\right)={\lambda }_N{\overline{Y}}_N\left(\frac{3}{8}{C}_{x_N}^2-\frac{1}{2}{C}_{y_N}{C}_{x_N}{\rho }_{x_N{y}_N}\right),$$

$$Bias\left({\overline{y}}_{BTrN}\right)\in \left[Bias\left({\overline{y}}_{BTrL}\right),Bias\left({\overline{y}}_{RrU}\right)\right].$$

$$MSE\left({\overline{y}}_{BTrN}\right)={\lambda }_N{\overline{Y}}_N^2\left(C_{y_N}^2+\frac{1}{4}{C}_{x_N}^2-C_{y_N}{C}_{x_N}{\rho }_{x_N{y}_N}\right),$$

(18)

$$MSE\left({\overline{y}}_{BTrN}\right)\in \left[MSE\left({\overline{y}}_{BTrL}\right),MSE\left({\overline{y}}_{BTrU}\right)\right].$$

$${\overline{y}}_{RrN}={\overline{y}}_{N}exp\left(\frac{({\overline{X}}_N+1)-({\overline{x}}_N+1)}{({\overline{X}}_N+1)+({\overline{x}}_N+1)}\right),$$

(19)

$${\overline{y}}_{RrN}\in \left[{\overline{y}}_{RrL},{\overline{y}}_{RrU}\right].$$

The bias and MSE of ${\overline{y}}_{RrN}$ are given as

$$Bias\left({\overline{y}}_{RrN}\right)={\lambda }_N{\overline{Y}}_N\left(\frac{3}{8}{\theta }_{Nr4}^2{C}_{x_N}^2-\frac{1}{2}{\theta }_{Nr4}{C}_{y_N}{C}_{x_N}{\rho }_{x_N{y}_N}\right),$$

where

$${\theta }_{Nr4}=\frac{{\overline{X}}_N}{{\overline{X}}_N+1},{\theta }_{Nr4}\in \left[{\theta }_{Lr4},{\theta }_{Ur4}\right],$$

$$Bias\left({\overline{y}}_{BTrN}\right)\in \left[Bias\left({\overline{y}}_{RrL}\right),Bias\left({\overline{y}}_{RrU}\right)\right].$$

$$MSE\left({\overline{y}}_{RrN}\right)={\lambda }_N{\overline{Y}}_N^2\left(C_{y_N}^2+\frac{1}{4}{\theta }_{Nr4}^2{C}_{x_N}^2-{\theta }_{Nr4}{C}_{y_N}{C}_{x_N}{\rho }_{x_N{y}_N}\right),$$

(20)

$$MSE\left({\overline{y}}_{RrN}\right)\in \left[MSE\left({\overline{y}}_{RrL}\right),MSE\left({\overline{y}}_{RrU}\right)\right].$$

The proposed neutrosophic ratio–exponential estimator by [30] is given as

$${\overline{y}}_{tpN}={\overline{y}}_N\left(k_1\frac{{\overline{X}}_N+1}{{\overline{x}}_N+1}+k_{2}exp\left(\frac{({\overline{X}}_N+1)-({\overline{x}}_N+1)}{({\overline{X}}_N+1)+({\overline{x}}_N+1)}\right)\right),$$

(21)

$${\overline{y}}_{tpN}\in \left[{\overline{y}}_{tpL},{\overline{y}}_{tpU}\right]$$

The mathematical expression for the bias of ${\overline{y}}_{tpN}$ is given as

$$\begin{array}{c}\hfill Bias\left({\overline{y}}_{tpN}\right)={\overline{Y}}_N\left[k_1\left(1+{\theta }_N\left({\theta }_{Nr4}{C}_{x_N}^2-{\tau }_N{C}_{x_N}{C}_{y_N}{\rho }_{x_N{y}_N}\right)\right)\right.\\ \hfill \left.+k_2\left(1+{\lambda }_N\left(\frac{3}{8}{\theta }_{Nr4}{C}_{x_N}^2-\frac{1}{2}{\tau }_N{C}_{x_N}{C}_{y_N}{\rho }_{x_N{y}_N}\right)\right)-1\right],\end{array}$$

(22)

$$Bias\left({\overline{y}}_{tpN}\right)\in \left[Bias\left({\overline{y}}_{tpL}\right),Bias\left({\overline{y}}_{tpU}\right)\right].$$

The mathematical expression for the minimum MSE of ${\overline{Y}}_{tpN}$ is given as

$$\begin{array}{c}\hfill MSE{\left({\overline{y}}_{tpN}\right)}_{min}={\overline{Y}}_N^2\left(1+A{k}_{1opt}^2+B{k}_{2opt}^2-2C{k}_{1opt}-2D{k}_{2opt}+2F{k}_{1opt}{k}_{2opt}\right),\end{array}$$

(23)

$$MSE{\left({\overline{y}}_{tpN}\right)}_{min}\in \left[MSE{\left({\overline{y}}_{tpL}\right)}_{min},MSE{\left({\overline{y}}_{tpU}\right)}_{min}\right],$$

where

$$A=1+\left({\lambda }_N{C}_{y_N}^2+3{\lambda }_N{\theta }_{Nr4}{C}_{x_N}^2-4{\lambda }_N{\theta }_{Nr4}N{C}_{x_N}{C}_{y_N}{\rho }_{x_N{y}_N}\right)$$

$$B=1+\left({\lambda }_N{C}_{y_N}^2+{\lambda }_N{\theta }_{Nr4}{C}_{x_N}^2-2{\lambda }_N{\theta }_{Nr4}{C}_{x_N}{C}_{y_N}{\rho }_{x_N{y}_N}\right)$$

$$C=1+\left({\lambda }_N{\theta }_{Nr4}{C}_{x_N}^2-{\lambda }_N{\theta }_{Nr4}{C}_{x_N}{C}_{y_N}{\rho }_{x_N{y}_N}\right)$$

$$D=1+\left(\frac{3}{8}{\lambda }_N{\theta }_{Nr4}{C}_{x_N}^2-\frac{1}{2}{\lambda }_N{\theta }_{Nr4}{C}_{x_N}{C}_{y_N}{\rho }_{x_N{y}_N}\right)$$

$$F=1+N\left({\lambda }_N{C}_{y_N}^2+\frac{15}{8}{\lambda }_N{\theta }_{Nr4}{C}_{x_N}^2-3{\lambda }_N{\theta }_{Nr4}{C}_{x_N}{C}_{y_N}{\rho }_{x_N{y}_N}\right)$$

$$k_{1opt}=\frac{DF-BC}{FF-AB},k_{2opt}=\frac{CF-AD}{FF-AB}$$

3.2. Proposed Generalized Neutrosophic Ratio-Type Estimators Using Neutrosophic Subsidiary Information

Let $x_{Ni}\in [x_{Li},x_{Ui}]$ contain K values. We introduce two variates $X_A:X_N\to \mathbb{R}$ and $X_S:X_N\to {\mathbb{R}}^{+}$, defined as

$$X_A=\sum _{j=L}^U\frac{X_{ji}}{K},i=1,2,3,\dots ,M.$$

$$X_S=\sqrt{\sum _{j=L}^U\frac{{(X_{ji}-X_{Ai})}^2}{K}},i=1,2,3,\dots ,M.$$

Let ${\overline{X}}_S$ be the population mean, $S_{XS}^2$ be the population variance, $C{V}_{XS}$ be the population coefficient of variation, ${\beta }_{1\left(X_S\right)}$ be the coefficient of skewness, and ${\beta }_{2\left(X_S\right)}$ be the coefficient of kurtosis of variable $X_S$. Let ${\rho }_{Y_N{X}_S}\in [{\rho }_{Y_L{X}_S},{\rho }_{Y_U{X}_S}]$ be the neutrosophic population correlation coefficient between $Y_N$ and $X_S$. Let $e_{N0}=\frac{{\overline{y}}_N-{\overline{Y}}_N}{{\overline{Y}}_N}$, $e_{N0}\in \left[e_{L0},e_{U0}\right]$, $e_{N1}=\frac{{\overline{x}}_N-{\overline{X}}_N}{{\overline{X}}_N}$, $e_{N1}\in \left[e_{L1},e_{U1}\right]$, $E\left[e_{N0}\right]=0$, $E\left(e_{N1}\right)=0$, $E\left(e_{N0}^2\right)={\lambda }_N{C}_{y_N}^2$, $E\left(e_{N1}^2\right)={\lambda }_N{C}_{x_N}^2$, $E\left(e_{N0}{e}_{N1}\right)={\lambda }_N{C}_{x_N}{C}_{y_N}{\rho }_{x_N{y}_N}$, and ${\lambda }_N=\frac{M_N-n_N}{M_N{n}_N}$, ${\lambda }_N\in [{\lambda }_L,{\lambda }_U]$. Let $\alpha$ and $\Psi$ represent the parametric values of variables $X_N$ and $X_S$ or $\alpha ,\Psi \in \mathbb{R}$. Let ${\tau }_N=\frac{\alpha {\overline{X}}_N}{\alpha {\overline{X}}_N+\Psi }$, ${\tau }_N\in \left[{\tau }_L,{\tau }_U\right]$.

3.2.1. Neutrosophic Ratio Class of Estimator

The proposed generalized neutrosophic ratio (GNR) class of estimators ${\overline{y}}_{NRTi}$ is defined as

$${\overline{y}}_{NRTi}={\overline{y}}_N\frac{\alpha {\overline{X}}_N+\Psi }{\alpha {\overline{x}}_N+\Psi },$$

(24)

$${\overline{y}}_{NRTi}\in \left[{\overline{y}}_{LRTi},{\overline{y}}_{URTi}\right]$$

and we have

$${\overline{y}}_{NRTi}-{\overline{Y}}_N={\overline{Y}}_N{e}_{N0}{\left(1+{\tau }_N{e}_{N1}\right)}^{-1}$$

(25)

The bias of ${\overline{y}}_{NRTi}$ up to the first-order approximation is given as

$$\begin{array}{c}\hfill Bias\left({\overline{y}}_{NRTi}\right)={\overline{Y}}_N\left[1+{\lambda }_N\left({\tau }_N^2{C}_{x_N}^2-{\tau }_N{C}_{x_N}{C}_{y_N}{\rho }_{x_N{y}_N}\right)\right]\end{array},$$

(26)

$$Bias\left({\overline{y}}_{NRTi}\right)\in \left[Bias\left({\overline{y}}_{LRTi}\right),Bias\left({\overline{y}}_{URTi}\right)\right]$$

The MSE of ${\overline{y}}_{NRTi}$ up to the first-order approximation is given as

$$MSE\left({\overline{y}}_{NRTi}\right)={\lambda }_N{\overline{Y}}_N^2\left[C_{y_N}^2+{\tau }_N^2{C}_{x_N}^2-2{\tau }_N{C}_{y_N}{C}_{x_N}{\rho }_{x_N{y}_N}\right],$$

(27)

$$MSE\left({\overline{y}}_{NRTi}\right)\in \left[MSE\left({\overline{y}}_{LRTi}\right),MSE\left({\overline{y}}_{URTi}\right)\right].$$

Some members of the proposed GNR class of estimator are given in Table 1.

Table 1. Some members of proposed GNR, GNE, and GNRE classes of estimator.

S,No	$\mathit{\alpha }$	$\mathbf{\Psi }$	${\overline{\mathit{y}}}_{{\mathit{NRT}}_{\mathit{i}}}$	${\overline{\mathit{y}}}_{{\mathit{NET}}_{\mathit{i}}}$	${\overline{\mathit{y}}}_{{\mathit{NRET}}_{\mathit{i}}}$
1	1	0	${\overline{y}}_{RN}$, [26]	${\overline{y}}_{BTrN}$, [26]
2	1	1		${\overline{y}}_{RrN}$, [26]	${\overline{y}}_{tpN}$, [30]
3	1	$C_{X_N}$	${\overline{y}}_{SDrRN}$, [26]
4	1	${\beta }_{2\left(X_N\right)}$	${\overline{y}}_{SKrRN}$, [26]
5	${\beta }_{2\left(X_N\right)}$	$C_{X_N}$	${\overline{y}}_{USrRN}$, [26]
6	${\beta }_{1\left(X_N\right)}$	${\overline{X}}_S$	${\overline{y}}_{NR{T}_1}$	${\overline{y}}_{NE{T}_1}$	${\overline{y}}_{NRE{T}_1}$
7	${\beta }_{2\left(X_N\right)}$	${\overline{X}}_S$	${\overline{y}}_{NR{T}_2}$	${\overline{y}}_{NE{T}_2}$	${\overline{y}}_{NRE{T}_2}$
8	${\beta }_{1\left(X_N\right)}$	${\overline{X}}_S+C{V}_{\left(X_S\right)}$	${\overline{y}}_{NR{T}_3}$	${\overline{y}}_{NE{T}_3}$	${\overline{y}}_{NRE{T}_3}$
9	${\beta }_{2\left(X_N\right)}$	${\overline{X}}_S+C{V}_{\left(X_S\right)}$	${\overline{y}}_{NR{T}_4}$	${\overline{y}}_{NE{T}_4}$	${\overline{y}}_{NRE{T}_4}$
10	${\beta }_{2\left(X_S\right)}$	${\overline{X}}_S+C{V}_{\left(X_S\right)}$	${\overline{y}}_{NR{T}_5}$	${\overline{y}}_{NE{T}_5}$	${\overline{y}}_{NRE{T}_5}$
11	${\beta }_{2\left(X_N\right)}$	${\overline{X}}_S-C{V}_{\left(X_S\right)}$	${\overline{y}}_{NR{T}_6}$	${\overline{y}}_{NE{T}_6}$	${\overline{y}}_{NRE{T}_6}$
12	${\beta }_{1\left(X_N\right)}$	${\overline{X}}_S+C{V}_{\left(X_N\right)}$	${\overline{y}}_{NR{T}_7}$	${\overline{y}}_{NE{T}_7}$	${\overline{y}}_{NRE{T}_7}$
13	${\beta }_{2\left(X_N\right)}$	${\overline{X}}_S+C{V}_{\left(X_N\right)}$	${\overline{y}}_{NR{T}_8}$	${\overline{y}}_{NE{T}_8}$	${\overline{y}}_{NRE{T}_8}$
14	${\beta }_{2\left(X_S\right)}$	${\overline{X}}_S+C{V}_{\left(X_N\right)}$	${\overline{y}}_{NR{T}_9}$	${\overline{y}}_{NE{T}_9}$	${\overline{y}}_{NRE{T}_9}$
15	${\beta }_{2\left(X_N\right)}$	${\overline{X}}_S-C{V}_{\left(X_N\right)}$	${\overline{y}}_{NR{T}_{10}}$	${\overline{y}}_{NE{T}_{10}}$	${\overline{y}}_{NRE{T}_{10}}$
16	${\beta }_{2\left(X_N\right)}-{\beta }_{2\left(X_S\right)}$	${\overline{X}}_S-C{V}_{\left(X_N\right)}$	${\overline{y}}_{NR{T}_{11}}$	${\overline{y}}_{NE{T}_{11}}$	${\overline{y}}_{NRE{T}_{11}}$
17	${\beta }_{1\left(X_N\right)}{\beta }_{1\left(X_S\right)}$	${\overline{X}}_S+C{V}_{\left(X_N\right)}$	${\overline{y}}_{NR{T}_{12}}$	${\overline{y}}_{NE{T}_{12}}$	${\overline{y}}_{NRE{T}_{12}}$
18	${\beta }_{2\left(X_N\right)}{\beta }_{2\left(X_S\right)}$	${\overline{X}}_S+C{V}_{\left(X_N\right)}$	${\overline{y}}_{NR{T}_{13}}$	${\overline{y}}_{NE{T}_{13}}$	${\overline{y}}_{NRE{T}_{13}}$
19	${\beta }_{2\left(X_N\right)}{\beta }_{1\left(X_N\right)}$	${\overline{X}}_S+C{V}_{\left(X_N\right)}$	${\overline{y}}_{NR{T}_{14}}$	${\overline{y}}_{NE{T}_{14}}$	${\overline{y}}_{NRE{T}_{14}}$
20	${\beta }_{2\left(X_S\right)}{\beta }_{1\left(X_S\right)}$	${\overline{X}}_S+C{V}_{\left(X_N\right)}$	${\overline{y}}_{NR{T}_{15}}$	${\overline{y}}_{NE{T}_{15}}$	${\overline{y}}_{NRE{T}_{15}}$
21	${\beta }_{2\left(X_N\right)}{\beta }_{2\left(X_S\right)}$	${\overline{X}}_S-C{V}_{\left(X_N\right)}$	${\overline{y}}_{NR{T}_{16}}$	${\overline{y}}_{NE{T}_{16}}$	${\overline{y}}_{NRE{T}_{16}}$
22	${\beta }_{1\left(X_N\right)}{\beta }_{1\left(X_S\right)}$	${\overline{X}}_S-C{V}_{\left(X_N\right)}$	${\overline{y}}_{NR{T}_{17}}$	${\overline{y}}_{NE{T}_{17}}$	${\overline{y}}_{NRE{T}_{17}}$
23	${\beta }_{2\left(X_N\right)}{\beta }_{1\left(X_N\right)}$	${\overline{X}}_S-C{V}_{\left(X_N\right)}$	${\overline{y}}_{NR{T}_{18}}$	${\overline{y}}_{NE{T}_{18}}$	${\overline{y}}_{NRE{T}_{18}}$
24	${\beta }_{2\left(X_S\right)}{\beta }_{1\left(X_S\right)}$	${\overline{X}}_S-C{V}_{\left(X_N\right)}$	${\overline{y}}_{NR{T}_{19}}$	${\overline{y}}_{NE{T}_{19}}$	${\overline{y}}_{NRE{T}_{19}}$
25	${\beta }_{1\left(X_N\right)}{\beta }_{1\left(X_S\right)}$	${\overline{X}}_S+C{V}_{\left(X_S\right)}$	${\overline{y}}_{NR{T}_{20}}$	${\overline{y}}_{NE{T}_{20}}$	${\overline{y}}_{NRE{T}_{20}}$
26	${\beta }_{2\left(X_N\right)}{\beta }_{2\left(X_S\right)}$	${\overline{X}}_S+C{V}_{\left(X_S\right)}$	${\overline{y}}_{NR{T}_{21}}$	${\overline{y}}_{NE{T}_{21}}$	${\overline{y}}_{NRE{T}_{21}}$
27	${\beta }_{2\left(X_N\right)}{\beta }_{1\left(X_N\right)}$	${\overline{X}}_S+C{V}_{\left(X_S\right)}$	${\overline{y}}_{NR{T}_{22}}$	${\overline{y}}_{NE{T}_{22}}$	${\overline{y}}_{NRE{T}_{22}}$
28	${\beta }_{2\left(X_S\right)}{\beta }_{1\left(X_S\right)}$	${\overline{X}}_S+C{V}_{\left(X_S\right)}$	${\overline{y}}_{NR{T}_{23}}$	${\overline{y}}_{NE{T}_{23}}$	${\overline{y}}_{NRE{T}_{23}}$
29	${\beta }_{2\left(X_N\right)}{\beta }_{2\left(X_S\right)}$	${\overline{X}}_S-C{V}_{\left(X_S\right)}$	${\overline{y}}_{NR{T}_{24}}$	${\overline{y}}_{NE{T}_{24}}$	${\overline{y}}_{NRE{T}_{244}}$
30	${\beta }_{2\left(X_N\right)}{\beta }_{1\left(X_N\right)}$	${\overline{X}}_S-C{V}_{\left(X_S\right)}$	${\overline{y}}_{NR{T}_{25}}$	${\overline{y}}_{NE{T}_{25}}$	${\overline{y}}_{NRE{T}_{25}}$
31	${\beta }_{2\left(X_S\right)}{\beta }_{1\left(X_S\right)}$	${\overline{X}}_S-C{V}_{\left(X_S\right)}$	${\overline{y}}_{NR{T}_{26}}$	${\overline{y}}_{NE{T}_{26}}$	${\overline{y}}_{NRE{T}_{26}}$

3.2.2. Neutrosophic Exponential Class of Estimator

The proposed generalized neutrosophic exponential (GNE) class of estimators ${\overline{y}}_{NETi}$ is defined as

$${\overline{y}}_{NE{T}_i}={\overline{y}}_{N}exp\left(\frac{(\alpha {\overline{X}}_N+\Psi )-(\alpha {\overline{x}}_N+\Psi )}{(\alpha {\overline{X}}_N+\Psi )+(\alpha {\overline{x}}_N+\Psi )}\right),$$

(28)

$${\overline{y}}_{NETi}\in \left[{\overline{y}}_{LETi},{\overline{y}}_{UETi}\right].$$

From Equation (28), we have

$${\overline{y}}_{NETi}-{\overline{Y}}_N=e_{N0}{\overline{Y}}_{N}Exp\left(\frac{{\tau }_N{e}_{N1}}{2}{\left(1+\frac{{\tau }_N{e}_{N1}}{2}\right)}^{-1}\right)$$

(29)

The mathematical expression for the bias of ${\overline{y}}_{NET}$ is given as

$$Bias\left({\overline{y}}_{NETi}\right)={\lambda }_N{\overline{Y}}_N\left[\frac{3}{8}{\tau }_N^2{C}_{x_N}^2-\frac{1}{2}{\tau }_N{C}_{y_N}{C}_{x_N}{\rho }_{x_N{y}_N}\right],$$

(30)

$$Bias\left({\overline{y}}_{NETi}\right)\in \left[Bias\left({\overline{y}}_{LETi}\right),Bias\left({\overline{y}}_{UETi}\right)\right].$$

The mathematical expression for the mean square error of ${\overline{y}}_{NETi}$ is given as

$$MSE\left({\overline{y}}_{NETi}\right)={\lambda }_N{\overline{Y}}_N^2\left[C_{y_N}^2+\frac{1}{4}{\tau }_N^2{C}_{x_N}^2-{\tau }_N{C}_{y_N}{C}_{x_N}{\rho }_{x_N{y}_N}\right],$$

(31)

$$MSE\left({\overline{y}}_{NETi}\right)\in \left[MSE\left({\overline{y}}_{LETi}\right),MSE\left({\overline{y}}_{UETi}\right)\right].$$

Some members of the proposed GNE class of estimator are given in Table 1.

3.2.3. Neutrosophic Ratio–Exponential Class of Estimator

The proposed generalized neutrosophic generalized ratio–exponential (GNRE) class of estimator ${\overline{y}}_{NRETi}$ is defined as follows:

$${\overline{y}}_{NRETi}={\overline{y}}_N\left[k_{1N}\frac{\alpha {\overline{X}}_N+\Psi }{\alpha {\overline{x}}_N+\Psi }+k_{2N}exp\left(\frac{(\alpha {\overline{X}}_N+\Psi )-(\alpha {\overline{x}}_N+\Psi )}{(\alpha {\overline{X}}_N+\Psi )+(\alpha {\overline{x}}_N+\Psi )}\right)\right],$$

(32)

$${\overline{y}}_{NRETi}\in \left[{\overline{y}}_{LRETi},{\overline{y}}_{URETi}\right]$$

Equation (32) can be written as follows:

$${\overline{y}}_{NRETi}={\overline{Y}}_N\left(1+e_{N0}\right)\left[k_{1N}{\left(1+{\tau }_N{e}_{N1}\right)}^{-1}+k_{2N}exp\left(-\frac{{\tau }_N{e}_{N1}}{2}{\left(1+\frac{{\tau }_N{e}_{N1}}{2}\right)}^{-1}\right)\right]$$

(33)

Expanding Equation (33) up to first-order approximation and subtracting ${\overline{Y}}_N$ from both sides, we have

$$\begin{array}{c}\hfill {\overline{Y}}_{NRETi}-{\overline{Y}}_N={\overline{Y}}_N\left[k_{1N}\left(1+e_{N0}-{\tau }_N{e}_{N1}-{\tau }_N{e}_{N0}{e}_{N1}+{\tau }_N^2{e}_{N1}^2\right)\right.\\ \hfill \left.+k_2\left(1+e_{N0}-\frac{{\tau }_N{e}_{N1}}{2}-\frac{{\tau }_N{e}_{N0}{e}_{N1}}{2}+\frac{3{\tau }_N^2{e}_{N1}^2}{8}\right)-1\right]\end{array}$$

(34)

Using Equation (34), the mathematical expression for the bias of ${\overline{Y}}_{NRETi}$ is given as

$$\begin{array}{c}\hfill Bias\left({\overline{y}}_{NRETi}\right)={\overline{Y}}_N\left[k_{1N}\left(1+{\lambda }_N\left({\tau }_N^2{C}_{x_N}^2-{\tau }_N{C}_{x_N}{C}_{y_N}{\rho }_{x_N{y}_N}\right)\right)\right.\\ \hfill \left.+k_{2N}\left(1+{\lambda }_N\left(\frac{3}{8}{\tau }_N^2{C}_{x_N}^2-\frac{1}{2}{\tau }_N{C}_{x_N}{C}_{y_N}{\rho }_{x_N{y}_N}\right)\right)-1\right],\end{array}$$

(35)

$$Bias\left({\overline{y}}_{NRETi}\right)\in \left[Bias\left({\overline{y}}_{LRETi}\right),Bias\left({\overline{y}}_{URETi}\right)\right]$$

Using Equation (34) and taking terms up to the first-order approximation, the mathematical expression for the MSE of ${\overline{Y}}_{NRETi}$ is given as

$$\begin{array}{c}\hfill MSE\left({\overline{y}}_{NRETi}\right)={\overline{Y}}_N^2\left(1+{\beta }_{1N}{k}_{1N}^2+{\beta }_{2N}{k}_{2N}^2-2{\beta }_{3N}{k}_{1N}-2{\beta }_{4N}{k}_{2N}+2{\beta }_{5N}{k}_{1N}{k}_{2N}\right),\end{array}$$

(36)

$$MSE\left({\overline{y}}_{NRETi}\right)\in \left[MSE\left({\overline{y}}_{LRETi}\right),MSE\left({\overline{y}}_{URETi}\right)\right],$$

where

$${\beta }_{1N}=1+{\lambda }_N\left(C_{y_N}^2+3{\tau }_N^2{C}_{x_N}^2-4{\tau }_N{C}_{x_N}{C}_{y_N}{\rho }_{x_N{y}_N}\right),{\beta }_{1N}\in \left[{\beta }_{1L},{\beta }_{1U}\right],$$

$${\beta }_{2N}=1+{\lambda }_N\left(C_{y_N}^2+{\tau }_N^2{C}_{x_N}^2-2{\tau }_N{C}_{x_N}{C}_{y_N}{\rho }_{x_N{y}_N}\right),{\beta }_{2N}\in \left[{\beta }_{2L},{\beta }_{2U}\right],$$

$${\beta }_{3N}=1+{\lambda }_N\left({\tau }_N^2{C}_{x_N}^2-{\tau }_N{C}_{x_N}{C}_{y_N}{\rho }_{x_N{y}_N}\right),{\beta }_{3N}\in \left[{\beta }_{3L},{\beta }_{3U}\right],$$

$${\beta }_{4N}=1+{\lambda }_N\left(\frac{3}{8}{\tau }_N^2{C}_{x_N}^2-\frac{1}{2}{\tau }_N{C}_{x_N}{C}_{y_N}{\rho }_{x_N{y}_N}\right),{\beta }_{4N}\in \left[{\beta }_{4L},{\beta }_{4U}\right],$$

$${\beta }_{5N}=1+{\lambda }_N\left(C_{y_N}^2+\frac{15}{8}{\tau }_N^2{C}_{x_N}^2-3{\tau }_N{C}_{x_N}{C}_{y_N}{\rho }_{x_N{y}_N}\right),{\beta }_{5N}\in \left[{\beta }_{5L},{\beta }_{5U}\right].$$

The real-valued constants $k_{1N}$ and $k_{2N}$ are selected that minimize $MSE\left({\overline{y}}_{NRETi}\right)$. Differentiating Equation (36) with respect to $k_{1N}$ and $k_{2N}$, we obtain

$$k_{1Nopt}=\frac{{\beta }_{4N}{\beta }_{5N}-{\beta }_{2N}{\beta }_{3N}}{{\beta }_{5N}{\beta }_{5N}-{\beta }_{1N}{\beta }_{2N}},k_{2Nopt}=\frac{{\beta }_{3N}{\beta }_{5N}-{\beta }_{1N}{\beta }_{4N}}{{\beta }_{5N}{\beta }_{5N}-{\beta }_{1N}{\beta }_{2N}}$$

The resultant minimum $MSE\left({\overline{y}}_{NRETi}\right)$ is

$$\begin{array}{c}\hfill MSE{\left({\stackrel{=}{y}}_{NERTi}\right)}_{min}={\overline{Y}}_N^2\left(1+{\beta }_{1N}{k}_{1Nopt}^2+{\beta }_{2N}{k}_{2Nopt}^2-2{\beta }_{3N}{k}_{1Nopt}-2{\beta }_{4N}{k}_{2Nopt}+2{\beta }_{5N}{k}_{1Nopt}{k}_{2Nopt}\right)\end{array}$$

(37)

$$MSE{\left({\overline{y}}_{NRETi}\right)}_{min}\in \left[MSE{\left({\overline{y}}_{LRETi}\right)}_{min},MSE{\left({\overline{y}}_{URETi}\right)}_{min}\right]$$

Some members of the generalized neutrosophic ratio–exponential (GNRE) class of estimators are presented in Table 1. It is mentioned that the existing neutrosophic estimators of the population mean are special cases of our proposed generalized neutrosophic estimator presented in Table 1.

4. Efficiency Comparison

The mathematical expression has been derived for the efficiency of the proposed neutrosophic class of estimators to its corresponding existing neutrosophic estimators.

Using Equations (10) and (27), the GNR class of estimator ${\overline{y}}_{NRTi}$ is more efficient than ${\overline{y}}_{NR}$ if

$${\rho }_{x_N{y}_N}\le \frac{C_{x_N}({\tau }_N+1)}{2C_{y_N}}$$

Using Equations (12) and (27), the GNR class of estimator ${\overline{y}}_{NRTi}$ is more efficient than ${\overline{y}}_{SDrN}$ if

$${\rho }_{x_N{y}_N}\le \frac{C_{x_N}({\tau }_N+{\theta }_{Nr1})}{2C_{y_N}}$$

Using Equations (14) and (27), the GNR class of estimator ${\overline{y}}_{NRTi}$ is more efficient than ${\overline{y}}_{SKrN}$ if

$${\rho }_{x_N{y}_N}\le \frac{C_{x_N}({\tau }_N+{\theta }_{Nr2})}{2C_{y_N}}$$

Using Equations (16) and (27), the GNR class of estimator ${\overline{y}}_{NRTi}$ is more efficient than ${\overline{y}}_{USrN}$ if

$${\rho }_{x_N{y}_N}\le \frac{C_{x_N}({\tau }_N+{\theta }_{Nr3})}{2C_{y_N}}$$

Using Equations (18) and (31), the GNE class of estimator ${\overline{y}}_{NETi}$ is more efficient than ${\overline{y}}_{BTrN}$ if

$${\rho }_{x_N{y}_N}\le \frac{C_{x_N}({\tau }_N+1)}{4C_{y_N}}$$

Using Equations (20) and (31), the GNR class of estimator ${\overline{y}}_{NRTi}$ is more efficient than ${\overline{y}}_{RrN}$ if

$${\rho }_{x_N{y}_N}\le \frac{C_{x_N}({\tau }_N+{\theta }_{Nr4})}{4C_{y_N}}$$

Using Equations (23) and (31), the GNRE class of estimator ${\overline{y}}_{NRETi}$ is more efficient than ${\overline{y}}_{tpN}$ if

$$\begin{array}{c}\hfill \left(A{k}_{1opt}^2+B{k}_{2opt}^2-2C{k}_{1opt}-2D{k}_{2opt}+2F{k}_{1opt}{k}_{2opt}\right)\\ \hfill -\left({\beta }_{1N}{k}_{1Nopt}^2+{\beta }_{2N}{k}_{2Nopt}^2-2{\beta }_{3N}{k}_{1Nopt}-2{\beta }_{4N}{k}_{2Nopt}+2{\beta }_{5N}{k}_{1Nopt}{k}_{2Nopt}\right)\ge 0\end{array}$$

For the empirical efficiency comparison, let ${\widehat{\theta }}_{1N}\in \left[{\widehat{\theta }}_{1L},{\widehat{\theta }}_{1U}\right]$ and ${\widehat{\theta }}_{2N}\in \left[{\widehat{\theta }}_{2L},{\widehat{\theta }}_{2U}\right]$ be two neutrosophic estimators of the neutrosophic population mean ${\theta }_{1N}\in \left[{\theta }_{1L},{\theta }_{1U}\right]$ having mean square errors $MSE\left({\widehat{\theta }}_{1N}\right)\in \left[MSE\left({\widehat{\theta }}_{1L}\right),MSE\left({\widehat{\theta }}_{1U}\right)\right]$ and $MSE\left({\widehat{\theta }}_{2N}\right)\in \left[MSE\left({\widehat{\theta }}_{2L}\right),{\widehat{MSE(\theta }}_{2U})\right].$ We used two criteria for the efficiency comparison between ${\widehat{\theta }}_{1N}$ and ${\widehat{\theta }}_{2N}$. The neutrosophic percentage relative efficiency (NPRE) criteria is defined as

$$NPRE=\frac{MSE\left({\widehat{\theta }}_{1N}\right)}{MSE\left({\widehat{\theta }}_{2N}\right)},NPRE\in [LPRE,UPRE].$$

The percentage relative efficiency total (PRET) criteria is defined as

$$PRET=\frac{MSET\left({\widehat{\theta }}_{1N}\right)}{MSET\left({\widehat{\theta }}_{2N}\right)}\times 100$$

where $MSET\left({\widehat{\theta }}_{1N}\right)=MSE\left({\widehat{\theta }}_{1L}\right)+MSE\left({\widehat{\theta }}_{1U}\right)$, $MSET\left({\widehat{\theta }}_{2N}\right)=MSE\left({\widehat{\theta }}_{2L}\right)+MSE\left({\widehat{\theta }}_{2U}\right).$

5. Simulation Study

Three simulated neutrosophic data sets are used for validating the theoretical and numerical efficiency comparisons of a proposed generalized class of neutrosophic estimators with existing neutrosophic estimators. The algorithm for the neutrosophic simulated data set has two steps. First, a bi-variate neutrosophic data set is generated from the bi-variate neutrosophic normal distribution of the study variable $Y_N\in [YL,YU]$ and auxiliary variable $X_N\in [XL,XU]$. That is, $\left(X_N,Y_N\right)\sim \mathcal{NN}\left({\mu }_N,{\Sigma }_N\right)$ , where ${\mu }_N$ is the neutrosophic mean vector and ${\Sigma }_N$ is the neutrosophic var-covariance matrix given as

$${\mu }_N=\left({\mu }_{X_N},{\mu }_{Y_N}\right),{\mu }_{X_N}\in [{\mu }_{X_L},{\mu }_{X_U}],{\mu }_{Y_N}\in [{\mu }_{Y_L},{\mu }_{Y_U}]$$

$${\Sigma }_N=\left[\begin{array}{cc}{\sigma }_{X_N}^2& {\sigma }_{X_N}{\sigma }_{Y_N}{\rho }_{X_N{Y}_N}\\ {\sigma }_{X_N}{\sigma }_{Y_N}{\rho }_{X_N{Y}_N}& {\sigma }_{Y_N}^2\end{array}\right]$$

where ${\sigma }_{X_N}\in \left[{\sigma }_{X_L},{\sigma }_{X_U}\right]$, ${\sigma }_{Y_N}\in \left[{\sigma }_{Y_L},{\sigma }_{Y_U}\right]$, and ${\rho }_{X_N{Y}_N}\in \left[{\rho }_{X_L{Y}_L},{\rho }_{X_U{Y}_U}\right].$ Second, the K = 100 uniformly distributed values are generated from $[X_L,X_U]$ and find the value of $X_A:[X_L,X_U]\to \mathbb{R}$ and $X_S:[X_L,X_U]\to {\mathbb{R}}^{+}$.

• The first neutrosophic data set, containing 3000 values, is generated from $\mathcal{NN}\left({\mu }_N,{\Sigma }_N\right)$ with ${\mu }_N=\left([130,250],[90,129]\right)$ and

  $${\Sigma }_N=\left[\begin{array}{cc}[{10}^2,6^2]& [10,6][5,9][0.10,-0.40]\\ [10,6][5,9][0.12,-0.35]& [5^2,9^2]\end{array}\right]$$
• The second neutrosophic data set, containing 3000 values, is generated from $\mathcal{NN}\left({\mu }_N,{\Sigma }_N\right)$ with ${\mu }_N=\left([20,25],[80,120]\right)$ and

  $${\Sigma }_N=\left[\begin{array}{cc}[{2.5}^2,5^2]& [2.5,5][3,7][0.40,0.50]\\ [2.5,5][3,7][0.40,0.50]& [3^2,7^2]\end{array}\right]$$
• The third neutrosophic data set, containing 3000 values, is generated from $\mathcal{NN}\left({\mu }_N,{\Sigma }_N\right)$ with ${\mu }_N=\left([11,26],[13,28]\right)$ and

  $${\Sigma }_N=\left[\begin{array}{cc}[5^2,3^2]& [5,3][7,9][-0.40,-0.50]\\ [5,3][7,9][-0.40,-0.50]& [7^2,9^2]\end{array}\right]$$

The statistical summaries of the above three simulated data sets are presented in Table 2, Table 3 and Table 4, respectively.

Table 2. Data summary of simulated population 1.

Variable	Mean	Variance	CV	${\mathit{\beta }}_1$	${\mathit{\beta }}_2$	${\mathit{\rho }}_{{\mathit{Y}}_{\mathit{N}}{\mathit{X}}_{\mathit{N}}}$
YN	[89.96268, 129.13892]	[24.81400, 81.61350]	[0.05537, 0.06996]	[0.00322, −0.06089]	[−0.10347, −0.16364]	[0.09739 , −0.39750]
XN	[129.83972, 249.86187]	[99.91385, 35.02842]	[0.07698, 0.02369]	[0.05101, −0.01263]	[0.05193, −0.02479]
XS	35.34425	13.96304	0.10572	0.06596	0.04418

Table 3. Data summary of simulated population 2.

Variable	Mean	Variance	CV	${\mathit{\beta }}_1$	${\mathit{\beta }}_2$	${\mathit{\rho }}_{{\mathit{Y}}_{\mathit{N}}{\mathit{X}}_{\mathit{N}}}$
YN	[84.97644, 125.21253]	[9.42978, 50.66704]	[0.03614, 0.05685]	[−0.00468, 0.00747]	[−0.02556, 0.03357]	[0.38504, 0.51247]
XN	[20.01850, 25.15033]	[6.11129, 24.03838]	[0.12349, 0.19494]	[0.04325, 0.04441]	[0.12058, 0.00489]	[0.00000, 0.00000]
XS	1.81335	1.59007	0.69539	0.72147	0.00965

Table 4. Data summary of simulated population 3.

Variable	Mean	Variance	CV	${\mathit{\beta }}_1$	${\mathit{\beta }}_2$	${\mathit{\rho }}_{{\mathit{Y}}_{\mathit{N}}{\mathit{X}}_{\mathit{N}}}$
YN	[13.08261, 28.38166]	[49.26777, 81.40849]	[0.53652, 0.31790]	[−0.01568, 0.01242]	[−0.07760, 0.08264]	[−0.40618, −0.50048]
XN	[11.04027, 25.95948]	[25.87714, 8.88683]	[0.46076, 0.11484]	[0.01566, −0.03767]	[−0.02383, −0.07052]	[0.00000, 0.00000]
XS	4.40090	3.03458	0.39583	0.07965	−0.13579

Let $B=630$, $c_0=130$, and ${\tilde{c}}^i=(10,23,31)$. The intuitionistic fuzzy cost function of $n_N$ is written as

$$130+(10,23,31)n=630$$

(38)

The intuitionistic fuzzy measurement cost ${\tilde{c}}^i=(10,23,31)$ is a linear triangular intuitionistic fuzzy number defined mathematically by Equation (39) and graphically by Figure 1:

$${\mu }_{{\tilde{c}}^i}\left(c\right)=\left\{\begin{array}{l}\frac{c-10}{23-10},10<c<23\hfill \\ 1,c=23\\ \frac{31-c}{31-23},23<c\le 31\\ \hfill 0,\mathrm{otherwise}.\end{array}\right., {\nu }_{{\tilde{c}}^i}\left(c\right)=\left\{\begin{array}{l}\frac{23-c}{23-10},10<c<23\hfill \\ 0,c=23\\ \frac{c-23}{31-23},23<c\le 31\\ \hfill 0,\mathrm{otherwise}.\end{array}\right.$$

(39)

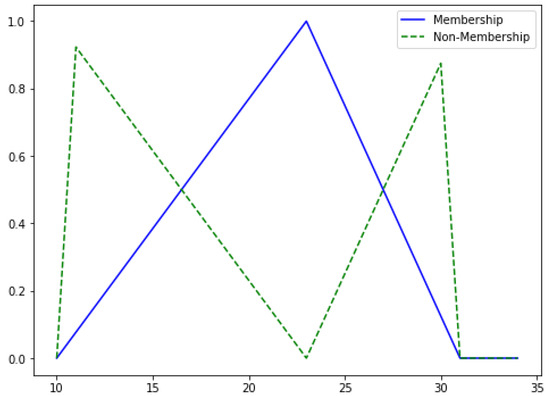
Figure 1. Triangular intuitionistic fuzzy measurement cost.

Using Equation (6), the intuitionistic fuzzy cost function given in Equation (38) can be converted into the classical form as

$$130+19.80n=630$$

$$\Rightarrow n=\frac{630-130}{19.80}=25.25\approx 25$$

Data Summary and Results

This section includes the statistical summary of three simulated data sets and the results of the estimation methods.

6. Discussion

The neutrosophic statistical approach is best for estimating the parameters of interest for uncertain and indeterminate data. Under such circumstances, the neutrosophic estimators of the population mean are more flexible and produce more efficient estimates. We proposed the GNR class of estimator ${\overline{y}}_{NRTi}$, GNE class of estimator ${\overline{y}}_{NETi}$, and GNRE class of estimator ${\overline{y}}_{NRETi}$ for the population mean in simple random sampling. The mathematical properties of the proposed estimators ${\overline{y}}_{NRTi}$, ${\overline{y}}_{NETi}$, and ${\overline{y}}_{NRETi}$ are derived up to the first-order approximation. The mathematical conditions have been derived for a theoretical efficiency comparison. The proposed neutrosophic estimators will perform better than neutrosophic estimators if these conditions are satisfied. The intuitionistic fuzzy set theory is the best alternative to classical set theory for making decisions in uncertain and fuzzy environments. The intuitionistic fuzzy cost function is introduced for decision making about per-unit measurement cost and sample size n under the fuzzy uncertain environment of simple random sampling. This cost function takes into account all possible values of the per-unit measurement cost collected through different sources like historical surveys, similar studies, pilot surveys, predicted costs, etc., and expert knowledge. The sample of 21 units is selected by the traditional linear cost function using an indicator function for deciding the per-unit measurement cost from (10, 23, 31) in the numerical study. The decided sample size under the classical approach is smaller than the proposed intuitionistic fuzzy approach. Because the precision of estimates is directly proportional to the sample size, the classical approach for deciding sample size under uncertain measurement costs will therefore produce smaller precision estimates. Table 2, Table 3 and Table 4 represent the statistical summary of the three simulated neutrosophic populations, 1, 2, and 3, respectively, with different levels of indeterminacy and correlation. The MSE and MSET of the existing neutrosophic ratio estimators ${\overline{y}}_{NR}$${\overline{y}}_{SDrRN}$, ${\overline{y}}_{SKrRN}$, and ${\overline{y}}_{USrRN}$ and the proposed GNR class of estimators ${\overline{y}}_{NRTi}(i=1,2,\dots ,26)$ are given in Table 5. Table 6 shows the MSE and MSET of the existing neutrosophic ratio estimators ${\overline{y}}_{BTrRN}$ and ${\overline{y}}_{RrN}$ and the proposed GNE class of estimators ${\overline{y}}_{NETi}(i=1,2,\dots ,26)$. Table 7 shows the MSE and MSET of the existing neutrosophic ratio–exponential estimator ${\overline{y}}_{tpN}$ and proposes the GNRE class of estimators ${\overline{y}}_{NRETi}(i=1,2,\dots ,26)$. We compared the efficiency of the existing neutrosophic estimators and the proposed GNR class of estimators, GNE class of estimators, and GNRE class of estimators with the neutrosophic estimator ${\overline{y}}_{NR}$ and the results are presented in Table 8, Table 9 and Table 10, respectively. Using PRET given in Table 8, it is noted that all members of the GNR class of estimators ${\overline{y}}_{NRTi}(i=1,2,\dots ,26)$ outperformed the existing neutrosophic estimator. ${\overline{y}}_{NRT6}$ produced the most efficient results for simulated population 1 and simulated population 3, and ${\overline{y}}_{NRT26}$ produced the most precise estimate of the neutrosophic mean for simulated population 2. From Table 9, the proposed GNE class of estimators ${\overline{y}}_{NETi}(i=1,2,\dots ,26)$ have higher efficiency than the existing exponential neutrosophic estimators ${\overline{y}}_{BTrRN}$ and ${\overline{y}}_{RrN}$ for all three simulated populations. Among ${\overline{y}}_{NETi}(i=1,2,\dots ,26)$, the estimator ${\overline{y}}_{NET11}$ produced the most efficient result for simulated population 1, the estimator ${\overline{y}}_{NET12}$ produced the most precise estimate for simulated population 2, and the estimator ${\overline{y}}_{NET5}$ produced the most efficient estimate for simulated population 3 based on the PRET. The proposed GNRE class of estimators ${\overline{y}}_{NRETi}(i=1,2,\dots ,26)$ is more efficient than the existing estimator ${\overline{y}}_{tpN}$ based on the NPRE and PRET as shown in Table 9. It can be observed that the estimator ${\overline{y}}_{NRET11}$ is most efficient for simulated population 1, the estimator ${\overline{y}}_{NRET1}$ produced the most precise estimate for the neutrosophic mean of simulation population 2, and the estimator ${\overline{y}}_{NRET9}$ produced the most efficient results for simulated population 3. All the proposed neutrosophic class estimators performed better than the existing respective neutrosophic estimators for all three simulated populations. The utilization of all the indeterminate values of the neutrosophic auxiliary variables in the proposed neutrosophic class of estimators is the main reason for producing more efficient results as compared to the respective existing neutrosophic estimators based only on extreme indeterminate values.

Table 5. MSE of generalized neutrosophic ratio class of estimators.

S,No	Estimator	Simulated Population 1		Simulated Population 2		Simulated Population 3
		MSE	MSET	MSE	MSET	MSE	MSET
1	${\overline{y}}_{RN}$	[2.62039, 4.47995]	7.10033	[3.75781, 18.57995]	22.33776	[4.75908, 4.81816]	9.57723
2	${\overline{y}}_{SDrRN}$	[2.61829, 4.47979]	7.09808	[3.71045, 18.27212]	21.98257	[4.59128, 4.80931]	9.40059
3	${\overline{y}}_{SKrRN}$	[2.61897, 4.48011]	7.09908	[3.71156, 18.57214]	22.28370	[4.76827, 4.82364]	9.59190
4	${\overline{y}}_{USrRN}$	[2.58068, 4.48615]	7.06683	[3.39087, 2.81246]	6.20333	[2.69187, 4.95460]	7.64646
5	${\overline{y}}_{NR{T}_1}$	[0.98961, 3.15546]	4.14507	[0.51214, 2.75074]	3.26287	[2.00787, 2.93006]	4.93793
6	${\overline{y}}_{NR{T}_2}$	[0.99042, 3.06895]	4.05936	[1.23625, 1.65660]	2.89285	[1.87344, 2.61138]	4.48481
7	${\overline{y}}_{NR{T}_3}$	[0.98948, 3.15572]	4.14519	[0.40905, 2.07641]	2.48546	[2.00345, 2.95787]	4.96132
8	${\overline{y}}_{NR{T}_4}$	[0.99028, 3.06949]	4.05977	[0.94167, 1.73141]	2.67308	[1.88003, 2.66911]	4.54914
9	${\overline{y}}_{NR{T}_5}$	[0.98407, 3.46520]	4.44927	[0.32600, 1.57056]	1.89656	[1.63234, 3.23046]	4.86280
10	${\overline{y}}_{NR{T}_6}$	[0.99056, 3.06839]	4.05895	[1.74167, 1.54196]	3.28363	[1.86556, 2.54490]	4.41046
11	${\overline{y}}_{NR{T}_7}$	[0.98951, 3.15552]	4.14503	[0.48684, 2.50371]	2.99054	[2.00280, 2.93869]	4.94149
12	${\overline{y}}_{NR{T}_8}$	[0.99032, 3.06907]	4.05939	[1.17250, 1.68099]	2.85349	[1.88101, 2.62905]	4.51006
13	${\overline{y}}_{NR{T}_9}$	[0.98410, 3.46564]	4.44974	[0.32070, 1.52289]	1.84360	[1.63292, 4.40972]	6.04264
14	${\overline{y}}_{NR{T}_{10}}$	[0.99052, 3.06882]	4.05934	[1.30635, 1.62891]	2.93526	[1.86413, 2.59294]	4.45707
15	${\overline{y}}_{NR{T}_{11}}$	[0.97836, 2.74398]	3.72234	[1.22364, 2.72553]	3.94916	[2.36208, 3.59385]	5.95593
16	${\overline{y}}_{NR{T}_{12}}$	[0.98132, 3.23219]	4.21351	[0.39378, 1.92481]	2.31859	[1.95815, 3.20884]	5.16699
17	${\overline{y}}_{NR{T}_{13}}$	[0.98220, 3.23056]	4.21276	[0.36297, 2.00563]	2.36860	[1.96431, 3.29127]	5.25558
18	${\overline{y}}_{NR{T}_{14}}$	[0.98190, 3.23926]	4.22116	[0.33513, 1.99082]	2.32595	[1.95313, 3.24686]	5.19999
19	${\overline{y}}_{NR{T}_{15}}$	[0.98168, 3.25507]	4.23675	[0.32765, 1.59527]	1.92292	[1.92087, 3.15364]	5.07451
20	${\overline{y}}_{NR{T}_{16}}$	[0.98219, 3.23055]	4.21274	[0.36147, 2.00463]	2.36610	[1.96665, 3.29447]	5.26113
21	${\overline{y}}_{NR{T}_{17}}$	[0.98131, 3.23218]	4.21349	[0.42656, 2.27291]	2.69947	[1.95905, 3.20774]	5.16679
22	${\overline{y}}_{NR{T}_{18}}$	[0.98190, 3.23926]	4.22116	[0.33513, 1.99082]	2.32595	[1.95313, 3.24686]	5.19999
23	${\overline{y}}_{NR{T}_{19}}$	[0.98167, 3.25509]	4.23676	[0.32441, 1.54539]	1.86980	[1.91308, 3.14942]	5.06251
24	${\overline{y}}_{NR{T}_{20}}$	[0.98133, 3.23220]	4.21353	[0.35142, 1.68926]	2.04068	[1.95820, 3.21005]	5.16825
25	${\overline{y}}_{NR{T}_{21}}$	[0.98220, 3.23058]	4.21278	[0.36536, 2.00646]	2.37182	[1.96445, 3.28775]	5.25220
26	${\overline{y}}_{NR{T}_{22}}$	[0.98190, 3.23926]	4.22116	[0.34169, 1.99457]	2.33626	[1.95312, 3.24583]	5.19895
27	${\overline{y}}_{NR{T}_{23}}$	[0.98169, 3.25503]	4.23671	[0.33434, 1.64950]	1.98384	[1.92042, 3.15824]	5.07866
28	${\overline{y}}_{NR{T}_{24}}$	[0.98219, 3.23054]	4.21273	[0.35578, 2.00233]	2.35811	[1.96645, 3.29887]	5.26533
29	${\overline{y}}_{NR{T}_{25}}$	[0.98189, 3.23927]	4.22116	[0.32184, 1.97603]	2.29787	[1.95289, 3.24909]	5.20197
30	${\overline{y}}_{NR{T}_{26}}$	[0.98167, 3.25513]	4.23680	[0.31861, 1.48661]	1.80521	[1.91375, 3.14357]	5.05732

Table 6. MSE of generalized neutrosophic exponential class of estimators.

S,No	Estimator	Simulated Population 1		Simulated Population 2		Simulated Population 3
		MSE	MSET	MSE	MSET	MSE	MSET
1	${\overline{y}}_{BTrRN}$	[1.32667, 3.76585]	5.09252	[0.97390, 4.38635]	5.36025	[2.99634, 3.91834]	6.91468
2	${\overline{y}}_{RrN}$	[1.32045, 3.76585]	5.08630	[0.89588, 4.38635]	5.28223	[2.88235, 3.91834]	6.80069
3	${\overline{y}}_{NE{T}_1}$	[0.97510, 3.19551]	4.17061	[0.32904, 1.52194]	1.85098	[1.98057, 3.07104]	5.05160
4	${\overline{y}}_{NE{T}_2}$	[0.97514, 3.14895]	4.12410	[0.44908, 1.80938]	2.25846	[1.91241, 2.86686]	4.77926
5	${\overline{y}}_{NE{T}_3}$	[0.97510, 3.19564]	4.17074	[0.31966, 1.48246]	1.80211	[1.97843, 3.08663]	5.06507
6	${\overline{y}}_{NE{T}_4}$	[0.97514, 3.14926]	4.12439	[0.39529, 1.85771]	2.25299	[1.91595, 2.90903]	4.82498
7	${\overline{y}}_{NE{T}_5}$	[0.97495, 3.34604]	4.32099	[0.34444, 1.74420]	2.08864	[1.71884, 2.42036]	4.13920
8	${\overline{y}}_{NE{T}_6}$	[0.97515, 3.14865]	4.12380	[0.54777, 1.71790]	2.26566	[1.90815, 2.81240]	4.72054
9	${\overline{y}}_{NE{T}_7}$	[0.97510, 3.19554]	4.17063	[0.32622, 1.50217]	1.82839	[1.97812, 3.07590]	5.05402
10	${\overline{y}}_{NE{T}_8}$	[0.97514, 3.14902]	4.12416	[0.43713, 1.82573]	2.26286	[1.91647, 2.88017]	4.79664
11	${\overline{y}}_{NE{T}_9}$	[0.97495, 3.34624]	4.32119	[0.33839, 1.69765]	2.03604	[1.72197, 2.48566]	4.20764
12	${\overline{y}}_{NE{T}_{10}}$	[0.97515, 3.14888]	4.12403	[0.46238, 1.78991]	2.25229	[1.90736, 2.85253]	4.75989
13	${\overline{y}}_{NE{T}_{11}}$	[0.98096, 2.90644]	3.88739	[0.44670, 2.32990]	2.77660	[2.13764, 3.40307]	5.54071
14	${\overline{y}}_{NE{T}_{12}}$	[0.98274, 3.23476]	4.21749	[0.31897, 1.48289]	1.80186	[1.95622, 3.21899]	5.17521
15	${\overline{y}}_{NE{T}_{13}}$	[0.98321, 3.23394]	4.21715	[0.36835, 2.00771]	2.37606	[1.95928, 3.25995]	5.21923
16	${\overline{y}}_{NE{T}_{14}}$	[0.98305, 3.23830]	4.22135	[0.35173, 2.00026]	2.35199	[1.95371, 3.23801]	5.19172
17	${\overline{y}}_{NE{T}_{15}}$	[0.98293, 3.24616]	4.22910	[0.34593, 1.76452]	2.11045	[1.93735, 3.19096]	5.12831
18	${\overline{y}}_{NE{T}_{16}}$	[0.98321, 3.23394]	4.21714	[0.36756, 2.00721]	2.37477	[1.96044, 3.26152]	5.22196
19	${\overline{y}}_{NE{T}_{17}}$	[0.98273, 3.23476]	4.21748	[0.32076, 1.48859]	1.80935	[1.95667, 3.21843]	5.17510
20	${\overline{y}}_{NE{T}_{18}}$	[0.98305, 3.23830]	4.22135	[0.35173, 2.00026]	2.35199	[1.95371, 3.23801]	5.19172
21	${\overline{y}}_{NE{T}_{19}}$	[0.98293, 3.24618]	4.22910	[0.34289, 1.72126]	2.06415	[1.93333, 3.18880]	5.12213
22	${\overline{y}}_{NE{T}_{20}}$	[0.98274, 3.23476]	4.21750	[0.31933, 1.50035]	1.81968	[1.95624, 3.21960]	5.17584
23	${\overline{y}}_{NE{T}_{21}}$	[0.98321, 3.23395]	4.21716	[0.36961, 2.00812]	2.37774	[1.95935, 3.25822]	5.21757
24	${\overline{y}}_{NE{T}_{22}}$	[0.98305, 3.23830]	4.22135	[0.35613, 2.00215]	2.35828	[1.95370, 3.23750]	5.19120
25	${\overline{y}}_{NE{T}_{23}}$	[0.98293, 3.24614]	4.22908	[0.35117, 1.80449]	2.15566	[1.93712, 3.19331]	5.13043
26	${\overline{y}}_{NE{T}_{24}}$	[0.98320, 3.23393]	4.21714	[0.36446, 2.00606]	2.37051	[1.96034, 3.26368]	5.22402
27	${\overline{y}}_{NE{T}_{25}}$	[0.98304, 3.23830]	4.22135	[0.33998, 1.99277]	2.33275	[1.95359, 3.23911]	5.19270
28	${\overline{y}}_{NE{T}_{26}}$	[0.98293, 3.24620]	4.22912	[0.33291, 1.63983]	1.97274	[1.93368, 3.18579]	5.11947

Table 7. MSE of generalized neutrosophic ratio–exponential class of estimators.

S,No	Estimator	Simulated Population 1		Simulated Population 2		Simulated Population 3
		MSE	MSET	MSE	MSET	MSE	MSET
1	${\overline{y}}_{tpN}$	[0.97490, 2.72566]	3.70056	[0.31859, 1.48196]	1.80055	[1.63155, 2.41954]	4.05109
2	${\overline{y}}_{NRE{T}_1}$	[0.97483, 2.72551]	3.70034	[0.31858, 1.48176]	1.80034	[1.62236, 2.41629]	4.03865
3	${\overline{y}}_{NRE{T}_2}$	[0.97483, 2.72549]	3.70032	[0.31858, 1.48187]	1.80045	[1.62107, 2.41501]	4.03608
4	${\overline{y}}_{NRE{T}_3}$	[0.97483, 2.72551]	3.70034	[0.31858, 1.48177]	1.80034	[1.62233, 2.41638]	4.03870
5	${\overline{y}}_{NRE{T}_4}$	[0.97483, 2.72549]	3.70032	[0.31858, 1.48188]	1.80046	[1.62114, 2.41529]	4.03644
6	${\overline{y}}_{NRE{T}_5}$	[0.97483, 2.72555]	3.70039	[0.31858, 1.48185]	1.80043	[1.61662, 2.41047]	4.02709
7	${\overline{y}}_{NRE{T}_6}$	[0.97483, 2.72549]	3.70032	[0.31859, 1.48185]	1.80044	[1.62099, 2.41463]	4.03562
8	${\overline{y}}_{NRE{T}_7}$	[0.97483, 2.72551]	3.70034	[0.31858, 1.48176]	1.80034	[1.62232, 2.41632]	4.03864
9	${\overline{y}}_{NRE{T}_8}$	[0.97483, 2.72549]	3.70032	[0.31858, 1.48187]	1.80045	[1.62115, 2.41510]	4.03625
10	${\overline{y}}_{NRE{T}_9}$	[0.97483, 2.72555]	3.70039	[0.31858, 1.48184]	1.80042	[1.61671, 2.41010]	4.02680
11	${\overline{y}}_{NRE{T}_{10}}$	[0.97483, 2.72549]	3.70032	[0.31859, 1.48186]	1.80045	[1.62097, 2.41491]	4.03588
12	${\overline{y}}_{NRE{T}_{11}}$	[0.97484, 2.72539]	3.70023	[0.31858, 1.48194]	1.80053	[1.62496, 2.41794]	4.04290
13	${\overline{y}}_{NRE{T}_{12}}$	[0.97484, 2.72552]	3.70036	[0.31858, 1.48177]	1.80035	[1.62192, 2.41708]	4.03900
14	${\overline{y}}_{NRE{T}_{13}}$	[0.97484, 2.72552]	3.70035	[0.31858 , 1.48190]	1.80049	[1.62197, 2.41729]	4.03926
15	${\overline{y}}_{NRE{T}_{14}}$	[0.97484, 2.72553]	3.70037	[0.31858, 1.48190]	1.80048	[1.62187, 2.41718]	4.03905
16	${\overline{y}}_{NRE{T}_{15}}$	[0.97484, 2.72552]	3.70036	[0.31858, 1.48186]	1.80044	[1.62156, 2.41694]	4.03850
17	${\overline{y}}_{NRE{T}_{16}}$	[0.97484, 2.72552]	3.70036	[0.31858, 1.48190]	1.80049	[1.62199, 2.41729]	4.03929
18	${\overline{y}}_{NRE{T}_{17}}$	[0.97484, 2.72552]	3.70036	[0.31858, 1.48176]	1.80034	[1.62192, 2.41708]	4.03901
19	${\overline{y}}_{NRE{T}_{18}}$	[0.97484, 2.72553]	3.70037	[0.31858, 1.48190]	1.80048	[1.62187, 2.41718]	4.03905
20	${\overline{y}}_{NRE{T}_{19}}$	[0.97484, 2.72552]	3.70036	[0.31858, 1.48185]	1.80043	[1.62148, 2.41693]	4.03841
21	${\overline{y}}_{NRE{T}_{20}}$	[0.97484, 2.72552]	3.70036	[0.31858, 1.48178]	1.80036	[1.62192, 2.41709]	4.03900
22	${\overline{y}}_{NRE{T}_{21}}$	[0.97484, 2.72552]	3.70035	[0.31858, 1.48190]	1.80049	[1.62197, 2.41728]	4.03925
23	${\overline{y}}_{NRE{T}_{22}}$	[0.97484, 2.72551]	3.70035	[0.31858, 1.48190]	1.80048	[1.62187, 2.41718]	4.03905
24	${\overline{y}}_{NRE{T}_{23}}$	[0.97484, 2.72552]	3.70036	[0.31858, 1.48187]	1.80045	[1.62155, 2.41695]	4.03851
25	${\overline{y}}_{NRE{T}_{24}}$	[0.97484, 2.72552]	3.70035	[0.31858, 1.48190]	1.80049	[1.62199, 2.41731]	4.03930
26	${\overline{y}}_{NRE{T}_{25}}$	[0.97484, 2.72551]	3.70035	[0.31858, 1.48190]	1.80048	[1.62187, 2.41719]	4.03905
27	${\overline{y}}_{NRE{T}_{26}}$	[0.97484, 2.72552]	3.70036	[0.31858, 1.48183]	1.80041	[1.62149, 2.41692]	4.03840

Table 8. NPRE and PRET of generalized neutrosophic ratio class of estimators.

S,No	Estimator	Simulated Population 1		Simulated Population 2		Simulated Population 3
		NPRE	PRET	NPRE	PRET	NPRE	PRET
1	${\overline{y}}_{RN}$	[100, 100]	100	[100, 100]	100	[[100, 100]	100
2	${\overline{y}}_{SDrRN}$	[100.08006, 100.00341]	100.03169	[101.27647, 101.68472]	101.61581	[103.65474, 100.18393]	101.87908
3	${\overline{y}}_{SKrRN}$	[100.05401, 99.99643]	100.01767	[101.24626, 100.04206]	100.24263	[99.80726, 99.88642]	99.84706
4	${\overline{y}}_{USrRN}$	[101.53861, 99.86177]	100.47412	[110.82149, 660.62933]	360.09302	[176.79476, 97.24620]	125.25053
5	${\overline{y}}_{NR{T}_1}$	[264.79028, 141.97433]	171.29583	[733.75067, 675.45388]	684.60409	[237.02090, 164.43889]	193.95234
6	${\overline{y}}_{NR{T}_2}$	[264.57410, 145.97668]	174.91247	[303.96788, 1121.57420]	772.17185	[254.02939, 184.50646]	213.54820
7	${\overline{y}}_{NR{T}_3}$	[264.82564, 141.96279]	171.29070	[918.67583, 894.81094]	898.73853	[237.54368, 162.89272]	193.03784
8	${\overline{y}}_{NR{T}_4}$	[264.61081, 145.95061]	174.89478	[399.05725, 1073.11367]	835.65698	[253.13828, 180.51558]	210.52849
9	${\overline{y}}_{NR{T}_5}$	[266.27983, 129.28388]	159.58410	[1152.71100, 1183.01279]	1177.80425	[291.54888, 149.14770]	196.94884
10	${\overline{y}}_{NR{T}_6}$	[264.53705, 146.00293]	174.93027	[215.75914, 1204.95912]	680.27717	[255.10118, 189.32614]	217.14807
11	${\overline{y}}_{NR{T}_7}$	[264.81606, 141.97174]	171.29743	[771.88175, 742.09796]	746.94653	[237.62152, 163.95598]	193.81281
12	${\overline{y}}_{NR{T}_8}$	[264.60086, 145.97083]	174.91149	[320.49588, 1105.29996]	782.82352	[253.00626, 183.26617]	212.35268
13	${\overline{y}}_{NR{T}_9}$	[266.27289, 129.26747]	159.56741	[1171.74313, 1220.04331]	1211.64125	[291.44619, 109.26216]	158.49422
14	${\overline{y}}_{NR{T}_{10}}$	[264.54715, 145.98255]	174.91344	[287.65733, 1140.63548]	761.01421	[255.29808, 185.81798]	214.87735
15	${\overline{y}}_{NR{T}_{11}}$	[267.83456, 163.26448]	190.74912	[307.10137, 681.70165]	565.63268	[201.47809, 134.06674]	160.80162
16	${\overline{y}}_{NR{T}_{12}}$	[267.02574, 138.60407]	168.51337	[954.29857, 965.28587]	963.41984	[243.03947, 150.15251]	185.35415
17	${\overline{y}}_{NR{T}_{13}}$	[266.78799, 138.67380]	168.54340	[1035.30500, 926.38958]	943.07990	[242.27734, 146.39206]	182.22986
18	${\overline{y}}_{NR{T}_{14}}$	[266.86859, 138.30148]	168.20799	[1121.29879, 933.28186]	960.37195	[243.66371, 148.39439]	184.17785
19	${\overline{y}}_{NR{T}_{15}}$	[266.92775, 137.62988]	167.58906	[1146.88947, 1164.69134]	1161.65802	[247.75630, 152.78061]	188.73203
20	${\overline{y}}_{NR{T}_{16}}$	[266.79029, 138.67420]	168.54411	[1039.58918, 926.85145]	944.07446	[241.98850, 146.24966]	182.03765
21	${\overline{y}}_{NR{T}_{177}}$	[267.02889, 138.60437]	168.51411	[880.95461, 817.45301]	827.48732	[242.92740, 150.20418]	185.36135
22	${\overline{y}}_{NR{T}_{18}}$	[266.86859, 138.30148]	168.20799	[1121.29879, 933.28186]	960.37195	[243.66371, 148.39439]	184.17785
23	${\overline{y}}_{NR{T}_{19}}$	[266.93056, 137.62888]	167.58854	[1158.36969, 1202.28249]	1194.66372	[248.76470, 152.98535]	189.17965
24	${\overline{y}}_{NR{T}_{20}}$	[267.02516, 138.60356]	168.51281	[1069.33186, 1099.88791]	1094.62597	[243.03298, 150.09614]	185.30905
25	${\overline{y}}_{NR{T}_{21}}$	[266.78756, 138.67313]	168.54271	[1028.51846, 926.00704]	941.79818	[242.26060, 146.54866]	182.34717
26	${\overline{y}}_{NR{T}_{22}}$	[266.86811, 138.30167]	168.20809	[1099.75875, 931.52769]	956.13262	[243.66566, 148.44125]	184.21471
27	${\overline{y}}_{NR{T}_{23}}$	[266.92723, 137.63159]	167.59059	[1123.95352, 1126.39894]	1125.98681	[247.81449, 152.55840]	188.57809
28	${\overline{y}}_{NR{T}_{24}}$	[266.79073, 138.67488]	168.54481	[1056.22998, 927.91600]	947.27518	[242.01318, 146.05455]	181.89243
29	${\overline{y}}_{NR{T}_{25}}$	[266.87167, 138.30118]	168.20816	[1167.59830, 940.26728]	972.10741	[243.69453, 148.29270]	184.10776
30	${\overline{y}}_{NR{T}_{26}}$	[266.93109, 137.62716]	167.58700	[1179.44595, 1249.82430]	1237.40299	[248.67820, 153.27011]	189.37364

Table 9. NPRE and PRET of generalized neutrosophic exponential class of estimators.

S,No	Estimator	Simulated Population 1		Simulated Population 2		Simulated Population 3
		NPRE	PRET	NPRE	PRET	NPRE	PRET
1	${\overline{y}}_{BTrN}$	[197.51566, 118.96238]	139.42659	[385.84991, 423.58601]	416.72974	[158.82949, 122.96425]	138.50576
2	${\overline{y}}_{RrN}$	[198.44674, 118.96238]	139.59722	[419.45387, 423.58601]	422.88519	[165.11079, 122.96425]	140.82732
3	${\overline{y}}_{NE{T}_1}$	[268.72953, 140.19515]	170.24690	[1142.04051, 1220.80954]	1206.80699	[240.28878, 156.89029]	189.58807
4	${\overline{y}}_{NE{T}_2}$	[268.71769, 142.26780]	172.16693	[836.77946, 1026.86755]	989.06978	[248.85292, 168.06400]	200.39140
5	${\overline{y}}_{NE{T}_3}$	[268.73135, 140.18927]	170.24170	[1175.56986, 1253.32238]	1239.53065	[240.54757, 156.09759]	189.08408
6	${\overline{y}}_{NE{T}_4}$	[268.71978, 142.25405]	172.15454	[950.65697, 1000.15444]	991.47015	[248.39304, 165.62739]	198.49271
7	${\overline{y}}_{NE{T}_5}$	[268.77059, 133.88815]	164.32193	[1090.99271, 1065.24390]	1069.49017	[276.87782, 199.06775]	231.37904
8	${\overline{y}}_{NE{T}_6}$	[268.71554, 142.28164]	172.17940	[686.02388, 1081.55337]	985.92659	[249.40848, 171.31855]	202.88420
9	${\overline{y}}_{NE{T}_7}$	[268.73086, 140.19383]	170.24587	[1151.91564, 1236.87663]	1221.71782	[240.58611, 156.64219]	189.49744
10	${\overline{y}}_{NE{T}_8}$	[268.71922, 142.26471]	172.16431	[859.65449, 1017.67007]	987.14530	[248.32505, 167.28739]	199.66555
11	${\overline{y}}_{NE{T}_9}$	[268.77061, 133.88009]	164.31427	[1110.49190, 1094.45442]	1097.11987	[276.37351, 193.83786]	227.61553
12	${\overline{y}}_{NE{T}_{10}}$	[268.71613, 142.27089]	172.16955	[812.71782, 1038.03854]	991.78203	[249.51085 168.90830]	201.20700
13	${\overline{y}}_{NE{T}_{11}}$	[267.12505, 154.13883]	182.65017	[841.22953, 797.45698]	804.49917	[222.63277, 141.58266]	172.85225
14	${\overline{y}}_{NE{T}_{12}}$	[266.64207, 138.49394]	168.35426	[1178.11411, 1252.95304]	1239.70493	[243.27971, 149.67914]	185.05994
15	${\overline{y}}_{NE{T}_{13}}$	[266.51331, 138.52885]	168.36784	[1020.16583, 925.43032]	940.11685	[242.89931, 147.79850]	183.49900
16	${\overline{y}}_{NE{T}_{14}}$	[266.55648, 138.34260]	168.20054	[1068.37183, 928.87577]	949.73692	[243.59172, 148.80005]	184.47138
17	${\overline{y}}_{NE{T}_{15}}$	[266.58847, 138.00737]	167.89238	[1086.29732, 1052.97294]	1058.43521	[245.64870, 150.99392]	186.75219
18	${\overline{y}}_{NE{T}_{16}}$	[266.51454, 138.52905]	168.36821	[1022.37397, 925.66123]	940.63007	[242.75529, 147.72724]	183.40290
19	${\overline{y}}_{NE{T}_{17}}$	[266.64380, 138.49409]	168.35465	[1171.53168, 1248.15801]	1234.57374	[243.22374, 149.70497]	185.06371
20	${\overline{y}}_{NE{T}_{18}}$	[266.55648, 138.34260]	168.20054	[1068.37183, 928.87577]	949.73692	[243.59172, 148.80005]	184.47138
21	${\overline{y}}_{NE{T}_{19}}$	[266.58999, 138.00688]	167.89214	[1095.93593, 1079.43687]	1082.17761	[246.15907, 151.09643]	186.97757
22	${\overline{y}}_{NE{T}_{20}}$	[266.64175, 138.49369]	168.35397	[1176.77507, 1238.37339]	1227.56367	[243.27647, 149.65095]	185.03733
23	${\overline{y}}_{NE{T}_{21}}$	[266.51308, 138.52851]	168.36749	[1016.69004, 925.23907]	939.45486	[242.89097, 147.87686]	183.55739
24	${\overline{y}}_{NE{T}_{22}}$	[266.55622, 138.34270]	168.20059	[1055.18562, 927.99891]	947.20560	[243.59270, 148.82348]	184.48977
25	${\overline{y}}_{NE{T}_{23}}$	[266.58819, 138.00823]	167.89314	[1070.08990, 1029.65023]	1036.23806	[245.67811, 150.88268]	186.67499
26	${\overline{y}}_{NE{T}_{24}}$	[266.51477, 138.52939]	168.36856	[1031.07157, 926.19344]	942.31804	[242.76759, 147.62960]	183.33065
27	${\overline{y}}_{NE{T}_{25}}$	[266.55814, 138.34245]	168.20065	[1105.30757, 932.36757]	957.57213	[243.60714, 148.74920]	184.43645
28	${\overline{y}}_{NE{T}_{26}}$	[266.59028, 138.00602]	167.89138	[1128.78376, 1133.03801]	1132.32009	[246.11523, 151.23903]	187.07480

Table 10. NPRE and PRET of neutrosophic generalized ratio–exponential class of estimators.

S,No	Estimator	Simulated Population 1		Simulated Population 2		Simulated Population 3
		NPRE	PRET	NPRE	PRET	NPRE	PRET
1	${\overline{y}}_{tpN}$	[268.78563, 164.36163]	191.87171	[1179.50961, 1253.74459]	1240.60936	[291.68994, 199.13527]	236.41111
2	${\overline{y}}_{NRE{T}_1}$	[268.80339, 164.37118]	191.88327	[1179.56139, 1253.91151]	1240.75495	[293.34208, 199.40302]	237.13919
3	${\overline{y}}_{NRE{T}_2}$	[268.80339, 164.37216]	191.88411	[1179.53356, 1253.81988]	1240.67514	[293.57587, 199.50865]	237.29027
4	${\overline{y}}_{NRE{T}_3}$	[268.80339, 164.37118]	191.88327	[1179.56181, 1253.90672]	1240.75112	[293.34909, 199.39570]	237.13626
5	${\overline{y}}_{NRE{T}_4}$	[268.80339, 164.37216]	191.88411	[1179.54617, 1253.81184]	1240.67094	[293.56321, 199.48523]	237.26949
6	${\overline{y}}_{NRE{T}_5}$	[268.80336, 164.36824]	191.88074	[1179.54595, 1253.83165]	1240.68704	[294.38396, 199.88450]	237.82004
7	${\overline{y}}_{NRE{T}_6}$	[268.80340, 164.37217]	191.88412	[1179.51477, 1253.83675]	1240.68538	[293.59117, 199.54030]	237.31776
8	${\overline{y}}_{NRE{T}_7}$	[268.80339, 164.37118]	191.88327	[1179.56177, 1253.91127]	1240.75482	[293.35014, 199.40073]	237.14018
9	${\overline{y}}_{NRE{T}_8}$	[268.80339, 164.37216]	191.88411	[1179.53625, 1253.81709]	1240.67337	[293.56134, 199.50116]	237.28022
10	${\overline{y}}_{NRE{T}_9}$	[268.80336, 164.36824]	191.88073	[1179.54859, 1253.84082]	1240.69499	[294.36824, 199.91561]	237.83710
11	${\overline{y}}_{NRE{T}_{10}}$	[268.80339, 164.37216]	191.88411	[1179.53067, 1253.82328]	1240.67737	[293.59399, 199.51682]	237.30197
12	${\overline{y}}_{NRE{T}_{11}}$	[268.80272, 164.37798]	191.88898	[1179.53409, 1253.75793]	1240.62478	[292.87305, 199.26725]	236.89023
13	${\overline{y}}_{NRE{T}_{12}}$	[268.80256, 164.37037]	191.88242	[1179.56150, 1253.90302]	1240.74806	[293.42329, 199.33749]	237.11892
14	${\overline{y}}_{NRE{T}_{13}}$	[268.80252, 164.37040]	191.88243	[1179.53679, 1253.78919]	1240.65075	[293.41293, 199.32082]	237.10369
15	${\overline{y}}_{NRE{T}_{14}}$	[268.80254, 164.36979]	191.88191	[1179.54297, 1253.79112]	1240.65347	[293.43178, 199.32967]	237.11611
16	${\overline{y}}_{NRE{T}_{15}}$	[268.80255, 164.37015]	191.88222	[1179.54533, 1253.82786]	1240.68383	[293.48794, 199.34926]	237.14827
17	${\overline{y}}_{NRE{T}_{16}}$	[268.80252, 164.37037]	191.88241	[1179.53707, 1253.78996]	1240.65143	[293.40901, 199.32019]	237.10197
18	${\overline{y}}_{NRE{T}_{17}}$	[268.80256, 164.37037]	191.88242	[1179.56201, 1253.90964]	1240.75354	[293.42176, 199.33772]	237.11859
19	${\overline{y}}_{NRE{T}_{18}}$	[268.80254, 164.36979]	191.88191	[1179.54297, 1253.79112]	1240.65347	[293.43178, 199.32967]	237.11611
20	${\overline{y}}_{NRE{T}_{19}}$	[268.80255, 164.37015]	191.88222	[1179.54661, 1253.83608]	1240.69077	[293.50191, 199.35018]	237.15346
21	${\overline{y}}_{NRE{T}_{20}}$	[268.80256, 164.37037]	191.88242	[1179.55943, 1253.89278]	1240.73933	[293.42320, 199.33724]	237.11871
22	${\overline{y}}_{NRE{T}_{21}}$	[268.80252, 164.37043]	191.88246	[1179.53635, 1253.78919]	1240.65067	[293.41271, 199.32151]	237.10411
23	${\overline{y}}_{NRE{T}_{22}}$	[268.80254, 164.37072]	191.88271	[1179.54126, 1253.79093]	1240.65299	[293.43181, 199.32988]	237.11627
24	${\overline{y}}_{NRE{T}_{23}}$	[268.80255, 164.37015]	191.88222	[1179.54319, 1253.82072]	1240.67762	[293.48874, 199.34826]	237.14782
25	${\overline{y}}_{NRE{T}_{24}}$	[268.80252, 164.37043]	191.88246	[1179.53817, 1253.79035]	1240.65195	[293.40935, 199.31933]	237.10147
26	${\overline{y}}_{NRE{T}_{25}}$	[268.80254, 164.37072]	191.88271	[1179.54788, 1253.79213]	1240.65521	[293.43221, 199.32922]	237.11593
27	${\overline{y}}_{NRE{T}_{26}}$	[268.80255, 164.37015]	191.88222	[1179.55115, 1253.85326]	1240.70560	[293.50071, 199.35146]	237.15398

7. Conclusions

The classical approach to decision making on the per-unit measurement cost in survey sampling is based on bi-valiant logic and modeled by a classical cost function. This approach may not deal with the uncertain, fuzzy nature of measurement costs and expert knowledge. The proposed intuitionistic fuzzy cost function models the fuzzy uncertainty in the measurement cost, taking into account all possible values and expert knowledge, by using a membership function. The estimation of the sample size under the proposed cost function is also more flexible and a generalization of the classical method. Moreover, the existing neutrosophic estimators of the population mean in simple random sampling are unable to utilize all the indeterminate and imprecise parts of the set of information collected through a sample survey or experimentation. These estimators are based on only extreme values in the neutrosophic data set. Utilizing the parametric value of the proposed function of the neutrosophic auxiliary variable, the proposed generalized neutrosophic ratio-type estimators are based on all indeterminate values and consequently produce more accurate and precise estimates of the indeterminate parameter of interest. The proposed neutrosophic methods of the estimation of the mean and sample size determination under fuzzy uncertainty can be potentially extended to other sampling designs.