Ninth-order Multistep Collocation Formulas for Solving Models of PDEs Arising in Fluid Dynamics: Design and Implementation Strategies
Abstract
1. Introduction
2. Design of NMCFS
Implementation Strategies of the NMCFs
3. Theoretical Analysis of the NMCFs
3.1. Introduction of the Analysis of the NMCFs
3.1.1. Order and Error Constant of the NMCFs
3.1.2. Consistency of the NMCFs (Omole et al. [40,41])
3.1.3. Zero-Stability of the NMCFs (Fatunla [42])
3.1.4. Convergence of the NMCFs (Henrici [39], Rufai et al. [43])
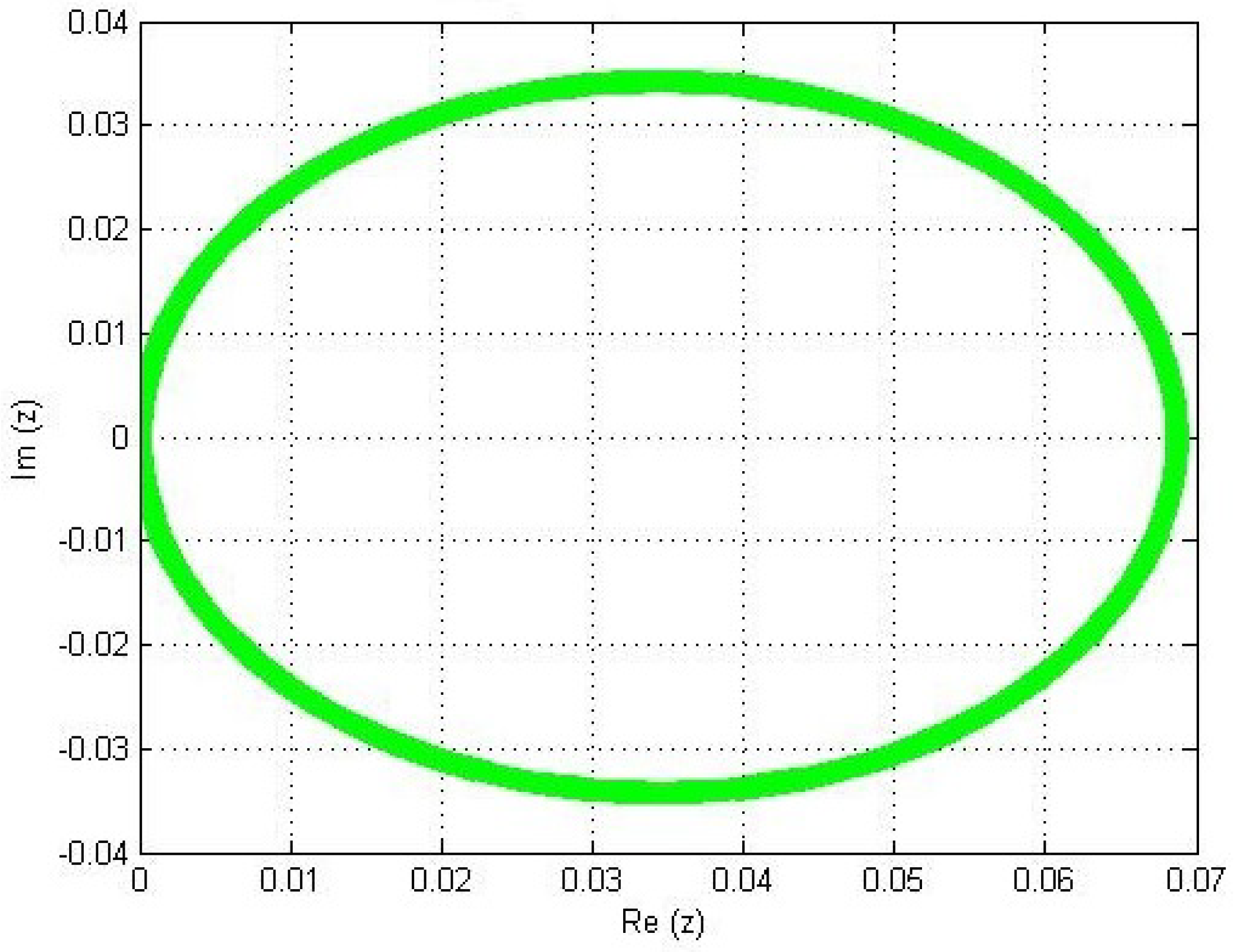
3.1.5. Region of Absolute Stability of the NMCFs (Yakubu et al. [21], Lambert [37])
4. Implementation Strategy
5. Numerical Examples
5.1. Test Problem One
5.2. Test Problem Two
5.3. Test Problem Three
5.4. Test Problem Four
5.5. Test Problem Five
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
Appendix D
References
- Liu, X.; Ahsan, M.; Ahmad, M.; Nisar, M.; Liu, X.; Ahmad, I.; Ahmad, H. Applications of Haar Wavelet-Finite Difference Hybrid Method and Its Convergence for Hyperbolic Nonlinear Schrodinger Equation with Energy and Mass Conversion. Energies 2021, 14, 7831. [Google Scholar] [CrossRef]
- Kamran, M.; Abbas, M.; Majeed, A.; Emadifar, H.; Nazir, T. Numerical Sim-ulation of Time Fractional BBM-Burger Equation Using Cubic B-Spline Functions. Hindawi J. Funct. Spaces 2022, 2022, 2119416. [Google Scholar]
- Kilic, S.S.S.; Celik, E. Complex Solutions to the Higher-Order Nonlinear Boussinesq Type Wave Equation Transform. Ric. Mat. 2022, 1–8. [Google Scholar]
- Akbarov, S.D.; Mehdiyev, M.A.; Zeynalov, A.M. Dynamic of the moving ring-load acting in the interior of the bi-layered hollow cylinder with imperfect contact between the layers. TWMS J. Pure Appl. Math. 2021, 12, 223–242. [Google Scholar]
- Chen, W.; Wu, W.X.; Teng, Z.D. Complete dynamics in a nonlocal dispersal two-strain SIV epidemic model with vaccination and latent delays. Appl. Comput. Math. 2020, 19, 360–391. [Google Scholar]
- Singh, J.; Kumar, D.; Kumar, S. An efficient computational method for local fractional transport equation occurring in fractal porous media. Comput. Appl. Math. 2020, 39, 137. [Google Scholar] [CrossRef]
- Mirzaee, F.; Rezaei, S.; Samadyar, N. Numerical solution of two-dimensional stochastic time-fractional sine-Gordon equation on non-rectangular domains using finite difference and meshfree methods. Eng. Anal. Bound. Elem. 2021, 127, 53–63. [Google Scholar] [CrossRef]
- Khan, A.; Khan, H.; Gómez-Aguilar, J.F.; Abdeljawad, T. Existence and Hyers-Ulam stability for a nonlinear singular fractional differential equations with Mittag-Leffler kernel. Chaos Solitons Fractals 2019, 127, 422–427. [Google Scholar] [CrossRef]
- Aliev, F.A.; Aliyev, N.A.; Hajiyeva, N.S.; Mahmudov, N.I. Some mathematical problems and their solutions for the oscillating systems with liquid dampers: A review. Appl. Comput. Math. 2021, 20, 339–365. [Google Scholar]
- Adeyefa, E.O.; Omole, E.O.; Shokri, A.; Yao, S.-W. Hermite Fitted Block Integrator for Solving Second-Order Anisotropic Elliptic Type PDEs. Fractal Fract. 2022, 6, 497. [Google Scholar] [CrossRef]
- Su, X.; Zhou, Y. A Fast High-Order Predictor–Corrector Method on Graded Meshes for Solving Fractional Differential Equations. Fractal Fract. 2022, 6, 516. [Google Scholar] [CrossRef]
- Awoyemi, D.O.; Idowu, M.O. A class of hybrid collocation methods for third order ordinary differential equations. Int. J. Comput. Math. 2005, 82, 1–7. [Google Scholar] [CrossRef]
- Iskandarov, S.; Komartsova, E. On the influence of integral perturbations on the boundedness of solutions of a fourth-order linear differential equation. TWMS J. Pure Appl. Math. 2022, 13, 3–9. [Google Scholar]
- Ashry, H.; Abd-Elhameed, W.M.; Moatimid, G.M.; Youssri, Y.H. Spectral Treatment of One and Two Dimensional Second-Order BVPs via Certain Modified Shifted Chebyshev Polynomials. Int. J. Appl. Comput. Math. 2021, 7, 248. [Google Scholar] [CrossRef]
- Asif, M. Haar Wavelet Approach for Numerical Solution of Three-dimensional Partial Differential Equations. Ph.D. Dissertation, University of Peshawar, Peshawar, Pakistan, 2017. [Google Scholar]
- Guo, L.; Xu, Y. Energy conserving local discontinuous Galerkin methods for the nonlinear Schrödinger equation with wave operator. J. Sci. Comput. 2015, 65, 622–647. [Google Scholar] [CrossRef]
- Aziz, I.; Khan, F. A comparative study of numerical integra-tion based on haar wavelets and hybrid functions. Comput. Math. Appl. 2010, 59, 2026–2036. [Google Scholar]
- Shiralashetti, S.C.; Kantli, M.H.; Deshi, A.B. Biorthogonal wavelet-based full-approximation schemes for the numerical solution of elasto-hydrodynamic lubrication problems. J. Math. Model. 2018, 6, 105–122. [Google Scholar]
- Saparova, B.; Mamytova, R.; Kurbanbaeva, N.; Ahmedov, A.A. A Haar Wavelet Series Solution of Heat Equation with Involution. J. Adv. Res. Fluid -Chanics Therm. Sci. 2021, 86, 50–55. [Google Scholar] [CrossRef]
- Takei, Y.; Iwata, Y. Numerical Scheme Based on the Implicit Runge-Kutta Method and Spectral Method for Calculating Nonlinear Hyperbolic Evolution Equations. Axioms 2022, 11, 28. [Google Scholar] [CrossRef]
- Yakubu, D.G.; Aminu, M.; Tumba, P.; Abdulhameed, M. An efficient family of second derivative Runge-Kutta collocation methods for oscillatory systems. J. Niger. Math. Soc. 2018, 37, 111–138. [Google Scholar]
- Zhao, E.; Huang, J. Boundary treatment of implicit-explicit Runge-Kutta method for hyperbolic systems with source terms. J. Comput. Phys. 2020, 423, 109828. [Google Scholar] [CrossRef]
- Mall, S.; Chakraverty, S. Single layer Chebyshev neural network model for solving elliptic partial differential equations. Neural Process. Lett. 2017, 45, 825–840. [Google Scholar] [CrossRef]
- Ghaffar, F.; Badshah, N.; Khan, M.A.; Islam, S. Multigrid method for 2D Helmholtz equation using higher order finite difference scheme accelerated by Krylov subspace. J. Appl. Environ. Biol. Sci. 2014, 4, 169–179. [Google Scholar]
- Ge, Y. Multigrid method and fourth-order compact difference discretization scheme with unequal meshsizes for 3D Poisson equation. J. Comput. Phys. 2010, 229, 6381–6391. [Google Scholar] [CrossRef]
- Gupta, M.M.; Kouatchou, J.; Zhang, J. Comparison of second and fourth order discretizations for multigrid Poisson solver. J. Comput. Phys. 1997, 132, 226–232. [Google Scholar] [CrossRef]
- Mulla, M.A.M.; Gaweash, A.M.A.; Bakur, H.Y.I. Numerical Solution of Parabolic in Partial Differential Equations (PDEs) in One and Two Space Variable. J. Appl. Math. Phys. 2022, 10, 311–321. [Google Scholar] [CrossRef]
- Harari, I.; Hughes, T.J. Finite element methods for the Helmholtz equation in an exterior domain model problem. Comput. Methods Appl. Mech. Eng. 1991, 87, 59–96. [Google Scholar] [CrossRef]
- Sunday, S.J.; Shokri, A.; Marian, D. Variable Step Hybrid Block Method for the Approximation of Kepler Problem. Fractal Fract. 2022, 6, 343. [Google Scholar] [CrossRef]
- Ramos, H.; Vigo-Aguiar, J. An almost L-stable BDF-type method for the numerical solution of stiff ODEs arising from the method of lines. Inter. J. Numer. Methods Partial. Differ. Equations 2006, 23, 1110–1121. [Google Scholar] [CrossRef]
- Ngwane, F.F.; Jator, S.N. A Trigonometrically Fitted Block Method for Solving Oscillatory Second-Order Initial Value Problems and Hamiltonian Systems. Inter. J. Diff. Eqn. 2017, 2017, 9293530. [Google Scholar] [CrossRef]
- Modebei, M.I.; Adeniyi, R.B.; Jator, S.N. Numerical approximation of fourth-order PDEs using block unification method. J. Niger. Math. Soc. 2020, 39, 47–68. [Google Scholar]
- Jator, S.N. Block Unification Scheme for Elliptic, Telegraph, and Sine-Gordon Partial Differential Equations. Am. J. Comput. Math. 2015, 5, 175–185. [Google Scholar] [CrossRef][Green Version]
- Olaiya, O.O.; Oduwole, H.K.; Odeyemi, J.K. Numerical solution of Black-Scholes Partial Differential Equation Using Direct Solution of Second-Order Ordinary Differential Equation With Two-Step Hybrid Block Method Of Order Seven. Sci. World J. 2019, 14, 23–29. [Google Scholar]
- Familua, A.B.; Omole, E.O.; Ukpebor, L.A. A Higher-order Block Method for Numerical Approximation of Third-order Boundary Value Problems in ODEs. J. Niger. Soc. Phys. Sci. 2022, 4, 706. [Google Scholar] [CrossRef]
- Milne, W.E. Numerical Solution of Differential Equations; John Wiley and Sons: Hoboken, NJ, USA, 1953. [Google Scholar]
- Lambert, J.D. Computational Methods in Ordinary Differential Equations; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1973. [Google Scholar]
- Jain, M.K.; Iyengar, S.K.; Jain, R.K. Numerical Methods for Scientific and Engineering Computation, 5th ed.; New Age International: Dhaka, Bangladesh, 2007; pp. 282–283. Available online: https://books.google.co.jp/books?hl=en&lr=&id=5XappvcENCMC&oi=fnd&pg=PA1&dq=Jain,+M.K.%3B+Iyengar,+S.K.%3B+Jain,+R.K.+Numerical+Methods+for+Scientific+and+Engineering+Computation,+5th+ed.,+2007%3B+pp.+282%E2%80%93283.&ots=RWHgTT0nnz&sig=BY3hSRTPK_x_M-a6G7H73_LbKUk#v=onepage&q&f=false (accessed on 19 July 2023).
- Henrici, P. Discrete Variable Method in Ordinary Differential Equations; John Wiley & Sons: New York, NY, USA, 1972. [Google Scholar]
- Omole, E.O.; Jeremiah, O.A.; Adoghe, L.O. A Class of Continuous Im-plicit Seventh-eight method for solving y′ = f(x,y) using power series as basic function. Int. J. Chem. Math. Phys. (IJCMP) 2020, 4, 39–50. [Google Scholar] [CrossRef]
- Omole, E.O.; Obarhua, F.O.; Familua, A.B.; Shokri, A. Algorithms of algebraic order nine for numerically solving second-order boundary and initial value problems in ordinary differential equations. Int. J. Math. Oper. Res. 2022, 25, 343–368. [Google Scholar] [CrossRef]
- Fatunla, S.O. Numerical Methods for Initial Value Problems in Ordinary Differential Equations; Academic Press Inc.: Cambridge, MA, USA; Harcourt Brace Jovanovich Publishers: New York, NY, USA, 1988. [Google Scholar]
- Rufai, M.A.; Shokri, A.; Omole, E.O. A One-Point Third-Derivative Hy-brid Multistep Technique for Solving Second-Order Oscillatory and Periodic Problems. Hindawi J. Math. 2023, 2023, 2343215. [Google Scholar] [CrossRef]
- Yigider, M.; Karabacak, M. The numerical solution of helmholtz equation via multivariate pade approximation. Int. J. Res. Eng. Technol. 2014, 4, 670–678. [Google Scholar]
- Lima, S.A.; Kamrujjaman, M.; Islam1, M.S. Numerical solution of con-vection diffusion reaction equations by a finite element method with error correlation. AIP Adv. 2021, 11, 085225. [Google Scholar] [CrossRef]
- Biala, T.A.; Jator, S.N. Block unification algorithm for 2d and 3d elliptic PDEs. J. Niger. Math. Soc. 2017, 36, 319–335. [Google Scholar]
- Xu, Q.; Wang, W. A New Parallel Iterative Algorithm for Solving 2D Poisson Equation. Numer. Methods Partial. DiffErential Equations 2011, 27, 749–1001. [Google Scholar] [CrossRef]
- Volkov, E.A.; Dosiyev, A.A.; Buranay, S.C. On the solution of a nonlocal problem. Comput. Math. Appl. 2013, 66, 330–338. [Google Scholar] [CrossRef]
| x | Exact Results | NMCFs Results | AEs in NMCFs |
|---|---|---|---|
| 0.1 | |||
| 0.2 | |||
| 0.3 | |||
| 0.4 | |||
| 0.5 | |||
| 0.6 | |||
| 0.7 | |||
| 0.8 | |||
| 0.9 | |||
| 1.0 |
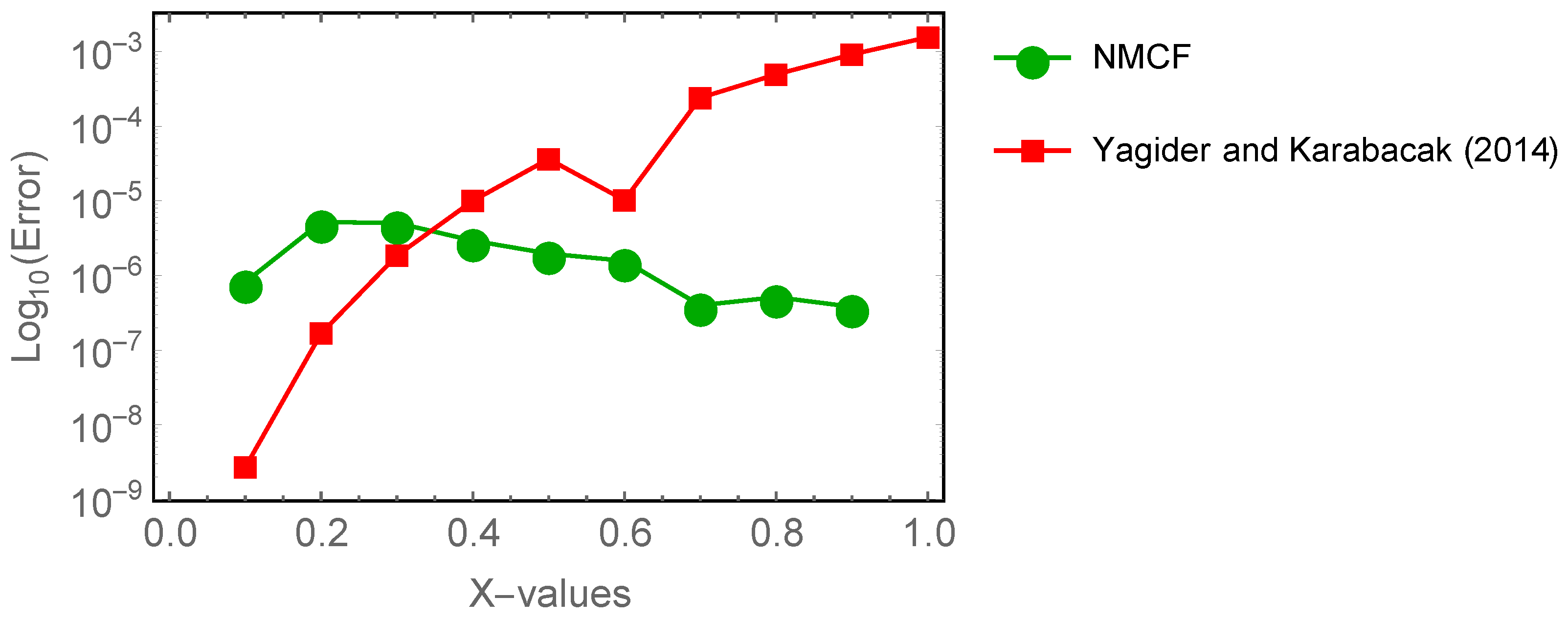
| x | AEs in NMCFs | AEs in Yagider and Karabacak [44] |
|---|---|---|
| 0.1 | ||
| 0.2 | ||
| 0.3 | ||
| 0.4 | ||
| 0.5 | ||
| 0.6 | ||
| 0.7 | ||
| 0.8 | ||
| 0.9 | ||
| 1.0 |
| x | Exact Results | NMCFs Results | AEs in NMCFs |
|---|---|---|---|
| 0.1 | |||
| 0.2 | |||
| 0.3 | |||
| 0.4 | |||
| 0.5 | |||
| 0.6 | |||
| 0.7 | |||
| 0.8 | |||
| 0.9 | |||
| 1.0 |
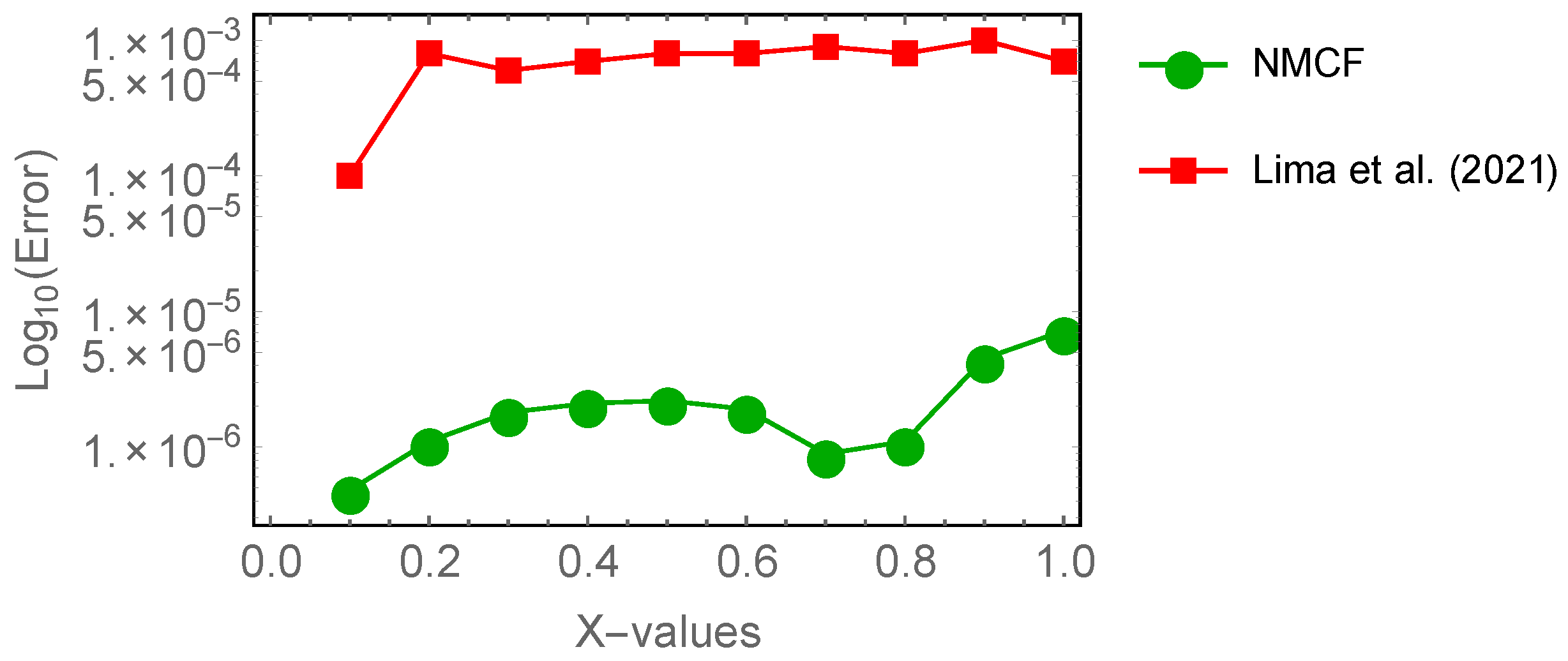
| x | AEs in NMCFs | AEs in Lima et al. [45] |
|---|---|---|
| 0.1 | ||
| 0.2 | ||
| 0.3 | ||
| 0.4 | ||
| 0.5 | ||
| 0.6 | ||
| 0.7 | ||
| 0.8 | ||
| 0.9 | ||
| 1.0 |
| x | Exact Results | NMCFs Results | AEs in NMCFs |
|---|---|---|---|
| 0.1 | |||
| 0.2 | |||
| 0.3 | |||
| 0.4 | |||
| 0.5 | |||
| 0.6 | |||
| 0.7 | |||
| 0.8 | |||
| 0.9 | |||
| 1.0 |
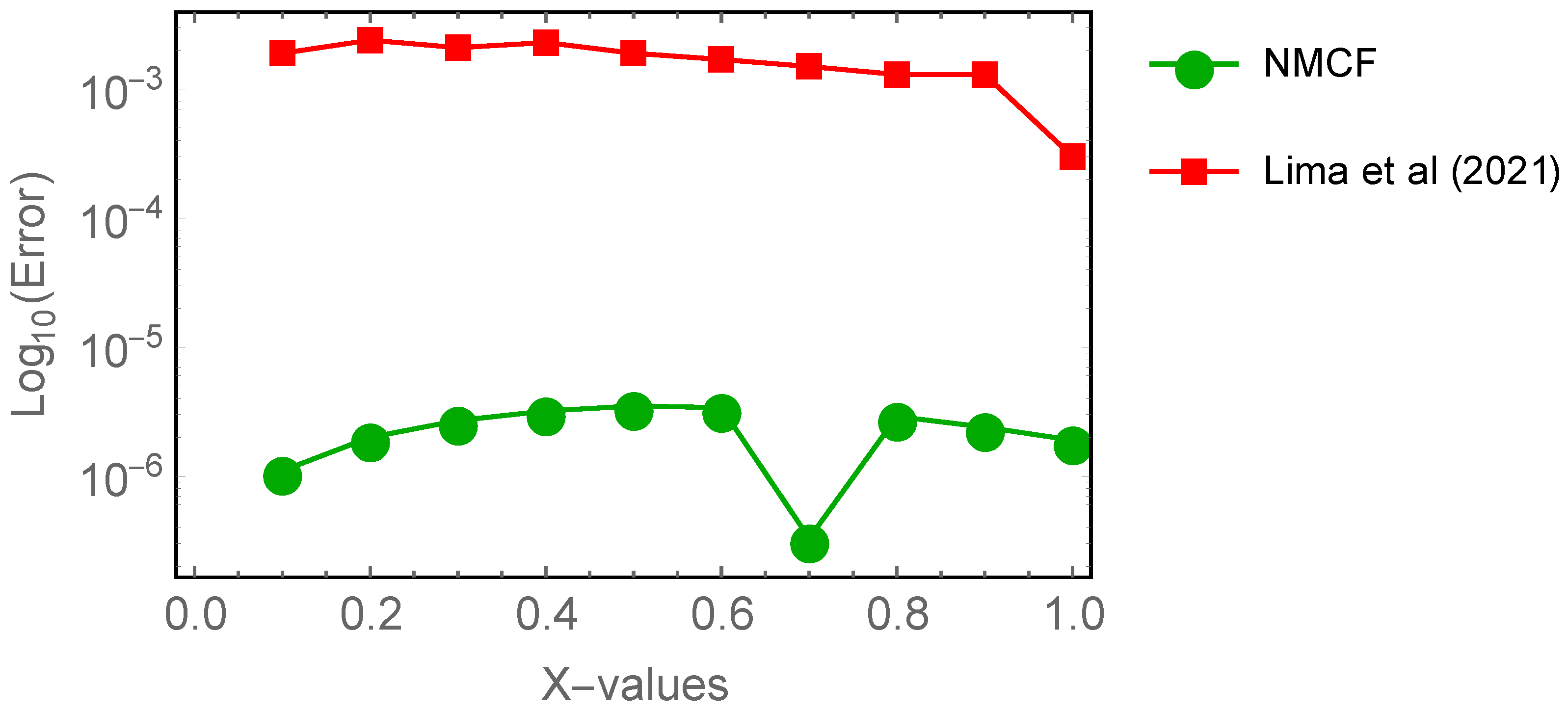
| x | AEs in NMCFs | AEs in Lima et al. [45] |
|---|---|---|
| 0.1 | ||
| 0.2 | ||
| 0.3 | ||
| 0.4 | ||
| 0.5 | ||
| 0.6 | ||
| 0.7 | ||
| 0.8 | ||
| 0.9 | ||
| 1.0 |
| N | Exact Results | NMCFs Results | AEs in NMCFs |
|---|---|---|---|
| 16 | |||
| 24 | |||
| 32 | |||
| 40 | |||
| 48 |
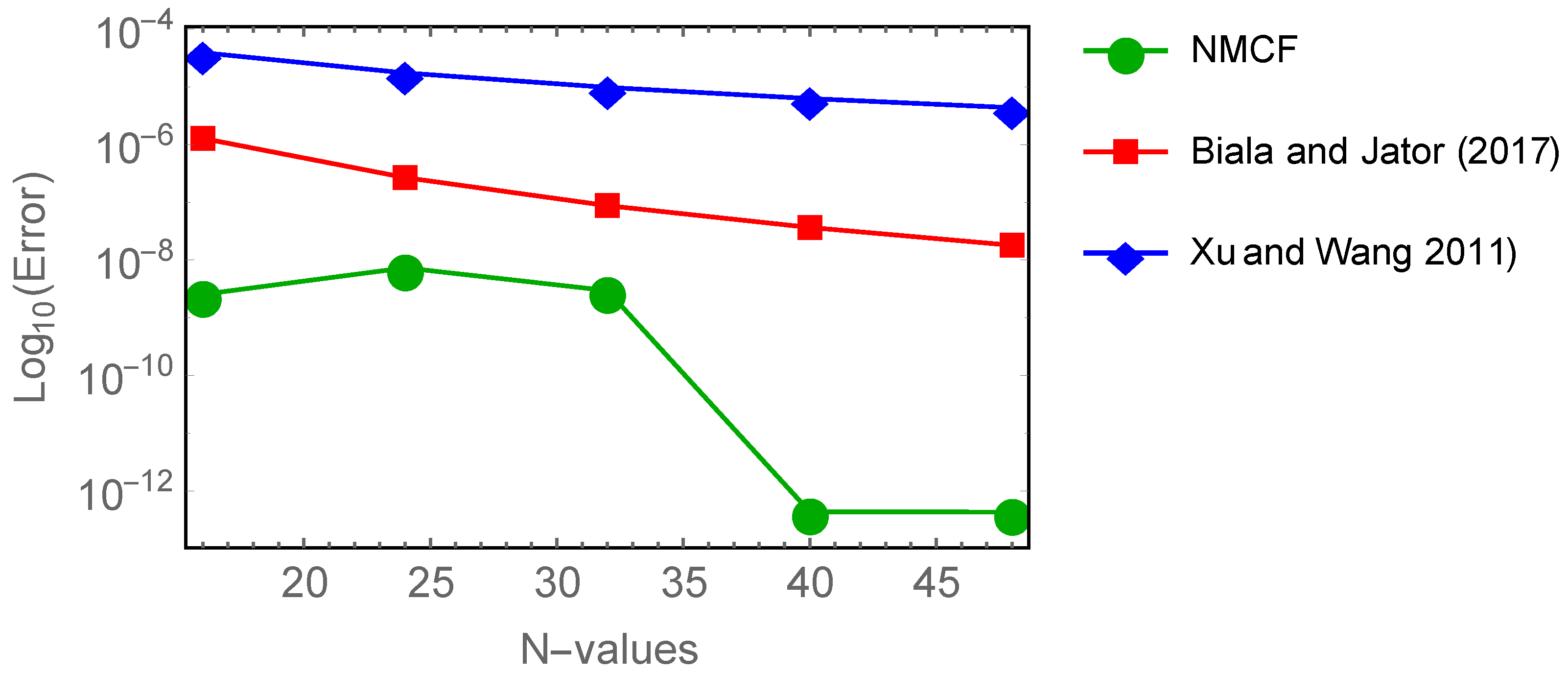
| N | AEs in NMCFs | AEs in Biala and Jator [46] | AEs in Xu and Wang [47] |
|---|---|---|---|
| 16 | |||
| 24 | |||
| 32 | |||
| 40 | |||
| 48 |
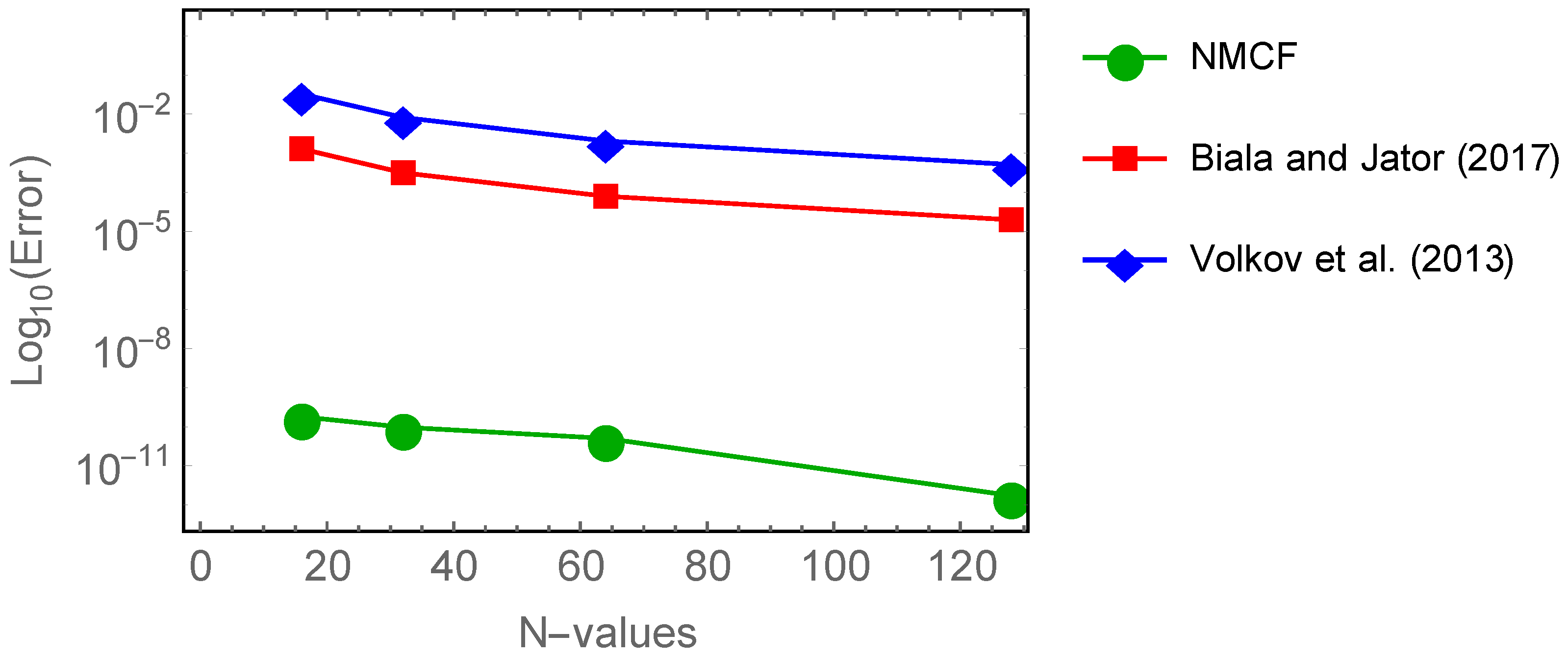
| N | Exact Results | NMCFs Results | AEs in NMCFs |
|---|---|---|---|
| 16 | |||
| 32 | |||
| 64 | |||
| 128 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Omole, E.O.; Adeyefa, E.O.; Ayodele, V.I.; Shokri, A.; Wang, Y. Ninth-order Multistep Collocation Formulas for Solving Models of PDEs Arising in Fluid Dynamics: Design and Implementation Strategies. Axioms 2023, 12, 891. https://doi.org/10.3390/axioms12090891
Omole EO, Adeyefa EO, Ayodele VI, Shokri A, Wang Y. Ninth-order Multistep Collocation Formulas for Solving Models of PDEs Arising in Fluid Dynamics: Design and Implementation Strategies. Axioms. 2023; 12(9):891. https://doi.org/10.3390/axioms12090891
Chicago/Turabian StyleOmole, Ezekiel Olaoluwa, Emmanuel Oluseye Adeyefa, Victoria Iyadunni Ayodele, Ali Shokri, and Yuanheng Wang. 2023. "Ninth-order Multistep Collocation Formulas for Solving Models of PDEs Arising in Fluid Dynamics: Design and Implementation Strategies" Axioms 12, no. 9: 891. https://doi.org/10.3390/axioms12090891
APA StyleOmole, E. O., Adeyefa, E. O., Ayodele, V. I., Shokri, A., & Wang, Y. (2023). Ninth-order Multistep Collocation Formulas for Solving Models of PDEs Arising in Fluid Dynamics: Design and Implementation Strategies. Axioms, 12(9), 891. https://doi.org/10.3390/axioms12090891








