First Entire Zagreb Index of Fuzzy Graph and Its Application

Abstract

The first entire Zagreb index (FEZI) is a graph parameter that has proven to be essential in various real-life scenarios, such as networking businesses and traffic management on roads. In this research paper, the FEZI was explored for a variety of fuzzy graphs, including star, firefly graph, cycle, path, fuzzy subgraph, vertex elimination, and edge elimination. This study presented several results, including determining the relationship between two isomorphic fuzzy graphs and between a path and cycle (connecting both end vertices of the path). This research also deals with the analysis of $\alpha$-cut fuzzy graphs and establishes bounds for some fuzzy graphs. To apply these findings to modern life problems, the research team utilized the results to identify areas that require more development in internet systems. These results have practical implications for enhancing the efficiency and effectiveness of internet systems. The conclusion drawn from this research can be used to inform future research and aid in the development of more efficient and effective systems in various fields.

1. Introduction

1.1. Research Background

In the modern day, fuzzy graph (FG) theory is one of the most applicable to regular life. So there are many researchers who are implementing FG theory, especially topological indices of fuzzy graphs. Rosenfeld [1], inspired by Zadeh’s [2] classical set (fuzzy set) in 1975, introduced the fuzziness for a graph, then, it is called a fuzzy graph. Additionally, this time he introduced several connective parameters of an FG and some applications of these parameters by Yeh et al. [3]. In [4,5], Sunitha et al. studied fuzzy block, fuzzy bridge, FSG, CFG, PFSG, fuzzy tree, fuzzy forest, fuzzy cut vertex, etc. The degree of a vertex $(d(v)/deg(v))$ in an FG is also discussed In [6]. The degree of an edge ($d_G(e)$) is also discussed in [7]. Further information on the FG hypothesis is provided in [8,9,10,11]. Bipolar and m-polar fuzzy graphs are discussed in [12,13]. The first Zagreb index is discussed in [14] and was inspired by the paper [15]. In a molecular graph of a chemical compound, we can calculate molecular descriptors by finding topological indices of this graph. A graph’s topology is described by these topological indices, which are numerical numbers. The Zagreb index, established in 1972 by Gutman and Trinajstic [16], is a degree-based topological index. The $pi$-electron energy of a conjugate system is determined using topological indices. In a crisp graph, many indices are defined but several issues in real life cannot be handled by these indices. So we can generalize these indices in fuzzy graphs. In this piece, we have introduced the FEZI in fuzzy graphs which is a major generalization of FEZI for crisp graphs. These indices are investigated from both a theoretical and an application point of view.

1.2. Research Question

These questions are covered in this paper:

• What is the FEZI upper bound for fuzzy graphs?
• What are the precise values or boundaries of FEZI for the firefly graph, star, path, cycle, etc.?
• What is the relation between the value of FEZI of a graph and its sub graph?
• What is the relation between the value of FEZI for two isomorphic graph?
• What is the relation for several graphs between the first Zagreb index and FEZI ?
• What are the applications of this index?

1.3. Objective of the Work

Various types of topological indices of a graph can be used for a variety of purposes and yield a wide range of outcomes for crisp graphs. However, in numerous applications, a crisp graph is not enough to solve it. We need to define a fuzzy graph to answer this question. In this paper, FEZI is defined and some results relating to sub graphs, paths, stars, firefly graphs, cycles, isomorphic graphs, etc. are given. At the end of this paper, we applied the first entire Zagreb index in internet network systems.

1.4. Structure of the Study

The structure of the article is as follows: in Section 2, some definitions are provided which are necessary for this study. In Section 3, we studied the FEZI of a fuzzy graph and provided some results on sub graphs, paths, stars, firefly graphs, cycles, etc. Also some relation between fuzzy graphs are provided. In Section 4, an application of the first entire Zagreb index in development in internet networking system is discussed.

2. Preliminaries

Here, we provide some fundamental definitions and theorems which are crucial to developing the later sections.

Let U be a universal set. An FS A on U is a mapping $\sigma :U\to [0,1]$. Here, $\sigma$ is the membership function of the FS A. A FS generally indicated by $A=(u,\sigma )$.

Assume that $F(\ne 0)$ is a known finite set. Then the fuzzy graph (FG) is a triplet, $G=(U,\omega ,\varrho )$, where $U(\ne 0)\subseteq F$ with $\omega :U\to [0,1]$ and $\varrho :U\times U\to [0,1]$ satisfying $\varrho (x_1,x_2)\le \omega (x_1)\wedge \omega (x_2)$. The set U is the set of vertices and $\epsilon :=((x_1,x_2):\varrho (x_1,x_2)>0)$ is the set of edges of the FG. $\omega (x_1)$ represents the membership value (MV) of the vertex $x_1$ and $\varrho$ represents the MV of the edge $(x_1,x_2)$ (or $x_1{x}_2$).

Let $G=(U,\omega ,\varrho )$ be an FG. Then, $H=(U^{\prime },{\omega }^{\prime },{\varrho }^{\prime })$ is called the PFSG of the FG G if $U^{\prime }\subset U,{\omega }^{\prime }(x_1)\le \omega (x_1),{\varrho }^{\prime }(x_1,x_2)\le \varrho (x_1,x_2)$ for all $x_1,x_2\in U^{\prime }$. If ${\omega }^{\prime }(x_1)=\omega (x_1)$ and ${\varrho }^{\prime }(x_1,x_2)\le \varrho (x_1,x_2)$ for all $x_1,x_2\in U^{\prime }$ then H is called FSG of the graph of the FG G.

For $x_1\in V$, we denote $G_{x_1}$ as an FSG of the FG $G=(V,\omega ,\varrho )$ with $\omega (x_1)=0$ and for $x_1{x}_2\in \epsilon$, $G_{x_1{x}_2}$ represents the FSG of the FG G with $\varrho (x_1{x}_2)=0$.

Let $x_0,x_1,\dots ,x_n$ all be vertices of an FG G. Then, the collection of vertices $P(x_0,x_1,\dots ,x_n)$ is a path in G if $\varrho (x_i,x_{i+1})\ne 0$ (for all i). The path’s length is n in this case. If $\varrho (x_0,x_n)>0$ for the path $P(x_0,x_1,\dots ,x_n)$ then it is called a cycle.

Let $x_0,x_1,\dots ,x_n$ be distinct vertices of a fuzzy graph G. Then, $G=(x_0,x_1,\dots ,x_n)$ is called a star if $\varrho (x_0,x_i)\ne 0$ for $i=1,2,\dots ,n$ and for all vertex except $x_0$ there is no edge between every two vertices, where $x_0$ is the center of the star.

In a graph G if $\varrho (x_i,x_j)\ge 0$ for all vertices $x_i$ and $x_j$, then it is called a complete graph. In a fuzzy graph $G=(V,\omega ,\varrho )$ if for every two vertex x and y satisfy the condition $\varrho (x,y)=\omega (x)\wedge \omega (y)$ then the graph is called a CFG.

Two FG $G_1=(V_1,{\omega }_1,{\varrho }_1)$ and $G_2=(V_2,{\omega }_2,{\varrho }_2)$ are called isomorphic to each other if there exists a bijective mapping $g:V_1\to V_2$ for any $x,y\in V_1$, ${\omega }_1(x)={\omega }_2(g(x))$ and ${\varrho }_2(g(x),g(y))={\varrho }_1(x,y)$.

Let $G=(V,E)$ be a crisp graph. Then, the first and second ZI are defined by $M_1^{\epsilon }={\displaystyle {\displaystyle \sum _{x\in V(G)UE(G)}}}{(deg(x))}^2$ and $M_2^{\epsilon }={\displaystyle {\displaystyle \sum _{\begin{array}{c}xiseitheradjacent\\ orincidenttoy\end{array}}}}deg(x)deg(y)$ [17].

The total degree of an FG with respect to vertices is indicated by $T_v(G)$ and is defined by $T_v(G)={\displaystyle {\displaystyle \sum _{v\in V(G)}}}{d}_G(v)$ [7]. Additionally, the total degree of an FG with respect to edge is indicated by $T_e(G)$ and is defined by $T_e(G)={\displaystyle {\displaystyle \sum _{e\in E(G)}}}{d}_G(e)$.

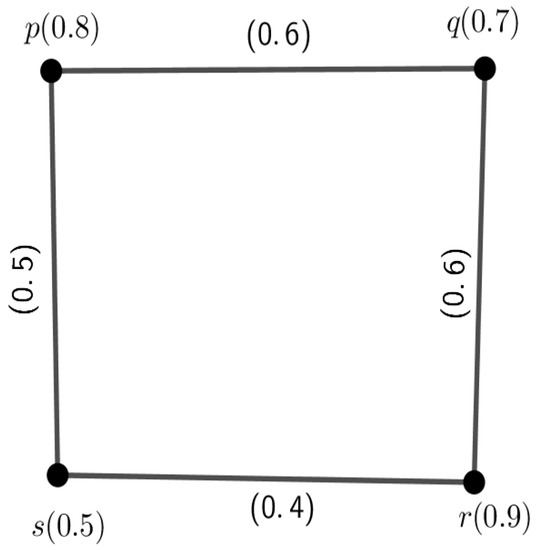
Example 1.

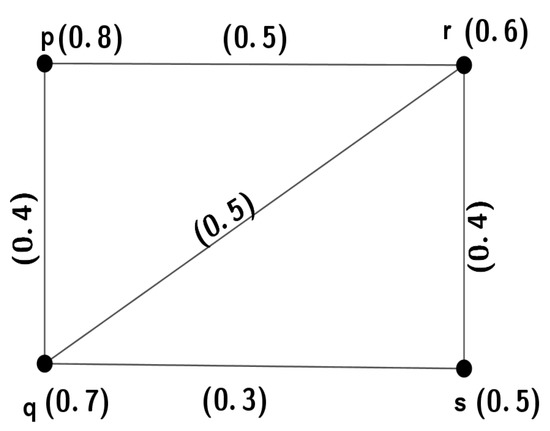
Let G be an FG with vertex set $V=\{p,q,r,s\}$ such that $\omega (p)=0.8,\omega (q)=0.7,\omega (r)=0.6,\omega (s)=0.5,\varrho (p,q)=0.4,\varrho (p,r)=0.5,\varrho (q,r)=0.5,\varrho (q,s)=0.3,\varrho (r,s)=0.4$, as shown in Figure 1. Then, $d(p)=0.9,d(q)=1.2,d(r)=1.4,d(s)=0.7,d(p,q)=1.3,d(p,r)=1.3,d(q,r)=1.6,d(q,s)=1.3,d(r,s)=1.3$ and $T_v(G)=0.9+1.2+1.4+0.7=4.2$ and $T_e(G)=1.3+1.3+1.3+1.6+1.3+1.3=6.8$.

Figure 1. A fuzzy graph.

3. First Entire Zagreb Index of Fuzzy Graphs

First entire Zagreb index (FEZI) have an important role for finding strength of vertices. The strength of vertices is important in fuzzy graph theory. Thus, in this section the FEZI of a fuzzy graph is initiated. Various properties and an application of FEZI for fuzzy graphs is given.

Definition 1.

Let G be an FG. Then, the FEZI of G is indicated by $M_1^z$ and is defined by: $M_1^z:={\displaystyle \sum _{x\in V(G)}}{(\omega (x)d(x))}^2+{\displaystyle \sum _{e\in E(G)}}{(\varrho (e)d(e))}^2$.

Example 2.

Let G be an FG with vertex set $V=\{p,q,r,s\}$ such that $\omega (p)=0.8,\omega (q)=0.7,\omega (r)=0.6,\omega (s)=0.5,\varrho (p,q)=0.4,\varrho (p,r)=0.5,\varrho (q,r)=0.5,\varrho (q,s)=0.3$ and $\varrho (r,s)=0.4$, shown in Figure 1. Then $d(p)=0.9,d(q)=1.2,d(r)=1.4,d(s)=0.7,d(p,q)=1.3,d(p,r)=1.3,d(q,r)=1.6,d(q,s)=1.3,d(r,s)=1.3$.

Now, $M_1^z={\displaystyle \sum _{xϵV(G)}}{(\omega (x)d(x))}^2+{\displaystyle \sum _{eϵE(G)}}{(\varrho (e)d(e))}^2$

$={(0.8\times 0.9)}^2+{(0.7\times 1.2)}^2+{(0.6\times 1.4)}^2+{(0.5\times 0.7)}^2+{(0.4\times 1.3)}^2+{(0.5\times 1.3)}^2+{(0.5\times 1.6)}^2+{(0.3\times 1.3)}^2+{(0.4\times 1.3)}^2$

= 3.7135.

Definition 2.

Let $(G,\omega ,\varrho )$ be an FG. Then, the second entire Zagreb index of G is indicated by $M_2^{ϵ}$ and is defined by $M_2^z:={\displaystyle \sum _{\begin{array}{c}u,vareadjacentto\\ eachother\end{array}}}\omega (u)d(u)\omega (v)d(v)+{\displaystyle \sum _{\begin{array}{c}visincident\\ toe\end{array}}}\omega (v)d(v)\varrho (e)d(e)$, where ω is the MV of a vertex and ϱ is the MV of an edge.

Example 3.

Let G be an FG with vertex set $V=\{p,q,r,s\}$ such that, $\omega (p)=0.6,\omega (q)=0.5,\omega (r)=0.4,\omega (s)=0.8,\varrho (p,r)=0.4,\varrho (q,r)=0.4,\varrho (r,s)=0.3$ shown in Figure 2. Then $d(p)=0.4,d(q)=0.4,d(r)=1.1,d(s)=0.3,d(p,r)=0.7,d(q,r)=0.7,d(r,s)=0.8$

Now, $M_2^z={\displaystyle \sum _{\begin{array}{c}u,vareadjacent\\ toeachother\end{array}}}\omega (u)d(u)\omega (v)d(v)+{\displaystyle \sum _{\begin{array}{c}visincident\\ toe\end{array}}}\omega (v)d(v)\omega (e)d(e)$

$=(0.4\times 0.5\times 0.4\times 1.1)+(0.4\times 0.6\times 0.4\times 1.1)+(0.3\times 0.8\times 0.4\times 1.1)+(0.4\times 0.7\times 0.4\times 0.7)+(0.4\times 0.3\times 0.7\times 0.8)+(0.4\times 0.3\times 0.7\times 0.8)+(0.4\times 0.6\times 0.4\times 0.7)+(0.4\times 0.5\times 0.4\times 0.7)+(0.8\times 0.3\times 0.3\times 0.8)+(0.4\times 0.7\times 0.4\times 1.1)+(0.4\times 0.7\times 0.4\times 1.1)+(0.4\times 0.3\times 0.8\times 1.1)=0.088+0.1056+0.1056+0.0784+0.0672+0.0672+0.0672+0.056+0.0576+0.1232+0.1232+0.1056=1.0448$.

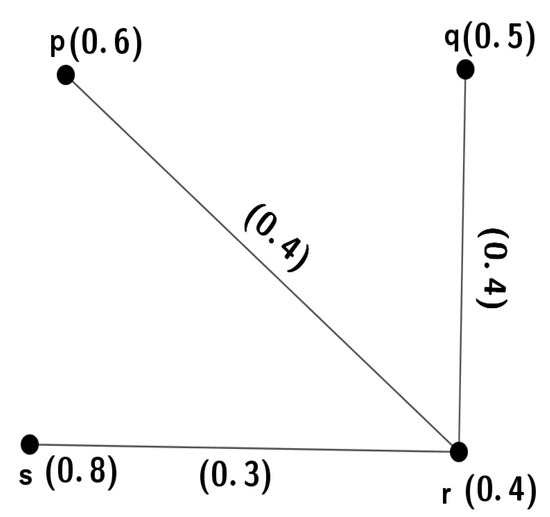
Figure 2. A fuzzy graph G with ${\mathrm{M}}_2^z$ = 1.0448.

Theorem 1.

Let the FG G have n vertices and m edges, then $M_1^z\le n^2{T}_v^2(G)+m^2{T}_e^2(G)$, where $T_v^2(G)$ and $T_e^2(G)$ represent the total degree with respect to vertex and total degree with respect to edge.

Proof. 

Now, the FEZI of G is given by

$M_1^z={\displaystyle \sum _{xϵV(G)}}{(\omega (x)d(x))}^2+{\displaystyle \sum _{eϵE(G)}}{(\varrho (e)d(e))}^2$.

Since $\sum {(pq)}^2\le \sum p^2\sum q^2$, we have

${\displaystyle \sum _{xϵV(G)}}{(\omega (x)d(x))}^2+{\displaystyle \sum _{eϵE(G)}}{(\varrho (e)d(e))}^2\le {\displaystyle \sum _{xϵV(G)}}{(\omega (x))}^2{\displaystyle \sum _{xϵV(G)}}{(d(x))}^2+{\displaystyle \sum _{eϵE(G)}}{(\varrho (e))}^2{\displaystyle \sum _{eϵE(G)}}{(d(e))}^2$

$\le {({\displaystyle \sum _{xϵV(G)}}\omega (x))}^2{({\displaystyle \sum _{xϵV(G)}}d(x))}^2+{({\displaystyle \sum _{eϵE(G)}}\varrho (e))}^2{({\displaystyle \sum _{eϵE(G)}}d(e))}^2$

$\le {({\displaystyle \sum _{xϵV(G)}}\omega (x))}^2{T}_v^2(G)+{({\displaystyle \sum _{eϵE(G)}}\varrho (e))}^2{T}_e^2(G)$.

Since $0\le \omega (x)\le 1$ and $0\le \varrho (e)\le 1$, therefore $M_1^z\le n^2{T}_v^2(G)+m^2{T}_e^2(G)$. □

Definition 3.

Let $G=(V,\omega ,\varrho )$ be an FG. Then FEZI at a vertex of G is indicated by $M_1^z(v)$ and is defined by $M_1^z(v):=M_1^z(G)-M_1^z(G_v)$ where $G_v=(V(G)-v,\omega ,\varrho )$.

Example 4.

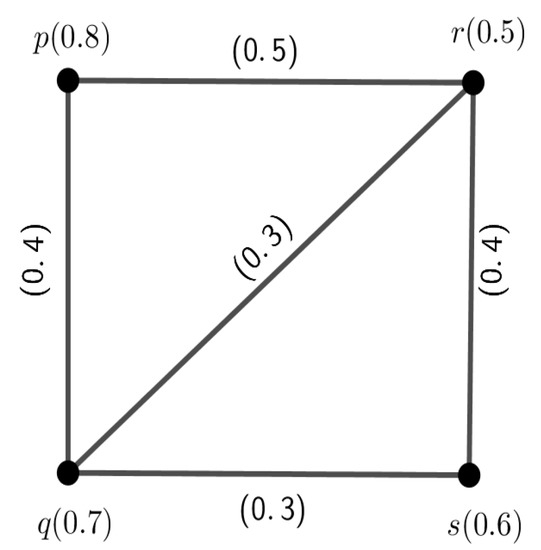
Let G be an FG with vertex set $V=\{p,q,r,s\}$ such that $\omega (p)=0.8,\omega (q)=0.7,\omega (r)=0.5,\omega (s)=0.6,\varrho (p,q)=0.4,\varrho (p,r)=0.5,\varrho (q,r)=0.5,\varrho (q,s)=0.3$ and $\varrho (r,s)=0.4$ shown in Figure 3. Then, $d(p)=0.9,d(q)=1.2,d(r)=1.4,d(s)=0.7,d(p,q)=1.3,d(p,r)=1.3,d(q,r)=1.6,d(q,s)=1.3,d(r,s)=1.3$.

Figure 3. A fuzzy graph G with $M_1^z(G)$ = 3.6458.

Now, $M_1^z={\displaystyle \sum _{xϵV(G)}}{(\omega (x)d(x))}^2+{\displaystyle \sum _{eϵE(G)}}{(\varrho (e)d(e))}^2$

$={(0.8\times 0.9)}^2+{(0.7\times 1.2)}^2+{(0.5\times 1.4)}^2+{(0.6\times 0.7)}^2+{(0.4\times 1.3)}^2+{(0.5\times 1.3)}^2+{(0.5\times 1.6)}^2+{(0.3\times 1.3)}^2+{(0.4\times 1.3)}^2$

So $M_1^z(G)=3.6458$.

Now the vertex p is removed from the graph G, then the graph of $G_p$ is shown in Figure 4. From the figure, $d(q)=0.6,d(r)=0.7,d(s)=0.7,d(q,r)=0.7,d(q,s)=0.7,d(r,s)=0.6$.

Figure 4. The FG $G_p$ obtained by deleting the vertex p from the above graph.

Now, $M_1^z(G_p)={\displaystyle \sum _{xϵV(G_p)}}{(\omega (x)d(x))}^2+{\displaystyle \sum _{eϵE(G_p)}}{(\varrho (e)d(e))}^2$

$={(0.7\times 0.6)}^2+{(0.5\times 0.7)}^2+{(0.6\times 0.7)}^2+{(0.3\times 0.7)}^2+{(0.6\times 0.4)}^2+{(0.3\times 0.7)}^2$. Therefore, $M_1^z(G_p)=0.6211$.

Then, the FEZI at p is $M_1^z(p)=3.6458-0.6211=3.0247$.

Theorem 2.

Suppose that H is an FG that is created by removing an edge from G. Then, $M_1^z(H)\le M_1^z(G)$.

Proof. 

Since $G=(V,\omega ,\varrho )$ is an FG and $H=(V^{\prime },{\omega }^{\prime },{\varrho }^{\prime })$ is a graph that is created by removing an edge from G so the MV of a vertex is the same in both graphs and the MV of edges are the same if it contains both E and $E^{\prime }$.

Then, the relation between the membership values of G and H is $\omega (x)\ge {\omega }^{\prime }(x)$ for all vertices x and $\varrho (e)\ge {\varrho }^{\prime }(e)$ for all edges.

This shows that $d(x)\ge d^{\prime }(x)$ for all vertices x. Additionally, $d(e)\ge d^{\prime }(e)$ for all edge e, where d and $d^{\prime }$ represent the degree of G and H.

Now, $M_1^z(G)={\displaystyle \sum _{xϵV(G)}}{(\omega (x)d(x))}^2+{\displaystyle \sum _{eϵE(G)}}{(\varrho (e)d(e))}^2$

$\ge {\displaystyle \sum _{xϵV(G)}}{({\omega }^{\prime }(x)d^{\prime }(x))}^2+{\displaystyle \sum _{eϵE(G)}}{({\varrho }^{\prime }(e)d^{\prime }(e))}^2$

$={\displaystyle \sum _{xϵV(H)}}{({\omega }^{\prime }(x)d^{\prime }(x))}^2+{\displaystyle \sum _{eϵE(H)}}{({\varrho }^{\prime }(e)d^{\prime }(e))}^2$

$=M_1^z(H)$.

Hence, $M_1^z(G)\ge M_1^z(H)$. □

Theorem 3.

If H is an FG that is obtained from G by deleting a vertex from G. Then, $M_1^z(H)\le M_1^z(G)$.

Proof. 

Since $G=(V,\omega ,\varrho )$ is an FG and $H=(V^{\prime },{\omega }^{\prime },{\varrho }^{\prime })$ is a graph that is created by removing a vertex from G.

So, $\omega (x)={\omega }^{\prime }(x)$ if $x\in V\cap V^{\prime }$ otherwise $\omega (x)>{\omega }^{\prime }(x)$. Additionally, $\varrho (e)={\varrho }^{\prime }(e)$ if $e\in E\cap E^{\prime }$ otherwise $\varrho (e)>{\varrho }^{\prime }(e)$. Then the relation between the membership values of $G=(V,\omega ,\varrho )$ and $H=(V^{\prime },{\omega }^{\prime },{\varrho }^{\prime })$ is $\omega (x)\ge {\omega }^{\prime }(x)$ for all vertices x and $\varrho (e)\ge {\varrho }^{\prime }(e)$ for all edges e. This shows that $d(x)\ge d^{\prime }(x)$ for all vertices x. Additionally, $d(e)\ge d^{\prime }(e)$ for all edges e. Here, d and $d^{\prime }$ represent the degrees of G and H.

Now, $M_1^z(G)={\displaystyle \sum _{xϵV(G)}}{(\omega (x)d(x))}^2+{\displaystyle \sum _{eϵE(G)}}{(\varrho (e)d(e))}^2$

$\ge {\displaystyle \sum _{xϵV(G)}}{({\omega }^{\prime }(x)d^{\prime }(x))}^2+{\displaystyle \sum _{eϵE(G)}}{({\varrho }^{\prime }(e)d^{\prime }(e))}^2$

$={\displaystyle \sum _{xϵV(H)}}{({\omega }^{\prime }(x)d^{\prime }(x))}^2+{\displaystyle \sum _{eϵE(H)}}{({\varrho }^{\prime }(e)d^{\prime }(e))}^2$

$=M_1^z(H)$. So, $M_1^z(G)\ge M_1^z(H)$. □

Example 5.

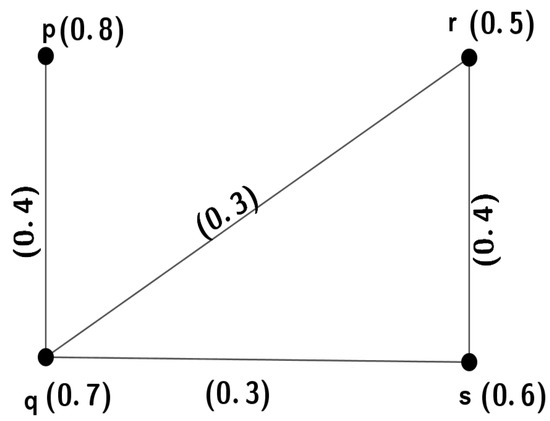
Let G be an FG with vertex set $V=\{p,q,r,s\}$ such that $\omega (p)=0.8,\omega (q)=0.7,\omega (r)=0.5,\omega (s)=0.6,\varrho (p,q)=0.4,\varrho (p,r)=0.5,\varrho (q,r)=0.5,\varrho (q,s)=0.3,\varrho (r,s)=0.4$ shown in Figure 3. Then $d(p)=0.9,d(q)=1.2,d(r)=1.4,d(s)=0.7,d(p,q)=1.3,d(p,r)=1.3,d(q,r)=1.6,d(q,s)=1.3$ and $d(r,s)=1.3$.

Now, $M_1^z(G)={\displaystyle \sum _{xϵV(G)}}{(\omega (x)d(x))}^2+{\displaystyle \sum _{eϵE(G)}}{(\varrho (e)d(e))}^2$.

$={(0.8\times 0.9)}^2+{(0.7\times 1.2)}^2+{(0.5\times 1.4)}^2+{(0.6\times 0.7)}^2+{(0.4\times 1.3)}^2+{(0.5\times 1.3)}^2+{(0.5\times 1.6)}^2+{(0.3\times 1.3)}^2+{(0.4\times 1.3)}^2=3.6458$.

The graph of H where the vertex p is deleted from G shown in Figure 4. From the figure, $d(q)=0.6,d(r)=0.7,d(s)=0.7,d(q,r)=0.7,d(q,s)=0.7,d(r,s)=0.6$.

Now, $M_1^z(H)={\displaystyle \sum _{xϵV(H)}}{(\omega (x)d(x))}^2+{\displaystyle \sum _{eϵE(H)}}{(\varrho (e)d(e))}^2$

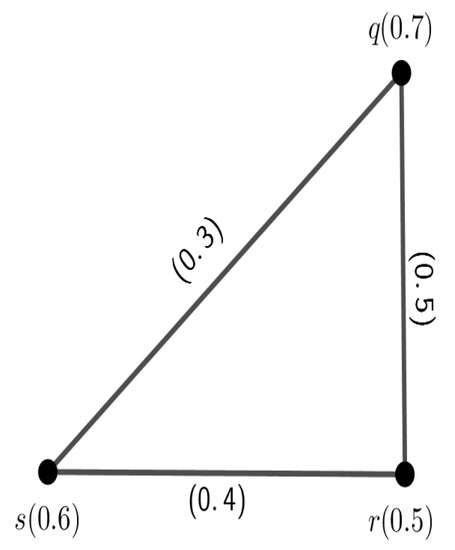
$={(0.7\times 0.6)}^2+{(0.5\times 0.7)}^2+{(0.6\times 0.7)}^2+{(0.3\times 0.7)}^2+{(0.6\times 0.4)}^2+{(0.3\times 0.7)}^2=0.6211$. The graph of K where the edge $pr$ is deleted from G is shown in Figure 5.

Figure 5. The FG obtained by deleting an edge from the graph in Figure 3.

From this figure, $d(p)=0.4,d(q)=1,d(r)=0.7,d(s)=0.7,d(p,q)=0.6,d(q,r)=1.1,d(q,s)=1.1,d(r,s)=1$

Now, $M_1^z(K)={\displaystyle \sum _{xϵV(K)}}{(\omega (x)d(x))}^2+{\displaystyle \sum _{eϵE(K)}}{(\varrho (e)d(e))}^2$

$={(0.8\times 0.4)}^2+{(0.7\times 1)}^2+{(0.5\times 0.7)}^2+{(0.6\times 0.7)}^2+{(0.6\times 0.4)}^2+{(0.3\times 1.1)}^2+{(0.3\times 1.1)}^2+{(0.4\times 1)}^2=1.3267$.

This shows that

• $M_1^z(G)\ge M_1^z(H)$.
• $M_1^z(G)\ge M_1^z(K)$.

Theorem 4.

Let G be an FG and H be an FSG of $G,$ then $M_1^z(G)\ge M_1^z(H)$.

Proof. 

Since $H=(V^{\prime },{\omega }^{\prime },{\varrho }^{\prime })$ is an FSG of $G=(V,\omega ,\varrho )$, therefore

$\omega (x)\ge {\omega }^{\prime }(x)$ for all vertices x and $\varrho (e)\ge {\varrho }^{\prime }(e)$ for all edges e. This sows that $d(x)\ge d^{\prime }(x)$ for all vertices x.

Additionally, $d(e)\ge d^{\prime }(e)$ for all edges e, where d and $d^{\prime }$ represent the degrees of G and H. Now, $M_1^z(G)={\displaystyle \sum _{xϵV(G)}}{(\omega (x)d(x))}^2+{\displaystyle \sum _{eϵE(G)}}{(\varrho (e)d(e))}^2$

$\ge {\displaystyle \sum _{xϵV(G)}}{({\omega }^{\prime }(x)d^{\prime }(x))}^2+{\displaystyle \sum _{eϵE(G)}}{({\varrho }^{\prime }(e)d^{\prime }(e))}^2$

$={\displaystyle \sum _{xϵV(H)}}{({\omega }^{\prime }(x)d^{\prime }(x))}^2+{\displaystyle \sum _{eϵE(H)}}{({\varrho }^{\prime }(e)d^{\prime }(e))}^2$

$=M_1^z(H)$

Hence, $M_1^z(G)\ge M_1^z(H)$. □

Theorem 5.

Let $G=(V,\omega ,\varrho )$ be an FG and $F=(V,\omega ,{\varrho }^{\prime })$ be the corresponding MST of G then $M_1^z(G)\ge M_1^z(F)$.

Proof. 

Since $F=(V,\omega ,{\varrho }^{\prime })$ is an MST of $G=(V,\omega ,\varrho )$ therefore F is an FSG of G. Then we can say from the above Theorem, $M_1^z(G)\ge M_1^z(F)$. □

Theorem 6.

Let G be an FG and let $G^{\alpha }=(V^{\prime },{\omega }^{\prime },{\varrho }^{\prime })$ be an α cut FG of $G=(V,\omega ,\varrho )$. Then, $M_1^z(G)\ge M_1^z(G^{\alpha })$ where the FG $G^{\alpha }$ is defined as $V^{\prime }=vϵV:\omega (v)\ge \alpha$ and ${\omega }^{\prime }(v)=\omega (v)$,${\varrho }^{,}(u,v)=\varrho (u,v)$ for all $u,vϵV^{\prime }$.

Proof. 

Since $G^{\alpha }$ is an FSG of the FG G, then by the above Theorem, $M_1^z(G)\ge M_1^z(G^{\alpha })$. □

Theorem 7.

Let G be an FG and let $0\le p_1\le p_2\le 1$ Then $M_1^z(G^{p_1})\ge M_1^z(G^{p_2})$.

Proof. 

Since $0\le p_1\le p_2\le 1$, therefore $G^{p_2}$ is a PFSG of $G^{p_1}$. Then, by the above Theorem, $M_1^z(G^{p_1})\ge M_1^z(G^{p_2})$. □

Corollary 1.

Let G be an FG and let $0\le p_1\le p_2\le p_3\le \dots \le p_n\le 1$.

Then, $M_1^z(G^{p_n})\le M_1^z(G^{p_{n-1}})\le \dots \le M_1^z(G^{p_2})\le M_1^z(G^{p_1})$.

Theorem 8.

Let $G=P(v_0,v_1,v_2,\dots ,v_n)$ be a path. Then,

• $M_1^z(G)=Z{F}_1(G)+{(\varrho (e_1)\varrho (e_2))}^2+{(\varrho (e_n)\varrho (e_{n-1}))}^2+{\displaystyle \sum _{i=2}^{i=n-1}}{\varrho }^2(e_i){(\varrho (e_{i-1})+\varrho (e_{i+1}))}^2$.
• $M_1^z(G)\le 8(n-1)$.

Proof. 

Given that $G=P(v_0,v_1,v_2,\dots ,v_n)$ is a path, there are $(n+1)$ vertices and n edges.

• Now,

  $$M_1^z(G)={\displaystyle \sum _{xϵV(G)}}{(\omega (x)d(x))}^2+{\displaystyle \sum _{eϵE(G)}}{(\varrho (e)d(e))}^2$$

  (1)
  Here, the degree of each vertex $v_i$, except $v_0$ and $v_n$, is $(\varrho (e_i)+\varrho (e_{i+1}))$ and the degree of $v_0$ is $\varrho (e_1)$ and degree of $v_n$ is $\varrho (e_n)$.
  Additionally, the degree of each edge $e_i$, except $e_1$ and $e_n$, is $(\varrho (e_{i-1})+\varrho (e_{i+1}))$ and the degree of $e_1$ is $e_2$, the degree of $e_n$ is $e_{n-1}$.
  Using this result, we have from $(1)$,
  $M_1^z(G)={({\omega }_0{\varrho }_1)}^2+{({\omega }_n{\varrho }_n)}^2+{\displaystyle \sum _{i=1}^{i=n-1}}{\omega }^2(v_i){(\varrho (e_i)+\varrho (e_{i+1}))}^2+{(\varrho (e_1)\varrho (e_2))}^2+$
  ${(\varrho (e_n)\varrho (e_{n-1}))}^2+{\displaystyle \sum _{i=2}^{i=n-1}}{\varrho }^2(e_i){(\varrho (e_{i-1})+\varrho (e_{i+1}))}^2$

  $$=Z{F}_1(G)+{(\varrho (e_1)\varrho (e_2))}^2+{(\varrho (e_n)\varrho (e_{n-1}))}^2+{\displaystyle \sum _{i=2}^{i=n-1}}{\varrho }^2(e_i){(\varrho (e_{i-1})+\varrho (e_{i+1}))}^2$$

  (2)
• From Equation $(2)$, we get
  $M_1^z(G)=Z{F}_1(G)+{(\varrho (e_1)\varrho (e_2))}^2+{(\varrho (e_n)\varrho (e_{n-1}))}^2+{\displaystyle \sum _{i=2}^{i=n-1}}{\varrho }^2(e_i){(\varrho (e_{i-1})+\varrho (e_{i+1}))}^2$.
  As $0\le \varrho (e_i)\le 1$ and $0\le \omega (v_i)\le 1$,
  $M_1^z(G)\le 2(2n-1)+1+1+4(n-2)$ (where $Z{F}_1(G)\le 2(2n-1)$)
  $=4n-2+2+4n-8$
  $=8n-8$.
  So, $M_1^z(G)\le 8(n-1)$.

□

Example 6.

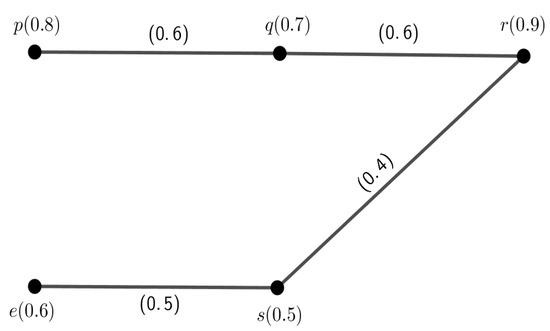
Let $A=P(p,q,r,s,e)$ be an FG with vertex set $V=p,q,r,s,e$ such that $\omega (p)=0.8,\omega (q)=0.7,\omega (r)=0.9,\omega (s)=0.5,\omega (e)=0.6,\varrho (p,q)=0.6,\varrho (q,r)=0.6,\varrho (r,s)=0.4,\varrho (s,e)=0.5$ shown in Figure 6. Then, $d(p)=0.6,d(q)=1.2,d(r)=1.0,d(s)=0.9,d(e)=0.5,d(p,q)=0.6,d(q,r)=1.0,d(r,s)=1.1$ and $d(s,e)=0.4$.

Figure 6. A fuzzy path G with $M_1^z(A)=2.7617$.

Now, $M_1^z(A)={\displaystyle \sum _{xϵV(A)}}{(\omega (x)d(x))}^2+{\displaystyle \sum _{eϵE(A)}}{(\varrho (e)d(e))}^2$

$={(0.8\times 0.6)}^2+{(0.7\times 1.2)}^2+{(0.9\times 1.0)}^2+{(0.5\times 0.9)}^2+{(0.6\times 0.5)}^2+{(0.6\times 0.6)}^2+{(0.6\times 1.0)}^2+{(0.4\times 1.1)}^2+{(0.5\times 0.4)}^2$

$=0.2304+0.7056+0.81+0.2025+0.09+0.1296+0.36+0.1936+0.04=2.7617$.

Theorem 9.

Let $G=P(v_0,v_1,v_2,\dots ,v_n)$ be a path. If we take $v_0=v_n$, it becomes a cycle $H=C(v_0,v_1,v_2,\dots ,v_n)$. Then $M_1^z(G)\le M_1^z(H)$.

Proof. 

Let d and $d^{\prime }$ denote the degree of a vertex/edge in G and H respectively. Here, $d(v)=d^{\prime }(v)$ for all vertices except $v_0$ and $v_n$. Now, $d(v_0)=e_1$ and $d(v_n)=e_n$ and $d^{\prime }(v_0)=e_1+e_n$. Additionally, $d(e)=d^{\prime }(e)$ for all edges except $e_1$ and $e_n$. Now, $d(e_1)=e_2$ and $d(e_n)=e_{n-1}$ and $d^{\prime }(e_1)=e_2+e_n,d^{\prime }(e_n)=e_1+e_{n-1}$.

Now, $M_1^z(G)={\displaystyle \sum _{vϵV(G)}}{(\omega (v)d(v))}^2+{\displaystyle \sum _{eϵE(G)}}{(\varrho (e)d(e))}^2$

$={(\omega (v_0)d(v_0))}^2+{(\omega (v_n)d(v_n))}^2+{\displaystyle \sum _{vϵV(G)-v_0,v_n}}{(\omega (v)d(v))}^2+{(\varrho (e_1)d(e_1))}^2+{(\varrho (e_n)d(e_n))}^2+{\displaystyle \sum _{eϵE(G)-e_1,e_n}}{(\varrho (e)d(e))}^2$

$={({\omega }^{\prime }(v_0)e_1)}^2+{({\omega }^{\prime }(v_n)e_n)}^2+{\displaystyle \sum _{vϵV(H)-v_0}}{({\omega }^{\prime }(v)d^{\prime }(v))}^2+{({\varrho }^{\prime }(e_1)e_2)}^2+{({\varrho }^{\prime }(e_n)e_{n-1})}^2+{\displaystyle \sum _{eϵE(H)-e_1,e_n}}{({\varrho }^{\prime }(e)d^{\prime }(e))}^2$

$={({\omega }^{\prime }(v_0)e_1)}^2+{({\omega }^{\prime }(v_0)e_n)}^2+{\displaystyle \sum _{vϵV(H)-v_0}}{({\omega }^{\prime }(v)d^{\prime }(v))}^2+{({\varrho }^{\prime }(e_1)e_2)}^2+{({\varrho }^{\prime }(e_n)e_{n-1})}^2+{\displaystyle \sum _{eϵE(H)-e_1,e_n}}{({\varrho }^{\prime }(e)d^{\prime }(e))}^2$

$={\omega }^{\prime }(v_0)({(e_1)}^2+{(e_n)}^2)+{\displaystyle \sum _{vϵV(H)-v_0}}{({\omega }^{\prime }(v)d^{\prime }(v))}^2+{({\varrho }^{\prime }(e_1)e_2)}^2+{({\varrho }^{\prime }(e_n)e_{n-1})}^2+{\displaystyle \sum _{eϵE(H)-e_1,e_n}}{({\varrho }^{\prime }(e)d^{\prime }(e))}^2$

$\le {\omega }^{\prime }(v_0){((e_1)+(e_n))}^2+{\displaystyle \sum _{vϵV(H)-v_0}}{({\omega }^{\prime }(v)d^{\prime }(v))}^2+{({\varrho }^{\prime }(e_1)(e_2+e_n))}^2+{({\varrho }^{\prime }(e_n)(e_{n-1}+e_1))}^2+{\displaystyle \sum _{eϵE(H)-e_1,e_n}}{({\varrho }^{\prime }(e)d^{\prime }(e))}^2$

$=M_1^z(H)$.

So, $M_1^z(G)\le M_1^z(H)$. □

Example 7.

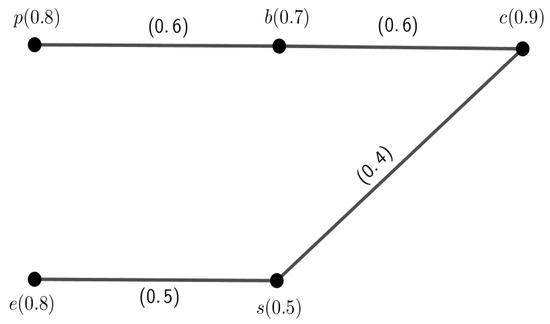
Let G be a path with vertex set $V=p,q,r,s,e$ such that $\omega (p)=0.8,\omega (q)=0.7,\omega (r)=0.9,\omega (s)=0.5,\omega (e)=0.8,\varrho (p,q)=0.6,\varrho (q,r)=0.6,\varrho (r,s)=0.4$ and $\varrho (s,e)=0.5$ shown in Figure 7.

Figure 7. A fuzzy path G with $M_1^z(G)$ = 2.8317.

Then, $d(p)=0.6,d(q)=1.2,d(r)=1.0,d(s)=0.9,d(e)=0.5,d(p,q)=0.6,d(q,r)=1.0,d(r,s)=1.1,d(s,e)=0.4$

Now, $M_1^z(G)={\displaystyle \sum _{xϵV(G)}}{(\omega (x)d(x))}^2+{\displaystyle \sum _{eϵE(G)}}{(\varrho (e)d(e))}^2$

$={(0.8\times 0.6)}^2+{(0.7\times 1.2)}^2+{(0.9\times 1.0)}^2+{(0.5\times 0.9)}^2+{(0.8\times 0.5)}^2+{(0.6\times 0.6)}^2+{(0.6\times 1.0)}^2+{(0.4\times 1.1)}^2+{(0.5\times 0.4)}^2$

$=0.2304+0.7056+0.81+0.2025+0.16+0.1296+0.36+0.1936+0.04=2.8317$.

Marge two vertex a and e in G, as shown in Figure 8.

Figure 8. A fuzzy graph H with $M_1^z(H)=3.7317$.

Then, $d(p)=1.1,d(q)=1.2,d(r)=1.0,d(s)=0.9,d(p,q)=1.1,d(q,r)=1.0,d(r,s)=1.1,d(s,p)=1.0.$

Now, $M_1^z(H)={\displaystyle \sum _{xϵV(H)}}{(\omega (x)d(x))}^2+{\displaystyle \sum _{eϵE(H)}}{(\varrho (e)d(e))}^2$

$={(0.8\times 1.1)}^2+{(0.7\times 1.2)}^2+{(0.9\times 1.0)}^2+{(0.5\times 0.9)}^2+{(0.6\times 1.1)}^2+{(0.6\times 1.0)}^2+{(0.4\times 1.1)}^2+{(0.5\times 1.0)}^2$

$=0.7744+0.7056+0.81+0.2025+0.4356+0.36+0.1936+0.25=3.7317$.

Theorem 10.

Let $G=C(v_0,v_1,\dots ,v_n)$ be a cycle. Then,

• $M_1^z(G)=Z{F}_1(G)+{(\varrho (e_1))}^2{(\varrho (e_2)+\varrho (e_n))}^2+{\displaystyle \sum _{i=2}^{i=n}}{(\varrho (e_i))}^2{(\varrho (e_{i-1})+\varrho (e_{i+1}))}^2$
• $M_1^z(G)\le 8(n+1)-4$.

Proof. 

Similar proof to Theorem 8. □

Theorem 11.

Let $G_1$ and $G_2$ be two fuzzy graphs and they are isomorphic to each other. Then, $M_1^z(G_1)=M_1^z(G_2)$.

Proof. 

As $G_1$ and $G_2$ are isomorphic to each other, then there exists a bijective mapping $\varphi :V_1\to V_2$ and for all $u,vϵV_1$ then ${\omega }_1(v)={\omega }_2(\varphi (v))$ and ${\varrho }_1(uv)={\varrho }_2(\varphi (u)\varphi (v))$

Then, $d_{G_1}(v)={\displaystyle \sum _{u\in V_1}}{\varrho }_1(uv)={\displaystyle \sum _{\varphi (u)\in V_2}}{\varrho }_2(\varphi (u)\varphi (v))=d_{G_2}(\varphi (v))$.

Now, $M_1^z(G)={\displaystyle \sum _{v\in V(G_1)}}{(\omega (v)d_{G_1}(v))}^2+{\displaystyle \sum _{uv\in E(G_1)}}{(\varrho (uv)d_{G_1}(uv))}^2$

$={\displaystyle \sum _{v\in V(G_2)}}{(\omega (\varphi (v))d_{G_2}(\varphi (v)))}^2+{\displaystyle \sum _{\varphi (u)\varphi (v)\in E(G_2)}}{(\varrho (\varphi (u)\varphi (v))d_{G_2}(\varphi (u)\varphi (v)))}^2$

$=M_1^z(G_2)$.

So, $M_1^z(G_1)=M_1^z(G_2).$ □

Theorem 12.

If $G=K_{1,p-1}$ (see Figure 9) is a star and satisfies the condition $\omega (o)\le \omega (v)$, where o is the center of the star, then the value of the FEZI is

Figure 9. Graph of $K_{1,p-1}$.

$M_1^z(G)={(\omega (o))}^2({\displaystyle \sum _{vϵV(G)-o}}{\omega (v)}^2+\omega {(o)}^2(p-1)(p^2-3p+3))$.

Proof. 

Given that $\omega (o)\le \omega (v)$, where o is the center of the star, so $\varrho (e)=\omega (o)$ for all edges. Now, $deg(v)$ for all $vϵV-o$ is given by $\varrho (ov)=\omega (o)$ and $deg(o)={\displaystyle \sum _{vϵV-o}}\varrho (ov)=(p-1)\omega (o)$ also $deg(e)=(p-2)\omega (o)$.

Now, $M_1^z(G)={\displaystyle \sum _{vϵV(G)}}{(\omega (v)deg(v))}^2+{\displaystyle \sum _{eϵE(G)}}{(\varrho (e)deg(e))}^2$

$={\displaystyle \sum _{vϵV(G)-o}}{(\omega (v)\omega (o))}^2+{(\omega (o)(p-1)\omega (o))}^2+{\displaystyle \sum _{eϵE(G)}}{(\omega (o)(p-2)\omega (o))}^2$

$={(\omega (o))}^2({\displaystyle \sum _{vϵV(G)-o}}{\omega (v)}^2+\omega {(o)}^2(p-1)(p^2-3p+3))$.

This shows that $M_1^z(G)={(\omega (o))}^2({\displaystyle \sum _{vϵV(G)-o}}{\omega (v)}^2+\omega {(o)}^2(p-1)(p^2-3p+3))$. □

Theorem 13.

If $G=S(a,b)$ is a double star, $c_1$ is the center of the first star and $c_2$ is the center of the second star and satisfies the condition $\omega (c_1)=\omega (c_2)\le \omega (v)$ for all $vϵV(G)$, then $M_1^z(G)=Z{F}_{1}G+{\omega (c_1)}^4(a^3+b^3+{(a+b)}^2)$.

Proof. 

Since $\omega (c_1)=\omega (c_2)\le \omega (v)$ for all $vϵV(G)$,

$\varrho (c_{1}u)=\omega (c_1),\varrho (c_{2}v)=\omega (c_2)=\omega (c_1)$.

Additionally, $deg(u)=\omega (c_1),deg(v)=\omega (c_2)=\omega (c_1)$,

$deg(c_1)=(a+1)\omega (c_1),deg(c_2)=(b+1)\omega (c_2)=(b+1)\omega (c_1)$,

$deg(u{c}_1)=a\omega (c_1),deg(u{c}_2)=b\omega (c_2)=b\omega (c_1),deg(c_1{c}_2)=(a+b)\omega (c_1)$.

Now, $M_1^z={\displaystyle \sum _{xϵV(G)}}{(\omega (x)d(x))}^2+{\displaystyle \sum _{eϵE(G)}}{(\varrho (e)d(e))}^2$

$=Z{F}_1(G)+{\displaystyle \sum _{eϵE(G_1)}}{(\varrho (e)deg(e))}^2+{\displaystyle \sum _{eϵE(G_2)}}{(\varrho (e)deg(e))}^2+{\varrho (c_1{c}_2)deg(c_1{c}_2)}^2$

$=Z{F}_1(G)+{\displaystyle \sum _{eϵE(G_1)}}{(\omega (c_1)a\omega (c_1))}^2+{\displaystyle \sum _{eϵE(G_2)}}{(\omega (c_1)b\omega (c_1))}^2+{(\omega (c_1)(a+b)\omega (c_1))}^2$

$=Z{F}_1(G)+{\omega (c_1)}^4(a^3+b^3+{(a+b)}^2)$

$M_1^z(G)=Z{F}_{1}G+{\omega (c_1)}^4(a^3+b^3+{(a+b)}^2)$. □

Theorem 14.

For a firefly graph $F_{s,t,p-2s-2t-1}$, if the MV of each vertex as well as the edge is one, then the value of the FEZI is $M_1^z(G)=p+10s+4t-1+{(p-t-1)}^2+(p-t-1){(p-t-2)}^2$.

Proof. 

Since the MV of each vertex and each edge is one, the number of vertices with degree 1 is $p-2s-2t-1+t=p-2s-t-1$,

the number of vertices with degree 2 is $2s+t$,

and $deg(c)=2(p+s-1)-(p-2s-t-1)-2(2s+t)=p-t-1$,

the number of edges with degree 1 is t,

the number of edges with degree 2 is s,

the remaining (p-t-1) edges have degree $(p-t-2)$.

Then, the FEZI is $M_1^z(G)={\displaystyle \sum _{xϵV(G)}}{(\omega (x)d(x))}^2+{\displaystyle \sum _{eϵE(G)}}{(\varrho (e)d(e))}^2$

$=(p-2s-t-1)+4(2s+t)+{(p-t-1)}^2+t+4s+(p-t-1){(p-t-2)}^2$$=p+10s+4t-1+{(p-t-1)}^2+(p-t-1){(p-t-2)}^2$. □

Corollary 2.

If $s=t=0$, then for a firefly graph,

$M_1^z(G)={(\omega (c))}^2({\displaystyle \sum _{vϵV(G)-c}}{\omega (v)}^2+\omega {(c)}^2(n-1)(n^2-3n+3)).$

If we put $s=t=0$ in $F_{s,t,n-2s-2t-1}$, then the graph is a star similar to $K_{1,n-1}$

So, $M_1^z(G)=M_1^z(K_{1,n-1})={(\omega (c))}^2({\displaystyle \sum _{vϵV(G)-c}}{\omega (v)}^2+\omega {(c)}^2(n-1)(n^2-3n+3))$.

4. Application of FEZI for Fuzzy Graphs to Find out the State Which Require More Development for Internet System

4.1. Model Construction

In the modern day, the internet is the most important part of our regular life. Here in this paper, we analyzed the Reliance Jio infocomm Ltd internet system in India. The data of Reliance Jio infocomm Ltd internet users are given in Table 1. These data were taken from https://dot.gov.in/sites/default/files/2022, accessed on 15 December 2022. Then, we constructed a Reliance Jio infocomm Ltd internet system graph (see Figure 10). Here, the whole graph is similar to a star where Reliance Jio infocomm Ltd (C) is the center of the star and each state is a pendent vertex of the star.

Table 1. Data of internet users for all states.

State	Internet Users (in Million)	Total Population (in Million)	Population Percentage of the State
Andhra Pradesh (A.P)	56.06	52.883	4
Assam (AS)	14.14	35.4	2.6
Bihar (BI)	48.11	125.1	9.2
Delhi (DE)	38.89	31.2	2.3
Gujrat (GU)	43.68	70.7	5.2
Haryana (HA)	16.74	29.9	2.2
Himachal Pradesh (H.P)	5.89	7.45	0.50
Jammu and Kashmir (J.K)	7.55	13.6	1.0
Karnataka (KA)	43.68	67.3	4.9
Kerala (KE)	24.92	35.4	2.6
Madhya Pradesh (M.P)	47.78	85.6	6.3
Maharashtra (MA)	61.12	125.5	9.3
Odisha (OD)	19.02	44.2	3.3
Punjab (PU)	25.1	30.6	2.2
Rajasthan (RA)	41.75	80.2	5.9
Tamil Nadu (T.N)	49.17	76.7	5.6
Uttar Pradesh (U.P)	91.35	233.4	17.2
West Bengal (W.B)	49.1	98.7	7.3

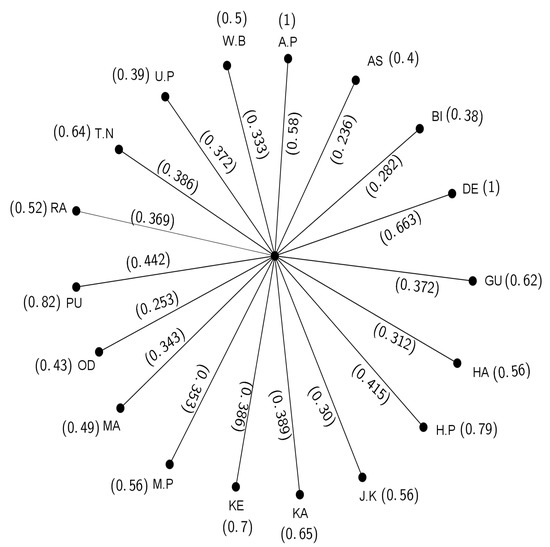
Figure 10. Fuzzy graph of internet network of Reliance jio.

4.2. Representation of Membership Values

Now, the MV of a vertex is denoted as $\omega (S)$ according to the formula below:

∧ {1,$\frac{Totalinternetusersinthestate}{Totalpopulationinthestate}$}.

Here we see that $\omega (S)\in [0,1]$, since there is an edge between center C and a state S. The $MV$ of this edge is denoted as $\varrho (CS)$ and is defined by the following formula:

∧{1,$\frac{TotalJiointernetusersinthisstateS}{TotalpopulationinthisstateS}+\frac{PopulationpersentageinthisstateS}{100}$}.

Here, we see that $\varrho (CS)\in [0,1]$.

The membership values are given in the Table 2 and Table 3.

Table 2. Some values with respect to internet users.

State	Jio Internet Users (Million)	$\frac{\mathbf{Total}\mathbf{internet}\mathbf{users}}{\mathbf{Total}\mathbf{population}}$	$\frac{\mathbf{Jio}\mathbf{internet}\mathbf{users}}{\mathbf{Total}\mathbf{population}}$	$\frac{\mathbf{Jio}\mathbf{internet}\mathbf{users}}{\mathbf{Total}\mathbf{population}}+\frac{\mathbf{population}\mathbf{percentage}}{100}$
A.P	28.9	1.06	0.54	0.58
AS	7.3	0.4	0.21	0.236
BI	24.82	0.38	0.19	0.282
DE	20.06	1.25	0.64	0.663
GU	22.53	0.62	0.32	0.372
HA	8.64	0.56	0.29	0.312
H.P	3.03	0.79	0.41	0.415
J.K	3.89	0.56	0.29	0.30
KA	22.53	0.65	0.34	0.389
KE	12.86	0.70	0.36	0.386
M.P	24.65	0.56	0.29	0.353
MA	31.54	0.49	0.25	0.343
OD	9.81	0.43	0.22	0.253
PU	12.95	0.82	0.42	0.442
RA	21.54	0.52	0.27	0.369
T.N	25.37	0.64	0.33	0.386
U.P	47.13	0.39	0.20	0.372
W.B	25.34	0.5	0.26	0.333

Table 3. Membership values and degrees of the FG of Figure 10.

State	MV of the State (Vertex)	Degree of the State (Vertex) = MV of the Edge	Degree of an Edge between State and Center of the Star
A.P	1	0.58	6.060
AS	0.4	0.236	6.550
BI	0.38	0.282	6.504
DE	1	0.663	6.123
GU	0.62	0.372	6.414
HA	0.56	0.312	6.474
H.P	0.79	0.415	6.371
J.K	0.56	0.30	6.486
KA	0.65	0.389	6.397
KE	0.70	0.386	6.400
M.P	0.56	0.353	6.433
MA	0.49	0.343	6.443
OD	0.43	0.253	6.533
PU	0.82	0.442	6.344
RA	0.52	0.369	6.417
T.N	0.64	0.386	6.400
U.P	0.39	0.372	6.414
W.B	0.5	0.333	6.453

Then the value of the FEZI is given by

$$M_1^z(G)={\displaystyle \sum _{vϵV(G)}}{(\omega (v)d(v))}^2+{\displaystyle \sum _{eϵE(G)}}{(\varrho (e)d(e))}^2=112.02.$$

The FEZI of states (vertex) are given in the Table 4, and they are calculated by the formula $M_1^z(State)=M_1^z(G)-M_1^z(G_{State})$.

Table 4. Value of first entire Zagreb index for all states.

State	${\mathit{M}}_1^{\mathit{z}}(\mathit{G}-\mathbf{State})$	${\mathit{M}}_1^{\mathit{z}}(\mathbf{State})$
A.P	111.68	0.34
AS	112.01	0.01
BI	112.01	0.01
DE	111.58	0.44
GU	111.97	0.05
HA	111.99	0.03
H.P	111.91	0.11
J.K	111.99	0.03
KA	111.96	0.06
KE	111.95	0.07
M.P	111.98	0.04
MA	111.99	0.03
OD	112.01	0.01
PU	111.89	0.13
RA	111.98	0.04
T.N	111.96	0.06
U.P	112.00	0.02
W.B	111.99	0.03

4.3. Decision Making

From the Table 4, we have $M_1^z(AS)=M_1^z(BI)=M_1^z(OD)<M_1^z(U.P)<M_1^z(HA)=M_1^z(J.K)=M_1^z(MA)=M_1^z(W.B)<M_1^z(M.P)=M_1^z(RA)<M_1^z(GU)<M_1^z(KA)=M_1^z(TN)<M_1^z(KE)<M_1^z(H.P)<M_1^z(PU)<M_1^z(A.P)<M_1^z(DE)$.

Now, the least FEZI of a vertex indicates that the vertex is most crucial for the development of internet network systems. Here, the first entire Zagreb index of two or more states is equal. In this situation, we will find the population percentage of these states who cannot use the internet. Then, the state having the largest population percentage that does not use the internet becomes the first to develop an internet network system.

Here, the percentages of the population who do not use the internet (PP) of the states are as follows: PP(AS) = 21.26, PP(BI) = 25.18, PP(OD) = 76.99, PP(HA) = 13.16, PP(J.K) = 6.05, PP(MA) = 64.38, PP(W.B) = 49.6, PP(M.P) = 37.82, PP(RA) = 38.45, PP(KA) = 23.62, PP(T.N) = 27.53. Then we can order the states as follows, and needing more development:

Odisha, Bihar, Assam, Uttar Pradesh, Maharashtra, West Bengal, Haryana, Jammu and Kashmir, Rajasthan, Madhya Pradesh, Gujrat, Tamil Nadu, Karnataka, Kerala, Himachal Pradesh, Punjab, Andhra Pradesh, Delhi.

5. Conclusions

In this article, the FEZI (first entire Zagreb index) was introduced as a graph parameter to quantify the structural characteristics of a graph. This study introduced several results and established relationships between various isomorphic graphs and $\alpha$-cut fuzzy graphs. Additionally, the paper provided bounds for some fuzzy graphs and applied these results to real-life problems in the field of internet system development. The precise values or boundaries of FEZI with regards to graphs such as the firefly graph, star, path, cycle, and others, were explored in this study. The relationship between the value of the FEZI of a graph and its subgraph, two isomorphic graphs, and the first Zagreb index and FEZI were also described here. To analyze the Reliance Jio infocomm Ltd. internet system in India, this paper constructed an internet system graph. In this graph, the least FEZI of a vertex indicates that the vertex is most crucial for the development of the internet network system, and the first entire Zagreb index of two or more states is equal. According to this paper, the state with the highest proportion of people who do not use the internet is the first to develop an internet network system. The first entire Zagreb index is also important in biochemistry, chemical graph theory, spectral graph theory, etc.