Reliability Class Testing and Hypothesis Specification: NBRULC−t_∘ Characterizations with Applications for Medical and Engineering Data Modeling

Abstract

Due to the complexity of the data being generated day in and day out in many practical domains, as a result of the development of scales for rating the success or failure of reliability, a new domain of reliability called the classes of life and determinant probability distributions has been presented. This article introduces novel statistical probability models for the reliability class of life test under different reliability processes in the age range $t_{\circ }$. Several probabilistic properties and features were derived and rigorously screened to test the new reliability class. According to the U-statistic, a novel hypothesis test was created to evaluate the exponentiality property. The comparative efficiency of the test according to Pitman’s asymptotic efficiency was examined and compared with other reliability classes. To prove the superiority of the new reliability class, some probability models were utilized, including the Weibull, Makeham, gamma, and linear failure rate models. Moreover, critical point simulations of the null Monte Carlo distribution and some applications of the censored and uncensored data were implemented to validate the class test listed by the reliability analysis.

1. Introduction

In the statistical sciences, the process of hypothesis testing involves making an analyzed assumption about a population parameter for testing. To test the null hypothesis against an alternative hypothesis, analysts use a sample of the population. The null hypothesis usually states that two parameters are identical. For example, one can claim that the content means the payout is zero. The alternative hypothesis, such as “population means yield is not equal to zero” is essentially the opposite of the null hypothesis. Since they contradict each other, only one of them can be true.

Several classes of life models have been reported to reflect the different components of aging. In dependency, economics, queuing, epidemiology, scheduling, and other fields, the convex ascending order of random variables determined by the comparison of increasing and convex expectation functions has found wide use. A growing convex system has many applications in queuing theory, dependability, operations research, economics, and other fields. Stoyan [1], for example, used this arrangement to determine the ideal sample size for an experimental design. By comparing queues and stochastic processes, Ross [2] offered various applications of this ordering. Using a specific distribution order allows characterizing and creating new definitions of aging categories. The aging phenomenon refers to the fact that an older system rather than a younger one has a shorter residual life in some static sense. The lifespan distribution classes, such as increasing failure rate (IFR), increasing failure rate average (IFRA), and new better than used (NBU), have thoroughly been researched usingreliability theory and its applications to derive practical constraints for the reliability of components or modules. The properties of maintaining life distribution classes under different reliability processes should also be studied for the same reason. These processes are generated by related systems, which may include identical or different components. Minimum and maximum component life, which are configured by the serial and parallel systems, respectively, are two important reliability measures.

Another well-liked action is warp, which is associated with cold standby systems. A lifetime distribution class is indicated as closed within a reliability process if the lifetime distributions of system components indicate that the lifetime distribution for the class as a whole also belongs to the class. It has long been found to be very useful in reliability theory for classifying life distributions according to aging characteristics. The most-well-known classes of life distributions that Barlow and Broshan [3] examined are the characteristics of aging for our IFR, IFRA, and NBU. The new better than used convex ordering (NBUC) and new worse than used convex ordering (NWUC) aging qualities were both presented by Cao and Wang [4] as extensions of NBU. Most of the traits connected to NBUC were investigated in Pellerey [5]. For the new better than used in the increasing convex average order (NBUCA) class based on the Laplace transform, see Al-Gashgari et al. [6]. A new better than used convex ordering moment generation function (NBUC_mgf) class was discussed by Abu-Youssef et al. [7]. For the exponential better than equilibrium life in convex (EBELC) class, see Mahmoud et al. [8]. Many aging categories/classes for life distributions at specific ages have been explored from a variety of perspectives by statisticians and reliability analysts. More information can be found in Hollander et al. [9]; Ebrahimi and Habbibullah [10] considered the question of how to prove that the quality of an item, as measured by its residual life, has decreased after a certain period of time of time $t_{\circ }.$ This problem/issue may arise, for example, if one wishes to prove that the probability of failure has increased since the beginning of the process in order to justify the demand for certain maintenance activities at time $t_{\circ }$. Given that $t_{\circ }$ is a given or definite period of interest, it is reasonable to assume that $t_{\circ }$ is known. See Renea and Samanieg [11] for NBU$-t_{\circ }$, Ahmad [12], Zehui and Xiaohu [13] for IFRA$-t_{\circ }$ and NBU$-t_{\circ }$, Mahmoud et al. [14] for NBUE$-t_{\circ }$, Mahmoud et al. [15] for NBURFR$-t_{\circ }$, Pandit and Anuradha [16] for NBU$-t_{\circ }$, Gadallah [17] for NBU${}_{mgf}-t_{\circ }$, Abdul Alim [18] for NBUFR$-t_{\circ }$, Mahmoud et al. [19] for NBUL$-t_{\circ }$, Elbatal [20] for NBUC$-t_{\circ }$ and NBU(2)$-t_{\circ }$, and EL-Sagheer [21] for NBRUL$-t_{\circ }$. The main objective of the research is that in nonparametric testing of life distributions, we discovered a lack of test efficiency and a weak test power. To account for the effectiveness and strength of the test, we developed a brand-new reliability class test of the life distribution called a new better than renewal used in the Laplace transform in increasing convex order at age $t_{\circ }$ (NBRULC$-t_{\circ }$).

In actual life, there are instances when the system’s components gradually deteriorate up to time $t_{\circ }$, the length of the warranty period most manufacturers provide, and are then renewed by the replacement of spare parts at time $t_{\circ }$. In this situation, renewal aims to improve system usability, but is unable to restore the system to its previous state at age $t_{\circ }$. For instance, the Aviation Administration decided that an airplane engine component needs to be replaced after many hours of flying. According to the airlines, this substitution is at best unneeded and might potentially be damaging to the aircraft. Airlines use operating data to determine whether an airplane engine is still as good as new after hours of renewal to back up their claim.

In the medical field, according to experts in the field of cancer, a person who has just received a diagnosis of a certain type of cancer has a significantly lower chance of surviving than someone alive for five years ($=t_{\circ }$) since receiving the diagnosis. (In fact, such survivors are frequently labeled as “cured”.) There may be a desire to test the cancer professionals’ beliefs.

Furthermore, for instance, a component that a manufacturer claims exhibits “infant mortality” has a declining failure rate over the range $\left[0,t_{\circ }\right]$. This notion is based on knowledge gained for related components. One wants to know if a used component of a certain age has a stochastically longer residual life than a fresh component. If so, he/she will test a certain portion of his/her output over the range $\left[0,t_{\circ }\right]$ and then sell the components that have survived to customers who require high-reliability components (such as a spacecraft assembly) at a premium price. To confirm or deny his/her preconceived notion, he/she wants to test this theory. The development of a new class of life distribution (NBRULC$-t_{\circ }$), a discussion of its characterization, and a comparison of the exponentiality and NBRULC$-t_{\circ }$ class using the $U_n$-statistic are the main points of this essay.

2. NBRULC$-{\mathit{t}}_{\circ }$ Class: Interpretation and Characterization

2.1. Interpretation

A survival function $\overline{F}\left(x\right)$ for a positive random variable X is considered a new better (worse) than renewal used in the Laplace transform order, $X\in$NBRUL (NWRUL), iff

$${\int }_0^{\infty }{\int }_{x+t}^{\infty }{e}^{-mx}\overline{F}\left(u\right)dudx\le (\ge ){\int }_0^{\infty }{\int }_t^{\infty }{e}^{-mx}\overline{F}\left(x\right)\overline{F}\left(u\right)dudx,x,t,m\ge 0,$$

where x is the value of the random variable X, m represents the parameter of the exponential distribution, and t is the time after a period of operation $t_{\circ }$ ($t_{\circ }>0$) (see Mahmoud et al. [22]). Depending on this concept, Etman et al. [23] defined a new class, in the so-called anew better (worse) than renewal used in Laplace transform in increasing convex order, say NBRULC (NWRULC), as follows

$${\int }_0^{\infty }{\int }_{x+t}^{\infty }{e}^{-mx}{\overline{W}}_F\left(u\right)dxdu\le (\ge ){\int }_0^{\infty }{\int }_t^{\infty }{e}^{-mx}\overline{F}\left(x\right){\overline{W}}_F\left(u\right)dxdu,x,t,m\ge 0,$$

or

$${\int }_0^{\infty }{e}^{-mx}\Gamma (x+t)dx\le {\int }_0^{\infty }{e}^{-mx}\overline{F}\left(x\right)\Gamma \left(t\right)dx,$$

where $\Gamma (x+t)={\int }_{x+t}^{\infty }{\overline{W}}_F\left(u\right)du.$ According to the definitions of Mahmoud et al. [22] and Etman et al. [23], a new class of life distributions known as NBRULC at age $t_{\circ }$, say (NBRULC$-t_{\circ }$), is defined. A survival function $\overline{F}\left(x\right)$ for a non-negative random variable X is considered new better (worse) than renewal used in the Laplace transform in increasing convex order at age ${\mathit{t}}_{\circ }$, $(X\in$NBRULC$-t_{\circ }($NWRULC$-t_{\circ }\left)\right)$, iff

$${\int }_0^{\infty }{\int }_{t_{\circ }}^{\infty }{e}^{-mx}{\overline{W}}_F\left(x+u\right)dxdu\le (\ge ){\int }_0^{\infty }{\int }_{t_{\circ }}^{\infty }{e}^{-mx}\overline{F}\left(x\right){\overline{W}}_F\left(u\right)dxdu,x,t_{\circ },m\ge 0,$$

or

$${\int }_0^{\infty }{\int }_{x+t_{\circ }}^{\infty }{e}^{-mx}{\overline{W}}_F\left(u\right)dxdu\le (\ge ){\int }_0^{\infty }{\int }_{t_{\circ }}^{\infty }{e}^{-mx}\overline{F}\left(x\right){\overline{W}}_F\left(u\right)dxdu,$$

and this could be rewritten as

$${\int }_0^{\infty }{e}^{-mx}\Gamma (x+t_{\circ })dx\le {\int }_0^{\infty }{e}^{-mx}\overline{F}\left(x\right)\Gamma \left(t_{\circ }\right)dx.$$

Remark 1. 

It is clear that NBRUL$\Rightarrow$NBRULC$\Rightarrow$NBRULC$-t_{\circ }$.

2.2. Characterization

2.2.1. Convolution Property

The convolution property of reliability classes is a property that states that if a system has a certain reliability class, such as IFR or NBU, then any convolution of systems with the same reliability class will also have the same reliability class. A systems wrap is a system consisting of various components connected in series, such that the system fails when any of the components fail. The reliability class is a way to describe how the failure rate of a system has changed over time. One possible application of the convolution property of reliability classes is the reliability analysis of systems consisting of different components connected in series. For example, one can use the convolution property to determine whether a system consisting of regenerative convolutions has a certain reliability class, such as IFR or NBU. Regeneration is a process that defines the time between successive failures of a system that is either repaired or replaced after each failure. Some possible properties of reliability classes are: Save property This property states that if a system has a certain reliability class, such as IFR or NBU, any subsystem or component of the system will have the same reliability class. This characteristic indicates that adding more components to the system will not improve the reliability class; Close property This property states that if a system has a certain reliability class, such as IFR or NBU, then any function in the system that maintains its failure rate will also have the same reliability class. For example, if the system has an IFR class, then the reciprocal or logarithm will also have an IFR class; Duality property This property states that if a system has a certain reliability class, such as IFR or NBU, its dual system will have the opposite reliability class, such as DFR or NWU. A dual system is a system with the same failure rate as the original system but with an inverted time scale. For example, if a system has an IFR class, its dual system will have a DFR class. One possible way to use the properties of reliability classes to analyze systems is to perform a RAMS analysis. Using the properties of reliability classes, one can determine how the failure rate of a system changes over time and how it affects its availability and maintainability. For example, one can use the save property to compare reliability classes for different components or subsystems of a system. One can also use the closure property to apply different functions to the system and see how they affect the reliability class. One can also use the duality property to find system duality and compare reliability classes.

Theorem 1. 

The NBRULC$-t_{\circ }$ class is preserved under convolution.

Proof. 

It is known that the convolution of two independent NBRULC$-t_{\circ }$ lifetime distributions, $F_1$ and $F_2$, can be formulated as

$$\overline{F}\left(u\right)={\int }_0^{\infty }{\overline{F}}_1(u-z)d{F}_2\left(z\right).$$

Therefore,

$$\begin{array}{ccc}\hfill {\int }_0^{\infty }{\int }_{t_{\circ }}^{\infty }{\int }_{x+y}^{\infty }{e}^{-mx}\overline{F}\left(u\right)dudydx& =& {\int }_0^{\infty }{e}^{-mx}{\int }_{t_{\circ }}^{\infty }{\int }_{x+y}^{\infty }{\int }_0^{\infty }{\overline{F}}_1(u-z)d{F}_2\left(z\right)dudydx\hfill \\ & =& {\int }_0^{\infty }{\int }_0^{\infty }{\int }_{t_{\circ }}^{\infty }{\int }_{x+y}^{\infty }{e}^{-mx}{\overline{F}}_1(u-z)dudydxd{F}_2\left(z\right).\hfill \end{array}$$

Since ${\overline{F}}_1$ is NBRULC$-t_{\circ }$, then

$$\begin{array}{ccc}\hfill {\int }_0^{\infty }{\int }_{t_{\circ }}^{\infty }{\int }_{x+y}^{\infty }{e}^{-mx}\overline{F}\left(u\right)dudydx& \le & {\int }_0^{\infty }{\int }_0^{\infty }{\int }_{t_{\circ }}^{\infty }{\int }_y^{\infty }{e}^{-mx}{\overline{F}}_1\left(x\right){\overline{F}}_1(u-z)dudydxd{F}_2\left(z\right)\hfill \\ & \le & {\int }_0^{\infty }{e}^{-mx}{\overline{F}}_1\left(x\right){\int }_{t_{\circ }}^{\infty }{\int }_y^{\infty }{\int }_0^{\infty }{\overline{F}}_1(u-z)d{F}_2\left(z\right)dudydx\hfill \\ & \le & {\int }_0^{\infty }{e}^{-mx}{\overline{F}}_1\left(x\right){\int }_{t_{\circ }}^{\infty }{\int }_y^{\infty }\overline{F}\left(u\right)dudydx,\hfill \end{array}$$

and by using ${\overline{F}}_i\left(x\right)\le \overline{F}\left(x\right)$ for $i=1,2$, we obtain

$${\int }_0^{\infty }{\int }_{t_{\circ }}^{\infty }{\int }_{x+y}^{\infty }{e}^{-mx}\overline{F}\left(u\right)dudydx\le {\int }_0^{\infty }{\int }_{t_{\circ }}^{\infty }{\int }_y^{\infty }{e}^{-mx}\overline{F}\left(x\right)\overline{F}\left(u\right)dudydx,$$

which completes the proof. □

2.2.2. Mixture Property

The mixing property of reliability classes is a property that states that if a system has a certain reliability class, such as IFR or NBU, any combination of systems with the same reliability class will also have the same reliability class. A mixture of systems is a system consisting of different components chosen randomly according to some probability distribution. The reliability class is a way to describe how the failure rate of a system has changed over time. One possible application of the mixture characteristic for reliability classes is the reliability analysis of systems consisting of different components with different lifetimes and different failure rates. For example, one can use the admixture property to determine whether a system consisting of a mixture of regeneration processes has a certain reliability class, such as IFR or NBU. Regeneration is a process that defines the time between successive failures of a system that is either repaired or replaced after each failure. One possible example of a system consisting of a mixture of regeneration processes is a system that detects and separates impulsive sources based on impulse spacing. The pulse spacing of each source is modeled as a regeneration process, which means that the time between successive pulses is a random variable that depends only on the previous impulse. The system receives a mixture of pulses from different sources and tries to determine which source each pulse belongs to. This is called deinterlacing of regeneration mixtures. The system filters out mixtures of regeneration processes using a method called maximum likelihood estimation (MLE). MLE is a technique that searches for the most likely values of statistical model parameters that fit the observed data. In this case, the system attempts to find the most likely values of the pulse spacing distributions for each source that fit the observed mixture of pulses. The system then assigns each pulse to the source that has the highest probability of generating it. Some of the potential advantages and disadvantages of MLE are: Advantages: It is easy to apply and can handle different types of statistical models. It has lower variance than other methods, which means it is less affected by sampling error. It is also unbiased with increasing sample size, which means that it converges to the true value of the coefficient. It is statistically well understood and has desirable properties such as consistency, efficiency, and approximate normality. Disadvantages: May be computationally intensive or intractable for some complex models. It may also be sensitive to outliers or model selection error. It does not account for prior information or parameter uncertainty. It may also result in biased estimates for small sample sizes.

Theorem 2. 

The NWRULC$-t_{\circ }$ class is preserved under mixture.

Proof. 

It is obvious that $F\left(u\right)$ is the mixture of $F_{\gamma }$, where each $F_{\gamma }$ is NWRULC$-t_{\circ }$, where

$$\overline{F}\left(u\right)={\int }_0^{\infty }{\overline{F}}_{\gamma }\left(u\right)dG\left(\gamma \right),$$

then

$$\begin{array}{ccc}\hfill {\int }_0^{\infty }{\int }_{t_{\circ }}^{\infty }{\int }_{x+y}^{\infty }{e}^{-mx}\overline{F}\left(u\right)dudydx& =& {\int }_0^{\infty }{\int }_{t_{\circ }}^{\infty }{\int }_{x+y}^{\infty }{\int }_0^{\infty }{e}^{-mx}{\overline{F}}_{\gamma }\left(u\right)dG\left(\gamma \right)dudydx\hfill \\ & =& {\int }_0^{\infty }{\int }_0^{\infty }{\int }_{t_{\circ }}^{\infty }{\int }_{x+y}^{\infty }{e}^{-mx}{\overline{F}}_{\gamma }\left(u\right)dudydxdG\left(\gamma \right),\hfill \end{array}$$

since $F_{\gamma }$ is NWRULC$-t_{\circ }$, then

$${\int }_0^{\infty }{\int }_0^{\infty }{\int }_{t_{\circ }}^{\infty }{\int }_{x+y}^{\infty }{e}^{-mx}{\overline{F}}_{\gamma }\left(u\right)dudydxdG\left(\gamma \right)\ge {\int }_0^{\infty }\left\{{\int }_0^{\infty }{\int }_{t_{\circ }}^{\infty }{\int }_y^{\infty }{e}^{-mx}{\overline{F}}_{\gamma }\left(x\right){\overline{F}}_{\gamma }\left(u\right)dudydx\right\}dG\left(\gamma \right).$$

Chebyshev’s inequality for similarity-ordered functions yields the following results

$$\begin{array}{ccc}\hfill {\int }_0^{\infty }{\int }_{t_{\circ }}^{\infty }{\int }_{x+y}^{\infty }{e}^{-mx}\overline{F}\left(u\right)dudydx& \ge & {\int }_0^{\infty }{\int }_0^{\infty }{e}^{-mx}{\overline{F}}_{\gamma }\left(x\right)dG\left(\gamma \right)dx{\int }_{t_{\circ }}^{\infty }{\int }_y^{\infty }{\int }_0^{\infty }{\overline{F}}_{\gamma }\left(u\right)dG\left(\gamma \right)dudy\hfill \\ & \ge & {\int }_0^{\infty }{e}^{-mx}\overline{F}\left(x\right)dx.{\int }_{t_{\circ }}^{\infty }{\int }_y^{\infty }\overline{F}\left(u\right)dudy\hfill \\ & \ge & {\int }_0^{\infty }{\int }_{t_{\circ }}^{\infty }{\int }_y^{\infty }{e}^{-mx}\overline{F}\left(x\right)\overline{F}\left(u\right)dudydx,\hfill \end{array}$$

which complete the proof. □

Chebyshev’s inequality is a mathematical theorem that gives a limit on the probability that a random variable will deviate from its mean by more than a certain number of standard deviations. It can be used to estimate how likely it is that extreme values will be observed in a data set.

2.2.3. Homogeneous Poisson Shock Model

Homogeneous Poisson shock model is a type of stochastic model that describes system failure due to random shocks that occur according to the homogeneous Poisson process. Homogeneous Poisson process is a process that counts the number of events that occur in a given time period, where the events are independent and have a constant rate. The shock model assumes that each shock causes some damage to the system, and the system fails when the total damage exceeds a certain threshold. Poisson homogeneous shock models can be used to model various phenomena such as insurance claims, health impairment, or machine failure. For example, one can use a homogeneous Poisson shock model to estimate the probability of a car crashing due to random mechanical failures that occur at a constant rate over time. There are different types of trauma models depending on the nature and distribution of trauma and the damage it causes. For example, some common types of shock models are: Heterogeneous Poisson shock models, where shocks occur according to an in-homogeneous Poisson process with a variable rate over time; delta models-shocks, where shocks occur at fixed intervals and deal a fixed amount of damage; trigger shock models, where shocks occur in groups or combinations and deal a variable amount of damage; mixed shock models, where shocks are a mixture of different types of shock models. Note that these types of shock models differ from the types of circulatory shock that affect the human body, such as septic shock, cardiogenic shock, hypovolemic shock, or anaphylactic shock. Some of the potential advantages and disadvantages of inhomogeneous Poisson shock models are: Advantages: they can capture changes in the shock rate over time, which may better reflect the reality of some phenomena than a constant rate. They can also accommodate different types of shock rate functions, such as periodic, linear, exponential, or arbitrary functions. According to the disadvantages: they may be more complex and difficult to analyze than homogeneous Poisson shock models. It may also require more data and assumptions to estimate the parameters of the shock rate function. Some potential advantages and disadvantages of homogeneous Poisson shock models are: Advantages: They are simple and easy to analyze, as they only require one parameter to describe the shock rate. They can also model various phenomena such as insurance claims, health declines, or machine failures, by interpreting shocks as different types of events that affect the system. Disadvantages: It may not capture the fluctuation of shock rate over time, which may not reflect the reality of some phenomena that have variable or non-constant rates. They may also be too restrictive or unrealistic for some applications that require more flexibility or complexity in the shock model. Suppose the device is subjected to a series of shocks of force k that occur randomly according to the Poisson process. Let us say the device has a probability ${\overline{P}}_s$ of surviving the first s shocks, where $1={\overline{P}}_0\ge {\overline{P}}_1\ge ...$. Denote $P_j={\overline{P}}_{j-1}-{\overline{P}}_j,j\ge 1$. As a result, the device’s survival feature is provided by

$$\overline{H}\left(t_{\circ }\right)=\sum _{s=0}^{\infty }{\overline{P}}_s\frac{{\left(k{t}_{\circ }\right)}^s}{s!}{e}^{-k{t}_{\circ }},k,t_{\circ }\ge 0,$$

(1)

where k is the intensity constant in the shock model and s represents the number of the shocks. This shock model has undergone research by Esary et al. [24] for different aging properties, Klefsjo [25] for HNBUE, and EL-Sagheer et al. [26] for NBRUL.

Definition 1. 

A discrete distribution $P_s,s=0,1,...,\infty$ is said to have a discrete new better (worse) than renewal used in the Laplace transform in increasing convex order at age t${}_{\circ }$ (NBRULC$-t_{\circ }$) (NWRULC$-t_{\circ }$) if

$$\sum _{i=0}^{\infty }\sum _{l=j}^{\infty }\sum _{r=i+l}^{\infty }{z}^i{\overline{P}}_r\le (\ge )\sum _{i=0}^{\infty }\sum _{l=j}^{\infty }\sum _{r=l}^{\infty }{z}^i{\overline{P}}_i{\overline{P}}_r,0\le z\le 1.$$

(2)

Theorem 3. 

If ${\overline{P}}_s$ is discrete NBRULC$-t_{\circ }$, then $\overline{H}\left(t_{\circ }\right)$ given by (1) is NBRULC$-t_{\circ }$.

Proof. 

Demonstrate that

$${\int }_0^{\infty }{\int }_{t_{\circ }}^{\infty }{\int }_{x+y}^{\infty }{e}^{-mx}\overline{H}\left(u\right)dudydx\le {\int }_0^{\infty }{\int }_{t_{\circ }}^{\infty }{\int }_y^{\infty }{e}^{-mx}\overline{H}\left(x\right)\overline{H}\left(u\right)dudydx.$$

Upon using (1), we obtain

$$\begin{array}{ccc}\hfill {\int }_0^{\infty }{\int }_{t_{\circ }}^{\infty }{\int }_{x+y}^{\infty }{e}^{-mx}\overline{H}\left(u\right)dudydx& =& {\int }_0^{\infty }{\int }_{t_{\circ }}^{\infty }{\int }_{x+y}^{\infty }{e}^{-mx}\sum _{s=0}^{\infty }{\overline{P}}_s\frac{{\left(ku\right)}^s}{s!}{e}^{-ku}dudydx\hfill \\ & =& {\int }_0^{\infty }{\int }_{t_{\circ }}^{\infty }{e}^{-mx}\sum _{s=0}^{\infty }{\overline{P}}_s\frac{1}{s!}{\int }_{x+y}^{\infty }{\left(ku\right)}^s{e}^{-ku}dudydx\hfill \\ & =& \frac{1}{k}{\int }_0^{\infty }{\int }_{t_{\circ }}^{\infty }{e}^{-mx}\sum _{s=0}^{\infty }{\overline{P}}_s\frac{1}{s!}\sum _{r=0}^s\frac{s!{\left[k(x+y)\right]}^r}{r!}{e}^{-k(x+y)}dydx,\hfill \end{array}$$

where ${\int }_{x+y}^{\infty }{\left(ku\right)}^s{e}^{-ku}du=\frac{1}{k}{\sum }_{r=0}^s\frac{s!{\left[k(x+y)\right]}^r}{r!}{e}^{-k(x+y)}$:

$$\begin{array}{ccc}\hfill {\int }_0^{\infty }{\int }_{t_{\circ }}^{\infty }{\int }_{x+y}^{\infty }{e}^{-mx}\overline{H}\left(u\right)dudydx& =& \frac{1}{k}{\int }_0^{\infty }{\int }_{t_{\circ }}^{\infty }{e}^{-mx}\sum _{s=0}^{\infty }{\overline{P}}_s\sum _{r=0}^s\frac{e^{-k(x+y)}}{r!}\sum _{j=0}^r\left(\genfrac{}{}{0pt}{}{r}{j}\right){\left(ky\right)}^{r-j}{\left(kx\right)}^{j}dydx\hfill \\ & =& \frac{1}{k}\sum _{s=0}^{\infty }{\overline{P}}_s\sum _{r=0}^s\sum _{j=0}^r\left(\genfrac{}{}{0pt}{}{r}{j}\right){\int }_{t_{\circ }}^{\infty }\frac{e^{-ky}}{r!}{\left(ky\right)}^{r-j}{\int }_0^{\infty }{\left(kx\right)}^j{e}^{-x(m+k)}dxdy\hfill \\ & =& \frac{1}{k^2}\sum _{j=0}^{\infty }\sum _{r=j}^{\infty }\sum _{s=r}^{\infty }{\overline{P}}_s\frac{1}{(r-j)!}{\left[\frac{k}{m+k}\right]}^{j+1}{\int }_{t_{\circ }}^{\infty }{\left(ky\right)}^{r-j}{e}^{-ky}dy,\hfill \end{array}$$

Let $l=r-j$:

$$\begin{array}{ccc}\hfill {\int }_0^{\infty }{\int }_{t_{\circ }}^{\infty }{\int }_{x+y}^{\infty }{e}^{-mx}\overline{H}\left(u\right)dudydx& =& \frac{1}{k^2}\sum _{j=0}^{\infty }\sum _{l=0}^{\infty }\sum _{s=l+j}^{\infty }{\overline{P}}_s\frac{1}{l!}{\left[\frac{k}{m+k}\right]}^{j+1}{\int }_{t_{\circ }}^{\infty }{\left(ky\right)}^l{e}^{-ky}dy\hfill \\ & =& \frac{1}{k^3}\sum _{j=0}^{\infty }\sum _{s=l+j}^{\infty }\sum _{l=0}^{\infty }\sum _{n=0}^l{\overline{P}}_s{\left[\frac{k}{m+k}\right]}^{j+1}\frac{{\left(k{t}_{\circ }\right)}^n}{n!}{e}^{-k{t}_{\circ }}\hfill \\ & =& \frac{1}{k^3}\sum _{j=0}^{\infty }\sum _{s=l+j}^{\infty }\sum _{n=0}^{\infty }\sum _{l=n}^{\infty }{\overline{P}}_s{\left[\frac{k}{m+k}\right]}^{j+1}\frac{{\left(k{t}_{\circ }\right)}^n}{n!}{e}^{-k{t}_{\circ }}\hfill \\ & =& \frac{1}{k^3}\sum _{n=0}^{\infty }\sum _{j=0}^{\infty }\sum _{l=n}^{\infty }\sum _{s=l+j}^{\infty }{\overline{P}}_s{\left[\frac{k}{m+k}\right]}^{j+1}\frac{{\left(k{t}_{\circ }\right)}^n}{n!}{e}^{-k{t}_{\circ }},\hfill \end{array}$$

since F is NBRULC$-t_{\circ }$:

$$\begin{array}{ccc}\hfill {\int }_0^{\infty }{\int }_{t_{\circ }}^{\infty }{\int }_{x+y}^{\infty }{e}^{-mx}\overline{H}\left(u\right)dudydx& \le & \frac{1}{k^3}\sum _{n=0}^{\infty }\sum _{j=0}^{\infty }\sum _{l=n}^{\infty }\sum _{s=l}^{\infty }{\overline{P}}_j{\overline{P}}_s\frac{{\left(k{t}_{\circ }\right)}^n}{n!}{e}^{-k{t}_{\circ }}.{\left[\frac{k}{m+k}\right]}^{j+1}\hfill \\ & \le & \frac{1}{k^2}\sum _{j=0}^{\infty }\sum _{s=l}^{\infty }\sum _{n=0}^{\infty }\sum _{l=n}^{\infty }{\overline{P}}_j{\overline{P}}_s\frac{{\left(k{t}_{\circ }\right)}^n}{n!}{e}^{-k{t}_{\circ }}{\int }_0^{\infty }\frac{{\left(kx\right)}^j}{j!}{e}^{-x(m+k)}dx\hfill \\ & \le & \frac{1}{k^2}{\int }_0^{\infty }\sum _{j=0}^{\infty }\sum _{s=l}^{\infty }\sum _{l=0}^{\infty }\sum _{n=0}^l{\overline{P}}_j{\overline{P}}_s\frac{{\left(k{t}_{\circ }\right)}^n}{n!}{e}^{-k{t}_{\circ }}\frac{{\left(kx\right)}^j}{j!}{e}^{-x(m+k)}dx\hfill \\ & \le & \frac{1}{k}{\int }_0^{\infty }\sum _{j=0}^{\infty }\sum _{l=0}^{\infty }\sum _{s=l}^{\infty }{\overline{P}}_j{\overline{P}}_s{\int }_{t_{\circ }}^{\infty }\frac{{\left(ky\right)}^l}{l!}{e}^{-ky}dy.\frac{{\left(kx\right)}^j}{j!}{e}^{-x(m+k)}dx\hfill \\ & \le & \frac{1}{k}{\int }_0^{\infty }\sum _{j=0}^{\infty }\sum _{s=0}^{\infty }\sum _{l=0}^s{\overline{P}}_j{\overline{P}}_s{\int }_{t_{\circ }}^{\infty }\frac{{\left(ky\right)}^l}{l!}{e}^{-ky}dy.\frac{{\left(kx\right)}^j}{j!}{e}^{-x(m+k)}dx\hfill \\ & \le & {\int }_0^{\infty }{\int }_{t_{\circ }}^{\infty }{\int }_y^{\infty }{e}^{-mx}\sum _{j=0}^{\infty }{\overline{P}}_j\frac{{\left(kx\right)}^j}{j!}{e}^{-kx}\sum _{s=0}^{\infty }{\overline{P}}_s\frac{{\left(ku\right)}^s}{s!}{e}^{-ku}dudydx\hfill \\ & \le & {\int }_0^{\infty }{\int }_{t_{\circ }}^{\infty }{\int }_y^{\infty }{e}^{-mx}\overline{H}\left(x\right)\overline{H}\left(u\right)dudydx.\hfill \end{array}$$

Reversing the inequalities leads to the proof for the NWRULC$-t_{\circ }$ class. □

3. Testing against NBRULC$-{\mathit{t}}_{\circ }$ Alternatives

In this segment, we considered the possibility that $H_{\circ }:F$ is exponential in contrast to the corresponding hypothesis $H_1:F$ that it is not exponential, but NBRULC$-t_{\circ }$. Building our test statistic requires applying the following snippet/lemma.

Lemma 1. 

If the random variable X has a distribution function F that belongs to the NBRULC$-t_{\circ }$ class, then

$$\frac{t_{\circ }}{m}{\mu }_{\left(2\right)}\xi \left(m\right)-\frac{1}{2m}{\mu }_{\left(3\right)}\xi \left(m\right)-\frac{t_{\circ }^2}{2m}\mu \xi \left(m\right)\ge \frac{t_{\circ }}{m^2}\mu -\frac{1}{m^2}{\mu }_{\left(2\right)}-\frac{e^{m{t}_{\circ }}}{m^3}\mu \xi \left(m\right)+\frac{1}{m^3}\mu ,m>0,$$

(3)

where

$$\xi \left(m\right)=E{e}^{-mX}={\int }_0^{\infty }{e}^{-mx}dF\left(x\right),{\mu }_{\left(r\right)}=E\left(X^r\right).$$

Proof. 

Since F is $NBRULC-t_{\circ }$, then

$${\int }_0^{\infty }{e}^{-mx}\Gamma (x+t_{\circ })dx\le {\int }_0^{\infty }{e}^{-mx}\overline{F}\left(x\right)\Gamma \left(t_{\circ }\right)dx,x,t_{\circ }\ge 0.$$

Integrating all sides with regard to t over $[0,\infty )$ results in

$${\int }_0^{\infty }{\int }_0^{\infty }{e}^{-mx}\Gamma (x+t_{\circ })dxdt\le {\int }_0^{\infty }{\int }_0^{\infty }{e}^{-mx}\overline{F}\left(x\right)\Gamma \left(t_{\circ }\right)dxdt.$$

(4)

Setting

$$\begin{array}{ccc}\hfill I_1& =& {\int }_0^{\infty }{\int }_0^{\infty }{e}^{-mx}\Gamma (x+t_{\circ })dxdt\hfill \\ & =& \frac{1}{2}E{\int }_0^{\infty }{\int }_0^{\infty }{e}^{-mx}{(X-x-t_{\circ })}^{2}I(X>x+t_{\circ })I(X>t)dxdt\hfill \\ & =& \frac{1}{2}E{\int }_0^X{\int }_0^{X-t_{\circ }}{e}^{-mx}{(X-x-t_{\circ })}^{2}dxdt\hfill \\ & =& \frac{1}{2}E{\int }_0^X{\int }_0^{X-t_{\circ }}[(X^2-2X{t}_{\circ }+t_{\circ }^2)e^{-mx}+(2t_{\circ }-2X)x{e}^{-mx}+x^2{e}^{-mx}]dxdt\hfill \\ & =& \frac{1}{2}E{\int }_0^X[\frac{X^2}{m}-\frac{2X{t}_{\circ }}{m}+\frac{2t_{\circ }}{m^2}-\frac{2X}{m^2}-\frac{2}{m^3}{e}^{-m(X-t_{\circ })}+\frac{t_{\circ }^2}{m}+\frac{2}{m^3}]dt.\hfill \end{array}$$

Therefore,

$$I_1=\frac{1}{2m}{\mu }_{\left(3\right)}-\frac{t_{\circ }}{m}{\mu }_{\left(2\right)}+\frac{t_{\circ }}{m^2}\mu -\frac{1}{m^2}{\mu }_{\left(2\right)}-\frac{e^{m{t}_{\circ }}}{m^3}\mu \xi \left(m\right)+\frac{t_{\circ }^2}{2m}\mu +\frac{1}{m^3}\mu .$$

(5)

Similarly, if we set

$$\begin{array}{ccc}\hfill I_2& =& {\int }_0^{\infty }{\int }_0^{\infty }{e}^{-mx}\overline{F}\left(x\right)\Gamma \left(t_{\circ }\right)dxdt\hfill \\ & =& E{\int }_0^{\infty }\Gamma \left(t_{\circ }\right){\int }_0^{\infty }{e}^{-mx}I(X>x)dxdt\hfill \\ & =& (\frac{1}{m}-\frac{1}{m}\xi \left(m\right)){\int }_0^{\infty }\Gamma \left(t_{\circ }\right)dt\hfill \\ & =& \frac{1}{2}(\frac{1}{m}-\frac{1}{m}\xi \left(m\right))E{\int }_0^{\infty }{(X-t_{\circ })}^{2}I(X>t)dt\hfill \\ & =& \frac{1}{2}E[\frac{1}{m}-\frac{1}{m}\xi \left(m\right)]{\int }_0^X{(X-t_{\circ })}^{2}dt,\hfill \end{array}$$

then

$$I_2=\frac{1}{2m}{\mu }_{\left(3\right)}-\frac{t_{\circ }}{m}{\mu }_{\left(2\right)}+\frac{t_{\circ }^2}{2m}\mu -\frac{1}{2m}{\mu }_{\left(3\right)}\xi \left(m\right)+\frac{t_{\circ }}{m}{\mu }_{\left(2\right)}\xi \left(m\right)-\frac{t_{\circ }^2}{2m}\mu \xi \left(m\right).$$

(6)

Substituting (5) and (6) into (4), we obtain

$$\frac{t_{\circ }}{m}{\mu }_{\left(2\right)}\xi \left(m\right)-\frac{1}{2m}{\mu }_{\left(3\right)}\xi \left(m\right)-\frac{t_{\circ }^2}{2m}\mu \xi \left(m\right)\ge \frac{t_{\circ }}{m^2}\mu -\frac{1}{m^2}{\mu }_{\left(2\right)}-\frac{e^{m{t}_{\circ }}}{m^3}\mu \xi \left(m\right)+\frac{1}{m^3}\mu ,$$

and the proof is complete. The following entry point is suggested:

$$\delta ={\int }_0^{\infty }{\int }_0^{\infty }{e}^{-mx}\overline{F}\left(x\right)\Gamma \left(t_{\circ }\right)dxdt-{\int }_0^{\infty }{\int }_0^{\infty }{e}^{-mx}\Gamma (x+t_{\circ })dxdt,$$

then

$$\delta =\frac{t_{\circ }}{m}{\mu }_{\left(2\right)}\xi \left(m\right)-\frac{1}{2m}{\mu }_{\left(3\right)}\xi \left(m\right)+\left(\frac{2e^{m{t}_{\circ }}-m^2{t}_{\circ }^2}{2m^3}\right)\mu \xi \left(m\right)+\frac{1}{m^2}{\mu }_{\left(2\right)}-\left(\frac{m{t}_{\circ }+1}{m^3}\right)\mu .$$

One can notice that the value of $\delta$ under $H_{\circ }$ equals $\lambda ,$ where

$$\lambda =\frac{(t_{\circ }-1)(2m^2-2m)-2(1-e^{m{t}_{\circ }})-m^2{t}_{\circ }^2}{2m^3(m+1)}.$$

Consider that $\Delta =\delta -\lambda ,$$\Delta$ could be expressed as follows:

$$\begin{array}{ccc}\hfill \Delta (m,t_{\circ })& =& \frac{t_{\circ }}{m}{\mu }_{\left(2\right)}\xi \left(m\right)-\frac{1}{2m}{\mu }_{\left(3\right)}\xi \left(m\right)+\left(\frac{2e^{m{t}_{\circ }}-m^2{t}_{\circ }^2}{2m^3}\right)\mu \xi \left(m\right)+\frac{1}{m^2}{\mu }_{\left(2\right)}\hfill \\ & & -\left(\frac{m{t}_{\circ }+1}{m^3}\right)\mu -\left(\frac{(t_{\circ }-1)(2m^2-2m)-2(1-e^{m{t}_{\circ }})-m^2{t}_{\circ }^2}{2m^3(m+1)}\right).\hfill \end{array}$$

An unbiased estimator of $\delta$ is given by

$$\begin{array}{ccc}\hfill \widehat{\Delta }(m,t_{\circ })& =& \frac{1}{n^2{\overline{X}}^4}\sum _{i=1}^n\sum _{j=1}^n[\frac{t_{\circ }}{m}{X}_i^2{e}^{-m{X}_j}-\frac{1}{2m}{X}_i^3{e}^{-m{X}_j}+\left(\frac{2e^{m{t}_{\circ }}-m^2{t}_{\circ }^2}{2m^3}\right)X_i{e}^{-m{X}_j}+\frac{1}{m^2}{X}_i^2\hfill \\ & & -\left(\frac{m{t}_{\circ }+1}{m^3}\right)X_i-\left(\frac{(t_{\circ }-1)(2m^2-2m)-2(1-e^{m{t}_{\circ }})-m^2{t}_{\circ }^2}{2m^3(m+1)}\right)].\hfill \end{array}$$

(7)

Now, set

$$\begin{array}{ccc}\hfill \phi (X_i,X_j)& =& \frac{t_{\circ }}{m}{X}_i^2{e}^{-m{X}_j}-\frac{1}{2m}{X}_i^3{e}^{-m{X}_j}+\left(\frac{2e^{m{t}_{\circ }}-m^2{t}_{\circ }^2}{2m^3}\right)X_i{e}^{-m{X}_j}+\frac{1}{m^2}{X}_i^2\hfill \\ & & -\left(\frac{m{t}_{\circ }+1}{m^3}\right)X_i-\left(\frac{(t_{\circ }-1)(2m^2-2m)-2(1-e^{m{t}_{\circ }})-m^2{t}_{\circ }^2}{2m^3(m+1)}\right).\hfill \end{array}$$

(8)

The test statistic $\widehat{\Delta }(m,t_{\circ })$ has asymptotic features that are reported in the following theorem: □

Theorem 4. 

(i) As $n\to \infty ,[\widehat{\Delta }(m,t_{\circ })-\Delta (m,t_{\circ })]$ is asymptotically normal with mean 0 and variance ${\sigma }^2(m,t_{\circ })/n,$ where

$$\begin{array}{ccc}\hfill {\sigma }^2(m,t_{\circ })& =& Var\{\frac{t_{\circ }}{m}{X}^2\xi \left(m\right)-\frac{1}{2m}{X}^3\xi \left(m\right)+\left(\frac{2e^{m{t}_{\circ }}-m^2{t}_{\circ }^2}{2m^3}\right)X\xi \left(m\right)+\frac{1}{m^2}{X}^2\hfill \\ & & -\left(\frac{m{t}_{\circ }+1}{m^3}\right)X+\frac{t_{\circ }}{m}{\mu }_{\left(2\right)}{e}^{-mX}-\frac{1}{2m}{\mu }_{\left(3\right)}{e}^{-mX}+\left(\frac{2e^{m{t}_{\circ }}-m^2{t}_{\circ }^2}{2m^3}\right)\mu e^{-mX}\hfill \\ & & +\frac{1}{m^2}{\mu }_{\left(2\right)}-\left(\frac{m{t}_{\circ }+1}{m^3}\right)\mu -\left(\frac{(t_{\circ }-1)(2m^2-2m)-2(1-e^{m{t}_{\circ }})-m^2{t}_{\circ }^2}{m^3(m+1)}\right)\}.\hfill \end{array}$$

(9)

(ii) Under $H_{\circ ,}$ the variance tends to

$$\begin{array}{ccc}\hfill {\sigma }_{\circ }^2(m,t_{\circ })& =& \frac{1}{6m^6{(1+m)}^5(1+2m)}\left[4\right\{9m^9+181m^8+462m^7+360m^6+42m^5\hfill \\ & & -46m^4+4m^3+2m^2-m+1+e^{2m{t}_{\circ }}{(1+m)}^2(m^3+7m^2+5m+1)\hfill \\ & & +e^{m{t}_{\circ }}(6m^7+6m^6-20m^5-34m^4-4m^3-6m-2)\}\hfill \\ & & -8m{t}_{\circ }\{8m^8+66m^7+154m^6+126m^5+26m^4-13m^3+m^2+m-1\hfill \\ & & +e^{m{t}_{\circ }}(2m^6+2m^5-10m^4-15m^3-3m^2-+3m+1)\}\hfill \\ & & +4m^2{t}_{\circ }^2\{m^7+27m^6+73m^5+78m^4+24m^3-4m^2+2m+2\hfill \\ & & -e^{m{t}_{\circ }}{(1+m)}^2(m^3+7m^2+5m+1)\}+4m^3{t}_{\circ }^2(2m^6+2m^5-10m^4\hfill \\ & & -15m^3-3m^2-+3m+1)+m^4{t}_{\circ }^4{(1+m)}^2(m^3+7m^2+5m+1)].\hfill \end{array}$$

(10)

Proof. 

Using standard U-statistics theory (see Lee [27]),

$${\sigma }^2=Var\{E[\phi (X_1,X_2)\mid X_1]+E[\phi (X_1,X_2)\mid X_2]\}.$$

(11)

Using (8), we can find $E[\phi (X_1,X_2)\mid X_1]$ and $E[\phi (X_1,X_2)\mid X_2]$ as follows

$$\begin{array}{ccc}\hfill E[\phi (X_1,X_2)& \mid & X_1]=\frac{t_{\circ }}{m}{X}^2\xi \left(m\right)-\frac{1}{2m}{X}^3\xi \left(m\right)+\left(\frac{2e^{m{t}_{\circ }}-m^2{t}_{\circ }^2}{2m^3}\right)X\xi \left(m\right)\hfill \\ & & +\frac{1}{m^2}{X}^2-\left(\frac{(t_{\circ }-1)(2m^2-2m)-2(1-e^{m{t}_{\circ }})-m^2{t}_{\circ }^2}{2m^3(m+1)}\right),\hfill \end{array}$$

(12)

and

$$\begin{array}{ccc}\hfill E[\phi (X_1,X_2)& \mid & X_2]=\frac{t_{\circ }}{m}{\mu }_{\left(2\right)}{e}^{-mX}-\frac{1}{2m}{\mu }_{\left(3\right)}{e}^{-mX}+\left(\frac{2e^{m{t}_{\circ }}-m^2{t}_{\circ }^2}{2m^3}\right)\mu e^{-mX}+\frac{1}{m^2}{\mu }_{\left(2\right)}\hfill \\ & & -\left(\frac{m{t}_{\circ }+1}{m^3}\right)\mu -\left(\frac{(t_{\circ }-1)(2m^2-2m)-2(1-e^{m{t}_{\circ }})-m^2{t}_{\circ }^2}{2m^3(m+1)}\right).\hfill \end{array}$$

(13)

Upon using (11–13), (9) is obtained. □

4. Pitman’s Asymptotic Efficiency of $\widehat{\Delta }(\mathbf{m},{\mathbf{t}}_{\circ })$

Pitman’s asymptotic efficiency is a concept that measures the relative performance of two statistical tests in terms of their sample sizes. It is defined as the boundary of the proportion of minimum sample sizes required for each test to achieve a given level of significance and power, at which the alternative hypothesis approaches the null hypothesis. A higher Pitman’s efficiency means that the test requires fewer observations than another test to achieve the same accuracy. One possible application of the asymptotic Pitman efficiency is to compare different tests for different statistical problems and select the most efficient one. For example, one can use the asymptotic Pitman efficiency to compare different tests of equality of means, variances, or proportions between two populations. The asymptotic Pitman efficiency can also be used to compare different tests for the independence, correlation, or regression of two variables. Pitman efficiency can help the approach choose the best test for a given problem based on the minimum sample size required. Some potential limitations or assumptions of the asymptotic Pitman efficiency are: It is based on asymptotic results, which means that it may not be accurate for small or medium sample sizes. It also depends on the rate of convergence of test statistics for their finite distributions; sensitive to alternative hypothesis selection and level of significance. May not reflect performance of tests for alternatives or other levels; it does not take into account other factors that may influence test selection, such as robustness, simplicity, or interpretability. It also does not take into account the loss function or the cost of errors. Using the following probability models, the efficiency of the Pitman’s asymptotic efficiency (PAE) technique is assessed in this segment for the linear failure rate (LFR), Weibull, and Makeham distributions:

(i)

The linear failure rate distribution (LFRD):

$${\overline{F}}_1\left(u\right)=e^{-u-\frac{\theta }{2}{u}^2},u,\theta \ge 0.$$

(ii)

The Weibull distribution (WD):

$${\overline{F}}_2\left(u\right)=e^{-u^{\theta }},u\ge 0,\theta >0.$$

(iii)

The Makeham distribution (MD):

$${\overline{F}}_3\left(u\right)=e^{-u-\theta \left(u+e^{-u}-1\right)},u,\theta \ge 0.$$

Be aware that ${\overline{F}}_1\left(u\right)$ and ${\overline{F}}_3\left(u\right)$ reduce to exponential distributions for $\theta =0$, while ${\overline{F}}_2\left(u\right)$ reduces to an exponential distribution for $\theta =1$. The PAE is defined by

$$\mathrm{PAE}\left(\widehat{\Delta }(m,t_{\circ })\right)=\frac{1}{{\sigma }_{\circ }\left(m\right)}{\left|\frac{d}{d\theta }\delta (m,t_{\circ })\right|}_{{}_{\theta \to {\theta }_{\circ }}}.$$

At $m=5.2,t_{\circ }=0.01$, this leads to

$$\mathrm{PAE}[\widehat{\Delta }(m,t_{\circ }),\mathrm{Weibull}]=1.107,\mathrm{PAE}[\widehat{\Delta }(m,t_{\circ }),\mathrm{LFR}]=1.126,$$

and

$$\mathrm{PAE}[\widehat{\Delta }(m,t_{\circ }),\mathrm{Makeham}]=0.332,\mathrm{where}{\sigma }_{\circ }(m,t_{\circ })=0.291785.$$

In

Table 1. The PAE test is compared to some competitive distributions.

Tests	MD	LFRD	WD
Abdel-Aziz [28]	$0.184$	$0.535$	$0.223$
Kango [29]	$0.144$	$0.433$	$0.132$
El-Morshedy et al. [30]	$0.155$	$0.769$	$0.707$
Our test with $\Delta \left(5.2,0.01\right)$	$0.332$	$1.126$	$1.107$

, different tests based on probability distributions are compared with the PAE test that is offered.

It is noted that the other tests that were studied in [28,29,30] do not depend on $t_{\circ }$, while our proposed test depends on $t_{\circ }$ and, therefore, gave better results compared to the results mentioned in Table 1.

5. Monte Carlo Simulation

Monte Carlo simulation is a mathematical technique that uses random samples to estimate the possible outcomes of an uncertain event. It was invented by John von Neumann and Stanislaw Ulam during World War II. A Monte Carlo simulation works by predicting a set of outcomes based on an estimated range of values rather than fixed input values. It uses a probability distribution to generate random samples and then calculates the results for each sample. By repeating this process several times, it creates a distribution of possible outcomes that can be analyzed statistically. Some of the probability distributions that can be used in a Monte Carlo simulation are: the uniform distribution, all values have an equal probability of occurrence; Normal distribution, values are symmetrically distributed around a mean and a standard deviation; lognormal distribution, the values are positively skewed and have a logarithmic relationship with the mean and standard deviation; Exponential distribution, the values decrease exponentially and have a constant rate coefficient; binomial distribution, values are discrete and represent the number of successes in a fixed number of trials with a fixed probability of success; and Poisson distribution, the values are discrete and represent the number of events that occur in a fixed time interval or space with a fixed rate parameter. A Monte Carlo simulation can be used to estimate the probability of an event occurring by following these steps: select the event whose probability you want to estimate and select the random variables that affect it; determine the probability distribution of each random variable, and generate random samples from it; evaluate the event for each sample, and count how often it occurs; Divide the number of iterations by the total number of samples, and multiply by 100 to get the percentage; Repeat this process several times, and calculate the mean and standard deviation of the percentages. This will give you an estimate of the probability of the event and the uncertainty surrounding it.

5.1. Critical Points

A critical value in a statistic is a distribution point for a test statistic under the null hypothesis that identifies a set of values that invite a rejection of the null hypothesis. This group is called the critical region or rejection region. One-sided tests usually have one critical value and two-sided tests usually have two critical values. A critical value and a p-value are two different approaches to the same outcome: enabling you to support or reject the null hypothesis in a test. The difference is: a critical value is a fixed value that depends on the significance level and the type of test. You are comparing the test statistic to the critical value to make a decision. If the test statistic is more extreme than the critical value, you reject the null hypothesis. Whereas, p-value is a calculated value based on the test statistic and distribution under the null hypothesis. The probability value is compared to the level of importance to make a decision. If the p-value is less than or equal to the level of significance, you reject the null hypothesis. According to the statistical literature, there is no definitive answer to which approach is better: critical value or probability value. Both have advantages and disadvantages, depending on the situation and preference. Some factors to consider are: Critical values are easier to use when you have a table of values for common tests and significance levels. p-values are easier to use when you have a calculator or software that can calculate them for any test and any level of significance; Critical values are more intuitive and visual, as they show the boundary between rejecting and not rejecting the null hypothesis. p-values are more accurate and informative, because they show the exact probability of obtaining the test statistic or more extreme under the null hypothesis; Critical values are more conservative and less likely to make a type I error (rejecting the null hypothesis when it is true). 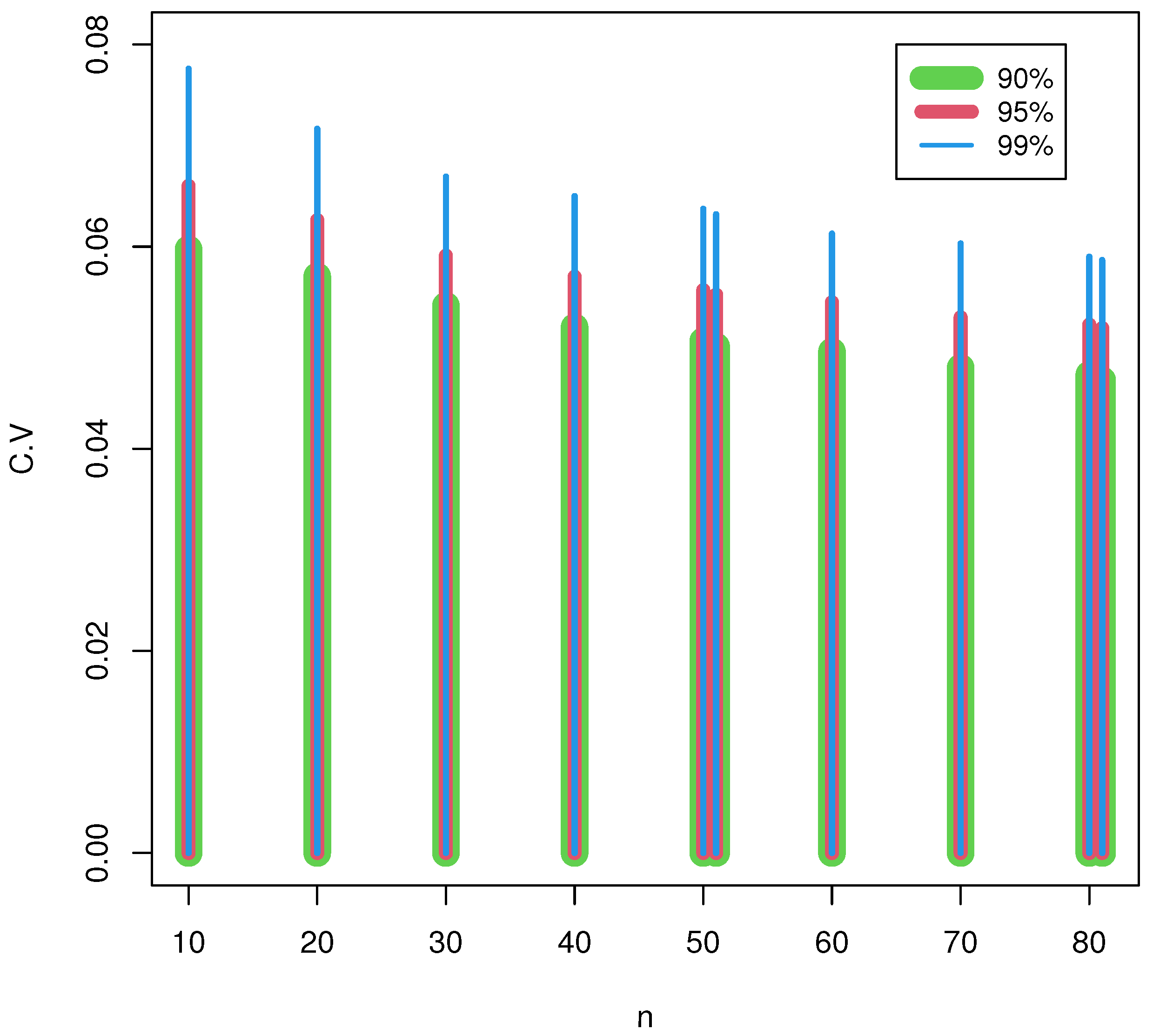p-values are more flexible and less likely to make a type II error (not rejecting the null hypothesis when it is false). This segment mimics the null Monte Carlo distribution’s critical points utilizing 10,000 size-generated samples with $n=5\left(5\right)50$. The upper percentile of ${\Delta }_n(5.2,0.01)$ for $90\%,95\%$, and $99\%$ was determined. The critical values rose with the rising confidence levels and fell with the rising sample sizes, as noted in

Table 2. The upper percentile of ${\Delta }_n(5.2,0.01)$.

n	Confidence Levels
	$\mathbf{90}\%$	$\mathbf{95}\%$	$\mathbf{99}\%$
5	$0.596320$	$1.382520$	$7.164070$
10	$0.184443$	$0.322756$	$0.986428$
15	$0.124193$	$0.190007$	$0.424041$
20	$0.092698$	$0.130198$	$0.275838$
25	$0.076891$	$0.104348$	$0.194681$
30	$0.067978$	$0.090650$	$0.156101$
35	$0.061213$	$0.081146$	$0.134843$
39	$0.055776$	$0.074077$	$0.123571$
40	$0.055441$	$0.072820$	$0.121345$
43	$0.053529$	$0.069936$	$0.115660$
45	$0.051139$	$0.067655$	$0.107019$
50	$0.049032$	$0.063827$	$0.099458$

and Figure 1, respectively.

5.2. Power Estimates of ${\Delta }_n(5.2,0.01)$ Test

Power estimates in Statistics are calculations that help you determine the minimum sample size for your study. Strength is the probability that the null hypothesis will be correctly rejected when it is false. It is based on four main components: effect size, difference size or relationship between variables of interest; significance level, probability of making a type I error (rejecting the null hypothesis when it is true); sample size and number of observations or study participants; and power, the probability of making a correct decision (rejecting the null hypothesis when it is false). If you know or have estimates for any three of these components, you can calculate the fourth using energy analysis. Energy analysis can help you design your study more efficiently and avoid wasting resources or missing out on important effects. A confidence interval is a range of values within which you would expect your estimate to fall if you retested, within a certain level of confidence. Statistical confidence is another way of describing probability. Power and confidence intervals are related in the following ways: Both power and confidence are probabilities dependent on the level of significance and sample size. A higher significance level or larger sample size will increase both power and confidence; Both strength and confidence are affected by impact size. A larger effect size will increase the strength and narrow the confidence interval; Both strength and confidence are inversely related. A higher power means a lower probability of making a type II error (not rejecting the null hypothesis when it is false), but also a higher probability of making a type I error (rejecting the null hypothesis when it is true). A higher confidence means a lower probability of making a type I error, but also a lower probability of making a type II error. Based on the 10,000 samples given in

Table 3. Power estimates of ${\Delta }_n(5.2,0.01)$.

n	$\mathit{\theta }$	LFRD	WD	GD
10	2 3 4	$0.5768$ $0.7960$ $0.9185$	$0.9614$ $0.9951$ $0.9992$	$0.9945$ $1.0000$ $1.0000$
20	2 3 4	$0.9764$ $0.9993$ $1.0000$	$1.0000$ $1.0000$ $1.0000$	$1.0000$ $1.0000$ $1.0000$
30	2 3 4	$0.9998$ $1.0000$ $1.0000$	$1.0000$ $1.0000$ $1.0000$	$1.0000$ $1.0000$ $1.0000$

, the power of the proposed test was estimated at the $(1-\alpha )\%$ confidence level, $\alpha =0.05$. Assume appropriate parameter values of $\theta$ for the LFRD, WD, and gamma distribution (GD), respectively, at $n=10,20$ and 30. Table 3 shows that the test we used ${\Delta }_n(5.2,0.01)$ has good power for all other options.

5.3. Testing against NBRULC$-t_{\circ }$ Class for Censored Data

A test statistic is suggested to compare $H_{\circ }$ versus $H_1$ using data that have been randomly right-censored. In a life-testing model or clinical study where patients may be lost (censored) before the completion of a study, such censored data are typically the only information available. Formally, this experimental scenario can be represented as follows. Assume that n objects are tested, with $X_1,X_2,...,X_n$ designating each object’s actual lifespan. Assuming a continuous life distribution F, we let $X_1,X_2,...,X_n$ be independently and identically distributed (i.i.d). Assume that, by a continuous life distribution G, $Y_1,Y_2,...,Y_n$ are i.i.d. Furthermore, consider the Xs and Ys to be independent variables. We observed the pairs in the randomly right-censored model $(Z_j,{\delta }_j),$$j=1,...,n,$ where $Z_j=min(X_i,Y_j)$ and

$${\delta }_j=\left\{\begin{array}{ccc}1,\hfill & \mathrm{if}\hfill & Z_j=X_j(j-\mathrm{th}\mathrm{observation}\mathrm{is}\mathrm{uncensored})\hfill \\ 0,\hfill & \mathrm{if}\hfill & Z_j=Y_j(j-\mathrm{th}\mathrm{observation}\mathrm{is}\mathrm{censored}).\hfill \end{array}\right.$$

Let $Z_{\left(0\right)}=0<Z_{\left(1\right)}<Z_{\left(2\right)}<.....<Z_{\left(n\right)}$ signify the ordered Zs and ${\delta }_{\left(j\right)}$ be ${\delta }_j$ comparable to $Z_{\left(j\right)}.$ Using the censored data ($Z_j,{\delta }_j$), $j=1,...,n.$ Kaplan and Meier [31] proposed the product limit estimator:

$${\overline{F}}_n\left(X\right)=\prod _{[j:Z(j)\le X]}{\{(n-j)/(n-j+1)\}}^{{\delta }_{\left(j\right)}},X\in [0,Z_{\left(n\right)}].$$

Now, for testing $H_{\circ }:{\Delta }_c(m,t_{\circ })=0$ against $H_1:{\Delta }_c(m,t_{\circ })>0,$ using the data that were right-censored randomly, we recommend the following test statistic:

$$\begin{array}{ccc}\hfill \Delta (m,t_{\circ })& =& \frac{t_{\circ }}{m}{\mu }_{\left(2\right)}\xi \left(m\right)-\frac{1}{2m}{\mu }_{\left(3\right)}\xi \left(m\right)+\left(\frac{2e^{m{t}_{\circ }}-m^2{t}_{\circ }^2}{2m^3}\right)\mu \xi \left(m\right)+\frac{1}{m^2}{\mu }_{\left(2\right)}\hfill \\ & & -\left(\frac{m{t}_{\circ }+1}{m^3}\right)\mu -\left(\frac{(t_{\circ }-1)(2m^2-2m)-2(1-e^{m{t}_{\circ }})-m^2{t}_{\circ }^2}{2m^3(m+1)}\right).\hfill \end{array}$$

where $\xi \left(m\right)={\int }_0^{\infty }{e}^{-mx}d{F}_n\left(x\right)$. It is possible to rewrite ${\Delta }_c(m,t_{\circ })$ for computing purposes as

$$\begin{array}{ccc}\hfill {\Delta }_c(m,t_{\circ })& =& \frac{t_{\circ }}{m}\tau \eta -\frac{1}{2m}\Phi \eta +\left(\frac{2e^{m{t}_{\circ }}-m^2{t}_{\circ }^2}{2m^3}\right)\Omega \eta +\frac{1}{m^2}\tau \hfill \\ & & -\left(\frac{m{t}_{\circ }+1}{m^3}\right)\Omega -\left(\frac{(t_{\circ }-1)(2m^2-2m)-2(1-e^{m{t}_{\circ }})-m^2{t}_{\circ }^2}{2m^3(m+1)}\right),\hfill \end{array}$$

where

$$\begin{array}{ccc}\hfill \Omega & =& \sum _{s=1}^n\left[\prod _{m=1}^{s-1}{C}_m^{\delta \left(m\right)}\left(Z_{\left(s\right)}-Z_{(s-1)}\right)\right],\hfill \\ \hfill \eta & =& \sum _{j=1}^n{e}^{-m{Z}_{\left(j\right)}}[\prod _{p=1}^{j-2}{C}_p^{\delta \left(p\right)}-\prod _{p=1}^{j-1}{C}_p^{\delta \left(p\right)}],\hfill \\ \hfill \tau & =& 2\sum _{i=1}^n\left[\prod _{v=1}^{i-1}{Z}_{\left(i\right)}{C}_v^{\delta \left(v\right)}\left(Z_{\left(i\right)}-Z_{(i-1)}\right)\right],\hfill \\ \hfill \Phi & =& 3\sum _{i=1}^n\left[\prod _{v=1}^{i-1}{Z}_{\left(i\right)}^2{C}_v^{\delta \left(v\right)}\left(Z_{\left(i\right)}-Z_{(i-1)}\right)\right],\hfill \end{array}$$

and

$$d{F}_n\left(Z_j\right)={\overline{F}}_n\left(Z_{j-1}\right)-{\overline{F}}_n\left(Z_j\right),c_s=\left[n-s\right]{\left[n-s+1\right]}^{-1}.$$

To make the test invariant, let

$${\widehat{\Delta }}_c(m,t_{\circ })=\frac{{\Delta }_c(m,t_{\circ })}{{\overline{Z}}^4},\mathrm{where}\overline{Z}=\sum _{i=1}^n\frac{Z_{\left(i\right)}}{n}.$$

The critical percentiles of the ${\widehat{\Delta }}_c$ test for sample sizes $n=10\left(10\right)80,51,81$ are shown in

Table 4. The upper percentile of ${\widehat{\Delta }}_c$ at $m=5.2,t_{\circ }=0.01$.

n	$90\%$	$95\%$	$99\%$
10	$0.059725$	$0.066002$	$0.077595$
11	$0.059405$	$0.065565$	$0.076262$
20	$0.057046$	$0.062618$	$0.071659$
21	$0.056410$	$0.061686$	$0.070329$
30	$0.054140$	$0.059101$	$0.066920$
40	$0.052021$	$0.057016$	$0.064999$
50	$0.050652$	$0.055694$	$0.063739$
51	$0.050105$	$0.055233$	$0.063203$
60	$0.049608$	$0.054491$	$0.061288$
70	$0.048010$	$0.052997$	$0.060309$
80	$0.047323$	$0.052271$	$0.059003$
81	$0.046768$	$0.051935$	$0.058674$

and Figure 2. Using the Mathematica 12 program, the common exponential distribution was used to obtain the critical values at $m=5.2,t_{\circ }=0.01$ and 10,000 replications for the null Monte Carlo distribution.

Following Figure 2 and Table 4, the critical values rose with the rises in the confidence level and fell with the rising sample sizes, respectively.

5.4. Power Estimates of Test ${\Delta }_c(m,t_{\circ })$

According to the three different Weibull, LFR, and gamma distributions based on 10,000 samples, the power of our test was evaluated at a significance level $\alpha =0.05$ with occasion parameter values of $\theta$ at $n=10,20$ and 30. For all other options,

Table 5. Power estimates of ${\Delta }_c(5.2,0.01)$.

n	$\mathit{\theta }$	WD	LFRD	GD
10	2 3 4	$0.9596$ $0.9991$ $1.0000$	$0.9871$ $0.9977$ $0.9995$	$0.9992$ $1.0000$ $1.0000$
20	2 3 4	$0.9228$ $0.9952$ $0.9999$	$0.9763$ $0.9942$ $0.9982$	$0.9997$ $1.0000$ $1.0000$
30	2 3 4	$0.9055$ $0.9947$ $0.9999$	$0.9738$ $0.9925$ $0.9987$	$0.9996$ $0.9999$ $1.0000$

demonstrates that the power estimates of our test ${\Delta }_c(5.2,0.01)$ were good.

6. Applications to Real Data: Censored and Uncensored Observations

Controlled (censored) data is only partially known data, which means that some information is missing or incomplete. Uncensored data is fully known data, which means that all information is available and complete. Controlled data can present challenges for statistical analysis, as it requires special methods and assumptions to deal with missing or incomplete information. Unsupervised (Uncensored) data is easier to analyze, because it does not have these issues.

6.1. Non-Censored Data

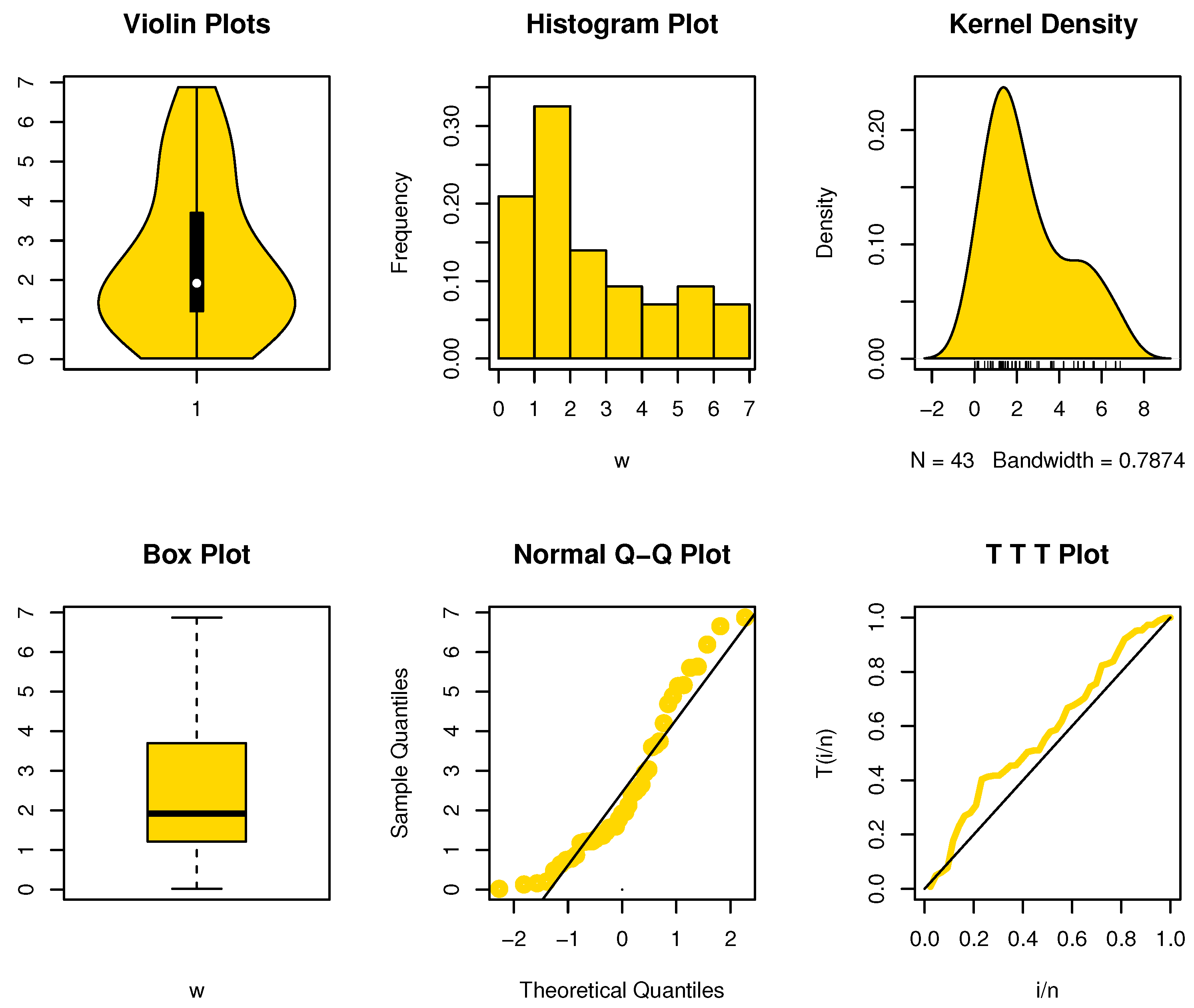
6.1.1. Dataset I: Aircraft’s Air Conditioning

The number of operational days between successive failures of an aircraft’s air conditioning system is a classic real dataset that Keating et al. [32] examined. This information is documented.

3.750	0.417	2.500	7.750	2.542	2.042	0.583
1.000	2.333	0.833	3.292	3.500	1.833	2.458
1.208	4.917	1.042	6.500	12.917	3.167	1.083
1.833	0.958	2.583	5.417	8.667	2.917	4.208
8.667

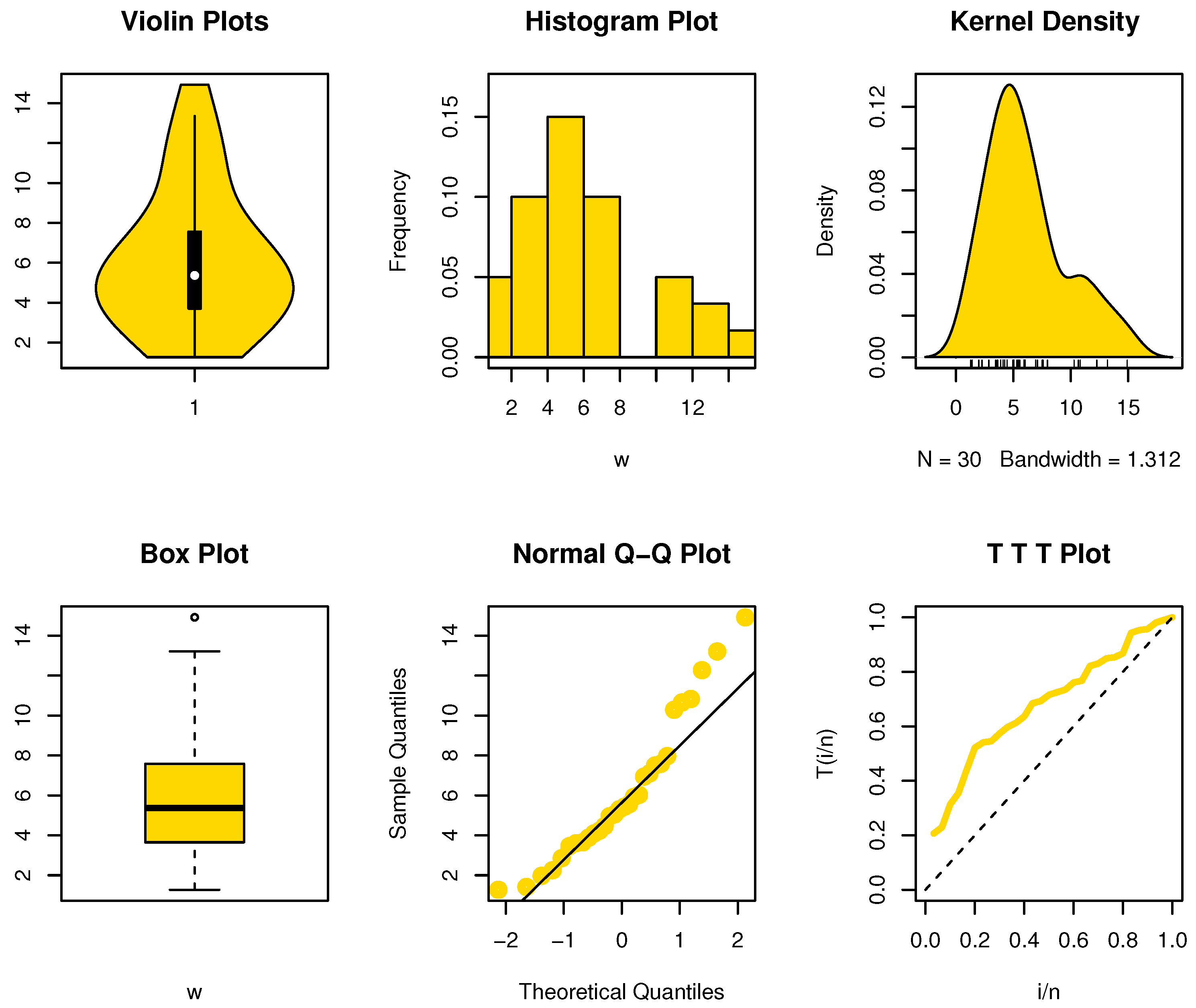
The shape of the data can be seen in Figure 3, and it is noted that there is an extreme observation and the kernel density is right-skewed. The $\Delta (5.2,0.01)=0.0023287$ was obtain, and this number is less than the value in Table 2’s tabulated value. The significance level of $\alpha =0.05$ makes it clear. The NBRULC$-t_{\circ }$ attribute is not met by this type of data; hence, this is true.

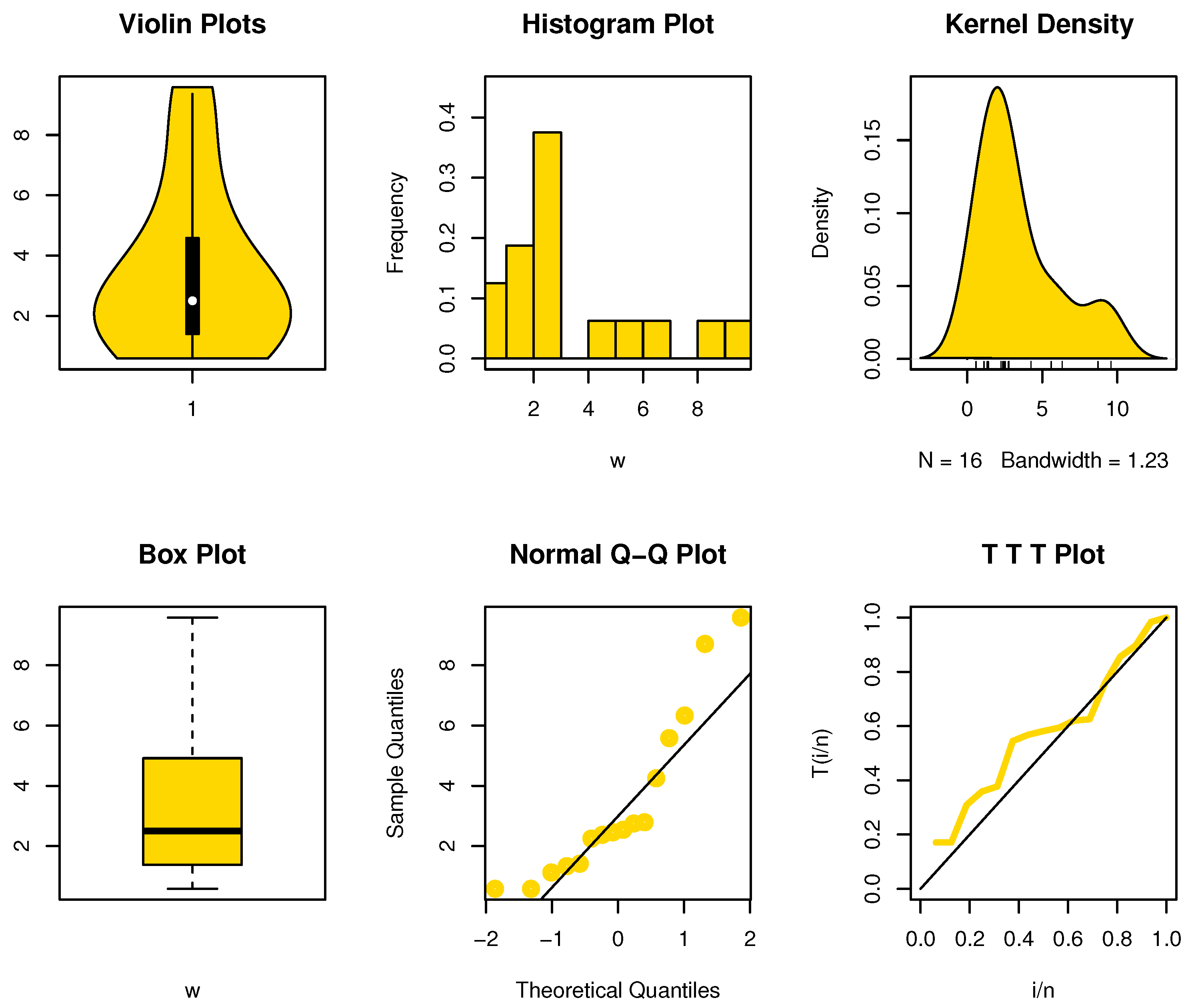
6.1.2. Dataset II: Air Conditioning in a Boeing 720 Aircraft

The dataset below shows the 16 operational days between consecutive air conditioning system failures in a Boeing 720 aircraft (see Edgeman et al. [33]).

4.25	8.708	0.583	2.375	2.25	1.333	2.792	2.458
5.583	6.333	1.125	0.583	9.583	2.75	2.542	1.417

Visualization plots of the data can be listed in Figure 4, and it was observed that there is no extreme observation and that the intensity of the kernel tends to the right. When $\Delta (5.2,0.01)=0.0023405$ was obtained, it is smaller than the relevant critical value in Table 2, and the null hypotheses, which demonstrate that the dataset has an exponential feature, are accepted.

6.1.3. Dataset III: Leukemia

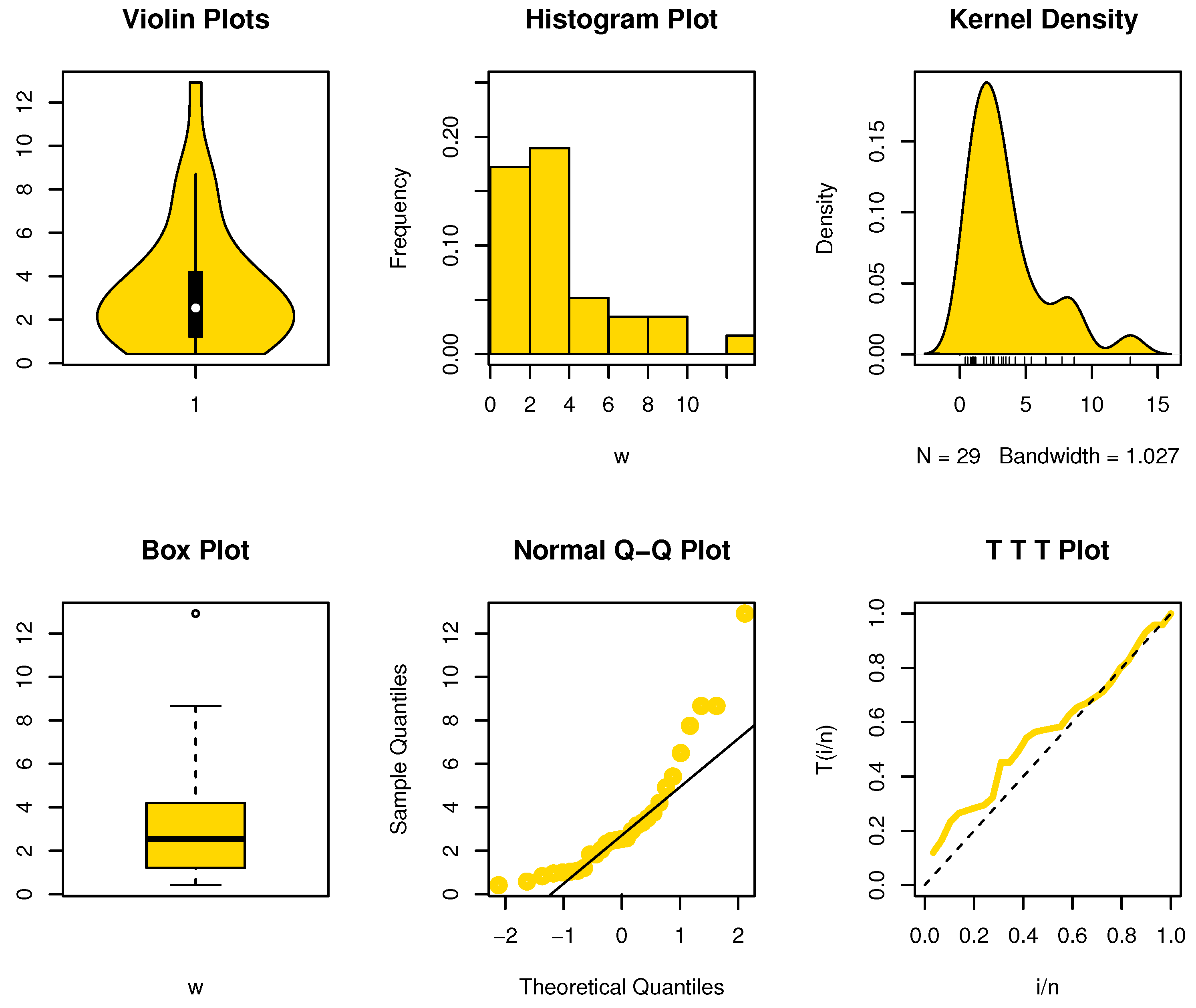
Consider the dataset below, which was compiled by Kotz and Johnson [34] and shows the survival periods (in years) of 43 patients who had a specific type of leukemia after their diagnosis.

0.019	0.129	0.159	0.203	0.485	0.636	0.748	0.781	0.869	1.175
1.206	1.219	1.219	1.282	1.356	1.362	1.458	1.564	1.586	1.592
1.781	1.923	1.959	2.134	2.413	2.466	2.548	2.652	2.951	3.038
3.6	3.655	3.754	4.203	4.690	4.888	5.143	5.167	5.603	5.633
6.192	6.655	6.874

The data representation plots are reported in Figure 5, and it was found that there are no extreme observations and the nucleation intensity tends to the right. We obtained a value of $\Delta (5.2,0.01)=0.0066037$, which is below the crucial value in Table 2. The null hypotheses were then accepted, proving that the dataset possesses exponential properties.

6.1.4. Dataset IV: COVID-19 in Italy

This data represents the COVID-19 mortality rate in Italy from 27 February to 27 April 2020 (see Almongy et al. [35]). The data are

$4.571$	$7.201$	$3.606$	$8.479$	$11.410$	$8.961$	$10.919$	$10.908$	$6.503$
$18.474$	$11.010$	$17.337$	$16.561$	$13.226$	$15.137$	$8.697$	$15.787$	$13.333$
$11.822$	$14.242$	$11.273$	$14.330$	$16.046$	$11.950$	$10.282$	$11.775$	$10.138$
$9.037$	$12.396$	$10.644$	$8.646$	$8.905$	$8.906$	$7.407$	$7.445$	$7.214$
$6.194$	$4.640$	$5.452$	$5.073$	$4.416$	$4.859$	$4.408$	$4.639$	$3.148$
$4.040$	$4.253$	$4.011$	$3.564$	$3.827$	$3.134$	$2.780$	$2.881$	$3.341$
$2.686$	$2.814$	$2.508$	$2.450$	$1.518$

Data representation plots are presented in Figure 6, and it is clear that there are no extreme observations and the nucleation intensity tends to the right. When $\Delta (5.2,0.01)=0.000377$ was obtained, it is smaller than the relevant critical value in Table 2, and the null hypotheses, which demonstrate that the dataset has an exponential feature, are accepted.

6.1.5. Dataset V: COVID-19 in the Netherlands

These data represent the COVID-19 mortality rate (see EL-Sagheer et al. [36]). The data are

$14.918$	$10.656$	$12.274$	$10.289$	$10.832$	$7.099$	$5.928$	$13.211$
$7.968$	$7.584$	$5.555$	$6.027$	$4.097$	$3.611$	$4.960$	$7.498$
$6.940$	$5.307$	$5.048$	$2.857$	$2.254$	$5.431$	$4.462$	$3.883$
$3.461$	$3.647$	$1.974$	$1.273$	$1.416$	$4.235$

The data representation plots are sketched in Figure 7, and it was found that there is an extreme observation and the intensity of nucleation tends to the right. At the significance level $\alpha =0.05,$$\Delta (5.2,0.01)=0.000661$ is smaller than the corresponding critical value in Table 2. This indicates that the type of data does not match the NBRULC$-t_{\circ }$ attribute.

6.2. Censored Data

6.2.1. Dataset VI: Myelogenous Blood Cancer

According to the International Bone Marrow Transplant Registry, 101 patients with advanced acute myelogenous blood cancer are represented by the following datasets (see Ghitany and Al-Awadhi [37]). The data can be listed as:

0.030	0.493	0.855	1.184	1.283	1.480	1.776	2.138	2.500
2.763	2.993	3.224	3.421	4.178	4.441+	5.691	5.855+	6.941+
6.941	7.993+	8.882	8.882	9.145+	11.480	11.513	12.105+	12.796
12.993+	13.849+	16.612+	17.138+	20.066	20.329+	22.368+	26.776+	28.717+
28.717+	32.928+	33.783+	34.221+	34.770+	39.539+	41.118+	45.033+	46.053+
46.941+	48.289+	57.401+	58.322+	60.625+

Consider the entire set of survival data (both censored and uncensored). At a $95\%$ confidence level, ${\Delta }_c(5.2,0.01)=-3.83989\times {10}^{27}$ is less than the critical value shown in Table 4. Then, we agree with $H_{\circ }$, which asserts that the dataset has exponential features. The leukemia-free survival times for the 51 autologous transplant patients are (in months)

0.658	0.822	1.414	2.500	3.322	3.816	4.737	4.836+	4.934
5.033	5.757	5.855	5.987	6.151	6.217	6.447+	8.651	8.717
9.441+	10.329	11.480	12.007	12.007+	12.237	12.401+	13.059+	14.474+
15.000+	15.461	15.757	16.480	16.711	17.204+	17.237	17.303+	17.664+
18.092	18.092+	18.750+	20.625+	23.158	27.730+	31.184+	32.434+	35.921+
42.237+	44.638+	46.480+	47.467+	48.322+	56.086

It was discovered that ${\Delta }_c(5.2,0.01)=-3.23764\times {10}^{38}$, smaller than the critical value of Table 4, was obtained. At the significance level $\alpha =0.05$, it is obvious. This suggests that the data type does not align with the NBRULC$-t_{\circ }$ attribute.

6.2.2. Dataset VII: Melanoma

Consider the data in Susarla and Van Ryzin [38]. These data show 46 melanoma patients’ survival rates. Of them, 35 correspond to entire lifetimes (non-censored data). The censored observations are listed in order:

13	14	19	19	20	21	23	23	25	26
26	27	27	31	32	34	34	37	38	38
40	46	50	53	54	57	58	59	60	65
65	66	70	85	90	98	102	103	110	118
124	130	136	138	141	234

The censored observations are ordered as follows:

16	21	44	50	55	67	73	76	80	81
86	93	100	108	114	120	124	125	129	130
132	134	140	147	148	151	152	152	158	181
190	193	194	213	215

If we consider the entire set of survival data (both censored and uncensored), we found that the critical value in Table 4 is more than our result, which is ${\Delta }_c(5.2,0.01)=-2.78737\times {10}^{39}$. The data’s exponential qualities are thus clear to us.

7. Concluding Remarks

The emphasis on reliability has increased during the past few years among manufacturing companies, the government, and civilian groups. Attempts are being made by agencies to purchase systems that have higher reliability and require less frequent maintenance as a result of current worries regarding government spending. Buying products that are more dependable and require less upkeep is our top priority as consumers. Quality that holds up over time is reliable. Quality is related to craftsmanship and manufacture; thus, if something does not work or fails quickly after it is acquired, one would consider its quality to be bad. Poor reliability would, however, be present if, over time, product parts started to fail sooner than planned. Thus, the difference between quality and reliability is related to the passage of time and, more specifically, the product lifetime. The new life distribution class known as NBRULC$-t_{\circ }$ is now a part of family of life distribution renewal classes. Convolution, mixture, and homogeneous shock models, among other reliability approaches, have all been used to create studies of closure qualities. After comparing the offered class test to some rival tests using the Weibull, LFR, gamma, and Makeham models, it was found that the suggested class performed well. A Monte Carlo simulation was run to evaluate the performance of NBRULC$-t_{\circ }$. It was discovered that, as the confidence levels climb and the sample sizes rise, the critical values also tend to rise. Furthermore, the power estimates of the suggested test were accurate based on the simulation results. To demonstrate the viability of the suggested NBRULC$-t_{\circ }$ class, certain applications in the engineering and medical (censored and uncensored scenarios) domains were examined and addressed. Through the results, we concluded the following:

• This class of life distribution was more efficient than the rest of the other classes that were compared with it, and its testing strength was strong.
• Table 1 revealed that, in all proposed distributions, our test was more effective than other tests, as predicted by the PAEs.