Graphs with Strong Proper Connection Numbers and Large Cliques

Abstract

In this paper, we mainly investigate graphs with a small (strong) proper connection number and a large clique number. First, we discuss the (strong) proper connection number of a graph G of order n and $\omega \left(G\right)=n-i$ for $1⩽i⩽3$. Next, we investigate the rainbow connection number of a graph G of order n, $diam\left(G\right)\ge 3$ and $\omega \left(G\right)=n-i$ for $2⩽i⩽3$.

1. Introduction

We only consider graphs that are undirected, simple, finite, and connected in this paper. For terminology and notation that are not defined here, we refer to [1].

In 2008, Chartrand et al. [2] introduced the concept of rainbow connection. For an edge-colored graph G, if each pair of vertices is connected by a rainbow path, where its edges are assigned different colors, then G is said to be rainbow-connected. An edge-coloring that makes G rainbow-connected is said to be a rainbow coloring of G. The rainbow connection number of G, denoted by $rc\left(G\right)$, is the smallest number of colors that are needed to make G rainbow-connected. Obviously, $rc\left(G\right)=1$ if and only if G is complete, and $rc\left(G\right)\ge diam\left(G\right)$. As a natural generalization of the rainbow connection number, the concept of the vertex rainbow connection number was presented by Krivelevich et al. [3], and the concept of the total rainbow connection number was introduced by Liu et al. [4]. There are abundant research results on this topic. In [5], Schiermeyer proved that a connected graph G with n vertices has $rc\left(G\right)<\frac{4n}{\delta \left(G\right)+1}+4$. Huang et al. [6] provided upper bounds of the rainbow connection number of outerplanar graphs with small diameters. In [7], Li et al. studied the vertex rainbow connection numbers of some graph operations. Ma et al. [8] investigated the total rainbow connection numbers of some special graphs. The reader should also consult [9] for a survey and [10] for a monograph.

Inspired by the concept of rainbow connection, Borozan et al. [11] proposed the concept of proper connection, and Andrews et al. [12] presented the concept of strong proper connection. A path is called a proper path in an edge-colored graph if its adjacent edges are assigned distinct colors. An edge-colored graph G is said to be properly connected if any two vertices are connected by a proper path, and G is said to be strongly properly connected if every pair of vertices is connected by a proper geodesic. An edge-coloring $\theta$ of graph G is called a proper-path coloring if it makes G properly connected, and $\theta$ is called a strong proper coloring if it makes G strongly properly connected. The proper connection number of G, denoted by $pc\left(G\right)$, is the smallest number of colors that are needed to make G properly connected. The strong proper connection number of G, denoted by $spc\left(G\right)$, is the smallest number of colors that are needed to make G strongly properly connected. From these definitions, it is easy to establish that $pc\left(G\right)=spc\left(G\right)=1$ if and only if G is complete. In [13,14], Huang et al. presented an upper bound for the proper connection number of a graph in terms of the bridge-block tree of the graph and investigated the proper connection number of the complement of a graph. Li et al. [15] used dominating sets to study the proper connection number of a graph. Ma and Zhang [16] characterized all connected graphs of size m with (strong) proper connection number $m-4$. For more details, we refer the reader to a survey [17].

Some results regarding the (vertex) rainbow connection numbers of graphs with a large clique number are available; see [18,19]. These results motivated us to consider the (strong) proper connection numbers of graphs with a large clique number. In this paper, we mainly discuss the (strong) proper connection number of a graph G of order n and $\omega \left(G\right)=n-i$ for $1⩽i⩽3$. Moreover, we also investigate the rainbow connection number of a graph G of order n, $diam\left(G\right)\ge 3$ and $\omega \left(G\right)=n-i$ for $2⩽i⩽3$.

2. (Strong) Proper Connection and Clique Number

In this section, we investigate graphs with a small (strong) proper connection number and a large clique number. We first introduce some definitions that will be used later.

A Hamiltonian path in a graph G is a path containing every vertex of G. A graph with a Hamiltonian path is called a traceable graph. Recall that a clique of a graph is a set of mutually adjacent vertices, and that the maximum size of a clique of graph G, i.e., the clique number of G, is denoted $\omega \left(G\right)$. For a connected graph G, we say Q is a subgraph of G which induces a maximum clique and $V\left(F\right)=V\left(G\right)\backslash V\left(Q\right)$. We say $N_Q\left(u\right)$ is the set of neighbors of u in Q and $d_Q\left(u\right)=\left|N_Q\left(u\right)\right|$. Additionally, we say $E\left[V\right(F),V(Q\left)\right]$ is the set of edges of G between vertices of $V\left(F\right)$ and vertices of $V\left(Q\right)$. Next, we present the following three useful propositions.

Proposition 1 ([12]).

Let G be a non-complete graph. If G is traceable, then $pc\left(G\right)=2$.

Proposition 2 ([12]).

For a non-trivial connected graph G that contains a bridge, if b is the maximum number of bridges incident with a vertex in G, then $spc\left(G\right)\ge pc\left(G\right)\ge b$.

Proposition 3 ([18]).

Let G be a connected graph of order n and size m. If $\left(\genfrac{}{}{0pt}{}{n-1}{2}\right)+1\le m\le \left(\genfrac{}{}{0pt}{}{n}{2}\right)-1$, then $rc\left(G\right)=2$.

As an immediate consequence of Proposition 3, we have the following Lemma.

Lemma 1. 

Let G be a connected graph of order n and size m. If $\left(\genfrac{}{}{0pt}{}{n-1}{2}\right)+1\le m\le \left(\genfrac{}{}{0pt}{}{n}{2}\right)-1$, then $pc\left(G\right)=spc\left(G\right)=2$.

Theorem 1. 

Let G be a connected graph of order n. If $\omega \left(G\right)=n+1-i$ for $i\in \{1,2\}$, then $pc\left(G\right)=spc\left(G\right)=i$.

Proof. 

If $i=1$, then $\omega \left(G\right)=n$, which implies that G is a complete graph. Thus, $pc\left(G\right)=spc\left(G\right)=1$. If $i=2$, then $\omega \left(G\right)=n-1$. Since G is connected, we obtain $\left|E\left(G\right)\right|\ge \left(\genfrac{}{}{0pt}{}{n-1}{2}\right)+1$, and so $\left(\genfrac{}{}{0pt}{}{n-1}{2}\right)+1\le \left|E\left(G\right)\right|\le \left(\genfrac{}{}{0pt}{}{n}{2}\right)-1$. Hence, $pc\left(G\right)=spc\left(G\right)=2$ by Lemma 1. □

Theorem 2. 

Let G be a connected graph of order $n\ge 4$ and $\omega \left(G\right)=n-2$. Let Q be a maximum clique of G and $V\left(G\right)\backslash V\left(Q\right)=\{u_1,u_2\}$. Then, either $pc\left(G\right)=spc\left(G\right)=2$ or one of the following holds:

(i) 

$4\le n\le 5$, $G[V\left(G\right)\backslash V\left(Q\right)]\cong 2K_1$ and $N_Q\left(u_1\right)=N_Q\left(u_2\right)=\left\{v\right\}$.

(ii) 

$n\ge 6$, $G[V\left(G\right)\backslash V\left(Q\right)]\cong 2K_1$ and $N_Q\left(u_1\right)=N_Q\left(u_2\right)=\left\{v\right\}$.

Moreover, we have $pc\left(G\right)=spc\left(G\right)=3$ for (i), $pc\left(G\right)=2$, and $spc\left(G\right)=3$ for (ii).

Proof. 

Let $F=G\left[V\right(G)\backslash V(Q\left)\right]$ and let $\theta$ be an edge-coloring of G. We prove this theorem by analyzing the structure of F.

Case 1. $F\cong K_2$. Since G is connected, it follows that $max\{d_Q\left(u_1\right),d_Q\left(u_2\right)\}\ge 1$. Note that G is traceable, and we have $pc\left(G\right)=2$ by Proposition 1. The following edge-coloring $\theta$ with two colors makes G strongly properly connected: color $u_1{u}_2$ and all edges of $E\left(Q\right)$ with 1, and color all edges of $E\left[V\right(F),V(Q\left)\right]$ with 2. Thus, $spc\left(G\right)=2$.

Case 2. $F\cong 2K_1$. Since G is connected, it follows that $min\{d_Q\left(u_1\right),d_Q\left(u_2\right)\}\ge 1$. Assume that $N_Q\left(u_1\right)\cap N_Q\left(u_2\right)=Ø$. Observe that G is traceable, and we have $pc\left(G\right)=2$ by Proposition 1. Assign an edge-coloring $\theta$ with two colors to G as follows: color all edges of $E\left(Q\right)$ with 1 and all edges of $E\left[V\right(F),V(Q\left)\right]$ with 2. It is clear that G is strongly properly connected with the above edge-coloring. Hence, $spc\left(G\right)=2$.

Assume that $N_Q\left(u_1\right)\cap N_Q\left(u_2\right)\ne Ø$ and $d_Q\left(u_1\right)=d_Q\left(u_2\right)=1$. Without a loss of generality, let $v\in N_Q\left(u_1\right)\cap N_Q\left(u_2\right)$. If $n=4$, then $G\cong K_{1,3}$. Hence, $pc\left(G\right)=spc\left(G\right)=3$. If $n=5$, then $G\cong G_1$, where $G_1$ is obtained by adding two pendant edges to a vertex of $K_3$. Thus, $pc\left(G\right)=spc\left(G\right)=3$. Now we consider $n\ge 6$. Let $V\left(Q\right)=\{v,w_1,w_2,\dots ,w_{n-3}\}$. Define an edge-coloring $\theta$ of G with two colors as follows: $\theta \left(u_{1}v\right)=\theta \left(w_1{w}_{n-3}\right)=1$; $\theta \left(u_{2}v\right)=\theta \left(v{w}_{n-4}\right)=2$; color the sequence $v{w}_1{w}_2\cdots w_{n-3}v$ alternately with 1 and 2 starting with $\theta \left(v{w}_1\right)=1$; and color the remaining edges arbitrarily with 1 and 2. We can check that G is properly connected with the above edge-coloring, and so $pc\left(G\right)=2$. If $\theta$ is a strong proper coloring of G, then $\theta \left(u_{1}v\right)\ne \theta \left(u_{2}v\right)\ne \theta \left(v{w}_1\right)$, and thus $spc\left(G\right)\ge 3$. On the other hand, we define a strong proper coloring ${\theta }^{\prime }$ of G with three colors as follows: ${\theta }^{\prime }\left(u_{1}v\right)=1$, ${\theta }^{\prime }\left(u_{2}v\right)=2$, and color all edges of $E\left(Q\right)$ with 3. Thus, $spc\left(G\right)=3$.

Assume that $N_Q\left(u_1\right)\cap N_Q\left(u_2\right)\ne Ø$ and $max\{d_Q\left(u_1\right),d_Q\left(u_2\right)\}\ge 2$. Without a loss of generality, let $v\in N_Q\left(u_1\right)\cap N_Q\left(u_2\right)$ and $d_Q\left(u_1\right)\ge 2$. Observe that G is traceable, and we obtain $pc\left(G\right)=2$ by Proposition 1. Assign an edge-coloring $\theta$ with two colors to G as follows: $\theta \left(u_{1}v\right)=1$; $\theta \left(u_{2}v\right)=\theta \left(u_{1}w\right)=2$ for any $w\in N_Q\left(u_1\right)\backslash \left\{v\right\}$; and color the remaining edges with 1. It is clear that $\theta$ is a strong proper coloring of G. Hence, $spc\left(G\right)=2$. □

Theorem 3. 

Let G be a connected graph of order $n\ge 5$, $diam\left(G\right)=2$, and $\omega \left(G\right)=n-3$. Let Q be a maximum clique of G and $V\left(G\right)\backslash V\left(Q\right)=\{u_1,u_2,u_3\}$. Then, either $pc\left(G\right)=spc\left(G\right)=2$ or one of the following holds:

(i) 

$G[V\left(G\right)\backslash V\left(Q\right)]\cong P_3$, where $u_1{u}_2,u_2{u}_3\in E\left(G\right)$, $d_Q\left(u_2\right)=0$, $min\{d_Q\left(u_1\right),d_Q\left(u_3\right)\}=1$, $N_Q\left(u_1\right)\cup N_Q\left(u_3\right)=V\left(Q\right)$ and $N_Q\left(u_1\right)\cap N_Q\left(u_3\right)=Ø$.

(ii) 

$n=6$, $G[V\left(G\right)\backslash V\left(Q\right)]\cong K_2+K_1$, where $u_1{u}_2\in E\left(G\right)$, and $N_Q\left(u_1\right)=N_Q\left(u_2\right)=N_Q\left(u_3\right)=\left\{v\right\}$.

(iii) 

$n\ge 7$, $G[V\left(G\right)\backslash V\left(Q\right)]\cong K_2+K_1$, where $u_1{u}_2\in E\left(G\right)$, and $N_Q\left(u_1\right)=N_Q\left(u_2\right)=N_Q\left(u_3\right)=\left\{v\right\}$.

(iv) 

$G[V\left(G\right)\backslash V\left(Q\right)]\cong K_2+K_1$, where $u_1{u}_2\in E\left(G\right)$, $N_Q\left(u_1\right)\cap N_Q\left(u_2\right)\cap N_Q\left(u_3\right)=\left\{v\right\}$, $min\{d_Q\left(u_1\right),d_Q\left(u_2\right)\}=d_Q\left(u_3\right)=1$ and $d_Q\left(u_1\right)+d_Q\left(u_2\right)\ge 3$.

(v) 

$G[V\left(G\right)\backslash V\left(Q\right)]\cong K_2+K_1$, where $u_1{u}_2\in E\left(G\right)$, $N_Q\left(u_1\right)\cap N_Q\left(u_3\right)\ne Ø$, $N_Q\left(u_2\right)\cap N_Q\left(u_3\right)\ne Ø$, $d_Q\left(u_1\right)=d_Q\left(u_2\right)=1$, $d_Q\left(u_3\right)=2$ and $N_Q\left(u_1\right)\cap N_Q\left(u_2\right)=Ø$.

(vi) 

$n=5$, $G[V\left(G\right)\backslash V\left(Q\right)]\cong 3K_1$ and $N_Q\left(u_1\right)=N_Q\left(u_2\right)=N_Q\left(u_3\right)=\left\{v\right\}$.

(vii) 

$n\ge 6$, $G[V\left(G\right)\backslash V\left(Q\right)]\cong 3K_1$ and $N_Q\left(u_1\right)=N_Q\left(u_2\right)=N_Q\left(u_3\right)=\left\{v\right\}$.

(viii) 

$G[V\left(G\right)\backslash V\left(Q\right)]\cong 3K_1$, $|(N_Q\left(u_1\right)\cap N_Q\left(u_2\right))\cup (N_Q\left(u_1\right)\cap N_Q\left(u_3\right))\cup (N_Q\left(u_2\right)\cap N_Q$

$\left(u_3\right)\left)\right| =1$, $N_Q\left(u_1\right)\cap N_Q\left(u_2\right)\cap N_Q\left(u_3\right)\ne Ø$ and $d_Q\left(u_1\right)+d_Q\left(u_2\right)+d_Q\left(u_3\right)\ge 4$.

(ix) 

$G[V\left(G\right)\backslash V\left(Q\right)]\cong 3K_1$, $|(N_Q\left(u_1\right)\cap N_Q\left(u_2\right))\cup (N_Q\left(u_1\right)\cap N_Q\left(u_3\right))\cup (N_Q\left(u_2\right)\cap N_Q$

$\left(u_3\right)\left)\right| =2$, $N_Q\left(u_1\right)\cap N_Q\left(u_2\right)\cap N_Q\left(u_3\right)\ne Ø$ and $d_Q\left(u_1\right)+d_Q\left(u_2\right)+d_Q\left(u_3\right)=5$.

Moreover, we have $pc\left(G\right)=2$ and $spc\left(G\right)=3$ for (i), (iii), (iv), (v), (viii), and (ix); $pc\left(G\right)=spc\left(G\right)=3$ for (ii); $pc\left(G\right)=spc\left(G\right)=4$ for (vi); and $pc\left(G\right)=3$ and $spc\left(G\right)=4$ for (vii).

Proof. 

Let $F=G\left[V\right(G)\backslash V(Q\left)\right]$ and let $\theta$ be an edge-coloring of G. We prove this theorem by analyzing the structure of F.

Case 1. $F\cong K_3$. Observe that G is traceable, and so $pc\left(G\right)=2$ by Proposition 1. The following edge-coloring $\theta$ with two colors induces a strong proper coloring of G: color all edges of $E\left(F\right)$ and $E\left(Q\right)$ with 1, and color all edges of $E\left[V\right(F),V(Q\left)\right]$ with 2. Thus, $spc\left(G\right)=2$.

Case 2. $F\cong P_3$, where $u_1{u}_2,u_2{u}_3\in E\left(G\right)$. Assume that $min\{d_Q\left(u_1\right),d_Q\left(u_2\right),d_Q\left(u_3\right)\}\ge 1$. Note that G is traceable, and we have $pc\left(G\right)=2$ by Proposition 1. Assign a strong proper coloring $\theta$ with two colors to G as follows: $\theta \left(u_1{u}_2\right)=1$; $\theta \left(u_2{u}_3\right)=2$; and color all edges of $E\left(Q\right)$ with 1 and all edges of $E\left[V\right(F),V(Q\left)\right]$ with 2. Hence, $spc\left(G\right)=2$.

Assume that $min\{d_Q\left(u_1\right),d_Q\left(u_2\right),d_Q\left(u_3\right)\}=0$. Since $diam\left(G\right)=2$, it follows that $d_Q\left(u_1\right)\ge 1$, $d_Q\left(u_2\right)=0$, $d_Q\left(u_3\right)\ge 1$, and $N_Q\left(u_1\right)\cup N_Q\left(u_3\right)=V\left(Q\right)$. Observe that G is traceable, and we obtain $pc\left(G\right)=2$ by Proposition 1. Next, we only consider the strong proper connection number of graph G under this assumption.

Suppose $N_Q\left(u_1\right)\cap N_Q\left(u_3\right)=Ø$ and $min\{d_Q\left(u_1\right),d_Q\left(u_3\right)\}=1$. Without a loss of generality, let $d_Q\left(u_1\right)=1$ and $N_Q\left(u_1\right)=\left\{v\right\}$. If there exists a strong proper coloring $\theta$ of G with two colors, then $\theta \left(u_1{u}_2\right)\ne \theta \left(u_2{u}_3\right)$. Without a loss of generality, let $\theta \left(u_1{u}_2\right)=1$ and $\theta \left(u_2{u}_3\right)=2$. Since $u_2{u}_{1}v$ is the unique $u_2-v$ geodesic and $u_2{u}_{3}w$ is the unique $u_2-w$ geodesic for any $w\in N_Q\left(u_3\right)$, it follows that $\theta \left(u_{1}v\right)=2$ and $\theta \left(u_{3}w\right)=1$. Note that $u_{1}vw$ is the unique $u_1-w$ geodesic for any $w\in N_Q\left(u_3\right)$, and so $\theta \left(vw\right)=1$. There is no proper geodesic between $u_3$ and v, which is a contradiction. Thus, $spc\left(G\right)\ge 3$. Assign an edge-coloring ${\theta }^{\prime }$ with three colors to G as follows: ${\theta }^{\prime }\left(u_1{u}_2\right)={\theta }^{\prime }\left(u_{3}w\right)=1$ for any $w\in N_Q\left(u_3\right)$, ${\theta }^{\prime }\left(u_2{u}_3\right)={\theta }^{\prime }\left(u_{1}v\right)=2$, and color all edges of $E\left(Q\right)$ with 3. Obviously, ${\theta }^{\prime }$ is a strong proper coloring of G, and so $spc\left(G\right)=3$.

Suppose $N_Q\left(u_1\right)\cap N_Q\left(u_3\right)=Ø$ and $min\{d_Q\left(u_1\right),d_Q\left(u_3\right)\}\ge 2$. Let $N_Q\left(u_1\right)=\{v_1,v_2,\dots ,v_t\}$ and $N_Q\left(u_3\right)=\{w_1,w_2,\dots ,w_k\}$, where $t+k=n-3$. Assign an edge-coloring $\theta$ with two colors to G such that G is strongly properly connected: $\theta \left(u_1{u}_2\right)=\theta \left(v_1{w}_1\right)=\theta \left(u_3{w}_1\right)=\theta \left(u_3{w}_i\right)=\theta \left(v_2{w}_i\right)=1$ for $2\le i\le k$, $\theta \left(u_2{u}_3\right)=\theta \left(v_1{w}_k\right)=\theta \left(u_1{v}_1\right)=\theta \left(u_1{v}_j\right)=\theta \left(w_1{v}_j\right)=2$ for $2\le j\le t$, and color the remaining edges arbitrarily with 1 and 2. Hence, $spc\left(G\right)=2$.

Suppose $N_Q\left(u_1\right)\cap N_Q\left(u_3\right)\ne Ø$, and say $v\in N_Q\left(u_1\right)\cap N_Q\left(u_3\right)$. This implies that $min\{d_Q\left(u_1\right),d_Q\left(u_3\right)\}\ge 2$. Color $u_1{u}_2$, $u_2{u}_3$, $u_{1}v$ and all edges of $E\left(Q\right)$ with 1, and color the remaining edges with 2. Clearly, G is strongly properly connected with the above edge-coloring, and so $spc\left(G\right)=2$.

Case 3. $F\cong K_2+K_1$, where $u_1{u}_2\in E\left(G\right)$. Since G is connected, we obtain $d_Q\left(u_3\right)\ge 1$. We distinguish the following three subcases.

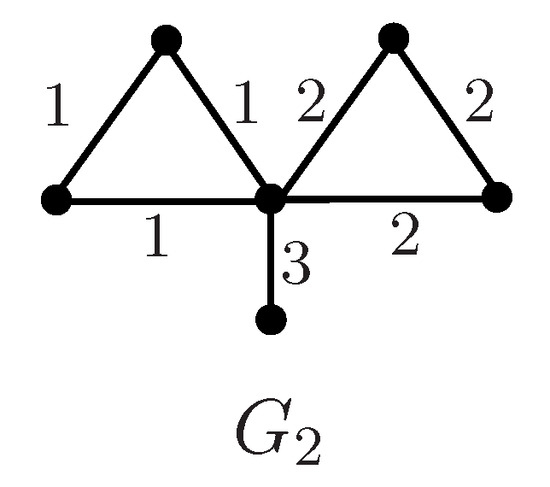
Subcase 3.1. $d_Q\left(u_3\right)=1$. Let $N_Q\left(u_3\right)=\left\{v\right\}$. Since $diam\left(G\right)=2$, we have $d_Q\left(u_1\right)\ge 1$, $d_Q\left(u_2\right)\ge 1$ and $v\in N_Q\left(u_1\right)\cap N_Q\left(u_2\right)$. Assume that $d_Q\left(u_1\right)=d_Q\left(u_2\right)=1$. This implies $n\ge 6$. If $n=6$, then $G\cong G_2$, where $G_2$ is displayed in Figure 1. Thus, $pc\left(G\right)=spc\left(G\right)=3$. Now we consider $n\ge 7$. Let $V\left(Q\right)=\{w_1,w_2,\dots ,w_{n-4},v\}$. Assign an edge-coloring $\theta$ with two colors to G as follows: $\theta \left(u_1{u}_2\right)=\theta \left(u_{1}v\right)=\theta \left(u_{2}v\right)=\theta \left(w_{i}v\right)=\theta \left(w_j{w}_{n-4}\right)=1$ for $1\le i\le n-5$ and $2\le j\le n-5$, $\theta \left(u_{3}v\right)=\theta \left(w_{n-4}v\right)=\theta \left(w_1{w}_{n-4}\right)=\theta \left(w_1{w}_2\right)=2$, and color the remaining edges arbitrarily with 1 and 2. It is easy to verify that $\theta$ is a proper-path coloring of G. Thus, $pc\left(G\right)=2$. If G is strongly properly connected with an edge-coloring $\theta$, then $\theta \left(u_{1}v\right)\ne \theta \left(u_{3}v\right)\ne \theta \left(w_{1}v\right)$, and so $spc\left(G\right)\ge 3$. Assign an edge-coloring ${\theta }^{\prime }$ with three colors to G as follows: ${\theta }^{\prime }\left(u_1{u}_2\right)={\theta }^{\prime }\left(u_{1}v\right)={\theta }^{\prime }\left(u_{2}v\right)=1$, ${\theta }^{\prime }\left(u_{3}v\right)=2$, and color all edges of $E\left(Q\right)$ with 3. We can check that G is strongly properly connected with the above edge-coloring. Hence, $spc\left(G\right)=3$.

Figure 1. The graph $G_2$ with a strong proper coloring.

Assume that $min\{d_Q\left(u_1\right),d_Q\left(u_2\right)\}=1$ and $d_Q\left(u_1\right)+d_Q\left(u_2\right)\ge 3$. Without a loss of generality, let $d_Q\left(u_1\right)\ge 2$ and $d_Q\left(u_2\right)=1$. Observe that G is traceable, and we have $pc\left(G\right)=2$ by Proposition 1. If G is strongly properly connected with an edge-coloring $\theta$, then $\theta \left(u_{2}v\right)\ne \theta \left(u_{3}v\right)\ne \theta \left(wv\right)$, where $w\in V\left(Q\right)\backslash N_Q\left(u_1\right)$. Hence, $spc\left(G\right)\ge 3$. Define an edge-coloring ${\theta }^{\prime }$ of G with three colors such that G is strongly properly connected: ${\theta }^{\prime }\left(u_1{u}_2\right)={\theta }^{\prime }\left(u_{1}v\right)={\theta }^{\prime }\left(u_{2}v\right)=1$, and color all edges of $E\left(Q\right)$ with 3 and the remaining edges with 2. Thus, $spc\left(G\right)=3$.

Assume that $min\{d_Q\left(u_1\right),d_Q\left(u_2\right)\}\ge 2$. Note that G is traceable, and so $pc\left(G\right)=2$ by Proposition 1. Assign a strong proper coloring $\theta$ with two colors to G as follows: $\theta \left(u_1{u}_2\right)=\theta \left(u_{1}v\right)=\theta \left(u_{2}v\right)=1$, and color all edges of $E\left(Q\right)$ with 1 and the remaining edges with 2. Hence, $spc\left(G\right)=2$.

Subcase 3.2. $d_Q\left(u_3\right)=2$. Let $N_Q\left(u_3\right)=\{u,v\}$. Since $diam\left(G\right)=2$, we obtain $N_Q\left(u_1\right)\cap N_Q\left(u_3\right)\ne Ø$ and $N_Q\left(u_2\right)\cap N_Q\left(u_3\right)\ne Ø$. Observe that G is traceable, and we have $pc\left(G\right)=2$ by Proposition 1.

Assume that $d_Q\left(u_1\right)=d_Q\left(u_2\right)=1$ and $N_Q\left(u_1\right)\cap N_Q\left(u_2\right)\ne Ø$. Let $u\in$$N_Q\left(u_1\right)\cap N_Q\left(u_2\right)$. There exists a strong proper coloring $\theta$ of G with two colors as follows: $\theta \left(u_1{u}_2\right)=\theta \left(u_{1}u\right)=\theta \left(u_{2}u\right)=\theta \left(u_{3}v\right)=1$, $\theta \left(u_{3}u\right)=2$, and color all edges of $E\left(Q\right)$ with 2. Thus, $spc\left(G\right)=2$.

Assume that $d_Q\left(u_1\right)=d_Q\left(u_2\right)=1$ and $N_Q\left(u_1\right)\cap N_Q\left(u_2\right)=Ø$. Let $N_Q\left(u_1\right)=\left\{u\right\}$, $N_Q\left(u_2\right)=\left\{v\right\}$ and $V\left(Q\right)=\{w_1,w_2,\dots ,w_{n-5},u,v\}$. If there exists a strong proper coloring $\theta$ of G with two colors, then $\theta \left(u_{1}u\right)\ne \theta \left(u{u}_3\right)$. Without a loss of generality, let $\theta \left(u_{1}u\right)=1$ and $\theta \left(u{u}_3\right)=2$. Since $u_{1}u{w}_1$ is the unique $u_1-w_1$ geodesic, it follows that $\theta \left(u{w}_1\right)=2$. Note that $u_{2}v{u}_3$ is the unique $u_2-u_3$ geodesic, and so $\theta \left(u_{2}v\right)\ne \theta \left(v{u}_3\right)$. We first consider $\theta \left(u_{2}v\right)=1$ and $\theta \left(v{u}_3\right)=2$. Since $u_{2}v{w}_1$ is the unique $u_2-w_1$ geodesic, we have $\theta \left(v{w}_1\right)=2$. There is no proper geodesic between $u_3$ and $w_1$, which is a contradiction. Next, we consider $\theta \left(u_{2}v\right)=2$ and $\theta \left(v{u}_3\right)=1$. Note that $u_{2}v{w}_1$ is the unique $u_2-w_1$ geodesic, so we obtain $\theta \left(v{w}_1\right)=1$. There is no proper geodesic between $u_3$ and $w_1$, which is a contradiction. Hence, $spc\left(G\right)\ge 3$. Allocate a strong proper coloring ${\theta }^{\prime }$ with three colors to G as follows: ${\theta }^{\prime }\left(u_1{u}_2\right)={\theta }^{\prime }\left(u_{1}u\right)={\theta }^{\prime }\left(u_{2}v\right)=1$, ${\theta }^{\prime }\left(u{u}_3\right)={\theta }^{\prime }\left(v{u}_3\right)=2$, and color all edges of $E\left(Q\right)$ with 3. Thus, $spc\left(G\right)=3$.

Assume that $d_Q\left(u_1\right)+d_Q\left(u_2\right)\ge 3$ and $N_Q\left(u_1\right)\cap N_Q\left(u_2\right)\ne Ø$. Without a loss of generality, let $d_Q\left(u_1\right)\ge 2$ and $w\in N_Q\left(u_1\right)\cap$$N_Q\left(u_2\right)$. Consider $u\in N_Q\left(u_1\right)\cap N_Q\left(u_2\right)$ or $v\in N_Q\left(u_1\right)\cap N_Q\left(u_2\right)$. Without a loss of generality, let $u\in N_Q\left(u_1\right)\cap N_Q\left(u_2\right)$. The following edge-coloring $\theta$ with two colors makes G strongly properly connected: $\theta \left(u_{1}u\right)=\theta \left(u_{2}u\right)=\theta \left(u_1{u}_2\right)=1$, $\theta \left(u_{3}u\right)=2$, and color all edges of $E\left(Q\right)$ with 2 and the remaining edges with 1. Hence, $spc\left(G\right)=2$. Consider $u\notin N_Q\left(u_1\right)\cap N_Q\left(u_2\right)$ and $v\notin N_Q\left(u_1\right)\cap N_Q\left(u_2\right)$. Then, $min\{d_Q\left(u_1\right),d_Q\left(u_2\right)\}\ge 2$. Without a loss of generality, let $u\in N_Q\left(u_1\right)$ and $v\in N_Q\left(u_2\right)$. Assign an edge-coloring $\theta$ with two colors to G as follows: $\theta \left(u_{1}w\right)=\theta \left(u_{2}w\right)=\theta \left(u_1{u}_2\right)=\theta \left(u_{1}u\right)=\theta \left(u_{3}v\right)=1$, $\theta \left(u_{3}u\right)=\theta \left(u_{2}v\right)=2$, and color all edges of $E\left(Q\right)$ with 2 and the remaining edges with 1. It is not difficult to verify that $\theta$ is a strong proper coloring of G, and so $spc\left(G\right)=2$.

Assume that $d_Q\left(u_1\right)+d_Q\left(u_2\right)\ge 3$ and $N_Q\left(u_1\right)\cap N_Q\left(u_2\right)=Ø$. Without a loss of generality, let $d_Q\left(u_1\right)\ge 2$, $u\in N_Q\left(u_1\right)$, and $v\in N_Q\left(u_2\right)$. There exists an edge-coloring $\theta$ with two colors such that G is strongly properly connected, as follows: $\theta \left(u_1{u}_2\right)=\theta \left(u_{2}v\right)=\theta \left(u_{3}u\right)=1$, $\theta \left(u_{1}u\right)=\theta \left(u_{3}v\right)=2$, and color all edges of $E\left(Q\right)$ with 2 and the remaining edges with 1. Hence, $spc\left(G\right)=2$.

Subcase 3.3. $d_Q\left(u_3\right)\ge 3$. Note that G is traceable, and we obtain $pc\left(G\right)=2$ by Proposition 1. Assume that $d_Q\left(u_1\right)=d_Q\left(u_2\right)=1$ and $N_Q\left(u_1\right)\cap N_Q\left(u_2\right)=Ø$. Let $N_Q\left(u_1\right)\cap N_Q\left(u_3\right)=\left\{u\right\}$ and $N_Q\left(u_2\right)\cap N_Q\left(u_3\right)=\left\{v\right\}$. Assign a strong proper coloring $\theta$ with two colors to G as follows: $\theta \left(u_1{u}_2\right)=\theta \left(u_{1}u\right)=\theta \left(u_{2}v\right)=1$, $\theta \left(u_{3}u\right)=\theta \left(u_{3}v\right)=2$, and color all edges of $E\left(Q\right)$ with 2 and the remaining edges with 1. Thus, $spc\left(G\right)=2$.

Assume that either $d_Q\left(u_1\right)=d_Q\left(u_2\right)=1$ and $N_Q\left(u_1\right)\cap N_Q\left(u_2\right)\ne Ø$, or $d_Q\left(u_1\right)+d_Q\left(u_2\right)\ge 3$. An analogous edge-coloring to that presented in Subcase 3.2 induces a strong proper coloring of G with $spc\left(G\right)=2$.

Case 4. $F\cong 3K_1$. Since $diam\left(G\right)=2$, it follows that $N_Q\left(u_1\right)\cap N_Q\left(u_2\right)\ne Ø$, $N_Q\left(u_1\right)\cap N_Q\left(u_3\right)\ne Ø$ and $N_Q\left(u_2\right)\cap N_Q\left(u_3\right)\ne Ø$. This case is demonstrated by the following three subcases.

Subcase 4.1. $|(N_Q\left(u_1\right)\cap N_Q\left(u_2\right))\cup (N_Q\left(u_1\right)\cap N_Q\left(u_3\right))\cup (N_Q\left(u_2\right)\cap N_Q\left(u_3\right))| =1$. This implies that $|N_Q\left(u_1\right)\cap N_Q\left(u_2\right)\cap N_Q\left(u_3\right)| =1$. Let $N_Q\left(u_1\right)\cap N_Q\left(u_2\right)\cap N_Q\left(u_3\right)=\left\{v\right\}$. Assume that $d_Q\left(u_1\right)=d_Q\left(u_2\right)=d_Q\left(u_3\right)=1$. Then, $spc\left(G\right)\ge pc\left(G\right)\ge 3$ by Proposition 2. If $n=5$, then $G\cong K_{1,4}$. Hence, $pc\left(G\right)=spc\left(G\right)=4$. Now we consider $n\ge 6$. Let $V\left(Q\right)=\{v,w_1,w_2,\dots ,w_{n-4}\}$. Assign an edge-coloring $\theta$ with three colors to G as follows: $\theta \left(u_{1}v\right)=1$; $\theta \left(u_{2}v\right)=2$; $\theta \left(u_{3}v\right)=3$; $\theta \left(w_1{w}_{n-4}\right)=3$ if n is even, $\theta \left(w_1{w}_{n-4}\right)=2$ if n is odd; color the sequence $w_{1}v{w}_2{w}_3\cdots w_{n-4}$ alternately with 1 and 2 starting with $\theta \left(w_{1}v\right)=1$; and color the remaining edges arbitrarily with 1 and 2. It is not difficult to check that $\theta$ is a proper-path coloring of G. Thus, $pc\left(G\right)=3$. Suppose G has a strong proper coloring $\theta$, we have $\theta \left(u_{1}v\right)\ne \theta \left(u_{2}v\right)\ne \theta \left(u_{3}v\right)\ne \theta \left(w_{1}v\right)$, and so $spc\left(G\right)\ge 4$. On the other hand, there exists a strong proper coloring ${\theta }^{\prime }$ of G with four colors, as follows: ${\theta }^{\prime }\left(u_{1}v\right)=1$, ${\theta }^{\prime }\left(u_{2}v\right)=2$, ${\theta }^{\prime }\left(u_{3}v\right)=3$, and color all edges of $E\left(Q\right)$ with 4. Therefore, we have $spc\left(G\right)=4$.

Assume that $d_Q\left(u_1\right)+d_Q\left(u_2\right)+d_Q\left(u_3\right)\ge 4$. Without a loss of generality, let $d_Q\left(u_1\right)\ge 2$, and say $u\in N_Q\left(u_1\right)\backslash \left\{v\right\}$. Let $V\left(Q\right)=\{u,v,w_1,w_2,\dots ,w_{n-5}\}$ with $n\ge 6$. The following edge-coloring $\theta$ with two colors makes G properly connected: $\theta \left(u_{1}v\right)=\theta \left(u_{2}v\right)=\theta \left(uv\right)=1$, $\theta \left(u_{3}v\right)=2$, color the sequence $v{w}_1{w}_2\cdots w_{n-5}u{u}_1$ alternately with 2 and 1 starting with $\theta \left(v{w}_1\right)=2$, and color the remaining edges arbitrarily with 1 and 2. Thus, $pc\left(G\right)=2$. Suppose G has a strong proper coloring $\theta$, we have $\theta \left(u_{1}v\right)\ne \theta \left(u_{2}v\right)\ne \theta \left(u_{3}v\right)$, and so $spc\left(G\right)\ge 3$. On the other hand, there exists a strong proper coloring ${\theta }^{\prime }$ of G with three colors, as follows: ${\theta }^{\prime }\left(u_{1}u\right)={\theta }^{\prime }\left(u_{2}v\right)=1$, ${\theta }^{\prime }\left(u_{3}v\right)=2$, ${\theta }^{\prime }\left(u_{1}v\right)=3$, and color all edges of $E\left(Q\right)$ with 3 and the remaining edges with 1. Hence, $spc\left(G\right)=3$.

Subcase 4.2. $|(N_Q\left(u_1\right)\cap N_Q\left(u_2\right))\cup (N_Q\left(u_1\right)\cap N_Q\left(u_3\right))\cup (N_Q\left(u_2\right)\cap N_Q\left(u_3\right))| =2$. Since $diam\left(G\right)=2$, we obtain $N_Q\left(u_1\right)\cap N_Q\left(u_2\right)\cap N_Q\left(u_3\right)\ne Ø$, and say $v\in N_Q\left(u_1\right)\cap N_Q\left(u_2\right)\cap N_Q\left(u_3\right)$. Without a loss of generality, we consider $|N_Q\left(u_1\right)\cap N_Q\left(u_2\right)| =2$, and say $u\in (N_Q\left(u_1\right)\cap N_Q\left(u_2\right))\backslash \left\{v\right\}$. Assign an analogous edge-coloring to that presented in Subcase 4.1 to G that satisfies $d_Q\left(u_1\right)+d_Q\left(u_2\right)+d_Q\left(u_3\right)\ge 4$. Obviously, G is properly connected, and so $pc\left(G\right)=2$.

Assume that $d_Q\left(u_1\right)+d_Q\left(u_2\right)+d_Q\left(u_3\right)=5$. Suppose that there exists a strong proper coloring $\theta$ of G with two colors. Note that $u_{1}v{u}_3$ is the unique $u_1-u_3$ geodesic, and $u_{2}v{u}_3$ is the unique $u_2-u_3$ geodesic. Without a loss of generality, let $\theta \left(u_{1}v\right)=\theta \left(u_{2}v\right)=1$ and $\theta \left(u_{3}v\right)=2$. Since $u_{3}vw$ is the unique $u_3-w$ geodesic, where $w\in V\left(Q\right)\backslash \{u,v\}$, it follows that $\theta \left(vw\right)=1$. In order to have a proper geodesic connecting $u_2$ and w, we have $\theta \left(u_{2}u\right)\ne \theta \left(uw\right)$. Similarly, for the sake of having a proper geodesic between $u_1$ and $u_2$, we obtain $\theta \left(u_{1}u\right)\ne \theta \left(u_{2}u\right)$. Then, $\theta \left(uw\right)=\theta \left(u_{1}u\right)$, and so there is no proper geodesic connecting $u_1$ and w, which is a contradiction. Thus, $spc\left(G\right)\ge 3$. Now we assign a strong proper coloring ${\theta }^{\prime }$ with three colors to G as follows: ${\theta }^{\prime }\left(u_{1}u\right)={\theta }^{\prime }\left(u_{1}v\right)={\theta }^{\prime }\left(u_{2}v\right)=1$, ${\theta }^{\prime }\left(u_{2}u\right)={\theta }^{\prime }\left(u_{3}v\right)=2$, and color all edges of $E\left(Q\right)$ with 3. Hence, $spc\left(G\right)=3$.

Assume that $d_Q\left(u_1\right)+d_Q\left(u_2\right)+d_Q\left(u_3\right)\ge 6$. Suppose $d_Q\left(u_3\right)=1$. This implies that $max\{d_Q\left(u_1\right),d_Q\left(u_2\right)\}\ge 3$. Without a loss of generality, we consider $d_Q\left(u_1\right)\ge 3$, and say $w\in N_Q\left(u_1\right)\backslash \{u,v\}$. The following edge-coloring $\theta$ with two colors makes G strongly properly connected: $\theta \left(u_{1}u\right)=\theta \left(u_{1}v\right)=\theta \left(u_{2}v\right)=1$, $\theta \left(u_{2}u\right)=\theta \left(u_{3}v\right)=\theta \left(u_{1}w\right)=2$, and color all edges of $E\left(Q\right)$ with 1 and the remaining edges with 2. Thus, $spc\left(G\right)=2$. Suppose $d_Q\left(u_3\right)\ge 2$. Let $z\in N_Q\left(u_3\right)\backslash \left\{v\right\}$, where $u=z$ is possible. Assign an edge-coloring $\theta$ with two colors to G as follows: $\theta \left(u_{1}u\right)=\theta \left(u_{1}v\right)=\theta \left(u_{2}v\right)=\theta \left(u_{3}z\right)=1$, $\theta \left(u_{2}u\right)=\theta \left(u_{3}v\right)=2$, and color all edges of $E\left(Q\right)$ with 2 and the remaining edges with 1. Obviously, $\theta$ is a strong proper coloring of G, and so $spc\left(G\right)=2$.

Subcase 4.3. $|(N_Q\left(u_1\right)\cap N_Q\left(u_2\right))\cup (N_Q\left(u_1\right)\cap N_Q\left(u_3\right))\cup (N_Q\left(u_2\right)\cap N_Q\left(u_3\right))| \ge 3$, and let $\{w_1,w_2,w_3\}\subseteq (N_Q\left(u_1\right)\cap N_Q\left(u_2\right))\cup (N_Q\left(u_1\right)\cap N_Q\left(u_3\right))\cup (N_Q\left(u_2\right)\cap N_Q\left(u_3\right))$. Up to isomorphism, we only need to consider the following two cases.

Let $\{u_1{w}_1,u_1{w}_2,u_2{w}_1,u_2{w}_3,u_3{w}_2,u_3{w}_3\}\subseteq E[V\left(F\right),V\left(Q\right)]$. Assign an edge-coloring $\theta$ with two colors to G such that G is strongly properly connected: $\theta \left(u_1{w}_1\right)=\theta \left(u_2{w}_3\right)=\theta \left(u_3{w}_2\right)=1$, $\theta \left(u_1{w}_2\right)=\theta \left(u_2{w}_1\right)=\theta \left(u_3{w}_3\right)=2$, and color all edges of $E\left(Q\right)$ with 2 and the remaining edges with 1. Hence, $pc\left(G\right)=spc\left(G\right)=2$.

Let $\{u_1{w}_1,u_1{w}_2,u_1{w}_3,u_2{w}_1,u_2{w}_2,u_2{w}_3,u_3{w}_1\}\subseteq E[V\left(F\right),V\left(Q\right)]$. The following edge-coloring $\theta$ with two colors makes G strongly properly connected: $\theta \left(u_1{w}_2\right)=\theta \left(u_2{w}_3\right)=\theta \left(u_3{w}_1\right)=1$, $\theta \left(u_1{w}_1\right)=\theta \left(u_2{w}_1\right)=\theta \left(u_2{w}_2\right)=2$, and color all edges of $E\left(Q\right)$ with 2 and the remaining edges with 1. Thus, $pc\left(G\right)=spc\left(G\right)=2$. □

Theorem 4. 

Let G be a connected graph of order $n\ge 5$, $diam\left(G\right)\ge 3$, and $\omega \left(G\right)=n-3$. Let Q be a maximum clique of G and $V\left(G\right)\backslash V\left(Q\right)=\{u_1,u_2,u_3\}$. Then, either $pc\left(G\right)=spc\left(G\right)=2$ or one of the following holds:

(i) 

$G[V\left(G\right)\backslash V\left(Q\right)]\cong P_3$, where $u_1{u}_2,u_2{u}_3\in E\left(G\right)$, $d_Q\left(u_1\right)=d_Q\left(u_3\right)=0$, and $d_Q\left(u_2\right)=1$.

(ii) 

$G[V\left(G\right)\backslash V\left(Q\right)]\cong P_3$, where $u_1{u}_2,u_2{u}_3\in E\left(G\right)$, $d_Q\left(u_1\right)=d_Q\left(u_3\right)=0$, and $d_Q\left(u_2\right)\ge 2$.

(iii) 

$G[V\left(G\right)\backslash V\left(Q\right)]\cong P_3$, where $u_1{u}_2,u_2{u}_3\in E\left(G\right)$, $min\{d_Q\left(u_1\right),d_Q\left(u_3\right)\}=1$, $d_Q\left(u_2\right)=0$, $N_Q\left(u_1\right)\cup N_Q\left(u_3\right)\ne V\left(Q\right)$, and $N_Q\left(u_1\right)\cap N_Q\left(u_3\right)=Ø$.

(iv) 

$5\le n\le 6$, $G[V\left(G\right)\backslash V\left(Q\right)]\cong K_2+K_1$, where $u_1{u}_2\in E\left(G\right)$, $N_Q\left(u_1\right)=N_Q\left(u_3\right)=\left\{v\right\}$, and $d_Q\left(u_2\right)=0$.

(v) 

$n\ge 7$, $G[V\left(G\right)\backslash V\left(Q\right)]\cong K_2+K_1$, where $u_1{u}_2\in E\left(G\right)$, $N_Q\left(u_1\right)=N_Q\left(u_3\right)=\left\{v\right\}$, and $d_Q\left(u_2\right)=0$.

(vi) 

$G[V\left(G\right)\backslash V\left(Q\right)]\cong K_2+K_1$, where $u_1{u}_2\in E\left(G\right)$, $d_Q\left(u_2\right)\ge 1$, $N_Q\left(u_1\right)=N_Q\left(u_3\right)=\left\{v\right\}$, $N_Q\left(u_2\right)\cap N_Q\left(u_3\right)=Ø$, and $N_Q\left(u_1\right)\cup N_Q\left(u_2\right)\ne V\left(Q\right)$.

(vii) 

$5\le n\le 6$, $G[V\left(G\right)\backslash V\left(Q\right)]\cong 3K_1$, $N_Q\left(u_1\right)\cap N_Q\left(u_2\right)\cap N_Q\left(u_3\right)=Ø$, $|N_Q\left(u_1\right)\cap N_Q\left(u_2\right)| =1$, and $d_Q\left(u_1\right)=d_Q\left(u_2\right)=d_Q\left(u_3\right)=1$.

(viii) 

$n=6$, $G[V\left(G\right)\backslash V\left(Q\right)]\cong 3K_1$, $N_Q\left(u_1\right)\cap N_Q\left(u_2\right)\cap N_Q\left(u_3\right)=Ø$, $|N_Q\left(u_1\right)\cap N_Q\left(u_2\right)| =1$, $d_Q\left(u_1\right)=d_Q\left(u_2\right)=1$, and $d_Q\left(u_3\right)=2$.

(ix) 

$n\ge 7$, $G[V\left(G\right)\backslash V\left(Q\right)]\cong 3K_1$, $N_Q\left(u_1\right)\cap N_Q\left(u_2\right)\cap N_Q\left(u_3\right)=Ø$, $|N_Q\left(u_1\right)\cap N_Q\left(u_2\right)| =1$, $d_Q\left(u_1\right)=d_Q\left(u_2\right)=1$, and $d_Q\left(u_3\right)\ge 1$.

(x) 

$G[V\left(G\right)\backslash V\left(Q\right)]\cong 3K_1$, $N_Q\left(u_1\right)\cap N_Q\left(u_2\right)\cap N_Q\left(u_3\right)=Ø$, $|N_Q\left(u_1\right)\cap N_Q\left(u_2\right)| =1$, $N_Q\left(u_1\right)\cap N_Q\left(u_3\right)\ne Ø$, $d_Q\left(u_1\right)=2$, and $d_Q\left(u_2\right)=d_Q\left(u_3\right)=1$.

Moreover, we have $pc\left(G\right)=2$ and $spc\left(G\right)=3$ for (ii), (iii), (v), (vi), (viii), (ix), and (x) and $pc\left(G\right)=spc\left(G\right)=3$ for (i), (iv), and (vii).

Proof. 

Let $F=G\left[V\right(G)\backslash V(Q\left)\right]$, and let $\theta$ be an edge-coloring of G. We prove this theorem by the following two cases.

Case 1. $diam\left(G\right)=3$. We distinguish the following four subcases by analyzing the structure of F.

Subcase 1.1. $F\cong K_3$. Note that G is traceable, and we have $pc\left(G\right)=2$ by Proposition 1. Assign an edge-coloring $\theta$ with two colors to G as follows: color all edges of $E\left(F\right)$ and $E\left(Q\right)$ with 1, and color all edges of $E\left[V\right(F),V(Q\left)\right]$ with 2. It is obvious that $\theta$ is a strong proper coloring of G, and so $spc\left(G\right)=2$.

Subcase 1.2. $F\cong P_3$, where $u_1{u}_2,u_2{u}_3\in E\left(G\right)$. Assume that $d_Q\left(u_1\right)=d_Q\left(u_3\right)=0$. Suppose $d_Q\left(u_2\right)=1$, and let $N_Q\left(u_2\right)=\left\{v\right\}$. Then, $spc\left(G\right)\ge pc\left(G\right)\ge 3$ by Proposition 2. Now we define a strong proper coloring $\theta$ of G with three colors as follows: $\theta \left(u_1{u}_2\right)=1$, $\theta \left(u_2{u}_3\right)=2$, $\theta \left(u_{2}v\right)=3$, and color all edges of $E\left(Q\right)$ with 1. Thus, $pc\left(G\right)=spc\left(G\right)=3$. Suppose $d_Q\left(u_2\right)\ge 2$, and let $u,v\in N_Q\left(u_2\right)$. Assign an edge-coloring $\theta$ with two colors to G as follows: $\theta \left(u_1{u}_2\right)=\theta \left(u_{2}u\right)=\theta \left(vw\right)=1$ for any $w\in V\left(Q\right)\backslash \{u,v\}$, $\theta \left(u_2{u}_3\right)=\theta \left(u_{2}v\right)=\theta \left(uv\right)=\theta \left(uw\right)=2$ for any $w\in V\left(Q\right)\backslash \{u,v\}$, and color the remaining edges arbitrarily with 1 and 2. We can check that G is properly connected with the above edge-coloring, and so $pc\left(G\right)=2$. If G is strongly properly connected with an edge-coloring $\theta$, then $\theta \left(u_1{u}_2\right)\ne \theta \left(u_2{u}_3\right)\ne \theta \left(u_{2}u\right)$. Thus, $spc\left(G\right)\ge 3$. Assign a strong proper coloring ${\theta }^{\prime }$ with three colors to G as follows: ${\theta }^{\prime }\left(u_1{u}_2\right)=1$, ${\theta }^{\prime }\left(u_2{u}_3\right)=2$, and color all edges of $E\left[V\right(F),V(Q\left)\right]$ with 3 and all edges of $E\left(Q\right)$ with 1. Thus, $spc\left(G\right)=3$.

Assume that $min\{d_Q\left(u_1\right),d_Q\left(u_3\right)\}=0$ and $max\{d_Q\left(u_1\right),d_Q\left(u_3\right)\}\ge 1$. Without a loss of generality, let $d_Q\left(u_3\right)=0$ and $d_Q\left(u_1\right)\ge 1$. Since $diam\left(G\right)=3$, it follows that $d_Q\left(u_2\right)\ge 1$. Note that G is traceable, and we have $pc\left(G\right)=2$ by Proposition 1. The following edge-coloring $\theta$ with two colors makes G strongly properly connected: $\theta \left(u_1{u}_2\right)=1$, $\theta \left(u_2{u}_3\right)=2$, and color all edges of $E\left(Q\right)$ with 2 and all edges of $E\left[V\right(F),V(Q\left)\right]$ with 1. Hence, $spc\left(G\right)=2$.

Assume that $d_Q\left(u_1\right)\ge 1$ and $d_Q\left(u_3\right)\ge 1$. Since $diam\left(G\right)=3$, it follows that $d_Q\left(u_2\right)=0$ and $N_Q\left(u_1\right)\cup N_Q\left(u_3\right)\ne V\left(Q\right)$. Observe that G is traceable, and we have $pc\left(G\right)=2$ by Proposition 1. Now, we only consider the strong proper connection number of graph G under this assumption.

Suppose $N_Q\left(u_1\right)\cap N_Q\left(u_3\right)=Ø$ and $min\{d_Q\left(u_1\right),d_Q\left(u_3\right)\}=1$. Without a loss of generality, we consider $d_Q\left(u_1\right)=1$, and say $N_Q\left(u_1\right)=\left\{u\right\}$. If there exists a strong proper coloring $\theta$ of G with two colors, then $\theta \left(u_1{u}_2\right)\ne \theta \left(u_2{u}_3\right)$. Without a loss of generality, let $\theta \left(u_1{u}_2\right)=1$ and $\theta \left(u_2{u}_3\right)=2$. Note that $u_2{u}_{1}u$ is the unique $u_2-u$ geodesic, and $u_2{u}_{3}v$ is the unique $u_2-v$ geodesic for any $v\in N_Q\left(u_3\right)$; then, $\theta \left(u_{1}u\right)=2$ and $\theta \left(u_{3}v\right)=1$. Since $u_{1}uv$ is the unique $u_1-v$ geodesic for any $v\in N_Q\left(u_3\right)$, we have $\theta \left(uv\right)=1$. There is no proper geodesic between $u_3$ and u, which is a contradiction. Thus, $spc\left(G\right)\ge 3$. On the other hand, we assign a strong proper coloring ${\theta }^{\prime }$ with three colors to G as follows: ${\theta }^{\prime }\left(u_1{u}_2\right)={\theta }^{\prime }\left(u_{3}v\right)=1$ for any $v\in N_Q\left(u_3\right)$, ${\theta }^{\prime }\left(u_2{u}_3\right)={\theta }^{\prime }\left(u_{1}u\right)=2$, and color all edges of $E\left(Q\right)$ with 3. Hence, $spc\left(G\right)=3$.

Suppose $N_Q\left(u_1\right)\cap N_Q\left(u_3\right)=Ø$ and $min\{d_Q\left(u_1\right),d_Q\left(u_3\right)\}\ge 2$. Let $N_Q\left(u_1\right)=\{w_1,w_2,\dots ,w_t\}$ and $N_Q\left(u_3\right)=\{v_1,v_2,\dots ,v_k\}$, where $t+k<n-3$. Assign an edge-coloring $\theta$ with two colors to G as follows: $\theta \left(u_1{u}_2\right)=\theta \left(w_1{v}_1\right)=\theta \left(u_3{v}_1\right)=\theta \left(u_3{v}_i\right)=\theta \left(w_2{v}_i\right)=1$ for $2\le i\le k$, $\theta \left(u_2{u}_3\right)=\theta \left(w_1{v}_k\right)=\theta \left(u_1{w}_1\right)=\theta \left(u_1{w}_j\right)=\theta \left(v_1{w}_j\right)=2$ for $2\le j\le t$, $\theta \left(v_{1}w\right)=2$ and $\theta \left(w_{1}w\right)=1$ for any $w\in V\left(Q\right)\backslash \{N_Q\left(u_1\right)\cup N_Q\left(u_3\right)\}$, and color the remaining edges arbitrarily with 1 and 2. It is clear that $\theta$ is a strong proper coloring of G, and so $spc\left(G\right)=2$.

Suppose $N_Q\left(u_1\right)\cap N_Q\left(u_3\right)\ne Ø$, and let $v\in N_Q\left(u_1\right)\cap N_Q\left(u_3\right)$. Consider $d_Q\left(u_1\right)=d_Q\left(u_3\right)=1$. Color $u_1{u}_2$ and all edges of $E\left(Q\right)$ with 1, and color $u_2{u}_3$, $u_{1}v$ and $u_{3}v$ with 2. Obviously, the above edge-coloring makes G strongly properly connected. Thus, $spc\left(G\right)=2$. Consider $min\{d_Q\left(u_1\right),d_Q\left(u_3\right)\}=1$ and $max\{d_Q\left(u_1\right),d_Q\left(u_3\right)\}\ge 2$. Without a loss of generality, let $d_Q\left(u_1\right)=1$ and $d_Q\left(u_3\right)\ge 2$. Assign a strong proper coloring $\theta$ with two colors to G as follows: $\theta \left(u_1{u}_2\right)=\theta \left(u_2{u}_3\right)=\theta \left(u_{3}v\right)=1$, $\theta \left(u_{1}v\right)=\theta \left(u_{3}w\right)=2$ for any $w\in N_Q\left(u_3\right)\backslash \left\{v\right\}$, and color all edges of $E\left(Q\right)$ with 1. Hence, $spc\left(G\right)=2$. Consider $min\{d_Q\left(u_1\right),d_Q\left(u_3\right)\}\ge 2$. Allocate a strong proper coloring $\theta$ with two colors to G as follows: $\theta \left(u_1{u}_2\right)=\theta \left(u_2{u}_3\right)=\theta \left(u_{3}v\right)=1$, and color all edges of $E\left(Q\right)$ with 1 and the remaining edges with 2. Thus, $spc\left(G\right)=2$.

Subcase 1.3. $F\cong K_2+K_1$, where $u_1{u}_2\in E\left(G\right)$. Since G is connected, we have $d_Q\left(u_3\right)\ge 1$ and $max\{d_Q\left(u_1\right),d_Q\left(u_2\right)\}\ge 1$. Without a loss of generality, let $d_Q\left(u_1\right)\ge 1$. Assume that $d_Q\left(u_2\right)=0$. Since $diam\left(G\right)=3$, it follows that $N_Q\left(u_1\right)\cap N_Q\left(u_3\right)\ne Ø$, and let $v\in N_Q\left(u_1\right)\cap N_Q\left(u_3\right)$.

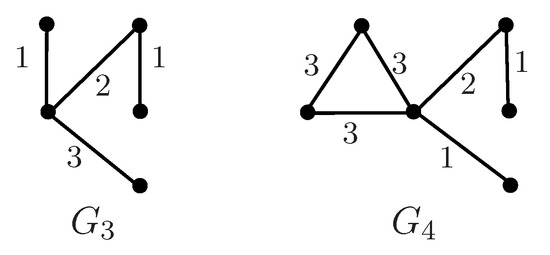
Suppose $d_Q\left(u_1\right)=d_Q\left(u_3\right)=1$. If $n=5$, then $G\cong G_3$, where $G_3$ is displayed in Figure 2. Hence, $pc\left(G\right)=spc\left(G\right)=3$. If $n=6$, then $G\cong G_4$, where $G_4$ is shown in Figure 2. Thus, $pc\left(G\right)=spc\left(G\right)=3$. Now, we consider $n\ge 7$. Let $V\left(Q\right)=\{w_1,w_2,\dots ,w_{n-4},v\}$. Assign an edge-coloring $\theta$ with two colors to G as follows: $\theta \left(u_1{u}_2\right)=\theta \left(u_{3}v\right)=\theta \left(w_{n-4}{w}_1\right)=1$, $\theta \left(u_{1}v\right)=\theta \left(w_{2}v\right)=2$, color the sequence $v{w}_1{w}_2\cdots w_{n-4}v$ alternately with 1 and 2 starting with $\theta \left(v{w}_1\right)=1$, and color the remaining edges arbitrarily with 1 and 2. We can verify that $\theta$ is a proper-path coloring of G. Thus, $pc\left(G\right)=2$. If G has a strong proper coloring $\theta$, then $\theta \left(u_{1}v\right)\ne \theta \left(u_{3}v\right)\ne \theta \left(v{w}_1\right)$, and so $spc\left(G\right)\ge 3$. On the other hand, there exists a strong proper coloring ${\theta }^{\prime }$ of G with three colors: assign 1 to $u_1{u}_2$ and $u_{3}v$, assign 2 to $u_{1}v$, and assign 3 to all edges of $E\left(Q\right)$. Therefore, $spc\left(G\right)=3$.

Figure 2. The graphs $G_3$ and $G_4$ with a strong proper coloring.

Suppose $d_Q\left(u_1\right)=1$ and $d_Q\left(u_3\right)\ge 2$. Note that G is traceable, and we have $pc\left(G\right)=2$ by Proposition 1. Allocate an edge-coloring $\theta$ with two colors to G as follows: $\theta \left(u_{1}v\right)=\theta \left(u_{3}w\right)=1$ for any $w\in N_Q\left(u_3\right)\backslash \left\{v\right\}$, $\theta \left(u_1{u}_2\right)=\theta \left(u_{3}v\right)=2$, and color all edges of $E\left(Q\right)$ with 2. Obviously, $\theta$ is a strong proper coloring of G, and so $spc\left(G\right)=2$.

Suppose $d_Q\left(u_1\right)\ge 2$ and $d_Q\left(u_3\right)=1$. Observe that G is traceable, and we obtain $pc\left(G\right)=2$ by Proposition 1. The following edge-coloring $\theta$ with two colors makes G strongly properly connected: $\theta \left(u_{1}v\right)=\theta \left(u_1{w}_1\right)=1$ for any $w_1\in N_Q\left(u_1\right)\backslash \left\{v\right\}$, $\theta \left(u_1{u}_2\right)=\theta \left(u_{3}v\right)=2$, and color all edges incident with v in $E\left(Q\right)$ with 1 and the remaining edges with 2. Hence, $spc\left(G\right)=2$.

Suppose $d_Q\left(u_1\right)\ge 2$ and $d_Q\left(u_3\right)\ge 2$. Note that G is traceable, and we have $pc\left(G\right)=2$ by Proposition 1. Define a strong proper coloring $\theta$ of G with two colors as follows: $\theta \left(u_{1}v\right)=1$, $\theta \left(u_1{u}_2\right)=\theta \left(u_{3}v\right)=2$, and color all edges of $E\left(Q\right)$ with 2 and the remaining edges with 1. Thus, $spc\left(G\right)=2$.

Assume that $d_Q\left(u_2\right)\ge 1$. Since $diam\left(G\right)=3$, it follows that $min\left\{\right|N_Q\left(u_1\right)\cap N_Q\left(u_3\right)|$,

$|N_Q\left(u_2\right)\cap N_Q\left(u_3\right)\left|\right\}=0$. Suppose $max\left\{\right|N_Q\left(u_1\right)\cap N_Q\left(u_3\right)|,|N_Q\left(u_2\right)\cap N_Q\left(u_3\right)\left|\right\}\ge 1$. Without a loss of generality, we consider $|N_Q\left(u_2\right)\cap N_Q\left(u_3\right)\left|\right\}=0$ and $|N_Q\left(u_1\right)\cap N_Q\left(u_3\right)| \ge 1$, and say $v\in N_Q\left(u_1\right)\cap N_Q\left(u_3\right)$. Observe that G is traceable, and we have $pc\left(G\right)=2$ by Proposition 1. Now, we only consider the strong proper connection number of graph G under this supposition.

We first consider $|N_Q\left(u_1\right)\cap N_Q\left(u_3\right)| \ge 2$. The following edge-coloring $\theta$ with two colors makes G strongly properly connected: color $u_1{u}_2$, $u_{3}v$ and all edges of $E\left(Q\right)$ with 2, and color the remaining edges with 1. Hence, $spc\left(G\right)=2$.

Next, we consider $|N_Q\left(u_1\right)\cap N_Q\left(u_3\right)| =1$. Let $d_Q\left(u_1\right)\ge 2$. Assign a strong proper coloring $\theta$ with two colors to G: color $u_{1}v$ and all edges of $E\left(Q\right)$ with 1, and color the remaining edges with 2. Hence, $spc\left(G\right)=2$. Let $d_Q\left(u_3\right)\ge 2$. Define a strong proper coloring $\theta$ of G with two colors as follows: color $u_1{u}_2$, $u_{3}v$ and all edges of $E\left(Q\right)$ with 2, and color the remaining edges with 1. Thus, $spc\left(G\right)=2$. Let $d_Q\left(u_1\right)=d_Q\left(u_3\right)=1$ and $N_Q\left(u_1\right)\cup N_Q\left(u_2\right)=V\left(Q\right)$. Allocate an edge-coloring $\theta$ with two colors to G: color $u_1{u}_2$, $u_{1}v$ and all edges of $E\left(Q\right)$ with 1, and color the remaining edges with 2. We can check that G is strongly properly connected with the above edge-coloring, and so $spc\left(G\right)=2$. Let $d_Q\left(u_1\right)=d_Q\left(u_3\right)=1$ and $N_Q\left(u_1\right)\cup N_Q\left(u_2\right)\ne V\left(Q\right)$. If $\theta$ is a strong proper coloring of G, then $\theta \left(u_{1}v\right)\ne \theta \left(u_{3}v\right)\ne \theta \left(vw\right)$, where $w\in V\left(Q\right)\backslash \{N_Q\left(u_1\right)\cup N_Q\left(u_2\right)\}$. Thus, $spc\left(G\right)\ge 3$. On the other hand, there exists an edge-coloring ${\theta }^{\prime }$ with three colors such that G is strongly properly connected: color $u_{1}v$ with 1 and all edges of $E\left(Q\right)$ with 3, and color the remaining edges with 2. Hence, $spc\left(G\right)=3$.

Suppose $max\left\{\right|N_Q\left(u_1\right)\cap N_Q\left(u_3\right)|,|N_Q\left(u_2\right)\cap N_Q\left(u_3\right)\left|\right\}=0$. Observe that G is traceable, and we have $pc\left(G\right)=2$ by Proposition 1. Assign an edge-coloring $\theta$ with two colors to G as follows: color $u_1{u}_2$ and all edges of $E\left(Q\right)$ with 2, and color all edges of $E\left[V\right(F),V(Q\left)\right]$ with 1. It is clear that $\theta$ is a strong proper coloring of G, and so $spc\left(G\right)=2$.

Subcase 1.4. $F\cong 3K_1$. Since $diam\left(G\right)=3$, it follows that $min\left\{\right|N_Q\left(u_1\right)\cap N_Q\left(u_2\right)|,|N_Q$

$\left(u_1\right)\cap N_Q\left(u_3\right)|,|N_Q\left(u_2\right)\cap N_Q\left(u_3\right)\left|\right\}=0$. Assume that $max\left\{\right|N_Q\left(u_1\right)\cap N_Q\left(u_2\right)|,|N_Q\left(u_1\right)\cap N_Q\left(u_3\right)|,|N_Q\left(u_2\right)\cap N_Q\left(u_3\right)\left|\right\}=0$. The following edge-coloring $\theta$ with two colors makes G strongly properly connected: color all edges of $E\left(Q\right)$ with 2, and color all edges of $E\left[V\right(F),V(Q\left)\right]$ with 1. Thus, $pc\left(G\right)=spc\left(G\right)=2$. Assume that $max\left\{\right|N_Q\left(u_1\right)\cap N_Q\left(u_2\right)|,$

$|N_Q\left(u_1\right)\cap N_Q\left(u_3\right)|,|N_Q\left(u_2\right)\cap N_Q\left(u_3\right)\left|\right\}\ge 1$. Without a loss of generality, we consider $|N_Q\left(u_1\right)\cap N_Q\left(u_2\right)| \ge 1$, and say $u\in N_Q\left(u_1\right)\cap N_Q\left(u_2\right)$.

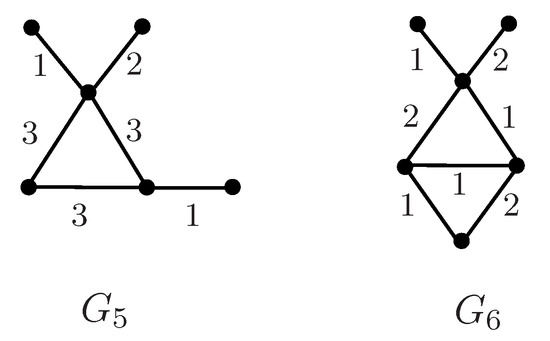
Suppose $d_Q\left(u_1\right)=d_Q\left(u_2\right)=1$. If $\theta$ is a strong proper coloring of G, then $\theta \left(u_{1}u\right)\ne \theta \left(u_{2}u\right)\ne \theta \left(uw\right)$, where $w\in V\left(Q\right)\backslash \left\{u\right\}$. Hence, $spc\left(G\right)\ge 3$. On the other hand, there exists a strong proper coloring ${\theta }^{\prime }$ of G with three colors, as follows: ${\theta }^{\prime }\left(u_{1}u\right)=1$, ${\theta }^{\prime }\left(u_{2}u\right)=2$, and color all edges of $E\left(Q\right)$ with 3 and the remaining edges with 1. Thus, $spc\left(G\right)=3$. Next, we discuss the proper connection number of G. If $n=5$, then $G\cong G_3$, where $G_3$ is displayed in Figure 2. Hence, $pc\left(G\right)=3$. We consider $n=6$. If $d_Q\left(u_3\right)=1$, then $G\cong G_5$. Thus, $pc\left(G\right)=3$. If $d_Q\left(u_3\right)=2$, then $G\cong G_6$. Hence, $pc\left(G\right)=2$. The graphs $G_5$ and $G_6$ are shown in Figure 3. Now, we consider $n\ge 7$. Let $V\left(Q\right)=\{u,v,w_1,w_2,\dots ,w_{n-5}\}$ and $v\in N_Q\left(u_3\right)$. Assign an edge-coloring $\theta$ with two colors to G as follows: $\theta \left(u_{1}u\right)=\theta \left(u_{3}v\right)=\theta \left(u{w}_{n-6}\right)=1$; $\theta \left(u_{2}u\right)=\theta \left(w_{n-5}v\right)=2$; color $w_{n-6}v$ with 1 for $n=7$ and $w_{n-6}v$ with 2 for $n\ge 8$; color the sequence $uv{w}_1{w}_2\cdots w_{n-5}u$ alternately with 2 and 1 starting with $\theta \left(uv\right)=2$; and color the remaining edges arbitrarily with 1 and 2. We can check that G is properly connected with the above edge-coloring, and so $pc\left(G\right)=2$.

Figure 3. The graphs $G_5$ and $G_6$ with a proper-path coloring.

Suppose $max\{d_Q\left(u_1\right),d_Q\left(u_2\right)\}\ge 2$. Without a loss of generality, let $d_Q\left(u_1\right)\ge 2$, and say $w\in N_Q\left(u_1\right)\backslash \left\{u\right\}$. We first consider $N_Q\left(u_1\right)\cap N_Q\left(u_3\right)=Ø$. The following edge-coloring $\theta$ with two colors makes G strongly properly connected: $\theta \left(u_{1}u\right)=1$, $\theta \left(u_{1}w\right)=\theta \left(u_{2}u\right)=2$, color all edges of $E\left(Q\right)$ with 1 and all edges incident with $u_3$ in $E\left[V\right(F),V(Q\left)\right]$ with 2, and color the remaining edges with 1. Thus, $pc\left(G\right)=spc\left(G\right)=2$.

Next, we consider $N_Q\left(u_1\right)\cap N_Q\left(u_3\right)\ne Ø$ and say $w_1\in N_Q\left(u_1\right)\cap N_Q\left(u_3\right)$. Let $d_Q\left(u_1\right)=2$ and $d_Q\left(u_2\right)=d_Q\left(u_3\right)=1$. The following edge-coloring $\theta$ with two colors makes G properly connected: color all edges of $E\left(Q\right)$ with 1 and the remaining edges with 2. Hence, $pc\left(G\right)=2$. If there exists a strong proper coloring $\theta$ of G with two colors, then $\theta \left(u_{1}u\right)\ne \theta \left(u_{2}u\right)$. Without a loss of generality, let $\theta \left(u_{1}u\right)=1$ and $\theta \left(u_{2}u\right)=2$. Since $u_{2}u{w}_1{u}_3$ is the unique $u_2-u_3$ geodesic, it follows that $\theta \left(u{w}_1\right)=1$ and $\theta \left(u_3{w}_1\right)=2$. Note that $u_1{w}_1{u}_3$ is the unique $u_1-u_3$ geodesic, and thus $\theta \left(u_1{w}_1\right)=1$. Since $u_{2}uv$ is the unique $u_2-v$ geodesic and $u_3{w}_{1}v$ is the unique $u_3-v$ geodesic, we obtain $\theta \left(uv\right)=\theta \left(w_{1}v\right)=1$, where $v\in V\left(Q\right)\backslash \{u,w_1\}$. There is no proper geodesic connecting $u_1$ and v, which is a contradiction. Hence, $spc\left(G\right)\ge 3$. On the other hand, we assign a strong proper coloring ${\theta }^{\prime }$ with three colors to G as follows: ${\theta }^{\prime }\left(u_{1}u\right)={\theta }^{\prime }\left(u_3{w}_1\right)=1$, ${\theta }^{\prime }\left(u_{2}u\right)={\theta }^{\prime }\left(u_1{w}_1\right)=2$, and color all edges of $E\left(Q\right)$ with 3. Therefore, $spc\left(G\right)=3$. Let $d_Q\left(u_1\right)\ge 3$. The following edge-coloring $\theta$ of G with two colors makes G strongly properly connected: $\theta \left(u_{1}u\right)=\theta \left(u_1{w}_1\right)=1$, $\theta \left(u_{2}u\right)=\theta \left(u_3{w}_1\right)=\theta \left(u_{1}w\right)=2$, where $w\in N_Q\left(u_1\right)\backslash \{u,w_1\}$, and color the remaining edges with 1. Thus, $pc\left(G\right)=spc\left(G\right)=2$. Let $max\{d_Q\left(u_2\right),d_Q\left(u_3\right)\}\ge 2$. Without a loss of generality, we consider $d_Q\left(u_2\right)\ge 2$. Define an edge-coloring $\theta$ of G with two colors as follows: $\theta \left(u_{1}u\right)=\theta \left(u_3{w}_1\right)=\theta \left(u_{2}z\right)=1$, where $z\in N_Q\left(u_2\right)$, $\theta \left(u_1{w}_1\right)=\theta \left(u_{2}u\right)=2$, and color all edges of $E\left(Q\right)$ with 2 and the remaining edges with 1. Obviously, $\theta$ is a strong proper coloring of G, and so $pc\left(G\right)=spc\left(G\right)=2$.

Case 2. $diam\left(G\right)\ge 4$. Since $diam\left(G\right)\ge 4$, it follows that $F\cong P_3$ or $F\cong K_2+K_1$. Assume that $F\cong P_3$, where $u_1{u}_2,u_2{u}_3\in E\left(G\right)$. Since $diam\left(G\right)\ge 4$, we have $min\{d_Q\left(u_1\right),d_Q\left(u_3\right)\}=0$, $max\{d_Q\left(u_1\right),d_Q\left(u_3\right)\}\ge 1$, and $d_Q\left(u_2\right)=0$. Without a loss of generality, let $d_Q\left(u_1\right)\ge 1$ and $d_Q\left(u_2\right)=d_Q\left(u_3\right)=0$. Note that G is traceable, and we have $pc\left(G\right)=2$ by Proposition 1. The following edge-coloring $\theta$ with two colors makes G strongly properly connected: color $u_1{u}_2$ and all edges of $E\left(Q\right)$ with 2, and color the remaining edges with 1. Thus, $spc\left(G\right)=2$.

Assume that $F\cong K_2+K_1$, where $u_1{u}_2\in E\left(G\right)$. Since $diam\left(G\right)\ge 4$, we have $min\{d_Q\left(u_1\right),d_Q\left(u_2\right)\}=0$, $max\{d_Q\left(u_1\right),d_Q\left(u_2\right)\}\ge 1$, and $d_Q\left(u_3\right)\ge 1$. Without a loss of generality, let $d_Q\left(u_1\right)\ge 1$, $d_Q\left(u_2\right)=0$ and $N_Q\left(u_1\right)\cap N_Q\left(u_3\right)=Ø$. Observe that G is traceable, and we obtain $pc\left(G\right)=2$ by Proposition 1. Assign a strong proper coloring $\theta$ with two colors to G as follows: color $u_1{u}_2$ and all edges of $E\left(Q\right)$ with 2, and color the remaining edges with 1. Hence, $spc\left(G\right)=2$. □

3. Rainbow Connection and Clique Number

Kemnitz and Schiermeyer [18] considered the rainbow connection number of graph G of order n, $diam\left(G\right)=2$, and $\omega \left(G\right)=n-i$ for $2⩽i⩽3$. In this section, we investigate the rainbow connection number of graph G of order n, $diam\left(G\right)\ge 3$, and $\omega \left(G\right)=n-i$ for $2⩽i⩽3$.

Theorem 5. 

Let G be a connected graph of order n, $diam\left(G\right)\ge 3$, and $\omega \left(G\right)=n-2$. Let Q be a maximum clique of G and $V\left(G\right)\backslash V\left(Q\right)=\{u_1,u_2\}$. Then, $rc\left(G\right)=3$.

Proof. 

Let $F=G\left[V\right(G)\backslash V(Q\left)\right]$ and let $\theta$ be an edge-coloring of G. Since $diam\left(G\right)\ge 3$, we have $rc\left(G\right)\ge diam\left(G\right)\ge 3$. Assume that $F\cong K_2$. Since $diam\left(G\right)\ge 3$, we obtain $max\{d_Q\left(u_1\right),d_Q\left(u_2\right)\}\ge 1$ and $min\{d_Q\left(u_1\right),d_Q\left(u_2\right)\}=0$. The following edge-coloring $\theta$ with three colors makes G rainbow-connected: color $u_1{u}_2$ with 1 and all edges of $E\left[V\right(F),V(Q\left)\right]$ with 2, and color all edges of $E\left(Q\right)$ with 3. Thus, $rc\left(G\right)=3$.

Assume that $F\cong 2K_1$. Since G is a connected graph with $diam\left(G\right)\ge 3$, it follows that $d_Q\left(u_1\right)\ge 1$, $d_Q\left(u_2\right)\ge 1$ and $N_Q\left(u_1\right)\cap N_Q\left(u_2\right)=Ø$. Assign an edge-coloring $\theta$ with three colors to G as follows: assign 1 to all edges that are incident with $u_1$, assign 2 to all edges that are incident with $u_2$, and assign 3 to all edges of $E\left(Q\right)$. It is not difficult to check that G is rainbow-connected with the above edge-coloring, and so $rc\left(G\right)=3$. □

Theorem 6. 

Let G be a connected graph of order n, $diam\left(G\right)\ge 3$, and $\omega \left(G\right)=n-3$. Let Q be a maximum clique of G and $V\left(G\right)\backslash V\left(Q\right)=\{u_1,u_2,u_3\}$. Then, either $rc\left(G\right)=3$, or $rc\left(G\right)=4$ if and only if one of the following holds.

(i) 

$G[V\left(G\right)\backslash V\left(Q\right)]\cong P_3$, where $u_1{u}_2,u_2{u}_3\in E\left(G\right)$, $d_Q\left(u_1\right)=d_Q\left(u_3\right)=0$, and $d_Q\left(u_2\right)=1$.

(ii) 

$G[V\left(G\right)\backslash V\left(Q\right)]\cong K_2+K_1$, where $u_1{u}_2\in E\left(G\right)$, $d_Q\left(u_2\right)=0$, $d_Q\left(u_1\right)=d_Q\left(u_3\right)=1$, and $N_Q\left(u_1\right)\cap N_Q\left(u_3\right)\ne Ø$.

(iii) 

$G[V\left(G\right)\backslash V\left(Q\right)]\cong 3K_1$, $N_Q\left(u_1\right)\cap N_Q\left(u_2\right)\cap N_Q\left(u_3\right)=Ø$, $|N_Q\left(u_1\right)\cap N_Q\left(u_2\right)| =1$, and $d_Q\left(u_1\right)=d_Q\left(u_2\right)=d_Q\left(u_3\right)=1$.

(iv) 

$G[V\left(G\right)\backslash V\left(Q\right)]\cong P_3$, where $u_1{u}_2,u_2{u}_3\in E\left(G\right)$, $d_Q\left(u_1\right)\ge 1$, and $d_Q\left(u_2\right)=d_Q\left(u_3\right)=0$.

(v) 

$G[V\left(G\right)\backslash V\left(Q\right)]\cong K_2+K_1$, where $u_1{u}_2\in E\left(G\right)$, $d_Q\left(u_1\right)\ge 1$, $d_Q\left(u_2\right)=0$, $d_Q\left(u_3\right)\ge 1$, and $N_Q\left(u_1\right)\cap N_Q\left(u_3\right)=Ø$.

Proof. 

Let $F=G\left[V\right(G)\backslash V(Q\left)\right]$, and let $\theta$ be an edge-coloring of G. We prove this theorem by the following two cases.

Case 1. $diam\left(G\right)=3$. We have $rc\left(G\right)\ge diam\left(G\right)=3$. We distinguish the following four subcases by analyzing the structure of F.

Subcase 1.1. $F\cong K_3$. The following edge-coloring $\theta$ with three colors makes G rainbow-connected: $\theta \left(u_1{u}_2\right)=\theta \left(u_2{u}_3\right)=\theta \left(u_1{u}_3\right)=1$, and color all edges of $E\left(Q\right)$ with 3 and all edges of $E\left[V\right(F),V(Q\left)\right]$ with 2. Thus, $rc\left(G\right)=3$.

Subcase 1.2. $F\cong P_3$, where $u_1{u}_2,u_2{u}_3\in E\left(G\right)$. Assume that $d_Q\left(u_1\right)=d_Q\left(u_3\right)=0$. Suppose $d_Q\left(u_2\right)=1$, and say $N_Q\left(u_2\right)=\left\{u\right\}$. If an edge-coloring $\theta$ is a rainbow coloring of G, then $\theta \left(u_1{u}_2\right)\ne \theta \left(u_2{u}_3\right)\ne \theta \left(u_{2}u\right)\ne \theta \left(uv\right)$, where $v\in V\left(Q\right)\backslash \left\{u\right\}$. Hence, $rc\left(G\right)\ge 4$. Allocate a rainbow coloring ${\theta }^{\prime }$ with four colors to G as follows: ${\theta }^{\prime }\left(u_1{u}_2\right)=1$, ${\theta }^{\prime }\left(u_2{u}_3\right)=2$, ${\theta }^{\prime }\left(u_{2}u\right)=3$, and color all edges of $E\left(Q\right)$ with 4. Thus, $rc\left(G\right)=4$. Suppose $d_Q\left(u_2\right)\ge 2$, and say $u,v\in N_Q\left(u_2\right)$. The following edge-coloring $\theta$ with three colors makes G rainbow-connected: $\theta \left(u_1{u}_2\right)=\theta \left(u_{2}u\right)=1$, $\theta \left(u_2{u}_3\right)=\theta \left(u_{2}v\right)=2$, and color the remaining edges with 3. Hence, $rc\left(G\right)=3$.

Assume that $min\{d_Q\left(u_1\right),d_Q\left(u_3\right)\}=0$ and $max\{d_Q\left(u_1\right),d_Q\left(u_3\right)\}\ge 1$. Without a loss of generality, let $d_Q\left(u_3\right)=0$ and $d_Q\left(u_1\right)\ge 1$. Since $diam\left(G\right)=3$, we have $d_Q\left(u_2\right)\ge 1$. Define an edge-coloring $\theta$ of G with three colors as follows: $\theta \left(u_1{u}_2\right)=1$, $\theta \left(u_2{u}_3\right)=2$, and color all edges of $E\left[V\right(F),V(Q\left)\right]$ with 1 and all edges of $E\left(Q\right)$ with 3. We can check that G is rainbow-connected with the above edge-coloring, and so $rc\left(G\right)=3$.

Assume that $d_Q\left(u_1\right)\ge 1$ and $d_Q\left(u_3\right)\ge 1$. Since $diam\left(G\right)=3$, it follows that $d_Q\left(u_2\right)=0$ and $N_Q\left(u_1\right)\cup N_Q\left(u_3\right)\ne V\left(Q\right)$. The following edge-coloring $\theta$ with three colors makes G rainbow-connected: $\theta \left(u_1{u}_2\right)=1$, $\theta \left(u_2{u}_3\right)=2$, assign 3 to all edges of $E\left(Q\right)$, assign 2 to the edges of $E\left[V\right(F),V(Q\left)\right]$ which are incident with $u_1$, and assign 1 to the edges of $E\left[V\right(F),V(Q\left)\right]$ which are incident with $u_3$. Thus, $rc\left(G\right)=3$.

Subcase 1.3. $F\cong K_2+K_1$, where $u_1{u}_2\in E\left(G\right)$. Since G is connected, we obtain $d_Q\left(u_3\right)\ge 1$ and $max\{d_Q\left(u_1\right),d_Q\left(u_2\right)\}\ge 1$. Without a loss of generality, let $d_Q\left(u_1\right)\ge 1$.

Assume that $d_Q\left(u_2\right)=0$. Since $diam\left(G\right)=3$, we have $N_Q\left(u_1\right)\cap N_Q\left(u_3\right)\ne Ø$, and say $u\in N_Q\left(u_1\right)\cap N_Q\left(u_3\right)$. Suppose $d_Q\left(u_1\right)=d_Q\left(u_3\right)=1$. If there exists a rainbow coloring $\theta$ of G with three colors, then $\theta \left(u_2{u}_1\right)\ne \theta \left(u_{1}u\right)\ne \theta \left(u{u}_3\right)$. Without a loss of generality, let $\theta \left(u_2{u}_1\right)=1$, $\theta \left(u_{1}u\right)=2$ and $\theta \left(u{u}_3\right)=3$. In order to have a rainbow path connecting $u_2$ and v for any $v\in V\left(Q\right)\backslash \left\{u\right\}$, let $\theta \left(uv\right)=3$. There is no rainbow path between $u_3$ and v, which is a contradiction. Thus, $rc\left(G\right)\ge 4$. On the other hand, the following edge-coloring ${\theta }^{\prime }$ with four colors makes G rainbow-connected: ${\theta }^{\prime }\left(u_2{u}_1\right)=1$, ${\theta }^{\prime }\left(u_{1}u\right)=2$, ${\theta }^{\prime }\left(u{u}_3\right)=3$, and color all edges of $E\left(Q\right)$ with 4. Hence, $rc\left(G\right)=4$. Suppose $max\{d_Q\left(u_1\right),d_Q\left(u_3\right)\}\ge 2$. We first consider $d_Q\left(u_1\right)\ge 2$, and say $v\in N_Q\left(u_1\right)\backslash \left\{u\right\}$. Assign an edge-coloring $\theta$ with three colors to G as follows: $\theta \left(u_2{u}_1\right)=1$, $\theta \left(u_{1}u\right)=2$, $\theta \left(u_{3}u\right)=\theta \left(u_{1}v\right)=3$, and color the remaining edges with 2. It is obvious that G is rainbow-connected with the above edge-coloring, and so $rc\left(G\right)=3$. Next, we consider $d_Q\left(u_3\right)\ge 2$, and say $w\in N_Q\left(u_3\right)\backslash \left\{u\right\}$. Define a rainbow coloring $\theta$ of G with three colors as follows: $\theta \left(u_2{u}_1\right)=1$, $\theta \left(u_{1}u\right)=\theta \left(u_{3}w\right)=2$, $\theta \left(u_{3}u\right)=3$, and color all edges of $E\left(Q\right)$ with 3 and the remaining edges with 2. Thus, $rc\left(G\right)=3$.

Assume that $d_Q\left(u_2\right)\ge 1$. Since $diam\left(G\right)=3$, we obtain $min\left\{\right|N_Q\left(u_1\right)\cap N_Q\left(u_3\right)|,|N_Q$

$\left(u_2\right)\cap N_Q\left(u_3\right)\left|\right\}=0$. Suppose $max\left\{\right|N_Q\left(u_1\right)\cap N_Q\left(u_3\right)|,|N_Q\left(u_2\right)\cap N_Q\left(u_3\right)\left|\right\}\ge 1$. Without a loss of generality, let $|N_Q\left(u_1\right)\cap N_Q\left(u_3\right)| \ge 1$ and $|N_Q\left(u_2\right)\cap N_Q\left(u_3\right)| =0$. Let $u\in N_Q\left(u_1\right)\cap N_Q\left(u_3\right)$ and $v\in N_Q\left(u_2\right)$. The following edge-coloring $\theta$ with three colors makes G rainbow-connected: $\theta \left(u_{1}u\right)=\theta \left(u_{2}v\right)=1$, $\theta \left(u_{3}u\right)=2$, and color the remaining edges with 3. Hence, $rc\left(G\right)=3$. Suppose $max\left\{\right|N_Q\left(u_1\right)\cap N_Q\left(u_3\right)|,|N_Q\left(u_2\right)\cap N_Q\left(u_3\right)\left|\right\}=0$. Let $w\in N_Q\left(u_1\right),v\in N_Q\left(u_2\right)$ and $u\in N_Q\left(u_3\right)$, where $w=v$ is possible. Allocate an edge-coloring $\theta$ with three colors to G: $\theta \left(u_1{u}_2\right)=\theta \left(u_{3}u\right)=1$, $\theta \left(u_{1}w\right)=\theta \left(u_{2}v\right)=2$, and color the remaining edges with 3. We can verify that G is rainbow-connected with the above edge-coloring, and so $rc\left(G\right)=3$.

Subcase 1.4. $F\cong 3K_1$. Since $diam\left(G\right)=3$, it follows that $min\left\{\right|N_Q\left(u_1\right)\cap N_Q\left(u_2\right)|,|N_Q$

$\left(u_1\right)\cap N_Q\left(u_3\right)|,|N_Q\left(u_2\right)\cap N_Q\left(u_3\right)\left|\right\}=0$. Assume that $max\left\{\right|N_Q\left(u_1\right)\cap N_Q\left(u_2\right)|,|N_Q\left(u_1\right)\cap N_Q\left(u_3\right)|,|N_Q\left(u_2\right)\cap N_Q\left(u_3\right)\left|\right\}=0$. Let $u\in N_Q\left(u_1\right),v\in N_Q\left(u_2\right)$ and $w\in N_Q\left(u_3\right)$. The following edge-coloring $\theta$ with three colors makes G rainbow-connected: $\theta \left(u_{1}u\right)=\theta \left(vw\right)=\theta \left(vz\right)=1$; $\theta \left(uv\right)=\theta \left(u_{3}w\right)=\theta \left(uz\right)=2$; $\theta \left(u_{2}v\right)=\theta \left(uw\right)=\theta \left(wz\right)=3$ for any $z\in V\left(Q\right)\backslash \{u,v,w\}$; and color the remaining edges with 1. Thus, $rc\left(G\right)=3$.

Assume that $max\left\{\right|N_Q\left(u_1\right)\cap N_Q\left(u_2\right)|,|N_Q\left(u_1\right)\cap N_Q\left(u_3\right)|,|N_Q\left(u_2\right)\cap N_Q\left(u_3\right)\left|\right\}\ge 1$. Without a loss of generality, let $|N_Q\left(u_1\right)\cap N_Q\left(u_2\right)| \ge 1$, and say $u\in N_Q\left(u_1\right)\cap N_Q\left(u_2\right)$. Suppose $d_Q\left(u_1\right)=d_Q\left(u_2\right)=d_Q\left(u_3\right)=1$. If an edge-coloring $\theta$ is a rainbow coloring of G, then $\theta \left(u_{1}u\right)\ne \theta \left(u_{2}u\right)\ne \theta \left(uv\right)\ne \theta \left(u_{3}v\right)$, where $\left\{v\right\}=N_Q\left(u_3\right)$. Thus, $rc\left(G\right)\ge 4$. On the other hand, we define a rainbow coloring ${\theta }^{\prime }$ of G with four colors as follows: ${\theta }^{\prime }\left(u_{1}u\right)=1,{\theta }^{\prime }\left(u_{2}u\right)=2,{\theta }^{\prime }\left(u_{3}v\right)=3$, and color all edges of $E\left(Q\right)$ with 4. Hence, $rc\left(G\right)=4$. Suppose $max\{d_Q\left(u_1\right),d_Q\left(u_2\right)\}\ge 2$. Without a loss of generality, let $d_Q\left(u_1\right)\ge 2$, and say $w\in N_Q\left(u_1\right)\backslash \left\{u\right\}$. Assign an edge-coloring $\theta$ with three colors to G: $\theta \left(u_{1}u\right)=\theta \left(u_{2}u\right)=1$; $\theta \left(u_{1}w\right)=\theta \left(u_{3}v\right)=2$, where $v\in N_Q\left(u_3\right)$ and $v=w$ is possible; and color the remaining edges with 3. Obviously, the edge-coloring $\theta$ is a rainbow coloring of G, and so $rc\left(G\right)=3$. Suppose $d_Q\left(u_3\right)\ge 2$, and say $v_1,v_2\in N_Q\left(u_3\right)$. The following edge-coloring $\theta$ with three colors makes G rainbow-connected: $\theta \left(u_{1}u\right)=\theta \left(u_3{v}_1\right)=1$, $\theta \left(u_{2}u\right)=\theta \left(u_3{v}_2\right)=2$, and color the remaining edges with 3. Thus, $rc\left(G\right)=3$.

Case 2. $diam\left(G\right)\ge 4$. We obtain $rc\left(G\right)\ge diam\left(G\right)\ge 4$. Since $diam\left(G\right)\ge 4$, it follows that $F\cong P_3$ or $F\cong K_2+K_1$. Assume that $F\cong P_3$, where $u_1{u}_2,u_2{u}_3\in E\left(G\right)$. Since $diam\left(G\right)\ge 4$, we have $min\{d_Q\left(u_1\right),d_Q\left(u_3\right)\}=0$, $max\{d_Q\left(u_1\right),d_Q\left(u_3\right)\}\ge 1$, and $d_Q\left(u_2\right)=0$. Without a loss of generality, let $d_Q\left(u_1\right)\ge 1$ and $d_Q\left(u_2\right)=d_Q\left(u_3\right)=0$. Allocate a rainbow coloring $\theta$ with four colors to G as follows: color $u_1{u}_2$ with 2 and $u_2{u}_3$ with 1, and color all edges of $E\left[V\right(F),V(Q\left)\right]$ with 3 and all edges of $E\left(Q\right)$ with 4. Therefore, $rc\left(G\right)=4$.

Assume that $F\cong K_2+K_1$, where $u_1{u}_2\in E\left(G\right)$. Since $diam\left(G\right)\ge 4$, it follows that $min\{d_Q\left(u_1\right),d_Q\left(u_2\right)\}=0$, $max\{d_Q\left(u_1\right),d_Q\left(u_2\right)\}\ge 1$, and $d_Q\left(u_3\right)\ge 1$. Without a loss of generality, let $d_Q\left(u_1\right)\ge 1$, $d_Q\left(u_2\right)=0$, and $N_Q\left(u_1\right)\cap N_Q\left(u_3\right)=Ø$. The following edge-coloring $\theta$ with four colors makes G rainbow-connected: $\theta \left(u_1{u}_2\right)=1$, $\theta \left(u_{1}u\right)=2$, and $\theta \left(u_{3}v\right)=3$, where $u\in N_Q\left(u_1\right)$ and $v\in N_Q\left(u_3\right)$, and color the remaining edges with 4. Hence, $rc\left(G\right)=4$. □