Abstract
This research work is devoted to undertaking a dynamical system representing SARS-CoV-19 disease under the concept of piecewise fractional-order derivative using the Caputo concept since long-memory and short-memory terms are not well explained by ordinary fractional differential equations. It has been found that for such disruption, piecewise operators of fractional derivatives have been found useful in many cases. Therefore, we study a compartmental model of susceptible and infected individuals under the concept of piecewise derivative. We establish the existence theory of the considered model by using some Banach and Schauder fixed-point theorems. Keeping the importance of stability, a pertinent result related to the said area is also developed. The said concept of stability is based on the concept given by Ulam and Hyers. Further, to derive the numerical results, we use the Euler method to develop a numerical scheme for the considered model. Using real available data, we have presented various graphical presentations of two compartments against different fractional orders and various values of isolation parameters. The crossover behaviors in the dynamics can be clearly observed, which is explained by the piecewise operators, not the usual fractional-order derivative.
Keywords:
SARS-CoV-19 model; fractional differential equations; stability; existence theory; numerical scheme MSC:
34A08; 37Mxx; 92-XX; 92Bxx
1. Introduction
Mathematical models play a vital role in the analysis, spreading, and predictions of infectious diseases. They are very important in understanding how to analyze efficient control of viruses and also prevention efforts [1,2,3]. There are various infectious diseases, with compartmental models ranging from the SIR model to some more complicated ones [4]. There are a lot of diseases, such as Dengue fever, Hanta fever, and Leptospirosis, that are widely spreading throughout the world [5,6]. Diseases that spread from one person to another through various are called infectious diseases. Additionally, noninfectious diseases are caused by inherited or environmental factors. Throughout history, infectious diseases have resulted in the loss of a huge number of human lives. The latest epidemic, which originated in China, is known as SARS-CoV-19. It is a serious respiratory infection with a high mortality rate. China gained control over the SARS outbreak because of a combination of restrictions and effective prevention measures. Among other viral diseases, the recent COVID-19 pandemic has produced a worldwide disaster, including over eight million individuals affected and a mortality-to-recovery ratio that looks to be in a favorable proportion. Despite the fact that COVID-19 has been known about and researched for a long time by medical professionals and researchers, many individuals are unaware of the condition. Vaccinations and antiviral medications to prevent or cure the infection are still unavailable [7,8,9]. In contrast to SARS-CoV 2003, COVID-19 has a considerable and lengthy incubation time. Recently, some remarkable work has been published on the mentioned disease model, such as [10,11].
Here, it should be kept in mind that epidemiology is the branch of science that essentially deals with the mathematical modeling of the spread of diseases. Moreover, mathematical modeling in epidemiology is concerned with describing the spread of disease and its effect on people. During the past 70 years, the study of infectious disease dynamics has matured into a rich interdisciplinary field at the intersection of mathematics, epidemiology, computational physics, ecology, evolutionary biology, immunology, sociology, and public health. Therefore, such and related infectious diseases could be modeled via different mathematical tools. The most common techniques for modeling epidemic diseases include ordinary differential equations, partial differential equations, and stochastic and delay differential equations. There has been a lot of research on the mathematical models for infectious diseases with the consideration of fractional and fractal-fractional operators, for instance, see [12,13,14].
There are numerous definitions of fractional calculus that were successfully applied to different systems where some nice properties of the underlying systems were derived by the researchers [15,16,17]. Physical phenomena frequently undergo sudden changes that standard derivatives of either fractional or integer ordering struggle to adequately describe since ordinary fractional differential operators involve long memory and hence cannot accommodate those evolutionary processes that depend upon short memory. The aforesaid property has been discussed in detail in [18,19] by using the concept of piecewise derivative of fractional order. Hence, it has been concluded by the authors that the mentioned aspect of fractional calculus can be used as a powerful tool to describe many real-world variations in their dynamical behaviors. Following the mentioned importance, authors [20] have extended the said concepts of fractional calculus to define other forms of operators involving piecewise form. Comparatively to a conventional fractional derivative, the above-mentioned operators are more commonly able to characterize such phenomena. The authors of [21] established some qualitative results using the aforesaid concept.
Coupled systems, due to the wide range of applications, have attracted the attention of many researchers. Because of their extensive applications in many fields, including the synchronization of chaos theory, coupled systems consisting of real order equations have been researched thoroughly. In this regard, various systems involving usual fractional derivatives have been studied in [22,23,24,25]. The concept of piecewise has been extended to coupled systems recently. For instance, the authors of [26] studied the existence and stability results of a model involving piecewise derivative using the non-singular derivative concept. The authors of [27] used the piecewise forms of fractional calculus and addressed the qualitative aspects of a coupled problem of blood therapy. These novel operators are quite useful since they allow one to examine a mathematical model using both classical operators as well as fractional operators in a single interval that is separated into two sub-intervals. These operators have provided researchers with a fresh avenue to investigate cross-over behaviors. For some details, we refer to [28,29,30,31].
Here, it should be keep in mind that usual fractional order models provide almost identical results up to the peak of the number of infected humans, whereas the later phase of the epidemic is more accurately modeled by the system using the modified parameters. Moreover, we demonstrate that a nonlinear fractional order differential equation model can simulate the dynamics of the epidemic much more accurately than the classical model based on first derivatives. However, the crossover behaviors in the dynamics cannot be well elaborated by using classical or usual fractional order models. The concerned effect can be more precisely described by using the concept of piecewise fractional-order derivatives. Most of the COVID-19 mathematical models have been studied by using the concept of fractional ordinary derivatives with singuler or non-singular kernels. However, the concept of piecewise derivatives has been very rarely used for the aforementioned models. Motivated by these benefits, we investigate the proposed COVID-19 model using classical and Caputo piecewise operators. Here, in this work, we intend to use the techniques of [32] and investigate the dynamical aspects of a generalized epidemic model. The classical form of the proposed model has been studied in [33] and described as
In the above model, and represent the susceptible and infected individuals, respectively, at any time period t. We extend the operator to piecewise form and consider the model (1) as
where represents the piecewise operator with order . The nomenclatures involved in the model (2) are described in Table 1.

Table 1.
Nomenclature involve in model (2) and their description.
Stability is an important consequence of applied analysis. Different concepts about stability analysis have been used in literature. Here, we will use the concepts given by Ulam and Hyers. The mentioned concepts have been used in many research articles, such as [34,35]. We will use the typical fixed-point theorems of Banach, Schauder, and Arzelá and the Ulam–Hyers type of stability results associated with the proposed model to be investigated. We enrich this section by formulating a new model. Additionally, we construct the flow charts of the interaction of different compartments of the model with each other.
2. Preliminaries
Fundamentals concepts, lemmas, and notions are recollected from frictional differential calculus. This detail is examined in [20,32].
Definition 1.
The piecewise version of the Riemann–Liouville integral of a continuous function , where is defined as
Definition 2.
The piecewise classical and arbitrary order derivative in the sense of Caputo is given by
Lemma 1.
The solution of
is given by
3. Qualitative Results
To discuss the dynamical properties of the proposed model, we will consider the product and Banach spaces. Let
and
are the Banach spaces endowed with the norms and , respectively. In addition, the product space is also a Banach space, with the norm defined by
Corollary 1.
Using Lemma 1, the solution of the system (2) is given by
For the analysis, we must show that the below data-dependence results are true.
- (A1):
- There exist constants and such that for every
- (A2):
- For constants , , , and , the following assertions (also called the growth condition) are satisfied
To establish the theory related to the existence of solution, firstly, we need to define
by
Furthermore, one can express these operators in extended form as
and
Theorem 1.
Under the assumption , the problem (2) has a unique solution if the condition holds, where
Proof.
Consider and in ; we prove the results as follow:
Cases-I: At , then from (9)
Taking the maximum value of both sides of (11), we have
Repeating the above procedure for the operator given in (10) at as
Hence, using one has from (14) that
Next, we prove the results for .
Cases-II: Let then one has
Applying assumption after simplification, one has from (16)
Repeating the same procedure for second operator on , we have
Let ; then, (19) yields
Thus, we have from (20)
Hence, if , hence all the conditions of Banach theorem hold. Thus, (2) has at most one solution. □
Theorem 2.
The considered system (2) has at least one solution under the hypothesis .
Proof.
If is closed and convex, such that and there exist two operators as
then we derive the proof as
Case-I:At
Step-1: If at one has
In the same way for the second operator, one has
Let and and Then, (27) implies that
where
Hence, Thus, H is bounded and ; this implies that with
Case-II: For for at one has
In the same line, one has also
Thus one has
Using for easiness the notions and Then Now if then Additionally H is bounded. Moreover, at
Step-2: Since Hence are continuous in the same domain. Now to show that is equi-continuous, Let then one has
and
Since are bounded in H is also bounded, which implies uniformly continuity; hence, we obtain
Now if then
Hence (30), we see if in the right side, which becomes zero, so
Additionally, is bounded over , so it is uniformly continuous and hence
Similarly, we have
Thus, H is equi-continuous. As a result, all of the requirements for approximately compactness are met, and H has at least one fixed value. Subsequently, a solution to model (2) exists. □
4. Ulam–Hyers Stability Analysis
Stability is an important branch of qualitative analysis. Here, we establish the said aspect using the Ulam–Hyers concept.
Definition 3.
The solution satisfies the given system of inequalities for any such that
is said to be Ulam–Hyers stable if there exists a unique solution and constant with
Let a function f does not depend upon and such that ; then,
Remark 1.
Lemma 2.
Proof.
□
Theorem 3.
Model (2) is Ulam–Hyers stable if and where
Proof.
If is the unique solution and is any solution of (2), then for and in view of assumption , and using Lemma 2, one has
and
Let us use ; then, we have from (41)
In the same line for we have
and
For easiness, we put ; then, (45) yields
Hence, the solution is Ulam -Hyers stable.
Furthermore, whenever a function (constant or increasing) from exists such that Then, by using (47), we have
with which proves that considered system is generalized Ulam–Hyers stable. □
5. Numerical Scheme
We provide a method for computing answers numerically to our suggested system (2). We create a framework for our simulation solution using the laws of definite integrals. We must build the approach for the first DE of the system (2) and then apply it to the following equations. The scheme (to be developed) has been explained and applied in detail in [36]. We extended the usual RK2 formula for the concept of the piecewise derivative. The classical form of the said scheme has been given in [37]. For the classical order derivative in and the fractional order Caputo derivative We write (2) using with as
Now, the numerical scheme based on RK2 method can be written for (49) by using first equation as
where and
In the same fashion, we can write for the second equation of the system (49) as
6. Results and Discussion
Here in this section, we present a numerical discussion to the proposed model by using the given values of the Table 2. In addition, take initial values as given in [7] as = 220 millions, = 0.142 million.

Table 2.
Nomenclature and numerical values are taken from [7].
Using Matlab 16, we present the graphical presentation of the considered model for different fractional order in Figure 1, Figure 2, Figure 3 and Figure 4, respectively. Here, we consider an isolation rate of approximately 30%.
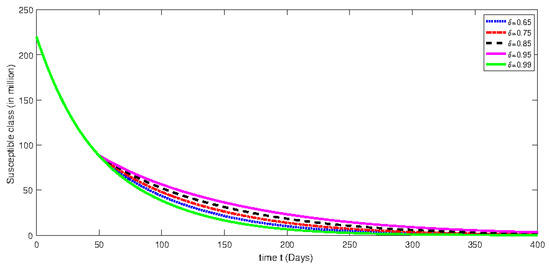
Figure 1.
Numerical solution for susceptible class for the given days and using different fractional orders with isolation rate of 30%.
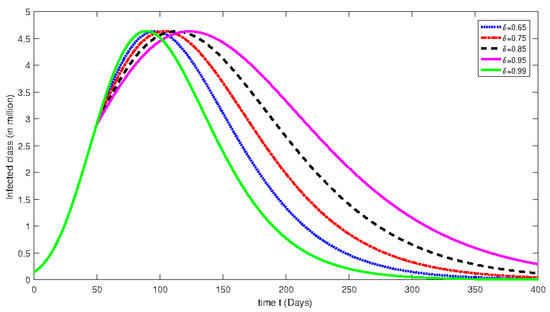
Figure 2.
Numerical solution for infected class for the given days and using different fractional orders with isolation rate of 30%.
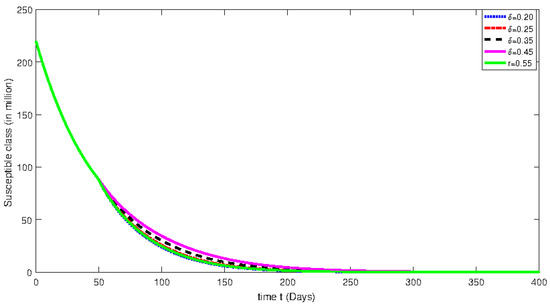
Figure 3.
Numerical solution for susceptible class for the given days and using different fractional orders with isolation rate of 30%.
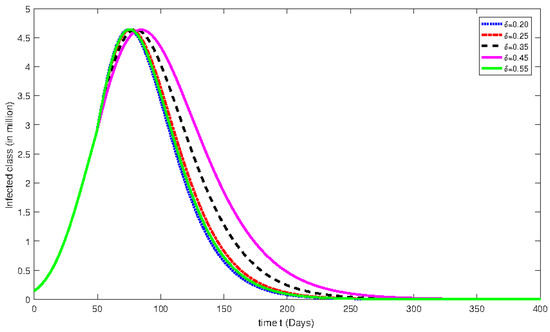
Figure 4.
Numerical solution for infected class for the given days and using different fractional orders with isolation rate of 30%.
Further, we present the graphical presentation of the considered model for different fractional order in Figure 5, Figure 6, Figure 7 and Figure 8, respectively. Here, we consider an isolation rate of approximately 50%.
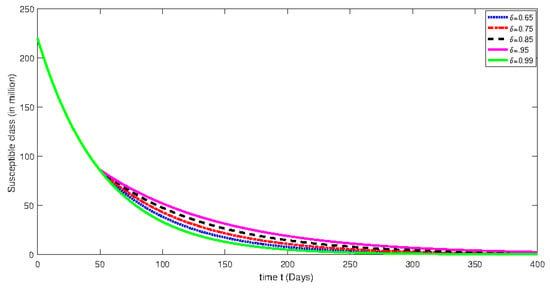
Figure 5.
Numerical solution for susceptible class for the given days and using different fractional orders with isolation rate of 50%.
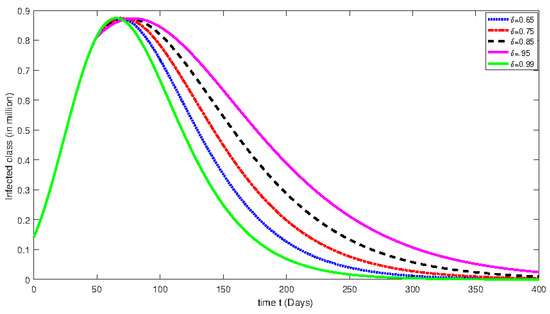
Figure 6.
Numerical solution for infected class for the given days and using different fractional orders with isolation rate of .
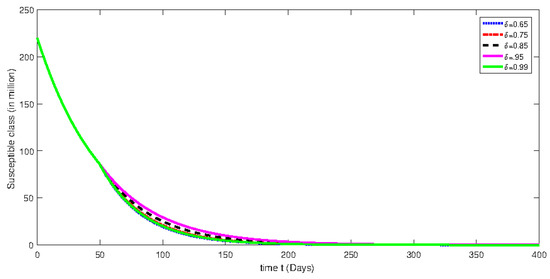
Figure 7.
Numerical solution for susceptible class for the given days and using different fractional orders with isolation rate of 50%.
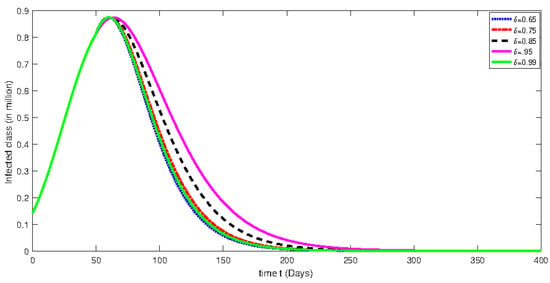
Figure 8.
Numerical solution for infected class for the given days and using different fractional orders with isolation rate of 50%.
In addition, to see the effect of greater isolation on the dynamics, we present the graphical presentation of the considered model for different fractional order in Figure 9, Figure 10, Figure 11 and Figure 12, respectively. Here, we consider isolation rate approximately 70%.
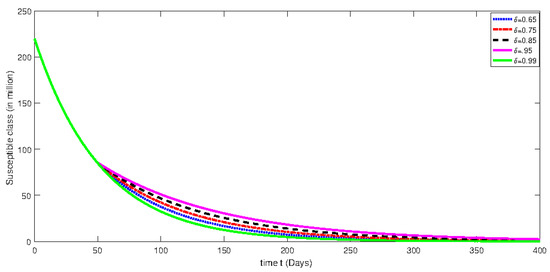
Figure 9.
Numerical solution for susceptible class for the given days and using different fractional orders with isolation rate of 70%.
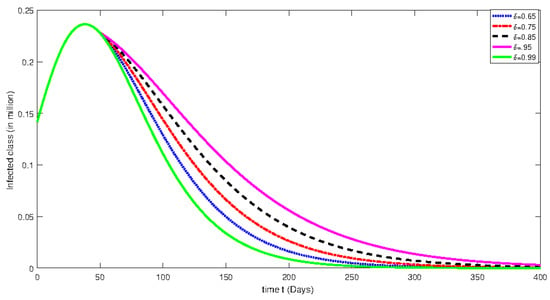
Figure 10.
Numerical solution for infected class for the given days and using different fractional orders with isolation rate of 70%.

Figure 11.
Numerical solution for susceptible class for the given days and using different fractional orders with isolation rate of 70%.
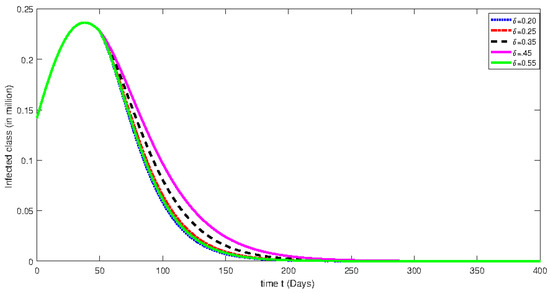
Figure 12.
Numerical solution for infected class for the given days and using different fractional orders with isolation rate of 70%.
From Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12, we see that at greater fractional order the effect of memory is more clear. Additionally, with the passage of time, the population of susceptible class is decreasing until it becomes stable and the convergent effect can be observed clearly. On the other hand, an infected class population initially increases for less than 100 days and then decreases. Moreover, the dynamical behavior effect has also been investigated by using various rate of isolation. The greater the isolation value, the smaller the spreading of the infection process will be. On the other hand, we see that the effect of memory is decreasing when the fractional order values are decreasing. The dynamical behaviors of both classes are the same as mentioned earlier. Further, the change in dynamical behavior near the point t = 100 can be observed clearly. After the mentioned point, the dynamics assume the multi-behaviors. This multi-behavior can only be clearly and brilliantly detected by using the piecewise derivative concept.
7. Conclusions
In this research work, we study a dynamical model that predicts COVID-19 disease infection. We have used a piecewise derivative concept to detect the multi-behavior concept and short memory effect in the dynamics of the considered system. We have proved some conditions for the existence of at least one solution and its uniqueness through a fixed-point approach. Additionally, we have used some numerical tools to study the numerical analysis of the proposed model. Using some real data, we have presented the numerical analysis of the corresponding compartments graphically against various fractional orders. Additionally, the effect of isolation has been verified by using various values of it. The greater the isolation effect, the less will be the chance of spreading of infection. Here, it is remarkable that using the Caputo type of fractional derivative, we bring forth a concept of “memory-dependent derivative”, which is simply expressed in an integral form of a ordinary and fractional derivative with a kernel function on a slipping interval. In the same way, high-order derivatives can also be accorded with the first-order one. Comparatively, the form of kernel function for the fractional type has been kept fixed, although for the memory-dependent type it can be selected freely corresponding to the necessity of applications. So, this kind of definition is better than the fractional one for reflecting the memory effect (the instantaneous rate of change depends on the past state). The important mathematical model describing the evolution of infectious diseases is called compartmental models. The foundation was built by Kermack and Mckendrick in 1927 for the first time to study the spread of the infectious diseases in community. The fractional derivative epidemic models provide a powerful instrument for the incorporation of memory and the hereditary properties of the systems as opposed to the integer-order models, where such effects are ignored or difficult to incorporate. In addition, when fitting data, the fractional models have one more degree of freedom than the integer-order model. The proposed model is a very simple model that contains two compartments, and many other classes have been ignored. Here, we have established the qualitative analysis of the existence theory of solution and numerical interpretation. However, in future, we will include more classes like exposed, recovered, asymptomatic, hospitalized, and vaccinated classes to form a more complex model under the piecewise derivatives with different form of kernels. However, from present results, we concluded that the piecewise derivative can help to understand the effect of the short memory effect in the dynamical systems, which cannot be explained through an ordinary fractional-order derivative.
Author Contributions
S.K. wrote the draft. Z.A.K. edited the paper. H.A. included the formal analysis. S.Z. included the numerical part. The revised version has been checked and approved by all of the authors. All authors have read and agreed to the published version of the manuscript.
Funding
The APC has been funded by Princess Nourah bint Abdulrahman University.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All of the data used are included within the paper.
Acknowledgments
Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R8). Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Goyal, M.; Baskonus, H.M.; Prakash, A. An efficient technique for a time fractional model of lassa hemorrhagic fever spreading in pregnant women. Eur. Phys. J. Plus 2019, 134, 482. [Google Scholar] [CrossRef]
- Gao, W.; Veeresha, P.; Prakasha, D.G.; Baskonus, H.M.; Yel, G. New approach for the model describing the deathly disease in pregnant women using Mittag-Leffler function. Chaos Solitons Fractals 2020, 134, 109696. [Google Scholar] [CrossRef]
- Khan, M.A.; Atangana, A. Modeling the dynamics of novel Coronavirus (2019–nCov) with fractional derivative. Alex. Eng. J. 2020, 59, 2379–2389. [Google Scholar] [CrossRef]
- Shah, K.; Alqudah, M.A.; Jarad, F.; Abdeljawad, T. Semi-analytical study of Pine Wilt Disease model with convex rate under Caputo-Febrizio fractional-order derivative. Chaos Solitons Fractals 2020, 135, 109754. [Google Scholar] [CrossRef]
- Xu, C.; Alhejaili, W.; Saifullah, S.; Khan, A.; Khan, J.; El-Shorbagy, M.A. Analysis of Huanglongbing disease model with a novel fractional piecewise approach. Chaos Soliton Fractals 2022, 161, 112316. [Google Scholar] [CrossRef]
- Qu, H.; Saifullah, S.; Khan, J.; Khan, A.; ur Rahman, M.; Zheng, G. Dynamics of Leptospirosis disease in the context of piecewise classical-global and classical-Caputo fractional operators. Fractals 2022, 30, 2240216. [Google Scholar] [CrossRef]
- Arfan, M.; Shah, K.; Abdeljawad, T.; Mlaiki, N.; Ullah, A. A Caputo Power law model prediciting the spread of the COVID-19 out breaking Pakistan. Alex. Eng. J. 2021, 60, 447–456. [Google Scholar]
- Wrapp, D.; Wang, N.; Corbett, K.S.; Goldsmith, J.A.; Hsieh, C.L.; Abiona, O.; Graham, B.S.; McLellan, J.S. Cryo-EM structure of the 2019-nCoV spike in the prefusion conformation. Science 2020, 367, 1260–1263. [Google Scholar] [CrossRef]
- Rothe, C.; Schunk, M.; Sothmann, P.; Bretzel, G.; Froeschl, G.; Wallrauch, C.; Zimmer, T.; Thiel, V.; Janke, C.; Guggemos, W.; et al. Transmission of 2019-nCoV infection from an asymptomatic contact in Germany. N. Engl. J. Med. 2020, 382, 970–971. [Google Scholar] [CrossRef]
- Ahmad, Z.; Arif, M.; Ali, F.; Khan, I.; Nisar, K.S. A report on COVID-19 epidemic in Pakistan using SEIR fractional model. Sci. Rep. 2020, 10, 22268. [Google Scholar] [CrossRef]
- Ahmad, Z.; Khan, N.; Arif, M.; Murtaza, S.; Khan, I. Dynamics of fractional order SIR model with a case study of COVID-19 in Turkey. City Univ. Int. J. Comput. Anal. 2020, 4, 18–35. [Google Scholar]
- Algahtani, O.J.J. Comparing the Atangana-Baleanu and Caputo-Fabrizio derivative with fractional order: Allen Cahn model. Chaos Solitons Fractals 2016, 89, 552–559. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Hilfer, R. Mathematical and physical interpretations of fractional derivatives and integrals. Handb. Fract. Calc. Appl. 2019, 1, 47–85. [Google Scholar]
- Caputo, M.; Fabrizio, M. On the notion of fractional derivative and applications to the hysteresis phenomena. Meccanica 2017, 52, 3043–3052. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonl. Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Ionescu, C.; Lopes, A.; Copot, D.; Machado, J.T.; Bates, J.H. The role of fractional calculus in modeling biological phenomena: A review. Commun. Nonl. Sci. Numer. Simul. 2017, 51, 141–159. [Google Scholar] [CrossRef]
- Wu, G.C.; Zeng, D.Q.; Baleanu, D. Fractional impulsive differential equations: Exact solutions, integral equations and short memory case. Fract. Calc. Appl. Anal. 2019, 22, 180–192. [Google Scholar] [CrossRef]
- Wu, G.C.; Luo, M.; Huang, L.L.; Banerjee, S. Short memory fractional differential equations for new memristor and neural network design. Nonlinear Dyn. 2020, 100, 3611–3623. [Google Scholar] [CrossRef]
- Atangana, A.; Araz, S.I. New concept in calculus: Piecewise differential and integral operators. Chaos Solitons Fractals 2021, 145, 110638. [Google Scholar] [CrossRef]
- Shah, K.; Deljawad, T.; Abdalla, B.; Abualrub, M.S. Utilizing fixed point approach to investigate piecewise equations with non-singular type derivative. AIMS Math. 2022, 7, 14614–14630. [Google Scholar] [CrossRef]
- Shah, K.; Ahmad, I.; Nieto, J.J.; Rahman, G.U.; Abdeljawad, T. Qualitative investigation of nonlinear fractional coupled pantograph impulsive differential equations. Qual. Theory Dyn. Syst. 2022, 21, 131. [Google Scholar] [CrossRef]
- Ahmad, M.; Zada, A.; Alzabut, J. Stability analysis of a nonlinear coupled implicit switched singular fractional differential system with p-Laplacian. Adv. Differ. Equat. 2019, 2019, 436. [Google Scholar] [CrossRef]
- Nawaz, Y.; Arif, M.S.; Abodayeh, K. A numerical scheme for fractional mixed convection flow over flat and oscillatory plates. J. Comput. Nonlinear Dyn. 2022, 17, 071008. [Google Scholar] [CrossRef]
- Laksaci, N.; Boudaoui, A.; Shatanawi, W.; Shatnawi, T.A. Existence results of global solutions for a coupled implicit Riemann–Liouville fractional integral equation via the vector kuratowski measure of noncompactness. Fractal Fract. 2022, 6, 130. [Google Scholar] [CrossRef]
- Shah, K.; Abdeljawad, T. Study of a mathematical model of COVID-19 outbreak using some advanced analysis. Waves Random Complex Media 2022, 2022, 1–18. [Google Scholar] [CrossRef]
- Shah, K.; Abdeljawad, T.; Alrabaiah, H. On coupled system of drug therapy via piecewise equations. Fractals 2022, 30, 2240206. [Google Scholar] [CrossRef]
- Xu, C.; Liu, Z.; Pang, Y.; Saifullah, S.; Inc, M. Oscillatory, crossover behavior and chaos analysis of HIV-1 infection model using piece-wise Atangana-Baleanu fractional operator: Real data approach. Chaos Soliton Fractals 2022, 164, 112662. [Google Scholar] [CrossRef]
- Saifullah, S.; Ahmad, S.; Jarad, F. Study on the dynamics of a piecewise Tumour-Immune interaction model. Fractals 2022, 30, 2240233. [Google Scholar] [CrossRef]
- Abdelmohsen, S.A.M.; Yassen, M.F.; Ahmad, S.; Abdelbacki, A.M.M.; Khan, J. Theoretical and numerical study of the rumours spreading model in the framework of piecewise derivative. Eur. Phys. J. Plus 2022, 137, 738. [Google Scholar] [CrossRef]
- Ahmad, S.; Yassen, M.F.; Alam, M.M.; Alkhati, S.; Jarad, F.; Riaz, M.B. A numerical study of dengue internal transmission model with fractional piecewise derivative. Results Phys. 2022, 39, 105798. [Google Scholar] [CrossRef]
- Shah, K.; Abdeljawad, T.; Ali, A. Mathematical analysis of the Cauchy type dynamical system under piecewise equations with Caputo fractional derivative. Chaos Solitons Fractals 2022, 161, 112356. [Google Scholar] [CrossRef]
- Pais, R.J.; Taveira, N. Predicting the evolution and control of the COVID-19 pandemic in Portugal. F1000 Research 2020, 9, 283. [Google Scholar] [CrossRef] [PubMed]
- Tunç, C.; Bixcxer, E. Hyers-Ulam-Rassias stability for a first order functional differential equation. J. Math. Fund. Sci. 2015, 47, 143–153. [Google Scholar] [CrossRef]
- Tunç, C.; Tunxcx, O.; Yao, J. On the new qualitative results in integro-differential equations with Caputo fractional derivative and multiple kernels and delays. J. Nonl. Convex Anal. 2022, 23, 2577–2591. [Google Scholar]
- Arshad, M.S.; Baleanu, D.; Riaz, M.B.; Abbas, M. A novel 2-Stage Fractional Runge-Kutta Method for a Time Fractional Logistic Growth Model. Discret. Dyn. Nat. Soc. 2020, 2020, 1020472. [Google Scholar] [CrossRef]
- Fu, Z.J.; Tang, Z.C.; Zhao, H.T.; Li, P.W.; Rabczuk, T. Numerical solutions of the coupled unsteady nonlinear convection-diffusion equations based on generalized finite difference method. Eur. Phys. J. Plus 2019, 134, 1–20. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).