Investigation of the F* Algorithm on Strong Pseudocontractive Mappings and Its Application

Abstract

In the context of uniformly convex Banach space, this paper focuses on examining the strong convergence of the $F^{*}$ iterative algorithm to the fixed point of a strongly pseudocontractive mapping. Furthermore, we demonstrate through numerical methods that the $F^{*}$ iterative algorithm converges strongly and faster than other current iterative schemes in the literature and extends to the fixed point of a strong pseudocontractive mapping. Finally, under a nonlinear quadratic Volterra integral equation, the application of our findings is shown.

1. Introduction

Throughout this work, Z will be a real Banach space and X a uniformly convex set. H is considered to be a self-map, $D\left(H\right)$ is the domain of the map H, and $F\left(X\right)$ is the set of fixed points of the map H.

A self-mapping H is said to be

• L-Lipschitizian if there exists $L>1$ such that for all $x,y\in D\left(H\right)$

  $$\parallel Hx-Hy\parallel \le L\parallel x-y\parallel ,$$

  if $L=1$, then H is called nonexpansive, while H is called a contraction if $L\in [0,1)$.
• k-strongly pseudocontractive if there exists a constant $k>1$ such that

  $$\left[\parallel x-y\parallel \le \parallel x-y+r\left(I-H\right)x-r\left(I-H\right)y\parallel \right],\forall x,y\in D\left(H\right)and\forall r<0.$$
• Accretive if $\exists j\left(x-y\right)\in J\left(x-y\right)$ such that

  $$[⟨Hx-Hy,j\left(x-y\right)⟩\le {\parallel x-y\parallel }^2],$$
  $\forall x,y\in D\left(H\right).$

Remark 1.

From [1], (2) and (3) above are equivalent.

Remark 2.

From inequality (2) above, ref. [2] obtained the following inequalities:

$$⟨Hx-Hy,j\left(x-y\right)⟩\le k{\parallel x-y\parallel }^2$$

and

$$⟨Hx-Hy,j\left(x-y\right)⟩\le (1-k){\parallel x-y\parallel }^2.$$

Then, the mapping H is considered to be strongly pseudocontractive if $k\in \left(0,1\right).$

Remark 3.

A strongly pseudocontractive mapping is said to be a strongly ϕ-pseudocontractive mapping, given ϕ defined as $\varphi \left(s\right)=k$ for $k\in (0,1),$ where the converse is not needed to be true.

4.

A mapping H is said to be strongly $\varphi$-pseudocontractive if $\forall x,y\in Z,\exists j(x-y)\in J(x-y)$ and having a strictly increasing function $\varphi :[0,\infty )\to [0,\infty )$ with $\varphi \left(0\right)=0$ such that

$$⟨Hx-Hy,j(x-y)⟩\le {\parallel x-y\parallel }^2-\varphi \left(\parallel x-y\parallel \right)\parallel x-y\parallel .$$

Remark 4.

A strongly ϕ-pseudocontractive mapping is said to be generalized strongly Φ-pseudocontractive mapping with $\mathrm{\Phi }:\left[0,\infty \right)\to \left[0,\infty \right)$ defined by $\mathrm{\Phi }\left(s\right)=\varphi \left(s\right)$ where the converse is not needed to be true.

5.

A mapping H is said to be generalized strongly $\mathrm{\Phi }$-pseudocontractive ∀$x,y\in Z$, having $j\left(x-y\right)\in J\left(x-y\right)$ and a strictly increasing function $\mathrm{\Phi }:[0,\infty )\to [0,\infty )$ with $\mathrm{\Phi }\left(0\right)=0,$ such that

$$⟨Hx-Hy,j(x-y)⟩\le {\parallel x-y\parallel }^2-\mathrm{\Phi }\left(\parallel x-y\parallel \right).$$

Picard iteration: In 1890 [3], Picard discovered an iterative scheme called Picard iteration which was used to estimate fixed points of nonexpansive mappings:

$$\left\{\begin{array}{c}{p}_0\in Z\hfill \\ p_{n+1}=H{p}_n.\hfill \end{array}\right.$$

The Mann iterative approach was developed in [4] to estimate fixed points of nonexpansive mappings:

$$\left\{\begin{array}{c}{p}_0\in Z\hfill \\ p_{n+1}=\left(1-r_n\right)p_n+r_{n}H{p}_n.\hfill \end{array}\right.$$

Also, it was known that the Mann iterative scheme fails to converge to a fixed point of pseudocontractive mapping. The author in [5] established a two-step Mann (Ishikawa) iterative scheme which was firstly used to estimate fixed points of pseudocontractive mappings. The iterative scheme was later used on nonexpansive mappings without any assumption on the convexity of the Banach space:

$$\left\{\begin{array}{c}{p}_0\in Z\hfill \\ p_{n+1}=\left(1-r_n\right)p_n+r_{n}H{q}_n\hfill \\ q_n=\left(1-s_n\right)p_n+s_{n}H{p}_n.\hfill \end{array}\right.$$

S iteration: A two-step iterative scheme called an S iterative scheme was initiated in [6] and was applied for nearly asymptotically nonexpansive mapping:

$$\left\{\begin{array}{c}{p}_0\in Z\hfill \\ p_{n+1}=\left(1-r_n\right)H{p}_n+r_{n}H{q}_n\hfill \\ q_n=\left(1-s_n\right)p_n+s_{n}H{p}_n.\hfill \end{array}\right.$$

Normal-S iteration: Sahu established in [2] an iterative scheme called the normal-S iterative scheme for nonexpansive mapping, defined as

$$\left\{\begin{array}{c}{p}_0\in Z\hfill \\ p_{n+1}=H\left(\left(1-r_n\right)p_n+r_{n}H{p}_n\right).\hfill \end{array}\right.$$

${\mathit{F}}^{*}$ iteration: To determine the fixed points of weak contractions in Banach spaces, the authors in [7] developed a novel two-step iterative approach known as $F^{*}$ iteration. It was demonstrated that the built-in method firmly converges to the fixed point of weak contractions. Additionally, it was demonstrated that the $F^{*}$ iterative scheme converged to a fixed point more quickly than the Picard, Mann, Ishikawa, S, normal-S, and Varat iterative schemes:

$$\left\{\begin{array}{c}{p}_0\in Z\hfill \\ p_{n+1}=H{q}_n\hfill \\ q_n=H\left(\left(1-r_n\right)p_n+r_{n}H{p}_n\right).\hfill \end{array}\right.$$

However, the $F^{*}$ iteration produced a data-dependent result. Additionally, numerical illustrations were provided to corroborate their findings. Their findings were also applied to estimate the solution of the Volterra integral equation that is both nonlinear and quadratic. Finally, in the researchers’ work there arose an open question: “Can the sequence $\left\{p_n\right\}$ generated by the $F^{*}$ iterative scheme converge to a fixed point of nonexpansive or pseudocontractive mappings?”

In response to this, our research is motivated by employing pseudocontractive mappings for the convergence of the sequence $\left\{p_n\right\}$ generated by iteration to a fixed point. To achieve the desired result, certain existing inequalities in convex Banach spaces were utilized following the assumption of the existence of a fixed point. Other necessary conditions for convergence of the sequence generated by the $F^{*}$ algorithm to the fixed point of strong pseudocontractive mapping were also obtained.

1.1. Various Results on Convergence

In [8], the following iteration method was considered:

$$p_{n+1}=x_n^{\left(1\right)}H(x_n^{\left(2\right)}H(\dots H(x_n^{\left(k\right)}H{p}_n+(1-x_n^{\left(k\right)})p_n+u_n^{\left(k\right)})+\dots )+(1-x_n^{\left(2\right)})P_n+u_n^{\left(2\right)})+(1-x_n^{\left(1\right)})p_n+u_n^{\left(1\right)},$$

(1)

$n=1,2,3,\dots ,$ where $0\le u_n^{\left(i\right)}\le 1$, for all $n\ge 1$ and $i=1,2,\dots ,k.$

Given a sequence $\left(p_n\right)$ in Z satisfying (1), $u_n^{\left(i\right)}=0$ for all $n=1$ and for all $i\in \{1,\dots ,k\}$ and the real sequence $\left\{u_n^{\left(i\right)}\right\}$, $i=1,2,\dots ,k$ satisfying

(c₁)

$0\le u_n^{\left(i\right)}\le u<1and{\sum }_{n=0}^{\infty }\left|\right|u_n^{\left(i\right)}\left|\right|\le \infty$;

(c₂)

$0\le u_n^{\left(i\right)}\le 1,i=2,\dots ,k$;

(c₃)

${\sum }_{n=1}^{\infty }(u_n^{\left(1\right)}{u}_n^{\left(2\right)}+\dots +u_n^{\left(1\right)}{u}_n^{\left(2\right)}\dots u_n^{\left(k\right)})<\infty$;

(c₄)

${lim}_{n\to \infty }(u_n^{\left(2\right)}+u_n^{\left(2\right)}{u}_n^{\left(3\right)}+\dots +u_n^{\left(2\right)}{u}_n^{\left(3\right)}\dots u_n^{\left(k\right)}=0.$

If $H\left(p_n^{\left(i\right)}\right)$ are bounded sets, then $\left\{p_n\right\}$ converges strongly to $p\in F\left(H\right)$ and $F\left(H\right)$ is a singleton.

In [9], the author proposed a new iterative scheme which was used in investigating the estimations of fixed points for nonexpansive mappings. The proposed iterative scheme generalized both Mann [4] and Ishikawa [5] iterative schemes, which have been studied rigorously by many researchers for estimating fixed points solutions of nonlinear mapping in Banach spaces. Stevic, in [8], examined the convergence of the iterative scheme given in (1) for strongly pseudocontractive mappings and a class of difference inequalities was examined which frequently appears in the investigation of the proposed iterative scheme. The newly introduced iterative scheme was later used in [8] to examine the convergence for strongly pseudocontractive mappings.

Theorem 1

([10]). Given that Z is a real Banach space with a uniformly convex dual space $Z^{*}$ and D is a bounded closed convex subset of Z. If $H:D\to D$ is a single-valued Lipschitz strongly pseudocontractive mapping, then the Ishikawa iterative scheme of H converges strongly to a unique fixed point of H.

Theorem 2.

Assume that Z is a real uniformly smooth Banach space and D is a bounded closed convex and nonempty subset of Z. Given that $H:D\to D$ is a strongly pseudocontractive map such that $H{p}^{*}=p^{*}$ for some $p^{*}\in K$. Setting $\{r_n\}$, $\left\{s_n\right\}$ to be real sequences satisfying the following conditions:

(a.) 

$0\le r_n$, $s_n\le 1$∀$n\ge 0$;

(b.) 

${lim}_{n\infty }{r}_n=0$; ${lim}_{n\infty }{s}_n=0$;

(c.) 

${\sum }_{n=0}^{\infty }{r}_n=\infty$.

So, for arbitrary $p_0\in D$, the sequence $\left\{p_n\right\}$ given in the iterative form by

$$\left\{\begin{array}{c}{p}_0\in Z,\hfill \\ p_{n+1}=\left(1-r_n\right)p_n+r_{n}H{q}_n,\hfill \\ q_n=\left(1-s_n\right)p_n+s_{n}H{p}_n,\hfill \end{array}\right.$$

converges strongly to $p^{*}$. However, $p^{*}$ is unique.

Theorem 3

([11]). Given that Z is a real Banach space with a uniformly convex dual $Z^{*}$, D is a nonempty closed convex bounded subset of Z, and $H:D\to D$ is a continuous strongly pseudocontractive mapping. So, the Ishikawa iterative sequence $\{{p_n\}}_{n=0}^{\infty }$ defined in [5] converges strongly to the unique fixed point of H.

Theorem 4.

Let $p_0$ be an arbitrary point in Z. Suppose $\left\{p_n\right\}$ is a sequence in Z which satisfies the recursive Formula (1), $\left\{t_n\right\}$ is a sequence in Z such that

$${\vartheta }_n=\parallel p_{n+1}-(1-x_n^{\left(1\right)})p_n-x_n^{\left(1\right)}H{p}_n^{\left(1\right)}-u_n^{\left(1\right)}\parallel ,n=0,1,\dots$$

where $\left(u_n^{\left(i\right)}\right)$ is a set of sequences in a real Banach space Z and $\left(x_n^i\right)$ such that $i=1,k,$ are k real sequences in $[0,1]$ satisfying under the following conditions:

(c₁.)

${\sum }_{n=0}^{\infty }\parallel u_n^{\left(1\right)}\parallel \le \infty$;

(c₂.)

${lim}_{n\to \infty }\parallel u_n^{\left(i\right)}\parallel =0$, $i=2,k$;

(c₃.)

${lim}_{n\to \infty }{x}_n^{\left(i\right)}=0$, $i=1,k$;

(c₄.)

${\sum }_{n=1}^{\infty }{x}_n^{\left(i\right)}=\infty$.

Then,

(i) 

the sequence $\left\{p_n\right\}$ is almost H-stable;

(ii) 

${lim}_{n\to \infty }{p}_{n+1}=p\in f\left(H\right)$ implies ${lim}_{n\to \infty }\vartheta =0$.

1.2. Nonlinear Quadratic Volterra Integral Equation

The authors in [12] investigated the monotonicity properties of the superposition operator and its applications. It was stated that an application of the monotonicity properties directly examines the solvability of a quadratic Volterra integral equation given in the form

$$x\left(z\right)=g\left(z\right)+f\left(z,x\left(z\right)\right){\int }_0^{z}u\left(z,\tau ,x\left(\tau \right)\right)d\tau ,$$

(2)

where x and g are elements of a Frechet space J, f is a linear continuous map from $J\to J$, and u is a nonlinear map from $J\to J$ such that $z\in J=\left[0,1\right].$

Several problems in science, physics, engineering and related disciplines lead to linear and nonlinear Volterra integral equations of both the first and second kind. These equations are often difficult to solve analytically but an approximated solution can be provided using numerical techniques (see [13,14,15,16,17,18]).

1.3. Useful Lemmas

The lemmas below will be helpful in showing our main results.

Lemma 1

([19]). Suppose $J:Z\to Z^2$ is a normalized duality mapping; then,

$${\parallel a+b\parallel }^2\le {\parallel a\parallel }^2+2⟨b,j(a+b)⟩,$$

(3)

for all $a,b\in Z$ where $j(a+b)\in J(a+b).$

Lemma 2

([11]). Given that ${\left\{{\mu }_n\right\}}_{n=0}^{\infty }$ is a set of non-negative real sequences satisfying

$${\mu }_{n+1}\le \left(1-{\gamma }_n\right){\mu }_n+{\sigma }_n,$$

(4)

where ${\gamma }_n\in \left[0,1\right]$, ${\sum }_{n=1}^{\infty }{\gamma }_n=\infty ,$ and ${\sigma }_n=o\left({\gamma }_n\right).$ Then, ${\mu }_n\to 0$ as $n\to \infty .$

2. Main Results

In this section, we will prove the strong convergence theorem for the $F^{*}$ iterative method for a strongly pseudocontractive mapping in uniformly convex Banach space.

Theorem 5.

Let Z be a real Banach space with a uniformly convex dual $Z^{*},$D be a nonempty closed convex bounded subset of Z and $H:D\to D$ be a continuous strongly pseudocontractive mapping. Then, the $F^{*}$ iterative sequence ${\left\{p_n\right\}}_{n=1}^{\infty }$ defined by

$$\left\{\begin{array}{c}{p}_0\in Z,\hfill \\ p_{n+1}=H{q}_n,\hfill \\ q_n=H\left(\left(1-r_n\right)p_n+r_{n}H{p}_n\right),\hfill \end{array}\right.$$

(5)

where $\left\{r_n\right\}$ and $\left\{p_n\right\}$ converges strongly to the unique fixed point of H.

Proof. 

The existence of a fixed point follows from [20].

Let p be a unique fixed point of H. Since $H:D\to D$ is strongly pseudocontractive, $I-H$ is strongly accretive, where I is the identity operator and for every $x,y\in D$

$$\begin{array}{cc}\hfill {\parallel p_{n+1}-p\parallel }^2& ={\parallel H{q}_n-p\parallel }^2\hfill \\ \hfill & =⟨H\left(H\left(\left(1-r_n\right)p_n+r_{n}H{p}_n\right)\right)-Hp,j\left(p_{n+1}-p\right)⟩\hfill \\ \hfill & \le k{\parallel H\left(\left(1-r_n\right)p_n+r_{n}H{p}_n\right)-p\parallel }^2\hfill \\ \hfill & =k⟨H\left(\left(1-r_n\right)p_n+r_{n}H{p}_n\right)-Hp,j\left(q_n-p\right)⟩\hfill \\ \hfill & \le k^2{\parallel \left(1-r_n\right)p_n+r_{n}H{p}_n-p\parallel }^2=k^2{\parallel p_n-r_n{p}_n+r_{n}H{p}_n+r_n{p}_n-r_n{p}_n-p\parallel }^2\hfill \\ \hfill & =k^2{\parallel r_n\left(H{p}_n-p\right)+\left(1-r_n\right)\left(p_n-p\right)\parallel }^2\hfill \\ \hfill & \le k^2{\left(1-r_n\right)}^2{\parallel p_n-p\parallel }^2+2r_n{k}^2⟨H{p}_n-p,j\left(z_n-P\right)⟩\hfill \\ \hfill & \le k^2{\left(1-r_n\right)}^2{\parallel p_n-p\parallel }^2+2r_n{k}^2⟨H{p}_n-p,j\left(z_n-P\right)-j\left(p_n-P\right)⟩\hfill \\ & +2r_n{k}^2⟨H{p}_n-p,j\left(p_n-P\right)⟩\hfill \\ \hfill & \le k^2{\left(1-r_n\right)}^2{\parallel p_n-p\parallel }^2+2r_n{k}^3{\parallel p_n-p\parallel }^2+2r_n{k}^2⟨H{p}_n-p,j\left(z_n-P\right)-j\left(p_n-P\right)⟩\hfill \\ \hfill & =k^2\left({\left(1-r_n\right)}^2+2r_{n}k{\parallel p_n-p\parallel }^2+2r_n⟨H{p}_n-p,j\left(z_n-P\right)-j\left(p_n-P\right)⟩\right)\hfill \\ \end{array}$$

Recall that $0<k<1$ implies $0<k^2<1$, which gives the inequality below

$$\begin{array}{cc}\hfill {\parallel p_{n+1}-p\parallel }^2& \le \left({\left(1-r_n\right)}^2+2r_{n}k{\parallel p_n-p\parallel }^2+2r_n⟨H{p}_n-p,j\left(z_n-P\right)-j\left(p_n-P\right)⟩\right)\hfill \\ & =\left(1-\left(2r_n-r_n^2-2r_{n}k\right)\right){\parallel p_n-p\parallel }^2+2r_n⟨H{p}_n-p,j\left(z_n-P\right)-j\left(p_n-P\right)⟩\hfill \\ & =\left(1-r_n\left(2-r_n-2k\right)\right){\parallel p_n-p\parallel }^2+2r_n⟨H{p}_n-p,j\left(z_n-P\right)-j\left(p_n-P\right)⟩\hfill \\ \end{array}$$

where

$${\alpha }_n=⟨H{p}_n-p,j\left(z_n-P\right)-j\left(p_n-P\right)⟩.$$

Now, we shall show ${\alpha }_n\to 0$ as $n\to \infty$. We observed that $\{H{p}_n-Hp\}$ is bounded; then, to show ${\alpha }_n\to 0$ as $n\to \infty$, it suffices to show

$$j\left(z_n-P\right)-j\left(p_n-P\right)\to 0\mathrm{as}n\to \infty .$$

Truly, since $X^{*}$ is uniformly convex, j is uniformly continuous on any bounded subset of X. Noting that

$$\left(z_n-p\right)-\left(p_n-p\right)=z_n-p_n=\left(1-r_n\right)p_n+r_{n}H{p}_n-p_n=r_{n}H{p}_n-r_n{p}_n\to 0\mathrm{as}n\to \infty .$$

so we see that

$$j\left(z_n-P\right)-j\left(p_n-P\right)\to 0\mathrm{as}n\to \infty .$$

where

$${\sigma }_n=2r_n⟨H{p}_n-p,j\left(z_n-p\right)-j\left(p_n-p\right)⟩.$$

We choose a large positive integer N such that for all $n\le N$, then

$$\frac{1-r_n}{2}<k<\frac{2-r_n}{2}.$$

Thus, the above inequality yields

$${\parallel p_{n+1}-p\parallel }^2\le \left(1-r_n\left(2-r_n-2k\right)\right){\parallel p_n-p\parallel }^2+{\sigma }_n.$$

(6)

Setting ${\mu }_n={\parallel p_n-p\parallel }^2$ and ${\gamma }_n=r_n\left(2-r_n-2k\right)$. Then,

$${\mu }_{n+1}\le \left(1-{\gamma }_n\right){\mu }_n+{\sigma }_n,$$

with

$${\gamma }_n\in \left[0,1\right],\sum _{n=1}^{\infty }{\gamma }_n=\infty ,$$

and

$${\sigma }_n=o\left(r_n\right).$$

By Lemma 2, (6) yields ${\mu }_n\to 0$ as $n\to \infty$. □

3. Application to Nonlinear Quadratic Volterra Integral Equation

In this section, the solution estimated by the $F^{*}$ iterative process for a nonlinear quadratic Volterra integral problem will be discussed. So, we look at Equation (2) for the nonlinear quadratic Volterra integral, taking into account that the following claims are true:

(D₁)

$g\in C\left(J\right)$ and g is non-negative and nondecreasing on $J=\left[0,1\right].$

(D₂)

The function $f:J\times K\to \mathbb{R}$ such that the following restrictions hold:

(i)

f on the set $J\times K$ is continuous;

(ii)

For $x\in K$, $z\in J$ both fixed, the functions $z\to f\left(z,x\right)$ and $x\to f\left(z,x\right)$ are increasing on J and K, respectively, and $f=f\left(z,x\right)$ is Lipschitz with respect to x, given that $g_0=g\left(0\right)=min\{g\left(z\right),z\in J\}$. However, f is positive on the set $J\times K,$ since $K\subset {\mathbb{R}}^{+}$ is not bounded and $h_0\in K$.

(D₃)

An increasing function $k\left(t\right)=k:\left[g_0,+\infty \right]\to {\mathbb{R}}^{+}$:

$|f\left(z,x_1\right)-f\left(z,x_2\right)|\le K\left(t\right)|x_1-x_2|$, for any $z\in J$ and ∀$x_1,x_2\in \left[g_0,t\right]$.

(D₄)

A function $u:J\times J\times \mathbb{R}\to \mathbb{R}$ is continuous, such that $u:J\times J\times {\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$, for arbitrarily fixed $\tau \in J$ and $x\in {\mathbb{R}}^{+}$ and the function $z\to u\left(z,\tau ,x\right)$ is increasing on J.

(D₅)

A nondecreasing map $m:{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}:u\left(z,\tau ,x\right)\le m\left(x\right)$ for $z,\tau \in J$ and $x\ge 0.$

(D₆)

There is a positive solution $t_0$ for the inequality

$$\parallel g\parallel +\left(rk\left(t\right)+E_1\right)m\left(t\right)\le t,$$

where $E_1=sup\{f\left(z,0\right):z\in J\}$. Moreover, $k\left(t_0\right)m\left(t_0\right)<1$.

Now, the existence result follows as proved in [12] and which was later used in [7].

Theorem 6.

Under the assertions $\left(D_1\right)$–$\left(D_6\right)$, Equation (2) has a minimum of a solution $x=x\left(z\right)\in C\left(J\right)$ that is increasing and positive on the interval $J.$ There follow some assertions for the estimation of the result of the integral Equation (2). Let $P=\{x\in C\left(J\right):x\left(z\right)\ge h_o$ for $z\in J\}$⊂$C\left(W\right)$ and $P_{t_0}=\{x\in P:\parallel x\parallel \le t_0\}$, where $t_0>0$ comes from assertion $\left(D_6\right)$, $P_{t_0}$ is nonempty since $t_0\le h_0$ is a closed bounded convex subset of $C\left(J\right)$.

If the Lipschitz condition $u\left(z,\tau ,x\right)$ with respect to x holds, i.e., for $z,\tau \in J$ and for $x_1,x_2\in P_{t_o}$, then ∃$N>0$:

$$\parallel u\left(z,\tau ,x_1\right)-u\left(z,\tau ,x_2\right)\parallel \le N\parallel x_1-x_2\parallel .$$

$\left(\chi \right)$$t_0$ in assertion $\left(D_6\right)$ satisfies the following inequality:

$$0<(m\left(t_0\right)K\left(t_0\right)+\left(t_{0}K\left(t_0\right)+E_1\right))<1.$$

So, we define an operator H on the set $P_{t_0}$ by

$$Hx\left(z\right)=g\left(z\right)+f\left(z,x\left(z\right)\right){\int }_0^{z}u\left(z,\tau ,x\left(\tau \right)\right)d\tau ,\forall z\in J.$$

(7)

According to the proof provided in [12], H transforms the set $P_{t_0}$ into itself as well as P. Additionally, H has at least one fixed point in $P_{t_0}$ and is continuous on $P_{t_0}$.

Now, we show that the operator H is strongly pseudocontraction on $P_{t_0}$, and then, for $z\in J$, we have

$$\begin{array}{cc}\hfill {\parallel Hx\left(z\right)-Hy\left(z\right)\parallel }^2& ={\parallel f\left(z,x\left(z\right)\right){\int }_0^{z}u\left(z,\tau ,x\left(\tau \right)\right)d\tau -f\left(z,y\left(z\right)\right){\int }_0^{z}u\left(z,\tau ,y\left(\tau \right)\right)d\tau \parallel }^2\hfill \\ \hfill & =\parallel f\left(z,x\left(z\right)\right){\int }_0^{z}u\left(z,\tau ,x\left(\tau \right)\right)d\tau -f\left(z,y\left(z\right)\right){\int }_0^{z}u\left(z,\tau ,x\left(\tau \right)\right)d\tau \hfill \\ \hfill & +f\left(z,y\left(z\right)\right){\int }_0^{z}u\left(z,\tau ,x\left(\tau \right)\right)d\tau -f\left(z,y\left(z\right)\right){\int }_0^{z}u\left(z,\tau ,y\left(\tau \right)\right){d\tau \parallel }^2\hfill \\ \hfill & \le \left[\parallel f\left(z,x\left(z\right)\right){\int }_0^{z}u\left(z,\tau ,x\left(\tau \right)\right)d\tau -f\left(z,y\left(z\right)\right){\int }_0^{z}u\left(z,\tau ,x\left(\tau \right)\right)d\tau \parallel \right.\hfill \\ \hfill & +{\left.\parallel f\left(z,y\left(z\right)\right){\int }_0^{z}u\left(z,\tau ,x\left(\tau \right)\right)d\tau -f\left(z,y\left(z\right)\right){\int }_0^{z}u\left(z,\tau ,y\left(\tau \right)\right)d\tau \parallel \right]}^2\hfill \\ \hfill & \le {\left[k\left(t_0\right)\parallel x\left(z\right)-y\left(z\right)\parallel {\int }_0^z\left|u\left(z,\tau ,x\left(\tau \right)\right)\right|d\tau +\left|f\left(z,y\left(z\right)\right)\right|{\int }_0^z|u\left(z,\tau ,x\left(\tau \right)\right)-u\left(z,\tau ,y\left(\tau \right)\right)|d\tau \right]}^2\hfill \\ \hfill & \le {\left[m\left(t_0\right)k\left(t_0\right)\parallel x\left(z\right)-y\left(z\right)\parallel +\left(t_{0}k\left(t_0\right)+E_1\right)N\parallel x\left(z\right)-y\left(z\right)\parallel \right]}^2\hfill \\ \hfill & ={\left[\left(m\left(t_0\right)k\left(t_0\right)+\left(t_{0}k\left(t_0\right)+E_1\right)N\right)\parallel x\left(z\right)-y\left(z\right)\parallel \right]}^2\hfill \\ \hfill & ={\left(m\left(t_0\right)k\left(t_0\right)+\left(t_{0}k\left(t_0\right)+E_1\right)N\right)}^2{\parallel x\left(z\right)-y\left(z\right)\parallel }^2\hfill \end{array}$$

By assumption $\left(\chi \right)$, we have that

$$\left(m\left(t_0\right)k\left(t_0\right)+\left(t_{0}k\left(t_0\right)+E_1\right)N\right)<1.$$

Let $k={\left(m\left(t_0\right)k\left(t_0\right)+\left(t_{0}k\left(t_0\right)+E_1\right)N\right)}^2$ and by $\left(\chi \right)$, we have $\sqrt{k}<1\Rightarrow k<1.$

Thus, operator S is a pseudocontraction which satisfies the inequality below:

$${\parallel Hx\left(z\right)-Hy\left(z\right)\parallel }^2=⟨Hx\left(z\right)-Hy\left(z\right),j\left(x\left(z\right)-y\left(z\right)\right)⟩\le k{\parallel x\left(z\right)-y\left(z\right)\parallel }^2.$$

Taking $Y=C\left(J\right)$, $C=P_{t_0}$, and H as in Equation (7), we obtain our desired result.

As stated in Theorem 2, we consider that $p^{*}$ is the fixed point of $H.$ So, we show that $p_n\to p^{*}$ as $n\to \infty$. Substituting the iterative scheme $\left(5\right)$, Equation $\left(7\right)$, and conditions $\left(D_1\right)$–$\left(D_4\right)$, we have

$$\begin{array}{cc}\hfill \parallel z_n\left(z\right)-p\left(z\right)\parallel & =\parallel \left(1-r_n\right)p_n\left(z\right)+r_{n}H{p}_n\left(z\right)-p\left(z\right)\parallel \hfill \\ & =\parallel \left(1-r_n\right)p_n\left(z\right)+r_{n}H{p}_n\left(z\right)-r_{n}p\left(z\right)+r_{n}p\left(z\right)-p\left(z\right)\parallel \hfill \\ & =\parallel \left(1-r_n\right)\left(p_n\left(z\right)-p\left(z\right)\right)+r_n\left(H{p}_n\left(z\right)-p\left(z\right)\right)\parallel \hfill \\ \hfill & \le \left(1-r_n\right)\parallel p_n\left(z\right)-p\left(z\right)\parallel +r_n\parallel H{p}_n\left(z\right)-p\left(z\right)\parallel \hfill \\ \hfill & =\left(1-r_n\right)\parallel p_n\left(z\right)-p^{*}\left(z\right)\parallel +r_n\parallel f(z,p_n\left(z\right)){\int }_0^{z}u(z,\tau ,p_n\left(\tau \right))d\tau \hfill \\ \hfill & -f(z,p^{*}\left(z\right)){\int }_0^{z}u(z,\tau ,p_n\left(\tau \right))d\tau \parallel \hfill \\ \hfill & \le \left(1-r_n\right)\parallel p_n\left(z\right)-p^{*}\left(z\right)\parallel +r_n\parallel f(z,p_n\left(z\right)){\int }_0^{z}f(z,\tau ,p_n\left(\tau \right))d\tau -f(z,p^{*}\left(z\right)){\int }_0^{z}u(z,\tau ,p_n\left(\tau \right))d\tau \parallel \hfill \\ & +r_n\parallel f(z,p^{*}\left(z\right)){\int }_0^{z}u(z,\tau ,p_n\left(\tau \right))d\tau -f(z,p^{*}\left(z\right)){\int }_0^{z}u(z,\tau ,p_n\left(\tau \right))d\tau \parallel \hfill \\ \hfill & \le \left(1-r_n\right)\parallel p_n\left(z\right)-p^{*}\left(z\right)\parallel +k\left(t_0\right)r_n\parallel p_n\left(z\right)-p^{*}\left(z\right)\parallel {\int }_0^z\left|u(z,\tau ,p_n\left(\tau \right))\right|d\tau \hfill \\ & +r_n\parallel f(z,p^{*}\left(z\right))\left({\int }_0^{z}u(z,\tau ,p_n\left(\tau \right))d\tau \right.\left.-{\int }_0^{z}u(z,\tau ,p^{*}\left(\tau \right))d\tau \right)\parallel \hfill \\ \hfill & \le \left(1-r_n\right)\parallel p_n\left(z\right)-p^{*}\left(z\right)\parallel +k\left(t_0\right)r_n\parallel p_n\left(z\right)-p^{*}\left(z\right)\parallel {\int }_0^z\left|u(z,\tau ,p_n\left(\tau \right))\right|\hfill \\ & +r_n\parallel f(z,p^{*}\left(z\right))\parallel \left({\int }_0^z|u(z,\tau ,p_n\left(\tau \right))-u(z,\tau ,p^{*}\left(\tau \right))|d\tau \right)\hfill \\ \hfill & \le \left(1-r_n\right)\parallel p_n\left(z\right)-p^{*}\left(z\right)\parallel +r_{n}m\left(t_0\right)k\left(t_0\right)\parallel p_n\left(z\right)-p^{*}\left(z\right)\parallel +r_n\left(t_{0}k\left(t_0\right)+E_1\right)N\parallel p_n\left(z\right)-p^{*}\left(z\right)\parallel \hfill \end{array}$$

$$\therefore \parallel z_n\left(z\right)-p^{*}\left(z\right)\parallel \le \left[(1-r_n)+r_n\{m\left(t_0\right)k\left(t_0\right)+r_n\left(t_{0}k\left(t_0\right)+E_1\right)N\}\right]\parallel p_n\left(z\right)-p^{*}\left(z\right)\parallel$$

(8)

$$\begin{array}{c}\parallel q_n\left(z\right)-p^{*}\left(z\right)\parallel =\parallel H{z}_n\left(z\right)-p^{*}\left(z\right)\parallel \hfill \\ =\parallel f(z,z_n\left(z\right)){\int }_0^{z}u(z,\tau ,z_n\left(\tau \right))d\tau -f(z,p^{*}\left(z\right)){\int }_0^{z}u(z,\tau ,p_n\left(\tau \right))d\tau \parallel \\ \le \parallel f(z,z_n\left(z\right)){\int }_0^{z}u(z,\tau ,z_n\left(\tau \right))d\tau -f(z,p^{*}\left(z\right)){\int }_0^{z}u(z,\tau ,z_n\left(\tau \right))d\tau \parallel \\ +\left|f(z,p^{*}\left(z\right)){\int }_0^{z}u(z,\tau ,z_n\left(\tau \right))d\tau \right.\left.-f(z,p^{*}\left(z\right)){\int }_0^{z}u(z,\tau ,p^{*}\left(\tau \right))d\tau \right|\\ \le \parallel f(z,z_n\left(\tau \right))-f(z,p^{*}\left(z\right))\parallel |{\int }_0^{z}u(z,\tau ,z_n\left(\tau \right))d\tau |+\parallel f(z,p^{*})\parallel |{\int }_0^{z}u(z,\tau ,z_n\left(\tau \right))d\tau -{\int }_0^{z}u(z,\tau ,p^{*}\left(\tau \right))d\tau |\\ \le k\left(t_0\right)\parallel z_n\left(z\right)-p^{*}\left(z\right)\parallel {\int }_0^z|u(z,\tau ,p_n)|d\tau +\left(t_{0}k\left(t_0\right)+E_1\right)N\parallel z_n\left(z\right)-p^{*}\left(z\right)\parallel \\ \hfill =m\left(t_0\right)k\left(t_0\right)\parallel z_n\left(z\right)-p^{*}\left(z\right)\parallel +\left(t_{0}k\left(t_0\right)+E_1\right)N\parallel z_n\left(z\right)-p^{*}\left(z\right)\parallel \end{array}$$

$$\therefore \parallel q_n\left(z\right)-p^{*}\left(z\right)\parallel \le \left[m\left(t_0\right)k\left(t_0\right)+\left(t_{0}k\left(t_0\right)+E_1\right)N\right]\parallel z_n\left(z\right)-p^{*}\left(z\right)\parallel$$

(9)

Substituting (8) into (9), we have

$$\begin{array}{cc}\hfill & \parallel q_n\left(z\right)-p^{*}\left(z\right)\parallel \le [m\left(t_0\right)k\left(t_0\right)+\left(t_{0}k\left(t_0\right)+E_1\right)N][(1-r_n)+r_n\{m\left(t_0\right)k\left(t_0\right)+(t_{0}k\left(t_0\right)\hfill \\ & +E_1\left)N\right\}]\parallel p_n\left(z\right)-p^{*}\left(z\right)\parallel \hfill \end{array}$$

(10)

$$\begin{array}{c}\parallel p_{n+1}\left(z\right)-p^{*}\left(z\right)\parallel =\parallel H{q}_n\left(z\right)-p^{*}\left(z\right)\parallel \hfill \\ =\parallel f(z,q_n\left(z\right)){\int }_0^{z}u(z,\tau ,q_n\left(\tau \right))d\tau -f(z,p^{*}\left(z\right)){\int }_0^{z}u(z,\tau ,p^{*}\left(\tau \right))d\tau \parallel \\ \le \parallel f(z,q_n\left(z\right)){\int }_0^{z}u(z,\tau ,q_n\left(\tau \right))d\tau -f(z,p^{*}\left(z\right)){\int }_0^{z}u(z,\tau ,q_n\left(\tau \right))d\tau \parallel \\ +\parallel f(z,p^{*}\left(z\right)){\int }_0^{z}u(z,\tau ,q_n\left(\tau \right))d\tau -f(z,p^{*}\left(z\right)){\int }_0^{z}u(z,\tau ,p^{*}\left(\tau \right))d\tau \parallel \\ \le k\left(t_0\right)\parallel q_n\left(z\right)-p^{*}\left(z\right)\parallel {\int }_0^z\left|u(z,\tau ,p_n\left(\tau \right))\right|d\tau +\left(t_{0}k\left(t_0\right)+E_1\right)N\parallel q_n\left(z\right)-p^{*}\left(z\right)\parallel \\ \hfill =m\left(t_0\right)k\left(t_0\right)\parallel q_n\left(z\right)-p^{*}\left(z\right)\parallel +\left(t_{0}k\left(t_0\right)+E_1\right)N\parallel q_n\left(z\right)-p^{*}\left(z\right)\parallel \end{array}$$

therefore,

$$\parallel p_{n+1}\left(z\right)-p^{*}\left(z\right)\parallel \le \left[m\left(t_0\right)k\left(t_0\right)+\left(t_{0}k\left(t_0\right)+E_1\right)N\right]\parallel q_n\left(z\right)-p^{*}\left(z\right)\parallel .$$

(11)

Substituting (10) into (11):

$$\begin{array}{cc}\hfill & \parallel p_{n+1}\left(z\right)-p^{*}\left(z\right)\parallel \le {\left[m\left(t_0\right)k\left(t_0\right)+\left(t_{0}k\left(t_0\right)+E_1\right)N\right]}^2[(1-r_n)+r_n\{m\left(t_0\right)k\left(t_0\right)\hfill \\ & +\left(t_{0}k\left(t_0\right)+E_1\right)N\left\}\right]\parallel p_n\left(z\right)-p^{*}\left(z\right)\parallel .\hfill \end{array}$$

(12)

Applying assumption $\chi$:

$$m\left(t_0\right)k\left(t_0\right)+\left(t_{0}k\left(t_0\right)+E_1\right)N<1,$$

which implies also that

$${\left[m\left(t_0\right)k\left(t_0\right)+\left(t_{0}k\left(t_0\right)+E_1\right)N\right]}^2<1,$$

then, we have Equation (12) as

$$\begin{array}{cc}\hfill \parallel p_{n+1}\left(z\right)-p^{*}\left(z\right)\parallel \le \left[(1-r_n)+r_n\{m\left(t_0\right)k\left(t_0\right)+\left(t_{0}k\left(t_0\right)+E_1\right)N\}\right]\parallel p_n\left(z\right)-p^{*}\left(z\right)\parallel & \\ \hfill =\left[1-r_n\left(1-\{m\left(t_0\right)k\left(t_0\right)+\left(t_{0}k\left(t_0\right)+E_1\right)N\}\right)\right]\parallel p_n\left(z\right)-p^{*}\left(z\right)\parallel \end{array}$$

$$\therefore \parallel p_{n+1}\left(z\right)-p^{*}\left(z\right)\parallel \le \left[1-r_n\left(1-\{m\left(t_0\right)k\left(t_0\right)+\left(t_{0}k\left(t_0\right)+E_1\right)N\}\right)\right]\parallel p_n\left(z\right)-p^{*}\left(z\right)\parallel .$$

Thus, it follows by induction that we have

$$\parallel p_{n+1}\left(z\right)-p^{*}\left(z\right)\parallel \le \parallel p_0\left(z\right)-p^{*}\left(z\right)\parallel \times \prod _{k=0}^n\{1-r_k\left(1-\left[\{m\left(t_0\right)k\left(t_0\right)+\left(t_{0}k\left(t_0\right)+E_1\right)N\}\right]\right)\}.$$

(13)

Since $r_k\in \left(0,1\right)$ for all $k\in \mathbb{N}$, using assumption $\left(\chi \right)$ gives

$$1-r_k\left(1-\left[\{m\left(t_0\right)k\left(t_0\right)+\left(t_{0}k\left(t_0\right)+E_1\right)N\}\right]\right)<1.$$

Accepting the fact that $exp(-y)\ge 1-y$, ∀$y\in \left(0,1\right)$, where Equation $\left(13\right)$ can be written as

$$\parallel p_{n+1}\left(z\right)-p^{*}\left(z\right)\parallel \le \parallel p_0\left(z\right)-p^{*}\left(z\right)\parallel exp-\left(1-\left[\{m\left(t_0\right)K\left(t_0\right)+\left(t_{0}k\left(t_0\right)+E_1\right)N\}\right]\right)\sum _{k=0}^n{r}_k$$

taking the ${lim}_{n\to \infty }$ of both sides, it yields ${lim}_{n\to \infty }\parallel p_n\left(z\right)-p^{*}\left(z\right)\parallel =0$, implying $p_n\left(z\right)\to p^{*}\left(z\right).$

Hence, the sequence $p_n$ generated by $F^{*}$ iterative scheme (5) converges strongly to the unique solution of integral Equation (7).

4. Numerical Examples

Example 1.

Let $Y=\mathbb{R}=\left(-\infty ,\infty \right)$ be a Banach space with usual norm and $C=\left[0,\infty \right)$. Let $R\left(H\right)=\left[0,\frac{2}{3}\right)$. The map $H:C\to C$ is a self-mapping defined by

$$Hx=\frac{x}{3\left(1+x\right)}$$

for all $x\in C$. We can easily verify that H is a strongly pseudocontractive mapping and has a fixed point $p=0$. Now, we choose $r_n=0.85$ and $s_n=0.15$ with the initial guess $p_0=5$.

From Table 1, we observe that the numerical results for $F^{*}$ iterative scheme (5) converge strongly and faster to zero at the sixth iteration when compared to the normal-S iterative scheme, which is the closest and converges among the other iterative schemes presented for the Volterra integral equation. Hence, the $F^{*}$ iterative scheme converges faster and better than the other iterative schemes existing in the literature. We present a graphical representation of our result in Figure 1.

Table 1. Comparison of different iterative schemes for Example 1.

Iter No.	${\mathit{F}}^{*}$	Picard	Mann	Ishikawa	Normal-S	$\mathbf{S}$
1	5	5	5	5	5	5
2	$0.0473333$	$0.2777778$	$0.9861111$	$0.2714574$	$0.1655010$	$0.9797900$
3	$0.0021545$	$0.0724638$	$0.2885927$	$0.0657739$	$0.0203615$	$0.2777725$
4	$0.0001035$	$0.0225225$	$0.1067441$	$0.0188694$	$0.0028783$	$0.0977829$
5	$0.0000050$	$0.0073421$	$0.0433388$	$0.0056526$	$0.0004148$	$0.0374809$
6	$0.0000000$	$0.0024295$	$0.0182701$	$0.0017147$	$0.0000602$	$0.0148500$
7	$0.0000000$	$0.0008079$	$0.0078242$	$0.0005221$	$0.0000099$	$0.0059613$
8	$0.0000000$	$0.0002691$	$0.0033733$	$0.0001592$	$0.0000015$	$0.0024057$
9	$0.0000000$	$0.0000897$	$0.0014586$	$0.0000485$	$0.0000000$	$0.0009729$
10	$0.0000000$	$0.0000299$	$0.0006315$	$0.0000148$	$0.0000000$	$0.0003938$
11	$0.0000000$	$0.0000100$	$0.0002735$	$0.0000045$	$0.0000000$	$0.0001595$
12	$0.0000000$	$0.0000033$	$0.0001185$	$0.0000014$	$0.0000000$	$0.0000646$
13	$0.0000000$	$0.0000011$	$0.0000513$	$0.0000000$	$0.0000000$	$0.0000262$
14	$0.0000000$	$0.0000000$	$0.0000222$	$0.0000000$	$0.0000000$	$0.0000106$
15	$0.0000000$	$0.0000000$	$0.0000096$	$0.0000000$	$0.0000000$	$0.0000043$
16	$0.0000000$	$0.0000000$	$0.0000018$	$0.0000000$	$0.0000000$	$0.0000017$
17	$0.0000000$	$0.0000000$	$0.0000010$	$0.0000000$	$0.0000000$	$0.0000000$
18	$0.0000000$	$0.0000000$	$0.0000000$	$0.0000000$	$0.0000000$	$0.0000000$

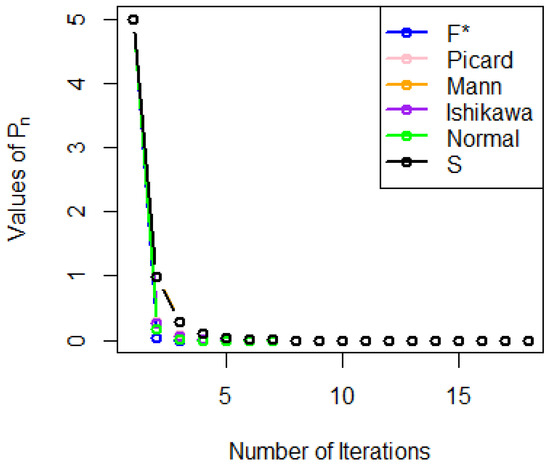
Figure 1. Figure to compare different iterative schemes for Example 1. $P_n$ are the values obtained during the iteration as n increases.

Example 2.

Let $Y=\mathbb{R}$ be a Banach space with usual norm and $C=\left[0,\infty \right)$. Let $R\left(H\right)=\left[0,\frac{6}{7}\right)$. The map $H:C\to C$ is a self-mapping defined by

$$Hx=\frac{x}{7\left(1+x\right)}$$

for all $x\in C$. We can easily verify that H is a strongly pseudocontractive mapping and has a fixed point $p=0$. Now, we choose $r_n=0.85$ and $s_n=0.15$, with the initial guess $p_0=5$.

From Table 2, we observe that the numerical results for $F^{*}$ iterative scheme (5) converge strongly and faster to zero at the fourth iteration when compared to the normal-S iterative scheme, which converges at the seventh iteration and is the closest to our algorithm among the other iterative schemes in the literature. We present a graphical representation of our result in Figure 2.

Table 2. Comparison of different iterative schemes for Example 2.

Iter No.	${\mathit{F}}^{*}$	Picard	Mann	Ishikawa	Normal-S	$\mathbf{S}$
1	5	5	5	5	5	5
2	$0.0088054$	$0.1190476$	$0.8511905$	$0.1162349$	$0.0656867$	$0.8483777$
3	$0.0000484$	$0.0151976$	$0.1835123$	$0.0133737$	$0.0024346$	$0.1785341$
4	$0.0000002$	$0.0021386$	$0.0463552$	$0.0016812$	$0.0000942$	$0.0430757$
5	$0.0000000$	$0.0003049$	$0.0033292$	$0.0002136$	$0.0000037$	$0.0108503$
6	$0.0000000$	$0.0000435$	$0.0009023$	$0.0000272$	$0.0000001$	$0.0027646$
7	$0.0000000$	$0.0000062$	$0.0002448$	$0.0000035$	$0.0000000$	$0.0007065$
8	$0.0000000$	$0.0000001$	$0.0000664$	$0.0000004$	$0.0000000$	$0.0000180$
9	$0.0000000$	$0.0000000$	$0.0000180$	$0.0000000$	$0.0000000$	$0.0000462$
10	$0.0000000$	$0.0000000$	$0.0000050$	$0.0000000$	$0.0000000$	$0.0000118$
11	$0.0000000$	$0.0000000$	$0.0000013$	$0.0000000$	$0.0000000$	$0.0000030$
12	$0.0000000$	$0.0000000$	$0.0000003$	$0.0000000$	$0.0000000$	$0.0000007$
13	$0.0000000$	$0.0000000$	$0.0000000$	$0.0000000$	$0.0000000$	$0.0000000$

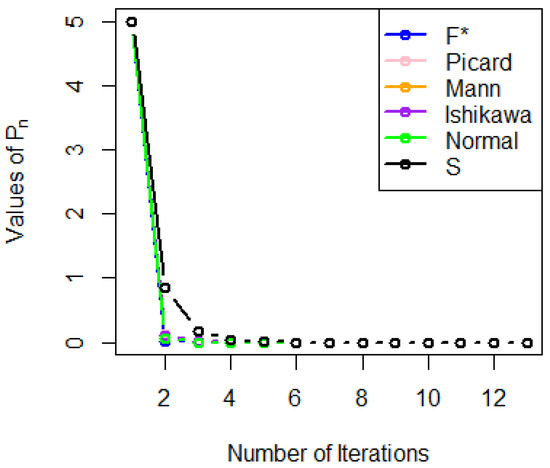
Figure 2. Figure to compare different iterative schemes for Example 2. $P_n$ are the values obtained during the iteration as n increases.

5. Conclusions

The historical development and application of pseudocontractive mapping with fixed point theory were extensively discussed in [21] and are a major subject of this work. In this paper, we investigated the convergence of an $F^{*}$ iterative scheme for a strongly pseudocontractive mapping on a uniformly convex Banach space. Using numerical examples, it has been found that the approach converges more quickly than the Picard, Mann, Ishikawa, S, normal-S iterative schemes for a strongly pseudocontractive mapping. This research work has studied the use of all of the generalized classes of strongly pseudocontractive mappings.