Abstract
Every red–blue coloring of the edges of a graph G results in a sequence , , …, of pairwise edge-disjoint monochromatic subgraphs () of size i, such that is isomorphic to a subgraph of for . Such a sequence is called a Ramsey chain in G, and is the maximum length of a Ramsey chain in G, with respect to a red–blue coloring c. The Ramsey index of G is the minimum value of among all the red–blue colorings c of G. If G has size m, then for some positive integer k. It has been shown that there are infinite classes S of graphs, such that for every graph G of size m in S, if and only if . Two of these classes are the matchings and paths of size m. These are both subclasses of linear forests (a forest of which each of the components is a path). It is shown that if F is any linear forest of size m with , then . Furthermore, if F is a linear forest of size , where , that has at most components, then , while for each integer t with there is a linear forest F of size with t components, such that .
MSC:
05C05; 05C15; 05C35; 05C55; 05C70
1. Introduction
For every graph G of size m, there is a unique positive integer k, such that . The graph G is said to have an ascending subgraph decomposition {, , …, } into k (pairwise edge-disjoint) subgraphs of G if is isomorphic to a proper subgraph of for . The following conjecture was stated in [1].
The Ascending Subgraph Decomposition Conjecture Every graph has an ascending subgraph decomposition.
This conjecture has drawn the attention of many researchers but has never been proved or disproved. There are many papers dealing with this conjecture (see [2,3,4,5,6,7,8,9], for example). Among the several classes of graphs for which the conjecture has been verified are regular graphs (see [3,10]). Two classes of graphs for which the conjecture can easily be verified are matchings (consisting of m components ) and stars : that is, for every positive integer m, where , there is an ascending subgraph decomposition {, , …, } of the graph G if either or , such that is isomorphic to a proper subgraph of for . If , the subgraphs are matchings and if , each subgraph is a star.
By a red–blue edge coloring (or simply a red–blue coloring) of a graph G, every edge of G is colored red or blue. Such an edge coloring is also referred to as a 2-edge coloring. In [11], the concept of ascending subgraph decomposition was extended to graphs possessing a red–blue coloring. Suppose that a red–blue coloring of a graph or is given, where . It was shown in [12] that there is not only an ascending subgraph decomposition {, , …, } of G but one in which each subgraph is monochromatic as well. This (perhaps unexpected) observation led to another concept, which is related to some topics in Ramsey Theory, named for the British mathematician Frank Ramsey [13]. Ramsey theory is one of the most studied areas in combinatorics and graph theory, with many highly nontrivial and beautiful results (see [14,15,16,17,18,19,20,21,22], for example). We refer to the books [11,23] for basic definitions and notation in graph theory that are not defined here.
Let G be a graph (without isolated vertices) of size m with a red–blue coloring c. A subgraph H of G is monochromatic if all edges of H are colored the same. A Ramsey chain of G with respect to c is a sequence , , …, of pairwise edge-disjoint subgraphs of G, such that each subgraph () is monochromatic of size i and is isomorphic to a subgraph of for . Each subgraph () in a Ramsey chain is called a link of the chain. The maximum length of a Ramsey chain of G with respect to c is the (ascending) Ramsey index of G. The Ramsey index of G is defined by Consequently, if for some graph G, then for every red–blue coloring of G, there is a Ramsey chain of length k in G, while there exists at least one red–blue coloring for which there is no Ramsey chain of length greater than k. These concepts were introduced and studied in [11,12], using somewhat different technology, and they were studied further in [24,25]. An immediate observation on Ramsey indexes of graphs was presented in [12].
Observation 1
([12]). If G is a graph of size m where for a positive integer k, then .
The result obtained on matchings and stars can therefore be stated as follows:
Theorem 1
([12]). If , where , then
In [24], the question was posed as to whether there are other infinite classes S of graphs, such that for every sufficiently large integer m and each graph G of size m in S, it follows that if and only if . In [24,25], this concept was studied for cycles and paths. As the emphasis here is on the size of a graph, let denote a cycle of size m and a path of size m: that is, is a path of order .
Theorem 2
([12,25]). If , where , then
A linear forest is a forest of which every component is a path. Here, we are only concerned with linear forests without isolated vertices. Paths and matchings are linear forests, namely, the linear forests with the minimum and maximum number of components. The goal here is to determine whether Theorems 1 and 2 can be extended to include linear forests distinct from paths and matchings.
2. Ramsey Indexes of Linear Forests
We saw in Theorems 1 and 2 that if or for a positive integer m, then if and only if . As and are both linear forests, this raises the question whether the same result holds for all linear forests of size m. This question can be answered immediately. The linear forest consisting of components where with has Ramsey index , not k. The red–blue coloring of F that assigns red to both edges of and blue to all other edges does not result in a Ramsey chain of length k, since a Ramsey chain of length k would require that and ; however, . On the other hand, and by Theorem 1; therefore, by Observation 2.
Each of the linear forests , , , , , has size , where . In each of these linear forests, a red–blue coloring is given in Figure 1 that shows that its Ramsey index is . In Figure 1, a bold edge indicates a red edge and a thin edge indicates a blue edge.
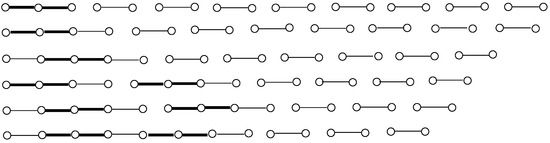
Figure 1.
Linear forests of size 10 with Ramsey index 3.
Each of the six linear forests in Figure 1 has t components for . The examples in Figure 1 suggest that determining for a linear forest F may depend not only on its size but the number of components of F as well. First, we present a result that gives the Ramsey index of linear forests of size m, where for any positive integer k. Prior to doing this, we state some useful information from three results presented in [24,25].
Observation 2
([24]). If H and G are graphs, such that , then . Consequently, if for each graph H of size m, then for every graph G of size .
Theorem 3
([25]). Let be an integer. For every set of t integers, such that and , every linear forest of size n can be decomposed into the matchings , , …, .
Proposition 1
([25]). Let for some integer . For every two positive integers and with and , there exists a partition of into two subsets and , where , , and , such that and .
We now apply Observations 1 and 2, Theorem 3, and Proposition 1, to establish the following result.
Theorem 4.
If H is a linear forest of size m, where for some integer , then .
Proof.
As by Observation 1, it remains only to verify that : that is, to verify that H has a Ramsey chain of length k for every 2-edge coloring of H. It suffices to assume that by Observation 2. Let c be a 2-edge coloring of H using the colors 1 and 2. We show that there is a Ramsey chain of length k in H. For , let be the linear forest in H induced by the edges of H colored i. Let have size where . Therefore, . We now consider five cases, according to whether or .
Case 1: ; thus, . As , it follows that . Because , it follows by Theorem 3 that can be decomposed into , which is a Ramsey chain of length k in H.
Case 2: ; thus, . As , it follows that . Because , it follows by Theorem 3 that can be decomposed into . As , there is a Ramsey chain of length k in H.
Case 3: ; thus, . Suppose first that ; then, . The linear forest can be decomposed into and , while the linear forest contains either or . In either case, H contains a Ramsey chain of length . Hence, we may assume that . Let F be a linear forest of size in . As , it follows that . Because , it follows by Theorem 3 that F can be decomposed into . As can be decomposed into and , there is a Ramsey chain of length k in H.
Case 4: ; thus, , and so, . Therefore, . As , it follows by Theorem 3 that can be decomposed into . Let F be a linear forest of size 3 in . As F can be decomposed into and , there is a Ramsey chain of length k in H.
Case 5: ; thus, and . Let F be a linear forest of size in . Consequently, , , and . By Proposition 1, there exists a partition of into two subsets and , where , and , such that and . Hence, can be decomposed into and F can be decomposed into , resulting in a Ramsey chain of length k in H. □
We illustrate the proof of Theorem 4 for the linear forest of size consisting of paths of sizes 5 and 6. Then, and . Five red–blue colorings of are given in Figure 2, to reflect the five cases for in the proof, where a bold edge indicates a red edge and a thin edge indicates a blue edge. For , an edge labeled i belongs to the link in a Ramsey chain of length 4 in , and the unlabeled edge is not used in R.
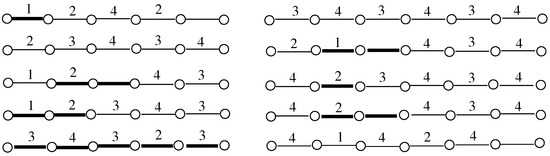
Figure 2.
Red–blue colorings of of size 11.
3. Binomial Linear Forests
From the results obtained in Section 2, it follows that investigating for a linear forest F of size m, we need only be concerned when for some integer . Thus, it is convenient to introduce terminology for this class of linear forests. A linear forest is k-binomial (or simply binomial) if its size is for some positive integer k. For example, a 3-binomial linear forest has size 6, a 4-binomial linear forest has size 10, and a 5-binomial linear forest has size 15. We begin with an observation that is a consequence of Theorem 4 and Observation 2.
Corollary 1.
If H is a k-binomial linear forest where , then . Furthermore, both values and k are attainable.
Proof.
First, by Observation 1. By Theorem 4, every linear forest of size has Ramsey index . Hence, by Observation 2. Therefore, . As and , both values and k are attainable. □
By Theorem 4 and Corollary 1, if H is a 3-binomial linear forest, then . We now determine the exact value of the Ramsey index of every 3-binomial linear forest. All 3-binomial linear forests are listed below:
Proposition 2.
Let H be a 3-binomial linear forest. Then, if and only if
Proof.
Let . First, observe that the linear forests H in X are the only 3-binomial linear forests containing a subgraph , such that and, consequently, contains no copies of . Let c be a 2-edge coloring of H that assigns the color 1 to the two edges of F and the color 2 to all other edges of H. We claim that there is no Ramsey chain of length 3 in H. Assume, to the contrary, that there is a Ramsey chain of length 3 in H. As the size of H is 6, it follows that is a decomposition of H. Necessarily, , and so, . As , this is impossible. Therefore, by Corollary 1.
For the converse, suppose that . We show that . As by Observation 1, it suffices to show that . Let c be a 2-edge coloring of H using the colors 1 and 2, where is the number of the edges in the subgraph of H colored i for and . Thus, and . We consider all possible pairs :
- ★
- If , then and is a linear forest of size 5. As , it follows by Theorem 3 that can be decomposed into . Thus, is a Ramsey chain of length 3 in H.
- ★
- If , then . First, suppose that . Then, is a linear forest of size 4, and so, can be decomposed into and a subgraph of size 3. As every graph of size 3 contains , it follows that is a Ramsey chain of length 3 in H. Next, suppose that . As , it follows that . Thus, . If , then can be decomposed into and . Thus, is a Ramsey chain of length 3 in H. If , then or . As can be decomposed into and , it follows that is a Ramsey chain of length 3 in H. If , then . As can be decomposed into and , it follows that is a Ramsey chain of length 3 in H.
- ★
- If , then can be decomposed into and and contains . Thus, is a Ramsey chain of length 3 in H.
□
We now consider k-binomial linear forests for integers . The following two results provide useful information on 2-edge colorings of k-binomial linear forests for .
Proposition 3.
For a k-binomial linear forest H where , let c be a 2-edge coloring of H using the colors 1 and 2. For , let be the subgraph of H induced by the edges of H colored i, where has size and . If , then is a Ramsey chain of length k in H and .
Proof.
We consider five cases, depending on whether or .
Case 1: . Let . As for and , it follows by Theorem 3 that can be decomposed into . Thus, is a Ramsey chain of length k in H and .
Case 2: . Thus, and . As , it follows that . Because is a linear forest of size and and when , it follows by Theorem 3 that can be decomposed into ; thus, is a Ramsey chain of length k in H and .
Case 3: . The subgraph can be decomposed into and . As for and , it follows by Theorem 3 that can be decomposed into . Thus, is a Ramsey chain of length k in H and .
Case 4: . Then, and . As , it follows that :
- ★
- Let . Then, is a linear forest of size 6. As , it follows by Theorem 3 that can be decomposed into . Thus, is a Ramsey chain of length 4 in H.
- ★
- Let . Then, can be decomposed into and . As and when , it follows by Theorem 3 that can be decomposed into . Thus, is a Ramsey chain of length k in H and .
Case 5: . By Proposition 1, there exists a partition of into two sets and , where , and , such that and . As , it follows by Theorem 3 that can be decomposed into the matchings , , …, and can be decomposed into the matchings , , …, . Consequently, is a Ramsey chain of length k in H and . □
Proposition 4.
For a k-binomial linear forest H where , let c be a 2-edge coloring of H using the colors 1 and 2. For , let be the subgraph of H induced by the edges of H colored i, where has size and . If
- (a)
- and has at least pairwise edge-disjoint copies of or
- (b)
- and has at least pairwise edge-disjoint copies of ,
then , , , , …, is a Ramsey chain of length k in H.
Proof.
First, suppose that and has at least pairwise edge-disjoint copies of , which are denoted by , , …, . Then, the number of edges of not belonging to any () is
and so, these edges of can be decomposed into
in such a way that for . Consequently, , , , , …, is a Ramsey chain of length k in H.
Next, suppose that . Then, can be decomposed into and . The subgraph has at least pairwise edge-disjoint copies of , which are denoted by , , …, . Then, the number of edges of not belonging to any () is
and so, these edges of can be decomposed into
in such a way that for . Consequently, , , , , …, is a Ramsey chain of length k in H. □
With the aid of Observation 1 and Propositions 3 and 4, we are able to establish the following result.
Theorem 5.
If H is a k-binomial linear forest, where with at most components, then .
Proof.
As by Observation 1, it remains to show that . Thus, we show that every 2-edge coloring of H produces a Ramsey chain of length k in H. Let c be a 2-edge coloring of H using the colors 1 and 2. For , let be the linear forest in H induced by the edges of H colored i, where has size with and components. By Proposition 3, if , then there is a Ramsey chain of length k in H. Thus, we may assume that . We consider these two cases, depending on whether or .
Case 1: . Then, is a linear forest of size . Let . Then, . Let be the components of , where has size for . Thus, . Let p be the maximum number of pairwise edge-disjoint copies of in . In each component (), the maximum number of pairwise edge-disjoint copies of is , and so, at most one edge of does not belong to these pairwise edge-disjoint copies of in . Hence, at most one edge in each () does not belong to any of these p pairwise edge-disjoint copies of in . As , it follows that
Therefore, there are at least pairwise edge-disjoint copies of in . By Proposition 4, there is a Ramsey chain of length k in H.
Case 2: . Then, can be decomposed into and . Here, is a linear forest of size . Let . Then, . Let be the components of , where has size for . Thus, . Let be the number of these components having odd size. If has even size, then let . If has odd size, then let be the subgraph of obtained by removing a pendant edge from , where is empty if . Hence, every subgraph has even size for and every nonempty linear forest can be decomposed into copies of . The size of the linear forest consisting of is, therefore, , which is an even number. As , it follows that
As is even, it follows that . Therefore, the number of pairwise edge-disjoint copies of in (and in as well) is at least . By Proposition 4, there is a Ramsey chain of length k in H. □
Next, we illustrate Theorem 5 for some 4-binomial forests of size 10, for which the number of components is 1, 2, or . Figure 3 shows red–blue colorings of the linear forests , , and of size 10, where four bold edges are red edges and six thin edges are blue edges. For , an edge labeled i belongs to the link in a Ramsey chain of length 4 in the linear forest.

Figure 3.
Red–blue colorings of three 4-binomial linear forests of size 10.
4. Binomial Linear Forests with an Intermediate Number of Components
By Theorems 1 and 5, every k-binomial linear forest where with t components, such that either or , has Ramsey index k. A natural question concerns whether these bounds on t can be improved. As we will see, no such improvement is possible. First, we provide a necessary and sufficient condition for a k-binomial linear forest to have Ramsey index .
Theorem 6.
A k-binomial linear forest H, where has Ramsey index if and only if
- (a)
- H contains a subgraph , such that has at most pairwise edge-disjoint copies of or
- (b)
- H contains a subgraph , such that has at most pairwise edge-disjoint copies of .
Proof.
First, we show that if H is a k-binomial linear forest where , such that neither (a) nor (b) holds, then . As by Observation 1, it remains to show that . Let c be a 2-edge coloring of H using the colors 1 and 2. For , let be the linear forest in H induced by the edges of H colored i. Let have size , where . By Proposition 3, there is a Ramsey chain of length k in H if . Thus, we may assume that :
- ★
- If , let . As (a) does not occur, it follows that has at least pairwise edge-disjoint copies of . Hence, H has a Ramsey chain of length k by Proposition 4.
- ★
- If , let . As (b) does not occur, it follows that has at least pairwise edge-disjoint copies of . Hence, H has a Ramsey chain of length k by Proposition 4.
For the converse, suppose that H is a k-binomial linear forest where , such that either (a) or (b) occurs. We show that . As by Corollary 4, it remains to show that . We consider two cases, according to whether (a) or (b) occurs.
Case 1: occurs. Let be a subgraph of H, such that has at most pairwise edge-disjoint copies of . Let c be a 2-edge coloring of H that assigns the color 1 to the two edges of F and the color 2 to all other edges of H. Then and . We claim that there is no Ramsey chain of length k with respect to c. Assume, to the contrary, that there is a Ramsey chain of length k in H. As the size of H is , it follows that is a decomposition of H. Necessarily, , and so, for , which implies that contains at least pairwise edge-disjoint copies of , which contradicts the fact that has at most pairwise edge-disjoint copies of . Thus, , and so, .
Case 2: occurs. Let be a subgraph of H, such that has at most pairwise edge-disjoint copies of . Let c be a 2-edge coloring of H that assigns the color 1 to the four edges of F and the color 2 to all other edges of H. Then, and . We claim that there is no Ramsey chain of length k, with respect to c. Assume, to the contrary, that there is a Ramsey chain of length k in H. As is a decomposition of H, it follows that either (i) is decomposed into and or (ii) . If (i) occurs, then for , which implies that contains at least pairwise edge-disjoint copies of , which contradicts the fact that has at most pairwise edge-disjoint copies of . If (ii) occurs, then contains a copy of and contains two edge-disjoint copies of for , which implies that contains at least pairwise edge-disjoint copies of , which contradicts the fact that has at most pairwise edge-disjoint copies of . Thus, , and so, . □
We have now seen for a linear forest H of size m where and that by Theorems 1, 4, and 5, if (i) or (ii) and H has t components, where or , then . Consequently, it remains only to consider those k-binomial linear forests with an intermediate number t of components, namely, . Let c be any 2-edge coloring of H using the colors 1 and 2, resulting in the monochromatic subgraphs and of sizes and , respectively, where . By Proposition 3, if , then . By Proposition 4 and Theorem 6, if , then . Furthermore, by Theorem 6, if , then only when contains at least pairwise edge-disjoint copies of ; otherwise, . Moreover, if , then only when has at least pairwise edge-disjoint copies of ; otherwise, . All of these suggest the need for only considering those 2-edge colorings of H for which and determining whether there is (a) any 2-edge coloring of H where , such that has fewer than pairwise edge-disjoint copies of or (b) any 2-edge coloring of H where , such that has fewer than pairwise edge-disjoint copies of . If there is a 2-edge coloring of H resulting in (a) or (b), then ; otherwise, . Therefore, to determine the Ramsey index of a k-binomial linear forest H where with an intermediate number t of components with , it suffices to study the 2-edge colorings of H, such that , such that possesses the minimum number of pairwise edge-disjoint copies of .
Each k-binomial linear forest H with t of components can be expressed as , where and . The maximum number of pairwise edge-disjoint copies of in H is . Now, let c be any 2-edge coloring of H using the colors 1 and 2 resulting in the monochromatic subgraphs and of sizes and , respectively, where and . First, we make some observations. If , then the maximum number of pairwise edge-disjoint copies of in is either or ; while, if , then the maximum number of pairwise edge-disjoint copies of in is , , or . We are now prepared to present the following result.
Theorem 7.
Let be a k-binomial linear forest of size for some integer with t components, where , where is the maximum number of pairwise edge-disjoint copies of in H:
- (1)
- If , then .
- (2)
- If and H contains two components of even size 4 or more, then ; otherwise, .
- (3)
- If and H contains at least one component of even size 4 or more, then ; otherwise, .
- (4)
- If , then .
Proof.
We first verify (1). Suppose that . By Observation 1, it suffices to show that for every 2-edge coloring c of H. Let c be a 2-edge coloring of H using the colors 1 and 2. For , let be the linear forest in H induced by the edges of H colored i where has size and . By Proposition 3, we may assume that . If , then the number of pairwise edge-disjoint copies of in is at least . As , it follows that by Theorem 6. If , then the number of pairwise edge-disjoint copies of in is at least . As , it follows that by Theorem 6. Therefore, .
Next, we verify (2). Suppose that :
- ★
- First, assume that H contains two components, and , where are both even. Define a 2-edge coloring c of H using the colors 1 and 2, such that and is placed in H in such a way that each of and contains a copy of of and the number of pairwise edge-disjoint copies of in is . Thus, by Theorem 6, and so, .
- ★
- Next, assume that H contains at most one component of even order 4 or more. Let c be any 2-edge coloring of H using the colors 1 and 2. For , let be the linear forest in H induced by the edges of H colored i where has size and . By Proposition 3, we may assume that . If , then the number of pairwise edge-disjoint copies of in is at least , and so, by Theorem 6. If , then, since H contains at most one component of even order 4 or more, any placement of in H produces at least pairwise edge-disjoint copies of in . It follows by Theorem 6 that . Therefore, .
We now verify (3). Suppose that :
- ★
- First, assume that H contains at least one component where is even. Define a 2-edge coloring c of H using the colors 1 and 2, such that and is placed in , in such a way that the number of pairwise edge-disjoint copies of in is . It follows by Theorem 6 that , and so, .
- ★
- Next, assume that H contains no component of even order 4 or more. Let c be any 2-edge coloring of H using the colors 1 and 2, where is the linear forest of size in H induced by the edges of H colored i and . By Proposition 3, we may assume that . If , then the number of pairwise edge-disjoint copies of in is at least , and so, by Theorem 6. If , then, as H contains no component of even order 4 or more, any placement of in H produces at least pairwise edge-disjoint copies of in . It follows by Theorem 6 that . Therefore, .
Finally, we verify (4). Suppose that . Define a 2-edge coloring c of H using the colors 1 and 2, such that . Then, the number of pairwise edge-disjoint copies of in is at least . As , it follows by Theorem 6 that , and so, . □
We have seen (by Theorems 1 and 5) that if H is a k-binomial linear forest where with t components, whether or , then . With the aid of Theorem 7, we are now able to show that these bounds on t cannot be improved.
Theorem 8.
For every two integers t and k where and , there is a k-binomial linear forest H with t components, such that .
Proof.
For each integer i with where , we construct a k-binomial linear forest with components, such that . In particular, has components and has components.
For an integer , let , where if k is even and and if is odd. Thus, are both even. As the size of is , it follows that is a k-binomial linear forest with components. The maximum number of pairwise edge-disjoint copies of in is . As and has two components of even size 4 or more, it follows by Theorem 7 that .
Next, let . Then, is a k-binomial linear forest with components. The maximum number of pairwise edge-disjoint copies of in is and has the component of even size 4 or more. By Theorem 7, . Next, let . Then, is a k-binomial linear forest with components. The maximum number of pairwise edge-disjoint copies of in is and has the component of even size 4 or more. By Theorem 7, .
Next, let . Then, is a k-binomial linear forest with components. The maximum number of pairwise edge-disjoint copies of in is . We continue this procedure, reducing the size of components greater than 1 until we arrive at
Here, is a k-binomial linear forest with components. For each integer i with , the maximum number of pairwise edge-disjoint copies of in is , and so, by Theorem 7. □
To illustrate Theorem 7, we consider and . For , we construct a 5-binomial linear forest with components, such that :
- ★
- Let , where and . As has 2 components and of even size 4 or more, by Theorem 7.
- ★
- Let , where and . As has the component of size 4, it follows by Theorem 7 that .
- ★
- Let , where and . As has the component of size 4, it follows by Theorem 7 that .
- ★
- For , let, where and ,, where and ,, where and ,, where and , and, where and .As , it follows by Theorem 7 that for .
We saw that the 5-binomial linear forest has 7 components and . This does not imply that every 5-binomial linear forest with 7 components has Ramsey index 4. For example, is also a 5-binomial linear forest with 7 components and the maximum number of pairwise edge-disjoint copies of in F is . As F has no component of even size 4 or more, it follows by Theorem 7 that .
5. Closing Comments
From the information obtained on Ramsey chains of linear forest, a question remains, namely that of determining information on Ramsey chains of other familiar classes of graphs. For every graph G of size m that has been investigated where , it has been shown that either or . This leads to the following problem:
Problem 1.
Let G be a graph of size m with for some positive integer k. Is it true that either or ?
Author Contributions
Equal contributions by all authors. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
We thank the anonymous referees whose valuable suggestions resulted in an improved paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Alavi, Y.; Boals, A.J.; Chartrand, G.; Erdős, P.; Oellermann, O.R. The ascending subgraph decomposition problem. Congr. Numer. 1987, 58, 7–14. [Google Scholar]
- Chen, H. On the ascending subgraph decomposition into matchings. J. Math. Res. Expo. 1994, 14, 61–64. [Google Scholar]
- Chen, H.; Ma, K. On the ascending subgraph decompositions of regular graphs. Appl. Math.—J. Chin. Univ. 1998, 13B, 165–170. [Google Scholar]
- Faudree, R.J.; Gould, R.J. Ascending subgraph decomposition for forests. Congr. Numer. 1990, 70, 221–229. [Google Scholar]
- Faudree, R.J.; Gould, R.; Jacobson, M.S.; Lesniak, L. Graphs with an ascending subgraph decomposition. Congr. Numer. 1988, 65, 33–42. [Google Scholar]
- Faudree, R.J.; Gyárfás, A.; Schelp, R.H. Graphs which have an ascending subgraph decomposition. Congr. Numer. 1987, 59, 49–54. [Google Scholar]
- Fink, J.F.; Straight, H.J. A note on path-perfect graphs. Discret. Math. 1981, 33, 95–98. [Google Scholar] [CrossRef]
- Fu, H. A note on the ascending subgraph decomposition problem. Discret. Math. 1990, 84, 315–318. [Google Scholar] [CrossRef]
- Ma, K.; Zhou, H.; Zhou, J. On the ascending star subgraph decomposition of star forest. Combinatorica 1994, 14, 307–320. [Google Scholar] [CrossRef]
- Fu, H.L.; Hu, W.H. Ascending subgraph decompositions of regular graphs. Discret. Math. 2002, 253, 11–18. [Google Scholar] [CrossRef]
- Ali, A.; Chartrand, G.; Zhang, P. Irregularity in Graphs; Springer: New York, NY, USA, 2021. [Google Scholar]
- Chartrand, G.; Zhang, P. The ascending Ramsey index of a graph. Symmetry 2023, 15, 523. [Google Scholar] [CrossRef]
- Ramsey, F.P. On a problem of formal logic. Proc. Lond. Math. Soc. 1930, 30, 264–286. [Google Scholar] [CrossRef]
- Chvátal, V. Tree-complete graph Ramsey numbers. J. Graph Theory 1977, 1, 93. [Google Scholar] [CrossRef]
- Erdős, P. Some remarks on the theory of graphs. Bull. Am. Math. Soc. 1947, 53, 292–294. [Google Scholar] [CrossRef]
- Erdős, P. Graph theory and probability II. Can. J. Math. 1961, 13, 346–352. [Google Scholar] [CrossRef]
- Erdős, P. Extremal problems in graph theory. In A Seminar on Graph Theory; Holt, Rinehart and Winston: New York, NY, USA, 1967; pp. 54–59. [Google Scholar]
- Erdős, P.; Rado, R. A combinatorial theorem. J. Lond. Math. Soc. 1950, 25, 249–255. [Google Scholar] [CrossRef]
- Erdös, P.; Szekeres, G. A combinatorial problem in geometry. Compos. Math. 1935, 2, 463–470. [Google Scholar]
- Graham, R.L.; Rothschild, B.L.; Spencer, J.H. Ramsey Theory, 2nd ed.; Wiley: New York, NY, USA, 2013. [Google Scholar]
- Greenwood, R.E.; Gleason, A.M. Combinatorial relations and chromatic graphs. Can. J. Math. 1955, 7, 1–7. [Google Scholar] [CrossRef]
- Radzisowski, S.P. Small Ramsey numbers. Electron. J. Comb. 2014. [Google Scholar] [CrossRef]
- Harary, F. Graph Theory; Addison-Wesley: Reading, MA, USA, 1969. [Google Scholar]
- Chartrand, G.; Chatterjee, R.; Zhang, P. Ramsey chains in graphs. Electron. J. Math. 2023, 6, 1–14. [Google Scholar] [CrossRef]
- Chatterjee, R.; Zhang, P. The Ramsey Indexes of Paths and Cycles. Department of Mathematics, Western Michigan University, Kalamazoo, MI, USA. 2023; Unpublished work. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).