Sharp Power Mean Bounds for Two Seiffert-like Means ^†

Abstract

The mean is a subject of extensive study among scholars, and the pursuit of optimal power mean bounds is a highly active field. This article begins with a concise overview of recent advancements in this area, focusing specifically on Seiffert-like means. We establish sharp power mean bounds for two Seiffert-like means, including the introduction and establishment of the best asymmetric mean bounds for symmetric means. Additionally, we explore the practical applications of these findings by extending several intriguing chains of inequalities that involve more than ten means. This comprehensive analysis provides a deeper understanding of the relationships and properties of these means.

1. Introduction

In the realm of mathematical inequalities, the concept of mean, in its various manifestations, holds a distinguished place. Mean, whether it be arithmetic, geometric, or one of its many counterparts, has been a steadfast companion to mathematicians throughout history. Its roots extend back to the earliest mathematical writings, where thinkers grappled with the notions of balance and fairness. From ancient civilizations to the luminaries of the Enlightenment, the concept of mean has played a pivotal role in shaping the discourse of mathematics.

As we embark on the journey of sharing our findings and insights, we do so with a profound reverence for the rich mathematical heritage and literature that have guided us to this juncture. Our objective is to weave a new thread into the intricate tapestry of inequalities, one that pays homage to the historical significance of mean while pushing the boundaries of mathematical knowledge.

The symmetrical beauty inherent in mathematical inequalities resonates with the aesthetics of a finely crafted masterpiece. It is as though mean serves as a mathematical brushstroke, imbuing the canvas of equations and proofs with an artistic touch.

In our pursuit, we are akin to intrepid explorers navigating uncharted territory, and we celebrate mean as our guiding compass through the labyrinth of mathematical inequalities. We acknowledge its role not only as a scientific cornerstone but also as an artistic element that enriches our mathematical journey.

Throughout the paper, we consider the condition that $a,b>0$ with $a\ne b$. For $r\in \mathbb{R}$, the power mean of order r of the positive real numbers a and b is defined by

$$A_r\equiv A_r\left(a,b\right)={\left(\frac{a^r+b^r}{2}\right)}^{1/r}\mathrm{if}r\ne 0\mathrm{and}{A}_0\equiv A_0\left(a,b\right)=\sqrt{ab},$$

(1)

which has the following properties:

(i) The function $r\mapsto A_r\left(a,b\right)$ is continuous and increasing on $\mathbb{R}$ (see [1]), and is log-concave on $\left(0,\infty \right)$ and log-convex on $(-\infty ,0)$ (see [2]).

(ii) The function $r\mapsto 2^{1/r}{A}_r\left(a,b\right)$ is strictly decreasing and log-convex on $\left(0,\infty \right)$ (Lemma 6 [3]).

More generally, the power mean of order r of a and b with weight $w\in \left(0,1\right)$ is defined by

$$A_r\left(a,b;w\right)={\left(w{a}^r+\left(1-w\right)b^r\right)}^{1/r}\mathrm{if}r\ne 0\mathrm{and}{A}_0\left(a,b;w\right)=a^w{b}^{1-w},$$

which satisfies that $r\mapsto A_r\left(a,b;w\right)$ is increasing on $\mathbb{R}$ for fixed $w\in \left(0,1\right)$.

As special cases, we have $A=A\left(a,b\right)=A_1\left(a,b\right)$, $G=G\left(a,b\right)=A_0\left(a,b\right)$, $H=H\left(a,b\right)=A_{-1}\left(a,b\right)$, which are the arithmetic mean, geometric mean and harmonic mean, respectively.

Various symmetric and homogeneous bivariate means exist, including the Heronian mean $He(a,b)$, the logarithmic mean $L(a,b)$ and the identric (exponential) mean $I(a,b)$, which are defined by

$$He\left(a,b\right)=\frac{a+b+\sqrt{ab}}{3},L\left(a,b\right)=\frac{a-b}{lna-lnb},I\left(a,b\right)=e^{-1}{\left(\frac{a^a}{b^b}\right)}^{1/(a-b)},$$

respectively. The three means have sharp lower and upper bounds in terms of power means, namely,

$$\begin{array}{ccc}\hfill A_{ln2/ln3}\left(a,b\right)<He\left(a,b\right)<A_{2/3}\left(a,b\right),& & \hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill A_0\left(a,b\right)<L\left(a,b\right)<A_{1/3}\left(a,b\right),& & \hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill A_{2/3}\left(a,b\right)<I\left(a,b\right)<A_{ln2}\left(a,b\right),& & \hfill \end{array}$$

(4)

where all orders of these power means in the above three double inequalities are the best possible. The inequalities (2), (3), and (4) are derived from references [4], [5], and [6,7], respectively.

There are also three bivariate means of the same form, which are the first Seiffert mean $P(a,b)$ [8], the second Seiffert mean $T(a,b)$ [9] and Neuman–Sándor mean $NS\left(a,b\right)$ [10], which are defined by

$$P\left(a,b\right)=\frac{a-b}{2arcsin\frac{a-b}{a+b}},T\left(a,b\right)=\frac{a-b}{2arctan\frac{a-b}{a+b}},NS\left(a,b\right)=\frac{a-b}{2arsinh\frac{a-b}{a+b}},$$

(5)

respectively. The three means also have the best power mean bounds, which are

$$\begin{array}{ccc}\hfill A_{ln2/ln\pi }\left(a,b\right)<P\left(a,b\right)<A_{2/3}\left(a,b\right),& & \hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill A_{ln2/(ln\pi -ln2)}\left(a,b\right)<T\left(a,b\right)<A_{5/3}\left(a,b\right),& & \hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill A_{ln2/[ln(ln(3+2\sqrt{2}))]}\left(a,b\right)<NS(a,b)<A_{4/3}(a,b).& & \hfill \end{array}$$

(8)

The inequalities (6), (7), and (8) are derived from references [11,12,13], [14,15], and [3,15,16], respectively.

Moreover, Yang [17] introduced two new means defined by

$$U\left(a,b\right)=\frac{a-b}{\sqrt{2}arctan\frac{a-b}{\sqrt{2ab}}}\mathrm{and}V\left(a,b\right)=\frac{a-b}{\sqrt{2}arsinh\frac{a-b}{\sqrt{2ab}}},$$

which also have the sharp lower and upper power mean bounds:

$$\begin{array}{ccc}\hfill A_{ln4/\left(2ln\pi -ln2\right)}\left(a,b\right)<U\left(a,b\right)<A_{4/3}\left(a,b\right),& & \hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill A_0\left(a,b\right)<V\left(a,b\right)<A_{2/3}\left(a,b\right).& & \hfill \end{array}$$

(10)

The inequalities (9) and (10) are derived from references [18] and [19], respectively.

Other bivariate means and the best bounds for them can be seen in the following articles:

(i) Gauss arithmetic–geometric mean [20];

(ii) Toader mean [21] and the best power mean bounds were established in [22], Corollary (1) [23], Theorem 22 [24];

(iii) Toader–Qi mean, see Theorem 3.4 [25];

(iv) Sándor mean, see [26,27];

(v) Sándor–Yang mean, see [17,28].

In particular, it is worth mentioning that, inspired by the first and second Seiffert means, Witkowski [29] introduced the Seiffert-like mean defined by

$$M_f\left(a,b\right)=\frac{\left|a-b\right|}{2f\left(\frac{\left|a-b\right|}{a+b}\right)},$$

(11)

where f is defined on $\left(0,1\right)$ satisfying

$$\frac{t}{1+t}<f\left(t\right)<\frac{t}{1-t},$$

and is called the Seiffert functions. Clearly, the Seiffert functions have two important properties:

$$\underset{t\to 0}{lim}f\left(0\right)=0\mathrm{and}\underset{t\to 0}{lim}\frac{f\left(t\right)}{t}=1.$$

(12)

Letting $f=arcsin,arctan,arsinh,artanh$ in (11) produces the first and second Seiffert means, Nueman–Sándor mean, and logarithmic mean. Taking $f=sinh$, tan in (11) gives

$$\begin{array}{ccc}\hfill M_{sinh}\left(a,b\right)& =& \frac{a-b}{2sinh\left(\frac{a-b}{a+b}\right)},\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill M_{tan}\left(a,b\right)& =& \frac{a-b}{2tan\left(\frac{a-b}{a+b}\right)},\hfill \end{array}$$

(14)

which are called the hyperbolic sine mean and tangent mean of a and b, respectively. Recently, the two new means, namely $M_{sinh}\left(a,b\right)$ and $M_{tan}\left(a,b\right)$, caught the attention of some scholars, and several bounds for the two new means have been established. Witkowski [29] presented a chain of comparison inequalities among the Seiffert-like means L, P, $M_{tan}$, $M_{sinh}$, and A:

$$L<\left\{\begin{array}{c}P\\ M_{tan}\end{array}\right\}<M_{sinh}<A,$$

where the means in the curly brackets are not comparable. In 2020, Nowicka and Witkowski [30] provided the optimal weighted power mean bounds $A_p(A,G;w)$ ($p=\pm 1$, $\pm 2$) for the two new means $M_{sinh}$ and $M_{tan}$. In another paper [31], the authors established the best weighted power mean bounds $A_p(A,H;w)$ ($p=\pm 1$, $\pm 2$) for $M_{sinh}$ and $M_{tan}$, which were generalized by Zhu [32], Zhu and Malešević [33] as follows: the double inequalities

$$\begin{array}{ccc}\hfill {\left(\frac{2}{3}{A}^q+\frac{1}{3}{H}^q\right)}^{1/q}& <& M_{tan}<{\left(\frac{2}{3}{A}^p+\frac{1}{3}{H}^p\right)}^{1/p},\hfill \\ \hfill {\left(\frac{5}{6}{A}^s+\frac{1}{6}{H}^s\right)}^{1/s}& <& M_{sinh}<{\left(\frac{5}{6}{A}^r+\frac{1}{6}{H}^r\right)}^{1/r},\hfill \end{array}$$

hold for $p\ge \left(ln(3/2)\right)/ln\left(tan1\right)$, $q\le 4/5$ and $r\ge 32/25$, $s\le \left(ln(6/5)\right)/ln\left(sinh1\right)$.

Other types of bounds for the two new means $M_{sinh}$ and $M_{tan}$ can be seen in [34,35,36].

From the published literature, however, there seems to be a gap in the research on power mean bounds for the two new means. The aim of this paper is to find the best power mean bounds for them. Our main results read as follows:

Theorem 1. 

The double inequality

$$A_p\left(a,b\right)<M_{sinh}\left(a,b\right)<A_q\left(a,b\right)$$

(15)

holds if and only if $p\le 2/3$ and $q\ge p_1=\left(ln2\right)/\left(ln2+lnsinh1\right)=0.811\dots$

Theorem 2. 

Let $p,q>0$ and ${\alpha }_p=1-{\left(2sinh1\right)}^{-p}$. If $b>a>0$, then the double inequality

$$A_p\left(a,b;{\alpha }_p\right)<M_{sinh}\left(a,b\right)<A_q\left(a,b;{\alpha }_q\right)$$

(16)

holds if and only if $p\ge 1$ and $0<q\le p_1=\left(ln2\right)/\left(ln2+lnsinh1\right)=0.811\dots$ Refer to Figure 1 and Figure 2. Moreover, $p\mapsto A_p\left(a,b;{\alpha }_p\right)$ is decreasing on $\left(0,\infty \right)$.

Figure 1. The graph of $A_p\left(a,b;{\alpha }_p\right)$ and $M_{sinh}(a,b)$ when $b=1$ and $a\in (0,1)$. From this, it can be observed that the double inequality (16) holds. The symmetric mean $M_{sinh}(a,1)$ is controlled by the asymmetric means $A_p(a,1;{\alpha }_p)$, with $A_1$ and $A_{p_1}$ being its sharp lower and upper bounds.

Figure 2. The graph of $A_p\left(a,b;{\alpha }_p\right)-M_{sinh}(a,b)$ when $b=1$ and $a\in (0,1)$. $A_1(a,1;{\alpha }_1)$ and $A_{p_1}(a,1;{\alpha }_{p_1})$ represent the sharp lower and upper bounds of $M_{sinh}$. Once exceeded, they are inevitably breached, as illustrated by the example $A_{0.9}(a,1;{\alpha }_{0.9})$ taken here.

Theorem 3. 

The double inequality

$$A_p\left(a,b\right)<M_{tan}\left(a,b\right)<A_q\left(a,b\right)$$

(17)

holds if and only if $p\le 1/3$ and $q\ge p_0=\left(ln2\right)/\left(ln2+lntan1\right)=0.610\dots$

Theorem 4. 

Let $p,q>0$ and ${\beta }_p=1-{\left(2tan1\right)}^{-p}$. If $b>a>0$, then the double inequality

$$A_p\left(a,b;{\beta }_p\right)<M_{tan}\left(a,b\right)<A_q\left(a,b;{\beta }_q\right)$$

(18)

holds if and only if $p\ge 1$ and $0<q\le p_0=\left(ln2\right)/\left(ln2+lntan1\right)=0.610\dots$ Refer to Figure 3 and Figure 4. Moreover, $p\mapsto A_p\left(a,b;{\beta }_p\right)$ is decreasing on $\left(0,\infty \right)$.

Figure 3. The graph of $A_p\left(a,b;{\beta }_p\right)$ and $M_{tan}(a,b)$ when $b=1$ and $a\in (0,1)$. From this, it can be observed that the double inequality (18) holds. The symmetric mean $M_{tan}(a,1)$ is controlled by the asymmetric means $A_p(a,1;{\beta }_p)$, with $A_1$ and $A_{p_0}$ being its sharp lower and upper bounds.

Figure 4. The graph of $A_p\left(a,b;{\beta }_p\right)-M_{tan}(a,b)$ when $b=1$ and $a\in (0,1)$. $A_1(a,1;{\beta }_1)$ and $A_{p_0}(a,1;{\beta }_{p_0})$ represent the sharp lower and upper bounds of $M_{tan}$. Once exceeded, they are inevitably breached, as illustrated by the example $A_{0.7}(a,1;{\beta }_{0.7})$ taken here.

The organization of the remaining sections of this paper is structured as follows. In Section 2, four tools and three monotonicity results are listed, which are needed to prove our main results. Proofs of Theorems 1–4 are presented in Section 3. In the fourth section, several chains of inequalities for means including eight old means and two new Seiffert-like means are established.

2. Preliminaries

2.1. Tools

Several tools are required for establishing our main results. The first tool is the so-called L’Hospital monotonic rule (LMR).

Proposition 1 

(Theorem 2 [37]). Let $-\infty <a<b<\infty$, and let $f,g:[a,b]\to \mathbb{R}$ be continuous functions that are differentiable on $\left(a,b\right)$, with $f\left(a\right)=g\left(a\right)=0$ or $f\left(b\right)=g\left(b\right)=0$. Assume that $g^{\prime }\left(x\right)\ne 0$ for each x in $(a,b)$. If $f^{\prime }/g^{\prime }$ is increasing (decreasing) on $(a,b)$ then so is $f/g$.

To introduce the second tool, we introduce an important auxiliary function $H_{f,g}$, which appeared in [38] and was called Yang’s H–function in [39]. For $-\infty \le a<b\le \infty$, let f and g be differentiable on $(a,b)$ and $g^{\prime }\ne 0$ on $(a,b)$. Then the function $H_{f,g}$ is defined by

$$H_{f,g}=\frac{f^{\prime }}{g^{\prime }}g-f.$$

(19)

If f and g are twice differentiable on $(a,b)$, then

$$\begin{array}{ccc}\hfill {\left(\frac{f}{g}\right)}^{\prime }& =& \frac{g^{\prime }}{g^2}\left(\frac{f^{\prime }}{g^{\prime }}g-f\right)=\frac{g^{\prime }}{g^2}{H}_{f,g},\hfill \end{array}$$

(20)

$$\begin{array}{ccc}\hfill H_{f,g}^{{}^{\prime }}& =& {\left(\frac{f^{\prime }}{g^{\prime }}\right)}^{\prime }g.\hfill \end{array}$$

(21)

The following proposition was proved in [38] and is called the L’Hospital piece monotonic rule (LPMR).

Proposition 2. 

Let $-\infty \le a<b\le \infty$. Let f and g be differentiable functions on $(a,b)$ and let $H_{f,g}$ be defined by (19). Suppose that (i) $g^{\prime }\ne 0$ on $(a,b)$; (ii) $f\left(b^{-}\right)=g\left(b^{-}\right)=0$; (iii) there is a $c\in \left(a,b\right)$ such that $f^{\prime }/g^{\prime }$ is increasing (respectively, decreasing) on $\left(a,c\right)$ and decreasing (respectively, increasing) on $\left(c,b\right)$. Then, we have the following:

(i) When $g^{\prime }>0$ and $H_{f,g}\left(a^{+}\right)\le 0\left(respectively,\ge 0\right)$, or $g^{\prime }<0$ and $H_{f,g}\left(a^{+}\right)\ge 0\left(respectively,\le 0\right)$, $f/g$ is decreasing (respectively, increasing) on $\left(a,b\right)$;

(ii) When $g^{\prime }>0$ and $H_{f,g}\left(a^{+}\right)>0\left(respectively,<0\right)$, or $g^{\prime }<0$ and $H_{f,g}\left(a^{+}\right)<0\left(respectively,>0\right)$, there is a unique number $x_b\in \left(a,b\right)$ such that $f/g$ is increasing (respectively, decreasing) on $\left(a,x_b\right)$ and decreasing (respectively, increasing) on $\left(x_b,b\right)$.

A significant role in addressing the monotonicity of power series ratios is played by the third tool, which involves the monotonicity rule for the ratio of two power series as discussed in [40].

Proposition 3. 

Let $A\left(t\right)={\sum }_{n=0}^{\infty }{a}_n{t}^n$ and $B\left(t\right)={\sum }_{n=0}^{\infty }{b}_n{t}^n$ be two real power series converging on $\left(-r,r\right)$ ($r>0$) with $b_n>0$ for all n. If the sequence ${\{a_n/b_n\}}_{n\ge 0}$ is increasing (decreasing), then so is the ratio $A\left(t\right)/B\left(t\right)$ on $\left(0,r\right)$.

The fourth tool, established in Theorem 2.1 [41] by Yang, Chu, and Wang, provides a fresh monotonicity rule for power series ratios when the sequence ${\{a_n/b_n\}}_{n\ge 0}$ is initially increasing (respectively, decreasing), then decreasing (respectively, increasing). The following proposition appeared in [42], which is a slightly modified version of Theorem 2.1 [41].

Proposition 4. 

Let $f\left(t\right)={\sum }_{k=0}^{\infty }{a}_k{t}^k$ and $g\left(t\right)={\sum }_{k=0}^{\infty }{b}_k{t}^k$ be two real power series converging on $\left(-r,r\right)$ and $b_k>0$ for all k. Suppose that for certain $m\in \mathbb{N}$, the sequences ${\left\{a_k/b_k\right\}}_{0\le k\le m}$ and ${\left\{a_k/b_k\right\}}_{k\ge m}$ are both non-constant, and they are increasing (respectively, decreasing) and decreasing (respectively, increasing), respectively. Then the function $f/g$ is strictly increasing (respectively, decreasing) on $\left(0,r\right)$ if and only if $H_{f,g}\left(r^{-}\right)\ge 0\left(respectively,\le 0\right)$. If $H_{f,g}\left(r^{-}\right)<0$$\left(respectively,>0\right)$, then there exists $t_0\in \left(0,r\right)$ such that the function $f/g$ is strictly increasing (respectively, decreasing) on $\left(0,t_0\right)$ and strictly decreasing (respectively, increasing) on $\left(t_0,r\right)$.

Propositions 3 and 4 are very efficient to study for certain special functions, see for example [43,44,45,46,47,48,49,50,51,52].

2.2. Three Monotonicity Results

The following two monotonicity results are crucial to prove Theorems 5 and 6.

Lemma 1. 

The function

$${\varphi }_{sinh}\left(t\right)=\frac{t\left(1-t^2\right)\left[2t{cosh}^{2}t-\left(2cosht+tsinht\right)sinht\right]}{\left[sinht-t\left(1-t\right)cosht\right]\left[sinht-t\left(t+1\right)cosht\right]}$$

(22)

is decreasing from $\left(0,1\right)$ onto $\left(0,1/3\right)$.

Lemma 2. 

The function

$${\varphi }_{tan}\left(t\right)=\frac{2t\left(1-t^2\right)\left(sint-tcost\right)cost}{\left(t^2-t+sintcost\right)\left(t^2+t-sintcost\right)}$$

(23)

is decreasing from $\left(0,1\right)$ onto $\left(0,2/3\right)$.

We first prove Lemma 1.

Proof of Lemma 1. 

Let

$$\begin{array}{ccc}\hfill g_1\left(t\right)& =& -t\left(1-t^2\right)\left[2t{cosh}^{2}t-\left(2cosht+tsinht\right)sinht\right],\hfill \\ \hfill g_2\left(t\right)& =& -\left[sinht-t\left(1-t\right)cosht\right]\left[sinht-t\left(t+1\right)cosht\right].\hfill \end{array}$$

Then ${\varphi }_{sinh}\left(t\right)=g_1\left(t\right)/g_2\left(t\right)$. Using the product-to-sum formula and expanding in power series yield

$$\begin{array}{ccc}\hfill 2g_1\left(t\right)& =& \left(t^2-1\right)\left(t^{2}cosh2t-2tsinh2t+3t^2\right)\hfill \\ & =& \left(t^2-1\right)\left[\sum _{n=1}^{\infty }\frac{2^{2n-2}}{\left(2n-2\right)!}{t}^{2n}-\sum _{n=1}^{\infty }\frac{2^{2n}}{\left(2n-1\right)!}{t}^{2n}+3t^2\right]\hfill \\ & =& \left(t^2-1\right)\sum _{n=2}^{\infty }\frac{\left(2n-5\right)2^{2n-2}}{\left(2n-1\right)!}{t}^{2n}\hfill \\ & =& \sum _{n=3}^{\infty }\frac{\left(2n-7\right)2^{2n-4}}{\left(2n-3\right)!}{t}^{2n}-\sum _{n=2}^{\infty }\frac{\left(2n-5\right)2^{2n-2}}{\left(2n-1\right)!}{t}^{2n}\hfill \\ & =& \sum _{n=3}^{\infty }\frac{\left(2n-2\right)\left(2n-1\right)\left(2n-7\right)2^{2n-4}}{\left[\left(2n-3\right)!\right]\left(2n-2\right)\left(2n-1\right)}{t}^{2n}-\sum _{n=3}^{\infty }\frac{\left(2n-5\right)2^{2n-2}}{\left(2n-1\right)!}{t}^{2n}-\frac{-2^2}{3!}{t}^4\hfill \\ & =& \sum _{n=3}^{\infty }\frac{\left(n-1\right)\left(2n-1\right)\left(2n-7\right)2^{2n-3}-2\left(2n-5\right)2^{2n-3}}{\left(2n-1\right)!}{t}^{2n}+\frac{2}{3}{t}^4\hfill \\ & =& \sum _{n=2}^{\infty }{a}_n{t}^{2n},\hfill \end{array}$$

where

$$a_2=\frac{2}{3}\mathrm{and}{a}_n=\frac{\left(2n-3\right)\left(2n^2-7n-1\right)2^{2n-3}}{\left(2n-1\right)!}\mathrm{for}n\ge 3;$$

$$\begin{array}{ccc}\hfill 2g_2\left(t\right)& =& t^{4}cosh2t-t^{2}cosh2t-cosh2t+2tsinh2t+t^4-t^2+1\hfill \\ & =& \sum _{n=2}^{\infty }\frac{2^{2n-4}}{\left(2n-4\right)!}{t}^{2n}-\sum _{n=1}^{\infty }\frac{2^{2n-2}}{\left(2n-2\right)!}{t}^{2n}\hfill \\ & & -\sum _{n=0}^{\infty }\frac{2^{2n}}{\left(2n\right)!}{t}^{2n}+\sum _{n=1}^{\infty }\frac{2^{2n}}{\left(2n-1\right)!}{t}^{2n}+t^4-t^2+1\hfill \\ & =& 2t^4+\sum _{n=3}^{\infty }\frac{\left(2n-1\right)\left(2n^3-5n^2+n+4\right)2^{2n-2}}{\left(2n\right)!}{t}^{2n}\hfill \\ & =& \sum _{n=2}^{\infty }{b}_n{t}^{2n},\hfill \end{array}$$

where

$$b_2=2\mathrm{and}{b}_n=\frac{\left(2n-1\right)\left(2n^3-5n^2+n+4\right)2^{2n-2}}{\left(2n\right)!}\mathrm{for}n\ge 3.$$

Obviously, $b_n>0$ for $n\ge 2$. To use Proposition 4, we have to observe the monotonicity of the sequence ${\left\{a_n/b_n\right\}}_{n\ge 2}$. A direct verification gives

$$\frac{a_2}{b_2}=\frac{1}{3}\mathrm{and}\frac{a_n}{b_n}=\frac{n\left(2n-3\right)\left(2n^2-7n-1\right)}{\left(2n-1\right)\left(2n^3-5n^2+n+4\right)}\mathrm{for}n\ge 3,$$

and then,

$$d_2=\frac{a_3}{b_3}-\frac{a_2}{b_2}=-\frac{9}{20}-\frac{1}{3}=-\frac{47}{60}<0,$$

$$d_n=\frac{a_{n+1}}{b_{n+1}}-\frac{a_n}{b_n}=8\frac{4n^6-n^4-20n^3+6n^2+6n-3}{\left(2n-1\right)\left(2n+1\right)\left(2n^3+n^2-3n+2\right)\left(2n^3-5n^2+n+4\right)}>0$$

for $n\ge 3$. This shows that the sequence ${\left\{a_n/b_n\right\}}_{n\ge 2}$ is decreasing for $n=2,3$ and increasing for $n\ge 3$. If we show that $H_{g_1,g_2}\left(1\right)<0$, then by Proposition 4, we deduce that ${\varphi }_{sinh}=g_1/g_2$ is decreasing on $\left(0,1\right)$. A direct computation yields

$$g_1\left(1\right)=0\mathrm{and}{g}_2\left(1\right)=\left(2cosh1-sinh1\right)sinh1>0.$$

Differentiation leads to

$$\begin{array}{ccc}\hfill g_1^{{}^{\prime }}\left(t\right)& =& \left(3t^2-1\right)\left[2t{cosh}^{2}t-\left(2cosht+tsinht\right)sinht\right]\hfill \\ & & -t\left(1-t^2\right)\left(2tcosht-3sinht\right)\left(sinht\right),\hfill \\ \hfill g_2^{{}^{\prime }}\left(t\right)& =& -\left[2tcosht+\left(t^2-t\right)sinht\right]\left[sinht-t\left(t+1\right)cosht\right]\hfill \\ & & +\left[sinht-t\left(1-t\right)cosht\right]\left[2tcosht+t\left(t+1\right)\left(sinht\right)\right],\hfill \end{array}$$

which yields

$$\begin{array}{ccc}\hfill g_1^{{}^{\prime }}\left(1\right)& =& cosh2-2sinh2+3=-0.491\dots <0,\hfill \\ \hfill g_2^{{}^{\prime }}\left(1\right)& =& 3cosh2+1>0.\hfill \end{array}$$

We then obtain

$$H_{g_1,g_2}\left(1\right)=\frac{g_1^{{}^{\prime }}\left(1\right)}{g_2^{{}^{\prime }}\left(1\right)}{g}_2\left(1\right)-g_1\left(1\right)<0.$$

An easy check gives ${lim}_{t\to 0}{\varphi }_{sinh}\left(0\right)=1/3$ and ${\varphi }_{sinh}\left(1\right)=0$, thereby completing the proof. □

For proving Lemma 2, we need the following lemmas.

Lemma 3. 

For $\left|t\right|<\pi$, we have

$$\begin{array}{ccc}\hfill \frac{1}{sint}& =& \frac{1}{t}+\sum _{n=1}^{\infty }\frac{2^{2n}-2}{\left(2n\right)!}\left|B_{2n}\right|t^{2n-1},\hfill \end{array}$$

(24)

$$\begin{array}{ccc}\hfill \frac{cost}{sint}& =& \frac{1}{t}-\sum _{n=1}^{\infty }\frac{2^{2n}}{\left(2n\right)!}\left|B_{2n}\right|t^{2n-1}\hfill \end{array}$$

(25)

$$\begin{array}{ccc}\hfill \frac{1}{{sin}^{2}t}& =& \frac{1}{t^2}+\sum _{n=1}^{\infty }\frac{\left(2n-1\right)2^{2n}}{\left(2n\right)!}\left|B_{2n}\right|t^{2n-2},\hfill \end{array}$$

(26)

$$\begin{array}{ccc}\hfill \frac{cost}{{sin}^{2}t}& =& \frac{1}{t^2}-\sum _{n=1}^{\infty }\frac{\left(2n-1\right)\left(2^{2n}-2\right)}{\left(2n\right)!}\left|B_{2n}\right|t^{2n-2}.\hfill \end{array}$$

(27)

Proof. 

The power series representations (24) and (25) were listed in Equations (4.3.68) and (4.3.70) [53]. The third and fourth power series representations follow from

$$\frac{1}{{sin}^{2}t}=-{\left(\frac{cost}{sint}\right)}^{\prime }\mathrm{and}\frac{cost}{{sin}^{2}t}=-{\left(\frac{1}{sint}\right)}^{\prime },$$

which completes the proof. □

The Bernoulli numbers $B_n$ are defined by the exponential generating function

$$\frac{x}{e^x-1}-1+\frac{x}{2}=\sum _{n=2}^{\infty }\frac{B_n}{n!}{x}^n\left|x\right|<2\pi .$$

The function $x/\left(e^x-1\right)-1+x/2$ is even on $\mathbb{R}$, $B_{2n+1}=0$ for $n\in \mathbb{N}$. An analytic expression exists for even orders, $B_{2n}={(-1)}^{n-1}\frac{2\left(2n\right)!}{{\left(2\pi \right)}^{2n}}{\sum }_{s=1}^{\infty }{s}^{-2n}={(-1)}^{n-1}\frac{2\left(2n\right)!}{{\left(2\pi \right)}^{2n}}\zeta \left(2n\right)$ for $n\ge 1$, where $\zeta (·)$ is the Riemann zeta function. The following lemma was proved in [54] (see also [55]).

Lemma 4. 

For $k\in \mathbb{N}$, Bernoulli numbers $B_{2k}$ satisfy

$$\frac{2^{2k+2}-1}{2^{2k}-1}\frac{{\pi }^2}{\left(2k+1\right)\left(2k+2\right)}<\frac{\left|B_{2k}\right|}{\left|B_{2k+2}\right|}<\frac{2^{2k+1}-1}{2^{2k-1}-1}\frac{{\pi }^2}{\left(2k+1\right)\left(2k+2\right)}.$$

(28)

Now, we are able to prove Lemma 2.

Proof of Lemma 2. 

Let

$$\begin{array}{ccc}\hfill \xi \left(2t\right)& =& 8t\left(sint-tcost\right)cost,\hfill \\ \hfill \eta \left(2t\right)& =& 4\left(t^2-t+sintcost\right)\left(t^2+t-sintcost\right).\hfill \end{array}$$

Then

$${\varphi }_{tan}\left(t\right)=\left(1-t^2\right)\frac{\xi \left(2t\right)}{\eta \left(2t\right)}.$$

Since $sint-tcost>0$ and $cost>0$ for $t\in \left(0,\pi /2\right)$, we have

$$\xi \left(s\right)=4s\left(sin\frac{s}{2}-\frac{s}{2}cos\frac{s}{2}\right)cos\frac{s}{2}=2ssins-s^{2}coss-s^2>0$$

for $s\in \left(0,\pi \right)$. Similarly, we have

$$\eta \left(s\right)=\left(\frac{1}{2}{s}^2-s+sins\right)\left(\frac{1}{2}{s}^2+s-sins\right)=\frac{1}{4}{s}^4-s^2+2ssins-{sin}^{2}s>0$$

for $s\in \left(0,\pi \right)$ due to ${\eta }_1\left(s\right)=\left(s^2/2-s+sins\right)>0$ and ${\eta }_2\left(s\right)=\left(s^2/2+s-sins\right)>0$ for $s\in \left(0,\pi \right)$. In fact, since

$${\eta }_1^{{}^{″}}\left(s\right)=1-sins>0,{\eta }_2^{{}^{″}}\left(s\right)=1+sins>0$$

for $s\in \left(0,\infty \right)$, and ${\eta }_j\left(0\right)={\eta }_j^{{}^{\prime }}\left(0\right)=0$ for $j=1,2$, we immediately get that ${\eta }_1\left(s\right)$, ${\eta }_2\left(s\right)>0$ for $s\in \left(0,\infty \right)$. Thus, if we prove that $s\mapsto \eta \left(s\right)/\xi \left(s\right)$ is increasing on $\left(0,\pi \right)$, then the function $s\mapsto \xi \left(s\right)/\eta \left(s\right)$ is positive and decreasing on $\left(0,\pi \right)$, and then, so is $t\mapsto {\varphi }_{tan}\left(t\right)$ on $\left(0,1\right)$.

Now, expanding in power series leads to

$$\begin{array}{ccc}\hfill \frac{\eta \left(s\right)}{{sin}^{2}s}& =& \frac{s^4/4-s^2+2ssins-{sin}^{2}s}{{sin}^{2}s}=\frac{1}{4}\frac{s^4}{{sin}^{2}s}-\frac{s^2}{{sin}^{2}s}+2\frac{s}{sins}-1\hfill \\ & =& \frac{1}{4}{s}^2+\sum _{n=1}^{\infty }\frac{\left(2n-1\right)2^{2n-2}}{\left(2n\right)!}\left|B_{2n}\right|s^{2n+2}-\left(1+\sum _{n=1}^{\infty }\frac{\left(2n-1\right)2^{2n}}{\left(2n\right)!}\left|B_{2n}\right|s^{2n}\right)\hfill \\ & & +2\left(1+\sum _{n=1}^{\infty }\frac{2^{2n}-2}{\left(2n\right)!}\left|B_{2n}\right|s^{2n}\right)-1=\sum _{n=1}^{\infty }{a}_n{s}^{2n},\hfill \end{array}$$

where $a_1=1/4$ and for $n\ge 2$,

$$a_n=\frac{\left(2n\right)\left(2n-1\right)\left(2n-3\right)2^{2n-4}\left|B_{2n-2}\right|-\left(\left(2n-3\right)2^{2n}+4\right)\left|B_{2n}\right|}{\left(2n\right)!};$$

$$\begin{array}{ccc}\hfill \frac{\xi \left(s\right)}{{sin}^{2}s}& =& \frac{-s^2-s^{2}coss+2ssins}{{sin}^{2}s}=-\frac{s^2}{{sin}^{2}s}-\frac{s^{2}coss}{{sin}^{2}s}+2\frac{s}{sins}\hfill \\ & =& -\left(1+\sum _{n=1}^{\infty }\frac{\left(2n-1\right)2^{2n}}{\left(2n\right)!}\left|B_{2n}\right|s^{2n}\right)\hfill \\ & & -\left(1-\sum _{n=1}^{\infty }\frac{\left(2n-1\right)\left(2^{2n}-2\right)}{\left(2n\right)!}\left|B_{2n}\right|s^{2n}\right)+2+\sum _{n=1}^{\infty }\frac{2\left(2^{2n}-2\right)}{\left(2n\right)!}\left|B_{2n}\right|s^{2n}\hfill \\ & =& \sum _{n=1}^{\infty }\frac{2^{2n+1}-4n-2}{\left(2n\right)!}\left|B_{2n}\right|s^{2n}:=\sum _{n=1}^{\infty }{b}_n{s}^{2n},\hfill \end{array}$$

where

$$b_n=\frac{2^{2n+1}-4n-2}{\left(2n\right)!}\left|B_{2n}\right|.$$

It is easy to check that $b_n>0$ for $n\ge 1$, $a_1/b_1=3/2$ and for $n\ge 2$

$$\begin{array}{ccc}\hfill \frac{a_n}{b_n}& =& \frac{\left(2n\right)\left(2n-1\right)\left(2n-3\right)2^{2n-4}\left|B_{2n-2}\right|-\left(\left(2n-3\right)2^{2n}+4\right)\left|B_{2n}\right|}{\left(2^{2n+1}-4n-2\right)\left|B_{2n}\right|}\hfill \\ & =& \frac{\left(2n\right)\left(2n-1\right)\left(2n-3\right)2^{2n-4}}{2^{2n+1}-4n-2}\frac{\left|B_{2n-2}\right|}{\left|B_{2n}\right|}-\frac{\left(2n-3\right)2^{2n}+4}{2^{2n+1}-4n-2}.\hfill \end{array}$$

Then, $a_2/b_2=20/11$, $a_3/b_3=154/57$, and then,

$$d_1=\frac{a_2}{b_2}-\frac{a_1}{b_1}=\frac{7}{22}>0\mathrm{and}{d}_2=\frac{a_3}{b_3}-\frac{a_2}{b_2}=\frac{554}{627}>0.$$

We next show that $d_n=a_{n+1}/b_{n+1}-a_n/b_n>0$ for $n\ge 3$. Using Lemma 4 yields

$$\frac{a_n}{b_n}<\frac{\left(2n\right)\left(2n-1\right)\left(2n-3\right)2^{2n-4}}{2^{2n+1}-4n-2}\frac{2^{2n-1}-1}{2^{2n-3}-1}\frac{{\pi }^2}{2n\left(2n-1\right)}-\frac{\left(2n-3\right)2^{2n}+4}{2^{2n+1}-4n-2},$$

$$\begin{array}{ccc}\hfill \frac{a_{n+1}}{b_{n+1}}& =& \frac{\left(2n+2\right)\left(2n+1\right)\left(2n-1\right)2^{2n-2}}{2^{2n+3}-4n-6}\frac{\left|B_{2n}\right|}{\left|B_{2n+2}\right|}-\frac{\left(2n-1\right)2^{2n+2}+4}{2^{2n+3}-4n-6}\hfill \\ & >& \frac{\left(2n+2\right)\left(2n+1\right)\left(2n-1\right)2^{2n-2}}{2^{2n+3}-4n-6}\frac{2^{2n+2}-1}{2^{2n}-1}\frac{{\pi }^2}{\left(2n+1\right)\left(2n+2\right)}\hfill \\ & & -\frac{\left(2n-1\right)2^{2n+2}+4}{2^{2n+3}-4n-6}.\hfill \end{array}$$

Then,

$$\begin{array}{ccc}\hfill d_n& :& =\frac{a_{n+1}}{b_{n+1}}-\frac{a_n}{b_n}>\frac{\left(2n-1\right)2^{2n-2}}{2^{2n+3}-4n-6}\frac{2^{2n+2}-1}{2^{2n}-1}{\pi }^2-\frac{\left(2n-1\right)2^{2n+2}+4}{2^{2n+3}-4n-6}\hfill \\ & & -\frac{\left(2n-3\right)2^{2n-4}}{2^{2n+1}-4n-2}\frac{2^{2n-1}-1}{2^{2n-3}-1}{\pi }^2+\frac{\left(2n-3\right)2^{2n}+4}{2^{2n+1}-4n-2}\hfill \\ & =& \frac{4\left({\pi }^2-4\right)2^{8n}-c_3\left(n\right)2^{6n}+c_2\left(n\right)2^{4n}+c_1\left(n\right)2^{2n}-128}{4\left(2^{2n}-1\right)\left(2^{2n}-8\right)\left(2^{2n}-2n-1\right)\left(2^{2n+2}-2n-3\right)}\hfill \end{array}$$

where

$$\begin{array}{ccc}\hfill c_3\left(n\right)& =& 6\left({\pi }^2-4\right)n^2+21{\pi }^{2}n+\left(4{\pi }^2-178\right),\hfill \\ \hfill c_2\left(n\right)& =& 12\left(5{\pi }^2-18\right)n^2-450+5{\pi }^2,\hfill \\ \hfill c_1\left(n\right)& =& 12\left(16-{\pi }^2\right)n^2+416-5{\pi }^2.\hfill \end{array}$$

An easy verification yields that $c_i\left(n\right)>0$ for $i=1,2,3$ and $n\ge 3$, and

$$c_1\left(n\right)2^{2n}-128\ge c_1\left(2\right)2^4-128=16\left(1176-53{\pi }^2\right)>0$$

for $n\ge 2$; also, using an obvious inequality

$$2^{2n}={\left(1+3\right)}^n>1+3n+\frac{3^{2}n\left(n-1\right)}{2}=\frac{1}{2}\left(9n^2-3n+2\right),$$

we obtain that

$$\begin{array}{ccc}\hfill 4\left({\pi }^2-4\right)2^{2n}-c_3\left(n\right)& >& 4\left({\pi }^2-4\right)\frac{1}{2}\left(9n^2-3n+2\right)\hfill \\ & & -\left[6\left({\pi }^2-4\right)n^2+21{\pi }^{2}n+\left(4{\pi }^2-178\right)\right]\hfill \\ & =& 4\left({\pi }^2-4\right)n^2-\left(9{\pi }^2-8\right)n+54>0\mathrm{for}n\ge 3,\hfill \end{array}$$

which leads to $4\left({\pi }^2-4\right)2^{8n}-c_3\left(n\right)2^{6n}>0$ for $n\ge 3$. It then follows that $d_n>0$ for $n\ge 3$. Consequently, the sequence ${\left\{a_n/b_n\right\}}_{n\ge 1}$ is increasing, and by Lemma 3, so is the function $s\mapsto \eta \left(s\right)/\xi \left(s\right)$ on $\left(0,\pi \right)$. An easy computation yields

$$\underset{t\to 0}{lim}{\varphi }_{tan}\left(t\right)=\frac{2}{3}\mathrm{and}{\varphi }_{tan}\left(1\right)=0,$$

which completes the proof. □

Finally, we prove the decreasing property of $p\mapsto A_p\left(y,x;1-c^p\right)$, which is needed to prove Theorems 2 and 4.

Lemma 5. 

Let $x>y>0$ and $c\in \left(0,1\right)$. The function

$$p\mapsto A_p\left(y,x;1-c^p\right)={\left(\left(1-c^p\right)y^p+c^p{x}^p\right)}^{1/p}$$

is decreasing on $\left(0,\infty \right)$ with

$$\underset{p\to 0}{lim}{A}_p\left(y,x;1-c^p\right)=xand\underset{p\to \infty }{lim}{A}_p\left(y,x;1-c^p\right)=max\left\{cx,y\right\}.$$

Proof. 

Let $t=x/y$. Then

$$A_p\left(y,x;1-c^p\right)=yc{\left(t^p+c^{-p}-1\right)}^{1/p},t\in \left(1,\infty \right).$$

Differentiation yields

$$\begin{array}{ccc}\hfill \frac{\partial ln{A}_p}{\partial t}& =& \frac{t^{p-1}}{t^p+c^{-p}-1},\hfill \\ \hfill \frac{\partial }{\partial p}\left(\frac{\partial ln{A}_p}{\partial t}\right)& =& \frac{c^{-p}{t}^{p-1}\left(1-c^p\right)}{{\left(t^p+c^{-p}-1\right)}^2}\left(lnt-\frac{lnc}{c^p-1}\right).\hfill \end{array}$$

Since $c\in \left(0,1\right)$ and $t\in \left(1,\infty \right)$, we see that there is a $t_0>1$ such that ${\partial }^{2}ln{A}_p/\left(\partial p\partial t\right)<0$ for $t\in \left(1,t_0\right)$ and ${\partial }^{2}ln{A}_p/\left(\partial p\partial t\right)>0$ for $t\in \left(t_0,\infty \right)$, where $t_0=exp\left(\left(lnc\right)/\left(c^p-1\right)\right)$. This implies that the function $t\mapsto \left(\partial ln{A}_p\right)/\partial p$ is decreasing on $\left(1,t_0\right)$ and increasing on $\left(t_0,\infty \right)$. Note that

$$\frac{\partial ln{A}_p}{\partial p}=\frac{1}{p}\frac{t^{p}lnt-c^{-p}lnc}{t^p+c^{-p}-1}-\frac{1}{p^2}ln\left(t^p+c^{-p}-1\right).$$

An easy computation yields

$$\underset{t\to 1^{+}}{lim}\frac{\partial ln{A}_p}{\partial p}=0\mathrm{and}\underset{t\to \infty }{lim}\frac{\partial ln{A}_p}{\partial p}=0.$$

It then follows that

$$\frac{\partial ln{A}_p}{\partial p}<max\left\{\underset{t\to 1^{+}}{lim}\frac{\partial ln{A}_p}{\partial p},\underset{t\to \infty }{lim}\frac{\partial ln{A}_p}{\partial p}\right\}=0,$$

which proves the decreasing property of $p\mapsto A_p\left(y,x;1-c^p\right)$ on $\left(0,\infty \right)$. The required limit values can be derived by the L’Hospital rule. This completes the proof. □

3. Proofs of Main Results

Due to the symmetry and homogeneous of the means $M_f\left(a,b\right)$ and $A_p\left(a,b\right)$, we assume that $b>a>0$ and let $x=a/b\in \left(0,1\right)$. Then, the desired inequalities are equivalent to

$$A_p\left(x,1\right)<M_f\left(x,1\right)<A_q\left(x,1\right)$$

(29)

for $x\in \left(0,1\right)$, where $f=tan,sinh$. We prove Theorems 1–4 by considering the monotonicity pattern of the ratio ${\mathcal{U}}_f\left(x\right)/\mathcal{V}\left(x\right)$ on $\left(0,1\right)$, where

$${\mathcal{U}}_f\left(x\right)=M_f^p\left(x,1\right)-1\mathrm{and}\mathcal{V}\left(x\right)=x^p-1.$$

Figure 5 and Figure 6 present the graphs of $f=sinh$ and $f=tan$ of ${\mathcal{U}}_f\left(x\right)/\mathcal{V}\left(x\right)$, respectively. We observe the following patterns in the monotonicity of the ratio ${\mathcal{U}}_f\left(x\right)/\mathcal{V}\left(x\right)$ on $\left(0,1\right)$: (i) increase for certain values of p; (ii) decrease for certain values of p; and (iii) increase first and then decrease gradually for certain values of p.

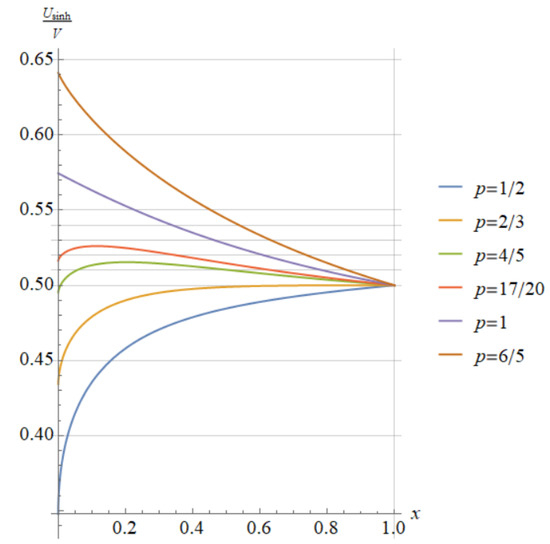
Figure 5. ${\mathcal{U}}_{sinh}/\mathcal{V}$ for different values of the parameter p.

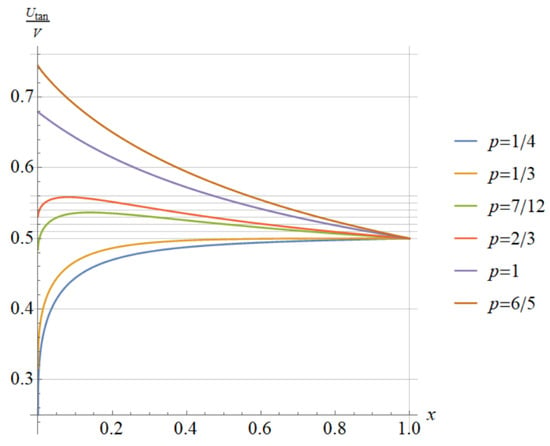
Figure 6. ${\mathcal{U}}_{tan}/\mathcal{V}$ for different values of the parameter p.

Now, we give a strict proof. Differentiation yields

$$\frac{{\mathcal{U}}_f^{{}^{\prime }}}{{\mathcal{V}}^{\prime }}=\frac{p{M}_f^{p-1}{M}_f^{{}^{\prime }}}{p{x}^{p-1}}=\frac{M_f^{p-1}}{x^{p-1}}{M}_f^{{}^{\prime }},$$

(30)

$$\begin{array}{ccc}\hfill {\left(\frac{{\mathcal{U}}_f^{{}^{\prime }}}{{\mathcal{V}}^{\prime }}\right)}^{\prime }& =& \left(p-1\right){\left(\frac{M_f}{x}\right)}^{p-2}\frac{x{M}_f^{{}^{\prime }}-M_f}{x^2}{M}_f^{{}^{\prime }}+{\left(\frac{M_f}{x}\right)}^{p-1}{M}_f^{{}^{″}}\hfill \\ & =& \frac{M_f^{p-2}}{x^p}\left[\left(p-1\right)\left(x{M}_f^{{}^{\prime }}-M_f\right)M_f^{{}^{\prime }}+x{M}_f{M}_f^{{}^{″}}\right].\hfill \end{array}$$

Assume that $\left(x{M}_f^{{}^{\prime }}-M_f\right)M_f^{{}^{\prime }}\ne 0$ for $x\in \left(0,1\right)$. Then

$${\left(\frac{{\mathcal{U}}_f^{{}^{\prime }}}{{\mathcal{V}}^{\prime }}\right)}^{\prime }=\frac{M_f^{p-2}}{x^p}\left(x{M}_f^{{}^{\prime }}-M_f\right)M_f^{{}^{\prime }}\left(p-1+\frac{x{M}_f{M}_f^{{}^{″}}}{\left(x{M}_f^{{}^{\prime }}-M_f\right)M_f^{{}^{\prime }}}\right).$$

(31)

In order to determine the sign of ${\left({\mathcal{U}}_f^{{}^{\prime }}/{\mathcal{V}}^{\prime }\right)}^{\prime }$ on $\left(0,1\right)$, we have to find the supremum and infimum of

$${\mathsf{\Phi }}_f\left(x\right)=\frac{x{M}_f{M}_f^{{}^{″}}}{\left(x{M}_f^{{}^{\prime }}-M_f\right)M_f^{{}^{\prime }}}$$

(32)

on $\left(0,1\right)$.

Lemma 6. 

Let f be an odd function on $\left(-1,1\right)$ and third-order differentiable on $\left[0,1\right]$. If $t\left(1\pm t\right)f^{\prime }\left(t\right)-f\left(t\right)\ne 0$ on $\left(0,1\right)$, then ${\mathsf{\Phi }}_f\left(x\right)$ defined by (32) can be expressed as

$${\mathsf{\Phi }}_f\left(x\right)=\frac{t\left(1-t^2\right)\left[2f\left(t\right)f^{\prime }\left(t\right)+tf\left(t\right)f^{″}\left(t\right)-2t{f}^{\prime }{\left(t\right)}^2\right]}{\left[t\left(t-1\right)f^{\prime }\left(t\right)+f\left(t\right)\right]\left[t\left(t+1\right)f^{\prime }\left(t\right)-f\left(t\right)\right]}={\varphi }_f\left(t\right)$$

(33)

for $t\in \left(0,1\right)$ with

$${\mathsf{\Phi }}_f\left(0^{+}\right)={\varphi }_f\left(1^{-}\right)=0\mathrm{and}{\mathsf{\Phi }}_f\left(1^{-}\right)={\varphi }_f\left(0^{+}\right)=\frac{1}{3}{f}^{‴}\left(0\right).$$

Proof. 

Let $t=\left(1-x\right)/\left(1+x\right)$. Then $x=\left(1-t\right)/\left(1+t\right)$ and

$$M_f\left(x,1\right)=\frac{1-x}{2f\left(\left(1-x\right)/\left(1+x\right)\right)}=\frac{t}{\left(1+t\right)f\left(t\right)}$$

for $t\in \left(0,1\right)$. Differentiation yields

$$\begin{array}{ccc}\hfill M_f^{{}^{\prime }}& \equiv & M_f^{{}^{\prime }}\left(x,1\right)=\frac{d}{dt}\left(\frac{t}{\left(1+t\right)f}\right)/\frac{dx}{dt}\hfill \\ & =& \frac{\left(1+t\right)f-t\left(f+\left(t+1\right)f^{\prime }\right)}{{\left(1+t\right)}^2{f}^2}\left(-\frac{{\left(t+1\right)}^2}{2}\right)=\frac{1}{2}\frac{t\left(t+1\right)f^{\prime }-f}{f^2},\hfill \end{array}$$

(34)

$$\begin{array}{ccc}\hfill M_f^{{}^{″}}& \equiv & M_f^{{}^{″}}\left(x,1\right)=\frac{d}{dt}\left(\frac{1}{2}\frac{t\left(t+1\right)f^{\prime }-f}{f^2}\right)/\frac{dx}{dt}\hfill \\ & =& \frac{1}{2}\frac{\left(\left(2t+1\right)f^{{}^{\prime }}+t\left(t+1\right)f^{″}-f^{\prime }\right)f^2-2f{f}^{\prime }\left(t\left(t+1\right)f^{\prime }-f\right)}{f^4}\left(-\frac{{\left(t+1\right)}^2}{2}\right)\hfill \\ & =& \frac{1}{4}{\left(t+1\right)}^3\frac{2t{\left(f^{\prime }\right)}^2-f\left(2f^{\prime }+t{f}^{″}\right)}{f^3}.\hfill \end{array}$$

Then

$$x{M}_f^{{}^{\prime }}-M_f=\frac{1-t}{1+t}\frac{1}{2}\frac{t\left(t+1\right)f^{\prime }-f}{f^2}-\frac{t}{\left(1+t\right)f}=\frac{1}{2}\frac{\left(t-t^2\right)f^{\prime }-f}{f^2}.$$

(35)

Since $f\left(t\right)-t\left(1\pm t\right)f^{\prime }\left(t\right)\ne 0$ on $\left(0,1\right)$, we see that $\left(x{M}_f^{{}^{\prime }}-M_f\right)M_f^{{}^{\prime }}\ne 0$ for $x\in \left(0,1\right)$. Then

$$\begin{array}{ccc}\hfill {\mathsf{\Phi }}_f\left(x\right)& =& \frac{x{M}_f{M}_f^{{}^{″}}}{\left(x{M}_f^{{}^{\prime }}-M_f\right)M_f^{{}^{\prime }}}=\frac{1-t}{1+t}\frac{t}{\left(1+t\right)f}\frac{1}{4}{\left(t+1\right)}^3\frac{2t{\left(f^{\prime }\right)}^2-f\left(2f^{\prime }+t{f}^{″}\right)}{f^3}/\hfill \\ & & \left[\frac{1}{2}\frac{\left(t-t^2\right)f^{\prime }-f}{f^2}\frac{1}{2}\frac{t\left(t+1\right)f^{\prime }-f}{f^2}\right]\hfill \\ & =& \frac{t\left(1-t^2\right)\left[\left(2f^{\prime }+t{f}^{″}\right)f-2t{\left(f^{\prime }\right)}^2\right]}{\left[t\left(t-1\right)f^{\prime }+f\right]\left[t\left(t+1\right)f^{\prime }-f\right]}.\hfill \end{array}$$

As shown in (12), $f\left(0\right)=0$, $f^{\prime }\left(0\right)={lim}_{t\to 0}f\left(t\right)/t=1$. Moreover, since f is an odd function on $\left(-1,1\right)$, we easily see that $f^{″}\left(0\right)=0$. Using the L’Hospital rule gives that, as $t\to 0$,

$$\frac{t\left(t-1\right)f^{\prime }\left(t\right)+f\left(t\right)}{t^2}\to \frac{2t{f}^{\prime }\left(t\right)+t\left(t-1\right)f^{″}\left(t\right)}{2t}\to f^{\prime }\left(0\right)-\frac{1}{2}{f}^{″}\left(0\right)=1,$$

(36)

$$\frac{t\left(1+t\right)f^{\prime }\left(t\right)-f\left(t\right)}{t^2}\to \frac{2t{f}^{\prime }\left(t\right)+t\left(1+t\right)f^{″}\left(t\right)}{2t}\to f^{\prime }\left(0\right)+\frac{1}{2}{f}^{″}\left(0\right)=1,$$

$$\frac{f\left(t\right)\left(2f^{\prime }\left(t\right)+t{f}^{″}\left(t\right)\right)-2t{f}^{\prime }{\left(t\right)}^2}{t^3}\to \frac{tf\left(t\right)f^{‴}\left(t\right)-3f^{″}\left(t\right)\left(t{f}^{\prime }\left(t\right)-f\left(t\right)\right)}{3t^2}$$

$$=\frac{1}{3}\frac{f\left(t\right)}{t}{f}^{‴}\left(t\right)-f^{″}\left(t\right)\frac{t{f}^{\prime }\left(t\right)-f\left(t\right)}{t^2}\to \frac{1}{3}{f}^{‴}\left(0\right)-f^{″}\left(0\right)\frac{f^{″}\left(0\right)}{2}=\frac{1}{3}{f}^{‴}\left(0\right),$$

which implies that

$${\mathsf{\Phi }}_f\left(1^{-}\right)={\varphi }_f\left(0^{+}\right)=\frac{1}{3}{f}^{‴}\left(0\right).$$

Due to the differentiability of f on $\left[0,1\right]$, $f\left(t\right)$, $f^{\prime }\left(t\right)$ and $f^{″}\left(t\right)$ are bounded on $\left[0,1\right]$, and therefore, ${\mathsf{\Phi }}_f\left(0^{+}\right)={\varphi }_f\left(1^{-}\right)=0$, which completes the proof. □

Remark 1. 

Under the conditions as Lemma 6, it follows from the limit relations ${lim}_{t\to 0}f\left(t\right)/t=1$ and (36) that

$$\underset{x\to 1}{lim}{M}_f^{{}^{\prime }}\left(x,1\right)=\underset{t\to 0}{lim}\frac{1}{2}\frac{t\left(t+1\right)f^{\prime }-f}{f^2}=\frac{1}{2}\underset{t\to 0}{lim}\frac{t^2}{f^2}\underset{t\to 0}{lim}\frac{t\left(t+1\right)f^{\prime }-f}{t^2}=\frac{1}{2},$$

which implies that

$$\underset{x\to 1^{-}}{lim}\frac{{\mathcal{U}}_f\left(x\right)}{\mathcal{V}\left(x\right)}=\underset{x\to 1}{lim}\frac{{\mathcal{U}}_f^{{}^{\prime }}\left(x\right)}{{\mathcal{V}}^{\prime }\left(x\right)}=\frac{1}{2}.$$

(37)

On the other hand, it is readily seen that

$$\underset{x\to 0^{+}}{lim}\frac{{\mathcal{U}}_f\left(x\right)}{\mathcal{V}\left(x\right)}=\underset{x\to 0^{+}}{lim}\frac{M_f^p\left(x,1\right)-1}{x^p-1}=1-\frac{1}{2^p{f}^p\left(1\right)}\mathrm{if}p>0.$$

(38)

3.1. Proofs of Theorems 1 and 2

We first observe the monotonic pattern of ${\mathcal{U}}_{sinh}\left(x\right)/\mathcal{V}\left(x\right)$ on $\left(0,1\right)$, which is displayed in the following theorem.

Theorem 5. 

The following statements are valid.

(i) If $0<p\le 2/3$, the ratio ${\mathcal{U}}_{sinh}/\mathcal{V}$ is increasing on $\left(0,1\right)$, and therefore, the double inequality

$${\alpha }_p<\frac{M_{sinh}^p\left(x,1\right)-1}{x^p-1}<\frac{1}{2}$$

holds, where ${\alpha }_p=1-1/{\left(2sinh1\right)}^p$, or equivalently,

$${\left(\frac{x^p+1}{2}\right)}^{1/p}<M_{sinh}\left(x,1\right)<{\left({\alpha }_p{x}^p+1-{\alpha }_p\right)}^{1/p}$$

(39)

for $x\in \left(0,1\right)$.

(ii) If $p\ge 1$, the ratio ${\mathcal{U}}_{sinh}/\mathcal{V}$ is decreasing on $\left(0,1\right)$, and therefore, the double inequality

$$\frac{1}{2}<\frac{M_{sinh}^p\left(x,1\right)-1}{x^p-1}<{\alpha }_p$$

holds, or equivalently,

$${\left({\alpha }_p{x}^p+1-{\alpha }_p\right)}^{1/p}<M_{sinh}\left(x,1\right)<{\left(\frac{x^p+1}{2}\right)}^{1/p}$$

(40)

for $x\in \left(0,1\right)$.

(iii) If $2/3<p<1$, there is an $x_0$ such that the ratio ${\mathcal{U}}_{sinh}/\mathcal{V}$ is increasing on $\left(0,x_0\right)$ and decreasing on $\left(x_0,1\right)$, and therefore, the inequality

$$min\left\{\frac{1}{2},{\alpha }_p\right\}\le \frac{M_{sinh}^p\left(x,1\right)-1}{x^p-1}$$

holds for $x\in \left(0,1\right)$. In particular, when $min\left\{1/2,{\alpha }_p\right\}=1/2$, that is, $\frac{ln2}{ln2+lnsinh1}\le p<1$, the inequality

$$M_{sinh}\left(x,1\right)<{\left(\frac{x^p+1}{2}\right)}^{1/p}$$

(41)

holds for $x\in \left(0,1\right)$; when $min\left\{1/2,{\alpha }_p\right\}={\alpha }_p$, that is, $2/3<p\le \frac{ln2}{ln2+lnsinh1}$, the inequality

$$M_{sinh}\left(x,1\right)<{\left({\alpha }_p{x}^p+1-{\alpha }_p\right)}^{1/p}$$

(42)

holds for $x\in \left(0,1\right)$.

Proof. 

Let $f\left(t\right)=sinht$. Then $f^{\prime }\left(t\right)=cosht$ and $f^{″}\left(t\right)=sinht$. By (33)–(35), we see that

$$\begin{array}{ccc}\hfill M_{sinh}^{{}^{\prime }}\left(x,1\right)& =& \frac{1}{2}\frac{t\left(t+1\right)cosht-sinht}{{sinh}^{2}t},\hfill \\ \hfill x{M}_{sinh}^{{}^{\prime }}\left(x,1\right)-M_{sinh}\left(x,1\right)& =& \frac{1}{2}\frac{\left(t-t^2\right)cosht-sinht}{{sinh}^{2}t},\hfill \end{array}$$

(43)

and ${\mathsf{\Phi }}_{sinh}\left(x\right)={\varphi }_{sinh}\left(t\right)$, where ${\varphi }_{sinh}\left(t\right)$ is defined by (22). Clearly, $M_{sinh}^{{}^{\prime }}\left(x,1\right)>0$ for $x\in \left(0,1\right)$. Since

$${\left[\left(t-t^2\right)cosht-sinht\right]}^{\prime }=-t\left(2cosht-sinht+tsinht\right)<0$$

for $t>0$, we have that $\left(t-t^2\right)cosht-sinht<0$ for $t>0$, which implies that

$x{M}_{sinh}^{{}^{\prime }}\left(x,1\right)-M_{sinh}\left(x,1\right)<0$ for $x\in \left(0,1\right)$. Then, by (31), we have that

$$sgn{\left[\frac{{\mathcal{U}}_{sinh}^{{}^{\prime }}\left(x\right)}{{\mathcal{V}}^{\prime }\left(x\right)}\right]}^{\prime }=-sgn\left(p-1+{\mathsf{\Phi }}_{sinh}\left(x\right)\right):=-sgn\mu \left(x\right).$$

(44)

Lemma 1 tells us that ${\varphi }_{sinh}\left(t\right)$ is decreasing in t from $\left(0,1\right)$ onto $\left(0,1/3\right)$ which, by Lemma 6 and $x=\left(1-t\right)/\left(1+t\right)$, implies that the function ${\mathsf{\Phi }}_{sinh}\left(x\right)$ ($={\varphi }_{sinh}\left(t\right)$) is increasing in x from $\left(0,1\right)$ onto $\left(0,1/3\right)$.

(i) If $0<p\le 2/3$, then $p-1+{\mathsf{\Phi }}_{sinh}\left(x\right)\le 0$ for $x\in \left(0,1\right)$, and so ${\left({\mathcal{U}}_{sinh}^{{}^{\prime }}/{\mathcal{V}}^{\prime }\right)}^{\prime }\ge 0$ for $x\in \left(0,1\right)$. It follows from Proposition 1 that ${\mathcal{U}}_{sinh}/\mathcal{V}$ is increasing on $\left(0,1\right)$. This together with (37) and (38) yields

$$1-\frac{1}{2^p{sinh}^{p}1}=\underset{x\to 0^{+}}{lim}\frac{{\mathcal{U}}_{sinh}\left(x\right)}{\mathcal{V}\left(x\right)}<\frac{{\mathcal{U}}_{sinh}\left(x\right)}{\mathcal{V}\left(x\right)}<\underset{x\to 1^{-}}{lim}\frac{{\mathcal{U}}_{sinh}\left(x\right)}{\mathcal{V}\left(x\right)}=\frac{1}{2}$$

for $x\in \left(0,1\right)$, which implies (39).

(ii) If $p\ge 1$, then $p-1+{\mathsf{\Phi }}_{sinh}\left(x\right)\ge 0$ for $x\in \left(0,1\right)$, and so ${\left({\mathcal{U}}_{sinh}^{{}^{\prime }}/{\mathcal{V}}^{\prime }\right)}^{\prime }\le 0$ for $x\in \left(0,1\right)$. It follows from Proposition 1 that ${\mathcal{U}}_{sinh}/\mathcal{V}$ is decreasing on $\left(0,1\right)$, and therefore, the inequalities

$$\frac{1}{2}<\frac{{\mathcal{U}}_{sinh}\left(x\right)}{\mathcal{V}\left(x\right)}<1-\frac{1}{2^p{sinh}^{p}1}$$

hold for $x\in \left(0,1\right)$, which implies (40).

(iii) In the case of $p\in \left(2/3,1\right)$, since $\mu \left(x\right)=p-1+{\mathsf{\Phi }}_{sinh}\left(x\right)$ is increasing on $\left(0,1\right)$ with $\mu \left(0^{+}\right)=p-1<0$ and $\mu \left(1^{-}\right)=p-2/3>0$, there is an $x_0\in \left(0,1\right)$ such that $\mu \left(x\right)<0$ for $x\in \left(0,x_0\right)$ and $\mu \left(x\right)>0$ for $x\in \left(x_0,1\right)$. This, by (44), implies that ${\left({\mathcal{U}}_{sinh}^{{}^{\prime }}/{\mathcal{V}}^{\prime }\right)}^{\prime }>0$ for $x\in \left(0,x_0\right)$ and ${\left({\mathcal{U}}_{sinh}^{{}^{\prime }}/{\mathcal{V}}^{\prime }\right)}^{\prime }<0$ for $x\in \left(x_0,1\right)$. To use Proposition 2, we also need the signs of ${\mathcal{V}}^{\prime }$ and $H_{{\mathcal{U}}_{sinh},\mathcal{V}}\left(0^{+}\right)$. By (43), it is derived that

$$M_{sinh}^{{}^{\prime }}\left(0^{+},1\right)=\frac{1}{2}\underset{t\to 1^{-}}{lim}\frac{t\left(t+1\right)cosht-sinht}{{sinh}^{2}t}=\frac{2cosh1-sinh1}{2{sinh}^{2}1}=0.691\dots ,$$

which together with $M_{sinh}\left(0^{+},1\right)=1/\left(2sinh1\right)$ gives

$$\begin{array}{ccc}\hfill H_{{\mathcal{U}}_{sinh},\mathcal{V}}\left(x\right)& =& \frac{{\mathcal{U}}_{sinh}^{{}^{\prime }}\left(x\right)}{{\mathcal{V}}^{\prime }\left(x\right)}\mathcal{V}\left(x\right)-{\mathcal{U}}_{sinh}\left(x\right)\hfill \\ & =& \frac{M_{sinh}^{p-1}\left(x,1\right)M_{sinh}^{{}^{\prime }}\left(x,1\right)}{x^{p-1}}\left(x^p-1\right)-\left[M_{sinh}^p\left(x,1\right)-1\right]\hfill \\ & \to & 1-\frac{1}{{\left(2sinh1\right)}^p}\mathrm{as}x\to 0^{+}.\hfill \end{array}$$

Since $p\in \left(2/3,1\right)$, we see that $H_{{\mathcal{U}}_{sinh},\mathcal{V}}\left(0^{+}\right)>0$. Clearly, ${\mathcal{V}}^{\prime }\left(x\right)=p{x}^{p-1}>0$. It then follows from Proposition 2 that there is an $x_0\in \left(0,1\right)$ such that ${\mathcal{U}}_{sinh}/\mathcal{V}$ is increasing on $\left(0,x_0\right)$ and decreasing on $\left(x_0,1\right)$, and therefore, we have

$$min\left\{\frac{1}{2},1-\frac{1}{{\left(2sinh1\right)}^p}\right\}\le \frac{{\mathcal{U}}_{sinh}\left(x\right)}{\mathcal{V}\left(x\right)}=\frac{M_{sinh}^p\left(x,1\right)-1}{x^p-1}$$

for $x\in \left(0,1\right)$. In particular, when $1-{\left(2sinh1\right)}^{-p}\ge 1/2$, that is, $\left(ln2\right)/\left(ln2+lnsinh1\right)\le p<1$, the inequality (41) holds for $x\in \left(0,1\right)$; when $1-{\left(2sinh1\right)}^{-p}\le 1/2$, that is, $2/3<p\le \left(ln2\right)/\left(ln2+lnsinh1\right)$, the inequality (42) holds for $x\in \left(0,1\right)$. The proof is thus proved. □

We are now in a position to prove Theorems 1 and 2.

Proof of Theorem 1. 

Assume that $b>a>0$ and let $x=a/b$. Then, the double inequality (15) is equivalent to

$${\left(\frac{x^p+1}{2}\right)}^{1/p}<M_{sinh}\left(x,1\right)<{\left(\frac{x^q+1}{2}\right)}^{1/q}$$

(45)

for $x\in \left(0,1\right)$. The sufficiency follows from the inequalities (39)–(41) in Theorem 5.

We prove the necessity by the reduction to absurdity. First, we prove that the necessary condition for which the second inequality of (45) holds for $x\in \left(0,1\right)$ is $q\ge p_1$.

Assume that $q\le 2/3$ such that the second inequality of (45) holds for $x\in \left(0,1\right)$. By Theorem 5 (i), we have the first inequality of (39) for $p=q$, which is clearly a contradiction.

Assume that $q\in \left(2/3,p_1\right)$ such that the second inequality of (45) holds for $x\in \left(0,1\right)$. By Theorem 5 (iii), there is an $x_0$ such that the ratio ${\mathcal{U}}_{sinh}/\mathcal{V}$ is increasing on $\left(0,x_0\right)$ and decreasing on $\left(x_0,1\right)$. Then

$$\frac{1}{2}=\underset{x\to 1^{-}}{lim}\frac{{\mathcal{U}}_{sinh}\left(x\right)}{\mathcal{V}\left(x\right)}<\frac{{\mathcal{U}}_{sinh}\left(x\right)}{\mathcal{V}\left(x\right)}\mathrm{for}x\in \left(x_0,1\right),$$

that is,

$$M_{sinh}\left(x,1\right)<A_q\left(x,1\right)\mathrm{for}x\in \left(x_0,1\right).$$

On the other hand, $q<p_1$ implies that ${\alpha }_q<1/2$, that is,

$${\alpha }_q=\underset{x\to 0^{+}}{lim}\frac{{\mathcal{U}}_{sinh}\left(x\right)}{\mathcal{V}\left(x\right)}<\underset{x\to 1^{-}}{lim}\frac{{\mathcal{U}}_{sinh}\left(x\right)}{\mathcal{V}\left(x\right)}=1/2.$$

Then there is an $x_1\in \left(0,x_0\right)$ such that ${\mathcal{U}}_{sinh}\left(x_1\right)/\mathcal{V}\left(x_1\right)=1/2$. Then

$$\frac{{\mathcal{U}}_{sinh}\left(x\right)}{\mathcal{V}\left(x\right)}<\frac{{\mathcal{U}}_{sinh}\left(x_1\right)}{\mathcal{V}\left(x_1\right)}=\frac{1}{2}\mathrm{for}x\in \left(0,x_1\right),$$

which implies that

$$A_q\left(x,1\right)<M_{sinh}\left(x,1\right)\mathrm{for}x\in \left(0,x_1\right).$$

These also yield a contradiction. This proves the necessary condition such that the second inequality of (45) holds for $x\in \left(0,1\right)$.

In the same way, we can prove that the necessary condition for which the first inequality of (45) to hold for $x\in \left(0,1\right)$ is $p\le 2/3$, and the proof is complete. □

Proof of Theorem 2. 

Let $x=a/b$. Then the double inequality (16) is equivalent to

$${\left({\alpha }_p{x}^p+1-{\alpha }_p\right)}^{1/p}<M_{sinh}\left(x,1\right)<{\left({\alpha }_q{x}^q+1-{\alpha }_q\right)}^{1/q}$$

(46)

for $x\in \left(0,1\right)$. The sufficiency follows from the inequalities (40)–(42) in Theorem 5.

The necessity can be proved by the reduction to absurdity. We first prove that the necessary condition such that the second inequality of (46) holds for $x\in \left(0,1\right)$ is $0<q\le p_1$.

Assume that $q\ge 1$ such that the second inequality of (46) holds for $x\in \left(0,1\right)$. Then by Theorem 5 (ii), the first inequality of (40) holds for $x\in \left(0,1\right)$ and $p=q$, which yields a contradiction.

Assume that $q\in \left(p_1,1\right)$ such that the second inequality of (46) holds for $x\in \left(0,1\right)$. By Theorem 5 (iii), there is an $x_0$ such that the ratio ${\mathcal{U}}_{sinh}/\mathcal{V}$ is increasing on $\left(0,x_0\right)$ and decreasing on $\left(x_0,1\right)$. Then

$${\alpha }_q=\underset{x\to 0^{+}}{lim}\frac{{\mathcal{U}}_{sinh}\left(x\right)}{\mathcal{V}\left(x\right)}<\frac{{\mathcal{U}}_{sinh}\left(x\right)}{\mathcal{V}\left(x\right)}\mathrm{for}x\in \left(0,x_0\right),$$

that is,

$$M_{sinh}\left(x,1\right)<A_q\left(x,1;{\alpha }_q\right)\mathrm{for}x\in \left(0,x_0\right).$$

On the other hand, $q>p_1$ implies that ${\alpha }_q>1/2$, that is,

$${\alpha }_q=\underset{x\to 0^{+}}{lim}\frac{{\mathcal{U}}_{sinh}\left(x\right)}{\mathcal{V}\left(x\right)}>\underset{x\to 1^{-}}{lim}\frac{{\mathcal{U}}_{sinh}\left(x\right)}{\mathcal{V}\left(x\right)}=1/2.$$

Then there is an $x_1\in \left(x_0,1\right)$ such that ${\mathcal{U}}_{sinh}\left(x_1\right)/\mathcal{V}\left(x_1\right)={\alpha }_q$, and therefore,

$$\frac{{\mathcal{U}}_{sinh}\left(x\right)}{\mathcal{V}\left(x\right)}<\frac{{\mathcal{U}}_{sinh}\left(x_1\right)}{\mathcal{V}\left(x_1\right)}={\alpha }_q\mathrm{for}x\in \left(x_1,1\right),$$

which implies that

$$M_{sinh}\left(x,1\right)>A_q\left(x,1;{\alpha }_q\right)\mathrm{for}x\in \left(x_1,1\right).$$

These yield a contradiction. This proves the necessary condition such that the second inequality of (46) holds for $x\in \left(0,1\right)$.

In a similar way, we can prove that the necessary condition for which the first inequality of (46) to hold for $x\in \left(0,1\right)$ is $p\ge 1$.

Taking $\left(y,x\right)=\left(a,b\right)$ and $c=1/\left(2sinh1\right)$ in Lemma 5, the decreasing property of $p\mapsto A_p\left(a,b;{\alpha }_p\right)$ on $\left(0,\infty \right)$ follows. This completes the proof. □

3.2. Proofs of Theorems 3 and 4

We begin with observing the monotonic pattern of ${\mathcal{U}}_{tan}\left(x\right)/\mathcal{V}\left(x\right)$ on $\left(0,1\right)$, which is contained in the following theorem.

Theorem 6. 

The following statements are valid.

(i) If $0<p\le 1/3$, the ratio ${\mathcal{U}}_{tan}/\mathcal{V}$ is increasing on $\left(0,1\right)$, and therefore, the double inequality

$${\beta }_p<\frac{M_{tan}^p\left(x,1\right)-1}{x^p-1}<\frac{1}{2}$$

holds, where ${\beta }_p=1-1/\left(2^p{tan}^{p}1\right)$, or equivalently,

$${\left(\frac{x^p+1}{2}\right)}^{1/p}<M_{tan}\left(x,1\right)<{\left({\beta }_p{x}^p+1-{\beta }_p\right)}^{1/p}$$

(47)

for $x\in \left(0,1\right)$.

(ii) If $p\ge 1$, the ratio ${\mathcal{U}}_{tan}/\mathcal{V}$ is decreasing on $\left(0,1\right)$, and therefore, the double inequality

$$\frac{1}{2}<\frac{M_{tan}^p\left(x,1\right)-1}{x^p-1}<{\beta }_p$$

holds, or equivalently,

$${\left({\beta }_p{x}^p+1-{\beta }_p\right)}^{1/p}<M_{tan}\left(x,1\right)<{\left(\frac{x^p+1}{2}\right)}^{1/p}$$

(48)

for $x\in \left(0,1\right)$.

(iii) If $1/3<p<1$, there is an $x_0$ such that the ratio ${\mathcal{U}}_{tan}/\mathcal{V}$ is increasing on $\left(0,x_0\right)$ and decreasing on $\left(x_0,1\right)$, and therefore, the inequality

$$min\left\{\frac{1}{2},{\beta }_p\right\}\le \frac{M_{tan}^p\left(x,1\right)-1}{x^p-1}$$

holds for $x\in \left(0,1\right)$. In particular, when $min\left\{1/2,{\beta }_p\right\}=1/2$, that is, $\left(ln2\right)/\left(ln2+lntan1\right)\le p<1$, the inequality

$$M_{tan}\left(x,1\right)<{\left(\frac{x^p+1}{2}\right)}^{1/p}$$

(49)

holds for $x\in \left(0,1\right)$; when $min\left\{1/2,{\beta }_p\right\}={\beta }_p$, that is, $1/3<p\le \left(ln2\right)/\left(ln2+lntan1\right)$, the inequality

$$M_{tan}\left(x,1\right)<{\left({\beta }_p{x}^p+1-{\beta }_p\right)}^{1/p}$$

(50)

holds for $x\in \left(0,1\right)$.

Proof. 

Let $f\left(t\right)=tant$. Then $f^{\prime }\left(t\right)=1/{cos}^{2}t$ and $f^{″}\left(t\right)=\left(2sint\right)/{cos}^{3}t$. By (33)–(35), we see that

$$\begin{array}{ccc}\hfill M_{tan}^{{}^{\prime }}\left(x,1\right)& =& \frac{1}{2}\frac{t^2+t-sintcost}{{sin}^{2}t}>0,\hfill \\ \hfill x{M}_{tan}^{{}^{\prime }}\left(x,1\right)-M_{tan}\left(x,1\right)& =& -\frac{1}{2}\frac{t^2-t+costsint}{{sin}^{2}t}<0,\hfill \end{array}$$

(51)

and ${\mathsf{\Phi }}_{tan}\left(x\right)={\varphi }_{tan}\left(t\right)$, where ${\varphi }_{tan}\left(t\right)$ is defined by (23). As shown in the proof of Lemma 2, ${\eta }_1\left(s\right)=\left(s^2/2-s+sins\right)>0$ and ${\eta }_2\left(s\right)=\left(s^2/2+s-sins\right)>0$ for $s\in \left(0,\pi \right)$, which indicate that

$$M_{tan}^{{}^{\prime }}\left(x,1\right)>0\mathrm{and}x{M}_{tan}^{{}^{\prime }}\left(x,1\right)-M_{tan}\left(x,1\right)<0$$

for $x\in \left(0,1\right)$. Then, by (31), we have that

$$sgn{\left[\frac{{\mathcal{U}}_{tan}^{{}^{\prime }}\left(x\right)}{{\mathcal{V}}^{\prime }\left(x\right)}\right]}^{\prime }=-sgn\left(p-1+{\mathsf{\Phi }}_{tan}\left(x\right)\right):=-sgn\nu \left(x\right).$$

(52)

Lemma 2 tells us that ${\varphi }_{tan}\left(t\right)$ is decreasing in t from $\left(0,1\right)$ onto $\left(0,2/3\right)$ which, by Lemma 6 and $x=\left(1-t\right)/\left(1+t\right)$, implies that the function ${\mathsf{\Phi }}_{tan}\left(x\right)$ ($={\varphi }_{tan}\left(t\right)$) is increasing in x from $\left(0,1\right)$ onto $\left(0,2/3\right)$.

(i) If $0<p\le 1/3$, then $p-1+{\mathsf{\Phi }}_{tan}\left(x\right)\le 0$ for $x\in \left(0,1\right)$, and so ${\left({\mathcal{U}}_{tan}^{{}^{\prime }}/{\mathcal{V}}^{\prime }\right)}^{\prime }\ge 0$ for $x\in \left(0,1\right)$. It follows from Proposition 1 that ${\mathcal{U}}_{tan}/\mathcal{V}$ is increasing on $\left(0,1\right)$. This together with (37) and (38) yields

$$1-\frac{1}{2^p{tan}^{p}1}=\underset{x\to 0^{+}}{lim}\frac{{\mathcal{U}}_{tan}\left(x\right)}{\mathcal{V}\left(x\right)}<\frac{{\mathcal{U}}_{tan}\left(x\right)}{\mathcal{V}\left(x\right)}<\underset{x\to 1^{-}}{lim}\frac{{\mathcal{U}}_{tan}\left(x\right)}{\mathcal{V}\left(x\right)}=\frac{1}{2}$$

for $x\in \left(0,1\right)$, which implies (47).

(ii) If $p\ge 1$, then $p-1+{\mathsf{\Phi }}_{tan}\left(x\right)\ge 0$ for $x\in \left(0,1\right)$, and so ${\left({\mathcal{U}}_{tan}^{{}^{\prime }}/{\mathcal{V}}^{\prime }\right)}^{\prime }\le 0$ for $x\in \left(0,1\right)$. It follows from Proposition 1 that ${\mathcal{U}}_{tan}/\mathcal{V}$ is decreasing on $\left(0,1\right)$, and therefore, the inequalities

$$\frac{1}{2}<\frac{{\mathcal{U}}_{tan}\left(x\right)}{\mathcal{V}\left(x\right)}<1-\frac{1}{2^p{tan}^{p}1}$$

hold for $x\in \left(0,1\right)$, which implies (48).

(iii) In the case of $p\in \left(1/3,1\right)$, since $\nu \left(x\right)=p-1+{\mathsf{\Phi }}_{tan}\left(x\right)$ is increasing on $\left(0,1\right)$ with $\nu \left(0^{+}\right)=p-1<0$ and $\nu \left(1^{-}\right)=p-1/3>0$, there is an $x_0\in \left(0,1\right)$ such that $\nu \left(x\right)<0$ for $x\in \left(0,x_0\right)$ and $\nu \left(x\right)>0$ for $x\in \left(x_0,1\right)$. This, by (52), implies that ${\left({\mathcal{U}}_{tan}^{{}^{\prime }}/{\mathcal{V}}^{\prime }\right)}^{\prime }>0$ for $x\in \left(0,x_0\right)$ and ${\left({\mathcal{U}}_{tan}^{{}^{\prime }}/{\mathcal{V}}^{\prime }\right)}^{\prime }<0$ for $x\in \left(x_0,1\right)$. To use Proposition 2, we also need the signs of ${\mathcal{V}}^{\prime }$ and $H_{{\mathcal{U}}_{tan},\mathcal{V}}\left(0^{+}\right)$. By (51), it is derived that

$$M_{tan}^{{}^{\prime }}\left(0^{+},1\right)=\frac{1}{2}\underset{t\to 1^{-}}{lim}\frac{t^2+t-sintcost}{{sin}^{2}t}=\frac{4-sin2}{4{sin}^{2}1}=1.0910\dots ,$$

which together with $M_{tan}\left(0^{+},1\right)=1/\left(2tan1\right)$ gives

$$\begin{array}{ccc}\hfill H_{{\mathcal{U}}_{tan},\mathcal{V}}\left(x\right)& =& \frac{{\mathcal{U}}_{tan}^{{}^{\prime }}\left(x\right)}{{\mathcal{V}}^{\prime }\left(x\right)}\mathcal{V}\left(x\right)-{\mathcal{U}}_{tan}\left(x\right)\hfill \\ & =& \frac{M_{tan}^{p-1}\left(x,1\right)M_{tan}^{{}^{\prime }}\left(x,1\right)}{x^{p-1}}\left(x^p-1\right)-\left[M_{tan}^p\left(x,1\right)-1\right]\hfill \\ & \to & 1-\frac{1}{{\left(2tan1\right)}^p}\mathrm{as}x\to 0^{+}.\hfill \end{array}$$

Since $p\in \left(1/3,1\right)$, we see that $H_{{\mathcal{U}}_{tan},\mathcal{V}}\left(0^{+}\right)>0$. Clearly, ${\mathcal{V}}^{\prime }\left(x\right)=p{x}^{p-1}>0$. It then follows from Proposition 2 that there is an $x_0\in \left(0,1\right)$ such that ${\mathcal{U}}_{tan}/\mathcal{V}$ is increasing on $\left(0,x_0\right)$ and decreasing on $\left(x_0,1\right)$, and therefore, we have

$$min\left\{\frac{1}{2},1-\frac{1}{{\left(2tan1\right)}^p}\right\}\le \frac{{\mathcal{U}}_{tan}\left(x\right)}{\mathcal{V}\left(x\right)}=\frac{M_{tan}^p\left(x,1\right)-1}{x^p-1}$$

for $x\in \left(0,1\right)$. In particular, when $1-{\left(2tan1\right)}^{-p}\ge 1/2$, that is, $\left(ln2\right)/\left(ln2+lntan1\right)\le p<1$, the inequality (49) holds for $x\in \left(0,1\right)$. The proof is thus proved. □

We are now in a position to prove Theorems 3 and 4.

Proof of Theorem 3. 

Assume that $b>a>0$ and let $x=a/b$. It suffices to prove that the double inequality (17) for $\left(a,b\right)=\left(x,1\right)$, that is,

$${\left(\frac{x^p+1}{2}\right)}^{1/p}<M_{tan}\left(x,1\right)<{\left(\frac{x^q+1}{2}\right)}^{1/q},$$

(53)

holds for $x\in \left(0,1\right)$ if and only if $p\le 1/3$ and $q\ge p_0=\left(ln2\right)/\left(ln2+lntan1\right)$. The sufficiency follows from the inequalities (47)–(49) in Theorem 6.

The necessity can be proved by the reduction to absurdity. Clearly, to prove the necessity for which the second inequality of (53) holds for $x\in \left(0,1\right)$, it suffices to prove $q\notin \left(1/3,p_0\right)$. Assume that $q\in \left(1/3,p_0\right)$ such that the second inequality of (53) holds for $x\in \left(0,1\right)$. By Theorem 6 (iii), there is an $x_0$ such that the ratio ${\mathcal{U}}_{tan}/\mathcal{V}$ is increasing on $\left(0,x_0\right)$ and decreasing on $\left(x_0,1\right)$. Then

$$\frac{1}{2}=\underset{x\to 1^{-}}{lim}\frac{{\mathcal{U}}_{tan}\left(x\right)}{\mathcal{V}\left(x\right)}<\frac{{\mathcal{U}}_{tan}\left(x\right)}{\mathcal{V}\left(x\right)}\mathrm{for}x\in \left(x_0,1\right),$$

that is,

$$M_{tan}\left(x,1\right)<A_q\left(x,1\right)\mathrm{for}x\in \left(x_0,1\right).$$

On the other hand, $q<p_0$ implies that ${\beta }_q<1/2$, that is,

$${\beta }_q=\underset{x\to 0^{+}}{lim}\frac{{\mathcal{U}}_{tan}\left(x\right)}{\mathcal{V}\left(x\right)}<\underset{x\to 1^{-}}{lim}\frac{{\mathcal{U}}_{tan}\left(x\right)}{\mathcal{V}\left(x\right)}=1/2.$$

$$lim{\mathcal{U}}_{tan}\left(0^{+}\right)/\mathcal{V}\left(0^{+}\right)<{\mathcal{U}}_{tan}\left(1^{-}\right)/\mathcal{V}\left(1^{-}\right).$$

Then there is an $x_1\in \left(0,x_0\right)$ such that ${\mathcal{U}}_{tan}\left(x_1\right)/\mathcal{V}\left(x_1\right)=1/2$, and therefore,

$$\frac{{\mathcal{U}}_{tan}\left(x\right)}{\mathcal{V}\left(x\right)}<\frac{{\mathcal{U}}_{tan}\left(x_1\right)}{\mathcal{V}\left(x_1\right)}=\frac{1}{2}\mathrm{for}x\in \left(0,x_1\right),$$

which implies that

$$M_{tan}\left(x,1\right)>A_q\left(x,1\right)\mathrm{for}x\in \left(0,x_1\right).$$

These yield a contradiction.

In a similar way, we can prove that the necessary condition for which the first inequality of (53) holds for $x\in \left(0,1\right)$ is $p\le 1/3$.

This completes the proof. □

Using the same method as the proof of Theorem 2, we can easily prove Theorem 4, the details of which are omitted.

4. Chains of Inequalities for Means

From Theorems 1 and 3 as well inequalities (2), (3), (4), (6), (9) and (10), we find that the means $He(a,b)$, $L_2(a,b)$, $I\left(a,b\right)$, $P(a,b)$, $M_{sinh}\left(a,b\right)$, ${\left(M_{tan}\right)}_2\left(a,b\right)$ have the same power mean $A_{2/3}(a,b)$, where

$$M_p\left(a,b\right)=M{\left(a^p,b^p\right)}^{1/p}\mathrm{if}p\ne 0\mathrm{and}{M}_0\left(a,b\right)=\underset{p\to 0}{lim}{M}_p\left(a,b\right)$$

is the so-called “p-order M mean” or “power-type mean” (see [56]). Then a question arises naturally: what is the relationship among these means? It was established in Remark 4 [56] that

$$L_2(a,b)<P(a,b)<N{S}_{1/2}(a,b)<He(a,b)<A_{2/3}(a,b)<I\left(a,b\right),$$

(54)

and in Theorems 3.1 and 3.2 [57] that

$$c_0{L}_4\left(a,b\right)\le U\left(a,b\right)\mathrm{and}U\left(a,b\right)<P_2\left(a,b\right),$$

(55)

where $c_0=0.9991\dots$ The inequalities (55) are equivalent to

$$c_0^2{L}_2\left(a,b\right)\le U_{1/2}\left(a,b\right)\mathrm{and}{U}_{1/2}\left(a,b\right)<P\left(a,b\right).$$

(56)

Taking into account (54) and Propositions 5–7, we obtain a nice chain of inequalities for means.

Theorem 7. 

The inequalities

$$\begin{array}{cc}V\left(a,b\right)& <L_2\left(a,b\right)<P\left(a,b\right)<N{S}_{1/2}\left(a,b\right)<He\left(a,b\right)\hfill \\ & <A_{2/3}\left(a,b\right)<I\left(a,b\right)<M_{sinh}\left(a,b\right)<{\left(M_{tan}\right)}_2\left(a,b\right)\hfill \end{array}$$

(57)

hold.

Combining (56) and (57), the following corollary is immediate.

Corollary 1. 

The inequalities

$$\begin{array}{cc}{c}_0^{2}V\left(a,b\right)& <c_0^2{L}_2\left(a,b\right)<U_{1/2}\left(a,b\right)<P\left(a,b\right)<N{S}_{1/2}\left(a,b\right)<He\left(a,b\right)\hfill \\ & <A_{2/3}\left(a,b\right)<I\left(a,b\right)<M_{sinh}\left(a,b\right)<{\left(M_{tan}\right)}_2\left(a,b\right)\hfill \end{array}$$

(58)

hold, where $c_0=0.9991\dots$ is the best constants.

Remark 2. 

It was conjectured in Conjecture 1 [56] that $NS(a,b)<T_p(a,b)$ holds if and only if $p\ge 4/5$. Then by Equation (4.3) [56], $T_{2/5}(a,b)$ can be interpolated between $N{S}_{1/2}\left(a,b\right)$ and $He\left(a,b\right)$ in (57) and (58).

The main results of the literature [13,14,15] are summarized in the inequalities (6)–(8). In conjunction with the new results (17) and (57) of this paper, the following corollary can be derived.

Corollary 2. 

The inequalities

$$\begin{array}{cc}L\left(a,b\right)& <A_p\left(a,b\right)<P\left(a,b\right)<N{S}_{1/2}\left(a,b\right)\hfill \\ & <He\left(a,b\right)<A_{2/3}\left(a,b\right)<I\left(a,b\right)<M_{sinh}\left(a,b\right)\hfill \\ & <{\left(M_{tan}\right)}_2\left(a,b\right)<A_q\left(a,b\right)<T\left(a,b\right)<A_r\left(a,b\right).\hfill \end{array}$$

(59)

hold, where $1/3\le p\le \left(ln2\right)/ln\pi$, $\left(2ln2\right)/\left(ln2+lntan1\right)\le q\le \left(ln2\right)/(ln\pi -ln2)$ and $r\ge 5/3$.

Proof. 

By (57), it suffices to prove the first two inequalities and the last three inequalities. The first two ones follow from the second one of (3) and the first one of (6) with the increasing property of $p\mapsto A_p\left(a,b\right)$ on $\mathbb{R}$. Replacing $\left(a,b\right)$ by $\left(a^2,b^2\right)$ and taking the square root in the second one of (17) gives

$${\left(M_{tan}\right)}_2\left(a,b\right)<A_q\left(a,b\right),$$

where $q\ge 2p_0=\left(2ln2\right)/\left(ln2+lntan1\right)=1.220\dots$ This, in combination with (7) and the increasing property of $p\mapsto A_p\left(a,b\right)$ on $\mathbb{R}$ proves the last three inequalities, thereby completing the proof. □

Next, we prove Propositions 5–7.

Proposition 5. 

The double inequality

$$I\left(a,b\right)<M_{sinh}\left(a,b\right)<\frac{e}{2sinh1}I\left(a,b\right)$$

holds.

Proof. 

Assume that $b>a>0$ and let $x=a/b$. Then, it suffices to prove that

$$0<h_1\left(x\right)<ln\frac{e}{2sinh1}$$

for $x\in \left(0,1\right)$, where

$$h_1\left(x\right)=ln\left(1-x\right)-ln2-lnsinh\left(\frac{1-x}{1+x}\right)-\left(\frac{-xlnx}{1-x}-1\right).$$

Differentiation yields

$${\left(1-x\right)}^2{h}_1^{{}^{\prime }}\left(x\right)=2\frac{{\left(1-x\right)}^2}{{\left(x+1\right)}^2}coth\left(\frac{1-x}{1+x}\right)+lnx=h_2\left(\frac{1-x}{1+x}\right),$$

where

$$h_2\left(t\right)=2t^{2}cotht+ln\frac{1-t}{1+t},t\in \left(0,1\right).$$

Differentiation again yields

$$h_2^{{}^{\prime }}\left(t\right)=4t\frac{cosht}{sinht}-2\frac{t^2}{{sinh}^{2}t}+\frac{2}{t^2-1}=-\frac{h_3\left(t\right)}{\left(1-t^2\right){sinh}^{2}t},$$

where

$$h_3\left(t\right)=2t^{3}sinh2t-2tsinh2t+cosh2t+2t^2-2t^4-1.$$

Expanding in power series leads to

$$\begin{array}{ccc}\hfill h_3\left(t\right)& =& 2\sum _{n=2}^{\infty }\frac{2^{2n-3}}{\left(2n-3\right)!}{t}^{2n}-2\sum _{n=1}^{\infty }\frac{2^{2n-1}}{\left(2n-1\right)!}{t}^{2n}+\sum _{n=0}^{\infty }\frac{2^{2n}}{\left(2n\right)!}{t}^{2n}+2t^2-2t^4-1\hfill \\ & =& \sum _{n=3}^{\infty }\frac{\left(2n-1\right)\left(n^2-n-1\right)}{\left(2n\right)!}{\left(2t\right)}^{2n}>0\hfill \end{array}$$

for $t>0$. This implies that $h_2^{{}^{\prime }}\left(t\right)<0$ for $t\in \left(0,1\right)$, which yields that $h_2\left(t\right)<{lim}_{t\to 0}{h}_2\left(t\right)=0$ for $t\in \left(0,1\right)$. It in turn implies that $h_1^{{}^{\prime }}\left(x\right)<0$ for $x\in \left(0,1\right)$, and therefore,

$$0=\underset{x\to 1^{-}}{lim}{h}_1\left(x\right)<h_1\left(x\right)<\underset{x\to 0^{+}}{lim}{h}_1\left(x\right)=1-ln\left(sinh1\right)-ln2,$$

which completes the proof. □

Proposition 6. 

The inequality

$$\sqrt{M_{tan}\left(a^2,b^2\right)}>M_{sinh}\left(a,b\right)$$

holds.

Proof. 

Assume that $b>a>0$ and let $x=\left(b-a\right)/\left(b+a\right)$. Then

$$\frac{a}{b}=\frac{1-x}{1+x}\mathrm{and}\frac{b^2-a^2}{a^2+b^2}=\frac{2x}{x^2+1}.$$

The required inequality is equivalent to

$$\begin{array}{ccc}\hfill 0& <& \frac{b^2-a^2}{2tan\frac{b^2-a^2}{b^2+a^2}}-{\left(\frac{b-a}{2sinh\frac{b-a}{b+a}}\right)}^2=\frac{b^2-a^2}{2}\left(cot\frac{2x}{x^2+1}-\frac{x}{2{sinh}^{2}x}\right)\hfill \\ & =& \frac{b^2-a^2}{2}\frac{x}{2{sinh}^{2}x}cot\frac{2x}{x^2+1}\left(\frac{2{sinh}^{2}x}{x}-tan\frac{2x}{x^2+1}\right).\hfill \end{array}$$

If we prove that

$$h_4\left(x\right)=arctan\left(\frac{2{sinh}^{2}x}{x}\right)-\frac{2x}{x^2+1}>0$$

for $x\in \left(0,1\right)$, then the required inequality follows. Since

$$\frac{2{sinh}^{2}x}{x}=\frac{1}{x}\left(cosh2x-1\right)=\sum _{n=1}^{\infty }\frac{2^{2n}}{\left(2n\right)!}{x}^{2n-1}>2x+\frac{2}{3}{x}^3,$$

it suffices to prove that

$$h_5\left(x\right)=arctan\left(2x+\frac{2}{3}{x}^3\right)-\frac{2x}{x^2+1}>0$$

for $x\in \left(0,1\right)$. Differentiation yields

$$h_5^{{}^{\prime }}\left(x\right)=2\frac{x^4\left(4x^4+29x^2+39\right)}{{\left(x^2+1\right)}^2\left(4x^6+24x^4+36x^2+9\right)}>0,$$

which implies that $h_5\left(x\right)>{lim}_{x\to 0}{h}_5\left(x\right)=0$ for $x\in \left(0,1\right)$, thereby completing the proof. □

Proposition 7. 

The inequality

$$V\left(a,b\right)<L_2\left(a,b\right)$$

holds.

Proof. 

Assume that $b>a>0$ and let $x=a/b$. Then the required inequality is equivalent to

$${\left(\frac{1-x}{\sqrt{2}arsinh\frac{1-x}{\sqrt{2x}}}\right)}^2<\frac{1-x^2}{-2lnx},$$

which is, in turn, equivalent to

$$h_6\left(x\right)={\left(arsinh\frac{1-x}{\sqrt{2x}}\right)}^2+\frac{{\left(1-x\right)}^2}{1-x^2}lnx>0$$

for $x\in \left(0,1\right)$. Differentiation yields

$$\frac{x\sqrt{x^2+1}}{x+1}{h}_6^{{}^{\prime }}\left(x\right)=-arsinh\frac{1-x}{\sqrt{2x}}-\frac{2xlnx+x^2-1}{{\left(x+1\right)}^3}\sqrt{x^2+1}=h_7\left(x\right),$$

$$\begin{array}{ccc}\hfill h_7^{{}^{\prime }}\left(x\right)& =& \frac{x+1}{2x\sqrt{x^2+1}}-\frac{\left(x+1\right)\left(5x^2-2x+5\right)-2\left(x-1\right)\left(x^2-x+1\right)lnx}{\sqrt{x^2+1}{\left(x+1\right)}^4}\hfill \\ & =& \frac{-4x\left(1-x\right)\left(x^2-x+1\right)}{2x{\left(x+1\right)}^4\sqrt{x^2+1}}{h}_8\left(x\right),\hfill \end{array}$$

where

$$h_8\left(x\right)=lnx-\frac{\left(1-x^2\right)\left(x^2-4x+1\right)}{4x\left(x^2-x+1\right)}.$$

Differentiation again yields

$$h_8^{{}^{\prime }}\left(x\right)=\frac{1}{4}\frac{{\left(1-x\right)}^2{\left(x+1\right)}^4}{x^2{\left(x^2-x+1\right)}^2}>0$$

for $x\in \left(0,1\right)$. Then $h_8\left(x\right)<h_8\left(1\right)=0$ for $x\in \left(0,1\right)$, which indicates that $h_7^{{}^{\prime }}\left(x\right)>0$ for $x\in \left(0,1\right)$, and hence, $h_7\left(x\right)<h_7\left(1\right)=0$ for $x\in \left(0,1\right)$. This leads to $h_6^{{}^{\prime }}\left(x\right)<0$ for $x\in \left(0,1\right)$, which gives $h_6\left(x\right)>h_6\left(1\right)=0$ for $x\in \left(0,1\right)$, and the proof is complete. □

5. Concluding Remarks

In this paper, we established the best power mean bounds for the Seiffert-like means $M_{sinh}\left(a,b\right)$ and $M_{tan}\left(a,b\right)$ by using monotone rules for the ratios of two functions (power series). These results enrich the mean value theory, and our ideas and techniques used in this paper can be applied to study other means and certain special functions.

Finally, we present several remarks.

Remark 3. 

In general, a mean bound for a symmetric mean is also symmetric, for example, the bounds given in (15) and (17) are symmetric means. It is interesting, however, that the bounds given in (16) and (18) are asymmetric means. It is valuable and challenging to find the best asymmetric mean bounds for a symmetric mean.

Remark 4. 

As a byproduct, we can give the maximum relative errors estimating $M_{sinh}$ by $A_{2/3}$. In fact, by Theorem 5 (i), we see that the function

$$x\mapsto \frac{1}{2}-\frac{M_{sinh}^p\left(x,1\right)-1}{x^p-1}=\frac{M_{sinh}^p\left(x,1\right)-\left(x^p+1\right)/2}{1-x^p}$$

is positive and decreasing on $\left(0,1\right)$ for $0<p\le 2/3$ as is the function $x\mapsto 2\left(1-x^p\right)/\left(x^p+1\right)$. Then the function

$$x\mapsto \frac{M_{sinh}^p\left(x,1\right)-\left(x^p+1\right)/2}{1-x^p}\frac{2\left(1-x^p\right)}{\left(x^p+1\right)}={\left(\frac{M_{sinh}\left(x,1\right)}{A_p\left(x,1\right)}\right)}^p-1$$

is decreasing on $\left(0,1\right)$, and so is $M_{sinh}\left(x,1\right)/A_p\left(x,1\right)$ on $\left(0,1\right)$ for $0<p\le 2/3$. It then follows that

$$1=\underset{x\to 1}{lim}\frac{M_{sinh}\left(x,1\right)}{A_p\left(x,1\right)}<\frac{M_{sinh}\left(x,1\right)}{A_p\left(x,1\right)}<\underset{x\to 0}{lim}\frac{M_{sinh}\left(x,1\right)}{A_p\left(x,1\right)}=\frac{2^{1/p-1}}{sinh1},$$

which, by setting $x=a/b$ and $p=2/3$, gives

$$A_{2/3}\left(a,b\right)<M_{sinh}\left(a,b\right)<\frac{\sqrt{2}}{sinh1}{A}_{2/3}\left(a,b\right),$$

or equivalently,

$$0<\frac{M_{sinh}\left(a,b\right)-A_{2/3}\left(a,b\right)}{M_{sinh}\left(a,b\right)}<1-\frac{sinh1}{\sqrt{2}}=0.169\dots$$

Remark 5. 

Similarly, using Theorem 6 (i), we can prove that

$$A_{1/3}\left(a,b\right)<M_{tan}\left(a,b\right)<\frac{4}{tan1}{A}_{1/3}\left(a,b\right),$$

or equivalently,

$$0<\frac{M_{tan}\left(a,b\right)-A_{1/3}\left(a,b\right)}{M_{tan}\left(a,b\right)}<1-\frac{tan1}{4}=0.610\dots$$

Remark 6. 

Based on the eight inequalities listed in Introduction and the new ones (15) and (17), we observe that the ten means $He$, L, I, P, T, $NS$, U, V, $M_{sinh}$, and $M_{tan}$ have the sharp power mean bounds $A_p$ (sharp at $a/b\to 1$), where p is a rational fraction in the lowest terms with the denominator of 3. Is there a pattern?