Abstract
This article introduces a novel paradigm for enhancing the administration of decisions regarding sustainable energy planning. This is achieved by deploying novel spherical fuzzy aggregation operators that have been meticulously tailored to address the inherent complexities of uncertainty and imprecision prevalent in energy planning datasets. These operators vastly increase the precision and efficacy of decision-making processes, thereby transforming the entire sustainable energy landscape. This study focuses predominantly on the complex domain of multi-attribute decision-making (MADM), in which the interplay of parameters is characterized by a discernible hierarchy of importance. This method generates aggregation operators based on the assignment of non-negative real values to clearly defined priority echelons, a framework known as priority degrees. This effort results in the development of two notable prioritized operators: the “spherical fuzzy prioritized averaging operator with priority degrees” and the “spherical fuzzy prioritized geometric operator with priority degrees”. The efficacy of these conceptual frameworks is vividly demonstrated through the application of extensive case studies, in which observable results clearly demonstrate their superiority over conventional methodologies. The empirical findings unequivocally demonstrate the superiority of the proposed operators, resonating with substantial performance and efficiency improvements. This study not only adds a seminal dimension to the field of sustainable energy management but also reveals a revolutionary application of spherical fuzzy aggregation operators at the forefront of effective decision-making paradigms. The seamless fusion of theoretical innovation and practical utility outlines a path forward, with transformative prospects and far-reaching implications for the sustainable energy landscape.
Keywords:
aggregation operators; decision-making; sustainable energy management; spherical fuzzy set MSC:
03E72; 94D05; 90B50
1. Introduction
Fuzzy multi-attribute decision-making (FMADM) is a mathematical approach to making decisions that involves taking into account multiple, often conflicting, criteria. This method is used to handle situations where the decision-making process is not straightforward and requires the consideration of multiple factors. FMADM is widely used in various fields, including engineering, economics, management, and medicine, to mention a few. FMADM finds use in the realm of engineering, specifically in the domain of product design and development. This methodology is employed when there exists a need to evaluate and take into account various factors, such as cost, quality, and performance, in the decision-making process. The application of the FMADM methodology enables engineers to effectively assess and identify the most optimal design solution, considering the inherent trade-offs that exist among various criteria. This methodology can also be applied in the context of project management to effectively determine task prioritization and resource allocation, while considering many criteria including time constraints, budget limitations, and available resources. In the field of economics, the FMADM approach is employed to assess investment prospects by considering many factors like return on investment, risk, and market circumstances. The aforementioned methodology can also be applied within the context of portfolio management, wherein it aids in identifying the most advantageous distribution of assets by considering several factors, including but not limited to risk tolerance and investment objectives. Within the realm of management, the utilization of the FMADM approach is employed to assess the efficacy of workers, departments, and organizations [1].
This evaluation process encompasses the consideration of various criteria, including but not limited to productivity, quality, and customer satisfaction. This strategy may also be applied in the context of resource allocation, wherein the allocation of resources is contingent upon various variables encompassing cost, efficiency, and risk. Within the field of medicine, the employment of the FMADM approach is prevalent for the purpose of assessing and comparing various treatment alternatives. This method allows for the consideration of several criteria, including but not limited to the efficacy of the treatment, potential adverse effects, and associated costs. This methodology can also be applied in the context of medical decision-making in order to ascertain the optimal course of action, taking into account many elements like patient medical records, diagnostic outcomes, and patient preferences [2].
The utilization of FMADM has numerous advantages. Firstly, the utilization of various criteria enables a more comprehensive assessment of available possibilities. Furthermore, this approach facilitates the incorporation of both subjective and objective factors, hence allowing for the consideration of stakeholders’ ideas and preferences. In conclusion, the FMADM framework facilitates the integration of uncertainty, hence enabling the management of scenarios characterized by incomplete or uncertain information. The FMADM approach holds significant importance and is used in the realm of decision-making, finding extensive application across many domains. The framework offers a structured approach to assess various alternatives by considering several criteria, enabling the incorporation of both subjective and objective factors, while also accommodating uncertainties. The utilization of FMADM enables decision-makers to enhance the quality and efficacy of their decisions by considering the trade-offs among several criteria [3].
The utilization of aggregation operators is of paramount importance in the process of decision-making, as they facilitate the amalgamation of several factors into a unified decision. An aggregation operator refers to a mathematical function that consolidates several values into a singular outcome, hence offering a means to incorporate and evaluate various criteria in the process of decision-making. There exist various forms of aggregating operators, such as weighted sum, weighted product, and ordered weighted averaging (OWA). The weighted sum operator is a fundamental and extensively employed aggregation operator. The process entails the allocation of weights to individual criteria, followed by the summation of these weighted values to yield a conclusive result [4]. The utilization of the weighted product operator is applicable in situations when the criteria exhibit interdependence, whereby the outcome of one criterion has an impact on the outcome of another criterion. The utilization of the OWA operator is employed in situations when the criteria exhibit varying levels of importance, necessitating the decision-maker to establish a hierarchy among them [5].
The significance of clean and sustainable energy is growing in prominence due to global imperatives such as the mitigation of greenhouse gas emissions, enhancement of energy resilience, and facilitation of economic progress. By placing reliance on renewable energy sources, it is possible to diminish our reliance on conventional fossil fuels, mitigate the adverse effects of energy production on the environment and public health, and provide support for endeavors aimed at addressing climate change [6]. The importance of fostering a more sustainable future necessitates the allocation of appropriate attention and assistance. The various MADM methodology is a systematic strategy employed to assess and analyze various criteria, which are frequently contradictory in nature, during the decision-making process. Within the realm of clean and sustainable energy, MADM possesses the potential to serve as a valuable instrument for decision-makers in evaluating the inherent compromises associated with diverse energy sources, technologies, and regulations [7].
The concept of fuzzy sets was introduced by Zadeh in 1965 as a means to address the handling of uncertain and imprecise data within decision-making contexts [8]. Fuzzy sets provide membership grades to elements of a set within the range of values from 0 to 1. This technique is a deviation from traditional or deterministic methodologies, which may not consistently yield optimal results in volatile or uncertain situations. The significance of Zadeh’s contributions in this field lies in the adaptation of set theoretic principles from crisp examples to fuzzy sets. Subsequently, scholars have identified a multitude of applications for fuzzy sets, encompassing domains such as data science, intelligent systems, clinical diagnosis, and other related fields. The membership function is a fundamental attribute of a fuzzy set; yet, the management of intricate fuzzy data might provide difficulties. Atanassov [9] presented a solution to address this difficulty by introducing the concept of intuitionistic fuzzy set (IFS), which represents an enhanced iteration of the fuzzy set by incorporating degrees of both membership and non-membership. In recent decades, there has been a growing utilization of IFSs by researchers to address the challenges posed by ambiguity and vagueness in data. Aggregation operators (AOs) play a crucial role in the integration of information and the combination of operational factors for different options. Various types of have been suggested for IFSs. Yager introduced the concept of Pythagorean fuzzy set [10] and q-rung orthopair fuzzy set [11]. Although the IFS theory has found extensive application across several industries, it may not possess the capacity to adequately account for situations requiring subjective human viewpoints, such as voting. Voting often necessitates the consideration of multiple replies, including affirmative, abstention, negative, and rejection. In order to tackle this matter, Cuong introduced the notion of “picture fuzzy set” (PFS), which encompasses different levels of “positive membership degree” (PMD), “neutral membership degree” (NMD), and “negative membership degree” (NMD) ranging from 0 to 1. It is important to note that these degrees must adhere to the constraint that their sum equals unity, as stated in Cuong’s works [12]. Nevertheless, there are instances where PFS may fail to provide a suitable resolution. In order to mitigate this constraint, a number of scholars have put forth the notion of SFPS. To address this limitation, several researchers proposed the concept of SFPS. Gundogdu and Kahraman [13] developed SFPSs to provide decision-makers with more flexibility to address decision-making challenges and uncertainty. Gundogdu and Kahraman proposed the spherical fuzzy TOPSIS [14], spherical fuzzy WASPAS [15], and spherical fuzzy VIKOR techniques [16]. Ashraf and Saleem proposed the GRA approach for the SF linguistic set [17]. Additionally, Zeng et al. [18], Rafiq et al. [19], and Jaller and Otay [20] have contributed extensive research on SPFSs.
Some exsiting AOs for SPFSs are given in Table 1.

Table 1.
Some AOs for SPFSs.
1.1. Research Aims and Motivations
In the course of our everyday experiences, we encounter many scenarios that necessitate the utilization of a mathematical function with the ability to condense a set of integers into a singular value. Consequently, the AO investigation holds considerable importance in MCDM issues. In light of their extensive application across various disciplines, a considerable number of scholars have recently directed their attention towards the topic of data aggregation. Nevertheless, it is not uncommon to encounter situations in which the elements to be combined have a clear hierarchical structure. In the context of purchasing a plot of land for residential construction, it is imperative to consider the factors of utility access, location, and cost. It is essential to avoid situations where utility access is paid for in terms of location, or when location is paid for in terms of cost. In the given scenario, there exists a stringent hierarchy of prioritization among parameters, with P1 being of higher priority than P2, and P2 being of higher priority than P3. Akram et al. proposed the utilization of spherical fuzzy prioritized AOs as a solution to address this particular challenge. The notion of determining the degrees of priority among several priority orders enhances the flexibility of the prioritized operators. The selection of the priority degree vector by the DM should be determined by their own preferences and the inherent characteristics of the problem at hand. To better elucidate the concept of priority degrees, let us examine the aforementioned instance of acquiring a plot. A priority degree, which is a non-negative real number, will be assigned to each priority level. Given the preceding case, it can be observed that P1 is more than P2, and P2 is greater than P3. The prioritizing relationship between the first priority order P1 and P2 is denoted as P1 P2, where d1 represents the degree of priority assigned to P1, with the constraint that . In a similar vein, the second priority order P2 is assigned the priority degree d2, where d2 is greater than the priority degree of P3 and is bounded between 0 and 1. Consequently, the prioritized criteria P1 > P2 > P3 are associated with a two-dimensional vector , and this relationship is represented as P1 P2 P3. Given the advantageous nature of the SPFS in addressing MCDM problems, it becomes imperative to construct novel prioritized AOs utilizing priority degrees.
1.2. Organization of the Paper
The remainder of this article is organized as follows. Section 2 provides a number of key SPFS concepts. In Section 3, we examined how the SPF prioritized AOs based on the priority vector operates. In Section 4, we present a method for solving MCDM problems using new AOs. Section 5 contains an application for selecting a sustainable energy source. Section 6 finishes with some concluding observations and future proposals.
2. Preliminaries
In this portion of the research, we will focus on the fundamentals and basic rules of SPFSs.
Definition 1
([13]). Assume SPFS in is given as
where defines the “degree of positive membership”, “degree of neutral membership”, and “degree of negative membership” of the alternative and , respectively, we have
Definition 2
([13]). Let and be SPFNs. , then
(1)
(2)
(3)
(4)
(5)
(6)
(7)
Definition 3
([13]). Let be the SPFN, “score function” (SF) of is defined as
. However, in some cases, the SF is not particularly useful for SPFN. As a result, using the SF to evaluate the SPFNs is insufficient. We are adding a new function, which is an “accuracy function” (AF).
Definition 4.
Let be the SPFN, then an AF of is defined as
.
To assist this sort of study, we propose additional SF, . We can see that .
Definition 5
([24]). Presume that is a conglomeration of SPFNs and SPFWA, if
where is the set of all SPFNs, and is weight vector of , s.t. & . Then, the SPFWA is called the “picture fuzzy weighted average operator”.
Theorem 1.
Let be the conglomeration of SPFNs, we can find by
Definition 6
([24]). Presume that is the conglomeration of SPFN, and SPFWG:, if
where is the set of all SPFNs, and is weight vector of , such that & . Then, the SPFWG is called the "picture fuzzy weighted geometric operator".
Theorem 2.
Let be the conglomeration of SPFNs; we can find SPFWG by
3. Spherical Fuzzy Prioritized AOs with PDs
In this section, AOs with PDs for SPFNs are presented.
3.1. SPFPA Operator
Presume is the assemblage of SPFNs, “there is a prioritization among these SPFNs expressed by the strict priority orders , where indicates that the SPFN has higher priority than . is the dimensional vector of PDs. The assemblage of such SPFNs with strict priority orders and PDs is denoted by .”
Definition 7.
SPFPA operator is a mapping from to and given as,
where , , for each and . Then, SPFPA is called “picture fuzzy prioritized averaging operators with PDs”.
Theorem 3.
where , , for each and .
Presume is the conglomeration of SPFNs, we also define SPFPA by
Proof.
By “mathematical induction”. For
Then
This demonstrates that Equation (2) is valid for ; now suppose that Equation (2) is correct for , i.e.,
Now for ,
This demonstrates that Equation (2) applies for . Therefore,
□
Theorem 4.
Presume that is the conglomeration of SPFNs, and
Then,
where , , for each and .
Theorem 5.
Presume that if is an SPFN having the characteristics , then
Proof.
Let be the SPFN. Then, by assumption, we have gives , and . By Definition 7, we have . Then, by using Theorem 3, we obtain
□
Corollary 1.
If is the conglomeration of largest SPFNs, i.e., for all g, then
Proof.
We would immediately establish a corollary analogous to Theorem 5. □
Corollary 2.
If is the smallest SPFN, i.e., , then
Proof.
□
Theorem 6.
Presume that and are two conglomerations of SPFNs, if and is an SPFN, then
1.
2.
3.
4.
Proof.
This is trivial by definition. □
SPFPA operator satisfied following properties.
Characteristic: 1
Presume that is the conglomeration of SPFNs, then we have
Proof.
Given that, , from this we have,
by this we obtain,
□
Characteristic: 2
Presume that is the conglomeration of SPFNs and for all g, then we have
Proof.
Given that, , from this we have,
and . Hence
□
Characteristic: 3
Presume that is the conglomeration of SPFNs and or 1, then we have
Proof.
Here, for each we have
because, ,
and
for each . Hence,
□
Characteristic: 4
Presume that is the conglomeration of SPFNs and for all , and , then we have
Proof.
Given that, . So,
for each .
So,
and for each .
for each .
Hence,
□
Characteristic: 5
Presume that is the conglomeration of SPFNs and or 0, then we have
Proof.
Given that, . So,
for each .
So,
and for each .
for each .
Hence,
□
3.2. SPFPG Operator
Definition 8.
An SPFPG operator is a mapping from to and defined as,
where , , for each and . Then SPFPG is called "picture fuzzy prioritized geometric operator with PDs".
Theorem 7.
where , , for each and .
Presume is the conglomeration of SPFNs, we can also find SPFPG by
Proof.
This is identical to Theorem 3. □
Theorem 8.
Presume that is the conglomeration of SPFNs, and
Then,
where , , for each , and .
Proof.
Proof is same as Theorem 4. □
Theorem 9.
Presume that if is an SPFN having the characteristic, , then
Proof.
Let be the SPFN. Then, by assumption, we have gives , and . By Definition 8, we have . Then, by using Theorem 7, we obtain
□
Corollary 3.
If is the conglomeration of largest SPFNs, i.e., for all g, then
Proof.
We can easily obtain a corollary similar to Theorem 9. □
Corollary 4.
If is the smallest SPFN, i.e., , then
Theorem 10.
Presume that and are two conglomerations of SPFNs, if and is an SPFN, then
1.
2.
3.
4.
Proof.
This is trivial by definition. □
SPFPG operator also satisfied the following properties.
Characteristic: 1
Presume that is the conglomeration of SPFNs, then
Characteristic: 2
Presume that is the conglomeration of SPFNs and ∀g, then
Characteristic: 3
Presume that is the conglomeration of SPFNs and or 1, then
Characteristic: 4
Presume that is the conglomeration of SPFNs and for all , and , then
Characteristic: 5
Presume that is the conglomeration of SPFNs and or 0, then
4. Proposed Methodology Based on Developed AOs
Let and be the alternatives and criterion, respectively; priorities are given among the criterion by strict priority relation. , indicate that parameter has a greater priority than with degree for . DM gave their opinion matrix , where is for the alternate as per the parameter by DM. The matrix D has converted into normalized matrix by the given formula ,
where show the compliment of .
The recommended operators will be added to the MCDM, which will necessitate the former procedures.
Step 1:
Acquire the decision matrix in the format of SPFNs from DM.
Step 2:
There is no need for normalization if all indicators are of the same kind. The matrix has been amended to “transforming response matrix, ” by Equation (18).
Step 3:
Aggregate for all alternates by utilizing the SPFPA (or SPFPG) operator.
Step 4:
Compute the total score from all alternative assessments.
Step 5:
The SF was used to classify the alternatives, and the most appropriate option was chosen.
5. Case Study
The integration of sustainable energy planning is fundamentally interconnected with decision-making processes across multiple levels, encompassing individual families, national governments, and international organizations. The establishment of this link is fundamental in the pursuit of sustainable energy development objectives and in effectively tackling the worldwide issues of climate change, limited resources, and environmental deterioration. The initial step in sustainable energy planning is the establishment of well-defined objectives and priorities. It is imperative for all stakeholders, including politicians, energy businesses, and individuals, to establish a clear and context-specific definition of sustainability. The decision-making process encompasses the evaluation of environmental, social, and economic concerns, alongside the assessment of long-term energy requirements.
The significance of clean and sustainable energy is escalating due to the global demand for energy to fuel national economies, coupled with the imperative to mitigate adverse environmental consequences. The demand for renewable and sustainable energy sources has experienced substantial growth in recent years. This surge can be attributed to several factors, such as the escalating prices associated with conventional fossil fuels, mounting apprehensions over climate change, and the imperative to mitigate greenhouse gas emissions [27]. This article aims to explore the significance and applications of clean and sustainable energy, as well as its pivotal role in fostering a more sustainable future.
- Reducing Greenhouse Gas Emissions: The mitigation of greenhouse gas emissions can be achieved by the use of clean and sustainable energy sources, thereby addressing the primary driver of global warming. When traditional fossil fuels, including coal, oil, and natural gas, are utilized as energy sources, they release significant quantities of carbon dioxide and other greenhouse gases into the atmosphere. In contrast, renewable energy sources, including wind, solar, and hydropower, do not generate direct emissions and exhibit much reduced indirect emissions in comparison to fossil fuels [28].
- Cost-Effective: Clean and sustainable energy is frequently exhibiting a growing tendency towards cost competitiveness when compared to conventional fossil fuels in numerous instances. The costs associated with renewable energy technologies, such as wind turbines and solar panels, have experienced a substantial reduction in recent years and are projected to sustain a downward trend. Moreover, it is worth noting that renewable energy sources exhibit significantly lower operational costs in comparison to conventional fossil fuels. This disparity arises due to the susceptibility of fossil fuels to price changes and geopolitical concerns [29].
- Improving Energy Security: The utilization of clean and sustainable energy sources has the potential to enhance energy security through the mitigation of reliance on imported fossil fuels. Countries can enhance their energy independence and mitigate the risks associated with price volatility and supply disruptions by depending on energy sources that are readily accessible within their own borders [30].
- Creating Jobs: The adoption of a clean and sustainable energy system has the potential to generate novel employment prospects in various sectors, including the installation, maintenance, and manufacturing of renewable energy technologies. Furthermore, the advancement of novel energy technologies has the potential to foster economic expansion and catalyze innovation [31].
- Enhancing Public Health: The utilization of clean and sustainable energy resources has the potential to enhance public health through the mitigation of air and water pollution. These forms of pollution have been linked to many health complications, including respiratory ailments, cardiovascular disorders, and malignancies. Moreover, it is worth noting that renewable energy sources exhibit significantly lower levels of noise emissions compared to conventional fossil fuels, hence mitigating the adverse effects of noise pollution on human health.
- Aiding Rural Development: Clean and sustainable energy sources have the potential to facilitate the provision of electricity to remote and rural areas, which frequently lack access to conventional grid networks. The provision of modern energy services through this initiative can have a substantial influence on the development of rural areas, facilitating economic growth and enhancing access to essential resources.
- Supporting Climate Action: The use of clean and sustainable energy sources plays a pivotal role in the worldwide endeavor to address climate change. Renewable energy sources have the potential to decelerate the progression of global warming and alleviate its adverse consequences, including elevated sea levels, heightened frequency and severity of natural calamities, and alterations in precipitation patterns, through the reduction in greenhouse gas emissions [32].
The significance of clean and sustainable energy is growing in prominence due to global imperatives such as the mitigation of greenhouse gas emissions, enhancement of energy resilience, and facilitation of economic progress. By placing reliance on renewable energy sources, it is possible to diminish our reliance on conventional fossil fuels, mitigate the adverse effects of energy production on the environment and public health, and provide support for endeavors aimed at addressing climate change. The importance of fostering a more sustainable future cannot be overstated, and it warrants significant attention and support. Figure 1 illustrates the interconnectedness between several factors and sustainable energy, including decision-making, waste management, biofuels, climate change, pollution, and other relevant issues. We take papers from PubMed and make a Figure 1 by VOS viewer.
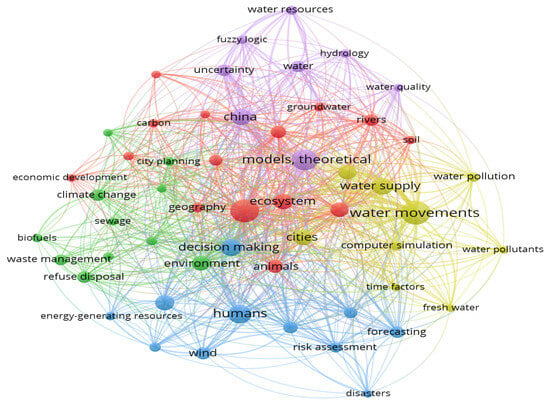
Figure 1.
Relation of different aspects with sustainable energy.
The various MADM methodology is a systematic strategy employed to assess and analyze various criteria, which frequently exhibit conflicting characteristics during the decision-making process. Within the realm of clean and sustainable energy, MADM can serve as a valuable instrument for decision-makers to evaluate the inherent compromises associated with various energy sources, technologies, and policies. This article aims to explore the applications of MADM within the realm of clean and sustainable energy, emphasizing its significance in fostering a more sustainable future.
- Evaluating Energy Sources: The MADM approach can be employed to assess and compare different renewable energy sources, including solar, wind, hydro, and bioenergy, in relation to conventional fossil fuels like coal, oil, and natural gas [30]. Various factors that may be taken into account throughout the review process include technical feasibility, economic viability, environmental effect, and social acceptability. This can assist decision-makers in selecting the energy source that is most suitable for their particular requirements and conditions.
- Assessing Energy Technologies: The MADM technique can be employed to assess and contrast various energy systems, including wind turbines, solar panels, and hydropower plants. The evaluation process may take into account several factors, such as technical performance, cost, environmental effect, and reliability. This can assist decision-makers in selecting the technology that is most suitable for their particular requirements and circumstances [29].
- Prioritizing Energy Policies: The MADM methodology can be effectively employed to establish priority rankings for energy policies and projects, including but not limited to renewable energy objectives, subsidies, and tax credits. The evaluation process may encompass various factors, such as cost-effectiveness, feasibility, environmental impact, and social acceptability. This can assist decision-makers in selecting policies and initiatives that have a higher probability of accomplishing their energy objectives and facilitating a shift toward a more sustainable energy framework.
- Evaluating Energy Projects: The MADM technique can be employed for the assessment and comparison of distinct energy projects, including wind farms, solar power plants, and hydropower schemes. The review process may encompass various factors, such as economic viability, environmental effect, social acceptability, and technological feasibility. This approach can assist decision-makers in selecting projects that have a higher probability of attaining their energy objectives and facilitating a shift toward a more sustainable energy framework.
- Balancing Trade-Offs: The MADM approach can be employed to effectively manage the trade-offs that arise from the utilization of diverse energy sources, technologies, and policies. For instance, renewable energy sources such as wind and solar power exhibit the advantageous characteristics of being sustainable and emitting minimal amounts of greenhouse gases. However, it is worth noting that these energy sources may also entail adverse consequences for animals and local residents. In contrast, hydro and bioenergy have the potential to generate minimal levels of greenhouse gas emissions; however, it is important to acknowledge that these energy sources can also exert adverse effects on water resources and ecosystems. The utilization of MADM can assist decision-makers in selecting the most suitable energy source, technology, or policy that effectively manages the inherent trade-offs and facilitates the transition toward a more sustainable energy system [32].
- Incorporating Stakeholder Perspectives: The MADM can serve as a valuable tool for integrating the viewpoints of diverse stakeholders, including governmental entities, energy corporations, environmental advocacy groups, and local communities. The review process may encompass various factors, such as technical feasibility, economic viability, environmental effect, and social acceptability. This can assist decision-makers in selecting the optimal energy source, technology, or policy that is most likely to effectively accomplish their energy objectives while considering the concerns and perspectives of many stakeholders.
The MADM technique serves as a valuable instrument for decision-makers in assessing the inherent trade-offs associated with various energy sources, technologies, and policies within the realm of clean and sustainable energy. By integrating many criteria and considering the perspectives of different stakeholders, MADM can facilitate the advancement toward a sustainable energy system and foster a more equitable and balanced approach to making energy-related decisions. As the global community confronts the pressing issues of mitigating greenhouse gas emissions and enhancing energy security, the relevance and significance of MADM will progressively escalate [33]. DM has more than 15 years of experience in the renewable energy industry in a variety of capacities. He possesses a Bachelor’s and a Master’s degree in environmental engineering and energy policy and management, respectively. He began their career as an engineer at a prominent solar panel manufacturer, where he gained practical knowledge of renewable energy technologies.
6. Numerical Illustration
Suppose the decision-making dilemma of determining the best candidate for the renewable energy sector. Presume the conglomeration of alternatives, = Wave Energy, = Wind Energy, = Nuclear Energy, and = Wind Energy and Wave Energy. These possibilities are evaluated using four criteria, = cost, = innovation, = environmental aspects, and = international collaboration. “Prioritized in strict priority order” is . PDs are = (2, 1, 3).
6.1. With SPFPA Operator
Step 1:
Obtain matrix by DM, which is shown in Table 2.

Table 2.
Rating given by DM.
Step 2:
In this case, no criteria are cost-type criteria, all are the benefit type, so there is no need for normalization. Normalized SPF decision matrix given in Table 3.

Table 3.
Normalized SPF decision matrix.
Step 3:

Table 4.
SPF-aggregated values .
Step 4:
Compute the score for all SPF-aggregated values .
Step 5:
Ranks according to SFs.
So,
is best alternative among all other alternatives.
6.2. With SPFPG Operator
Step 1:
Obtain matrix by DM, which is shown in Table 5.

Table 5.
Rating given by DM.
Step 2:
In this case, no criteria are cost-type criteria, all are the benefit type, so there is no need for normalization. Normalized SPF decision matrix given in Table 6.

Table 6.
Normalized SPF decision matrix.
Step 3:

Table 7.
SPF-aggregated values .
Step 4:
Compute the score for all SPF-aggregated values .
Step 5: Ranks according to SFs.
So,
is the best alternative among all other alternatives.
6.3. Comparison with Existing AOs
Proposed AOs are contrasted against a significant number of existing AOs in this section. We obtain a comparable optimal solution by solving the data with previously established AOs, which we then employ to equalize our results. This demonstrates that the AO is effective and long-lasting. Several previously-published AOs are outperformed by the methodology presented in this paper. To confirm that our ideal solution is the best, we test it with a wide spectrum of existing operators. The fact that we both arrive at the same optimal conclusion indicates that our proposed AOs are reliable. Comparison anaylsis is given in Table 8.

Table 8.
Comparison of proposed operators with some exiting operators.
7. Conclusions
This paper presents a novel methodology for managing decision-making processes effectively within the context of sustainable energy planning. The proposed strategy makes use of innovative spherical fuzzy prioritized evaluation objects. These operators incorporate the concept of level prioritization, enabling a more comprehensive and sophisticated approach to decision-making. The results of the conducted case studies provide empirical evidence for the efficacy of this particular strategy, demonstrating superior performance in comparison to conventional approaches. This article makes a substantial contribution by proposing a more precise and efficient approach to sustainable energy planning and decision-making. This study provides valuable insights for experts in the relevant field and emphasizes the potential of fuzzy spherical prioritized analytical objects as a decision-making tool.
In the not-too-distant future, the operators and methodologies described above will be utilized in a wide variety of applications, including analysis of networks, risk evaluation, cognitive psychology, learning by reinforcement, processing of signals, and a variety of others with uncertain contexts. During the process of aggregating future efforts, one of our goals is to conduct an analysis of the interrelationships that exist between attribute pairs. In addition, we plan to establish more comprehensive information metrics that will assist us in comprehending the information that we come into contact with on a daily basis.
Author Contributions
Conceptualization, M.A. and S.S.; methodology, M.A. and S.S.; software, M.A. and S.S.; validation, M.A., R.K., S.S. and Y.Y.; formal analysis, Y.Y.; resources, S.S. and R.K.; data curation, M.A. and S.S.; writing—original draft preparation, M.A. and S.S.; writing—review and editing, Y.Y.; visualization, Y.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R259), Princess Nourah bint Abdulrahman University, Saudi Arabia.
Data Availability Statement
The data used to support the findings of the study are included within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Riaz, M.; Farid, H.M.A. Enhancing green supply chain efficiency through linear Diophantine fuzzy soft-max aggregation operators. J. Ind. Intell. 2023, 1, 8–29. [Google Scholar] [CrossRef]
- Kausar, R.; Farid, H.M.A.; Riaz, M. A numerically validated approach to modeling water hammer phenomena using partial differential equations and switched differential-algebraic equations. J. Ind. Intell. 2023, 1, 75–86. [Google Scholar] [CrossRef]
- Farid, H.M.A.; Riaz, M. q-rung orthopair fuzzy Aczel–Alsina aggregation operators with multi-criteria decision-making. Eng. Appl. Artif. Intell. 2023, 122, 106105. [Google Scholar] [CrossRef]
- Kausar, R.; Riaz, M.; Yasin, Y.; Deveci, M.; Pamucar, D. Measuring Efficiency of Retrieval Algorithms with Schweizer-Sklar Information Aggregation. Inf. Sci. 2023, 647, 119438. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Z.; Lu, Z. Multi-objective load dispatch for microgrid with electric vehicles using modified gravitational search and particle swarm optimization algorithm. Appl. Energy 2022, 306, 118018. [Google Scholar] [CrossRef]
- Cheng, B.; Wang, M.; Zhao, S.; Zhai, Z.; Zhu, D.; Chen, J. Situation-Aware Dynamic Service Coordination in an IoT Environment. IEEE/ACM Trans. Netw. 2017, 25, 2082–2095. [Google Scholar] [CrossRef]
- Chen, Y. Research on collaborative innovation of key common technologies in new energy vehicle industry based on digital twin technology. Energy Rep. 2022, 8, 15399–15407. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inform. Contr. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Yager, R.R. Pythagorean fuzzy subsets. In Proceedings of the IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS), 2013 Joint, Edmonton, AB, Canada, 24–28 June 2013; pp. 57–61. [Google Scholar]
- Yager, R.R. Generalized orthopair fuzzy sets. IEEE Trans. Fuzzy Syst. 2017, 25, 1222–1230. [Google Scholar] [CrossRef]
- Cuong, B.C. Picture fuzzy sets-first results. In Part 1. Seminar Neuro-Fuzzy Systems with Applications; Technical Report; Institute of Mathematics: Hanoi, Vietnam, 2013. [Google Scholar]
- Gundogdu, F.K.; Kahraman, C. Spherical fuzzy sets and spherical fuzzy TOPSIS method. J. Intell. Fuzzy Syst. 2019, 36, 337–352. [Google Scholar] [CrossRef]
- Gundogdu, F.K.; Kahraman, C. A novel fuzzy TOPSIS method using emerging interval-valued spherical fuzzy sets. Eng. Appl. Artif. Intell. 2019, 85, 307–323. [Google Scholar] [CrossRef]
- Gundogdu, F.K.; Kahraman, C. Extension of WASPAS with spherical fuzzy sets. Informatica 2019, 30, 269–292. [Google Scholar] [CrossRef]
- Gundogdu, F.K.; Kahraman, C. A novel VIKOR method using spherical fuzzy sets and its application to warehouse site selection. J. Intell. Fuzzy Syst. 2019, 37, 1197–1211. [Google Scholar] [CrossRef]
- Ashraf, S.; Abdullah, S.; Mahmood, T. GRA method based on spherical linguistic fuzzy Choquet integral environment and its application in multi-attribute decision-making problems. Math. Sci. 2018, 12, 263–275. [Google Scholar] [CrossRef]
- Zeng, S.; Hussain, A.; Mahmood, T.; Ali, M.I.; Ashraf, S.; Munir, M. Covering-Based Spherical Fuzzy Rough Set Model Hybrid with TOPSIS for Multi-Attribute Decision-Making. Symmetry 2019, 11, 547. [Google Scholar] [CrossRef]
- Rafiq, M.; Ashraf, S.; Abdullah, S.; Mahmood, T.; Muhammad, S. The cosine similarity measures of spherical fuzzy sets and their applications in decision-making. J. Intell. Fuzzy Syst. 2019, 36, 6059–6073. [Google Scholar] [CrossRef]
- Jaller, M.; Otay, I. Evaluating Sustainable Vehicle Technologies for Freight Transportation Using Spherical Fuzzy AHP and TOPSIS. In Intelligent and Fuzzy Techniques: Smart and Innovative Solutions. Proceedings of the INFUS 2020 Conference, Istanbul, Turkey, 21–23 July 2020; Kahraman, C., Cevik Onar, S., Oztaysi, B., Sari, I., Cebi, S., Tolga, A., Eds.; Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2021; Volume 1197. [Google Scholar]
- Jin, Y.; Ashraf, S.; Abdullah, S. Spherical Fuzzy Logarithmic Aggregation Operators Based on Entropy and Their Application in Decision Support Systems. Entropy 2019, 21, 628. [Google Scholar] [CrossRef]
- Ashraf, S.; Abdullah, S.; Mahmood, T. Spherical fuzzy Dombi aggregation operators and their application in group decision making problems. J. Ambient. Intell. Humaniz. Comput. 2020, 11, 2731–2749. [Google Scholar] [CrossRef]
- Akram, M.; Alsulami, S.; Khan, A.; Karaaslan, F. Multi-criteria group decision-making using spherical fuzzy prioritized weighted aggregation operators. Int. J. Comput. Intell. Syst. 2020, 13, 1429–1446. [Google Scholar] [CrossRef]
- Ashraf, S.; Abdullah, S. Emergency decision support modeling for COVID-19 based on spherical fuzzy information. Int. J. Intell. Syst. 2020, 35, 1601–1645. [Google Scholar] [CrossRef]
- Riaz, M.; Farid, H.M.A. Multicriteria decision-making with proportional distribution based spherical fuzzy fairly aggregation operators. Int. J. Intell. Syst. 2022, 37, 7079–7109. [Google Scholar] [CrossRef]
- Jin, H.; Ashraf, S.; Abdullah, S.; Qiyas, M.; Bano, M.; Zeng, S. Linguistic spherical fuzzy aggregation operators and their applications in multi-attribute decision making problems. Mathematics 2019, 7, 413. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Yuan, X.; Shen, Y.; Lu, Z.; Wang, Z. Adaptive Dynamic Surface Control with Disturbance Observers for Battery/Supercapacitor-based Hybrid Energy Sources in Electric Vehicles. IEEE Trans. Transp. Electrif. 2022. [Google Scholar] [CrossRef]
- Fu, Q.; Li, Z.; Ding, Z.; Chen, J.; Luo, J.; Wang, Y.; Lu, Y. ED-DQN: An event-driven deep reinforcement learning control method for multi-zone residential buildings. Build. Environ. 2023, 242, 110546. [Google Scholar] [CrossRef]
- Li, P.; Hu, J.; Qiu, L.; Zhao, Y.; Ghosh, B.K. A Distributed Economic Dispatch Strategy for Power–Water Networks. IEEE Trans. Control. Netw. Syst. 2022, 9, 356–366. [Google Scholar] [CrossRef]
- Chen, H.; Wu, H.; Kan, T.; Zhang, J.; Li, H. Low-carbon economic dispatch of integrated energy system containing electric hydrogen production based on VMD-GRU short-term wind power prediction. Int. J. Electr. Power Energy Syst. 2023, 154, 109420. [Google Scholar] [CrossRef]
- Liu, X.; Li, Z.; Fu, X.; Yin, Z.; Liu, M.; Yin, L.; Zheng, W. Monitoring House Vacancy Dynamics in The Pearl River Delta Region: A Method Based on NPP-VIIRS Night-Time Light Remote Sensing Images. Land 2023, 12, 831. [Google Scholar] [CrossRef]
- Tong, D.; Sun, Y.; Tang, J.; Luo, Z.; Lu, J.; Liu, X. Modeling the interaction of internal and external systems of rural settlements: The case of Guangdong, China. Land Use Policy 2023, 132, 106830. [Google Scholar] [CrossRef]
- Cui, Z.; Sheng, H.; Yang, D.; Wang, S.; Chen, R.; Ke, W. Light Field Depth Estimation For Non-Lambertian Objects via Adaptive Cross Operator. IEEE Trans. Circuits Syst. Video Technol. 2023. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).