EEG-Based Person Identification and Authentication Using Deep Convolutional Neural Network

Abstract

Using biometric modalities for person recognition is crucial to guard against impostor attacks. Commonly used biometric modalities, such as fingerprint scanners and facial recognition, are effective but can easily be tampered with and deceived. These drawbacks have recently motivated the use of electroencephalography (EEG) as a biometric modality for developing a recognition system with a high level of security. The majority of existing EEG-based recognition methods leverage EEG signals measured either from many channels or over a long temporal window. Both set limits on their usability as part of real-life security systems. Moreover, nearly all available methods use hand-engineered techniques and do not generalize well to unknown data. The few EEG-based recognition methods based on deep learning suffer from an overfitting problem, and a large number of model parameters must be learned from only a small amount of available EEG data. Leveraging recent developments in deep learning, this study addresses these issues and introduces a lightweight convolutional neural network (CNN) model consisting of a small number of learnable parameters that enable the training and evaluation of the CNN model on a small amount of available EEG data. We present a robust and efficient EEG-based recognition system using this CNN model. The system was validated on a public domain benchmark dataset and achieved a rank-1 identification result of 99% and an equal error rate of authentication performance of 0.187%. The system requires only two EEG channels and a signal measured over a short temporal window of 5 s. Consequently, this method can be used in real-life settings to identify or authenticate biometric security systems.

1. Introduction

A biometric recognition system aims to identify or authenticate individuals from the patterns of their physical or behavioral characteristics [1]. Common physical modalities include fingerprints, face images, voice, and iris. Behavioral modalities rely on an individual’s comportment, such as analyzing gait patterns in which an individual is identified based on his/her walking patterns. Each biometric modality has benefits and limitations; one of the main problem of these modalities is spoofing. The reliable authentication of an individual’s identity is an issue of high importance, particularly in organizations that require a high-level security system, such as governmental facilities and private companies. This need has motivated the use of electroencephalography (EEG) as a biometric modality in security systems. EEG measures the electrical activity of the brain. It is usually employed in medicine to detect various neurological disorders, such as sleep disorders [2], epilepsy [3], and brain tumors. In addition, it is applied for post-stroke rehabilitation [4], emotion recognition [5], and it is used for brain–computer interfaces, in which brain signals are leveraged to control external activities. Brain signals are sensitive to the mental state of an individual, making the fabrication or theft of EEG signals practically impossible. This property makes it a particularly attractive modality for use within a high-level security system.

EEG has great potential as a biometric modality. The main challenge is to design a suitable method to identify and authenticate a person using his/her EEG brain signals. The majority of existing EEG-based recognition techniques leverage hand-engineered features that do not achieve sufficiently high recognition results, as reported in [6,7]. Convolutional neural network (CNN)-based models have achieved impressive results in different fields, such as image classification and voice recognition [8,9]. Two prior studies [10,11] leveraged deep CNN for EEG-based identification and authentication. Although the reported results are better than those obtained with methods based on hand-engineered features, their CNN models are tremendously large in terms of the number of learnable parameters compared to the amount of available training data. A learning model with a relatively large number of parameters compared to the amount of training data usually suffers from overfitting. Consequently, it does not generalize well to unseen data. To the best of our knowledge, a dependable EEG-based recognition method that can be implemented in a high-level security application does not yet exist. Moreover, existing methods are impractical as part of a security system due to the highly complex CNN models [10,11], a large number of requisite channels [11,12], and an extended signal length, usually requiring 10 s or more to perform recognition [13].

To address the issues mentioned above, we propose a robust EEG-based person recognition system. Developing such a system utilizing deep learning is challenging due to the limited number of available EEG signals. The complexity of a CNN model depends on the number of learnable weights and biases. If the model size correlates with the available data volume for training, then the model has good generalization. However, if the model’s capacity is large compared to the input, the model may memorize the training data, causing an overfitting problem. This work proposes a lightweight, deep CNN model for accurate individual detection using EEG signals to address these challenges. The proposed CNN model is lightweight in the sense that it involves a small number of learnable parameters and addresses the overfitting problem. It has a small number of parameters but has sufficient capacity to learn discriminative EEG-based features for person recognition. The model requires only two channels and a 5 s signal length to implement a compact and robust EEG-based person identification and authentication system.

The main contribution of this research is the development of a reliable and accurate EEG-based person recognition system. The specific contributions of this work are as follows:

• A deep CNN model is designed based on a pyramidal architecture with a relatively low parameter complexity and high capacity for achieving good recognition performance on raw EEG signals. The model architecture design is suitable for EEG signals. It considers an EEG signal to be a one-dimensional vector in the temporal domain, leveraging one-dimensional convolutions to process EEG signals.
• Using the designed lightweight CNN model, a robust EEG-based recognition system is developed for person identification and authentication that is suitable for deployment in high-level security systems.
• A thorough evaluation of the system is conducted using a benchmark dataset.
• We found a relationship between brain regions and people identification, as shown in Section 4.2. To the best of our knowledge, no research has provided this connection.

The rest of the paper is organized as follows. Section 2 provides a literature review of related works. Section 3 describes the proposed system, and Section 4 discusses the evaluation criteria, implementation details, results, and analyses. Finally, the conclusion summarizes the findings and discusses future work.

2. Related Work

This section presents an overview of the state-of-the-art EEG-based biometrics recognition methods, which are categorized based on two scenarios: identification and authentication.

2.1. Identification System

Recently, a number of methods for identification based on hand-engineered features [6,7,13,14,15,16] and deep learning [10,11,12,17,18] have been published. Table 1 provides a summary of these methods.

Table 1. EEG-based Identification Methods. Notations: CL—Classifier, S—Subjects, C—EEG channels, PL—Pattern/Instance length, L1—Cityblock distance, PSD—Power spectral density, COH—Spectral coherence connectivity, AR—Autoregressive, PCA—Principal component analysis, MPCA—Multilinear PCA, KNN—K-nearest neighbors, FLDA—Fischer linear discriminant classifier, PLV—Phase Locking Index, RHO—Synchronization index measures deviation of relative phase, GVAE—Graph Variational Auto Encoder.

Paper	Feature	CL	Database	S, C	PL	Acc (%)	Learnable Parameters
Rocca et al., 2014 [14]	PSD, COH	L1	PhysioNet	108, 56	10 s	100.00	N/A
Maiorana et al., 2015 [15]	AR, PSD, COH	L1	Private	50, 7	5 s	90.00	N/A
Maiorana et al., 2016 [6]	AR	L1	Private	50, 19	5 s	88.00	N/A
Maiorana et al., 2016 [7]	PCA, MPCA	KNN	PhysioNet	30, 19	5 s	71.00	N/A
Suppiah and Vinod 2018 [13]	PSD	FLDA	PhysioNet	109, 1	12 s	97.00
Wang et al., 2020 [16]	RHO	Mahalanobis distance	PhysioNet	109, 64	1 s	98.83	N/A
Mao et al., 2017 [10]	Raw EEG	CNN	BCIT	100, 64	1 s	97.00	N/A
Sun et al., 2019 [11]	Raw EEG	CNN, LSTM	PhysioNet	109, 16	1 s	99.58	505,281,566
Sun et al., 2019 [11]	Raw EEG	CNN, LSTM	PhysioNet	109, 4	1 s	94.28	505,281,566
Wang et al., 2019 [12]	PLV	GCNN	PhysioNet	109, 64	5.5 s	99.98	81,901
Wang et al., 2019 [12]	PLV	GCNN	Private	59, 46	5.5 s	98.96	N/A
Behrouzi and Hatzinakos 2022 [17]	GVAE	SVM	PhysioNet	109, 64	1 s	99.78	258
Bidgoly et al., 2022 [18]	Raw EEG	CNN	PhysioNet	109, 3	1 s	98.04	N/A

The summary indicates that deep learning-based methods generally result in better performance than those based on hand-engineered features. The hand-engineered features-based method of Rocca et al. [14] shows the best accuracy (100%); it uses a 10 s long EEG signal segment with 56 channels, which makes them impractical for real security systems. In addition, La Rocca et al. used a benchmark dataset for EEG recognition, the EEG Motor Movement/imagery dataset [19]; however, they reported only 108 subjects for their study and failed to mention why one subject was removed. The recent works of Sun et al. [11] and Wang et al. [12] proposed CNN-based solutions capable of achieving high accuracy results from short signal lengths. However, they both require a larger number of channels and fail to demonstrate comparable results when the number of channels decreases. Although the work in [18] obtained high accuracy with few channels, CNN models also have high parameter complexities and are prone to overfitting.

2.2. Authentication System

The number of related works on biometric authentication is limited compared to the identification. In [20], Das et al. used only hand-engineered features, while Schons et al. [21] and Sun et al. [11] employed deep learning techniques. Furthermore, the work by Sun et al. [11] is the only one that covers both the identification and authentication problems. An overview of these methods is given in Table 2.

Table 2. EEG-based Authentication. Notations: CL—Classifier, S—Subjects, C—EEG channels, PL—Pattern/instance length, L2—Euclidean distance, EER—Equal Error Rate.

Paper	Features	CL	Protocol	S, C	PL	EER (%)
Das et al., 2016 [20]	EEG Sub-bands	Cosine	Private	50, 17	600 ms	8.00
Jijomon and Vinod 2018 [22]	EEG Sub-band, PSD	Cross Correlation	PhysioNet	109, 10	7.5 s	0.016
Schons et al., 2018 [21]	EEG Sub-bands, CNN	L2	PhysioNet	109, 64	12 s	0.19
Sun et al., 2019 [11]	Raw EEG	CNN, LSTM	PhysioNet	109, 16	1 s	0.41
Sun et al., 2019 [11]	Raw EEG	CNN, LSTM	PhysioNet	109, 4	1 s	0.56

The overview in the table shows that overall deep learning-based methods outperform hand-engineered features-based methods. Solutions to the authentication problem proposed in [11,20,21] either use a large number of channels and/or a long signal length. Only the work presented in [20] used a signal length of less than a second; however, the EER of the method is very high (8%). Sun et al. [11] achieved 0.56% EER using a short signal length but with four channels. In conclusion, a robust, lightweight system for EEG-based recognition is still an open research issue. The majority of researchers focus solely on the identification problem and neglect the authentication problem.

3. Proposed Method

This section starts with the problem definition and then presents an overview of the proposed system, which is followed by the design of the proposed CNN model, the dataset and the proposed data augmentation technique, and finally, the training procedure.

3.1. Problem Definition

Let ${\mathit{R}}^{C\times T}$ be the space of EEG signal segments captured from p subjects. Any $\mathit{x}\in {\mathit{R}}^{C\times T}$ is an EEG signal segment consisting of C channels and a temporal window of n seconds sampled into T points, i.e., $\mathit{x}=\left[\mathit{x}\left(t_1\right), \mathit{x}\left(t_2\right), \dots , \mathit{x}\left(t_T\right)\right]$ where $x\left(t_i\right)\in {\mathit{R}}^C$. Moreover, let $l\in \mathit{L}=\left\{1, 2, \dots , P\right\}$ be the set of labels/identifiers of p subjects. We deal with two recognition problems: (i) identification problem, i.e., to predict the label $l$ (i.e., the identity of a subject) from the EEG signal segments $\mathit{x}$ of an unknown subject, and (ii) authentication problem, i.e., to verify the identity claim of a subject given the label (the subject identity) and the EEG signal segments $\mathit{x}$. Each problem is a matching problem and involves an enrollment phase.

3.2. Enrollment Phase

In this phase, EEG signal segments from the known subjects are acquired, and feature vectors are extracted from them and stored in the database along with their identities (labels), as shown in Figure 1. Using a time window of a fixed size (e.g., 3 s (base window size)), EEG signal segments are captured from each subject. Different methods, such as hand-engineered or deep learning, can be used to extract the features. Due to the superior performance of deep learning in many recognition applications, we employ deep learning for feature extraction and propose a lightweight CNN model for this purpose. Details of the CNN model are given in the following section. An EEG signal is passed to the CNN model, and the features are extracted from the final softmax layer. The EEG signal consists of two EEG channels that achieved the highest recognition results: channel numbers 64 and 45. The details are discussed in the Results section.

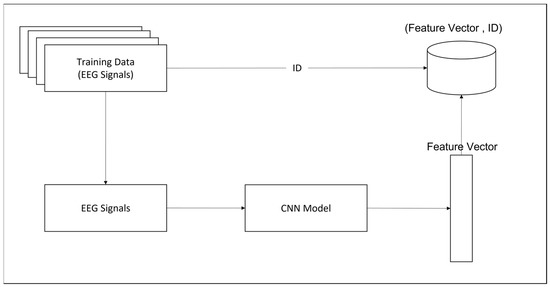
Figure 1. Enrollment Phase.

3.3. Identification Problem

In this problem, the label $l$ of an unknown $x$ is predicted. The design of the system for this problem is shown in Figure 2. Using a time window of a fixed size (e.g., 5 s), $x$ is captured from a query subject, and then $x$ is split with the base window size into M overlapping segments $x_1, x_2,\dots ,x_M.$Each $x_i$ is passed through the CNN model, and the n-dimensional feature vector is extracted using a fully connected layer (FC2). The extracted M feature vectors are fused by averaging the corresponding features as shown in the Equation (1) below:

$$\begin{array}{c}Feature 1\\ Feature 2\\ \begin{array}{c}⋮\\ Feature n\end{array}\end{array}\left[\begin{array}{c}{X}_{11}\\ X_{12}\\ \begin{array}{c}⋮\\ X_{1n}\end{array}\end{array}\right]+\left[\begin{array}{c}{X}_{21}\\ X_{22}\\ \begin{array}{c}⋮\\ X_{2n}\end{array}\end{array}\right]+\dots \dots +\left[\begin{array}{c}{X}_{m1}\\ X_{m2}\\ \begin{array}{c}⋮\\ X_{mn}\end{array}\end{array}\right]=\left[\begin{array}{c}{X}_{1/m}\\ X_{2/m}\\ \begin{array}{c}⋮\\ X_{n/m}\end{array}\end{array}\right] \begin{array}{c} f_{q1}\\ f_{q2}\\ \begin{array}{c}⋮\\ f_{\mathit{qn}}\end{array}\end{array}$$

(1)

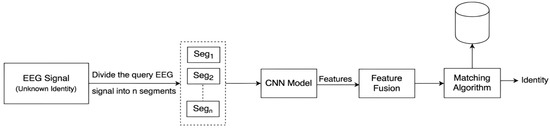
Figure 2. Identification System.

Finally, the query fused feature vector $f_q$ is passed to the matching algorithm, which measures the similarity between $f_q$ and the feature vectors $f_e$ enrolled in the database using a distance measure $d\left(f_q, f_e\right)$, i.e., Manhattan distance (L1). The query feature vector is compared to all enrolled feature vectors. The predicted label of the query subject is the label of the subject whose enrolled feature vector in the database is the most similar to that of the query subject.

3.4. Authentication Problem

The authentication problem substantiates whether $\mathit{x}$ belongs to the subject with an identifier $l$ when the pair ($\mathit{x}$, $l$) is given. The design of the system for this problem is illustrated in Figure 3. The query feature vector $f_q$ is computed from $\mathit{x}$ using the technique described in Section 3.3. It is compared only to the enrolled feature vectors $f_e$ with the same identity $l$. The query subject is predicted as genuine or an impostor using the following threshold:

$$\left(f_{q }, f_e\right)\in \left\{\begin{array}{c}Genuine if d\left(f_{q }, f_e\right)\le threshold\\ Impostor otherwise \end{array} \right.$$

(2)

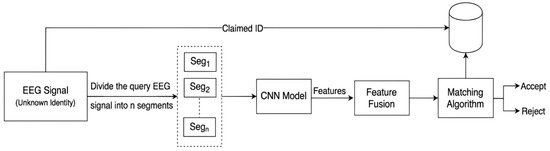
Figure 3. Authentication System.

3.5. The Proposed Lightweight CNN Model

The core component of each system is the deep CNN model used for feature extraction. Training a deep CNN model requires a large amount of training data, but the available EEG data are limited. Therefore, to avoid the overfitting problem, we propose a lightweight deep CNN model.

A lightweight CNN model means that the model involves a small number of learnable parameters (a few thousand in comparison to millions), and a small amount of data is needed for learning. As the availability of raw EEG signals is limited, a small number of training examples can be generated, even with data augmentation. For this reason, only a lightweight CNN model is suitable for raw EEG signals to avoid the overfitting problem. The focus of the proposed work is to use only two EEG channels with a sampling rate of 160 and a small window of 3 s to enhance useability. This results in EEG instances with a size of 160 × 2 × 3 = 960 samples such that for each channel, 480 samples were obtained compared to a very small RGB image 32 × 32 × 3 = 3072 samples. This is why the model must be lightweight. As the sample size becomes smaller, the model needs to be lighter so that it can generalize well and not memorize the data.

The model is designed to minimize the number of learnable parameters. This can be achieved by adopting a pyramid architecture, which was previously demonstrated to achieve high accuracy results in EEG-related problems [23,24]. In this architecture, the number of filters of convolution (CONV) layers decreases as we go deeper, unlike in the usual CNN model designs. It significantly reduces the number of learnable parameters and generalizes better to unknown data (Section 4.4). The CNN filter size was inspired by the VGGNet model used for classifying the ImageNet dataset [25], in which the filter size is restricted to 5 × 5 and 3 × 3. However, as the proposed model takes EEG signals, which consist of one-dimensional (1D) channels, as input instead of two-dimensional spatial images, we modified the filter height to 1, resulting in filters with sizes of 5 × 1 and 3 × 1.

The model consists of two main blocks, as illustrated in Figure 4. Figure 4a shows the CONV block, which takes the input, feeds it to the CONV layer, and then moves it to the Batch Normalization (BN) layer. A Scaled Exponential Linear Units (SeLU) activation function is applied to introduce nonlinearity to the output. SeLU is defined as follows:

$$f\left(x\right)=\left\{\begin{array}{c}\mathsf{\lambda }x \mathrm{if} x>0\\ \mathsf{\lambda }\mathsf{\alpha }\left({\mathrm{e}}^x-1\right) \mathrm{if} x\le 0, \end{array}\right.$$

where the hyperparameters λ and α are to λ ≈ 1.0507 $\mathsf{\alpha }$≈ 1.6733.

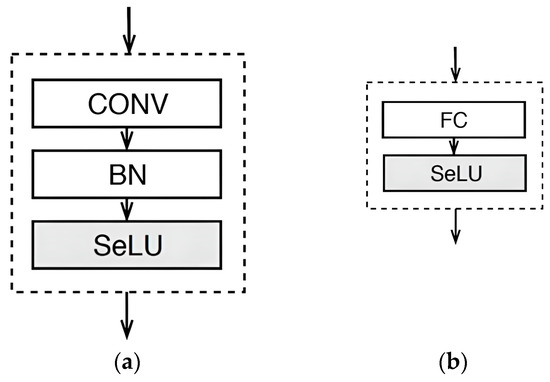
Figure 4. Building Blocks of the CNN Model. (a) CONV Block, (b) FC Block.

Figure 4b illustrates the FC block. Each convolution layer is followed by a max-pooling layer to control the number of learnable parameters. After the final pooling layer, the output is flattened and fed to the FC blocks. The dropout layer is placed before the final FC layer, with a rate of 0.3 to minimize model overfitting [26]. Before training, the data are normalized using a z-score transformation. The baseline CNN model is depicted in Figure 5.

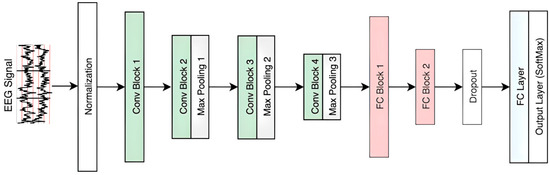
Figure 5. Proposed CNN Model for EGG-based Recognition.

Table 3 shows the detailed CNN model architecture. The model starts with a 5 × 1 filter size and the largest number of filters (64). The number of filters then decreases by half to 32, and the filter size changes to 3 × 1. The last CONV block ends with a 3 × 1 filter size and the smallest number of filters (16). Two FC blocks followed with 100 neurons in the first and 35 neurons in the second. The final FC layer is used for classification, in which the number of neurons is equal to the number of subjects (109). The output of this FC layer is fed into the softmax layer. The final row of the table highlights the number of learnable parameters used in the model, i.e., 74,071 parameters. This number is very small compared to, for example, the 18,529,390 learnable parameters of the CNN model used in [21]. Although this model does not require big data for training, the available data are very small. To avoid the overfitting problem, we introduce data augmentation to enlarge the dataset. This ensures that the amount of training data is large enough compared to the model’s learning capacity. More details are presented in Section 3.6.1.

Table 3. CNN Model Network Architecture.

Layer Name	#Filters #Neurons	Filter Size/Stride/Pad	Input Shape	Learnable Parameters
Input Layer	-	-	2 × 480	-
CONV Block 1	64	1 × 5/1/0	2 × 480	384
CONV Block 2	32	1 × 5/1/0	2 × 476 × 64	10,272
Max Pooling 1	-	1 × 3/1/0	2 × 472 × 32	-
CONV Block 3	32	1 × 3/1/0	2 × 157 × 32	3104
Max Pooling 2	-	1 × 3/1/0	2 × 155 × 32	-
CONV Block 4	16	1 × 3/1/0	2 × 51 × 32	1552
Max Pooling 3		1 × 3/1/0	2 × 49 × 32	-
FC Block 1	100	-	512	51,300
FC Block 2	35	-	100	3535
Dropout (0.3)	-	-	-	-
FC	109	-	35	3924
SoftMax	-	-	-	-
Total Parameters				74,071

3.6. Datasets and Data Augmentation

To develop the system, we used the benchmark dataset [19] used in state-of-the-art methods of person recognition based on EEG signals. The data were hosted and maintained by PhysioNet [27] and developed by Schalk et al. [28]. The data were recorded from 109 subjects following the international 10–10 montage system. The proposed system used the recordings in the dataset, which corresponded to Eyes Opened (EO) and Eyes Closed (EC) in the rest state. Each recording comprised 60 s of raw EEG signals sampled at 160 Hz and captured from 64 channels.

The dataset has been leveraged in several of the state-of-the-art studies reviewed in Section 2. This dataset is large, with a number of subjects greater than 100. The large number of channels recorded provides flexibility in evaluating different channel combinations to find the most suitable ones for recognition tasks. The dataset contains 14 recording sessions, with two of these sessions applying the EO and EC resting-state protocols.

We use an EEG signal of a fixed temporal length (e.g., 3 s) as an input instance of the CNN model. The duration of the EEG signal recorded from each subject is 60 s. Therefore, the total number of training and testing instances from each subject without overlapping is 20 = (160 × 60)/(160 × 3) for only EO or EC and 40 for both. The total number of instances from all subjects is 40 × 109 = 4360 for training and testing. However, the model has 74,071 learnable parameters, which are almost 17 times larger than the data size. This number is insufficient for the training and evaluation of a deep CNN model. For this reason, a data augmentation step is applied before training. Data augmentation was first proposed by Fraschini et al. in [29], in which they used a stride of 20 samples. In the current study, we propose using a smaller stride of five samples and merging the EO and EC for training and testing.

To develop a robust model, we used 10-fold cross-validation. The partition of the signal for every fold ensures that there is no overlap between training, validation, and testing. The following data training schema is used for fine-tuning the model hyperparameters and comparing the different input arrangements. Finally, the feature fusion step is used for testing the model, where data augmentation is no longer needed.

3.6.1. Data Training Schema

An EEG signal from each subject with a duration of 60 s (9600 samples) is divided into three parts: 36 s for training, 12 s for validation, and 12 s for testing. The training records of 36 s are generated from the first 5760 samples. A sliding window of 3 s with a stride of 5 samples (0.03125 s) is applied over the signal to create the training instances. For validation and testing, the stride of the sliding window is 1 s (i.e., 160 samples), as illustrated in Figure 6. The partition of the signal assures that there is no overlap between training, validation, and testing. This step is executed in the EO and EC protocols. In this case, the number of training instances is 230,426 and that of validation and testing instances is 2180 each.

Figure 6. Data Augmentation Schema 1.

3.6.2. Feature Fusion Schema

This schema is used in conjunction with the feature–fusion step. In this case, for testing, a window of 5 s is used to extract test instances from the test region of the signal, ensuring no overlapping. This produces two records from the EO protocol and another two from the EC protocol. Finally, the 5 s testing records are divided into segments (Seg) of 3 s, where Seg ∈ [3, 4, 5] with overlapping, as shown in Table 4. The features are extracted from each segment with the CNN model and fused, as shown in Equation (1).

Table 4. Distance Fusion Segments.

# of Seg	Seg-1	Seg-2	Seg-3	Seg-4	Seg-5
3	0 s–3 s	1 s–4 s	2 s–5 s
4	0 s–3 s	0.75 s–3.75 s	1.25 s–4.25 s	2 s–5 s
5	0 s–3 s	0.5 s–3.5 s	1 s–4 s	1.5 s–4.5 s	2 s = 5 s

3.7. Training CNN Model

The model is trained with the Adadelta optimizer using its default parameters [30]. The training dataset is normalized and shuffled, and a batch of 64 samples is randomly selected for each iteration. The training is stopped when the validation accuracy no longer improves over 10 epochs or when it begins to decrease. Figure 7 illustrates one of the model training sessions. The model training progressed correctly, with validation and training accuracy being close. The model reached its highest validation accuracy at 20 ± 5 epochs; each epoch took from 70 to 120 s depending on the allocated resource from Google each time (please see Section 3.8).

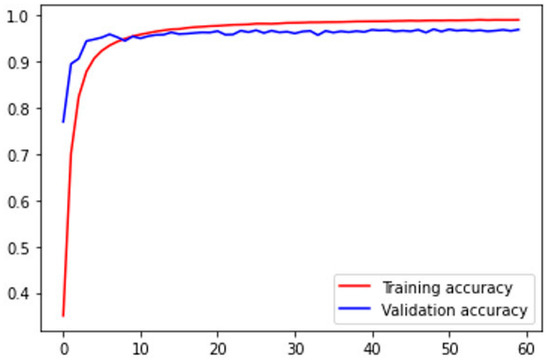
Figure 7. Model Training.

3.8. Implementation

The main programming language used for development is python 3. The CNN model was trained using the high-level API Keras 2.2.5 and Tensor-Flow 1.15.0 as a backend. TensorFlow is a distributed machine learning system made available by Google. The experiments were conducted in Google’s Colaboratory service enabling the use of Google’s GPU hardware. All results analyses were performed in Matlab.

4. Results and Analysis

This section describes the procedure used to evaluate the proposed method and explores the effects of using individual EEG channels on recognition performance. We then show how the pyramidal model architecture affects model size. The system’s performance in identification and authentication tasks is presented with a comparison and discussion of related works. Finally, a correlation analysis of the EEG frequency bands is presented.

4.1. Evaluation Procedure

An EEG-based recognition system depends on the signal length and the number of EEG channels used as inputs. A number of experiments were performed to identify the best and minimal number of EEG channels for input into the CNN model. For each input or parameter selection, the model was trained and tested five times using the data training schema (Section 3.4). Of these five independent trials, the best results in terms of accuracy were reported for comparison. The model training was stopped when validation accuracy began to decrease or when no improvement was observed. The weights of the model demonstrated to have the highest validation accuracy were then retrieved. The final identification and authentication systems were evaluated using 10-fold cross-validation, and the average performance was reported.

The results of the system are reported using commonly used metrics. For authentication, the results are reported using the false acceptance rate (FAR), false reject rate, equal error rate (EER), receiver operating characteristic (ROC) curve, and detection error tradeoff (DET). The identification system results are reported using accuracy and cumulative matching characteristic (CMC). One-tailed Wilcoxon tests at significance levels of 0.05 and 0.01 were conducted on the results of Section 4.6 and Section 4.7 to determine whether the difference between the median of the two groups was statistically significant [31].

4.2. The Effect of Individual Channels and Acquisition Protocols

To examine the effect of individual channels, experiments were conducted using the proposed CNN model. In this case, the input consists of single-channel signals comprising 480 samples, and the activation function was SeLU. All 64 channels were individually tested based on data from resting-state protocols: EO, EC, and EO+EC. These experiments served two purposes: to determine which channels had the greatest discriminative potential to reveal an individual’s identity and to determine whether the merging of these protocols during training improved the model performance. Simultaneously, this experiment revealed which brain region held the most discriminative features for person identification.

The ranking of the channels is illustrated in Figure 8 for the EO+EC results. The green color indicates the best channels for recognition and is found to be concentrated in the temporal, parietal, and occipital regions. Figure 8 also shows the relationship between the brain areas and how they relate to identifying people using EEG signals.

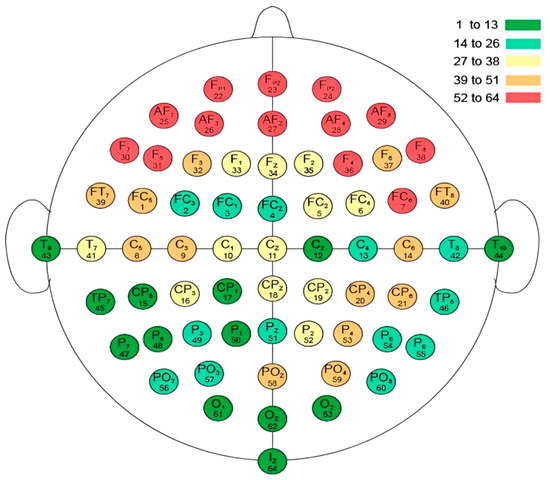
Figure 8. The Relationship between Brain Regions and Person Identification.

Table 5 identifies channel 64 as the best channel for identification in all three cases, which is consistent with the findings of Suppiah and Vinod in [13]. The electrode of channel 64 is placed on the inion bump, which is known as the internal occipital protuberance. These experiments also reveal that merging the protocols outperforms separate protocols.

Table 5. Top 10 Channel Ranking for (a) eyes opened (EO), (b) eyes closed (EC), (c) eyes opened and closed (EO+EC).

	(a) EO		(b) EC		(c) EO+EC
Rank	Channel #	Acc (%)	Channel #	Acc (%)	Channel #	Acc (%)
1	64	88.87	64	87.27	64	92.48
2	62	82.68	45	81.08	45	86.29
3	47	82.45	42	81.08	61	86.25
4	56	82.22	47	79.82	62	84.91
5	61	82.22	61	79.59	47	84.51
6	42	81.99	43	79.36	43	84.23
7	10	81.53	62	78.78	63	83.25
8	43	81.3	56	76.61	44	83.19
9	45	81.19	44	76.38	12	83.02
10	52	81.07	63	75.69	48	82.97

4.3. Model Selection

This section describes the experiments performed to fine-tune the model to identify the best optimizer, activation function, and loss function. These tests were performed using 3 s long signals from the top two ranking channels. Table 6 presents the results from the highest to the lowest accuracy. The selection starts from the activation function, which is followed by the loss function and ends with the selection of the highest-performing optimizer.

Table 6. Model Selection.

(a) Activation Function		(b) Loss Function		(c) Optimizer
Function	Acc (%)	Function	Acc (%)	Optimizer	Acc (%)
SeLU [32]	97.88	Cross-entropy	97.88	Adadelta [30]	98.25
Prelu [33]	97.52	Hinge	97.53	RMSProp [34]	97.88
LeakyReLU (0.1) [35]	96.88	Kullback Leibler Divergence	97.53	Adam [36]	97.61
ReLU [37]	96.83			Nadam [38]	97.56
ELU [39]	96.51			Adamax [40]	97.29
Thresholded ReLU (0.1) [41]	95.96			SGD [42]	96.97
				Adagrad [43]	96.83

4.4. Number of Channels and Segment Length

The next investigation of model performance varied the segment length and number of channels. Each increase in the number of channels resulted in an increase in the number of learnable parameters, as illustrated in Figure 9. The channels were selected based on experiments reported in Section 4.2 and Table 5c; then, we varied the length of the segment for the best two channels obtained. The major improvement in accuracy by 5% was noticed using two channels and a 3 s segment length compared to using a 1 s segment length. It is clear that the model utilizing two channels as input shows a major improvement in the resulting accuracy; please see the results in Table 7. Each column shows an approximately 1% improvement compared to the model with a fewer number of channels. The model clearly produces high recognition results, regardless of the signal length. Even with a signal length of 1 s, the model achieves a recognition rate of 98.31% and more for the models with 8, 9, and 10 channels.

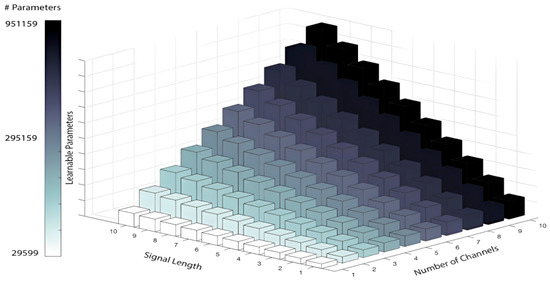
Figure 9. Number of Learnable Parameters in Terms of Signal Length and Number of Channels.

Table 7. Segment Length and Number of Channels.

	Number of Channels
		1	2	3	4	5	6	7	8	9	10
Segment Length	1 s	78.24	92.2	93.99	95.6	96.06	97.28	97.24	98.31	98.77	98.62
	2 s	89.99	96.49	97.53	98.24	98.08	98.79	98.54	99.41	99.2	99.58
	3 s	92.24	97.98	98.62	98.57	99.08	99.22	99.17	99.35	99.44	99.77
	4 s	93.78	98.75	98.72	99.33	99.33	99.54	99.49	99.49	99.59	99.38
	5 s	95.01	98.68	98.5	99.08	99.25	99.65	99.42	99.48	99.71	99.77
	6 s	95.28	98.88	99.08	99.34	99.08	99.73	99.73	99.08	99.54	99.54
	7 s	96.33	98.54	98.54	98.92	99.08	99.61	99.77	99.31	99.23	99.38
	8 s	95.5	98.25	98.8	98.62	98.99	99.44	99.35	99.62	99.44	99.44
	9 s	95.64	99.08	99.08	98.5	98.62	99.65	99.19	99.54	98.08	99.54
	10 s	95.87	98.16	98.13	98.74	98.01	99.38	99.69	99.08	99.23	99.08

4.5. The Effect of Pyramid Architecture on Model Size

A well-trained deep CNN model can generalize to unknown data if the number of learnable parameters is small, effectively preventing model memorization of the training data (i.e., overfitting). The number of learnable parameters can be controlled in a number of ways. One way is to design a network such that the initial CONV blocks contain the largest number of filters, and the terminal CONV blocks contain the fewest number of filters. Table 8 shows the differences between the proposed model and its reverse; the differences are bolded. The reversed model increases the number of learnable parameters starting at CONV block 4, resulting in a model size three times that of the proposed model. To compare the performance of the two models, we used schema-2 with 10-fold cross-validation. A Wilcoxon test with (p < 0.01) indicated that there was no statistical difference between the proposed (M1) and its reverse.

Table 8. Different Model Architectures, where: F: filters, #N: number of neurons, No: not in the model.

		M1 (Proposed)		Reverse of M1		M2		M3
Layer Name	F/Stride/Pad	#F #N	Parameters	#F #N	Parameters	#F #N	Parameters	#F #N	Parameters
Input Layer	-	-	-	-	-	-	-	-	-
CONV Block 1	1 × 5/1/0	64	384	16	96	64	384	64	384
CONV Block 2	1 × 5/1/0	32	10,272	32	2592	32	10,272	32	10,272
Max Pooling 1	1 × 3/1/0	-	-	-	-	-	-	-	-
CONV Block 3	1 × 3/1/0	32	3104	32	3104	16	1552	32	3104
Max Pooling 2	1 × 3/1/0	-	-	-	-	-	-	-	-
CONV Block 4	1 × 3/1/0	16	1552	64	6208	No		16	1552
Max Pooling 3	1 × 3/1/0	-	-	-	-	No		-	-
CONV Block 5	1 × 3/1/0	No		No		No		16	784
FC Block 1	-	100
FC Block 2	-	35
Dropout (0.3)	-	-	-		-		-		-
FC	-	109	3204	109	3924	109	11,009	109	3924
SoftMax	-	-	-	-	-	-	-	-	-
Total Parameters			74,071		224,359		186,517		74,935
Acc %			97.77 ± 0.82		97.64 ± 1.00		96.5 ± 1.15		97.24 ± 0.91

The different model architectures are shown in Table 8. M1 represents the proposed model. The architecture is based on the use of four CONV blocks. To investigate the number of CONV blocks, M2 with three CONV blocks and M3 with five CONV blocks were tested. Both M2 and M3 have only one FC block with a different number of neurons. A Wilcoxon test with p < 0.05 shows that M1 outperforms M2 at a 5% significant level. This indicates that a model with a minimal number of parameters is preferred over a model with a large number of parameters. Another test with p < 0.01 shows no statistical difference between M1 and M3. However, M1 is preferred because of its simpler architecture and slightly smaller number of learnable parameters. For these reasons, M1 was chosen as the final model.

4.6. Identification System Results

The CNN model is trained with segment lengths of 3 s using schema 2 and then evaluated using schema 3. While the training pattern length used is 3 s, the test record is 5 s long. Again, the two highest-ranking channels, 64 and 45, are used as input. The feature vectors are extracted from the output of the final softmax layer, and the extracted feature vectors are fused, as detailed in Equation (1). To measure the similarity between the two vectors, the matching algorithm uses the L1 metric. Table 9 shows the results of the 10-fold cross-validation with and without feature-level fusion. For fusion, we used three methods and found that the max was better than the other methods. In every fold, the training datasets and test datasets were different. Despite this difference, the results for all folds were consistent, indicating the proposed method’s generalization. Figure 10 shows the CMC curve of the top 10 ranks using the feature-level fusion of the best combination of 5 s–4 seg.

Table 9. Identification System Results (Rank 1).

Fold Number	3 s (%)	5 s–3 Seg (%)			5 s–4 Seg (%)			5 s–5 Seg (%)
		Min	Avg	Max	Min	Avg	Max	Min	Avg	Max
Fold 1	97.02	98.17	98.85	98.39	98.62	98.39	98.85	98.17	98.39	98.17
Fold 2	97.49	99.08	99.08	99.08	98.17	98.62	98.85	98.62	98.62	98.85
Fold 3	97.49	99.08	98.39	98.62	99.31	99.31	98.31	99.08	98.85	98.62
Fold 4	98.39	99.54	99.31	99.77	99.31	98.85	99.54	99.54	99.31	99.54
Fold 5	98.62	99.54	99.31	99.54	99.77	99.77	99.77	99.77	99.54	99.77
Fold 6	98.62	99.31	98.31	99.54	99.31	99.08	99.54	99.31	99.31	99.31
Fold 7	97.82	99.54	98.62	99.54	99.77	98.85	99.54	99.08	98.62	99.54
Fold 8	98.05	99.31	98.39	99.31	99.31	99.08	99.08	99.08	98.62	99.08
Fold 9	97.94	99.31	98.85	99.08	99.08	99.08	99.31	99.54	99.31	99.54
Fold 10	98.28	99.77	99.08	99.54	99.54	99.54	99.54	99.54	99.31	99.54
Avg ± std	98.06 ± 0.47	99.26 ± 0.44	98.91 ± 0.36	99.24 ± 0.44	99.21 ± 0.49	99.05 ± 0.41	99.33 ± 0.31	99.17 ± 0.48	98.99 ± 0.41	99.19 ± 0.5

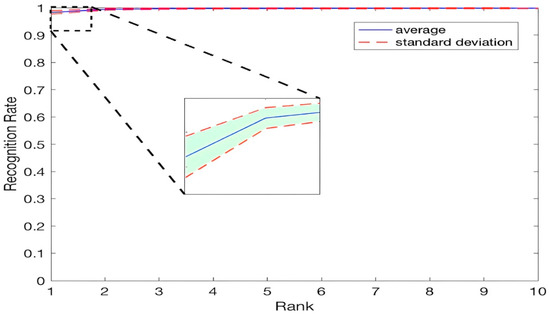
Figure 10. CMC Curve for the Top 10 Rank.

The Wilcoxon test shows a 5% statistically significant difference between using 5 s with feature fusion and 3 s without feature fusion. The 5 s–4 seg combination shows the best results, but there is no significant difference between it and the 5 s–3 seg or the 5 s–5 seg combination. Moreover, there is no significant difference between the feature fusion methods in the identification system results.

4.7. Authentication System Results

The authentication system uses schemes and feature-level fusion in the same way as the identification system. The main difference is that instead of identifying the subject, the ID of the subject is fed with the input, and the system compares the input ID to the stored subject ID. The authentication system then returns a response of either acceptance or rejection. Table 10 presents the results of the 10-fold cross-validation with and without feature-level fusion. Table 11 shows the detailed results of the authentication system. The case of 5 s–3 seg using AVG in feature fusion has the lowest EER of 0.187%. Figure 11 illustrates the ROC curve, and Figure 12 shows the DET curve using the 5 s–3 seg results. The ROC and DET curves are generated from 436 genuine (intra-class) pairs and 47,088 impostor (inter-class) pairs.

Table 10. Authentication System Results (EER).

Fold Number	3 s (%)	5 s–3 Seg (%)			5 s–4 Seg (%)			5 s–5 Seg (%)
		Min	Avg	Max	Min	Avg	Max	Min	Avg	Max
Fold 1	1.00	0.93	0.46	0.72	0.80	0.46	0.70	1.15	0.46	0.70
Fold 2	0.56	0.70	0.23	0.44	0.81	0.23	0.69	0.92	0.23	0.82
Fold 3	0.35	0.69	0.21	0.19	0.46	0.23	0.45	0.69	0.23	0.20
Fold 4	0.24	0.46	0.23	0.46	0.46	0.23	0.45	0.23	0.23	0.46
Fold 5	0.23	0.23	0.23	0.23	0.23	0.23	0.23	0.23	0.23	0.23
Fold 6	0.44	0.46	0.23	0.23	0.46	0.23	0.45	0.46	0.23	0.23
Fold 7	0.54	0.69	0.02	0.23	0.58	0.03	0.25	0.69	0.02	0.47
Fold 8	0.32	0.46	0.03	0.03	0.92	0.23	0.04	0.70	0.23	0.03
Fold 9	0.34	0.69	0.23	0.23	0.46	0.23	0.46	0.46	0.23	0.64
Fold 10	0.24	0.12	0.00	0.02	0.46	0.01	0.23	0.23	0.01	0.23
Avg ± std	0.42 ± 0.23	0.54 ± 0.24	0.187 ± 0.16	0.27 ± 0.21	0.57 ± 0.22	0.21 ± 0.12	0.39 ± 0.20	0.57 ± 0.31	0.21 ± 0.12	0.40 ± 0.25

Table 11. Authentication System 5 s–3 seg Results.

Metrics	Avg ± Std
EER	0.187% ± 0.16%
Minimum Half Total EER	0.12% ± 0.1%
Authentication Rate at 1% FAR	99.93% ± 0.15%
Authentication Rate at 0.1% FAR	99.77% ± 0.22%
Authentication Rate at 0.01%	99.11% ± 0.51%

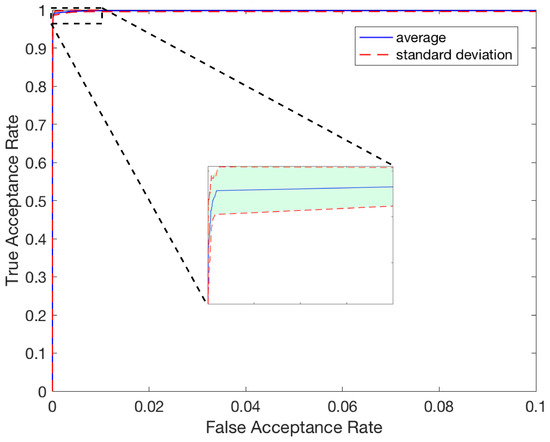
Figure 11. ROC Curve.

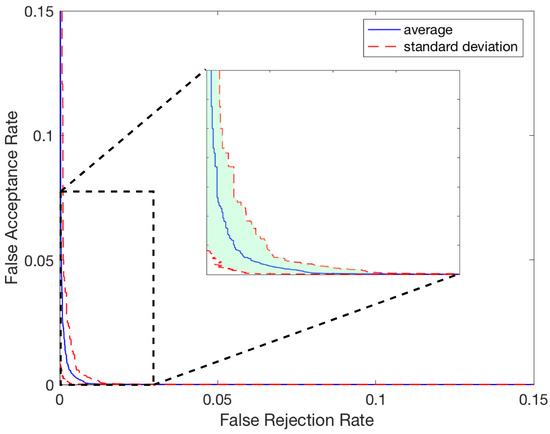
Figure 12. DET Curve.

The authentication system’s mean results using 5 s is 0.19% EER, while the 3 s mean is 0.43%. The Wilcoxon test with p < 0.05 indicates a statistically significant difference between the 5 s and 3 s group median. Moreover, the proposed method achieves a minimal EER of 0.0012. The authentication rate shows an impressive performance of 99% and higher for different thresholds of 1%, 0.1%, and 0.01%.

5. Discussion

5.1. Model Size and Signal Length

The proposed method generates excellent results while leveraging only two EEG channels and a short signal length of 5 s. The proposed model has 74,071 learnable parameters, which is considerably smaller than those in the work of Sun et al. [11] with 505,281,566 parameters and Schons et al. [21] with 78,857,325 learnable parameters. This is mainly due to the pyramidal nature of the model. The statistics are provided in Table 12. All the studies listed in Table 12 for comparison used the motor/imagery dataset.

Table 12. Learnable Parameters and Data Size.

	Learnable Parameters	Number of Training Instances
Schons et al., 2018 [21]	78,857,325	42,696
Sun et al., 2019 [11]	505,281,566	177,040
Wang et al., 2019 [12]	N/A	33,795
Current Work	74,071	230,426

Keeping the model size small in relation to the number of training instances is the key to making the model learn discriminative patterns and not memorize the data. By doing so, the model can easily be generalized to unseen data.

Wang et al., 2019 [12] used a solution based on deep learning that achieved high recognition results. However, the study only mentioned the summarized configuration of its GCNN model, and the number of learnable parameters was unclear. In their study, a connectivity graph is constructed from an EEG signal, which requires 64 channels for recognition. Using a large number of electrodes is not practical for recognition, and it involves complex pre-processing to build the connectivity graph. In comparison, our method uses only two channels and is appropriate for practical deployment. Moreover, it does not require any complex pre-processing and directly takes EEG signals as input.

5.2. Comparison to Related Work

The proposed CNN architecture processes the EEG signal using 1D convolutions until it reaches the fully connected layer. Sun et al. [11] used a similar processing method in their CONV blocks and incorporated an LSTM at the end of their model. The use of an LSTM slowed down their model compared to the proposed model, which depends only on CONV blocks and incorporates two-terminal FC layers.

In Section 4.2, this study recommends merging the EO and EC protocols to further improve the model learning capabilities, which supports [11,12], in which the merged states led to improvements in model training. Comparing our system to state-of-the-art studies, our approach has several distinct advantages. (i) It has a fixed channel position. (ii) It requires only two channels, whereas [12] used 64 and [11] used 16 channels. (iii) Only a short signal length of 5 s is required. As shown in Table 13, most of the studies used more than 5 s. (iv) The system can be used for both identification and authentication while providing high-level security. The former qualities make the method easy to incorporate in real-life scenarios.

Table 13. Comparison to Related Studies.

	Method	Channels	Length	Acc (%)	EER (%)
Rocca et al., 2014 [14]	PSD, COH, L1	15	10 s	100	-
Schons et al., 2018 [21]	EEG [30:50], CNN	64	12 s	-	0.19
Suppiah et al., 2018 [13]	PSD, FLDA	1	12 s	97	-
Sun et al., 2019 [11]	Raw EEG, CNN, LSTM	16	1 s	99.58	0.41
Sun et al., 2019 [11]	Raw EEG, CNN, LSTM	4	1 s	94.28	0.56
Wang et al., 2019 [12]	PLV, GCNN	64	5.5 s	99.98	-
Wang et al., 2020 [16]	RHO, Mahalanobis distance	64	1 s	98.83	-
Behrouzi and Hatzinakos 2022 [17]	GVAE, SVM	64	1 s	99.78	-
Bidgoly et al., 2022 [18]	Raw EEG, CNN, Cosine	3	1 s	98.04	1.96
Current Study	Raw EEG, CNN, L1	2	5 s	99.05	0.187

Table 13 compares the results of the proposed method to those of state-of-the-art studies. All the listed studies used the PhysioNet dataset. Rocca et al. [14] based their system on the functional connectivity of EEG brain signals. Their work was the foundation of many subsequent studies, including Wang et al. [12], which calculates within-frequency and cross-frequency functional connectivity estimates. Behrouzi and Hatzinakos [17] used a graph variational auto-encoder (GVAE) for extracting features and SVM for identification. Although these methods achieved high recognition results, they required a large number of channels of 15, 64, and 64, respectively. The same problem was encountered in [10,21].

Suppiah and Vinod [13] used a single channel, but their study design required the removal of a considerable number of samples. Their relaxation criterion condition considered the first 30 s of a recording to be of insufficient quality for identification. Furthermore, they required a long signal of 12 s. In [11], Sun et al. proposed a model that combined 1D CONV methods with an LSTM. They used a short signal length of 1 s and 16 channels as input. Unfortunately, their method could not sustain a sufficiently high result when they reduced the input to four channels. A 10-fold cross-validation evaluation procedure was used. Conversely, the proposed method was demonstrated to be robust and effective for real-life security systems, given its achievement of low EER and high rank-1 accuracy.

5.3. Correlation between CNN Features and EEG Frequency Bands

A challenge in training a deep CNN model using EEG data rather than images is the difficulty of interpreting EEG patterns that the network has learned.

The proposed model uses raw EEG data for training and classification. Therefore, to understand what triggers feature activation, the features from the second FC block (35 neurons) are extracted and correlated with the power spectral density (PSD) of each frequency band. By calculating the correlation between the features and the EEG frequency band, we can infer which frequency band is responsible for the features. This correlation technique was first suggested and used by [44] to explore how CNN learns features from spectral amplitude. Amin et al. further showed the method’s efficiency in [45], revealing the relationship between the frequency band and the CNN output. In the current study, their technique is used to show the important frequency band for EEG-based person recognition and further verify that the model is learning correctly.

Prior to the correlation step, the EEG signal is passed to the Welch periodogram algorithm for calculating the PSD of the delta (0.5–3 Hz), theta (3–8 Hz), alpha (8–13 Hz), beta (13–30 Hz), gamma (30–50 Hz), and high gamma (50 Hz and above) frequency bands. The frequency bands’ PSDs were then correlated with the extracted features. The two-channel correlation results used as input are illustrated in Figure 13. The blue color indicates the negative coefficients, and the red color denotes the positive coefficients. The correlation between the learned features and the EEG sub-bands demonstrates that the proposed model focuses its learning on the EEG signals from the higher frequency bands: beta, gamma, and high gamma. The correlation increases with each of the higher frequency bands.

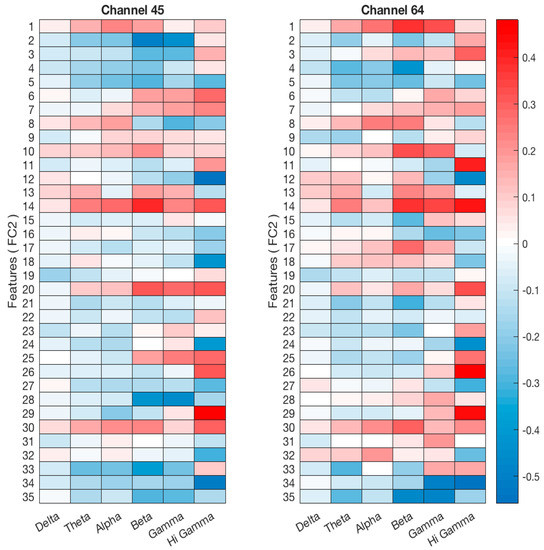
Figure 13. Correlation Coefficients between the EEG Sub-bands and CNN Features. The x-axis represents the frequency bands (Delta, Theta, Alpha, Beta, and Gamma), and the y-axis represents the features extracted from the fully connected layer (FC2).

Wang et al. [12] used EEG in the gamma and beta sub-bands as a model input and reported them as two important sub-bands for EEG-based people identification. Schons et al. [21] found that the gamma band plays an important role in recognition. The proposed model has the advantage of learning information from raw EEG without using hand-engineered methods. This gives our model the distinct advantage of learning all useful patterns in the higher-frequency bands without neglecting relevant information in the lower sub-bands.

6. Conclusions and Future Work

This study addresses the challenges in EEG-based person recognition. By developing a lightweight and robust system based on a deep CNN model, the proposed solution consumes raw EEG as input and leverages the CNN’s ability to automatically extract discriminative features that are useful to determine an individual’s identity. A series of experiments was conducted to select the minimal input vector size to create the lightweight model. Each EEG channel was individually tested to determine the best set for identifying individuals. These experiments revealed that the highest-ranking channel electrode was placed on the inion bump. We described the specifications of the recognition system for both identification and authentication tasks. Each task comprised a lightweight CNN model that required only a small number of learnable parameters, whose performance was further enhanced using feature fusion. The system required only a small input vector from two channels and a recording length of 5 s. As a result, the system was compact, easy to store, and could generalize well to unknown data. As shown in Section 5.2, the system outperformed the existing methods introduced in the literature review.

The system is valuable for high-level security systems and can be used by different government and private agencies. Future studies may consider evaluating the model using a dataset comprising multiple recording sessions and human states while performing different tasks, such as attention-based or imaginary-based tasks. Eventually, the system could be extended to perform continuous authentication, strengthening the security level inside the facilities.