Abstract
The unknown friction factor from the implicit Colebrook equation cannot be expressed explicitly in an analytical way, and therefore to simplify the calculation, many explicit approximations can be used instead. The accuracy of such approximations should be evaluated only throughout the domain of interest in engineering practice where the number of test points can be chosen in many different ways, using uniform, quasi-uniform, random, and quasi-random patterns. To avoid picking points with undetected errors, a sufficient minimal number of such points should be chosen, and they should be distributed using proper patterns. A properly chosen pattern can minimize the required number of testing points that are sufficient to detect maximums of the error. The ability of the Sobol quasi-random vs. random distribution of testing points to capture the maximal relative error using a sufficiently small number of samples is evaluated. Sobol testing points that are quasi-randomly distributed can cover the domain of interest more evenly, avoiding large gaps. Sobol sequences are quasi-random and are always the same, which allows the exact repetition of scientific results.
1. Introduction
The Colebrook equation, formally established in 1939 for calculating the flow friction through pipes, is empirical but widely accepted in engineering practice as an informal standard [1]. It is based on an experiment from 1937 performed by Colebrook and White, who tested flow through a set of pipes with their inner surfaces ranging from smooth to very rough [2]. The equation was later developed solely by Colebrook [1]; Equation (1). Its graphical interpretation is given by Rose [3] and was later reevaluated by Moody [4]. Two non-dimensional parameters are used as input, the Reynolds number Re [5] and the roughness of the inner pipe surface ε [6]. An unfortunate circumstance is that the Colebrook equation is expressed in an implicitly given logarithmic form with respect to the unknown Darcy’s flow friction factor f, which cannot be extracted analytically.
where:
f—turbulent Darcy’s flow friction factor (dimensionless)–index 0 refers to the accurate solution obtained iteratively after a sufficient number of iterations.
Re—Reynolds number (dimensionless); Re = u·D/ν where u is flow velocity (in m/sec), ν is the kinematic viscosity of fluid (in m2/sec), and D is inner diameter of pipe (in m).
ε—relative roughness of inner pipe surface (dimensionless); ε =ε*/D where ε* is the height of the protrusion in the inner surface of the pipe wall above the viscose fluid layer (in m), and D is the inner diameter of pipe (in m) where ε* << D (ε* typically goes from 0.0015 mm for PVC pipes through to about 3.0 mm for rough concrete pipes [7]).
ln—natural logarithm.
The Colebrook equation is used in engineering practice for the Reynolds number Re between 4000 and 108, and for the relative roughness of an inner pipe surface ε between 0 and 0.05, i.e., for a turbulent condition of flow.
The Colebrook equation in its implicitly given native form can be solved only iteratively [8,9,10,11]. Therefore, to simplify the everyday life of engineers, various very accurate explicit approximations have been developed over time [12,13,14,15,16]. The distribution of the relative error δ% over the domain of applicability of the Colebrook equation is uneven and is different for every new approximation [17,18]. This error should be evaluated in a sufficient number of points dispersed over the domain of applicability in engineering practice, and the points should be uniformly, randomly or quasi-randomly distributed. This communication shows how to use Sobol’s quasi-random distribution for such purposes. The Colebrook equation is widely used in many scientific disciplines where fluid flow occurs [19,20,21,22], and hence evaluation of the error and its distribution is essential for the ability to check and repeat scientific findings.
2. Estimation of Error; Testing Patterns and Quantity of Points
This section describes the calculation of the relative error δ% of the chosen approximation of the Colebrook equation and evaluates different quantities of testing points and related patterns, i.e., their distribution over the domain of its applicability in engineering practice.
2.1. Relative Error
The relative error δ% of any explicit approximation should be calculated in reference to the solution of the original implicitly given Colebrook equation. Its native implicitly given form is usually solved in an iterative process after sufficient iterations f0 [8,9,10,11] (as the Colebrook equation is empirical, its accuracy can be disputed, but for this study, it is treated as accurate [23,24,25]). The relative error δ% is calculated as , where f is obtained using the chosen explicit approximation (the testing approximation in this communication is given in Equation (2)). The goal is to find a worst case, which is represented by the maximum relative error, i.e., to find a combination of input parameters for the largest approximation error. For this reason, a sufficiently large number of sample points from the domain of the Colebrook equation has to be chosen and those points are chosen using Sobol’s sampling, a type of quasi-random sampling which is capable of detecting picks of the relative error more efficiently than the classical Monte Carlo sampling, as fewer evaluation points of quasi-Monte Carlo points are required. Consequently, quasi-Monte Carlo sampling overperforms the classical Monte Carlo sampling [26].
The results do not depend only on the number of testing points, but also on their distribution.
2.2. Chosen Approximation for Tests
Explicit approximations of the Colebrook equation should be both accurate and simple for computation (a smaller number of floating-point operations requiring execution in a computer’s processor increases the computational efficiency) [27,28,29,30,31,32]. In general, an approximation with a smaller number of logarithmic and exponential functions is more efficient (each non-integer power and exponential function should be calculated approximately as two logarithmic functions [27]).
For the tests performed in this communication, an approximation given by Praks and Brkić [31] is used; Equation (2). It was chosen from a selection of the simplest and most accurate approximations, which included the approximations of Vatankhah [33], Lamri [34], Lamri and Easa [35], etc.
The parameters in Equation (2) are numerically optimized to minimize the maximal relative error δ% [36]. Such variation of the numerical values of parameters does not only change the value of the maximal relative error δ%, but also changes the distribution of the error over the domain of applicability of the Colebrook equation in engineering practice [17,18]. Therefore, the results depend on both the number of testing points and on their distribution.
The maximal relative error δ% of Equation (2) is estimated by Praks and Brkić [31] to be around 0.0012% using up to 2 to 8 million Sobol’s quasi-random testing points. Using the same methodology for estimation of the maximal relative error δ% as in Brkić [14], with 740 quasi-uniform testing points, it is estimated to be up to 0.00120421% (it was additionally tested using 740 points and confirmed up to 0.001204% by Brkić and Stajić [15], who used VBA coding for MS Excel).
2.3. Distribution of Testing Points
The domain of applicability in engineering practice of the Colebrook equation should be tested using a sufficient number of points. Otherwise, the highest value of the relative error δ% can be overlooked, because it can be located among the chosen testing points. Therefore, the testing points should sufficiently cover the domain of applicability of the Colebrook equation using an appropriate pattern to avoid such undetected picks of error which can occur among the testing points.
Some authors recommend a few million testing points while others suggest even less than a thousand, chosen using various patterns such as uniform, quasi-uniform, random, and quasi-random. For such purposes, Yıldırım [13] uses 10 thousand uniformly distributed points, Brkić [14] uses 740 quasi-uniformly distributed points, Shaik et al. [25] one million, while Praks and Brkić [30,31] use even 2 to 8 million quasi-Monte Carlo points.
In this communication, results obtained using a random pattern of points for testing are compared with the Sobol quasi-random points [37,38,39,40,41], always using an equal number of testing points.
In further text, the methodology on how to use Sobol’s quasi-random sequence for testing of the approximations of the Colebrook equation is shown. It is compared with quasi-random testing points generated in MS Excel [14,15].
Other approaches for random [42,43] and quasi-random sequence testing are available [44].
2.3.1. Sobol’s Quasi-Random Testing Points
This communication does not describe how the algorithm for generating Sobol sequences works [37,38,39,40,41]. It is focused on how to use it to test the explicit approximations of the Colebrook equation. Compared with random sampling, Sobol numbers offer a lower discrepancy (they fill the space of possibilities more evenly), and because of that ability, they have been chosen for testing.
The Sobol quasi-Monte Carlo sampling is a complex procedure, which requires a specialized software tool. For Sobol quasi-Monte Carlo sampling in Matlab, the open-source software can be downloaded for free [37], or alternatively, open-source SciPy library of Python can be used for the Sobol sequence [45].
Because, the Colebrook equation has two input parameters, i.e., the Reynolds number Re, and the relative roughness of inner pipe surface ε, two-dimensional Sobol sequences [39] are used in the tests performed here. Using Sobol’s two-dimensional sequence [S1i, S2i], values of the Reynolds number Re between 4000 and 108 can be generated, as well for the relative roughness of inner pipe surface ε between 0 and 0.05. Sobol’s numbers are always between 0 and 1, and the Reynolds number Re can be generated using the first dimension of the Sobol two-dimensional sequence S1i, while the relative roughness of the inner pipe surface ε using the second S2i, as shown in Equation (3):
The Sobol sequence is defined for values between zero and one. On the other hand, the input parameters of the Colebrook equation cover large intervals. For example, Reynolds numbers vary from 4000 to 108, and ε between 0 and 0.05, while to normalize it, Equation (4) is used, where and represent a normalized value, i.e., a value between 0 and 1 (for example a random number or quasi-random number of the Sobol sequence):
Logarithms and the 10x functions were used in the transformation to sufficiently cover the large interval of input parameters of the Colebrook equation (especially for the Reynolds numbers). As the Reynold numbers Re of the Colebrook equation are between 4000 and 108, the procedure for the generation can be expressed as 10^(Renorm*(Remax − Remin) + Remin), where Remin = log10(4000) and Remax = log10(108) = 8. Consequently, the expression for the generation of Reynold numbers Re of the Colebrook equation can be approximated as Re~10.0^(4.3979*Renorm + 3.6021), as 103.6021~4000 represents the minimal Reynold number of the Colebrook equation. Moreover, 4.3979 + 3.6021 = 8, which represents the maximal Reynold number 108, where for Renorm = 0→Re~4000 and for Renorm = 1→Re~108. Similarly, the relative roughness ε of the pipeline between εmin = log10(3.1808 × 10−7) and εmax = log10(0.05) can be generated from εnorm as ε = 10^(εnorm*(εmax − εmin) + εmin) where the expression can be approximated for the Colebrook equation as ε~10.0^(5.1964*xnorm − 6.4975) because for εnorm = 0→ε~0 and for εnorm = 1→ε~0.05.
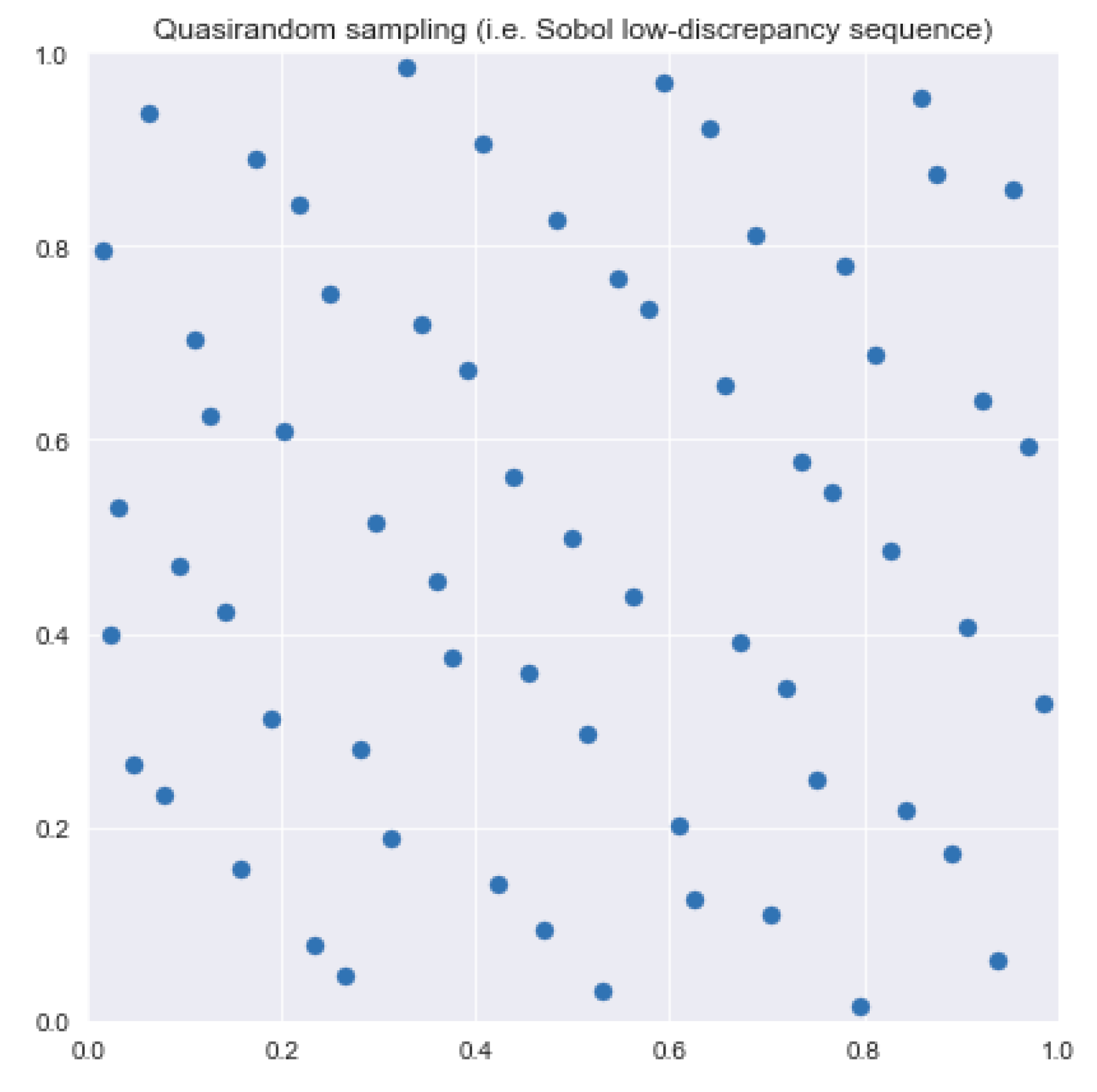
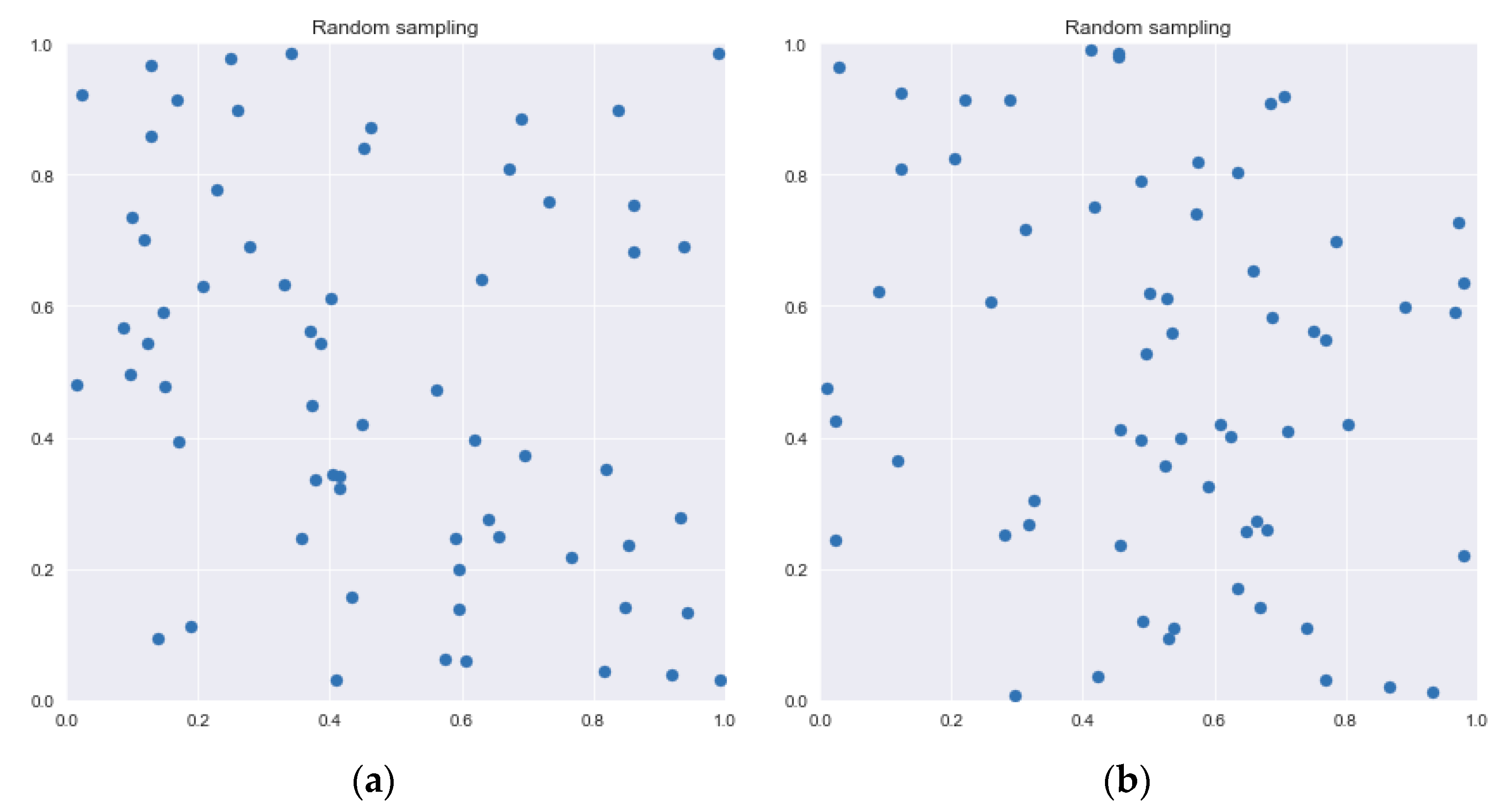
The Sobol sequence is not random, and in our case, the starting pattern is always identical, as in Figure 1 where 64 two-dimension points are shown. By comparing Figure 1 and Figure 2, it can be seen that such sequences more thoroughly cover the domain of the Colebrook equation than random sampling.
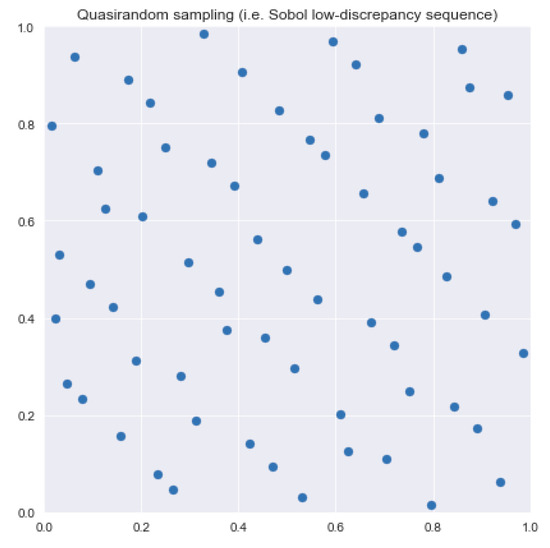
Figure 1.
Sobol’s points for n = 6, 2n = 64.
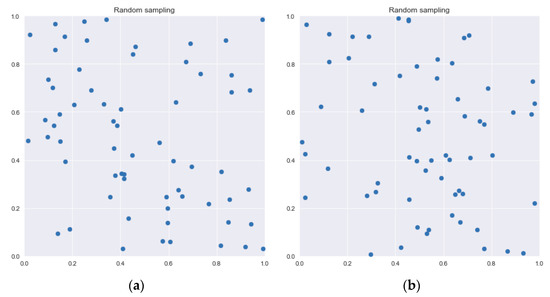
Figure 2.
Random distribution of testing points; (a) the first example, (b) the second example.
Using Sobol’s quasi-random tests, the maximal relative error δ% of Equation (2) for n = 6, for 64 sampling points is 0.00120432%, for 740 sampling points the same results (the maximal error was already detected in the first 64 samples), while for n = 11, 2n = 2048 is up to 0.00120441%.
Compared with the methodology by Brkić [14] with 740 quasi-uniform testing points with the error estimated up to 0.00120421%, Sobol’s quasi-random testing captured an even higher error of 0.00120432%, with only n = 6, 2n = 64 sampling points.
Sobol’s points and solutions of Equations (1) and (2) are shown in Table 1.

Table 1.
Sobol’s points and solutions of Equations (1) and (2).
2.3.2. Random Sampling
Instead of [S1i, S2i], Equation (3) used Excel function “Rand()”. This will always generate different testing patterns as shown in Figure 2.
The maximal relative error δ% in all tests for the approximation from Equation (2) is always evaluated to be around 0.0012% using random sampling.
3. Conclusions
The Colebrook equation depends on two input parameters: the Reynolds number Re and the relative roughness ε of the pipeline. As the input parameters have a large variance of possible values (the Reynolds number Re varies from 4000 to 108 and the inner pipe surface varies from 3.1808 × 10−7 to 0.05), every new approximation of the Colebrook equation should be discovered by the evaluation of a large number of possible combinations of input parameters. For this reason, a method is required, which is able to identify a limited number of pairs suitable for the building of a new approximation. This communication shows that the Sobol quasi-Monte Carlo method requires, for the same accuracy of the Colebrook approximation, a less number of evaluations of the Colebrook equation than the classical Monte-Carlo method.
The findings of this communication for 2048 and even for 64 quasi-random points give comparable results as 740 uniform points of logarithmic scale [14]. Moreover, Sobol’s test points are not random, but quasi-random, and so such an approach is deterministic (which is useful for comparisons of calculations [46,47,48]). Finally, the Sobol quasi-random approach is preferable, as it fills the sampling space more evenly. Thus, the chance to neglect some parts of the examined domain is minimized for the Sobol quasi-random approach.
Author Contributions
Conceptualization, P.P. and D.B.; methodology, P.P. and D.B.; software, P.P.; validation, P.P. and D.B.; formal analysis, D.B.; investigation, P.P.; resources, P.P.; data curation, P.P. and D.B.; writing—original draft preparation, D.B.; writing—review and editing, D.B. and P.P.; visualization, P.P.; supervision, D.B.; project administration, P.P. and D.B.; funding acquisition, P.P. All authors have read and agreed to the published version of the manuscript.
Funding
The work has been supported by the Technology Agency of the Czech Republic through the project CEET—“Center of Energy and Environmental Technologies” TK03020027.
Data Availability Statement
Data and methods used in the research are presented in sufficient detail in this communication so that other researchers can replicate the work.
Acknowledgments
We thank John Cawley from IT4Innovations, who as a native speaker kindly checked the correctness of English expressions throughout the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Colebrook, C.F. Turbulent flow in pipes with particular reference to the transition region between the smooth and rough pipe laws. J. Inst. Civ. Eng. 1939, 11, 133–156. [Google Scholar] [CrossRef]
- Colebrook, C.; White, C. Experiments with fluid friction in roughened pipes. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1937, 161, 367–381. [Google Scholar] [CrossRef]
- Brown, G.O. The history of the Darcy-Weisbach equation for pipe flow resistance. In Proceedings of the Environmental and Water Resources History Sessions at ASCE Civil Engineering Conference and Exposition, Washington, DC, USA, 3–7 November 2002; pp. 34–43. [Google Scholar] [CrossRef] [Green Version]
- Moody, L.F. Friction factors for pipe flow. Trans. ASME 1944, 66, 671–684. [Google Scholar]
- Jackson, D.; Launder, B. Osborne Reynolds and the publication of his papers on turbulent flow. Annu. Rev. Fluid Mech. 2007, 39, 19–35. [Google Scholar] [CrossRef] [Green Version]
- Kaur, K.; Annus, I.; Vassiljev, A.; Kändler, N. Determination of pressure drop and flow velocity in old rough pipes. Proceedings 2018, 2, 590. [Google Scholar] [CrossRef] [Green Version]
- Carvajal, J.; Zambrano, W.; Gómez, N.; Saldarriaga, J. Turbulent flow in PVC pipes in water distribution systems. Urban Water J. 2020, 17, 503–511. [Google Scholar] [CrossRef]
- Brkić, D. Solution of the implicit Colebrook equation for flow friction using Excel. Spreadsheets Educ. 2017, 10, 4663. Available online: https://sie.scholasticahq.com/article/4663 (accessed on 12 August 2021).
- Praks, P.; Brkić, D. Advanced iterative procedures for solving the implicit Colebrook equation for fluid flow friction. Adv. Civ. Eng. 2018, 2018, 5451034. [Google Scholar] [CrossRef] [Green Version]
- Praks, P.; Brkić, D. Choosing the optimal multi-point iterative method for the Colebrook flow friction equation. Processes 2018, 6, 130. [Google Scholar] [CrossRef] [Green Version]
- Olivares, A.; Guerra, R.; Alfaro, M.; Notte-Cuello, E.; Puentes, L. Experimental evaluation of correlations used to calculate friction factor for turbulent flow in cylindrical pipes. Rev. Int. Métodos Numér. Cálc. Diseño Ing. 2019, 35, 15. [Google Scholar] [CrossRef]
- Gregory, G.A.; Fogarasi, M. Alternate to standard friction factor equation. Oil Gas J. 1985, 83, 120–127. [Google Scholar]
- Yıldırım, G. Computer-based analysis of explicit approximations to the implicit Colebrook–White equation in turbulent flow friction factor calculation. Adv. Eng. Softw. 2009, 40, 1183–1190. [Google Scholar] [CrossRef]
- Brkić, D. Review of explicit approximations to the Colebrook relation for flow friction. J. Pet. Sci. Eng. 2011, 77, 34–48. [Google Scholar] [CrossRef] [Green Version]
- Brkić, D.; Stajić, Z. Excel VBA-Based User Defined Functions for highly precise Colebrook’s pipe flow friction approximations: A comparative overview. Facta Univ. Ser. Mech. Eng. 2021, 19, 253–269. [Google Scholar] [CrossRef]
- Qiu, M.; Ostfeld, A. A head formulation for the steady-state analysis of water distribution systems using an explicit and exact expression of the Colebrook–White equation. Water 2021, 13, 1163. [Google Scholar] [CrossRef]
- Winning, H.K.; Coole, T. Explicit friction factor accuracy and computational efficiency for turbulent flow in pipes. Flow Turbul. Combust. 2013, 90, 1–27. [Google Scholar] [CrossRef]
- Winning, H.K.; Coole, T. Improved method of determining friction factor in pipes. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 941–949. [Google Scholar] [CrossRef]
- Samadifar, M.; Toghraie, D. Numerical simulation of heat transfer enhancement in a plate-fin heat exchanger using a new type of vortex generators. Appl. Therm. Eng. 2018, 133, 671–681. [Google Scholar] [CrossRef]
- Rahmati, A.R.; Akbari, O.A.; Marzban, A.; Toghraie, D.; Karimi, R.; Pourfattah, F. Simultaneous investigations the effects of non-Newtonian nanofluid flow in different volume fractions of solid nanoparticles with slip and no-slip boundary conditions. Therm. Sci. Eng. Prog. 2018, 5, 263–277. [Google Scholar] [CrossRef]
- Shahsavar, A.; Godini, A.; Sardari, P.T.; Toghraie, D.; Salehipour, H. Impact of variable fluid properties on forced convection of Fe3O4/CNT/water hybrid nanofluid in a double-pipe mini-channel heat exchanger. J. Therm. Anal. Calorim. 2019, 137, 1031–1043. [Google Scholar] [CrossRef]
- Barnoon, P.; Toghraie, D.; Eslami, F.; Mehmandoust, B. Entropy generation analysis of different nanofluid flows in the space between two concentric horizontal pipes in the presence of magnetic field: Single-phase and two-phase approaches. Comput. Math. Appl. 2019, 77, 662–692. [Google Scholar] [CrossRef]
- Zahreddine, H. Accurate explicit analytical solution for Colebrook-White equation. Mech. Res. Commun. 2021, 111, 103646. [Google Scholar] [CrossRef]
- Muzzo, L.E.; Matoba, G.K.; Ribeiro, L.F. Uncertainty of pipe flow friction factor equations. Mech. Res. Commun. 2021, 116, 103764. [Google Scholar] [CrossRef]
- Shaikh, M.M.; Massan, S.R.; Wagan, A.I. A sixteen decimal places’ accurate Darcy friction factor database using non-linear Colebrook’s equation with a million nodes: A way forward to the soft computing techniques. Data Brief 2019, 27, 104733. [Google Scholar] [CrossRef] [PubMed]
- Sobol, I.M. Uniformly distributed sequences with an additional uniform property. USSR Comput. Math. Math. Phys. 1976, 16, 236–242. [Google Scholar] [CrossRef]
- Clamond, D. Efficient resolution of the Colebrook equation. Ind. Eng. Chem. Res. 2009, 48, 3665–3671. [Google Scholar] [CrossRef] [Green Version]
- Giustolisi, O.; Berardi, L.; Walski, T.M. Some explicit formulations of Colebrook–White friction factor considering accuracy vs. computational speed. J. Hydroinform. 2011, 13, 401–418. [Google Scholar] [CrossRef] [Green Version]
- Biberg, D. Fast and accurate approximations for the Colebrook equation. J. Fluids Eng. 2017, 139, 031401. [Google Scholar] [CrossRef]
- Brkić, D.; Praks, P. Accurate and efficient explicit approximations of the Colebrook flow friction equation based on the Wright ω-function. Mathematics 2019, 7, 34. [Google Scholar] [CrossRef] [Green Version]
- Praks, P.; Brkić, D. Review of new flow friction equations: Constructing Colebrook explicit correlations accurately. Rev. Int. Métodos Numér. Cálc. Diseño Ing. 2020, 36, 41. [Google Scholar] [CrossRef]
- Praks, P.; Brkić, D. One-log call iterative solution of the Colebrook equation for flow friction based on Padé polynomials. Energies 2018, 11, 1825. [Google Scholar] [CrossRef] [Green Version]
- Vatankhah, A.R. Approximate analytical solutions for the Colebrook equation. J. Hydraul. Eng. 2018, 144, 06018007. [Google Scholar] [CrossRef]
- Lamri, A.A. Discussion of “Approximate analytical solutions for the Colebrook equation”. J. Hydraul. Eng. 2020, 146, 07019012. [Google Scholar] [CrossRef] [Green Version]
- Lamri, A.A.; Easa, S.M. Computationally efficient and accurate solution for Colebrook equation based on Lagrange theorem. J. Fluids Eng. 2021, 144, 014504. [Google Scholar] [CrossRef]
- Brkić, D.; Ćojbašić, Ž. Evolutionary Optimization of Colebrook’s Turbulent Flow Friction Approximations. Fluids 2017, 2, 15. [Google Scholar] [CrossRef] [Green Version]
- Sobol, I.M.; Turchaninov, V.I.; Levitan, Y.L.; Shukhman, B.V. Quasi-Random Sequence Generators; Distributed by OECD/NEA Data Bank; Keldysh Institute of Applied Mathematics; Russian Academy of Sciences: Moscow, Russia, 1992; Available online: https://ec.europa.eu/jrc/sites/jrcsh/files/LPTAU51.rar (accessed on 12 January 2021).
- Bratley, P.; Fox, B.L. Algorithm 659: Implementing Sobol’s quasirandom sequence generator. ACM Trans. Math. Softw. TOMS 1988, 14, 88–100. [Google Scholar] [CrossRef]
- Joe, S.; Kuo, F.Y. Constructing Sobol sequences with better two-dimensional projections. SIAM J. Sci. Comput. 2008, 30, 2635–2654. [Google Scholar] [CrossRef] [Green Version]
- Joe, S.; Kuo, F.Y. Remark on algorithm 659: Implementing Sobol’s quasirandom sequence generator. ACM Trans. Math. Softw. TOMS 2003, 29, 49–57. [Google Scholar] [CrossRef]
- Fox, B.L. Algorithm 647: Implementation and relative efficiency of quasirandom sequence generators. ACM Trans. Math. Softw. TOMS 1986, 12, 362–376. [Google Scholar] [CrossRef]
- Hamlet, R. Random testing. Encycl. Softw. Eng. 1994, 2, 971–978. [Google Scholar] [CrossRef]
- Hamlet, D. When only random testing will do. In Proceedings of the 1st International Workshop on Random Testing, Portland, ME, USA, 20 July 2006; pp. 1–9. [Google Scholar] [CrossRef]
- Chen, T.Y.; Merkel, R. Quasi-random testing. IEEE Trans. Reliab. 2007, 56, 562–568. [Google Scholar] [CrossRef]
- Engine for Generating (Scrambled) Sobol’ Sequences. Available online: https://docs.scipy.org/doc/scipy/reference/reference/generated/scipy.stats.qmc.Sobol.html (accessed on 12 January 2022).
- Ashraf, A.; Pervaiz, S.; Haider Bangyal, W.; Nisar, K.; Ibrahim, A.; Rodrigues, J.J.P.C.; Rawat, D.B. Studying the Impact of Initialization for Population-Based Algorithms with Low-Discrepancy Sequences. Appl. Sci. 2021, 11, 8190. [Google Scholar] [CrossRef]
- Bangyal, W.H.; Nisar, K.; Ibrahim, A.; Haque, M.R.; Rodrigues, J.J.P.C.; Rawat, D.B. Comparative Analysis of Low Discrepancy Sequence-Based Initialization Approaches Using Population-Based Algorithms for Solving the Global Optimization Problems. Appl. Sci. 2021, 11, 7591. [Google Scholar] [CrossRef]
- Wang, L.; Defo, M.; Xiao, Z.; Ge, H.; Lacasse, M.A. Stochastic Simulation of Mould Growth Performance of Wood-Frame Building Envelopes under Climate Change: Risk Assessment and Error Estimation. Buildings 2021, 11, 333. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).