Abstract
Marine controlled source electromagnetic (CSEM) is an efficient method to explore ocean resources. The amplitudes of marine CSEM signals decay rapidly with the measuring offsets. The signal is easily contaminated by various kinds of noise when the offset is large. These noise include instrument internal noise, dipole vibration noise, seawater motion noise and environmental noise Suppressing noise is the key to improve data quality and interpretation accuracy. Sparse representation based denoising method has been used for denoising for a long time. provides a new way to remove noise. Under the framework of sparse representation, the denoising effect is closely related to the chosen transform matrix. This matrix is called dictionary and its column named atom. In general, the stronger the correlation between signal and dictionary is, the sparser representation will be, and further the better the denoising effect will be. In this article, a new method based on dictionary learning is proposed for marine CSEM denoising. Firstly, the signal segments suffering little from noise are captured to compose the training set. Then the learned dictionary is trained from the training set via K-singular value decomposition (K-SVD) algorithm. Finally, the learned dictionary is used to sparsely represent the contaminated signal and reconstruct the filtered one. The effectiveness of the proposed approach is verified by a synthetic data denoising experiment, in which windowed-Fourier-transform (WFT) and wavelet-transform (WT) denoising methods and three dictionaries (discrete-sine-transform (DST) dictionary, DST-wavelet merged dictionary and the learned dictionary) under a sparse representation framework are tested. The results demonstrate the superiority of the proposed dictionary-learning-based denoising method. Finally, the proposed approach is applied to field data denoising process, coupled with DST and DST-wavelet dictionaries based denoising methods. The outcomes further proves that the propsoed approach is effective and superior for marine CSEM data denoising.
1. Introduction
Marine CSEM is frequently used in hydrocarbon and other undersea resources exploration [1,2]. The principle and working flow of frequency domain marine CSEM are illustrated in Figure 1. A horizontal electric source, towed close to the bottom, is utilized to transmit an electromagnetic signal. Several receivers are deployed on the seafloor with a certain rule to record electromagnetic signals.
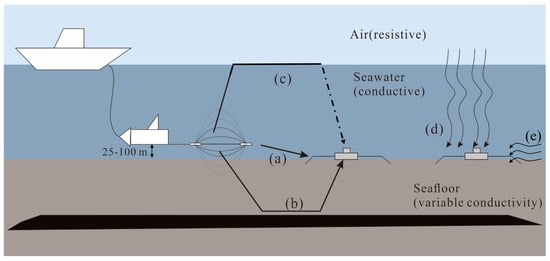
Figure 1.
The work flow of marine CSEM is illustrated. There are five components in the signal recorded at the receiver, (a) direct wave, (b) reflection-refraction wave, (c) air wave, (d) natural electromagnetic field variations and (e) noise.
The marine CSEM system is sensitive to the resistive reservoir embedded in the conductive seabed [3]. The amplitude of signal decays rapidly with the transmitter-receiver offset. When the offset is large, the power of recorded signal is weak and easily contaminated by different kinds of noise. Suppressing the noise influence is crucial to improve data quality and interpretation accuracy in marine CSEM data processing.
According to the literature [4], there are five noise types based on their originating sources:
- (1)
- Dipole vibrations. The vibration of receiver arm will induce a voltage, whose magnitude is comparable to the target signal [5].
- (2)
- Seafloor currents. Seafloor currents will induce voltages that always have a low frequency closely related to the currents [6].
- (3)
- Natural electromagnetic field variations. The changes of natural electromagnetic field can influence the recorded signal, such as magnetotelluric.
- (4)
- Internal electrode and amplifier noise. This noise comes from the internal part of the instrument.
- (5)
- Air waves. Air waves can seriously affect the data quality in shallow water exploration. Its influence will be weakened with the increase of seawater depth. Despite the disagreement whether air waves are noise or not, many scholars still try to remove it [7].
Nowadays, most denoising methods are aiming at removing single noise type, and the denoised results are illustrated by the magnitude value offset (MVO) plot. The MVO plot extracts single frequency components and plots its magnitude along offset [8]. Myer proposed to remove noise by multi-windows stacking, and the denoising results were affected by the length of the selected window [9]. The canonical denoising methods, WFT (windowed Fourier transform) and WT (wavelet transform), are still investigated [10]. Besides, many methods are proposed to remove noise for marine CSEM data. Time domain filters and noise estimation methods are proposed to remove random noise [11]. Time-varying bilateral filter is proposed to solve the low signal-to-noise ratio (SNR) problem [5]. Adaptive filter is also introduced to marine CSEM data denoising procedure [12]. Most of the studies are focused on removing Gaussian noise or a single noise type, but noise is often presented in a varying combination of various types so that a more complete approach may be desired.
Utilizing the hypothesis that signal and noise behavior differently in sparse domain, sparse representation based denoising method gains focus recently. Zhang introduced compressive sensing (CS) into marine CSEM denoising procedure, which can suppress various kinds of noise [13]. Li denoised magnetotelluric data using mathematical morphology filtering and sparse representation [14]. Xue denoised airborne EM data by K-SVD based denoising algorithm, in which the noise is assumed as Gaussian white noise and the training set is composed by contaminated signal [15]. Tang denoised magnetotelluric data using dictionary learning, where the training set is constructed from the interferences [16]. Denoising under the sparse representation framework is closely related to the correlation between signal and the chosen dictionary. Generally, the stronger the correlation between signal and dictionary is, the better the denoising effect will be [17].
In this article, we propose to denoise marine CSEM by constructing a dictionary based on the features of the signals via a dictionary learning algorithm, which is the continuation and extension of our former work [18]. In theory, the learned dictionary has stronger correlation than any given dictionaries, and can achieve better denoising effect. Firstly, the theory and principle of the proposed approach, as well as the working flow of dictionary learning based denoising procedure are briefly described. Then, numerical experiments are carried out for synthetic data with different denoising methods, including classical WFT and WT denoising methods and three dictionaries (DST, DST-wavelet and learned dictionaries) under sparse representation framework. After that, all three dictionaries are applied to the field data, and their denoising effects are compared by MVO plots. Finally, denoising performances of different methods are compared and conclusions are drawn.
2. Theory and Methodology
2.1. Dictionary Learning Based on K-SVD Algorithm
The method promoted in this article is built on the assumption of signal sparse representation. Signal can be represented as a linear combination of the columns from the dictionary:
where is named dictionary and its columns named atoms, is the coefficient vector, and is the error tolerance. Especially, when there are only K non-zero coefficients in and , then the signal has a sparse representation with dictionary . The sparse representation of the target signal is closely related to the matrix . And pre-specified transform matrices, such as discrete sine transform (DST) and wavelet transform (WT) matrix, are always chosen as the dictionary [13]. The matrix can also be designed as an over-complete dictionary, in which the number of rows is larger than columns [19]. Now the widely used sparse reconstruction algorithm is orthogonal matching pursuit (OMP) [20] with the basic flow listed in Figure 2.

Figure 2.
The pseudocode of OMP algorithm.
The transmitting signal of marine CSEM is a square wave or binary symmetric wave, they both are sparse in frequency domain [9]. Generally, noise is considered as non-sparse in most of the transform domains. Then the denoising problem is transformed to the sparse representation and reconstruction problem of noisy signal. Zhang (2020) used discrete sine transform matrix (DST) as the dictionary and reported good results. However, given the unknown character of noise, an ideal sparse representation should be self-adaptive, flexible and simple. We suggest that it would be more appropriate to construct the dictionary based on the signals features. Hence, we introduce dictionary learning algorithm to construct an adaptive dictionary based on the characteristics of the signal.
Dictionary learning is a machine learning method, which trains the dictionary and gains the sparse coefficients from the given data. Theoretically, the trained dictionary contains the prototype of the given data and provides a sparse representation for similar signal. The objective function of dictionary learning is [21]:
where means norm, which presents the count of non-zeros elements in target vector. This equation means to search for the sparsest representation coefficients vector under the allowed error .
The frequently used dictionary learning algorithm is K-SVD algorithm [22]. The objective function is illustrated as
where is the learned dictionary, is the matrix of original signal, is the sparse representation matrix, is the aimed sparsity, F means Frobenius norm.
Equation (3) can not be solved directly, here we solve it iteratively. In the sparse representation stage, is fixed, and the above optimization problem becomes classical sparse representation problem The penalty term of Equation (3) can be decoupled as
These N distinct problems can be solved by OMP algorithm.
In the dictionary learning stage, both and are fixed, take only one atom in the dictionary and the corresponding kth row in denoted as , here T means transposition. Then the Equation (4) can be expressed as
where stands for the error matrix for all except the k-th atom.
Applying SVD to matrix directly will lead to some mistakes [22]. A remedy is defining as the group of indices pointing to examples that use the atom , thus
Define as a matrix with the size , in which ones are on the th entries and zeros others. Define to shrink the row vector by discarding zeros entries, the same action is applied to error matrix as . Then we solve the equivalent minimization problem
by using SVD directly. Decompose , define the solution for as the first column of and the coefficient vector as the first column of multiplied by . The algorithm flow of K-SVD is illustrated in Figure 3.

Figure 3.
The pseudocode of K-SVD algorithm.
2.2. Denoising Flow of the Proposed Algorithm
The denoising procedure for marine CSEM data is presented in Figure 4. Once setting the segment length and the target frequency, the input raw time series can be filtered by the given approach. The noise suppressing effect is evaluated by SNR and MAE values. Besides, the denoising results are evaluated by MVO or MVT plots intuitively.
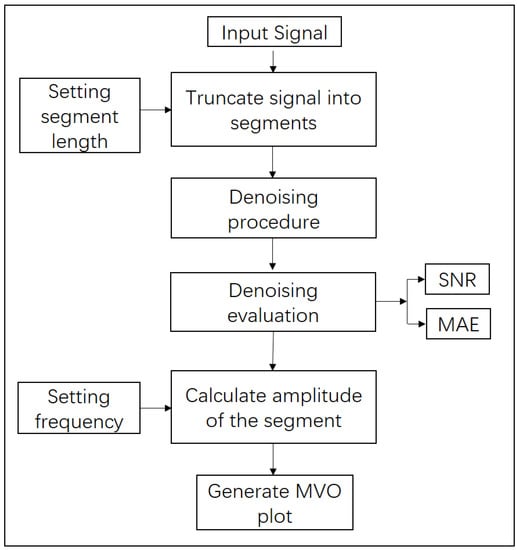
Figure 4.
Flow chart of the denoising technique described in this article. There are three inputs including the target signal, the setting window length and frequency. Note that the denoising processing and evaluation procedure are defined for time series, and the denoising effect is illustrated through MVO plots at given frequencies.
The denoising procedure of the proposed approach is given in Figure 5. Once given the initial dictionary, the selection of training set is vital for the proposed method. The training set signal should suffer little from noise and have similar features with the target one. The marine CSEM receivers are settled on the seafloor and the transmitter is dragged along the pre-specified line. When the transmitter-receiver offset is relatively small, the signal is suffering little from the noise. As a result, the signal with small offset is intercepted to construct the training set.
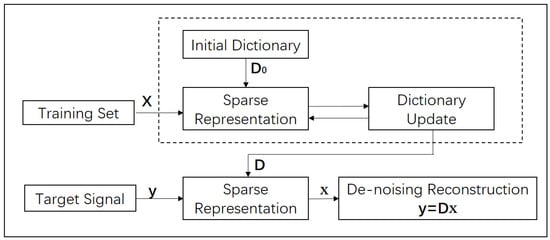
Figure 5.
Flow chart of denoising procedure by dictionary learning. The dashed line box contains the dictionary learning procedure, where an initial dictionary for the training set is provided.
In this article, DST dictionary is given as the initial dictionary, and the learned one is generated from the training set via K-SVD algorithm. Then target signal is decomposed and reconstructed with the learned dictionary. All these above are built on theory, the following part will verify the effectiveness of dictionary leaning algorithm in numerical experiments and field data applications.
3. Synthetic Data Examples
The canonical 1D reservoir model used to generate simulated data is shown in Figure 6a. For forward simulation, we adopt the open source software [23]. Setting the transmitting frequency 0.5 Hz, the velocity of transmitter 1 m/s, and sampling interval 0.1 m, we obtain the spectral response as shown in Figure 6b,c.
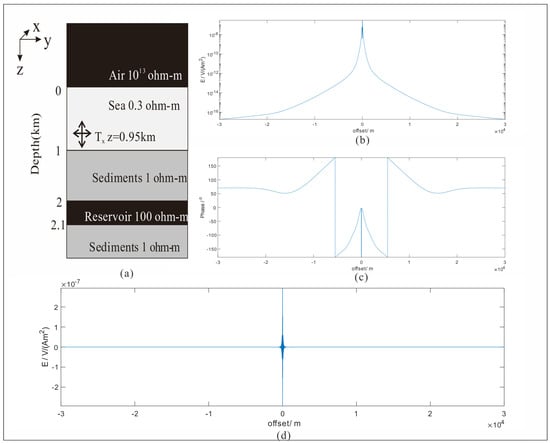
Figure 6.
The canonical reservoir model and the CSEM response. (a) is the canonical model (comes from Myer 2011). There is a half-space air layer with the resistivity ohm-m, a 1000 m deep seawater layer with 0.3 ohm-m, and a sediment layer with 1 ohm-m. Besides, a 100 m thick and 100 ohm-m high resistive layer is buried 1000 m below the seafloor. The transmitter is dragged along Y-axis at 50 m above the seafloor. The receiver is located at the original point of Y-axis. (b) illustrates the MVO (magnitude versus offset) plot of marine CSEM signal, and the maximum value appears at the receiver location. (c) shows the PVO (phase versus offset) plot of the signal. (d) is the modulating signal to simulate the recorded signal.
To simulate the recorded time series, we modulate the signal by
where is the correlation function between location and time, and are the magnitude and phase values respectively. The simulated time series is shown in Figure 6d, in which most details are obscure. Here in this article, we only use magnitude curves, as the phase curves are easily disturbed by noise. As we set the depth of sea to 1000 m, the airwave effect is ignored. Assuming all noise is additive, we add four types of noise.
- (1)
- Random noise. Magnitudes are integer multiples of the noise floor V/(Am2), and the average value is zero [24].
- (2)
- Internal noise. This kind of noise originates from the circuitry of the equipment, and the magnitude is set as of clear signal to simulate the amplifier noise [13].
- (3)
- Impulse noise. Thirty positive impulses with the magnitude V/(Am2) are added randomly to the signal to simulate the accidental interferences.
- (4)
- Low frequency noise. The motion of seawater is complex and so is the noise caused by this movement. The noise has multiple frequencies surrounding low frequency. To simply the research, we use five low frequency sine signals with the frequency 0.01, 0.02, 0.03, 0.04 and 0.05 Hz separately to simulate the seawater motion influence.
These noise types are illustrated in Figure 7a–d, corresponding to the four kinds of noise, respectively. Figure 7e is the overall view of the contaminated signal, most details are imperceptible in this overall view. Figure 7f is the partially enlarged view of Figure 7e, where it is obvious that the signal is contaminated by random noise and impulse noise. Figure 7g is the time-frequency plot of the contaminated signal, in which the impulse noise is shown as vertical stripes and five low frequency noise sources are shown as cross stripes at corresponding locations.
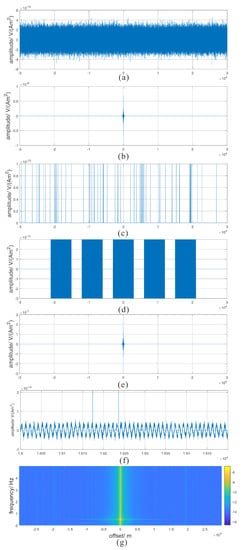
Figure 7.
All the added noise and the contaminated signal. (a) illustrates the random noise, (b) shows the internal noise, (c) presents impulses to simulate dipole vibrations and (d) shows low frequency noise to simulate seawater motions. (e) is the overview of the contaminated signal, in which the clear signal comes from the above simulation, (f) is the partial enlarged view of the signal (g) presents the time-frequency characters of the contaminated signal.
3.1. Numerical Experiment I
This example verifies the hypothesis that effective signal is sparse with learned dictionaries, while noise is not. As former literature proved that DST and DST-wavelet dictionaries perform well for marine CSEM data denoising [13], these two dictionaries are choosen as the control group. The training set is constructed by signal segments with amplitudes higher than V/(Am2) from the contaminated signal. Choose DST dictionary as the initial dictionary, the learned dictionary is constructed via K-SVD algorithm and marked as DL. In this experiment, three segments of raw noise free signal are intercepted to verify the convergence of all these three dictionaries. The segments of added noise with the same locations are also intercepted to verify the non-sparse features with these dictionaries. Each segment is decomposed and reconstructed with three different dictionaries, and the residual ratio along with the iteration times plots are illustrated in Figure 8.
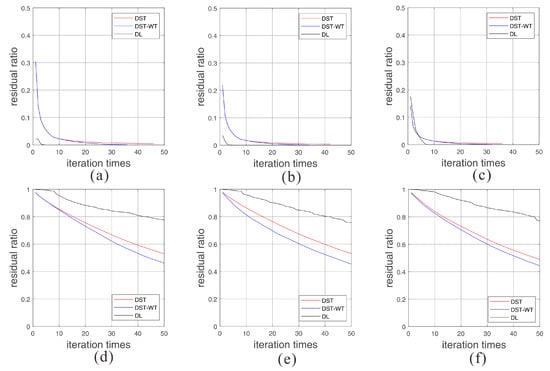
Figure 8.
The convergent performances with three dictionaries of different segments with locations from far, middle and near offset. (a–c) are the convergence performance of intercepted raw noise free signals. (d–f) are the convergence performance of four kinds of added noise with the same locations. In this figure, DST means discrete sine transform dictionary, DST-WT represents the merged dictionary of discrete sine transform and wavelet transform, and DL represents the dictionary generated by learning method.
Figure 8a–c present the convergent performances of noise free signal at far, middle and near offsets with three dictionaries, separately. Reconstruction errors reduce to constants after certain times of iteration for all three segments with all three dictionaries. Besides, reconstruction errors reduce to after 10 times iteration for all these noise free signals with each dictionary. In detail, DST-wavelet merged dictionary performs better than DST dictionary. And the learned dictionary has the best convergent performance among them, for the reconstruction error remains constant after few times of iteration. The results prove the sparsity of the effective signal with the three dictionaries and the superiority of the learned dictionary. Figure 8d–f illustrate the convergent performances of added noise with the same locations with the above noise free signal. The results are apparent that noise is not sparse with all three dictionaries. In detail, the learned dictionary performs worst for the sparse representation of noise. This experiment verifies the base hypothesis of the proposed denoising approach, that the effective signal of marine CSEM can be sparse represented while the noise is not.
3.2. Numerical Experiment II
In the second experiment, we compare the performance of the denoising methods, windowed Fourier transform (WFT) and wavelet transform (WT) to the proposed method based on dictionary learning by applying the methods to a contaminated signal. Fourier and wavelet transforms are common methods in time series analysis [25]. The results of different denoising methods are shown in Figure 9.
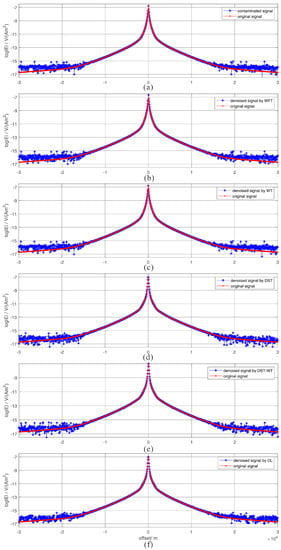
Figure 9.
The denoising results of different methods for synthetic data. (a) is the comparison MVO plot between original and contaminated signals, (b) is the contrast plot between denoising results after WFT (windowed Fourier transform) and the original signal, (c) is the comparison MVO plot between denoising results of wavelet transform and the original signal. (d) is the contrast plot between denoising results under DST (discrete sine transform) dictionary and the original signal. (e) is the comparison MVO plot between denoising result under DST-wt (discrete sine transform and wavelet transform merged dictionary) dictionary and original signal (f) is the denoising result under learned dictionary.
Figure 9a compares the MVO plots between noise free signal and the contaminated one. Figure 9b illustrates the MVO plots of the noise free signal and the filtered one by WFT. The MVO plot of the filtered signal at large offset is almost the same with the noisy one, which illustrates the ineffectiveness of the WFT method.
Figure 9c displays the denoising outcomes after wavelet transform. Here we employ sym4 wavelet and decompose the contaminated signal into four levels. Sym4 is a member of symlet wavelets, which are modified Daubechies wavelets with increased symmetry. For each level, we calculate the soft threshold according the minimax principle [26,27]. It is shown that the wavelet transform is not sufficiently effective for marine CSEM signal denoising.
Comparing all three dictionaries (DST, DST-wavelet and the learned dictionaries) by setting the maximum iteration time to 10 and applying them to the denoising procedure, the obtained results are illustrated in Figure 9d–f. Figure 9d presents the MVO plot comparison between the noise free signal and the filtered one with DST dictionary. In general, the overall trend of the filtered signal is coincides with the noise free one. In detail, the influences of impulses are suppressed to some extent. Figure 9e presents the denoising performance under DST-wavelet merged dictionary. The denoising performance of the merged dictionary is almost the same with the DST dictionary. For impulses suppressing, the DST dictionary performs better. Figure 9f shows the results with the proposed dictionary learning based denoising approach. From the overall view, the trend of filtered signal is almost the same with others. However, the proposed approach obviously remove impulse noise when the absolute offset is larger than m. Generally speaking, the proposed approach gains the best denoising result among all these methods.
In this experiment, signal-noise-ratio (SNR) and root-mean-square error (RMSE) are used to evaluate the denoising effect, they are defined as
where means the original signal, and represents the filtered signal.
The amplitude of effective signal changes rapidly with the transmitter-receiver offset. It’s meaningless to calculate the SNR and RMSE values for the whole signal. Besides, improving the data quality at large offset is the ultimate goal for this article. Here we intercept two segments, 20,000–20,120 m and 21,000–21,120 m, form large offset to calculate SNR and RMSE values. The denoising results of different methods are listed in Table 1. The three largest SNR and three smallest RMSE values are bold to enhance readability.

Table 1.
The comparison of different denoising methods.
The denoising results with DST and DST-wavelet dictionaries are good for both segments, which proves the effectiveness of the sparse representation based denoising method. The outcomes of the learned dictionary is the best among all these methods. This comparison further proves the superiority of the proposed method. Both qualitative comparison and quantitative calculation all illustrate the superiority of the proposed dictionary learning based denoising approach.
4. Real Data Application
The field marine CSEM survey was carried out by Guangzhou Marine Geological Survey (GMGS) in March 2016. The employed detection system was developed by key laboratory of Geo-detection in China University of Geoscience independently [28,29,30].
The study area is located in Qiongdongnan Basin, which is an important gas hydrate prospecting basin in the northern slope of South China Sea. The seafloor bathymetry is fairly flat, and the water depth is between 1343 m and 1354 m [31]. A 4500 m profile perpendicular to the geological strike was arranged along a NW-SE direction in the Qiongdongnan Basin. It comprises 10 sites with a space of 500 m. The main target of this article is denoising, and we select the 2nd receiver (R2) as the study object. The four time series recorded in R2, Ex, Ey, Hx and Hy, are illustrated in Figure 10.
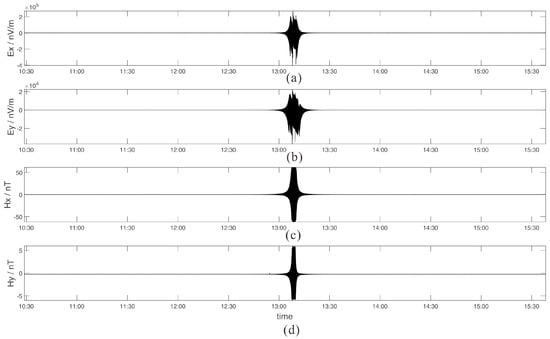
Figure 10.
Four horizontal electromagnetic components of the 2nd receiver. (a) is the Ex component, (b) is the Ey component, (c) shows the Hx component and (d) is the Hy component.
Figure 11a is the Ey time sequence recorded at R2 receiver, and most details are imperceptible in this figure. Figure 11b displays the 0.5 Hz MVT (magnitude versus time) plot with a window length of 60 s, where the segment between 12:00 and 14:00 suffers less from the influence of noise. In the field data denoising procedure, the training set is chosen from the segments that suffer less from noise. In other words, the segment between 12:00 and 14:00 is chosen as the training set. Then a learned dictionary is trained by K-SVD algorithm, marked as DL.
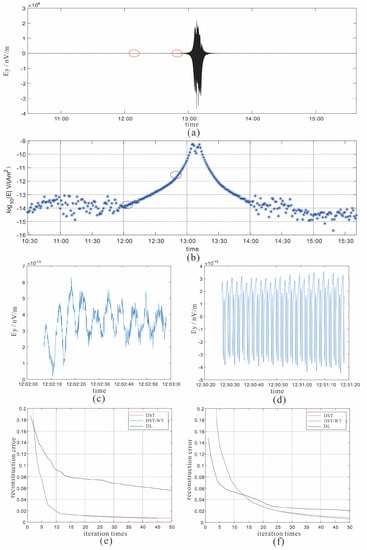
Figure 11.
The characters of Ey component. (a) is the time sequence, (b) is the 0.5 Hz MVT plot, (c,d) are segments intercepted from (a), corresponding to red circles in (a), or the black circles in (b). (e,f) are the convergence performance under three dictionaries, in which red lines represent DST dictionary, blue lines represent DST-wavelet merged dictionary and black lines represent the learned dictionary.
Figure 11c,d are selected from the time sequence, and their location are illustrated by the black circles in Figure 11b. It appears that the data presented in Figure 11c correspond to the part that suffers from the influence of noise and the data in Figure 11d is affected less by noise. Figure 11e is the reconstruction error of the first segment under three different dictionaries. DST and DST-wavelet dictionaries all have good convergence performance, and the performance of DST-wavelet dictionary is a little better than single DST dictionary. After 15 times of iteration, the reconstruction error stops to reduce for the learned dictionary. The reason for this phenomenon is that this segment still suffers from the influence of noise. This phenomenon changes in Figure 11f, where the target segment suffers less from noise.
The Ey components of R2 undergo the denoising procedure by DST, DST-wavelet and learned dictionary, separately, and the results are illustrated in Figure 12 and Figure 13. Figure 12 illustrates the 0.5 Hz MVT plots with three different dictionaries, Figure 12a the DST dictionary, Figure 12b the merged dictionary and Figure 12c the learned dictionary. Compared with the scattered raw field data, the segments between 10:30 and 12:00 with three different dictionaries are less scattered, and the same phenomenon appears between 14:30 and 15:30. It yields that all three dictionaries suppress noise successfully at large offset. Especially the segment between 14:00 and 14:30, the proposed approach presents obvious centralized characteristic. Considering the morphology of simulated signal, here we deduce that the proposed method yields the best denoising results.
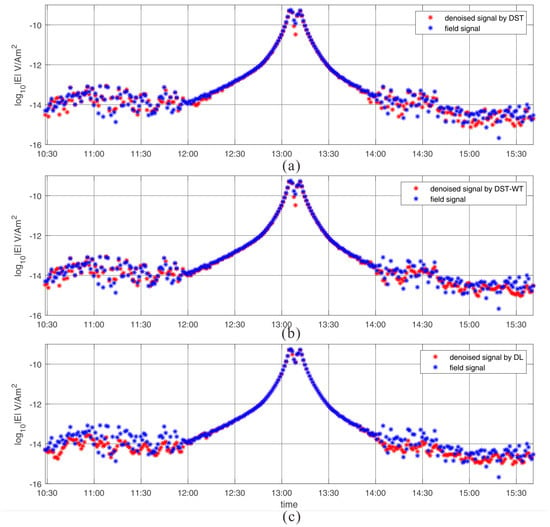
Figure 12.
The MVT plot at frequency 0.5 Hz for field data. (a) is the denoising result under DST dictionary, (b) is the denoising outcome under DST-wavelet merged dictionary and (c) is the denoising result under learned dictionary.
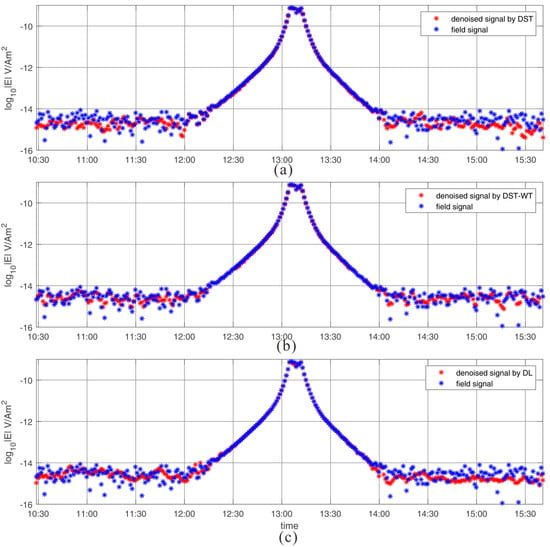
Figure 13.
The MVT plots at frequency 1.5 Hz for field data. (a) is the denoising result under DST dictionary, (b) is the denoising outcome under DST-wavelet merged dictionary and (c) is the denoising result under learned dictionary.
Figure 13 shows the 1.5 Hz MVT plots with three different dictionaries, respectively. Compared with the raw field data, the segments between 10:30 and 12:00 present obvious less scattered features with three dictionaries, which yields the denoising effect of these three dictionaries. The same appearance occurs at the segments between 14:30 and 15:30. And the difference of the segment between 14:00 and 14:30 yields that the proposed dictionary learning based denoising method are smoother than the other two, which further proves the best denoising performance.
Compared with other denoising methods, the MVT plots at 0.5 Hz of the proposed approach gains the smoother overall trend than others. Besides, the proposed method effectively removes outliers, which are considered as noise. The 1.5 Hz MVT plots further verify this phenomenon. The filed data applications of different methods proves the superiority of the proposed approach.
5. Conclusions
The amplitudes of marine CSEM signals change rapidly with transmitter-receiver offset. When the offset is large, the effective signal is easily contaminated by different kinds of noise. Suppressing the noise influence is vital to improve data quality. In this article, a dictionary learning based noise suppressing approach is proposed for marine CSEM data. Firstly, an adaptive dictionary is learned by the training data. The training data set is constructed by signal suffers little from noise, such as the signal with small offset. Secondly, the contaminated signal is sparsely represented with the learned data. Finally, the sparse representation coefficients are sieved and used to reconstruct the filtered signal. After these procedures, all kinds of noise are suppressed for marine CSEM signal.
The effectiveness of the proposed method is verified in numerical experiments, compared with the classical WFT and WT denoising methods. The first numerical experiment verifies the base hypothesis that the effective signal is sparse while the noise is not. The second experiment carries out qualitative comparison by MVO curves and quantitative comparison by SNR and RMSE values. Both qualitative and quantitative comparisons all prove the superiority of the proposed dictionary learning based denoising approach.
Besides, the dictionary learning based method, coupled with the given DST and DST-wavelet dictionaries, are applied to field data denoising process. The DST dictionary has similar denoising results as the DST-wavelet dictionary, and the learned dictionary performs best among them, both in 0.5 Hz and 1.5 Hz MVT curves. The comparison further verifies the superiority of the proposed denoising method.
In this article, we set the maximum iteration time to 10 and the reconstruction error as the unified stop criterion. However, the power of signal varies rapidly with the offset. Even the noise floor is set as constant, the SNR values still vary with the offset. As a result, the stop criterions should vary with the offset to gain the best denoising result. The adoptive stop criteria for the dictionary learning based denoising approach still need further research.
Author Contributions
Conceptualization, P.Z. and X.P.; methodology, P.Z., software, J.L. Denoising marine controlled source electromagnetic data based on dictionary learning. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Open Funding of Key Laboratory of Metallogenic Prediction of Nonferrous Metals and Geological Environment Monitoring (Central South University) 2021YSJS11, National Natural Science Foundation (CN) 42004107, Natural Science Foundation of Hunan Province (CN) under grant 2021JJ40723 and 2021JJ30814.
Data Availability Statement
The open source software used in this article is listed below: 1D CSEM Modeling: https://marineemlab.ucsd.edu/ (accessed on 20 May 2021). By using this code, the forward simulation will be carried out easily. However, the field data is secretive as the requirement.
Acknowledgments
We appreciate the editor for their suggestions to improve this paper. We also appreciate Kerry Key and Michal Aharon et al. for their open source code software, which is the base of this work. Besides, we appreciate the help from Zhenwei Guo in the writing of this article, his constructive suggestions help us to improve this work.
Conflicts of Interest
We declare that we have no financial and personal relationships with other people or organizations that can inappropriately influence our work, there is no professional or other personal interest of any nature or kind in any product, service and/or company that could be construed as influencing the position presented in, or the review of, the manuscript entitled, ’Denoising marine controlled source electromagnetic data based on dictionary learning’.
Abbreviations
| CSEM | controlled source electromagnetic |
| WFT | windowed Fourier transform |
| WT | wavelet transform |
| DST | discrete sine transform |
| OMP | orthogonal matching pursuit |
| target signal | |
| sparse coefficients vector | |
| dictionary | |
| error | |
| the calculated sparse coefficients vector | |
| residual for the ith iteration | |
| index set for the column number for ith iteration | |
| column set for ith iteration |
References
- Constable, S.; Srnka, L.J. An introduction to marine controlled-source electromagnetic methods for hydrocarbon exploration. Geophysics 2007, 72, WA3–WA12. [Google Scholar] [CrossRef]
- Peng, R.; Hu, X.; Chen, B.; Li, J. 3-D marine controlled-source electromagnetic modeling in electrically anisotropic formations using scattered scalar–vector potentials. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1500–1504. [Google Scholar] [CrossRef]
- Constable, S. Ten years of marine CSEM for hydrocarbon exploration. Geophysics 2010, 75, 75A67–75A81. [Google Scholar] [CrossRef] [Green Version]
- Pethick, A.M. Multidimensional Computation and Visualisation for Marine Controlled Source Electromagnetic Methods. Ph.D. Thesis, Curtin University, Perth, WA, Australia, 2013. [Google Scholar]
- Liu, N. Preprocessing and Research of Denoising Methods for Marine Controlled Source Electromagnetic Data. Ph.D. Thesis, Jilin University, Changchun, China, 2015. (In Chinese). [Google Scholar]
- Zili, Z. Theory Research and Application of Ocean Electromagnetic Field. Ph.D. Thesis, China University of Geosciences, Wuhan, China, 2009. [Google Scholar]
- Yin, C.; Liu, Y.; Weng, A.; Jia, D.; Ben, F. Research on marine controlled-source electromagnetic method airwave. J. Jilin Univ. (Earth Sci. Ed.) 2012, 42, 1506–1520. [Google Scholar]
- Behrens, J.P. The Detection of Electrical Anisotropy in 35 Ma Pacific Lithosphere: Results from a Marine Controlled-Source Electromagnetic Survey and Implications for Hydration of the Upper Mantle; University of California: San Diego, CA, USA, 2005. [Google Scholar]
- Myer, D.; Constable, S.; Key, K. Broad-band waveforms and robust processing for marine CSEM surveys. Geophys. J. Int. 2011, 184, 689–698. [Google Scholar] [CrossRef] [Green Version]
- Hsu, S.K.; Chiang, C.W.; Evans, R.L.; Chen, C.S.; Chiu, S.D.; Ma, Y.F.; Chen, S.C.; Tsai, C.H.; Lin, S.S.; Wang, Y. Marine controlled source electromagnetic method used for the gas hydrate investigation in the offshore area of SW Taiwan. J. Asian Earth Sci. 2014, 92, 224–232. [Google Scholar] [CrossRef]
- Xin, L.; Wen-bo, W.; Jian-en, J. Study on improving MCSEM signal-to-noise ratio. Prog. Geophys. 2009, 24, 1047–1050. [Google Scholar]
- Li, Z. Study on Marine Controlled-Source Electromagnetic Data De-Noising Based on Adaptive Filtering Method. Ph.D. Thesis, China University of Geosciences, Wuhan, China, 2017. [Google Scholar]
- Zhang, P.; Deng, M.; Jing, J.; Chen, K. Marine controlled-source electromagnetic method data de-noising based on compressive sensing. J. Appl. Geophys. 2020, 177, 104011. [Google Scholar] [CrossRef]
- Li, G.; Liu, X.; Tang, J.; Li, J.; Ren, Z.; Chen, C. De-noising low-frequency magnetotelluric data using mathematical morphology filtering and sparse representation. J. Appl. Geophys. 2020, 172, 103919. [Google Scholar] [CrossRef]
- Xue, S.Y.; Yin, C.C.; Su, Y.; Liu, Y.H.; Wang, Y.; Liu, C.H.; Xiong, B.; Sun, H.F. Airborne electromagnetic data denoising based on dictionary learning. Appl. Geophys. 2020, 17, 306–313. [Google Scholar] [CrossRef]
- Tang, J.; Li, G.; Zhou, C.; Ren, Z.; Xiao, X.; Liu, Z.j. Denoising AMT data based on dictionary learning. Chin. J. Geophys. 2018, 61, 3835–3850. [Google Scholar]
- Ma, J.; Plonka, G. The curvelet transform. IEEE Signal Process. Mag. 2010, 27, 118–133. [Google Scholar] [CrossRef]
- Zhang, P.; Pan, X.; Guo, Z.; Ge, Z.; Liu, J. Application of dictionary learning in marine CSEM denoising. In Proceedings of the First International Meeting for Applied Geoscience & Energy (Society of Exploration Geophysicists), Denver, CO, USA, 26 September–1 October 2021; pp. 528–532. [Google Scholar]
- Mallat, S.G.; Zhang, Z. Matching pursuits with time-frequency dictionaries. IEEE Trans. Signal Process. 1993, 41, 3397–3415. [Google Scholar] [CrossRef] [Green Version]
- Tropp, J.A.; Gilbert, A.C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef] [Green Version]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Aharon, M.; Elad, M.; Bruckstein, A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. Signal Process. 2006, 54, 4311–4322. [Google Scholar] [CrossRef]
- Key, K. 1D inversion of multicomponent, multifrequency marine CSEM data: Methodology and synthetic studies for resolving thin resistive layers. Geophysics 2009, 74, F9–F20. [Google Scholar] [CrossRef]
- Myer, D.; Constable, S.; Key, K.; Glinsky, M.E.; Liu, G. Marine CSEM of the Scarborough gas field, Part 1: Experimental design and data uncertainty. Geophysics 2012, 77, E281–E299. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Oldenburg, D.W. Rapid construction of equivalent sources using wavelets. Geophysics 2010, 75, L51–L59. [Google Scholar] [CrossRef]
- Daubechies, I. Ten Lectures on Wavelets; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1992. [Google Scholar]
- Lv, P.; Wu, X.; Zhao, Y.; Chang, J. Noise removal for semi-airborne data using wavelet threshold and singular value decomposition. J. Appl. Geophys. 2022, 201, 104622. [Google Scholar] [CrossRef]
- Kai, C.; Jian-En, J.; Qing-Xian, Z.; Xian-Hu, L.; Guang-Hong, T.; Meng, W. Ocean bottom EM receiver and application for gas-hydrate detection. Chin. J. Geophys. 2017, 60, 4262–4272. [Google Scholar]
- Wang, M.; Deng, M.; Wu, Z.; Luo, X.; Jing, J.; Chen, K. The deep-tow marine controlled-source electromagnetic transmitter system for gas hydrate exploration. J. Appl. Geophys. 2017, 137, 138–144. [Google Scholar] [CrossRef]
- Jian-En, J.; Zhong-Liang, W.; Ming, D.; Qing-Xian, Z.; Xian-Hu, L.; Guang-Hong, T.; Kai, C.; Meng, W. Experiment of marine controlled-source electromagnetic detection in a gas hydrate prospective region of the South China Sea. Chin. J. Geophys. 2016, 59, 2564–2572. [Google Scholar]
- Jing, J.E.; Chen, K.; Deng, M.; Zhao, Q.X.; Luo, X.H.; Tu, G.H.; Wang, M. A marine controlled-source electromagnetic survey to detect gas hydrates in the Qiongdongnan Basin, South China Sea. J. Asian Earth Sci. 2019, 171, 201–212. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).