Estimating Magma Crystallization Temperatures Using High Field Strength Elements in Igneous Rocks

Abstract

Indirect calculation of magma crystallization temperatures is an important subject for geologists to know the petrogenesis of igneous rocks. During magma evolution from generation to crystallization, several processes control the behavior of elements. In this research, we obtained two new methods for the thermometry of magma by using high field strength elements (HFSEs; Zr, Hf, Ce, Y, and Ti) abundances in igneous rocks. The first was T_(K) = −15,993/(lnC_Zr + lnC_Hf − 21.668), where C_Zr and C_Hf are the bulk-rock Zr and Hf contents in ppm, and T is the temperature in Kelvin. This equation was specially formulated to address metaluminous to peraluminous rocks with M < 2 [(Na + K + 2Ca)/(Al × Si)] (cation ratio) and SiO₂ > 63 wt.%. The second was T_(K) = −20,914/(ln(C_Hf + C_Y + C_Ce) + (ln(C_Zr/TiO₂) − 31.153). C_Hf, C_Y, and C_Ce, and C_Zr are Hf, Y, Ce, and Zr contents (ppm) in the whole rocks. The second equation is more suitable for peralkaline to alkaline rocks with M > 2 and a wide range of SiO₂. Both equations are applicable for temperatures from 750 °C to 1400 °C. These two equations are simple and robust thermometry methods and predict similar values in the range of T_Zr thermometry, which has previously been suggested for magma crystallization temperature.

1. Introduction

Indirect estimation of magma crystallization temperature by using the composition of the whole rock is a challenging subject in igneous petrology. This matter is an important subject for understanding the evolution of igneous rocks, and there are different thermometry methods based on the mineral equilibria and compositions in igneous and metamorphic rocks [1,2,3,4,5,6,7,8,9,10,11]. Here, we briefly mention some common thermometry methods in igneous rocks, including Zr content in rutile in equilibrium with quartz and zircon (T(°C) = 127.8 × ln (Zr in ppm) − 10) [12]), Ti incorporation in zircon (T_ZircTi (°C) = $\frac{5080}{6.01-\log \left(\mathrm{Ti} \mathrm{in} \mathrm{zircon};\mathrm{ppm}\right) + \log ({\mathsf{\alpha }}_{{\mathrm{TiO}}_2)}}-273)$ [1]), and Ti in quartz (T(°C) = $\left(-\frac{376}{\mathrm{logTi}{\left(\mathrm{ppm}\right)}_{\mathrm{qtz}}-5.69}\right)-273)$ [2]. Apatite saturation thermometry is particularly applicable for peraluminous rocks [4]. The Fe-Ti oxide composition in the intrusive rocks is valuable for the determination of the temperature and oxygen fugacity [5]. Two feldspars thermometry has a long history and was developed by several researchers [6,7,8]. The composition of plagioclase is sensitive to the temperature in the magmatic melts. Accordingly, plagioclase compositions are a respectable thermometer in igneous rocks [13,14,15,16]. Likewise, Ghiorso and Evans [17] developed a new approach of thermometry in the oxide solid solution of Fe₂O₃-FeTiO₃-MgTiO₃-MnTiO₃ with less Al₂O_3.

Zircon saturation thermometry (T_Zr) is dependent on the Zr concentration in the felsic melt (W&H83) [18]. Both the WandH83 and the revised T_Zr formula (B13) [19] are widely established for the estimation of magma crystallization temperature for mostly aluminous compositions. Conclusively, the zircon saturation thermometry was revised and updated for the calculation of the intermediate to felsic alkaline melt temperatures higher than 800 °C by Gervasoni et al. [20], which we, here, refer to as the G16 equation.

There are some glitches with thermometry methods, including the following: (1) most granitic rocks do not commonly show a pure melt composition because they are cumulate [21,22] or driven by incomplete separation of residue minerals from the melt [23]; (2) the estimated temperature from mineral couples represents the temperature of subsolidus equilibrium, not the crystallization temperature, and, furthermore, it is also more sensitive to reactions in granitic rocks [24,25]. Moreover, geological processes, such as weathering, hydrothermal alteration, and metamorphism could affect the minerals’ compositions [26].

Zircon saturation thermometry is frequently used to estimate magma crystallization temperature. Zircon is a host for high field strength elements (HFSEs) and rare earth elements [20,27,28,29]. Among the HFSEs, Th, U, Zr, Ti, Nb, Ta, and Hf are immobile during various types of geological processes, such as weathering, alteration, and metamorphism [30,31,32]. In the present research, we to show the relationship between HFSEs (Nb, Ta, Zr, Hf, Th, U, Ce, Y, and Ti) content in igneous rocks and magma crystallization temperatures, by using a large number of various types of whole rock compositions. We suggest two new equations for the estimation of magma crystallization temperature based on whole rock chemistry.

2. Source Data and Method

A total of 994 whole-rock datasets were selected from http://georoc.mpch-mainz.gwdg.de/georoc/ (accessed on 29 August 2021). These data were selected from various magmatic rocks from different areas. Contents of Nb, Ta, Zr, Hf, Th, U, Ce, Y, and major elements are reported in Supplementary Materials Tables S1 and S2, including metaluminous to peraluminous and peralkaline to alkaline compositions, respectively. The Kolmogorov–Smirnov (K-S) [33] test was used to check the normality of the data distribution. All distributions of Nb, Ta, Zr, Hf, Th, U, Ce, Y, Ti (herein used as TiO₂ in wt.%), were nonnormal (Kolmogorov-Smirnov v alues < 0.01). Skewness values were positive for all studied elements. Probability (P) values with less than 0.05 and 0.01 were considered to indicate significant differences (confidence levels of 0.95% and 0.99%, respectively).

3. Zr Saturation Temperature, A Review

Watson and Harrison [18] suggested that the zircon saturation in granitic melts is related to the Zr content, melt composition, and magma crystallization temperature. Based on their calculation, the M value (M = [Na + K + 2Ca]/[Si × Al]) could be an outstanding compositional proxy that is calculated based on the molar values of each component and is expressed as Equation (1):

$${\mathrm{T}}_{\mathrm{Zr}}(°\mathrm{C}) = \frac{\mathrm{12,900}}{\ln \frac{\mathrm{497,600}}{\mathrm{Zr}\left(\mathrm{ppm}\right)} + 3.8 + 0.85\left(\mathrm{M}-1\right)}-273$$

(1)

This equation (herein referred to as WandH83) was calibrated for M ranging from 0.9 to 1.9 and it did not work for peralkaline rocks. This equation worked well for low-Fe magma [34]. Equation (1) (herein referred to as B13) has been updated by Boehnke et al. [19] as follows (B13):

$${\mathrm{T}}_{\mathrm{Zr}}(°\mathrm{C}) = \frac{10108}{\ln \frac{\mathrm{497,600}}{\mathrm{Zr}\left(\mathrm{ppm}\right)} + 1.48 + 1.16\left(\mathrm{M}-1\right)}-273$$

(2)

The WandH83 and B13 zircon saturation temperature models also do not support estimated temperature for the samples with M > 2, high alkali composition, and higher temperatures. Gervasoni et al. [20] updated the T_Zr calculation for melts with M > 2, and ASI (ASI = [Al₂O₃/(CaO + Na₂O + K₂O)]) [35] ranging from 0.49 to 1.4. Fe-poor and also more alkaline compositions than those were used by WandH83 and B13 in the following Equation (3):

$${\mathrm{T}}_{\mathrm{Zr}}(°\mathrm{C}) = \frac{\mathrm{lnZr}\left(\mathrm{ppm}\right)-4.29 + 1.35 \mathrm{InG}}{0.0056}$$

(3)

Here G is the molar ratio (3[Al₂O₃] + [SiO₂])/([Na₂O] + [K₂O] + [CaO] + [MgO] + [FeO]), and Zr (ppm) is the value of Zr in the rock/glass/melt (herein refer to G16).

G16 can be used for more alkaline, intermediate to felsic rocks. Notably, the WandH83, B13, and G16 zircon saturation temperatures were calibrated for temperatures of 800 to 1200 °C [20,36], and the temperature results came with higher uncertainty of at least 50 °C [20].

The first experiment on zircon saturation temperature for basaltic magma was done by Shao et al. [37]. They suggested a refined model as Equation (4) (refer to S19):

ln C_Zr(melt) = (3.313 ± 0.349) – (1.35 ± 0.1) × lnG + (0.0065 ±0.0003) × T_k

(4)

• C_Zr(melt) = Zr concentration in melt (ppm)
• T = Temperature (K)
• G = (3[Al₂O₃] + [SiO₂])/([Na₂O] + [K₂O] + [CaO] + [MgO] + [FeO]) (molar proportion)

The M and G parameters of zircon saturation models were revised, for temperatures from 750 to 1400 °C, with a large range of compositions from mafic to felsic rocks (peralkaline to peraluminous). Based on this calibration two models were suggested [36]. Model 1 is more suitable for estimating the temperature of metaluminous to peraluminous magmas (refer to S20-1), as shown in Equation (5) [36]:

$${\mathrm{lnC}}_{\mathrm{Zr}}\left(\mathrm{melt}\right) = (14.297 \pm 0.308) + (0.964 \pm 0.066) \times \mathrm{M} - \frac{\left(1113\pm 374\right)}{\mathrm{T}}$$

(5)

Model 2 was revised to the G parameter and is used for estimation of the temperature in alkaline to peralkaline rocks (herein referred to as S20- 2) as in Equation (6) [36]:

$${\mathrm{lnC}}_{\mathrm{Zr}}\left(\mathrm{melt}\right) = (18.99 \pm 0.423) – (1.069 \pm 0.102) \times \mathrm{lnG} - \frac{\left(\mathrm{12,288}\pm 543\right)}{\mathrm{Tk}}$$

(6)

T_Zr has been applied to predict the minimum temperature for magmas initially under-saturated in Zr [38,39], which is controlled by magma composition. Zr is an incompatible element, and it does not enter the rocks forming minerals during magma crystallization. Its values gradually increase during magma differentiation. Furthermore, the dissolution of Zr-bearing minerals increases Zr content in the melt and finally enters the zircon crystals [39]. Therefore, T_Zr varies during the fractional and crystallization of magma [18,39,40].

During magma fractionation, late-stage magmatic rocks have a high content of Zr and estimated high T_Zr temperature, compared to less differentiated mafic rocks. To reinforce this concept, silicic and mafic magmas were compared by Siégel et al. [26].

Accordingly, during fractional crystallization of mafic melts, Zr content increases, and M decreases [41]. Mafic magma needs a high Zr content for crystallization of the zircon and it will not happen without a high rate of magma fractionation [26]. Therefore, T_Zr in the mafic rocks is significantly lower than the magma crystallization temperature (T_Zr < T_Magma). T_Zr in the mafic magma has not yet been fully calibrated, but it could still be meaningful if the degree of zircon- undersaturation of magma is determined [26].

During magma fractionation, the Zr contents in the granitic and dioritic rocks are less than the Zr contents in the melt. In this case, T_Zr < T_Magma [40], and, also, in highly evolved magma, the Zr content in the late stage crystallized rocks is higher than that in Zr_Magma, which causes the overestimation of T_Zr [39]. Hence, the pegmatite rocks, which represent the late stage of magma crystallization, mislead us in estimating the magma crystallization temperature. Subsequently, it is necessary to emphasize that T_Zr is the temperature at the onset of zircon crystallization and is not equal to the magma crystallization temperature (T_Magma).

T_Zr may be close the magma temperature (T_Magma) if the rocks and melt composition are the same. Phenocryst-free felsic volcanic rocks, due to quick quenching, could be more likely for T_Zr = T_Magma [18]. This difference is clear in contemporary plutonic–volcanic rocks [40]. Collins et al. [38] mentioned that T_Zr is a reliable estimate for partial melting temperatures in felsic (silicic) rocks with SiO₂ ranging from 65 to 70 wt.%, because zircon is saturated and T_Zr is equal to the T_Magma.

In this research, the chemistries of around 1000 (994) whole rocks, with a wide range of compositions and tectonic settings, were investigated. We assessed the relationship between HFSE contents in the whole rocks and magma temperature with various compositions, from the mafic to felsic, and with the peralkaline to peraluminous affinity. We opted to apply Shao’s two refined models [36]. Consequently, we selected two sets of data including 915 databases of metaluminous and peraluminous rocks throughout the world with M < 2 and SiO₂ > 63% wt.%, and T_Zr was calculated by S20-1 Equation (5) for these rocks. Furthermore, 79 peralkaline to alkaline rocks with M > 2 and SiO₂ > 45 wt.% were selected to estimate the temperature based on the S20-2 model (Equation (6)).

In our dataset, we considered that the T_Zr was not equal to the T_Magma and that it showed the temperature of zircon crystallization. Here, the estimation of magma crystallization temperature for all datasets was calculated by using Equations (5) and (6), presented in Tables S1 and S2.

4. Results

4.1. Major Oxides Relationships with T_Zr

The selected samples were plotted in the metaluminous and peraluminous to peralkaline in an [Al₂O₃]/[(Na₂O + K₂O)] versus [Al₂O₃]/[(CaO + Na₂O + K₂O)] variation diagram [42] (Figure 1).

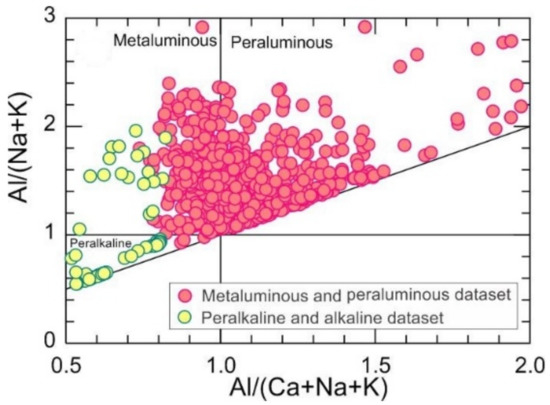
Figure 1. Variation of Al/(Na + K) versus Al/(Ca + Na + K) [42] shows the composition of selected rocks changed from peralkaline to peraluminous. The geochemical data in use in this research was collected from 994 whole rocks datasets on the http://georoc.mpch-mainz.gwdg.de/georoc/ (accessed on 29 August 2021). The 915 databases of metaluminous and peraluminous rocks throughout the world with M < 2 [M = (Na + K + 2Ca]/(Si × Al] and SiO₂ > 63% wt.% (Table S1) and the 79 peralkaline to alkaline bulk rock database with M > 2, and SiO₂ > 45wt.% (Table S2).

To evaluate the effect of the major components of the whole rock, M and G parameters, of the magma crystallization temperature, were calculated. Then, the M and G parameter calculated values were plotted against the temperatures (Figure 2 and Figure 3) which were calculated on the basis of the equations S20-1 and S20-2. Based on Equation (1), the M values had a clear correlation with the temperature. Here, we briefly used M∝W&H83 [18,19], and also G values were consistent with temperature based on Equation (3). G∝G16 in the calculation of Gevasoni et al. are presented in [20]. Nevertheless, our selected data showed that M was not correlated with T_Zr, based on equation S20-1 (R² = 0.21; Figure 2f). Despite this, G denoted a positive correlation with T_Zr in the S20-2 model (R² = 0.87, Figure 3h). Meanwhile, [SiO₂] showed a high positive correlation (R² = 0.82), [MgO], [CaO], and [Al₂O₃] showed a high to a moderate negative relationship (R² = 0.84; R² = 0.61, R² = 0.51, respectively) with T_Zr. Hence, we agreed that the concept of T_Zr and its experimental calibration in the calculation of zircon saturation thermometry by Watson and Harrison [18] and all revisions of T_Zr were robust. However, its application in bulk rock composition (M) has some errors, which were recently discussed by Duan et al. [40].

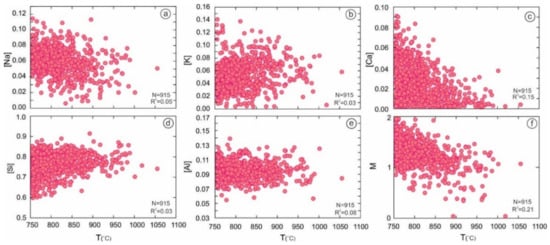
Figure 2. (a–f) Plot of the main members of whole rocks M value [(Na + K + 2Ca]/(Si × Al] (cation ratio) versus T_Zr for the metaluminous to peraluminous dataset (Temperature is estimated by S20-1); (n = 915 from metaluminous and peraluminous with M < 2 and SiO₂ > 63% wt.%, table, accessed on 29 August 2021).

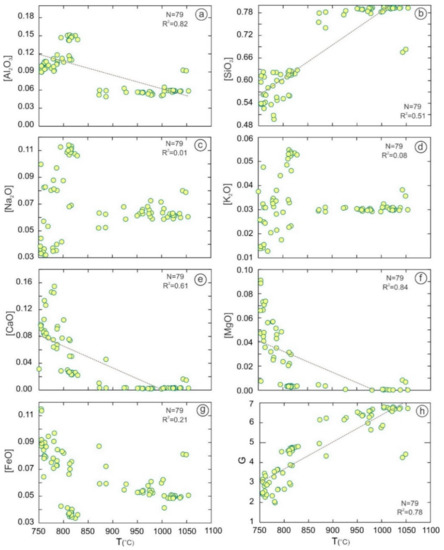
Figure 3. (a–h) G variation (3[Al₂O₃] + [SiO₂])/([Na₂O] + [K₂O] + [CaO] + [MgO] + [FeO]) versus the T_Zr (which calculated based on the Equation (S20-2)) in peralkaline to alkaline dataset. G∝G16 in experimental data of Gervasoni et al. [20];. Nevertheless, there was a clear relationship among the [Al₂O₃], [SiO₂], [CaO], [MgO], and G versus T_Zr (n = 79 peralkaline to alkaline rocks with M > 2, and SiO₂ > 45wt.%, http://georoc.mpch-mainz.gwdg.de/georoc/, accessed on 29 August 2021).

4.2. HFSEs Considerations in Magma Crystallization Temperature

All HFSEs are typically incompatible and are generally concentrated in accessory minerals. Zircon is the main host for HFSEs (Nb, Ta, Zr, Hf, Th, U), and Ti is widely used for determining the temperature of magma when zircon is saturated [18]. Therefore, the behavior of Zr in granitic melts is an important factor to estimation of zircon saturation temperature. In the following, we present some geochemical pairs of Nb-Ta, Zr-Hf, and Th-U with some petrogenesis index, such as Zr/TiO₂ and Zr + Nb + Ce + Y, to show how the distribution of the HFSEs in the melts are controlled by temperature.

4.2.1. Nb and Ta’s Relationship with T_Zr

The elements Nb and Ta are not fractionated during most geological processes [43] and are poorly soluble in solution [44]. The contents of Nb and Ta in the bulk crust are approximately 8 and 0.7 ppm, respectively [45]. Niobium (Nb) is mostly concentrated in alkaline rocks, such as alkali granite and alkaline mafic and ultramafic rocks, and Ta accompanies Nb with abundances of one-tenth to one-fifteenth [46].

To evaluate the relationship between the temperature and Nb and Ta concentrations, the temperature was calculated based on WandH83 [18], G16 [20], and S20 [36] (Tables S1 and S2). In Nb-Tzr in Figure 4a–d there is no evidence of aa significant relationship between zircon saturation temperature and Nb (R² = 0.08, Figure 4a; R² = 0.34, Figure 4b). Meanwhile, there is a frail positive and linear correlation between Ta concentration and temperature in the metaluminous and peraluminous datasets (R² = 0.02; Figure 4c) (here, T is estimated from the zircon saturation thermometer in Equation (5)). Nevertheless, a positive linear correlation between T_Zr and C_Ta (R² = 0.69) appears in the alkaline and peralkaline rocks (Figure 4d) with Equation (7) as follows:

T(°C) = −0.265C_Ta(ppm)² + 19.65C_Ta + 729.58

(7)

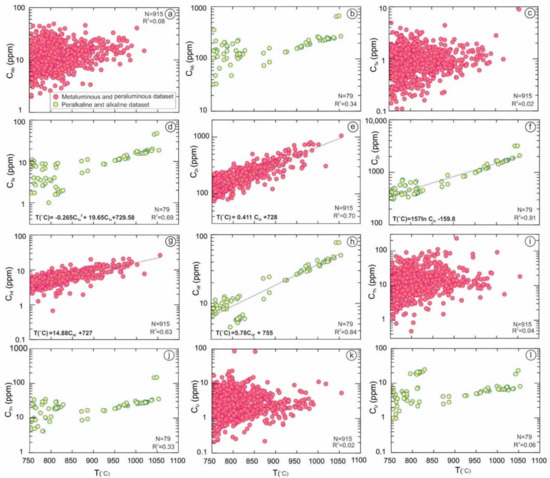
Figure 4. (a,b) Nb versus the temperature (a) in the metaluminous to peraluminous rocks, (b) Peralkaline to the alkaline dataset. (c,d) C_Ta versus the temperature (c) in metaluminous to the peraluminous dataset, (d) in peralkaline to the alkaline dataset. C_Nb is not correlated to the temperature but Ta∝T in the peralkaline to the alkaline dataset. C_Zr versus the temperature (e), in metaluminous to the peraluminous dataset, (f) in peralkaline to alkaline Plot C_Hf versus the temperature (g) in metaluminous to the peraluminous dataset, (h) in peralkaline to the alkaline dataset. The pattern shows that the temperature in whole rocks has a strong positive relationship with Zr and Hf in both datasets. C_Th versus the temperature in the metaluminous to peraluminous dataset (i), and in the peralkaline to alkaline dataset (j) (Temperature is estimated by S20-2). U abundances versus the temperature in metaluminous to peraluminous (k) and in peralkaline to alkaline dataset (l). C_Th and C_U are depended on the temperature in bulk composition. (Note: Temperature calculated based on the S20-1 in metaluminous to peraluminous dataset (n = 915) and Equation (S20-2) for the peralkaline to alkaline (n =179) dataset, n = 994, http://georoc.mpch-mainz.gwdg.de/georoc/, accessed on 29 August 2021).

C_Ta = Ta values (ppm) in whole rock.

4.2.2. Zr-Hf of Whole Rocks and Their Relationship to the T_Zr

Accessory minerals, such as zircon and ilmenite, can control the concentrations of Zr and Hf during partial melting and magma differentiation [47]. Additionally, Zr and Hf are immobile [48]. The plotting of the Zr-Hf versus the calculated temperature shows a positive correlation between Zr and Hf contained in the whole-rock composition and temperature (Figure 4e–h). In the peraluminous and metaluminous datasets, there was a positive linear regression (R² = 0.71) between temperature and Zr at the >99% confidence level (p < 0.01) (Figure 4e) (Equation (8)). The correlation diagrams and equations appear as follows:

T(°C) = 0.411 C_Zr(ppm) + 728

(8)

As shown in Figure 4f, alkaline and peralkaline rocks showed a higher correlation (R² = 0.91) between T_Zr and Zr, and Equation (9) describes the trend (Figure 4f):

T(°C) = 157ln C_Zr(ppm) − 159.8

(9)

Moreover, there was a significant positive correlation between the zircon saturation temperature and Hf (R² = 0.63) (p ≤ 0.001, Figure 4g) for the peraluminous and metaluminous rocks:

T(°C) = 14.88C_{Hf (ppm)} + 727

(10)

In alkaline and peralkaline rocks (p ≤ 0.001; Figure 4h; R² = 0.84):

T(°C) = 5.78C_Hf (ppm) + 755

(11)

These equations show T∝Zr and T∝Hf.

4.2.3. Th and U of Whole Rocks and Their Relationship to Tzr

U ^{+ 4} and Th ^{+ 4} with an ionic radii of 1.00 A° and 1.05 A° [49] are common substitutes for Zr ^{+ 4} in zircon grains [50].

Plotting of Th and U of the bulk rocks versus the Tzr did not confirm a significant correlation for the metaluminous to peraluminous, and also for the peralkaline to alkaline rocks (Figure 4i–l). The scattering of Th and U (Figure 4i–l), showed that their concentrations in the magma were not affected by melt temperature.

4.3. Geochemical Index Relationship to T_Zr

The immobile elements, especially HFSEs, are good indicators for discriminating geological classification and geotectonic signatures [51,52]. The Zr/TiO₂ ratios showed a robust positive correlation (R² = 0.90) with estimated temperature from zircon saturation thermometry at the >99% confidence level (p ≤ 0.001, Figure 5a) in the alkaline and peralkaline databases. This meant that the Zr/TiO₂∝ T_Zr and Zr/TiO₂ ratio increased with rising temperatures of magma (Figure 5a), according to the following equation:

T(°C) = 505.94 (Zr/TiO₂)^0.077

(12)

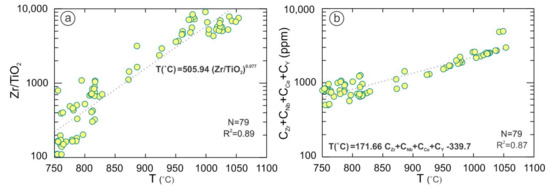
Figure 5. HFSE- based parameters (a) Zr/TiO₂ and (b) C_Zr + C_Nb + C_Ce + C_Y versus T (°C) with a strong correlation with temperature in peralkaline and alkaline rocks (n = 79 peralkaline to alkaline rocks with M > 2, and SiO₂ > 45wt.%, http://georoc.mpch-mainz.gwdg.de/georoc/, accessed on 29 August 2021.

Immobile elements, such as Zr, Y, and Nb, are mainly used for discriminating geological settings, especially in alkaline rocks. Ce increases during the magma differentiation in alkaline rocks [53]. Zr + Nb + Ce + Y versus T_Zr variation (Figure 5b) showed a strong positive correlation (R² = 0.87) in the alkaline rocks at the >99% confidence level (p ≤ 0.001) with a simple equation as follows:

T(°C) = 171.66 (C_Zr + C_Nb + C_Ce + C_Y) − 339.7

(13)

5. Discussion

Due to the diffusion rates in tetravalent cations, such as Zr, Hf, Th, U, Ce, Ga, and Ti, being too slow, with low immobility of these elements during the geological process, they are worthy geochemical tracers [54] and geothermometers. Zirconium and Ti have known elements for geothermometric assessment, by using Ti substances in zircon, quartz and also Zr values in rutile, and Ti contents in quartz [1,55,56,57,58]. The rest of the HFSEs show similar characteristics. Here, we discuss and highlight how the HFSE abundances are controlled by magma temperature.

5.1. Nb-Ta, Zr-Hf, and Th-U Values Are Related to Magma Composition and Temperature

The contents of Nb and Ta (Tables S1 and S2) in the alkaline rocks were much higher than those in the other igneous rocks (Table S2). Tantalum and Nb, with large ionic charges, large ionic radials, and also low partition coefficients, cannot enter the crystal lattices of the main rocks forming minerals. Therefore, their abundances increase in the melts. Furthermore, too low degrees of partial melting or highly fractionated magmas can be rich in these two elements [32,59]. Niobium (Nb) is usually concentrated in peralkaline granites [60], whereas Ta is concentrated in peraluminous granite and pegmatite [61]. The concentrations of Nb and Ta are too low in the bulk rock composition (Table S1 and S2) and their contents do not show a clear correlation with temperature in metaluminous to peralkaline rocks (Figure 4a–d). Nonetheless, Ta has a lower coefficient than Nb [62], and Ta contents in peralkaline and alkaline samples showed a clear relationship with temperature (Figure 4d).

5.2. Zr and Hf’s Relationship to the Magma Composition

Zirconium and Hf were more concentrated in the igneous alkaline rocks (Table S2). Zirconium, Hf, Nb, and Ta abundances are controlled by the crystallization of accessory minerals, such as zircon, baddeleyite, perovskite, and pyrochlore [63]. Zr solubility in alkaline melts is high [64]. Hf solubility is higher than that of Zr in peraluminous magma [62]. Hafnium and Zr have similar solid/melt distribution coefficients Dzr = D_Hf [32], and they also showed a strong relation with magma temperature (Figure 4e–h)

5.3. Th and U Relationship to Whole-Rock and Magma Crystallization Temperatures

Thorium (Th) and U are incompatible during the melting of the mantle and increase in felsic rocks [65]. Thorium and U enter accessory minerals, such as zircon, monazite, apatite, and allanite, without a clear relationship to magma temperature (Figure 4i–l). Nevertheless, their abundances increase in high degrees of fractional crystallization [66]. In highly evolved magma, the distribution coefficient for both Th and U is high, and T_Zr is overestimated in relation to the temperature of magma [39]. Hence, highly evolved magma was ignored in this research.

5.4. Suggestion Geothermometer

To check the applicability of the relationship between HFSEs and zircon saturation temperatures, we collected various compositions from mafic to felsic and peralkaline to peraluminous compositions around the world (http://georoc.mpch-mainz.gwdg.de/georoc/, accessed on 29 August 2021). Here, we summarize our findings for metaluminous to peraluminous and peralkaline to alkaline compositions rocks.

5.4.1. (Zr-Hf) Metalumous–Peralumous Temperature Model

As shown in Figure 6, the lnC_Zr + 0.964(M − 1) value for the whole rocks was related to temperature. Herein, by fitting 915 samples of metaluminous and peraluminous composition, we developed a new equation between lnC_Zr + 0.964(M-1), lnC_Zr, LnC_Hf, and 1000/T as follows:

lnC_Zr(ppm)-0.964(M − 1) = 0.9369 × lnC_{Zr(ppm) +} 0.0956

(14)

R² = 0.71, (Figure 7a).

T_(K) = −8392.3/(lnC_Zr(ppm) − 12.8)

(15)

R² = 0.71, (Figure 7b).

lnC_{Zr (ppm)} − 0.964(M − 1) = 0.7543lnC_{Hf (ppm)} + 3.7516

(16)

R² = 0.58, (Figure 7c)

T_(K) = −7721.8/(lnC_{Hf (ppm)} − 7.7897)

(17)

R² = 0.58, (Figure 7d).

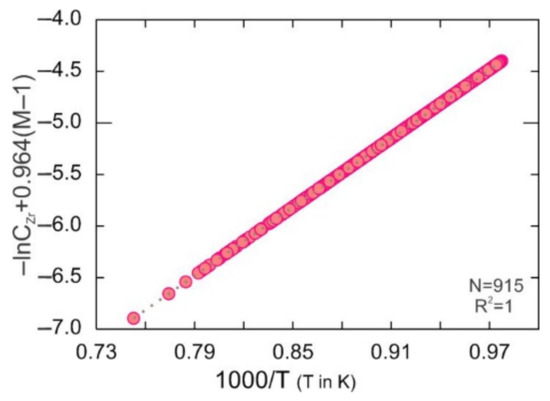
Figure 6. Variation of −lnC_Zr + 0.964(M − 1) vs. 1000/T (T_K) to refine the zircon saturation for metaluminous to peraluminous rocks which are modeled by the equation of S20-1.

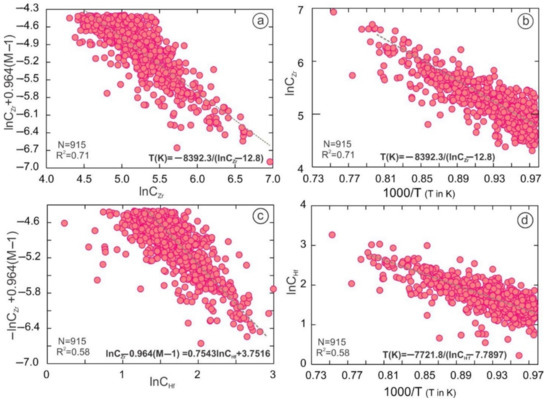
Figure 7. (a–d) lnC_Zr, lnC_Hf vs. −lnC_Zr + 0.964(M − 1) and 1000/T (T in K) are plotted for the metaluminous to peraluminous rocks. InC_Zr and lnC_Hf to lnC_Zr + 0.964(M − 1) and 1000/T (T in K) infer a negative correlation (n = 915, and M < 2. http://georoc.mpch-mainz.gwdg.de/georoc/, accessed on 29 August 2021).

The concentrations of Zr and Hf in the whole rocks, calculated based on equation S20-1 (Equations (14)–(17)), showed a strong positive regression with the temperature (Figure 7a–d). Therefore, Equations (14) and (16) were combined to evaluate the relationship between the composition and C_Zr + C_Hf in the metaluminous to the peraluminous dataset, as follows:

lnC_{Zr (ppm)} − 0.964(M −1) = 1.4391 × (lnC_Zr(ppm) + lnC_Hf(ppm) + 0.2936

(18)

R² = 0.71, (Figure 8a)

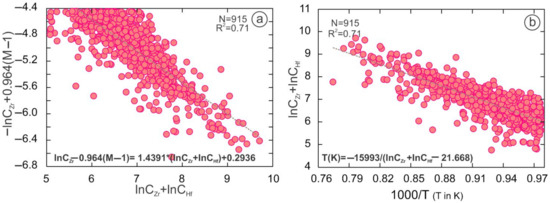
Figure 8. (a) lnC_Zr + lnC_Hf to lnC_Zr + 0.964(M–1) and 1000/T (T in K) show a negative correlation (b) Accordingly, C_Zr + C_Hf in bulk composition could be related to the temperature. (n = 915, and M < 2 http://georoc.mpch-mainz.gwdg.de/georoc/, accessed on 29 August 2021).

The concentration of Zr and Hf in the whole rock in the metaluminous to the peraluminous rocks showed a good correlation with the main components of the S20-1 and magma crystallization temperatures (Equations (14)–(17)). Therefore, we tried to obtain an equation based on Zr-Hf abundances in the whole rock data in the metaluminous to the peraluminous rocks based on a linear correlation between the lnC_{Zr (ppm)} + lnC_{Hf (ppm)} and temperature. Finally, by fitting the 915 samples, we proposed a temperature model in the metaluminous to the peraluminous rocks by using the abundances of the Zr and Hf in the whole rock as follows (Equation (19)) (p value < 0.001) (Figure 8b):

T_(K) = −15993/(lnC_{Zr (ppm)} + lnC_{Hf (ppm)} − 21.668)

(19)

It is notable that the estimation of the temperature was done based on the HFSE contents in the whole rock and calibrated based on the S20-1 and was appropriate for a temperature from 750 to 1400 °C, M < 2, and SiO₂ > 63 wt.%.

5.4.2. Temperature Model Based on the HFSE Abundances in the Peralkaline–Alkaline Rocks

Alkaline magmas have a high contents of Na⁺, K⁺, Ca⁺², and M⁺², which are network modifiers and are known to breakdown silicate bonds and make non-bridging oxygen [67]. Additionally, alkaline melts have an open structure chain, and the sheet is kept apart because they are less polymerized with low viscosity. Accordingly, it is difficult for Zr⁺⁴ to combine with SiO₄ tetrahedra and crystallize zircon [68]. Perhaps, this could explain the higher contents of Zr in the alkaline melts. In the alkaline and peralkaline melts, concerning increasing T_Zr, several parameters were proposed to increase, including Zr, Hf, Zr/TiO₂, and Ce + Y + Nb + Zr.

As shown in Figure 9, the lnC_Zr + 1.069lnG value was related to the temperature (R² = 0.99). To check the applicability of using HFSE abundances in the whole rocks to the main component of S20-2 and temperature, we plotted the contents of Zr, Hf, Zr/TiO₂, and Zr + Nb + Ce + Y versus the lnC_Zr −1.069lnG and 1000/T_K. (the main parameters of S20-2 equation) as below:

lnC_{Zr (ppm)} − 1.069lnG = 0.643lnC_{Ta (ppm)} + 4.4097

(20)

R² = 0.57, (Figure 10a)

T _(K) = −8202/(lnC_Ta(ppm) − 9.119)

(21)

R² = 0.52, (Figure 10b).

lnC_Zr(ppm) − 1.069lnG = 1.092LnC_Zr(ppm) − 1.5708

(22)

R² = 0.87, (Figure 10c).

T _(K) = −7699/(lnC_Zr(ppm) − 13.39)

(23)

R² = 0.89, (Figure 10d)

lnC_Zr(ppm) − 1.069lnG = 0.869 × lnC_Hf(ppm) + 3.2587

(24)

R² = 0.85, (Figure 10e).

T (K) = −9309/(lnC_Hf(ppm) − ;10.9)

(25)

R² = 0.83, (Figure 10f).

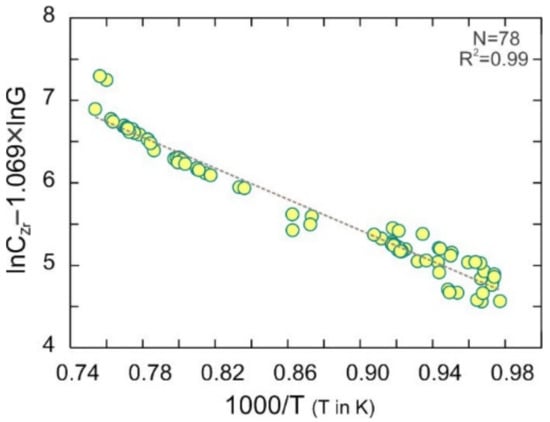
Figure 9. lnC_Zr + 1.069lnG vs. 1000/T (T in K) based on Equation (S20-2) for the peralkaline to alkaline rocks.

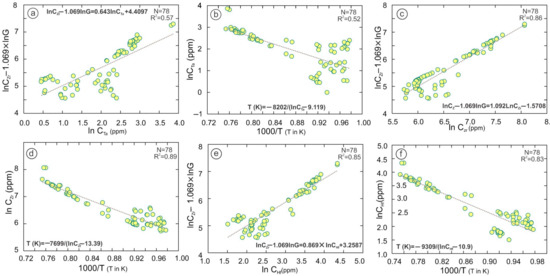
Figure 10. (a–f) Plot lnC_Ta, lnC_Zr, and lnC_Hf versus the lnCZr–1.069lnG and 1000/T in the peralkaline to alkaline rocks which is showing a clear correlation except for C_Ta.

lnC_{Zr(ppm) -}1.069lnG = 0.4622(ln(C_Zr(ppm)/TiO_2(wt.%)) + 2.375

(26)

R² = 0.64, (Figure 11a).

T_(K) = −14507/((lnZr_(ppm)/TiO₂(wt.% in bulk rock) –19.89)

(27)

R² = 0.76, (Figure 11b).

lnC_Zr(ppm)-1.069lnG = 1.202(lnC_Zr + C_Nb + C_Ce + C_Y) _(ppm) −2.87

(28)

R² = 0.83, (Figure 12a).

T_(K) = −6733/(ln(C_Zr + C_Nb + C_Ce + C_Y) _(ppm) − 12.992)

(29)

R² = 0.85, (Figure 12b).

Concerning the temperature, four parameters were proposed, including Zr, Hf, (Zr + Nb + Ce + Y), and Zr/TiO₂. As discussed previously, the abundances of Hf, Nb, Ce, Y and Zr/TiO₂ showed a clear correlation with temperature (Equations (21)–(29). Herein, we tried to find an equation for estimating magma crystallization temperature based on HFSE abundances in the peralkaline to alkaline rocks, based on Equations (21)–(29). To optimize the calculation of the coefficient, Nb and Ta were ignored. Using Equations (21) to (29) we obtained the following:

lnC_Zr(ppm)− 1.069lnG = 0.3877 ln(C_Hf + C_Y + C_Ce) (ppm) + (ln(C_Zr(ppm)/TiO_2(wt.%)) + 0.6762

(30)

R² = 0.80, (Figure 12c)

The abundances of Hf, Nb, Ce, Y and Zr/TiO₂ ratios _in in the peralkaline to alkaline rocks showed a clear relationship to the main parameters of the S20-2 equation. So, herein, due to the strong correlation between the ln(C_Hf + C_Y + C_Ce) _(ppm) + (ln(C_Zr(ppm)/TiO_2(wt.%)) and temperature (T_K), the following equation could be suggested for estimating the magma temperature for these rocks (Equation (31)):

T_(K) = −20914/(ln (C_Hf + C_Y + C_Ce) _(ppm) + (ln(C_Zr(ppm)/TiO_2(wt.%)) − 31.153)

(31)

R² = 0.88, (Figure 12d).

This model is appropriate for obtaining the temperature of magma for a wide range of compositions of mafic to felsic peralkaline and peraluminous whole-rock data (M > 2) and is calibrated, based on S20-2 Equation 6 and for T > 750 °C to <1400 °C.

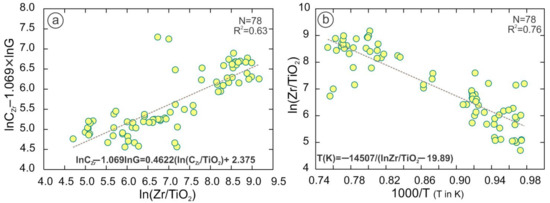
Figure 11. (a,b) ln(C_Zr/TiO₂) in bulk composition correlate to lnC_Zr − 1.069lnG and 1000/T.

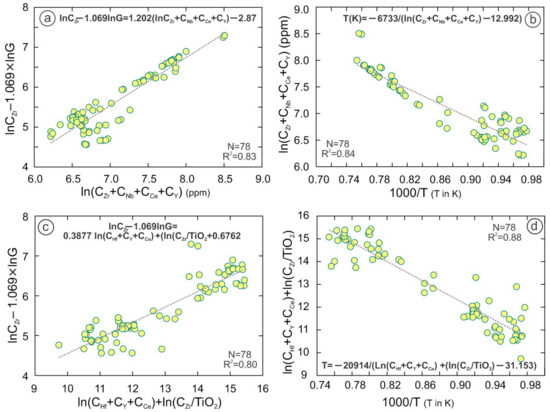
Figure 12. (a,b) ln (C_Zr + C_Nb + C_Ce + C_Y) correlate to lnC_Zr − 1.069lnG and 1000/T. (c,d) The suggesting HFSEs parameter ln(C_Zr + C_Nb + C_Ce + C_Y) + ln(CZr/TiO₂) versus the lnC_Zr − 1.069lnG and 1000/T indicate that this parameter could be dependent on the temperature.

5.5. Testing the Equations

To test our suggested equations in the metaluminous and peraluminous rocks (Equation 19), we selected the peraluminous granite in southern Saqqez, northeast of Iran [69] (Table 1). These samples were plutonic (granite and granodiorite) to volcanic (andesite, rhyolite, and dacite). The pluton displayed M = 1.08 to 1.74, which were within the experimental range of WandH83 and B13. We calculated T_Zr for these rocks based on equations WandH83, B13, S20-1, and our suggested equations (Figure 13a–c, Table 1). For fifteen samples, the average temperature of our model (Equation 19), based on HFSEs in whole rock, was 692°C (531 °C–792 °C) and, calculated by S20-1, it was 712 °C (556 °C–812 °C), calculated by WH83 it was 723 °C (584 °C–810 °C) and calculated by B13 it was 675 °C (515 °C–779 °C) (Figure 13a–c).

Table 1. Chemical composition of 18 selected peraluminous granite in southern Saqqez, northeast of Iran [69,70]. Temperatures are estimated from the revised T_Zr (temperature of zircon saturation) by Watson and Harrison [18], Boenke et al. [19] and Shao [36address metaluminous to peraluminous rocks with] and suggested model for metaluminous and peraluminous rocks in degrees Celsius. [M = (Na + K + 2Ca]/(Si × Al).

SAMPLE NAME	ROCK NAME	SiO2	TiO2	Al2O3	Fe2O3	FeO	MnO	MgO	CaO	Na2O	K2O	P2O5	LOI	Zr	Nb	Th	U	Ta	Hf	M	W&H83	B13	S20-1	T Suggested Model
		Wt.%	Wt.%	Wt.%	Wt.%	Wt.%	Wt.%	Wt.%	Wt.%	Wt.%	Wt.%	Wt.%	Wt.%	ppm	ppm	ppm	ppm	ppm	ppm		(°C)	(°C)	(°C)	(°C)
HMP-7	Rhyolite	76.0	0.140	13.6	1.59	1.43	0.050	0.310	0.160	3.52	3.55	0.050	1.02	89.0	12.1	9.34	2.12	0.986	3.22	1.00	764	727	759	726
HMP-9	Rhyolite	73.7	0.170	14.6	2.30	2.07	0.050	0.320	0.810	5.08	1.77	0.050	1.11	101	20.0	8.11	2.18	1.48	3.42	1.14	764	724	758	738
HMP-10	Rhyolite	69.9	0.330	14.4	2.57	2.31	0.100	0.980	3.02	2.68	2.19	0.050	3.85	61.8	9.05	7.31	1.86	0.689	2.17	1.22	719	669	706	681
HMP-17	Dacite	69.2	0.420	15.0	3.38	3.04	0.050	1.31	2.66	4.38	2.00	0.150	1.42	78.7	4.18	5.76	1.52	0.272	2.47	1.42	724	670	711	702
PKM-1	Granodiorite	68.1	0.580	15.8	4.37	3.93	0.080	1.47	2.14	3.39	2.16	0.050	1.81	49.0	6.72	6.92	1.62	0.402	1.90	1.11	708	660	695	661
PKM-4	Granite	75.1	0.320	14.3	0.760	0.684	0.050	0.410	0.85	7.15	0.05	0.050	0.700	169	9.94	5.30	1.71	0.771	4.92	1.34	794	752	789	797
PKM-5	Granodiorite	63.2	0.900	16.2	5.90	5.31	0.120	1.93	4.53	4.91	0.27	0.110	1.91	34.7	10.5	6.56	1.46	0.801	1.41	1.64	650	584	628	627
PGM-23	Granodiorite	68.3	0.530	14.2	4.67	4.20	0.100	1.47	4.15	3.48	0.79	0.050	2.29	10.1	3.97	3.16	0.72	0.235	0.60	1.46	585	515	557	532
PGM-24	Granodiorite	68.8	0.570	14.9	3.55	3.20	0.150	2.37	3.06	4.05	0.52	0.050	2.06	17.0	4.51	4.41	0.876	0.263	1.04	1.28	626	563	602	578
PGM-29	Rhyolite	77.2	0.180	12.3	1.24	1.12	0.050	0.180	0.290	4.05	4.01	0.050	0.44	73.4	5.25	7.70	1.66	0.384	2.42	1.28	729	678	716	697
PGM-30	Rhyolite	73.0	0.390	14.7	2.42	2.18	0.050	0.120	0.230	6.83	1.67	0.060	0.51	127	6.37	5.88	1.38	0.494	3.90	1.34	769	723	761	761
PKH-1	Granite	70.3	0.430	15.4	2.95	2.66	0.080	0.680	1.88	4.58	2.34	0.050	1.31	57.6	10.2	9.51	1.81	0.689	2.43	1.29	709	656	694	683
PKH-2	Granodiorite	67.5	0.370	17.2	3.24	2.92	0.080	0.900	2.35	3.16	3.20	0.050	1.81	174	17.8	9.14	2.37	1.31	4.74	1.14	811	779	812	797
PKH-4	Granite	69.7	0.440	15.3	3.57	3.21	0.070	1.58	0.480	4.42	2.39	0.050	2.02	103	5.69	5.20	1.17	0.400	3.01	1.03	773	738	770	731
PKH-5	Granite	71.6	0.390	15.6	2.64	2.38	0.050	1.31	0.160	4.04	2.31	0.050	1.90	55.4	6.42	6.00	1.29	0.515	2.01	0.875	734	695	726	670
KMG-9	Granite	70.5	0.362	15.2	3.22	2.90	0.059	0.950	2.25	3.28	4.17	0.102	0.540	122	12.8	14.0	2.38	1.29	3.58	1.37	763	716	755	753
KMG-10	Granite	69.5	0.361	15.1	3.14	2.83	0.058	0.950	2.30	3.32	4.13	0.101	0.420	103	12.9	13.4	1.70	1.31	3.43	1.39	748	698	737	739
KMG-11	Granite	71.7	0.331	15.3	2.90	2.61	0.049	0.840	1.82	2.72	3.50	0.095	0.670	138	13.2	13.5	1.58	0.400	4.11	1.09	795	762	794	770
KMG-14	Granite	72.5	0.188	14.0	2.37	2.13	0.029	0.420	1.44	3.47	4.85	0.062		124	5.16	10.8	2.42	0.930	4.12	1.40	762	714	753	763
MGF-10	Granite	67.1	0.523	16.2	3.96	3.56	0.070	1.39	3.00	3.36	3.95	0.137	0.620	140	15.4	14.4	2.25	0.900	3.96	1.46	767	719	759	769
KMG-1	Granite	75.0	0.128	13.6	0.910	0.819	0.009	0.160	0.780	3.09	5.32	0.025	0.520	73.9	8.46	24.0	3.96		2.62	1.27	731	680	718	702
KMG-2	Granite	76.8	0.031	13.1	0.740	0.666	0.011	0.060	0.620	3.39	4.95	0.017	0.250	77.9	9.10	25.2	3.87		3.98	1.27	735	685	722	731
KMG-4	Granite	72.7	0.209	13.9	2.05	1.85	0.060	0.460	1.62	3.42	4.05	0.052	0.510	79.6	10.1	13.6	1.79	1.24	2.69	1.33	732	681	719	708
KMG-6	Granite	73.1	0.202	14.1	1.88	1.69	0.038	0.380	1.49	3.23	4.73	0.048	0.580	96.9	9.85	17.9	2.01	1.57	3.17	1.33	747	698	737	730
MGF-7	Granite	73.9	0.147	14.4	1.76	1.58	0.009	0.360	1.34	2.85	5.19	0.033	0.690	136	6.96	11.0	1.55	0.660	4.07	1.26	781	739	775	769

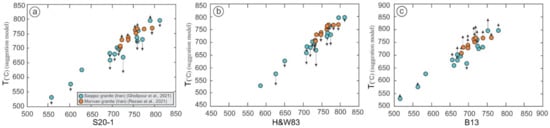
Figure 13. The correlation of the present suggested model temperature with the previously published equations (a) S20-1 [36], (b) W&H83 [18], and (c) B13 [19] for some metaluminous to peraluminous igneous rocks [69,70]. That shows the HFSEs in bulk rocks chemistry have a clear relation to the magma crystallization temperature and it is more consistent with zircon saturation temperature at higher than 750 °C. The length of the arrow shows the differences in the suggested temperature here with T(S20-1), W&H83, and B13, respectively.

Notably, our model for estimating the temperature in the metaluminous to peraluminous rocks was calibrated by the S20-1 limitation of 750 °C to 1400 °C, M < 2, and SiO₂ > 63%. In this study, only three samples showed temperatures higher than 750 °C, and the calculated temperatures based on our model, S20-1, WandH83, and B13, in these samples included PKM4 sample (granite): our model: 796 °C, S20-1: 789 °C; WandH83: 794 °C and B13: 751 °C. PGM-30 (rhyolite) our model: 761 °C, S20-1: 761 °C, WandH83: 769 °C, B13: 723 °C. PKH-2 (granodiorite): Our equation: 796 °C, S20-1: 812 °C, WandH83: 810 °C and B13: 779 °C (Table 1). The difference range of our suggested model was −56 to 8, −64 to 3, and −25 to 45 with S20-1, WandH83, and B13 (Figure 13; Table 1). Based on a comparison of these new equations with the previous models, our result was consistent with S20-1, WandH83, and B13 and suggested the possibility of using HFSE concentrations in whole-rock data for the estimation of temperature.

Another example for the testing of our model was Marivan granitoid body in the northern part of the Sanandaj-Sirjan zone [70]. Ten peraluminous granite samples with SiO₂ > 63% were selected. Zircon U–Pb dating indicated the late Eocene age for this body [70]. The range of Zr abundances changed from 73.9 to 140 ppm. This pluton had M values that changed from 1.08-1.46, all of which were within the experimental range specified by the WandH83, B13, S20-1, and our suggestion model (Figure 13a–c). Zircon saturation temperatures from this pluton were calculated by using WandH83, B13, and S20-1 equations, and our suggested equation. For the ten samples, the average of our model was 743°C (702°C-770 °C), of S20-1, it was 747 °C (717 °C–793 °C), of WandH13, 756 °C (730 °C-794 °C) and of B13, 709 °C (680 °C–761 °C) (Table 1). As mentioned before, just 5 samples indicated temperatures higher than 750 °C. KMG-9: our model: 752 °C, S20-1: 755 °C, W&H83: 763 °C, B13:716 °C. KMG-11: our model: 770 °C, S20-1: 793 °C; WH83:794 °C: B13: 761 °C. KMG-19: our model: 763 °C; S20-1: 753 °C; WH83: 762 °C; B13: 713 °C (Table 1). MGF-10: our model: 768 °C, S20-1: 759 °C; WH83: 767 °C: B13: 718 °C. MGF-7: our model: 768 °C, S20-1: 775 °C; W&H83; 780 °C: B13: 739 °C (Table 1). The difference range of our suggested model in Marivan granitoid was −23 to 10, −29 to 2, and 9 to 50 °C (Figure 13; Table 1). By using Equation (30), in general, our model yielded temperatures between those of previous models (WH, B13, S20-1) and they overlapped with each other.

To assess the applicability of our model in alkaline igneous rocks, 26 samples from the Basin and Range from geochemical data (http://georoc.mpch-mainz.gwdg.de/georoc/, accessed on 29 August 2021, were selected [71,72,73,74,75,76,77,78,79,80,81] (Figure 14, Table 2). These data had SiO₂ ranging from 40.5 to 67.7 wt.% and M > 2, and all had the specified range of S20-2 and our model. The temperature was calculated by the suggested model in peralkaline to alkaline rocks (Equation 31) and the results compared with the results using S20-2 (Table 2). The results are presented in Table 2 and Figure 14. As shown in Figure 14, the temperature was calculated based on equation S20-2, and our model was more consistent.

Figure 14. The assessment of estimated temperature in the suggested model for peralkaline to alkaline rocks versus estimated temperature by using S20-1. The correlation shows that HFSE-based thermometry mode could be used to estimate temperature and it is extremely close to zircon saturation temperature for peralkaline to alkaline data. The length of the arrow shows the differences in suggested temperature in here with S20-2 (n = 26 sample alkaline of Basin and Range from geochemical data http://georoc.mpch-mainz.gwdg.de/georoc/, accessed on 29 August 2021 [71,72,73,74,75,76,77,78,79,80,81]).

Table 2. The chemical composition of 26 alkaline selected samples from the Basin and Range from geochemical data (http://georoc.mpch-mainz.gwdg.de/georoc/, accessed on 29 August 2021). Temperatures are estimated from the revised T_Zr (temperature of zircon saturation) by Shao [36] (S20-2) and our suggested model for alkaline and peralkaline composition rock in degrees Celsius.

Rock Name	SiO2	TiO2	Al2O3	FeOT	CaO	MgO	MnO	K2O	Na2O	P2O5	Y	Zr	Nb	Ce	Nd	Yb	Hf	Ta	Th	U	M	G	S20-2	T Suggested Model
	Wt.%	Wt.%	Wt.%	Wt.%	Wt.%	Wt.%	Wt.%	Wt.%	Wt.%	Wt.%	ppm	ppm	ppm	ppm	ppm	ppm	ppm	ppm	ppm	ppm	ppm	ppm	(°C)	(°C)
	56.6	1.14	17.1	6.41	6.98	3.91	0.090	2.95	3.59	0.490	25.0	273	15.2	184	87.0	2.18	6.20	0.800	18.8	2.10	2.06	3.62	750	752
Pantellerite	67.7	0.31	10.5	4.70	3.10	0.280	0.160	4.16	4.83	0.140	227	3450	313	676	228	29.7	90.4	19.6	140	23.8	2.26	5.75	1096	1118
	55.7	1.32	17.1	7.68	5.90	3.25	0.170	3.86	4.78	0.710	43.0	434	39.0	154		4.16	10.3	1.800	9.50		2.19	3.48	788	766
	65.9	0.250	12.2	2.41	6.44	0.250	0.130	4.40	4.77	0.100	105	579	88.0	292		9.32	18.0	4.100	32.0		2.72	5.23	859	923
	50.0	0.070	10.5	1.00	3.64	1.09	0.010	3.94	8.45	0.010	59.0	165	69.0	47.4	41.7	5.56	7.70	4.900	69.0	14.7	3.46	4.02	718	842
Basalt	44.5	1.42	13.5	9.11	9.25	12.4	0.173	2.63	5.43	0.772	30.0	295	56.7	227	86.8	2.57	5.66	3.15	20.6	4.51	4.60	1.59	687	755
Basalt	47.8	1.03	16.7	8.89	7.65	10.2	0.280	2.98	2.99	0.658	25.8	257	37.7	195	83.2	2.05	5.79	2.19	15.5	3.34	2.60	2.17	701	756
Basalt	48.5	1.30	15.1	8.53	10.28	9.54	0.130	3.10	1.84	0.853	25.1	236	33.9	309	16.8	2.03	5.25	1.54	15.6	2.97	3.24	2.08	691	761
Basalt	40.5	1.23	16.6	9.84	9.71	14.0	0.314	2.58	3.50	0.903	33.4	315	57.7	173	72.6	2.93	6.48	3.34	12.5	2.87	3.74	1.57	690	755
Basalt	43.0	1.04	18.2	8.82	9.69	12.5	0.275	2.03	2.80	0.773	36.4	366	46.8	301	116	3.24	8.31	3.51	38.5	7.68	2.96	1.86	716	797
Basalt	48.5	1.20	15.0	8.17	12.9	7.14	0.144	3.68	2.08	0.498	33.8	383	46.8	161	69.3	3.02	8.85	3.86	14.2	3.42	3.99	2.10	730	763
Syenite	49.6	1.59	18.9	7.76	7.52	3.49	0.147	4.78	4.62	0.865	37.7	369	47.1	295	110	3.42	8.18	3.47	38.5	7.53	2.51	3.04	761	774
Basalt	46.1	1.29	14.6	9.89	8.73	12.2	0.188	2.73	2.75	0.661	33.1	315	49.9	178	65.8	3.18	6.15	3.68	16.4	3.71	3.34	1.79	701	753
Basalt	47.6	1.78	18.0	8.56	8.55	4.96	0.164	3.47	4.90	1.18	27.9	341	48.2	227	96.1	2.12	7.36	3.32	11.2	2.63	2.87	2.59	739	751
Andesite	55.4	1.38	15.2	6.49	6.48	4.23	0.100	3.70	3.02	0.630	35.0	474	37.0	195	85.1	2.60	10.9	2.03	24.9		2.20	3.44	795	776
Basanite	51.7	1.80	12.7	6.50	6.40	5.70	0.130	8.40	2.00	1.50	105	652		82.0	43.0	1.30	18.3	1.30	3.40	1.40	3.24	2.64	798	771
Basanite	53.3	1.57	12.3	6.02	4.65	7.36	0.100	8.22	2.16	1.56	31.0	803		50.0	25.0	1.20	17.4	0.800	2.70	0.00	2.87	2.65	818	751
Basanite	51.0	1.50	11.6	7.40	7.40	9.20	0.160	7.00	2.00	1.60	25.0	575		91.0	48.0	1.50	14.0	0.900	4.20	1.50	3.83	2.09	764	750
Basalt	43.7	1.40	10.8	9.60	10.2	15.0	0.210	3.00	2.80	1.60	45.0	382		134	68.0	1.70	8.80	1.10	6.50	1.80	5.43	1.37	694	752
Leucitite	46.5	1.98	10.1	9.92	8.97	12.7	0.170	5.41	2.14	1.37	47.0	840		239	113	2.34	16.0	1.00	19.0	2.30	5.25	1.52	768	800
Leucitite,	46.6	1.81	10.6	9.17	9.13	12.1	0.160	4.75	1.99	1.30	51.0	798		214	102	2.34	16.0	1.80	17.0	2.20	4.79	1.61	769	798
Leucitite	49.0	1.53	14.4	8.41	9.63	9.05	0.160	3.58	2.17	0.950	45.0	479		161	76.8	2.55	11.0	1.30	14.0	2.20	3.31	2.11	749	766
Absarokite	45.3	1.21	11.7	8.67	10.0	12.6	0.180	4.20	3.18	2.00	29.0	471	25	208	95.0	2.10	11.0	1.10	9.90	2.60	5.04	1.55	721	784
Minette	51.1	1.79	12.7	7.51	8.71	7.27	0.130	5.93	2.60	1.45	23.0	842	20	102	53.0	1.70	14.0	0.800	3.10	1.00	3.79	2.25	806	764
Absarokite	49.6	1.57	11.2	6.47	8.71	12.0	0.100	5.94	2.08	1.62	21.0	678	25	194	94.0	1.10	14.0	1.00	7.30	1.90	4.43	1.81	765	786
Absarokite	49.9	1.57	11.3	6.44	8.68	11.6	0.100	6.10	2.03	1.63	20.0	576	22	164	82.0	1.10	15.0	1.00	7.60	2.10	4.36	1.85	753	770
Trachyandesite	57.1	1.04	15.5	7.52	6.68	4.29	0.080	3.84	2.95	0.480	34.0	290	12.0	145		2.74	6.43	0.810	16.0		2.20	3.36	749	752
Basalt	48.8	1.79	16.9	10.5	9.19	5.73	0.180	1.64	3.44	1.10	37.0	426		204		2.46	8.09	1.62	12.3		2.69	2.49	754	759
Basalt	50.9	1.44	17.0	9.29	8.47	5.09	0.170	1.69	3.16	0.990	28.0	379		199		2.35	7.61	1.47	11.7		2.34	2.84	756	761
Basalt	50.6	1.53	17.3	9.84	8.61	5.23	0.180	1.87	3.27	1.10	37.0	392		209		2.33	7.56	1.41	11.6		2.42	2.74	756	764
Basalt	49.1	1.61	17.2	9.91	8.70	5.20	0.170	1.66	3.35	1.14	15.0	408		213		2.30	7.79	1.50	10.8		2.47	2.68	757	759
Basalt	47.1	2.17	16.1	10.6	9.34	5.35	0.170	2.00	3.81	1.35	29.0	428		258		2.30	7.88	1.67	9.65		3.03	2.37	750	758
Minette	51.2	1.84	13.0	7.68	8.51	7.10	0.140	5.46	2.80	1.43	23.0	816	21.0	105	54.0	1.70	15.0	0.800	2.90	1.00	3.61	2.30	805	762

6. Conclusions

Most previous models for magma crystallization temperature were based on the mineral composition and Zr saturation index. Here, we present two simple models, using whole-rocks chemistry without any complicated calculations. Whole-rock chemistry, especially HSFE abundances, can be considered a new method for estimating the magma temperature for intermediate to felsic rocks and entire alkaline rocks. The estimation temperature by using our suggested models shows similar ranges to the zircon saturation temperature.