A Block-Based Division Reversible Data Hiding Method in Encrypted Images

Abstract

Due to the increased digital media on the Internet, data security and privacy protection issue have attracted the attention of data communication. Data hiding has become a topic of considerable importance. Nowadays, a new challenge consists of reversible data hiding in the encrypted image because of the correlations of local pixels that are destroyed in an encrypted image; it is difficult to embed secret messages in encrypted images using the difference of neighboring pixels. In this paper, the proposed method uses a block-based division mask and a new encrypted method based on the logistic map and an additive homomorphism to embed data in an encrypted image by histogram shifting technique. Our experimental results show that the proposed method achieves a higher payload than other works and is more immune to attack upon the cryptosystem.

1. Introduction

Data hiding is a technique in which secret messages are embedded into digital media by making non-perceptible slight changes to the cover media. Data hiding can be categorized as irreversible or reversible. The difference between reversible and irreversible data hiding approaches is that, in the former, secret messages can be extracted from the stego-media and the original cover media can be recovered without distortion. On the other hand, in the irreversible data hiding approach, the original cover media cannot be recovered without loss of information.

Reversible data hiding can be used in many applications, therefore, this approach has been extensively studied. In 2003, Tian [1] proposed the difference expansion (DE) method, which is based on the difference expansion transform of pairs of pixels. In 2004, Alattar [2] extended Tian’s method using a difference expansion of vectors, instead of pairs, to increase the payload. Thodi and Rodriquez [3] proposed a new difference expansion scheme, termed the prediction error expansion. In 2006, Ni et al. [4] proposed a reversible data hiding method based on the histogram shifting. The method utilizes the peak point to embed secret messages and shift the pixels between the peak point and zero or the minimum points of the histogram of an image. In 2011, D. Coltuc [5] reduced the embedding distortion of the prediction error expansion reversible watermarking. Gao et al. [6] developed a novel framework for lossless data embedding (LDE) by combining the advantages of the generalized statistical quantity histogram (GSQH) and histogram-based embedding. Li et al. [7] proposed a prediction-error expansion (PEE) for selecting pixels from smooth areas for data embedding, while leaving pixels from rough areas unchanged. In 2012, Wu et al. [8] developed an embedding method and investigated the predictive ability of the new prediction scheme. In 2009, Hong et al. [9] established a histogram of the difference between original pixels and the corresponding predicted values, and used two bins (0 and −1) to achieve a high payload. In 2013, Wang et al. [10] presented a novel framework that can be used to design two-dimensional (2D) reversible data-hiding schemes, while Li et al. [11] proposed a two-dimensional difference histogram modification scheme. Ou et al. [12] exploited image redundancy using the prediction-error expansion. In 2014, Fu et al. [13] exploited the similarity among adjacent pixels and used side-match predictors for obtaining the histogram of prediction errors, to achieve a high embedding capacity. In 2013, Li et al. [14] proposed the pixel value ordering (PVO) method, in which the maximal- (minimal-) value pixel in a block is either increased (decreased) or unchanged to hide one bit. Peng et al. [15] improved the embedding procedure using spatial information associated with pixels. Ou et al. [16] proposed the PVO-k algorithm to adaptively modify the block according to the numbers of maximal- and minimal-valued pixels. Qu et al. [17] proposed a pixel-wise PVO to achieve a higher payload while maintaining marked image fidelity.

In some applications, cover media are encrypted first for privacy reasons, and then secret messages are embedded into the encrypted media. To prevent the content of the cover media from being exposed to an unauthorized user, the content owner encrypts the image before communication. After encryption, the encrypted image will destroy the correlations of local pixels; it is difficult to embed secret messages in encrypted images using the difference of neighboring pixels. This leads to a new challenge consisting of reversible data hiding in encrypted image.

In 2011, Zhang [18] proposed a novel reversible data hiding scheme for encrypted images by modifying a part of the encrypted data. In 2011, Lai et al. [19] proposed a new technique using mosaic image encryption. In 2012, Hong et al. [20] improved Zhang’s method by using a side-match technique in the encrypted image. In 2014, Li et al. [21] used a random diffusion strategy in the encrypted image. Wu and Sun [22] proposed a different strategy based on prediction error. In 2015, Li et al. [23] proposed a method for reversible data hiding in encrypted images using cross-division and an additive homomorphism. Liao and Shu [24] calculated the complexity of image blocks and proposed a new, more precise function to calculate the complexity of image blocks. Pan et al. [25] did not concatenate the neighboring block’s border pixels to the current block, but only used the current block itself. In 2016, Cao et al. [26] fully exploited the correlations of neighbor pixels, and then proposed a novel method for high-capacity separable reversible data hiding in encrypted images. Qian and Zhang [27] assumed the original grayscale image with all pixel values falling into [0, 255], and the image size as M × N, where both M and N are the power of 2. The image owner turns the original image into plain bits by decomposing each pixel into 8 bits. In 2017, Khanam and Kim [28] proposed two reversible data hiding systems using an enhanced embedding pattern and offering a high payload. Yi and Zhou [29] first introduced binary-block embedding in a binary image. Xiao et al. [30] proposed a system which consists of three phases: image encryption, data embedding, and data extraction or image recovery. However, Li et al.’s method [23] achieves high payload and perfect image recovery. In their approach, a non-overlapping cross-division mask is first established for a cover image, and then the cover image is encrypted using the RC4 cryptosystem and the additive homomorphism.

The RC4 cryptosystem is simple to implement, but many studies suggest that RC4 is insecure [31,32,33,34,35,36,37]. Fluhrer and McGrew [31] described a way to distinguish RC4 outputs from random strings using 230 data. Mantin and Shamir [32] presented a better distinguisher which requires only 28 data. Roos [33] discovered a class of weak keys that reduces their effective size by five bits. Grosul and Wallach [34] showed that for large keys whose size is close to N words, RC4 is vulnerable to a related key attack. In addition, Knudsen et al. [35], Golić [36], and Mister and Tavares [37], provided more analysis on the security of RC4.

To overcome the drawback associated with using the RC4 cryptosystem, in this paper, we propose a novel encryption method, based on the logistic map and an additive homomorphism.

The remainder of this paper is organized as follows. Section 2 provides a brief literature review, while Section 3 describes the proposed method. The experimental results and discussion are presented in Section 4, and finally, some concluding remarks are provided in Section 5.

2. Related Work

In this section, we focus on introducing the method of Li et al. [23] and refer more to the method sub-stages for improving the payload and security. Firstly, a two-way difference histogram shifting technique is introduced to embedding secret messages for increasing the payload. Secondly, the method of Li et al. is described in detail with examples. Finally, we use logistic map nonlinear chaotic system instead of RC4 cryptosystem in encrypted procedure improve the security.

2.1. Histogram Shifting

In 2006, Ni et al. proposed the histogram shifting method. This method focuses on high visual quality with little distortion, in which the peak point of the image histogram is utilized for data embedding. In order to increase the payload, the spatial correlation in the image is exploited by considering the differences between adjacent pixels and uses a two-way histogram shifting to embed secret message.

The commonly used difference histogram shifting embedding procedure contains the following steps. First, for a chosen peak point d_i, we propose a two-way histogram shifting; the following shift or expansion is performed:

$$d_i\prime =\{\begin{array}{c}{d}_i+1,\mathrm{if}{d}_i>1\hfill \\ d_i+b,b\in \left\{0,1\right\},\mathrm{if}{d}_i=1\\ d_i-b,b\in \left\{0,1\right\},\mathrm{if}{d}_i=0\\ d_i-1,\mathrm{if}{d}_i<0\end{array}$$

(1)

where b ∊ {0, 1} is a secret message bit. Figure 1a shows an example two-way difference histogram. Suppose the secret bit stream is “101011001000...”; then, Figure 1b shows the histogram obtained after embedding.

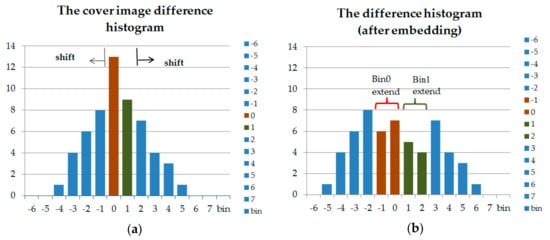
Figure 1. An example two-way difference histogram shifting. (a) The cover image difference histogram. (b) The difference histogram (after embedding).

The implementation will be introduced in the next section.

2.2. The Method of Li et al.

In the approach of Li et al., a cross-shaped mask was used with a non-overlapping cross-division (Figure 2) to retain the same difference between the neighboring pixels in the cross-block.

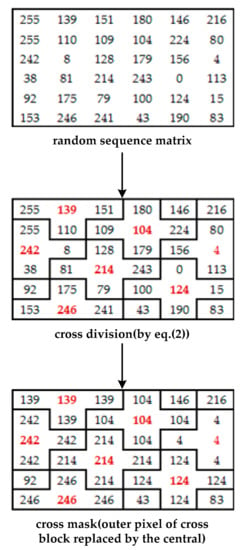
Figure 2. A 6 × 6 example of the mask matrix in the method of Li et al.

The encryption method proposed by Li et al. [23] is explained as follows.

• Step 1: The cover image is established using a cross-shaped mask with a non-overlapping cross division (Figure 2). Assuming the central pixels of the divided image in the cross-division block as N_r,c (where r is row and c is column), the neighboring pixels are N_r,c−1, N_r,c+1, N_r−1,c, and N_r+1,c. Equation (2) is used for expressing the relationship between pixels:

  $$\begin{array}{l}\{\begin{array}{l}r=r\\ c=(2\times r)\mathrm{mod}5+5\times m\end{array}\\ \forall r=1,2,\dots ,d_1;m=0,1,\dots ,\lfloor \frac{d_2-(2\times r)\mathrm{mod}5}{5}\rfloor \end{array}$$

  (2)

  where d₁ and d₂ represent the image’s height and width.
• Step 2: Encrypt the cover image using the RC4 cryptosystem and an additive homomorphism:

  $$E_{r,c}=(N_{r,c}+M_{r,c})\mathrm{mod}256$$

  (3)

  where E_r,c, N_r,c, and M_r,c represent the encrypted pixel, the original pixel, and the mask value, respectively.
• Step 3: Calculate the difference between the central pixels and their neighboring pixels in the non-overlapping cross-division block. After that, histogram shifting (described in Section 2.1) is used to embed secret messages into neighboring pixels.

In the above example, Figure 1a, two bins (0 and 1) are needed for difference histogram shifting in Figure 1b. The other bins (except 0 and 1) shift to the left and right. If d_i = 0 (bin 0), the to-be-embedded b secret bit is 0, the value of d_i (bin 0) is intact (d_i′ = d_i). Otherwise, if b = 1, the value of d_i is decremented by 1(d_i′ = d_i − 1). Furthermore, if d_i = 1 (bin 1), the selected d_i is left unchanged or incremented by “1” if the embedded bit b is “0” (d_i′ = d_i) or “1” (d_i′ = d_i + 1), respectively. After that, the value of each bin d_i (except d_i = 0 or 1) is shifted toward the outer side by 1.

For the secret message of “0110 0111 0001 0100 110 …”, the stego image difference histogram after embedding is shown in Figure 7b.

2.3. Logistic Map

The RC4 cryptosystem is simple to implement, but it is insecure. Instead of the RC4 cryptosystem, in this paper we propose a novel encryption method based on the logistic map and an additive homomorphism. The logistic map is a nonlinear chaotic system, which is characterized by randomness and sensitivity to the initial seed.

The major drawback of the logistic map is its key sensitivity, which depends on the system parameter u and on the initial seed x₀. The logistic map (Equation (4)) is a nonlinear chaotic system, characterized by randomness and sensitivity to the initial seed (Figure 3), and has been utilized in cryptography for the generation of sequences. Mathematically, the logistic map is written as

$$x_{n+1}=u{x}_n(1-x_n)$$

(4)

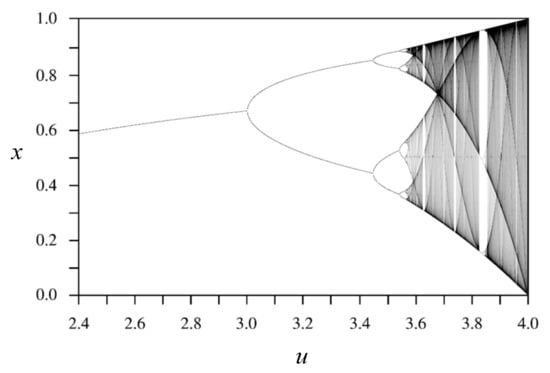
Figure 3. Bifurcation diagram for the logistic map.

The temporal series of values generated by the logistic map are unpredictable and are very sensitive with respect to initial conditions; thus, this system offers high immunity to a variety of attacks on cryptosystems.

3. Proposed Method

Li et al. [23] have developed a difference-histogram-based reversible data hiding approach which has not been explored fully. In this study, we propose a block-based division mask instead of a cross-shaped division mask to fully exploit embeddable cases; the approach is schematized in Figure 4. In addition, we propose a novel encryption method based on the logistic map and an additive homomorphism.

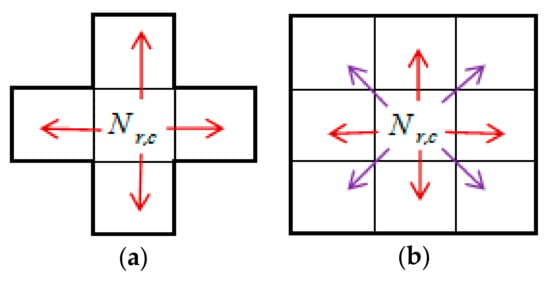
Figure 4. Comparison of explored cases. (a) The method of Li et al.; (b) The proposed method.

3.1. Block-Based Division Method

For example, in Figure 6, firstly, the cover image is divided into 3 × 3 non-overlapping blocks. If the width and height of the cover image are not dividable by 3, the block subdivision in the boundary region is adjusted according to the number of residual pixels in the boundary region (Figure 5).

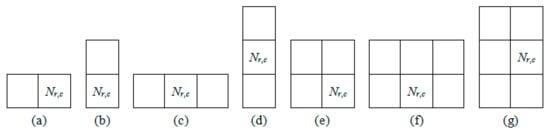
Figure 5. (a–g) Different-sized blocks in the boundary region.

Then, the logistic map matrix is created and the values are transformed into the range corresponding to gray-level pixels (e.g., the remainder of x_i is multiplied by 256 and then rounded to integer). After that, the logistic map matrix is also divided into 3 × 3 non-overlapping blocks. Finally, for each 3 × 3 block the central pixel is used to replace its neighboring pixels.

Because adjacent pixels in the cover image are strongly correlated, using the mask matrix yields much higher peak points (Figure 7a) compared with the method of Li et al. [23] (Figure 9a).

3.2. Encryption Procedure

The following outlines this procedure:

• Step 1: The cover image is divided into 3 × 3 non-overlapping blocks.
• Step 2: The initial values of x₀ ($0<x_0<1$) and u (bifurcation parameter, $3.569945<u\le 4$) are given by Equation (4), and the logistic map equation $x_{n+1}=u{x}_n(1-x_n)$ is used for the original image’s pixels, which are further transformed into the range corresponding to grey-scale pixels (e.g., the remainder of x_i is multiplied by 256 and then rounded to integer), and the block-based mask is developed.

For example, in Figure 6, the cover image is divided into four 3 × 3 blocks. Corresponding to the cover image, denote u = 4 and x₀ = 0.00000001, we establish the logistic map matrix. Then, the mask matrix is created by expanding the center pixel value to its neighboring pixels for each 3 × 3 block.

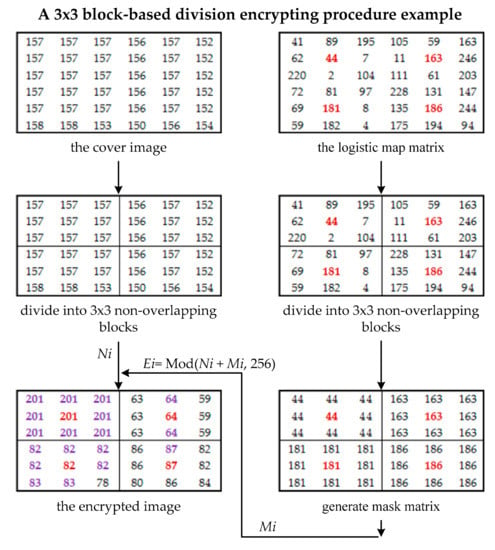
Figure 6. An example 3 × 3 block-based division encrypting procedure.

An additive homomorphism is applied to generate the encrypted image (Figure 6).

3.3. Embedding Procedure

The embedding and extraction methods are the same as those of Li et al. [23], using histogram shifting. Theoretically, every block can embed at most 8 message bits.

Figure 7a shows a histogram that was generated from Figure 6. For the secret bit stream of “0110 0111 0001 0100 110 …”, the stego image difference histogram is shown in Figure 7b.

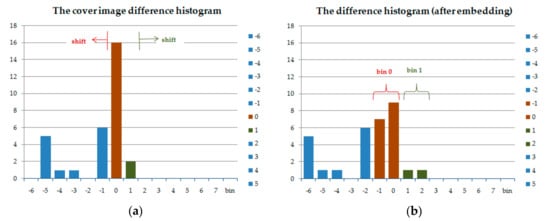
Figure 7. Difference histogram shifting using block division. (a) The cover image difference histogram; (b) The difference histogram (after embedding).

The block-based division contains more pixels (nine, as in the encrypted image in Figure 6) than the cross-division (five, as in the encrypted image in Figure 8). Because, in natural images, neighboring pixels are strongly correlated, the block-based division efficiently increases the embedding capacity.

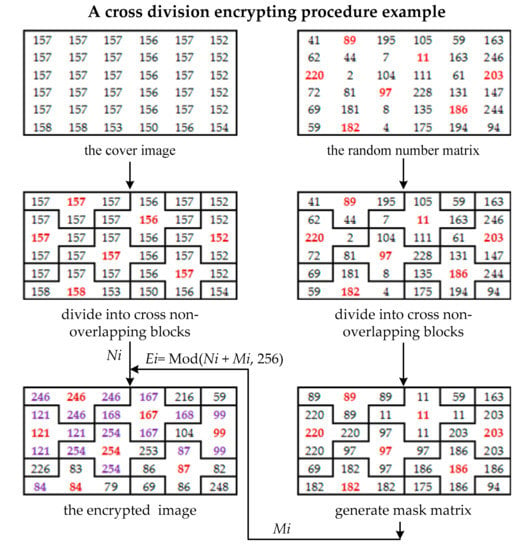
Figure 8. An example cross-division encryption procedure.

The two-way difference histogram for the encrypted image (Figure 6) is shown in Figure 7a, while Figure 7b shows the difference histogram after embedding.

An example cross-division embedding procedure is shown in the following.

The two-way difference histogram for the encrypted image (Figure 8) is shown in Figure 9a, while Figure 9b shows the difference histogram after embedding.

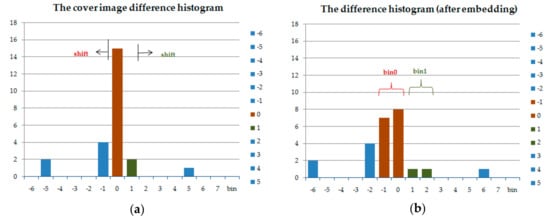
Figure 9. Difference histogram shifting using cross-division. (a) The cover image difference histogram; (b) The difference histogram (after embedding).

3.4. Extraction Procedure

The receiver side can extract the embedded data and recover the original cover image perfectly. The following outlines this procedure:

• Step 1: Generate the difference histogram of the stego image.
• Step 2: The difference histogram is shifted conversely to extract the secret data.
• Step 3: Therefore, the original image is recovered exactly.
• Step 4: Reorganize the extracted data to retrieve the embedded additional message perfectly.

Firstly, the receiver can obtain the same mask matrix only when the receiver denotes u = 4 and x₀ = 0.00000001. Otherwise, the receiver will get the wrong secret bits and cannot recover the original cover image. For each 3 × 3 block, calculate the difference between the center pixel and its neighboring pixels. Collect all the differences to generate the difference histogram of the stego image (Figure 9b). Then, the difference histogram is shifted conversely to extract the secret data (Figure 9a). Finally, reorganize the extracted data by Equation (3).

4. Experimental Results

In this section, we evaluate the results of some experiments performed using the proposed method and provide some discussion on the embedding capacity, peak signal-to-noise ratio (PSNR), entropy, and correlation coefficients. This section contains the description of detailed comparisons of experiments performed using this method and the method of Li et al. [23], by shifting the difference histogram.

Six standard test images (“Lena”, “Baboon”, “Peppers”, “Jet”, “Scene”, and “Tiffany”) from the SIPI image database were selected as cover images; these images and their corresponding stego images generated using the proposed method are shown in Table 1.

Table 1. Cover images and their corresponding stego images generated using the proposed method.

	Cover Image	Stego Image
Lena
Baboon
Peppers
Jet
Scene
Tiffany

In the following, we show the experimental results that prove that the proposed method achieves higher embedding capacity and high immunity with respect to a variety of attacks on cryptosystems.

Table 2, Table 3, Table 4 and Table 5 list the experimental results for the proposed method and the method of Li et al. [23], in terms of their embedding capacity (bits), PSNR, entropy, and correlation coefficients.

Table 2. Comparison of embedding capacities of the proposed method and the method of Li et al.

	Proposed Method	Li et al.
Lena	39,241	38,155
Baboon	13,220	12,852
Peppers	32,432	28,266
Jet	58,565	57,058
Scene	27,722	24,166
Tiffany	47,200	45,043

Table 3. Comparison of PSNR values (dB) of the proposed method and the method of Li et al.

	Proposed Method	Li et al.
Lena	9.223157	9.156620
Baboon	9.509704	9.491607
Peppers	8.920476	8.845069
Jet	7.987589	7.986285
Scene	8.239897	8.221679
Tiffany	6.873964	6.866277

Table 4. Comparison of entropies of the proposed method and the method of Li et al.

	Proposed Method	Li et al.
Lena	7.999079	7.999010
Baboon	7.999247	7.999158
Peppers	7.999114	7.999192
Jet	7.998732	7.999125
Scene	7.999109	7.999164
Tiffany	7.998823	7.999067

Table 5. Comparison of correlation coefficients of the proposed method and the method of Li et al.

	Proposed Method	Li et al.
Lena	−0.000713	0.012889
Baboon	−0.001393	0.003908
Peppers	0.011101	−0.006034
Jet	−0.000428	0.006841
Scene	−0.001599	−0.003999
Tiffany	0.005251	0.003879

First, theoretically, the ideal embedding capacity is 8/9 bits per pixel (bpp), which is higher than the value of 4/5 bpp reported by Li et al. In our experiments, all the cover images are sized 512 × 512. The proposed method can be divided into 28,900 3 × 3 blocks and 340 2 × 3 blocks (near the border part). Theoretically, each 3 × 3 block and 2 × 3 block can embed maximally 8 and 5 secret bits. The total number of embeddable pixels is 232,900 (28,900 × 8 + 340 × 5 = 232,900). Comparing with Li et al.’s method, they divided into 52,020 cross-shaped blocks and 408 broken-blocks (near the border part). Theoretically, each cross-shaped block and each broken-block can embed maximally 4 and 3 secret bits. The total number of embeddable pixels is 209,304 (52,020 × 4 + 408 × 3 = 209,304), which is less than that of the proposed method. The experimental result also proves that the proposed method is superior to the method of Li et al. (Table 2).

Second, in general, PSNR is used to evaluate the image quality, where PSNR is defined as follows:

$$\mathrm{PSNR}=10\times {\log }_{10}\frac{{255}^2}{\mathrm{MSE}}$$

(5)

where the mean square error (MSE) is defined as

$$\mathrm{MSE}=\frac{1}{w\times h}{\displaystyle \sum _{r=1}^w{\displaystyle \sum _{c=1}^h{(N_{r,c}-N{\prime }_{r,c})}^2}}$$

(6)

with w and h denoting the image dimensions, and $N_{r,c}$ and $N{\prime }_{r,c}$ representing the pixel at row r and column c of the cover image and the stego image, respectively. Low values of PSNR imply low discrimination. The proposed method yields almost the same PSNR value as the method of Li et al. (Table 3).

Third, the entropy equation of a gray-level image s is defined as

$$H\left(s\right)=N(x_i){\log }_2\frac{1}{N\left(x_i\right)}$$

(7)

where N(x_i) stands for the gray-level pixel equal to the appearance probability of i. High entropy corresponds to high confusion. The proposed method yields almost the same value of entropy as the method of Li et al. (Table 4).

Fourthly, the correlation coefficient is a statistical measure of the correlation between adjacent pixels in the image. The correlation coefficient (Corr) is defined as

$$Cor{r}_{x_1{x}_2}=\frac{\mathrm{cov}\left(x_1,x_2\right)}{\sqrt{D\left(x_1\right)}\sqrt{D\left(x_2\right)}}$$

(8)

where x₁ and x₂ are the image values of gray-level images, and D(x₁) and D(x₂) are the variances of x₁ and x₂. The definition is shown as

$$D\left(x_1\right)=\frac{1}{n}{{\displaystyle \sum _{i=1}^n\left(x_{1i}-E\left(x_1\right)\right)}}^2$$

(9)

where E(x₁) and E(x₂) are the expected values of x₁ and x₂, defined as

$$E\left(x_1\right)=\frac{1}{n}{\displaystyle \sum _{i=1}^n{x}_{1i}}$$

(10)

The covariance cov(x₁, x₂) between x₁ and x₂ is defined as follows:

$$\mathrm{cov}\left(x_1,x_2\right)=\frac{1}{n}{\displaystyle \sum _{i=1}^{n}E\left(x_{1i}-E\left(x_1\right)\right)\left(x_{2i}-E\left(x_2\right)\right)}$$

(11)

The correlation coefficients of the considered encrypted images approach ideal values (zero). These confirm that the chaotic encryption algorithm yields zero correlation, suggesting that attackers cannot obtain valuable information by exploiting statistical attacks. A smaller correlation coefficient indicates stronger resistance to statistical attacks. Both the proposed method and the method of Li et al. yield nearly zero values (Table 5).

Finally, we conclude that, compared with the method of Li et al., the proposed method achieves higher embedding capacity, almost the same PSNR (low values of PSNR correspond to low discrimination), almost the same entropy (high entropy corresponds to high confusion), and nearly zero correlation.

5. Conclusions

Owing to the insecurity of the RC4 cryptosystem, here we proposed to use the logistic chaotic map instead. The logistic map is a nonlinear chaotic system, characterized by randomness and sensitivity to the initial seed. The major drawback of the logistic map is the key sensitivity, which depends on a single system parameter u and an initial seed x₀. In addition, we proposed a block-based division mask instead of a cross-shaped division mask to fully exploit embeddable cases and increase the embedding capacity.

Theoretically, the ideal embedding capacity of the proposed method is 8/9 bpp, which is better than that achieved by the method of Li et al. (4/5 bpp). The experimental result in Table 2 also proves this. Besides this, the experimental results in Table 3 show that the proposed method has low discrimination. The experimental results in Table 4 show that the proposed method has high confusion. The experimental results in Table 5 show that the proposed method achieves high immunity with respect to a variety of attacks the cryptosystem.

The proposed method not only guarantees perfect data extraction and recovery of the original cover image, but also provides a better embedding capacity compared with Li et al.’s methods.