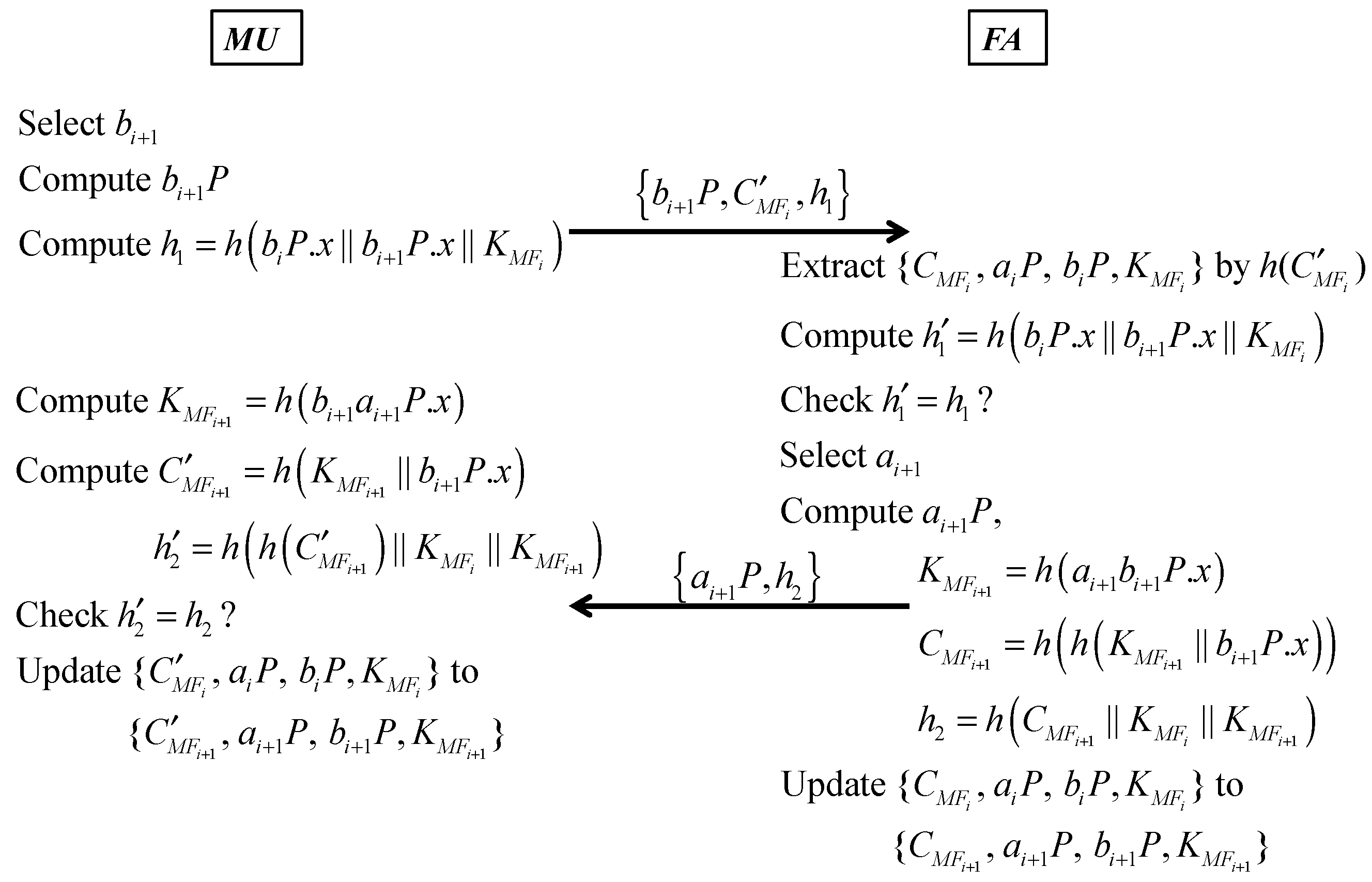A Secure Mobility Network Authentication Scheme Ensuring User Anonymity

Abstract

With the rapid growth of network technologies, users are used to accessing various services with their mobile devices. To ensure security and privacy in mobility networks, proper mechanisms to authenticate the mobile user are essential. In this paper, a mobility network authentication scheme based on elliptic curve cryptography is proposed. In the proposed scheme, a mobile user can be authenticated without revealing who he is for user anonymity, and a session key is also negotiated to protect the following communications. The proposed mobility network authentication scheme is analyzed to show that it can ensure security, user anonymity, and convenience. Moreover, Burrows-Abadi-Needham logic (BAN logic) is used to deduce the completeness of the proposed authentication scheme.

1. Introduction

With the rapid growth of network technologies, users are used to accessing various services with their mobile devices. As a result, mobile devices and mobility networks play an important role in people’s daily lives. There are three entities in mobility networks; mobile user, home agent and foreign agent. Before being able to access mobile services, a mobile user needs to register with the home agent. After successful registration, the mobile user with a mobile device can access mobile services. These mobile services are provided by the home agent directly or a foreign agent. If the requested mobile service is provided by a foreign agent, the registered mobile user needs the home agent’s help to have himself/herself authenticated by the foreign agent. An illustration of mobility networks is shown in Figure 1, where a mobile user with a mobile device can be regarded as a mobile node. Plenty of mobility network applications are proposed and utilized because they provide great convenience.

Although mobility networks bring people great convenience and advantages, security threats exist. First, the transmission medium is a public but insecure channel such that an attacker can easily eavesdrop or intercept the transmitted data. Second, when a mobile user enters a service domain dominated by a new foreign agent, the mobile user has to access services via the new foreign agent. In this condition, two issues raise: (1) how the mobile user determines whether the foreign agent is legal; and (2) how the foreign agent determines whether the mobile user is legal. That is, the mobile user and the foreign agent have to authenticate each other. Unfortunately, in the beginning, no secret is shared between them. Third, because the mobile user is a visitor, the foreign agent serves the mobile user when he continuously stays. The mobile user may continuously stay, but the mobile user may not request mobile services continuously. This denotes that the mobile user and the foreign agent do not always communicate with each other. In such a condition, it is a challenge for the mobile user and the foreign agent to ensure each other’s legality after they have already authenticated each other. Forth, a mobile user may roam. Because the transmission medium is public, anyone can eavesdrop. If an attacker wants to trace a mobile user, he can eavesdrop and use the intercepted messages to obtain required information.

To ensure security of mobility networks, many authentication protocols are proposed [1,2,3,4,5,6,7,8,9,10]. In 2004, Zhu and Ma proposed an authentication scheme with anonymity for wireless environments based on the hash function and smart cards [5]. Later, Lee et al. [6] analyzed Zhu and Ma’s scheme and found that Zhu and Ma’s scheme does not provide mutual authentication and cannot resist forgery attack. In 2006, Lee et al. [7] proposed an enhancement to improve Zhu and Ma’s authentication scheme for wireless networks. In 2009, Chang et al. [8] analyzed Lee et al.’s scheme [7] and pointed out that Lee et al.’s scheme still suffers from forgery attack and also proposed an improvement.

In 2014, Kuo et al. [9] showed that Chang et al.’s scheme cannot ensure anonymity for mobile users and proposed an improvement. Kuo et al. claimed that their scheme could ensure efficiency and security in mobility networks and provide anonymity for mobile users. In 2015, Lu et al. [10] showed that Kuo et al.’s scheme suffers from three drawbacks, vulnerability to insider attack, unfriendly password changes, and no local validation. They also proposed an authentication scheme to remedy these drawbacks. Later, Chang et al. [11] found that Kuo et al.’s scheme [9] is vulnerable to the other two weaknesses in 2016. First, Kuo et al.’s scheme cannot resist man-in-the-middle attacks when a mobile user and a foreign agent negotiate the session key. Via this security flaw, an attacker can impersonate a mobile user and negotiate the session key with the foreign agent. Second, Kuo et al.’s scheme cannot resist the synchronization problem. An attacker only needs to modify the transmitted data in password change phase such that a legal mobile user is unable to be authenticated by the home agent anymore. Lu et al. [10] claimed that their scheme could defend against replay attack and provide mobile user anonymity.

After thoroughly analyzing Lu et al.’s scheme, Chang et al. found that it possesses three drawbacks [12]. First, Lu et al.’s scheme is vulnerable to replay attack in authentication with key agreement phase. An attacker only needs to eavesdrop and resend the intercepted message with a new timestamp to cheat the foreign agent and the home agent. Second, user anonymity is not ensured as claimed because some transmitted parameters are fixed. Third, a random number chosen by the mobile user in registration phase is not stored in his/her smart card. As a result, the mobile user’s smart card cannot compute one essential parameter to have himself/herself authenticated by the home agent in authentication with key agreement phase.

In addition to mobility networks, privacy is also an important topic in different types of networks. To ensure privacy and security in different types of networks, related security mechanisms are proposed [13,14,15,16,17,18]. After analyzing the previous authentication schemes, the weaknesses that they suffer from and the security mechanisms of other networks, we propose a mobility network authentication scheme by considering the following four properties to ensure security and convenience.

Property 1: user anonymity

User anonymity needs to be ensured to prevent an unauthorized party from tracing a specific user. It denotes that only the authorized parties can know who the user is.

Property 2: resistance to common attacks

The proposed authentication scheme should be able to resist common attacks to ensure security.

Property 3: local password change

A mobile user should be able to change his/her password locally and at will without accessing the home agent to make the authentication scheme more convenient and user-friendly.

Property 4: mutual authentication between any two of a mobile user, a foreign agent and the home agent

In a mobility network authentication scheme, any two of a mobile user, a foreign agent and the home agent have to authenticate each other mutually to make sure that the other communication parties are legal.

The rest of this paper is organized as follows. The proposed scheme is shown in Section 2. The corresponding analysis is given in Section 3. Further discussions including comparisons and authentication proof using Burrows-Abadi-Needham logic (BAN logic) [19] are made in Section 4. Finally, some conclusions are given in Section 5.

2. The Proposed Secure Mobility Network Authentication Scheme Ensuring User Anonymity

In this section, we propose a user anonymity-ensured mobility network authentication scheme for mobility networks based on elliptic curve cryptography. Our scheme is composed of five phases: registration phase, login phase, authentication and establishment of the session key phase, update session key phase, and password change phase. A mobile user has to register with the home agent before accessing mobile services. In the registration phase, a mobile user registers with the home agent, the home agent stores parameters in a smart card, and the home agent issues it to the user. The mobile user and the home agent communicate via a secure channel. And the home agent stores parameters in a smart card securely because the smart card only can be accessed and modified by privilege users or administrators. In the login phase, a mobile user inserts his smart card into his terminal device. This denotes that the mobile user and the smart card can exchange required data via the terminal device. The terminal device possesses computational capacities and has a user interface to show the authentication progress or the response. The terminal device will execute computational operations on behalf of the mobile user. The terminal device should be personal or protected with proper security mechanisms such as firewalls. For simplicity, the communications between the mobile user and the smart card will be omitted, and the operations executed by either the user or the terminal device will be denoted by the user. In both the authentication and establishment of the session key phase and the update session key phase, data is transmitted via public channels. Notations used in our mobility network authentication scheme are listed in

Table 1. Notations used in our mobility network authentication scheme.

Symbol	Definition
MU	A mobile user
FA	A foreign agent
HA	The home agent
IDA	The identifier of an entity A
h(·)	A collision free one-way hash function
pMU	The password chosen by MU
PWMU	The secret of MU that is computed by IDMU and pMU
RA	A random nonce chosen by an entity A
p	A prime greater than 2160
n	A prime greater 2160
P	A point on the elliptic curve Ep(a, b) of order n, where a, b ∈ Zp, Ep(a, b): y2 = x3 + ax + b and 4a3 + 27b2 ≠ 0
P.x	The x coordinate of the point P
pHA-MU	The secret key of HA for MU
pFA-HA	The secret key shared between HA and FA
||	Concatenation operator
⊕	Exclusive-or operator

. The details are as follows.

2.1. Registration Phase

In this phase, if MU wants to access the roaming service, he/she must register with HA at first. Registration phase is depicted in Figure 2, and the details are as follows:

Step 1:

MU selects his/her password p_MU and identifier ID_MU.

Step 2:

MU sends ID_MU and p_MU to HA via a secure channel.

Step 3:

After HA receives {ID_MU, p_MU} from MU, HA checks if ID_MU does not exist. If it does hold, HA generates a random nonce R_MU and the secret key p_HA-MU for MU.

Step 4:

HA computes PW_MU = h(ID_MU || p_MU), U = h(p_HA-MU || R_MU), W = PW_MU ⊕ R_MU, V = R_MU ⊕ p_HA-MU and L = h(ID_MU || R_MU || PW_MU).

Step 5:

HA stores {ID_HA, L, W, V, h(·)} into a smart card and issues it to MU via a secure channel.

Step 6:

HA stores {U, R_MU, p_HA-MU} into HA’s database for MU.

2.2. Login Phase

After registering with HA, MU can login with the smart card issued in registration phase to access the roaming service. Login phase is depicted in Figure 3, and the details are as follows:

Step 1:

MU inserts his/her smart card into his/her terminal device and enters ID_MU and p_MU.

Step 2:

The smart card computes PW_MU = h(ID_MU || p_MU), R_MU = W ⊕ PW_MU, and L′ = h(ID_MU || R_MU || PW_MU).

Step 3:

The smart card checks if L′ is equal to L. If it does not hold, the smart card aborts the process and accumulates the number of times for L′ is not equal to L. If the entered ID_MU and p_MU make L′ and L differ from each other three consecutive times, the smart card will be locked automatically. Note that the counter will be reset to zero when the entered ID_MU and p_MU have L′ equal L.

2.3. Authentication and Establishment of the Session Key Phase

After the login phase, the authentication and establishment of the session key phase is executed. In this phase, MU can be authenticated anonymously and negotiate a session key with FA while roaming. In the proposed scheme, HA and FA share a secret key p_FA-HA in advance, where different FA’s possess different p_FA-HA’s. The authentication and establishment of the session key phase is depicted in Figure 4, and the details are as follows:

Step 1:

The smart card generates a new random nonce $R_{{MU}_{new}}$ and selects a random number b₀.

Step 2:

The smart card computes b₀P, R_MU = PW_MU ⊕ W, p_HA-MU = R_MU ⊕ V, S₁ = h(p_HA-MU || R_MU), S₂ = R_MU ⊕ $R_{{MU}_{new}}$, and S₃ = h(R_MU ⊕ h(p_HA-MU || $R_{{MU}_{new}}$) || b₀P.x).

Step 3:

MU sends {ID_HA, S₁, S₂, S₃, b₀P} to FA and stores {b₀, $R_{{MU}_{new}}$}.

Step 4:

After FA receives {ID_HA, S₁, S₂, S₃, b₀P}, FA selects a new random number a₀ and computes a₀P and $S_{{FA}_1}$ = h(a₀P.x || b₀P.x || p_FA-HA).

Step 5:

FA stores the information {ID_HA, b₀P, a₀, a₀P} and sends {ID_FA, S₁, S₂, S₃, a₀P, b₀P, $S_{{FA}_1}$} to HA.

Step 6:

When HA receives {ID_FA, S₁, S₂, S₃, a₀P, b₀P, $S_{{FA}_1}$}, HA uses S₁ to get the corresponding data {R_MU, p_HA-MU} from its database because the matched {R_MU, p_HA-MU} makes S₁ = h(p_HA-MU || R_MU). Then HA computes $R_{{MU}_{new}}$ = S₂ ⊕ R_MU, S′₃ = h(R_MU ⊕ h(p_HA-MU || $R_{{MU}_{new}}$) || b₀P.x), and $S_{{FA}_1}^{\prime }$ = h(a₀P.x || b₀P.x || p_FA-HA).

Step 7:

HA checks if S′₃ = S₃ and $S_{{FA}_1}^{\prime }=S_{{FA}_1}$. If they both hold, HA selects a new random number c₀ and computes c₀P and S₄ = h(c₀b₀P.x || a₀P.x || ID_FA || ID_HA || R_MU || $R_{{MU}_{new}}$); otherwise, HA aborts this authentication request and terminates this phase. After that, HA updates U and R_MU stored in its database to h(p_HA-MU || $R_{{MU}_{new}}$) and $R_{{MU}_{new}}$, respectively. Note that the original U = S₁ and the original R_MU are also stored in HA’s database to resist the synchronization problem. That is, the original U instead of the updated one will be searched to find the corresponding data {the original R_MU, p_HA-MU} when only HA’s data is updated.

Step 8:

HA computes $S_{{FA}_2}$ = h(c₀a₀P.x || b₀P.x || p_FA-HA) and sends {ID_HA, c₀P, S₄, $S_{{FA}_2}$} to FA.

Step 9:

After receiving {ID_HA, c₀P, S₄, $S_{{FA}_2}$} from HA, FA checks if ID_HA exists in its database. If it does exist, FA computes $S_{{FA}_2}^{\prime }$ = h(a₀c₀P.x || b₀P.x || p_FA-HA) and checks if $S_{{FA}_2}^{\prime }=S_{{FA}_2}$. If it does hold, FA computes $K_{{MF}_0}$ = h(a₀b₀P.x) and $C_{{MF}_0}$ = h(h($K_{{MF}_0}$ || b₀P.x)); otherwise, FA terminates this phase directly.

Step 10:

FA sends {ID_FA, S₄, a₀P, c₀P, $C_{{MF}_0}$} to MU.

Step 11:

When MU receives {ID_FA, S₄, a₀P, c₀P, $C_{{MF}_0}$}, MU computes S′₄ = h(b₀c₀P.x || a₀P.x || ID_FA || ID_HA || R_MU || $R_{{MU}_{new}}$) and checks whether S₄ is equal to S′₄. If it does not hold, MU terminates this phase directly; otherwise, MU computes the session key $K_{{MF}_0}$ = h(b₀a₀P.x), $C_{{MF}_0}^{\prime }$ = h($K_{{MF}_0}$ || b₀P.x), and $C_{{MF}_0}^{″}$ = h($C_{{MF}_0}^{\prime }$), and checks if $C_{{MF}_0}=C_{{MF}_0}^{″}$. If it does not hold, MU terminates this phase directly; otherwise, MU computes $B_{{MF}_0}$ = h(c₀P.x || $K_{{MF}_0}$), updates W to W_new = PW_MU ⊕ $R_{{MU}_{new}}$ and V to V_new = $R_{{MU}_{new}}$ ⊕ p_HA-MU and stores $C_{{MF}_0}^{\prime }$, a₀P, b₀P, and the session key $K_{{MF}_0}$.

Step 12:

MU sends {$B_{{MF}_0}$} to FA.

Step 13:

After obtaining {$B_{{MF}_0}$}, FA computes $B_{{MF}_0}^{\prime }$ = h(c₀P.x || $K_{{MF}_0}$) and checks if $B_{{MF}_0}=B_{{MF}_0}^{\prime }$. If it does not hold, FA terminates this phase directly; otherwise, FA stores {$C_{{MF}_0}$, a₀P, b₀P, $K_{{MF}_0}$} into its database.

After the above, FA and MU share the session key $K_{{MF}_0}$. Thereupon, the communication between FA and MU can be protected by $K_{{MF}_0}$.

2.4. Update Session Key Phase

After being authenticated by HA via FA, MU can update the session key shared with FA for some security issues while staying in the same FA continuously. For generality, assume that MU has stayed in the same FA and updated the session i times. Thus, the secret key shared between FA and MU is $K_{{MF}_i}$ = h(a_ib_iP.x) = h(b_ia_iP.x) while FA and MU store {$C_{{MF}_i}$, a_iP, b_iP, $K_{{MF}_i}$} and {$C_{{MF}_i}^{\prime }$, a_iP, b_iP, $K_{{MF}_i}$}, respectively. Update session key phase is depicted in Figure 5, and the details are as follows:

Step 1:

MU selects a new random number b_i+1 and computes b_i+1P and h₁ = h(b_iP.x || b_i+1P.x || $K_{{MF}_i}$).

Step 2:

MU sends {b_i+1P, $C_{{MF}_i}^{\prime }$, h₁} to FA.

Step 3:

After receiving {b_i+1P, $C_{{MF}_i}^{\prime }$, h₁}, FA checks if $h(C_{{MF}_i}^{\prime })$ exists in its database, where $h(C_{{MF}_i}^{\prime })$ = $C_{{MF}_i}$. If it does not exist, FA terminates this phase; otherwise, FA extracts {$C_{{MF}_i}$, a_iP, b_iP, $K_{{MF}_i}$} from its database.

Step 4:

FA computes h′₁ = h(b_iP.x || b_i+1P.x || $K_{{MF}_i}$) and checks if h′₁ is equal to h₁. If it does not hold, FA terminates this phase; otherwise, FA selects a new random number a_i+1 and computes a_i+1P, $K_{{MF}_{i+1}}$ = h(a_i+1b_i+1P.x), $C_{{MF}_{i+1}}$ = h(h($K_{{MF}_{i+1}}$ || b_i+1P.x)) and h₂ = h($C_{{MF}_{i+1}}||K_{{MF}_i}||K_{{MF}_{i+1}}$).

Step 5:

FA updates {$C_{{MF}_i}$, a_iP, b_iP, $K_{{MF}_i}$} to {$C_{{MF}_{i+1}}$, a_i+1P, b_i+1P, $K_{{MF}_{i+1}}$} in its database and sends {a_i+1P, h₂} to MU.

Step 6:

When MU receives {a_i+1P, h₂} from FA, MU computes $K_{{MF}_{i+1}}$ = h(b_i+1a_i+1P.x), $C_{{MF}_{i+1}}^{\prime }$ = h($K_{{MF}_{i+1}}$ || b_i+1P.x), and h′₂ = h(h($C_{{MF}_{i+1}}^{\prime }$) || $K_{{MF}_i}||K_{{MF}_{i+1}}$). Then, MU checks if h′₂ is equal to h₂. If it does not hold, MU terminates this phase; otherwise, MU updates {$C_{{MF}_i}^{\prime }$, a_iP, b_iP, $K_{{MF}_i}$} to {$C_{{MF}_{i+1}}^{\prime }$, a_i+1P, b_i+1P, $K_{{MF}_{i+1}}$} in the mobile device.

If this phase is terminated by MU or FA and MU still wants to access the roaming service, login phase is executed immediately.

2.5. Password Change Phase

MU can change his/her password with his/her smart card at will without HA’s help. Password change phase is depicted in Figure 6, and the details are as follows:

Step 1:

MU inserts his/her smart card into his/her terminal device and enters ID_MU and p_MU.

Step 2:

The smart card computes PW_MU = h(ID_MU || p_MU), R_MU = W ⊕ PW_MU and L′ = h(ID_MU || R_MU || PW_MU).

Step 3:

The smart card checks if L′ is equal to L. If it does not hold, the smart card aborts the process.

Step 4:

If L′ equals L, MU selects the new password $p_{{MU}_{new}}$ and sends it to the smart card. Note that this approach can be executed by entering $p_{{MU}_{new}}$ with an embedded keyboard.

Step 5:

When the smart card receives the new password $p_{{MU}_{new}}$, it will ask MU to enter $p_{{MU}_{new}}$ again for correctness. If the reentered password is different from the previous one, the smart card will inform MU of this issue. MU may resend the new password or terminate this phase. If the reentered password and the previous one are the same, the smart card computes ${PW}_{{MU}_{new}}$, W_new = ${PW}_{{MU}_{new}}$ ⊕ R_MU and L_new = h(ID_MU || R_MU || ${PW}_{{MU}_{new}}$). Then, the smart card updates W to W_new and L to L_new.

3. Property Analysis

In this section, we analyze our proposed scheme’s security and convenience by taking the following four properties into consideration: (1) user anonymity; (2) resistance to common attacks; (3) local password change; and (4) mutual authentication. In the following, we discuss our scheme to show that it possesses these properties.

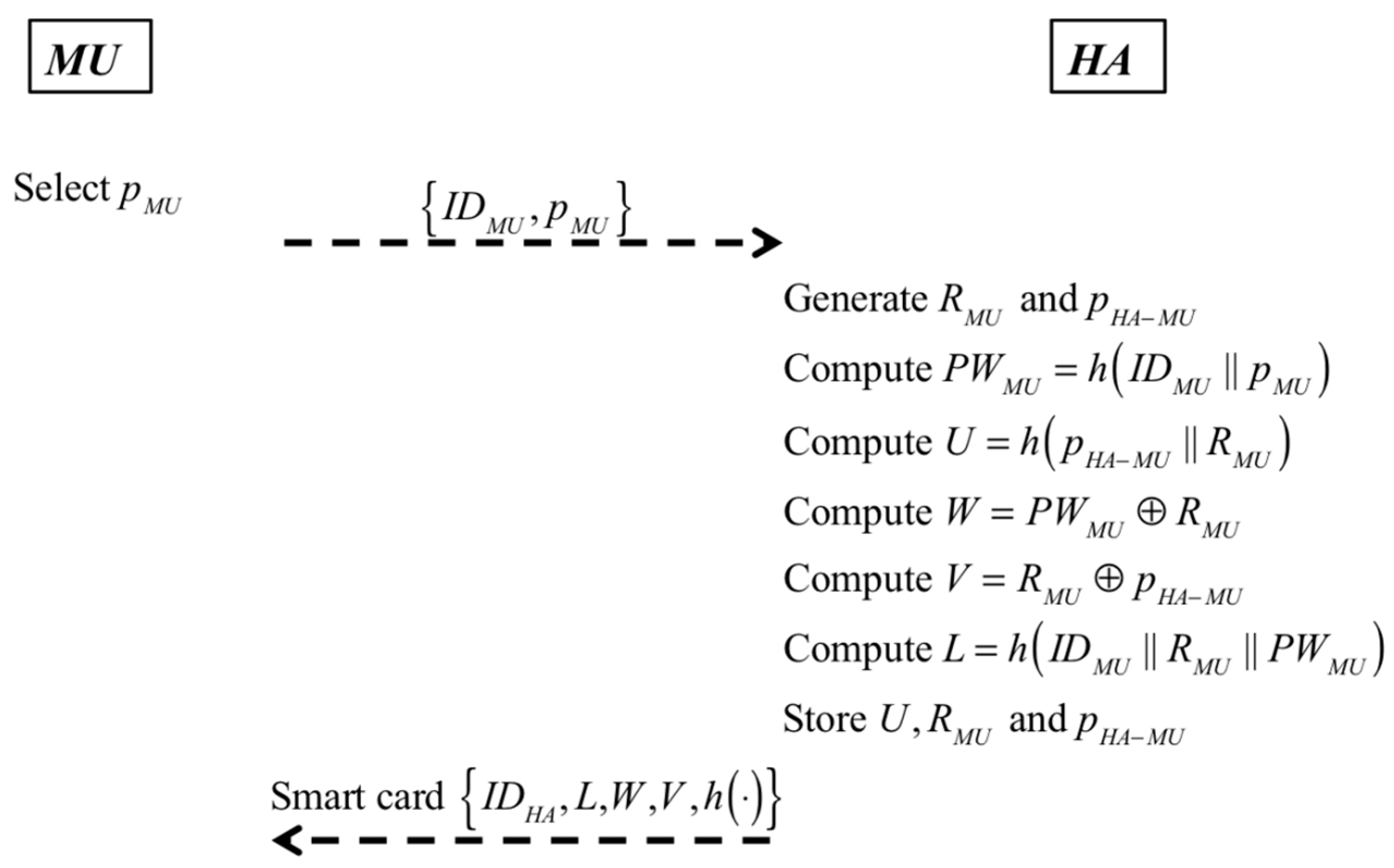
3.1. User Anonymity

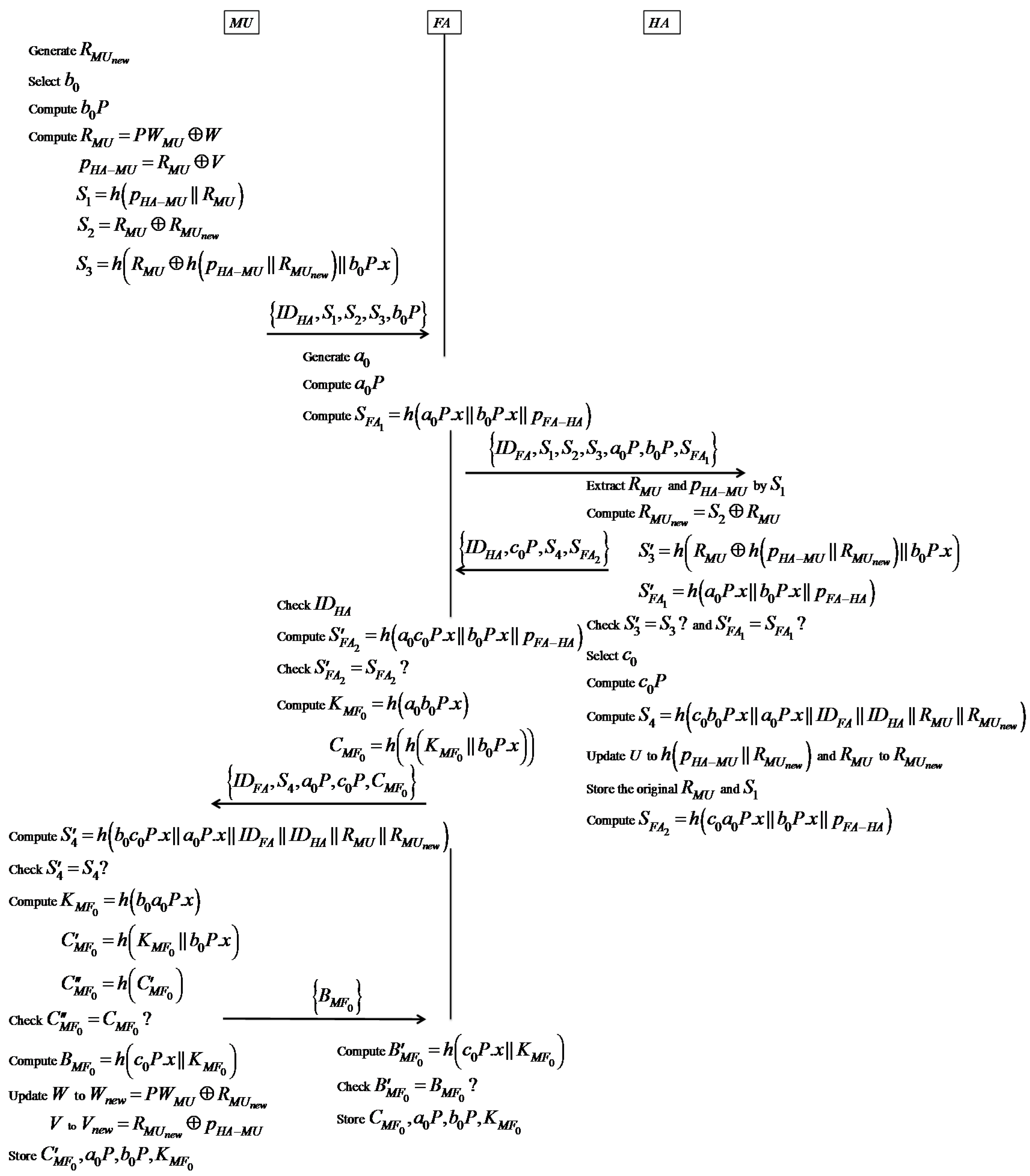
In our proposed scheme, MU’s real identifier is concealed in PW_MU = h(ID_MU || p_MU) and is never transmitted when MU wants to access the roaming service. In authentication and establishment of the session key phase, MU sends {ID_HA, S₁, S₂, S₃, b₀P} to FA, where S₁ = h(p_HA-MU || R_MU), S₂ = R_MU ⊕ $R_{{MU}_{new}}$, and S₃ = h(R_MU ⊕ h(p_HA-MU || $R_{{MU}_{new}}$) || b₀P.x). After authenticating MU and FA successfully, HA sends {ID_HA, c₀P, S₄, $S_{{FA}_2}$} to FA, where S₄ = h(c₀b₀P.x || a₀P.x || ID_FA || ID_HA || R_MU || $R_{{MU}_{new}}$). Parameters S₁, S₂, S₃, and S₄ contain MU’s specific information R_MU and $R_{{MU}_{new}}$ and are transmitted via public channels. Because R_MU and $R_{{MU}_{new}}$ will be updated in each session, it denotes that S₁, S₂, S₃, and S₄ in one session differ from those in other sessions. That is, no constant parameter is transmitted for MU in different sessions, and our scheme ensures user anonymity.

3.2. Resistance to Common Attacks

To show that the proposed authentication scheme can resist common attacks to ensure security, common attacks, man-in-the-middle attack, desynchronization attack, insider attack, replay attack, and offline secret key guessing attack are taken into consideration. These attacks are chosen for security analysis because of the following reasons. First, HA, MU, and FA transmit data via public channels. It is essential to protect all communication parties from being threatened by an attacker without being detected when the authentication scheme is in progress. This denotes that the proposed scheme has to resist man-in-the-middle attack. Second, in authentication and establishment of the session key phase of the proposed scheme, the random nonce R_MU kept by HA will be updated to $R_{{MU}_{new}}$ after MU is authenticated successfully, and MU will update W to W_new = PW_MU ⊕ $R_{{MU}_{new}}$ and V to V_new = $R_{{MU}_{new}}$ ⊕ p_HA-MU after MU is assured that $C_{{MF}_0}=C_{{MF}_0}^{″}$. If only HA updates U to h(p_HA-MU || $R_{{MU}_{new}}$) and R_MU to $R_{{MU}_{new}}$ while W and V are not updated, MU may be regarded as an illegal user. That is, the proposed scheme has to resist desynchronization attacks to ensure that an authorized mobile user can access the service even when the new authentication parameters are modified by an attacker. Third, the proposed scheme has to resist insider attacks such that no one can impersonate a legal mobile user even when a malicious insider with privileges can access the home agent’s database. Forth, the proposed scheme has to resist replay attack such that no one can impersonate MU to cheat FA and HA by sending the intercepted data transmitted in previous sessions. Fifth, because the computational capacities of computers progress rapidly, an attacker can eavesdrop to get transmitted messages and analyze them offline. That is, an attacker may attempt to retrieve the secrets p_HA-MU and p_FA-HA by mounting an offline secret key guessing attack. The corresponding analysis is given as follows.

In authentication and establishment of the session key phase, an attacker may mount a man-in-the-middle attack by impersonating a communication party to establish the session key with another innocent communication party. First, we assume an attacker tries to impersonate MU and establish the session key with FA by modifying b₀P. However, this approach will never succeed because MU computes S₃ = h(R_MU ⊕ h(p_HA-MU || $R_{{MU}_{new}}$) || b₀P.x) for HA and HA verifies b₀P by checking whether S₃ = S′₃. FA can also verify b₀P by checking whether $S_{{FA}_2}^{\prime }=S_{{FA}_2}$. On the other hand, if the attacker tries to impersonate FA and establish the session key with MU by modifying a₀P, this approach will never succeed because HA can verify a₀P by checking whether $S_{{FA}_1}^{\prime }=S_{{FA}_1}$ and MU can verify a₀P by checking whether S₄ = S′₄. In the update session key phase, FA authenticates MU by checking if h₁ = h′₁ and MU authenticates FA by checking if h₂ = h′₂ Because of the above reasons, our scheme can resist man-in-the-middle attacks.

In the authentication and establishment of the session key phase, an attacker may attempt to mount a desynchronization attack by disturbing the authentication process after HA updates U to h(p_HA-MU || $R_{{MU}_{new}}$) and R_MU to $R_{{MU}_{new}}$ in its database. Although MU does not update W and V in his/her smart card, MU still can be authenticated by HA successfully because HA stores the original R_MU and the original U. Because of the above reasons, our scheme can resist desynchronization attack.

Assume that a malicious insider with privileges tries to get MU’s private data in HA’s database to impersonate MU. In our proposed scheme, this attack cannot be mounted successfully because HA does not store a user’s password and his/her real identifier. No insider can obtain p_MU and ID_MU to compute MU’s secret PW_MU, where PW_MU = h(ID_MU || p_MU). Therefore, our scheme can resist insider attack.

In authentication and establishment of the session key phase, anyone can eavesdrop to intercept the transmitted data because the channel is public. In Step 3, MU sends {ID_HA, S₁, S₂, S₃, b₀P} to FA and stores $R_{{MU}_{new}}$, where S₁ = h(p_HA-MU || R_MU), S₂ = R_MU ⊕ $R_{{MU}_{new}}$, and S₃ = h(R_MU ⊕ h(p_HA-MU || $R_{{MU}_{new}}$) || b₀P.x). In Step 10, FA sends {ID_FA, S₄, a₀P, c₀P, $C_{{MF}_0}$} to MU, where $C_{{MF}_0}$ = h(h($K_{{MF}_0}$ || b₀P.x)) = h(h(h(a₀b₀P.x) || b₀P.x)). In Step 12, MU sends {$B_{{MF}_0}$} to FA, where $B_{{MF}_0}$ = h(c₀P.x || $K_{{MF}_0}$). In Step 13, FA computes $B_{{MF}_0}^{\prime }$ = h(c₀P.x || $K_{{MF}_0}$) and checks if $B_{{MF}_0}$ = $B_{{MF}_0}^{\prime }$ to determine whether MU is legal. After an attacker eavesdrops, he may use the intercepted data to cheat HA and FA to access services. However, the attacker cannot mount a reply attack successfully because of the following. $K_{{MF}_0}$ = h(a₀b₀P.x) and $B_{{MF}_0}$ = h(c₀P.x || $K_{{MF}_0}$) = h(c₀P.x || h(a₀b₀P.x)). If the attacker wants to cheat, he has to obtain a₀b₀P. Although a₀P and b₀P are available, the attacker knows neither a₀ nor b₀ because of the difficulty of solving the elliptic curve discrete logarithm problem (ECDLP). As a result, the attacker cannot compute a₀b₀P to obtain $B_{{MF}_0}$. Since $B_{{MF}_0}$ cannot be obtained by the attacker, he cannot be authenticated by FA successfully by retransmitting the intercepted data. Therefore, our scheme can resist replay attack.

In the authentication and establishment of the session key phase, HA authenticates FA by checking whether $S_{{FA}_1}^{\prime }=S_{{FA}_1}$, and FA authenticates HA by checking whether $S_{{FA}_2}^{\prime }=S_{{FA}_2}$, where $S_{{FA}_1}$ = h(a₀P.x || b₀P.x || p_FA-HA) and $S_{{FA}_2}$ = h(c₀a₀P.x || b₀P.x || p_FA-HA). The secret p_FA-HA shared between FA and HA is contained in both $S_{{FA}_1}$ and $S_{{FA}_2}$. Although a₀P, b₀P and c₀P are available, an attacker cannot compute c₀a₀P because of the difficulty of solving ECDLP. On the other hand, MU authenticates HA by checking whether S₄ = S′₄ and HA authenticates MU by checking whether S₃ = S′₃, where S₄ = h(c₀b₀P.x || a₀P.x || ID_FA || ID_HA || R_MU || $R_{{MU}_{new}}$) and S₃ = h(R_MU ⊕ h(p_HA-MU || $R_{{MU}_{new}}$) || b₀P.x). The secret p_HA-MU shared between MU and HA is contained in the transmitted parameters S₁ and S₃, where S₁ = h(p_HA-MU || R_MU). If an attacker wants to obtain p_HA-MU, he has to guess R_MU at the same time. This makes retrieving p_HA-MU hard. Because of the above, offline secret key guessing attacks cannot be mounted on the proposed scheme.

3.3. Local Password Change

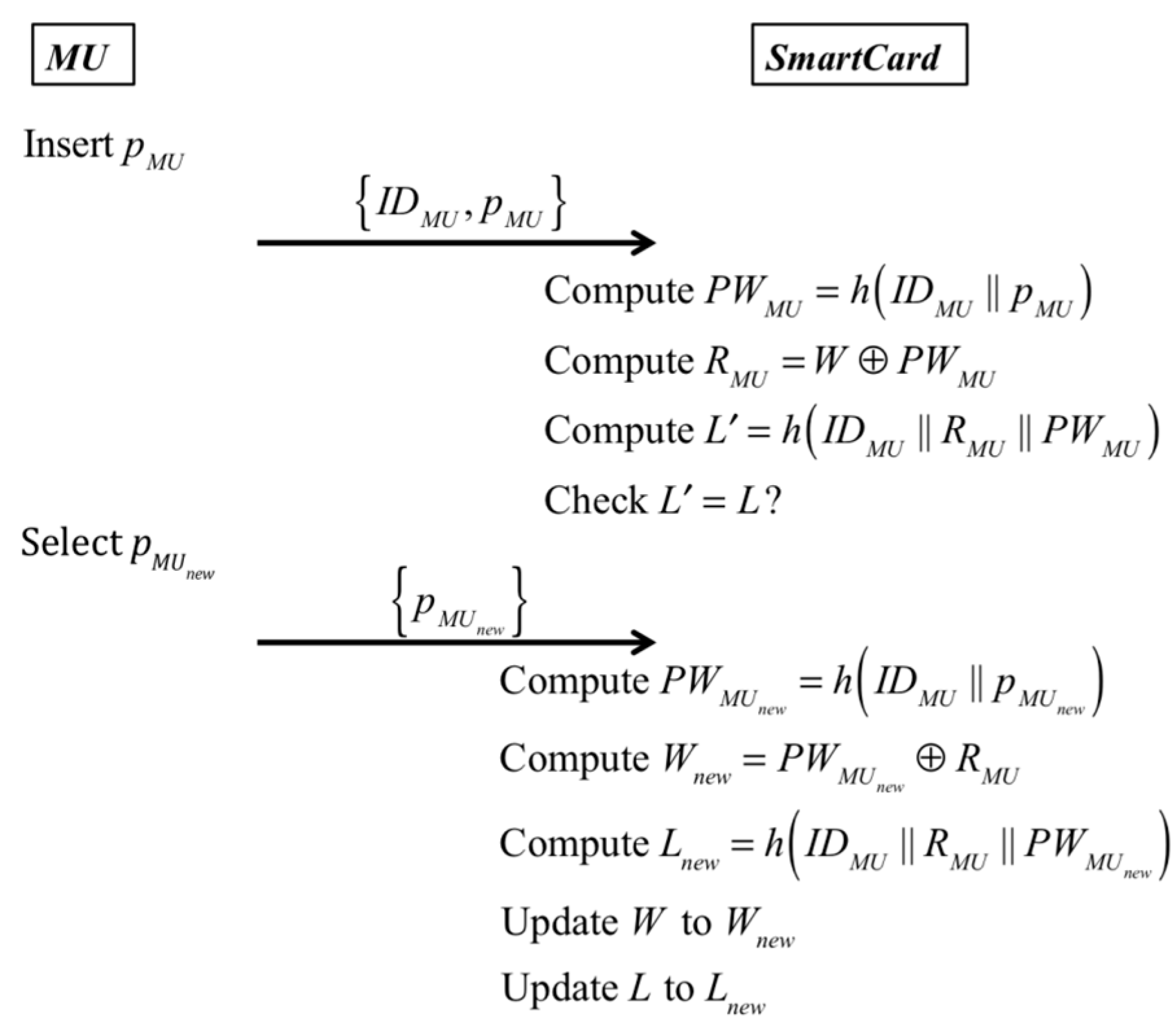
In our proposed scheme, MU can locally update his/her password. When MU wants to change his/her password PW_MU to the new password ${PW}_{{MU}_{new}}$, he/she does not need to connect to HA. This means a user can change his/her password at will.

3.4. Mutual Authentication

First, we make discussions on communication parties MU, FA and HA in authentication and establishment of the session key phase by the following three cases.

Case 1: Mutual authentication between FA and HA

HA authenticates FA by checking whether $S_{{FA}_1}^{\prime }=S_{{FA}_1}$, and FA authenticates HA by checking whether $S_{{FA}_2}^{\prime }=S_{{FA}_2}$, where $S_{{FA}_1}$ = h(a₀P.x || b₀P.x || p_FA-HA) and $S_{{FA}_2}$ = h(c₀a₀P.x || b₀P.x || p_FA-HA). Because p_FA-HA is only known to FA and HA, it denotes that only FA and HA can compute the correct parameters to be authenticated successfully. That is, our proposed scheme provides mutual authentication between FA and HA.

Case 2: Mutual authentication between MU and HA

MU authenticates HA by checking whether S₄ = S′₄, and HA authenticates MU by checking whether S₃ = S′₃, where S₄ = h(c₀b₀P.x || a₀P.x || ID_FA || ID_HA || R_MU || $R_{{MU}_{new}}$) and S₃ = h(R_MU ⊕ h(p_HA-MU || $R_{{MU}_{new}}$) || b₀P.x). Only MU and HA can compute the correct parameters to be authenticated successfully because p_HA-MU, $R_{{MU}_{new}}$ and R_MU are only known to MU and HA. As the result, our proposed scheme provides mutual authentication between MU and HA.

Case 3: Mutual authentication between MU and FA

In authentication and establishment of the session key phase, MU authenticates HA by checking if S₄ = S′₄, where S₄ = h(c₀b₀P.x || a₀P.x || ID_FA || ID_HA || R_MU || $R_{{MU}_{new}}$). Because only HA and MU know p_HA-MU, $R_{{MU}_{new}}$ and R_MU, only HA can compute c₀b₀P and S₄. If S₄ = S′₄, it denotes (1) a₀P is valid because S₄ contains a₀P.x and (2) FA has been already authenticated by HA. Then, MU computes the session key $K_{{MF}_0}$ = h(b₀a₀P.x), $C_{{MF}_0}^{\prime }$ = h($K_{{MF}_0}$ || b₀P.x), and $C_{{MF}_0}^{″}$ = h($C_{{MF}_0}^{\prime }$) and checks if $C_{{MF}_0}=C_{{MF}_0}^{″}$. If $C_{{MF}_0}=C_{{MF}_0}^{″}$, it denotes that FA really knows $K_{{MF}_0}$ = h(a₀b₀P.x). Because MU has already authenticated HA, MU is assured that only FA knows a₀ to compute $K_{{MF}_0}$. As a result, FA is authenticated successfully by MU. Thereupon, MU computes $B_{{MF}_0}$ = h(c₀P.x || $K_{{MF}_0}$) and sends it to FA. After obtaining {$B_{{MF}_0}$}, FA computes $B_{{MF}_0}^{\prime }$ = h(c₀P.x || $K_{{MF}_0}$) and checks if $B_{{MF}_0}=B_{{MF}_0}^{\prime }$. If $B_{{MF}_0}=B_{{MF}_0}^{\prime }$, FA is assured that MU knows b₀ to compute $K_{{MF}_0}$. FA has authenticated HA by checking if $S_{{FA}_2}^{\prime }=S_{{FA}_2}$, where $S_{{FA}_2}$ = h(c₀a₀P.x || b₀P.x || p_FA-HA). It denotes (1) b₀P is valid because $S_{{FA}_2}$ contains b₀P.x and (2) MU has been already authenticated by HA. As a result, MU is authenticated successfully by FA. Therefore, our proposed scheme provides mutual authentication between MU and FA.

Second, we make discussions on communication parties MU and FA in the update session key phase. Because MU and FA have already shared the session key $K_{{MF}_i}$ = h(a_ib_iP.x) in the previous session, they can use $K_{{MF}_i}$ and the stored data to authenticate each other. At the moment, FA stores {$C_{{MF}_i}$, a_iP, b_iP, $K_{{MF}_i}$} and MU stores {$C_{{MF}_i}^{\prime }$, a_iP, b_iP, $K_{{MF}_i}$}, where $C_{{MF}_0}^{\prime }$ = h($K_{{MF}_0}$ || b₀P.x) and $C_{{MF}_0}$ = h(h($K_{{MF}_0}$ || b₀P.x)) = h($C_{{MF}_0}^{\prime }$). MU selects r b_i+1, computes b_i+1P and h₁ = h(b_iP.x || b_i+1P.x || $K_{{MF}_i}$), and sends {b_i+1P, $C_{{MF}_i}^{\prime }$, h₁} to FA. After receiving {b_i+1P, $C_{{MF}_i}^{\prime }$, h₁}, FA checks if $h(C_{{MF}_i}^{\prime })$ exists in its database, where $h(C_{{MF}_i}^{\prime })$ = $C_{{MF}_i}$. Because it is hard to find the input of the hash function with a known hash value, this search approach protects MU from being traced even he stays in FA’s service domain and implies MU‘s legality. After finding the matched $C_{{MF}_i}$, FA extracts {$C_{{MF}_i}$, a_iP, b_iP, $K_{{MF}_i}$} from its database and selects a_i+1. FA computes h′₁ = h(b_iP.x || b_i+1P.x || $K_{{MF}_i}$) and checks if h′₁ = h₁. If h′₁ = h₁, it denotes (1) MU indeed knows $K_{{MF}_i}$ and (2) b_i+1P is valid. FA authenticates MU successfully. Then, FA computes a_i+1P, $K_{{MF}_{i+1}}$ = h(a_i+1b_i+1P.x), $C_{{MF}_{i+1}}$ = h(h($K_{{MF}_{i+1}}$ || b_i+1P.x)) and h₂ = h($C_{{MF}_{i+1}}||K_{{MF}_i}||K_{{MF}_{i+1}}$). FA updates {$C_{{MF}_i}$, a_iP, b_iP, $K_{{MF}_i}$} to {$C_{{MF}_{i+1}}$, a_i+1P, b_i+1P, $K_{{MF}_{i+1}}$} in its database and sends {a_i+1P, h₂} to MU. After receiving {a_i+1P, h₂}, MU computes $K_{{MF}_{i+1}}$ = h(b_i+1a_i+1P.x), $C_{{MF}_{i+1}}^{\prime }$ = h($K_{{MF}_{i+1}}$ || b_i+1P.x), and h′₂ = h(h($C_{{MF}_{i+1}}^{\prime }$) || $K_{{MF}_i}||K_{{MF}_{i+1}}$). Then, MU checks if h′₂ = h₂. If h′₂ = h₂, it denotes that FA indeed knows $K_{{MF}_i}$ and $K_{{MF}_{i+1}}$. MU authenticates FA successfully. As a result, mutual authentication is ensured in update session key phase.

4. Further Discussions

In this section, we first make comparisons between the proposed scheme and the related works, and BAN logic is then used to deduce the completeness of the proposed authentication scheme.

4.1. Comparisons

In the following, we present a discussion of the properties of the proposed scheme and the related works. The term “Local password change” denotes whether the mobile user can locally change his password without the home agent’s help in the corresponding scheme. The term “Anonymity” denotes whether the corresponding scheme can ensure user anonymity. The term “Insider attack resistance” denotes whether the corresponding scheme can resist insider attack. The term “Man-in-the-middle attack resistance” denotes whether the corresponding scheme can resist man-in-the-middle attack. The term “The synchronization problem resistance” denotes whether the corresponding scheme can resist the synchronization problem. “Replay attack resistance” denotes whether the corresponding scheme can resist replay attack. The comparisons between our scheme and the related works are given in

Table 2. Comparisons between our scheme and the related works.

Schemes	Ours	Kuo et al.’s [9]	Lu et al.’s [10]
Local password change	Yes	No	Yes
Anonymity	Yes	Yes	No
Insider attack resistance	Yes	No	Yes
Man-in-the-middle attack resistance	Yes	No	Yes
The synchronization problem resistance	Yes	No	Yes
Replay attack resistance	Yes	Yes	No

. According to the comparisons, it is assured that our scheme can resist common attacks and ensure security and convenience at the same time while others cannot.

4.2. BAN Logic-Based Authentication Proof

In the following, BAN logic is used to deduce the completeness of the proposed authentication scheme. Notations used in BAN logic are listed in

Table 3. Notations used in Burrows-Abadi-Needham logic (BAN logic).

Symbol	Definition
A, B	Principals indicate general instances participating in a protocol.
$A|\equiv M$	A believes the statement M.
$A⊲M$	A sees M.
$A|~M$	A once said M.
$A\Rightarrow M$	A has jurisdiction over M.
#(M)	M is a fresh message.
<M>N	Formula M is combined with formula N.
(M, N)	M or N is one part of message (M, N).
(M)K	M is hashed with the secret K.
$A\stackrel{K}{\leftrightarrow }B$	K is the secret shared between A and B.

.

Fundamental rules for BAN logic analysis are listed as follows:

• RBL1 (Message Meaning Rule 1): $\frac{A|\equiv A\stackrel{N}{\leftrightarrow }B, A⊲<M{>}_N}{A|\equiv B|~M}$.
• RBL2 (Message Meaning Rule 2): $\frac{A|\equiv A\stackrel{K}{\leftrightarrow }B, A⊲{(M)}_K}{A|\equiv B|~M}$.
• RBL3 (Nonce Verification Rule): $\frac{A|\equiv \#(M),A|\equiv B|~M}{A|\equiv B|\equiv M}$.
• RBL4 (Jurisdiction Rule): $\frac{A|\equiv B\Rightarrow M,A|\equiv B|\equiv M}{A|\equiv M}$.
• RBL5 (Freshness Conjunction Rule): $\frac{A|\equiv \#(M)}{A|\equiv \#(M,N)}$.
• RBL6 (Belief Rule): $\frac{A|\equiv (M),A|\equiv (N)}{A|\equiv (M,N)}$.
• RBL7 (Session Key Rule): $\frac{A|\equiv \#(M),A|\equiv B|\equiv M}{A|\equiv A\stackrel{K}{\leftrightarrow }B}$.

The following goals must be satisfied by using the above rules to ensure the security of the proposed authentication scheme under BAN logic.

Goal 1:

$HA|\equiv MU\stackrel{R_{M{U}_{new}},\hspace{0.17em}{c}_0{b}_{0}P}{\leftrightarrow }HA$.

Goal 2:

$HA|\equiv MU|\equiv MU\stackrel{R_{M{U}_{new}},\hspace{0.17em}{c}_0{b}_{0}P}{\leftrightarrow }HA$.

Goal 3:

$MU|\equiv MU\stackrel{R_{M{U}_{new}},\hspace{0.17em}\hspace{0.17em}{b}_0{c}_{0}P}{\leftrightarrow }HA$.

Goal 4:

$MU|\equiv HA|\equiv MU\stackrel{R_{M{U}_{new}},\hspace{0.17em}\hspace{0.17em}{b}_0{c}_{0}P}{\leftrightarrow }HA$.

Goal 5:

$HA|\equiv FA\stackrel{c_0{a}_{0}P}{\leftrightarrow }HA$.

Goal 6:

$HA|\equiv FA|\equiv FA\stackrel{c_0{a}_{0}P}{\leftrightarrow }HA$.

Goal 7:

$FA|\equiv FA\stackrel{a_0{c}_{0}P}{\leftrightarrow }HA$.

Goal 8:

$FA|\equiv HA|\equiv FA\stackrel{a_0{c}_{0}P}{\leftrightarrow }HA$.

Goal 9:

$MU|\equiv FA\stackrel{K_{M{F}_0}}{\leftrightarrow }MU$.

Goal 10:

$MU|\equiv FA|\equiv FA\stackrel{K_{M{F}_0}}{\leftrightarrow }MU$.

Goal 11:

$FA|\equiv FA\stackrel{K_{M{F}_0}}{\leftrightarrow }MU$.

Goal 12:

$FA|\equiv MU|\equiv FA\stackrel{K_{M{F}_0}}{\leftrightarrow }MU$.

Idealized transformation of the proposed scheme is as follows:

IM1: MU → FA: ID_HA, S₁, S₂, S₃, b₀P:

$$\{I{D}_{HA},h(p_{HA-MU}||R_{MU}),<R_{M{U}_{new}}{>}_{R_{MU}},<b_{0}P{>}_{R_{MU}\oplus h(p_{HA-MU}||R_{M{U}_{new}})},b_{0}P\}.$$

IM2: FA → HA: ID_FA, S₁, S₂, S₃, a₀P, b₀P, $S_{{FA}_1}$:

$$\{I{D}_{FA},h(p_{HA-MU}||R_{MU}),<R_{M{U}_{new}}{>}_{R_{MU}},<b_{0}P{>}_{R_{MU}\oplus h(p_{HA-MU}||R_{M{U}_{new}})},a_{0}P,b_{0}P,(a_{0}P,b_{0}P{)}_{p_{FA-HA}}\}.$$

IM3: HA → FA: ID_HA, c₀P, S₄, $S_{{FA}_2}$:

$$\{I{D}_{HA},c_{0}P,(c_0{b}_{0}P,a_{0}P,b_{0}P,R_{M{U}_{new}}{)}_{R_{MU}},(c_0{a}_{0}P,b_{0}P{)}_{P_{FA-HA}}\}.$$

IM4: FA → MU: ID_FA, S₄, a₀P, c₀P, $C_{{MF}_0}$:

$$\{I{D}_{FA},(c_0{b}_{0}P,a_{0}P,b_{0}P,R_{M{U}_{new}}{)}_{R_{MU}},a_{0}P,c_{0}P,(b_{0}P{)}_{K_{M{F}_0}}\}.$$

To evaluate the proposed scheme, assumptions regarding the preliminary state are shown as follows:

A1:

$MU|\equiv MU\stackrel{R_{MU},\hspace{0.17em}\hspace{0.17em}{p}_{HA-MU}}{\leftrightarrow }HA$.

A2:

$HA|\equiv MU\stackrel{R_{MU},\hspace{0.17em}\hspace{0.17em}{p}_{HA-MU}}{\leftrightarrow }HA$.

A3:

$FA|\equiv FA\stackrel{\hspace{0.17em}\hspace{0.17em}{p}_{FA-HA}}{\leftrightarrow }HA$.

A4:

$HA|\equiv FA\stackrel{\hspace{0.17em}\hspace{0.17em}{p}_{FA-HA}}{\leftrightarrow }HA$.

A5:

$MU|\equiv \#(b_0)$.

A6:

$FA|\equiv \#(a_0)$.

A7:

$HA|\equiv \#(c_0)$.

A8:

$HA|\equiv MU\Rightarrow b_{0}P$.

A9:

$FA|\equiv MU\Rightarrow b_{0}P$.

A10:

$MU|\equiv FA\Rightarrow a_{0}P$.

A11:

$HA|\equiv FA\Rightarrow a_{0}P$.

A12:

$MU|\equiv HA\Rightarrow c_{0}P$.

A13:

$FA|\equiv HA\Rightarrow c_{0}P$.

Considering IM1 and IM2 of the idealized forms:

IM1: MU → FA: ID_HA, S₁, S₂, S₃, b₀P:

$$\{I{D}_{HA},h(p_{HA-MU}||R_{MU}),<R_{M{U}_{new}}{>}_{R_{MU}},<b_{0}P{>}_{R_{MU}\oplus h(p_{HA-MU}||R_{M{U}_{new}})},b_{0}P\}.$$

IM2: FA → HA: ID_FA, S₁, S₂, S₃, a₀P, b₀P, $S_{{FA}_1}$:

$$\{I{D}_{FA},h(p_{HA-MU}||R_{MU}),<R_{M{U}_{new}}{>}_{R_{MU}},<b_{0}P{>}_{R_{MU}\oplus h(p_{HA-MU}||R_{M{U}_{new}})},a_{0}P,b_{0}P,(a_{0}P,b_{0}P{)}_{p_{FA-HA}}\}.$$

By applying seeing rule, we have

S1: FA$⊲$ID_HA, S₁, S₂, S₃, b₀P:

$$\{I{D}_{HA},h(p_{HA-MU}||R_{MU}),<R_{M{U}_{new}}{>}_{R_{MU}},<b_{0}P{>}_{R_{MU}\oplus h(p_{HA-MU}||R_{M{U}_{new}})},b_{0}P\}.$$

S2: HA$⊲$ID_FA, S₁, S₂, S₃, a₀P, b₀P, $S_{{FA}_1}$:

$$\{I{D}_{FA},h(p_{HA-MU}||R_{MU}),<R_{M{U}_{new}}{>}_{R_{MU}},<b_{0}P{>}_{R_{MU}\oplus h(p_{HA-MU}||R_{M{U}_{new}})},a_{0}P,b_{0}P,(a_{0}P,b_{0}P{)}_{p_{FA-HA}}\}.$$

By S2, A2, and RBL1, we have

S3:

$HA|\equiv MU|~${h(pHA-MU || RMU),$<R_{M{U}_{new}}{>}_{R_{MU}}$, $<b_{0}P{>}_{R_{MU}\oplus h(p_{HA-MU}||R_{M{U}_{new}})}$, b0P}.

By S3, A5, A8, RBL3, RBL4, and RBL7, we have

S4:

$HA|\equiv MU\stackrel{R_{M{U}_{new}},\hspace{0.17em}{c}_0{b}_{0}P}{\leftrightarrow }HA$.

Goal 1

By S4, A7, A12, and RBL4, we have

S5:

$HA|\equiv MU|\equiv MU\stackrel{R_{M{U}_{new}},\hspace{0.17em}{c}_0{b}_{0}P}{\leftrightarrow }HA$.

Goal 2

By S2, A4, and RBL2, we have

S6:

$HA|\equiv FA|~${IDFA, a0P, ${(a_{0}P,b_{0}P)}_{p_{FA-HA}}$}.

By S6, A6, A11, RBL3, RBL4, and RBL7, we have

S7:

$HA|\equiv FA\stackrel{c_0{a}_{0}P}{\leftrightarrow }HA$

Goal 5

By S7, A7, A13, and RBL4, we have

S8:

$HA|\equiv FA|\equiv FA\stackrel{c_0{a}_{0}P}{\leftrightarrow }HA$.

Goal 6

Considering IM3 of the idealized form:

IM3: HA → FA: ID_HA, c₀P, S₄, $S_{{FA}_2}$:

$$\{I{D}_{HA},c_{0}P,(c_0{b}_{0}P,a_{0}P,b_{0}P,R_{M{U}_{new}}{)}_{R_{MU}},(c_0{a}_{0}P,b_{0}P{)}_{P_{FA-HA}}\}.$$

By applying seeing rule, we have

S9: FA$⊲$ID_HA, c₀P, S₄, $S_{{FA}_2}$:

$$\{I{D}_{HA},c_{0}P,(c_0{b}_{0}P,a_{0}P,b_{0}P,R_{M{U}_{new}}{)}_{R_{MU}},(c_0{a}_{0}P,b_{0}P{)}_{P_{FA-HA}}\}.$$

By S9, A3, A7, A13, RBL2, RBL3, RBL4, and RBL7, we have

S10:	$FA|\equiv HA|~${IDHA, c0P, ${(c_0{a}_{0}P,b_{0}P)}_{P_{FA-HA}}$},

S11:

$FA|\equiv FA\stackrel{a_0{c}_{0}P}{\leftrightarrow }HA$,

Goal 7

S12:

$FA|\equiv HA|\equiv FA\stackrel{a_0{c}_{0}P}{\leftrightarrow }HA$, and

Goal 8

S13:	$FA|\equiv MU|~b_{0}P$.

By S13, A5, and A9, we have

S14:

$FA|\equiv FA\stackrel{K_{M{F}_0}}{\leftrightarrow }MU$ and

Goal 11

S15:

$FA|\equiv MU|\equiv FA\stackrel{K_{M{F}_0}}{\leftrightarrow }MU$

Goal 12

Considering IM4 of the idealized form:

IM4: FA → MU: ID_FA, S₄, a₀P, c₀P, $C_{{MF}_0}$:

$$\{I{D}_{FA},(c_0{b}_{0}P,a_{0}P,b_{0}P,R_{M{U}_{new}}{)}_{R_{MU}},a_{0}P,c_{0}P,(b_{0}P{)}_{K_{M{F}_0}}\}.$$

By applying seeing rule, we have

S16: MU$⊲$ID_FA, S₄, a₀P, c₀P, $C_{{MF}_0}$:

$$\{I{D}_{FA},(c_0{b}_{0}P,a_{0}P,b_{0}P,R_{M{U}_{new}}{)}_{R_{MU}},a_{0}P,c_{0}P,(b_{0}P{)}_{K_{M{F}_0}}\}.$$

By S16, A1, and RBL1, we have

S17:

$MU|\equiv HA|~${${(c_0{b}_{0}P,a_{0}P,b_{0}P,R_{M{U}_{new}})}_{R_{MU}}$, a0P, c0P}.

By S17, A7, A12, RBL3, RBL4, and RBL7, we have

S18:	$HA|\equiv MU\stackrel{R_{M{U}_{new}},\hspace{0.17em}{c}_0{b}_{0}P}{\leftrightarrow }HA$ and	Goal 3
S19:	$MU|\equiv HA|\equiv MU\stackrel{R_{M{U}_{new}},\hspace{0.17em}\hspace{0.17em}{b}_0{c}_{0}P}{\leftrightarrow }HA$.	Goal 4

By S16, A6, A10, RBL3, RBL4, and RBL7, we have

S20:	$MU|\equiv FA\stackrel{K_{M{F}_0}}{\leftrightarrow }MU$ and	Goal 9
S21:	$MU|\equiv FA|\equiv FA\stackrel{K_{M{F}_0}}{\leftrightarrow }MU$.	Goal 10

The above BAN logic analysis formally proves the authentication process has any two of MU, FA, and HA authenticate each other and the shared secrets are established as claimed.

5. Conclusions

In this paper, we propose a user anonymity-ensured mobility network authentication scheme after analyzing the previous related schemes and the weaknesses that they suffer from. In our scheme, first the parameters for negotiating the session key are verified. In the authentication and establishment of the session key phase, $S_{{FA}_1}$ and S₄ are employed by HA and MU to verify a₀P, and S₃ and $S_{{FA}_2}$ are employed by HA and FA to verify b₀P. In the update session key phase, h₁ and h₂ are employed by MU and FA to authenticate each other. Second, HA does not store MU’s password anymore and MU can change his/her password locally without connecting to HA. Third, the smart card authenticates MU before the authentication and establishment of the session key phase and password change phase. Forth, no fixed parameters are transmitted, to ensure user anonymity.

Via these new approaches, the proposed mobility network authentication scheme can defend against the weaknesses that the previous schemes suffer from. The proposed scheme is also analyzed to show that it ensures security and convenience and can be applied to mobility networks.