Abstract
A novel localization method based on multiple signal classification (MUSIC) algorithm is proposed for positioning an electric dipole source in a confined underwater environment by using electric dipole-receiving antenna array. In this method, the boundary element method (BEM) is introduced to analyze the boundary of the confined region by use of a matrix equation. The voltage of each dipole pair is used as spatial-temporal localization data, and it does not need to obtain the field component in each direction compared with the conventional fields based localization method, which can be easily implemented in practical engineering applications. Then, a global-multiple region-conjugate gradient (CG) hybrid search method is used to reduce the computation burden and to improve the operation speed. Two localization simulation models and a physical experiment are conducted. Both the simulation results and physical experiment result provide accurate positioning performance, with the help to verify the effectiveness of the proposed localization method in underwater environments.
1. Introduction
Estimation of source position has many important application areas including underwater localization, electroencephalography (EEG) and underwater navigation. In the last decades, the acoustic based locating method has played a main role in underwater localization [1,2]. However, the complexity and uncertain characteristics of underwater environments, such as the varying temperature and density, multi-path propagation, Doppler effect, and propagation delay, seriously influence the acoustic propagation and underwater channel [3,4,5]. The electromagnetic based localization method would not be affected by these drawbacks because the electromagnetic field propagates much faster than that of the sound wave [6,7]. Moreover, the underwater electromagnetic noise is much lower and more stable [8,9].
Underwater localization based on electromagnetic waves has been investigated recently. In the work [10], a self-localization method based on the attenuation of electromagnetic waves is presented. However, the localization accuracy decreases because of the boundary of the test model. Daegil Park et al. provided a received signal strength method to locate the source in a two dimensional plane by using commercial high frequency sensors [6]. However, high frequency electromagnetic wave based localization in seawater suffers from the serious attenuation because of the small skin depth, which limits its development. As a result, it is a challenge to locate an excitation source with high frequency electromagnetic facilities. Localization based on quasi-static electric fields provides better performance in the near field area, which has lower attenuation compared with the high frequency signals in conducting media. Underwater localization methods based on electric fields are also studied in works [11,12]. In Lebastard’s work [11], a bio-inspired method has been proposed to improve the localization performance using the Unscented Kalman filter. The work [12] proposed a locating algorithms using electric sense based on the measurement electric field re-emitted by secondary dipole. However, the electric field re-emitted by a secondary dipole that is usually much weaker than the primary field, which limits the localization region. Moreover, in practice, in a shallow sea environment, the seabed has rugged terrains, yielding a complex boundary condition, which will strongly affect the localization.
Considering the challenge of the underwater target localization in a complex confined environment, this paper proposes a novel solution for the underwater localization based on the boundary element method (BEM) theory and multiple signal classification (MUSIC) This localization method is prominent in magnetoencephalography (MEG) and EEG source analysis [13,14,15], where BEM can accurately describe the boundary model and the MUSIC provides a good performance, and it does not suffer from the problem of non-convexity [16]. In this method, we first discretize the boundary of the finite region using BEM. Then, the distribution of scalar potential on the boundary is derived. The sensors, electric dipole array, are set in the locating region, and one of the electric dipole is set as the reference point, which are different from electric field based methods in an infinite region or the classical EEG method using several electric dipole pairs. The potential difference between each electric dipole and the reference point consists of two components, namely the contribution of the electric dipole source itself and the contribution of the boundary. The position of the electric dipole source can be located via finding the minimum eigenvalue of the estimated gain matrix and the noise subspace by using the MUSIC algorithm. Generally, the electric dipole source carries out a controllable single frequency signal, which is independent of the environmental disturbances and noise. The MUSIC algorithm scans all possible source locations and estimates whether a source in its location [17], which results in a great amount of computation. To overcome this drawback and reduce the scan time, we also propose a global-multiple region-conjugate gradient (CG) hybrid search method in this paper. The effectiveness of the proposed method is investigated and compared with the source in infinite space model. The results strongly suggest that the proposed algorithm is effective in underwater localization.
2. Localization of Electric Dipole Source in Finite Region
2.1. Localization Model of Electric Dipole Source
The electric dipole source in the underwater localization problem is equivalent to a quasi-static electric field in a closed body, which is shown in Figure 1, and the discussions and details of the quasi-static electric field approximation can be found in [18]. The potential of each point in region is , and the boundary is defined as . It can be considered that the conductive of the water in region is far greater than that in the external region, which means there is no current field out of the region . According to the electrostatic field theory [19], we have the base Laplace equation with a Neumann boundary condition, which are shown in (1) and (2):
where f is the source distribution in region and n is the norm vector on boundary surface pointing into the region . The potential of observation point on boundary surface can be written as:
where denotes the Cauchy’s principal value integration. W is the test function, which is expressed in three-dimensional space as:
is the position of the source point on the boundary surface .
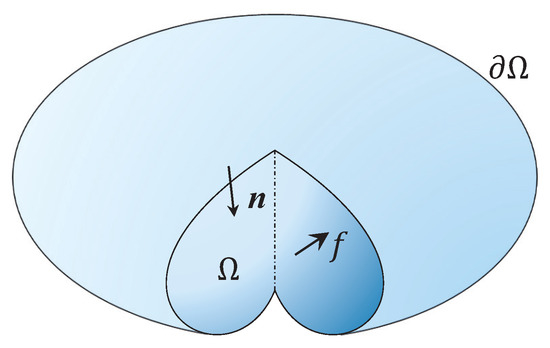
Figure 1.
Electrostatic field problem in finite region.
The boundary surface is discretized with N triangular patches for numerical calculation. We have:
where , donates the ith triangular patch of with the norm vector and represents the conductivity of the material in the localization region.
We assume that the electric dipole source is located at point in with a dipole moment . The matrix equation resulted from (5) can be written explicitly as:
where is the element of the surface impedance matrix , donates the unknown potential on , represents the potential contribution of the electric dipole source on the boundary surface, donates the transpose operation, , and and are the unit vectors in x, y and z directions, respectively.
In order to measure the potential in the locating area, electrodes are set at points in the water as receiving antenna array where . We take the th electrode as reference point. By inversing the operation, the voltage between the kth electrode and reference point are obtained:
where:
It can be seen from (12) that the voltage consists of the potential contribution on the boundary surface and the contribution of the electric dipole source itself. Thus, we obtain the matrix equation , which is given by:
We refer to as the dipole gain matrix [20] that maps a dipole at into a set of measurements, which is a matrix. It should be noted that for the electric dipole in infinite media, there would be no boundary in the area. As a result, the matrices and will not exist. Thus, we define it as the boundless model. If the boundary exists, we define it as the boundary model.
2.2. Localization Based on the Multiple Signal Classification Algorithm
The electric dipole source is associated with a low frequency sine current excitation, as the electric dipole source is a controllable source. We assume that the orientation of the electric dipole source is fixed during measurements. The data are acquired as:
where is the moment of the electric dipole source at time , . is the potential difference column vector at time , which has been explicitly illustrated in (16). The additive noise matrix is assumed to be zero mean with covariance , where denotes the expected value of the argument, is the Hermitian transpose operator, and denotes the identity matrix. The white noise covariance can probably be estimated using sufficiently long periods of measurement data for this study. The expected value of the matrix outer product may be represented under the zero-mean white noise assumption:
As is a Hermitian matrix of rank K, it can be decomposed as after eigenvalue decomposition where is the eigenvectors. represents the corresponding diagonal matrix of nonzero eigenvalues, which can be stated as:
According to [20], the eigenvectors may be rewritten as , where is the signal subspace and is the noise subspace. In this model, there is only one electric dipole source, and the signal subspace is matrix, and the noise subspace is matrix.
The position of the electric dipole source can be found by scanning the locating region and finding the minima generalized eigenvalue of , where indicates the generalized eigenvalue of the matrix pair given in parenthesis [21]. The eigenvector corresponding to the minima generalized eigenvalue represents the orientation of the electric dipole source. The algorithmic steps required for locating the electric dipole source in a confined environment from the original measured voltage data are given as follows.
- Step 1: Discretize the boundary of the locating area and calculate the boundary matrix according to the prior information about the boundary. By inverting the boundary matrix, we have .
- Step 2: By measuring the voltage of each channel of the receiving antenna array, the matrix is formed with the size of .
- Step 3: According to (23), the covariance matrix can be constructed.
- Step 4: Obtain the required signal subspace and noise subspace via the eigendecomposition of the constructed matrix .
- Step 5: Mesh the locating area with a set of spatial points .
- Step 6: Calculate the matrix according to (17) with the estimated dipole source position , .
- Step 7: Obtain the eigenvalues , and via the generalized eigendecomposition , where .
- Step 8: Find the global minima of . The dipole source position is estimated by .
Alternatively, is defined as the spatial spectrum in the locating area. The electric dipole source can also be located by scanning the locating area and finding the peak of . In the classical localization method, all possible source locations should be scanned in Step 5 of the localization procedure [17]. For example, scanning a region with size of 1 m × 1 m × 1 m with 10 mm interval will yield eigenvalue decomposition operations, which is not suitable for underwater localization. To reduce calculation and improve the location accuracy, we propose a novel global-multiple region-CG hybrid search method. The task is divided into four steps:
- Step 1: Scan the entire locating region with the interval of by the use of point-by-point scan method, and output the estimation position .
- Step 2: Scan the local region near the estimation position with the interval of , where .
- Step 3: If m equals to M, go to Step 4. Otherwise, update the estimation position , update the interval by , reduce the searching range and go to Step 2.
- Step 4: Estimate the position by using the CG method and output the final estimation position.
The first step leads to eigenvalue decomposition operations. The second step yields eigenvalue decomposition operations. In the fourth step, the CG method leads to eigenvalue decomposition operations. Therefore, the hybrid search method ceases eigenvalue decomposition operations.
3. Numerical Examples
In this section, we present a simulation model to illustrate the features of our proposed localization method. A cube with edge length of 1 m is filled with water with the conductivity of . The boundary surfaces of the simulation model are discretized into 6272 triangular patches with the average edge length of 0.03 m. 9 electrodes are located in the simulation model, which compose a receiving antenna array. The simulation model is shown in Figure 2. Table 1 illustrates the position of each electrode, and we set the electrode with the index number nine as the reference point.
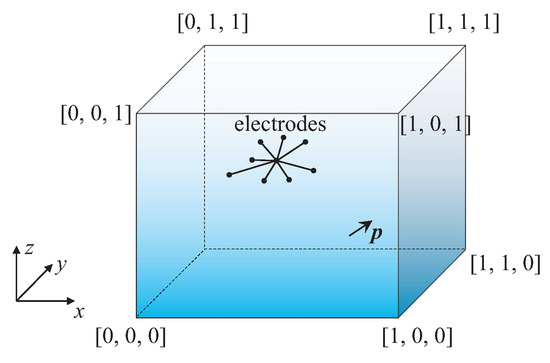
Figure 2.
Simulation model with nine electrodes.

Table 1.
The positions of the nine electrodes located in the simulation model.
We assume that the electric dipole source is on the plane . The low frequency sinusoidal current excitation of 100 Hz is loaded on the dipole with the dipole moment . In order to study the performance of the localization method in details, three possible situations are investigated: electric dipole source being far from boundary , close to boundary surface and close to the edge . The upper plot of Figure 3 shows the response of the receiving antenna array to the simulated noiseless source with 100 sample points and 1 ms sampling period, where the electric dipole source is located at . Then, we add white Gaussian noise to all data points, and the squared Frobenius norm of the noise matrix is one-tenth that of the squared Frobenius norm of the noiseless signal matrix, which yields the final signal-to-noise ratio (SNR) equal to 20 dB [21,22]. The lower plot of Figure 3 shows the response of the receiving antenna array for the signal plus noise data.
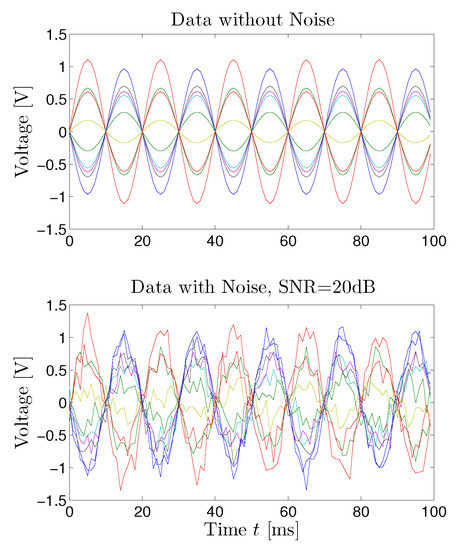
Figure 3.
The upper plot shows the response of the receiving antenna array to the simulated noiseless source with 100 sample points. The lower plot shows the response of the receiving antenna array for the signal plus noise data such that the signal-to-noise ratio (SNR) is 20 dB.
Figure 4 displays the spatial spectrum as an image whose intensities are proportional to the primary value, where the electric dipole source is at positions , and for an SNR of 20 dB. From Figure 4, we can see that there are errors between the estimation positions and the actual locations because of the noise. By calculating the cost function, the estimation positions , and are obtained, with the errors of 0.009 m, 0.013 m and 0.027 m, respectively. It can also be seen from Figure 4 that the highlight area in (c) is larger than (b) and (a), making it difficult to distinguish the estimated position and the background. The reason is that the distance from the electric dipole source at is smaller than the edge length of the triangular element. As a result, the effect of the triangular element shape to the field description should not be neglected.
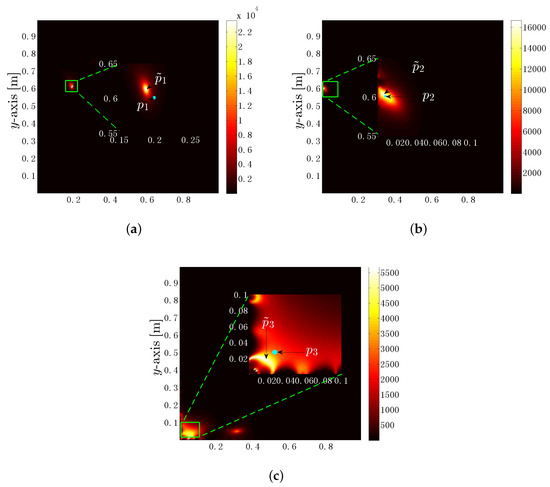
Figure 4.
Imaging the spatial spectrum on the plane z. (a) m for estimating the position of electric dipole source at ; (b) m for estimating the position of electric dipole source at ; (c) m for estimating the position of electric dipole source at . The highlight blue spot indicates the true location.
In this simulation, we have mm, mm, mm, mm, mm, mm, and , . Thereby, the hybrid search method yields a total of eigenvalue decomposition operations. According to statistics, the calculations by using CG method are much smaller than that of local search method, which can be neglected. Compared with the 10 mm interval point-by-point scan method, the hybrid search method can reduce 95.2% calculations with less than 1 mm resolution. The comparison shows that the hybrid search method could reduce the locating time effectively.
In order to further evaluate the accuracy of the proposed localization method, it is compared with the localization method in boundless model. We use a line as the simulation tracking trail, where . The root mean square (RMS) errors, under a different noise level, are depicted in Figure 5. It is clearly shown in Figure 5 that the localization method in the boundless model has much higher RMS errors compared with our proposed localization method in boundary model for a different SNR level. For the proposed localization method, there are relatively lower RMS errors in the interval . However, the RMS errors increase when the electric dipole source is close to the boundary surface. That is because the shape of the triangular element should not be neglected. Moreover, the distance between the electric dipole source and electrode antenna array are further when the electric dipole source is close to the boundary surface, resulting in lower signal amplitude. The proposed localization method has a minimum RMS error of 0.025 m for SNR = 10 dB, 0.016 m for SNR = 15 dB and 0.009 m for SNR = 20 dB, indicating that the proposed localization method has good performance for underwater electric dipole source locating.
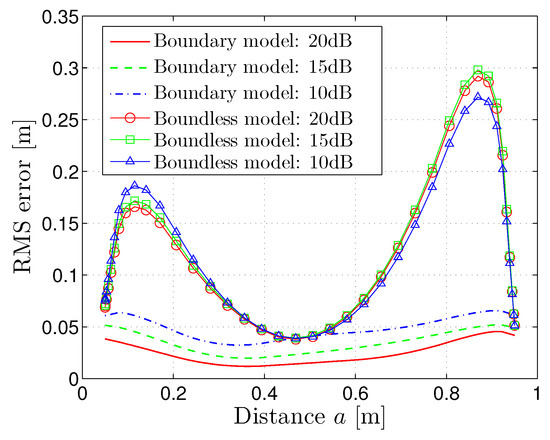
Figure 5.
The root mean square (RMS) errors under difference noise level.
We propose another simulation model to study the performance of the localization method in shallow sea environment, which is shown in Figure 6. The boundary surfaces of the experiment model are discretized into 4888 triangular patches with the average edge length of 6 m. The conductivity of the sea is assumed to be . The receiving antenna array with nine electrodes are located in the experiment model, which are listed in Table 2. The low frequency sinusoidal current excitation of 100 Hz is loaded on the dipole with the dipole moment . The data samples used in this experiment model are . An autonomous underwater vehicle (AUV) travels along a trail . Figure 7 presents the RMS errors at difference position, which are compared with the boundless model.
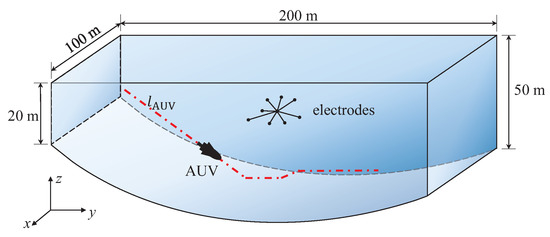
Figure 6.
Experiment model for autonomous underwater vehicle (AUV) localization in shallow sea.

Table 2.
The positions of the nine electrodes located in the experiment model.
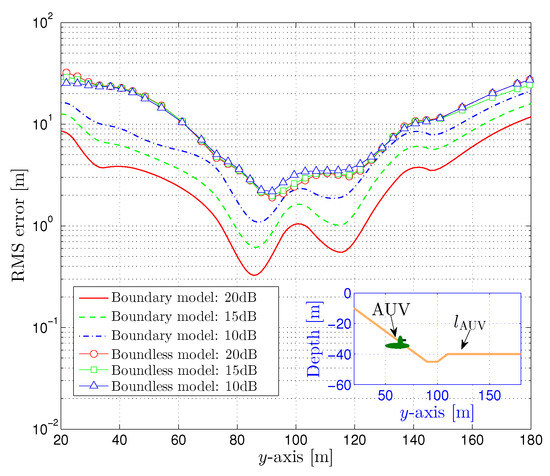
Figure 7.
The performance of AUV localization at a different position.
The results show that the RMS errors of localization increase with the noise level rising. However, there are much higher RMS errors in the boundless model compared with our proposed localization method in boundary model for each SNR level, indicating that the proposed localization method has better locating accuracy. We can also notice that the proposed localization method shows good performance in interval , with the minimum RMS error of 0.3 m at SNR = 20 dB, 0.6 m at SNR = 15 dB and 1.1 m at SNR = 10 dB. However, the RMS errors increase when the electric dipole source gets close to the boundary surface, because the distance between the electric dipole source and electrode antenna array are further than the electric dipole source is to the boundary surface, resulting in a lower signal amplitude. However, the errors have been in an acceptable range.
In order to make the proposed method more easily implemented in engineering applications, we study the localization accuracy under different number of receiving electrodes. We assume that the AUV is located at position . The RMS errors of the position estimates versus the SNR are given in Figure 8. In Figure 8, we also plot the RMS errors of boundless model estimates. We can see from Figure 8 that the RMS errors decrease as the number receiving electrodes increases. It is obvious that the proposed method provides smaller RMS errors than those of the boundless model for the same SNR and electrodes number. We can also notice that the RMS errors do not significantly decrease as the electrodes number increases in the boundless model. However, the proposed method provides significantly better localization performance when the electrodes number increases.
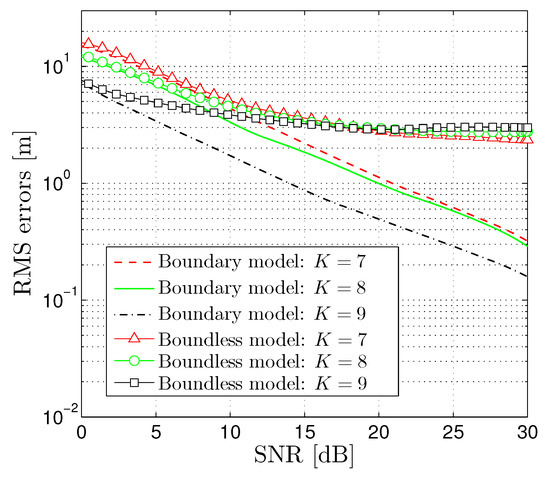
Figure 8.
RMS errors for different number of electrodes versus SNR.
In this section, two numerical simulations are proposed to analyze the performance of the proposed localization method. Comparisons of the boundary model and boundless model with different SNR show that the proposed localization method provides higher localization accuracy, which can be used as a precise localization system in confined underwater environments. Additionally, it should be noted that the size of the gain matrix of the boundless model is much smaller than that of the boundary model. As a result, localization based on the boundless model would reduce the computation burden for eigendecomposition. In the scenario of deep ocean localization, the electric dipole and the receiving antenna array are far from the surface and the seabed, where the field contribution by the boundary can be neglected. It means that the boundless model can also provide acceptable localization accuracy in deep ocean localization with a smaller computational burden.
4. Experiment
To further verify the effectiveness of proposed localization method, a set of localization experiment is developed in our laboratory environment. A cylindrical plastic pipe is used as a mobile electric dipole source, with diameter of 8 mm, length of 100 mm. Two metal sheets cover the ends of the cylindrical plastic pipe as the electrodes of the dipole source. We create a uniform circular array receiving antenna (UCARA) with nine electrodes, the detail of which is shown in Figure 9. A diagram of this experiment is proposed in Figure 10. The dipole source is mounted on a horizontal movable gantry workbench with a size of 3 m by m. This allows us to move the dipole source along the pre-programmed trail with high geometric resolution. The depth of the water in the tank is m, and the conductivity of the water is set to be 4 S/m, which is close to the conductivity of sea water.
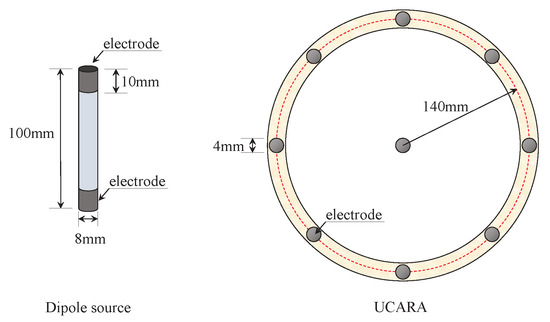
Figure 9.
The electric dipole source and uniform circular array receiving antenna (UCARA) , left the physical size of the electric dipole source, right side the size of UCARA.

Figure 10.
Tank experiment environment.
In this experiment, the source frequency is 100 Hz, where the dipole moment A along the x-axis and output power of W. The positions of the electrodes in the UCARA are known and fixed, which are listed in Table 3, where the ninth electrode is set as the common ground. During the measurement, we set the dipole source at the point , where , which are named , , , and . The voltage data on the UCARA are measured by the use of an eight channel analog digital converter (ADC) with a 1 kHz sample rate and 16 bit precision. For locating the dipole source, we use 100 measured voltage data to model each channel. In order to find out the dipole source, the spatial spectra are plotted in Figure 11, where is the estimated position of , . Localization results obtained from the localization experiment with the dipole source is shown in Figure 11. 300 independent measurements are carried out for each test point, and the comparisons between estimated positions and their actual positions are also given in Table 4. From the Table 4, we can find that the maximum root mean square (RMS) error is m. The estimation errors may be caused by the following reasons. Firstly, the dipole source in the experiment is not an ideal dipole, which has physical dimensions in practice. Secondly, the shell of the UCARA can affect the distribution of the electric field of the UCARA. Finally, the actual position of the dipole source may be slightly moved during measurement because of the water wave. Although some experimental results slightly offset the center position, the localization accuracy is still good. These results prove that the proposed localization scheme can be used as a precise localization system in underwater environments.

Table 3.
The electrode positions of the UCARA.
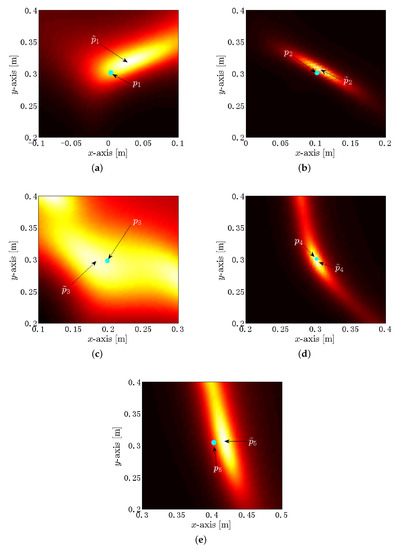
Figure 11.
Spatial spectra based on the measured data. (a) is the estimation for ; (b) is the estimation for ; (c) is the estimation for ; (d) is the estimation for ; and (e) is the estimation for .

Table 4.
The estimated positions of the electric dipole source in different positions.
5. Conclusions
In this paper, a novel method based on BEM and the MUSIC algorithm is proposed for underwater electric dipole source localization. The BEM is utilized to discretize the continuous surface function and transpose it to a matrix equation, which accurately describes the field contribution by the boundary. The canonical MUSIC algorithm is used to estimate the location of the electric dipole source. In comparison with the least squares methods, MUSIC provides a better performance without non-convexity. In order to speed up the localization operation, a global-multiple region-CG hybrid search method is introduced. From the simulation results, 95.2% computation burden is effectively reduced by using the hybrid search method. Both the simulation results and the physical experiment show that the new method and the algorithm we presented in this paper can realize high accuracy for locating an electric dipole source in a confined underwater environment. In addition, we also research how the noise level and the distance between electric dipole source and receiving antenna array impact the errors of location. In our further work, we will do more research and experiments to acquire much more accurate results.
Acknowledgments
This research has been supported by the National Key Research and Development Program of China-Government Corporation Special Program (2016YFE0111100), Fundamental Research Funds for the Central Universities (GK2080260160 and GK2080260166).
Author Contributions
Yidong Xu did the mathematical modeling and the simulations. He also wrote the draft of the paper. Wei Xue and Yingsong Li put forward to the idea and checked the simulation of this paper. Yingsong Li, Lili Guo and Wenjing Shang contributed to the revisions and the discussion of the results.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Carroll, P.; Zhou, S.; Zhou, H.; Xu, X.; Cui, J.H.; Willett, P. Underwater Localization and Tracking of Physical Systems. J. Electr. Comput. Eng. 2012, 2012, 2. [Google Scholar] [CrossRef]
- Lefort, R.; Real, G.; Drémeau, A. Direct regressions for underwater acoustic source localization in fluctuating oceans. Appl. Acoust. 2017, 116, 303–310. [Google Scholar] [CrossRef]
- Li, B.; Zhou, S.; Stojanovic, M.; Freitag, L.; Willett, P. Multicarrier Communication over Underwater Acoustic Channels with Nonuniform Doppler Shifts. IEEE J. Ocean. Eng. 2008, 33, 198–209. [Google Scholar]
- Esmaiel, H.; Jiang, D. Review Article: Multicarrier Communication for Underwater Acoustic Channel. Int. J. Commun. Netw. Syst. Sci. 2013, 6, 361–376. [Google Scholar] [CrossRef]
- Rango, F.D.; Veltri, F.; Fazio, P. A multipath fading channel model for underwater shallow acoustic communications. In Proceedings of the IEEE International Conference on Communications (ICC), Ottawa, ON, Canada, 10–15 June 2012; pp. 3811–3815. [Google Scholar]
- Park, D.; Kwak, K.; Kim, J.; Wan, K.C. Underwater sensor network using received signal strength of electromagnetic waves. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 1052–1057. [Google Scholar]
- Quintanadíaz, G.; Menarodríguez, P.; Pérezálvarez, I.; Jiménez, E.; Dortanaranjo, B.P.; Zazo, S.; Pérez, M.; Quevedo, E.; Cardona, L.; Hernández, J. Underwater Electromagnetic Sensor Networks—Part I: Link Characterization. Sensors 2017, 17, 189. [Google Scholar] [CrossRef] [PubMed]
- Soderberg, E.F. ELF noise in the sea at depths from 30 to 300 meters. J. Geophys. Res. 1969, 74, 2376–2387. [Google Scholar] [CrossRef]
- Zazo, J.; Macua, S.V.; Zazo, S.; Pérez, M.; Pérez-Álvarez, I.; Jiménez, E.; Cardona, L.; Brito, J.H.; Quevedo, E. Underwater Electromagnetic Sensor Networks, Part II: Localization and Network Simulations. Sensors 2016, 16, 2176. [Google Scholar] [CrossRef] [PubMed]
- Duecker, D.A.; Geist, A.R.; Hengeler, M.; Kreuzer, E.; Pick, M.A.; Rausch, V.; Solowjow, E. Embedded Spherical Localization for Micro Underwater Vehicles Based on Attenuation of Electro-Magnetic Carrier Signals. Sensors 2017, 17, 959. [Google Scholar] [CrossRef] [PubMed]
- Lebastard, V.; Chevallereau, C.; Amrouche, A.; Jawad, B.; Girin, A.; Boyer, F.; Gossiaux, P.B. Underwater robot navigation around a sphere using electrolocation sense and Kalman filter. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 4225–4230. [Google Scholar]
- Boyer, F.; Lebastard, V.; Chevallereau, C.; Servagent, N. Underwater Reflex Navigation in Confined Environment Based on Electric Sense. IEEE Trans. Robot. 2013, 29, 945–956. [Google Scholar] [CrossRef]
- Mosher, J.C.; Leahy, R.M. EEG and MEG source localization using recursively applied (RAP) MUSIC. In Proceedings of the Conference Record of The Thirtieth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 3–6 November 1996; pp. 1201–1207. [Google Scholar]
- Mosher, J.C.; Leahy, R.M.; Lewis, P.S. EEG and MEG: Forward solutions for inverse methods. IEEE Trans. Bio-Med. Eng. 1999, 46, 245–259. [Google Scholar] [CrossRef]
- Hong, J.H.; Ahn, M.; Kim, K.; Jun, S.C. Localization of coherent sources by simultaneous MEG and EEG beamformer. Med. Biol. Eng. Comput. 2013, 51, 1121–1135. [Google Scholar] [CrossRef] [PubMed]
- Shahbazi, F.; Ewald, A.; Nolte, G. Self-Consistent MUSIC: An approach to the localization of true brain interactions from EEG/MEG data. Neuroimage 2015, 112, 299. [Google Scholar] [CrossRef] [PubMed]
- Shahbazi, F.; Ziehe, A.; Nolte, G. Self-Consistent MUSIC algorithm to localize multiple sources in acoustic imaging. In Proceedings of the 4th Berlin Beamforming Conference, Berlin, Germany, 22–23 February 2012. [Google Scholar]
- Heller, L.; Hulsteyn, D.B.V. Brain stimulation using electromagnetic sources: Theoretical aspects. Biophys. J. 1992, 63, 129–138. [Google Scholar] [CrossRef]
- Katsikadelis, J. Boundary Elements. Theory and Applications; Elsevier Science: Oxford, UK, 2002. [Google Scholar]
- Mosher, J.C.; Leahy, R.M. Recursive MUSIC: A framework for EEG and MEG source localization. IEEE Trans. Biomed. Eng. 1998, 45, 1342–1354. [Google Scholar] [CrossRef] [PubMed]
- Sekihara, K.; Poeppel, D.; Marantz, A.; Koizumi, H.; Miyashita, Y. Noise covariance incorporated MEG-MUSIC algorithm: A method for multiple-dipole estimation tolerant of the influence of background brain activity. IEEE Trans. Biomed. Eng. 1997, 44, 839–847. [Google Scholar] [CrossRef] [PubMed]
- Mosher, J.C.; Leahy, R.M. Source localization using recursively applied and projected (RAP) MUSIC. IEEE Trans. Signal Process. 1999, 47, 332–340. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).