Abstract
Deduplication is an efficient data reduction technique, and it is used to mitigate the problem of huge data volume in big data storage systems. Content defined chunking (CDC) is the most widely used algorithm in deduplication systems. The expected chunk size is an important parameter of CDC, and it influences the duplicate elimination ratio (DER) significantly. We collected two realistic datasets to perform an experiment. The experimental results showed that the current approach of setting the expected chunk size to 4 KB or 8 KB empirically cannot optimize DER. Therefore, we present a logistic based mathematical model to reveal the hidden relationship between the expected chunk size and the DER. This model provides a theoretical basis for optimizing DER by setting the expected chunk size reasonably. We used the collected datasets to verify this model. The experimental results showed that the R2 values, which describe the goodness of fit, are above 0.9, validating the correctness of this mathematic model. Based on the DER model, we discussed how to make DER close to the optimum by setting the expected chunk size reasonably.
1. Introduction
Deduplication is an efficient data reduction technique, and it is used to mitigate the problem of huge data volume in big data storage systems. At present, deduplication is widely used in secondary storage systems such as backup or archival systems [1,2,3,4], and is also gradually used in primary storage systems, such as file systems [5,6]. Content defined chunking (CDC) [7] can achieve high duplicate elimination ratios (DERs), and therefore is the most widely used data chunking algorithm. DER indicates the ratio of the eliminated data processed by the deduplication, and is used as an essential indicator to evaluate the deduplication effect. Therefore, improving DER has been an important research area for the storage community. After a deduplication process, a storage system needs to store unique and meta data. The unique data refers to the data that is judged as new by a deduplication process. The metadata refers to the data that saves the address information of a data chunk that is used to rebuild a data stream. This will occur while a restoration is needed in a backup system, or a file read is requested in a primary storage system. The expected chunk size is an important parameter in CDC algorithms and needs to be set before the deduplication is enabled. A smaller chunk size results in a large number of metadata and hence requires a significant amount of storage space, but it will reduce the unique data size, and vice versa. Thus, the expected chunk size will influence DER significantly and is an important parameter in CDC [8]. The researcher has pointed out that a reasonable setting of the expected chunk size could increase DER significantly [9]. To increase DER, the researcher has been focusing on improving chunking algorithms; however, few studies have been done on how to set the expected chunk size reasonably to increase DER. Nowadays, researchers consider 4 KB or 8 KB empirically as the reasonable expected chunk size. However, these values lack both theoretical proof and verification with realistic datasets.
To verify whether setting the expected chunk size to 4 KB or 8 KB can improve DER, we collected two realistic datasets to perform the experiment. The datasets are: (1) Linux kernel source codes; and (2) multiple SQLite backup data while running the Transaction Processing Performance Council-C (TPC-C) benchmark. The experimental results showed that setting the expected chunk size to 4 KB or 8 KB cannot optimize DER. To study how to set the expected chunk size reasonably in order to optimize DER, we propose a logistic based mathematical model to reveal the hidden relationship between the expected chunk size and the DER. Two realistic datasets were used to verify this model. The experimental results showed that the R2 values, which describe the goodness of fit, are above 0.9, validating the correctness of this mathematic model. Based on this model, we discussed how to set the expected chunk size to make DER close to the optimum.
Our contributions in this paper are the following:
- (1)
- With two realistic datasets, we showed that the expected chunk size 4 KB or 8 KB that is currently considered reasonable, cannot optimize DER.
- (2)
- We present a logistic based mathematical model to reveal the hidden relationship between the DER and the expected chunk size. The experimental results with two realistic datasets showed that this mathematical model is correct.
- (3)
- Based on the proposed model, we discussed how to set the expected chunk size to make DER close to the optimum.
2. Related Work
DER is an essential metric to evaluate the deduplication effect. Thus, to increase DER is an important study in the deduplication research area. At present, researchers mainly focus on improving data chunking algorithms to increase DER. The purpose of data chunking algorithms is to divide a data stream into a series of chunks that are used as the basic units to detect duplicated data. Currently, there are three kinds of data chunking algorithms: (1) single instance store (SIS)— under this method, the whole file is used as the basic unit to perform a deduplication. The representatives are SIS in Windows 2000 (NT 5.0, Microsoft, Redmond, WA, USA) [10] and DeDu [11]. The problem of the single instance store is its low DER; (2) fixed sized partitioning (FSP)—this algorithm divides the file into fixed sized chunks, which are used as basic units to perform a deduplication. The representatives of FSP are Venti [4] and Oceanstore [12]. Compared with SIS, FSP improved DER significantly. However, the effectiveness of this approach on DER is highly sensitive to the sequence of edits and modifications performed on consecutive versions of an object. For example, an insertion of a single byte at the beginning of a file can change the content of all chunks in the file resulting in no sharing with existing chunking; and (3) content defined chunking (CDC). CDC employs Rabin’s fingerprints [13] to choose partition points in the object. Using fingerprints allows CDC to “remember” the relative points at which the object was partitioned in previous versions without maintaining any state information. By picking the same relative points in the object to be chunk boundaries, CDC localizes the new chunks created in every version to regions where changes have been made, keeping all other chunks the same. CDC was first applied in LBFS (A Low-bandwidth Network File System) [7]. Moreover, lots of chunking algorithms are developed based on CDC to improve DER [9,14,15,16]. Because CDC can avoid the problem of data shifting and is widely used, and is also the basic foundation of many improved algorithms, we study the influence of expected chunk size on DER in CDC based deduplication.
The expected chunk size is an important parameter in CDC algorithms, and will affect DER significantly. Thus, it is important to study how to set the expected chunk size reasonably to improve DER. Nowadays, researchers suggest setting the expected chunk size by rule of thumb. For example, 4 KB [17] or 8 KB [3,7,18] are considered reasonable by some researchers; Symantec Storage Foundation 7.0 (Mountain View, CA, USA) recommends a chunk size of 16 KB or higher [19]; IBM (Armonk, NY, USA) mentioned the average chunk size for most deduplicated files is about 100 KB [20]. However, these expected chunk sizes lack either theoretical proof or experimental evaluation. Suzaki [21] studied the effect of chunk size from 4 KB to 512 KB on Input/Output (I/O) optimization by experiments, and showed large chunks (256 KB) were effective. However, the main concern of Suzaki’s work is to optimize I/O rather than DER by setting chunk size, whereas, we focus on the impact of chunk size on DER in this paper.
3. Background
3.1. The Symbol Definitions
In Table 1, we defined the symbols that will be used in this paper.

Table 1.
The symbol definitions.
3.2. The Principal of CDC
In this paper, our study was based on the original implementation of CDC, which was first proposed in LBFS [7]. The principal of the CDC algorithm is shown in Figure 1. A 48 byte window slides continuously from the beginning of the data stream. The rabin fingerprint [13] of the current window data is calculated and then this fingeprint is judged on whether its low-order x bits equals a magic value. Thus, the boundary can be judged by whether the condition rabin_fp & mask==mask-1 is met. The rabin_fp represents the rabin fingerprint of the current window data; mask is a predefined binary value and is used to obtain the low-order x bits of the fingerprint. For example, if mask is set to 1111 in binary, the low-order 4 bits will be obtained. The magic value could be set to mask-1 or any value less than or equal to mask.
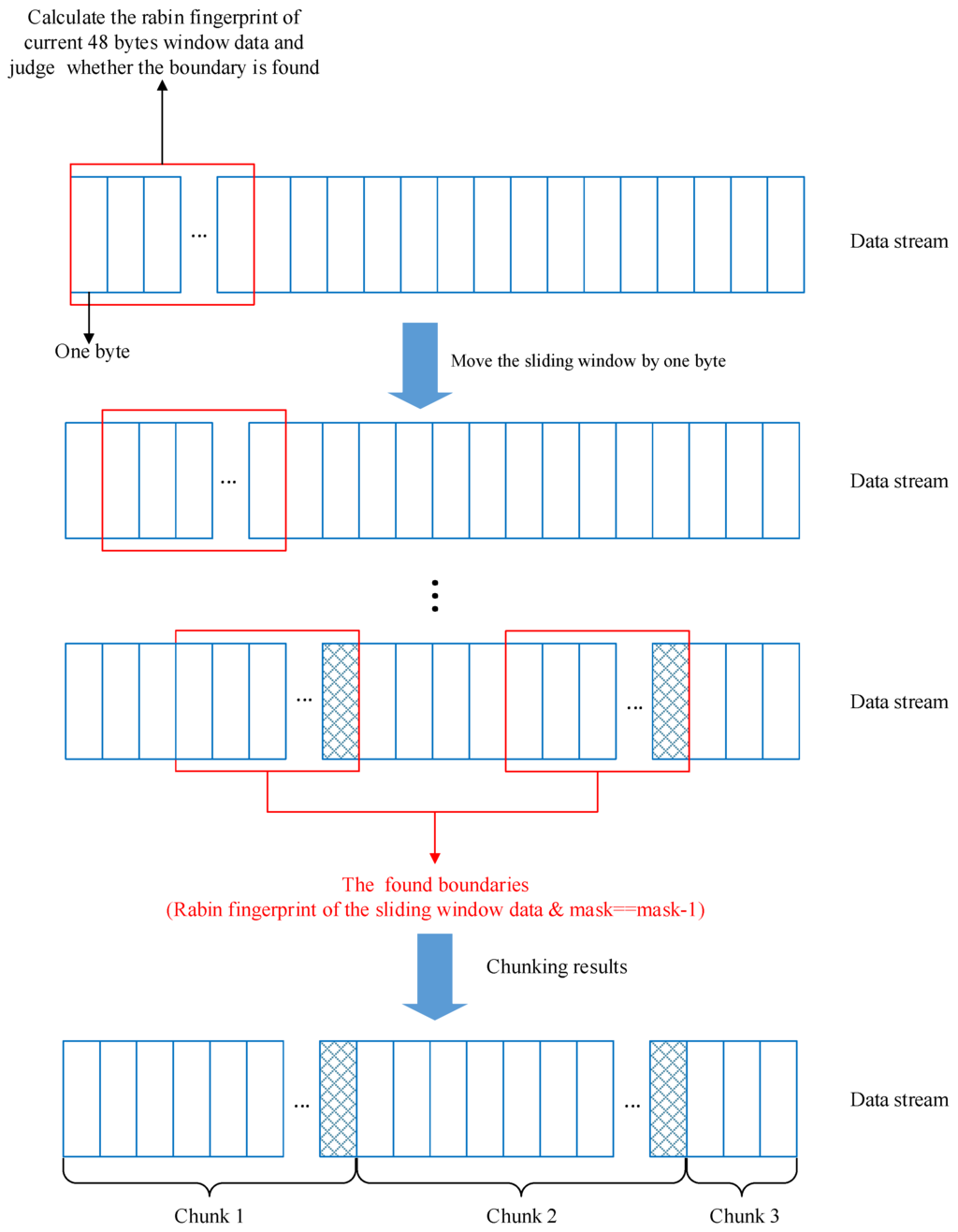
Figure 1.
The principal of Content defined chunking (CDC) algorithm.
If the condition is met, the last byte of the current window is used as the boundary of the chunk. After the window sliding finished, the formed boundaries divide the data stream into a series of data chunks with variable lengths. To avoid the chunks being too large or too small, the maximum and minimum value of the chunks need to be set. The window slides from a minimum chunk size position, and if the chunk size is bigger than maximum, the last byte of the current window is set as the boundary enforced.
3.3. The Expected Chunk Size
The process of the CDC algorithm is to slide a window by one byte and judge whether the current position is a boundary. Since the rabin hash function [13] generates a fingerprint with input data uniformly, the probability that low-order x bits of a region’s fingerprint equals a chosen value is 1/2x. This chunking process can be considered a Bernoulli trial; thus, the expected boundaries number X obeys Binomial distribution, as
In Equation (1), S is the length of the data stream; W is the size of the sliding window; and x is the length of the mask. For example, if x = 4, then mask = 1111; if x = 3, then mask = 111.
The expectation of boundaries number is:
The expectation of chunks number is:
We assume the expected chunk size μ is far less than the data stream length S. Therefore, the expected chunk size is:
Equation (4) shows that the expected chunk size μ is decided by the mask length x, and these two variables have an exponential relationship.
4. Modeling DER with the Expected Chunk Size
Three kinds of data need to be stored after the deduplication: (1) Unique data—this data is judged as not existing in the storage system by the CDC algorithm; (2) Metadata—this data contains the address information of the chunks to rebuild the data stream; (3) Fingerprint index—the Secure Hash Algorithm-1 (SHA-1) or MD5 hash value of each unique data is used as its fingerprint. All fingerprints are stored in a lookup index to detect whether a new chunk is duplicated with the existing chunks.
4.1. Modeling the Metadata Size
For the data that is formed after the chunking algorithm, no matter if it is duplicated or not, its corresponding metadata needs to be stored. The metadata saves the actual address information of the current chunk in the storage system, and it is used to retrieve its corresponding chunk if a read behavior is needed. The total metadata number of a data stream equals the total chunks number, and it can be computed as follows:
Supposing the size of one metadata is m, then the mathematical model of the metadata size is:
4.2. Modeling the Unique and Index Data Size
We use Su to denote the sum of unique and index data size. We cannot derive the relationship between Su and expected chunk size μ theoretically. Consequently, we observed a large number of real datasets and found that the curve of the relationship between Su and μ is S shaped. The growth ratio is urgent first and then slow, and the curve has a upper bound. Thus, we consider the logistic function is the appropriate model to describe the relationship between Su and μ. Figure 2 shows three representatives of the relationship curves. Three datasets are: (1) 310 versions of Linux kernel source codes [22]; (2) 12 dumps of Wikipedia pages [23]; and (3) 90 backups of SQLite [24] while running TPC-C [25] benchmark. In Figure 2, the x-axis represents the expected chunk size (decided by mask length); and the y-axis represents the data size of unique and index (MB).
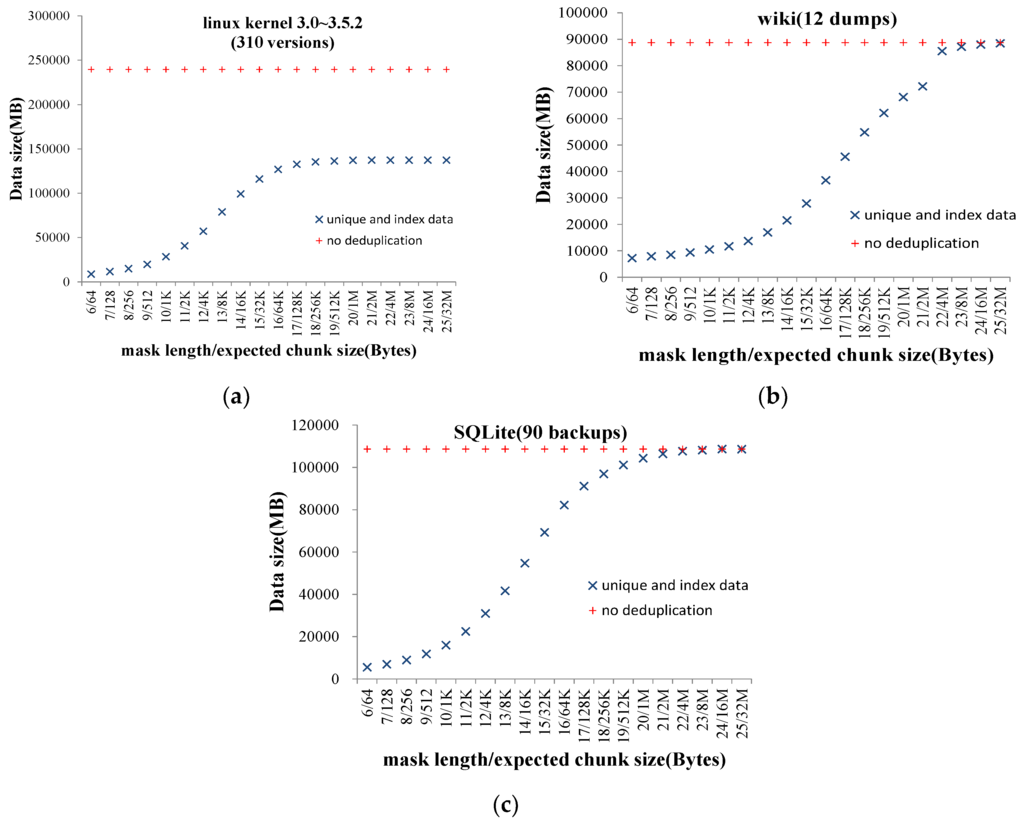
Figure 2.
The curve of the relationship between the unique data size and the expected chunk size. (a)linux kernel source codes; (b) wikipedia dumps; (c) SQLite backups.
The logistic function is defined as follows:
where L is the upper bound of the logistic function; k is the steepness of the curve; and x0 is the x-value of the curve’s midpoint.
In Figure 2, it can be seen that the increase of mask lengths beyond 15 changes the data size very slightly in the linux kernel dataset. This is because the files in this set are simply smaller, which means that individual source code files with 64 KB are rare. When mask length is beyond 15, the CDC algorithm becomes SIS, resulting in the whole file being processed for the de-duplication. Thus, the increase of mask length has very little impact on unique data size. Anyway, the original data size So could be considered as the upper bound of the unique data size.
When x is beyond 15, the index data size is rather small and can be ignored; therefore, the upper bound of the unique and index data size is the original data size So before deduplication. Thus, the mathematical model of the unique and index data size is:
4.3. Modeling the DER
The data size that needs to be stored after deduplication equals the sum of the meta data size, the unique data size, and the index data size. It can be computed as:
According to the definition of DER, the mathematical model of the relationship between the DER and the expected chunk size is:
where m is the size of one meta data, and its value depends on specific implementation of the deduplication system, and it is a constant value. k and x0 are the parameters of logistic function and they are described above. These two values need to be estimated.
5. Experiment
5.1. Experimental Setup
We used the open source deduplication program deduputil [26] to perform the experiment. Deduputil supports a variety of chunking algorithms, including CDC.
The configuration of the server used for the experiment is described as follows:
- (1)
- CPU: 2 Intel Xeon E5-2650 v2 2.6 GHz 8-core processors;
- (2)
- RAM: 128 GB DDR3;
- (3)
- Disk: 1.2 T MLC PCIe SSD card;
- (4)
- Operating system: CentOS release 6.5 (Final).
5.2. Datasets
We collected two realistic datasets for the experiment, with the following information:
- (1)
- The Linux kernel source code dataset [22]. The total size is 233.95 GB, and the total versions are 260, including version from 3.0 to 3.4.63;
- (2)
- The SQLite [24] period backup dataset while running the TPC-C benchmark [25]. The total size is 148 GB, and the total backups are 90.
Because the data size increases in a real storage system, we simulate this characterization to comprehensively observe the experimental results, which means that we perform the experiment by setting the dataset size from small to large. In the Linux kernel experiment, we used the first 60 versions to perform the first experiment. Afterwards, we performed the experiment at the interval of 50 versions. That means we performed the first experiment with the first 60 versions, and the second experiment with the first 110 versions until all the experiments were finished. In the SQLite experiment, we used the first 20 backups for the first experiment, and then performed the experiment at intervals of 20 backups. The minimum and maximum need to be set in the CDC algorithm, and we set the minimum to 64 B and the maximum to 32 MB. Consequently, the expected chunk size range that needs to be observed is 64 B–32 MB.
5.3. Experimental Results
The experimental results are shown in Figure 3 and Figure 4. The x-axis represents the expected chunk size (decided by mask length); and the y-axis represents the DER. The results show that DER is not optimal by setting the expected chunk size to 4 KB or 8 KB in all experiments. Moreover, the results also show that the expected chunk size that optimizes DER varies among different datasets. Even in the same type of dataset, the expected chunk size that optimizes the DER varies as the data volume increases. Thus, we need to set the expected chunk size according to the specific dataset to optimize DER.
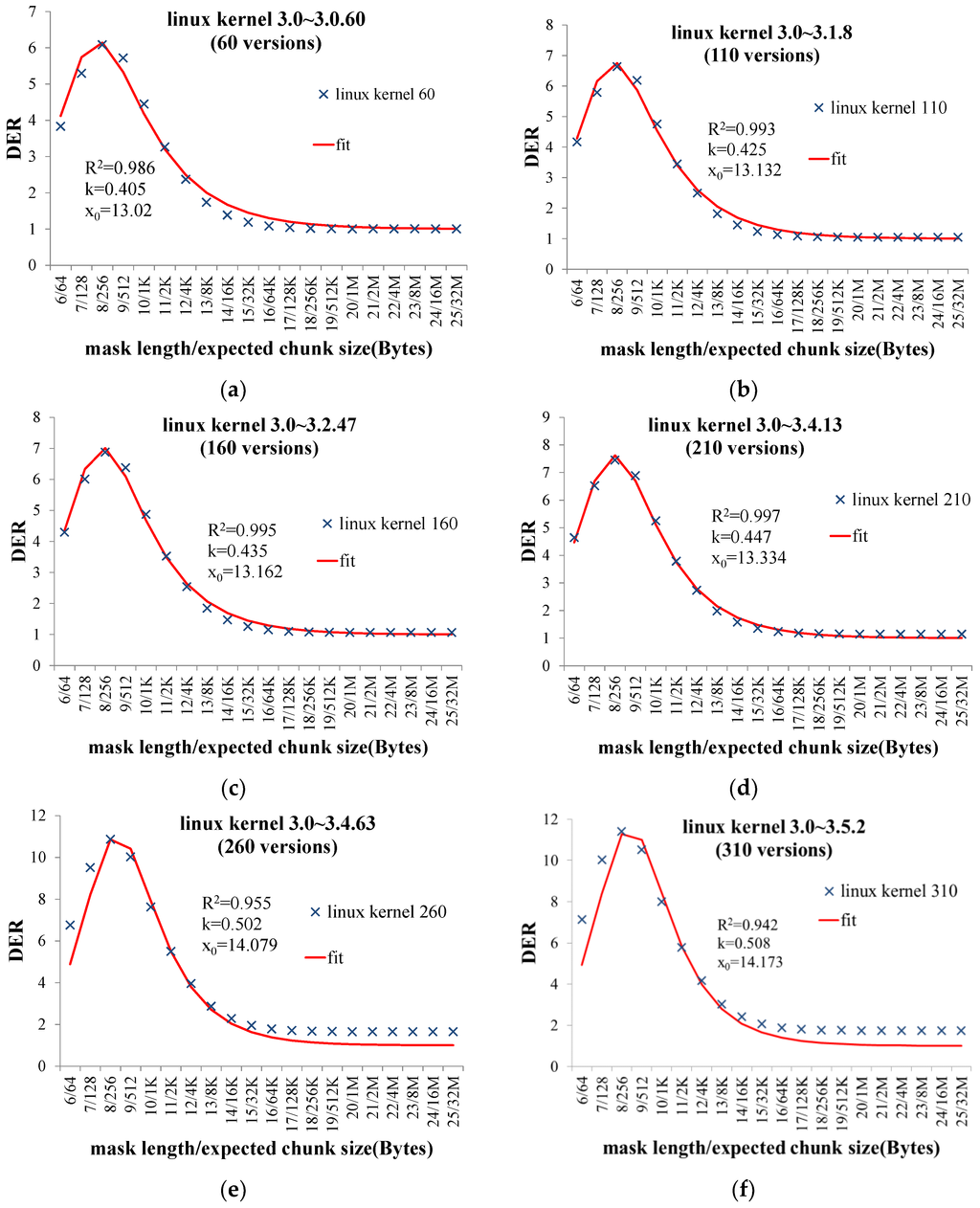
Figure 3.
The experimental results of Linux kernel datasets. (a) 60 versions; (b) 110 versions; (c) 160 versions; (d) 210 versions; (e) 260 versions; (f) 310 versions.
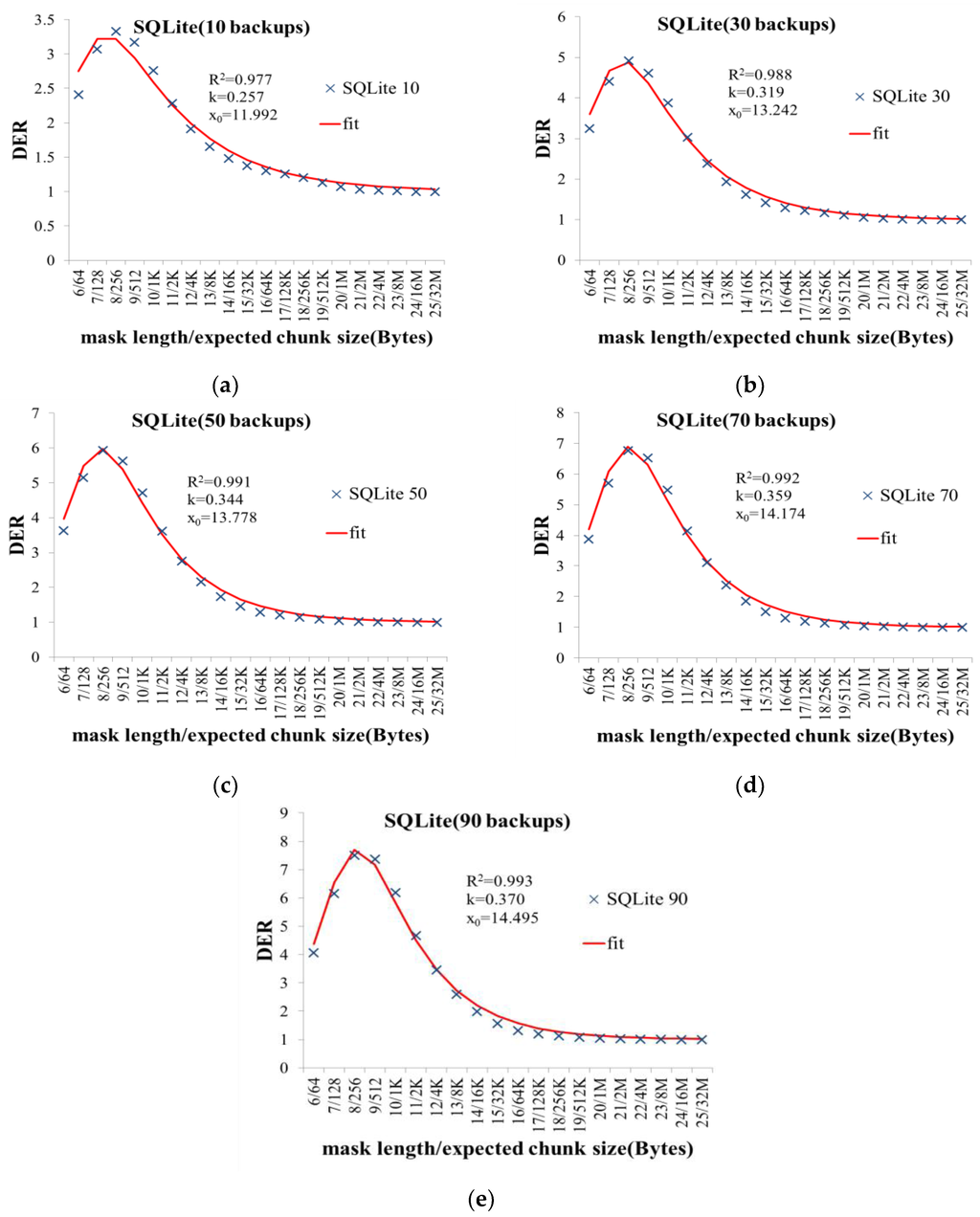
Figure 4.
The experimental results of SQLite backup datasets. (a) 10 backups; (b) 30 backups; (c) 50 backups; (d) 70 backups; (e) 90 backups.
We use R2 value to reflect the goodness of fit of the mathematical model that describes the relationship between the DER and the expected chunk size. The range of R2 is 0~1. The closer the R2 is to 1, the better the goodness of fit. The experimental results show that the R2 values of the experiments are above 0.9, validating that the mathematical model can correctly reflect the relationship between the DER and the expected chunk size.
5.4. Discussion of Optimizing DER by Setting the Expected Chunk Size
Once the expected chunk size is set, it cannot be changed. Otherwise, DER will decrease because a lot of new coming duplicated data chunks will be detected as new due to their changed chunk size. Thus, the expected chunk size should be set under the consideration of making the DER optimum while the data volume grows to a large scale in the future. In Figure 3 and Figure 4, the experimental results show that in the same dataset, the parameters k and x0 of the DER mathematical model increase slowly, and the increase ratio declines as the data volume grows. Based on this observed rule, in practice, we can obtain the initial values of these two parameters of the DER model by analyzing a small amount of historical data in a storage system. Then, we revise the values. For example, we can add 0.3–0.5 to k and add 4–9 to x0. The revisions can be used as the predicted values of the model parameters under the assumption that the data volume of the storage system grows to a large scale in future. With the predicted values, we can calculate the corresponding expected chunk size and set it in the CDC algorithm. Compared with setting the expected chunk size empirically to 4 KB or 8 KB, this approach could make DER of a storage system much closer to the optimum.
From the experimental results, it can be seen that the higher DER is, the bigger the two parameters k and x0 are. Thus, if we cannot obtain the initial values of the two parameters, they could be set according to their estimated DER, which can be obtained empirically for specific datasets or by the method proposed in [27]. For a dataset with high DER, we recommend setting the k to 0.5–0.8, and x0 to 15–20; for a dataset with low DER, we recommend setting the k less than 0.5, and x0 to less than 15. With these parameters, the expected chunk size can be calculated. Of course, this approach is not very precise to optimize DER. Consequently, in the future, we will study the theoretical relationship between the DER and the two parameters and then hope to propose a more precise approach to improve DER.
6. Conclusions
In this paper, we collected two datasets: (1) Linux kernel source codes; and (2) multiple SQLite backup data while running the TPC-C benchmark, to verify whether setting the expected chunk size to 4 KB or 8 KB can improve DER. The experimental results show that setting the expected chunk size to 4 KB or 8 KB cannot optimize DER. To reasonably set the expected chunk size, we present a logistically based mathematical model to reveal the hidden relationship between the expected chunk size and the DER. Two realistic datasets were used to verify this model. The experimental results show that the R2 value, which describes the goodness of fit, is above 0.9, validating the correctness of this mathematic model. Based on this model, we discussed how to set the expected chunk size to make DER close to the optimum.
Acknowledgments
The authors would like to thank the anonymous reviewers for providing insightful comments and providing directions for additional work which has vastly improved this paper. Helena Moreno Chacón helped us check the English of this paper, and we greatly appreciate her efforts. This work was supported by the National Natural Science Foundation of China (Grant No. 61572394), the National Key Research and Development Plan of China (Grant No. 2016YFB1000303), and the Shenzhen Fundamental Research Plan (Grant No. JCYJ20120615101127404 & JSGG20140519141854753).
Author Contributions
Longxiang Wang proposed the model and solved it, carried out the analysis; Xiaoshe Dong provided guidance for this paper; Xingjun Zhang was the research advisor; Fuliang Guo contributed to the revisions and collected experiment data; Yinfeng Wang and Weifeng Gong contributed to the revisions and advice on experiments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- EMC. (2012), EMC DATA DOMAIN white papaer. Available online: http://www.emc.com/collateral/software/white-papers/h7219-data-domain-data-invul-arch-wp.pdf (accessed on 18 July 2016).
- Dubnicki, C.; Gryz, L.; Heldt, L.; Kaczmarczyk, M.; Kilian, W.; Strzelczak, P.; Szczepkowski, J.; Ungureanu, C.; Welnicki, M. Hydrastor: A scalable secondary storage. In Proceedings of the 7th USENIX Conference on File and Storage Technologies, San Francisco, CA, USA, 24–27 February 2009; pp. 197–210.
- Min, J.; Yoon, D.; Won, Y. Efficient deduplication techniques for modern backup operation. IEEE Trans. Comput. 2011, 60, 824–840. [Google Scholar] [CrossRef]
- Quinlan, S.; Dorward, S. Venti: A New Approach to Archival Data Storage. In Proceedings of the 1st USENIX Conference on File and Storage Technologies, Monterey, CA, USA, 28–30 January 2002; pp. 89–101.
- Tsuchiya, Y.; Watanabe, T. DBLK: Deduplication for primary block storage. In Proceedings of the IEEE 27th Symposium on Mass Storage Systems and Technologies, Denver, CO, USA, 23–27 May 2011; pp. 1–5.
- Srinivasan, K.; Bisson, T.; Goodson, G.; Voruganti, K. iDedup: Latency-aware, inline data deduplication for primary storage. In Proceedings of the 10th USENIX conference on File and Storage Technologies, San Jose, CA, USA, 14–17 February 2012; pp. 24–35.
- Muthitacharoen, A.; Chen, B.; Mazieres, D. A low-bandwidth network file system. In Proceedings of the Eighteenth ACM Symposium on Operating Systems Principles, Banff, AB, Canada, 21–24 October 2001; pp. 174–187.
- You, L.L.; Karamanolis, C. Evaluation of efficient archival storage techniques. In Proceedings of the 21st IEEE/12th NASA Goddard Conference on Mass Storage Systems and Technologies, Greenbelt, MD, USA, 13–16 April 2004; pp. 227–232.
- Romański, Ł.H.B.; Kilian, W.; Lichota, K.; Dubnicki, C. Anchor-driven subchunk deduplication. In Proceedings of the 4th Annual International Conference on Systems and Storage, Haifa, Israel, 30 May–1 June 2011; pp. 1–13.
- Bolosky, W.J.; Corbin, S.; Goebel, D.; Douceur, J.R. Single instance storage in Windows 2000. In Proceedings of the 4th USENIX Windows Systems Symposium, Seattle, WA, USA, 3–4 August 2000; pp. 13–24.
- Sun, Z.; Shen, J.; Yong, J. A novel approach to data deduplication over the engineering-oriented cloud systems. Integr. Comput. Aided Eng. 2013, 20, 45–57. [Google Scholar]
- Kubiatowicz, J.; Bindel, D.; Chen, Y.; Czerwinski, S.; Eaton, P.; Geels, D.; Gummadi, R.; Rhea, S.; Weatherspoon, H.; Weimer, W.; et al. OceanStore: An architecture for global-scale persistent storage. SIGPLAN Not. 2000, 35, 190–201. [Google Scholar] [CrossRef]
- Rabin, M.O. Fingerprint by Random Polynomials. (TR-15–81)1981. Available online: http://www.xmailserver.org/rabin.pdf (accessed on 18 July 2016).
- Kruus, E.; Ungureanu, C.; Dubnicki, C. Bimodal content defined chunking for backup streams. In Proceedings of the 8th USENIX Conference on File and Storage Technologies, San Jose, CA, USA, 23–26 February 2010; pp. 239–252.
- Eshghi, K.; Tang, H.K. A framework for analyzing and improving content-based chunking algorithms. 2005. Hewlett-Packard Labs Technical Report TR 30. Available online: http://www.hpl.hp.com/techreports/2005/HPL-2005–30R1.pdf (accessed on 18 July 2016).
- Bobbarjung, D.R.; Jagannathan, S.; Dubnicki, C. Improving duplicate elimination in storage systems. ACM Trans. Storage 2006, 2, 424–448. [Google Scholar] [CrossRef]
- Lillibridge, M.; Eshghi, K.; Bhagwat, D.; Deolalikar, V.; Trezise, G.; Camble, P. Sparse indexing: Large scale, inline deduplication using sampling and locality. In Proceedings of the 7th USENIX Conference on File and Storage Technologies, San Francisco, CA, USA, 24–27 February 2009; pp. 111–123.
- Debnath, B.; Sengupta, S.; Li, J. ChunkStash: Speeding up inline storage deduplication using flash memory. In Proceedings of the 2010 USENIX Conference on USENIX Annual Technical Conference, Boston, MA, USA, 23–25 June 2010; pp. 1–16.
- Symantec. About Deduplication Chunk Size. Available online: https://sort.symantec.com/public/documents/vis/7.0/aix/productguides/html/sf_admin/ch29s01s01.htm (accessed on 18 July 2016).
- IBM. (2016). Determining the Impact of Deduplication on a Tivoli Storage Manager Server Database and Storage Pools. Available online: http://www-01.ibm.com/support/docview.wss?uid=swg21596944 (accessed on 18 July 2016).
- Suzaki, K.; Yagi, T.; Iijima, K.; Artho, C.; Watanabe, Y. Impact on Chunk Size on Deduplication and Disk Prefetch. In Recent Advances in Computer Science and Information Engineering, 125 ed.; Springer: Berlin, Germany, 2012; Volume 2, pp. 399–413. [Google Scholar]
- Linux. (2016). The Linux Kernel Archives. Available online: http://kernel.org/ (accessed on 18 July 2016).
- Wikipedia. (2015). svwiki dump. Available online: http://dumps.wikimedia.org/svwiki/20150807/ (accessed on 18 July 2016).
- D.RichardHipp. (2016), SQLite homepage. Available online: http://sqlite.org/ (accessed on 18 July 2016).
- TPCC. (2010, 2009–02–11). TPC BENCHMARK™ C Standard Specification. Available online: http://www.tpc.org/tpc_documents_current_versions/pdf/tpc-c_v5.11.0.pdf (accessed on 18 July 2016).
- Liu, A. Deduputil homepage. Available online: https://sourceforge.net/projects/deduputil/ (accessed on 18 July 2016).
- Harnik, D.; Khaitzin, E.; Sotnikov, D. Estimating Unseen Deduplication-from Theory to Practice. In Proceedings of the 14th USENIX Conference on File and Storage Technologies (FAST 16), Santa Clara, CA, USA, 22–25 February 2016; pp. 277–290.
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).