Unveiling the Dynamics of the Universe
Abstract
:1. Introduction
2. Scalar-tensor Theories
2.1. General Formalism
2.2. Conformal Picture
2.3. Cosmological Dynamics
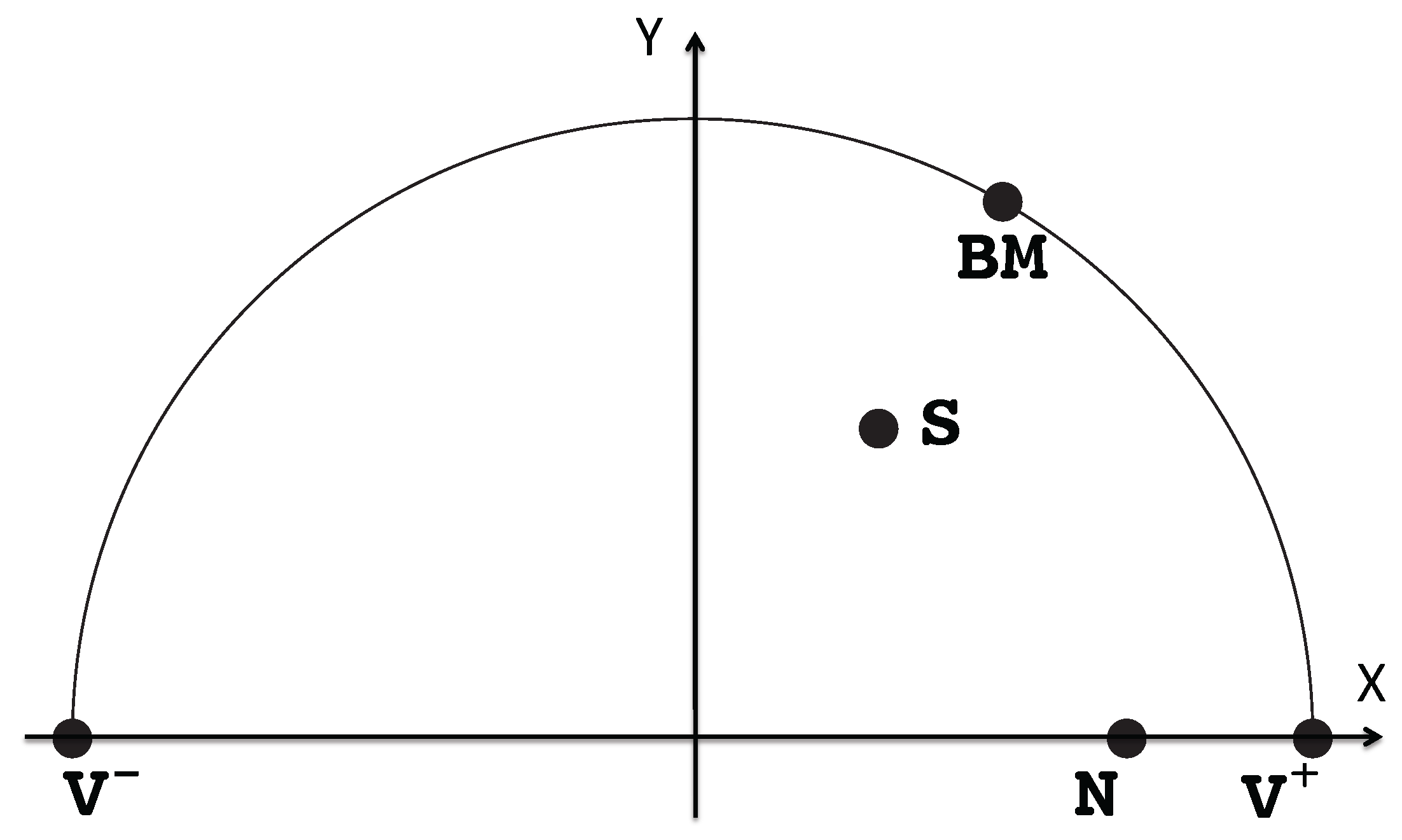
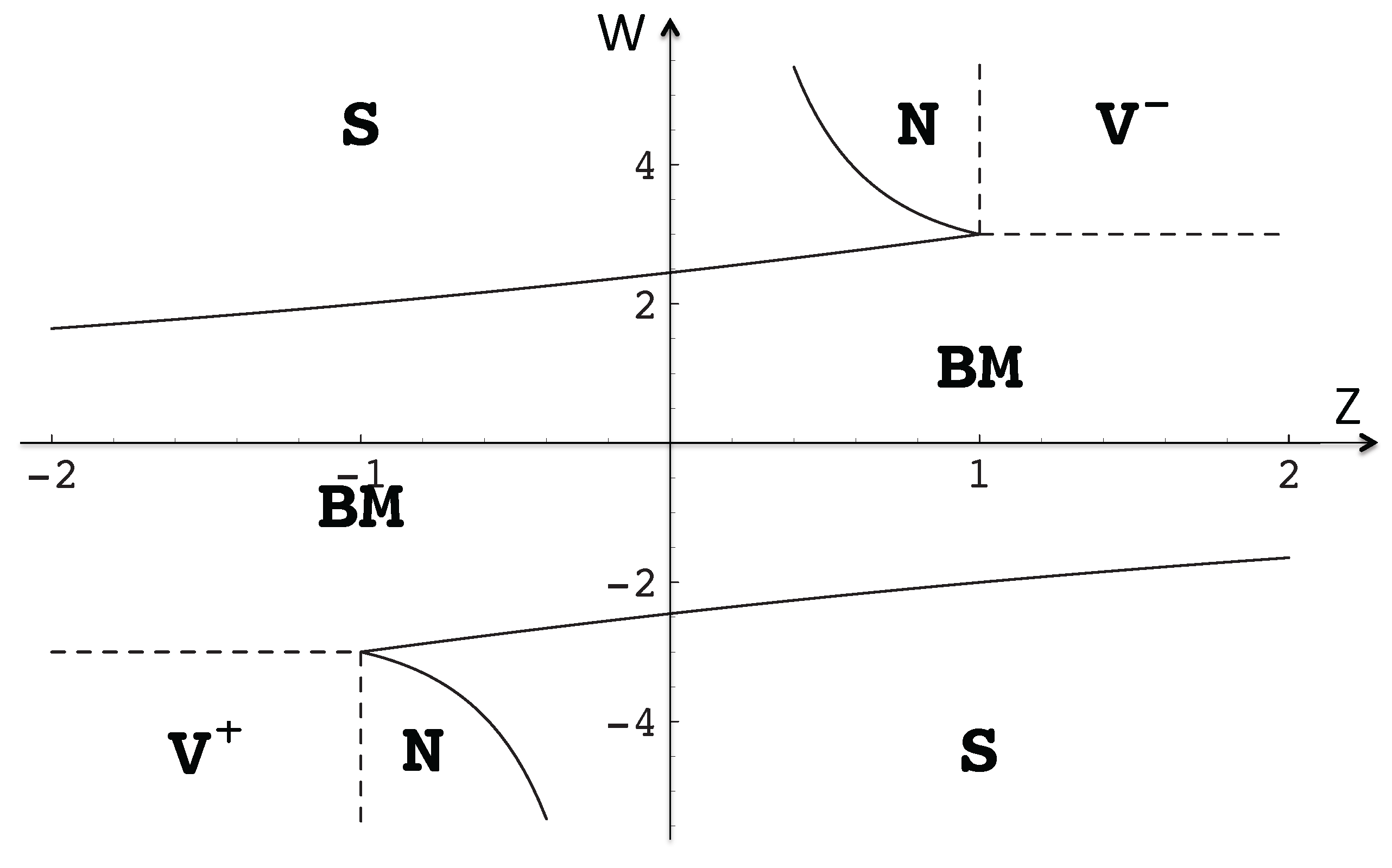
- . This case corresponds to de Sitter solutions, dominated by the scalar field, and arise at non-vanishing maxima or minima of the potential V. Notice that may be different from 0. These solutions are attractors at minima of V and repellors at maxima of V.
- . The second case corresponds to matter dominated solutions with at maxima or minima of m. Note however that the system (15)–(18) is singular when , translating the fact that the variables in use are not regular. In the original variables, this second class of solutions exists provided that V has also an extremum, or is identically zero.
- , which lies on the invariant line , provided . These solutions (BM) correspond to those found in [114].
- , that lies in the interior of the phase space domain, provided that
2.4. Assisted Quintessence
2.4.1. General Equations
2.4.2. Scalar Field Dominated Solution
2.4.3. Scaling Solution
2.4.4. Scalar Potential Independent Solutions
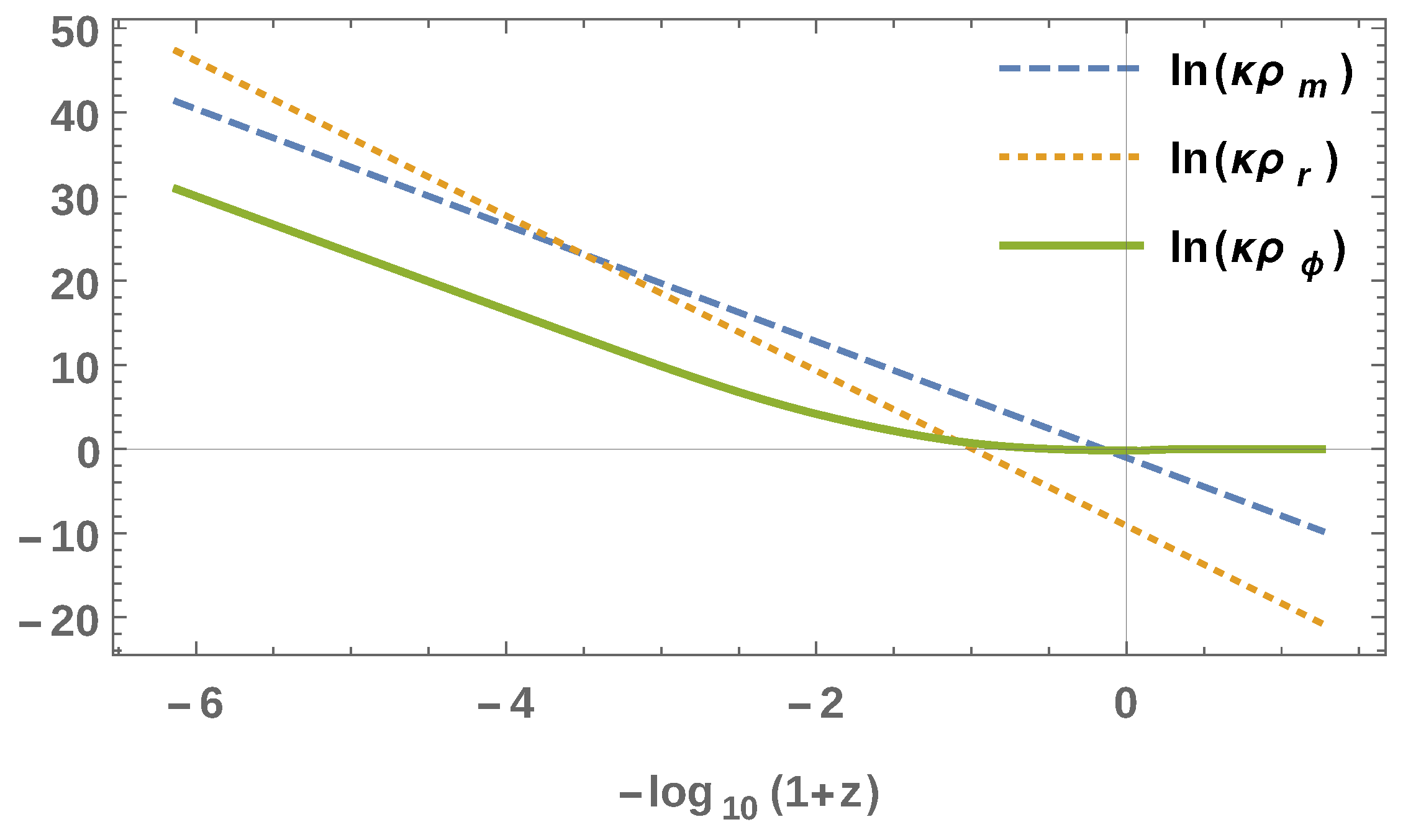
- First, we have the kinetic dominated solutions where all the energy density for the dark sector is due to the kinetic energy of the scalar fields. In this instance, we have .
- As a second possibility, we have a contribution from the kinetic energy and the matter energy densities for the dark sector. In this case we have . This will be true for any matter species α since the sum is constrained to yield the same for all matter species.
- Finally, as a third possibility we have a matter dominated scenario. This has been investigated previously in the literature for the case of a single field with two matter components [128,130,131,132]. If we extend this to more than one field, we will see that there is a consistency condition imposed on the values of the couplings to allow a flat direction in the field space, otherwise this solution will be non existent. This is by its nature a transient solution since the matter contribution will eventually decay away and the scaling solution or the scalar field dominated solution will take over. However, this can be an interesting scenario for model building since it allows the dark matter sector to have a significant contribution before the acceleration of the Universe.
3. Horndeski Theories and Self-tuning
3.1. Dynamical Screening
- The field equation evaluated at the critical point has to be trivially satisfied leading the value of the field free to screen. This implies that the minisuperspace Lagrangian density at the critical point takes the form
- The full scalar equation of motion must depend on to allow for a non-trivial cosmological dynamics before screening. This leads to a condition equivalent to (45) if .
3.2. Requiring the Existence of a de Sitter Critical Point:
3.2.1. Linear Terms: “The Magnificent Seven”
3.2.2. Non-linear Terms
3.3. Cosmology of the Models
3.3.1. Example of a Linear Model
3.3.2. Example of a Non-Linear Model
3.4. Summary
4. Modified Theories of Gravity and Extensions
4.1. Modified Theories of Gravity
4.1.1. General Formalism
4.1.2. Discriminating between Dark Energy and Modified Gravity Models
4.1.3. Late-Time Cosmic Acceleration
4.2. Curvature-Matter Couplings in Gravity
4.3. The Palatini Approach
4.3.1. Quadratic Cosmology from Gravity-matter Coupling
4.3.2. Bouncing Cosmologies in Born-Infeld-like Gravity Models
4.4. Hybrid Metric-Palatini Gravity
4.4.1. General Formalism
4.4.2. Unifying Local Tests and the Late-Time Cosmic Acceleration
4.4.3. Future Outlook: More gEneral Hybrid Metric-Palatini Theories
4.5. Slow-Roll Inflation in Gravity
4.5.1. Inflationary Parameters
4.5.2. Inflation in Gravity
5. Topological Defects
5.1. Spontaneous Symmetry Breaking and Topological Defects
5.2. A VOS Model for Topological Defect Networks of Arbitrary Dimensionality
5.3. Observational Signatures of Topological Defects
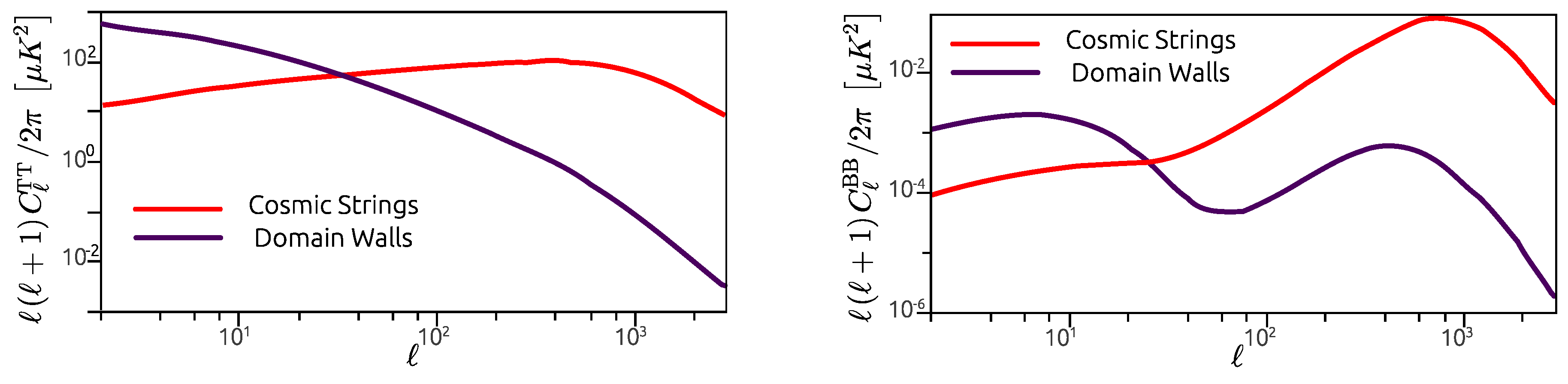
5.3.1. CMB Anisotropies
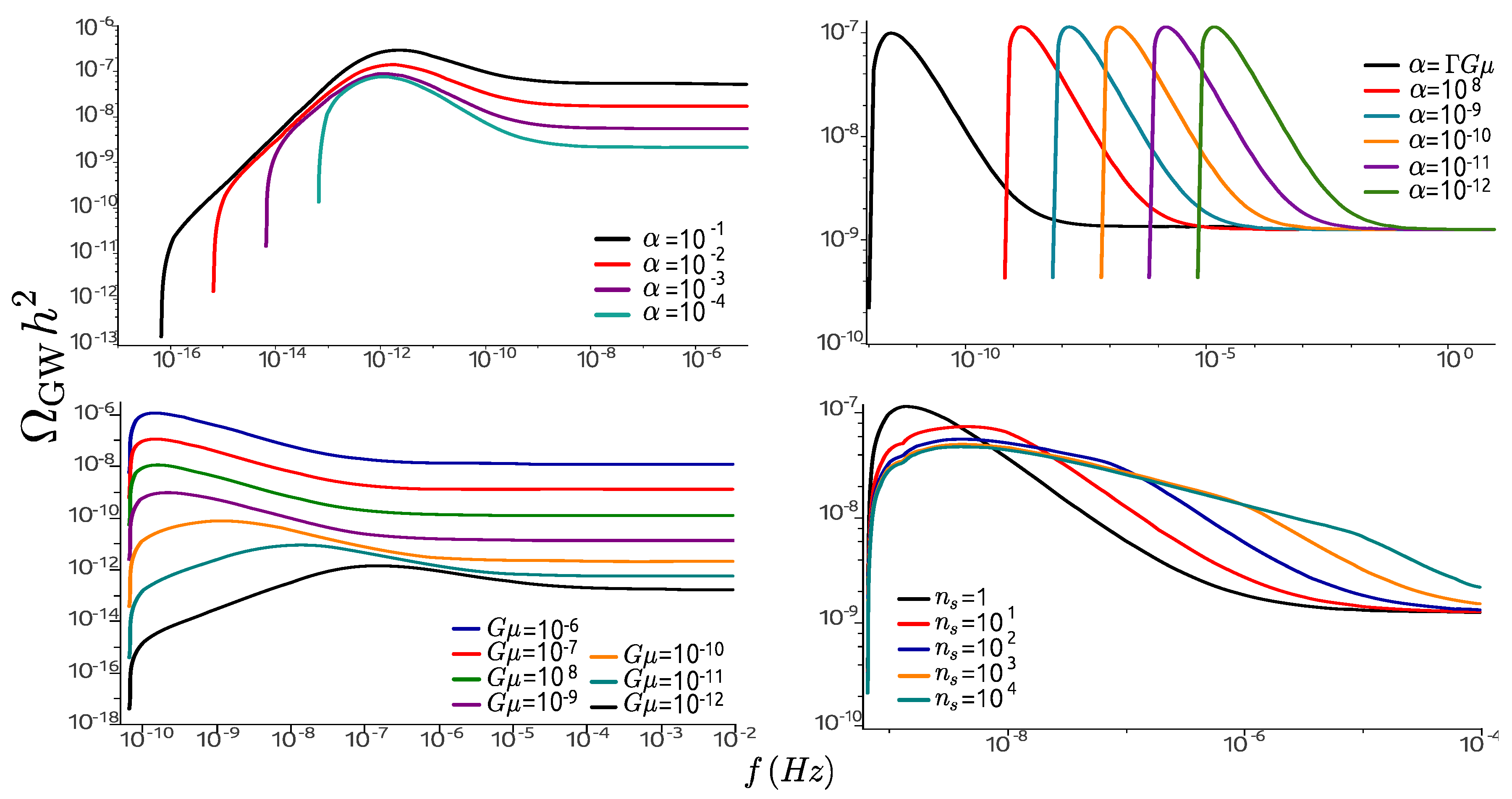
5.3.2. The Stochastic Gravitational Wave Background
6. Cosmological Tests with Galaxy Clusters at CMB Frequencies
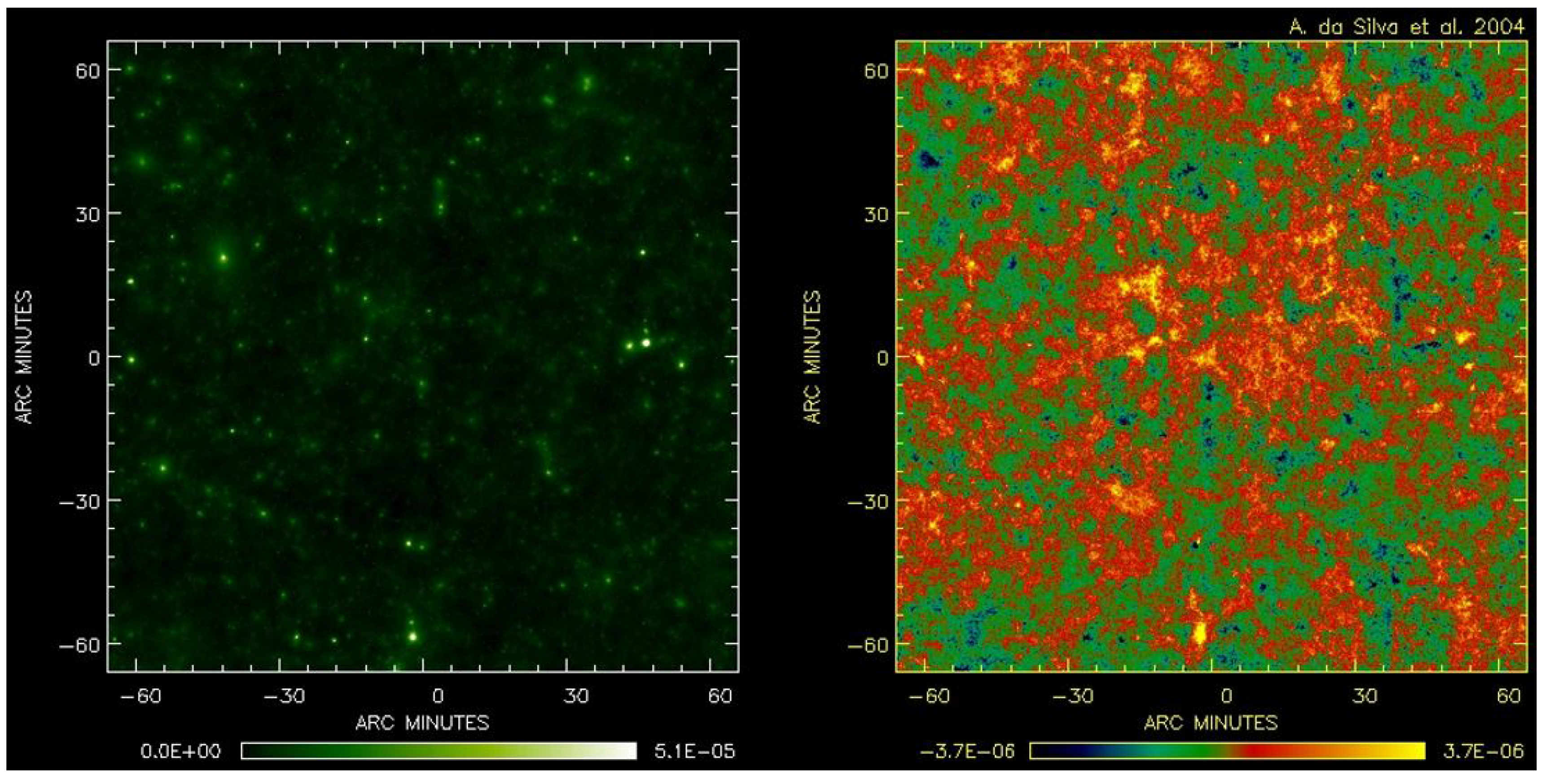
6.1. Galaxy Clusters
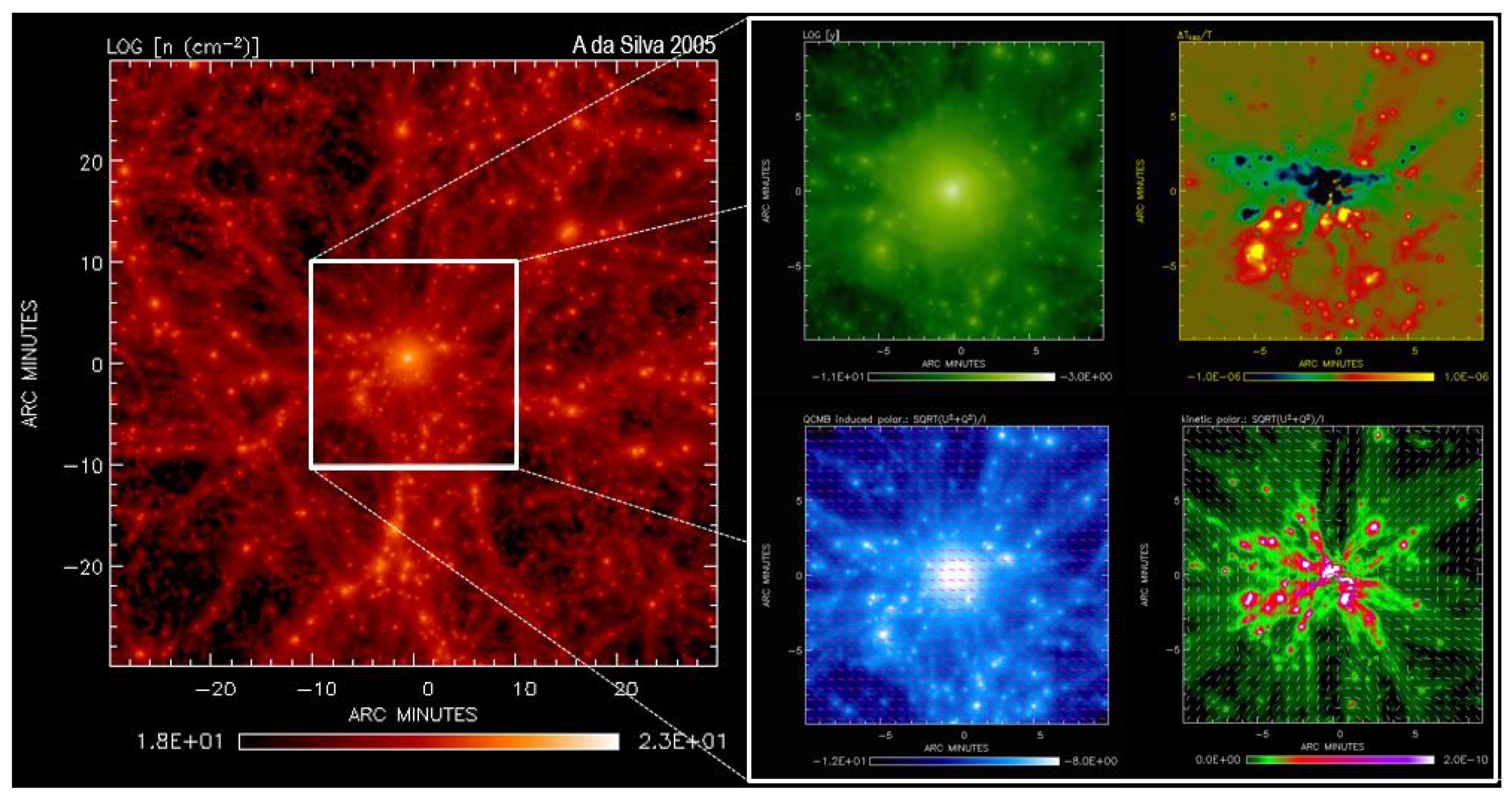
6.2. The SZ Effect: Temperature and Polarization Signal
6.3. Cosmological Tests Using SZ Cluster Surveys
6.3.1. SZ Cluster Counts
6.3.2. SZ Power Spectra
6.3.3. Probing New Physics with the SZ Clusters
6.4. Probing Primordial Non-Gaussianities with Galaxy Clusters
6.4.1. Parametrizing Primordial Non-Gaussianity
6.4.2. The Non-Gaussian Mass Function
6.4.3. Biased Cosmological Parameter Estimation with Cluster Counts
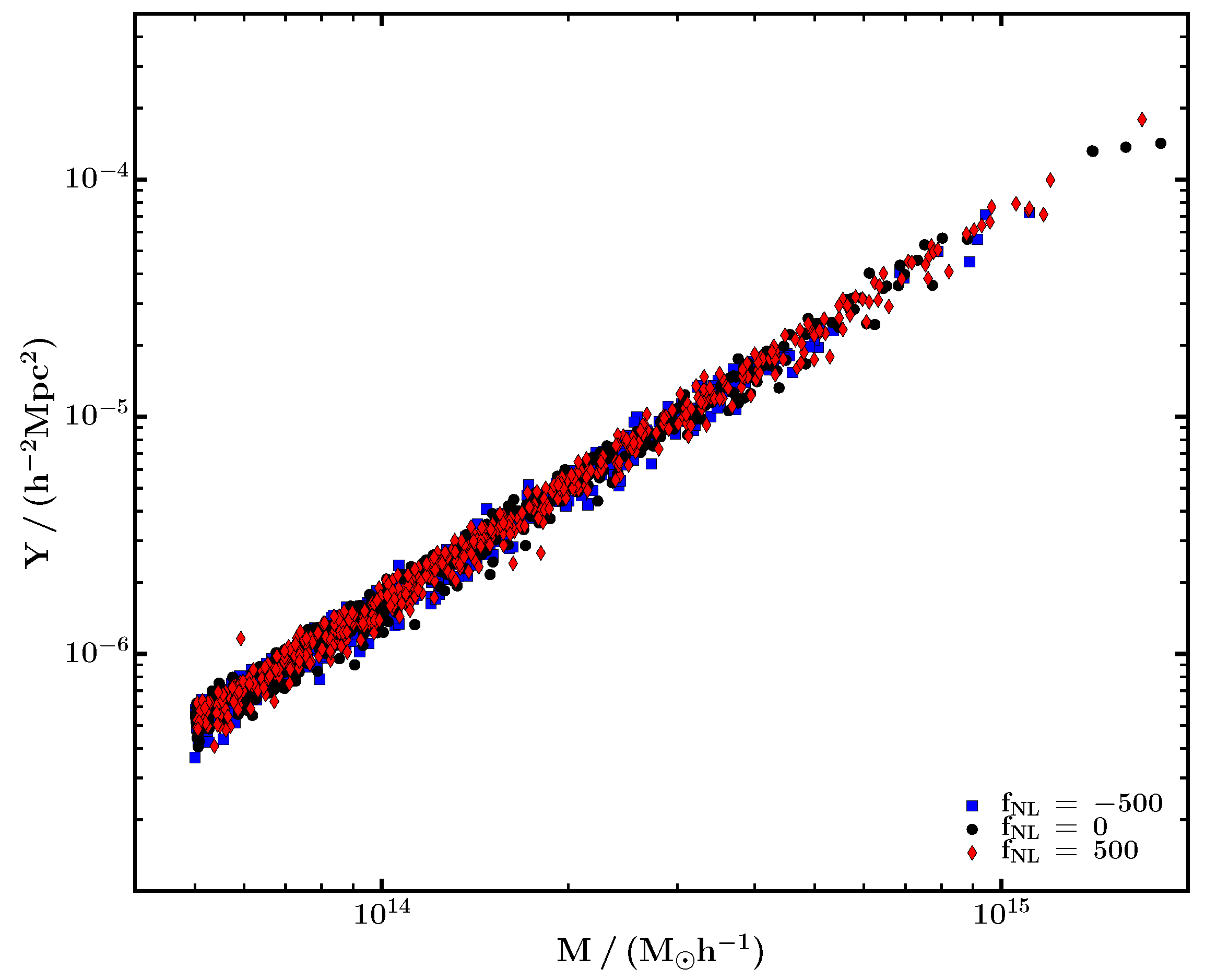
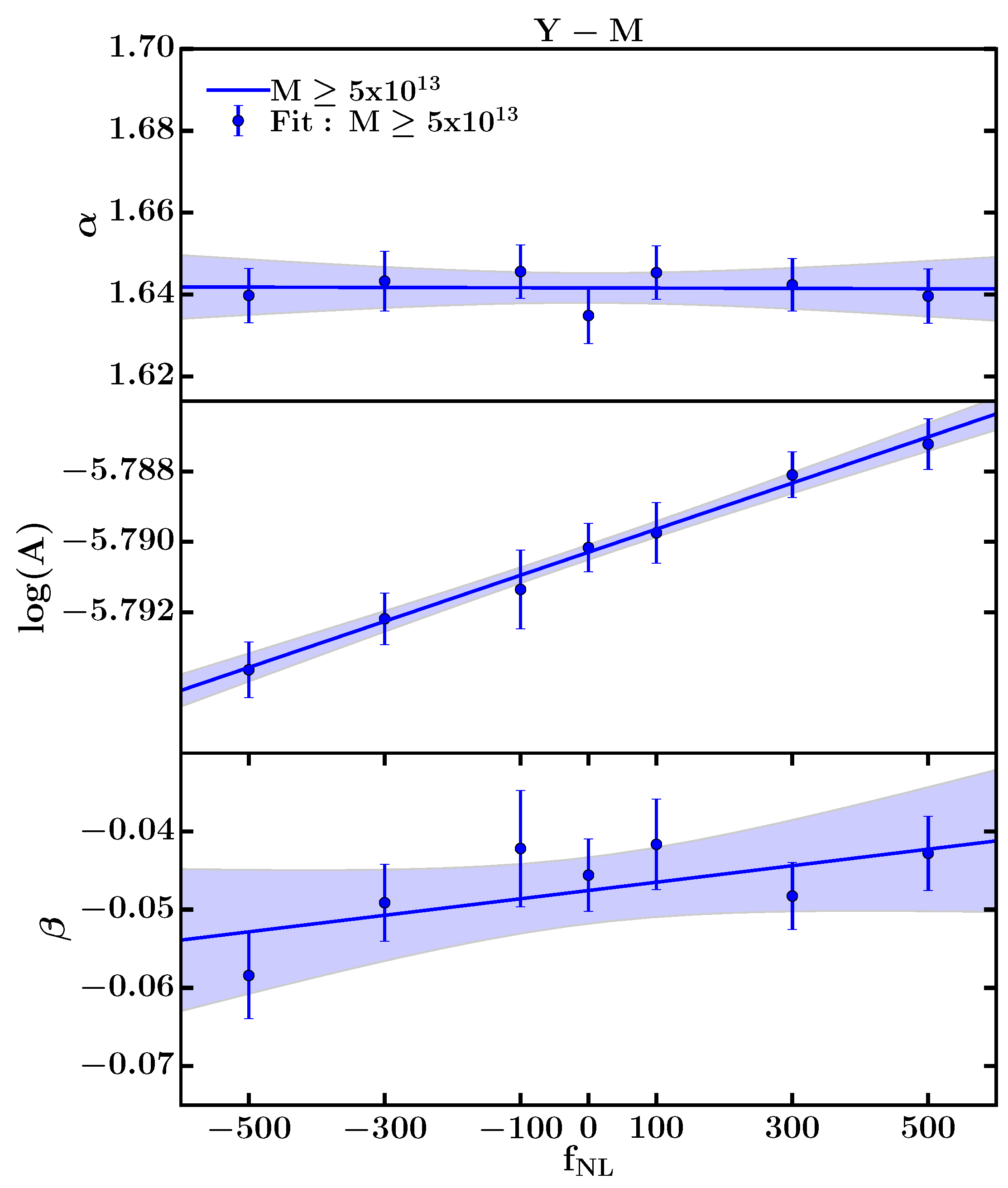
6.4.4. The Impact of pRimordial Non-Gaussianities on Galaxy Clusters Scaling Relations
7. Testing Gravity with Weak Lensing
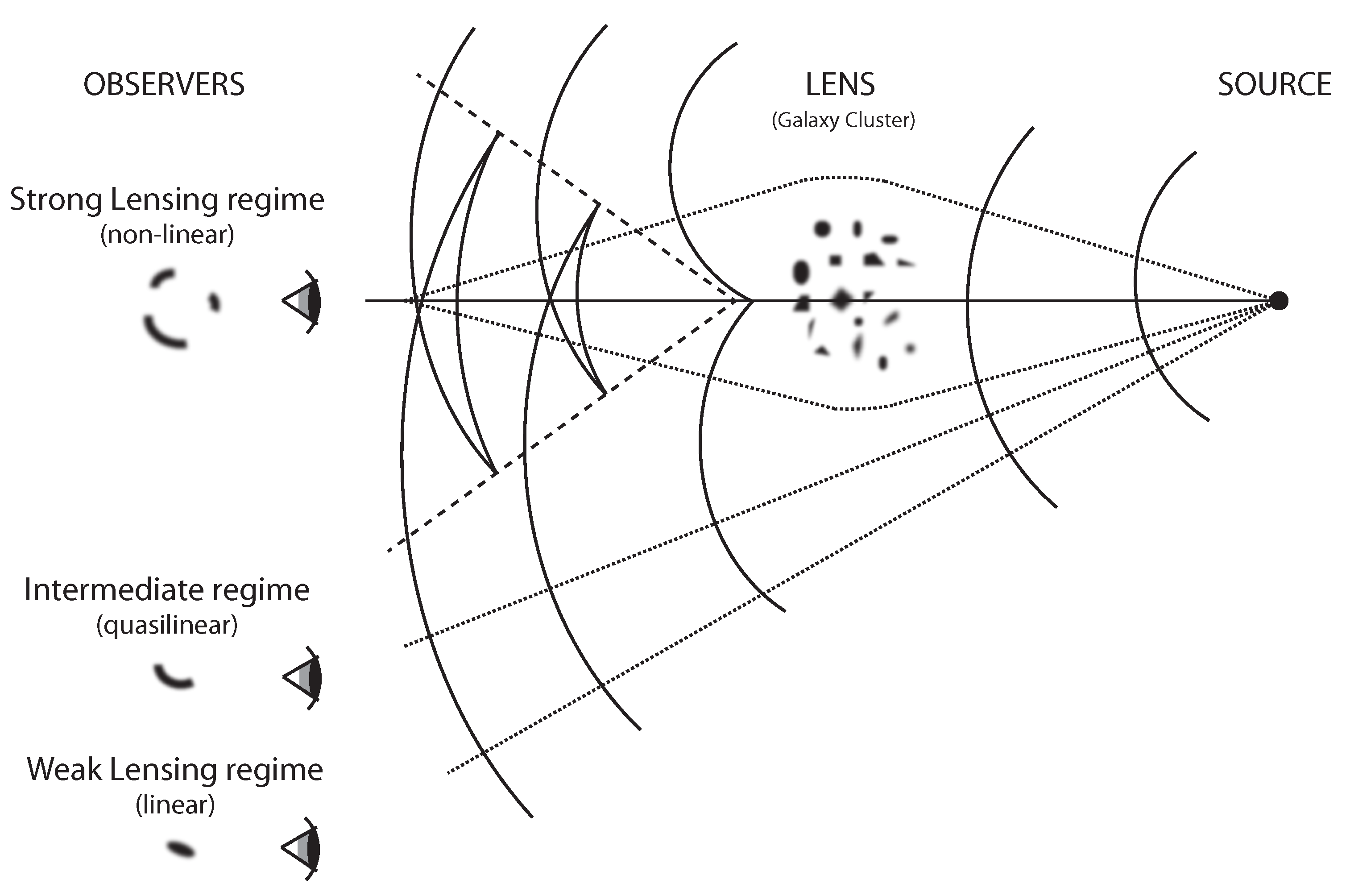
7.1. Gravitational Lensing
7.2. Cosmic Shear
7.3. Testing Deviations from General Relativity
7.4. Testing Gravity with Future Cosmic Shear Data
8. Angular Distribution of Cosmological Parameters as a Measurement of Spacetime Inhomogeneities
8.1. Method of Local Parameter Estimation
8.2. Average over the Local Parameter Estimation
9. Summary and Conclusion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Omega and Lambda from 42 high redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiattia, A.; Diercks, A.; Garnavich, P.M.; Craig, G.; Hogan, C.J.; Jha, S.; Kishner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Maartens, R. Brane world gravity. Living Rev. Rel. 2004, 7, 7. [Google Scholar] [CrossRef]
- Dvali, G.R.; Gabadadze, G.; Porrati, M. 4-D gravity on a brane in 5-D Minkowski space. Phys. Lett. B 2000, 485, 208. [Google Scholar] [CrossRef]
- de Rham, C.; Hofmann, S.; Khoury, J.; Tolley, A.J. Cascading Gravity and Degravitation. J. Cosmol. Astropart. Phys. 2008, 0802, 011. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Faraoni, V. f(R) Theories of Gravity. Rev. Mod. Phys. 2010, 82, 451. [Google Scholar] [CrossRef]
- De Felice, A.; Tsujikawa, S. f(R) theories. Living Rev. Rel. 2010, 13, 3. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M. Extended Theories of Gravity. Phys. Rept. 2011, 509, 167. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rept. 2011, 505, 59. [Google Scholar] [CrossRef]
- Lobo, F.S.N. The Dark side of gravity: Modified theories of gravity. In Dark Energy-Current Advances and Ideas; Research Signpost: Kerala, India, 2009; pp. 173–204. [Google Scholar]
- Capozziello, S. Curvature quintessence. Int. J. Mod. Phys. D 2002, 11, 483. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified gravity with negative and positive powers of the curvature: Unification of the inflation and of the cosmic acceleration. Phys. Rev. D 2003, 68, 123512. [Google Scholar] [CrossRef]
- Carroll, S.M.; Duvvuri, V.; Trodden, M.; Turner, M.S. Is cosmic speed-up due to new gravitational physics? Phys. Rev. D 2004, 70, 043528. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753–1936. [Google Scholar] [CrossRef]
- Brans, C.; Dicke, R.H. Mach’s principle and a relativistic theory of gravitation. Phys. Rev. 1961, 124, 925–935. [Google Scholar] [CrossRef]
- De Rham, C. Massive Gravity. Living Rev. Rel. 2014, 17, 7. [Google Scholar] [CrossRef]
- Horndeski, G.W. Second-order scalar-tensor field equations in a four-dimensional space. Int. J. Theor. Phys. 1974, 10, 363. [Google Scholar] [CrossRef]
- Charmousis, C.; Copeland, E.J.; Padilla, A.; Saffin, P.M. Self-tuning and the derivation of a class of scalar-tensor theories. Phys. Rev. D 2012, 85, 104040. [Google Scholar] [CrossRef]
- Martín-Moruno, P.; Nunes, N.J.; Lobo, F.S.N. Horndeski theories self-tuning to a de Sitter vacuum. Phys. Rev. D 2015, 91, 084029. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Where new gravitational physics comes from: M Theory? Phys. Lett. B 2003, 576, 5. [Google Scholar] [CrossRef]
- Parker, L.; Toms, D.J. Quantum Field Theory in Curved Spacetime: Quantized Fields and Gravity; Cambridge University Press: Oxford, UK, 2009. [Google Scholar]
- Cembranos, J.A.R. Dark matter from R2 gravity. Phys. Rev. Lett. 2009, 102, 141301. [Google Scholar] [CrossRef] [PubMed]
- Bamba, K.; Odintsov, S.D. Inflationary cosmology in modified gravity theories. Symmetry 2015, 7, 220. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, A.N.; Armitage-Caplan, C.; Ashdown, A.M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; et al. Planck 2013 results. XXII. Constraints on inflation. Astron. Astrophys. 2014, 571, A22. [Google Scholar]
- Hu, W.; Sawicki, I. Models of f(R) Cosmic Acceleration that Evade Solar-System Tests. Phys. Rev. D 2007, 76, 064004. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unifying inflation with LambdaCDM epoch in modified f(R) gravity consistent with Solar System tests. Phys. Lett. B 2007, 657, 238. [Google Scholar] [CrossRef]
- Olmo, G.J. Palatini Approach to Modified Gravity: f (R) Theories and Beyond. Int. J. Mod. Phys. D 2011, 20, 413. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Liberati, S. Metric-affine f (R) theories of gravity. Annals Phys. 2007, 322, 935. [Google Scholar] [CrossRef]
- Harko, T.; Koivisto, T.S.; Lobo, F.S.N.; Olmo, G.J. Metric-Palatini gravity unifying local constraints and late-time cosmic acceleration. Phys. Rev. D 2012, 85, 084016. [Google Scholar] [CrossRef]
- Linder, E.V. Einstein’s Other Gravity and the Acceleration of the Universe. Phys. Rev. D 2010, 81, 127301. [Google Scholar] [CrossRef]
- Cai, Y.F.; Capozziello, S.; De Laurentis, M.; Saridakis, E.N. f (T) Teleparallel Gravity and Cosmology. 2015; arXiv:1511.07586 [gr-qc]. [Google Scholar]
- Harko, T.; Lobo, F.S.N.; Otalora, G.; Saridakis, E.N. Nonminimal torsion-matter coupling extension of f(T) gravity. Phys. Rev. D 2014, 89, 124036. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.N.; Otalora, G.; Saridakis, E.N. gravity and cosmology. J. Cosmol. Astropart. Phys. 2014, 1412, 021. [Google Scholar] [CrossRef]
- van Dam, H.; Veltman, M.J.G. Massive and massless Yang-Mills and gravitational fields. Nucl. Phys. B 1970, 22, 397. [Google Scholar] [CrossRef]
- Zakharov, V. I. Linearized gravitation theory and the graviton mass. JETP Lett. 1970, 12, 312. [Google Scholar]
- Avelino, P.P.; Martins, C.J.A.P.; Menezes, J.; Menezes, R.; Oliveira, J.C.R.E. Frustrated expectations: Defect networks and dark energy. Phys. Rev. D 2006, 73, 123519. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. [Planck Collaboration]. Planck 2015 results. XIII. Cosmological parameters. 2015; arXiv:1502.01589 [astro-ph.CO]. [Google Scholar]
- Avelino, P.P.; Sousa, L. Observational Constraints on Varying-Alpha Domain Walls. Universe 2015, 1, 6–16. [Google Scholar] [CrossRef]
- Anthonisen, M.; Brandenberger, R.; Scott, P. Constraints on cosmic strings from ultracompact minihalos. Phys. Rev. D 2015, 92, 023521. [Google Scholar] [CrossRef]
- Barton, A.; Brandenberger, R.H.; Lin, L. Cosmic Strings and the Origin of Globular Clusters. J. Cosmol. Astropart. Phys. 2015, 1506, 022. [Google Scholar] [CrossRef]
- Bramberger, S.F.; Brandenberger, R.H.; Jreidini, P.; Quintin, J. Cosmic String Loops as the Seeds of Super-Massive Black Holes. J. Cosmol. Astropart. Phys. 2015, 1506, 007. [Google Scholar] [CrossRef] [PubMed]
- Avelino, P.P.; Liddle, A.R. Cosmological perturbations and the reionization epoch. Mon. Not. Roy. Astron. Soc. 2004, 348, 105. [Google Scholar] [CrossRef]
- Weinberg, D.H.; Mortonson, M.J.; Eisenstein, D.J.; Hirata, C.; Riess, A.G.; Rozo, E. Observational probes of cosmic acceleration. Phys. Rep. 2013, 530, 87–255. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, E.; Battaner, R.; et al. Planck Collaboration, Planck 2015 results. XIII. Cosmological parameters. 2015; arXiv:1502.01589. [Google Scholar]
- Aghanim, N.; Majumdar, S.; Silk, J. Secondary anisotropies of the CMB. Rep. Prog. Phys. 2008, 71, 066902. [Google Scholar] [CrossRef]
- Sunyaev, R.A.; Zeldovich, Y.B. The Sunyaev-Zel’dovich effect. Comments Astrophys. Space Phys. 1972, 4, 173. [Google Scholar]
- Birkinshaw, M. The Sunyaev-Zel’dovich effect. Phys. Rep. 1999, 310, 97. [Google Scholar] [CrossRef]
- Bartelmann, M.; Schneider, P. Weak Gravitational Lensing. Phys. Rep. 2001, 340, 297–472. [Google Scholar] [CrossRef]
- Laureijs, R.; Amiaux, J.; Arduini, S.; Brinchmann, J.; Cole, R.; Cropper, M.; Dabin, C.; Duvet, L.; Ealet, A.; Garilli, B.; et al. Euclid Definition Study Report. 2011; arXiv:1110.3193. [Google Scholar]
- Winther, H.A.; Schmidt, F.; Barreira, A.; Arnold, C.; Sownak Bose, S.; Claudio Llinares, C.; Marco Baldi, M.; Falck, B.; Hellwing, W.A.; Koyama, K.; et al. Modified gravity N-body code comparison project. Mon. Not. Roy. Astron. Soc. 2015, 454, 4208–4234. [Google Scholar] [CrossRef] [Green Version]
- Semboloni, E.; Hoekstra, H.; Schaye, J.; van Daalen, M.P.; McCarthy, I.J. Quantifying the effect of baryon physics on weak lensing tomography. Mon. Not. Roy. Astron. Soc. 2011, 417, 2020–2035. [Google Scholar] [CrossRef]
- Bull, P.; Akrami, Y.; Adamek, J.; Baker, T.; Bellini, E.; Beltran-Jimenez, J.; Bentivegna, E.; Camera, S.; Clesse, S.; Davis, J.H. Beyond Λ CDM: Problems, solutions, and the road ahead. Phys. Dark Universe 2016, 12, 56–99. [Google Scholar] [CrossRef] [Green Version]
- Joudaki, S.; Blake, C.; Heymans, C.; Choi, A.; Harnois-Deraps, J.; Hildebrandt, H.; Joachimi, B.; Johnson, A.; Mead, A.; Parkinson, D.; et al. CFHTLenS revisited: Assessing concordance with Planck including astrophysical systematics. 2016; arXiv: 1601.05786. [Google Scholar]
- Schwarz, D.; Copi, C.; Huterer, D.; Starkman, G. CMB Anomalies after Planck. 2015; arXiv: 1510.07929. [Google Scholar]
- Acquaviva, V.; Bartolo, N.; Matarrese, S.; Riotto, A. Gauge-invariant second-order perturbations and non-Gaussianity from inflation. Nucl. Phys. B 2003, 667, 119. [Google Scholar]
- Maldacena, J. Non-gaussian features of primordial fluctuations in single field inflationary models. J. High Energy Phys. 2003, 5, 13. [Google Scholar] [CrossRef]
- Bartolo, N.; Komatsu, E.; Matarrese, S.; Riotto, A. Non-Gaussianity from inflation: Theory and observations. Phys. Rep. 2003, 402, 103. [Google Scholar] [CrossRef]
- Komatsu, E.; Afshordi, N.; Bartolo, N.; Baumann, D.; Bond, J.R.; Buchbinder, E.I.; Byrnes, C.T.; Chen, X.; Chung, D.J.H.; Cooray, A.; et al. Non-Gaussianity as a Probe of the Physics of the Primordial Universe and the Astrophysics of the Low Redshift Universe. 2003; arXiv:0902.4759 [astro-ph.CO]. [Google Scholar]
- Lyth, D.H.; Wands, D. Generating the curvature perturbation without an inflaton. Phys. Lett. B 2002, 524, 5. [Google Scholar] [CrossRef]
- Bartolo, N.; Matarrese, S.; Riotto, A. Non-Gaussianity in the curvaton scenario. Phys. Rev. D 2004, 69, 043503. [Google Scholar] [CrossRef]
- Sasaki, M.; Väliviita, J.; Wands, D. Non-Gaussianity of the primordial perturbation in the curvaton model. Phys. Rev. D 2006, 74, 103003. [Google Scholar] [CrossRef]
- Lehners, J.-L.; Steinhardt, P.J. Non-Gaussian density fluctuations from entropically generated curvature perturbations in ekpyrotic models. Phys. Rev. D 2008, 77, 063533. [Google Scholar] [CrossRef]
- Lehners, J.-L. Ekpyrotic Nongaussianity: A Review. Adv. Astron. 2010, 903907. [Google Scholar] [CrossRef]
- Yokoyama, S.; Soda, J. Primordial statistical anisotropy generated at the end of inflation. J. Cosmol. Astropart. Phys. 2008, 8, 005. [Google Scholar] [CrossRef]
- Karčiauskas, M.; Dimopoulos, K.; Lyth, D.H. Anisotropic non-Gaussianity from vector field perturbations. Phys. Rev. D 2009, 80, 023509. [Google Scholar] [CrossRef]
- Dimastrogiovanni, E.; Bartolo, N.; Matarrese, S.; Riotto, A. Non-Gaussianity and Statistical Anisotropy from Vector Field Populated Inflationary Models. Adv. Astron. 2010, 752670. [Google Scholar] [CrossRef]
- Polarski, D.; Starobinsky, A.A. Isocurvature perturbations in multiple inflationary models. Phys. Rev. D 1994, 50, 6123. [Google Scholar] [CrossRef]
- Mukhanov, V.F.; Steinhardt, P.J. Density perturbations in multifield inflationary models. Phys. Lett. B 1998, 422, 52. [Google Scholar] [CrossRef]
- Rigopoulos, G.I.; Shellard, E.P.S.; van Tent, B.J.W. Large non-Gaussianity in multiple-field inflation. Phys. Rev. D 2006, 73, 083522. [Google Scholar] [CrossRef]
- Byrnes, C.T.; Choi, K.-Y. Review of Local Non-Gaussianity from Multifield Inflation. Adv. Astron. 2010, 724525. [Google Scholar] [CrossRef]
- Carvalho, C.S.; Marques, K. Angular distribution of cosmological parameters: Measurement of inhomogeneities from type Ia supernovae. 2015; arXiv: 1512.07869 [astro-ph/CO]. [Google Scholar]
- Billyard, A.; Coley, A. On the correspondence between exact solutions in Kaluza-Klein theory and in scalar tensor theories. Mod. Phys. Lett. A 1997, 12, 2121. [Google Scholar] [CrossRef]
- Barrow, J.D.; Tipler, F.J. The Anthropic Cosmological Principle; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Wands, D. Extended gravity theories and the Einstein-Hilbert action. Class. Quant. Grav. 1994, 11, 269. [Google Scholar] [CrossRef]
- Barrow, J.D.; Cotsakis, S. Inflation and the Conformal Structure of Higher Order Gravity Theories. Phys. Lett. B 1988, 214, 515. [Google Scholar] [CrossRef]
- Kalara, S.; Kaloper, N.; Olive, K.A. Theories of Inflation and Conformal Transformations. Nucl. Phys. B 1990, 341, 252. [Google Scholar] [CrossRef]
- Malquarti, M.; Copeland, E.J.; Liddle, A.R.; Trodden, M. A New view of k-essence. Phys. Rev. D 2003, 67, 123503. [Google Scholar] [CrossRef]
- Bergmann, P.G. Comments on the scalar tensor theory. Int. J. Theor. Phys. 1968, 1, 25. [Google Scholar] [CrossRef]
- Wagoner, R.V. Scalar tensor theory and gravitational waves. Phys. Rev. D 1970, 1, 3209. [Google Scholar] [CrossRef]
- Nordtvedt, N. PostNewtonian metric for a general class of scalar tensor gravitational theories and observational consequences. Astrophys. J. 1970, 161, 1059. [Google Scholar] [CrossRef]
- Will, C.M. The Confrontation between General Relativity and Experiment. Living Rev. Rel. 2014, 17, 4. [Google Scholar] [CrossRef]
- Wald, R.M. General Relativity; University of Chicago Press: Chicago, IL, USA, 1984; p. 491. [Google Scholar]
- Damour, T.; Nordtvedt, K. Tensor-scalar cosmological models and their relaxation toward general relativity. Phys. Rev. D 1993, 48, 3436. [Google Scholar] [CrossRef]
- Damour, T.; Esposito-Farèse, G. Tensor multiscalar theories of gravitation. Class. Quantum Grav. 1992, 9, 2093. [Google Scholar] [CrossRef]
- Thorne, K.S.; Will, C.M. Theoretical Frameworks for Testing Relativistic Gravity. I. Foundations. Astrophys. J. 1971, 163, 595. [Google Scholar] [CrossRef]
- Mimoso, J.P.; Nunes, A.M. General relativity as a cosmological attractor of scalar tensor gravity theories. Phys. Lett. A 1998, 248, 325. [Google Scholar] [CrossRef]
- Banerjee, N.; Sen, S. Does Brans-Dicke theory always yield general relativity in the infinite omega limit? Phys. Rev. D 1997, 56, 1334. [Google Scholar] [CrossRef]
- Billyard, A.; Coley, A.; Ibanez, J. On the asymptotic behavior of cosmological models in scalar tensor theories of gravity. Phys. Rev. D 1999, 59, 023507. [Google Scholar] [CrossRef]
- Mimoso, J.P.; Nunes, A. A Qualitative Analysis of the Attractor Mechanism of General relativity. Astrophys. Space Sci. 2003, 283, 661. [Google Scholar] [CrossRef]
- Faraoni, V.; Gunzig, E. Einstein frame or Jordan frame? Int. J. Theor. Phys. 1999, 38, 217. [Google Scholar] [CrossRef]
- Flanagan, E.E. The Conformal frame freedom in theories of gravitation. Class. Quant. Grav. 2004, 21, 3817. [Google Scholar] [CrossRef]
- Olmo, G.J. Violation of the Equivalence Principle in Modified Theories of Gravity. Phys. Rev. Lett. 2007, 98, 061101. [Google Scholar] [CrossRef] [PubMed]
- Capozziello, S.; de Ritis, R.; Marino, A.A. Some aspects of the cosmological conformal equivalence between “Jordan frame” and “Einstein frame”. Class. Quant. Grav. 1997, 14, 3243. [Google Scholar] [CrossRef]
- Capozziello, S.; Lobo, F.S.N.; Mimoso, J.P. Energy conditions in modified gravity. Phys. Lett. B 2014, 730, 280. [Google Scholar] [CrossRef]
- Capozziello, S.; Lobo, F.S.N.; Mimoso, J.P. Generalized energy conditions in Extended Theories of Gravity. Phys. Rev. D 2015, 91, 124019. [Google Scholar] [CrossRef]
- Dicke, R.H. Mach’s principle and invariance under transformation of units. Phys. Rev. 1962, 125, 2163. [Google Scholar] [CrossRef]
- Nariai, H. On the Green’s function in an expanding universe and its role in the problem of Mach’s principle. Progr. Theor. Phys. 1968, 40, 49. [Google Scholar] [CrossRef]
- O’Hanlon, J.; Tupper, B.O.J. Vacuum-field solutions in the Brans-Dicke theory. Il Nuovo Cimento 1972, 7, 305. [Google Scholar] [CrossRef]
- Barrow, J.D.; Mimoso, J.P. Perfect fluid scalar-tensor cosmologies. Phys. Rev. D 1994, 50, 3746. [Google Scholar] [CrossRef]
- Barrow, J.D. Scalar-tensor cosmologies. Phys. Rev. D 1993, 47, 5329. [Google Scholar] [CrossRef]
- Mimoso, J.P.; Wands, D. Massless fields in scalar—Tensor cosmologies. Phys. Rev. D 1995, 51, 477. [Google Scholar] [CrossRef]
- Nunes, A.; Mimoso, J.P. On the potentials yielding cosmological scaling solutions. Phys. Lett. B 2000, 488, 423. [Google Scholar] [CrossRef]
- Charters, T.C.; Nunes, A.; Mimoso, J.P. Stability analysis of cosmological models through Liapunov’s method. Class. Quant. Grav. 2001, 18, 1703. [Google Scholar] [CrossRef]
- Mimoso, J.P.; Nunes, A. General relativity as an attractor to scalar tensor gravity theories. Astrophys. Space Sci. 1999, 261, 327. [Google Scholar] [CrossRef]
- Nunes, A.; Mimoso, J.P.; Charters, T.C. Scaling solutions from interacting fluids. Phys. Rev. D 2001, 63, 083506. [Google Scholar] [CrossRef]
- Santos, C.; Gregory, R. Cosmology in Brans-Dicke theory with a scalar potential. Ann. Phys. 1997, 258, 111. [Google Scholar] [CrossRef]
- Holden, D.J.; Wands, D. Phase-plane analysis of Friedmann-Robertson-Walker cosmologies in Brans-Dicke gravity. Class. Quant. Grav. 1998, 15, 3271. [Google Scholar] [CrossRef]
- Carloni, S.; Dunsby, P.K.S.; Capozziello, S.; Troisi, A. Cosmological dynamics of Rn gravity. Class. Quant. Grav. 2005, 22, 4839. [Google Scholar] [CrossRef]
- Kuusk, P.; Jarv, L.; Saal, M. Scalar-tensor cosmologies: General relativity as a fixed point of the Jordan frame scalar field. Int. J. Mod. Phys. A 2009, 24, 1631. [Google Scholar] [CrossRef]
- Jarv, L.; Kuusk, P.; Saal, M. Potential dominated scalar-tensor cosmologies in the general relativity limit: Phase space view. Phys. Rev. D 2010, 81, 104007. [Google Scholar] [CrossRef]
- Faraoni, V. Phase space geometry in scalar-tensor cosmology. Ann. Phys. 2005, 317, 366. [Google Scholar] [CrossRef]
- Tsujikawa, S. Modified gravity models of dark energy. Lect. Notes Phys. 2010, 800, 99. [Google Scholar]
- Amendola, L. Scaling solutions in general nonminimal coupling theories. Phys. Rev. D 1999, 60, 043501. [Google Scholar] [CrossRef]
- Barrow, J.D.; Maeda, K. Extended inflationary universes. Nucl. Phys. 1990, B341, 294. [Google Scholar] [CrossRef]
- Uzan, J.P. Cosmological scaling solutions of nonminimally coupled scalar fields. Phys. Rev. D 1999, 59, 123510. [Google Scholar] [CrossRef]
- Liddle, A.R.; Mazumdar, A.; Schunck, F.E. Assisted inflation. Phys. Rev. D 1998, 58, 061301. [Google Scholar] [CrossRef]
- Malik, K.A.; Wands, D. Dynamics of assisted inflation. Phys. Rev. D 1999, 59, 123501. [Google Scholar] [CrossRef]
- Copeland, E.J.; Mazumdar, A.; Nunes, N.J. Generalized assisted inflation. Phys. Rev. D 1999, 60, 083506. [Google Scholar] [CrossRef]
- Kim, S.A.; Liddle, A.R.; Tsujikawa, S. Dynamics of assisted quintessence. Phys. Rev. D 2005, 72, 043506. [Google Scholar] [CrossRef]
- Tsujikawa, S. General analytic formulae for attractor solutions of scalar-field dark energy models and their multi-field generalizations. Phys. Rev. D 2006, 73, 103504. [Google Scholar] [CrossRef]
- Ohashi, J.; Tsujikawa, S. Assisted dark energy. Phys. Rev. D 2009, 80, 103513. [Google Scholar] [CrossRef]
- Karwan, K. Dynamics of entropy perturbations in assisted dark energy with mixed kinetic terms. J. Cosmol. Astropart. Phys. 2011, 1102, 007. [Google Scholar] [CrossRef]
- Zlatev, I.; Wang, L.M.; Steinhardt, P.J. Quintessence, cosmic coincidence, and the cosmological constant. Phys. Rev. Lett. 1999, 82, 896. [Google Scholar] [CrossRef]
- Amendola, L. Perturbations in a coupled scalar field cosmology. Mon. Not. Roy. Astron. Soc. 2000, 312, 521. [Google Scholar] [CrossRef]
- Holden, D.J.; Wands, D. Selfsimilar cosmological solutions with a nonminimally coupled scalar field. Phys. Rev. D 2000, 61, 043506. [Google Scholar] [CrossRef]
- Amendola, L. Coupled quintessence. Phys. Rev. D 2000, 62, 043511. [Google Scholar] [CrossRef]
- Brookfield, A.W.; van de Bruck, C.; Hall, L.M.H. New interactions in the dark sector mediated by dark energy. Phys. Rev. D 2008, 77, 043006. [Google Scholar] [CrossRef]
- Baldi, M. Multiple Dark Matter as a self-regulating mechanism for dark sector interactions. Ann. Phys. 2012, 524, 602. [Google Scholar] [CrossRef]
- Amendola, L.; Barreiro, T.; Nunes, N.J. Multifield coupled quintessence. Phys. Rev. D 2014, 90, 083508. [Google Scholar] [CrossRef]
- Piloyan, A.; Marra, V.; Baldi, M.; Amendola, L. Supernova constraints on Multi-coupled Dark Energy. J. Cosmol. Astropart. Phys. 2013, 1307, 42. [Google Scholar] [CrossRef]
- Piloyan, A.; Marra, V.; Baldi, M.; Amendola, L. Linear Perturbation constraints on Multi-coupled Dark Energy. J. Cosmol. Astropart. Phys. 2014, 1402, 45. [Google Scholar] [CrossRef]
- Baldi, M. Cold dark matter halos in Multi-coupled Dark Energy cosmologies: Structural and statistical properties. Phys. Dark Univ. 2014, 3, 4. [Google Scholar] [CrossRef]
- Armendariz-Picon, C.; Mukhanov, V.F.; Steinhardt, P.J. Essentials of k-essence. Phys. Rev. D 2001, 63, 103510. [Google Scholar] [CrossRef]
- Deffayet, C.; Pujolas, O.; Sawicki, I.; Vikman, A. Imperfect Dark Energy from Kinetic Gravity Braiding. J. Cosmol. Astropart. Phys. 2010, 1010, 026. [Google Scholar] [CrossRef]
- Woodard, R.P. Avoiding dark energy with 1/r modifications of gravity. Lect. Notes Phys. 2007, 720, 403. [Google Scholar]
- Deffayet, C.; Gao, X.; Steer, D.A.; Zahariade, G. From k-essence to generalised Galileons. Phys. Rev. D 2011, 84, 064039. [Google Scholar] [CrossRef]
- Deffayet, C.; Esposito-Farese, G.; Vikman, A. Covariant Galileon. Phys. Rev. D 2009, 79, 084003. [Google Scholar] [CrossRef]
- Nicolis, A.; Rattazzi, R.; Trincherini, E. The Galileon as a local modification of gravity. Phys. Rev. D 2009, 79, 064036. [Google Scholar] [CrossRef]
- Zumalacárregui, M.; García-Bellido, J. Transforming gravity: From derivative couplings to matter to second-order scalar-tensor theories beyond the Horndeski Lagrangian. Phys. Rev. D 2014, 89, 064046. [Google Scholar] [CrossRef]
- Gleyzes, J.; Langlois, D.; Piazza, F.; Vernizzi, F. Healthy theories beyond Horndeski. Phys. Rev. Lett. 2015, 114, 211101. [Google Scholar] [CrossRef] [PubMed]
- Gleyzes, J.; Langlois, D.; Piazza, F.; Vernizzi, F. Exploring gravitational theories beyond Horndeski. J. Cosmol. Astropart. Phys. 2015, 1502, 18. [Google Scholar] [CrossRef] [Green Version]
- Weinberg, S. The Cosmological Constant Problem. Rev. Mod. Phys. 1989, 61, 1. [Google Scholar] [CrossRef]
- Carroll, S.M. The Cosmological constant. Living Rev. Rel. 2001, 4, 1. [Google Scholar] [CrossRef]
- Kaloper, M.; Padilla, A. Vacuum Energy Sequestering: The Framework and Its Cosmological Consequences. Phys. Rev. D 2014, 90, 084023. [Google Scholar] [CrossRef]
- Charmousis, C.; Copeland, E.J.; Padilla, A.; Saffin, P.M. General second order scalar-tensor theory, self tuning, and the Fab Four. Phys. Rev. Lett. 2012, 108, 051101. [Google Scholar] [CrossRef] [PubMed]
- Martín-Moruno, P.; Nunes, N.J.; Lobo, F.S.N. Attracted to de Sitter: Cosmology of the linear Horndeski models. J. Cosmol. Astropart. Phys. 2015, 1505, 33. [Google Scholar] [CrossRef]
- Martín-Moruno, P.; Nunes, N.J. Attracted to de Sitter II: Cosmology of the shift-symmetric Horndeski models. J. Cosmol. Astropart. Phys. 2015, 1509, 56. [Google Scholar] [CrossRef]
- Penrose, R. Gravitational collapse and space-time singularities. Phys. Rev. Lett 1965, 14, 57. [Google Scholar] [CrossRef]
- Penrose, R. Gravitational collapse: The role of general relativity. Riv. Nuovo Cim. Numero Speciale 1969, 1, 252. [Google Scholar]
- Hawking, S.W. Singularities in the universe. Phys. Rev. Lett 1966, 17, 444. [Google Scholar] [CrossRef]
- Jungman, G.; Kamionkowski, M.; Griest, K. Supersymmetric dark matter. Phys. Rept. 1996, 267, 195. [Google Scholar] [CrossRef]
- Green, M.; Schwarz, J.; Witten, E. Superstring Theory; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Thiemann, T. Lectures on loop quantum gravity. Lect. Notes Phys. 2003, 631, 41. [Google Scholar]
- Birrell, N.D.; Davies, P.C.W. Quantum Fields in Curved Space; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Buchdahl, H.A. Non-linear Lagrangians and cosmological theory. Mon. Not. Roy. Astron. Soc. 1970, 150, 1. [Google Scholar] [CrossRef]
- Barrow, J.D.; Ottewill, A.C. The Stability of General Relativistic Cosmological Theory. J. Phys. A 1983, 16, 2757. [Google Scholar] [CrossRef]
- Ferraris, M.; Francaviglia, M.; Volovich, I. The Universality of vacuum Einstein equations with cosmological constant. Class. Quant. Grav. 1994, 11, 1505. [Google Scholar] [CrossRef]
- Vollick, D.N. 1/R Curvature corrections as the source of the cosmological acceleration. Phys. Rev. D 2003, 68, 063510. [Google Scholar] [CrossRef]
- Meng, X.H.; Wang, P. Palatini formation of modified gravity with ln R terms. Phys. Lett. B 2004, 584, 1. [Google Scholar] [CrossRef]
- Poplawski, N.J. Interacting dark energy in f(R) gravity. Phys. Rev. D 2006, 74, 084032. [Google Scholar] [CrossRef]
- Li, B.; Chan, K.C.; Chu, M.C. Constraints on f(R) Cosmology in the Palatini Formalism. Phys. Rev. D 2007, 76, 024002. [Google Scholar] [CrossRef]
- Li, B.; Barrow, J.D.; Mota, D.F. The Cosmology of Ricci-Tensor-Squared gravity in the Palatini variational approach. Phys. Rev. D 2007, 76, 104047. [Google Scholar] [CrossRef]
- Iglesias, A.; Kaloper, N.; Padilla, A.; Park, M. How (Not) to Palatini. Phys. Rev. D 2007, 76, 104001. [Google Scholar] [CrossRef]
- Amendola, L.; Appleby, S.; Bacon, D.; Baker, T.; Baldi, M.; Bartolo, N.; Blanchard, A.; Bonvin, C.; Borgani, S.; Branchini, E.; et al. Cosmology and fundamental physics with the Euclid satellite. Living Rev. Rel. 2013, 16, 6. [Google Scholar] [CrossRef]
- Capozziello, S.; Carloni, S.; Troisi, A. Quintessence without scalar fields. Recent Res. Dev. Astron. Astrophys. 2003, 1, 625. [Google Scholar]
- Sotiriou, T.P. Modified Actions for Gravity: Theory and Phenomenology. 2007; arXiv:gr-qc/0710.4438. [Google Scholar]
- Vikman, A. Can dark energy evolve to the phantom? Phys. Rev. D 2005, 71, 023515. [Google Scholar] [CrossRef]
- Cai, Y.F.; Saridakis, E.N.; Setare, M.R.; Xia, J.Q. Quintom Cosmology: Theoretical implications and observations. Phys. Rept. 2010, 493, 1. [Google Scholar] [CrossRef]
- Bertolami, O.; Boehmer, C.G.; Harko, T.; Lobo, F.S.N. Extra force in f(R) modified theories of gravity. Phys. Rev. D 2007, 75, 104016. [Google Scholar] [CrossRef]
- Bertolami, O.; Páramos, J. Do f(R) theories matter? Phys. Rev. D 2008, 77, 084018. [Google Scholar] [CrossRef]
- Bertolami, O.; Páramos, J. On the non-trivial gravitational coupling to matter. Class. Quant. Grav. 2008, 25, 245017. [Google Scholar] [CrossRef]
- Faraoni, V. A viability criterion for modified gravity with an extra force. Phys. Rev. D 2007, 76, 127501. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Gravity assisted dark energy dominance and cosmic acceleration. Phys. Lett. B 2004, 599, 137. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Dark energy and cosmic speed-up from consistent modified gravity. PoS WC 2004, 2004, 24. [Google Scholar]
- Allemandi, G.; Borowiec, A.; Francaviglia, M.; Odintsov, S.D. Dark energy dominance and cosmic acceleration in first order formalism. Phys. Rev. D 2005, 72, 063505. [Google Scholar] [CrossRef]
- Mukohyama, S.; Randall, L. A Dynamical approach to the cosmological constant. Phys. Rev. Lett. 2004, 92, 211302. [Google Scholar] [CrossRef] [PubMed]
- Harko, T.; Koivisto, T.S.; Lobo, F.S.N. Palatini formulation of modified gravity with a nonminimal curvature-matter coupling. Mod. Phys. Lett. A 2011, 26, 1467. [Google Scholar] [CrossRef]
- Koivisto, T. Covariant conservation of energy momentum in modified gravities. Class. Quant. Grav. 2006, 23, 4289. [Google Scholar] [CrossRef]
- Bertolami, O.; Paramos, J.; Harko, T.; Lobo, F.S.N. Non-minimal curvature-matter couplings in modified gravity. 2008; arXiv:0811.2876 [gr-qc]. [Google Scholar]
- Sotiriou, T.P.; Faraoni, V. Modified gravity with R-matter couplings and (non-)geodesic motion. Class. Quant. Grav. 2008, 25, 205002. [Google Scholar] [CrossRef]
- Schutz, B.F. Perfect Fluids in General Relativity: Velocity Potentials and a Variational Principle. Phys. Rev. D 1970, 2, 2762. [Google Scholar] [CrossRef]
- Brown, J.D. Action functionals for relativistic perfect fluids. Class. Quant. Grav. 1993, 10, 1579. [Google Scholar] [CrossRef]
- Bertolami, O.; Lobo, F.S.N.; Páramos, J. Non-minimum coupling of perfect fluids to curvature. Phys. Rev. D 2008, 78, 064036. [Google Scholar] [CrossRef]
- Hawking, S.W.; Ellis, G.F.R. The Large Scale Structure of Spacetime; Cambridge University Press: Cambridge, UK, 1973. [Google Scholar]
- Falk, J. Theory of elasticity of coherent inclusions by means of nonmetric geometry. J. Elast. 1981, 11, 359. [Google Scholar] [CrossRef]
- Kröner, E. The continuized crystal—A bridge between micro and macromechanics? Z. Angew. Math. Mech. 1986, 66, T284–T292. [Google Scholar]
- Clayton, J.D. Nonlinear Mechanics of Crystals; Springer: Maryland, MD, USA, 2011. [Google Scholar]
- Lobo, F.S.N.; Olmo, G.J.; Rubiera-Garcia, D. Crystal clear lessons on the microstructure of spacetime and modified gravity. Phys. Rev. D 2015, 91, 124001. [Google Scholar] [CrossRef]
- Olmo, G.J.; Rubiera-Garcia, D. The quantum, the geon, and the crystal. Int. J. Mod. Phys. D 2015, 24, 1542013. [Google Scholar] [CrossRef]
- Olmo, G.J.; Rubiera-Garcia, D. Importance of torsion and invariant volumes in Palatini theories of gravity. Phys. Rev. D 2013, 88, 084030. [Google Scholar] [CrossRef]
- Olmo, G.J.; Rubiera-Garcia, D. Palatini f (R) black holes in nonlinear electrodynamics. Phys. Rev. D 2011, 84, 124059. [Google Scholar] [CrossRef]
- Exirifard, Q.; Sheikh-Jabbari, M.M. Lovelock gravity at the crossroads of Palatini and metric formulations. Phys. Lett. B 2008, 661, 158. [Google Scholar] [CrossRef]
- Borunda, M.; Janssen, B.; Bastero-Gil, M. Palatini versus metric formulation in higher curvature gravity. J. Cosmol. Astropart. Phys. 2008, 2008, 0811. [Google Scholar] [CrossRef] [PubMed]
- Olmo, G.J.; Rubiera-Garcia, D. Brane-world and loop cosmology from a gravity-matter coupling perspective. Phys. Lett. B 2015, 740, 73. [Google Scholar] [CrossRef]
- Bojowald, M. Loop quantum cosmology. Living Rev. Rel. 2008, 11, 4. [Google Scholar] [CrossRef]
- Ashtekar, A.; Singh, P. Loop Quantum Cosmology: A Status Report. Class. Quant. Grav 2011, 28, 213001. [Google Scholar] [CrossRef]
- Maartens, R.; Koyama, K. Brane-World Gravity. Living Rev. Rel 2010, 13, 5. [Google Scholar] [CrossRef]
- Ashtekar, A.; Pawlowski, T.; Singh, P. Quantum nature of the big bang. Phys. Rev. Lett. 2006, 96, 141301. [Google Scholar] [CrossRef] [PubMed]
- Barragan, C.; Olmo, G.J.; Sanchis-Alepuz, H. Bouncing Cosmologies in Palatini f (R) Gravity. Phys. Rev. D 2009, 80, 024016. [Google Scholar] [CrossRef]
- Olmo, G.J.; Rubiera-Garcia, D. Nonsingular black holes in f (R) theories. Universe 2015, 1, 173. [Google Scholar] [CrossRef]
- Bambi, C.; Cardenas-Avendano, A.; Olmo, G.J.; Rubiera-Garcia, D. Wormholes and nonsingular space-times in Palatini f(R) gravity. Phys. Rev. D 2016, 93, 064016. [Google Scholar] [CrossRef]
- Barragan, C.; Olmo, G.J. Isotropic and Anisotropic Bouncing Cosmologies in Palatini Gravity. Phys. Rev. D 2010, 82, 084015. [Google Scholar] [CrossRef]
- Deser, S.; Gibbons, G.W. Born-Infeld-Einstein actions? Class. Quant. Grav 1998, 15, L35. [Google Scholar] [CrossRef]
- Bañados, M.; Ferreira, P.G. Eddington’s theory of gravity and its progeny. Phys. Rev. Lett 2010, 105, 011101. [Google Scholar] [CrossRef] [PubMed]
- Jiménez, J.B.; Heisenberg, L.; Olmo, G.J. Infrared lessons for ultraviolet gravity: The case of massive gravity and Born-Infeld. J. Cosmol. Astropart. Phys. 2014, 1411, 004. [Google Scholar] [CrossRef] [PubMed]
- Olmo, G.J.; Rubiera-Garcia, D.; Sanchez-Puente, A. Geodesic completeness in a wormhole spacetime with horizons. Phys. Rev. D. 2015, 92, 044047. [Google Scholar] [CrossRef]
- Bazeia, D.; Losano, L.; Olmo, G.J.; Rubiera-Garcia, D.; Sanchez-Puente, A. Classical resolution of black hole singularities in arbitrary dimension. Phys. Rev. D 2015, 92, 044018. [Google Scholar] [CrossRef]
- Olmo, G.J.; Rubiera-Garcia, D.; Sanchez-Puente, A. Classical resolution of black hole singularities via wormholes. Eur. Phys. J. C 2016, 76, 143. [Google Scholar] [CrossRef]
- Odintsov, O.D.; Olmo, G.J.; Rubiera-Garcia, D. Born-Infeld gravity and its functional extensions. 2014, 90, 044003. [Google Scholar]
- Hawking, S. Gravitationally collapsed objects of very low mass. Mon. Not. Roy. Astron. Soc. 1971, 152, 75. [Google Scholar] [CrossRef]
- Lobo, F.S.N.; Olmo, O.J.; Rubiera-Garcia, D. Semiclassical geons as solitonic black hole remnants. J. Cosmol. Astropart. Phys. 2013, 1307, 011. [Google Scholar] [CrossRef]
- Chen, P.; Ong, Y.C.; Yeom, D.H. Black Hole Remnants and the Information Loss Paradox. 2014; arXiv:1412.8366 [gr-qc]. [Google Scholar]
- Capozziello, S.; Harko, T.; Koivisto, T.S.; Lobo, F.S.N.; Olmo, G.J. Cosmology of hybrid metric-Palatini f(X)-gravity. J. Cosmol. Astropart. Phys. 2013, 1304, 11. [Google Scholar] [CrossRef]
- Capozziello, S.; Harko, T.; Koivisto, T.S.; Lobo, F.S.N.; Olmo, G.J. Wormholes supported by hybrid metric-Palatini gravity. Phys. Rev. D 2012, 86, 127504. [Google Scholar] [CrossRef]
- Capozziello, S.; Harko, T.; Koivisto, T.S.; Lobo, F.S.N.; Olmo, G.J. The virial theorem and the dark matter problem in hybrid metric-Palatini gravity. J. Cosmol. Astropart. Phys. 2013, 1307, 24. [Google Scholar] [CrossRef]
- Capozziello, S.; Harko, T.; Koivisto, T.S.; Lobo, F.S.N.; Olmo, G.J. Hybrid metric-Palatini gravity. Universe 2015, 1, 199. [Google Scholar] [CrossRef]
- Mukhanov, V. Physical Foundations of Cosmology; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Liddle, A.R.; Lyth, D.H. Cosmological Inflation and Large-Scale Structure; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Dodelson, S. Modern Cosmology; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Ade, P.A.R.; Aghanim, A.N.; Arnaud, M.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2015 results. XX. Constraints on inflation. 2015; arXiv:1502.02114 [astro-ph.CO]. [Google Scholar]
- Lidsey, J.E.; Liddle, A.R.; Kolb, E.W.; Copeland, E.J.; Barreiro, T.; Abney, M. Reconstructing the inflation potential: An overview. Rev. Mod. Phys. 1997, 69, 373. [Google Scholar] [CrossRef]
- Elizalde, E.; Nojiri, S.; Odintsov, S.D.; Saez-Gomez, D.; Faraoni, V. Reconstructing the universe history, from inflation to acceleration, with phantom and canonical scalar fields. Phys. Rev. D 2008, 77, 106005. [Google Scholar] [CrossRef]
- Bamba, K.; Nojiri, S.; Odintsov, S.D. Reconstruction of scalar field theories realizing inflation consistent with the Planck and BICEP2 results. Phys. Lett. B 2014, 737, 374. [Google Scholar] [CrossRef]
- Capozziello, S.; Faraoni, V. Beyond Einstein Gravity; Springer: Dordrecht, The Netherlands, 2010. [Google Scholar]
- De la Cruz-Dombriz, A.; Saez-Gomez, D. Black holes, cosmological solutions, future singularities, and their thermodynamical properties in modified gravity theories. Entropy 2012, 14, 1717. [Google Scholar] [CrossRef] [Green Version]
- Saez-Gomez, D. Modified f (R) gravity from scalar-tensor theory and inhomogeneous EoS dark energy. Gen. Rel. Grav. 2009, 41, 1527. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Saez-Gomez, D. Cosmological reconstruction of realistic modified F(R) gravities. Phys. Lett. B 2009, 681, 74. [Google Scholar] [CrossRef]
- Bamba, K.; Nojiri, S.; Odintsov, S.D.; Sáez-Gómez, D. Inflationary universe from perfect fluid and F(R) gravity and its comparison with observational data. Phys. Rev. D 2014, 90, 124061. [Google Scholar] [CrossRef]
- De Felice, A.; Tsujikawa, S.; Elliston, G.; Tavakol, R. Chaotic inflation in modified gravitational theories. J. Cosmol. Astropart. Phys. 2011, 1108, 021. [Google Scholar] [CrossRef]
- Starobinsky, A.A. A New Type of Isotropic Cosmological Models Without Singularity. Phys. Lett. B 1980, 91, 99. [Google Scholar] [CrossRef]
- Copeland, E.J.; Rahmede, C.; Saltas, I.D. Asymptotically Safe Starobinsky Inflation. Phys. Rev. D 2015, 91, 103530. [Google Scholar] [CrossRef]
- De la Cruz-Dombriz, A.; Elizalde, E.; Odintsov, S.D.; Saez-Gomez, D. Spotting deviations from R2 inflation. 2016; arXiv:1603.05537 [gr-qc]. [Google Scholar]
- Sasaki, M.; Stewart, E.D. A General analytic formula for the spectral index of the density perturbations produced during inflation. Prog. Theor. Phys. 1996, 95, 71. [Google Scholar] [CrossRef]
- Avelino, P.P.; Menezes, R.; Sousa, L. p-brane dynamics in N+1-dimensional FRW universes. Phys. Rev. D 2009, 79, 043519. [Google Scholar] [CrossRef]
- Sousa, L.; Avelino, P.P. p-brane dynamics in (N+1)-dimensional FRW universes: A unified framework. Phys. Rev. D 2011, 83, 103507. [Google Scholar]
- Sousa, L.; Avelino, P.P. The cosmological evolution of p-brane networks. Phys. Rev. D 2011, 84, 063502. [Google Scholar] [CrossRef]
- Martins, C.J.A.P.; Shellard, E.P.S. Quantitative string evolution. Phys. Rev. D 1996, 54, 2535. [Google Scholar] [CrossRef]
- Martins, C.J.A.P.; Shellard, E.P.S. Extending the velocity dependent one scale string evolution model. Phys. Rev. D 2002, 65, 043514. [Google Scholar] [CrossRef]
- Leite, A.M.M.; Martins, C.J.A.P.; Shellard, E.P.S. Accurate Calibration of the Velocity-Dependent One-Scale Model for Domain Walls. Phys. Lett. B 2013, 718, 740. [Google Scholar] [CrossRef]
- Oliveira, M.F.; Avgoustidis, A.; Martins, C.J.A.P. Cosmic string evolution with a conserved charge. Phys. Rev. D 2012, 85, 083515. [Google Scholar] [CrossRef]
- Avgoustidis, A.; Shellard, E.P.S. Velocity-Dependent Models for Non-Abelian/Entangled String Networks. Phys. Rev. D 2008, 78, 103510. [Google Scholar] [CrossRef]
- Nunes, A.S.; Avgoustidis, A.; Martins, C.J.A.P.; Urrestilla, J. Analytic Models for the Evolution of Semilocal String Networks. Phys. Rev. D 2011, 84, 063504. [Google Scholar] [CrossRef]
- Martins, C.J.A.P. Evolution of Hybrid Defect Networks. Phys. Rev. D 2009, 80, 083527. [Google Scholar] [CrossRef]
- Avelino, P.P.; Martins, C.J.A.P. Primordial adiabatic fluctuations from cosmic defects. Phys. Rev. Lett. 2000, 85, 1370. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.H.P.; Avelino, P.P.; Shellard, E.P.S.; Allen, B. Cosmic strings, loops, and linear growth of matter perturbations. Int. J. Mod. Phys. D 2002, 11, 61. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; et al. [Planck Collaboration], Planck 2013 results. XXV. Searches for cosmic strings and other topological defects. Astron. Astrophys. 2014, 571, A25. [Google Scholar]
- Bardeen, J.M. Gauge Invariant Cosmological Perturbations. Phys. Rev. D 1980, 22, 1882. [Google Scholar] [CrossRef]
- Martin, J.; Ringeval, C.; Vennin, V. How Well Can Future CMB Missions Constrain Cosmic Inflation? J. Cosmol. Astropart. Phys. 2014, 1410, 038. [Google Scholar] [CrossRef]
- Sousa, L.; Avelino, P.P. Cosmic Microwave Background anisotropies generated by domain wall networks. Phys. Rev. D 2015, 92, 083520. [Google Scholar] [CrossRef]
- Pogosian, P.; Vachaspati, T. Cosmic microwave background anisotropy from wiggly strings. Phys. Rev. D 1999, 60, 083504. [Google Scholar] [CrossRef]
- Pogosian, L.; Wasserman, I.; Wyman, M. On vector mode contribution to CMB temperature and polarization from local strings. 2006; astro-ph/0604141. [Google Scholar]
- Vilenkin, A. Gravitational radiation from cosmic strings. Phys. Lett. B 1981, 107, 47. [Google Scholar] [CrossRef]
- Brandenberger, R.H.; Albrecht, A.; Turok, N. Gravitational Radiation from Cosmic Strings and the Microwave Background. Nucl. Phys. B 1986, 277, 605. [Google Scholar] [CrossRef]
- Sanidas, S.A.; Battye, R.A.; Stappers, B.W. Constraints on cosmic string tension imposed by the limit on the stochastic gravitational wave background from the European Pulsar Timing Array. Phys. Rev. D 2012, 85, 122003. [Google Scholar] [CrossRef]
- Sousa, L.; Avelino, P.P. Stochastic Gravitational Wave Background generated by Cosmic String Networks: Velocity-Dependent One-Scale model versus Scale-Invariant Evolution. Phys. Rev. D 2013, 88, 023516. [Google Scholar] [CrossRef]
- Aasi, J.; Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.R.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Advanced LIGO. Class. Quant. Grav. 2015, 32, 074001. [Google Scholar]
- Accadia, T.; Agathos, M.; Allocca, A.; Astone, P.; Ballardin, G.; Barone, F.; Barsuglia, M.; Basti, A.; Bauer, T.S.; Bejger, M.; et al. Advanced Virgo Interferometer: A Second Generation Detector for Gravitational Waves Observation. 2015; arXiv:1408.3978 [gr-qc]. [Google Scholar]
- Dufaux, J.F. Cosmological Backgrounds of Gravitational Waves and eLISA. ASP Conf. Ser. 2013, 467, 91. [Google Scholar]
- Manchester, R.N. The Parkes Pulsar Timing Array. AIP Conf. Proc. 2008, 983, 584. [Google Scholar] [CrossRef]
- Ferdman, R.D.; van Haasteren, R.; Bassa, C.G.; Burgay, M.; Cognard, I.; Corongiu, A.; D’Amico, N.; Desvignes, G.; Hessels, J.W.T.; Janssen, G.H.; et al. The European Pulsar Timing Array: Current efforts and a LEAP toward the future. Class. Quant. Grav. 2010, 27, 084014. [Google Scholar] [CrossRef] [Green Version]
- Hiramatsu, T.; Kawasaki, M.; Saikawa, K. On the estimation of gravitational wave spectrum from cosmic domain walls. J. Cosmol. Astropart. Phys. 2014, 1402, 031. [Google Scholar] [CrossRef]
- Hiramatsu, T.; Kawasaki, M.; Saikawa, K. Gravitational Waves from Collapsing Domain Walls. J. Cosmol. Astropart. Phys. 2010, 1005, 032. [Google Scholar] [CrossRef]
- Bleem, L.E.; Stalder, B.; de Haan, T.; Aird, K.A.; Allen, S.W.; Applegate, D.E.; Ashby, L.N.; Bautz, M.; Bayliss, M.; Benson, B.A.; et al. Galaxy Clusters discovered via the Sunyaev-Zel’dovic effect in the 2500-square-degree SPT-SZ Survey. Astrophys. J. Suppl. 2015, 216, 27. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck Collaboration, Planck 2015 results. XXIV. Cosmology from Sunyaev-Zeldovich cluster counts. 2015; arXiv:1502.01597. [Google Scholar]
- André, P.; Baccigalupi, C.; Banday, A.; Barbosa, D.; Barreiro, B.; Bartlett, J.; Bartolo, N.; Battistelli, E.; Battye, R.; Bendo, G.; et al. PRISM (Polarized Radiation Imaging and Spectroscopy Mission): An extended white paper. J. Cosmol. Astropart. Phys. 2014, 2, 006. [Google Scholar]
- Ramos, E.P.R.G.; da Silva, A.J.C.; Liu, G.-C. Cosmic Microwave Background Induced Polarization from Single Scattering by Clusters of Galaxies and Filaments. Astrophys. J. 2012, 757, 44. [Google Scholar] [CrossRef]
- Jenkins, A.; Frenk, C.S.; White, S.D.M.; Colberg, J.M.; Cole, S.; Evrard, A.E.; Couchman, H.M.P.; Yoshida, N. The mass function of dark matter haloes. Mon. Not. Roy. Astron. Soc. 2001, 321, 372. [Google Scholar] [CrossRef] [Green Version]
- Press, W.H.; Schechter, P. Formation of Galaxies and Clusters of Galaxies by Self-Similar Gravitational Condensation. Astrophys. J. 1974, 187, 425. [Google Scholar] [CrossRef]
- Kravtsov, A.V.; Borgani, S. Formation of Galaxy Clusters. Ann. Rev. Astron. Astrophys. 2012, 50, 353. [Google Scholar] [CrossRef]
- Wagner, C.; Verde, L. N-body simulations with generic non-Gaussian initial conditions II: Halo bias. J. Cosmol. Astropart. Phys. 2012, 3, 002. [Google Scholar] [CrossRef] [PubMed]
- Achitouv, I.; Baldi, M.; Puchwein, E.; Weller, J. The Imprint of f(R) Gravity on Non-Linear Structure Formation. 2015; arXiv:1511.01494. [Google Scholar]
- Nunes, N.J.; da Silva, A.C.; Aghanim, N. Number counts in homogeneous and inhomogeneous dark energy models. Astron. Astrophys. 2006, 450, 899. [Google Scholar] [CrossRef]
- Kaiser, N. Evolution and clustering of rich clusters. Mon. Not. Roy. Astron. Soc. 1986, 222, 323. [Google Scholar] [CrossRef]
- Kay, S.T.; da Silva, A.C.; Aghanim, N.; Blanchard, A.; Liddle, A.R.; Puget, J.-L.; Sadat, R.; Thomas, P.A. The evolution of clusters in the CLEF cosmological simulation: X-ray structural and scaling properties. Mon. Not. Roy. Astron. Soc. 2007, 377, 317. [Google Scholar] [CrossRef]
- Da Silva, A. C.; Catalano, A.; Montier, L.; Pointecouteau, E.; Lanoux, J.; Giard, M. The impact of dust on the scaling properties of galaxy clusters. Mon. Not. Roy. Astron. Soc. 2009, 396, 849. [Google Scholar] [CrossRef]
- Aghanim, N.; da Silva, A.C.; Nunes, N.J. Cluster scaling relations from cosmological hydrodynamic simulations in a dark-energy dominated universe. Astron. Astrophys. 2009, 496, 637. [Google Scholar] [CrossRef]
- Trindade, A.M.M.; da Silva, A. Effect of Priomordial non-Gaussianities on Galaxy Clusters Scaling Relations. 2016; arXiv:1603.09270. [Google Scholar]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. A Universal Density Profile from Hierarchical Clustering. Astrophys. J. 1997, 490, 493. [Google Scholar] [CrossRef]
- Nagai, D.; Kravtsov, A.V.; Vikhlinin, A. Effects of Galaxy Formation on Thermodynamics of the Intracluster Medium. Astrophys. J. 2007, 668, 1. [Google Scholar] [CrossRef]
- Da Silva, A.C.; Barbosa, D.; Liddle, A.R.; Thomas, P.A. Hydrodynamical simulations of the Sunyaev-Zel’dovich effect: The kinetic effect. Mon. Not. Roy. Astron. Soc. 2001, 326, 155. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Barrena, R.; Bartlett, J.G.; et al. Planck Collaboration, Planck 2015 results. XXVII. The Second Planck Catalogue of Sunyaev-Zeldovich Sources. 2015; arXiv:1502.01598. [Google Scholar]
- Ade, P.A.R.; Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; et al. Planck Collaboration, Planck 2013 results. XX. Cosmology from Sunyaev-Zeldovich cluster counts. Astron. Astrophys. 2014, 571, A20. [Google Scholar]
- Ade, P.A.R.; Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; et al. Planck Collaboration, Planck 2013 results. XXI. Power spectrum and high-order statistics of the Planck all-sky Compton parameter map. Astron. Astrophys. 2014, 571, A21. [Google Scholar]
- Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; Battaner, E.; et al. Planck Collaboration, Planck 2015 results. XXII. A map of the thermal Sunyaev-Zeldovich effect. 2015; arXiv:1502.01596. [Google Scholar]
- De Martino, I.; Atrio-Barandela, F.; da Silva, A.; Ebeling, H.; Kashlinsky, A.; Kocevski, D.; Martins, C.J.A.P. Measuring the Redshift Dependence of the Cosmic Microwave Background Monopole Temperature with Planck Data. Astrophys. J. 2012, 757, 144. [Google Scholar] [CrossRef]
- De Martino, I.; Génova-Santos, R.; Atrio-Barandela, F.; Ebeling, H.; Kashlinsky, A.; Kocevski, D.; Martins, C.J.A.P. Constraining the Redshift Evolution of the Cosmic Microwave Background Blackbody Temperature with PLANCK Data. Astrophys. J. 2015, 808, 128. [Google Scholar] [CrossRef]
- Rudjord, Ø.; Hansen, F.K.; Lan, X.; Liguori, M.; Marinucci, D.; Matarrese, S. An Estimate of the Primordial Non-Gaussianity Parameter fNL Using the Needlet Bispectrum from WMAP. Astrophys. J. 2009, 701, 369. [Google Scholar]
- Komatsu, E.; Dunkley, J.; Nolta, M.R.; Bennett, C.L.; Gold, B.; Hinshaw, G.; Jarosik, N.; Larson, D.; Limon, M.; Page, L.; et al. Five-Year Wilkinson Microwave Anisotropy Probe Observations: Cosmological Interpretation. Astrophys. J. S. 2009, 180, 330. [Google Scholar] [CrossRef]
- Curto, A.; Martínez-González, E.; Barreiro, R.B. Improved Constraints on Primordial Non-Gaussianity for the Wilkinson Microwave Anisotropy Probe 5-Year Data. Astrophys. J. 2009, 706, 399. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; et al. Planck Collaboration, Planck 2013 results. XXIV. Constraints on primordial non-Gaussianity. Astron. Astrophys. 2014, 571, A24. [Google Scholar]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; et al. Planck Collaboration, Planck 2015 results. XVII. Constraints on primordial non-Gaussianity. 2015; arXiv:1502.01592 [astro-ph.CO]. [Google Scholar]
- Sefusatti, E.; Komatsu, E. Bispectrum of galaxies from high-redshift galaxy surveys: Primordial non-Gaussianity and nonlinear galaxy bias. Phys. Rev. D 2007, 76, 083004. [Google Scholar] [CrossRef]
- Matarrese, S.; Verde, L. The Effect of Primordial Non-Gaussianity on Halo Bias. Astrophys. J. Lett. 2008, 677, L77. [Google Scholar] [CrossRef]
- Giannantonio, T.; Porciani, C.; Carron, J.; Amara, A.; Pillepich, A. Constraining primordial non-Gaussianity with future galaxy surveys. Mon. Not. Roy. Astron. Soc. 2012, 422, 2854. [Google Scholar] [CrossRef]
- Schäfer, B.M.; Grassi, A.; Gerstenlauer, M.; Byrnes, C.T. A weak lensing view on primordial non-Gaussianities. Mon. Not. Roy. Astron. Soc. 2012, 421, 797. [Google Scholar] [CrossRef]
- Hilbert, S.; Marian, L.; Smith, R.E.; Desjacques, V. Measuring primordial non-Gaussianity with weak lensing surveys. Mon. Not. Roy. Astron. Soc. 2012, 426, 2870. [Google Scholar] [CrossRef]
- Tashiro, H.; Ho, S. Constraining primordial non-Gaussianity with CMB-21 cm cross-correlations? Mon. Not. Roy. Astron. Soc. 2013, 431, 2017. [Google Scholar] [CrossRef]
- Takeuchi, Y.; Ichiki, K.; Matsubara, T. Application of cross correlations between CMB and large-scale structure to constraints on the primordial non-Gaussianity. Phys. Rev. D 2012, 85, 043518. [Google Scholar] [CrossRef]
- Robinson, J.; Baker, J.E. Evolution of the cluster abundance in non-Gaussian models. Mon. Not. Roy. Astron. Soc. 2000, 311, 781. [Google Scholar] [CrossRef]
- Matarrese, S.; Verde, L.; Jimenez, R. The Abundance of High-Redshift Objects as a Probe of Non-Gaussian Initial Conditions. Astrophys. J. 2000, 541, 10. [Google Scholar] [CrossRef]
- Kamionkowski, M.; Verde, L.; Jimenez, R. The void abundance with non-gaussian primordial perturbations. J. Cosmol. Astropart. Phys. 2009, 1, 010. [Google Scholar] [CrossRef]
- Lam, T.Y.; Sheth, R.K.; Desjacques, V. The initial shear field in models with primordial local non-Gaussianity and implications for halo and void abundances. Mon. Not. Roy. Astron. Soc. 2009, 399, 1482. [Google Scholar] [CrossRef] [Green Version]
- D’Amico, G.; Musso, M.; Noreña, J.; Paranjape, A. Excursion sets and non-Gaussian void statistics. Phys. Rev. D 2011, 83, 023521. [Google Scholar] [CrossRef]
- Sekiguchi, T.; Yokoyama, S. Void bias from primordial non-Gaussianities. 2012; arXiv:1204.2726 [astro-ph.CO]. [Google Scholar]
- Fergusson, J.R.; Shellard, E.P.S. Shape of primordial non-Gaussianity and the CMB bispectrum. Phys. Rev. D 2009, 80, 043510. [Google Scholar] [CrossRef]
- LoVerde, M.; Miller, A.; Shandera, S.; Verde, L. Effects of scale-dependent non-Gaussianity on cosmological structures. J. Cosmol. Astropart. Phys. 2008, 4, 014. [Google Scholar] [CrossRef]
- Giannantonio, T.; Porciani, C. Structure formation from non-Gaussian initial conditions: Multivariate biasing, statistics, and comparison with N-body simulations. Phys. Rev. D 2010, 81, 063530. [Google Scholar] [CrossRef]
- Maggiore, M.; Riotto, A. The Halo Mass Function from Excursion Set Theory. III. Non-Gaussian Fluctuations. Astrophys. J. 2010, 717, 526. [Google Scholar] [CrossRef]
- D’Amico, G.; Musso, M.; Noreña, J.; Paranjape, A. An improved calculation of the non-Gaussian halo mass function. J. Cosmol. Astropart. Phys. 2011, 2, 001. [Google Scholar] [CrossRef]
- LoVerde, M.; Smith, K.M. The non-Gaussian halo mass function with fNL, gNL and τNL. J. Cosmol. Astropart. Phys. 2011, 8, 003. [Google Scholar] [CrossRef]
- Achitouv, I.E.; Corasaniti, P.S. Non-Gaussian halo mass function and non-spherical halo collapse: Theory vs. simulations. J. Cosmol. Astropart. Phys. 2012, 2, 2. [Google Scholar] [CrossRef] [PubMed]
- D’Aloisio, A.; Zhang, J.; Jeong, D.; Shapiro, P.R. Halo statistics in non-Gaussian cosmologies: The collapsed fraction, conditional mass function and halo bias from the path-integral excursion set method. Mon. Not. Roy. Astron. Soc. 2013, 428, 2765. [Google Scholar] [CrossRef]
- Zentner, A.R. The Excursion Set Theory of Halo Mass Functions, Halo Clustering, and Halo Growth. Intern. J. Mod. Phys. D 2007, 16, 763. [Google Scholar] [CrossRef]
- Maggiore, M.; Riotto, A. The Halo Mass Function from Excursion Set Theory. I. Gaussian Fluctuations with Non-Markovian Dependence on the Smoothing Scale. Astrophys. J. 2010, 711, 907. [Google Scholar] [CrossRef]
- Trindade, A.M.M.; Avelino, P.P.; Viana, P.T.P. A new signature of primordial non-Gaussianities from the abundance of galaxy clusters. Mon. Not. Roy. Astron. Soc. 2012, 424, 1442. [Google Scholar] [CrossRef]
- Trindade, A.M.M.; Avelino, P.P.; Viana, P.T.P. Biased cosmological parameter estimation with galaxy cluster counts in the presence of primordial non-Gaussianities. Mon. Not. Roy. Astron. Soc. 2013, 435, 782. [Google Scholar] [CrossRef]
- Da Silva, A.C.; Kay, S.T.; Liddle, A.R.; Thomas, P.A. Hydrodynamical simulations of the Sunyaev-Zel’dovich effect: Cluster scaling relations and X-ray properties. Mon. Not. Roy. Astron. Soc. 2004, 348, 1401. [Google Scholar] [CrossRef]
- Schneider, P.; Ehlers, J.; Falco, E.E. Gravitational Lenses; Springer: Berlin, Germany, 1992. [Google Scholar]
- Schneider, P.; Kochanek, C.S.; Wambsganss, J. Gravitational Lensing: Strong, Weak and Micro; Springer: Berlin, Germany, 2006. [Google Scholar]
- Narayan, R.; Bartelmann, M. Gravitational Lensing. In Formation of Structure in the Universe; Dekel, A., Ostriker, J.P., Eds.; Cambridge University Press: Cambridge, UK, 1999; p. 360. [Google Scholar]
- Bartelmann, M. Gravitational Lensing. Class. Quantum Gravity 2010, 27, 233001. [Google Scholar] [CrossRef]
- Fort, B.; Mellier, Y. Arc(let)s in clusters of galaxies. Astron. Astrophys. Rev. 1994, 5, 239–292. [Google Scholar] [CrossRef]
- Valdes, F.; Jarvis, J.F.; Tyson, J.A. Alignment of faint galaxy images—Cosmological distortion and rotation. Astrophys. J. 1983, 271, 431–441. [Google Scholar] [CrossRef]
- Mould, J.; Blandford, R.; Villumsen, J.; Brainerd, T.; Smail, I.; Small, T.; Kells, W. A search for weak distortion of distant galaxy images by large-scale structure. Mon. Not. Roy. Astron. Soc. 1994, 271, 31–38. [Google Scholar] [CrossRef]
- Schneider, P.; van Waerbeke, L.; Jain, B.; Kruse, G. A new measure for cosmic shear. Mon. Not. Roy. Astron. Soc. 1998, 296, 873–892. [Google Scholar] [CrossRef]
- Van Waerbeke, L.; Mellier, Y.; Erben, T.; Cuillandre, J.C.; Bernardeau, F.; Maoli, R.; Bertin, E.; McCracken, H.J.; Le Fèvre, O.; Fort, B.; et al. Detection of correlated galaxy ellipticities from CFHT data: First evidence for gravitational lensing by large-scale structures. Astron. Astrophys. 2000, 358, 30–44. [Google Scholar]
- Bacon, D.J.; Refregier, A.R.; Ellis, R.S. Detection of weak gravitational lensing by large-scale structure. Mon. Not. Roy. Astron. Soc. 2000, 318, 625–640. [Google Scholar] [CrossRef]
- Wittman, D.M.; Tyson, J.A.; Kirkman, D.; Dell’Antonio, I.; Bernstein, G. Detection of weak gravitational lensing distortions of distant galaxies by cosmic dark matter at large scales. Nature 2000, 405, 143–148. [Google Scholar] [CrossRef] [PubMed]
- Kaiser, N.; Wilson, G.; Luppino, G. Large-Scale Cosmic Shear Measurements. 2000; arXiv:astro-ph/0003338. [Google Scholar]
- Hetterscheidt, M.; Simon, P.; Schirmer, M.; Hildebrandt, H.; Schrabback, T.; Erben, T.; Schneider, P. GaBoDS: The Garching-Bonn deep survey. VII. Cosmic shear analysis. Astron. Astrophys. 2007, 468, 859–876. [Google Scholar] [CrossRef]
- Fu, L.; Semboloni, E.; Hoekstra, H.; Kilbinger, M.; van Waerbeke, L.; Tereno, I.; Mellier, Y.; Heymans, C.; Coupon, J.; Benabed, K.; et al. Very weak lensing in the CFHTLS wide: Cosmology from cosmic shear in the linear regime. Astron. Astrophys. 2008, 479, 9–25. [Google Scholar] [CrossRef]
- Erben, T.; Hildebrandt, H.; Miller, L.; van Waerbeke, L.; Heymans, C.; Hoekstra, H.; Kitching, T.D.; Mellier, Y.; Benjamin, J.; Blake, C.; et al. CFHTLenS: The Canada-France-Hawaii Telescope Lensing Survey—Imaging data and catalogue products. Mon. Not. Roy. Astron. Soc. 2013, 433, 2545–2563. [Google Scholar] [CrossRef]
- Miller, L.; Heymans, C.; Kitching, T.D.; van Waerbeke, L.; Erben, T.; Hildebrandt, H.; Hoekstra, H.; Mellier, Y.; Rowe, B.T.P.; Coupon, J.; et al. Bayesian galaxy shape measurement for weak lensing surveys—III. Application to the Canada-France-Hawaii Telescope Lensing Survey. Mon. Not. Roy. Astron. Soc. 2013, 429, 2858–2880. [Google Scholar] [CrossRef]
- Benjamin, J.; Van Waerbeke, L.; Heymans, C.; Kilbinger, M.; Erben, T.; Hildebrandt, H.; Hoekstra, H.; Kitching, T.D.; Mellier, Y.; Miller, L.; et al. CFHTLenS tomographic weak lensing: quantifying accurate redshift distributions. Mon. Not. Roy. Astron. Soc. 2013, 431, 1547–1564. [Google Scholar] [CrossRef]
- Heymans, C.; Van Waerbeke, L.; Miller, L.; Erben, T.; Hildebrandt, H.; Hoekstra, H.; Kitching, T.D.; Mellier, Y.; Simon, P.; Bonnett, C.; et al. CFHTLenS: the Canada-France-Hawaii Telescope Lensing Survey. Mon. Not. Roy. Astron. Soc. 2012, 427, 146–166. [Google Scholar] [CrossRef]
- Simpson, F.; Heymans, C.; Parkinson, D.; Blake, C.; Kilbinger, M.; Benjamin, J.; Erben, T.; Hildebrandt, H.; Hoekstra, H.; Kitching, T.D.; et al. CFHTLenS: Testing the laws of gravity with tomographic weak lensing and redshift-space distortions. Mon. Not. Roy. Astron. Soc. 2012, 429, 2249–2263. [Google Scholar] [CrossRef]
- Dossett, J.N.; Ishak, M.; Parkinson, D.; Davis, T.M. Constraints and tensions in testing general relativity from Planck and CFHTLenS data including intrinsic alignment systematics. Phys. Rev. D 2015, 92, 023003. [Google Scholar] [CrossRef]
- Harnois-Déraps, J.; Munshi, D.; Valageas, P.; van Waerbeke, L.; Brax, P.; Coles, P.; Rizzo, L. Testing modified gravity with cosmic shear. Mon. Not. Roy. Astron. Soc. 2015, 454, 2722–2735. [Google Scholar] [CrossRef]
- Munshi, D.; Valageas, P.; Van Waerbeke, L.; Heavens, A. Cosmology with Weak Lensing Surveys. Phys. Rep. 2008, 462, 67–121. [Google Scholar] [CrossRef] [Green Version]
- Kilbinger, M. Cosmology with cosmic shear observations: A review. Rep. Prog. Phys. 2015, 78, 086901. [Google Scholar] [CrossRef] [PubMed]
- Ma, C.P.; Bertschinger, E. Cosmological Perturbation Theory in the Synchronous and Conformal Newtonian Gauges. Astrophys. J. 1995, 455, 7. [Google Scholar] [CrossRef] [Green Version]
- Baker, T.; Ferreira, P.G.; Skordis, C.; Zuntz, J. Towards a fully consistent parameterization of modified gravity. J. Cosmol. Astropart. Phys. 2012, 6, 32. [Google Scholar]
- Bertschinger, E. On the Growth of Perturbations as a Test of Dark Energy and Gravity. Astrophys. J. 2006, 648, 797–806. [Google Scholar] [CrossRef]
- Caldwell, R.; Cooray, A.; Melchiorri, A. Constraints on a new post-general relativity cosmological parameter. Phys. Rev. D 2007, 76, 023507. [Google Scholar] [CrossRef]
- Hu, W.; Sawicki, I. Parametrized post-Friedmann framework for modified gravity. Phys. Rev. D 2007, 76, 104043. [Google Scholar] [CrossRef]
- Amendola, L.; Kunz, M.; Sapone, D. Measuring the dark side (with weak lensing). J. Cosmol. Astropart. Phys. 2008, 4, 13. [Google Scholar] [CrossRef]
- Tereno, I.; Semboloni, E.; Schrabback, T. COSMOS weak-lensing constraints on modified gravity. Astron. Astrophys. 2011, 530, 68. [Google Scholar] [CrossRef]
- Schrabback, T.; Hartlap, J.; Joachimi, B.; Kilbinger, M.; Simon, P. Evidence of the accelerated expansion of the Universe from weak lensing tomography with COSMOS. Astron. Astrophys. 2010, 516, 63. [Google Scholar] [CrossRef]
- Hu, W. Power Spectrum Tomography with Weak Lensing. Astrophys. J. Lett. 1999, 522, L21–L24. [Google Scholar] [CrossRef]
- Daniel, S.F.; Linder, E.V.; Smith, T.L.; Caldwell, R.R.; Cooray, A.; Leauthaud, A.; Lombriser, L. Testing general relativity with current cosmological data. Phys. Rev. D 2010, 81, 123508. [Google Scholar] [CrossRef]
- Linder, E.V. Cosmic growth history and expansion history. Phys. Rev. D 2005, 72, 043529. [Google Scholar] [CrossRef]
- Linder, E.V.; Cahn, R.N. Parameterized beyond-Einstein growth. Astropart. Phys. 2007, 28, 481–488. [Google Scholar] [CrossRef]
- Lewis, A.; Bridle, S. Cosmological parameters from CMB and other data: A Monte Carlo approach. Phys. Rev. D 2002, 66, 103511. [Google Scholar] [CrossRef]
- Komatsu, E.; Smith, K.M.; Dunkley, J.; Bennett, C.L.; Gold, B.; Hinshaw, G.; Jarosik, N.; Larson, D.; Nolta, M.R.; Page, L.; et al. Seven-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Interpretation. Astrophys. J. Suppl. 2011, 192, 18. [Google Scholar] [CrossRef]
- Eisenstein, D.; Hu, W. Baryonic Features in the Matter Transfer Function. Astrophys. J. 1998, 496, 605–614. [Google Scholar] [CrossRef]
- Smith, R.E.; Peacock, J.A.; Jenkins, A.; White, S.D.M.; Frenk, C.S.; Pearce, F.R.; Thomas, P.A.; Efstathiou, G.; Couchman, H.M.P. Stable clustering, the halo model and non-linear cosmological power spectra. Mon. Not. Roy. Astron. Soc. 2003, 341, 1311–1332. [Google Scholar] [CrossRef] [Green Version]
- Valageas, P.; Nishimichi, T.; Taruya, A. Matter power spectrum from a Lagrangian-space regularization of perturbation theory. Phys. Rev. D 2013, 87, 083522. [Google Scholar] [CrossRef]
- Leonard, C.D.; Baker, T.; Ferreira, P.G. Exploring degeneracies in modified gravity with weak lensing. Phys. Rev. D 2015, 91, 083504. [Google Scholar] [CrossRef]
- Takahashi, R.; Sato, M.; Nishimichi, T.; Taruya, A.; Oguri, M. Revising the Halofit Model for the Nonlinear Matter Power Spectrum. Astrophys. J. 2012, 761, 152–162. [Google Scholar] [CrossRef]
- Heitmann, K.; Lawrence, E.; Kwan, J.; Habib, S.; Higdon, D. The Coyote Universe Extended: Precision Emulation of the Matter Power Spectrum. Astrophys. J. 2014, 780, 111–129. [Google Scholar] [CrossRef]
- Zhao, G.B.; Pogosian, L.; Silvestri, A.; Zylberberg, J. Cosmological Tests of General Relativity with Future Tomographic Surveys. Phys. Rev. Lett. 2009, 103, 241301. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, F. Weak lensing probes of modified gravity. Phys. Rev. D 2008, 78, 043002. [Google Scholar] [CrossRef]
- Zhang, P.; Liguori, M.; Bean, R.; Dodelson, S. Probing gravity at cosmological scales by measurements which test the relationship between gravitational lensing and matter overdensity. Phys. Rev. Lett. 2007, 99, 141302. [Google Scholar] [CrossRef] [PubMed]
- Leonard, C.D.; Ferreira, P.G.; Heymans, C. Testing gravity with EG: Mapping theory onto observations. 2015; arXiv:1510.04287. [Google Scholar]
- Reyes, R.; Mandelbaum, R.; Seljak, U.; Baldauf, T.; Gunn, J.E.; Lombriser, L.; Smith, R.E. Confirmation of general relativity on large scales from weak lensing and galaxy velocities. Nature 2010, 464, 256–258. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kalus, B.; Schwarz, D. J.; Seikel, M.; Wiegand, A. Constraints on anisotropic cosmic expansion from supernova. Astron. Astrophys. 2013, 553, A56. [Google Scholar] [CrossRef]
- Wotjak, R.; Knebe, A.; Watson, W.A.; Iliev, I.T.; Heß, S.; Rapetti, D.; Yepes, G.; Gottlöber, S. Cosmic Variance of the Local Hubble Flow in Large-Scale Cosmological Simulations. Mon. Not. Roy. Astron. Soc. 2014, 438, 1805. [Google Scholar]
- Bengaly, C.A.P.; Bernui, A.; Alcaniz, J.S. Probing cosmological isotropy with Type Ia Supernova. Astrophys. J. 2015, 808, 39. [Google Scholar] [CrossRef]
- Cooray, A.; Holz, D.E.; Caldwell, R. Measuring Dark Energy Spatial Inhomogeneity with Supernova Data. J. Cosmol. Astropart. Phys. 2010, 11, 15. [Google Scholar] [CrossRef]
- Valkenburg, W.; Marra, V.; Clarkson, C. Testing the Copernican principle by constraining spatial homogeneity. Mon. Not. Roy. Astron. Soc. 2014, 438, 6. [Google Scholar] [CrossRef]
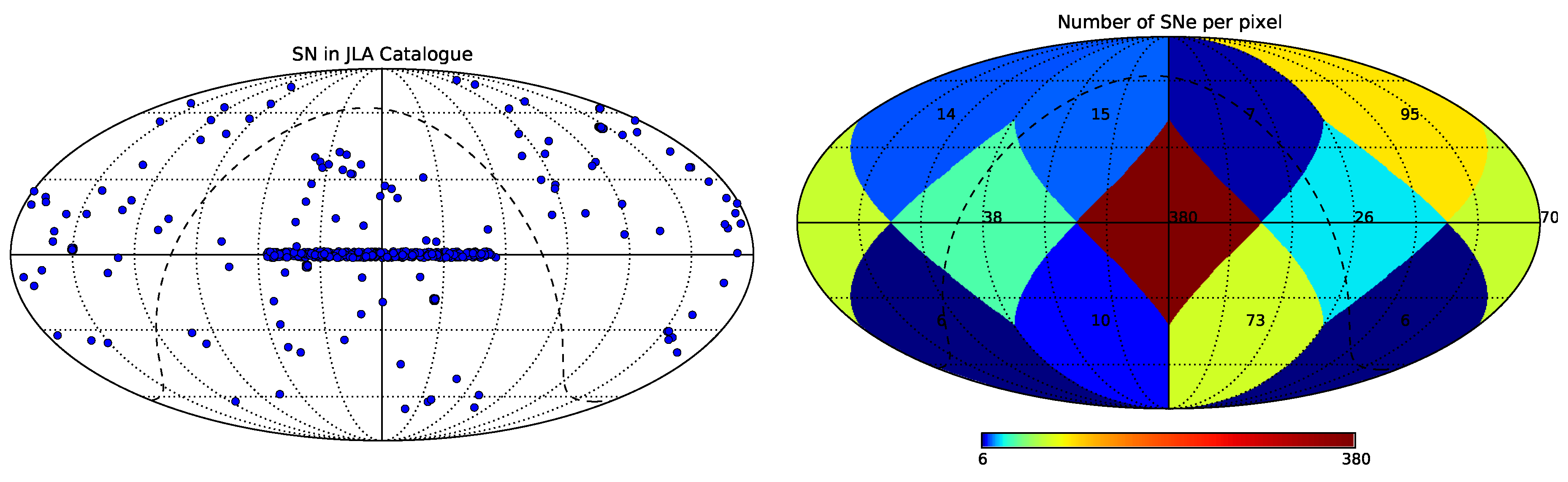
- Betoule, M.; Kessler, R.; Guy, J.; Mosher, J.; Hardin, D.; Biswas, R.; Astier, P.; El-Hage, P.; Konig, M.; Kuhlmann, S.; et al. Improved Cosmological Constraints from a Joint Analysis of the SDSS–II and SNLS Supernova Samples. Astron. Astrophys. 2014, 568, 32. [Google Scholar] [CrossRef] [Green Version]
- Górski, K.M.; Hivon, E.; Banday, A.J.; Wandelt, B.D.; Hansen, F.K.; Reinecke, M.; Bartelmann, M. HEALPix: A Framework for High-Resolution Discretization and Fast Analysis of Data Distributed on the Sphere. Astrophys. J. 2005, 622, 759. [Google Scholar] [CrossRef]
- Räsänen, S. Accelerated Expansion from Structure Formation. J. Cosmol. Astropart. Phys. 2006, 11, 3. [Google Scholar] [CrossRef]
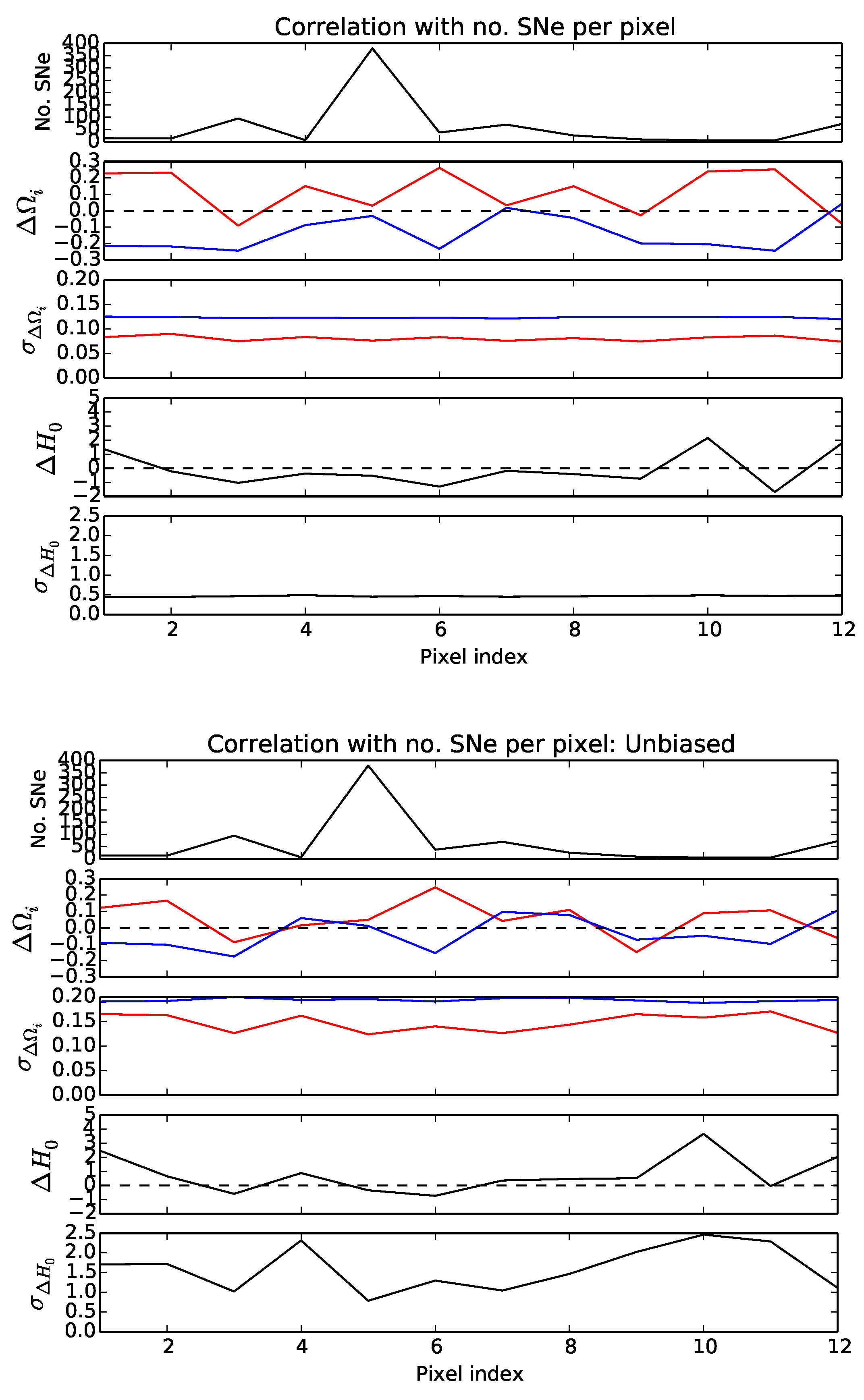
- Carvalho, C.S.; Basilakos, S. Angular distribution of cosmological parameters as a probe of inhomogeneities: A kinematic parametrisation. 2016; arXiv:1603.07519 [astro-ph.CO]. [Google Scholar]
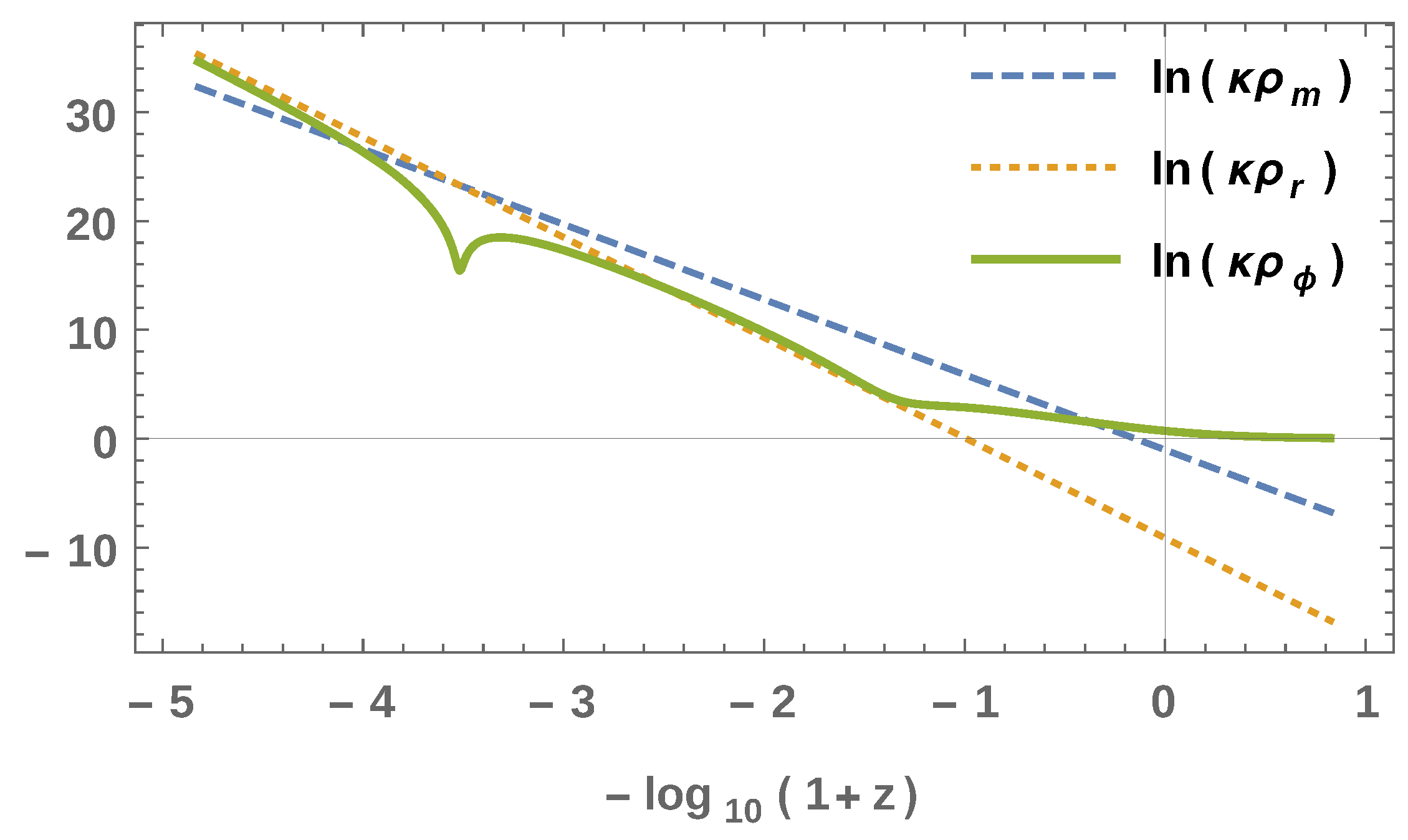

© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Avelino, P.; Barreiro, T.; Carvalho, C.S.; Da Silva, A.; Lobo, F.S.N.; Martín-Moruno, P.; Mimoso, J.P.; Nunes, N.J.; Rubiera-García, D.; Sáez-Gómez, D.; et al. Unveiling the Dynamics of the Universe. Symmetry 2016, 8, 70. https://doi.org/10.3390/sym8080070
Avelino P, Barreiro T, Carvalho CS, Da Silva A, Lobo FSN, Martín-Moruno P, Mimoso JP, Nunes NJ, Rubiera-García D, Sáez-Gómez D, et al. Unveiling the Dynamics of the Universe. Symmetry. 2016; 8(8):70. https://doi.org/10.3390/sym8080070
Chicago/Turabian StyleAvelino, Pedro, Tiago Barreiro, C. Sofia Carvalho, Antonio Da Silva, Francisco S.N. Lobo, Prado Martín-Moruno, José Pedro Mimoso, Nelson J. Nunes, Diego Rubiera-García, Diego Sáez-Gómez, and et al. 2016. "Unveiling the Dynamics of the Universe" Symmetry 8, no. 8: 70. https://doi.org/10.3390/sym8080070
APA StyleAvelino, P., Barreiro, T., Carvalho, C. S., Da Silva, A., Lobo, F. S. N., Martín-Moruno, P., Mimoso, J. P., Nunes, N. J., Rubiera-García, D., Sáez-Gómez, D., Sousa, L., Tereno, I., & Trindade, A. (2016). Unveiling the Dynamics of the Universe. Symmetry, 8(8), 70. https://doi.org/10.3390/sym8080070









