Abstract
The goal of image steganographic methods considers three main key issues: high embedding capacity, good visual symmetry/quality, and security. In this paper, a hybrid data hiding method combining the right-most digit replacement (RMDR) with an adaptive least significant bit (ALSB) is proposed to provide not only high embedding capacity but also maintain a good visual symmetry. The cover-image is divided into lower texture (symmetry patterns) and higher texture (asymmetry patterns) areas and these textures determine the selection of RMDR and ALSB methods, respectively, according to pixel symmetry. This paper has three major contributions. First, the proposed hybrid method enhanced the embedding capacity due to efficient ALSB utilization in the higher texture areas of cover images. Second, the proposed hybrid method maintains the high visual quality because RMDR has the closest selection process to generate the symmetry between stego and cover pixels. Finally, the proposed hybrid method is secure against statistical regular or singular (RS) steganalysis and pixel difference histogram steganalysis because RMDR is capable of evading the risk of RS detection attacks due to pixel digits replacement instead of bits. Extensive experimental tests (over 1500+ cover images) are conducted with recent least significant bit (LSB)-based hybrid methods and it is demonstrated that the proposed hybrid method has a high embedding capacity (800,019 bits) while maintaining good visual symmetry (39.00% peak signal-to-noise ratio (PSNR)).
1. Introduction
Internet evolution has led to the rapid transmission of digital content such as images, audio, text, and videos. Meanwhile, advancement of forgery tools and applications means that digital content can easily be altered, copied, and destroyed during transmission. In order to secure the transmission of data and prevent its manipulation, a security system provides two main disciplines: information encryption and information hiding (see Figure 1). Information encryption, or cryptography, is a process of transforming the data using a crypto-key so it becomes unintelligent. There are different client/server architectures [1,2] based applications employed the encryption algorithms to secure its data during transmission. On the other hand, information hiding is the art and science of hiding secret data such that its presence cannot be detected [3]. Information hiding can be further classified into watermarking and steganography (see Figure 1). Watermarking protects intellectual copyright and guarantees the integrity of transmitted data. In general, watermarking is useful for small sizes of information such as a company’s logo or author’s tags [3]. Steganography is the art of using the communication medium in such a way that it conceals the existence of secret data [3,4]. The communication medium can be image, text, audio, or video.
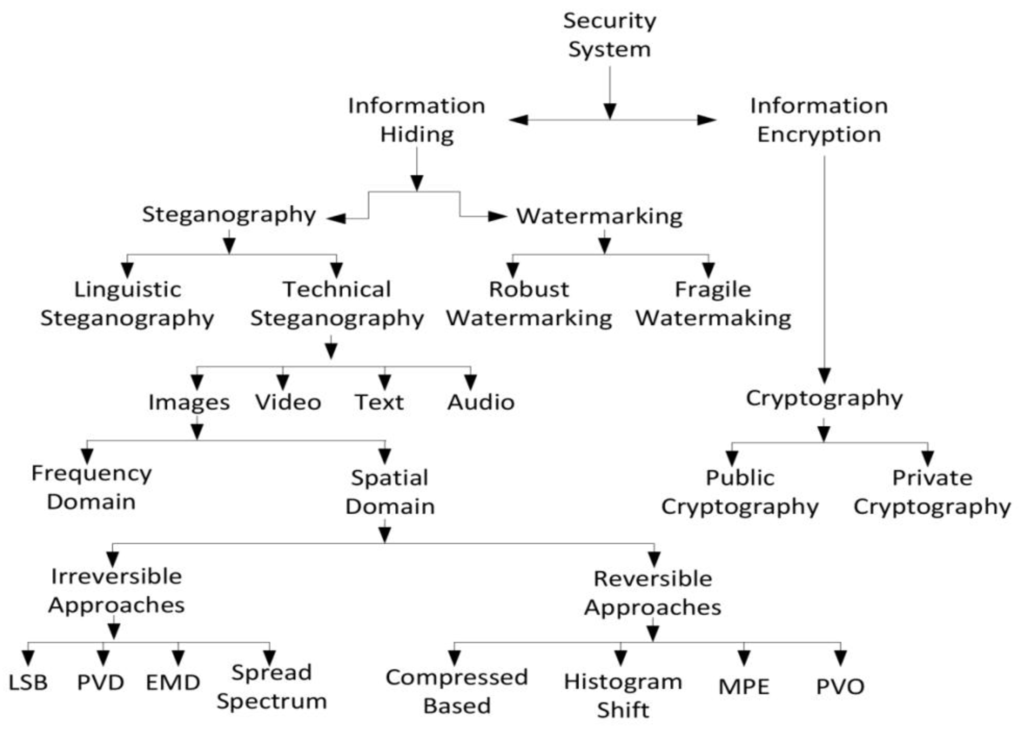
Figure 1.
General classification of information hiding systems.
Generally, the image steganographic method is evaluated by three key perspectives: capacity (the maximum payload that could be embedded into the cover-image), visual symmetry (the stego-image should be perceptually identical to its cover-image), and security (the stego-image must be resistant to steganalysis detection attacks). Hence, the ideal steganographic method should be simultaneously capable of high capacity, good visual symmetry, and undetectability. Most often, high payload steganographic methods introduce the distortion artifacts in stego-images and are vulnerable to steganalysis. Moreover, good visual quality steganographic methods suffer from the low payload. How to simultaneously achieve high capacity, visual symmetry, and security is a challenging research problem due to the contradictions between them.
Numerous image steganography methods are available in the literature. These methods are categorized into two major divisions, spatial and frequency domains. In the spatial domain, the secret data is embedded directly by modifying the pixel intensities, whereby, in the frequency domain, the information is embedded into the transformed coefficient of cover images. The frequency domain methods are more robust against detection attacks as compared to the spatial domain, but they have low payloads and are computationally expensive [5]. Conversely, the high payload, good visual quality, and low computational cost of the spatial domain make it useful for image steganography, so the proposed work carried out in this paper is based on the spatial domain.
Recently, data embedding applications have divided steganographic methods into reversible and irreversible approaches. The reversible steganographic methods reconstruct the original image after extracting the secret message from the stego-images. Such embedding approaches suffer from low payload as compared to irreversible methods. To increase the embedding capacity of reversible approaches, data compression methods are applied to the secret message before the embedding process [6,7]. In contrast, irreversible steganography attempts to achieve a high embedding payload and good visual symmetry without giving much attention to recovering the cover-image during the extraction process.
The fundamental and common irreversible image steganographic method is least significant bit (LSB) substitution [8]. It replaces bits of pixels to hide the secret data. In LSB-based methods, the payload is dependent on the utilization of least bit substitution; it directly affects the visual quality of stego-images. Optimal pixel adjustment process (OPAP) [9] was applied to LSB-based pixels to improve the visual quality of stego-image. Although LSB-based methods are efficient, due to asymmetry structures they can easily be exposed by statistical steganalysis detection attacks [10,11,12]. On the other hand, LSB matching (LSBM), also known as ±1 embedding, can solve or avoid the asymmetric structure of the LSB replacement method. Generally, in LSBM, if the secret bit does not match the LSB of the cover pixel, then a random ±1 is added to the cover pixel value. However, LSB matching does not lead to the asymmetric changes in the pixels. Consequently, it is more difficult to detect LSB matching than LSB replacement [12]. Furthermore, LSBM-based methods can be utilized to achieve n bpp secret data embedding [13].
With respect to undetectability, generally, modern steganographic methods prioritize high security instead of high payload or visual quality of stego-images. Therefore, the state-of-the-art highly undetectable stego (HUGO) [14] method is proposed based on the LSB matching algorithm. It consists of a high dimensional image model to calculate the distortions corresponding to a modification of each pixel by ±1, but can only hide up to 1 bpp. Similarly, wavelet obtained weights (WOW) [15], spatial universal wavelet relative distortion (S-UNIWARD) [16], HIgh Low Low (HILL) [17], and minimizing the power of optimal detector (MiPOD) [18] are targeted as highly secure steganographic methods with limited payload.
On the other hand, classical steganographic methods provide higher payload, usually more than 1 bpp. Wu and Tsai proposed a pixel value difference (PVD) method that embeds the secret data by readjusting the difference between two consecutive pixels and has a good visual symmetry [19]. In the literature, PVD-based methods considered different directions of pixels’ differences, along with human vision system (HVS) smoothness and edginess sensitivity, to determine the number of secret bits for embedding [20,21]. In general, PVD-based methods improved the visual quality; however, the difference histogram of stego-images deviated from the cover-image and was vulnerable to histogram analysis. Zhang and Wang introduced an exploiting modification direction (EMD) for data hiding, where n number of pixels were utilized to hide the (2n + 1) base secret digits [22]. Furthermore, different EMD-based methods [23,24,25,26] were proposed to improve the visual quality but suffered from low payload.
Researchers have also combined different singular steganographic techniques into hybrid data embedding methods. Generally, hybrid embedding methods utilized the advantages of existing singular steganographic approaches; for example, high payload of LSB and good imperceptibility of PVD methods are employed in [27,28,29,30,31]. Furthermore, the hybrid steganographic methods are more secure, because many steganalysis detection attacks are specifically designed to target a singular steganography method [10,11,12,32]. Thus hybrid embedding approaches generally confuse the statistical steganalysis methods used to detect the stego-images [33].
Wu et al. [27] proposed a hybrid embedding method based on LSB and PVD approaches. It divided the cover-image into edginess and smoothness levels; further, the LSB and PVD methods were applied on smooth and edge areas, respectively. Regardless of the fact that this method improved the payload and visual quality, it failed to resist RS-analysis detection attacks [10]. In [29,31], Jung proposed methods to combine LSB with multi-pixel differencing and PVD with modulus function. These methods improved hidden capacity and retained acceptable visual quality but suffered from low security. Yang et al. [34] enhanced Wu et al.’s [27] method by introducing a lower level readjustment strategy. This method improved visual quality and undetectability against RS detection attacks. However, the limitation of this method is that the pixel difference showed asymmetrical curves in the histogram. To obtain high payload and good visual quality, Khodaei et al. [28] combined the k-bit LSB with the PVD method. This method divided the pixels into three non-overlapping pixel blocks. The k-bit LSB method was applied to the base/center pixel and PVD was applied to the other two pixels of the block. Tsai et al. [30] enhanced the Khodaei et al. [28] method by introducing an adaptive m × n pixel blocks for selection of edge regions in the cover-image to increase the payload. However, this method reduced the visual quality of the stego-image. To obtain good visual quality and high payload, Hsiao Shan [35] proposed a multi-way PVD method by combining the tri-way PVD and mode selection process, while this combination improved the visual quality but has low payload as compared to [28]. Shen et al. suggested a reversible data embedding method by combining the PVD with modulus function for color images, thus having a low payload [36]. Moreover, Shen et al. [26] proposed another method with high capacity and good visual imperceptibility compared to that of Zhang and Wang [22]. This method combined the PVD and EMD methods and suffers from low payload as compared with the latest hybrid embedding methods [25,27,28,29,34]. Recently, Wu et al. [25] proposed a hybrid method for high payload and good visual quality by combining LSB, EMD, and modification of prediction errors (MPE) methods. This method provided two adaptive solutions for steganographic applications; the first solution targeted the good visual quality and the second solution is high hidden capacity. As we observed through experiments, Wu et al. [25] obtained a lower payload as compared with existing hybrid methods. Furthermore, this method is exposed by pixel difference histogram analysis (see Section 3.5).
It is observed that the aforementioned hybrid methods provide good payload and acceptable visual quality [37] in stego-images. However, all of the aforementioned methods can easily be exposed to state-of-the-art ensemble-based subtractive pixel adjacency matrix (SPAM) steganalysis methods [38]. This indicates that these methods are more concerned with the payload and visual quality than they are with undetectability. This is in spite of the fact that some of them are unable to provide a competent payload [25,27,28,29,31,34,35], and do not fully utilize the advantages of singular steganographic methods [25,27,28,29,34]. Furthermore, existing hybrid methods are unable to achieve simultaneous high payload, good visual quality, and undetectability (at least lower bpp) in one steganographic solution.
Motivated by the above facts, our main goal is to propose a hybrid steganographic method, which provides a high embedding capacity while maintaining good visual symmetry and structural undetectability against RS and difference histogram steganalysis. The paper contributions are as follows. First, we propose a novel singular steganographic right-most digit replacement (RMDR) method to provide 3 bpp for lower texture areas with improved visual quality. Second, we utilize the adaptive k-bit LSB OPAP [9] as an adaptive least significant bit (ALSB) method to improve hidden capacity for higher texture areas. Furthermore, we combine ALSB with RMDR into one steganographic approach to create a hybrid method that maintains the advantages of both (high payload and good visual quality).
The organization of the paper is as follows. This section discussed related work on LSB-based hybrid steganographic approaches. Section 2 proposes a hybrid steganographic method, with details of embedding and extraction procedures. In Section 3, detailed experimental results are presented and discussed. Conclusions and future directions are presented in Section 4.
2. Proposed Hybrid Data Embedding Method
In this section, we present a hybrid data embedding scheme. This hybrid method is based on two steganographic approaches, RMDR and ALSB [9]. RMDR is a novel proposed method for high visual quality and undetectability, while ALSB [9] is utilized to achieve high payload. In proposed hybrid embedding, the selection of k-bit ALSB with RMDR is inspired by following methods [25,27,34].
In the proposed scheme, the cover-image is divided into two regions inspired by [27] i.e., region-1 and region-2 for lower and higher texture areas, respectively, as shown in Table 1. Further, these texture regions are categorized into four Rn difference ranges based on the width, where n = 4, e.g., R1 [0, 31] to R4 [128, 255]. On the other hand, the second row of Table 1 shows the pre-estimated number of secret bits for embedding in each pixel. For example, the R1 range exists under region-1 and 3-bits secret data are used to embed in each pixel. Furthermore, these ranges can be dynamically generated depending on the steganographic requirement. For experiments, we propose the following regions and ranges of Table 1, which meet the proposed method goals, i.e., high payload and acceptable visual quality.

Table 1.
Proposed hybrid embedding method range table divisions as region-1 and region-2 levels, where k denotes the least bits for embedding.
The complete description of the proposed RMDR embedding and hybrid embedding methods are presented in Section 2.1 and Section 2.2. In addition, both proposed extraction parts of the above RMDR and hybrid methods are presented in Section 2.3 and Section 2.4.
2.1. RMDR Embedding Method
In the RMDR embedding process, the right-most digit of a pixel value is utilized for embedding the secret data, so a decomposition of the pixel value is required to separate the pixel digits. For this reason, a pixel value is decomposed into three digit levels. For example, a pixel value [0, 255] and its proposed decomposition of digit levels are denoted as left digit (LD), middle digit (MD), and right digit (RD), as described in Equation (1), where LD range ∈ [0, 2], MD and RD ranges ∈ [0, 9]. For example, if = 243, its LD, MD, and RD decomposed values are 2, 4, and 3, respectively. If a pixel value consists of only one/two digit(s) then a leading zero(s) is added to occupy the LD or MD, such as = 4 where LD and MD are 0 and RD is 4.
In the embedding process, the three secret bits are converted into stegoRD from Table 2. Table 2 consists of three columns, namely b, SRD0(b) and SRD1(b), where b is a three-bit secret decimal data, and SRD0(b) and SRD1(b) are the stegoRDs (mapped RDs) against b. In our experiments, the generation of mapping table (Table 2) is as follows: the three-bit secret digit, 23 range is [0, 7], and a pixel RD range is [0, 9]. The pixel RD range has two extra digits as {8, 9} that can be reused with three-bit secret digits as replacing with {3, 4} digit value. These two extra digits aim at minimizing the difference between cover and stego-pixels RDs. Alternatively, it can be adaptively generated by considering the frequency of RDs in cover images.

Table 2.
StegoRD decimal digit values mapping table for the RMDR embedding method.
In the RMDR embedding method, two cover pixels (, ) considered as a block () are utilized to hide the secret data. The six secret bits are divided and converted into two three-bit decimals; their equivalent stegoRD ((b) and (b)) values are derived from Table 2. Furthermore, the best nearest stego-pixels values are calculated with their stegoRDs. Finally, the resultant stego-block difference must exist in region-1 of Table 1. The detailed embedding steps with examples are described in Scheme 1.
Scheme 1.
Proposed RMDR embedding steps.
The above RMDR embedding method provides the embedding capacity of 3 bits per pixel (bpp), and its closest stego-pixel selection process provides good visual quality around the +38 dB peak signal-to-noise ratio (PSNR) of a stego-image. Furthermore, RMDR has the advantage of resisting RS-steganalysis detection attacks due to its digit replacement characteristics, as shown in Section 3.4.
2.2. Hybrid Embedding Method
The proposed hybrid embedding method concurrently utilized the digits and bits characteristics of pixels values to hide the secret data that confuse the statistical structural steganalysis methods. The proposed hybrid method partitioned the cover-image into two non-overlapping consecutive (horizontal) pixel blocks i.e., ). The pixel difference ) of each block is used to determine the region level of the block, as shown in Table 1. Furthermore, the pixel difference blocks belonging to region-1 and region-2 are employed by the RMDR (Section 2.1) and k-bit ALSB [9] embedding methods, respectively. However, from the experimental results, we found that some stego-blocks of region-2 can be switched to region-1 during the ALSB [9] embedding process. Therefore, the proposed method failed to recover 100% of the secret bits through the extraction process. For example, () = (146, 178) and secret bits are (1010 0010), where its difference d = |32|, belongs to region-2 of Table 1. Therefore, the ALSB embedding and extraction process would be applied to hide and recover the secret bits. So, after applying ALSB embedding, the stego-block values are () = (154, 178), and its new difference = |24|, where this stego-block loses its region consistency from region-2 to region-1 of Table 1. Therefore, the ALSB-based block of region-2 would be considered as the RMDR region-1 based block during the extraction process and the secret data would not be recovered with 100% accuracy. Hence, a readjustment process as in Equation (4) is applied on the ALSB-based stego-block () when a region inconsistency problem occurs. This readjustment process computes the new stego-block () while maintaining the region’s consistency and secret data. After applying Equation (4), the new = |40| of the resultant stego-block () = (138, 178) belongs to region-2 of Table 1, and 100% of the secret data can be recovered during the extraction process. Furthermore, the complete embedding steps are illustrated in Scheme 2.
where and pixels are computed as
Scheme 2.
Proposed hybrid embedding steps.
2.3. RMDR Extracting Method
The RMDR extracting method required the two stego-pixels as and of block(i) from stego-image (S) and Table 3 for extraction of stegoRDs. This extraction method extracts the RDs (i.e., and ) of and and finds its equivalent values from Table 3. Furthermore, the transformation and concatenation processes are applied on the extracted RDs. The RDMR extraction steps and its examples are given in Scheme 3.

Table 3.
RMDR extraction table for StegoRDs.
Scheme 3.
Proposed RMDR extraction steps.
2.4. Hybrid Extraction Method
The hybrid extraction process required the stego-image as input and range table division as listed in Table 1. Similar to the embedding process, the stego-image S is partitioned into two consecutive non-overlapped pixel blocks, i.e., ). If the difference of each block value ) exists in the region-1 level (Table 1), RMDR extraction (Section 2.3) is applied; otherwise, the k-bit ALSB OPAP [9] extraction method is employed. The extraction steps are given in Scheme 4.
Scheme 4.
Proposed hybrid extraction steps.
3. Experimental Results and Discussion
In this experimental section, the proposed hybrid method was implemented in MATLAB and tested on two well-known and standard image datasets. First, the proposed method was tested with the uncompressed color image database (UCID) [39], which consists of 1338 images with resolutions of 512 × 384 and 384 × 512. Furthermore, these RGB color images are converted into gray scale before testing. Second, we utilized the USC-SIPI [40] standard eight-bit (512 × 512, 256 × 256, and 1024 × 1024) test images, i.e., Lena, Baboon, Pepper, Jet, Barbara, Zelda, Tiffany, and Elaine, as shown in Figure 2. The secret data were generated by a pseudo-random numbers generator. In the experiments, the same experimental procedure (fixed k = 4) is applied to our proposed method and other hybrid methods [19,25,27,28,34]. The performance comparisons are evaluated based on measuring the embedding capacity, PSNR, bpp, universal quality index (Q), and security by RS-analysis, pixel difference histogram analysis, and SPAM features under ensemble classifier steganalysis. Furthermore, these experimental results are analyzed and shown in Section 3.1, Section 3.2, Section 3.3, Section 3.4, Section 3.5 and Section 3.6.

Figure 2.
Images for experiments (a–h).
3.1. Embedding Capacity and Visual Quality Analysis
This section analyzes the performance of hidden capacity and visual quality of proposed and existing methods in three parts. First, we compared the proposed hybrid method with existing well-known steganographic methods (i.e., LSB, PVD [19,41]), as shown in Table 4. Secondly, the proposed method was compared with existing LSB-based hybrid methods (i.e., Wu et al. [27], Yang et al. [34], Jung et al. [29], Khodaei et al. [28] and Wu et al. [25]) in Table 5. Third, the performance of the proposed method and existing hybrid methods are measured with complete UCID [39] and USC-SIPI [40] image datasets, as shown in Table 6.

Table 4.
Performance comparison between the proposed hybrid embedding method and singular steganographic methods.

Table 5.
Performance comparison of existing hybrid LSB-based (PVD, EMD, and MPE) methods against the proposed method.

Table 6.
Performance comparison with UCID [39] and USC-SIPI [40] image datasets of proposed and existing hybrid methods.
The number of secret bits embedded into a stego-image is considered to be the embedding capacity. The highest value of embedding capacity indicates a good payload. For evaluating the visual imperceptibility of stego-images, PSNR and mean square error (MSE) were calculated as in Equation (5). H and W represent the height and width of the cover-image and represent cover and stego-pixels, respectively. The highest value of PSNR indicates the good visual quality of a stego-image with respect to its cover-image.
where .
The embedding capacity and PSNR performance statistics of proposed and singular steganographic methods are shown in Table 4 for eight stego-images. The results show that the average hidden capacity (800,109 bits) of the proposed method is higher than for 3-bit LSB, (Wu and Tsai [19]) PVD, and (Yang et al.’s [41]) adaptive LSB methods. The proposed method’s PSNR was slightly lower than that of Wu and Tsai’s method [19] but the hidden capacity of the proposed method is almost double that of Wu and Tsai’s [19] (see Table 4). Moreover, Wu and Tsai’s method [19] suffers from pixel histogram steganalysis [27].
From the experimental results, as shown in Table 5, the proposed method has the highest average hidden capacity and simultaneously has higher PSNR as compared with existing LSB-based hybrid methods. This is due to the combination of RMDR and adaptive LSB methods because RMDR produces the good visual quality of stego-image at 3 bpp while the adaptive LSB method ensures the highest payload up to 800,019 bits. Finally, the performance of payload and PSNR are compared for UCID [39] and USC-SIPI [40] image datasets, as shown in Table 6. The experimental results show that the proposed method’s average payload in UCID [39] (554,156 bits) and the USC-SIPI [40] (1,636,102 bits) database are higher than for the existing methods. Similarly, the proposed method, PSNR, in UCID [39] (38.88 dB) and USC-SIPI [40] (38.32 dB) are the highest among others. This indicates that the proposed method outperformed the existing hybrid embedding method in simultaneously achieving high payload and visual quality. This is due to the fact that the proposed method keeps both RMDR (good visual quality) and adaptive LSB (high payload) advantages intact to efficiently utilize lower and higher texture areas during embedding procedure.
Furthermore, Figure 3 illustrates the bit plane decomposition of cover and proposed stego-images. The bit plane results show that the stego-image is almost visually identical to its cover-image, and can resist the bit plane analysis. Similarly, in Figure 4, the visual distortion artifacts of proposed and recent hybrid methods are compared for the Lena image. It shows that the proposed method has less human perceivable differences than compared methods. This is due to the fact that the proposed method uses the RMDR closest pixels selection process, which computes the best stego-pixels against its cover pixels.

Figure 3.
Bit plane comparison of cover and stego-images. (a)--(d).

Figure 4.
Stego-images and its specific zoomed area of (a) 3-bit LSB; (b) Khodaei et al. [28]; (c) Wu et al. [25]; and (d) the proposed method.
3.2. Universal Quality Index Analysis
A universal quality index Q measures the visual quality of an image [42]. Let and be the cover-image and stego-image, respectively. The quality Q is computed as in Equation (6):
where
The range of Q is [−1, +1]. The value 1 represents the best quality when Y = Z, or the stego-image is identical to its cover-image. From Table 7, the proposed method shows the value of Q against existing (3-LSB, Yang et al. [34], Khodaei et al. [28], and Wu et al. [25]) methods. Moreover, the value Q of the proposed method is closer to 1. This shows that the proposed method has similar fidelity between the cover and stego-image against the compared methods.

Table 7.
Universal quality index (Q) of proposed and existing LSB-based methods by Wang and Bovik [42].
3.3. Embedding Capacity versus PSNR
The embedding capacity vs. the PSNR for the proposed and existing methods [25,27,28,34] are depicted in Figure 5a–d except for the similar results for the first four test images. In Figure 5a, the methods were tested on the Lena image. The respective PSNR values at 20,000 hidden bits are 53.78 dB, 55.96 dB, 63.98 dB, 54.80 dB, and 55.70 dB for Wu et al., Yang et al., Wu et al., Khodaei et al., and the proposed methods. The proposed method reached its maximum of 793,810 hidden bits when the PSNR was 39.19 dB while the other three methods reached their maximum of 791,443 bits with PSNR at 37.56 dB. The experiment on the Baboon image showed that the maximum hidden capacity and PSNR of Wu et al. [27] (717,749 bits, 35.30 dB), Yang et al. [34] (717,749 bits, 36.19 dB), Wu et al. [25] (603,894 bits, 35.10 dB), Khodaei et al. [28] (809,435 bits, 34.85 dB), and the proposed method had a maximum of 820,776 bits with 38.03 dB PSNR, as depicted in Figure 5b. The proposed method gained up to +103,525 hidden bits and +1.86 PSNR against Yang et al. [34]. For the Pepper image, the embedding capacity of the proposed method had a maximum of 792,384 bits at 39.34 dB PSNR, as shown in Figure 5c. The PSNR in the Jet image at 20,000 embedding bits recorded for Wu et al. [27] is 53.67 dB, for Yang et al. [34] is 55.83 dB, for Wu et al. [25] is 64.00 dB, for Khodaei et al. [28] is 53.80 dB, and for the proposed method is 55.62 dB. The proposed method had a maximum embedding capacity and PSNR around 795,728 bits with 39.18 dB PSNR.
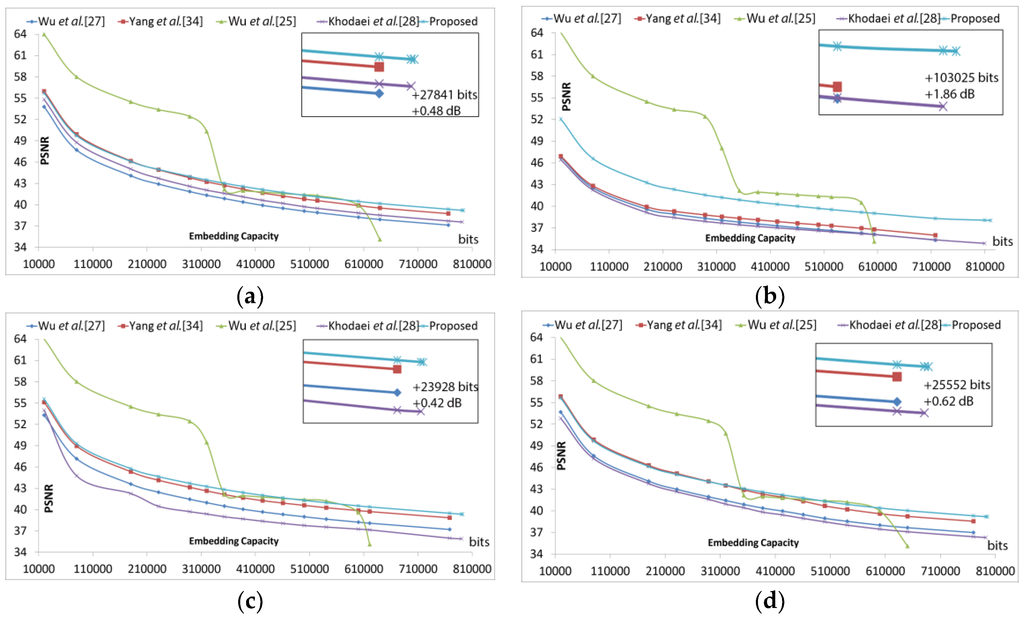
Figure 5.
Comparison graphs for various embedding capacities vs. PSNR: (a) Lena; (b) Baboon; (c) Pepper; (d) Jet.
Therefore, the graphs analysis in Figure 5 illustrates that the proposed method can achieve good and almost higher PSNR values without considering the different levels of embedding payload. It shows that the proposed method produces good visual symmetry irrespective of embedding payload. Among these test images, a prominent gain was achieved for the Baboon image. This shows that the proposed method is also suitable for both types of texture-based images and works better with higher texture images e.g., Baboon.
3.4. Security against Statistical RS-Steganalysis
The security of the proposed method against statistical RS-steganalysis [10] plays a significant role in detecting the hidden data inside the stego-images. In this section, the process of evaluating security against RS-analysis is divided into two parts. Firstly, RS-analysis is compared with the proposed RMDR and 3-bit LSB embedding approaches (see Figure 6). Secondly, RS-analysis is evaluated for the proposed hybrid approach (see Figure 7).
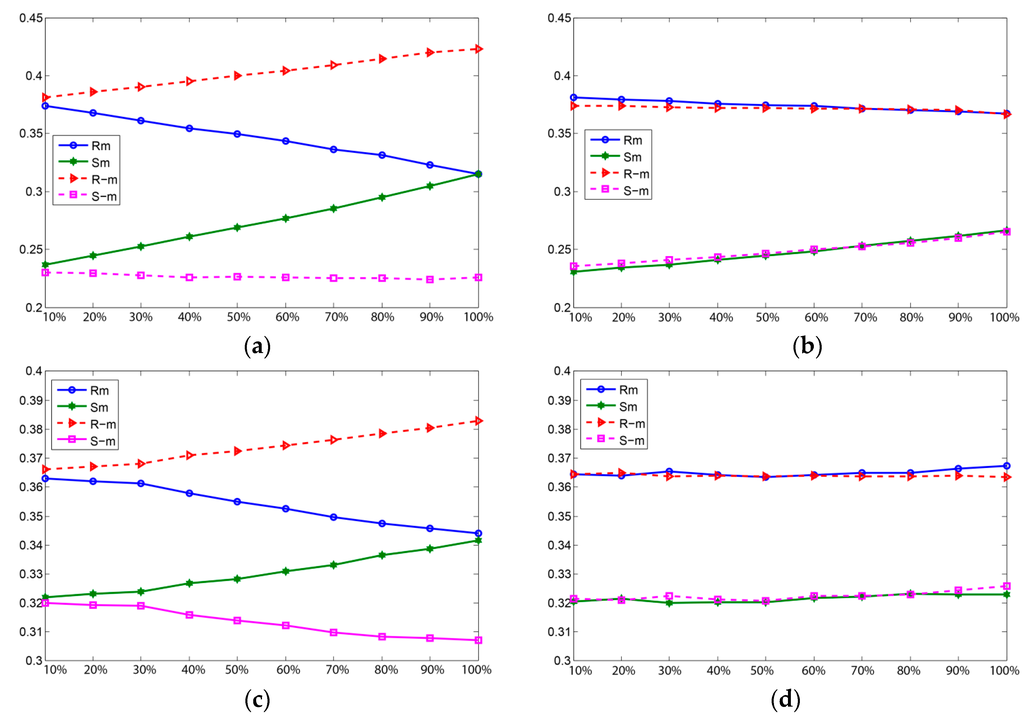
Figure 6.
RS-analysis graphs for 3-bit LSB vs. RMDR of stego-images. (a) Lena 3-bit LSB; (b) Lena RMDR; (c) Baboon 3-bit LSB; (d) Baboon RMDR.
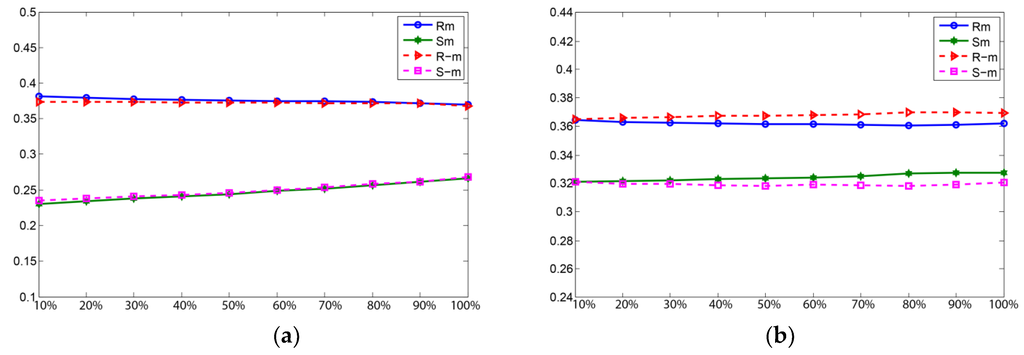
Figure 7.
RS-analysis graphs of Lena (a) and Baboon (b) images by the proposed method.
The RS-steganalysis method presents a discrimination function (DF) with flipping masks as M and –M, where M and –M are respectively. , , , and indicate the proportion of blocks, where the magnitude of DF increases or decreases on applying each block. If the parameters satisfies ≈ > ≈ , it indicates that there is no hidden data in the respective image. When an image has hidden data, and increases, whereas and decreases and exposed by RS-analysis.
The RS detection results can be seen in Figure 6a–d with 3-bit LSB and RMDR methods for the first two images, Lena and Baboon. In Figure 6a–d, the x-axis indicates the percentage of secret data inside the stego-image and the y-axis denotes the relative percentages of regular (, ) and singular (, ) groups when applying the above masks (M, −M). The comparison of RS-analysis between the RMDR and 3-bit LSB embedding methods is due to the similar embedding capacity of 3 bpp. The 3-bit LSB difference between the singular and regular groups increases with the addition of embedding capacity, as shown in Figure 6a,c. In the RMDR method, Figure 6b,d retained the closest differences in singular and regular groups up to 100% embedding capacity and proved the undetectability against RS-steganalysis of the RMDR method.
Figure 7a,b shows the RS detection analysis of the Lena and Baboon images with the proposed hybrid approach. In RS-analysis graphs, stego-images had both singular and regular parameters close to each other even with an increase in hidden data bits. This indicates that the proposed method has high security against statistical RS-analysis.
3.5. Pixel Difference Histogram Analysis
A pixel difference histogram is one of the potential steganalysis methods to expose the secret data of stego-images. The pixel difference histogram is computed by taking the differences of neighboring pixels with fall-off ranges between cover and stego-image. Figure 8 shows the pixel difference histograms of the Lena and Baboon stego-images using the Wu et al. method [25], the Khodaei et al. method [28], and the proposed method. In the case of Lena histogram (a), it is observed that the proposed stego-image histogram is well preserved against Wu et al. [25] and Khodaei et al. [28] methods. Similarly, for the Baboon stego-image comparison, Wu et al.’s method lost symmetry to keep its curves close to its cover-image difference histogram [25]. However, the proposed hybrid method provides more security by keeping the pixel difference histogram closer to the cover-image; it did not generate any noticeable artifacts under pixel difference histogram steganalysis detection attacks.
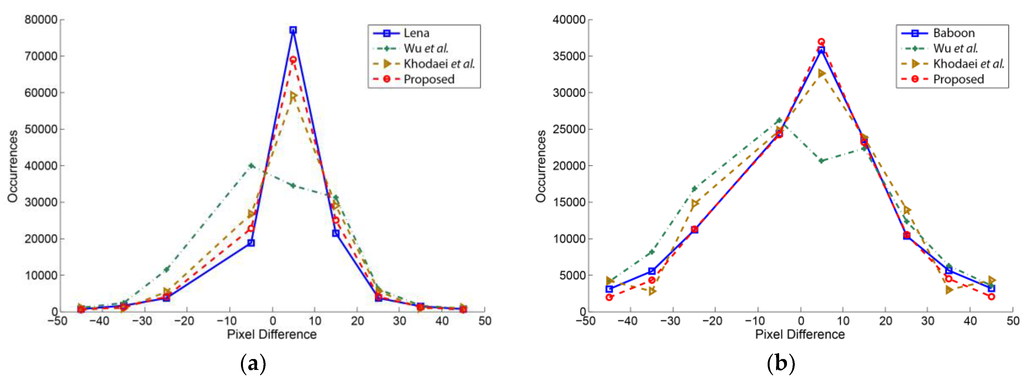
Figure 8.
Pixel difference histograms of cover and stego-images of the proposed method compared to the methods of Wu et al. [25] and Khodaei et al. [28] (a,b).
3.6. Undetectability under SPAM Analysis Using Ensemble Classifier
In this section, we analyzed the proposed method using an ensemble classifier with state-of-the-art modern steganalysis SPAM-based features [43]. The second order SPAM 686 feature set steganalyzer is very effective at detecting stego-images. In our experiment, the ensemble classifier and SPAM features are obtained from [38]. These features are evaluated on both UCID [39] and USC-SIPI [40] image datasets, where 500 cover and 500 stego-images are used for training and the rest are used for testing. For an undetectability comparison, the proposed method and two state-of-the-art LSB matching methods known as ±1 embedding and HUGO [14] are employed, as shown in Table 8. Table 8 consists of columns, namely bit rate as bits per pixel (bpp), true positive, false positive, true negative, false negative, and finally the detection error rate of the steganalysis method. To evaluate the performance, the higher classification error rate indicates the higher undetectability of a steganography approach.

Table 8.
Undetectabilityperformance under SPAM steganalysis with ensemble classifier for the proposed method as compared with the LSB matching and HUGO embedding methods.
As from Table 8, when the payload is 0.2 bpp, the proposed method has a higher error rate of 52.10%, while the LSBM (±1) and HUGO [14] had 25.30% and 51.80%, respectively. Generally, Table 8 shows that the proposed method has a higher detectability error rate than LSBM (±1) embedding method. Our method has a higher detectability error rate because the proposed method required fewer pixels to embed secret bits than the LSBM (±1) method. Suppose, in the worst case of LSBM (±1) embedding, it took (512 × 512) = (262,144) pixels to embed 262,144 secret bits. In the case of the proposed method, 85,948 pixels would be required to embed 262,144 bits due to the 3.05 bpp average embedding rate. So, the rest of the pixels in the proposed method would be unmodified, which would create less distortion from the artifacts’ impact on the stego-image during feature extraction. In addition, the proposed method has a similar error rate to the HUGO [14] method, but a lower computational complexity [14]. The overall results indicate that the proposed method has high undetectability at a lower embedding rate. However, for a higher embedding rate, SPAM + ensemble classifier can successfully steganalyze all the embedding methods, i.e., proposed, LSBM (±1), and HUGO [14].
4. Conclusions
In this work, we have presented a novel hybrid steganographic method with high payload and good visual symmetry, based on the adaptive LSB and RMDR methods. In order to conceal secret data, texture areas of the cover images are exploited according to the absolute difference of pixel pairs. Generally, lower texture areas of cover images are more noise sensitive to the higher texture areas. However, to embed secret data for low texture areas, we presented a closest stego-pixel selection process in the proposed RMDR method. Similarly, to obtain a larger payload in high texture areas, we employed the adaptive LSB embedding method to fully utilize the different variation of higher texture areas.
Compared with related LSB-based hybrid embedding approaches, the proposed method has significant advantages. First, the proposed method efficiently utilized the image texture areas against the PVD, ALSB, LSB + PVD, LSB + EMD + MPE methods, thereby enabling us to produce an embedded image with a significantly higher payload. Secondly, the proposed method reduces the visual distortion artifacts caused by different readjusting phases of the falling-off boundary, and underflow or overflow problems, which are serious in other hybrid LSB + PVD methods. Finally, the proposed method is able to resist statistical RS detection attack and pixel difference histogram attack, and has undetectability for a lower rate of bits per pixels embedding against modern nonstructural steganalysis, i.e., SPAM + ensemble classifier.
The proposed method, however, suffers from the following limitations. The nonstructural feature-based (SPAM + Ensemble classifier) steganalysis detection rate of our approach is essentially high at larger embedding bits per pixels. Second, the texture estimation is limited to two pixel pairs because it only considers a single (horizontal) direction. Third, there is no measure taken to encrypt secret data before the embedding process.
In the future, besides the merits achieved in this paper, we will attempt to improve in the following directions. Different pixel pair directions (i.e., diagonally, vertically) should be investigated to find a more efficient texture estimation for the embedding process. Secondly, a statistical model should be investigated, before and after embedding secret data, to minimize the embedding distortion artifacts from modern steganalysis detection attacks. Third, state-of-the-art compression methods should be investigated and applied to minimize the size of secret data before embedding, to retain undetectability against modern steganalysis. Finally, encryption of secret data should be investigated to enhance the security of secret messages.
Acknowledgments
The work was supported by the National University of Science and Technology, Islamabad, Pakistan under faculty development program abroad (grant number 0972/F008/HRD/FDP-14/); the Ministry of Education, Malaysia under the University of Malaya (High Impact Research Grant UM.C/625/1/HIR/MoE/FCSIT/17); and the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (No. 2015R1D1A1A01058019). We thank the anonymous reviewers for their valuable suggestions that improved the clarity of this article.
Author Contributions
All authors discussed the contents of the manuscript and contributed to its preparation. Mehdi Hussain and Ainuddin Wahid Abdul Wahab designed and implemented the proposed scheme; Noman Javed and Ki-Hyun Jung analyzed the simulation data and wrote the paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Fan, C.-I.; Tseng, Y.-F. Anonymous Multi-Receiver Identity-Based Authenticated Encryption with CCA Security. Symmetry 2015, 7, 1856–1881. [Google Scholar] [CrossRef]
- Shahzad, A.; Lee, Y.-K.; Kim, S.; Xiong, N.; Choi, J.-Y.; Cho, Y. Real Time MODBUS Transmissions and Cryptography Security Designs and Enhancements of Protocol Sensitive Information. Symmetry 2015, 7, 1176–1210. [Google Scholar] [CrossRef]
- Katzenbeisser, S.; Petitcolas, F. Information Hiding Techniques for Steganography and Digital Watermarking; Artech House: Boston, MA, USA, 2000. [Google Scholar]
- Subhedar, M.S.; Mankar, V.H. Current status and key issues in image steganography: A survey. Comput. Sci. Rev. 2014, 13, 95–113. [Google Scholar] [CrossRef]
- Kougianos, E.; Mohanty, S.P.; Mahapatra, R.N. Hardware assisted watermarking for multimedia. Comput. Electr. Eng. 2009, 35, 339–358. [Google Scholar] [CrossRef]
- Kuo, W.-C.; Kuo, S.-H.; Wuu, L.-C. Multi-Bit Data Hiding Scheme for Compressing Secret Messages. Appl. Sci. 2015, 5, 1033–1049. [Google Scholar] [CrossRef]
- Lee, C.F.; Weng, C.Y.; Sharma, A. Steganographic access control in data hiding using run-length encoding and modulo-operations. Secur. Commun. Netw. 2016, 9, 139–148. [Google Scholar] [CrossRef]
- Collins, J.C.; Agaian, S.S. Taxonomy for spatial domain LSB steganography techniques. In SPIE Sensing Technology+ Applications; International Society for Optics and Photonics: Baltimore, MD, USA, 2014; Volume 9120, p. 912006. [Google Scholar]
- Chan, C.-K.; Cheng, L.-M. Hiding data in images by simple LSB substitution. Pattern Recognit. 2004, 37, 469–474. [Google Scholar] [CrossRef]
- Fridrich, J.; Goljan, M.; Du, R. Reliable detection of LSB steganography in color and grayscale images. In Proceedings of the 2001 Workshop on Multimedia and Security: New Challenges, New York, NY, USA, 5 October 2001; pp. 27–30.
- Fillatre, L. Adaptive steganalysis of least significant bit replacement in grayscale natural images. IEEE Trans. Signal Process. 2012, 60, 556–569. [Google Scholar] [CrossRef]
- Zhang, J.; Cox, I.J.; Doërr, G. Steganalysis for LSB matching in images with high-frequency noise. In Proceedings of the IEEE 9th Workshop on Multimedia Signal Processing, Crete, Greece, 1–3 October 2007; pp. 385–388.
- Al-Dmour, H.; Al-Ani, A. Quality optimized medical image information hiding algorithm that employs edge detection and data coding. Comput. Methods Programs Biomed. 2016, 127, 24–43. [Google Scholar] [CrossRef] [PubMed]
- Pevný, T.; Filler, T.; Bas, P. Using high-dimensional image models to perform highly undetectable steganography. In Information Hiding; Springer: Berlin/Heidelberg, Germany, 2010; pp. 161–177. [Google Scholar]
- Holub, V.; Fridrich, J. Designing steganographic distortion using directional filters. In Proceedings of the 2012 IEEE International Workshop on Information Forensics and Security (WIFS), Tenerife, Spain, 2–5 December 2012; pp. 234–239.
- Holub, V.; Fridrich, J.; Denemark, T. Universal distortion function for steganography in an arbitrary domain. EURASIP J. Inf. Secur. 2014, 2014, 1–13. [Google Scholar] [CrossRef]
- Li, B.; Wang, M.; Huang, J.; Li, X. A new cost function for spatial image steganography. In Proceedings of the 2014 IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; pp. 4206–4210.
- Sedighi, V.; Fridrich, J.; Cogranne, R. Content-adaptive pentary steganography using the multivariate generalized Gaussian cover model. In IS&T/SPIE Electronic Imaging; International Society for Optics and Photonics: San Francisco, CA, USA, 2015. [Google Scholar]
- Wu, D.-C.; Tsai, W.-H. A steganographic method for images by pixel-value differencing. Pattern Recognit. Lett. 2003, 24, 1613–1626. [Google Scholar] [CrossRef]
- Lee, Y.-P.; Lee, J.-C.; Chen, W.-K.; Chang, K.-C.; Su, J.; Chang, C.-P. High-payload image hiding with quality recovery using tri-way pixel-value differencing. Inf. Sci. 2012, 191, 214–225. [Google Scholar] [CrossRef]
- Balasubramanian, C.; Selvakumar, S.; Geetha, S. High payload image steganography with reduced distortion using octonary pixel pairing scheme. Multimedia Tools Appli. 2014, 73, 2223–2245. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, S. Efficient steganographic embedding by exploiting modification direction. IEEE Commun. Lett. 2006, 10, 781–783. [Google Scholar] [CrossRef]
- Wang, X.-T.; Chang, C.-C.; Lin, C.-C.; Li, M.-C. A novel multi-group exploiting modification direction method based on switch map. Signal Process. 2012, 92, 1525–1535. [Google Scholar] [CrossRef]
- Kim, C. Data hiding by an improved exploiting modification direction. Multimedia Tools Appl. 2014, 69, 569–584. [Google Scholar] [CrossRef]
- Wu, K.-S.; Liao, W.-D.; Lin, C.-N.; Chen, T.-S. A high payload hybrid data hiding scheme with LSB, EMD and MPE. Imag. Sci. J. 2014, 63, 174–181. [Google Scholar] [CrossRef]
- Shen, S.-Y.; Huang, L.-H. A data hiding scheme using pixel value differencing and improving exploiting modification directions. Comput. Secur. 2015, 48, 131–141. [Google Scholar] [CrossRef]
- Wu, H.-C.; Wu, N.-I.; Tsai, C.-S.; Hwang, M.-S. Image steganographic scheme based on pixel-value differencing and LSB replacement methods. IEEE Proc. Vis. Image Signal Process. 2005, 152, 611–615. [Google Scholar] [CrossRef]
- Khodaei, M.; Faez, K. New adaptive steganographic method using least-significant-bit substitution and pixel-value differencing. IET Image Process. 2012, 6, 677–686. [Google Scholar] [CrossRef]
- Jung, K.-H. High-capacity steganographic method based on pixel-value differencing and LSB replacement methods. Imag. Sci. J. 2010, 58, 213–221. [Google Scholar] [CrossRef]
- Tsai, Y.-Y.; Chen, J.-T.; Chan, C.-S. Exploring LSB substitution and pixel-value differencing for block-based adaptive data hiding. Int. J. Netw. Secur. 2014, 16, 359–364. [Google Scholar]
- Jung, K.-H.; Ha, K.-J.; Yoo, K.-Y. Image data hiding method based on multi-pixel differencing and LSB substitution methods. In Proceedings of the International Conference on Convergence and Hybrid Information Technology, Daejeon, South Korea, 28–30 August 2008.
- Zaker, N.; Hamzeh, A. A novel steganalysis for TPVD steganographic method based on differences of pixel difference histogram. Multimedia Tools Appl. 2012, 58, 147–166. [Google Scholar] [CrossRef]
- Sajedi, H.; Jamzad, M. HYSA: hybrid steganographic approach using multiple steganography methods. Secur. Comm. Netw. 2011, 4, 1173–1184. [Google Scholar] [CrossRef]
- Yang, C.-H.; Weng, C.-Y.; Wang, S.-J.; Sun, H.-M. Varied PVD + LSB evading detection programs to spatial domain in data embedding systems. J. Syst. Softw. 2010, 83, 1635–1643. [Google Scholar] [CrossRef]
- Huang, H.-S. A combined image steganographic method using multi-way pixel-value differencing. In Proceedings of the Sixth International Conference on Graphic and Image Processing (ICGIP 2014), Beijing, China, 24–25 October 2015.
- Shen, S.; Huang, L.; Tian, Q. A novel data hiding for color images based on pixel value difference and modulus function. Multimedia Tools Appl. 2015, 74, 707–728. [Google Scholar] [CrossRef]
- Petitcolas, F.A.; Anderson, R.J. Evaluation of copyright marking systems. In Proceedings of the IEEE International Conference on Multimedia Computing and Systems, Florence, Italy, 7–11 June 1999.
- Implementation of the Ensemble Classifier (Using Weka) and the SPAM Features + HUGO Algorithm. Available online: http://dde.binghamton.edu/download/ (accessed on 20 April 2016).
- Schaefer, G.; Stich, M. UCID: An uncompressed color image database. In Proceedings of the SPIE, Storage and Retrieval Methods and Applications for Multimedia 2004, San Jose, CA, USA, 18 January 2004.
- The USC-SIPI Image Database. Available online: http://sipi.usc.edu/database/ (accessed on 1 September 2015).
- Yang, H.; Sun, X.; Sun, G. A high-capacity image data hiding scheme using adaptive LSB substitution. Radioengineering 2009, 18, 509. [Google Scholar]
- Wang, Z.; Bovik, A.C. A universal image quality index. IEEE Signal Process. Lett. 2002, 9, 81–84. [Google Scholar] [CrossRef]
- Pevny, T.; Bas, P.; Fridrich, J. Steganalysis by subtractive pixel adjacency matrix. IEEE Trans. Inf. Forensics Secur. 2010, 5, 215–224. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).