On Solutions for Linear and Nonlinear Schrödinger Equations with Variable Coefficients: A Computational Approach
Abstract
:1. Introduction
- Bose-Einstein condensates: , a, h constants and other coefficients are zero.
- Pulse dynamics in the dispersion-managed fibers [10]: , a is a constant and other coefficients are zero.
2. Soliton Solutions for VCNLS through Riccati Equations and Similarity Transformations
3. Riccati Systems with Parameters and Similarity Transformations
4. Crank-Nicolson Scheme for Linear Schrödinger Equation with Variable Coefficients Depending on Space
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rajendran, S.; Muruganandam, P.; Lakshmanan, M. Bright and dark solitons in a quasi-1D Bose–Einstein condensates modelled by 1D Gross–Pitaevskii equation with time-dependent parameters. Phys. D Nonlinear Phenom. 2010, 239, 366–386. [Google Scholar] [CrossRef]
- Agrawal, G.-P. Nonlinear Fiber Optics, 4th ed.; Academic Press: New York, NY, USA, 2007. [Google Scholar]
- Al Khawaja, U. A comparative analysis of Painlevé, Lax Pair and similarity transformation methods in obtaining the integrability conditions of nonlinear Schrödinger equations. J. Phys. Math. 2010, 51. [Google Scholar] [CrossRef]
- Brugarino, T.; Sciacca, M. Integrability of an inhomogeneous nonlinear Schrödinger equation in Bose-Einstein condensates and fiber optics. J. Math. Phys. 2010, 51. [Google Scholar] [CrossRef]
- Chen, H.-M.; Liu, C.S. Solitons in nonuniform media. Phys. Rev. Lett. 1976, 37, 693–697. [Google Scholar] [CrossRef]
- He, X.G.; Zhao, D.; Li, L.; Luo, H.G. Engineering integrable nonautonomous nonlinear Schrödinger equations. Phys. Rev. E. 2009, 79. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Li, Y. Designable inegrability of the variable coefficient nonlinear Schrödinger equations. Stud. Appl. Math. 2010, 126, 1–15. [Google Scholar] [CrossRef]
- He, J.S.; Charalampidis, E.G.; Kevrekidis, P.G.; Frantzeskakis, D.J. Rogue waves in nonlinear Schrödinger models with variable coefficients: Application to Bose-Einstein condensates. Phys. Lett. A 2014, 378, 577–583. [Google Scholar] [CrossRef]
- Kruglov, V.I.; Peacock, A.C.; Harvey, J.D. Exact solutions of the generalized nonlinear Schrödinger equation with distributed coefficients. Phys. Rev. E 2005, 71. [Google Scholar] [CrossRef] [PubMed]
- Marikhin, V.G.; Shabat, A.B.; Boiti, M.; Pempinelli, F. Self-similar solutions of equations of the nonlinear Schrödinger type. J. Exp. Theor. Phys. 2000, 90, 553–561. [Google Scholar] [CrossRef]
- Ponomarenko, S.A.; Agrawal, G.P. Do Solitonlike self-similar waves exist in nonlinear optical media? Phys. Rev. Lett. 2006, 97. [Google Scholar] [CrossRef] [PubMed]
- Ponomarenko, S.A.; Agrawal, G.P. Optical similaritons in nonlinear waveguides. Opt. Lett. 2007, 32, 1659–1661. [Google Scholar] [CrossRef] [PubMed]
- Raghavan, S.; Agrawal, G.P. Spatiotemporal solitons in inhomogeneous nonlinear media. Opt. Commun. 2000, 180, 377–382. [Google Scholar] [CrossRef]
- Serkin, V.N.; Hasegawa, A. Novel Soliton solutions of the nonlinear Schrödinger Equation model. Phys. Rev. Lett. 2000, 85. [Google Scholar] [CrossRef] [PubMed]
- Serkin, V.; Matsumoto, M.; Belyaeva, T. Bright and dark solitary nonlinear Bloch waves in dispersion managed fiber systems and soliton lasers. Opt. Commun. 2001, 196, 159–171. [Google Scholar] [CrossRef]
- Tian, B.; Shan, W.; Zhang, C.; Wei, G.; Gao, Y. Transformations for a generalized variable-coefficient nonlinear Schrödinger model from plasma physics, arterial mechanics and optical fibers with symbolic computation. Eur. Phys. J. B 2005, 47, 329–332. [Google Scholar] [CrossRef]
- Dai, C.-Q.; Wang, Y.-Y. Infinite generation of soliton-like solutions for complex nonlinear evolution differential equations via the NLSE-based constructive method. Appl. Math. Comput. 2014, 236, 606–612. [Google Scholar] [CrossRef]
- Wang, M.; Shan, W.-R.; Lü, X.; Xue, Y.-S.; Lin, Z.-Q.; Tian, B. Soliton collision in a general coupled nonlinear Schrödinger system via symbolic computation. Appl. Math. Comput. 2013, 219, 11258–11264. [Google Scholar] [CrossRef]
- Yu, F.; Yan, Z. New rogue waves and dark-bright soliton solutions for a coupled nonlinear Schrödinger equation with variable coefficients. Appl. Math. Comput. 2014, 233, 351–358. [Google Scholar] [CrossRef]
- Fibich, G. The Nonlinear Schrödinger Equation, Singular Solutions and Optical Collapse; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Kevrekidis, P.G.; Frantzeskakis, D.J.; Carretero-Gonzáles, R. Emergent Nonlinear Phenomena in Bose-Einstein Condensates: Theory and Experiment; Springer Series of Atomic, Optical and Plasma Physics; Springer: Berlin/Heidelberg, Germany, 2008; Volume 45. [Google Scholar]
- Suazo, E.; Suslov, S.-K. Soliton-Like solutions for nonlinear Schrödinger equation with variable quadratic Hamiltonians. J. Russ. Laser Res. 2010, 33, 63–83. [Google Scholar] [CrossRef]
- Sulem, C.; Sulem, P.L. The Nonlinear Schrödinger Equation; Springer: New York, NY, USA, 1999. [Google Scholar]
- Tao, T. Nonlinear dispersive equations: Local and global analysis. In CBMS Regional Conference Series in Mathematics; American Mathematical Society: Providence, RI, USA, 2006. [Google Scholar]
- Zakharov, V.-E.; Shabat, A.-B. Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of waves in nonlinear media. Soviet. Phys. JETP 1972, 34, 62–69. [Google Scholar]
- Suslov, S.-K. On integrability of nonautonomous nonlinear Schrödinger equations. Proc. Am. Math. Soc. 2012, 140, 3067–3082. [Google Scholar] [CrossRef]
- Talanov, V.I. Focusing of light in cubic media. JETP Lett. 1970, 11, 199–201. [Google Scholar]
- Perez-Garcia, V.M.; Torres, P.J.; Konotop, V.K. Similarity transformations for nonlinear Schrödinger equations with time-dependent coefficients. Physica D 2006, 221, 31–36. [Google Scholar] [CrossRef]
- Ablowitz, M.; Hooroka, T. Resonant intrachannel pulse interactions in dispersion-managed transmission systems. IEEE J. Sel. Top. Quantum Electron. 2002, 8, 603–615. [Google Scholar] [CrossRef]
- Marhic, M.E. Oscillating Hermite-Gaussian wave functions of the harmonic oscillator. Lett. Nuovo Cim. 1978, 22, 376–378. [Google Scholar] [CrossRef]
- Carles, R. Nonlinear Schrödinger equation with time dependent potential. Commun. Math. Sci. 2010, 9, 937–964. [Google Scholar] [CrossRef]
- López, R.M.; Suslov, S.K.; Vega-Guzmán, J.M. On a hidden symmetry of quantum harmonic oscillators. J. Differ. Equ. Appl. 2013, 19, 543–554. [Google Scholar] [CrossRef]
- Aldaya, V.; Cossío, F.; Guerrero, J.; López-Ruiz, F.F. The quantum Arnold transformation. J. Phys. A Math. Theor. 2011, 44, 1–6. [Google Scholar] [CrossRef]
- Feynman, R.P.; Hibbs, A.R. Quantum Mechanics and Path Integrals; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Cordero-Soto, R.; Lopez, R.M.; Suazo, E.; Suslov, S.K. Propagator of a charged particle with a spin in uniform magnetic and perpendicular electric fields. Lett. Math. Phys. 2008, 84, 159–178. [Google Scholar] [CrossRef]
- Lanfear, N.; López, R.M.; Suslov, S.K. Exact wave functions for a generalized harmonic oscillators. J. Russ. Laser Res. 2011, 32, 352–361. [Google Scholar] [CrossRef]
- López, R.M.; Suslov, S.K.; Vega-Guzmán, J.M. Reconstructing the Schrödinger groups. Phys. Scr. 2013, 87, 1–6. [Google Scholar] [CrossRef]
- Suazo, E.; Suslov, S.K. Cauchy problem for Schrödinger equation with variable quadratic Hamiltonians. 2011. to be submitted. [Google Scholar]
- Suazo, E. Fundamental Solutions of Some Evolution Equations. Ph.D. Thesis, Arizona State University, Tempe, AZ, USA, September 2009. [Google Scholar]
- Mahalov, A.; Suazo, E.; Suslov, S.K. Spiral laser beams in inhomogeneous media. Opt. Lett. 2013, 38, 2763–2766. [Google Scholar] [CrossRef] [PubMed]
- Koutschan, C.; Suazo, E.; Suslov, S.K. Fundamental laser modes in paraxial optics: From computer algebra and simulations to experimental observation. Appl. Phys. B 2015, 121, 315–336. [Google Scholar] [CrossRef]
- Escorcia, J.; Suazo, E. Blow-up results and soliton solutions for a generalized variable coefficient nonlinear Schrödinger equation. Available online: http://arxiv.org/abs/1605.07554 (accessed on 24 May 2016).
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation through Random Media, 2nd ed.; SPIE Press: Bellingham, WA, USA, 2005. [Google Scholar]
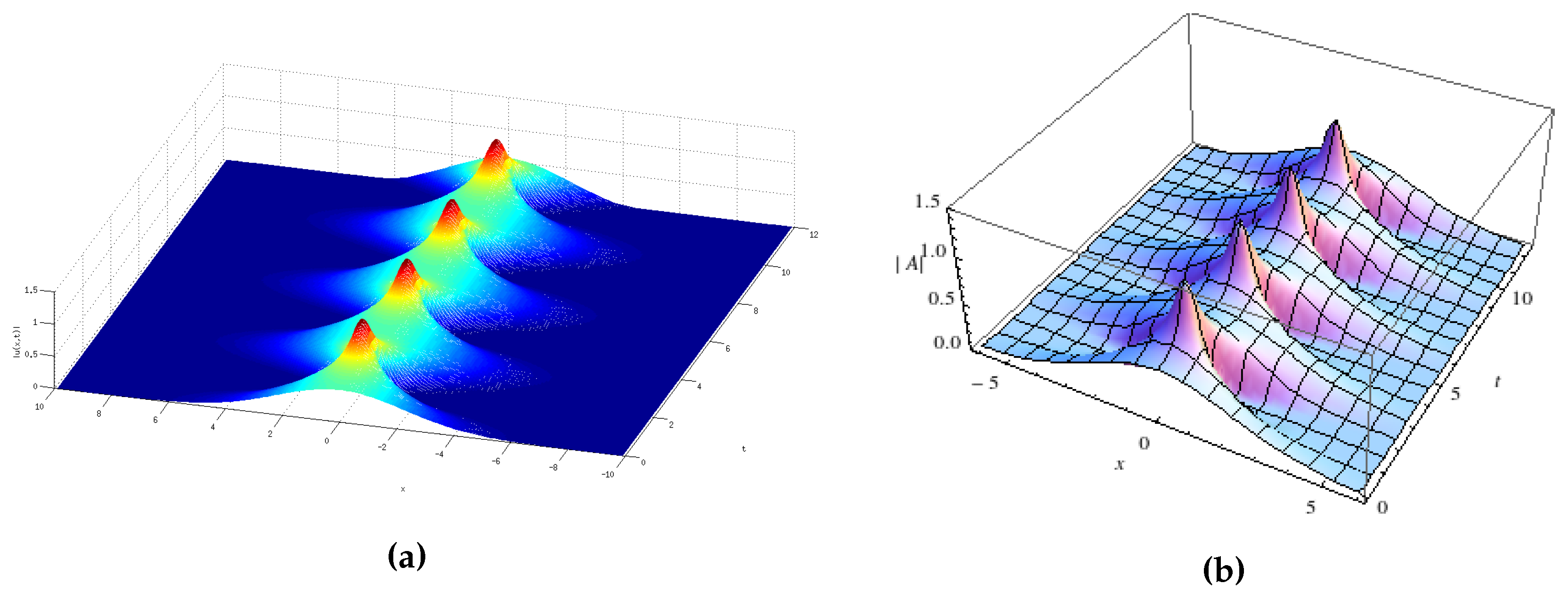
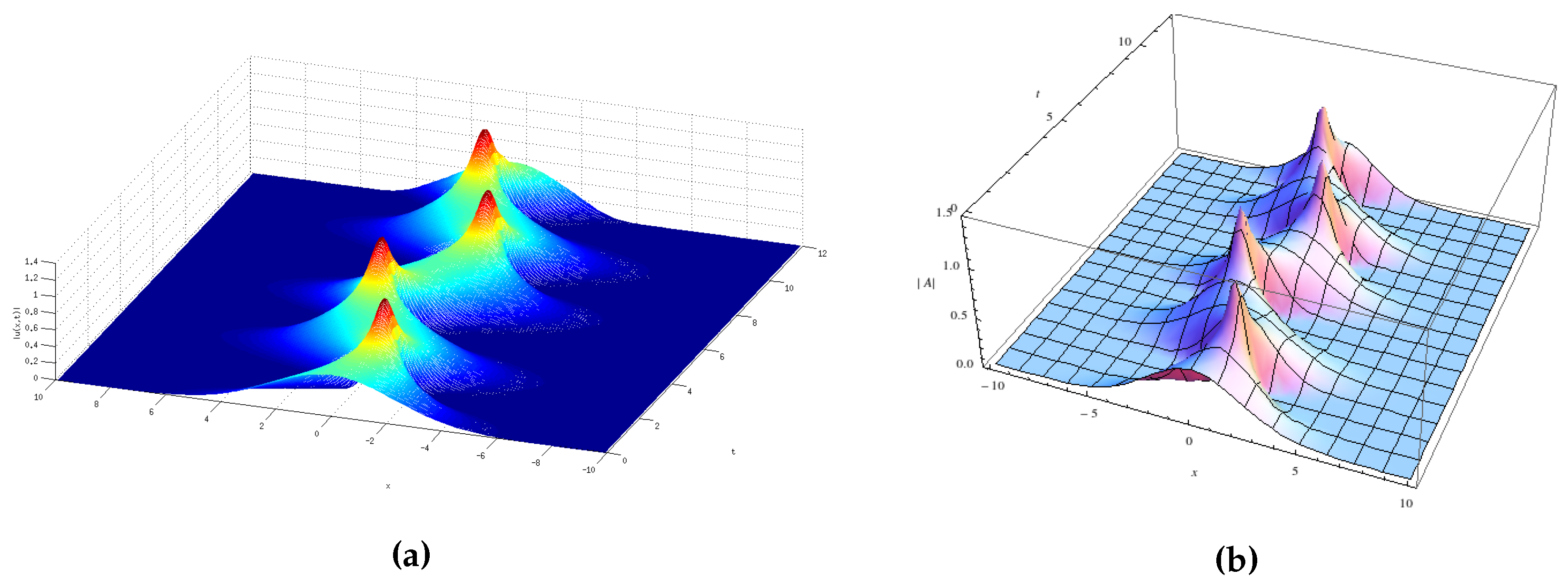
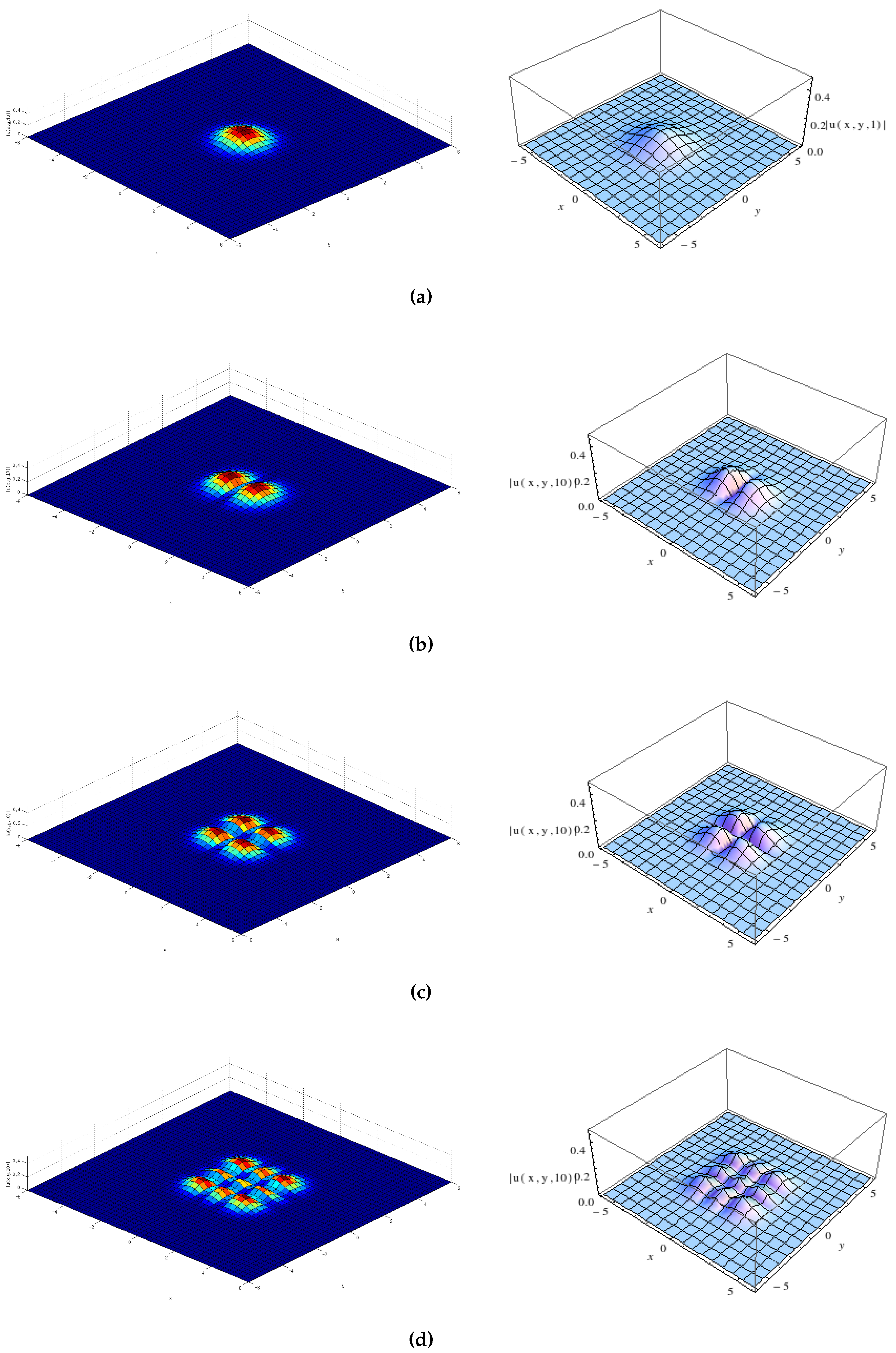

| # | Variable Coefficient NLS | Solutions () |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 | ||
| 11 | ||
| 12 | ||
| 13 | ||
| 14 | ||
| 15 | ||
| 16 | ||
| 17 | ||
| 18 |
| # | Riccati Equation | Similarity Transformation from Table 1 |
|---|---|---|
| 1 | 1 | |
| 2 | 2 | |
| 3 | 3 | |
| 4 | 1 | |
| 5 | 3 | |
| 6 | 4 | |
| 7 | 5 | |
| 8 | 3 | |
| 9 | 1 | |
| 10 | 8 | |
| 11 | 3 | |
| 12 | 6 | |
| 13 | 7 | |
| 14 | 1 | |
| 15 | 8 | |
| 16 | 9 | |
| 17 | 10 | |
| 18 | 10 | |
| 19 | 3 | |
| 20 | 1 | |
| 21 | 3 | |
| 22 | 1 | |
| 23 | 3 | |
| 24 | 1 | |
| 25 | 3 | |
| 26 | 1 | |
| 27 | 3 | |
| 28 | 1 | |
| 29 | 3 | |
| 30 | 1 | |
| 31 | 1 | |
| 32 | 5 | |
| 33 | 5 | |
| 34 | 5 | |
| 35 | 11 | |
| 36 | 12 | |
| 37 | 13 | |
| 38 | 14 | |
| 39 | 15 | |
| 40 | 16 | |
| 41 | 17 | |
| 42 | 18 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amador, G.; Colon, K.; Luna, N.; Mercado, G.; Pereira, E.; Suazo, E. On Solutions for Linear and Nonlinear Schrödinger Equations with Variable Coefficients: A Computational Approach. Symmetry 2016, 8, 38. https://doi.org/10.3390/sym8060038
Amador G, Colon K, Luna N, Mercado G, Pereira E, Suazo E. On Solutions for Linear and Nonlinear Schrödinger Equations with Variable Coefficients: A Computational Approach. Symmetry. 2016; 8(6):38. https://doi.org/10.3390/sym8060038
Chicago/Turabian StyleAmador, Gabriel, Kiara Colon, Nathalie Luna, Gerardo Mercado, Enrique Pereira, and Erwin Suazo. 2016. "On Solutions for Linear and Nonlinear Schrödinger Equations with Variable Coefficients: A Computational Approach" Symmetry 8, no. 6: 38. https://doi.org/10.3390/sym8060038
APA StyleAmador, G., Colon, K., Luna, N., Mercado, G., Pereira, E., & Suazo, E. (2016). On Solutions for Linear and Nonlinear Schrödinger Equations with Variable Coefficients: A Computational Approach. Symmetry, 8(6), 38. https://doi.org/10.3390/sym8060038






