M-Polynomial and Degree-Based Topological Indices of Polyhex Nanotubes

Abstract

The discovery of new nanomaterials adds new dimensions to industry, electronics, and pharmaceutical and biological therapeutics. In this article, we first find closed forms of M-polynomials of polyhex nanotubes. We also compute closed forms of various degree-based topological indices of these tubes. These indices are numerical tendencies that often depict quantitative structural activity/property/toxicity relationships and correlate certain physico-chemical properties, such as boiling point, stability, and strain energy, of respective nanomaterial. To conclude, we plot surfaces associated to M-polynomials and characterize some facts about these tubes.

1. Introduction

Nanoscience has attracted research interest because of its increasing applications and uses. Nanocrystals, nanowires, and nanotubes are three major categories of nanomaterials. Since the discovery of the carbon nanotubes in 1991, interest in one-dimensional nanomaterials has grown remarkable, and a phenomenal number of research articles are being published on nanotubes as well as on nanowires.

Material properties depend on molecular structure. In the context of chemical graph theory, this structure can be represented by a graph whose vertices represent atoms of nanomaterials and edges correspond to chemical bonds. Chemical graph theory contributes the lion’s share of efforts to predict the chemical properties of a nanomaterial without involving a wet lab. A graph G(V,E) with vertex set V(G) and edge set E(G) is connected if there is a path between any pair of vertices in G. A network is simply a connected graph having no multiple edges and loops. In a chemical graph, the degree of any vertex is at most 4. The distance between two vertices u and v is denoted as $d(u,v)=d_G(u,v)$ and is the length of the shortest path between u and v in graph G. The number of vertices of G adjacent to a given vertex v is the “degree” of this vertex and will be denoted by $d_v$. The concept of degree in graph theory is closely related (but not identical) to the concept of valence in chemistry. For details on the basics of graph theory, any standard text such as [1] can be of great help.

Several algebraic polynomials have useful applications in chemistry. The Hosoya polynomial is perhaps the best well-known example [2], and it plays a vital role in determining distance-based topological indices. Among other algebraic polynomials, M-polynomial [3] was introduced in 2015 and plays the same role in determining closed forms of many degree-based topological indices. These indices are actually score functions that capture a variety of physico-chemical properties of chemical compounds such as boiling point, heat of evaporation, heat of formation, chromatographic retention times, surface tension, and vapor pressure [4,5,6,7,8,9].

Definition 1.

Let G be a simple connected graph. The M-polynomial of G is defined as

$$M\left(G,x,y\right)={\displaystyle \sum _{\delta \le i\le j\le \mathsf{\Delta }}{m}_{ij}\left(G\right)x^i{y}^j}$$

where $\delta =\mathrm{Min}\left\{d_v\right|v\in \mathrm{V}\left(\mathrm{G}\right)\},$ $\mathsf{\Delta }=\mathrm{Max}\left\{d_v\right|v\in \mathrm{V}\left(\mathrm{G}\right)\},$ and $m_{ij}(G)$ is the number of edges $vu\in E(G)$ such that $\left\{d_v,d_u\right\}=\left\{i,j\right\}.$

In 1947, Wiener approximated the boiling point of alkanes as $\alpha W(G)+\beta P_3+\gamma$ where $\alpha ,$ $\beta$, and $\gamma$ are empirical constants, $W(G)$ is the Wiener index, and $P_3$ is the number of paths of length 3 in G [10]. The Wiener index was the first and is the most studied topological index, defined as ${\displaystyle \sum _{i<j}d(v_i,v_j)}$. In [11], Gutman and Trinajstic introduced Zagreb indices.

Let G be the simple connected graph. The first Zagreb index is defined as

$$M_1\left(G\right)={\displaystyle \sum _{v\in V(G)}{(d_v)}^2},$$

and the second Zagreb index is defined as

$$M_2\left(G\right)={\displaystyle \sum _{uv\in E(G)}{d}_u{d}_v}.$$

For detail about these indices, see [12,13].

The second modified Zagreb index is defined as

$${}^{m}M_2(G)={\displaystyle \sum _{uv\in E(G)}\frac{1}{d_u{d}_v}}.$$

The general Randic index is defined as

$$R_{\alpha }(G)={{\displaystyle \sum _{uv\in E(G)}(d_u{d}_v)}}^{\alpha },$$

where α is an arbitrary real number (see [14]).

Symmetric division index is defined as

$$SDD\left(G\right)={\displaystyle \sum _{uv\in E(G)}\left\{\frac{\min (d_u,d_v)}{\max (d_u,d_v)}+\frac{\max (d_u,d_v)}{\min (d_u,d_v)}\right\}}.$$

Recently, Munir et al. computed M-polynomials and related topological indices for Nanostar dendrimers [15], titania nanotubes [16], and circulant graphs [17]. The structures of Nanostar dendrimers and titania nanotubes are different from polyhex nanotubes from a geometrical point of view. Basic structural units of titania nanotubes are rectangles arranged differently for different types [16], whereas basic units of polyhex nanotubes are hexagons concatenated in different ways for different types. Nanostar dendrimers are macromolecules built on a tree-like structure [15]. Polyhex nanotubes have many applications in electronics, chemical processing, optics, and energy management [18,19] and are used in flat panel display screens [20], hydrogen storage, robotics and artificial muscles, chemical sensors, and photography. We refer the readers to [21,22,23] for further details about these nanomaterials.

In this report, we are interested in the geometry of two well-known polyhex nanotubes, namely zigzag polyhex $H{C}_6$ and armchair polyhex $V{C}_6$. These are single-walled carbon nanotubes made from a layer of graphenes and are cylindrical in shape. We computed the general closed forms of M-polynomials for these nanotubes and recovered many topological indices from it. We also plot the graphs of these M-polynomials here. The author in [24], using the definitions, computed closed forms of the first and second Zagreb indices and the Zagreb polynomials for these tubes. We also re-obtained the first and the second Zagreb indices by the use of the M-polynomial.

The following Table 1 relates some degree-based topological indices with the M-polynomial [3].

Table 1. Derivation of some degree-based topological indices from M-polynomial.

Topological Index	$f\left(x,y\right)$	Derivation from $M\left(G;x,y\right)$
First Zagreb	$x+y$	$(D_x+D_y)\left(M\left(G;x,y\right)\right){|}_{x=y=1}$
Second Zagreb	$xy$	$(D_x{D}_y)\left(M\left(G;x,y\right)\right){|}_{x=y=1}$
Second Modified Zagreb	$\frac{1}{xy}$	$(S_x{S}_y)\left(M\left(G;x,y\right)\right){|}_{x=y=1}$
General Randi$\acute{\mathrm{c}}\mathsf{\alpha }\in \mathbb{N}$	${\left(xy\right)}^{\alpha }$	$(D_x^{\alpha }{D}_y^{\alpha })\left(M\left(G;x,y\right)\right){|}_{x=y=1}$
General Randi$\acute{\mathrm{c}}\mathsf{\alpha }\in \mathbb{N}$	$\frac{1}{{\left(xy\right)}^{\alpha }}$	$(S_x^{\alpha }{S}_y^{\alpha })\left(M\left(G;x,y\right)\right){|}_{x=y=1}$
Symmetric Division Index	$\frac{x^2+y^2}{xy}$	$(D_x{S}_y+S_x{D}_y)\left(M\left(G;x,y\right)\right){|}_{x=y=1}$

where $D_x=x\frac{\partial (f\left(x,y\right)}{\partial x},D_y=y\frac{\partial (f\left(x,y\right)}{\partial y},S_x={\int }_0^x\frac{f\left(t,y\right)}{t}dt,S_y={\int }_0^y\frac{f\left(x,t\right)}{t}dt$.

.

2. Results and Discussion

In this section, we provide our main computational results. We divide this section into two subsections.

2.1. Zigzag Polyhex Nanotubes

If you roll graphene up into a seamless tube in such a way that carbon–carbon bonds are parallel to the axis of the tube, then we obtain zigzag polyhex nanotubes (Figure 1) represented as $H{C}_6[m,n]$, where m is the number of hexagons in a row, and n is the number of hexagons in a column. The following figures illustrate this.

Figure 1. The image of zigzag polyhex $H{C}_6$.

In the following theorem, we compute the M-polynomial of zigzag polyhex nanotube.

Theorem 1.

Let $H{C}_6[m,n]$ be the zigzag structure of Polyhex nanotube. Then,

$$M\left(H{C}_6[m,n],x,y\right)=4m{x}^2{y}^3+m\left(3n-2\right)x^3{y}^3.$$

Proof. 

From the 2D lattice of $H{C}_6[m,n]$, we can see that there are two partitions of vertices [25] $\left|V_{\left\{2\right\}}\right|=\left|\{v\in V\left(H{C}_6[m,n]\right)|d_v=2\}\right|=2m$ and $\left|V_{\left\{3\right\}}\right|=\left|\{v\in V\left(H{C}_6[m,n]\right)|d_v=3\}\right|=2mn$ with $\left|V(H{C}_6[m,n])\right|=2m(n+1)$. By handshaking lemma, we obtain $|E(G)|=m(3n+2)$.

The edge set of $H{C}_6\left[m,n\right]$ can be partitioned as $\left|E_{\left\{2,2\right\}}\right|=\left|\left\{uv\in E(H{C}_6[m,n]):d_u=2\mathrm{and}{d}_v=2\right\}\right|=0,$ $\left|E_{\left\{2,3\right\}}\right|=\left|\left\{uv\in E(H{C}_6[m,n]):d_u=2\mathrm{and}{d}_v=3\right\}\right|=4m$ and $\left|E_{\left\{3,3\right\}}\right|=\left|\left\{uv\in E\left(H{C}_6[m,n]\right):d_u=d_v=3\right\}\right|=\left|E(G)\right|-\left|E_{\{2,2\}}\right|-\left|E_{\{2,3\}}\right|=m(3n-2)$. In Figure 2, $E_{\left\{2,3\right\}}$ is marked red, and $E_{\left\{3,3\right\}}$ is marked black.

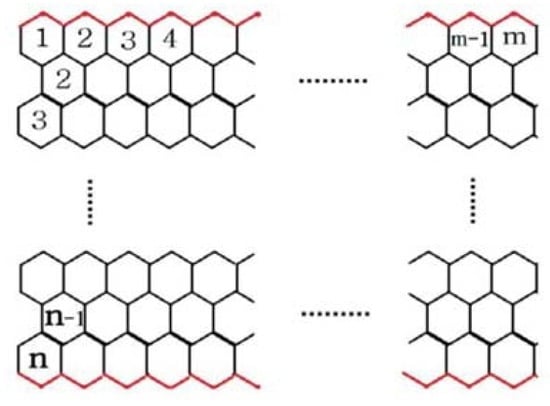
Figure 2. The 2-D lattice of $H{C}_6[m,n]$.

Thus, the M-polynomial of $H{C}_6[m,n]$ is

$$M\left(H{C}_6[m,n];x,y\right)=\sum _{i\le j}{m}_{ij}(H{C}_6[m,n])x^i{y}^j=4m{x}^2{y}^3+m\left(3n-2\right)x^3{y}^3.$$

Figure 3 is a graph for the M-polynomial of zigzag polyhex nanotube. This graph is a saddle surface.

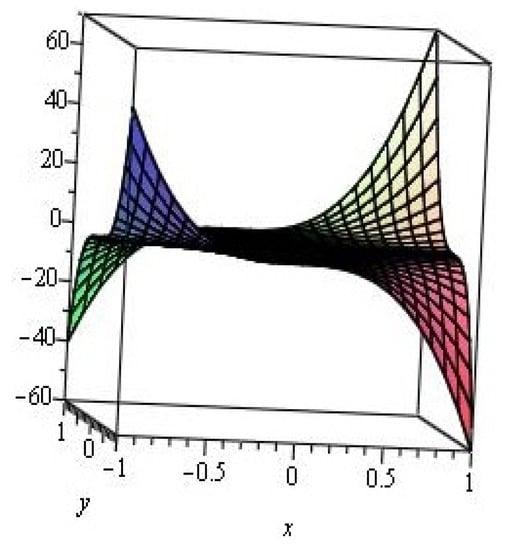
Figure 3. M-polynomial of the zigzag polyhex nanotube.

Theorem 2.

Let $H{C}_6[m,n]$ be the zigzag structure of Polyhex nanotube. Then,

$$M_1\left(H{C}_6[m,n]\right)=2m\left(4+9n\right).$$

$$M_2(H{C}_6[m,n])=3m(2+9n).$$

$${}^{m}M_2\left(H{C}_6[m,n]\right)=\frac{m}{9}\left\{4+3n\right\}.$$

$$R_a(H{C}_6[m,n])=3^{\alpha }m(2^{\alpha +2}+3^{\alpha }(3n-2)).$$

$$R_a(H{C}_6[m,n])=\frac{m}{3^{\alpha }}(2^{2-\alpha }-{2.3}^{-\alpha }+3^{1-\alpha }n).$$

$$SDD(H{C}_6[m,n])=\frac{2}{3}m(7+9n).$$

Proof. 

We leave the proof for the reader.

2.2. Armchair Polyhex Nanotubes

Now we turn our attention towards the armchair structure of the polyhex nanotube, $V{C}_6[m,n]$. If we roll graphene up into a seamless tube in such a way that carbon–carbon bonds are perpendicular to the axis of the tube, then we obtain armchair polyhex nanotube $V{C}_6[m,n]$ (Figure 4), where m is the number of hexagons in a row, and n is the number of hexagons in a column. Figure 4 and Figure 5 illustrate this.

Figure 4. Armchair polyhex nanotube $V{C}_6[m,n]$.

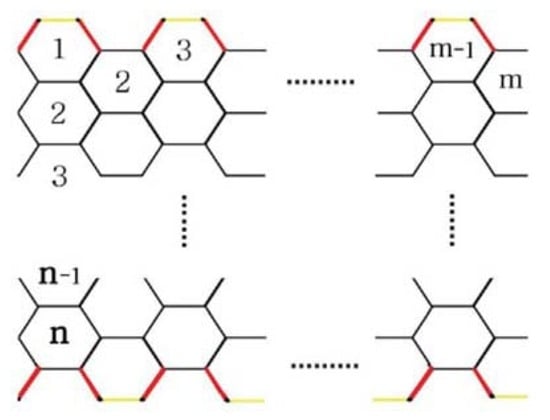
Figure 5. The 2-D lattice of $V{C}_6[m,n]$.

Theorem 3.

Let $V{C}_6[m,n]$ be the Armchair structure of Polyhex nanotube. Then,

$$M\left(V{C}_6[m,n];x,y\right)=m{x}^2{y}^2+2m{x}^2{y}^3+m\left(3n-1\right)x^3{y}^3.$$

Proof. 

The 2-D lattice of $V{C}_6[m,n]$ has $2m(n+1)$ vertices, with two partitions of vertices $\left|V_{\left\{2\right\}}=\{v\in V\left(V{C}_6[m,n]\right)|d_v=2\}\right|=2m$ and $\left|V_{\left\{3\right\}}=\{v\in V\left(V{C}_6[m,n]\right)|d_v=3\}\right|=2mn$. This shows that $V{C}_6[m,n]$ has 3mn + 2m edges. The edge set of $V{C}_6[m,n]$ has partitions as follows:

$\left|E_{\left\{2,2\right\}}\right|=\left|\left\{uv\in E\left(V{C}_6[m,n]\right):d_u=d_v=2\right\}\right|=\frac{m}{2}+\frac{m}{2}=m,$

$\left|E_{\left\{2,3\right\}}\right|=\left|\{uv\in E\left(V{C}_6[m,n]\right):d_u=2\mathrm{and}{d}_v=3\}\right|=2m,$

$\left|E_{\left\{3,3\right\}}\right|=\left|\left\{uv\in E\left(V{C}_6[m,n]\right)│d_u=d_v=3\right\}\right|=(3mn+2n)-m-2m=3mn-m$.

In Figure 5, $E_{\left\{2,2\right\}}$ is marked yellow, $E_{\left\{2,3\right\}}$ is marked red, and $E_{\left\{3,3\right\}}$ is marked black. Hence,

$$M\left(V{C}_6[m,n];x,y\right)=\sum _{i\le j}{m}_{ij}(V{C}_6[m,n])x^i{y}^j=m{x}^2{y}^2+\left(2m\right)x^2{y}^3+m\left(3n-1\right)x^3{y}^3.$$

Figure 6 is the graph for the M-polynomial of the armchair polyhex nanotube.

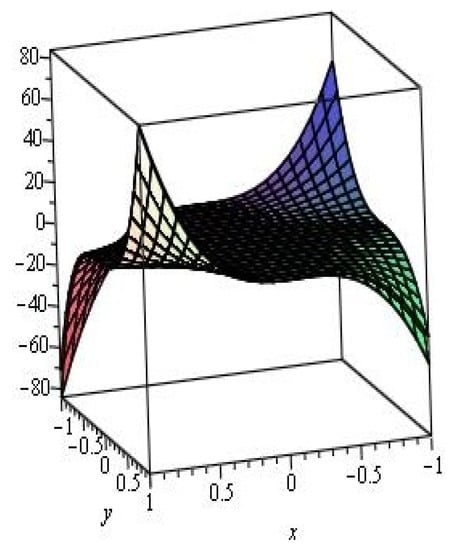
Figure 6. M-polynomial of the armchair polyhex nanotube.

Theorem 4.

Let $V{C}_6[m,n]$ be the Armchair structure of Polyhex nanotube. Then,

$$M_1\left(V{C}_6[m,n]\right)=8m+18mn.$$

$$M_2(V{C}_6[m,n])=(7+27n)m.$$

$${}^{m}M_2(V{C}_6[m,n])=\frac{m}{36}(17+12n).$$

$$R_a(V{C}_6[m,n])=\left[2^{2\alpha }+2^{\alpha +1}{3}^{\alpha }+3^{2\alpha }(3n-1)\right]m.$$

$$R_a(V{C}_6[m,n])=\left[2^{-2\alpha }+2^{1-\alpha }{3}^{\alpha }+3^{-2\alpha }(3n-1)\right]m.$$

$$SDD(V{C}_6[m,n])=\frac{m}{3}(13+18n).$$

3. Conclusions

In this article, closed forms of the M-polynomials for the armchair and the zigzag polyhex nanotubes are obtained. We also provide degree-based topological indices of Polyhex nanotubes. Topological indices thus calculated can help us to understand their physical features, chemical reactivity, and biological activities. From this point of view, topological indices can be regarded as score functions that map each molecular structure to a real number and are used as descriptors. These results can also play a vital role in the determination of the significance of Polyhex nanotubes in industry [18,19]. We invite other researchers to investigate topological indices of recently developed aluminosilicate/alumino-germanate nanotubes [26].