M-Polynomial and Degree-Based Topological Indices of Polyhex Nanotubes
Abstract
:1. Introduction
2. Results and Discussion
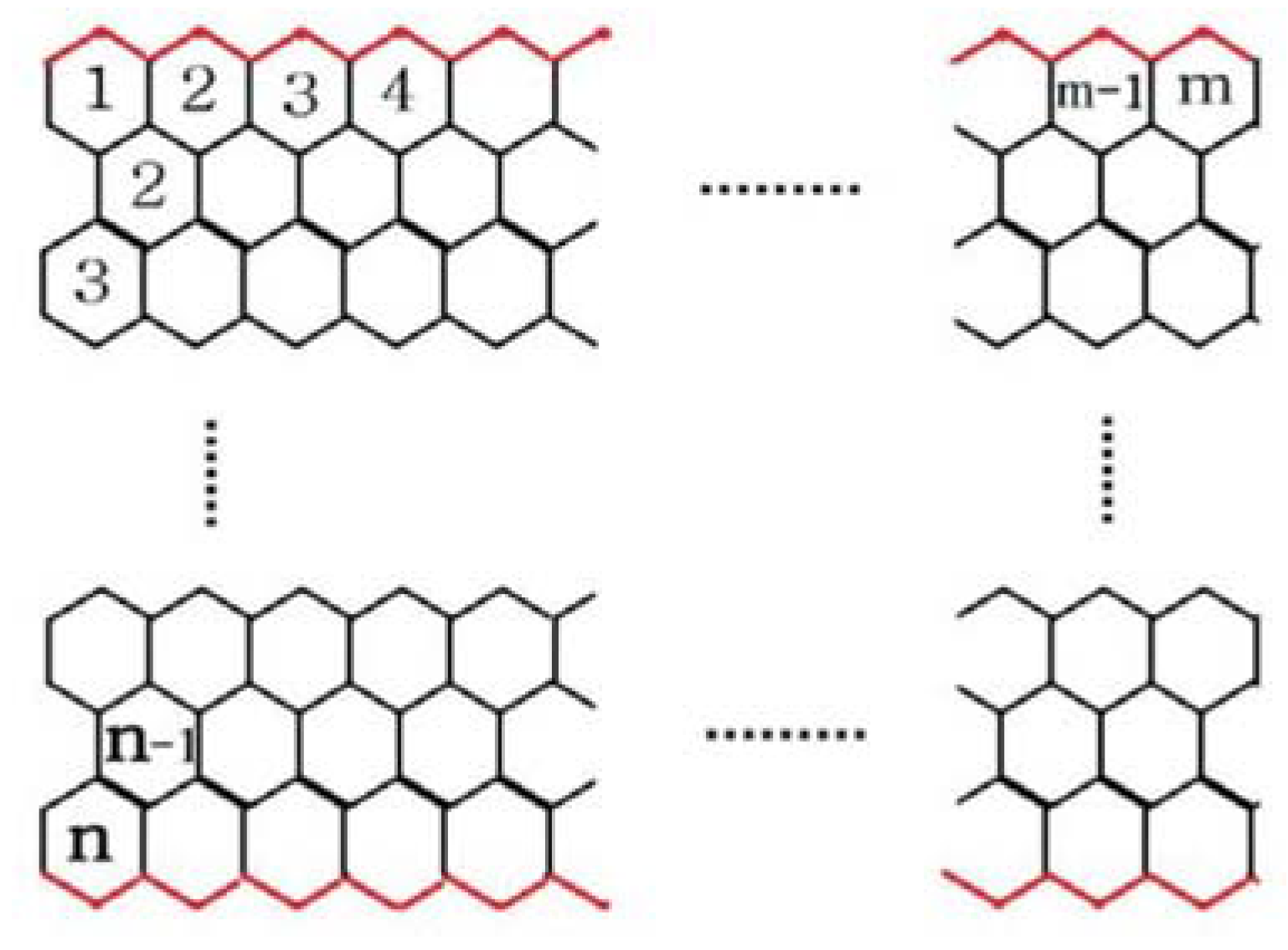
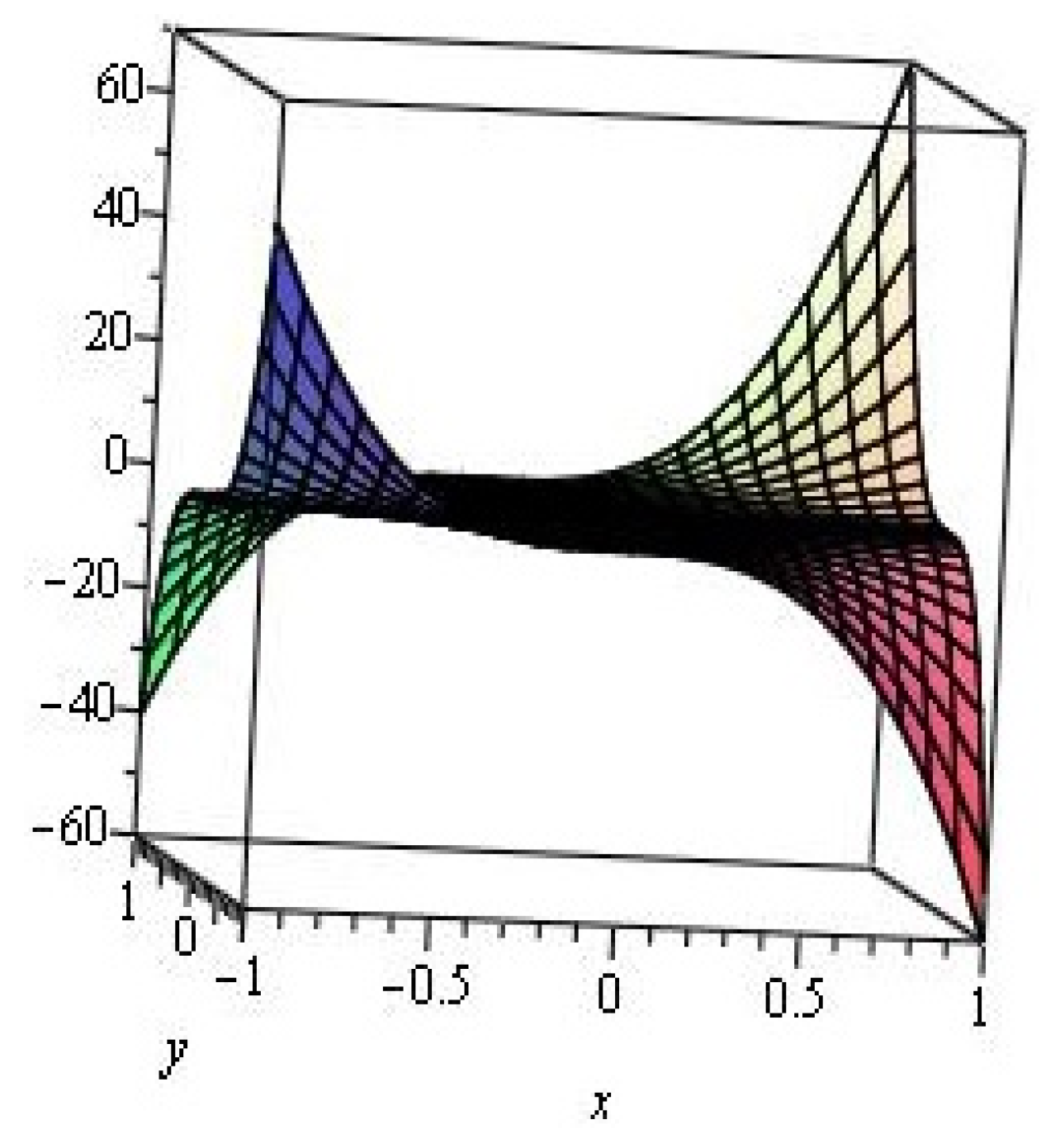
2.1. Zigzag Polyhex Nanotubes
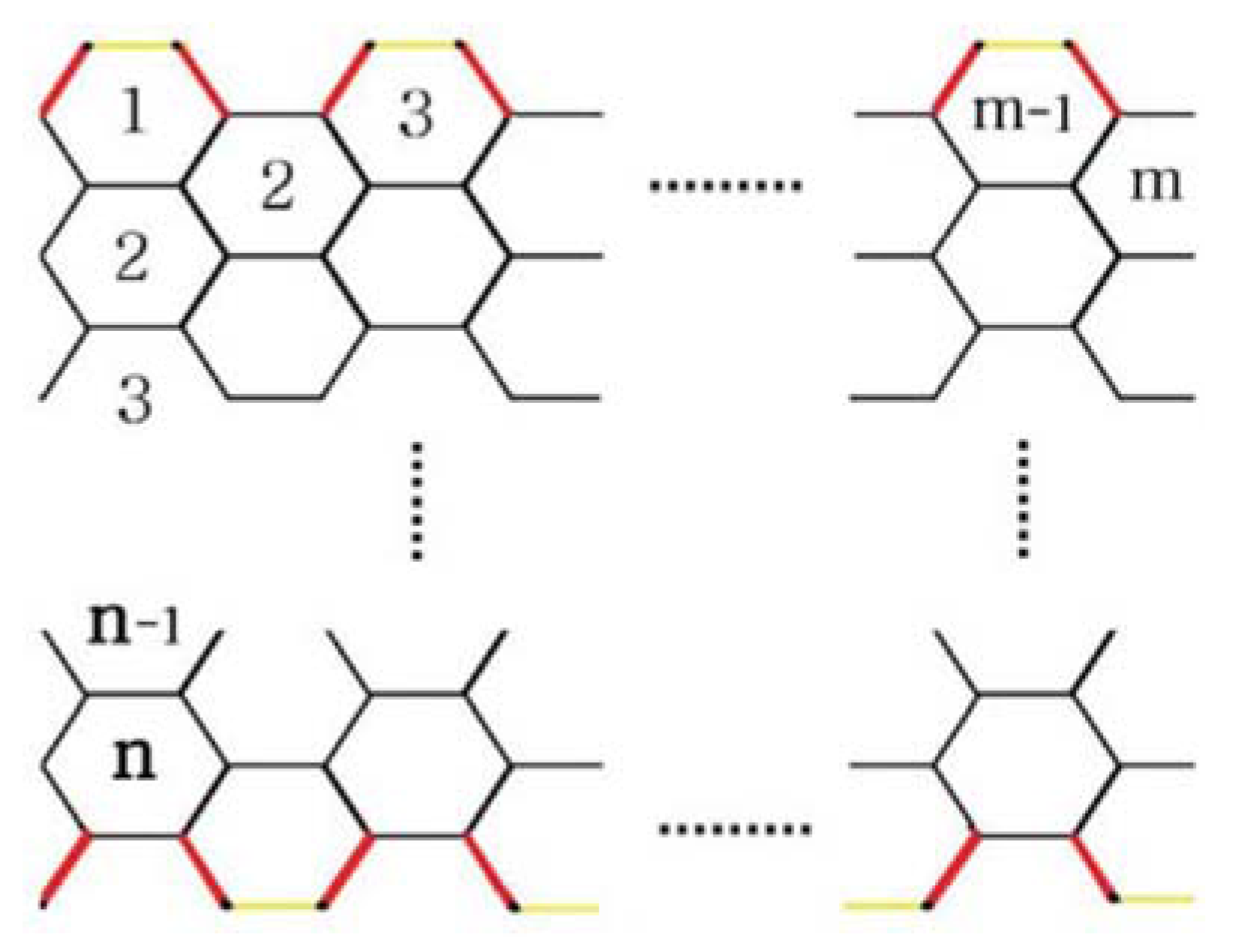
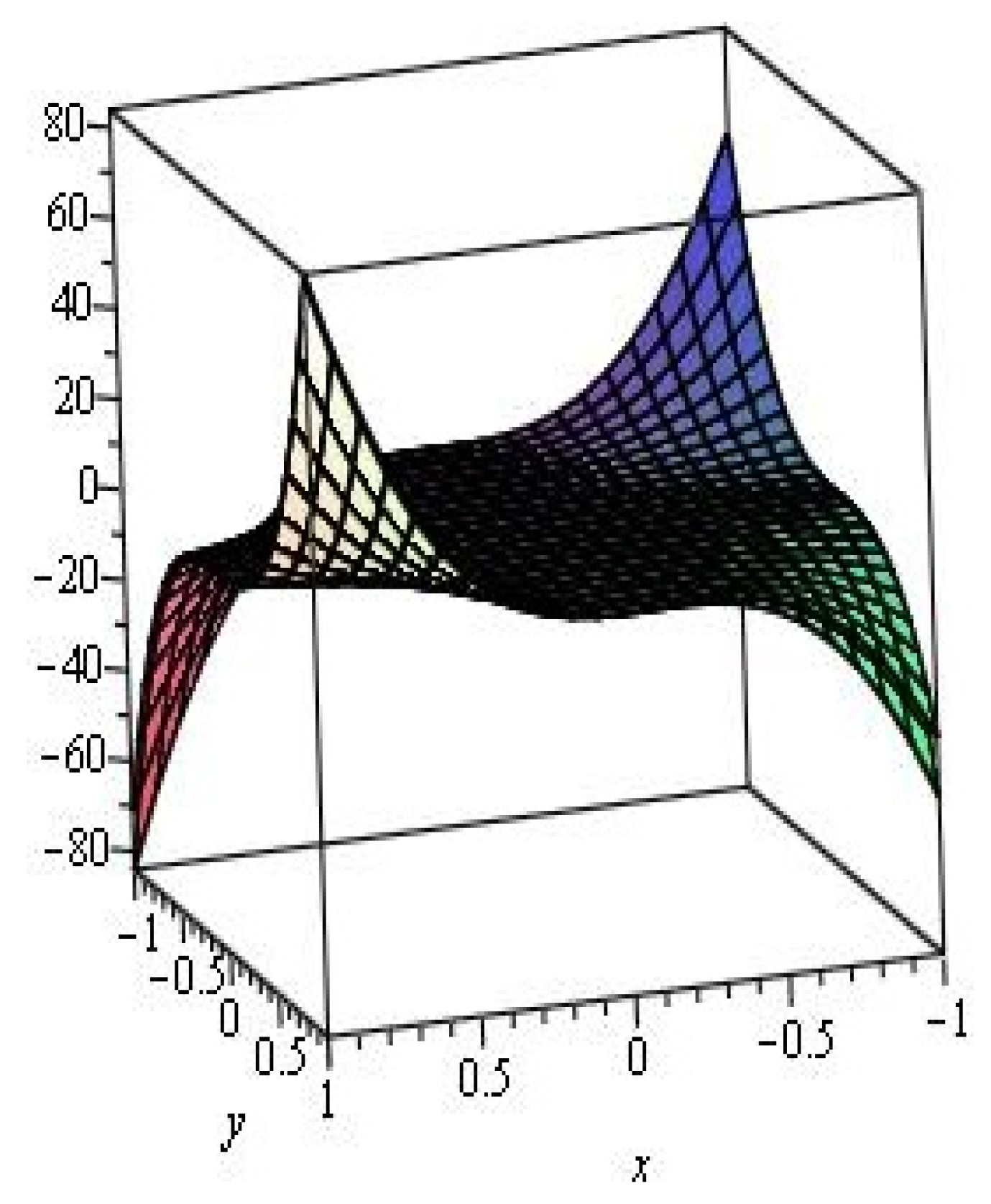
2.2. Armchair Polyhex Nanotubes
3. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- West, D.B. An Introduction to Graph Theory; Prentice-Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Gutman, I. Some properties of the Wiener polynomials. Graph Theory Notes New York 1993, 125, 13–18. [Google Scholar]
- Deutsch, E.; Klavzar, S. M-Polynomial and degree-based topological indices. Iran. J. Math. Chem. 2015, 6, 93–102. [Google Scholar]
- Rucker, G.; Rucker, C. On topological indices, boiling points, and cycloalkanes. J. Chem. Inf. Comput. Sci. 1999, 39, 788–802. [Google Scholar] [CrossRef]
- Klavžar, S.; Gutman, I. A Comparison of the Schultz molecular topological index with the Wiener index. J. Chem. Inf. Comput. Sci. 1996, 36, 1001–1003. [Google Scholar] [CrossRef]
- Brückler, F.M.; Došlić, T.; Graovac, A.; Gutman, I. On a class of distance-based molecular structure descriptors. Chem. Phys. Lett. 2011, 503, 336–338. [Google Scholar] [CrossRef]
- Deng, H.; Huang, G.; Jiang, X. A unified linear-programming modeling of some topological indices. J. Comb. Optim. 2015, 30, 826–837. [Google Scholar] [CrossRef]
- Deng, H.; Yang, J.; Xia, F. A general modeling of some vertex-degree based topological indices in benzenoid systems and phenylenes. Comp. Math. Appl. 2011, 61, 3017–3023. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, F. The Clar covering polynomial of hexagonal systems. Discret. Appl. Math. 1996, 69, 147–167. [Google Scholar] [CrossRef]
- Wiener, H. Structural determination of paraffin boiling points. J. Am. Chem. Soc. 1947, 69, 17–20. [Google Scholar] [CrossRef] [PubMed]
- Gutman, I.; Trinajstic, N. Graph theory, and molecular orbitals total F-electron energy of alternant hydrocarbons. Chem. Phys. Lett. 1972, 17, 535–538. [Google Scholar] [CrossRef]
- Das, K.C.; Gutman, I. Some properties of the second zagreb index. MATCH Commun. Math. Comput. Chem. 2004, 50, 103–112. [Google Scholar]
- Hao, J. Theorems about zagreb indices and modified zagreb indices. MATCH Commun. Math. Comput. Chem. 2011, 65, 659–670. [Google Scholar]
- Li, X.; Shi, Y. A Survey on the Randic Index. MATCH Commun. Math. Comput. Chem. 2008, 59, 127–156. [Google Scholar]
- Munir, M.; Nazeer, W.; Rafique, S.; Kang, S.M. M-polynomial and related topological indices of Nanostar dendrimers. Symmetry 2016, 8, 97. [Google Scholar] [CrossRef]
- Munir, M.; Nazeer, W.; Rafique, S.; Nizami, A.R.; Kang, S.M. M-polynomial and degree-based topological indices of titania nanotubes. Symmetry 2016, 8, 117. [Google Scholar] [CrossRef]
- Munir, M.; Nazeer, W.; Shahzadi, Z.; Kang, S.M. Some invariants of circulant graphs. Symmetry 2016, 8, 134. [Google Scholar] [CrossRef]
- Stover, D.; Normile, D. Buckytubes. Pop. Sci. 1992, 240, 31. [Google Scholar]
- The many faces of nanotech. Nat. Nanotechnol. 2007, 2, 585. [CrossRef]
- Wang, Q.H.; Yan, M.; Chang, R.P.H. Flat panel display prototype using gated carbon nanotube field emitters. Appl. Phys. Lett. 2001, 78, 1294. [Google Scholar] [CrossRef]
- Zhang, L.; Kucera, L.R.; Ummadisetty, S.; Nykaza, J.R.; Elabd, Y.A.; Storey, R.F.; Cavicchi, K.A.; Weiss, R.A. Supramolecular multiblock polystyrene–polyisobutylene copolymers via ionic interactions. Macromolecules 2014, 47, 4387–4396. [Google Scholar] [CrossRef]
- Chakrabarty, A.; Zhang, L.; Cavicchi, K.A.; Weiss, R.A.; Singha, N.K. Tailor-Made fluorinated copolymer/clay nanocomposite by cationic RAFT assisted pickering miniemulsion polymerization. Langmuir 2015, 31, 12472–12480. [Google Scholar] [CrossRef] [PubMed]
- Qiad, Z.; Zhang, L.; Stein, G.E.; Cavicchi, K.A.; Vogt, B.D. Unidirectional alignment of block copolymer films induced by expansion of a permeable elastomer during solvent vapor annealing. Macromolecules 2014, 47, 1109–1116. [Google Scholar]
- Farahani, M.R. Some connectivity indices and zagreb index of polyhex nanotubes. Acta. Chim. Slov. 2012, 59, 779–783. [Google Scholar] [PubMed]
- Iranmaneh, A.; Zeraatkar, M. Computing Ga index for some nanotubes. Optoelectron. Adv. Mater. Rapid Commun. 2010, 4, 1852–1855. [Google Scholar]
- Liou, K.H.; Kang, D.V. Defective single-walled aluminosilicate nanotubes: Structural stability and mechanical properties. ChemNanoMat 2016, 2, 189–195. [Google Scholar] [CrossRef]


| Topological Index | Derivation from | |
| First Zagreb | ||
| Second Zagreb | ||
| Second Modified Zagreb | ||
| General Randi | ||
| General Randi | ||
| Symmetric Division Index |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Munir, M.; Nazeer, W.; Rafique, S.; Kang, S.M. M-Polynomial and Degree-Based Topological Indices of Polyhex Nanotubes. Symmetry 2016, 8, 149. https://doi.org/10.3390/sym8120149
Munir M, Nazeer W, Rafique S, Kang SM. M-Polynomial and Degree-Based Topological Indices of Polyhex Nanotubes. Symmetry. 2016; 8(12):149. https://doi.org/10.3390/sym8120149
Chicago/Turabian StyleMunir, Mobeen, Waqas Nazeer, Shazia Rafique, and Shin Min Kang. 2016. "M-Polynomial and Degree-Based Topological Indices of Polyhex Nanotubes" Symmetry 8, no. 12: 149. https://doi.org/10.3390/sym8120149
APA StyleMunir, M., Nazeer, W., Rafique, S., & Kang, S. M. (2016). M-Polynomial and Degree-Based Topological Indices of Polyhex Nanotubes. Symmetry, 8(12), 149. https://doi.org/10.3390/sym8120149






