EMG Pattern Classification by Split and Merge Deep Belief Network
Abstract
:1. Introduction
2. Materials and Methods
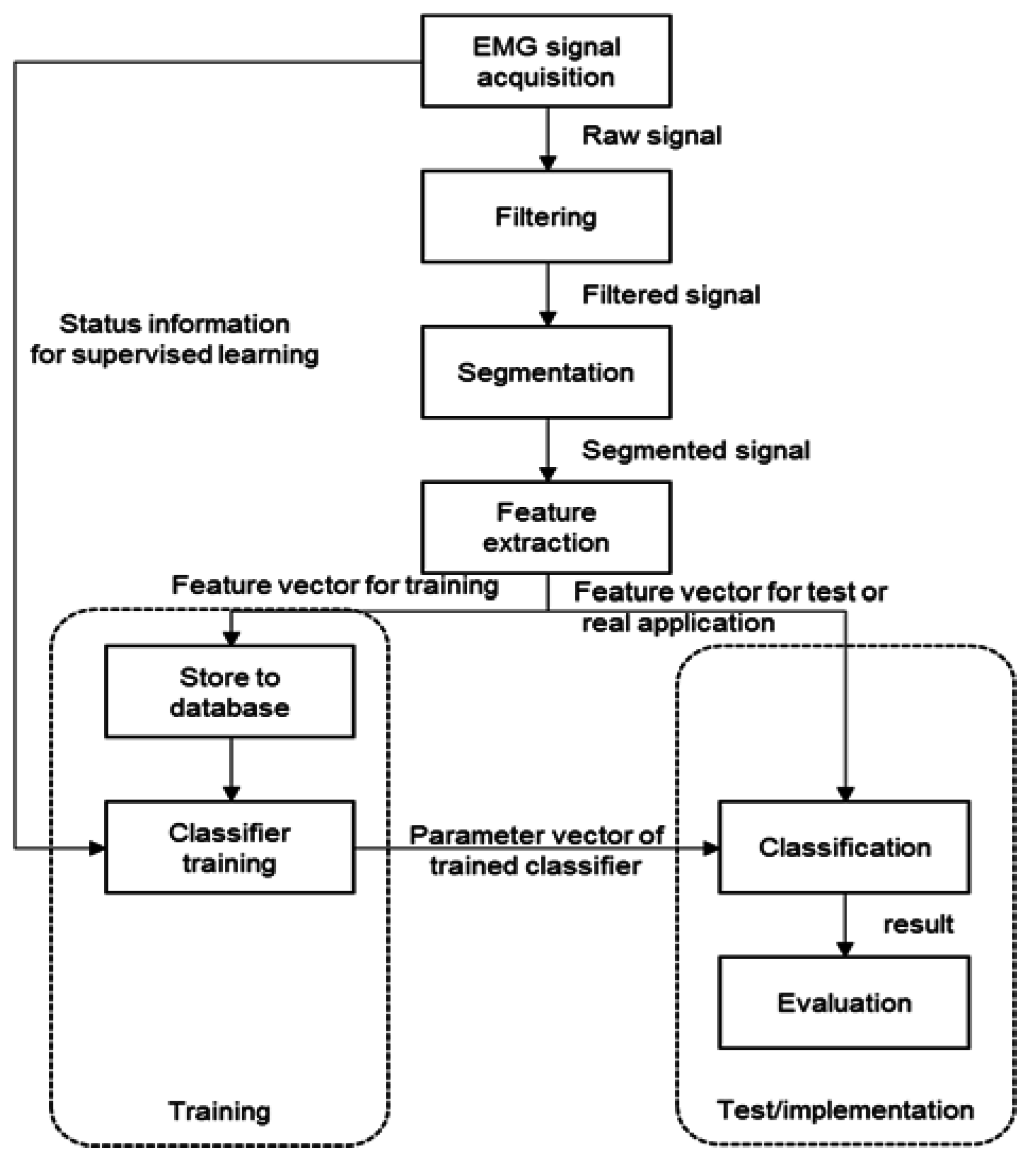
2.1. Pattern Recognition Process
2.2. Feature Extraction
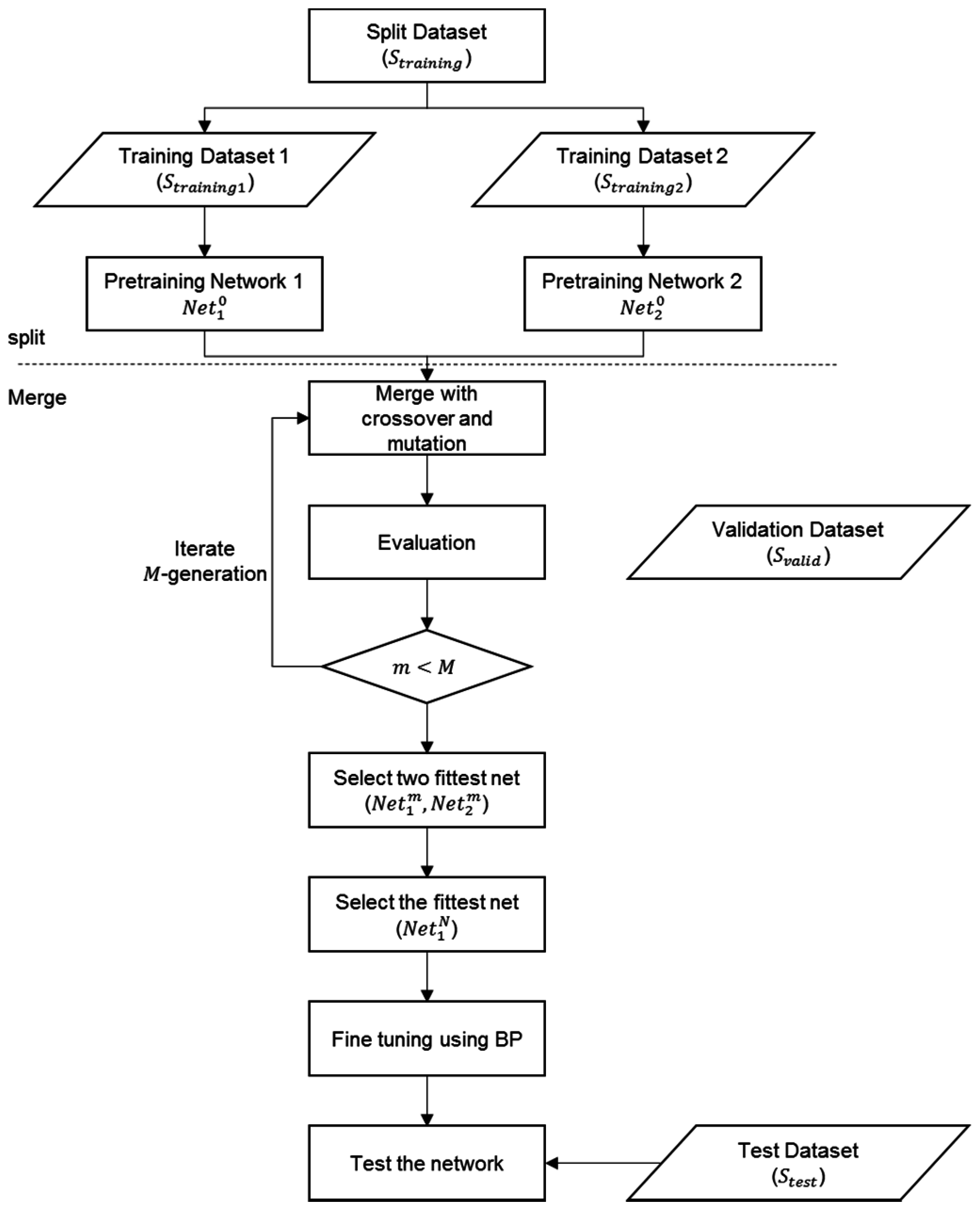
2.3. Split and Merge Deep Belief Network
2.4. Participants and EMG Signal Acquisition
2.5. Training and Test
3. Results
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| BP | Back Propagation |
| DAMV | Different Absolute Mean Value |
| DBN | Deep Belief Network |
| ECU | Extensor Carpi Ulnaris |
| EMG | Electromyography |
| FCU | Flexor Carpi Ulnaris |
| GA | Genetic Algorithm |
| GMM | Gaussian Mixture Model |
| LDA | Linear Discriminant Analysis |
| MAV | Mean Absolute Value |
| MLP | Multi-Layer Perceptron |
| RBM | Restricted Boltzmann Machine |
| SM-DBN | Split and Merge Deep Belief Network |
| SVM | Support Vector Machine |
| ZC | Zero Crossing |
References
- Hudgins, B.; Parker, P.; Scott, R. A new strategy for multifunction myoelectric control. IEEE Trans. Biomed. Eng. 1993, 40, 82–94. [Google Scholar] [CrossRef] [PubMed]
- Saridis, G.N.; Gootee, T.P. Emg pattern analysis and classification for a prosthetic arm. IEEE Trans. Biomed. Eng. 1982, 29, 403–412. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.W.; Lee, G.K. Gait angle prediction for lower limb orthotics and prostheses using an EMG signal and neural networks. Int. J. Control Autom. Syst. 2005, 3, 152–158. [Google Scholar]
- Ajiboye, A.; Weir, R. A heuristic fuzzy logic approach to EMG pattern recognition for multifunctional prosthesis control. IEEE Trans. Neural Syst. Rehabil. Eng. 2005, 13, 280–291. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Naik, G.R.; Huang, S.; Abraham, A.; Nguyen, H.T. Nonlinear multiscale Maximal Lyapunov Exponent for accurate myoelectric signal classification. Appl. Soft Comput. 2015, 36, 633–640. [Google Scholar] [CrossRef]
- Naik, G.R.; Nguyen, H.T. Nonnegative Matrix Factorization for the Identification of EMG Finger Movements: Evaluation Using Matrix Analysis. IEEE J. Biomed. Health Inform. 2015, 19, 478–485. [Google Scholar] [CrossRef] [PubMed]
- Naik, G.; Al-Timemy, A.; Nguyen, H. Transradial Amputee Gesture Classification Using an Optimal Number of sEMG Sensors: An Approach Using ICA Clustering. IEEE Trans. Neural Syst. Rehabil. Eng. 2015, 24, 837–846. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Zhou, P. A Novel Framework Based on FastICA for High Density Surface EMG Decomposition. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 24, 117–127. [Google Scholar] [CrossRef] [PubMed]
- Naik, G.R.; Dinesh, K.K.; Marimuthu, P. Signal processing evaluation of myoelectric sensor placement in low-level gestures: Sensitivity analysis using independent component analysis. Expert Syst. 2014, 31, 91–99. [Google Scholar] [CrossRef]
- Naik, G.R.; Dinesh, K.K. Subtle electromyographic pattern recognition for finger movements: A pilot study using BSS techniques. J. Mech. Med. Biol. 2012, 12, 1–19. [Google Scholar] [CrossRef]
- Naik, G.R.; Dinesh, K. Kumar, Identification of hand and finger movements using multi run ICA of surface electromyogram. J. Med. Syst. 2012, 36, 841–851. [Google Scholar] [CrossRef] [PubMed]
- Naik, G.R.; Acharyya, A.; Nguyen, H.T. Classification of finger extension and flexion of EMG and Cyberglove data with modified ICA weight matrix. In Proceedings of the 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Chicago, IL, USA, 26–30 August 2014; pp. 3829–3832.
- Xie, H.-B.; Huang, H.; Wu, J.; Liu, L. A comparative study of surface EMG classification by fuzzy relevance vector machine and fuzzy support vector machine. Physiol. Meas. 2015, 36, 191–206. [Google Scholar] [CrossRef] [PubMed]
- Palkowski, A.; Grzegorz, R. Basic Hand Gestures Classification Based on Surface Electromyography. Computat. Math. Methods Med. 2016, 2016, 6481282. [Google Scholar] [CrossRef] [PubMed]
- Young, A.J.; Smih, L.H.; Rouse, E.J.; Hargrove, L.J. Classification of simultaneous movements using surface EMG pattern recognition. IEEE Trans. Biomed. Eng. 2013, 60, 1250–1258. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Lee, S. EMG pattern recognition based on artificial intelligence techniques. IEEE Trans. Rehabil. Eng. 1998, 6, 400–405. [Google Scholar] [CrossRef] [PubMed]
- Mandryk, R.L.; Inkpen, K.M.; Calvert, T.W. Using psychophysiological techniques to measure user experience with entertainment technologies. Behav. Inf. Technol. 2006, 25, 141–158. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Ahsan, M.R.; Ibrahimy, M.I.; Khalifa, O.O. EMG signal classification for human computer interaction: A review. Eur. J. Sci. Res. 2009, 33, 480–501. [Google Scholar]
- Al-Angari, H.M.; Kanitz, G.; Tarantino, S.; Cipriani, C. Distance and mutual information methods for EMG feature and channel subset selection for classification of hand movements. Biomed. Signal Process. Control 2016, 27, 24–31. [Google Scholar] [CrossRef]
- Boudjellal, A.; Abed-Meraim, K.; Aissa-El-Bey, A. Sparsity-based algorithms for blind separation of convolutive mixtures with application to EMG signals. In Proceedings of the 2014 IEEE Workshop on Statistical Signal Processing (SSP), Jupiters, Gold Coast, Australia, 29 June–2 July 2014.
- Jeong, E.; Kim, S.; Song, Y.; Lee, S. Comparison of wrist motion classification methods using surface electromyogram. J. Central South Univ. 2013, 20, 960–968. [Google Scholar] [CrossRef]
- Shim, H.M.; Lee, S. Multi-channel electromyography pattern classification using deep belief networks for enhanced user experience. J. Central South Univ. 2015, 22, 1801–1808. [Google Scholar] [CrossRef]
- Hinton, G.; Osindero, S.; Teh, Y. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- An, H.; Shim, H.M.; Na, S.I.; Lee, S. Split and merge algorithm for deep learning and its application for additional classes. Pattern Recognit. Lett. 2015, 65, 137–144. [Google Scholar] [CrossRef]
- THE MNIST Database. Available online: http://yann.lecun.com/exdb/mnist/ (accessed on 18 April 2016).
- Karlssona, S.; Gerdle, B. Mean frequency and signal amplitude of the surface EMG of the quadriceps muscles increase with increasing torque—A study using the continuous wavelet transform. J. Electromyogr. Kinesiol. 2001, 11, 131–140. [Google Scholar] [CrossRef]
- Lee, S.; Kim, J.; Park, S. An enhanced feature extraction algorithm for EMG pattern classification. IEEE Trans. Rehabil. Eng. 1996, 4, 439–443. [Google Scholar] [PubMed]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Representations by Back-Propagating Errors. In Cognitive Modeling; The MIT Press: Cambridge, MA, USA, 1988; pp. 213–220. [Google Scholar]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef] [PubMed]
- Python Software Foundation. Python2.7.7. Available online: https://www.python.org/ (accessed on 18 April 2016).
- Scipy developers. Sciypy. Available online: https://www.scipy.org/ (accessed on 18 April 2016).
- Scikit-learn machine learning in Python. Available online: http://scikit-learn.org/ (accessed on 18 April 2016).
- Palm, R.B. DeepLearnToolbox. Available online: https://github.com/rasmusbergpalm/ (accessed on 18 April 2016).
- The R Foundation. The R Project for Statistical Computing. Available online: https://www.r-project.org/ (accessed on 18 April 2016).




| Parameter | Value |
|---|---|
| Channels | Flexor carpi ulnaris |
| Extensor carpi ulnaris | |
| Sampling rate | 1 kHz |
| Filter | 10–500 Hz 2nd order Butterworth |
| Data window | 166 ms Hamming window, 50% overlapped |
| Features | DAMV, DASDV, MAV, ZC |
| Number of Trials | DBN | SM-DBN | |
|---|---|---|---|
| 1 | 13.09 | 10.82 | |
| 2 | 12.64 | 11.36 | |
| 3 | 9.45 | 8.82 | |
| 4 | 12.64 | 12.36 | |
| 5 | 11.18 | 9.55 | |
| 6 | 12.45 | 11.09 | |
| 7 | 11.64 | 10.73 | |
| 8 | 11.73 | 9.73 | |
| 9 | 12.18 | 11.27 | |
| 10 | 13.00 | 11.36 | |
| Average | 12.00 | 10.709 | |
| Standard-deviation | 1.086 | 1.050 | |
| t-test | Confidence interval | 95% | |
| [0.2873556, 2.2946444] | |||
| t | 2.7027 | ||
| df | 17.979 | ||
| p-value | 0.0146 | ||
| alternative hypothesis | True difference in means is not equal to 0. | ||
| Number of Trials | SM-DBN | DBN | ||||
|---|---|---|---|---|---|---|
| Accuracy (%) | Sensitivity (TPR, %) | Specificity (FPR, %) | Accuracy (%) | Sensitivity (TPR, %) | Specificity (FPR, %) | |
| 1 | 89.18 | 89.27% | 2.90% | 86.91% | 86.98% | 3.56% |
| 2 | 88.64 | 88.73% | 3.08% | 87.36% | 87.44% | 3.46% |
| 3 | 91.18 | 91.29% | 2.34% | 90.55% | 90.83% | 2.53% |
| 4 | 87.64 | 87.74% | 3.37% | 87.36% | 87.43% | 3.46% |
| 5 | 90.45 | 90.58% | 2.55% | 88.82% | 89.02% | 3.02% |
| 6 | 88.91 | 89.11% | 3.00% | 87.55% | 87.80% | 3.42% |
| 7 | 89.27 | 89.34% | 2.90% | 88.36% | 88.36% | 3.16% |
| 8 | 90.27 | 90.31% | 2.59% | 88.27% | 88.37% | 3.19% |
| 9 | 88.73 | 88.87% | 3.04% | 87.82% | 87.74% | 3.28% |
| 10 | 88.64 | 88.70% | 3.07% | 87.00% | 87.12% | 3.48% |
| Average | 89.29 | 89.39% | 2.88% | 88.00% | 88.11% | 3.26% |
| Standard Deviation | 0.010522 | 0.010468119 | 0.003051907 | 0.01085 | 0.011446 | 0.003072 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shim, H.-m.; An, H.; Lee, S.; Lee, E.H.; Min, H.-k.; Lee, S. EMG Pattern Classification by Split and Merge Deep Belief Network. Symmetry 2016, 8, 148. https://doi.org/10.3390/sym8120148
Shim H-m, An H, Lee S, Lee EH, Min H-k, Lee S. EMG Pattern Classification by Split and Merge Deep Belief Network. Symmetry. 2016; 8(12):148. https://doi.org/10.3390/sym8120148
Chicago/Turabian StyleShim, Hyeon-min, Hongsub An, Sanghyuk Lee, Eung Hyuk Lee, Hong-ki Min, and Sangmin Lee. 2016. "EMG Pattern Classification by Split and Merge Deep Belief Network" Symmetry 8, no. 12: 148. https://doi.org/10.3390/sym8120148
APA StyleShim, H.-m., An, H., Lee, S., Lee, E. H., Min, H.-k., & Lee, S. (2016). EMG Pattern Classification by Split and Merge Deep Belief Network. Symmetry, 8(12), 148. https://doi.org/10.3390/sym8120148






