Abstract
Transaction privacy has attracted a lot of attention in the e-commerce. This study proposes an efficient and provable fair document exchange protocol with transaction privacy. Using the proposed protocol, any untrusted parties can fairly exchange documents without the assistance of online, trusted third parties. Moreover, a notary only notarizes each document once. The authorized document owner can exchange a notarized document with different parties repeatedly without disclosing the origin of the document or the identities of transaction participants. Security and performance analyses indicate that the proposed protocol not only provides strong fairness, non-repudiation of origin, non-repudiation of receipt, and message confidentiality, but also enhances forward secrecy, transaction privacy, and authorized exchange. The proposed protocol is more efficient than other works.1. Introduction
Parties involved in Internet-based e-commerce usually do not fully trust each other. This mutual distrust is a major motivator for the fair exchange of documents between parties. For example, many consumers desire to fairly purchase products such as digital film, video, or music from online merchants using electronic cash [1,2]. A fair document exchange protocol should provide the following basic security features [3,4] to enhance the security of e-commerce:
Strong fairness: Each party obtains the expected document from the other party at the end of the protocol. Neither party has any advantage if one party misbehaves or prematurely aborts.
Non-repudiation of origin (NOO): The sender of the document generates irrefutable origin evidence for the receiver that can be presented to a third party, who can determine if the sender is the authorized owner of a given document.
Non-repudiation of receipt (NOR): The designated receiver generates irrefutable receipt evidence for the sender of the document that can be presented to a third party, who can determine if the designated receiver has received a given document.
Message confidentiality: Only designated receivers can disclose the delivered document.
Previous researchers have proposed several fair exchange protocols. Fair exchange protocols can be classified into different groups based on the type of content exchanged: (i) fair document exchange protocols [4–10]; (ii) optimistic fair exchange protocols of digital signature [11–15]; (iii) electronic contract signing protocols [16–22]; and (iv) certified e-mail/e-goods delivery protocols [23–30]. Optimistic fair exchange protocols of digital signature and contract signing protocols exchange digital signatures fairly. The fair exchange protocols of digital signature that incorporate an offline trusted third party (TTP) are called optimistic [11]. In the optimistic fair exchange protocol of digital signature, the sender transmits the digital signature of origin to fairly obtain irrefutable evidence of receipt. In the contract signing protocol, the sender, and the receiver fairly exchanging their respective digital signatures for the same digital contract, which is already known by both parties. The concurrent signature scheme [31] is another mechanism for fairly exchanging signatures. After concurrent signature exchange, each signer believes that he himself will obtain the correct signature of the opposing party fairly. Upon release of the keystone, both signatures will bind to their true signer. Unfortunately, digital signatures limit the format and content of the message to be exchanged. However, it is not possible to implement fair document exchange protocol by modifying the optimistic fair exchange protocols of digital signature and the contract signing protocols or adopting concurrent signature mechanisms. In certified e-mail/e-goods delivery protocols, the sender can only fairly exchange a digital document based on the irrefutable receipt (i.e., the digital signature) of the designated receiver. Because of the specific characteristics of receipt in certified e-mail/e-goods delivery protocols, it is not possible to implement the fair document exchange protocol by altering certified e-mail/e-goods delivery protocols. A fair document exchange protocol enables the fair exchange of any type of digital document between mutually distrusting parties. Any type of digital document means that the message format and content are not restricted. For example, the document may be a piece of a password, business report, purchase order, a movie, electronic letter, digital content, or digital cash.
Digital rights management (DRM) [32,33] protects the document against unauthorized exchange, and further prevents the unauthorized party from re-exchanging the received notarized document in e-commerce. However, DRM cannot guarantee that irrelevant documents are fairly exchanged. In other words, DRM cannot ensure fairness. Therefore, both parties may obtain different advantages by unexpectedly aborting or misbehaving in the DRM system.
The involvement of a trusted third party (TTP) between mistrusting parties is necessary to ensure fairness in the fair document exchange protocol. Fair document exchange protocols can be classified into two types: (1) online TTP model, in which the TTP is actively involved in each exchanging transaction; (2) offline TTP model, in which the TTP is not involved in each exchanging transaction. The offline TTP only notarizes exchanged documents and intervenes in case of dispute between exchanging parties.
A fair document exchange protocol that adopts an online and centered trusted third party (TTP) could be expensive to maintain and may cause the communication bottleneck problem. Involving the online TTP in each transaction of the fair document exchange protocol remarkably decreases performance, especially in a multi-receiver context. Therefore, researchers have proposed several fair document exchange protocols with offline TTP [4,6–10]. The main idea of these studies is that the sender first sends the ciphertext of his/her own document before obtaining the expect document from the opposite party. Both parties will then fairly exchange the decryption keys of the ciphertext. A fair document exchange protocol includes two important functions, verifiability and recoverability, which are essential to ensuring strong fairness. Verifiability means that the legal receiver can verify the accuracy of the received ciphertext before obtaining the real document. Recoverability allows the legal receiver to recover the document with assistance of the offline TTP when the opposing party misbehaves or prematurely aborts the exchange.
There are two main strategies to ensure the verifiability and recoverability of exchanged messages in offline TTP models. In the first strategy [6–10], the offline TTP helps the sender encrypt the document, and then generates its certified commitment. However, the sender may attempt to fairly exchange the same document with many participants. This compromises transaction privacy because each participant gets the same certified commitment and ciphertext decryption key. For example, a vendor may fairly exchange the same product with many buyers in a multi-receiver e-commerce environment. This allows one buyer to identify other buyers buying the same product. Although the sender can require the offline TTP to re-generate a new certified commitment during each transaction to maintain the transaction privacy, the offline TTP must be online. This online model has some drawbacks. Therefore, fair document exchange protocols [6–10] based on this first strategy are not practical for multi-receiver e-commerce environments, which require transaction privacy.
In the second strategy, the offline TTP issues a certified commitment for each document using the public key-based verifiable encryption method [4]. This verifiable encryption method ensures that the designated receiver can verify the relationship between the received ciphertext and the expected document before obtaining the real document. However, the verifiable encryption method ensures that the bit length of the exchanged document is limited for each transaction in the fair document protocol. The sender must perform fair document exchange protocols many times for large exchanged documents, such as films. Thus, a fair document exchange protocol based on this second strategy is inefficient and unpractical. In addition, the transaction privacy of the fair document exchange protocol based on the verifiable encryption method [4] must be enhanced.
This paper proposes an efficient and provable fair document exchange protocol that differs from both of these strategies. The proposed protocol integrates encryption and digital signature by inspiring from the concept of extractable commitment technology. It not only ensures strong fairness, non-repudiation of origin, non-repudiation of receipt, and message confidentiality, but also provides the following security functions to enhance the security of fair document exchange:
Backward and forward secrecy: Nobody except the designated receiver can obtain the session key in the previous or next transaction, even if an adversary compromises the current session key.
Transaction privacy: Each transaction keeps the identity of the participants and the exchanging documents secret. In this case, a legal receiver who has obtained a document still cannot learn the behavior of the other transactions for the same document.
Authorized exchange: The receiver can verify the ownership of the notarized document to prevent unauthorized exchange. The proposed protocol prevents an unauthorized party from re-exchanging or re-distributing previously received documents.
Resisting the replay attack: No one can replay previous eavesdropped messages to impersonate legal participants or exchange documents with other participants.
In the proposed protocol, the notary notarizes each document only once and gives the recovery certificate to the authorized party. Verifiable documents, such as digital signatures or e-cash, do not need to be notarized in the proposed protocol. After notarization, the authorized party can use its recovery certificate to exchange the document with several different parties without adversely affecting transaction privacy. The offline notary does not need to store any messages or maintain any public catalog after notarizing the documents. These features make the proposed protocol practical and cost-effective for multi-receiver e-commerce environments.
The remainder of the paper is organized as follows. Section 2 defines some notations. Section 3 describes the proposed fair document exchange protocol. Section 4 demonstrates the security definitions and analyses. Section 5 discusses functionalities and performance. Finally, Section 6 provides some brief conclusions.
2. Preliminaries
In the fair document exchange, the notary T is an offline third party trusted by both participants. Thus, the notary T should not conspire with any participants. All parties have access to the public description information descA of MA and public description information descB of MB. For instance, the title, movie length, and film director are the public description information descA of a popular movie MA. Moreover, all public keys are certified by Certificate Authority (CA) and known by all participants. This paper uses the following notations:
A, B: The unique identities for Alice A and Bob B, respectively.
MA: The document that Alice A would like to transmit to Bob B for fair exchange.
MB: The document that Bob B would like to transmit to Alice A for fair exchange.
T: The unique identity for the notary T for the documents MA and MB.
descA, descB: The public description information of MA and MB, respectively.
PRu and PUu: RSA-based [34] private and public keys of user u, where u ∈ {A, B, T}. For example, PRA is the private key of Alice A, and so on.
E(PUu, X) and D(PRu, Y): RSA-based encryption and decryption algorithms, where the plaintext X and the ciphertext Y satisfy that Y = E(PUu, X) and X = D(PRu, Y).
S(PRu, X) and V(PUu, Y): RSA-based message recovery signature algorithms where the message X and the signature Y satisfy that Y = S(PRu, X) and X = V(PUu, Y).
E[Ki, X] and D[Ki, Y]: Symmetric encryption and decryption functions such as AES-128 [35], where the message X and the ciphertext Y satisfy that Y = E[Ki, X] and X = D[Ki, Y] using the same secret key Ki.
kT: The secret key of the notary T for symmetric encryption and decryption functions.
β: The bit length of the secret key of the symmetric encryption function.
H(.) and G(.): The collision-resistance one-way hash functions [36], where H:{0, 1}*→{0, 1}β and G:{0,1}*→{0,1}(3/2)β.
The bitwise exclusive-OR operator.
x|: The bit length of the value x.
3. Fair Document Exchange Protocol
The proposed fair document exchange protocol consists of three phases: notarization phase, fair exchange phase, and arbitration phase. The notary T notarizes the documents in the notarization phase. In the fair exchange phase, Alice A uses the notarized document MA to fairly exchange the notarized document MB with Bob B without notary involvement. If a dispute occurs, the offline notary helps both participants retrieve their documents in the arbitration phase. The proposed protocol integrates encryption and digital signature by the extractable commitment technology. The extractable commitment technology integrates encryption and digital signature via special padding process. The padding processes of the proposed protocol show in Steps N2 and N3 of the notarization phase, and Steps F1 and F2 of the fair exchange phase.
3.1. Notarization Phase
Without loss of generality, consider the following example to explain the procedures of the notarization phase. Alice A performs Steps (N1) to (N3) to obtain the recovery certificate CertA = {WA, vA, CA, descA, σA} and secret key KA for MA. Bob B runs the same procedure to obtain the recovery certificate CertB = {WB, vB, CB, descB, σB} and secret key KB for MB. The notary has to make sure the ownership of exchange document. The verifying ownership process is out of the scope of this paper. The step (N1) of the notarization phase should include the out-of-band method. Figure 1 shows a diagram of this phase.

Step (N1): Alice A sends the document MA and its description information descA to the notary T via the out-of-band method.
Step (N2): After verifying the ownership of MA, the notary T performs the following sub-steps to send back {πA, vA, Ω} to Alice A:
Step (N2-1): Randomly selects a secret key KA and number r1 such that KA = (kx||ky) and |kx| = |ky| = β/2, and |r1| = β.
Step (N2-2): Defines d1 = (ky||r1) and c1 = (kx||0β/2)⊕H(d1).
Step (N2-3): Computes four values wA = G(c1)⊕d1, vA = H(wA)⊕c1, πA = E(PUA, S(PRT, wA)) and CA = E[KA, MA], where PRT is the private key of the notary T.
Step (N2-4): Derives the warrant WA = E[kT, wA] and the signature σA = S(PRT, H(WA||vA||CA||descA||PUA)) using the private key PRT of the notary T.
Step (N2-5): Sends back {πA, vA, Ω} to Alice A, where the ciphertext Ω = E[KA, (WA||σA)].
Step (N3): Alice A runs the following sub-steps to obtain secret key KA and the recovery certificate CertA of MA:
Step (N3-1): Recovers the value wA from πA by computing V(PUT, D(PRA, πA)).
Step (N3-2): Derives three values c1 = H(wA)⊕vA, d1 = G(c1)⊕wA and u1 = c1⊕H(d1).
Step (N3-3): If the rightmost β/2 bits of u1 are “0”, then go to next sub-step. Otherwise, terminates this notarization process.
Step (N3-4): Assigns kx as the left-hand β/2 bits of u1 and ky as the left-hand β/2 bits of d1.
Step (N3-5): Generates the secret key KA = (kx||ky) and recovers the values (WA||σA) by computing D[KA, Ω].
Step (N3-6): Derives the ciphertext CA = E[KA, MA].
Step (N3-7): If V(PUT, σA) is equal to H(WA||vA||CA||descA||PUA), then stores the recovery certificate CertA = {WA, vA, CA, descA, σA} and secret key KA of MA. Otherwise, terminates this notarization process.
3.2. Fair Exchange Phase
Without loss of generality, consider the following example to explain the procedures of this phase. Alice A wants to obtain the document MB from Bob B in a fair way, and Bob B wants to obtain the document MA from Alice A in a fair way. Figure 2 shows the diagram of this phase, and the following subsection describes the steps in detail.
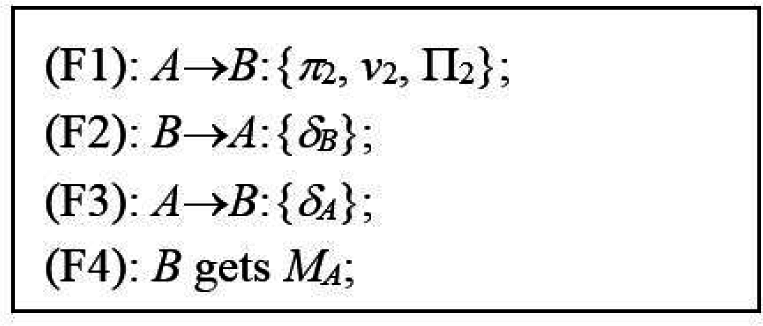
Step (F1): Alice A performs the following sub-steps to send the session information {π2, v2} and the ciphertext Π2 to Bob B:
Step (F1-1): Generates the request information req_info = (A||B||T||descA||descB||Tstamp), where Tstamp is time stamp.
Step (F1-2): Randomly selects a session key K2 and number r2 such that K2 = (x||y), |x| = |y| = β/2, and |r2| = β.
Step (F1-3): Defines d2 = (y||r2) and c2 = (x||0β/2)⊕H(d2).
Step (F1-4): Computes three values w2 = G(c2)⊕d2, π2 = E(PUB, (PUA||α2)) and v2 = H(w2)⊕c2, where α2 = S(PRA, (ϖ||w2)), where ϖ = H(CertA||req_info||w2).
Step (F1-5): Sends the session information {π2, v2} and the ciphertext Π2 to Bob B, where the ciphertext Π2 = E[K2, (CertA|| req_info)].
Step(F2): Bob B performs the following sub-steps to get session key K2 and the recovery certificate CertA of the document MA, and sends the ciphertext {δB} to Alice A:
Step (F2-1): Obtains (PUA||α2) by computing D(PRB, π2) and recovers (ϖ||w2) by computing V(PUA, α2).
Step (F2-2): Computes three values c2 = H(w2)⊕v2 and d2 = G(c2)⊕w2, u2 = c2⊕H(d2).
Step (F2-3): If the rightmost β/2 bits of u2 are “0”, then go to next sub-step. Otherwise, terminates this exchanging process.
Step (F2-4): Assigns x as the left-hand β/2 bits of u2 and y as the left-hand β/2 bits of d2.
Step (F2-5): Generates the session key K2 = (x||y) to recover the value (CertA||req_info) by computing D[K2, Π2], where CertA = {WA, vA, CA, descA, σA}. If ϖ ≠ H(CertA||req_info||w2) then terminates this exchanging process.
Step (F2-6): If V(PUT, σA) is not equal to H(WA||vA||CA||descA||PUA) then terminates this exchanging process because Alice A may not be the authorized owner of MA or CA is not the corrected cipher text of the expected document MA.
Step (F2-7): Checks the time stamp Tstamp and the identities of participants in req_info.
Step (F2-8): Generates the signature SB = S(PRB, H(req_info||CertA||MB)). SB is the irrefutable receipt of Bob B.
Step (F2-9): Sends the message δB = E[K2, (SB||KB||CertB)] back to Alice A, where KB is the secret key obtained from notarization phase. If Bob B is the original owner of the document MB, which is verifiable such as digital signature or e-cash, Bob B uses MB in place of (KB||CertB) in δB.
Step (F3): Alice A performs the following sub-steps to get MB and send the ciphertext {δA} back to Bob B:
Step (F3-1): Obtains the values (SB||KB||CertB) by computing D[K2, δB] where CertB = {WB, sB, CB, descB, σB} and gets the document MB = D[KB, CB]. If the document MB is verifiable, Alice A will get MB after decrypting δB.
Step (F3-2): If V(PUT, σB) is not equal to H(WB||sB||CB||descB||PUB) then terminates this exchanging process because MB may not be the expected document or Bob B may not be the authorized owner of MB.
Step (F3-3): Verifies descB for the document MB and checks whether V(PUB, SB) is equal to H(req_info||CertA||MB).
Step (F3-4): Generates irrefutable receipt SA = S(PRA, H(req_info||MA||MB)).
Step (F3-5): Sends the ciphertext δA = E[K2, (KA||SA)] back to Bob B.
Step (F4): Bob B recovers (KA||SA) by computing D[K2, δA], and obtains the document MA = D[KA, CA], where CA is included in CertA which Bob B has gotten in Step(F2). Finally, Bob B verifies descA for MA and checks whether V(PUA, SA) is equal to H(req_info||MA||MB). If this holds, the fair exchange phase is complete. Otherwise, Bob B can initiate the arbitration phase to maintain strong fairness.
3.3. Arbitration Phase
Any participants may prematurely abort the fair exchange phase. All possible arbitration cases are as follows:
Case 1: Alice A generates all messages of Step (F1) of the fair exchange phase to request for arbitration directly.
Case 2: After receiving {π2, v2, Π2} of Step (F1), Bob B generates all messages of Step (F2) and initiates the arbitration phase without sending back the message {δB} of Step (F2).
Case 3: Alice A obtains the ciphertext {δB} after Step (F2) but does not perform Step (F3).
To ensure strong fairness, Alice A and Bob B obtain the exchange documents MB and MA by initiating the arbitration phase, as in the Cases 2 and 3. The initiator of the arbitration phase provides the recovery certificate of the exchanged document to the other party. In Case 1, Alice A does not obtain the recovery certificate CertB from Bob B. In this case, notary T does not perform the arbitration phase with Alice A. In Case 2, Bob B generates the irrefutable receipt and uses the recovery certificate CertA to initiate the arbitration phase. Bob B passes all verifications of the notarization phase. In Case 3, Alice A always gets the document MB before sending the ciphertext {δA} of Step (F3) to Bob B. If Alice A prematurely stops sending the ciphertext {δA} of Step (F3) to Bob B, Bob B can initiate the arbitration phase with the messages {CertA, req_info, w2} received in Step (F1), two irrefutable evidences {α2, SB}, and his own document MB. In these two cases, the notary T first ensures the truthfulness of transaction, and then recovers the document MA for Bob B and sends the document MB to Alice A to maintain strong fairness in the fair document exchange protocol.
Step (A1): Checks two equations: V(PUA, α2) = w2 and V(PUB, SB) = H(req_info||CertA||MB). If one of them is false, then terminates the arbitration process because the requester is unable to provide irrefutable evidences for the truthfulness of transaction.
Step (A2): Checks the equivalence of V(PUT, σA) and H(WA||vA||CA||descA||PUA). If it is false, then terminates the arbitration process, where CertA = {WA, vA, CA, descA, σA}.
Step (A3): Derives the value wA = D[kT, WA].
Step (A4): Recovers the secret key KA using the values {wA, vA} as the procedures of Steps (N3-2) to (N3-5) of the notarization phase.
Step (A5): Recovers the document MA by computing D[KA, CA].
Step (A6): Sends the document MB to Alice A and the document MA to Bob B via the out-of-band method or the secure channel, simultaneously.
4. Security Analysis
This section demonstrates the security functions of the proposed protocol. The proposed protocol enhances the security of our draft protocol [37]. The draft protocol [37] only includes partial idea of the proposed protocol in this paper. This paper completely details our fair document exchange protocol and demonstrates its security by formal method. Specifically, Section 4.1 uses the random oracle technique [38] to prove message confidentiality. Next, Section 4.2 demonstrates backward and forward secrecy, and Section 4.3 proves transaction privacy. Section 4.4 proves non-repudiation of origin and receipt. Section 4.5 describes the authorized exchanging property. Section 4.6 proves the strong fairness of this approach. Finally, Section 4.7 discusses the replay attack.
4.1. Message Confidentiality
Message confidentiality means that the adversary cannot learn any information from the communication transcripts {π2, v2, Π2, δA, δB} of the proposed fair exchange phase. In the fair exchange phase, the session information {π2, v2} of Step (F1) is the most important ciphertext for protecting the session key K2. This session key K2 encrypts other ciphertexts {Π2, δA, δB} using a symmetric encryption algorithm such as AES-128 [35]. The session key K2 of the proposed protocol is random and independent for each transaction. To demonstrate the advantage probability on the adversary learning any information of the session key K2, Definition 1 defines an interactive game based on random oracle technique [38]. Based on Definition 1, Theorem 1 proves the advantage probability of an adversary that learns any information of the session key K2 from the session information {π2, v2}. By Theorem 1, Theorem 2 demonstrates the advantage probability of an adversary learning any information of the exchanged documents MA and MB. Finally, Theorem 3 proves that the proposed protocol provides the message confidentiality.
Definition 1 (Message confidentiality of the session information): The session information {π, v} of Step (F1) achieves the message confidentiality against adaptive chosen-ciphertext attacks (IND-CCA2) [39], if no probabilistic polynomial time (PPT) adversary V has a non-negligible advantage in the following interactive game:
Stage 1: The challenger generates the public/private key pair {PUU, PRU} of user U with respect to the security parameter. The private key PRU is kept secret while the public key PUU is given to the adversary V.
Stage 2: The adversary V makes a number of adaptively queries to the following oracles, i.e., each query may be based on the knowledge of previous replies.
Encryption oracle: The adversary V provides an arbitrary session key K and two distinct public keys {PUS, PUR} to query the encryption oracle (simulated by the challenger). The session information {π, v} for the sender S’s public key PUS and the designated receiver R’s public key PUR is returned if the public keys {PUS, PUR} are valid in the sense that {PUS, PUR} are in the range of Stage 1. Otherwise, rejects the query.
Decryption oracle: The adversary V provides the session information {π, v} with two distinct public keys {PUS, PUR} to query the decryption oracle. The session key K for the sender S’s public key PUS and the designated receiver R’s public key PUR is returned if the decryption oracle is successful and {PUS, PUR} are valid in the sense that {PUS, PUR} are in the range of Stage 1. Otherwise, rejects the query.
Stage 3: The adversary V produces two distinct session keys {K0, K1} to query the encryption oracle, where |K0| = |K1| = β. The challenger flips a coin λ←{0, 1} and sends back the challenge ciphertext {π*, v*} under the session key Kλ for the sender A and the designated receiver B.
Stage 4: The adversary makes a number of new queries as those in Stage 2 with restriction that it cannot query decryption oracle with the challenge ciphertext {π*, v*} of Stage 3.
Stage 5: At the end of the interactive game, the adversary V outputs a bit λ'. The adversary V wins the interactive game if λ' = λ. The advantage probability of the adversary V is defined as εkey = |Pr[λ' = λ]-1/2|.
Theorem 1. Let β be a security parameter. Under the random oracle model, if there exists a PPT algorithm that breaks the IND-CCA2 security of the session information {π, v} with advantage at least εkey, then there exists another PPT algorithm that solves the RSA problem with probability at least 2εkey − 2 × (qE + qD)/2β, where qE and qD represent the maximum number of encryption oracle and decryption oracle queries made by Adversary V during the game of Definition 1.
Proof. Assume that there exists Adversary V who wins the interactive game in Definition 1 of Section 4.1 with a non-negligible advantage. Algorithm Ψ then runs V as a subroutine to solve the RSA problem with a non-negligible advantage. Definition 3 defines the RSA problem.
Definition 3 (RSA Problem) [40]: Given the RSA-based public key PUU of party U and a ciphertext C(=E(PUU, M)), to compute the plaintext M.
Suppose Ψ is given a ciphertext C* and the public key PUB of the RSA problem, Ψ runs V as a subroutine to find the plaintext M* such that C* = E(PUB, M*). The term Ψ simulates the environment of interactive game in Definition 1 as follows:
Ψ maintains three lookup tables {τH, τG, τα} to simulate the H hash oracle, encryption oracle and decryption oracle. All oracles of the interactive game are defined as follows:
H oracle: For querying H(d), the oracle replies the previously defined value h from τH if τH has defined H(d) = h. Otherwise, the oracle returns a random value h and stores {d, h} in τH, where |h| = β.
Encryption oracle: Given the session key K = (x||y) and two distinct public keys {PUS, PUR}, the encryption oracle performs the following steps to return the session information {π, v}:
(E1): Checks the public keys {PUS, PUR} are in the range of Stage 1 of Definition 1. If PUS = PUR, then rejects the query.
(E2): Selects a random number r, where |r| = β.
(E3): Sets d = (y||r) and simulates H(d) as described in H oracle.
(E4): Computes c = (x||0β/2)⊕H(d). If the value G(c) has defined in τG, go to Step (E2).
(E5): Selects a random value α and sets (ϖ||w) = V(PUS, α), where |w| = (3/2)β.
(E6): Simulates H(w) as described in H oracle.
(E7): Computes v = H(w)⊕c. If the tuple (v, α) does not defined in τα, adds new tuple (v, α) into τα. Otherwise, go to Step (E5).
(E8): Defines G(c) = (w⊕d) and adds new record {c, (w⊕d)} into τG.
(E9): Returns the session information {π, v}, where π = E(PUR, (PUS||α)).
Decryption oracle: Given the session information {π, v} with two distinct public keys {PUS, PUR}, the decryption oracle performs the following steps to return the session key K:
(D1): Checks the public keys {PUS, PUR} are in the range of Stage 1 of Definition 1. If PUS = PUR, then rejects the query.
(D2): Looks for a tuple (v, *) of τα according to the index value v. If the tuple (v, *) does not define in τα, the oracle randomly selects a random value α. Otherwise, retrieves the value α from τα according to the index value v.
(D3): Checks the equation π = E(PUR, (PUS||α)). If it is incorrect, rejects the query.
(D4): Computes (ϖ||w) = V(PUS, α), where |w| = (3/2)β.
(D5): Simulates H(w) as described in H oracle and computes c = H(w)⊕v.
(D6): If G(c) has defined in τG, retrieves the defined value from τG. Otherwise, defines G(c) = g, where g is random value and |g| = (3/2)β.
(D7): Computes d = G(c)⊕w and simulates H(d) as described in H oracle.
(D8): Computes u = c⊕H(d). If the rightmost β/2 bits of u are “0”, then updates the tuple (v, α) of τα and the record {c, (w⊕d)} of τG. Otherwise, rejects the query.
(D9): Returns the session key K = (x||y), where x is the left-hand β/2 bits of u and y is the left-hand β/2 bits of d.
After completing Stage 2 of Definition 1, V produces two distinct session keys {K0, K1} and requests Ψ for a challenge ciphertext built under Sender A’s public key PUA and the designated Receiver B’s public key PUB, where PUA ≠ PUB.
In Stage 3 of Definition 1, Ψ generates the challenge ciphertext {π*, v*} to V such that π* = C* and the value v* is a random number, where |v*| = β.
In Stage 4 of Definition 1, Ψ answers V’s subsequence queries as in Stage 2 of Definition 1. Finally, V outputs a bit λ' in Stage 5 of Definition 1. Ψ queries the decryption oracle with {π*, v*} to derive the session key Kλ''. If λ'' = λ', Ψ searches τα to find out a tuple (v*, α*) such that π* = E(PUB, (PUA||α*)). Ψ returns the value (PUA||α*) as the plaintext M* of C*. In other words, Ψ derives the plaintext M* of C* even if Ψ only knows the ciphertext C* and the public key PUB.
When Ψ derives a session key Kλ'' by querying the decryption oracle with {π*, v*} and λ'' = λ', τα has stored the corresponding tuple (v*, α*) or the decryption oracle has selected the proper value α* in Step (D2) of decryption oracle such that α* can pass the verification π* = E(PUB, (PUA||α*)) of Step (D3). If V wins the interactive game (i.e., Kλ'' = Kλ') with advantage εkey, the probability that Ψ finds out a tuple (v*, α*) from τα such that π* = E(PUB, (PUA||α*)) is εkey. Due to π* = C* and C* = E(PUB, M*), the probability that Ψ solves M* = (PUA||α*) is εkey. Hence, Ψ solves the RSA problem with non-negligible advantage if V wins the interactive game with non-negligible advantage.
Analysis
The running time of Ψ is in polynomial of V’s running time. The simulated game is computationally indistinguishable from the real game. Note that this study perfectly simulates the H oracle and encryption oracle. Except in special cases, the decryption oracle queries are perfectly carried out too. The special case includes two sub-cases: the decryption oracle rejects the valid session information {π, v} or the decryption oracle accepts the invalid session information {π, v}.
Next, assess Ψ’s probability of success. Let E be the event that Algorithm Ψ solves the RSA problem by running V as subroutine. As long as the simulated game is perfectly simulated as a real game, the probability of E happening is the same as in a real attack. (i.e., an attack in which V interacts with real oracles.) In a real attack, we have
Rewriting Equation (1) leads to |Pr[λ' = λ]-(1/2)| ≤ (1/2)Pr[E]. According to Stage 5 of Definition 1, εkey = |Pr[λ' = λ]-(1/2)|. We can derive εkey ≤ (1/2)Pr[E]. In other words, Pr[E] ≥ 2εkey.
The probability that the simulated game is not perfect must be assessed. Except for a special cases, decryption oracle queries are carried out perfectly too. These special cases include two sub-cases: the decryption oracle rejects the valid session information {π, v} or the decryption oracle accepts the invalid session information {π, v}. However, each sub-case may be happen when τα has defined the corresponding tuple (v, α) by the encryption oracle or the decryption oracle with v. The occurrence probability for each sub-case is (qE + qD)/2β. Hence, the total probability for these sub-cases is not greater than 2 × (qE + qD)/2β. By eliminating the probability that the decryption oracle of the simulated game is not perfectly simulated as a real game, the probability of Ψ solving the RSA problem should be modified as
β should be larger than 128 bits such as AES-128, because β is a security parameter. The probability 2 × (qE + qD)/2β is negligible. Pr[E] is non-negligible if εkey is non-negligible. The probability of Ψ solving the RSA problem is non-negligible, if εkey is non-negligible and β is security parameter. Q.E.D.
Theorem 2. Given the communication transcripts of the fair exchange phase, the success probability of an adversary learning any information regarding the exchanged documents {MA, MB} is at most εmsg and εmsg ≤ Maximum{((1/2)εRSA + (qE + qD)/2β), εRSA, εAES}, where εRSA is the maximum probability of breaking the RSA asymmetric encryption algorithm and εAES is the maximum probability of breaking the symmetric encryption algorithm.
Proof. The session key K encrypts documents {MA, MB} in Steps (F2) and (F3) of the fair exchange phase. The session information {π, v} of Step (F1) of the fair exchange phase protects the session key K. Adversary V can get the session key K by breaking message confidentiality of the session information {π, v}. According to Equation (2) in the proof of Theorem 1, V constructs a PPT algorithm to break IND-CCA2 security of the session information {π, v} with the advantage probability at most εkey, εkey ≤ ((1/2)Pr[E] + (qE + qD)/2β), where Pr[E] is the probability of Algorithm Ψ solving the RSA problem by running V as subroutine in Theorem 1. This means that the maximum probability of V retrieving session key K from the session information {π, v} is at most ((1/2)εRSA + (qE + qD)/2β), because Pr[E] ≤ εRSA and εRSA is the maximum probability of breaking the RSA asymmetric encryption algorithm.
V can obtain the session key K if he gets the private keys {PRA, PRB} from Alice A and Bob B by breaking the RSA asymmetric encryption algorithm. The probability of this case is at most εRSA.
V directly retrieves digital documents {MA, MB} from the ciphertexts {δA, δB} by breaking the symmetric encryption algorithm. The probability of breaking symmetric encryption algorithm is εAES.
In summary, the success probability of an adversary learning any information of the exchanged documents {MA, MB} is at most εmsg, and εmsg ≤ Maximum{((1/2)εRSA + (qE + qD)/2β), εRSA, εAES}. Q.E.D.
Theorem 3. The proposed protocol provides message confidentiality.
Proof. In the AES-128 [35] symmetric encryption algorithm adopted in the proposed protocol, the bit length of the session key K is 128 bits (i.e., β = 128 bits). According to Theorem 2, the success probability of an adversary learning any information of the exchanged documents {MA, MB} is at most εmsg, and
Equation (3) is reduced to εmsg ≤ Maximum{εRSA, εAES}, because β = 128 bits and the probability (qE + qD)/2β is negligible when using AES-128. According to the National Institute of Standards and Technology (NIST) [41], the probability εRSA is negligible when the modulus of the RSA encryption algorithm is sufficiently large. The National Bureau of Standards [35] and NIST [41] further indicate that the probability εAES is also negligible for AES-128 symmetric encryption. The success probability of an adversary obtaining MA and MB is negligible. In other words, the proposed protocol provides sufficient message confidentiality. Q.E.D.
4.2. Backward and Forward Secrecy
The initiator, Alice A, randomly selects a session key K2 for each transaction in the fair exchange phase. The session key K2 is fully independent for different transactions. Even if adversaries obtain the current session key K2, they cannot derive the previous and subsequent session keys. The proposed protocol achieves backward and forward secrecy.
4.3. Transaction Privacy
Theorem 3 of Section 4.1 demonstrates the message confidentiality of the proposed protocol. Nobody except Alice A and Bob B can obtain the exact transaction information during the fair exchange phase. The session key K2 protects the exchanged document and its recovery certificate. Section 4.2 shows that the session key K2 for each transaction is random and independent. Even when someone exchanges the same document and its recovery certificate with different parties, transaction privacy remains intact.
4.4. Non-Repudiation of Origin and Non-Repudiation of Receipt
The initiator, Alice A, generates the ciphertexts {π, v, Π} to initiate the exchange session in Step (F1) of the fair exchange phase. Definition 2 defines the message unforgeability of the session information {π, v}. Theorem 4 proves that the success probability of Forger F forging the session information {π, v} is negligible. Theorem 5 proves that the success probability of Forger F forging {π, v, Π} the fair exchange phase is negligible.
Definition 2 (Message unforgeability of the session information): The session information {π, v} in Step (F1) of the fair exchange phase is existentially unforgeability against chosen-message attack (EUF-CMA) [42] if no probabilistic polynomial time (PPT) Forger F has a non-negligible advantage in the following game:
The challenger generates a key pair {PUU, PRU}. The private key PRU is kept secret while the public key PUU is given to Forger F.
Forger F adaptively makes a number of queries to H hash oracle, G hash oracle, the encryption oracle and the decryption oracle.
At the end of the game, the challenger gives Forger F a challenging session key K*. Forger F produces a session information {π*, v*} of K* and valid key pair {PUB, PRB} of the designated Receiver B. Forger F wins the game if the decryption oracle returns the session key K* for decryption query with {π*, v*} such that the session information {π*, v*} was not the output of an encryption query made during the game.
Theorem 4. Let β be a security parameter. Under the random oracle model, if there exists a PPT algorithm and the probability of the PPT algorithm breaking the EUF-CMA security of the session information {π, v} is at least εforge, then there exists another PPT algorithm which solves the RSA problem with a probability of at least (1 − qE × qG/2β) × (1 − ((qE + qD)/2β + (1 − (qE + qD)/2β)/2|α|)) × εforge, where qG, qE, and qD are the maximum number of G oracle, encryption oracle, and decryption oracle queries of Forger F during the game of Definition 2.
Proof. Assume that Forger F who wins the interactive game given in Definition 2 of Section 4.4 with a non-negligible advantage. Algorithm Γ runs F as a subroutine to solve the RSA problem with non-negligible advantage.
Suppose Γ is given a ciphertext C* and the public key PUA of the RSA problem, Γ runs F as a subroutine to find the plaintext M* such that C* = E(PUA, M*). Γ sets up a simulated environment of interactive game of Definition 2 as follows:
Γ maintains three lookup tables {τH, τG, τα} for simulating H hash oracle, G hash oracle, decryption oracle, and encryption oracle. F performs adaptive queries to the following oracles:
H oracle: this oracle is simulated as in the proof of Theorem 1.
G oracle: To query G(c) of F, the G oracle replies the defined value, if G(c) is defined in τG. Otherwise, the oracle randomly selects a challenging session key K(=(x||y)) and performs the following steps to return the value G(c):
(G1): Selects a random number r, where |r| = β.
(G2): Sets d = (y||r) and simulates H(d) as described in H oracle.
(G3): Computes c = (x||0β/2)⊕H(d).
(G4): Assigns the value (ϖ||w) = C*, where |w| = (3/2)β.
(G5): Simulates H(w) as described in H oracle.
(G6): Computes v = H(w)⊕c. If the tuple (v, *) does not define in τα, the oracle randomly selects a value α and adds new tuple (v, α) into τα.
(G7): Stores the session key K into the key set Λ.
(G8): Returns the value (w⊕d) and updates the record {c, w⊕d} of τG.
Encryption oracle: Given the session key K = (x||y) and two distinct public keys {PUS, PUR}, the encryption oracle performs the following steps to return the session information {π, v}:
(C1): Checks the public keys {PUS, PUR} are in the range of Stage (1) of Definition 2. If PUS = PUR, then rejects the query.
(C2): Selects a random number r, where |r| = β.
(C3): Sets d = (y||r) and simulates H(d) as described in H oracle.
(C4): Computes c = (x||0β/2)⊕H(d).
(C5): Selects a random value α and sets (ϖ||w) = V(PUA, α), where |w| = (3/2)β.
(C6): Simulates H(w) as described in H oracle.
(C7): Computes v = H(w)⊕c. If the tuple (v, α) does not defined in τα, adds new tuple (v, α) into τα. Otherwise, go to Step (C5).
(C8): If the value G(c) has defined in τG by G oracle, then Γ outputs “failure” and halts. If the value G(c) does not define in τG, defines G(c) = (w⊕d) and adds the record {c, (w⊕d)} into τG. Otherwise, go to Step (C2).
(C9): Returns the session information {π, v}, where π = E(PUR, (PUS||α)).
Decryption oracle: this oracle is simulated as in the proof of Theorem 1.
Finally, Γ simulates the last stage of Definition 2 by selecting a session key K* from the key set Λ and giving F a public key PUA and the challenging session key K*. F produces the receiver B’s key pair {PUB, PRB} and the forged ciphertext {π*, v*}. Γ retrieves K' by querying the decryption oracle with the forged ciphertext {π*, v*} of F. If K' = K*, Γ obtains (PUA||α*) by computing D(PRB, π*). Finally, Γ returns the value α* as the plaintext M* of C* such that M* = D(PRA, C*). In other words, Γ solves the RSA problem.
According to the restriction of Stage (3) in Definition 2, the forged ciphertext {π*, v*} of F cannot be the response of the encryption oracle. The encryption oracle does not define the tuple (v*, α*) of τα, which is related to K*. There are only two cases in which Γ can obtain the key K', and K' is equal to K* on querying the decryption oracle with {π*, v*} of F. The first case is that τα has stored the corresponding tuple (v*, α*) of {π*, v*}. In the second case, the decryption oracle selects the proper value α* in Step (D2) of the decryption oracle such that α* can pass the verification π* = E(PUB, (PUA||α*)) of Step (D3).
Because the G oracle defines the challenging session key K* when making G queries, the corresponding tuple (v*, α*) of {π*, v*} is defined at this time. If the decryption oracle can derive K' from {π*, v*} of F and K' = K*, Γ retrieves the corresponding value α* according to the index value v* from τα in Step (D2) of the decryption oracle. Moreover, Γ uses the corresponding value α* and Sender A’s public key PUA to generate the value (ϖ||w) by running the RSA-based message recovery procedure in Step (D4) (i.e., (ϖ||w) = V(PUA, α*)). If the decryption oracle returns the key K' and K' = K* during the decryption query ({π*, v*}), the value (ϖ||w) of Step (D4) and its extended parameters pass the verification of Step (D8). In other words, α* is the signature of the value (ϖ||w). Because the RSA-based message recovery algorithm is identical to RSA-based asymmetric encryption algorithm, the procedure in Step (D4) can also perform the RSA-based encryption procedure to get the ciphertext (ϖ||w) by encrypting the value α* with Sender A’s public key PUA. However, the G oracle assigns the value (ϖ||w) = C* in Step (G4) and K* is defined at the same time when making G queries. If K' = K*, α* is the plaintext M* of C*. Hence, the value α* which Γ obtained is the plaintext M* of C* when K' = K*. In other words, Γ solves the RSA problem in the first case.
In the second case, the value α* is the correct value selected by Step (D2) of the decryption oracle such that α* passes the verification π* = E(PUB, (PUA||α*)) of Step (D3) and τα does not define the corresponding tuple (v*, α*) of {π*, v*}. K* provided by Γ is derived through the query of the G oracle and the procedures of the query define one tuple (v*, α*) in τα. In other words, τα must define the tuple (v*, α*) for each K*. In the second case, if K' = K* and Step (D2) of the decryption oracle does not define any corresponding tuple (v*, *), it the forged ciphertext {π*, v*} of F is not the correct ciphertext of K*. The second case is a special case in which the decryption oracle accepts the invalid ciphertext, and the decryption oracle cannot perfectly reflect a real game. Γ cannot obtain M* of C* in this special case. The following assessment of the success probability on Γ solving the RSA problem precludes this special case.
This theorem assumes that when F successfully forges the ciphertext {π*, v*} for K* (i.e., F wins the interactive game), Γ can find out a tuple (v*, α*) from τα such that π* = E(PUB, (PUA||α*)). Because α* is the plaintext M* of C*, as demonstrated above, Γ can solve the RSA problem. Hence, these are a non-negligible probability of Γ solving the RSA problem if there is a non-negligible probability of F winning the interactive game.
Analysis
The running time of Γ is in polynomial of F’s running time. To see that the simulated game is computationally indistinguishable from the real game, note that the H oracle and G oracle can be simulated perfectly as a real game. When the encryption oracle performs Step (C8) and returns “failure”, the encryption oracle cannot be perfectly simulated as a real game. If Step (C8) does not return “failure”, the encryption oracle perfectly simulates a real game. The decryption oracle perfectly simulates the real game except for a special case. This special case includes two sub-cases: the decryption oracle rejects the valid session information {π, v} or the decryption oracle accepts the invalid session information {π, v}.
Next, assess Γ’s probability of success. If the encryption oracle returns “failure” or the decryption oracle makes an erroneous judgment while F queries the ciphertext, the simulated game does not perfectly reflect a real game. The success probability of Γ solving the RSA problem should preclude these two cases.
The first case occurs in the encryption query. During each encryption query, Γ attempts to define G(c) in Step (C8) of the encryption oracle. However, when the G oracle has defined G(c) in τG, the encryption oracle will return “failure”. The game makes at most qG queries to the G oracle. τG defines at most qG records, which are defined by G oracle. Moreover, the game makes at most qE queries to the encryption oracle. The probability that this case will happen is at most (qE × qG/2β). In other words, the probability that Γ does not fail during simulating the encryption oracle is at least
The second case occurs in the decryption query, and includes two sub-cases: the decryption oracle rejects the valid session information {π, v} or the decryption oracle accepts the invalid session information {π, v}. After querying the encryption oracle and the decryption oracle, τα defines the corresponding tuple (v, α). The corresponding tuple (v, α) may cause the decryption oracle to reject the valid session information {π, v}. The probability of this sub-case is at most (qE + qD)/2β. The decryption oracle may accept the invalid session information {π, v} when τα does not define the corresponding tuple (v, α) and the randomly selected value α at Step (D2) passes the verification of Step (D3). The probability of this sub-case is at most (1 − (qE + qD)/2β)/2|α|. The total probability for these sub-cases is not greater than (qE + qD)/2β + (1 − (qE + qD)/2β)/2|α|. In other words, the probability of the decryption oracle making an accurate judgment while F queries the decryption oracle is at least
If Γ perfectly simulates the real game and F wins the game, Γ can solve the RSA problem. The probability of F winning the game is at most εforge. According to Equations (4) and (5), Pr[F wins the game and Γ perfectly simulates the real game] ≥ (1 − qE × qG/2β) × (1 − ((qE + qD)/2β + (1 − (qE + qD)/2β)/2|α|)) × εforge. In other words, the probability that Γ solves the RSA problem is at least (1 − qE × qG/2β) × (1 − ((qE + qD)/2β + (1 − (qE + qD)/2β)/2|α|)) × εforge. Q.E.D.
Theorem 5. Given the public/private keys {PUB, PRB} of the designated receiver (i.e., Bob B) and Alice A’s public key PUA, the success probability of Forger F forging the ciphertexts {π, v, Π} and exchanging message MA in Step (F1) of the fair exchange phase is negligible.
Proof. Theorem 4 shows that εforge ≤ εRSA/(1 − qE × qG/2β) × (1 − ((qE + qD)/2β + (1 − (qE + qD)/2β)/2|α|)) if the probability of F wins the game is at most εforge, where εRSA is the maximum probability of breaking the RSA asymmetric encryption algorithm. β should be larger than 128 bits, as in the AES-128 algorithm, because β is security parameter. |α| is the bit length of RSA-based signature. The probability (1/(1 − qE × qG/2β) × (1 − ((qE + qD)/2β + (1 − (qE + qD)/2β)/2|α|))) is negligible. The probability εRSA is negligible when the modulus of the RSA encryption algorithm is sufficiently large. Hence, the probability εforge is negligible. In other words, the probability of F successfully forging the session information {π, v} in Step (F1) is negligible.
Step (F1) generates the other ciphertext {Π} using the session key K, and generates the session information {π, v} based on the session key K. The success probability of F forging the ciphertext {Π} is negligible because the success probability of F forging the session information {π, v} of K is negligible. In summary, the probability of F successfully generating the ciphertexts {π, v, Π} of exchanging message MA in Step (F1) of fair exchange phase is negligible. Q.E.D.
The message {δB} of Step (F2) includes the RSA-based signature SB of Bob B. The signature SB integrates the signature of the exchanged document MB and the receipts of the request information req_info and the recovery certificate CertA. The message {δB} is unforgeable if RSA-based signature is secure. The message {δA} of Step (F3) includes the RSA-based signature SA of Alice A. The signature SA integrates the signature of the exchanged document MA and the receipt of the exchanged document MB. The message {δA} is unforgeable if RSA-based signature is secure. Based on Theorem 5 and RSA-based signature, all communication transcripts in the proposed protocol are unforgeable. The proposed protocol provides the non-repudiation of origin and receipt because the adversary cannot forge exchanged messages.
4.5. Authorized Exchanging
In the proposed protocol, the notary notarizes each document only once and generates its recovery certificate. The recovery certificate includes the notary’s signature on the public key of the document owner. Bob B authenticates the ownership of MA in Step (F2-6) of the fair exchange phase using the recovery certificate of MA. Similarly, Alice A authenticates the ownership of MB in Step (F3-2) of the fair exchange phase based on the recovery certificate of MB. The sender should provide his or her signature of the document and its recovery certificate. This approach prevents the receiver from impersonating the authorized owner and re-distributing the received document to other parties using this protocol.
4.6. Strong Fairness
Any participants may prematurely abort the fair exchange phase. All possible arbitration cases are as follows.
Case 1: Alice A generates all messages of Step (F1) of the fair exchange phase to request for arbitration directly.
Case 2: After receiving {π2, v2, Π2} of Step (F1), Bob B generates all messages of Step (F2) and initiates the arbitration phase without sending back the message {δB} of Step (F2).
Case 3: Alice A obtains the ciphertext {δB} after Step (F2) but does not perform Step (F3).
Because Alice A does not have the recovery certificate CertB in Case 1, the notary stops the arbitration process and does not recover MB for Alice A. Neither Alice A nor Bob B obtains the exchanged document of the opposing party. In Case 2, Bob B is able to generate the irrefutable receipt first. Bob B uses his irrefutable receipt, the recovery certificate CertA, and MB to initiate the arbitration phase. Bob B passes all verifications of the notarization phase. The notary simultaneously helps Bob B recover MA and sends MB to Alice A. Both Alice A and Bob B get the exchanged document of the opposing party. In Case 3, Bob B initiates the arbitration phase with his irrefutable receipt, MB, and the recovery certificate CertA. As in Case 2, both Alice A and Bob B get the exchanged document of the opposing party. Clearly, the proposed protocol provides strong fairness.
If the document MB of Bob B is verifiable, such as a digital signature or e-cash, the notary does not need to notarize document MB. In this circumstance, Alice A should initiate the fair exchange protocol. If Bob B sends the wrong document MB to Alice A in Step (F2) of the fair exchange phase, Alice A checks that the verifiable document MB is incorrect directly and stops the exchange phase without sending the secret key KA in Step (F3). In this case, neither Alice A nor Bob B obtains the exchanged document of the opposing party. The proposed protocol provides fairness in this case even though the document MB is not notarized by the notary T.
4.7. Replay Attack
The adversary replays the messages {π2, v2, Π2} of Step (F1) in the fair exchange phase. The adversary attempts to impersonate Alice A to obtain the document MB. Bob B verifies the expired period of time stamp Tstamp and confirms the identities of both participants after decrypting the messages {π2, v2, Π2}. Bob B stops the fair exchange phase based on the replaying messages {π2, v2, Π2}. Theorem 2 demonstrates the message confidentiality of exchanged messages. Even if the adversary can quickly replay the communication transcripts between Alice A and Bob B in the valid time period, the adversary still cannot obtain the exchanged documents because only Alice A and Bob B can obtain the session key K2 from the exchanged messages. Thus, the proposed protocol can resist replay attack.
5. Discussions
This section analyzes the performance of the proposed approach and compares it with previous methods [4,6–10]. Alaraj’s method [5] assumes that initiator party has known the hash value of the encrypted exchange data of the responder party before performing the exchange protocol. It also assumes that the responder party has known the encryption of the initiator’s encryption key for this transaction before performing the exchange protocol. These two assumptions are not practical in the e-commerce via Internet. Besides, Alaraj’s method [5] includes many techniques of Zhang et al.’s method [10]. The computational cost of Alaraj’s method [5] is as well as Zhang et al.’s method [10]. The following comparisons do not include Alaraj’s method [5]. Section 5.1 compares functionalities. Section 5.2 makes comparisons based on computation and communication costs.
5.1. Functionalities Comparisons
Table 1 compares the functionalities of previous methods [4,6–10] with the proposed protocol. As Sections 4.2 and 4.3 show, the proposed approach protects the communication transcripts, ensuring transaction privacy and backward/forward secrecy without requiring an online notary. The transaction privacy and backward/forward secrecy of the other studies are vulnerable because the session key used to protect each document is fixed in the multi-receiver e-commerce environment. Examples include Alaraj and Munro’s protocols [6,7], Liang et al.’s protocol [4], Ray et al.’s protocols [8,9] and Zhang et al.’s protocol [10].

The notary T must ensure the truthfulness of the transaction based on the irrefutable receipts of each party in the proposed protocol whenever a dispute occurs between participants. The proposed protocol prevents the erroneous judgment that the notary has endorsed the forged transaction behavior. However, the notaries of the other studies in Table 1 cannot ensure the truthfulness of the transaction in the notarization phase.
Only the proposed protocol and Ray et al.’s [8,9] protocol provide complete non-repudiation of origin and non-repudiation of receipt because they adopt irrefutable signature of the sender and receipt of the receiver for each transaction. Using the verifiable recovery certificate, the receiver verifies the ownership of the exchanged document in Alaraj and Munro’s studies [6,7] and the proposed protocol. The only protocols to consider the replay attack are the proposed protocol and Ray et al.’s protocol [8,9]. Therefore, the proposed protocol is practical for fairly exchanging documents in a multi-receiver e-commerce environment.
5.2. Performance Evaluations
Table 2 shows the computational time of public key operations under the same security level [43]. The notations TRSA-SIG-DEC, TRSA-VFY-ENC, TPAIR, and TECSM in Table 2 represent one RSA signing/decryption with a 1024-bit modulus, one RSA verification/encryption with a 1024-bit modulus, one admissible bilinear pairing, and one elliptic curve-based scalar multiplication as suggested by IEEE Standard P1363.3 [44], respectively. The public operations in Table 2 are implemented by the standard cryptographic library, MIRACL (Multiprecision Integer and Rational Arithmetic C/C++ Library) [45]. The implementation platform consists of a 32-bit Intel Pentium IV processor at 3 GHz.

Table 3 compares the main computational costs of the fair exchange phase for the proposed protocol and previous studies [4,6–10]. The fair exchange phase of the propose protocol only requires six RSA-based verification/encryption operations and four RSA-based signing/decryption operations, and is therefore more efficient than previous RSA-based fair document exchange protocols [6–10]. Because it adopts a bilinear pairing function, Liang et al.’s fair document exchange protocol [4] has much higher computational cost than the proposed protocol under the same security level. The acceleration ratio in Table 3 shows that the proposed protocol is 123% to 435% faster than previous studies [4,6–10]. The acceleration ratio is the computational cost of the compared protocol divides by the computational cost of our protocol. Clearly, the proposed protocol is more efficient than previous studies.

The AES-128 algorithm has the same security strength as RSA with a 3072-bit modulus [41]. Table 4 compares the total communication cost and number of rounds to transmit messages (#round) in the fair exchange phase while using AES-128 and RSA-3072 key lengths recommended by the NIST [41]. Assume that the proposed protocol adopts a 16-bit identity of each participator, 128-bit public description information of each document, 16-bit timestamp, and a 3072-bit RSA-based signature are adopted in the proposed protocol. In the fair exchange phase of the proposed protocol, the message size in Step (F1) is |MA| + 10,112 bits. The message size in Step (F2) is |MB| + 6720 bits, and the message size in Step (F3) is 3200 bits. Hence, the total communication cost of the proposed fair exchange phase is |MA| + |MB| + 20,032 bits. Table 4 shows the total communication costs of previous works [4,6–10]. Alaraj and Munro’s protocols [6,7] and Liang et al.’s protocol [4] incur additional communication costs in producing receipts. Because Liang et al.’s protocol [37] adopts the public key-based verifiable encryption method, the bit length of the exchanged document is limited. Therefore, Liang et al.’s protocol [4] must divide exchanged documents into many blocks, and the communication cost is 9216 bits for each 3072-bit transaction document. Hence, Liang et al.’s protocol [4] requires more transaction sessions to exchange documents, especially for large documents such as films. In other words, Liang et al.’s protocol [4] is inefficient in exchanging large documents. However, Alaraj and Munro’s studies [6,7] and the current study improve efficiency by encrypting the document using a symmetric encryption algorithm, such as AES-128 [35]. As Table 4 shows, the proposed protocol saves about 109% to 169% + |MB| of the communication costs in previous studies [6–10]. Though the proposed protocol provides complete functionalities of fair document exchange, it still has lower communication costs.

6. Conclusions
This paper proposes an efficient and provable fair document exchange protocol that ensures transaction privacy in a multi-receiver e-commerce environment. In this approach, the offline notary notarizes each document only once. Authorized owners repeat fair exchanges with different parties without endangering participant privacy. Though the notary is offline, the proposed protocol still ensures transaction privacy in the multi-receiver e-commerce environment where other methods lose transaction privacy. This study demonstrates that the proposed protocol not only meets principal security requirements, but also enhances forward secrecy, transaction privacy, and authorized exchange. Moreover, the proposed protocol is more efficient than other fair document exchange methods in multi-receiver e-commerce.
Acknowledgments
The authors would like to express their appreciation to the anonymous reviewers for their valuable suggestions and comments. This research was partially supported by the Ministry of Science and Technology, Taiwan, under contract No.: 103-2221-E-032-037 and 97-2221-E-032-019.
Author Contributions
Ren-Junn Hwang and Chih-Hua Lai researched relation work and designed the scheme; Chih-Hua Lai performed and analyzed the data; Ren-Junn Hwang and Chih-Hua Lai wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Alshehri, M.; Aldabbas, H.; Sawle, J.; Baqar, M.A.B. Adopting E-commerce to user’s needs. Int. J. Comput. Sci. Eng. Surv. 2012, 3, 1–12. [Google Scholar]
- Simplot-Ryl, I.; Traore, I.; Everaere, P. Distributed architectures for electronic cash schemes: A survey. Int. J. Parallel Emergent Distrib. Syst. 2009, 24, 243–271. [Google Scholar]
- Asokan, N.; Schunter, M.; Waidner, M. Optimistic protocols for fair exchange. Proceedings of the 4th ACM Conference on Computer and Communications Security, Zurich, Switzerland, 1–4 April 1997; pp. 7–17.
- Liang, X.; Cao, Z.; Lu, R.; Qin, L. Efficient and secure protocol in fair document exchange. Comput. Stand. Interfaces. 2008, 30, 167–176. [Google Scholar]
- Alaraj, A.M. Optimizing One Fair Document Exchange Protocol. Int. J. Netw. Secur. Appl. 2012, 4. [Google Scholar] [CrossRef]
- Alaraj, A.; Munro, M. An e-commerce fair exchange protocol that enforces the customer to be honest. Int. J. Product Lifecycle Manag. 2008, 3, 114–131. [Google Scholar]
- Alaraj, A.; Munro, M. An efficient e-commerce fair exchange protocol that encourages customer and merchant to be honest. In Computer Safety, Reliability, and Security; Lecture Notes in Computer Science; Springer Berlin, Heidelberg: Berlin, Germany, 2008; pp. 193–206. [Google Scholar]
- Ray, I.; Ray, I.; Natarajan, N. An anonymous and failure resilient fair-exchange e-commerce protocol. Decis. Support Syst. 2005, 39, 267–292. [Google Scholar]
- Ray, I.; Zhang, H. Experiences in developing a fair-exchange e-commerce protocol using common off-the-shelf components. Electron. Commerce Res. Appl. 2008, 7, 247–259. [Google Scholar]
- Zhang, N.; Shi, Q.; Merabti, M.; Askwith, R. Practical and efficient fair document exchange over networks. J. Netw. Comput. Appl. 2006, 29, 46–61. [Google Scholar]
- Asokan, N.; Schunter, M.; Waidner, M. Optimistic fair exchange of digital signatures. IEEE J. Sel. Areas Commun. 2000, 18, 593–610. [Google Scholar]
- Gao, W.; Li, F.; Xu, B. An abuse-free optimistic fair exchange protocol based on BLS signature. Proceedings of International Conference on Computational Intelligence and Security, Suzhou, China, 13–17 December 2008; pp. 278–282.
- Gurgens, S.; Rudolph, C.; Vogt, H. On the security of fair non-repudiation protocols. Int. J. Inf. Secur. 2005, 4, 253–262. [Google Scholar]
- Hernandez-Ardieta, J.L.; Gonzalez-Tablas, A.I.; Alvarez, B.R. An optimistic fair exchange protocol based on signature policies. Comput. Secur. 2008, 27, 309–322. [Google Scholar]
- Sun, Y.; Gu, L.; Qing, S.; Zheng, S.; Yang, Y.; Sun, Y. New optimistic fair exchange protocol based on short signature. Int. Conf. Commun. Softw. Netw. 2010, 99–104. [Google Scholar]
- Bao, F.; Wang, G.; Zhou, J.; Zhu, H. Analysis and improvement of Micali’s fair contract signing protocol. In Information Security and Privacy; Lecture Notes in Computer Science; Springer Berlin, Heidelberg: Berlin, Germany, 2004; pp. 176–187. [Google Scholar]
- Chen, X.; Zhang, F.; Tian, H.; Kim, K. Three-round abuse-free optimistic contract signing with everlasting secrecy. Proceedings of the 14th Financial Cryptography and Data Security, Tenerife, Canary Islands, 25–28 January 2010; pp. 304–311.
- Frikken, K.B.; Atallah, M.J. Achieving fairness in private contract negotiation. Proceedings of the 9th Financial Cryptography and Data Security, Roseau, Dominica, 28 February–3 March 2005; pp. 270–284.
- Harn, L.; Lin, C. Contract signature in e-commerce. Comput. Electr. Eng. 2011, 37, 169–173. [Google Scholar]
- Mukhamedov, A.; Ryan, M. Fair multi-party contract signing using private contract signatures. Inf. Comput. 2008, 206, 272–290. [Google Scholar]
- Mukhamedov, A.; Ryan, M. Improved multi-party contract signing. Proceedings of the 11th Financial Cryptography and Data Security, Tobago, 12–15 February 2007; pp. 179–191.
- Wang, G. An Abuse-Free Fair Contract-Signing Protocol Based on the RSA Signature. IEEE Trans. Inf. Forensics Secur. 2010, 5, 158–168. [Google Scholar]
- Dodis, Y.; Lee, P.J.; Yum, D.H. Optimistic fair exchange in a multi-user setting. J. Univers. Comput. Sci. 2008, 14, 318–346. [Google Scholar]
- Imamoto, K.; Sakurai, K. A certified email system with receiver’s selective usage of delivery authority. In Progress in Cryptology—INDOCRYPT 2002; Lecture Notes in Computer Science; Springer Berlin, Heidelberg: Berlin, Germany, 2002; pp. 326–338. [Google Scholar]
- Ma, C.; Li, S.; Chen, K.; Liu, S. Analysis and improvement of fair certified e-mail delivery protocol. Comput. Stand. Interfaces. 2006, 28, 467–474. [Google Scholar]
- Ma, X.-L.; Cui, W.; Gu, L.-Z.; Yang, Y.-X.; Hu, Z.-M. A novel id-based verifiably encrypted signature without random oracle. Proceedings of the International Conference on Computational Intelligence and Security, Suzhou, China, 13–17 December 2008; pp. 359–363.
- Nenadic, A.; Zhang, Z.; Barton, S. Fair certified e-mail delivery. Proceedings of the 9th ACM Symposium on Applied Computing-Computer Security Track, Trento, Italy, 14–17 March 2004; pp. 391–396.
- Nenadic, A.; Zhang, N.; Shi, Q.; Goble, C. DSA-based verifiable and recoverable encryption of signatures and its application in certified e-goods delivery. Proceedings of the IEEE Conference on e-Technology, e-Commerce and e-Service, Hong Kong, China, 29 March–1 April 2005; pp. 94–99.
- Nenadic, A.; Zhang, N.; Shi, Q.; Goble, C. Certified e-mail delivery with DSA receipts. Proceedings of the 19th IEEE International Parallel and Distributed Processing Symposium, Denver, CO, USA, 3–8 April 2005; pp. 4–8.
- Oppliger, R. Certified mail: the next challenge for secure messaging. Commun. ACM. 2004, 47, 75–79. [Google Scholar]
- Chen, L.; Kudla, C.; Paterson, G.K. Concurrent signatures. In Advances in Cryptology—EUROCRYPT 2004; Lecture Notes in Computer Science; Springer Berlin, Heidelberg: Berlin, Germany, 2004; pp. 287–305. [Google Scholar]
- Buhse, W.; Meer, J. The open mobile alliance digital rights management. IEEE Signal Process. Mag. 2007, 140–143. [Google Scholar]
- Chen, C.-L. A secure and traceable E-DRM system based on mobile device. Expect Syst. Appl. 2007, 35, 878–886. [Google Scholar]
- Rivest, R.; Shamir, A.; Adleman, L. A method for obtaining digital signature and public key cryptosystems. Commun. ACM. 1978, 21, 120–126. [Google Scholar]
- National Bureau of Standards (NBS), NBS FIPS PUBS 197, Advanced Encryption Standard; U.S. Department of Commerce: Washington, DC, USA; November; 2001.
- National Institute of Standards and Technology (NIST), FIPS PUB 180-3, Secure Hash Standard (SHS); U.S. Department of Commerce: Washington, DC, USA; October; 2008.
- Hwang, R.J.; Lai, C.H. Provable Fair Document Exchange Protocol with Transaction Privacy for Multi-Buyer E-commerce. Proceedings of the 20th National Information Security Conference, Hsinchu, Taiwan, 27 May 2010; pp. 191–196.
- Bellare, M.; Rogaway, P. Random oracles are practical: A paradigm for designing efficient protocols. Proceedings of the 1st ACM Conference on Computer and Communication Security, Fairfax, VA, USA, 3–5 November 1993; pp. 62–73.
- Rackoff, C.; Simon, D.R. Non-interactive zero-knowledge proof of knowledge and chosen ciphertext attack. In Advances in Cryptology—CRYPTO ’91; Lecture Notes in Computer Science; Springer Berlin, Heidelberg: Berlin, Germany, 1992; pp. 433–444. [Google Scholar]
- Rivest, R.; Kaliski, B. RSA Problem. In Encyclopedia of Cryptography and Security; Springer: Berlin, Germany, 2005. [Google Scholar]
- National Institute of Standards and Technology (NIST), Special Publication (SP) 800-57, Part 1, Recommend for Key Management: General (Revised); U.S. Department of Commerce: Washington, DC, USA; March; 2007.
- Goldwasser, S.; Micali, S.; Rivest, R. A digital signature scheme secure against adaptive chosen-message attack. SIAM J. Comput. 1988, 17, 281–308. [Google Scholar]
- Cao, X.; Zeng, X.; Kou, W.; Hu, L. Identity-based anonymous remote authentication for value-added services in mobile networks. IEEE Trans. Veh. Technol. 2009, 58, 3508–3517. [Google Scholar]
- IEEE Standard P1363.3/D3, IEEE Standard for Identity-Based Cryptographic Techniques Using Pairings; IEEE: Piscataway, NJ, USA; April; 2008.
- Shamus Software Limited. Multiprecision Integer and Rational Arithmetic C/C++ Library (MIRACL), Available online: http://www.certivox.com/miracl accessed on 1 October 2014.
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).