Abstract
Fractal symmetry is symmetry across scale. If one looks at a branch of a tree its branching pattern is reminiscent of the tree as a whole. Plants exhibit a number of different symmetries, including bilateral, rotational, translational, and fractal; deviations from each of these types has been associated with organisms developing in stressful environments. Here, we explore the utilization and meaning of fractal analysis on annual growth ring production in woody plants. Early detection of stress in plants is difficult and the compounding effects of multiple or severe stressors can lead to irreversible damage or death. Annual wood production was used to produce a time series for individuals from stands classified as either high vigor or low vigor (a general measure of health). As a measure of symmetry over time, the fractal dimension of each time series was determined and compared among vigor classes. We found that individuals obtained from low vigor sites had a significantly lower fractal dimension than those from high vigor sites. These results agree with patterns found in a variety of other organisms, and we argue that the reduced fractal dimension is related to a loss in system complexity of stressed individuals.1. Introduction
Evaluating plant health remains a challenge despite numerous studies and significant progress in the field (see below). There is currently no direct measure for plant health and in fact, there is not even a clear definition (reviewed in [1]). What can be agreed upon is that prolonged stress to an organism reduces vigor which in turn reduces that individual’s general measure of health. Indicators of plant health are no different; typically defined on a comparative basis and measured indirectly through the description of observable traits (i.e., crown loss [2], percent damage [3], photosynthetic rates [4], net photosynthesis [5], critical wilting [6], insect damage (but see [7]), and various imaging techniques [8]). The presence of measurable change, however, implies an advanced stage of health decline which may or may not be reversible [9]. One method to detect underlying stress in a population is through measurements of developmental stability [10,11]. Although fluctuating asymmetry (random deviations from bilateral symmetry) is the most commonly used measurement, others include phyllotaxy, equiangular spirals, and fractal dimension [12]. For this study we focus on the fractal dimension of annual growth rings in trees.
Fractals derive their name because in many, but not all, cases they have non-integer dimensions [13,14]. True fractals display symmetry of scale, and are infinitely complex. Although natural objects are only approximate fractals, fractal geometry and analysis serve an important role in the natural sciences. One example is the replacement of smooth, Euclidean shapes historically used in models by more accurate fractal shapes, representative of many natural objects such as coast lines, clouds, and tree crowns [15,16]. The fractal dimension of an object is often used to describe the roughness of its surface or edge [17,18]. This type of analysis describes the ability of the object to fill space, and is useful when considering things like photosynthetic surface area (canopy cover [19]), surface gas exchange (leaf or stem surface area [20]), and water or nutrient acquisition (root systems [21]). Fractals are also well known for their property of self-similarity or scale-independence. The concept of self-similarity is important for parsimony and design models (e.g., structure of a fern [22]), developmental stability [12], and the prevalence of self-similar systems present in the natural world gives rise to questions regarding order and fundamental rules of nature [23]. A third application of fractal analysis describes the roughness of a time series, displaying symmetry of scale over time [24,25]. This type of fractal application has been widely used in the medical field to monitor heart rate, brain wave, blood pressure, and other biological processes in humans ([26] and references therein); however, this technique has only rarely been used to evaluate developmental stability in plants [12,27].
Correlations between fractal dimension and stress have been observed in numerous animal species. The fractal dimension of behavior patterns have been measured and correlated to general health or stress in chimpanzees [28], fathead minnows [29], Iberian ibex [30], and domestic hens [31]. In plants, fractal analysis has been used to correlate the fractal dimension of physical measurements (self-similarity) to stress. Two examples are differential shoot branching patterns across grazing and water stresses in green pepper [32], and differential root branching across a nitrogen gradient in corn [33]. Finally, it is worth mentioning that fractal measurement and analysis of human system processes over time has been widely explored. For example, the fractal dimension of an individual’s heart rate has been shown to be a reliable indicator of heart disease in humans [34,35], and the fractal dimension of electroencephalogram (EEG) activity, which detects electrical activity in the brain, has been correlated to Alzheimer’s [36]. In all of the cases described above, the fractal dimension of the measured trait decreased with increased stress.
Lipsitz [26] suggests that healthy organisms have complex systems. He argues that a complex system is better able to react to stress, and can do so quickly and on many levels. This idea is not a new one. Emlen et al. [37] outline what they refer to as the attractor hypothesis which is a theory that accounts for detailed adaptive responses of an organism to their continuously changing environments. In both accounts, disease or stress reduces the health of the organism, which can then impose a loss of complexity within the system and enhance susceptibility to additional diseases or stressors [26,37]. In the case of trees, growth depends on several variables, but, for example, is critically dependent on water availability. Precipitation is generally inconsistent with a high fractal dimension [38]. Individual trees respond to resource availability in a complex way. They grow more and store resources when resources available and less when they are limited. This is referred to as environmental buffering and the more successful an individual is in this buffering, the healthier it should be. In this study, we use fractal analysis to examine the time series produced from annual growth rings in low and high vigor trees. We then estimate and compare the fractal dimension of the time series between classifications to determine if the fractal dimension of annual growth can be used as an indicator of developmental stability in trees.
2. Methods
Eighteen trembling aspen (Populus tremuloides Michx.) increment cores were selected from a larger sample collected for a study on aspen decline in northern Minnesota. The subset of cores used in this study was selected based on age, with only the oldest trees being used due to the requirement of many annual rings needed to obtain an accurate estimate of fractal dimension. Tree age ranged from 62 to 118 years with an average age of 88.6 (Table 1). Samples were collected at breast height (1.4 m) in June and July 2009 (incomplete rings from 2009 were excluded from all analysis). All cores were prepared according to standard techniques [39], dated by hand, then read and cross-dated using COFECHA [40]. For this study, nine cores were selected from three stands classified as high vigor stands, and nine cores were selected from three stands classified as low vigor stands (for a total of 18 cores from six stands in two vigor classes). Vigor classification was based on visual assessment and verified with average annual stand growth over the last decade. High vigor stands were characterized by an average annual growth greater than 816 mm2·year−1 and low vigor stands by an average annual growth less than 452 mm2·year−1 [41]. Annual growth measurements are determined using basal area increment measurements. As the diameter of the tree increases, the same amount of wood production is represented by smaller and smaller rings. Therefore, ring width is a biased predictor of secondary growth so annual wood production, (i.e., basal area increment), is used.

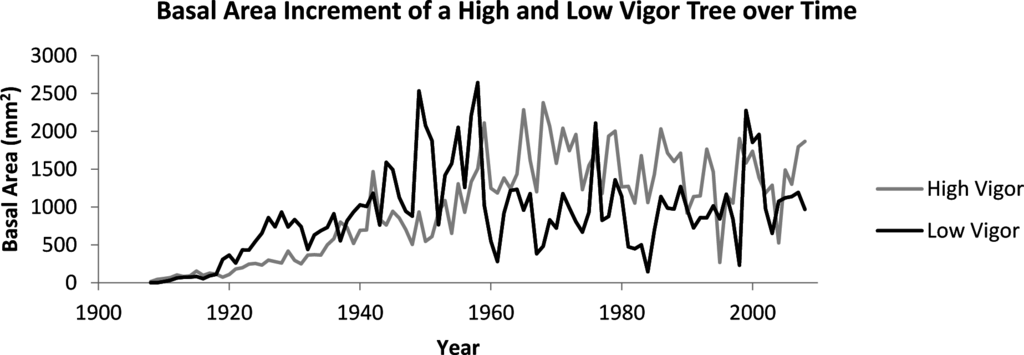
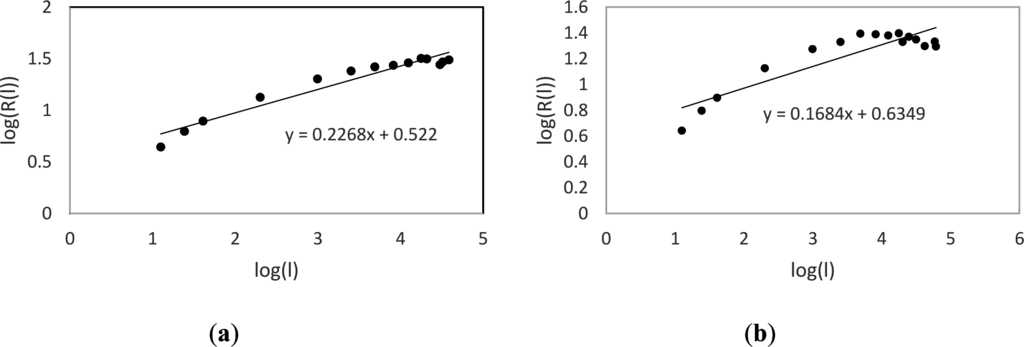
The set of basal area increment measurements for each tree was computed using ring widths and the dplR package for R [42] to produce a time series (Figure 1). The fractal dimension of each time series was calculated using a variation of the variogram estimator [25] which utilizes a lag ( ) of stationary increments. Specifically, if is the sample standard deviation of the time series from time to time and is the range of the time series observations from time to time , then is known as the rescaled range. If we then let be the average of all the rescaled range values for a given lag , then the Hurst coefficient can be calculated by determining the slope of the line obtained from plotting against for multiple values of (Figure 2 [43–45]). The Hurst coefficient (H) is directly related to fractal dimension (FD) by the equation for a given time series. Below is a summary of the algorithm used to estimate the fractal dimension of a tree core:
Measure annual tree ring widths and determine corresponding tree diameters (DBH) by commutatively adding ring radii.
Calculate annual basal area (BA) and produce a time series.
For each time lag (i.e., scale) l = 3, 4, 5, …, 90.
Calculate the standard deviation, , and range, , of the time series observations from year t = 1 to year t = l.
Repeat for all values of t applicable for the time series (i.e., ).
Calculate the rescaled range, , for each applicable t and the average rescaled range, , for each lag l.
Plot against for all values of and determine the slope of the line using least squares. The Hurst coefficient, H, is the slope of this line.
Calculate the fractal dimension, FD, using the equation: .
To determine if fractal dimension differed between vigor classes and if tree age had an effect on the results we used an ANCOVA with fractal dimension as the dependent variable, vigor classification as the independent variable, and age as the covariate (Table 1).
3. Results
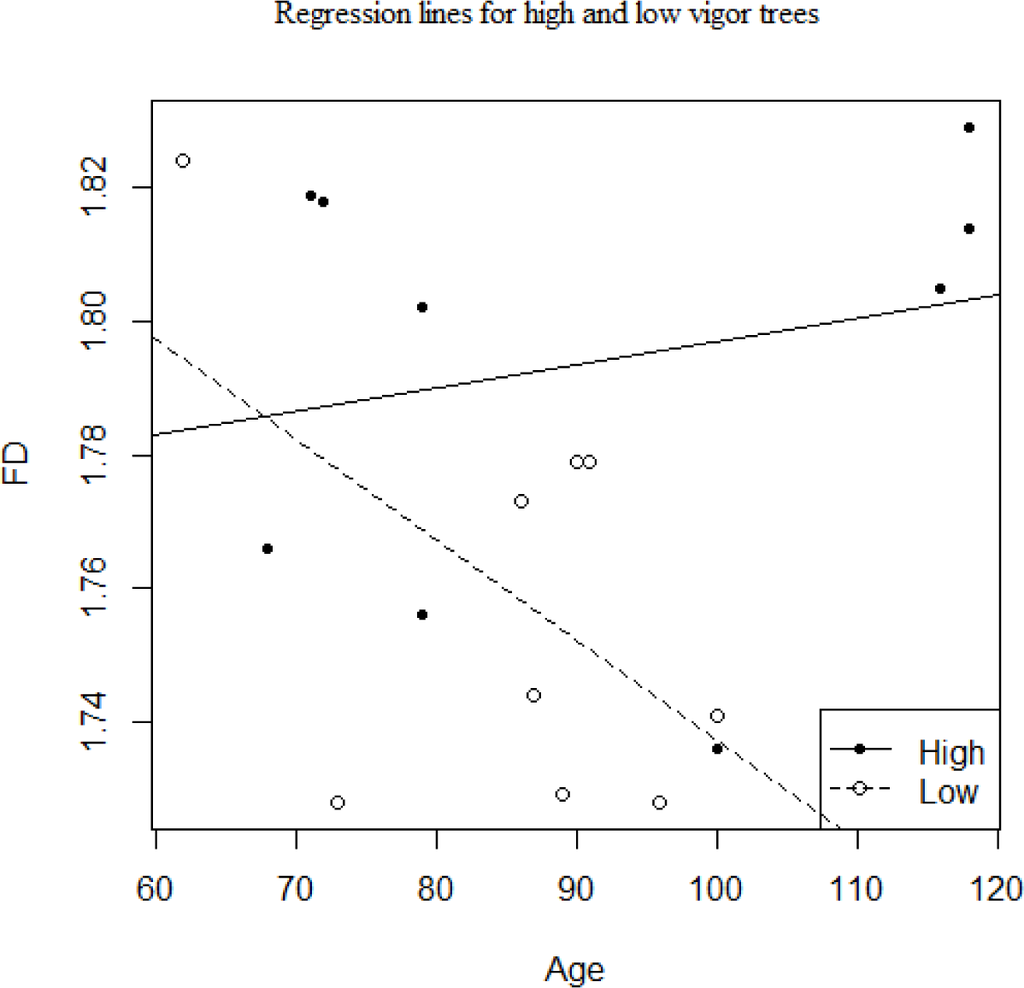
Low and high vigor trees display significantly different fractal dimensions (Table 2). Low vigor trees have an average fractal dimension of 1.758 ± 0.033 while high vigor trees have an average fractal dimension of 1.794 ± 0.033. The first ANCOVA model included age, vigor, and the interaction effect between age and vigor classification (Figure 2). Both age and the interaction between age and vigor classification were not significant (F = 0.045, P = 0.835 and F = 2.83, P = 0.114 respectively) while classification group was significant (F = 5.561, P = 0.033). The lack of a significant interaction effect indicates that the regression between age and fractal dimension is similar for both low and high vigor groups (Figure 3). A model without the interaction effect was then run. Again, age was not significant (F = 0.040, P = 0.844) while classification was (F = 4.95, P = 0.042). Finally, an ANOVA was used to compare the two models (F = 2.835, P = 0.1144). Insignificant results indicate that the removal of the interaction effect does not significantly affect the fit of the model. The only significant effect on the fractal dimension of an individual was the vigor classification group it was assigned to.

4. Discussion
Our results indicate that stressed trees display a lower fractal dimension in their growth patterns compared to healthy trees and coincides with previous studies across a variety of organisms. One way to compare results among studies is to calculate the ratio between the Hurst coefficient (slope of the log(l)-log(R(l)) graph) of healthy and stressed groups. In this study the average Hurst coefficient of the high vigor group was 0.853 times that of the low vigor group (HH/HL), a value comparable to values found in previous studies on animal behavior (0.803 [28]; 0.884 [29]; 0.74 and 0.798 [30]), plant growth (0.854 [32]; 0.871 [33]), and time series analysis of heart rhythms (the difference between healthy and various diseases ranged from 0.79 to 0.941 [36]).
While average growth rates confirmed our vigor classifications at the stand level, a decline in growth within an individual tree does not necessarily translate to a decline in health. Growth of a complex organism like a tree requires a suite of interconnected physical (i.e., apical and lateral growth, nutrient transportation, leaf and root production), chemical (i.e., hormone production and regulation, photosynthesis, respiration), and biological (i.e., dormancy, reproduction) processes. To help visualize how this complex system of processes may operate imagine a series of overlapping sine curves where the state space contains all vital life processes and the final output is growth. A system in its most basic state can be represented by a single curve (i.e., carbon sequestration). Alone, however, this process cannot support the tree. As the system becomes more complex, the number of curves increases (representing processes such as water and nutrient uptake and transport, respiration, and hormone production), each with a different frequency or amplitude. This complexity allows the organism to function smoothly; curves compensate for each other as peaks and troughs overlap. Consider that each curve contributes in some way to our final output which is growth. When there is only one curve, growth occurs in fits and starts. When there are many curves, growth occurs at a fairly constant and close to ideal rate, although the curves vary continuously. (It is important to understand that the ideal growth rate will itself fluctuate based on the environment and available resources). When stress is introduced to the system, energy is required to alleviate that stress-energy that must come from somewhere within the system. As a result, the system experiences a loss in complexity, which in turn affects growth, until the stress is relieved and the system recalibrates [9,46]. Based on this idea, the theory proposed by Emlen et al. [37] and Lipsitz [26], and evidence provided by previous studies, our results suggest that the fractal dimension of the tree ring data reflects an individual measure of developmental instability. The lower fractal dimension seen in the low vigor trees could be indicative of a lower state of system complexity (as we observed) due to stress which has diminished those individuals’ ability to respond dynamically to its environment. In another fundamental sense, the loss of dimension means literally a loss of the symmetry across time scales.
Growth and wood production (or biomass in general) is often used as a measure of health, and is thought to be a particularly sensitive indicator of stress [47]. Other energy and resource sinks including leaf, bud, and root production, maintenance, and storage tissue production all take precedence over secondary stem growth [48]. Reduced secondary growth is expected if there is a general lack of resources or if extra resources are required to fight disease, regenerate after defoliation, or otherwise respond to a disturbance. However, if there were little or no lasting effects of a stressful year on the individual, we expect that wood production would more or less reflect the environmental conditions of the year in which it was produced. In fact, this is often the case and a high correlation between annual precipitation and growth is a necessary assumption when tree ring chronologies are used to reconstruct historic climate data [49,50]. However, there are many studies that document the long term influence on growth by a single climatic [51] or herbivory [52] event (also see [1] and references therein).
The focus of this study was not to evaluate the mechanisms influencing stand vigor, only to examine the fractal dimensions within different vigor classes. However, the six stands represented in this study are similar with respect to soil, weather, and elevation; there is no natural gradient with which to further classify them, and all things being equal, we would expect the annual growth, vigor, and fractal dimensions to be similar. Clearly, differences among local site conditions exist, some of which are responsible for the variation in stand vigor. Differential competition, insect damage, and local weather patterns are all possible factors affecting stand vigor. For this study, however, we did not identify which factor(s) affect stand vigor but instead focused on the correlation between fractal dimension and stand vigor class.
5. Conclusions
Our results support the idea that healthy individuals exhibit higher system complexity compared to stressed individuals which can be measured by fractal analysis. Higher system complexity in healthy individuals allows for more efficient reactions to a fluctuating environment, maintaining homeostasis. Individuals from stands that had low vigor were not producing consistently smaller basal area increments compared to individuals from high vigor stands, but the pattern with which wood was produced differed. A healthy individual from a high vigor stand produced wood dynamically resulting in a rough time series; differential production between years presumably correlates well with available resources. A stressed individual from a low vigor stand produced wood in a less dynamic pattern, resulting in a time series that was less rough. If our interpretation is correct, the fractal dimension of tree ring growth provides a measure of developmental stability over time in woody plants.
The authors would like to thank John H. Graham and an anonymous reviewer for their comments which greatly improved this manuscript. The data used in this study was collected under a Base Evaluation Monitoring Grant by the Forest Health Monitoring Program of the US Forest Service. Support for JPS was provided by a Japanese Society for Promotion of Science Postdoctoral Fellowship.
Conflicts of Interest
The authors declare no conflict of interest.
Author Contributions
JPS collected and processed tree cores, did the analysis and wrote the paper. DMK and JBB obtained funding for the collection of data and contributed knowledge of field site locations. DCF helped write the paper and made conceptual contributions.
References
- Dobbertin, M. Tree growth as indicator of tree vitality and of tree reaction to environmental stress: A review. Eur. J. For. Res. 2005, 124, 319–333. [Google Scholar]
- Torelli, N.; Shortle, W.C.; Cufara, K.; Ferlin, F.; Smith, K.T. Detecting changes in tree health and productivity of silver fir in Slovenia. Eur. J. For. Pathol. 1999, 29, 189–197. [Google Scholar]
- Duchesne, L.; Ouimet, R.; Houle, D. Basal area growth of sugar maple in relation to acid deposition, stand health, and soil nutrients. J. Environ. Qual. 2002, 31, 1676–1683. [Google Scholar]
- Taylor, O.C.; Cardiff, E.A.; Mersereau, J.D. Apparent photosynthesis as a measure of air pollution damage. J. Air Pollut. Control Assoc. 1965, 15, 171–173. [Google Scholar]
- Myhre, A.; Forberg, E.; Aarnes, H.; Nilsen, S. Reduction of net photosynthesis in oats after treatments with low concentrations of ozone. Environ. Pollut. 1988, 53, 265–271. [Google Scholar]
- Denmead, O.T.; Shaw, R.H. The effects of soil moisture stress at different stages of growth on the development and yield of corn. Agron. J. 1960, 52, 272–274. [Google Scholar]
- Larsson, S. Stressful times for the plant stress—Insect performance hypothesis. Oikos 1989, 56, 277–283. [Google Scholar]
- Chaerle, L.; van der Straeten, D. Seeing is believing: Imaging techniques to monitor plant health. Biochim. Biophys. Acta. 2001, 1519, 153–166. [Google Scholar]
- Pedersen, B.S. The role of stress in the mortality of midwestern oaks as indicated by growth prior to death. Ecology 1998, 79, 79–93. [Google Scholar]
- Freeman, D.C.; Graham, J.H.; Emlen, J.M. Developmental stability in plants: Symmetries, stress, and epigenesis. Genetica 1993, 89, 97–119. [Google Scholar]
- Freeman, D.C.; Graham, J.H.; Emlen, J.M.; Tracy, M.; Hough, R.A.; Alados, C.L.; Escos, J. Plant developmental instability: New measures, applications, and regulation. In Developmental Instability: Causes and Consequences; Polack, M., Ed.; Oxford University Press: New York, NY, USA, 2002; pp. 927–1027. [Google Scholar]
- Graham, J.H.; Freeman, D.C.; Emlen, J.M. Developmental Stability: A Sensitive Indicator of Populations under Stress; Landis, W.G., Hughes, J.S., Lewis, M.A., Eds.; ASTM Special Technical Publication 1179; American Society for Testing and Materials: Phiadelphia, PA, USA, 1993; pp. 136–158. [Google Scholar]
- Mandlebrot, B.B. Fractals, Form, Chance, and Dimension; Freeman: San Francisco, NC, USA, 1977. [Google Scholar]
- Mandlebrot, B.B. The Fractal Geometry of Nature; Freeman: New York, NY, USA, 1983; pp. 1–58. [Google Scholar]
- Voss, R.F. Random fractals: Self-affinity in noise, music, mountains, and clouds. Physica D Nonlinear Phenom 1989, 38, 362–371. [Google Scholar]
- Zeide, B.; Pfeifer, P. A method for estimation of fractal dimension of tree crowns. For. Sci. 1991, 37, 1253–1265. [Google Scholar]
- Burrough, P.A. Fractal dimensions of landscapes and other environmental data. Nature 1981, 294, 240–242. [Google Scholar]
- Theiler, J. Estimating fractal dimension. J. Opt. Soc. Am. 1989, 7, 1056–1073. [Google Scholar]
- Critten, D.L. Fractal dimension relationships and values associated with certain plant canopies. J. Agric. Eng. Res. 1997, 67, 61–72. [Google Scholar]
- Kurth, W. Morphological models of plant growth: Possibilities and ecological relevance. Ecol. Model. 1994, 75, 299–308. [Google Scholar]
- Tatsumi, J.; Yamauchi, A.; Kono, Y. Fractal analysis of plant root systems. Ann. Bot. 1989, 64, 499–503. [Google Scholar]
- Prusinkiewicz, P.; Hanan, J. Linenmayer Systems, Fractals, and Plants; Springer-Verlag: New York, NY, USA, 1989. [Google Scholar]
- Stevens, P. Patterns in Nature; Atlantic Monthly Press Book: Boston, MA, USA, 1974. [Google Scholar]
- Bruno, R.; Raspa, G. Geostatistical characterization of fractal models and surfaces. Geostatistics 1989, 1, 77–89. [Google Scholar]
- Gneiting, T.; Sevcikova, H.; Percival, D.B. Estimators of fractal dimension: Assessing the roughness of time series and spatial data. Stat. Sci. 2010, 27, 247–277. [Google Scholar]
- Lipsitz, L.A. Dynamics of Stability: The physiological basis of functional health and frailty. J. Gerontol. Ser. A Biol. Sci. Med. Sci. 2002, 57, 115–125. [Google Scholar]
- Graham, J.H.; Duda, J.J.; Brown, M.L.; Kitchen, S.; Emlen, J.M.; Malol, J.; Bankstahl, E.; Krzysik, A.J.; Balbach, H.; Freeman, D.C.; et al. The effects of drought and disturbance on the growth and developmental instability of loblolly pine (Pinus taeda L.). Ecol. Indic. 2012, 20, 143–150. [Google Scholar]
- MacIntosh, A.J.J.; Alados, C.L.; Huffman, M.A. Fractal analysis of behavior in a wild primate: Behavioural complexity in health and disease. J. R. Soc. Interface. 2011, 8, 1497–1509. [Google Scholar]
- Alados, C.L.; Weber, D.N. Lead effects on the predictability of reproductive behavior in fathead minnows (Pimephales promelas): A mathematical model. Environ. Toxicol. Chem. 1999, 18, 2392–2399. [Google Scholar]
- Alados, C.L.; Escos, J.; Emlen, J.M. Fractal structure of sequential behavior patterns: An indicator of stress. Anim. Behav. 1996, 51, 437–443. [Google Scholar]
- Rutherford, K.M.D.; Haskell, M.J.; Glasbey, C.; Jones, R.B.; Lawrence, A.B. Detrended fluctuation analysis of behavioural responses to mild acute stressors in domestic hens. Appl. Anim. Behav. Sci. 2003, 83, 125–139. [Google Scholar]
- Escos, J.M.; Alados, C.L.; Emlen, J.M. Fractal structures and fractal functions as disease indicators. Oikos 1995, 74, 310–314. [Google Scholar]
- Eghball, B.; Settimi, J.R.; Maranville, J.W.; Parkhurst, A.M. Fractal analysis for morphological description of corn roots under nitrogen stress. Agron. J. 1993, 85, 287–289. [Google Scholar]
- Acharya, R.U.; Bhat, P.S.; Kannathal, N.; Rao, A.; Lim, C.M. Analysis of cardiac health using fractal dimension and wavelet transformation. ITBM-RBM 2005, 26, 133–139. [Google Scholar]
- Qtsuka, K.; Cornelissen, G.; Halberg, F. Circadian rhythmic fractal scaling of heart rate variability in health and coronary artery disease. Clin. Cardiol 2009, 20, 631–638. [Google Scholar]
- Jelles, B.; van Birgelen, J.H.; Slaets, J.P.J.; Hekster, R.E.M.; Jonkman, E.J.; Stam, C.J. Decrease on non-linear structure in the EEG of Alzheimer patients compared to healthy controls. Clin. Neurophysiol. 1999, 110, 1159–1167. [Google Scholar]
- Emlen, J.M.; Freeman, D.C.; Mills, A.; Graham, J.H. How organisms do the right thing: The attractor hypothesis. Chaos 1998, 8, 717–726. [Google Scholar]
- Selvi, T.S.; Selvaraj, S.R. Fractal Dimension Analysis of Northeast Monsoon of Tmil Nadu. Univers. J. Environ. Res. Technol. 2011, 1, 219–221. [Google Scholar]
- Speer, J.H. Fundamentals of Tree-Ring Research; University of Arizona Press: Tucson, AZ, USA, 2010. [Google Scholar]
- Holmes, R.L. Program COFECHA: Version 3; The University of Arizona: Tucson, AZ, USA, 1992. [Google Scholar]
- Sakai, A.K.; Burris, T.A. Growth in male and female aspen clones: A twenty-five year longitudinal study. Ecology 1985, 66, 1921–1927. [Google Scholar]
- Bunn, A.G. A dendrochronology program library in R (dplR). Dendrochronologia 2008, 26, 115–124. [Google Scholar]
- Hurst, H.E. Long term storage capacity of reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–808. [Google Scholar]
- Mandlebrot, B.B.; Wallis, J.R. Robustness of the rescaled range R/S in the measurement of non-cyclic long run statistical dependence. Water Resour. Res. 1969, 5, 967–988. [Google Scholar]
- Davies, R.B.; Hart, D.S. Tests for Hurst effect. Biometrika 1987, 74, 95–101. [Google Scholar]
- Manion, P.D. Tree Disease Concepts; Prentice-Hall: Englewood Cliffs, NJ, USA, 1981. [Google Scholar]
- Waring, R.H.; Pitman, G.B. Modifying lodgepole pine stands to change susceptibility to mountain pine beetle attack. Ecology 1985, 66, 889–897. [Google Scholar]
- Waring, R.H. Characteristics of trees predisposed to die. BioScience 1987, 37, 569–573. [Google Scholar]
- Fritts, H.C. Tree rings and Climate; Academic Press: New York, NY, USA, 1976. [Google Scholar]
- Grissino-Mayer, H.D. A 2129-year reconstruction of precipitation for northwestern New Mexico, USA. In Tree Rings, Environment, and Humanity; Dean, J.S., Meko, D.M., Swetnam, T.W., Eds.; Radiocarbon, Department of Geosciences, University of Arizona: Tucson, Arizona, USA, 1996; pp. 191–204. [Google Scholar]
- Lapointe-Garant, M.P.; Huang, J.G.; Geaizquierdo, G.; Raulier, F.; Bernier, P.; Berninger, F. Use of tree rings to study the effect of climate change on trembling aspen in Quebec. Glob. Change Biol. 2009, 16, 2039–2051. [Google Scholar]
- Speed, J.D.M.; Austrheim, G.; Hester, A.J.; Mysterud, A. Browsing interacts with climate to determine tree-ring increment. Funct. Ecol 2011, 25, 1018–1023. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).