The Perception of Symmetry in Depth: Effect of Symmetry Plane Orientation
Abstract
: The visual system is sensitive to symmetries in the frontoparallel plane, and bilateral symmetry about a vertical axis has a particular salience. However, these symmetries represent only a subset of the symmetries realizable in three-dimensional space. The retinal image symmetries formed when viewing natural objects are typically the projections of three-dimensional objects—animals, for example—that have a symmetry in depth. To characterize human sensitivity to depth symmetry, experiments measured observers’ ability to discriminate stereo displays that were symmetrically distributed in depth and those that were asymmetrically distributed. Disparity values were distributed about one of four planes passing through the z-axis and differing in frontoparallel orientation. Asymmetrical patterns were generated by perturbing one of these disparities. Symmetrical-asymmetrical discrimination thresholds were lowest for symmetry about the vertical plane and highest for the horizontal plane. Thresholds for discriminating repetitions and non-repetitions of depth values did not differ across the four planes, whereas discriminations for depth gradients differed from both the symmetry and repetition cases. The heightened sensitivity to symmetry in depth about the vertical plane is a 3-D analog of 2-D mirror-image symmetry performance and could be its source.1. Introduction
Symmetries exist in a variety of forms and their perceptual effect differs widely, from the subtle to the salient. Symmetry in the sense of reflection is the case most extensively studied (see [1–3] for reviews) and mirror-image symmetry about the vertical midline is a particularly salient example [4]. A number of reasons have been suggested for this salience, ranging from the collateral (a by-product of our symmetric visual systems [4–6]) to the adaptive (the advantage of detecting evolutionarily important visual objects, such as conspecifics and other animals). Animals are arguably the most conspicuous class of natural objects with bilaterally symmetry. The most consistently symmetrical of manufactured objects are those mimicking, accommodating, or adapted to humans or their bodily parts (clothing, furniture, eye-glasses, utensils, tools) and vehicles of all sorts, whose bilaterally symmetrical surfaces resemble those of animals for common adaptive reasons: Both differentiate “top” and “bottom” in order to negotiate the effect of gravity and both move in a preferred “forward” direction. Despite the variety and importance of object symmetry, relatively few studies have examined cases of symmetry that are more general than bilateral mirror-image symmetry presented in the observer’s frontoparallel plane.
Typically, planar symmetrical patterns are encountered as textures, markings on flat surfaces. Placing subsets of such a pattern at different depths allows interactions between planar and three-dimensional (3-D) representations to be studied [7–9]. However, the task of detecting the symmetry projected onto the x-y plane—the observer’s frontoparallel plane—makes the depth variation an irrelevant property. While most perceptual studies place planar patterns normal to the visual direction, skewing the pattern by means of a rotation about a line in the x-y plane gives access to more generic vantage points [7–19]. After the rotation, cues to the pattern’s symmetry can be indirect and more complex, for the retinal image is then typically asymmetrical. Another common source of symmetry is3-D objects, which often have multiple non-independent symmetries. The task of detecting the symmetry of a skewed 3-D object given a planar projection can be highly informative about shape recognition processes [18]. As with skewed planar symmetry, however, the object’s retinal image is generally asymmetric; reconstructions of the object as symmetric are inferences and asymmetric reconstructions are no less consistent with the evidence. Even so, there is evidence that humans tend to infer symmetry when it goes beyond, or even against, the visual information provided [19]. Yet there is also evidence that the detection of planar symmetry does not benefit from the addition of consistent 3-D symmetry cues [8]. Because depth information is often under-specified in the visual input and subject to inference, symmetry can function as an interpretive assumption in recognizing shapes that vary in depth, but there is little direct evidence about the processing of the symmetry of depth signals.
Thus, while a symmetrical retinal image usually requires that an object be viewed from a privileged vantage point, humans seem disposed to recover the symmetry of objects whether they are imaged symmetrically on the retina or not [10–19]. The symmetry of at least some 3-D objects might thus be assumed a priori. This study examines the hypothesis that the salience of symmetry of patterns confined to the frontoparallel plane is a special case of the salience of symmetry of 3-D objects. It considers the component needed to bridge this dimensional gap: symmetry in depth. The stimuli used are as simple as possible, their depth is defined by binocular disparity, and their symmetry is conserved in their retinal images. Experiment 1, introduced next, compares observers’ sensitivity to symmetrical depth across patterns with horizontally, vertically, or obliquely oriented symmetry planes, using sensitivity to repetition as a standard for comparison. Experiment 2 tests the generality of the results of the first experiment by using patterns with a different symmetry property.
2. Experiment 1
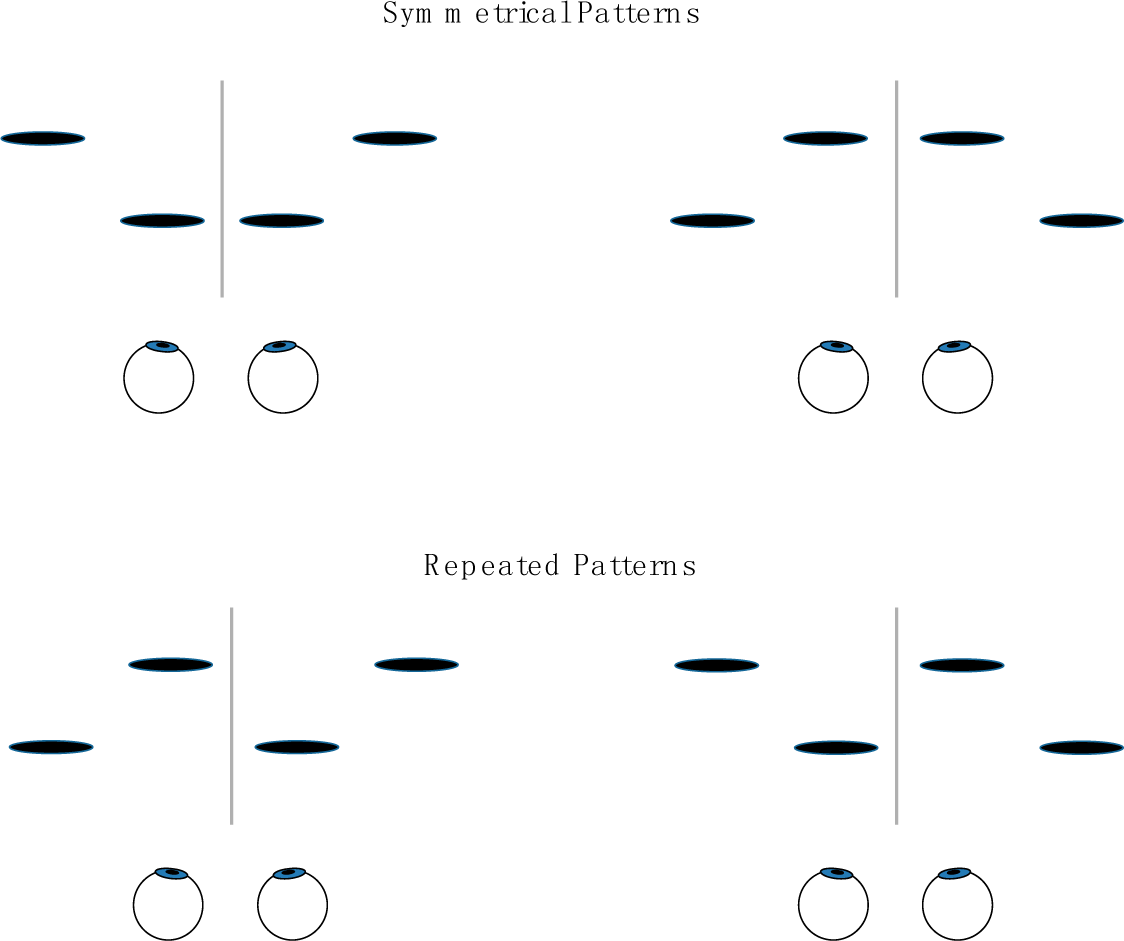
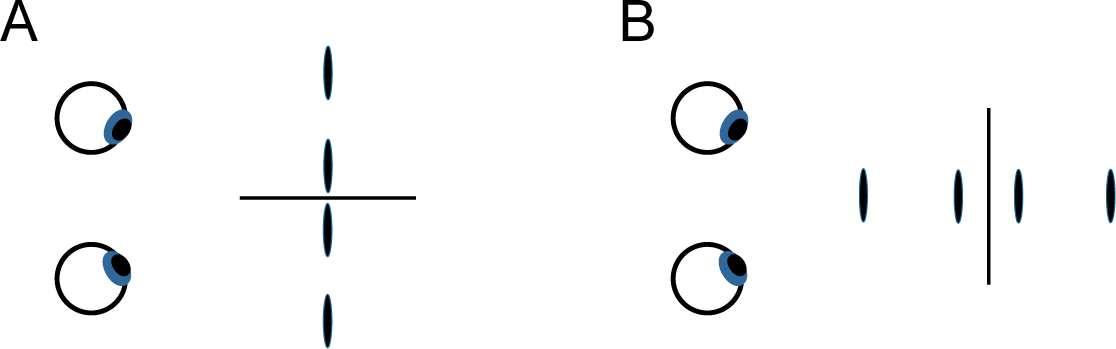
If the salience of two-dimensional frontoparallel bilaterally symmetrical patterns derives from, or is a special case of, humans’ sensitivity to the bilateral symmetry of 3-D objects, then an observer’s sensitivity to frontoparallel symmetry and to symmetry in depth should display similar effects of the orientation of the axis or plane around which the symmetry is arrayed Symmetry in the frontoparallel plane is typically most salient perceptually and most easily discriminated from asymmetrical variants when it is arrayed about a vertical axis [4,13,15,20–29]. Similarly, two patterns that are left-right reflections of one another tend to be difficult to discriminate [5]. For the case of depth symmetry, we will consider in Experiment 1 the simplest of cases, in which four disks are symmetrically deployed about a plane passing through the z-axis, as depicted relative to the eyes of the observer in Figure 1A, or asymmetrically deployed, as in Figure 1B (The geometric center of symmetrical and repeated patterns used in the experiments coincided with the origin of the coordinate system and with the fixation point on which observers’ eyes converged (see Section 5). The interocular axis was in the horizontal x-z plane and parallel to the x-axis; the y-axis was thus vertical and the z-axis ran through the observer’s sagittal plane.) This symmetry plane projects onto the x-y plane—from the observer’s perspective, the frontoparallel plane—with a vertical, horizontal, or oblique orientation, as in Figure 1C (see Section 5 for full specification of stimuli). Trial-to-trial variation of the stimuli was confined to the z-values of the individual disks making up the display. These z-values, defined by binocular disparity, were the only relevant task parameter and had values that were either symmetrical or asymmetrical (or, for purposes of comparison, repeated or non-repeated) on either side of the symmetry (or repetition) plane. The task was to discriminate symmetrical and asymmetrical depth (or repeated and non-repeated depth). Figure 2 shows the alternative stimulus configurations for symmetrical and repeating patterns. Common laboratory instances of planar mirror-image symmetry can be considered a special case of this type of display, the case where the depth of the pattern is constant. Constant depth values are equally consistent with a pattern’s having depth symmetry, depth repetition, or a depth gradient.
The relation between bilateral symmetry in the x-y plane and depth symmetry hinges on the matter of orientation. Different symmetry orientations are related by rotation. A bilateral symmetrical pattern in the x-y plane can be rotated within this plane to acquire a differently oriented symmetry axis. The same does not hold for symmetry in depth. A depth-symmetrical pattern like that in Figure 2A, if rotated within the x-z plane, does not preserve its depth symmetry relative to the observer. Instead, the rotation results in a skewed symmetry pattern, one having correponding elements in different depth planes. The depth-symmetric pattern must be rotated about a line, either the z-axis or a line parallel to the z-axis, in order to produce a differently oriented symmetry in depth. The rotation is in 3-D space, not within a plane. The rotation defines a family of depth-symmetrical patterns in 3-D (even if individual patterns are 2-D). A z-axis rotation changes the orientation of the symmetry; symmetry lines connecting correponding points are normal to a plane passing through the z-axis. For symmetry orientation to be relevant to a pattern’s description, the pattern’s symmetry axis or plane counts among its dimensions. The same applies to patterns repeated in depth.
Performance for detecting pattern symmetry was evaluated by contrasting it with performance for detecting pattern repetition. Differently oriented symmetry planes give the stimuli different spatial and retinal locations (Figure 1C). Repeated patterns had the same locations and component disparities as symmetrical patterns and serve to control for effects of variation in the intrinsic sensitivity of different locations. Moreover, the arrangement of the cyclopean positions of stimuli in the x-y plane is the same for both symmetrical and repeating patterns. This makes the pattern’s projection on the x-y plane identical for both symmetrical and repeated depth patterns and equally consistent with both of them. (The advantage of this arrangement in the x-y plane comes at the cost of muddying the interpretation of planar symmetry judgments collected from a 2-D rendering of the stimuli. Would the data tell us something about symmetry detection—or repetition detection?)
Displays like that of Figure 2A are only one of several options for probing depth symmetry. Figure 3 shows a more direct way to get a depth analog of mirror-image symmetry in the plane. Here, a symmetrical frontoparallel display (Figure 3A) has had its stimulus positions rotated 90° in the x-z plane, creating a depth symmetry (Figure 3B), a true “mirror-image” display from the observer’s perspective. The reasons for not using such a display here were pragmatic. Potential problems arise from depth range, disparity gradients, transparency or occlusion, and perceived near-far metrical differences.
Note, too, that the pattern elements used in the experiments were not arranged as in Figure 4. Here, the disks are symmetrical in the x-y plane about the y-axis, but symmetrical relations in depth would be confined to pairs of disks with the same horizontal position (of which there are four). If the disks of each pair independently had the same depth, we could say the pattern was symmetrical in depth. However, we could equally say it was repeated in depth. Two points are insufficient to distinguish reflection symmetry and repetition. The minimum required number of discrete stimuli aligned perpendicularly to a point on the symmetry or repetition plane is four, which is the number used here.
The repetition discrimination task used as a standard for comparison requires observers to make what are in effect “same-different” judgments. “Same” patterns are translated copies (forming a symmetry of another type). “Same-different” judgments can be computationally simple and quickly executed [30,31], so it is not immediately obvious that symmetry discrimination is the easier task (e.g., [32]). The relative salience and discriminability of symmetry and repetition may depend on whether the axis is seen to separate the two sides of a single object or two distinct objects [7,33]. However, the absolute depth discrimination performance for symmetrical and repeated patterns is not of primary interest here. Rather, interest focuses on performance as a function of the orientation of the symmetry and repetition planes. Detailed methods are to be found in Section 6.
Results
Observers discriminated symmetrical and asymmetrical as well as repeated and non-repeated depth configurations, with vertical, horizontal, or oblique planes of symmetry or repetition passing through the z-axis. A conspicuous feature of this experiment was the difficulty of the task for some of the observers. Of the four observers who participated, two could not do the symmetry task sufficiently well to establish threshold performance. One of these observers (both female) had months of prior experience in various stereo experiments, the other had a modest amount. Both had good stereoacuity. Modifying the stimulus size, contrast, texture, presentation duration (≤400 ms), and temporal envelope did not make the symmetry task performable for these observers (their repetition discrimination was similarly poor). A failure to understand the instructions (though not an inability to paraphrase them) is a possible cause but seems unlikely. The data of these two observers were disregarded from further consideration. The other two observers succeeded with the symmetry task and found repetitions more difficult.
For the two observers who succeeded with the symmetry task, data for the two disparity magnitude conditions (±2.0 and ±5.0 arcmin) used to render the symmetry and repeated patterns were proportional and were combined after scaling the 2 arcmin data. Likewise, data for the two oblique planes were similar and combined. Psychometric functions were fitted with cumulative Gaussian functions from which the threshold were determined. Thresholds for the task are the magnitudes of the disparity perturbations required for correctly discriminating the patterns presented in the two stimulus intervals at a level of 84%.
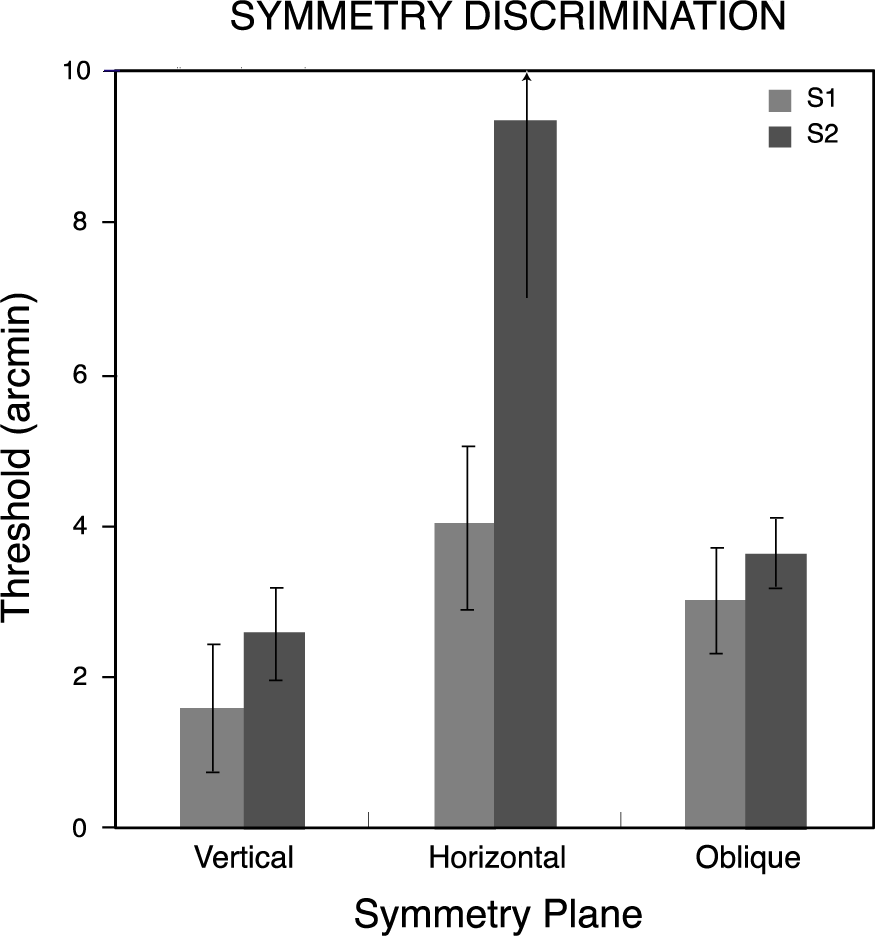
Figure 5 shows thresholds for symmetry discriminations for the two observers as a function of the symmetry plane orientation. Observers’ thresholds varied with the orientation of this plane, being lowest when the plane was vertical and highest when it was horizontal. Bootstrapped estimates of threshold variability for the three pairs of conditions were calculated using 4000-iteration Monte Carlo simulations [34] on the psychometric data for each observer and the resulting standard deviations bracket the threshold measures in Figure 5. Thresholds for the vertical plane were significantly lower (p< 0.05) than for the other orientations, and those for oblique planes were significantly lower than for the horizontal plane, for both observers.
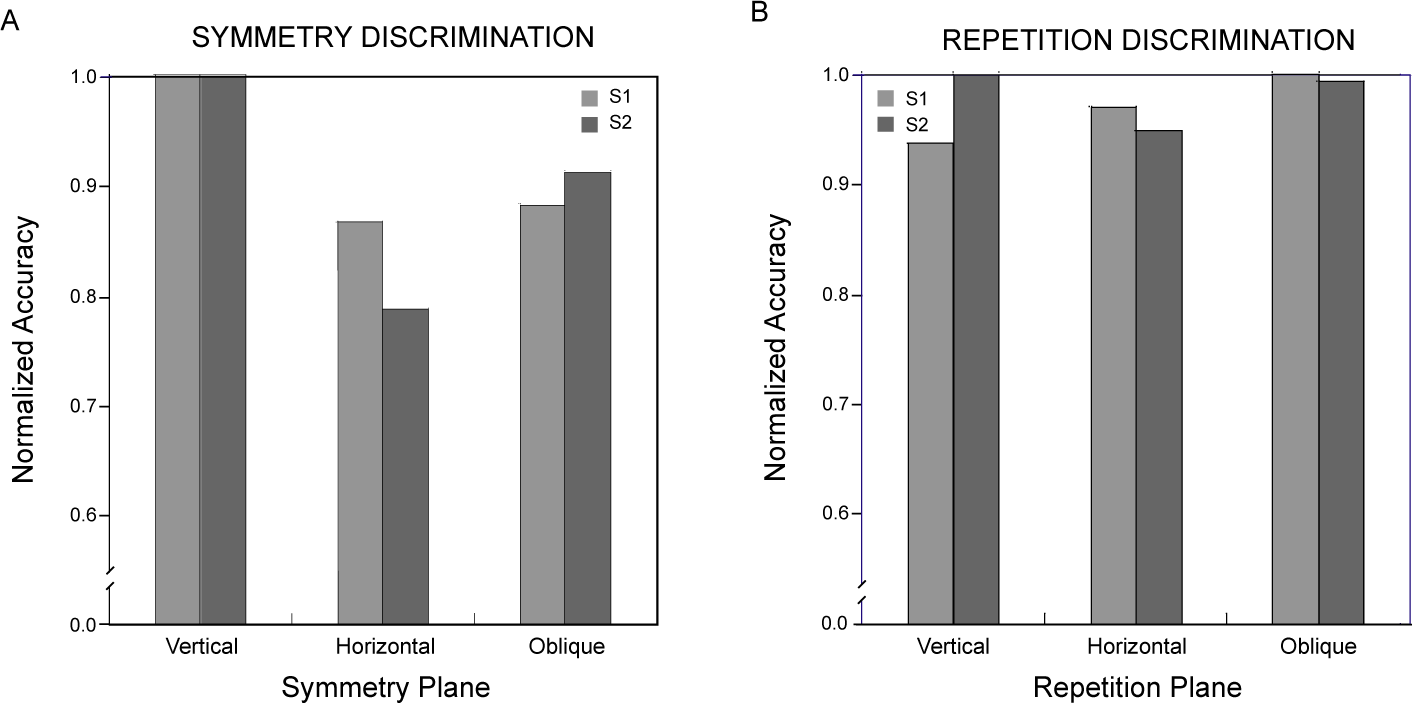
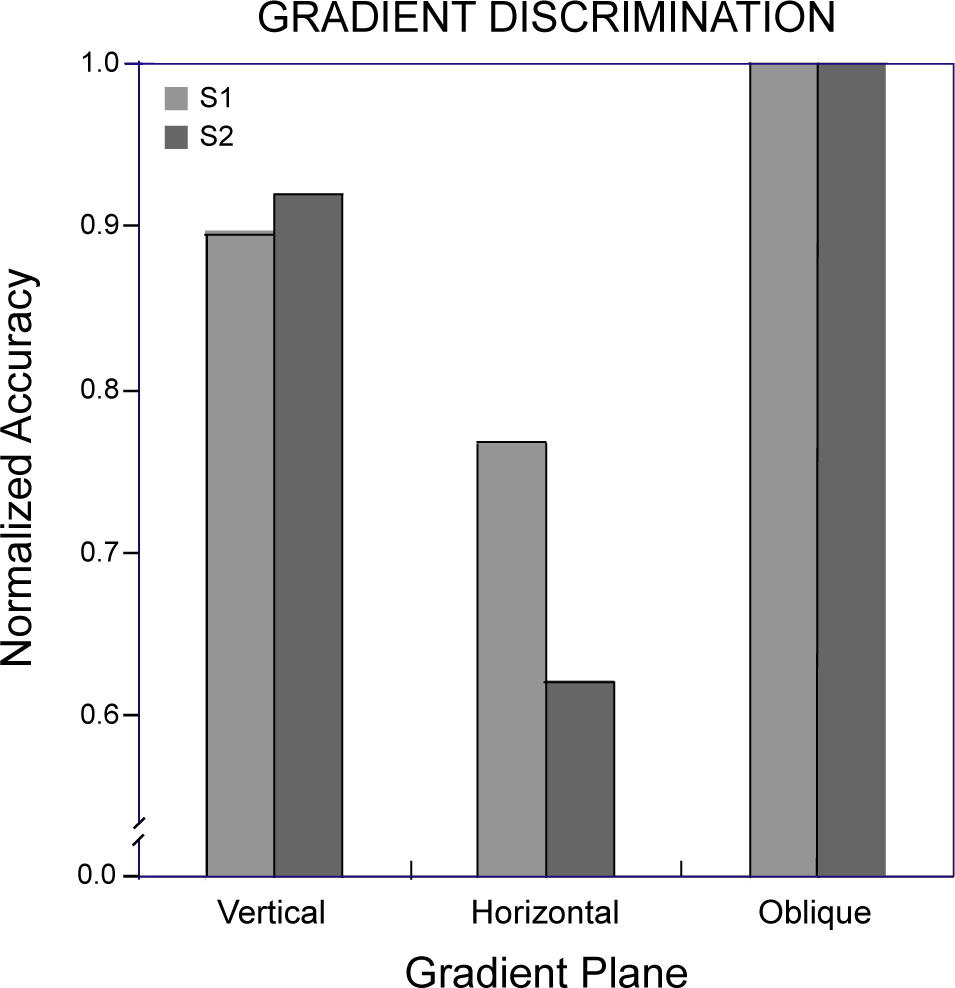
Symmetry discrimination was considerably easier overall for these observers than repetition discrimination. This difference was reflected in the constant stimulus values used for symmetry and repetition discriminations, which covered the same range in order to avoid diplopia in the repetition discrimination task (see Materials and Methods). Therefore, while comparable thresholds could not be obtained across the two discrimination conditions [34], performance accuracies could be compared over the same range of disparity perturbations. Logit-transformed proportion-correct responses for the two observers pooled across all levels of disparity were entered into a repeated-measures analysis of variance with pattern type (symmetry, repetition) and symmetry or repetition plane orientation (vertical, horizontal, oblique) as factors. Neither pattern type (F(1, 1) = 42.2) nor orientation (F(2, 2) = 10.5) attained significance in this analysis (p> 0.05), but their interaction did (F(2, 2) = 28.9, p< 0.05). Orthogonal comparisons of primary interest showed the vertically symmetrical patterns were discriminated more accurately than all other combinations of pattern type and orientation (Dunnett test, d(6, 5) = 0.23, p< 0.05). Accuracy for symmetry discriminations was 0.82 ± 0.066 (mean ± standard deviation) averaged across orientations and observers, while that for repetitions was 0.67 ± 0.013. The effect of orientation on repetition discrimination accuracy was not significant (F(1, 2) = 2.44, p> 0.25). The minute spread of repetition accuracies across orientations contrasts with the effect of symmetry orientation, accounting for the observed interaction. The relative differences across conditions in the proportion of correct discriminations appear in Figure 6, where scores for each observer have been normalized with respect to the most discriminable orientation.
The results show an effect of symmetry plane orientation that is a 3-D analog of the effect of symmetry axis orientation typically found in studies of symmetry in the frontoparallel plane [4,13,15,20–29]. In both the planar case, where symmetry is defined about an axis in the x-y plane, and the 3-D case, where symmetry is defined about a plane running through the z-axis, symmetry about the vertical has an advantage over other orientations. The lack of such an advantage for repetition in depth shows that pattern orientation (in this experiment, the orientation of the row of disks) is not the source of the difference in performance between vertical, horizontal, and oblique symmetry planes. For similar reasons, the different retinal positions of the stimuli are unlikely to have contributed to the effect of symmetry plane orientation. Instead, the effect of plane orientation is due to the depth pattern.
3. Experiment 2
In Experiment 1, individual disks had the same disparities and the same x-y locations whether they belonged to symmetrical patterns or to repeated patterns. Yet symmetry was considerably more discriminable than repetition. It is possible that this difference in task difficulty contributed to the different effects of orientation observed for symmetry and repetition discrimination. For example, a difficult task might have induced observers to adopt a different strategy than they used in an easier task. It is also unclear how specific to symmetry discrimination the difference among the orientations are. Would these differences hold for non-repeating redundant patterns generally? Or are they unique to bilateral reflective symmetry, or are all types of symmetry (excepting repetition) most discriminable about a vertical plane of symmetry? As a start to answering such questions, I selected a type of symmetry sufficiently different from the reflection used in Experiment 1 that it might return a different pattern of results and yet similar to it in that its level of discriminability—how easy the task was—would overlap with that recorded for symmetrical patterns in the first experiment. The pattern chosen was a depth gradient, as seen in Figure 7.
As is the case with the patterns used in Experiment 1, a linear depth gradient centered on the fixation plane can be described several ways. For example, it is a pattern with odd symmetry, which reverses its depth polarity across the plane of reflection, or it could be described as having a rotational or skewed centric symmetry. Intuitively, it had a simple description, differed from the even-symmetrical patterns of Experiment 1, and satisfied the requirements for Experiment 2.
Results
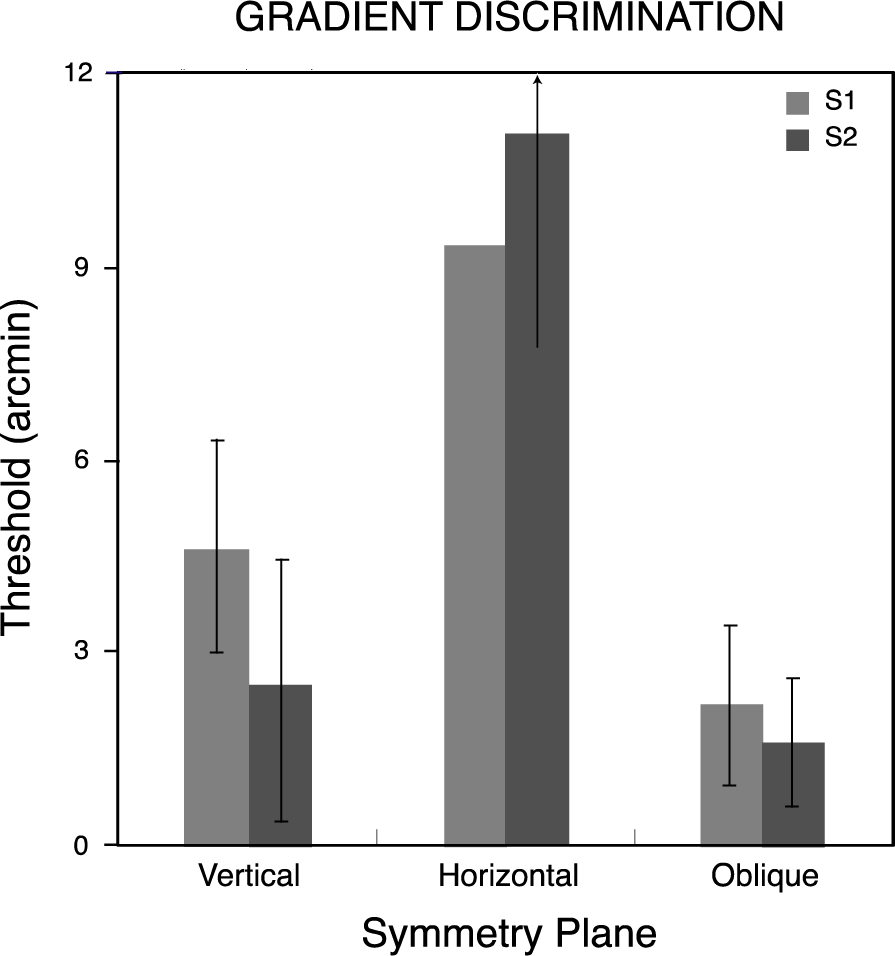
Thresholds were determined for depth-gradient discriminations by fitting the psychometric functions with cumulative Gaussians, as for symmetrical depth discriminations in Experiment 1. Each observer’s threshold for discriminating depth gradients about planes with vertical, horizontal and the two (pooled) oblique orientations appears in Figure 8, along with standard deviations calculated by the Monte Carlo method used in the first experiment [34]. As in the case for symmetry discriminations, gradient discrimination thresholds varied with the orientation of the pattern’s symmetry plane. However, for neither observer was threshold lowest for the vertically oriented plane. Observers were best able to discriminate linear depth gradients centered about an oblique plane, though the thresholds for oblique and vertical planes did not differ significantly (p> 0.05). The vertical plane (about which the disks are arranged with a horizontal gradient of horizontal disparities) and the horizontal plane (arranged with a vertical gradient of horizontal disparities) resulted in progressively lower sensitivity. Overall, thresholds here (mean = 5.2 arcmin) were similar to those for symmetry discriminations (mean = 4.1 arcmin). Both the symmetry and gradient data show surprisingly poor performance for depth discriminations about the horizontal plane. They differ, though, in the relative advantage for the vertical symmetry plane. Comparing normalized discrimination accuracy for gradient discriminations (Figure 9) with that for symmetric discriminations (Figure 6) shows there is no unique distribution of sensitivities to the orientations of depth symmetries in general.
4. Discussion
Mach’s observations in the 1880s [4] brought attention to the perceptual salience of frontoparallel mirror-image symmetry, in particular the salience of reflection about a vertical axis. Symmetry in depth deployed about a vertical plane appears to enjoy an analogous advantage. The stimuli used here were symmetric about a plane perpendicular to the frontoparallel plane. Observers were better at discriminating symmetric and asymmetric depth when this plane was vertical—the y-z plane—than other orientations tested, either the horizontal x-z plane or oblique planes with intermediate orientations. A preference for 3-D symmetry about the vertical is also found when observers give interpretations to random 2-D figures [35]. The frontoparallel symmetry of the stimuli used in the study—that is, the symmetry of the disks’ x-y values—is not implicated in this, for the advantage was specific to the even depth symmetry tested in Experiment 1 and did not appear for discrimination of depth repetition or depth gradients, despite the frontoparallel symmetry of all the stimuli. Thus, we can conclude that the enhanced discriminability of even-symmetric displays about the y-z plane does not result from their projected symmetry in the frontoparallel plane (or, for that matter, their projected repetition or uniform spacing), but rather from the reflection across the y-z plane.
Evidence that bilaterally symmetric 3-D objects share the perceptual salience found for mirror-image symmetry in the frontoparallel plane comes from other studies as well, which suggest that symmetry may be an a priori expectation brought to bear in the course of object recognition [10,11,19,36–40]. The symmetrical stimuli used here have a reflection about a plane in 3-D space, a property they share with many animals, plants, and man-made objects. When objects of this sort give rise to bilaterally symmetric retinal images, 2-D and 3-D symmetry information would be available simultaneously to mechanisms sensitive to both frontoparallel and depth symmetry. Analysis of the 2-D signals would not necessary represent a first stage, however. A viewpoint-independent analysis of 3-D object symmetry could in principle develop alongside or precede the analysis of 2-D image symmetry, whether this is represented monocularly or binocularly [41].
Indeed, Chen and Sio [9] raised this possibility in a recent study by showing that stereo-depth modulations selectively interfered with the detection of frontoparallel bilateral symmetry. Depth was a task-irrelevant attribute. Interference resulted when symmetrically positioned random dots near the symmetry axis were separated by a step modulation in depth. Modulations that kept these dots on a plane, even a tilted plane, did not interfere. Even though the dots’ cyclopean x-y coordinates were independent of the disparity manipulation, depth values that were inconsistent with a 2-D or 3-D symmetrical object interfered with the detection of 2-D symmetry. Thus, the detection of 2-D symmetry was best for patterns whose depth structure was symmetric, suggesting that 3-D shape is recovered in parallel or ahead of planar symmetry.
The even depth symmetry of the stimuli of Experiment 1 is common among animals, plants, and their parts. In their prototypical postures, objects of these types usually have vertical symmetry planes. A standing elephant and an up-right tree are examples, as opposed to a lying or obliquely oriented elephant and a toppled or leaning tree. These postures benefit both stability and mobility under the influence of gravity (however, whether the perceptual effects of symmetry orientation observed here are framed with respect to head-centric or gravitational coordinates—and hence whether the effect of the elephant’s apparent orientation is due to its posture or the observer’s—is unknown). Neither repetition in depth nor a depth gradient seems to come with as strong an a priori expectation for redundancy about any particular plane. This makes the poor performance for depth gradients centered about a horizontal plane rather puzzling. The properties of this specific pattern (and of repetition patterns, as well) that account for the performance deficits observed here are unknown. The issue of overall task difficulty is discussed more below.
4.1. Chirality
The symmetrical patterns used here have a double symmetry: They are symmetrical about a vertically, horizontally, or obliquely oriented plane through the z-axis, and also about a plane perpendicular to this one. The vertically symmetrical pattern, for example, is symmetrical about the sagittal plane and also the horizontal plane. This makes them achiral and gives them a rotational symmetry in addition to a reflectional symmetry. The repetition and gradient patterns also have rotational symmetries. This is a consequence of the symmetry of disks and of their spatial arrangement and is not a general property of symmetrical 3-D objects. Depth symmetrical patterns with a single symmetry plane are, like the left and right hands, chiral and cannot be brought into 3-D superposition by a combination of rotation and translation.
It is possible that observers used the patterns’ rotation symmetry strategically and it would be revealing if a less symmetrical depth pattern produced results different from those recorded here. For example, observers might have judged symmetry in Experiment 1 by mentally rotating the pattern and then checking for congruence [42]. They would fail if they used this strategy on chiral patterns. The patterns used here were the simplest possible. More complex and constraining patterns might provide tests of more detailed hypotheses.
4.2. On Task Difficulty
Two of the participants in Experiment 1 failed to contribute useful data. Neither one was stereo-deficient by other measures and both showed competence in other stereo tasks carried out on the same equipment. It is possible that their failure was in understanding the task or in finding a strategy compatible with it. The other observers found the repetition discrimination task to be difficult, requiring more attention than expected from other stereo tasks they had experience with. All the observers reported some difficulty in maintaining sustained attending to all four disks at once. They reported trying to assess the depth profile of a single, integrated pattern while having to fight off the strategy of comparing the depths of individual pairs of disks across the plane of symmetry or repetition. Consequently, they had the impression that many of their incorrect decisions rested on a comparison of just a single pair, there being either no time for a second comparison or no memory of the outcome of the first. (This constraint would likely affect repetition judgments most severely. The inner, most nearly foveal disks generally differ in depth whether the pattern is repeated or non-repeated. By contrast, symmetry judgments relying on these two disks would depend on a discrimination of depth equality and difference. Depth gradients should resemble repetitions in this regard, but each pattern type has a mixture of such post-hoc advantages and disadvantages.) Conversely, the two successful observers had the impression that it was their ability to see the pattern “as a whole” that made the symmetry task fairly easy. The difficulty, in short, seems to be one of stimulus integration, not symmetry discrimination.
Segmentation and grouping are known to affect the perception of planar symmetry and repetition. For example, symmetry has been shown to be easier to detect than repetition for patterns seen as single objects, whereas the reverse holds for patterns seen as two objects, one on either side of the symmetry or repetition axis [7,33,43]. The spatially separated components of the patterns used here might be grouped in several ways; they might be perceived as four disks. Changes to the patterns that make them perceptually integrated, appearing either as a single object or as two objects on opposite sides of the midline, might allow a template-matching strategy to replace one of pairwise depth comparisons of component disks. The spatial separation of the disks also made them independent and made the disparity perturbation non-redundant. Both the spatial discreteness of the pattern components and their independence are uncharacteristic of the features of naturally encountered objects, possibly contributing to the difficulty of the task, much as they do in the detection of planar skew symmetry [11,14].
The task of detecting skewed planar symmetry illustrates the advantage that connectivity and other grouping properties brings to symmetry discriminations, and presumably to surface shape judgments generally. Detecting the symmetry of disconnected dots in a skewed pattern is difficult, and sometimes impossible, but is much easier when the same symmetry is depicted by points connected by straight lines [11,14]. The same should hold for feature correspondence: corresponding features in a symmetrical pattern that are unique are, in effect, connected even if spatially discrete, when they are seen as groups of discrete pattern elements [15,17]. Such connections are a primary target of camouflage strategies.
Attributing deficits in stereo processing to disconnected stimuli seems at odds with results from Westheimer [44] and McKee [45]. They showed that discrete stimuli, such as two vertical lines, that yielded high stereoacuity produced much lower performance after extraneous stimulus elements linking them were added. Vertical lines joined by horizontal lines at their tops and bottoms form a rectangle or, joined at their midpoints, form an “H”. A possible interpretation of this phenomenon would point out that, unjoined, the vertical lines are perceptually independent stimuli and only weakly subject to the expectations of perspective. However, the perceptual grouping resulting from the linkage would engage the expectation of perspective cues to depth. The reason for this is symmetry: the rectangle, the “H”, and so on, are symmetrical objects and as such are expected to display the appropriate perspective changes when disparity skews them about the vertical axis. The result would be a pitting of the evidence of depth from disparity and the contrary evidence from perspective. Indeed, in naturalistic viewing conditions, with the availability of multiple cues to depth, the contribution of stereo information in the recovery of 3-D shape may be low [46]. Hence, symmetry in depth might be most effectively judged by cues other than, or in addition to, disparity—an additional source of task difficulty in the present experiments.
A more fundamental question about task difficulty is what information observers use in making a discrimination. Asymmetry detection experiment might be run in which the pattern presented on each trial is unpredictable and different from the pattern presented on any other trial. Whatever strategy the observer adopts, the conditions of the experiment require that the two sides of the pattern be compared in some fashion. However, this is not the case in the experiments reported here. Each trial in a block displayed a convex or a concave version of a symmetry pattern (or their repeated counterparts), each with a knowable set of parameters, or, on asymmetric trials, a perturbation of the pattern. With a knowledge of pattern parameters, an observer might identify the overall shape of the pattern (for example, convex or concave) and then attempt to match it against an appropriate template. Comparing the two sides of the pattern is not a requirement. One might then ask in what sense the task under this strategy is symmetry (or repetition) discrimination. Yet clearly, if symmetry discrimination were easier than repetition discrimination when this strategy is used, symmetry perception in some sense (or symmetry learning or matching or other process) would be implicated, just as it would be with strategies that are more unambiguously those of “symmetry discrimination”. Strategy choice is a possible source of some of the individual differences seen here. However, given the potential variety of strategies, evidence converging from many studies on a common picture would constrain the range of possible mechanisms. Among the few commonalities—even so, sometimes not observed [1,3]—is the advantage for bilateral symmetry about a vertical axis and, as seen here, a vertical (specifically, sagittal) plane.
4.3. Conclusions
Mach in the 1880s [4] showed that bilateral symmetry in the frontoparallel plane is most salient when distributed about a vertical axis. An analogous salience appears to hold for symmetry in depth. The symmetry examined here was a reflection about a plane perpendicular to the frontoparallel plane. The projection of the stimuli onto the frontoparallel plane has a symmetrical and repeating pattern. The vertical-plane advantage for depth discriminations of reflected 3-D stimuli is not due to the frontoparallel symmetry, however. The advantage appears for even symmetry in depth but not for repetition in depth or for the odd symmetry of a depth gradient. Therefore, we can conclude that the enhanced discriminability of depth about a vertical symmetry plane results from the reflection about this plane itself. In turn, the vertical plane advantage for depth symmetry might be the source of the advantage for detecting planar symmetry about the vertical axis.
5. Materials and Methods
5.1. Experiment 1
5.1.1. Stimuli
The pattern elements were truncated Gaussian disks, luminance increments displayed on a uniform background of lower intensity. Patterns consisted of four circular disks, which were evenly spaced and arranged along a line in the x-y plane. The disks’ z-axis values distinguished symmetric and repeated patterns. These values came in two sizes, either small or large. In the former group, symmetric patterns had disks with either of the following sets of spatially-ordered disparities (in arcmin of visual angle): [+2.0, −2.0, −2.0, + 2.0] or [−2.0, +2.0, +2.0, −2.0]. Those in the latter group were similar, but with values equal to ±5.0. Repeated patterns had either of two disparity sets: [+2.0, −2.0, +2.0, −2.0] or [−2.0, +2.0, −2.0, +2.0], or the same sequences with values of ±5.0 arcmin. Hence, symmetric and repeated patterns had the same cyclopean visual directions and the same disparities. They were distinguished only binocularly and only by the combination of disk position and disparity value.
Individual disks had visible diameters of approximately 1.2° of visual angle. The four disks of a pattern had uniform cyclopean spacing, with center-to-center separation of adjacent disks equaled 1.5° of visual angle in all conditions. The arrangement of disks varied with the orientation of the symmetry or repetition plane. These planes had four orientations: vertical, horizontal, the 45° oblique and the 135° oblique. Disks were arrayed horizontally in the first case, vertically in the second, along a 135° angle relative to the horizontal in the third and along a 45° angle in the fourth (see Figure 1C). Thus, the four symmetry or repetition planes were related by a rotation about the z-axis, as were the x-y positions of the disks.
Each symmetrical and repeating pattern was paired with an asymmetrical or non-repeating pattern. Each member of the pair appeared in one of the two intervals of a trial. The asymmetrical and non-repeating patterns were identical to their more regular counterparts across three of the four pattern disks. They differed only in the disparity of one, randomly selected disk.
The disks had a peak luminance of 26.8 cd/m2 and a Weber contrast of 0.3 against the background of 20.6 cd/m2. They were displayed on a 19 in. flat-screen CRT with 75 Hz. refresh rate. Only the green gun of the monitor was used, the others being fed through an attenuator to increase luminance resolution. The screen was viewed through the front-silvered mirrors of a modified Wheatstone stereoscope. The observer’s chin was supported by a chin-rest and a septum kept each eye’s view confined to half the screen. Viewing distance was 93 cm. The room was dimly illuminated (mean luminance: ~6 cd/m2) by an incandescent lamp.
5.1.2. Procedure
On each trial of the experiment, a symmetrical or repeating pattern appeared in one of two intervals. The other interval presented an asymmetrical or non-repeating pattern. The two patterns differed in the disparity of one disk. Thus, if the first interval displayed a symmetrical pattern with a concave depth profile, the depth profile displayed in the second interval was also concave with a perturbation in one position. Likewise, repeated patterns had the same depth profile in both intervals, plus the perturbation in one interval. The observer’s task was to discriminate the patterns by selecting the interval in which the symmetrical or repeated pattern appeared. Symmetry and repetition conditions were run in separate blocks of trials.
The perturbed disk in asymmetrical or non-repeating patterns had an increment (either positive or negative) added to the ±2.0 or ±5.0 arcmin disparity that defined the basic depth profile of the pattern. Disparity increments were selected for each observer based on pilot data, a single set of increments being chosen for all symmetry-plane orientations. (As discussed above, such increments could not be found for two of the observers.) Increments selected in this way showed repetition discrimination to be the more difficult task and resulted in reported diplopia. Diplopia was avoided by the expedient of using the symmetry increments for both symmetry and repetition discriminations.
A constant-stimulus procedure controlled the size of the disparity perturbation. Each trial’s perturbation value was selected at random from the set of increment values, which were sampled equally often in the 120-trial block. Five additional practice trials started the block. Observers were informed that the task was either symmetry discrimination or repetition discrimination before the start of the block of trials.
Each block of trials was devoted to a single condition defined by the type of depth relation (symmetrical, repeated) and the orientation of the plane of symmetry or repetition (vertical, horizontal, the two obliques). Three parameters varied from trial to trial within a block: (1) the interval (first or second) in which the symmetrical or repeating pattern appeared; (2) the size, polarity, and position of the perturbing disparity increment; (3) the polarity of the symmetrical or repeating pattern (e.g., convex or concave depth profile), which was the same across the two intervals of the trial. The symmetrical or repeated pattern had equal probability of appearing in the first and second interval. Each block was repeated 4 to 6 times, in random order, for the two observers capable of performing the task.
Each stimulus interval lasted 147 ms (11 video frames), with a 347 ms interstimulus interval separating the two intervals. The stimuli were positioned at the center of the monitor, where a fixation point appeared when the stimuli were not in view. Observers initiated each trial with a click of a mouse and identified the interval displaying the symmetrical or repeating pattern by clicking one of two on-screen buttons (labeled “1stInterval” and “2nd Interval”) that appeared after the second interval. Auditory feedback about the accuracy of this response followed the click.
5.1.3. Observers
Four observers—two female and two male (one the author), all with normal or corrected-to-normal visual acuity and normal stereo vision, three with considerable previous experience in stereo-depth experiments—participated in Experiment 1. All procedures carried out in the experiments followed the tenets of the World Medical Association Declaration of Helsinki and were approved by the Institutional Review Board of Syracuse University (IRB#12-214; 9/16/14). All participants in the experiments participated with their informed consent.
5.2. Experiment 2
5.2.1. Stimuli and Procedure
The method of Experiment 1 was repeated in Experiment 2, with one change: The pattern consisted of a row of four evenly spaced disks whose disparities varied linearly from one end to the other in the order −8.25, −2.75, +2.75, +8.25 arcmin, or the reverse sequence, from +8.25 arcmin to −8.25 arcmin. On randomly selected trials, the sequence of disparities from one end of the row of disks to the other went from positive to negative; on the remaining trials the sequence went from negative to positive. The disks were symmetrically distributed about the mid-point of the monitor. The disks were spaced 2.25° and 0.75° of visual angle on either side of the midpoint. Thus, the two outer disks formed a corresponding opposed-polarity pair, having the same disparity magnitudes and reversed disparity signs; the same holds for the two inner disks.
As in Experiment 1, the plane separating the two odd-reflected sides of the pattern passed through the z-axis with an orientation that was vertical, horizontal, or oblique (at either 45° or 135°). Each observer completed between eight and ten 120-trial blocks, plus warm-up trials at the start of each block, for each of the four orientation conditions. Remaining methodological details duplicated those of the first experiment.
5.2.2. Observers
The two observers who successfully completed Experiment 1 participated in Experiment 2.
Acknowledgments
This material is based upon work supported by the National Science Foundation under Grant Number NSF BCS-1257096. The author thanks Cherlyn Ng for sharing ideas and providing helpful suggestions and the three anonymous reviewers, whose comments were interesting, thoughtful, and useful for improving the manuscript.
Conflicts of Interest
The author declares no conflict of interest.
References
- Wagemans, J. Detection of visual symmetries. Spat. Vis. 1995, 9, 9–32. [Google Scholar]
- Treder, M.S. Behind the looking-glass: A review on human symmetry perception. Symmetry 2010, 2, 1510–1543. [Google Scholar]
- Van der Helm, P.A. Symmetry perception. In The Oxford Handbook of Perceptual Organisation; Wagemans, J., Ed.; Oxford University Press: Oxford, UK, 2014; pp. 1–26. [Google Scholar]
- Mach, E. The Analysis of Sensations; Dover: New York, NY, USA, 1959. [Google Scholar]
- Corballis, M.C.; Beale, I.L. Bilateral symmetry and behavior. Psychol. Rev. 1970, 77, 451–464. [Google Scholar]
- Julesz, B. Foundations of Cyclopean Perception; University of Chicago Press: Chicago, IL, USA, 1970. [Google Scholar]
- Treder, M.S.; van der Helm, P.A. Symmetry versus repetition in cyclopean vision: A microgenetic analysis. Vis. Res. 2007, 47, 2956–2967. [Google Scholar]
- Locher, P.J.; Smets, G. The influence of stimulus dimensionality and viewing orientation on detection of symmetry in dot patterns. Bull. Psychon. Soc. 1992, 30, 43–46. [Google Scholar]
- Chen, C.C.; Sio, L.T. 3D surface configuration modulates 2D symmetry detection. Vis. Res. 2015, 107, 86–93. [Google Scholar]
- Saunders, J.A.; Knill, D.C. Perception of 3D surface orientation from skew symmetry. Vis. Res. 2001, 41, 3163–3183. [Google Scholar]
- Sawada, T.; Pizlo, Z. Detection of skewed symmetry. J. Vis. 2008, 8, 1–18. [Google Scholar]
- Van der Vloed, G.; Csathó, A.; van der Helm, P.A. Symmetry and repetition in perspective. Acta Psychol. 2005, 120, 74–92. [Google Scholar]
- Wagemans, J.; Van Gool, L.; d’Ydewalle, G. Detection of symmetry in tachistoscopically presented dot patterns: Effects of multiple axes and skewing. Percept. Psychophys. 1991, 50, 413–427. [Google Scholar]
- Wagemans, J. Perceptual use of nonaccidental properties. Can. J. Psychol. 1992, 46, 236–279. [Google Scholar]
- Wagemans, J.; Van Gool, L.; d’Ydewalle, G. Orientational effects and component processes in symmetry detection. Q. J. Exp. Psychol. 1992, 44A, 475–508. [Google Scholar]
- Wagemans, J. Skewed symmetry: A nonaccidental property used to perceive visual forms. J. Exp. Psychol. Hum. Percept. Perform. 1993, 19, 364–380. [Google Scholar]
- Wagemans, J.; van Gool, L.; Swinnen, V.; van Horebeek, J. Higher-order structure in regularity detection. Vis. Res. 1993, 33, 1067–1088. [Google Scholar]
- Sawada, T. Visual detection of symmetry of 3D shapes. J. Vis. 2010, 10, 1–22. [Google Scholar]
- McBeath, M.K.; Schiano, D.J.; Tversky, B. Three-dimensional bilateral symmetry bias in judgments of figural identity and orientation. Psychol. Sci. 1997, 8, 217–223. [Google Scholar]
- Attneave, F. Symmetry information and memory for patterns. Am. J. Psychol. 1955, 68, 209–222. [Google Scholar]
- Barlow, H.B.; Reeves, B.C. The versatility and absolute efficiency of detecting mirror symmetry in random dot displays. Vis. Res. 1979, 19, 783–793. [Google Scholar]
- Corballis, M.C.; Roldan, C.E. On the perception of symmetrical and repeated patterns. Percept. Psychophys. 1974, 16, 136–142. [Google Scholar]
- Corballis, M.C.; Roldan, C.E. Detection of symmetry as a function of angular rotation. J. Exp. Psychol. Hum. Percept. Perform. 1975, 1, 221–230. [Google Scholar]
- Goldmeier, E. Similarity in visually perceived forms. Psychol. Issues. 1972, 8, 1–136. [Google Scholar]
- Kahn, J.I.; Foster, D.H. Horizontal-vertical structure in the visual comparison of rigidly transformed patterns. J. Exp. Psychol. Hum. Percept. Perform 1986, 12, 422–433. [Google Scholar]
- Palmer, S.E.; Hemenway, K. Orientation and symmetry: Effects of multiple, rotational, and near symmetries. J. Exp. Psychol. Hum. Percept. Perform 1978, 4, 691–702. [Google Scholar]
- Pashler, H. Coordinate frame for symmetry detection and object recognition. J. Exp. Psychol. Hum. Percept. Perform 1990, 16, 150–163. [Google Scholar]
- Rock, I.; Leaman, R. An experimental analysis of visual symmetry. Acta Psychol. 1963, 21, 171–183. [Google Scholar]
- Wenderoth, P. The salience of vertical symmetry. Perception 1994, 23, 221–236. [Google Scholar]
- Nickerson, R.S. Binary-classification reaction time: A review of some studies of human information-processing capabilities. Psychon. Monogr. Suppl. 1972, 4, 275–318. [Google Scholar]
- Farell, B. “Same”-“Different” judgments: A review of current controversies in perceptual comparisons”. Psychol. Bull. 1985, 98, 419–456. [Google Scholar]
- Corballis, M.C.; Miller, A.; Morgan, M.J. The role of left-right orientation in interhernispheric matching of visual information. Percept. Psychophys. 1971, 10, 385–388. [Google Scholar]
- Koning, A.; Wagemans, J. Detection of symmetry and repetition in one and two objects. Structures versus strategies. Exp. Psychol. 2009, 56, 5–17. [Google Scholar]
- Wichmann, F.A.; Hill, N.J. The psychometric function: II. Bootstrap-based confidence intervals and sampling. Percept. Psychophys. 2001, 63, 1314–1329. [Google Scholar]
- Schiano, D.J.; McBeath, M.K.; Chambers, K.W. Regularity of symmetry verticality guides perceptual judgments of objects. Am. J. Psychol. 2008, 121, 209–227. [Google Scholar]
- Freyd, J.; Tversky, B. Force of symmetry in form perception. Am. J. Psychol. 1984, 97, 109–126. [Google Scholar]
- King, M.; Meyer, G.E.; Tangney, J.; Biederman, I. Shape constancy and a perceptual bias towards symmetry. Percept. Psychophys. 1976, 19, 129–136. [Google Scholar]
- Li, Y.; Sawada, T.; Shi, Y.; Kwan, T.; Pizlo, Z. A. Bayesian model of binocular perception of 3D mirror symmetrical polyhedra. J. Vis. 2011, 11, 1–20. [Google Scholar]
- Pizlo, Z.; Sawada, T.; Li, Y.; Kropatsch, W.G.; Steinman, R.M. New approach to the perception of 3D shape based on veridicality, complexity, symmetry and volume. Vis. Res. 2010, 50, 1–11. [Google Scholar]
- Vetter, T.; Poggio, T. Symmetric 3D objects are an easy case for 2D object recognition. Spat. Vis. 1994, 8, 443–453. [Google Scholar]
- Tyler, C.W. Spatial form as inherently three-dimensional. In Seeing Spatial Form; Jenkin, M.R.M., Harris, R.L., Eds.; Oxford University Press: London, UK, 2005; pp. 67–88. [Google Scholar]
- Shepard, R.N.; Metzler, J. Mental rotation of three-dimensional objects. Science 1971, 171, 701–703. [Google Scholar]
- Baylis, G.C.; Driver, J. Obligatory edge assignment in vision: The role of figure and part segmentation in symmetry detection. J. Exp. Psychol. Hum. Percept. Perform 1995, 21, 1323–1342. [Google Scholar]
- Westheimer, G. The spatial sense of the eye. Investig. Ophthalmol. Vis. Sci. 1979, 18, 893–912. [Google Scholar]
- McKee, S.P. The spatial requirements for fine stereoacuity. Vis. Res. 1983, 23, 191–198. [Google Scholar]
- Pizlo, Z.; Li, Y.; Steinman, R.M. Binocular disparity only comes into play when everything else fails; a finding with broader implications than one might suppose. Spat. Vis. 2008, 21, 495–508. [Google Scholar]



© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farell, B. The Perception of Symmetry in Depth: Effect of Symmetry Plane Orientation. Symmetry 2015, 7, 336-353. https://doi.org/10.3390/sym7020336
Farell B. The Perception of Symmetry in Depth: Effect of Symmetry Plane Orientation. Symmetry. 2015; 7(2):336-353. https://doi.org/10.3390/sym7020336
Chicago/Turabian StyleFarell, Bart. 2015. "The Perception of Symmetry in Depth: Effect of Symmetry Plane Orientation" Symmetry 7, no. 2: 336-353. https://doi.org/10.3390/sym7020336
APA StyleFarell, B. (2015). The Perception of Symmetry in Depth: Effect of Symmetry Plane Orientation. Symmetry, 7(2), 336-353. https://doi.org/10.3390/sym7020336




