Abstract
We present the first provably-secure three-party password-only authenticated key exchange (PAKE) protocol that can run in only two communication rounds. Our protocol is generic in the sense that it can be constructed from any two-party PAKE protocol. The protocol is proven secure in a variant of the widely-accepted model of Bellare, Pointcheval and Rogaway (2000) without any idealized assumptions on the cryptographic primitives used. We also investigate the security of the two-round, three-party PAKE protocol of Wang, Hu and Li (2010) and demonstrate that this protocol cannot achieve implicit key authentication in the presence of an active adversary.1. Introduction
Protocols for password-only authenticated key exchange (PAKE) enable two or more parties to generate a shared, cryptographically-strong key (called a session key) from their easy-to-remember passwords. PAKE protocols are increasingly popular, and perhaps, due to the popularity of passwords, as explained by Herley and van Oorschot, “despite countless attempts to dislodge passwords (in the past 20 years), they are more widely used and firmly entrenched than ever” [1]. There has been an enormous amount of research effort expended on the design and analysis of PAKE protocols, and yet, there are still worthwhile contributions to be made even in the simple scenario of two protocol participants (also known as clients) with an online trusted server. In such a three-party model, the server provides its registered clients with a centralized authentication service, which allows each client to remember and manage only a single password. Password guessing attacks (also known as dictionary attacks) present a more subtle threat in the three-party model (compared to a two-party model), as a malicious client can attempt to mount such an attack against another client; see [2–6].
It is generally considered that the design of secure, yet efficient key exchange protocols (including password-based protocols) is notoriously difficult, and performing a security analysis for such protocols is complicated and error-prone; see, e.g., [7–9]. The many vulnerabilities identified in published protocols have highlighted the importance of rigorous security proofs in a well-defined formal model. In the provable-security paradigm for key exchange protocols, a reductionist proof approach is adopted to show that an efficient algorithm for breaking the protocol implies an efficient algorithm for solving another problem believed to be (computationally) hard. A complete mathematical proof under a well-established cryptographic assumption offers a strong assurance to protocol implementers that the protocol in hand achieves the desired security properties. The provable-security paradigm for key exchange protocols was made popular by Bellare and Rogaway [10], who introduced the first formal model of adversary capabilities with an associated definition of session-key security. Since then, it has been standard practice for protocol designers to provide proofs of security for their protocols in a widely-accepted security model.
A number of three-party PAKE protocols have been proposed over the last decade [2,3,5,6,11–25]. Many of these protocols have never been proven secure in any model [3,13,17–21] and/or have been found to be vulnerable to some attack(s) [2,3,5,6,8,18–20,23,26–32]. Some protocols [2,11,12,15,23,24] have been proven secure only in a restricted model, in which the adversary is not allowed to corrupt protocol participants, and thus, no attacks by malicious clients can be captured.
Reducing the number of communication rounds is an important practical consideration in designing key exchange protocols. Adopting the usual convention in the three-party (and multi-party) setting, we let a round consist of all protocol messages that can be sent in parallel; note that messages in the same round cannot be dependent on one another. So far, there have been several two-round key exchange protocols presented in the three-party setting.
The protocols of [15,24] are the only two-round, three-party PAKE protocols published with a claimed security proof (although the two protocols presented by Lee and Hwang [23] can run in two rounds (without key confirmation), and they are insecure in the presence of a malicious client [31]; both protocols are susceptible to a man-in-the-middle attack, as well as an offline dictionary attack). However, it was later found that both protocols are not secure against an active adversary, and their associated claims of provable security are invalid (see [2,8,32,33] and Section 3 of this paper).
The protocols of [34,35] were proven secure and require only two rounds, but these protocols assume a “hybrid” three-party setting where a server’s public key is required in addition to passwords.
The recent protocol of Tsai and Chang [30] can run in two rounds (without key confirmation), but this protocol only works in a hybrid setting that requires both a cryptographic key and a password pre-established between each client and the server (see [4,29,36–44] for other protocols designed to work in a hybrid setting).
Table 1 summarizes the security properties and known weaknesses of published two-round three-party PAKE protocols with (claimed) proofs of security. To the best of our knowledge, there exists no (provably) secure three-party PAKE protocol running in only two rounds.

We regard our contributions of this paper to be two-fold:
We present the first two-round, three-party PAKE protocol that is provably secure in a well-defined communication model; see Section 4. The communication model in which we work allows the adversary to corrupt protocol participants and, therefore, captures not only the notion of forward secrecy, but also attacks by malicious clients. We make no idealizing assumptions in our security proof. Similar to the protocols of [2,11,12,19,24], our protocol is generic in the sense that it can be constructed from any two-party PAKE protocol. If the underlying two-party protocol is round-optimal [45–47], then our three-party protocol runs in only two communication rounds.
We also present a previously unpublished flaw in an existing two-round, three-party PAKE protocol proposed by Wang, Hu and Li [24]; see Section 3.2. The Wang–Hu–Li protocol (named NWPAKE-2) was claimed to be provably secure in a variant of the Real-Or-Random (ROR) model. We reveal that the NWPAKE-2 protocol fails to achieve implicit key authentication in the presence of an active adversary who is not even registered with the server, which invalidates the “claimed” security proof.
The remainder of this paper is structured as follows: Section 2 describes a communication model along with the associated security definition. In Section 3, we revisit the NWPAKE-2 protocol of Wang, Hu and Li [24] and reveal a previously unpublished flaw in the protocol. We then present our proposed two-round, three-party PAKE protocol and prove its security in Section 4. The last section concludes the paper.
2. The Communication Model
We now describe a communication model adapted from the widely-accepted indistinguishability-based model of Bellare, Pointcheval and Rogaway [45]. This will be the model that is used to prove the security of our proposed three-party PAKE protocol.
2.1. Participants and Long-Term Keys
Let S be a trusted authentication server and the set of all clients registered with S. During registration, each client selects a password pwC from dictionary and shares pwC with S via a secure/authenticated channel. The password pwC is used as the long-term secret key between C and S. Any two clients C, may run a three-party PAKE protocol π with S at any point in time to establish a session key. Let . A user may execute the protocol multiple times (including concurrent executions) with the same or different participants. Thus, a single user could have many instances of it at a point of time. We denote instance i of user U by . We say that a client instance accepts when it successfully computes its session key in an execution of the protocol.
2.2. Partnering
Intuitively, two instances are partners if they participate in a protocol execution and establish a (shared) session key. Formally, partnering between instances is defined in terms of the notions of session identifiers and partner identifiers (see [48] on the role and the possible construct of session and partner identifiers as a form of partnering mechanism that enables the right session key to be identified in concurrent protocol executions). A session identifier (sid) is a string that uniquely identifies a protocol session and is usually defined as a function of the messages transmitted in the session. Let denote the sid of instance . A partner identifier (pid) is a sequence of identities of participants of a specific protocol session. Instances are given as input a pid before they can run the protocol. denotes the pid given to instance . In a typical session, there will be three participants, namely two clients C and C′ and the server S. We say that two instances and are partners if all of the following conditions are satisfied: (1) both and have accepted; (2) ; and (3) .
2.3. Adversary Capabilities
The probabilistic polynomial-time (PPT) adversary is in complete control of all communications between users, and its capabilities are modeled via a pre-defined set of oracle queries, as described below.
Execute( , ): This query models passive attacks against the protocol. It prompts an execution of the protocol between the instances , and and returns the transcript of the protocol execution to .
Send( , m): This query sends a message m to instance , modeling active attacks against the protocol. Upon receiving m, the instance proceeds according to the protocol specification. The message output by , if any, is returned to . A query of the form Send( , start:(C, C′, S)) prompts to initiate the protocol with .
Reveal : This query captures the notion of known key security (it is often reasonable to suppose that the adversary can obtain session keys from any sessions other than the one under attack) and, if has accepted, returns the session key back to . However, this session (key) will be rendered unfresh (see Definition 1).
Corrupt(U): This query returns U’s password pwU to . If U = S (i.e., the server is corrupted), all clients’ passwords stored by the server are returned. This query captures not only the notion of forward secrecy, but also attacks by malicious clients.
Test : This query is used to define the indistinguishability-based security of the protocol. If has accepted, then depending on a randomly-chosen bit b, is given either the real session key (when b = 1) or a random key drawn from the session-key space (when b = 0). is allowed to ask as many test queries as it wishes. All test queries are answered using the same value of the hidden bit b. Namely, the keys output by the test oracle are either all real or all random. However, we require that for each different set of partners, should access the test oracle only once.
Although Execute and Reveal oracles can be simulated by accessing Send and Test oracles, respectively, multiple times, the former (i.e., Execute and Reveal oracles) often makes it easier to prove the security of protocols and to understand the proofs, and for this reason, we allow both Execute and Reveal queries in our model. The number of queries asked by an adversary is referred to as the query complexity of the adversary (Q) and is represented as an ordered sequence of five non-negative integers, Q = (qexec, qsend, qreve, qcorr, qtest). These five non-negative integers are the numbers of queries that the adversary asked, respectively, of the Execute, Send, Reveal, Corrupt and Test oracles.
2.4. Security Definition
We define the security of a three-party PAKE protocol via the notion of freshness. Intuitively, a fresh instance is one that holds a session key that should not be known to the adversary , and an unfresh instance is one whose session key (or some information about the key) can be known by trivial means. The formal definition of freshness is explained in Definition 1.
Definition 1. An instance is fresh if none of the following occurs: (1) queries Reveal or Reveal , where is the partner of; and (2) queries Corrupt(U), for some, before or its partner accepts.
The security of a three-party PAKE protocol π is defined in the context of the following experiment:
Experiment Exp0:
Phase 1. makes any oracle queries at will as many times as it wishes, except that:
is not allowed to ask the Test query if the instance is unfresh.
is not allowed to ask the Reveal query if it has already made a Test query to or , where is the partner of .
Phase 2. Once decides that Phase 1 is over, it outputs a bit b′ as a guess on the hidden bit b chosen by the Test oracle. is said to succeed if b = b′.
Let Succ0 be the event that succeeds in the experiment Exp0. The advantage of in breaking the security of the authenticated key exchange protocol π is .
Definition 2. A three-party PAKE protocol π is AKE-secure if, for any PPT adversary A asking at most qsend Send queries, is only negligibly larger than c · qsend/|D|, where c is a constant.
To represent the security of protocol π in terms of the amount of resources used by adversaries, we let be defined as:
3. Revisiting Wang, Hu and Li’s (2010) NWPAKE-2 Protocol
Implicit key authentication is among the fundamental security properties that should be achieved by key exchange protocols. In this section, we show that the NWPAKE-2 protocol of Wang, Hu and Li [24] does not achieve implicit key authentication.
3.1. Protocol Description
Assume two clients A and B who want to establish a session key. Let S be the trusted server with which A and B shared their passwords pwA and pwB, respectively. The public parameters of the NWPAKE-2 protocol include: (1) a cyclic group of prime order q and a generator g of ; (2) a two-party PAKE protocol, 2PAKE; and (3) a pair of message authentication code (MAC) generation/verification algorithms (Mac, Ver), where Ver outputs a bit, with 1 meaning accept and 0 meaning reject. If the underlying two-party protocol, 2PAKE, is round-optimal, NWPAKE-2 completes in two communication rounds, as depicted in Figure 1. The protocol description is as follows:
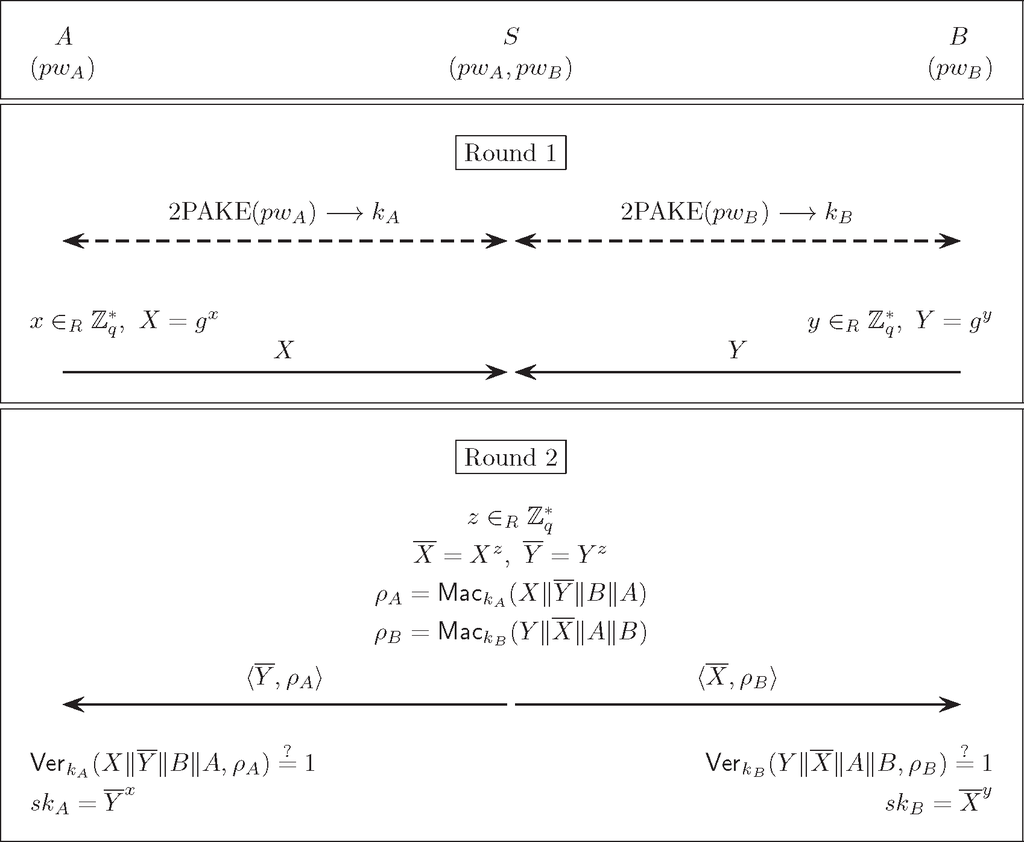
Step 1. A and S establish a secret key kA by running the two-party protocol, 2PAKE. Likewise, B and S establish a secret key kB.
Step 2. A (resp. B) selects a random
and sends X = gx (resp. Y = gy) to S.
Step 3. S chooses a random , computes:
and sends and to A and B, respectively.
Step 4. A and B abort if their received MAC is invalid. Otherwise, they will compute their respective session keys, and .
At the end of the protocol execution, A and B will compute the same session key skA = skB = gxyz.
3.2. Violating Implicit Key Authentication
We now assume that there exists an adversary C who is not registered with the server and demonstrate how C can easily violate the implicit key authentication property of NWPAKE-2.
C chooses a random , computes X′=gx′ and replaces X (sent by A to S) with X′.
Upon receipt of the “replaced” message, S will compute as , and therefore, B’s session key skB will be set to gx′yz.
C intercepts the message sent by S to A and then computes . In other words, C is able to compute B’s session key even though C is not B’s partner.
The design flaw exploited by the adversary is that the server S is provided with no means of authenticating the public values X and Y. Note that NWPAKE-2 exhibits a security weakness no matter which protocol is used for the instantiation of 2PAKE. Wang, Hu and Li [24] provide a proof sketch for the security of NWPAKE-2 in a model that allows Send queries. Any protocol proven secure in such a model should be secure against our above attack, and therefore, the security proof (sketch) for NWPAKE-2 is invalidated.
4. Our Proposed Protocol
This section presents our two-round, three-party PAKE protocol, which we denote as 2R3PAKE (“R” is for round) and proves its security in the communication model described in Section 2. The 2R3PAKE protocol can be viewed as a combined variant of the NWPAKE-2 protocol of Wang, Hu and Li [24] and the 3PKD protocol of Bellare and Rogaway [49]. 2R3PAKE is generic in the sense that it can be constructed from any secure two-party PAKE protocol. Our generic construction takes only one round of communication in addition to the number of rounds required to perform the underlying two-party protocol. Hence, applying our construction to a round-optimal two-party PAKE protocol immediately yields a three-party PAKE protocol running in two communication rounds.
4.1. Preliminaries
The security of 2R3PAKE is based on the decisional Diffie–Hellman assumption, the security of a message authentication code scheme, a two-party PAKE protocol, and a symmetric encryption scheme.
4.1.1. Decisional Diffie–Hellman Assumption
Consider a cyclic group having prime order q. Let g be a random generator of . Informally speaking, the Decisional Diffie–Hellman (DDH) problem for G is to distinguish between two distributions (ga, gb, gab) and (ga, gb, gc), where a, b and c are chosen at random from . We say that the DDH assumption holds in if it is computationally intractable to solve the DDH problem for . More formally, we define the advantage of an algorithm in solving the DDH problem for to be . We say that the DDH assumption holds in if is negligible for all PPT algorithms . denotes the maximum value of over all algorithms running in time at most t. A typical way of generating where the DDH assumption is believed to hold is to select two primes p, q, such that p = δq + 1 for some small δ ∈ ℕ (e.g., δ = 2), and let be the subgroup of prime order q in .
4.1.2. Message Authentication Codes
A message authentication code (MAC) scheme Σ is a triple of efficient algorithms (Gen, Mac, Ver), where: (1) the key generation algorithm Gen takes as input a security parameter 1ℓ and outputs a key k chosen uniformly at random from {0, 1}ℓ; (2) the MAC generation algorithm Mac takes as input a key k and a message m and outputs a MAC (also known as a tag) σ; and (3) the MAC verification algorithm Ver takes as input a key k, a message m and a MAC σ and outputs 1 if σ is valid for m under k or outputs 0 if σ is invalid. Let be the advantage of an adversary in violating the strong existential unforgeability of Σ under an adaptive chosen message attack. More precisely, is the probability that an adversary , who mounts an adaptive chosen message attack against Σ with oracle access to Mack(·) and Verk(·), outputs a message/tag pair (m, σ), such that: (1) Verk(m, σ) = 1; and (2) σ was not previously output by the oracle Mack(·) as a MAC on the message m. We say that the MAC scheme Σ is secure if is negligible for every PPT adversary . Let denote the maximum value of over all adversaries running in time at most t and asking at most qmac and qver queries to Mack(·) and Verk(·), respectively.
4.1.3. Two-Party PAKE Protocols
2R3PAKE takes as input a two-party PAKE protocol, 2PAKE. We assume that the given two-party protocol, 2PAKE, outputs session keys distributed in {0, 1}n, where n = 2ℓ, and is AKE-secure against an adversary who is given access to all of the oracles: Execute, Send, Reveal, Corrupt and Test. Let be the advantage of an adversary at breaking the AKE security of 2PAKE. We require that, for any PPT adversary asking at most qsend Send queries, is only negligibly larger than . denotes the maximum value of over all adversaries with time complexity at most t and query complexity at most Q.
4.1.4. Symmetric Encryption Schemes
A symmetric encryption scheme Ω is a triple of efficient algorithms (Gen, Enc, Dec) where: (1) the key generation algorithm Gen takes as input a security parameter 1ℓ and outputs a key k chosen uniformly at random from {0, 1}ℓ; (2) the encryption algorithm Enc takes as input a key k and a plain text message m and outputs a ciphertext c; and (3) the decryption algorithm Dec takes as input a key k and a ciphertext c and outputs a message m. We require that Deck(Enck(m)) = m holds for all k ∈ {0, 1}ℓ and all m ∈ , where is the plain text space. For an eavesdropping adversary against Ω and for a random bit b ∈R {0, 1}, consider the following experiment, , where “ind-seav” denotes indistinguishability against single eavesdropping:
For simplicity, we assume, in this experiment, that the security parameter 1ℓ is implicit in the description of Ω. Note that in the experiment, the adversary generates the plain text pair (m0, m1) and is given the ciphertext c, which is the encryption of either m0 or m1. Let be the advantage of an eavesdropper in breaking the indistinguishability of Ω, and let it be defined as:
We say that the symmetric encryption scheme Ω is secure (with respect to a single encryption) if is negligible for every PPT adversary . We use to denote the maximum value of over all adversaries running in time at most t.
We now claim that if a symmetric encryption scheme is secure with respect to a single encryption, then it is also secure with respect to multiple encryptions under different keys. For an integer n ≥ 1, consider the following experiment, , where “ind-meav” denotes indistinguishability against multiple eavesdropping:
Then, we define and
Lemma 1. For any symmetric encryption scheme Ω,
Proof. Let be a multiple eavesdropper attacking the indistinguishability of Ω, with advantage and time complexity t. The proof proceeds with a standard hybrid argument [50]. Consider a sequence of n + 1 hybrid experiments , where each is different from only in that each ci is set as follows:
The experiments and at the extremes of the sequence are identical to and , respectively. As we move from to in the sequence, we change the ξ-th ciphertext cξ from the encryption of m0, ξ to the encryption of m1,ξ. Since there are n such moves from to the inequality of the lemma follows immediately if we prove that the difference between the probabilities that outputs 1 in any two neighboring experiments and is at most . To complete the proof, it suffices to show that for any ,
Let . We will prove Equation (1) by constructing, from , a single eavesdropper who breaks the indistinguishability of Ω with advantage ε and time complexity t.
begins by invoking adversary , then proceeds to simulate the indistinguishability experiment for and, finally, ends by outputting whatever bit eventually outputs. In the simulated experiment, generates the ciphertexts exactly as in the hybrid experiment , except that it generates the ξ-th ciphertext cξ as follows:
When outputs the ξ-th plain text pair (m0,ξ, m1,ξ), outputs this as its own plain text pair in experiment , receives in return a ciphertext c and sets cξ = c.
It follows that:
The probability that outputs 1 when the given ciphertext c is the encryption of m0,ξ is equal to the probability that outputs 1 in the experiment .
The probability that outputs 1 when the given ciphertext c is the encryption of m1,ξ is equal to the probability that outputs 1 in the experiment .
This means that:
Since Aξ has time complexity t, it follows that by definition. This completes the proof of Equation (1) and, hence, the proof of Lemma 1. □
4.2. The 2R3PAKE Protocol
We assume that the following information has been pre-established and is known to all parties in the network: (1) a cyclic group of prime order q and a generator g of ; (2) a MAC scheme Σ = (Gen, Mac, Ver); (3) a two-party PAKE protocol 2PAKE; and (4) a symmetric encryption scheme Ω = (Gen, Enc, Dec). These public parameters can be determined by the server and broadcast to all registered clients. Let A and B be two clients who wish to establish a session key and S be the trusted server with which A and B have registered their passwords pwA and pwB, respectively. The partner identifier assigned to (an instance of) A (resp. B) is pidA (resp. pidB). Recall that pid is a sequence of identities of protocol participants; for simplicity, we assume that pidA = pidB = (A, B, S). Our 2R3PAKE protocol is depicted in Figure 2 and its description is as follows:
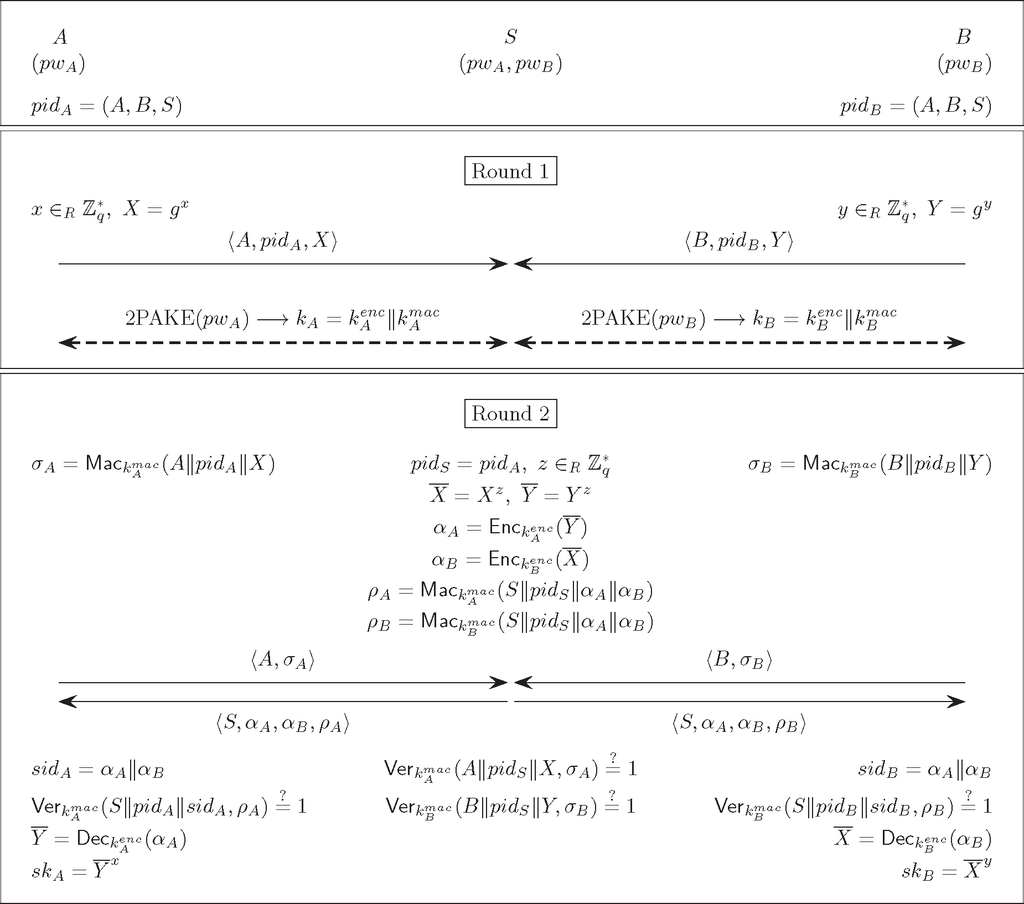
Step 1. A (resp. B) selects a random , computes X = gx (resp. Y = gy) and sends ⟨A, pidA, X⟩ (resp. ⟨B, pidB, Y⟩) to S.
Step 2. A and S establish a 2ℓ-bit key kA by running the two-party protocol, 2PAKE. Likewise, B and S establish a 2ℓ-bit key kB. Let and .
Step 3. A computes and sends ⟨A, σA⟩ to S. Similarly, B computes and sends ⟨B, σB⟩ to S
Step 4. S sets pidS = pidA, chooses a random and computes
S then sends ⟨S, αA, αB, ρA⟩ and ⟨S, αA, αB, ρB⟩ to A and B, respectively.
Step 5. A sets the session identifier, sidA = αA||αB, and verifies that . If the verification fails, A aborts the protocol. Otherwise, A recovers as and computes the session key, . B proceeds correspondingly; it aborts if , where sidB = αA║αB, and, otherwise, computes and .
Step 6. S checks that . If the check fails, S marks this transaction as invalid. For MAC σB, S checks its validity in the same way. (To prevent online dictionary attacks (unlike offline dictionary attacks, where password guesses can be verified offline, online dictionary attacks are the ones where the attacker verifies each password guess via an online transaction with the server), S may lock out a problematic client after a certain number of invalid transactions.)
Steps 1 and 2 constitute the first round of communication, while Steps 3 and 4 constitute the second communication round. It is trivial to note that in the presence of a passive adversary, A and B will compute session keys of the same value gxyz. We do not require 2PAKE to be instantiated with a protocol that provides either unilateral or mutual authentication, as 2R3PAKE already provides mutual authentication between the server and the clients (via the MAC values exchanged in the second round). Hence, any two-party protocol that provides implicit key authentication, including one-round protocols, will be a suitable candidate to instantiate 2PAKE. We emphasize that sending and in an encrypted form is necessary for the security of the protocol, as evidenced by the flaws discovered in previous two-round PAKE protocols (see Section 3 and [32]).
4.3. Security Proof
Theorem 1. For any adversary who has time complexity at most t and query complexity at most Q = (qexec, qsend, qreve, qcorr, qtest), its advantage in breaking the AKE security of 2R3PAKE is bounded by:
Proof. Let be a PPT adversary who attacks the AKE security of 2R3PAKE with time complexity t and query complexity Q = (qexec, qsend, qreve, qcorr, qtest). We prove the theorem by making a series of modifications to the experiment Exp0, bounding the difference in success probability between two consecutive (modified) experiments and ending up with an experiment in which has a success probability of 1/2 (i.e., has no advantage). By Succi, we denote the event that correctly guesses the hidden bit b in experiment Expi.
Before presenting the first modified experiment, we define the notion of a clean instance.
Definition 3. We say an instance is unclean if has queried Corrupt(U′) for some. Otherwise, we say it is clean.
Experiment Exp1. We modify the experiment by replacing each different 2ℓ-bit key (established by an execution of 2PAKE) with a random key drawn uniformly from {0, 1}2ℓ for all clean instances. The difference in success probability between Exp0 and Exp1 is bounded by:
Claim 1..
Proof. We prove the claim by constructing an adversary who attacks the AKE security of 2PAKE with advantage equal to . Let denote the 2ℓ-bit key held by instance .
chooses a random bit b ∈ {0, 1} and invokes the adversary . then simulates the oracles for as follows:
Execute queries. When an Execute( , , ) query is asked, first checks if A, B or S was previously corrupted.
If so, answers the Execute query as in experiment Exp0.
Otherwise, answers the query using its own oracles. first asks two queries Execute( , ) and Execute( , ). Let T2PAKE and T′2PAKE be two transcripts returned in response to the Execute queries. Next, makes the queries Test and Test and receives in return two keys and (either real or random). then generates the rest of the protocol messages, using and as and , respectively. Finally, returns these messages together with T2PAKE and T′2PAKE after ordering them properly.
Send queries. For each Send( , m) query, checks if m is a message for initiating a new session (of 2R3PAKE) or the Send query belongs to an execution of 2PAKE.
If both are untrue, responds to the query as in experiment Exp0.
Otherwise, answers it by making the same query to its own Send oracle. If the query prompts to accept, then checks if is clean.
If so, makes a Test query (unless the partner of has already been tested) and sets to be the output of this Test query.
Otherwise, makes a Reveal query and sets to be the output of this Reveal query.
Reveal queries. responds to the queries as per the protocol specification.
Corrupt queries. answers these queries using its own Corrupt oracle.
Test queries. responds to these queries based on the randomly chosen bit b at the beginning of the simulation. will return the real session key if b = 1 and a random key chosen uniformly at random from if b = 0.
At some point in time, will terminate and output its guess b′. When this happens, outputs 1 if b = b′ and 0 otherwise.
From the simulation, it is clear that:
The probability that outputs 1 when its Test oracle returns real session keys is equal to the probability that correctly guesses the bit b in experiment Exp0.
The probability that outputs 1 when its Test oracle returns random keys is equal to the probability that correctly guesses the bit b in experiment Exp1.
That is, . Since has at most time complexity t′ and query complexity Q′ = (2qexec, qsend, qsend, qcorr, 2qexec + qsend), it follows, by definition, that . This completes the proof of Claim 1.
Experiment Exp2. This experiment is different from Exp1, only in that it is aborted and the adversary does not succeed if the following event Forge occurs.
Forge: The event that the adversary makes a Send query of the form Send( , V║msg) for uncorrupted U and V, such that msg contains a MAC forgery.
Then, we have:
Claim 2..
Proof. Assuming that the event Forge occurs, we construct a forger who outputs, with a non-negligible probability, a forgery against the MAC scheme Σ. The forger is given oracle access to Mack(·) and Verk(·). The goal of is to produce a message/tag pair (m, σ), such that: (1) Verk(m, σ) = 1; and (2) σ was not previously output by the Mack(·) oracle on input m.
Let n be the number of all different MAC keys established via a Send query made by . Clearly, n ≤ qsend. begins by choosing a random α ∈ {1,…, n}. Let denote the α−th key among all of the n MAC keys and Sendα be a Send query that should be answered and/or verified using . invokes as a subroutine and handles the oracle calls of as in experiment Exp1, except that: it answers all Sendα queries by accessing its MAC generation and verification oracles. As a result, the α−th MAC key is never used during the simulation. If Forge occurs against an instance that holds , halts and outputs the message/tag pair generated by as its forgery. Otherwise, halts and outputs a failure indication.
If the guess α is correct, then the simulation is perfect, and achieves its goal. Namely, . Since n ≤ qsend, we get . As has at most time complexity t′ and makes at most two queries to Mack(·) and Verk(·),it follows, by definition, that . This completes the proof of Claim 2.
Experiment Exp3. We further modify the experiment so that Execute and Send oracles are simulated as in “the Exp3 modification” described below.
The Exp3 modification
When asks an Execute or Send query, the simulator answers it exactly as in experiment Exp2, except that it modifies the way of generating the ephemeral public values (denoted as X and Y in the protocol) as follows:
The simulator chooses two random v1, and computes and .
For each instance , the simulator chooses a random , computes:
and uses R as the ephemeral public value (i.e., as X or Y ) of .
Since the view of is identical between Exp2 and Exp3, it is straightforward to see that:
Claim 3.
Experiment Exp4. In this experiment, each and is computed as and (instead of as and ) if they are expected to be encrypted with a key held by a clean (server) instance. This is the only difference from Exp3.
Claim 4.
Proof. We prove the claim by constructing a multiple eavesdropper who attacks the indistinguishability of Ω with advantage equal to .
chooses a random bit b ∈ {0, 1} and invokes the adversary . then handles all of the oracle queries of as in experiment Exp3, except that it generates αA and αB for each clean server instance as follows:
outputs (X, ) and (Y, ) as its own (two) plain text pairs (in the indistinguishability experiment ), receives in return two ciphertexts c1 and c2 and sets αA = c2 and αB = c1. (Note, here, that c1 and c2 are encryptions of either X and Y or and .)
When outputs its guess b′, outputs 1 if b = b′ and 0 otherwise. It easily follows that:
The probability that outputs 1 when the first plain texts are encrypted in experiment is equal to the probability that succeeds in experiment Exp4.
The probability that outputs 1 when the second plain texts are encrypted in experiment is equal to the probability that succeeds in experiment Exp3.
Therefore, . Since eavesdrops at most qsend encryptions and has time complexity at most t′, Claim 4 follows immediately from Lemma 1 of Section 4.1.
Experiment Exp5. We now modify the way session keys are computed. For each clean instance and its partner instance, the shared session key is chosen uniformly at random from .
Claim 5.
Proof. We prove the claim by constructing an algorithm that solves the DDH problem in with advantage equal to .
On input, a DDH-problem instance ( , chooses a random bit b ∈ {0, 1}, invokes the adversary and simulates the oracles on its own. handles all of the queries of as in experiment Exp4, except for the following:
uses W1 and W2 in place of V1 and V2 (see “the Exp3 modification”).
For each clean instance
who sends and receives , or vice versa, sets the session key to be .
Later, when outputs its guess b′, outputs 1 if b = b′ and 0 otherwise.
The simulation above clearly shows that:
The probability that outputs 1 on a true Diffie–Hellman triple is equal to the probability that correctly guesses the bit b in experiment Exp4.
The probability that outputs 1 on a random triple is equal to the probability that correctly guesses the bit b in experiment Exp5.
Hence, . From this and since , we obtain the inequality of Claim 5.
In experiment Exp5, the session keys of all fresh instances are chosen uniformly at random from , and thus, the adversary obtains no information on the bit b chosen by the Test oracle. Therefore, it follows that Pr[Succ5] = 1/2. This result combined with Claims 1–5 yields the statement of Theorem 1.
5. Concluding Remarks
In this paper, we have proposed an efficient and secure three-party password-only authenticated key exchange protocol that requires only two communication rounds. We have rigorously proven the security of the protocol in a widely-accepted adversary model. Since our proof of security requires no idealizing assumptions, our proposed protocol would be considered equivalent to being provably secure in the standard model, as long as the building blocks are also instantiated with schemes proven secure in the standard model. For a more efficient implementation of our proposed protocol, Steps 3 and 6 (see the protocol description in Section 4.2) can be omitted if security against undetectable online dictionary attacks is not required. This simplified protocol would still be AKE-secure in the sense of Definition 2 (i.e., Theorem 1 also holds for the simplified protocol). We finally note that it seems impossible to design an AKE-secure, one-round key exchange protocol in the password-only, three-party setting, although we are unable to prove this statement formally.
Acknowledgments
This work was supported by Konkuk University.
Author Contributions
S.H. and D.W. conceived and designed the experiments; S.H. and J.P. performed the experiments; J.P. and D.W. analyzed the data; J.N. and K.C. proved the security of the protocol; J.N. and K.C. wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hervey, C.; van Oorschot, P. A research agenda acknowledging the persistence of passwords. IEEE Secur. Priv. 2012, 10, 28–36. [Google Scholar]
- Wang, W.; Hu, L. Efficient and provably secure generic construction of three-party password-based authenticated key exchange protocols, Proceedings of the INDOCRYPT 2006—7th International Conference on Cryptology, Kolkata, India, 11–13 December 2006; 4329, pp. 118–132.
- Nam, J.; Paik, J.; Kang, H.; Kim, U.; Won, D. An off-line dictionary attack on a simple three-party key exchange protocol. IEEE Commun. Lett. 2009, 13, 205–207. [Google Scholar]
- Lo, N.; Yeh, K. Cryptanalysis of two three-party encrypted key exchange protocols. Comput. Stand. Interfaces. 2009, 31, 1167–1174. [Google Scholar]
- Lin, C.; Hwang, T. On a simple three-party password-based key exchange protocol. Int. J. Commun. Syst. 2011, 24, 1520–1532. [Google Scholar]
- Wu, S.; Pu, Q.; Wang, S.; He, D. Cryptanalysis of a communication-efficient three-party password authenticated key exchange protocol. Inform. Sci. 2012, 215, 83–96. [Google Scholar]
- Choo, K.K.R.; Boyd, C.; Hitchcock, Y. Errors in computational complexity proofs for protocols, Proceedings of the ASIACRYPT 2005—11th International Conference on the Theory and Application of Cryptology and Information Security, Chennai, India, 4–8 December 2005; 3788, pp. 624–643.
- Choo, K.K.R.; Boyd, C.; Hitchcock, Y. Examining indistinguishability-based proof models for key establishment protocols, Proceedings of the ASIACRYPT 2005—11th International Conference on the Theory and Application of Cryptology and Information Security, Chennai, India, 4–8 December 2005; 3788, pp. 585–604.
- Choo, K.K.R.; Boyd, C.; Hitchcock, Y. The importance of proofs of security for key establishment protocols: Formal analysis of Jan–Chen, Yang–Shen–Shieh, Kim–Huh–Hwang–Lee, Lin–Sun–Hwang, and Yeh–Sun protocols. Comput. Commun. 2006, 29, 2788–2797. [Google Scholar]
- Bellare, M.; Rogaway, P. Entity authentication and key distribution, Proceedings of the 13th Annual International Cryptology Conference, Santa Barbara, CA, USA, 22–26 August 1993; 773, pp. 232–249.
- Abdalla, M.; Fouque, P.; Pointcheval, D. Password-based authenticated key exchange in the three-party setting, Proceedings of the Public Key Cryptography 2005, Les Diablerets, Switzerland, 23–26 January 2005; 3386, pp. 65–84.
- Abdalla, M.; Fouque, P.; Pointcheval, D. Password-based authenticated key exchange in the three-party setting. IEE Proc. Inform. Secur. 2006, 153, 27–39. [Google Scholar]
- Lin, C.; Sun, H.; Steiner, M.; Hwang, T. Three-party encrypted key exchange without server public-keys. IEEE Commun. Lett. 2001, 5, 497–499. [Google Scholar]
- Lee, T.; Hwang, T.; Lin, C. Enhanced three-party encrypted key exchange without server public keys. Comput. Secur. 2004, 23, 571–577. [Google Scholar]
- Abdalla, M.; Pointcheval, D. Interactive Diffie-Hellman assumptions with applications to password-based authentication. In Financial Cryptography and Data Security; Patrick,, A.S., Yung,, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 341–356. [Google Scholar]
- Wen, H.; Lee, T.; Hwang, T. Provably secure three-party password-based authenticated key exchange protocol using Weil pairing. IEE Proc. Commun. 2005, 152, 138–143. [Google Scholar]
- Lu, R.; Cao, Z. Simple three-party key exchange protocol. Comput. Secur. 2007, 26, 94–97. [Google Scholar]
- Chung, H.; Ku, W. Three weaknesses in a simple three-party key exchange protocol. Inform. Sci. 2008, 178, 220–229. [Google Scholar]
- Guo, H.; Li, Z.; Mu, Y.; Zhang, X. Cryptanalysis of simple three-party key exchange protocol. Comput. Secur. 2008, 27, 16–21. [Google Scholar]
- Kim, H.; Choi, J. Enhanced password-based simple three-party key exchange protocol. Comput. Electr. Eng. 2009, 35, 107–114. [Google Scholar]
- Huang, H. A simple three-party password-based key exchange protocol. Int. J. Commun. Syst. 2009, 22, 857–862. [Google Scholar]
- Dongna, E.; Cheng, Q.; Ma, C. Password authenticated key exchange based on RSA in the three-party settings, Proceedings of the Provable Security Conference 2009, Guangzhou, China, 11–13 November 2009; 5848, pp. 168–182.
- Lee, T.; Hwang, T. Simple password-based three-party authenticated key exchange without server public keys. Inform. Sci. 2010, 180, 1702–1714. [Google Scholar]
- Wang, W.; Hu, L.; Li, Y. How to construct secure and efficient three-party password-based authenticated key exchange protocols, Proceedings of The 6th China International Conference on Information Security and Cryptology, Shanghai, China, 20–24 October 2010; 6584, pp. 218–235.
- Chang, T.; Hwang, M.; Yang, W. A communication-efficient three-party password authenticated key exchange protocol. Inform. Sci. 2011, 181, 217–226. [Google Scholar]
- Nam, J.; Lee, Y.; Kim, S.; Won, D. Security weakness in a three-party pairing-based protocol for password authenticated key exchange. Inform. Sci. 2007, 177, 1364–1375. [Google Scholar]
- Phan, R.; Yau, W.; Goi, B. Cryptanalysis of simple three-party key exchange protocol (S-3PAKE). Inform. Sci. 2008, 178, 2849–2856. [Google Scholar]
- Yoon, E.; Yoo, K. Cryptanalysis of a simple three-party password-based key exchange protocol. Int. J. Commun. Syst. 2011, 24, 532–542. [Google Scholar]
- Liang, H.; Hu, J.; Wu, S. Re-attack on a three-party password-based authenticated key exchange protocol. Math. Comput. Model. 2013, 57, 1175–1183. [Google Scholar]
- Tsai, H.; Chang, C. Provably secure three party encrypted key exchange scheme with explicit authentication. Inform. Sci. 2013, 238, 242–249. [Google Scholar]
- Nam, J.; Choo, K.K.R.; Park, M.; Paik, J.; Won, D. On the security of a simple three-party key exchange protocol without server’s public keys. Sci. World J 2014, 479534:1–479534:7. [Google Scholar]
- Nam, J.; Choo, K.K.R.; Paik, J.; Won, D. An offline dictionary attack against Abdalla and Pointcheval’s key exchange in the password-only three-party setting. IEICE Trans. Fundam. Electr. Commun. Comput. Sci. 2015. in press. [Google Scholar]
- Szydlo, M. A note on Chosen-Basis Decisional Diffie-Hellman assumptions, Proceedings of the Financial Cryptography 2006, Anguilla, British West Indies, 27 February–2 March 2006; 4107, pp. 166–170.
- Yoneyama, K. Efficient and strongly secure password-based server aided key exchange, Proceedings of the INDOCRYPT 2008: 9th International Conference on Cryptology, Kharagpur, India, 14–17 December 2008; 5365, pp. 172–184.
- Zhao, J.; Gu, D. Provably secure three-party password-based authenticated key exchange protocol. Inform. Sci. 2012, 184, 310–323. [Google Scholar]
- Lin, C.; Sun, H.; Hwang, T. Three-party encrypted key exchange: Attacks and a solution. ACM SIGOPS Oper. Syst. Rev. 2000, 34, 12–20. [Google Scholar]
- Chang, C.; Chang, Y. A novel three-party encrypted key exchange protocol. Comput. Stand. Interfaces. 2004, 26, 471–476. [Google Scholar]
- Chen, H.; Chen, T.; Lee, W.; Chang, C. Security enhancement for a three-party encrypted key exchange protocol against undetectable on-line password guessing attacks. Comput. Stand. Interfaces. 2008, 30, 95–99. [Google Scholar]
- Yoon, E.; Yoo, K. Improving the novel three-party encrypted key exchange protocol. Comput. Stand. Interfaces. 2008, 30, 309–314. [Google Scholar]
- Chien, H.; Wu, T. Provably secure password-based three-party key exchange with optimal message steps. Comput. J 2009, 52, 646–655. [Google Scholar]
- Lou, D.; Huang, H. Efficient three-party password-based key exchange scheme. Int. J. Commun. Syst. 2011, 24, 504–512. [Google Scholar]
- Yang, J.; Cao, T. Provably secure three-party password authenticated key exchange protocol in the standard model. J. Syst. Softw. 2012, 85, 340–350. [Google Scholar]
- Lee, C.; Chen, S.; Chen, C. A computation-efficient three-party encrypted key exchange protocol. Appl. Math. Inform. Sci. 2012, 6, 573–579. [Google Scholar]
- Wu, S.; Chen, K.; Pu, Q.; Zhu, Y. Cryptanalysis and enhancements of efficient three-party password-based key exchange scheme. Int. J. Commun. Syst. 2013, 26, 674–686. [Google Scholar]
- Bellare, M.; Pointcheval, D.; Rogaway, P. Authenticated key exchange secure against dictionary attacks, Proceedings of the Eurocrypt 2000, Bruges, Belgium, 14–18 May 2000; 1807, pp. 139–155.
- Abdalla, M.; Pointcheval, D. Simple password-based encrypted key exchange protocols, Proceedings of the CT-RSA 2005, San Francisco, CA, USA, 14–18 February 2005; 3376, pp. 191–208.
- Katz, J.; Vaikuntanathan, V. Round-optimal password-based authenticated key exchange, Proceedings of the Theory of Cryptography Conference 2011, Providence, RI, USA, 28–30 March 2011; 6597, pp. 293–310.
- Choo, K.K.R. A proof of revised Yahalom protocol in the Bellare and Rogaway (1993) model. Comput. J 2007, 50, 591–601. [Google Scholar]
- Bellare, M.; Rogaway, P. Provably secure session key distribution—The three party case, Proceedings of the 27th ACM Symposium on Theory of Computing, Las Vegas, NV, USA, May 1995; pp. 57–66.
- Goldwasser, S.; Micali, S. Probabilistic encryption. J. Comput. Syst. Sci. 1984, 28, 270–299. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).