Abstract
The second-order differential equation for a damped harmonic oscillator can be converted to two coupled first-order equations, with two two-by-two matrices leading to the group Sp(2). It is shown that this oscillator system contains the essential features of Wigner’s little groups dictating the internal space-time symmetries of particles in the Lorentz-covariant world. The little groups are the subgroups of the Lorentz group whose transformations leave the four-momentum of a given particle invariant. It is shown that the damping modes of the oscillator correspond to the little groups for massive and imaginary-mass particles respectively. When the system makes the transition from the oscillation to damping mode, it corresponds to the little group for massless particles. Rotations around the momentum leave the four-momentum invariant. This degree of freedom extends the Sp(2) symmetry to that of SL(2, c) corresponding to the Lorentz group applicable to the four-dimensional Minkowski space. The Poincaré sphere contains the SL(2, c) symmetry. In addition, it has a non-Lorentzian parameter allowing us to reduce the mass continuously to zero. It is thus possible to construct the little group for massless particles from that of the massive particle by reducing its mass to zero. Spin-1/2 particles and spin-1 particles are discussed in detail.1. Introduction
We are quite familiar with the second-order differential equation
In Equation (1), when b = 0, the equation is that of a simple harmonic oscillator with the frequency . As b increases, the oscillation becomes damped. When b is larger than , the oscillation disappears, as the solution is a damping mode.
Consider that increasing b continuously, while difficult mechanically, can be done electrically using Equation (2) by adjusting the resistance R. The transition from the oscillation mode to the damping mode is a continuous physical process.
This b term leads to energy dissipation, but is not regarded as a fundamental force. It is inconvenient in the Hamiltonian formulation of mechanics and troublesome in transition to quantum mechanics, yet, plays an important role in classical mechanics. In this paper this term will help us understand the fundamental space-time symmetries of elementary particles.
We are interested in constructing the fundamental symmetry group for particles in the Lorentz-covariant world. For this purpose, we transform the second-order differential equation of Equation (1) to two coupled first-order equations using two-by-two matrices. Only two linearly independent matrices are needed. They are the anti-symmetric and symmetric matrices
These two matrices lead to the Sp(2) group consisting of two-by-two unimodular matrices with real elements. This group is isomorphic to the three-dimensional Lorentz group applicable to two space-like and one time-like coordinates. This group is commonly called the O(2, 1) group.
This O(2, 1) group can explain all the essential features of Wigner’s little groups dictating internal space-time symmetries of particles [1]. Wigner defined his little groups as the subgroups of the Lorentz group whose transformations leave the four-momentum of a given particle invariant. He observed that the little groups are different for massive, massless, and imaginary-mass particles. It has been a challenge to design a mathematical model which will combine those three into one formalism, but we show that the damped harmonic oscillator provides the desired mathematical framework.
For the two space-like coordinates, we can assign one of them to the direction of the momentum, and the other to the direction perpendicular to the momentum. Let the direction of the momentum be along the z axis, and let the perpendicular direction be along the x axis. We therefore study the kinematics of the group within the zx plane, then see what happens when we rotate the system around the z axis without changing the momentum [2].
The Poincaré sphere for polarization optics contains the SL(2, c) symmetry isomorphic to the four-dimensional Lorentz group applicable to the Minkowski space [3–7]. Thus, the Poincaré sphere extends Wigner’s picture into the three space-like and one time-like coordinates. Specifically, this extension adds rotations around the given momentum which leaves the four-momentum invariant [2].
While the particle mass is a Lorentz-invariant variable, the Poincaré sphere contains an extra variable which allows the mass to change. This variable allows us to take the mass-limit of the symmetry operations. The transverse rotational degrees of freedom collapse into one gauge degree of freedom and polarization of neutrinos is a consequence of the requirement of gauge invariance [8,9].
The SL(2, c) group contains symmetries not seen in the three-dimensional rotation group. While we are familiar with two spinors for a spin-1/2 particle in nonrelativistic quantum mechanics, there are two additional spinors due to the reflection properties of the Lorentz group. There are thus 16 bilinear combinations of those four spinors. This leads to two scalars, two four-vectors, and one antisymmetric four-by-four tensor. The Maxwell-type electromagnetic field tensor can be obtained as a massless limit of this tensor [10].
In Section 2, we review the damped harmonic oscillator in classical mechanics, and note that the solution can be either in the oscillation mode or damping mode depending on the magnitude of the damping parameter. The translation of the second order equation into a first order differential equation with two-by-two matrices is possible. This first-order equation is similar to the Schrödinger equation for a spin-1/2 particle in a magnetic field.
Section 3 shows that the two-by-two matrices of Section 2 can be formulated in terms of the Sp(2) group. These matrices can be decomposed into the Bargmann and Wigner decompositions. Furthermore, this group is isomorphic to the three-dimensional Lorentz group with two space and one time-like coordinates.
In Section 4, it is noted that this three-dimensional Lorentz group has all the essential features of Wigner’s little groups which dictate the internal space-time symmetries of the particles in the Lorentz-covariant world. Wigner’s little groups are the subgroups of the Lorentz group whose transformations leave the four-momentum of a given particle invariant. The Bargmann Wigner decompositions are shown to be useful tools for studying the little groups.
In Section 5, we note that the given momentum is invariant under rotations around it. The addition of this rotational degree of freedom extends the Sp(2) symmetry to the six-parameter SL(2, c) symmetry. In the space-time language, this extends the three dimensional group to the Lorentz group applicable to three space and one time dimensions.
Section 6 shows that the Poincaré sphere contains the symmetries of SL(2, c) group. In addition, it contains an extra variable which allows us to change the mass of the particle, which is not allowed in the Lorentz group.
In Section 7, the symmetries of massless particles are studied in detail. In addition to rotation around the momentum, Wigner’s little group generates gauge transformations. While gauge transformations on spin-1 photons are well known, the gauge invariance leads to the polarization of massless spin-1/2 particles, as observed in neutrino polarizations.
In Section 8, it is noted that there are four spinors for spin-1/2 particles in the Lorentz-covariant world. It is thus possible to construct 16 bilinear forms, applicable to two scalars, and two vectors, and one antisymmetric second-rank tensor. The electromagnetic field tensor is derived as the massless limit. This tensor is shown to be gauge-invariant.
2. Classical Damped Oscillators
For convenience, we write Equation (1) as
If ω = μ, both Equations (6) and (8) collapse into one solution
These three different cases are treated separately in textbooks. Here we are interested in the transition from Equation (6) to Equation (8), via Equation (10). For convenience, we start from μ greater than ω with μ′ given by Equation (9).
For a given value of μ, the square root becomes zero when ω equals μ. If ω becomes larger, the square root becomes imaginary and divides into two branches.
Given the solutions of Equations (6) and (10), it is convenient to use ψ(t) defined as
2.1. Two-by-Two Matrix Formulation
In order to convert this second-order equation to a first-order system, we introduce ψ1(t) and ψ2(t) satisfying two coupled differential equations
Using the Hermitian and anti-Hermitian matrices of Equation (3) in Section 1, we construct the linear combination
2.2. Transition from the Oscillation Mode to Damping Mode
It appears straight-forward to compute this expression by a Taylor expansion, but it is not. This issue was extensively discussed in the earlier papers by two of us [12,13]. The key idea is to write the matrix
Then the Taylor expansion leads to
If ω is sufficiently close to but smaller than μ, the matrix of Equation (25) becomes
We can rewrite this matrix as
The transition from Equation (31) to Equation (32) is continuous as they become identical when ∊ = 0. As ∊ changes its sign, the diagonal elements of above matrices tell us how cos(ω′t) becomes cosh(μ′t). As for the upper-right element element, − sin(ω′t) becomes sinh(μ′t). This non-analytic continuity is discussed in detail in one of the earlier papers by two of us on lens optics [13]. This type of continuity was called there “tangential continuity.” There, the function and its first derivative are continuous while the second derivative is not.
2.3. Mathematical Forms of the Solutions
In this section, we use the Heisenberg approach to the problem, and obtain the solutions in the form of two-by-two matrices. We note that
For the oscillation mode, the trace of the matrix is smaller than 2. The solution takes the form of
with trace 2 cos(x). The trace is independent of η.For the damping mode, the trace of the matrix is greater than 2.
with trace 2 cosh(x). Again, the trace is independent of η.For the transition mode, the trace is equal to 2, and the matrix is triangular and takes the form of
When x approaches zero, the Equations (33) and (34) take the formrespectively. These two matrices have the same lower-left element. Let us fix this element to be a positive number γ. ThenThen the matrices of Equation (36) becomeIf we introduce a small number ∊ defined asthe matrices of Equation (38) becomerespectively, with .
3. Groups of Two-by-Two Matrices
If a two-by-two matrix has four complex elements, it has eight independent parameters. If the determinant of this matrix is one, it is known as an unimodular matrix and the number of independent parameters is reduced to six. The group of two-by-two unimodular matrices is called SL(2, c). This six-parameter group is isomorphic to the Lorentz group applicable to the Minkowski space of three space-like and one time-like dimensions [14].
We can start with two subgroups of SL(2, c).
While the matrices of SL(2, c) are not unitary, we can consider the subset consisting of unitary matrices. This subgroup is called SU(2), and is isomorphic to the three-dimensional rotation group. This three-parameter group is the basic scientific language for spin-1/2 particles.
We can also consider the subset of matrices with real elements. This three-parameter group is called Sp(2) and is isomorphic to the three-dimensional Lorentz group applicable to two space-like and one time-like coordinates.
In the Lorentz group, there are three space-like dimensions with x, y, and z coordinates. However, for many physical problems, it is more convenient to study the problem in the two-dimensional (x, z) plane first and generalize it to three-dimensional space by rotating the system around the z axis. This process can be called Euler decomposition and Euler generalization [2].
First, we study Sp(2) symmetry in detail, and achieve the generalization by augmenting the two-by-two matrix corresponding to the rotation around the z axis. In this section, we study in detail properties of Sp(2) matrices, then generalize them to SL(2, c) in Section 5.
There are three classes of Sp(2) matrices. Their traces can be smaller or greater than two, or equal to two. While these subjects are already discussed in the literature [15–17] our main interest is what happens as the trace goes from less than two to greater than two. Here we are guided by the model we have discussed in Section 2, which accounts for the transition from the oscillation mode to the damping mode.
3.1. Lie Algebra of Sp(2)
The two linearly independent matrices of Equation (3) can be written as
The Hermitian matrix J2 generates the rotation matrix
Returning to the Lie algebra of Equation (43), since K1 and K3 are anti-Hermitian, and J2 is Hermitian, the set of commutation relation is invariant under the Hermitian conjugation. In other words, the commutation relations remain invariant, even if we change the sign of K1 and K3, while keeping that of J2 invariant. Next, let us take the complex conjugate of the entire system. Then both the J and K matrices change their signs.
3.2. Bargmann and Wigner Decompositions
Since the Sp(2) matrix has three independent parameters, it can be written as [15]
For the matrix of Equation (49), we can now consider the following three cases. Let us assume that χ is positive, and the angle θ is less than 90°. Let us look at the upper-right element.
If it is negative with [sinh χ < (cosh χ)sin α], then the trace of the matrix is smaller than 2, and the matrix can be written as
withIf it is positive with [sinh χ > (cosh χ)sin α)], then the trace is greater than 2, and the matrix can be written as
withIf it is zero with [(sinh χ = (cosh χ)sin α)], then the trace is equal to 2, and the matrix takes the form
The above repeats the mathematics given in Section 2.3.
Returning to Equations (52) and (53), they can be decomposed into
We note that both Equations (57) and (58) are written as similarity transformations. Thus
The question is what physics these decompositions describe in the real world. To address this, we study what the Lorentz group does in the real world, and study isomorphism between the Sp(2) group and the Lorentz group applicable to the three-dimensional space consisting of one time and two space coordinates.
3.3. Isomorphism with the Lorentz Group
The purpose of this section is to give physical interpretations of the mathematical formulas given in Section 3.2. We will interpret these formulae in terms of the Lorentz transformations which are normally described by four-by-four matrices. For this purpose, it is necessary to establish a correspondence between the two-by-two representation of Section 3.2 and the four-by-four representations of the Lorentz group.
Let us consider the Minkowskian space-time four-vector
In order to give physical interpretations to the three two-by-two matrices given in Equations (44)–(46), we consider rotations around the y axis, boosts along the x axis, and boosts along the z axis. The transformation is restricted in the three-dimensional subspace of (t, z, x). It is then straight-forward to construct those four-by-four transformation matrices where the y coordinate remains invariant. They are given in Table 1. Their generators also given. Those four-by-four generators satisfy the Lie algebra given in Equation (43).

4. Internal Space-Time Symmetries
We have seen that there corresponds a two-by-two matrix for each four-by-four Lorentz transformation matrix. It is possible to give physical interpretations to those four-by-four matrices. It must thus be possible to attach a physical interpretation to each two-by-two matrix.
Since 1939 [1] when Wigner introduced the concept of the little groups many papers have been published on this subject, but most of them were based on the four-by-four representation. In this section, we shall give the formalism of little groups in the language of two-by-two matrices. In so doing, we provide physical interpretations to the Bargmann and Wigner decompositions introduced in Section 3.2.
4.1. Wigner’s Little Groups
In [1], Wigner started with a free relativistic particle with momentum, then constructed subgroups of the Lorentz group whose transformations leave the four-momentum invariant. These subgroups thus define the internal space-time symmetry of the given particle. Without loss of generality, we assume that the particle momentum is along the z direction. Thus rotations around the momentum leave the momentum invariant, and this degree of freedom defines the helicity, or the spin parallel to the momentum.
We shall use the word “Wigner transformation” for the transformation which leaves the four-momentum invariant:
For a massive particle, it is possible to find a Lorentz frame where it is at rest with zero momentum. The four-momentum can be written as m(1, 0, 0, 0), where m is the mass. This four-momentum is invariant under rotations in the three-dimensional (z, x, y) space.
For an imaginary-mass particle, there is the Lorentz frame where the energy component vanishes. The momentum four-vector can be written as p(0, 1, 0, 0), where p is the magnitude of the momentum.
If the particle is massless, its four-momentum becomes p(1, 1, 0, 0). Here the first and second components are equal in magnitude.
The constant factors in these four-momenta do not play any significant roles. Thus we write them as (1, 0, 0, 0), (0, 1, 0, 0), and (1, 1, 0, 0) respectively. Since Wigner worked with these three specific four-momenta [1], we call them Wigner four-vectors.
All of these four-vectors are invariant under rotations around the z axis. The rotation matrix is
In addition, the four-momentum of a massive particle is invariant under the rotation around the y axis, whose four-by-four matrix was given in Table 1. The four-momentum of an imaginary particle is invariant under the boost matrix S(λ) given in Table 1. The problem for the massless particle is more complicated, but will be discussed in detail in Section 7. See Table 2.

4.2. Two-by-Two Formulation of Lorentz Transformations
The Lorentz group is a group of four-by-four matrices performing Lorentz transformations on the Minkowskian vector space of (t, z, x, y), leaving the quantity
In this two-by-two representation, the four-vector is written as
Since the G matrix starts with four complex numbers and its determinant is one by Equation (67), it has six independent parameters. The group of these G matrices is known to be locally isomorphic to the group of four-by-four matrices performing Lorentz transformations on the four-vector (t, z, x, y). In other words, for each G matrix there is a corresponding four-by-four Lorentz-transform matrix [7].
The matrix G is not a unitary matrix, because its Hermitian conjugate is not always its inverse. This group has a unitary subgroup called SU(2) and another consisting only of real matrices called Sp(2). For this later subgroup, it is sufficient to work with the three matrices R(θ), S(λ), and B(η) given in Equations (44)–(46) respectively. Each of these matrices has its corresponding four-by-four matrix applicable to the (t, z, x, y). These matrices with their four-by-four counterparts are tabulated in Table 1.
The energy-momentum four vector can also be written as a two-by-two matrix. It can be written as
The Lorentz transformation can be written explicitly as
Wigner’s little group consists of two-by-two matrices satisfying
If determinant of W is a positive number, then P is proportional to
For all three cases, the matrix of the form
For the massive particle with the four-momentum of Equation (76), the transformations with the rotation matrix of Equation (44) leave the P matrix of Equation (76) invariant. Together with the Z(ϕ) matrix, this rotation matrix leads to the subgroup consisting of the unitary subset of the G matrices. The unitary subset of G is SU(2) corresponding to the three-dimensional rotation group dictating the spin of the particle [14].
For the massless case, the transformations with the triangular matrix of the form
For a particle with an imaginary mass, a W matrix of the form of Equation (45) leaves the four-momentum of Equation (77) invariant.
Table 3 summarizes the transformation matrices for Wigner’s little groups for massive, massless, and imaginary-mass particles. Furthermore, in terms of their traces, the matrices given in this subsection can be compared with those given in Section 2.3 for the damped oscillator. The comparisons are given in Table 4.


Of course, it is a challenging problem to have one expression for all three classes. This problem has been discussed in the literature [12], and the damped oscillator case of Section 2 addresses the continuity problem.
5. Lorentz Completion of Wigner’s Little Groups
So far we have considered transformations applicable only to (t, z, x) space. In order to study the full symmetry, we have to consider rotations around the z axis. As previously stated, when a particle moves along this axis, this rotation defines the helicity of the particle.
In [1], Wigner worked out the little group of a massive particle at rest. When the particle gains a momentum along the z direction, the single particle can reverse the direction of momentum, the spin, or both. What happens to the internal space-time symmetries is discussed in this section.
5.1. Rotation around the z Axis
In Section 3, our kinematics was restricted to the two-dimensional space of z and x, and thus includes rotations around the y axis. We now introduce the four-by-four matrix of Equation (63) performing rotations around the z axis. Its corresponding two-by-two matrix was given in Equation (79). Its generator is
For each of these two-by-two matrices there is a corresponding four-by-four matrix generating Lorentz transformations on the four-dimensional Lorentz group. When these two-by-two matrices are imaginary, the corresponding four-by-four matrices were given in Table 1. If they are real, the corresponding four-by-four matrices were given in Table 5.

This set of commutation relations is known as the Lie algebra for the SL(2, c), namely the group of two-by-two elements with unit determinants. Their elements are complex. This set is also the Lorentz group performing Lorentz transformations on the four-dimensional Minkowski space.
This set has many useful subgroups. For the group SL(2, c), there is a subgroup consisting only of real matrices, generated by the two-by-two matrices given in Table 1. This three-parameter subgroup is precisely the Sp(2) group we used in Sections 3 and 3.2. Their generators satisfy the Lie algebra given in Equation (43).
In addition, this group has the following Wigner subgroups governing the internal space-time symmetries of particles in the Lorentz-covariant world [1]:
The Ji matrices form a closed set of commutation relations. The subgroup generated by these Hermitian matrices is SU(2) for electron spins. The corresponding rotation group does not change the four-momentum of the particle at rest. This is Wigner’s little group for massive particles. If the particle is at rest, the two-by-two form of the four-vector is given by Equation (76). The Lorentz transformation generated by J3 takes the form
Similar computations can be carried out for J1 and J2.There is another Sp(2) subgroup, generated by K1, K2, and J3. They satisfy the commutation relations
The Wigner transformation generated by these two-by-two matrices leave the momentum four-vector of Equation (77) invariant. For instance, the transformation matrix generated by K2 takes the formand the Wigner transformation takes the formComputations with K2 and J3 lead to the same result.Since the determinant of the four-momentum matrix is negative, the particle has an imaginary mass. In the language of the four-by-four matrix, the transformation matrices leave the four-momentum of the form (0, 1, 0, 0) invariant.
Furthermore, we can consider the following combinations of the generators:
Together with J3, they satisfy the the following commutation relations.In order to understand this set of commutation relations, we can consider an xy coordinate system in a two-dimensional space. Then rotation around the origin is generated byand the two translations are generated byfor the x and y directions respectively. These operators satisfy the commutations relations given in Equation (89).
The two-by-two matrices of Equation (88) generate the following transformation matrix.
5.2. E(2)-Like Symmetry of Massless Particles
From the four-by-four generators of K1,2 and J1,2, we can write
In the two-by-two representation, the electromagnetic four-potential takes the form
For massless spin-1/2 particles starting with the two-by-two expression of G(γ, ϕ) given in Equation (92), and considering the spinors
5.3. Boosts along the z Axis
In Sections 4.1 and 5.1, we studied Wigner transformations for fixed values of the four-momenta. The next question is what happens when the system is boosted along the z direction, with the transformation
We are interested in Lorentz transformations which leave a given non-zero momentum invariant. We can consider a Lorentz boost along the direction preceded and followed by identical rotation matrices, as described in Figure 1 and the transformation matrix as
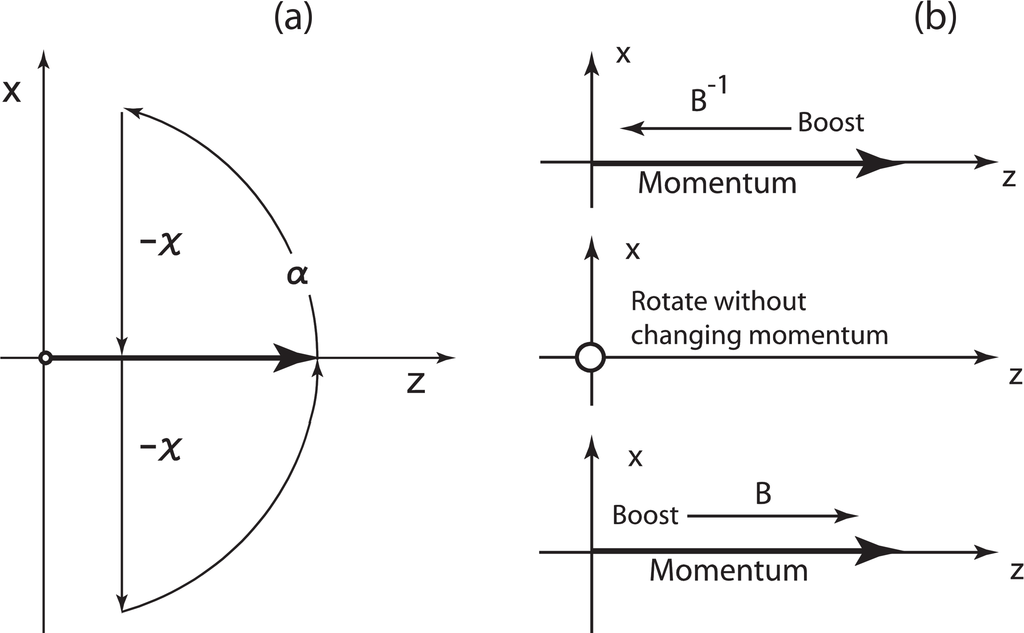
If the particle is massive, the off-diagonal elements of Equation (108) have opposite signs, and this matrix can be decomposed into
withandAccording to Equation (109) the first matrix (far right) reduces the particle momentum to zero. The second matrix rotates the particle without changing the momentum. The third matrix boosts the particle to restore its original momentum. This is the extension of Wigner’s original idea to moving particles.If the particle has an imaginary mass, the off-diagonal elements of Equation (108) have the same sign,
withandThis is also a three-step operation. The first matrix brings the particle momentum to the zero-energy state with p0 = 0. Boosts along the x or y direction do not change the four-momentum. We can then boost the particle back to restore its momentum. This operation is also an extension of the Wigner’s original little group. Thus, it is quite appropriate to call the formulas of Equations (109) and (112) Wigner decompositions.If the particle mass is zero with
the η parameter becomes infinite, and the Wigner decomposition does not appear to be useful. We can then go back to the Bargmann decomposition of Equation (107). With the condition of Equations (115) and (108) becomeswithThe decomposition ending with a triangular matrix is called the Iwasawa decomposition [16,22] and its physical interpretation was given in Section 5.2. The γ parameter does not depend on η.
Thus, we have given physical interpretations to the Bargmann and Wigner decompositions given in Section (3.2). Consider what happens when the momentum becomes large. Then η becomes large for nonzero mass cases. All three four-momenta in Equation (106) become
In Section 5.2, we concluded that the triangular matrix corresponds to gauge transformations. However, particles with imaginary mass are not observed. For massive particles, we can start with the three-dimensional rotation group. The rotation around the z axis is called helicity, and remains invariant under the boost along the z direction. As for the transverse rotations, they become gauge transformation as illustrated in Table 6.

5.4. Conjugate Transformations
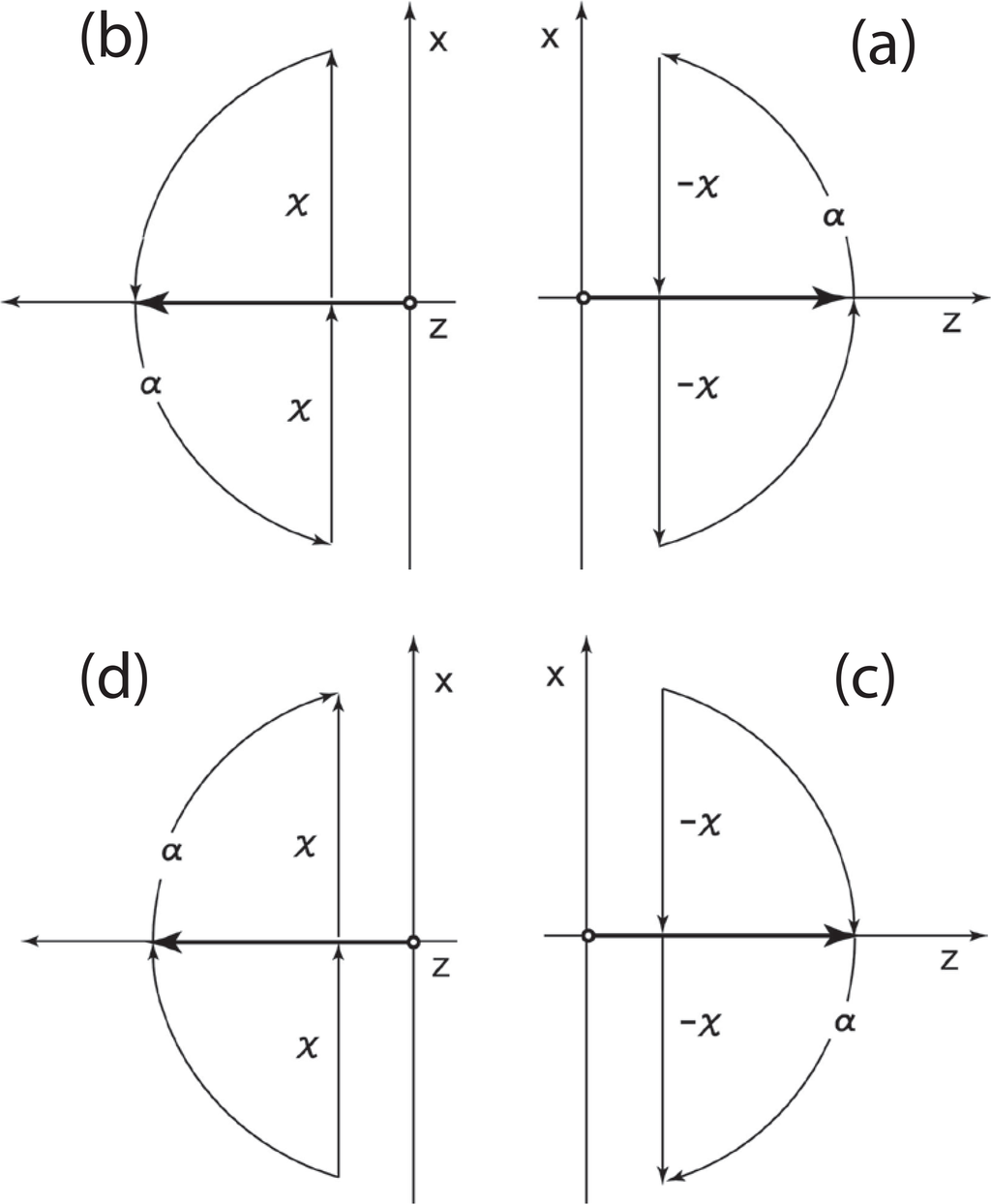
The most general form of the SL(2, c) matrix is given in Equation (66). Transformation operators for the Lorentz group are given in exponential form as:
Since we understand the rotation around the z axis, we can now restrict the kinematics to the zt plane, and work with the Sp(2) symmetry. Then the D matrices can be considered as Bargmann decompositions. First, D and Ḋ, and their Hermitian conjugates are
We can also consider changing the direction of rotations. Then they result in the Hermitian conjugates. We can write their matrices as
From the exponential expressions from Equation (119) to Equation (122), it is clear that
6. Symmetries Derivable from the Poincaré Sphere
The Poincaré sphere serves as the basic language for polarization physics. Its underlying language is the two-by-two coherency matrix. This coherency matrix contains the symmetry of SL(2, c) isomorphic to the the Lorentz group applicable to three space-like and one time-like dimensions [4,6,7].
For polarized light propagating along the z direction, the amplitude ratio and phase difference of electric field x and y components traditionally determine the state of polarization. Hence, the polarization can be changed by adjusting the amplitude ratio or the phase difference or both. Usually, the optical device which changes amplitude is called an “attenuator” (or “amplifier”) and the device which changes the relative phase a “phase shifter”.
Let us start with the Jones vector:
The optical beam can be attenuated differently in the two directions. The resulting matrix is
The polarization is not always along the x and y axes, but can be rotated around the z axis using Equation (79) generated by J2 given in Table 1.
Among the rotation angles, the angle of 45° plays an important role in polarization optics. Indeed, if we rotate the squeeze matrix of Equation (46) by 45°, we end up with the squeeze matrix of Equation (45) generated by K1 given also in Table 1.
Each of these four matrices plays an important role in special relativity, as we discussed in Sections 3.2 and 6. Their respective roles in optics and particle physics are given in Table 7.

The most general form for the two-by-two matrix applicable to the Jones vector is the G matrix of Equation (66). This matrix is of course a representation of the SL(2, c) group. It brings the simplest Jones vector of Equation (128) to its most general form.
6.1. Coherency Matrix
However, the Jones vector alone cannot tell us whether the two components are coherent with each other. In order to address this important degree of freedom, we use the coherency matrix defined as [3,23]
The angle ξ specifies the degree of coherency. If it is zero, the system is fully coherent, while the system is totally incoherent if ξ is 90°. This can therefore be called the “decoherence angle.”
While the most general form of the transformation applicable to the Jones vector is G of Equation (66), the transformation applicable to the coherency matrix is
6.2. Two Radii of the Poincaré Sphere
Let us write explicitly the transformation of Equation (136) as
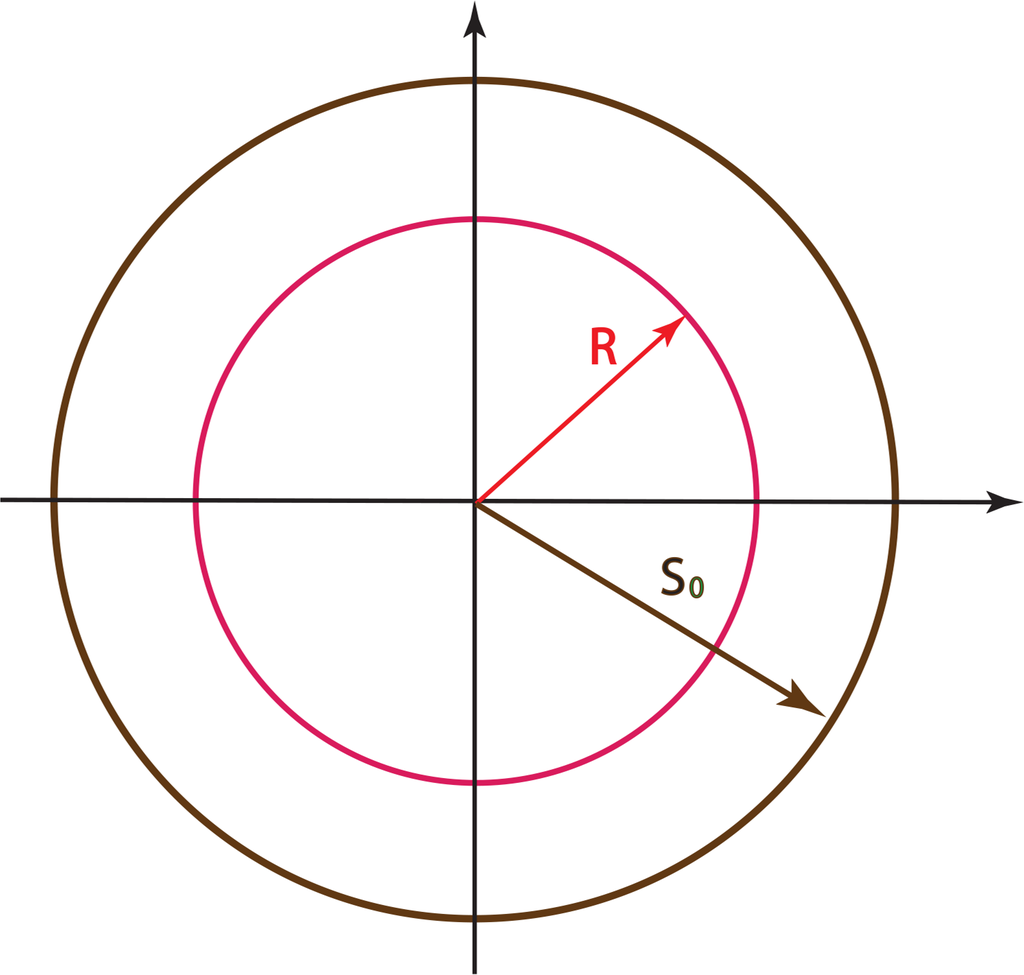
In the Jones vector of Equation (128), the amplitudes of the two orthogonal components are equal. Thus, the two diagonal elements of the coherency matrix are equal. This leads to S3 = 0, and the problem is reduced from the sphere to a circle. In the resulting two-dimensional subspace, we can introduce the polar coordinate system with
The radius R takes its maximum value S0 when ξ = 0°. It decreases as ξ increases and vanishes when ξ =90°. This aspect of the radius R is illustrated in Figure 3.
In order to see its implications in special relativity, let us go back to the four-momentum matrix of m(1, 0, 0, 0). Its determinant is m2 and remains invariant. Likewise, the determinant of the coherency matrix of Equation (132) should also remain invariant. The determinant in this case is
The coherency matrix then becomes
Since the Lorentz transformation leaves the determinant invariant, the change in this ξ variable is not a Lorentz transformation. It is of course possible to construct a larger group in which this variable plays a role in a group transformation [6], but here we are more interested in its role in a particle gaining a mass from zero or the mass becoming zero.
6.3. Extra-Lorentzian Symmetry
The coherency matrix of Equation (146) can be diagonalized to
Thus, with this extra variable, it is possible to study the little groups for variable masses, including the small-mass limit and the zero-mass case.
For a fixed value of p0, the (mass)2 becomes
This transition is illustrated in Figure 4. We are interested in reaching a point on the light cone from mass hyperbola while keeping the energy fixed. According to this figure, we do not have to make an excursion to infinite-momentum limit. If the energy is fixed during this process, Equation (152) tells the mass and momentum relation, and Figure 5 illustrates this relation.
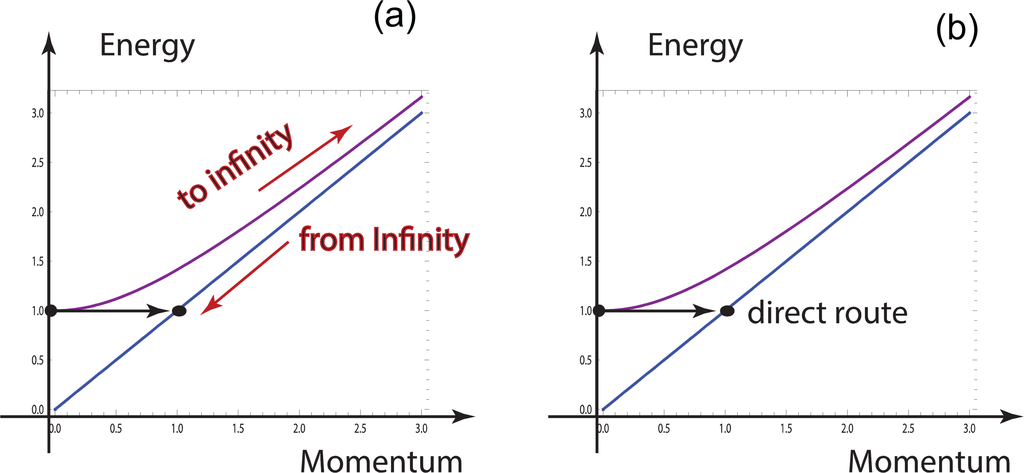
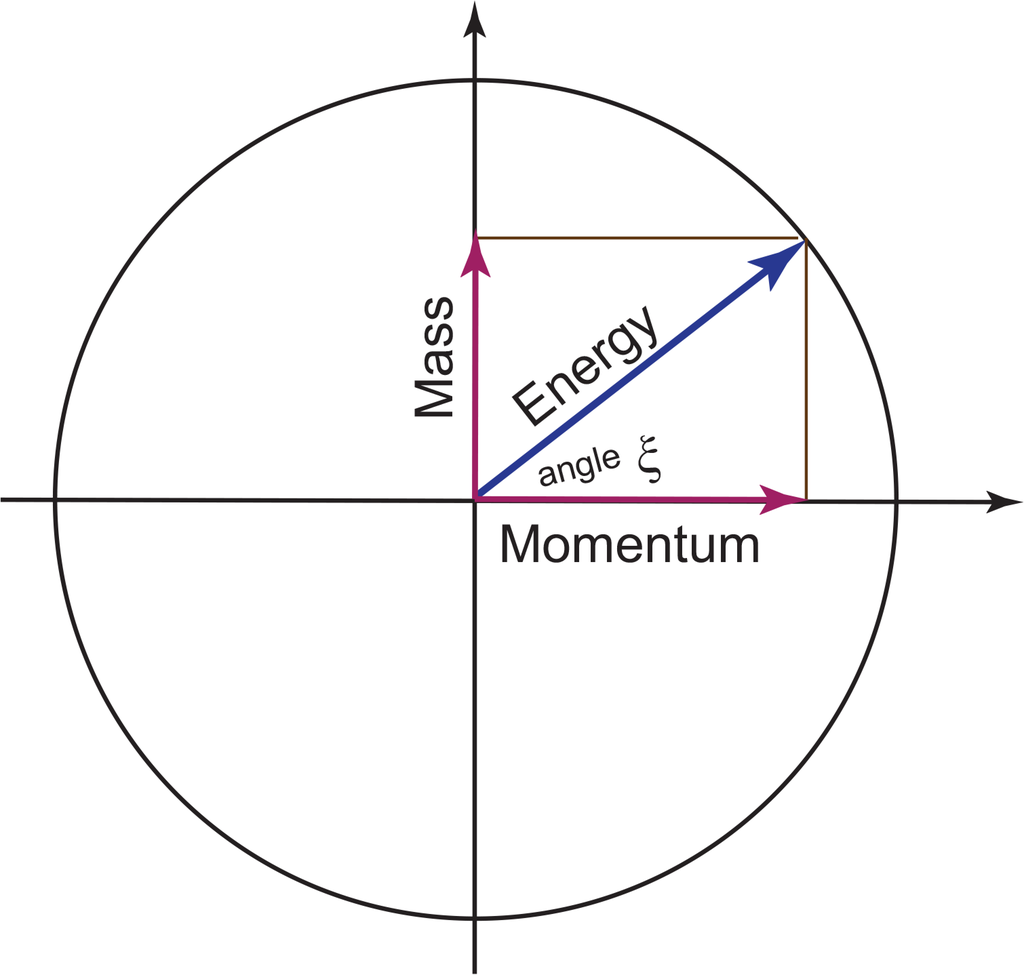
Within the framework of the Lorentz group, it is possible, by making an excursion to infinite momentum where the mass hyperbola coincides with the light cone, to then come back to the desired point. On the other hand, the mass formula of Equation (151) allows us to go there directly. The decoherence mechanism of the coherency matrix makes this possible.
7. Small-Mass and Massless Particles
We now have a mathematical tool to reduce the mass of a massive particle from its positive value to zero. During this process, the Lorentz-boosted rotation matrix becomes a gauge transformation for the spin-1 particle, as discussed Section 5.2. For spin-1/2 particles, there are two issues.
It was seen in Section 5.2 that the requirement of gauge invariance lead to a polarization of massless spin-1/2 particle, such as neutrinos. What happens to anti-neutrinos?
There are strong experimental indications that neutrinos have a small mass. What happens to the E(2) symmetry?
7.1. Spin-1/2 Particles
Let us go back to the two-by-two matrices of Section 5.4, and the two-by-two D matrix. For a massive particle, its Wigner decomposition leads to
Since the Lie algebra of SL(2, c) is invariant under the sign change of the Ki matrices, we can consider the “dotted” representation, where the system is boosted in the opposite direction, while the direction of rotations remain the same. Thus, the Wigner decomposition leads to
When the particle mass becomes very small,
When the particle mass becomes zero, they become
For neutrinos,
It was noted in Section 5.2 that the triangular matrices of Equation (160) perform gauge transformations. Thus, for Equations (161) and (162) the requirement of gauge invariance leads to the polarization of neutrinos. The neutrinos are left-handed while the anti-neutrinos are right-handed. Since, however, nature cannot tell the difference between the dotted and undotted representations, the Lorentz group cannot tell which neutrino is right handed. It can say only that the neutrinos and anti-neutrinos are oppositely polarized.
If the neutrino has a small mass, the gauge invariance is modified to
7.2. Small-Mass Neutrinos in the Real World
Whether neutrinos have mass or not and the consequences of this relative to the Standard Model and lepton number is the subject of much theoretical speculation [24,25], and of cosmology [26], nuclear reactors [27], and high energy experimentations [28,29]. Neutrinos are fast becoming an important component of the search for dark matter and dark radiation [30]. Their importance within the Standard Model is reflected by the fact that they are the only particles which seem to exist with only one direction of chirality, i.e., only left-handed neutrinos have been confirmed to exist so far.
It was speculated some time ago that neutrinos in constant electric and magnetic fields would acquire a small mass, and that right-handed neutrinos would be trapped within the interaction field [31]. Solving generalized electroweak models using left- and right-handed neutrinos has been discussed recently [32]. Today these right-handed neutrinos which do not participate in weak interactions are called “sterile” neutrinos [33]. A comprehensive discussion of the place of neutrinos in the scheme of physics has been given by Drewes [30]. We should note also that the three different neutrinos, namely νe, νμ, and ντ, may have different masses [34].
8. Scalars, Four-Vectors, and Four-Tensors
In Sections 5 and 7, our primary interest has been the two-by-two matrices applicable to spinors for spin-1/2 particles. Since we also used four-by-four matrices, we indirectly studied the four-component particle consisting of spin-1 and spin-zero components.
If there are two spin 1/2 states, we are accustomed to construct one spin-zero state, and one spin-one state with three degeneracies.
In this paper, we are confronted with two spinors, but each spinor can also be dotted. For this reason, there are 16 orthogonal states consisting of spin-one and spin-zero states. How many spin-zero states? How many spin-one states?
For particles at rest, it is known that the addition of two one-half spins result in spin-zero and spin-one states. In this paper, we have two different spinors behaving differently under the Lorentz boost. Around the z direction, both spinors are transformed by
Among the bilinear combinations given in Table 8, the following two are invariant under rotations and also under boosts.
Under the dot conjugation, the boost is performed in the opposite direction. Therefore it is the operation of space inversion, and S+ is a scalar while S− is called the pseudo-scalar.
8.1. Four-Vectors
Let us consider the bilinear products of one dotted and one undotted spinor as uu̇, uv̇, u̇v, vv̇, and construct the matrix
The form of Equation (176) for a particle or field with four-components, is given by (V0, Vz, Vx, Vy). The two-by-two form of this four-vector is
Let us go back to the matrix of Equation (180), we can construct another matrix U̇. Since the dot conjugation leads to the space inversion,
Thus, U of Equation (176) and U̇ of Equation (183) used up 8 of the 16 bilinear forms. Since there are two bilinear forms in the scalar and pseudo-scalar as given in Equation (175), we have to give interpretations to the six remaining bilinear forms.
8.2. Second-Rank Tensor
In this subsection, we are studying bilinear forms with both spinors dotted and undotted. In Section 8.1, each bilinear spinor consisted of one dotted and one undotted spinor. There are also bilinear spinors which are both dotted or both undotted. We are interested in two sets of three quantities satisfying the O(3) symmetry. They should therefore transform like
In order to construct the z component in this O(3) space, let us first consider
Next, in order to construct the x and y components, we start with g± as
Furthermore, fz, fx, and fy of Equations (190) and (193) transform like a three-dimensional vector. The same can be said for gi of Equations (190) and (195). Thus, they can grouped into the second-rank tensor
If the system is Lorentz-booted, fi and gi can be computed from Table 8. We are now interested in the symmetry of photons by taking the massless limit. According to the procedure developed in Section 6, we can keep only the terms which become larger for larger values of η. Thus,
Then the tensor of Equation (197) becomes
In order to address this question, let us go back to Equation (191). In the massless limit,
The B+ and E+ are for the photon spin along the z direction, while B− and E− are for the opposite direction. In 1964 [35], Weinberg constructed gauge-invariant state vectors for massless particles starting from Wigner’s 1939 paper [1]. The bilinear spinors uu and and v̇v̇ correspond to Weinberg’s state vectors.
8.3. Possible Symmetry of the Higgs Mechanism
In this section, we discussed how the two-by-two formalism of the group SL(2, c) leads the scalar, four-vector, and tensor representations of the Lorentz group. We discussed in detail how the four-vector for a massive particle can be decomposed into the symmetry of a two-component massless particle and one gauge degree of freedom. This aspect was studied in detail by Kim and Wigner [20,21], and their results are illustrated in Figure 6. This decomposition is known in the literature as the group contraction.
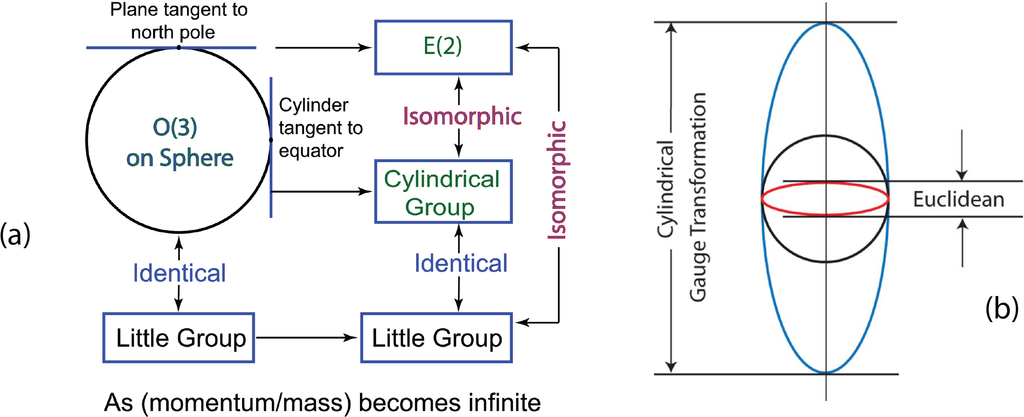
The four-dimensional Lorentz group can be contracted to the Euclidean and cylindrical groups. These contraction processes could transform a four-component massive vector meson into a massless spin-one particle with two spin components, and one gauge degree of freedom.
Since this contraction procedure is spelled out detail in [21], as well as in the present paper, its reverse process is also well understood. We start with one two-component massless particle with one gauge degree of freedom, and end up with a massive vector meson with its four components.
The mathematics of this process is not unlike the Higgs mechanism [36,37], where one massless field with two degrees of freedom absorbs one gauge degree freedom to become a quartet of bosons, namely that of W, Z± plus the Higgs boson. As is well known, this mechanism is the basis for the theory of electro-weak interaction formulated by Weinberg and Salam [38,39].
The word “spontaneous symmetry breaking” is used for the Higgs mechanism. It could be an interesting problem to see that this symmetry breaking for the two Higgs doublet model can be formulated in terms of the Lorentz group and its contractions. In this connection, we note an interesting recent paper by Dée and Ivanov [40].

9. Conclusions
The damped harmonic oscillator, Wigner’e little groups, and the Poincaré sphere belong to the three different branches of physics. In this paper, it was noted that they are based on the same mathematical framework, namely the algebra of two-by-two matrices.
The second-order differential equation for damped harmonic oscillators can be formulated in terms of two-by-two matrices. These matrices produce the algebra of the group Sp(2). While there are three trace classes of the two-by-two matrices of this group, the damped oscillator tells us how to make transitions from one class to another.
It is shown that Wigner’s three little groups can be defined in terms of the trace classes of the Sp(2) group. If the trace is smaller than two, the little group is for massive particles. If greater than two, the little group is for imaginary-mass particles. If the trace is equal to two, the little group is for massless particles. Thus, the damped harmonic oscillator provides a procedure for transition from one little group to another.
The Poincaré sphere contains the symmetry of the six-parameter SL(2, c) group. Thus, the sphere provides the procedure for extending the symmetry of the little group defined within the Lorentz group of three-dimensional Minkowski space to its full Lorentz group in the four-dimensional space-time. In addition, the Poincaré sphere offers the variable which allows us to change the symmetry of a massive particle to that of a massless particle by continuously decreasing the mass.
In this paper, we extracted the mathematical properties of Wigner’s little groups from the damped harmonic oscillator and the Poincaré sphere. In so doing, we have shown that the transition from one little group to another is tangentially continuous.
This subject was initiated by Inönü and Wigner in 1953 as the group contraction [41]. In their paper, they discussed the contraction of the three-dimensional rotation group becoming contracted to the two-dimensional Euclidean group with one rotational and two translational degrees of freedom. While the O(3) rotation group can be illustrated by a three-dimensional sphere, the plane tangential at the north pole is for the E(2) Euclidean group. However, we can also consider a cylinder tangential at the equatorial belt. The resulting cylindrical group is isomorphic to the Euclidean group [20]. While the rotational degree of freedom of this cylinder is for the photon spin, the up and down translations on the surface of the cylinder correspond to the gauge degree of freedom of the photon, as illustrated in Figure 6.
It was noted also that the Bargmann decomposition of two-by-two matrices, as illustrated in Figure 1 and Figure 2, allows us to study more detailed properties of the little groups, including space and time reflection reflection properties. Also in this paper, we have discussed how the scalars, four-vectors, and four-tensors can be constructed from the two-by-two representation in the Lorentz-covariant world.
In addition, it should be noted that the symmetry of the Lorentz group is also contained in the squeezed state of light [14] and the ABCD matrix for optical beam transfers [18]. We also mentioned the possibility of understanding the mathematics of the Higgs mechanism in terms of the Lorentz group and its contractions.
Acknowledgments
In his 1939 paper [1], Wigner worked out the subgroups of the Lorentz group whose transformations leave the four momentum of a given particle invariant. In so doing, he worked out their internal space-time symmetries. In spite of its importance, this paper remains as one of the most difficult papers to understand. Wigner was eager to make his paper understandable to younger physicists.
While he was the pioneer in introducing the mathematics of group theory to physics, he was also quite fond of using two-by-two matrices to explain group theoretical ideas. He asked one of the present authors (Young S. Kim) to rewrite his 1939 paper [1] using the language of those matrices. This is precisely what we did in the present paper.
We are grateful to Eugene Paul Wigner for this valuable suggestion.
Author Contributions
This paper is largely based on the earlier papers by Young S. Kim and Marilyn E. Noz, and those by Sibel Başkal and Young S. Kim. The two-by-two formulation of the damped oscillator in Section 2 was jointly developed by Sibel Başkal and Yound S. Kim during the summer of 2012. Marilyn E. Noz developed the idea of the symmetry of small-mass neutrinos in Section 7. The limiting process in the symmetry of the Poincaré sphere was formulated by Young S. Kim. Sibel Başkal initially constructed the four-by-four tensor representation in Section 8.
The initial organization of this paper was conceived by Young S. Kim in his attempt to follow Wigner’s suggestion to translate his 1939 paper into the language of two-by-two matrices. Sibel Başkal and Marilyn E. Noz tightened the organization and filled in the details.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wigner, E. On unitary representations of the inhomogeneous Lorentz Group. Ann. Math 1939, 40, 149–204. [Google Scholar]
- Han, D.; Kim, Y.S.; Son, D. Eulerian parametrization of Wigner little groups and gauge transformations in terms of rotations in 2-component spinors. J. Math. Phys 1986, 27, 2228–2235. [Google Scholar]
- Born, M.; Wolf, E. Principles of Optics, 6th ed; Pergamon: Oxford, UK, 1980. [Google Scholar]
- Han, D.; Kim, Y.S.; Noz, M.E. Stokes parameters as a Minkowskian four-vector. Phys. Rev. E 1997, 56, 6065–6076. [Google Scholar]
- Brosseau, C. Fundamentals of Polarized Light: A Statistical Optics Approach; John Wiley: New York, NY, USA, 1998. [Google Scholar]
- Başkal, S.; Kim, Y.S. De Sitter group as a symmetry for optical decoherence. J. Phys. A 2006, 39, 7775–7788. [Google Scholar]
- Kim, Y.S.; Noz, M.E. Symmetries shared by the Poincaré Group and the Poincaré Sphere. Symmetry 2013, 5, 233–252. [Google Scholar]
- Han, D.; Kim, Y.S.; Son, D. E(2)-like little group for massless particles and polarization of neutrinos. Phys. Rev. D 1982, 26, 3717–3725. [Google Scholar]
- Han, D.; Kim, Y.S.; Son, D. Photons, neutrinos and gauge transformations. Am. J. Phys 1986, 54, 818–821. [Google Scholar]
- Başkal, S.; Kim, Y.S. Little groups and Maxwell-type tensors for massive and massless particles. Europhys. Lett 1997, 40, 375–380. [Google Scholar]
- Leggett, A.; Chakravarty, S.; Dorsey, A.; Fisher, M.; Garg, A.; Zwerger, W. Dynamics of the dissipative 2-state system. Rev. Mod. Phys 1987, 59, 1–85. [Google Scholar]
- Başkal, S.; Kim, Y.S. One analytic form for four branches of the ABCD matrix. J. Mod. Opt 2010, 57, 1251–1259. [Google Scholar]
- Başkal, S.; Kim, Y.S. Lens optics and the continuity problems of the ABCD matrix. J. Mod. Opt 2014, 61, 161–166. [Google Scholar]
- Kim, Y.S.; Noz, M.E. Theory and Applications of the Poincaré Group; Reidel: Dordrecht, The Netherlands, 1986. [Google Scholar]
- Bargmann, V. Irreducible unitary representations of the Lorentz group. Ann. Math 1947, 48, 568–640. [Google Scholar]
- Iwasawa, K. On some types of topological groups. Ann. Math 1949, 50, 507–558. [Google Scholar]
- Guillemin, V.; Sternberg, S. Symplectic Techniques in Physics; Cambridge University Press: Cambridge, UK, 1984. [Google Scholar]
- Başkal, S.; Kim, Y.S. Lorentz Group in Ray and Polarization Optics. In Mathematical Optics: Classical, Quantum and Computational Methods; Lakshminarayanan, V., Calvo, M.L., Alieva, T., Eds.; CRC Taylor and Francis: New York, NY, USA, 2013; Chapter 9; pp. 303–340. [Google Scholar]
- Naimark, M.A. Linear Representations of the Lorentz Group; Pergamon: Oxford, UK, 1964. [Google Scholar]
- Kim, Y.S.; Wigner, E.P. Cylindrical group and masless particles. J. Math. Phys 1987, 28, 1175–1179. [Google Scholar]
- Kim, Y.S.; Wigner, E.P. Space-time geometry of relativistic particles. J. Math. Phys 1990, 31, 55–60. [Google Scholar]
- Georgieva, E.; Kim, Y.S. Iwasawa effects in multilayer optics. Phys. Rev. E 2001, 64. [Google Scholar] [CrossRef]
- Saleh, B.E.A.; Teich, M.C. Fundamentals of Photonics, 2nd ed; John Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- Papoulias, D.K.; Kosmas, T.S. Exotic Lepton Flavour Violating Processes in the Presence of Nuclei. J. Phys.: Conf. Ser 2013, 410, 012123:1–012123:5. [Google Scholar]
- Dinh, D.N.; Petcov, S.T.; Sasao, N.; Tanaka, M.; Yoshimura, M. Observables in neutrino mass spectroscopy using atoms. Phys. Lett. B 2013, 719, 154–163. [Google Scholar]
- Miramonti, L.; Antonelli, V. Advancements in Solar Neutrino physics. Int. J. Mod. Phys. E 2013, 22, 1–16. [Google Scholar]
- Li, Y.-F.; Cao, J.; Jun, Y.; Wang, Y.; Zhan, L. Unambiguous determination of the neutrino mass hierarchy using reactor neutrinos. Phys. Rev. D 2013, 88, 013008:1–013008:9. [Google Scholar]
- Bergstrom, J. Combining and comparing neutrinoless double beta decay experiments using different 584 nuclei. J. High Energy Phys 2013, 02, 093:1–093:27. [Google Scholar]
- Han, T.; Lewis, I.; Ruiz, R.; Si, Z.-G. Lepton number violation and W′ chiral couplings at the LHC. Phys. Rev. D 2013, 87, 035011:1–035011:25. [Google Scholar]
- Drewes, M. The phenomenology of right handed neutrinos. Int. J. Mod. Phys. E 2013, 22, 1330019:1–1330019:75. [Google Scholar]
- Barut, A.O.; McEwan, J. The four states of the massless neutrino with pauli coupling by spin-gauge invariance. Lett. Math. Phys 1986, 11, 67–72. [Google Scholar]
- Palcu, A. Neutrino Mass as a consequence of the exact solution of 3-3-1 gauge models without exotic electric charges. Mod. Phys. Lett. A 2006, 21, 1203–1217. [Google Scholar]
- Bilenky, S.M. Neutrino. Phys. Part. Nucl 2013, 44, 1–46. [Google Scholar]
- Alhendi, H. A.; Lashin, E. I.; Mudlej, A. A. Textures with two traceless submatrices of the neutrino mass matrix. Phys.Rev. D 2008, 77, 013009.1–013009.1-13. [Google Scholar]
- Weinberg, S. Photons and gravitons in S-Matrix theory: Derivation of charge conservation and equality of gravitational and inertial mass. Phys. Rev 1964, 135, B1049–B1056. [Google Scholar]
- Higgs, P.W. Broken symmetries and the masses of gauge bosons. Phys. Rev. Lett 1964, 13, 508–509. [Google Scholar]
- Guralnik, G.S.; Hagen, C.R.; Kibble, T.W.B. Global conservation laws and massless particles. Phys. Rev. Lett 1964, 13, 585–587. [Google Scholar]
- Weinberg, S. A model of leptons. Phys. Rev. Lett 1967, 19, 1265–1266. [Google Scholar]
- Weinberg, S. Quantum Theory of Fields, Volume II, Modern Applications; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Dée, A.; Ivanov, I.P. Higgs boson masses of the general two-Higgs-doublet model in the Minkowski-space formalism. Phys. Rev. D 2010, 81, 015012:1–015012:8. [Google Scholar]
- Inönü, E.; Wigner, E.P. On the contraction of groups and their representations. Proc. Natl. Acad. Sci. USA 1953, 39, 510–524. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).