Symmetry Adapted Assur Decompositions
Abstract
: Assur graphs are a tool originally developed by mechanical engineers to decompose mechanisms for simpler analysis and synthesis. Recent work has connected these graphs to strongly directed graphs and decompositions of the pinned rigidity matrix. Many mechanisms have initial configurations, which are symmetric, and other recent work has exploited the orbit matrix as a symmetry adapted form of the rigidity matrix. This paper explores how the decomposition and analysis of symmetric frameworks and their symmetric motions can be supported by the new symmetry adapted tools.1. Introduction
Assur decompositions of mechanisms date back to the work of the engineer, Leonid Assur [1], as a tool to simplify the analysis and synthesis of mechanisms. These techniques are widely used in the kinematical community. Several recent mathematical papers have reworked this approach using tools from rigidity theory, extending results from the plane to three-space (as well as higher d-dimensional space) and providing algorithms for decomposing pinned isostatic frameworks into these minimal components [2–6]. Other recent papers have developed mathematical tools and algorithms to analyze the behaviour of symmetric frameworks [7–10]. Given the examples of symmetric mechanisms, with fully symmetric motions, it is natural to consider how the symmetry-adapted tools can be used to decompose symmetric mechanisms for analysis, for synthesis and for control of these mechanisms.
Figure 1 shows two common mechanisms. The Stewart Platform of Figure 1a–c is a pinned isostatic structure, which is widely studied in mechanical engineering and robotics, and has appeared in previous papers on symmetry and rigidity [11,12]. The symmetry analysis adds further information about when coordinated drivers give a fully symmetric motion. The Grab Bucket (see, for example, ([13], p. 270)) depicted in Figure 1d is a common machine, which can be analyzed as a plane structure (see Section 6); this structure is pinned with mirror symmetry and does not fit the previous work on Assur decompositions of plane mechanisms [2,3].
We will apply the techniques developed for isostatic pinned graphs (which generate square matrices) to orbit rigidity matrices, which have independent rows and maximal rank among symmetry regular configurations. Consider the pinned framework in Figure 2a. Although this has the graph of a generically rigid framework in three-space, with the symmetry of the two mirrors, generating a dihedral symmetry group, the inner points not on the ground all move continuously, preserving this symmetry (b). In mechanical engineering, one can ask which drivers (say pistons) can be inserted to control this motion. Figure 2c shows one set of drivers, which, if they expand in a synchronised way, drive the framework along the path of the symmetric motion. The graph of this extended framework, or symmetric scheme, is generically redundant, but in the symmetry analysis of the associated orbit matrix, this is minimally rigid for symmetric motions, or -isostatic.
In our context, given a symmetry group , we can consider a framework that is minimally rigid for symmetric motions or pinned -isostatic (Figures 1, 2c and 3a). Graphs that are -symmetric and minimal pinned -isostatic will be called -Assur. Selecting any orbit of edges (i.e., each edge together with all its symmetric copies) under the action of the symmetry group as coordinated drivers will now generate a symmetric motion. There is a residual question whether this is the only resulting motion; and we will return to such questions below.
Overall, the paper extends the basic techniques of Assur decompositions and the impact of selected drivers to a new context, whenever the associated pinned orbit matrix is square and full rank. This analysis confirms that, if the underlying graph is also pinned isostatic, we get the equivalent Assur decomposition to an analysis on the underlying graph, confirming how symmetric orbits of drivers can drive symmetric motions. The symmetry analysis is simpler, because the group-labeled quotient graph (also called gain graph) and the resulting algebra of the orbit matrix are smaller. The symmetry-based analysis also extends other structures where the underlying graph is not pinned isostatic, extending the insight of Assur decompositions to new mechanisms and posing some new possibilities for the synthesis of mechanisms with symmetric motions.
We note that gain graphs have appeared in a number of papers on rigidity, whether the term gain graph was used explicitly or not [8,12,14–18], but were originally introduced by Zaslavsky, whose survey [19] is a great source of information.
We finish the introduction by outlining the paper.
In Section 2, we review the key concepts and definitions on pinned frameworks, Assur graphs and symmetric frameworks.
In Section 3, we develop combinatorial conditions on the pinned -gain graph that ensure -isostaticity.
In Section 4, we consider the broad class of “pinned -isostatic graphs”. With this square invertible pinned orbit matrix, we are guaranteed an appropriate set of directions on the edges, of out-degree equal to the number of columns of that vertex in this pinned orbit matrix. Any such -directed orientation gives a strongly-connected directed graph decomposition, and the components, along with their outgoing edges, are the -Assur graphs.
Section 5 examines the special subclass, where the underlying graph is also generically isostatic and remains isostatic at almost all -symmetric configurations. This extra assumption allows us to map between the d-Assur decomposition and the -Assur decomposition.
Section 6 examines examples of other types of pinned -isostatic frameworks, where the underlying graph is not pinned isostatic, but redundant and rigid, or is flexible. In those cases, only the -Assur decomposition is possible, and this new decomposition of the underlying graph provides additional insight for analysis and synthesis.
In the final section, we outline some extensions of our work based on the philosophy of applying the decomposition techniques to constraint systems that generate square matrices (Section 7).
2. Background
In this section, we recap relevant ideas from the literature on pinned frameworks, Assur graphs and symmetric frameworks.
2.1. Pinned Frameworks
We set Ĝ =(I, P ; E), where Ĝ is the (finite simple) graph with vertex set I ∪ P and edge set E. Vertices in I are referred to as inner and vertices in P are referred to as pinned. A pinned framework (Ĝ, p) is the combination of a pinned graph Ĝ with a map p : I ∪ P → ℝd. For simplicity, we will denote p(v) by pv for v ∈ I or P (Figures 1a,d, 2c and 3a). We refer to p as a configuration.
For a pinned framework (Ĝ, p) in ℝd, we define the pinned rigidity matrix to be the |E|× d|I| matrix with one row per edge and d columns per inner vertex as follows:
In the matrix, the displayed rows correspond to edges ij and ik where i, j ∈ I and k ∈ P. Unlike the standard rigidity matrix, note that the pinned rigidity matrix only has columns for inner vertices.
We call solutions U to the equation R(Ĝ, p) × UT =0 pinned infinitesimal motions of (Ĝ, p). If the only such motion is the zero motion then (Ĝ, p) is said to be pinned infinitesimally rigid. Equivalently (Ĝ, p) is pinned infinitesimally rigid if rank R(Ĝ, p)= d|I|. Moreover, (Ĝ, p) is pinned d-independent if the rows of R(Ĝ, p) are linearly independent and (Ĝ, p) is pinned d-isostatic if (Ĝ, p) is pinned infinitesimally rigid and pinned d-independent.
A pinned self-stress ω is an assignment of real weights to the edges of Ĝ, such that the following equilibrium condition holds:
For a given pinned graph Ĝ, let p vary over all of ℝd(|I|+|P|). For all q in an open subset U, R(Ĝ, q) has maximal possible rank. Any pinned framework (Ĝ, p) that achieves this rank is said to be regular. More strongly, a pinned framework is generic if the coordinates of the vertices, inner and pinned, form an algebraically independent set over ℚ.
We refer the reader to [2–4,6] for more detailed definitions and discussions on pinned frameworks.
2.2. Assur Decompositions
In this subsection, we review Assur decompositions of pinned d-isostatic frameworks. The reader can refer to [4] for further details, equivalent definitions and more examples.
A pinned graph Ĝ is pinned d-isostatic if there exists a pinned d-isostatic realisation of Ĝ in d-space. A d-Assur graph (in mechanical engineering, also known as an Assur group) is a minimal pinned d-isostatic graph, where minimal means that no proper subgraph (containing at least one inner vertex) is also a pinned d-isostatic graph. A d-directed orientation of a pinned graph Ĝ is an assignment of directions to the edges of Ĝ, such that every inner vertex has out-degree exactly d and every pinned vertex (ground vertex) has out-degree exactly zero (a sink in the directed graph). In ([4], Theorem 3.6), the natural necessary counting conditions were given for a pinned graph to be isostatic, and it was noted that any graph satisfying these counts has a d-directed orientation. However, for all d, there exist examples where a pinned graph has a d-directed orientation, but is not pinned d-isostatic.
Starting with a pinned d-isostatic graph Ĝ, a key initial step in the Assur decomposition is to generate a d-directed graph of Ĝ (for instance, via the pebble game [5,6]), where edges are directed toward the ground. The d-directed graph is then decomposed into its strongly connected components (i.e., maximally strongly connected subgraphs) [4]. More specifically, a strongly connected component decomposition of a pinned d-directed graph of Ĝ condenses all pins into a sink (ground) vertex, identifies the strongly connected components and condenses each such component to single vertices to obtain a directed acyclic graph and a partial order. Note that if any multiple edges arise during this identification process, we discard additional copies.
Two orientations of a graph are equivalent if corresponding vertices have the same out-degree. In [4], it was noted that equivalent orientations differ at most by reversing the orientations of cycles. This implies the following result:
Corollary 1 ([4]). Given two equivalent orientations of a graph, the strongly connected components are the same in both orientations.
An Assur decomposition is a decomposition of a pinned d-isostatic graph, where the individual components are the d-Assur graphs. This is exactly the strongly connected component decomposition. Each strongly connected component and its outgoing edges with ends becoming pins are the d-Assur components (see Figure 3).
In [4], additional connections and equivalent properties of d-Assur decompositions were presented via a lower triangular block decomposition of the pinned rigidity matrix, by permuting rows and columns following the partial order (see Theorem 3).
For any pinned isostatic graph Ĝ, the pinned rigidity matrix R(Ĝ, p) will be square. If it is not possible to permute the rows and columns into lower triangular blocks, then we say that R(Ĝ, p) is indecomposable. In general, we consider a lower triangular block decomposition of the rigidity matrix R(Ĝ, p), and hence, the graph Ĝ, by permuting the rows and columns into indecomposable blocks. This is illustrated in Figure 3.
If e is an edge in a pinned isostatic graph Ĝ, then we call e a driver in Ĝ −e. The terminology is used by mechanical engineers who often use such edges to drive motions, that is, they remove this edge, and hence, its length is allowed to change. This drives a unique motion in the framework (e.g., a piston) and, hence, can easily be controlled. Such motions can be understood by looking at the d-Assur decomposition.
We say that a d-Assur graph is strongly d-Assur if the infinitesimal motion created by removing any edge has a non-trivial velocity at each vertex. For d =2, this coincides ([4], Proposition 4.2) with the definition of two-Assur, but for d ≥ 3, it is an inequivalent notion (see [4] for examples that are three-Assur, but not strongly three-Assur). These examples are based on the fact that for d ≥ 3, the length of a non-edge may be determined by a non-rigid component (i.e., the lack of a combinatorial (counting) characterization of rigidity).
Removal of an edge (driver) from a component of a strongly d-Assur graph makes every vertex in every component above (in the partial order; see below) go into motion and keeps every component below fixed. Note, however, that removal of an edge from a component of a d-Assur graph may leave entire components above fixed.
We finish this subsection with a key result on d-Assur graphs. Since we will provide a different style of proof, to [4], for the symmetric analogue in Section 4, we first prove a proposition that allows us to state Theorems 3.3 and 3.4 in [4] in a single theorem.
We will often use the word ground as a colloquial term to refer to the set of pinned vertices.
Given a maximal lower triangular block decomposition of R(Ĝ, p), the induced directed block graph has one vertex per block plus a vertex Z for the ground. There is a directed block graph edge if there is a directed edge (A, B) that goes from the block A to a block B, which is upper left from it, i.e., if there is an edge with start vertex in A and end vertex in B. There is a directed edge (A, Z) to the ground if there is an edge in block A, which goes to a pinned vertex. See Figure 3c,d.
Proposition 2. Given a pinned isostatic graph Ĝ in dimension d and a maximal lower triangular block decomposition of R(Ĝ, p), the induced block graph is an acyclic directed graph D, with sink Z (the ground). Moreover the directions induce a partial order on the vertices of D.
Proof. The block-decomposition is lower triangular, so there is a linear order of the blocks by the position of their columns. Place Z at the bottom of the linear order. Observe that all directed block edges point down this linear order, because of the block lower-triangular pattern of the matrix. Therefore, there cannot be a cycle in this graph. The graph has a partial order on its vertices, and the linear order of the blocks is an extension of this partial order.
Remark 1. The lower triangular block decomposition is not unique. Given the partial order, any linear extension produces a lower-triangular block decomposition. Any two blocks that are incomparable in the partial order can be switched in the linear order. They can also be switched in the block decomposition by permuting the corresponding rows and columns.
Theorem 3 ([4]). For a pinned d-isostatic graph Ĝ and any d-directed orientation of Ĝ, the following are equivalent:
the d-Assur decomposition of Ĝ;
the decomposition into strongly connected components associated with the d-directed orientation;
the induced block graph from a maximal block-triangular decomposition of the pinned rigidity matrix.
We call the shared partial order from the three equivalent decompositions of Theorem 3 the d-Assur block graph.
2.3. Symmetric Graphs
For a finite simple graph G =(V, E), we let Aut(G) denote the automorphism group of G. An action of a group on G is a group homomorphism θ : → Aut(G). An action θ is called free on the vertices (resp., edges) if θ(x)(v) ≠ v for every v ∈ V (resp., θ(x)(e) ≠ e for every e ∈ E) and every non-trivial element x ∈ . We say that a graph G is -symmetric (with respect to θ) if acts on G via θ.
Throughout the paper, we will omit to specify the action θ if it is clear from the context. In that case, we also denote θ(x)(v) by xv.
For an -symmetric graph G =(V, E), the quotient graph G/ is a multigraph, whose vertex set is the set V/ of vertex orbits and whose edge set is the set E/ of edge orbits. Note that an edge orbit may be represented by a loop in G/ (see Figure 4).
While several distinct graphs may have the same quotient graph, a gain labeling makes this relation one-to-one if the underlying group action is free on V [12]. To see this, choose a representative vertex v from each vertex orbit under the group action. Then, each orbit is of the form v = {xv | x ∈}. If the action is free, an edge orbit connecting u and v in G/ can be written as {{xu, xyv}| x ∈} for a unique y ∈. We then orient the edge orbit from u to v in G/ and assign to it the gain y. This yields the quotient -gain graph (G/,ψ) of G, which is unique up to choices of representative vertices. The map ψ is also called the gain function of (G/,ψ). Note that a gain graph is a directed graph, but its orientation is only used as a reference orientation and may be changed, provided that we also modify ψ, so that if an edge has gain x in one orientation, then it has gain x−1 in the other direction.
The map c : G → H defined by c(xv)= v and c({xu, xψ(e)v})=(u, v) is called the covering map. In order to avoid confusion, throughout the paper, a vertex or an edge in a quotient gain graph H is denoted with the mark tilde (e.g., ṽ or ẽ) and the vertex and edge set of H is denoted by Ṽ and Ẽ, respectively. Then, the fiber c−1(ṽ) of a vertex ṽ ∈ Ṽ and the fiber c−1(ẽ) of an edge ẽ ∈ Ẽ coincide with a vertex orbit and an edge orbit, respectively, in G. For simplicity, the gain ψ(ẽ) of an edge ẽ ∈ Ẽ will sometimes also be denoted by ψẽ.
Finally, a graph Ĝ =(I, P ; E), where I is the set of inner vertices and P is the set of pinned vertices, is called -symmetric (with respect to θ) if for every x ∈, θ(x) maps pinned vertices to pinned vertices and inner vertices to inner vertices. The construction of the quotient -gain graph of Ĝ is of course completely analogous to the construction described above.
2.4. Symmetric Frameworks and Orbit Matrices
In this subsection, we introduce the basic terminology for symmetric frameworks and summarise the key results concerning “symmetry-forced” rigidity of frameworks. We begin with a discussion of “unpinned” symmetric frameworks.
A symmetry operation of a framework (G, p) in ℝd, where G =(V, E), is an isometry x of ℝd, such that for some αx ∈ Aut(G),we have x p(v)) = p(αx(v)) for all v ∈ V. The set of all symmetry operations of a framework (G, p) in ℝd forms a group under composition, called the point group of (G, p). Clearly, we may assume wlog that the point group of a framework is always a symmetry group, i.e., a subgroup of the orthogonal group O(ℝd).
We use the Schoenflies notation for the symmetry operations and symmetry groups in dimensions two and three considered in this paper, as this is one of the standard notations in the literature about symmetric structures (see [10,20–22], for example). The relevant groups in this paper are s, n and nv. s is a group of order two generated by a single reflection, n, n ≥ 1, is a cyclic group generated by a rotation Cn about the origin (in the plane) or an axis through the origin (in three-space) by an angle of and nv is a dihedral group that is generated by a rotation n and a reflection (whose reflectional plane contains the rotational axis of n in three-space).
Let be an abstract group and G = (V, E) be an -symmetric graph with respect to an action θ : → Aut(G). Suppose also that acts on ℝd via the homomorphism τ : → O(ℝd). Then, we say that a framework (G, p) is -symmetric (with respect to θ and τ) if:
Note that if (G, p) is -symmetric, then the point group of (G, p) is either equal to τ() or contains τ() as a subgroup [22].
Let H = (Ṽ, Ẽ) be the quotient graph of G with the covering map c : G → H. Then, it is convenient to fix a representative vertex v of each vertex orbit v = {xv : x ∈}, and define the quotient of p to be p̃ : H̃ → ℝd, so that there is a one-to-one correspondence between p and p̃ given by p(v)= p̃ (c(v)) for each representative vertex v.
An infinitesimal motion u : V → ℝd of an -symmetric framework (G, p) (with respect to θ and τ) is called fully -symmetric if:
We say that (G, p) is -symmetric (infinitesimally) rigid if every fully -symmetric infinitesimal motion of (G, p) is trivial (i.e., if it corresponds to a translation or rotation (or a combination of those) of (G, p))[10,12]. Moreover, the framework (G, p) is called -isostatic if it is minimally -symmetric infinitesimally rigid, i.e.,if (G, p) is -symmetric infinitesimally rigid and has no non-zero -symmetric self-stress. To simplify the detection of fully -symmetric motions and self-stresses of (G, p), the orbit rigidity matrix of (G, p) was introduced in [10].
Definition 4 (Schulze and Whiteley [10]). Let (G, p) be an -symmetric framework with respect to θ and τ, where G = (V, E) and θ acts freely on V. Further, let (H, ψ) be the quotient -gain graph of G, where H = (Ṽ, Ẽ). For each edge ẽ = (ũ, ṽ) ∈ Ṽ, the orbit (rigidity) matrix (H, ψ, p̃) of (G, p) has the following corresponding (d|Ṽ|-dimensional) row vector:
See also Example 2 in Section 3 for an example of an orbit matrix (for a pinned framework).
Remark 2. When the action θ is not free on the vertices of G, the number of columns in (H, ψ, p̃), corresponding to vertices that are fixed by non-trivial symmetry operations, are reduced accordingly. pecifically, let p(u) be a joint of the -symmetric framework (G, p) (with respect to θ and τ), let x be a symmetry operation in , which fixes p(u) (i.e., τ(x)(p(u)) = p(u)), and let Fx be the linear subspace of ℝd, which consists of all points a ∈ ℝd with τ(x)(a) = a. (In the applied sciences, the space Fx is sometimes also referred to as the symmetry element of x [20].) Then, the joint p(u) of any -symmetric framework (G, p) (with respect to θ and τ) must lie in the linear subspace
For example, if a joint p(u) of a s-symmetric framework (G, p) in three-space is fixed by the reflection s in s, and the symmetry element (reflection plane) Fs of s is the xy-plane, then the orbit matrix has only two columns corresponding to p(u) (since Fid ∩ Fs = ℝ3 ∩ Fs = Fs) and the two entries of each row are obtained by deleting the third coordinate of the corresponding row vectors p̃(ũ) − τ(ψẽ)p̃(ṽ) in Equation (3).
The following result summarises the key properties of the orbit matrix.
Theorem 5 ([10,12]). Let (G, p) be an -symmetric framework (with respect to θ and τ), and let (H, ψ) be the quotient -gain graph of G. Then, the solutions to (H, ψ, p̃)u = 0 are isomorphic to the space of fully -symmetric infinitesimal motions of (G, p). Moreover, the solutions to ωT(H, ψ, p̃) = 0 are isomorphic to the space of fully -symmetric self-stresses of (G, p).
We say that (G, p) is -regular if the orbit matrix (H, ψ, p̃) has maximal rank among all -symmetric realisations of G (see also [10,12]). Clearly, all -regular realisations of a given graph share the same -symmetric infinitesimal rigidity properties. Moreover, it was shown in [7,9] that for -regular frameworks, the existence of a non-trivial fully -symmetric infinitesimal motion guarantees the existence of a symmetry-preserving mechanism. Thus, for -regular frameworks, -symmetric infinitesimal rigidity and -symmetric (finite) rigidity are equivalent, and hence, a graph G is called -rigid (-isostatic) if there exists a -regular realisation of G, which is -symmetric (infinitesimally) rigid (-isostatic).
For -rigidity in the plane, there are Laman type theorems for all groups, except the “even order” dihedral groups of the form 2nv, n ≥ 1 [8,16]. To state these theorems, we need the following definitions (see also [8,12]).
Let (H, ψ) be an -gain graph with H = (Ṽ, Ẽ). A cycle in H is called balanced if the product of its edge gains is equal to the identity. (If is an additive group, we take the sum instead of the product.) More precisely, a cycle of the form ṽ1, ẽ1, ṽ2, ẽ2, ṽ3,..., ṽk, ẽk, ṽ1, is balanced if , where sign(ẽi) = 1 if ẽi is directed from ṽi to ṽi+1, and sign(ẽi) = −1 otherwise.
We say that an edge subset F ⊆ Ẽ is balanced if all cycles in F are balanced; otherwise, it is called unbalanced.
Definition 6. Let (H, ψ) be an -gain graph with H = (Ṽ, Ẽ), and let k, ℓ, m be nonnegative integers with m ≤ ℓ. (H, ψ) is called (k, ℓ, m)-gain-sparse if:
|F |≤ k|V (F)|− ℓ for any nonempty balanced F ⊆ Ẽ;
|F |≤ k|V (F)|− m for any nonempty F ⊆ Ẽ.
Example 1. Consider, for example, the gain-graph H shown in Figure 4b. H = (Ṽ, Ẽ) is (2, 3, 1)-gain tight, since |Ẽ| =5=2|Ṽ|− 1, and all the conditions in Definition 6 are satisfied. However, H is not (2, 3, 2)-gain sparse, for example, since there exists a loop at vertex one with gain C2, and for this subgraph, we have |F | =1 > 0=2|V (F)|− 2.
For -symmetric frameworks in the plane, where the action θ is free on the vertex set, we have the following elegant characterizations of -symmetric rigid graphs for the groups s and n.
Theorem 7 (Malestein and Theran [16], Jordán et al. [8]). Let be s or n for some n ≥ 2, τ : ℤ/nℤ → be a homomorphism, G = (V, E) be an -symmetric graph with θ : → Aut(G), where θ acts freely on V, and (G, p) be a two-dimensional -regular framework with respect to θ and τ. Then, (G, p) is -isostatic if and only if the quotient -gain graph (H, ψ) is (2, 3, 1)-gain-tight.
Note that the condition |F |≤ 2|V (F)|− 1 for any nonempty F ⊆ Ẽ in the quotient graph H = (Ṽ, Ẽ) in Theorem 7 reflects the fact that there is only a one-dimensional space of -symmetric trivial infinitesimal motions for the groups s and n in dimension two. In general, for any point group in dimension two or three, the dimension of the space of trivial -symmetric infinitesimalmotions can easily be read off from the character table of [20].
A similar, but slightly more complicated characterization of -rigid graphs for dihedral groups of the form (2n+1)v, n ≥ 1, was also established in [8]. However, for dihedral groups of the form 2nv, n ≥ 1, a combinatorial characterization of -rigid graphs in the plane is not known. For example, it was shown in [8] that Bottema’s mechanism (a realisation of the complete bipartite graph K4,4 with 2v symmetry in the plane) is falsely predicted to be 2v-symmetric rigid by the matroidal counts for the orbit matrix.
Remark 3. For -symmetric graphs, where the action θ is not free on the vertex set, no combinatorial characterizations for -rigidity have been derived yet. This is because for such graphs, the structure of the orbit matrix and the corresponding combinatorial counts become significantly more messy (recall Remark 2). However, in principle, we do not expect any major new difficulties to arise when making the extension of Theorem 7 to symmetric graphs with non-free group actions.
Clearly, in three-space, no combinatorial characterizations for -rigidity are known, since the problem of finding a combinatorial characterisation of rigid graphs (without symmetry) in dimensions d ≥ 3 remains a long-standing open problem in discrete geometry [23].
3. Symmetric Pinned Frameworks
Based on the discussion in the previous section, we are now ready to introduce the key concepts of pinned -isostatic graphs and -Assur graphs.
3.1. Basic Definitions
Let Ĝ = (I, P ; E) be a -symmetric pinned graph (with respect to the action θ : → Aut(G)), and let Ĥ = (Î, P̂; Ê) be the associated quotient -gain graph. Note that we always assume |P| > 0. Given a pinned -symmetric realisation of Ĝ (with respect to the action θ and the homomorphism τ : → (ℝd)), we define the (pinned) orbit matrix pin(Ĥ, ψ, p̃) of (Ĝ, p) as follows. There are d columns for every inner vertex ṽ ∈ Î and no columns for any pinned vertex. For an edge (ũ, ṽ) with ũ, ṽ ∈Î, there is a row in the pinned orbit matrix exactly like in the orbit matrix (see Definition 4). Moreover if an edge (ũ, ṽ) has ũ∈Î and ṽ∈ P̂, then the corresponding row in pin(Ĥ, ψ, p̃) is:
All solutions U to pin(Ĥ, ψ, p̃) × UT = 0 are called pinned fully -symmetric infinitesimal motions of (Ĝ, p). If the only such motion is the zero motion, then (Ĝ, p) is said to be pinned -symmetric infinitesimally rigid. Equivalently, (Ĝ, p) is pinned -symmetric infinitesimally rigid if rank pin(Ĥ, ψ, p̃) = d|Î|.
A pinned fully -symmetric self-stress of (Ĝ, p) is a pinned self-stress ω of (Ĝ, p) with the property that ωe = ωf whenever e and f belong to the same edge orbit under the action of θ. Note that it follows immediately from ([10], Theorem 8.3) that there exists a one-to-one correspondence between the pinned fully -symmetric self-stresses of (Ĝ, p) and the row dependencies of pin(Ĥ, ψ, p̃), i.e., the solutions ω to ωT pin(Ĥ, ψ, p̃) = 0. The framework (Ĝ, p) is called pinned -independent if the rows of pin(Ĥ, ψ, p̃) are linearly independent and (Ĝ, p) is pinned -isostatic if (Ĝ, p) is both pinned -independent and pinned -symmetric infinitesimally rigid.
Finally, (Ĝ, p) is called pinned -regular if pin(Ĥ, ψ, p̃) has maximal rank among all pinneds -symmetric realisations of Ĝ. Included in this definition is a level of regularity for the placement of the pinned vertices that may not be apparent in some of the figures. This arises since symmetry can, for example, force an orbit of vertices in a framework in three-space to be coplanar. There is some subtlety to analysing singular choices of pinning, which we do not pursue in this paper.
The following lemma gives several equivalent ways of defining a pinned -isostatic graph.
Lemma 8. Let Ĝ be a -symmetric pinned graph (with respect to θ and τ), and let Ĥ = (Î, P̂;Ê) be the corresponding quotient -gain graph. Further, suppose the action θ is free on the vertices of Ĝ. Then, the following are equivalent:
There exists a pinned -isostatic realisation of Ĝ in d-space;
Every -regular pinned realisation of Ĝ in d-space is -isostatic;
Pinned -regular realisations of Ĝ are pinned -rigid and |Ê| = d|Î|;
Pinned -regular realisations of Ĝ are pinned -independent and |Ê| = d|Î|.
Observe that, for any pinned -isostatic framework (Ĝ, p), the orbit matrix pin(Ĥ, ψ,p̃) is square and invertible. Note that this remains true even if θ does not act freely on the vertices of Ĝ.
Any -symmetric graph Ĝ (or, equivalently, its quotient -gain graph) satisfying the equivalent conditions in Lemma 8 is pinned -isostatic. Analogous to the non-symmetric situation, a -Assur graph is a minimal pinned -isostatic graph. Further, a -Assur graph is strongly -Assur if the removal of any edge of its quotient -gain graph (i.e., the removal of an edge orbit in the covering graph) puts all inner vertices of the covering graph into (a symmetry-preserving) motion.
Example 2. Consider the two-dimensional 3-symmetric (with respect to θ and τ) pinned framework (Ĝ, p) and the corresponding quotient 3-gain graph of Ĝ depicted in Figure 3 (and Figure 6). Let τ : 3 → (ℝ2) be the homomorphism defined by. Suppose pw = (−2, 3), pu = (−1, 2) and. Then, the pinned orbit matrix pin(Ĥ, ψ, p̃) of (Ĝ, p) is:
3.2. Counting Conditions for Pinned -isostatic Graphs
In this subsection, we prove an analogue of Theorem 3.6 in [4] giving necessary counting conditions for a pinned -symmetric graph, under a group action that is free on the vertices, to be pinned -isostatic. We then consider, for plane symmetry groups, when these counts are sufficient; that is, for the groups in Theorem 7, we prove analogues of ([2], Theorem 4).
We begin with an observation that follows immediately from Lemma 8 and Theorem 5. Before the statement, we note that a stronger conclusion, including information about the gains, is possible using the argument in [8]. We will not need this stronger version.
Theorem 9. Let be a symmetry group in dimension d, and let Ĝ be a pinned -symmetric graph (with respect to an action θ) with quotient -gain graph Ĥ = (Î, P̂;Ê). Further, let triv denote the dimension of the space of fully -symmetric trivial infinitesimal motions. Suppose θ acts freely on the vertices of Ĝ. Then, if Ĝ is pinned -isostatic, the following hold:
|Ê| = d|Î|;
every subgraph H′ = (I′,P′; E′) of Ĥ satisfies |E′|≤ d|I′|.
every subgraph of Ĥ with no pinned vertices is (d, ,triv)-gain sparse.
Proof. By the definition of pinned -isostatic, we have |Ê| = d|Î|. If either of the other two conditions fails, then any -symmetric realisation of Ĝ has a pinned fully -symmetric self-stress.
For example, if is a symmetry group s in dimension three, then trivs =3 and every subgraph of Ĥ with no pinned vertices must be (3, 6, 3)-gain sparse. Similarly, if is a symmetry group n, n ≥ 2,in dimension three, then triv s = 2 and every subgraph of Ĥ with no pinned vertices must be (3, 6, 2)-gain sparse (see also [10,11,20]).
For the plane symmetry groups in Theorem 7, we have both necessary and sufficient conditions for a pinned symmetric graph to be -isostatic.
Theorem 10. Let be a symmetry group s or n, n ≥ 2, in dimension two, and let Ĝ be a pinned -symmetric graph (with respect to an action θ) with quotient -gain graph Ĥ = (Î, P̂;Ê). Further, suppose θ acts freely on the vertices of Ĝ. Then, Ĝ is pinned -isostatic if and only if the following hold:
|Ê| =2|Î|;
every subgraph of Ĥ with no pinned vertices is (2, 3, 1)-gain sparse;
every subgraph H′ = (I′,P′; E′) of Ĥ with P′ ≠ ∅ satisfies |E′|≤ 2|I′|.
Proof. Replace the pinned vertices P̂ of Ĥ with the quotient -gain graph of a non-pinned -isostatic graph with vertex set P̂ and edge set F. (For example, if P̂ contains only a single vertex ṽ, then we attach a loop with a non-trivial gain to ṽ.) Let H* be the (non-pinned) quotient -gain graph with vertex setÎ ∪ P̂ and edge setÊ ∪ F. Then, by Theorem 7, the covering graph of H* is -isostatic if and only if the conditions in Theorem 10 are satisfied. This gives the result.
Any pinned graph Ĝ satisfying the counts in the first part of Theorem 10 is said to be pinned (2, 3, 1)-gain-tight.
Note that we can easily obtain analogous necessary counts for pinned -symmetric graphs to be pinned -isostatic in the case where the action θ is not free on the vertices. For example, for a symmetry group n which acts freely on the inner vertices of a pinned n-symmetric graph Ĝ, but not freely on the pinned vertices of Ĝ (i.e.,any n-symmetric framework has a pinned vertex at the origin), we obtain the necessary condition that every subgraph H′=(I′,P′; E′) of the quotient n-gain graph Ĥ, which contains the pinned vertex that is fixed by n, must satisfy |E|≤ 2|I |− 1. This is because rotations about the origin are the only fully n-symmetric infinitesimal motions (i.e., trivn = 1), and the fixed pinned vertex does not prevent such a trivial motion.
Similarly, the conditions in Theorem 10 remain unchanged for a group s in the plane, which acts freely on the inner, but not freely on the pinned vertices of a s-symmetric graph, since a pinned vertex removes all fully s-symmetric infinitesimal motions (translations along the mirror), regardless of whether it is fixed by the reflection or not.
We close this section by commenting on non-regular pinning. For non-symmetric frameworks, it is known that the analogue of Theorem 10 holds with arbitrary placement of the pinned vertices [2]. The proof utilises an inductive construction of all two-isostatic graphs. The graphs in Theorem 10 can also be characterised by an inductive construction [8], so we expect that the theorem can be extended to allow arbitrary pinning.
4. Decomposing Pinned -Isostatic Graphs
In Subsection 2.2, we recalled a description of the d-Assur graph decomposition of the pinned d-isostatic graphs that appeared in [4]. In this section, we extend the key results from d-Assur to -Assur graphs and introduce the -Assur decomposition via similar techniques. For any -isostatic graph Ĝ, the pinned orbit matrix pin(Ĥ, ψ, p̃) is square and invertible, and we are assured of getting an appropriate set of directions on the associated gain graph (the out-degree of a vertex is equal to the number of columns of that vertex in the pinned orbit matrix). Any orientation of the gain graph gives a unique strongly-connected directed graph decomposition, whose components with their outgoing edges are the -Assur graphs. We will state this precisely and also introduce strongly -Assur graphs.
One key point the reader should keep in mind is that the essential information for a -Assur decomposition is contained in the quotient graph. In terms of an -Assur decomposition, the group elements assigned to the edges of Ĥ are only relevant in the initial determination of whether the graph Ĝ is -isostatic.
Before we state the main results, we outline the -Assur decomposition informally and illustrate it on some examples.
Let Ĝ be a pinned -isostatic graph with a free group action on the vertices, and let Ĥ be its quotient pinned -gain graph. We first seek a minimal pinned -isostatic subgraph (i.e.,a -Assur graph), where the ground is the bottom layer. This will be above the ground component and is then collapsed into the ground. We then seek another minimal pinned -isostatic subgraph, collapsing it into the ground. This is then repeated until each vertex orbit belongs to some minimal pinned -isostatic subgraph. This is the -Assur decomposition. The -Assur decomposition will be carried out via the decomposition into strongly connected components of the directed gain graph.
An -directed orientation of a pinned -gain graph Ĥ is an assignment of directions to the edges of Ĥ, such that every inner vertex has out-degree exactly dimUp(u) (recall Remark 2) and every pinned vertex has out-degree exactly zero (see Proposition 11). Recall that when acts freely on the edge set, then dimUp(u) is exactly d. The strongly connected components in Ĥ, with its outgoing edges becoming pinned will correspond to the -Assur decomposition of the -directed orientation of a pinned -gain graph Ĥ (Theorem 13).
Recall that there is a one-to-one correspondence between the covering graph and the -gain graph. This implies that there is a one-to-one correspondence between a -Assur component of Ĝ and a -Assur component of Ĥ. In Ĥ, such components are connected, while in Ĝ, one component may consist of |S| disconnected subgraphs (compare Figures 3 and 6). This bijection justifies the terminology “component” for such disconnected subgraphs.
Example 3. Consider the pinned framework shown in Figure 6 with 3-symmetry in the plane. Note that this is the same framework as in Figure 3a. This framework is pinned isostatic in the plane, as well as pinned 3-isostatic. The 3-Assur decomposition of the covering graph is shown in Figure 6b, and the corresponding decomposition of the quotient 3-gain graph is shown in Figure 6d.
Example 4. Consider the pinned two-dimensional framework with s symmetry shown in Figure 7a. Unlike the previous example, the s-Assur decomposition (shown in Figure 7c) is not a tree in this case. Note that the framework in Figure 7a has the correct overall pinned count consisting of 28 edges and 14 inner vertices; however, this graph is not pinned two-isostatic (and not pinned two-rigid), as it has a generically dependent component (the subgraph induced by A, B, C, A′, B′and C′ is overbraced). Alternatively, if we ignore the vertices above this component, we can observe that this component is only attached to the ground via two edges (coloured in orange). Thus, without imposed symmetry, this graph does not have a two-Assur decomposition.
In standard Assur decompositions, to apply the decomposition, and to find the Assur components, the graph Ĝ must be pinned isostatic. However, for symmetric frameworks, even if the original underlying graph Ĝ is flexible or has redundancy, we may still find the symmetry-adapted Assur decomposition.
4.1. Pinned Symmetric Frameworks
Analogous to work in [4], we use the pinned orbit matrix for any pinned -isostatic graph Ĝ to generate the directed quotient -gain graph. Then, we relate the directed gain graph strongly connected component decomposition to a block decomposition of the pinned orbit matrix.
Proposition 11. Let Ĝ be a pinned -isostatic graph in dimension d. Then, there is a -directed orientation of the associated pinned -gain graph Ĥ = (Î, P̂;Ê).
Proof. By Theorem 9, we know that |Ê| = d|Î| and |Ê ′| ≤ |Î ′| for all subgraphs Ĥ′ of Ĥ. The proposition now follows quickly from a standard result on oriented sparse graphs first proven by Hakimi ([24], Theorem 2) (see also [25], Theorem 1, or [26], Lemma 6).
We remark also that the proof of Theorem 1 in [25] given in [27] reveals an efficient polynomial-time algorithm for obtaining the -directed orientation. The algorithm, being based around reversing directed paths, is similar to the well-known pebble game algorithm [6,28]. Clearly, this algorithm is independent of the dimension, group or action.
Given a maximal lower triangular block decomposition of pin(Ĥ, ψ, p̃), the induced -Assur block graph has one vertex per block plus a vertex Z for the ground. There is a directed block graph edge if there is a directed edge (A, B) that goes from the block A to a block B, which is upper left from it, i.e.,if there is an edge with start vertex in A and end vertex in B. There is a directed edge (A, Z) to the ground if there is an edge in block A, which goes to a pinned vertex. Recall Figure 6 and Example 2.
We now state, without proof, the obvious analogue of Proposition 2 for pinned -isostatic graphs; see also Remark 1.
Proposition 12. Given a pinned -isostatic graph Ĝ and a maximal lower triangular block decomposition of pin(Ĥ, ψ, p̃), the induced block graph is an acyclic directed graph D, with sink Z (the ground). Moreover, the directions induce a partial order on the vertices of D.
Next, we prove one of our main results, giving an extension of Theorem 3.4 in [4], to the symmetric setting.
Theorem 13. Let Ĝ be a pinned -isostatic graph. For any -directed orientation of the quotient -gain graph Ĥ, the following decompositions are equivalent:
the -Assur decomposition of Ĝ;
the decomposition into strongly connected components of the -directed orientation of Ĥ;
the induced block graph from a maximal block-triangular decomposition of pin(Ĥ, ψ, p̃).
Proof. (1) ⇒ (2). Let Ĝ1 be the -Assur component of Ĝ containing the ground, and let Ĥ1 be the corresponding component in Ĥ. By Proposition 11, there is a -directed orientation of Ĥ1. Choose any such orientation and suppose that Ĥ1 is not strongly connected. (Remember that Corollary 1 implies that our choice of -directed orientation is not important.) Now, consider a strongly connected component in Ĥ1 containing the ground, and let be its covering graph. Since Ĥ1 is pinned -isostatic, we have by Theorem 9. Moreover, if this inequality were strict, then the strongly connected component above , i.e., the graph , together with its edges to , would have too many edges, contradicting the fact that Ĥ1 is -isostatic. Thus, . Now, since Ĝ is -isostatic, we know that is -isostatic. This contradicts the minimality of Ĝ1, since . Repeating this argument for subsequent components completes the argument.
(2) ⇒ (3). Consider the strongly connected components containing the ground. With a permutation of rows and a permutation of column vertices, we place the corresponding vertices and edges at the top left of the pinned orbit matrix pin(Ĥ, ψ, p̃). If there are more strongly connected components, then the remaining rows and columns form a second block. Continuing this process for each of the blocks in the acyclic strongly connected component decomposition, we find the desired diagonal matrix block for each component of the decomposition.
(3) ⇒ (1). We consider minimal components and prove the contrapositive. Assume Ĝ is not minimal pinned -isostatic and there is a proper pinned -isostatic subgraph G*. We claim the pinned orbit matrix pin(Ĥ, ψ, p̃) decomposes. Indeed, if we permute the inner vertices and all of the edges associated with G* to the upper left corner of pin(Ĥ, ψ, p̃), the rest of these rows from G* are zero and the remaining columns and rows form a second block. This gives a block triangular decomposition of the pinned orbit matrix pin(Ĥ, ψ, p̃).
As a corollary, we observe that the equivalence is true for individual components in the decomposition.
Corollary 14. Let be a symmetry group in dimension d, and let Ĝ be a pinned -isostatic graph. Further, let Ĥ be the quotient -gain graph of Ĝ. Then, the following are equivalent:
Ĝ contains no proper pinned -isostatic subgraphs;
Ĥ is indecomposable for some (any) -directed orientation;
the pinned orbit matrix pin(Ĥ, ψ, p̃) has no proper block triangular decomposition.
We have shown that the -Assur block graph encodes all of the information about the -Assur decomposition. This bijection allows us to be slightly terse in subsequent examples and figures, referring only to the partial order (the -Assur block graph) rather than the -Assur decomposition.
4.2. -Drivers and Strongly -Assur Graphs
Assume we have a -Assur decomposition of a pinned graph Ĝ. If we replace an orbit of edges in this graph by a set of symmetric drivers (i.e., a set of edges simultaneously change their lengths in a coordinated, symmetric fashion), then the pinned framework will have a symmetric motion, which fixes the ground (and the ground includes an orbit of end-vertices of the edges that were converted to drivers).
Proposition 15. Let Ĝ be a pinned -isostatic graph with quotient -gain graph Ĥ.
For a -regular realisation, removing any edge from Ĥ generates a fully -symmetric finite motion in which some non-pinned vertices (of Ĝ) are in motion relative to the ground;
Given a -Assur decomposition of Ĝ, if an edge ẽ of Ĥ is removed, then, at any -regular realisation, there is no fully -symmetric infinitesimal motion with non-zero velocity at vertices in components below or incomparable to the component containing ẽ.
Proof. 1. The existence of a fully -symmetric infinitesimal motion follows from the definition of a pinned -isostatic graph. That a fully -symmetric infinitesimal motion implies a fully -symmetric finite motion follows from [9].
2. This follows directly from the definition of a -Assur decomposition.
In [4] it was shown that not all d-Assur graphs (when d > 2) are strongly d-Assur. This is connected to obstacles to a good combinatorial (counting) characterisation for three- and higher-dimensional bar and joint frameworks to be rigid. Similarly, we say that a -Assur graph is strongly -Assur if the -symmetric infinitesimal motion created by removing any edge orbit has a non-trivial velocity at each vertex. The example in Figure 8 is a -Assur graph, but it is not strongly -Assur. Therefore, as for graphs without imposed symmetry, being strongly -Assur is a stronger property than being -Assur.
Corollary 16. Let Ĝ be pinned -isostatic, and let Ĥ be the quotient -gain graph of Ĝ. Assume each component in the -Assur decomposition of (Ĝ and hence) Ĥ is strongly -Assur. Suppose an edge ẽ is removed from some component Ĥ*. Then, at a -regular realisation, there is a fully -symmetric finite motion in which all vertices in Ĥ* or in components above Ĥ* move.
Proof. The definition of a strongly -Assur graph Ĥ* guarantees that all inner vertices of Ĥ* are in motion. If there is a higher strongly -component in which some inner vertices are not in motion, then none of them are in motion, including the vertices at the heads of the outgoing edges of the component, since the -Assur component is -isostatic. This, in turn, means that some vertices of the components just below this are also not moving. Going down the -Assur decomposition, we conclude that the vertices of the strongly -component from which the orbit was removed are also not in motion. This is a contradiction.
For certain groups in the plane, we can show that there is no distinction between -Assur graphs and strongly -Assur graphs.
Proposition 17. Let be the symmetry group s or n in the plane, where n ≥ 2, and let act freely on the vertices of a pinned graph Ĝ. Then, Ĝ is -Assur if and only if it is strongly -Assur.
The proof is similar to ([4], Proposition 4.2).
Proof. By definition, strongly -Assur graphs are -Assur. For the converse, assume Ĝ is -Assur and delete an edge ũṽ from the corresponding -gain graph Ĥ. Theorem 9 implies that Ĥ −ũṽ satisfies |Ẽ| =2|Ĩ|− 1. Hence, the orbit matrix pin(Ĥ −ũṽ, ψ, p̃) admits a non-trivial solution U to the equation pin(Ĥ − ũṽ, ψ, p̃) × U =0. Let U = (U1,U2,...,U|Ẽ|)T. If Ui =0 for some i, then that inner vertex is still -rigidly connected to the ground. Therefore, Theorem 10 implies that vertex i must be contained in a pinned subgraph Ĥ′ with |Ẽ′| =2|Ĩ′|. The corresponding covering graph Ĝ ′ would then be pinned -isostatic, but Ĥ′ contains at most one of ũ and ṽ, implying that |Ĩ′| < |Ĩ|. This contradicts the minimality of Ĝ.
For more exotic symmetry groups, we do not know if the proposition holds. We do however note that in higher dimensions, the proposition fails and, hence, see the difficulty for even order dihedral groups in the plane (see the comments following Theorem 7) as a warning that there is the potential for the proposition above to break down in that case.
Finally, we note that while for the decomposition of an -isostatic framework into -Assur components, all of the essential information is given by the quotient graph (without the gain labeling of the edges), the gain labeling of the edges does become relevant in the synthesis of a framework from its -Assur components. For example, if we want to test a given framework for -isostaticity, then, we can decompose the framework (ignoring the gains) and then check whether each component is -isostatic (using the gains). This process of decomposing and carrying out the more complex analysis on the small pieces, then recombining with known rules for synthesis, is a standard engineering technique. It was this kind of analysis of the paths of the machine that motivated Assur to investigate the decomposition into as simple pieces as possible. In the synthesis from pieces, the gain labeling enables us to build up the entire graph from the components and to draw conclusions about the -symmetric rigidity properties of the original framework.
5. -Assur Graphs Which Are Pinned-Isostatic
In this section, we will analyse -Assur decompositions of -symmetric pinned graphs, which are both pinned -isostatic and pinned isostatic (i.e., there are also no symmetry-breaking motions or non-symmetric self-stresses). Examples of such graphs are shown in Figures 3, 9 and 10. Given such a graph (with a free group action), we will show in Theorem 19 that there exists a very strong connection between the Assur and the -Assur decompositions of the graph; essentially a bijection between them (see Figures 3 and 6).
For the symmetry group 3 in the plane, a pinned 3-symmetric graph, where 3 acts freely on the vertices, is pinned 3-isostatic if and only if it is pinned isostatic. This follows from Theorem 10 and the fact that for each of the three irreducible representations of 3, the rank properties of the corresponding orbit matrix are described by exactly the same counting conditions given in Theorem 10 (see [12]). More generally, we conjecture that for the rotational groups n, n > 2, in the plane, pinned n-isostaticity is equivalent to pinned isostaticity, provided that the action of n is free on the vertices and edges. In particular, this includes all odd-order rotational groups that act freely on the vertices.
However, note that if a pinned graph Ĝ = (I, P ; E) is n-isostatic, n ≥ 2,or s-isostatic in the plane, where the action is free on the vertices, but not on the edges, then we must have |E| < 2|I|, and hence, Ĝ is not pinned isostatic, but flexible [21]. For 2 or s in the plane, symmetry-breaking motions can also arise in 2-or s-isostatic pinned graphs if the action is free on both vertices and edges, due to a violation of the (2, 3, 2)-gain sparsity count (see Section 6 and [12]).
For -symmetric pinned graphs that are both pinned -isostatic and pinned isostatic, we show that if we remove an orbit of edges and convert those edges into actuators (drivers that are synchronised to change length at the same rate), then the resulting symmetry-preserving motion at a -regular configuration is the only motion of the structure. In other words, no symmetry-breaking motions can occur.
Proposition 18. Let Ĝ be a -symmetric pinned graph with -gain graph Ĥ = (Ĩ, P̃; Ẽ), and let p be a -symmetric configuration that is -regular. Let (Ĝ, p) be pinned isostatic. Let ẽ ∈ Ẽ have an orbit of edges F = {e1,e2,...,er}⊂ E. If we remove edges e1,e2,...,es from Ĝ and convert them into actuators, then there is a unique finite motion of (Ĝ − F, p).
Proof. Since (Ĝ, p) is pinned isostatic, (Ĝ, p) is also pinned -isostatic. Therefore, removing ẽ lowers the rank of the orbit matrix by one and induces a unique (up to scalar multiplication) solution ũ at p̃. This transfers to a fully -symmetric non-trivial infinitesimal motion u at p by Theorem 6.1 in [10]. If we take the pinned rigidity matrix R(Ĝ, p), with the orbit still present, then R(Ĝ, p)u = b, where b has equal non-zero entries for all the edges in ẽ. Since (Ĝ, p) is isostatic, R(Ĝ, p) is invertible, so the infinitesimal motion of (Ĝ − F, p) (with the edges of F converted into actuators, i.e., synchronised drivers) is unique. Moreover, because p is -regular, this extends locally to a finite motion of (Ĝ − F, p).
Example 5. Consider the example in Figure 10. A two-direction on the gain graph (b) induces a symmetric set of two-directions on the original graph. If we shift any orbit of edges from the bottom component into a symmetric set of drivers, then this has a four-fold symmetric motion, which moves all vertices. If we shift an orbit of edges from the top component into a symmetric set of drivers, then there is a 4-symmetric motion, which moves only the vertices in the top component.
If these drivers encounter a “dead end position” in which the drivers no longer can move, then the rank of the orbit matrix has dropped at this singular position, and there will be a fully symmetric self-stress. We conjecture that this symmetric self-stress must be non-zero on all edges in this graph. Whether this extends to all -Assur components is a question worth further investigation.
5.1. Mapping between Gain Graphs and Covering Graphs
We now formalise the relationship between components in the covering graph and the gain graph and, hence, prove our second main result.
Theorem 19. Let Ĝ be a pinned graph, and let act freely on the vertices and edges of Ĝ. Let Ĝ be pinned isostatic at every pinned -regular realisation, and let Ĥ be the corresponding -gain graph. Then, the projection of a d-Assur graph is a -Assur graph, and the lift of a -Assur graph is a set of inner-vertex disjoint sets of d-Assur graphs (possibly only one).
Proof. Firstly, Proposition 11 implies that Ĝ has a -directed orientation and Ĥ has a d-directed orientation. For any vertex ṽ in Ĥ and any vertex v in Ĝ in the fiber over ṽ, the out-degrees are equal by the definition of a gain graph and the assumption that the action is free on the vertices and edges. This proves that any -directed orientation of Ĥ lifts to a d-directed orientation of Ĝ. The converse is the same argument unless the given -directed orientation of Ĝ is not itself -symmetric. In this case, we note that the existence of a -symmetric -directed orientation is clear and then apply Corollary 1. Thus, we know that any -directed orientation of Ĥ lifts to a d-directed orientation of Ĝ and any d-directed orientation of Ĝ projects to a -directed orientation of Ĥ.
We now show that, for our given orientations, any strongly connected component of Ĥ lifts to a set of strongly connected components of Ĝ, and any strongly connected component of Ĝ projects to a strongly connected component of Ĥ. Let have elements id, a1,a2,...,am−1 (so, has order m). The group operation will be written additively in this proof. Suppose there is a directed cycle C̃n in Ĥ on vertices ṽ1, ṽ2,..., ṽn with gain gi on edge ṽi ṽi+1 for each i and that the corresponding vertex orbits in Ĝ are for 1 ≤ i ≤ n. Moreover, suppose k is the order of the subgroup of induced by the labels on the edges of C̃n. Each edge ṽi ṽi+1 lifts to an edge where r ∈ is the sum of the gains on the edges ṽ1ṽ2,..., ṽi−1ṽi. The path ,… visits v1 again on its k-th visit to a vertex in the orbit ṽ1 (and also visits each other vertex k times). For any vertex in the orbit of ṽ1 not visited by this cycle, repeat the path above. It will take m/k repetitions to ensure every vertex in the orbit of ṽ1 has been visited. Hence, C̃n corresponds to m/k directed cycles in Ĝ. This proves the first part of 2, lifting from Ĥ to Ĝ. Conversely, take any two vertex orbits in Ĥ that project from the same strongly connected component in Ĝ. Since there is a directed cycle in Ĝ connecting elements of the two orbits, the projection of this cycle into Ĥ will be a cycle (not necessarily simple) connecting the two orbits. The completes the proof of 2.
Theorem 3 implies the strongly connected components of Ĝ are the d-Assur components. Theorem 13 implies the strongly connected components of Ĥ are the -Assur components. The theorem follows.
We expect that the map between quotient and covering graphs contains enough information for the following stronger conclusion to be possible.
Conjecture 20. Let Ĝ be pinned isostatic at every -regular realisation, and let the action of be free on the vertices and edges. Then, a -Assur component is strongly -Assur if and only if the corresponding d-Assur components are strongly d-Assur.
Recall that for reflection and rotation symmetry in the plane, pinned graphs are -Assur if and only if they are strongly -Assur (see Proposition 17). Hence, the conjecture follows in those cases from Theorem 19. However, we still believe the conjecture in the cases where -Assur is a strictly weaker property than strongly -Assur.
5.2. Subgroup Assur Decompositions
In Figure 11, we observe that there is a correspondence among the distinct -block graphs induced by various subgroups. Specifically, when a symmetry group is a subgroup of , then the -gain graph of a -symmetric graph G is a projection of the -gain graph of G, and there is an induced projection from the -block graph to the -block graph. Conversely, there is a lifting of the -gain graph of G to the -gain graph of G. This illustrates a general principle. If Ĝ is -isostatic and -isostatic for some subgroup of , then the analysis in the previous subsection can be adapted to reveal the R-Assur decomposition. Let us mention one straightforward way in which this can be done. If Ĝ is pinned isostatic, we can simply apply Theorem 19 to and to separately. Here, composing the -quotient map with the -lifting map gives the quotient map from to . Similarly, composing the R-quotient map with the -lifting map gives us the lifting map from to .
Consider again Figure 11 and how this might be applied. Since we now know that we can choose any subgroup of 6 to apply a -Assur decomposition, we can make different choices of edge orbits to take as drivers depending on whether we want to see a 2, 3 or 6-symmetric motion. We can pick a set of drivers of size 6, 3, 2 (or 1 for the identity subgroup). Each choice will guarantee a motion with at least the symmetry of the subgroup we chose. It is more subtle to realise in this example that the motion being driven will not have additional symmetry!
6. -Assur Graphs Which Are Not Pinned Isostatic at -Regular Configurations
In Section 5, we focused on pinned -isostatic graphs that were also pinned isostatic. This assumption ensured that all -Assur components were also pinned isostatic and d-Assur. In that section, a key assumption was that the action of the group was free on the vertices and edges. Some previous -isostatic examples included components that were not isostatic without symmetry, and therefore, the underlying graph does not have a d-Assur decomposition without symmetry (Figures 1d and 7d). There are simple examples that illustrate the possible impact of fixed vertices generating redundancy (Figure 12a,b) and the possible impact of fixed edges giving flexible frameworks (Figure 12c,d).
More generally, there are symmetry groups and associated group actions that fix vertices, edges or both, where: (i) the -Assur components may be pinned redundant, but rigid at -regular configurations; (ii) the -Assur components may be pinned flexible (with symmetry breaking flexes), but independent at -regular configurations; or (iii) a -Assur component may be both redundant and flexible. We may also have a -Assur decomposition in which some components are isostatic, some are redundant and some are flexible. In all of these cases, the covering graph does not have a d-Assur decomposition, for a full comparison of Assur decompositions of the type described in Subsection 5.2. However, through exploring subgroups, we will see that two -Assur components for one group may now combine to a single -Assur component for a subgroup of .
While some of these examples are extreme, there are also several key examples, already mentioned in Figures 1d and 7d, which are used, or are usable, for controlling symmetric motions in mechanical engineering. We will return to the analysis of these examples below, as evidence that these additional types do contribute to the analysis of mechanical linkages and can contribute to the synthesis of new mechanical linkages.
6.1. -Assur Graphs Which Are Redundant and Rigid at -Regular Realisations
Variants of the graph in Figure 13 are redundant and rigid with different choices of drivers. They also have different -Assur decompositions depending on the symmetry group used for the analysis.
Example 6. Consider the three-dimensional pinned framework of Figures 2 and 13. The 2v-symmetric graphs all have |Î| =2, and the number of orbit matrix columns is equal to four. In (a) |Ê| =3, so there is a fully 2v-symmetric motion, while in (b), (c) |Ê| =4, and the graphs are -isostatic. However, they have counts, such as |E| =3|I| (Figure 13a), |E| =3|I|+1 (Figure 2c) and |E| =3|I|+4 (Figure 13c).
These examples leave questions about their -Assur decompositions, as well as what happens when we focus on one of the mirrors for the subgroup s. Figure 14 illustrates that when we move down to a subgroup of , two -Assur components can combine into a single R-Assur component. This is quite different from the behaviour guaranteed in ection 5.2 when there is a free action.
Example 7. If we take the underlying framework of Example 6, there are two possible pairs of mirrors (Figure 15). With mirrors through the vertices (a), the count is four columns and three rows, so the orbit matrix predicts one fully 2v-symmetric motion. With the other set of mirrors fixing the edges (b), we have three columns and four rows, predicting a fully 2v-symmetric self-stress. In fact, both the infinitesimal motion and the self-stress appear for the original framework, with different symmetries. In the extended symmetry analysis of [12], for (a), the self-stress appears as a dependence in their “anti-symmetric orbit matrix”. For (b), the self-stress if fully symmetric and the infinitesimal motion is in the kernel of their “anti-symmetric” matrix. Unusually, these two combine to give all of the information about the framework without either symmetry being forced.
When we stack two layers of this example, we gain insight into examples explored with cruder tools in [29]. For example, when stacking two copies, turned to have fixed vertices in one and fixed edges in the other, this double analysis provides clearer insights. The framework in (c) counts for the orbit matrix to have seven columns and seven rows, suggesting it might be pinned 2v-isostatic. However, (d) counts for the bottom layer to have a fully 2v-symmetric self-stress and the top layer to have the fully 2v-symmetric infinitesimal motion and, hence, not have a 2v-Assur decomposition. Given a framework with several choices of symmetry subgroups, we can get different information from different choices. These choices are a topic for further research.
6.2. -isostatic Graphs with All -regular Realisations Flexible without Forced Symmetry
We already saw that a pinned -isostatic graph may be flexible without forced symmetry, due to a fixed edge (Figure 12c,d). There is a slightly different type of flexibility that happens when the framework, along with the ground, is generically isostatic, but the number of pins needed under symmetry is too small to eliminate all trivial motions. The following example illustrates this.
Example 8. Consider the schematic of a Grab Bucket in Figure 16b, which has a single mirror in the plane ([13], p. 270). The quotient s-gain graph in Figure 16c confirms this has the correct count to be pinned s-isostatic with |Ê| = 7, |Î| =4, and, with the fixed vertex u, seven columns in the orbit matrix. The s-Assur block graph in (d) illustrates that the red edge is a driver that moves all of the inner vertices.
The covering graph, without forced symmetry, is independent, but does not have sufficient pins to make it pinned two-isostatic. There will be a trivial “swing” of the bucket around the top pin; something that is observed on any construction site. This swing is controlled by gravity pulling down on the bucket; and the desired motion is the mirror symmetric operation of the bucket, which is controlled by the driver. Our analysis does contribute clarifying information about the symmetric motion.
If we modify the pinning and make both of the two vertices on the mirror into the ground, then what remains is a pinned two-isostatic graph (|E| =12, |I| =6), without forced symmetry. What this analysis that is not based on the symmetry misses is the symmetric impact of changing the distance between these two pins!From the point of view of the -Assur components, it is the bottom component—a single bar—that is pinned -isostatic, but not pinned isostatic.
In practice, this image is one side of a three-dimensional framework, which has an added mirror symmetry between the two sides. In some images on the internet, the “ground” is expanded to two grounding sites, and the bucket retains a single swinging motion in addition to the driver-controlled motion, which preserves both mirrors. In others, the ground is pulled to a single pin, and the second vertex u may be on the intersection of the two mirrors or doubled (symmetrically). There is still a single fully-symmetric motion and, then, other incidental motions due to having insufficient ground vertices.
There is a variant of the Grab Bucket, which is the bottom component of Figure 7d.
Example 9. Consider the graph in Figure 17a, with ssymmetry and one fixed vertex on the mirror. The direct analysis of the gain graph, and the orbit matrix, shows this is a s-Assur graph. However, a direct count shows |E| =2|I|, while there is a non-trivial symmetry breaking motion with just the one vertex pinned. This guarantees an anti-symmetric self-stress. With the red edges (see Figure 17b) as coordinated drivers, we see an alternative mechanism for a Grab Bucket.
Finally, we present an extreme example of where our definitions of -Assur can take us.
Example 10. The framework in Figure 18a is pinned 2v-isostatic; with no edge orbits to the ground. This occurs because there are no fully 2v-symmetric trivial motions.
However, it is not pinned rigid, as it is unpinned when non-symmetric motions are allowed, with rotations around the origin, as well as translations. With two copies (Figure 18c), this is far from rigid once motions breaking the symmetry are permitted.
6.3. -Isostatic Graphs with Combined Components
We can combine components with different properties, some with isostatic graphs, some with redundant graphs, some with flexible graphs.
Example 11. Consider the two-dimensional framework with mirror symmetry shown in Figure 19a, with its gain graph Figure 19b and its s-Assur block graph in Figure 19c. The underlying graph of the framework in Figure 19a has a dependent lower component, an isostatic component (the middle) and a flexible upper component. Even the lower component is also not pinned rigid (it does not have enough pins).
Such composite structures can be synthesised by composing various -Assur graphs with the same symmetry. We might even compose several components with different symmetries, provided the attachments from the upper component(s) to the lower ones had the symmetry of the upper components. We have only scratched the surface of what can happen and what can be designed.
7. Extensions and Conclusions
In the same way that orbit matrices have proven useful in a number of broader settings, the analysis extends to other settings where we can create square pinned orbit matrices. In the next two subsections, we outline this principal in different settings.
7.1. Extensions to “Anti-Symmetric” Orbit Matrices
It was shown in [30] that the rigidity matrix R(G, p) of a -symmetric framework (G, p) can be transformed into a block-decomposed form, where each block Ri(G, p) corresponds to an irreducible representation ρi of the group . This breaks up the rigidity analysis of (G, p) into a number of independent subproblems [21,30]. In fact, the fully -symmetric rigidity properties of (G, p) are described by the block matrix R1(G, p) corresponding to the trivial irreducible representation ρ1 of . Thus, as shown in [10], this block matrix is equivalent to the orbit matrix defined in Definition 4.
In the recent paper [12], an orbit matrix was established for each of the blocks Ri(G, p) in the case where the group is abelian, and these new tools were successfully used to characterise -generic infinitesimally rigid graphs (i.e., graphs G with the property that -generic realisations of G do not have any non-trivial infinitesimal motions) in the plane for the groups s, 2 and 3. (Note that -generic is the natural analogue of generic for symmetric frameworks.)
Since the structure of the “anti-symmetric” orbit matrices is similar to the structure of the orbit matrix from Definition 4, we expect that the methods and results established in this paper can be extended to these other orbit matrices in a straightforward fashion. This would allow us to analyse symmetric frameworks for infinitesimal motions and stresses that break certain symmetries, but preserve others. However, note that an “anti-symmetric” infinitesimal motion typically does not extend to a finite motion [7,30].
7.2. Extensions to Matrices for Other Constraint Systems
All of the techniques (and even examples) of this paper extend directly to spherical linkages, which are studied in settings, such as [31] Chapters 7–10. Papers, such as [10], carry out the transfer for all orbit matrices, including the original rigidity matrix (where the group is the identity). There is no complication to transferring these transfer processes to pinned frameworks, and the -Assur decompositions will also transfer. All of the techniques also extend to cones; provided the cone point (or the cone point and its symmetric images) has the appropriate symmetry.
Periodic frameworks in the plane have been studied by a number of groups. Whether the lattice is fixed [18], partially variable or fully flexible [14,15], there is a natural rigidity matrix, which can be made square by pinning. Moreover periodic frameworks have been understood combinatorially using gain graphs. Hence, there is potential to use the techniques in this paper to generate Assur decompositions when one vertex in the fixed lattice can substitute for the ground.
In [32,33], frameworks in three-dimensions supported on fixed surfaces have been studied and symmetric analogues of Theorem 7 have been obtained [17]. The rigidity matrix has 3|V | columns and, when the framework is isostatic, 2|V|− k + |V| rows (where k is the number of isometries of ℝ3 admitted by the surface). When the surface admits no isometries of ℝ3 then no pinning is required. However, unlike the situation in Figure 18, all frameworks on such a surface can be considered as pinned. Otherwise, it seems like these frameworks should be decomposable into Assur components by pinning k degrees of freedom to make the matrix square and then applying the techniques in this paper.
In ([4], Subsection 5.1), it was outlined how to extend the equivalence of Assur decompositions to various alternative types of frameworks allowing bodies, bars, joints, pins, hinges, etc. All of these kinds of mechanisms occur in the mechanical engineering literature. All of the techniques and results of this paper will have analogous decompositions under symmetry, since the symmetry-adapted analogues of the basic rigidity results have recently been developed.
In [34], general CAD systems in three-dimensions were investigated with constraint matrices, which are analogs of the rigidity matrices for bodies and bars. It is natural to consider pinned CAD systems (essentially make one of the bodies the ground) and to also consider systems of symmetric CAD constraints. We anticipate that all of the decompositions described here will again extend to these more general sets of constraints.
7.3. Inductive Constructions
Inductive constructions can be a tool for the synthesis of mechanisms, including the synthesis of larger Assur components. We present the basic idea for -Assur decompositions via one fundamental recursive operation, and the reader can pull this back to a discussion without symmetry, when is the identity group. The reader interested in inductive constructions can consult [35].
For notational reasons, we discuss the case d =2 only. The one-extension deletes an edge of (H, ψ) and adds a new vertex and three new edges to (H, ψ). First, one chooses an edge ẽ of H (which will be deleted) and a vertex z̃ of H, which may be an end-vertex of ẽ. Then, one subdivides ẽ, with a new vertex ṽ and new edges ẽ1 and ẽ2, such that the tail of ẽ1 is the tail of ẽ and the head of ẽ2 is the head of ẽ. The gains of the new edges are assigned so that ψ(e1) · ψ(e2) = ψ(e). Finally, we add a third new edge, e3, to H. This edge is oriented from ṽ to z̃, and its gain is such that every two-cycle ẽiẽj, if it exists, is unbalanced. See also Figure 20.
In the covering graph, one-extension is one of a number of graph operations that preserve the underlying symmetry. Some of these can be recognised as performing standard, non-symmetric, Henneberg operations simultaneously [8,12,17,36].
Supplementary Videos
symmetry-06-00516-s001.zipAcknowledgments
We thank the anonymous referees for careful reading and helpful comments. The research was supported in part by a grant from NSERC (Canada) to Walter Whiteley.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Assur, L.V. Issledovanie Ploskih Sterznevyh Mehanizmov s Nizsimi Parami s Tocki Zreniya ih Struktury i Klassikacii; Artobolevski, I.I., Ed.; Izdat. Akademii Nauk SSSR: Moscow, Russia, 1952. [Google Scholar]
- Shai, O.; Servatius, B.; Whiteley, W. Combinatorial characterization of the Assur graphs from engineering. Eur. J. Comb 2010, 31, 1091–1104. [Google Scholar]
- Shai, O.; Servatius, B.; Whiteley, W. Geometric properties of Assur graphs. Eur. J. Comb 2010, 31, 1105–1120. [Google Scholar]
- Shai, O.; Sljoka, A; Whiteley, W. Directed graphs, decompositions, and spatial linkages. Discret. Appl. Math 2013, 161, 3028–3047. [Google Scholar]
- Sljoka, A.; Shai, O.; Whiteley, W. Checking mobility and decomposition of linkages via pebble game algorithm. In Proceedings of the American Society of Mechanical Engineers 2011 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Washington, DC, USA, 28–31 August 2011; pp. 493–502.
- Sljoka, A. Algorithms in Rigidity Theory with Applications to Protein Flexibility and Mechanical Linkages. Ph.D. Thesis, York University, Toronto, ON, Canada. 31 August 2012. Available online: http://www.math.yorku.ca/~adnanslj/adnanthesis.pdf (accessed on 17 June 2014). [Google Scholar]
- Kangwai, R.D.; Guest, S.D. Detection of finite mechanisms in symmetric structures. Int. J. Solids Struct 1999, 36, 5507–5527. [Google Scholar]
- Jordan, T.; Kaszanitzky, V.; Tanigawa, S. Gain-sparsity and Symmetry-forced Rigidity in the Plane; The Egerváry Research Group on Combinatorial Optimization Group (EGRES) Technical Report TR-2012-17; Operations Research Department, Eötvös University: Budapest, Hungary, 2012. [Google Scholar]
- Schulze, B. Symmetry as a sufficient condition for a finite flex. SIAM J. Discret. Math 2010, 24, 1291–1312. [Google Scholar]
- Schulze, B.; Whiteley, W. The orbit rigidity matrix of a symmetric framework. Discret. Comput. Geom 2011, 46, 561–598. [Google Scholar]
- Guest, S.D.; Schulze, B.; Whiteley, W. When is a symmetric body-bar structure isostatic? Int. J. Solids Struct 2010, 47, 2745–2754. [Google Scholar]
- Schulze, B.; Tanigawa, S. Infinitesimal rigidity of symmetric bar-joint frameworks. 2013. Available online: http://arxiv.org/abs/1308.6380 (accessed on 17 June 2014). [Google Scholar]
- Rosenauer, N.; Willis, A.H. Kinematics of Mechanisms; Dover: New York, NY, USA, 1967. [Google Scholar]
- Borcea, C.; Streinu, I. Periodic frameworks and flexibility. Proc. R. Soc. A 2010, 466, 2633–2649. [Google Scholar]
- Malestein, J.; Theran, T. Generic combinatorial rigidity of periodic frameworks. Adv. Math 2013, 233, 291–331. [Google Scholar]
- Malestein, J.; Theran, L. Frameworks with forced symmetry I: Reflections and rotations. 2013. Available online: http://arxiv.org/abs/1304.0398 (accessed on 17 June 2014). [Google Scholar]
- Nixon, A.; Schulze, B. Symmetry-forced rigidity of frameworks on surfaces. 2013. Available online: http://arxiv.org/abs/1312.1480 (accessed on 17 June 2014). [Google Scholar]
- Ross, E. The rigidity of periodic frameworks as graphs on a fixed torus. 2010. Available online: http://arxiv.org/abs/1202.6652 (accessed on 17 June 2014). [Google Scholar]
- Zaslavsky, T. A mathematical bibliography of signed and gain graphs and allied areas. Electron. J. Comb 1998, 5, 124. [Google Scholar]
- Bishop, D.M. Group Theory and Chemistry; Clarendon Press: Oxford, UK, 1973. [Google Scholar]
- Fowler, P.W.; Guest, S.D. A symmetry extension of Maxwell’s rule for rigidity of frames. Int. J. Solids Struct 2000, 37, 1793–1804. [Google Scholar]
- Schulze, B. Injective and non-injective realizations with symmetry. Contrib. Discret. Math 2010, 5, 59–89. [Google Scholar]
- Whiteley, W. Some Matroids from Discrete Applied Geometry. In Contemporary Mathematics; American Mathematical Society: Providence, RI, USA, 1996; Volume 197, pp. 171–311. [Google Scholar]
- Hakimi, S. On the degrees of the vertices of a directed graph. J. Frankl. Inst 1965, 279, 139–154. [Google Scholar]
- Frank, A.; Gyárfás, A. How to orient the edges of a graph? Combinatorics. In Proceedings of the 5th Hungarian Combinatorial Colloquium, Keszthely, Hungary, 28 June–3 July 1976; pp. 353–364.
- Haas, R.; Lee, A.; Streinu, I.; Theran, L. Characterizing sparse graphs by map decompositions. J. Comb. Math. Comb. Comput 2007, 62, 3–11. [Google Scholar]
- Berg, A.; Jordán, T. Algorithms for graph rigidity and scene analysis. In Lecture Notes in Computer Science 2832, In Proceedings of the 11th Annual European Symposium on Algorithms (ESA), Budapest, Hungary, 15–20 September 2003; Di Battista, G., Zwick, U., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 78–89. [Google Scholar]
- Hendrickson, B.; Jacobs, D. An algorithm for two-dimensional rigidity percolation: The pebble game. J. Comput. Phys 1997, 137, 346–365. [Google Scholar]
- Whiteley, W. Fragmentary and incidental behavior of columns, slabs and crystals. Philos. Trans. A Math. Phys. Eng. Sci 2013. [Google Scholar] [CrossRef]
- Schulze, B. Block-diagonalized rigidity matrices of symmetric frameworks and applications. Beitr. Algebra Geom 2010, 51, 427–466. [Google Scholar]
- McCarthy, J.M.; Soh, G.S. Interdisciplinary Applied Mathematics. In Geometric Design of Linkages, 2nd ed; Springer: New York, NY, USA, 2011; Volume 11. [Google Scholar]
- Nixon, A.; Owen, J.; Power, S. Rigidity of frameworks supported on surfaces. SIAM J. Discret. Math 2012, 26, 1733–1757. [Google Scholar]
- Nixon, A.; Owen, J.; Power, S. A Laman theorem for frameworks on surfaces of revolution. 2012. Available online: http://arxiv.org/abs/1210.7073 (accessed on 17 June 2014). [Google Scholar]
- Lee-St. John, A.; Sidman, J. Combinatorics and the rigidity of CAD systems. Comput. Aided Des 2013, 45, 473–482. [Google Scholar]
- Nixon, A.; Ross, E. One brick at a time: A survey of inductive constructions in rigidity theory. In Fields Institute Communications 70; (Rigidity and Symmetry); Connelly, R., Weiss, A., Whiteley, W., Eds.; Springer: New York, NY, USA, 2014; pp. 303–324. [Google Scholar]
- Schulze, B. Symmetric versions of Laman’s Theorem. Discret. Comput. Geom 2010, 44, 946–972. [Google Scholar]
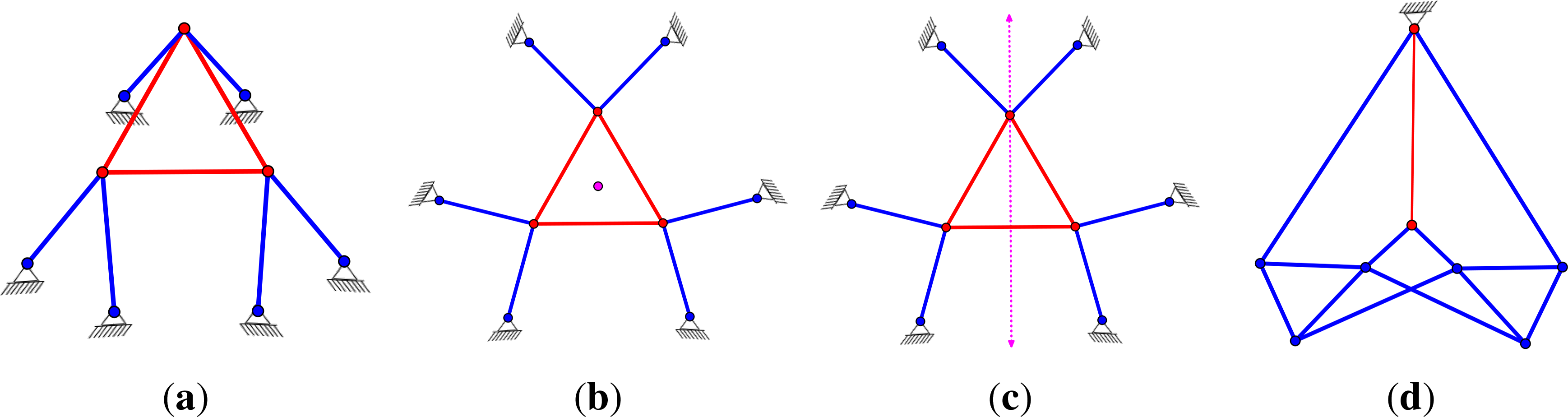
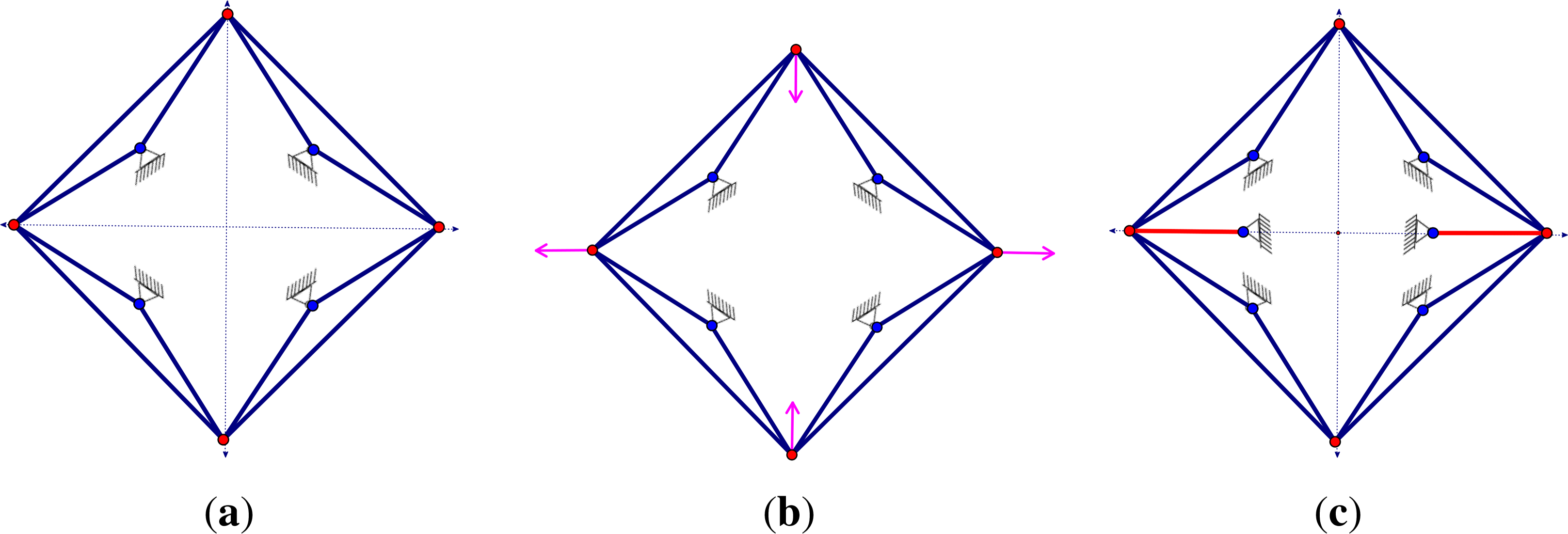
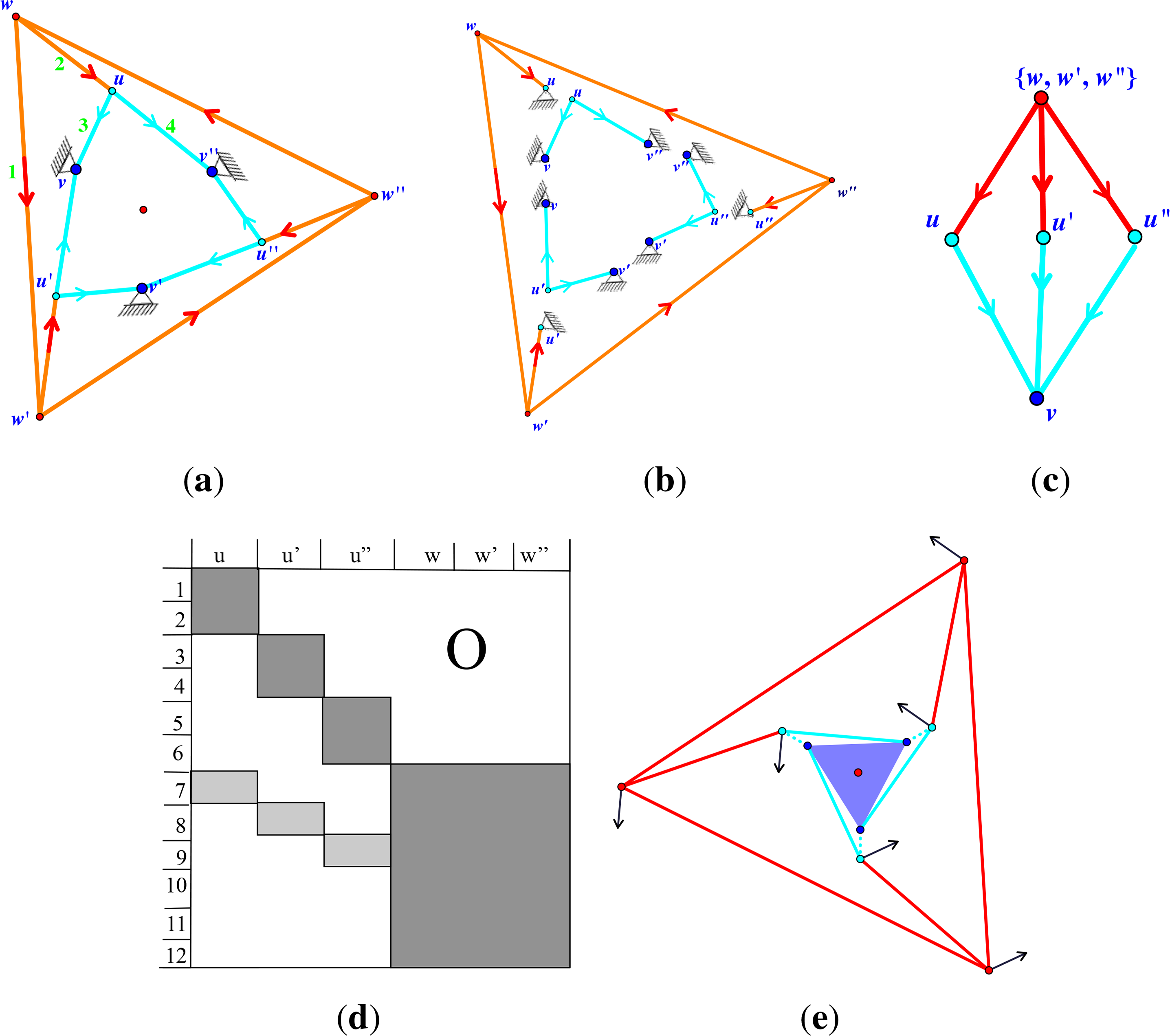
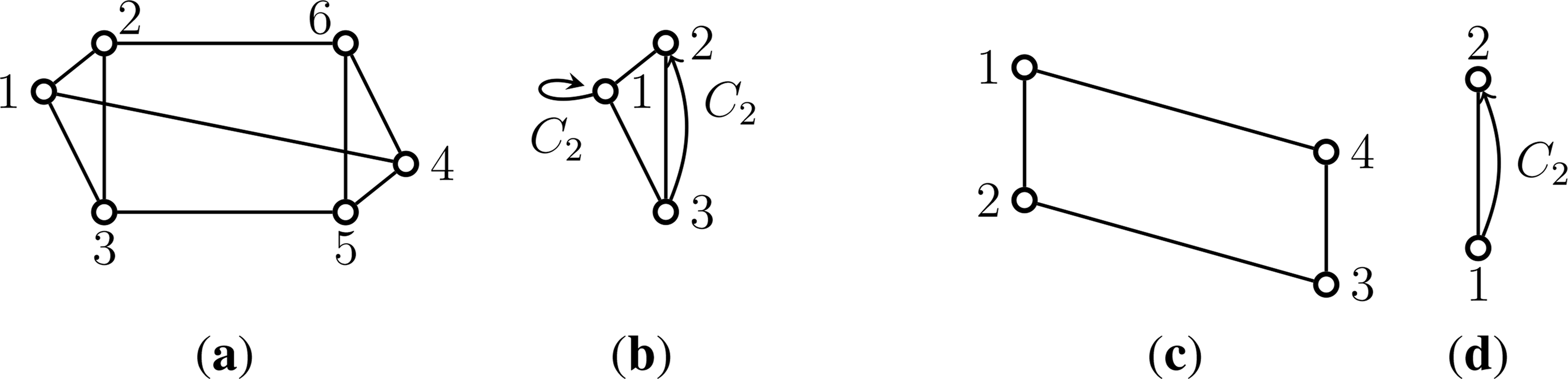
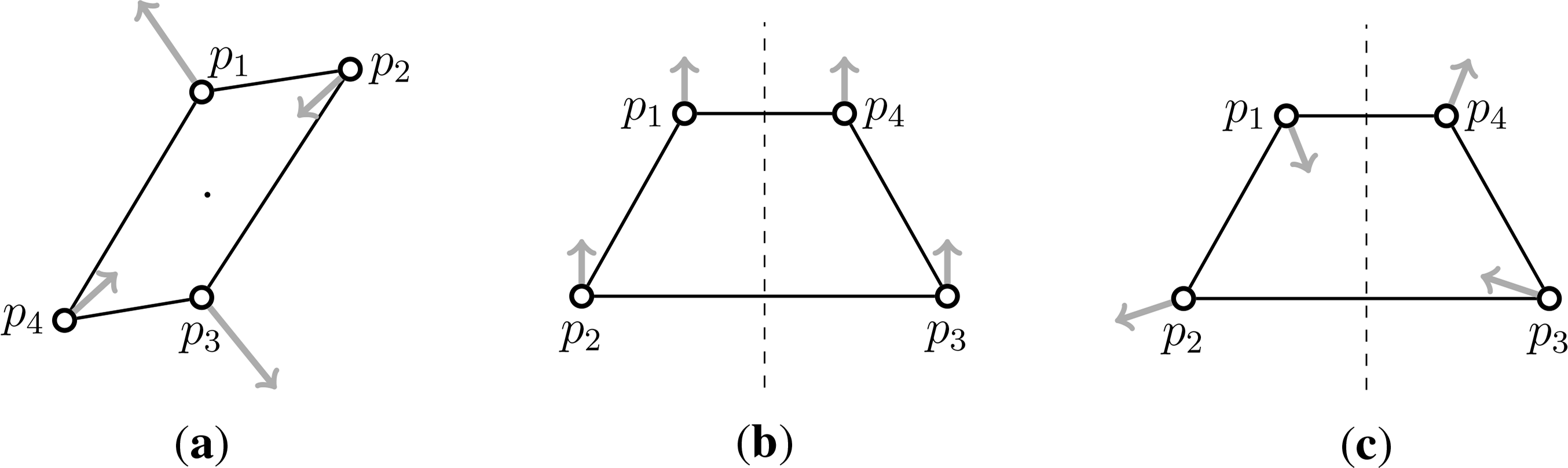
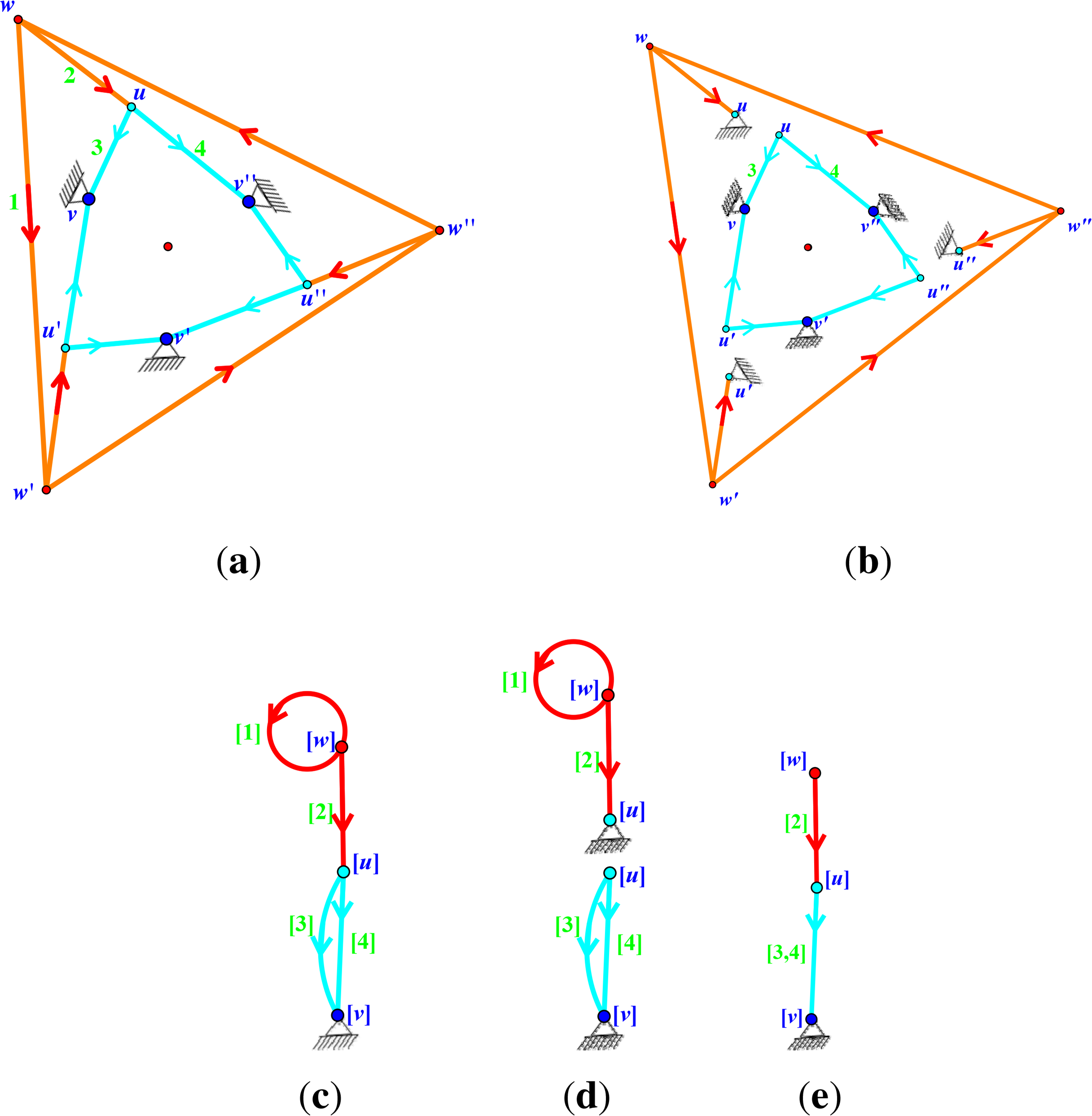
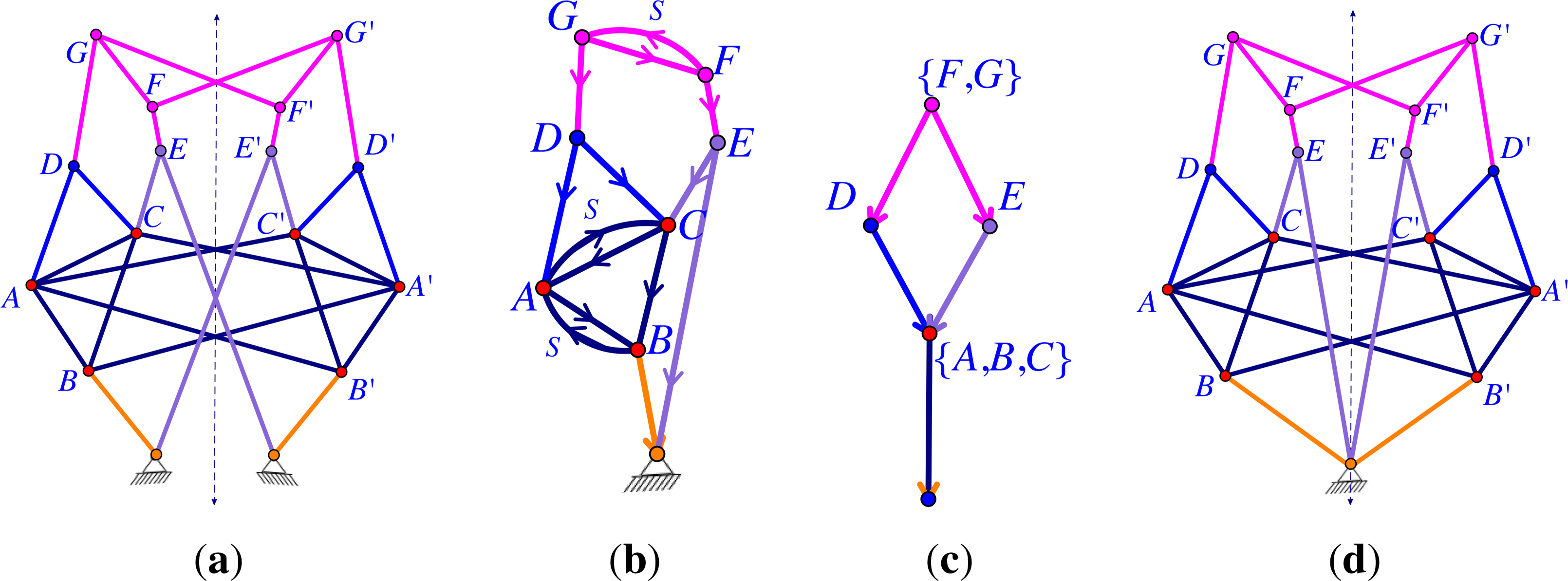
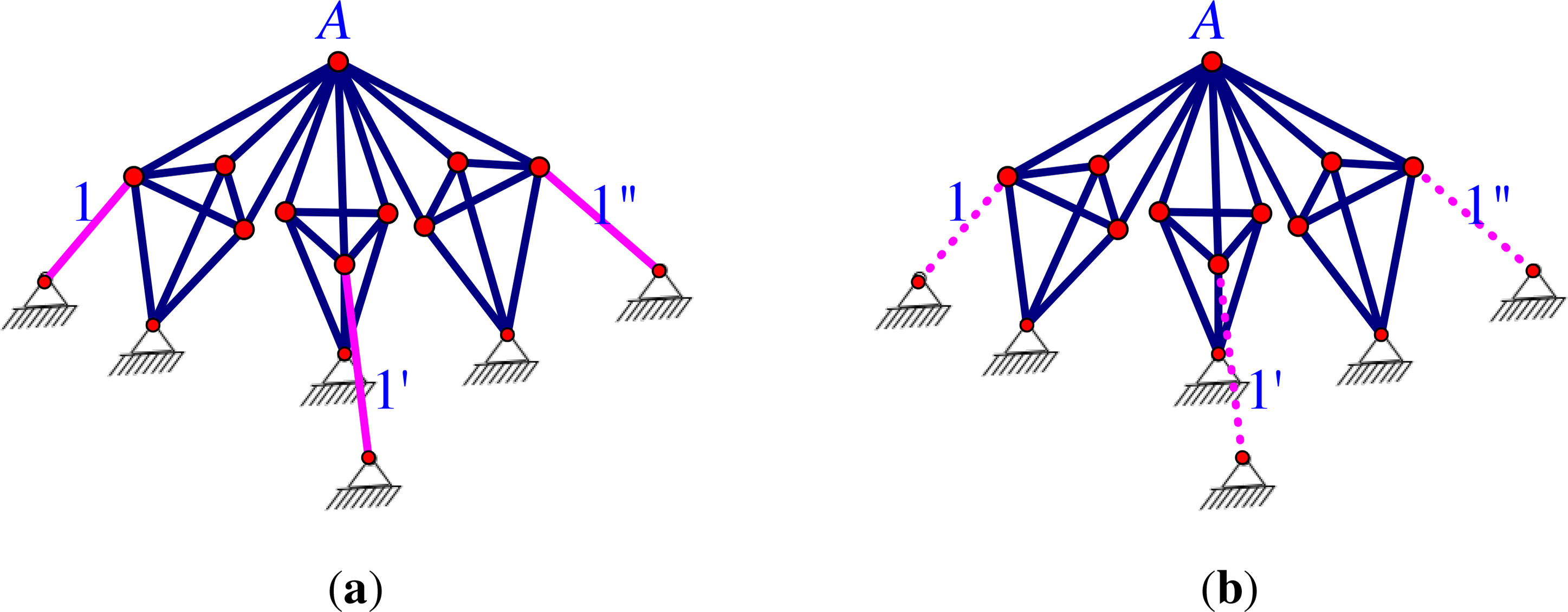
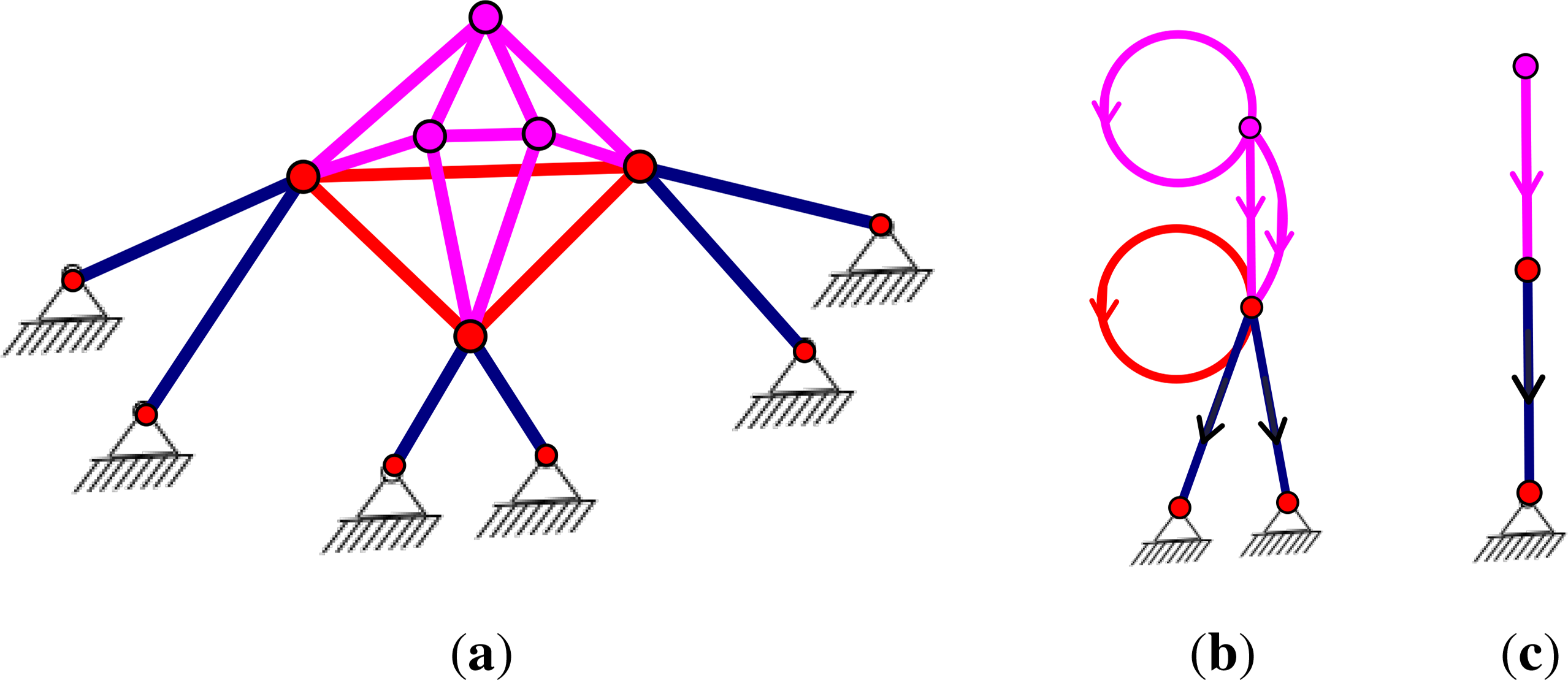
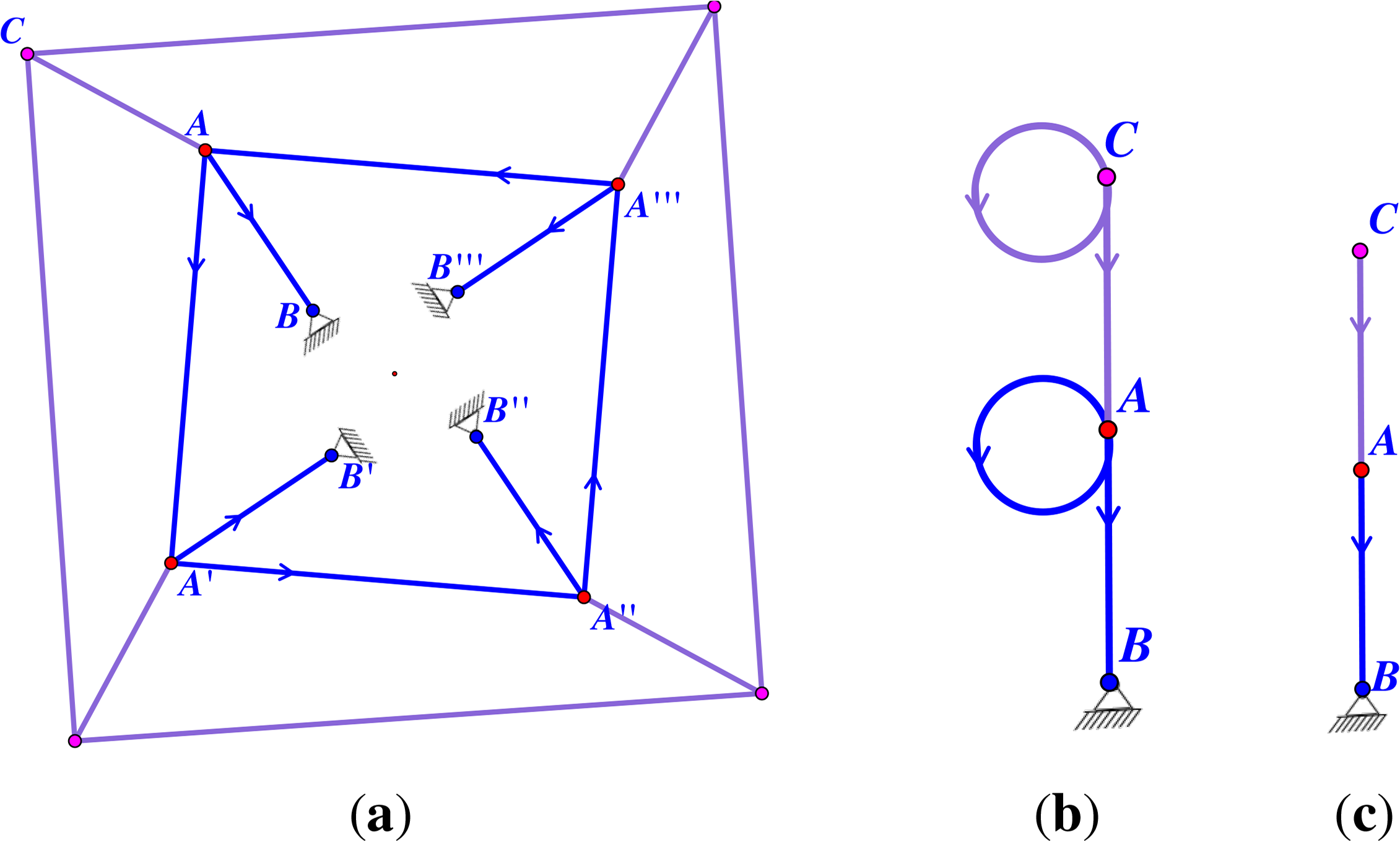
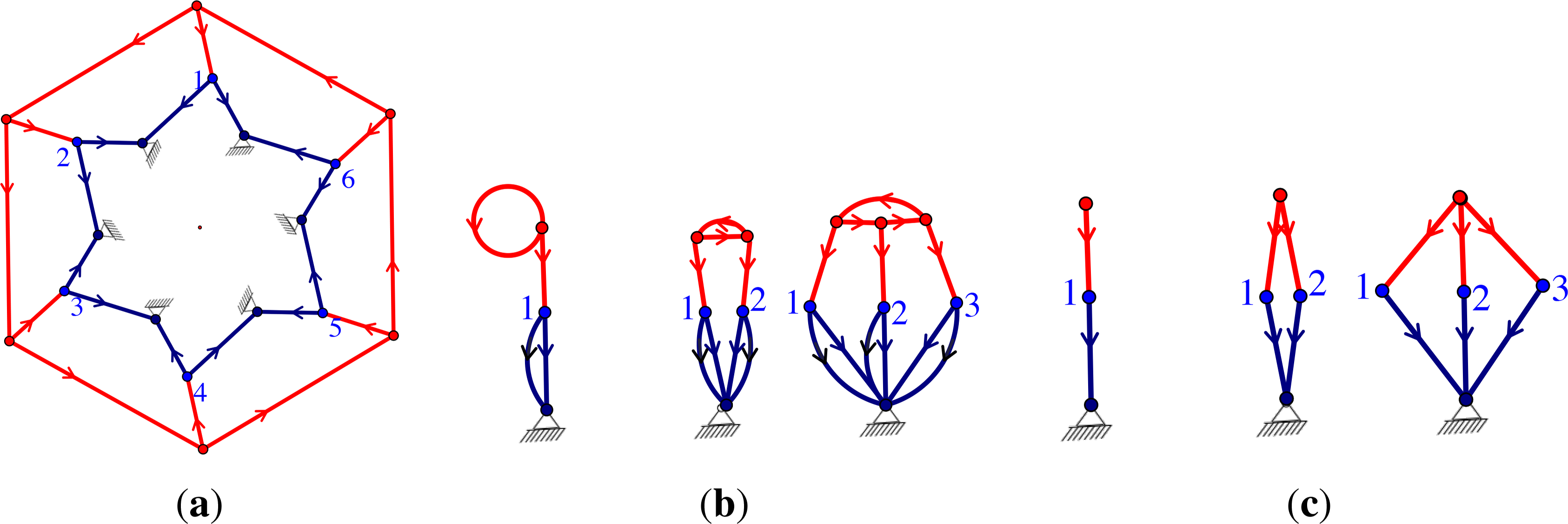
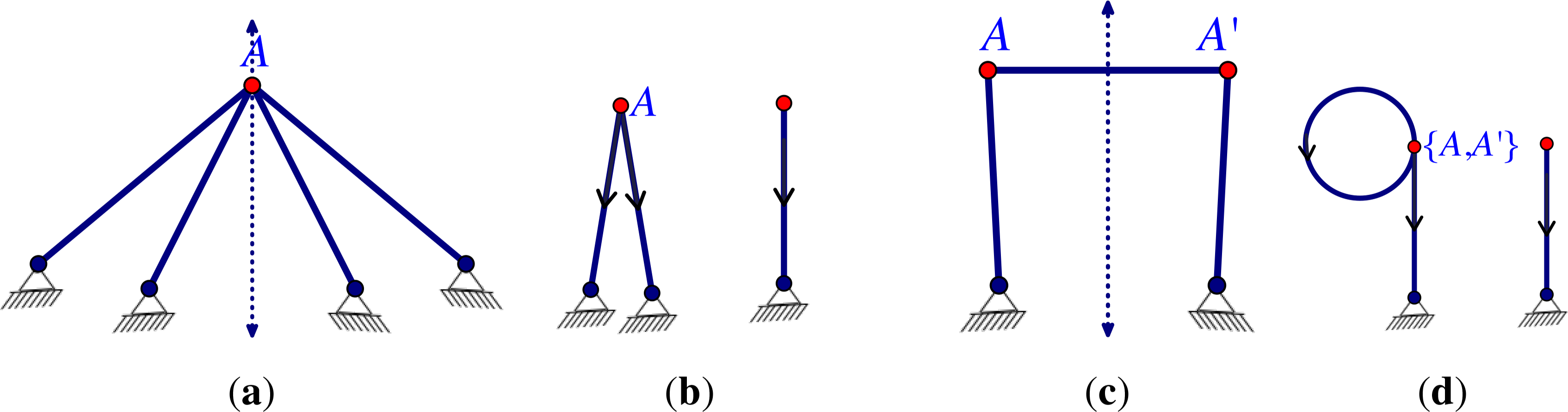
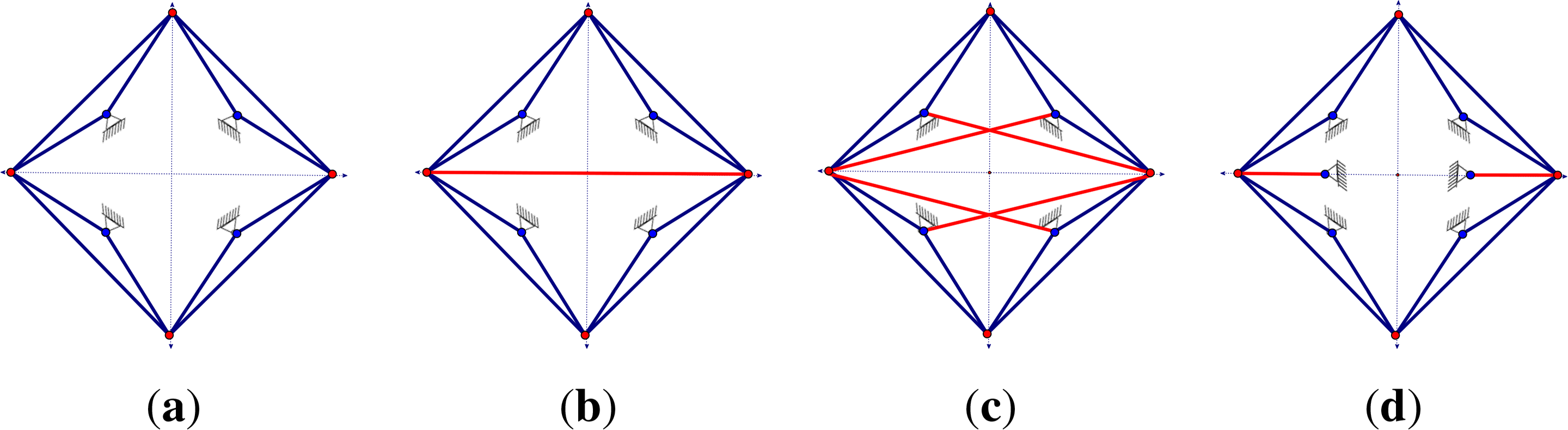
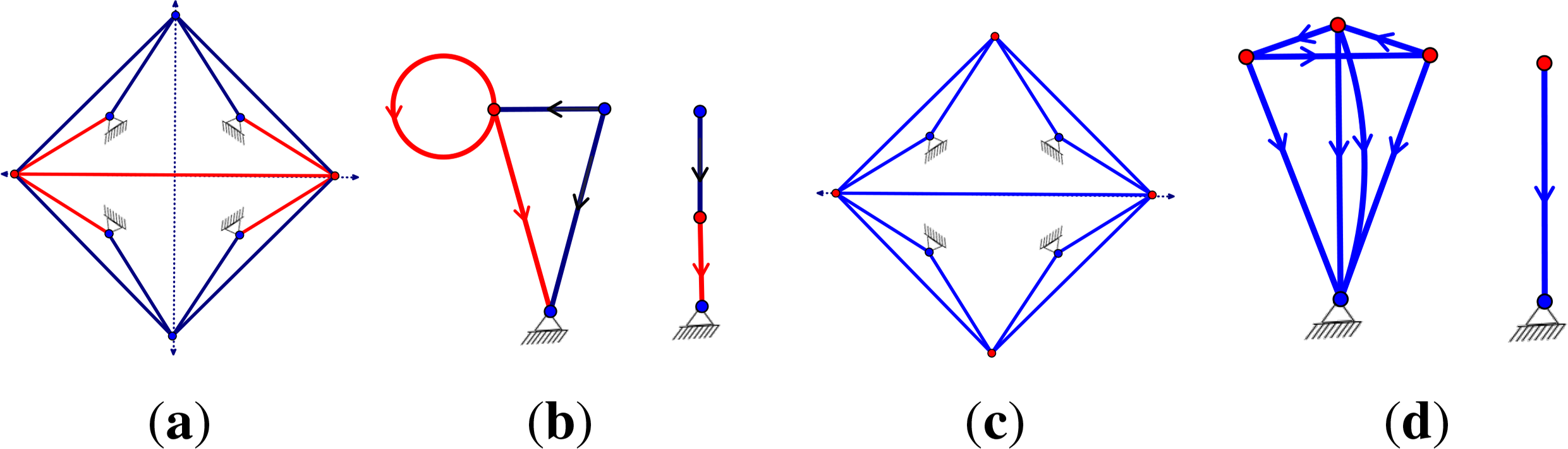
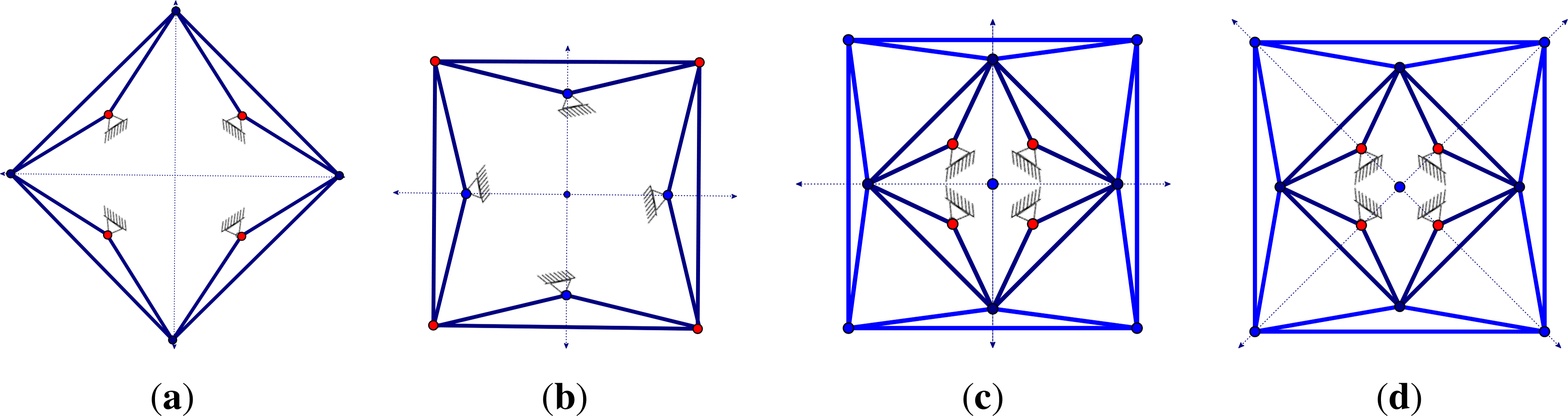
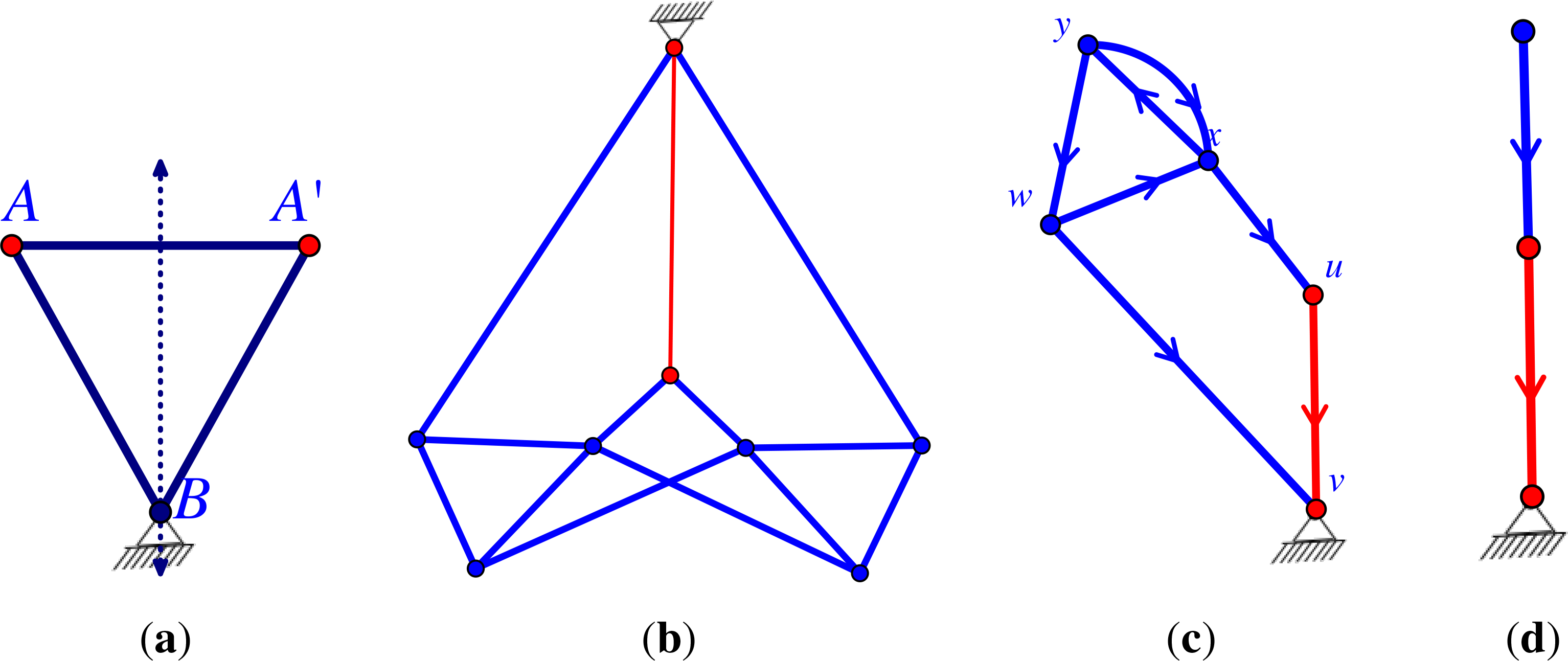
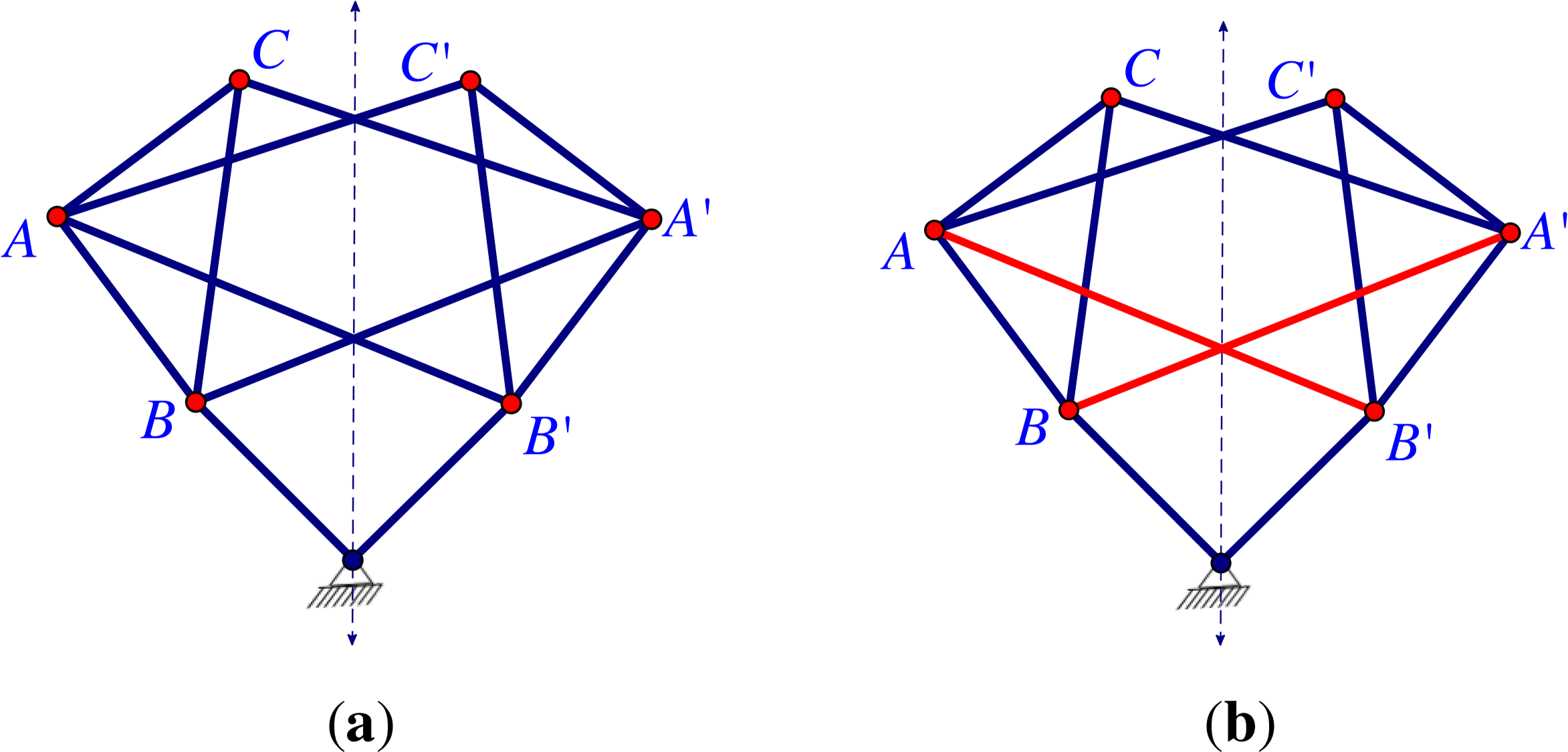
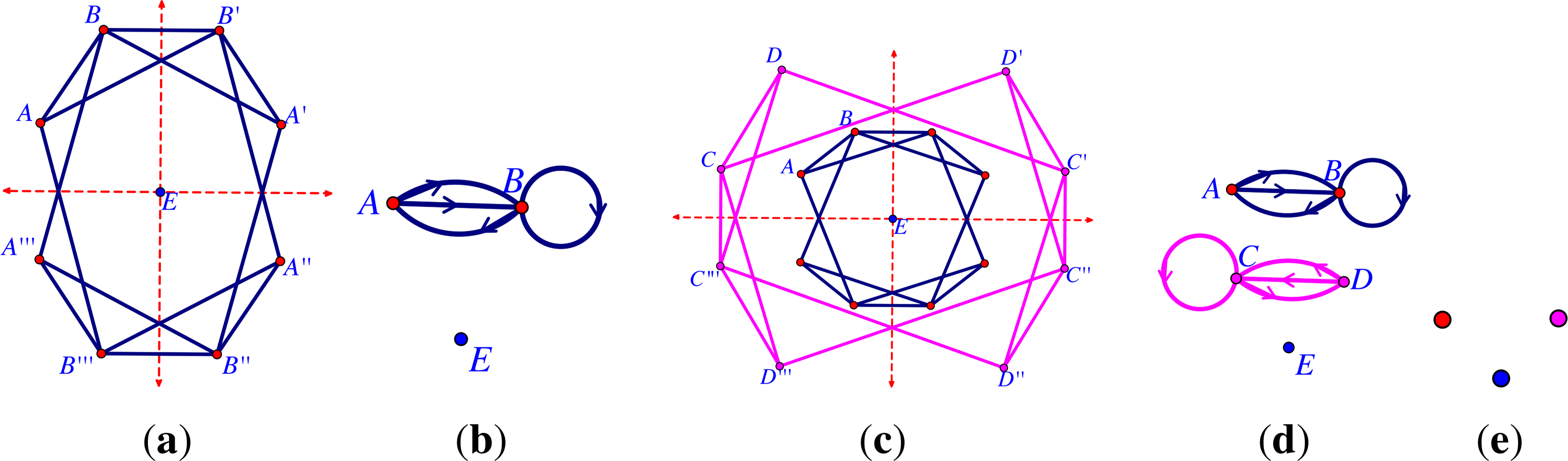
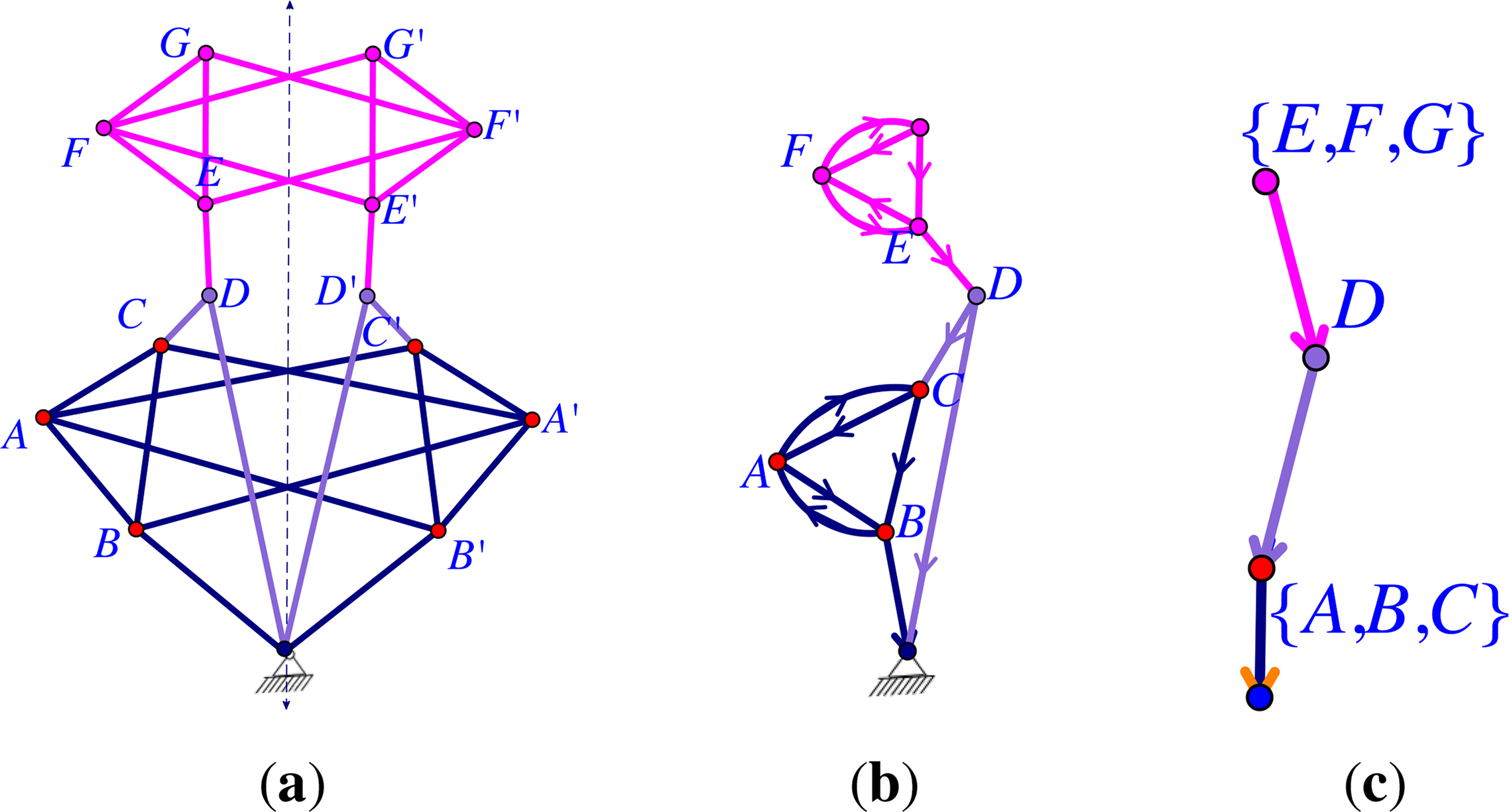
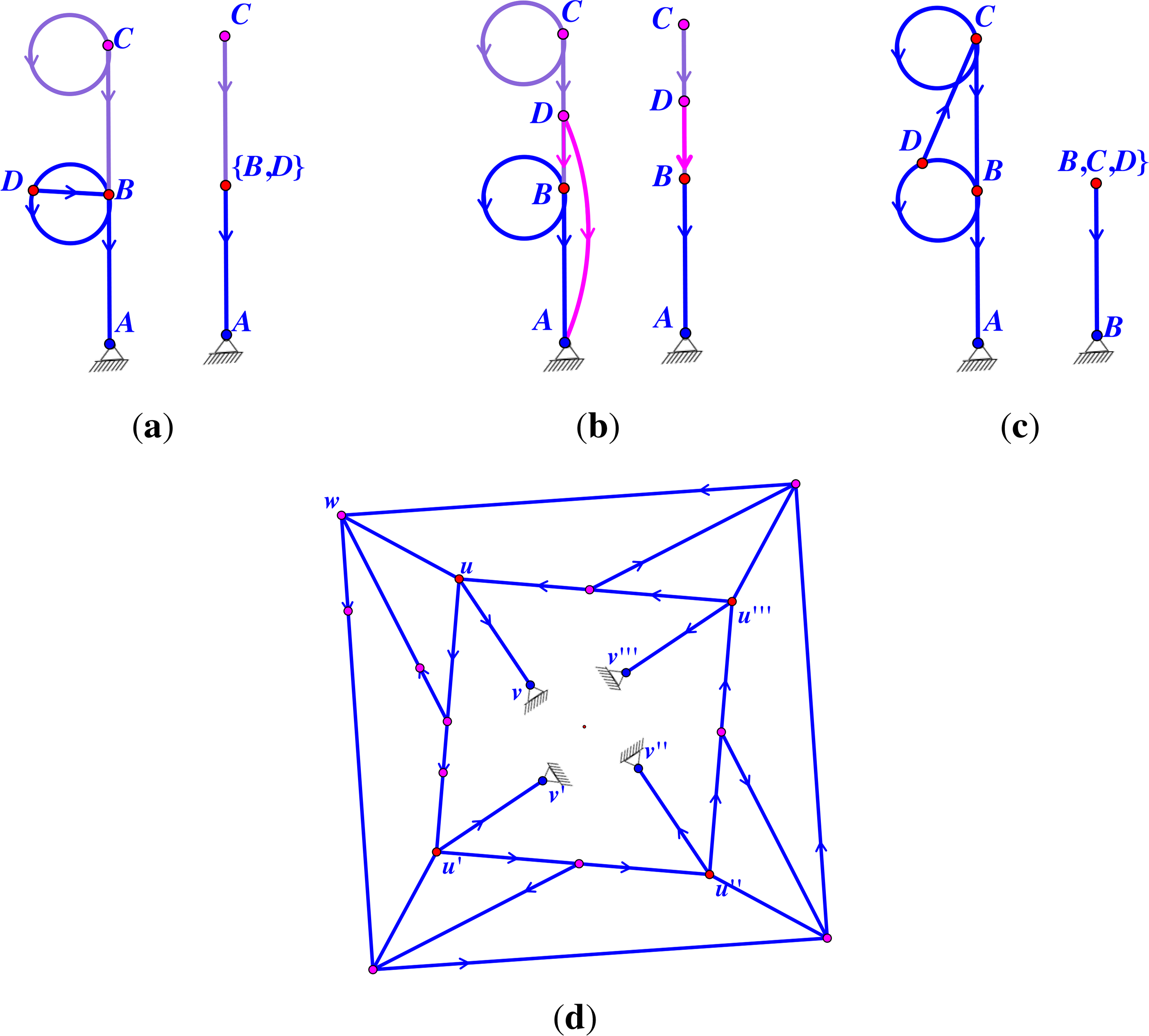
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Nixon, A.; Schulze, B.; Sljoka, A.; Whiteley, W. Symmetry Adapted Assur Decompositions. Symmetry 2014, 6, 516-550. https://doi.org/10.3390/sym6030516
Nixon A, Schulze B, Sljoka A, Whiteley W. Symmetry Adapted Assur Decompositions. Symmetry. 2014; 6(3):516-550. https://doi.org/10.3390/sym6030516
Chicago/Turabian StyleNixon, Anthony, Bernd Schulze, Adnan Sljoka, and Walter Whiteley. 2014. "Symmetry Adapted Assur Decompositions" Symmetry 6, no. 3: 516-550. https://doi.org/10.3390/sym6030516
APA StyleNixon, A., Schulze, B., Sljoka, A., & Whiteley, W. (2014). Symmetry Adapted Assur Decompositions. Symmetry, 6(3), 516-550. https://doi.org/10.3390/sym6030516



