Abstract
Periodic patterns and symmetries are striking visual properties that have been used decoratively around the world throughout human history. Periodic patterns can be mathematically classified into one of 17 different Wallpaper groups, and while computational models have been developed which can extract an image’s symmetry group, very little work has been done on how humans perceive these patterns. This study presents the results from a grouping experiment using stimuli from the different wallpaper groups. We find that while different images from the same wallpaper group are perceived as similar to one another, not all groups have the same degree of self-similarity. The similarity relationships between wallpaper groups appear to be dominated by rotations.
1. Introduction
Symmetry and tilings have been used in art and architecture throughout human history [1,2,3]. Two-dimensional periodic patterns can be classified into 17 different wallpaper groups based on the Euclidean plane isometries (translations, reflections, rotations and glides) that they possess. Islamic, Moorish and Egyptian architecture (see Figure 1) and the art of M. C. Escher are rich with ornate examples. The Alhambra palace contains examples of most, if not all, of the wallpaper groups [4,5]. These patterns are also used throughout everyday Western architecture (see Figure 2 for some examples).
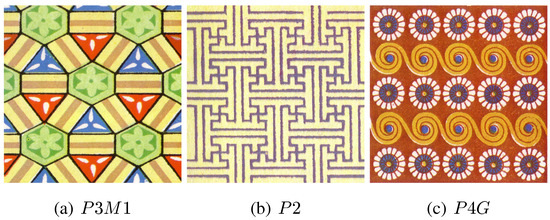
Figure 1.
Some examples of ornate symmetrical patterns.

Figure 2.
Some examples of everyday symmetrical patterns.
The reasons why symmetries in repeating patterns present such compelling impressions to human vision have been the subject of research over many decades. Gestalt theory recognised that symmetry contributes to the “goodness” of a form, promoting its emergence through the grouping of image elements. Subsequent experimental investigations have defined goodness (also termed salience) behaviourally, in terms of accuracy and speed of discriminating symmetrical forms from non-symmetrical ones, and resistance of discrimination to degradation of symmetry by noise. In dot patterns and geometrical forms, key findings have been that mirror symmetry (around a reflection axis) is more quickly and accurately detected than either translation or rotational symmetry [6,7]. Mirror symmetry is detected more quickly and accurately if a pattern is reflected in a vertical axis than in a horizontal one, and less well again if reflected in oblique axes [7]. A variety of theories have been proposed to explain these and other findings, in terms of the properties of either multiple processes of symmetry detection, or the properties of the representations of images that they generate (for a review, see [8], and for recent models see [9,10,11,12]).
In this paper, we will not address questions about the detection of symmetries in images, but instead will investigate how symmetries affect the appearance of two-dimensional patterns. The measurement of visual appearance is important in applied contexts as a means to determine how people describe and classify objects, materials and surfaces. Our understanding of the physical basis of visual appearance is greatest in the case of colour [13], whereas other properties have been less well explored. One of these is texture; fine-scale variation in surface height and reflectance that has constant statistical properties from one patch of a surface to another. The main perceptual dimensions along which people classify images of textures have been identified [14,15], and include roughness, directionality and regularity. However, progress has only been made in identifying the mathematical properties of surfaces that underlie these dimensions in a few specific cases, such as roughness in random-phase surfaces [16], and the effects of phase randomisation on the appearance of phase-rich surfaces [17].
Since the visual textures used in the creation or decoration of artificial surfaces often contain periodically repeating elements, it is interesting to ask how the symmetries present in such textures influence human perception of their appearance. Previous work on the appearance of patterns containing symmetries has tested their effects on aesthetic impressions, showing that there is a correlation between symmetric patterns and judgements of “beauty” in a pattern [18], or on perceived complexity. In the second case, [19] used “band” (or “frieze”) patterns consisting of a simple geometric form repeated (translated) along a single axis, with combinations of reflections, rotations and glide reflections defined by the seven symmetry groups that are possible for such a pattern. They concluded that processes of grouping these elements into larger perceived “motifs” partially overrode the effects of symmetry on judgements of complexity.
Here, we aim to use two-dimensional periodic patterns made up from patches of random-dot noise to measure the perceived similarity of exemplars from each of the wallpaper groups to other exemplars of the same group, and to exemplars of the other groups. To this end, a free-sorting experiment will be described in which observers were asked to sort a set of 85 patterns (i.e., 5 examples from each of the 17 groups) into subsets of similar appearance. Similarity matrices obtained by this sorting method have previously been used to identify the dimensions underlying human classification of visual textures (e.g., [14,15]). it is important to emphasise that observers in our experiment were not instructed to classify the stimulus patterns into subsets according to the symmetries present in them, and nor was their attention drawn to the fact that the patterns contained multiple symmetries or that they were relevant to the experiment. Computer vision models that can extract a pattern’s symmetry group from an image have been developed [20,21,22], but this is likely to be a highly skilled task for humans, completely unlike the judgements of visual similarity that we sought to obtain.
2. The 17 Wallpaper Groups
There are four Euclidean plane isometries: translation, rotation, reflection and glide. A translation involves shifting a plane by a displacement vector v. As we are dealing with periodic patterns, then for each wallpaper group P, there exists a such that P is invariant under the translation . (Note: this is only strictly true for patterns that repeat infinitely in two directions). A rotation, , involves rotating around a point c by an angle of result and a reflection involves reflecting the pattern in the line L (mirror symmetry). Finally a glide is a combination of a translation along the line L by distance d, followed by . The 17 different wallpaper groups all possess different Euclidean plane isometries, and a summary is given in Table 1. We use the standard Crystallographic notation for wallpaper groups [23]. For more details, see [24,25].

Table 1.
A summary of the 17 possible wallpaper groups. Note, rotation centres lie on reflection axes except for groups and . If a group has n rotations, this means that it is invariant under rotations of .
3. Methods
3.1. Stimuli
Five exemplars of each wallpaper group were created by tiling patches of white noise patterns. This gave a total of 85 textured stimuli. The white noise patches had an area pixels. Depending on the symmetry class, these patches were square, rectangular or triangular. Tiles were then created from the patches using reflections, rotations and glides. The advantage of using noise rather than textons is that it minimizes the role that patch (texton) similarity can have on the perceived similarity of the whole pattern. It is likely that the relative importance of symmetry group (global structure) and textons (local structure) will depend on other factors, such as spatial scale and contrast. Trying to investigate the effect of all of these variables on perceived similarity at the same time would require a prohibitive number of stimuli.
White noise was chosen as it allows us to create many equivalent instances of the same symmetry group, and it avoids the problems of tiling discontinuities that would arise if coloured noise were used. (For example, if coloured noise was used, there would be obvious edge discontinuities when a patch was tiled with a copy of itself rotated . As all the pixels in white noise are uncorrelated, this problem as avoided.) For textures with and rotations, the white noise patches were first up-sampled by a factor of eight. This was done as to minimise the loss of high frequencies due to bilinear interpolation when rotating the white noise patches. Once the tiled image had been created it was down-sampled back to its original scale. Finally a Gaussian filter ( pixels) was applied to all of the resulting tiled images in order to remove any high frequency artifacts that may have been introduced by the rotation operations. The standard deviation of pixel intensities was prior to printing.
These images were then printed onto card and cut into circles. This was done in order to encourage observers to choose their own preferred orientation for each image. An example image from each group is shown in Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25, Figure 26 and Figure 27.
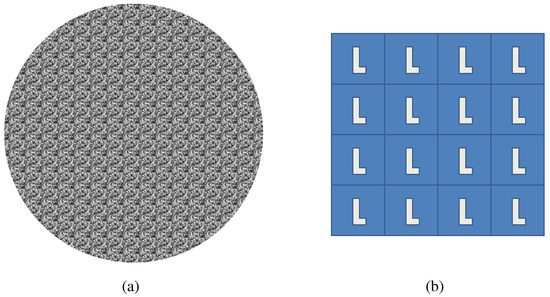
Figure 11.
P1. (a) Example stimuli; (b) Cell structure.
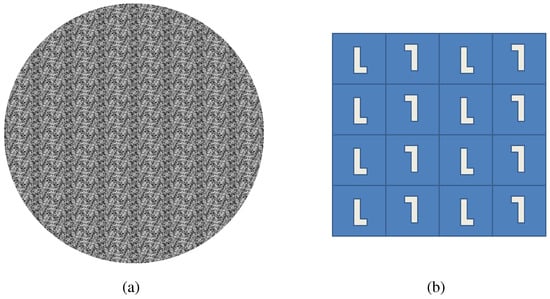
Figure 12.
P2. (a) Example stimuli; (b) Cell structure.
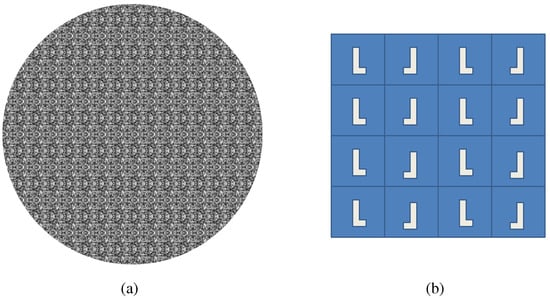
Figure 13.
PM. (a) Example stimuli; (b) Cell structure.
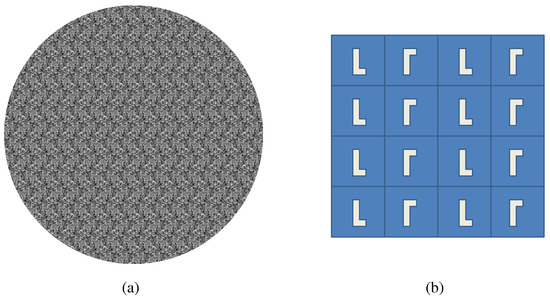
Figure 14.
PG. (a) Example stimuli; (b) Cell structure.
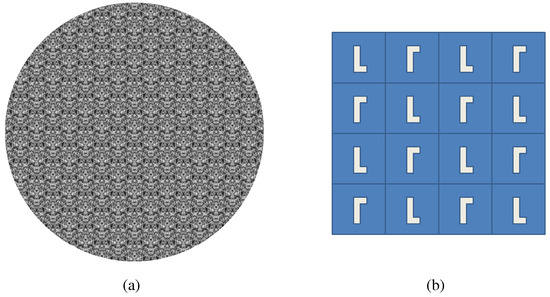
Figure 15.
CM. (a) Example stimuli; (b) Cell structure.
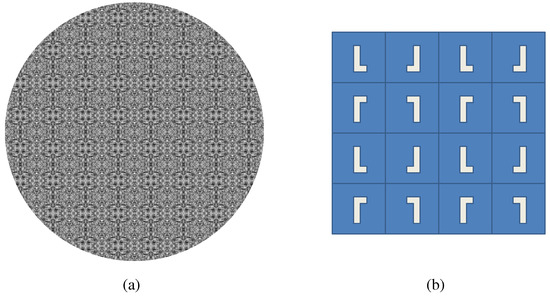
Figure 16.
PMM. (a) Example stimuli; (b) Cell structure.
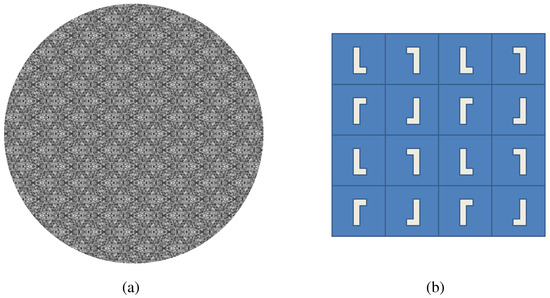
Figure 17.
PMG. (a) Example stimuli; (b) Cell structure.
Figure 18.
PGG. (a) Example stimuli; (b) Cell structure.
Figure 19.
CMM. (a) Example stimuli; (b) Cell structure.
Figure 20.
P4. (a) Example stimuli; (b) Cell structure.
Figure 21.
P4M. (a) Example stimuli; (b) Cell structure.
Figure 22.
P4G. (a) Example stimuli; (b) Cell structure.
Figure 23.
P3. (a) Example stimuli; (b) Cell structure.
Figure 24.
P3M1. (a) Example stimuli; (b) Cell structure.
Figure 25.
P31M. (a) Example stimuli; (b) Cell structure.
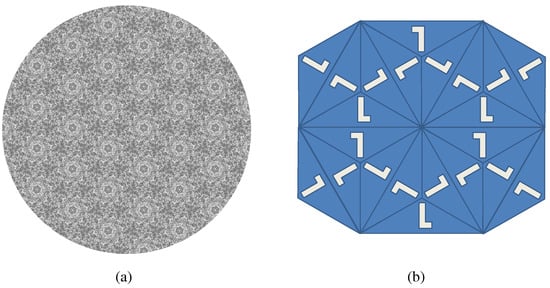
Figure 26.
P6. (a) Example stimuli; (b) Cell structure.
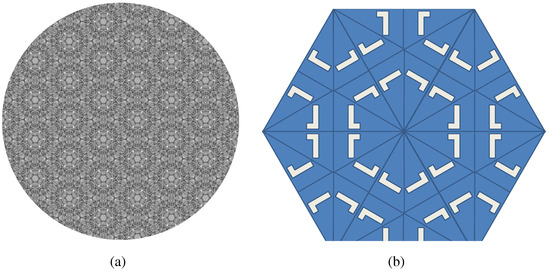
Figure 27.
P6M. (a) Example stimuli; (b) Cell structure.
3.2. Participants
15 participants (10 male, 5 female), ranging in age between 23 and 58 years, took part in the study. Some were familiar with experiments involving free sorting of textured images, but none with experiments on symmetrical patterns. They did not receive payment for their participation.
3.3. Procedure
Participants were presented with all the 85 images laid out randomly on a large table, and were instructed to classify them into as many subsets as they wished, by placing them into piles of any size. They were free to take as long as they wished to complete the task, and to move images between subsets until they were satisfied with their classification. They were not asked to group by symmetry, only that their subsets should consist of similar images. The experiment was carried out in a corner of a large office, screened from natural light and illuminated by normal overhead room lighting (two fluorescent tubes).
4. Results
Participants took between approximately 15 and 30 min to sort the images into subsets. Figure 3 shows the number of subsets made by different participants, and the distribution of the number of images in subsets of different sizes. The overall similarity matrix is shown in Figure 4.
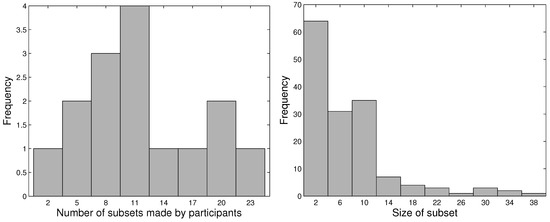
Figure 3.
Histograms showing (left) the number of subsets chosen by the participants; (right) the size of the subsets made.
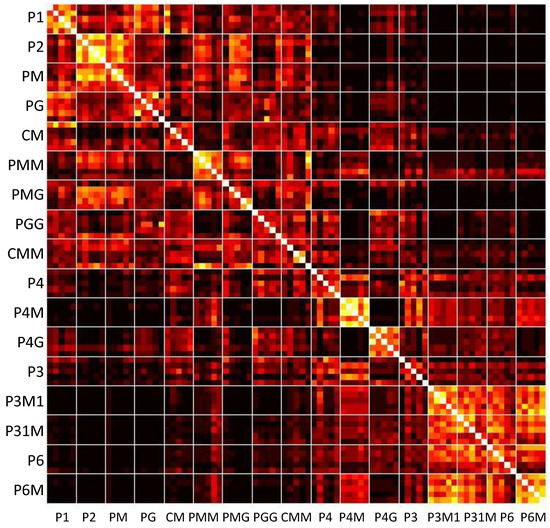
Figure 4.
Similarity matrix. Each row and column represents an image, and the colour of the pixel at position indicates the number of times image i was placed in a subset with image j. Brighter colours indicate increasing similarity. The high values along the diagonal are due to each image being classed as similar to itself. The images are grouped by symmetry group, as indicated by the white lines.
The first question we want to ask is whether participants classified images from the same wallpaper group as being similar to each other. Figure 5 shows how often images from a group were classed with other images from the same group. This was further analysed as follows: for each image I, the similarity matrix was used to retrieve the nth most similar images. A score, was given by the number of images belonging to the same wallpaper group as I among the n most similar (with a maximum of 4 as there were 5 instances of each wallpaper group in the set of images). The mean results for each wallpaper group are shown in Figure 6. As can be seen, images from the same wallpaper group are retrieved more often than would be expected by chance.
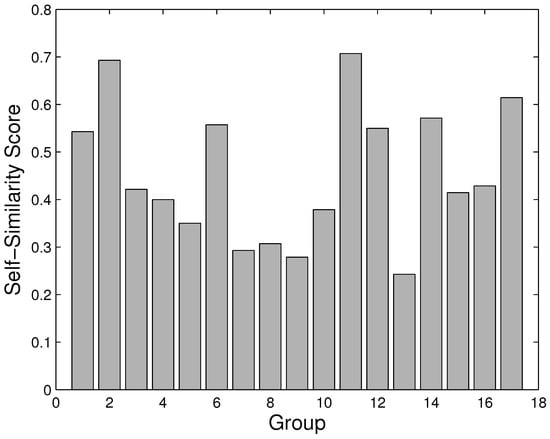
Figure 5.
The degree of self-similarity for each of the 17 wallpaper groups.
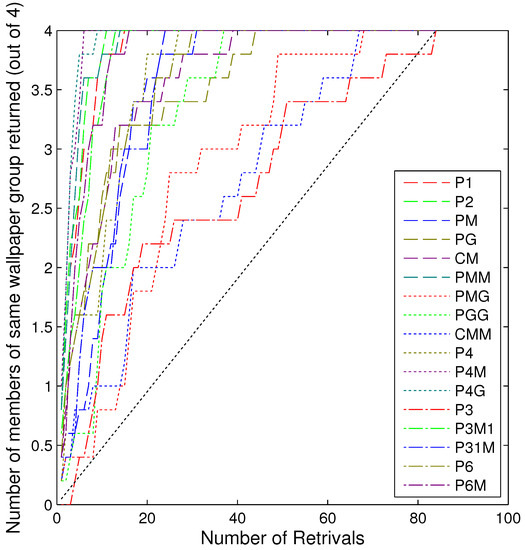
Figure 6.
Mean number of retrievals from the same wallpaper group. The dotted line shows the number of retrievals that would be expected by chance (hypergeometric distribution). Each line represents a different symmetry group.
However, we can clearly see from Figure 4 and Figure 6 that the participants did not use only an image’s wallpaper group when making subsets, and there is considerable overlap between the different groups. The perceived similarity between wallpaper groups is shown in Figure 7. This was constructed by collapsing the similarity matrix to obtain a value for each group, rather than each individual image. A group’s self-similarity was calculated as the mean number of times that a participant classified an image from a group with other images from the same group, divided by 4, giving a value in the range 0–1. In the figure, a group’s self-similarity is represented by the area of its shape symbol, with groups whose exemplars were consistently classified as similar to one another, such as and , represented by large shapes. Groups with a low degree of self-similarity, such as and , are represented by small shapes. The similarity of one group to another was calculated as the mean number of times that a participant classified an image from one group with an image from another, divided by 5 (since each image has five opportunities to be classified with an image in another group). In Figure 7, similarities between groups are represented by the thicknesses of the lines connecting their shape symbols. We can see that images from , and were perceived as very similar to one another. Likewise, , , and formed a coherent set of perceptually similar images.
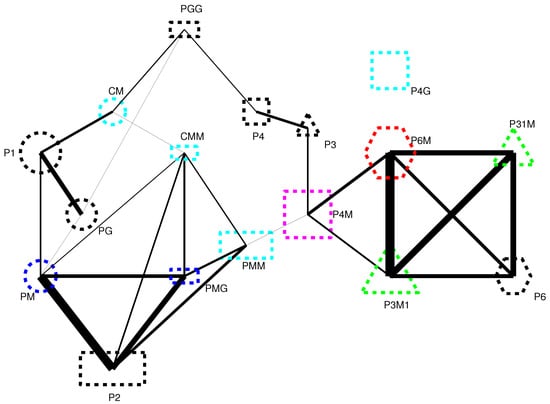
Figure 7.
Graph showing how similar the wallpaper groups are to each other. The different shapes represent a group’s rotations (circle = no rotations, rectangle = 1 rotation, square = 2 rotations, triangle = 3 rotations, hexagon = six rotations) and the colour represents the number of reflections (black = no reflections, dark blue = 1 reflection, light blue = two reflections, green = 3 reflections, pink = 4 reflections and red = 6 reflections). The size of the shapes represent how consistently participants grouped members from the same wallpaper group together, and the thickness of the connecting lines represents how similar the different wallpaper groups are to each other. Note: only the top quartile of inter-group similarities are shown.
The role of individual symmetries in determining perceived similarity was further explored with a multi-linear regression model. Each symmetry group was described using a feature vector where , and are the number of rotations, reflections and glides contained in the wallpaper group. These were then used to explore whether there is a link between the number of symmetries in a wallpaper group and its degree of self similarity. The results from the regression analysis suggest that this is not the case (, ).
A separate regression was performed on each inter-group comparison, giving 136 data points, and the dependent variables were , and for comparing wallpaper group i with group j. The results from this linear regression give a of only 0.181 (, ). Although the relationship is significant, the low value of implies that human observers do not decide whether to classify two images together or apart simply on the basis of the number of symmetries that they contain. Of the three independent variables, only was found to have a significant effect, with , .
5. Discussion
The aim of this study was to investigate the effect of symmetry on texture similarity judgements. In order to minimise the effect of texton similarity, we used patches of white noise as textons. The reasoning behind this was that any perceived structure arising from the properties of the wallpaper groups would be more apparent in observers’ classifications. The results show that images from the same group were classified together by human observers more often than would be expected by chance. The similarity relationships shown in Figure 7, and the results of the regression analyses, further indicate that the number of rotational symmetries in an image has a stronger influence on its classification than the numbers of either reflections or glides that are present. However, it is also clear from the results that images were not classified by wallpaper group, or number of rotational symmetries, alone, and that observers must have taken other visual properties into account in making classifications.
An important question in interpreting these results is their possible sensitivity to the particular random dot patterns that were repeated to create the images. It is well known that if stochastic patterns of textons such as dots are reflected around one or more two-fold symmetry axes, the groupings of textons that are perceived depend strongly on their initial arrangement. Observers’ classifications of symmetric patterns of this kind by visual similarity would clearly be dominated by specific arrangements of textons. However, the stimuli used here differed from those previously used in experiments on symmetry in containing many more repetitions of a texton (the random dot patch used as a seed), and in the fine scale at which the random dot texture was viewed (see examples of stimuli in Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25, Figure 26 and Figure 27). For two reasons, we argue that the classifications of these patterns would be robust to variation in the random dot seeds.
First, the similarity matrix (see Figure 4) shows that values in the 5 × 5 blocks of cells lying along the diagonal (ignoring cells representing self-similarities of single images) are higher than the average similarity value for pairs of images, implying that images drawn from the same wallpaper group were more often classified together in the same subset than randomly chosen pairs of images. If similarity was determined by random dot seeds alone, this pattern would not be observed.
Second, inspection of the sets of images in each wallpaper group shows that similar large-scale geometric structure emerges in all five exemplars, despite variations in detail caused by the random seed. Figure 8, Figure 9 and Figure 10 show examples from groups , and . Particular groups are characterised by structures such as grid patterns (e.g., PMM), striations (e.g., P2), or large geometric forms with characteristic triangular, circular or elliptical shapes (e.g., P6M). These structures are comparable to the “motifs” that [19] argued account in part for judgements of complexity in band patterns with different symmetry properties. It is probable that the influence of wallpaper group on classification that we have observed does not operate directly through recognition of symmetries, but instead through perceptual classification of the characteristic scales and shapes of the motifs that each group generates in images, whatever random dot seed is used.

Figure 8.
Examples of different instances of P2.

Figure 9.
Examples of different instances of PMM.

Figure 10.
Examples of different instances of P6M.
The results obtained in our experiment cannot be compared directly to those in the literature on symmetry detection, without knowing to what extent observers based their classification of images on their goodness, or salience, of the symmetries that they contained. This may well have been one factor underlying similarity judgements but, as we have seen, the motifs perceived in images were probably also important (cf. [19]). A further problem in comparing results is that observers had unlimited time to make classifications, and were free to move images between subsets until they were satisfied with them. Measures of reaction time from symmetry detection experiments may be relevant to any classification decisions that were made quickly, but not to those made more slowly and deliberately. For these reasons, the present data cannot be used to test models of symmetry detection. Even so, some tentative comparisons can be made with existing data on the salience of different symmetries.
Strother et al. [19] found that glide symmetry in band patterns made little contribution to judgements of complexity, and it appears also to have little effect on similarity judgements. The only difference between groups P1 and PG is that the latter contains a glide symmetry (neither contains reflection or rotation symmetries), and images from the two groups are frequently classified together (see Figure 7), consistent with the hypothesis that glide symmetry is not readily visible. However, the relative importance of reflection and rotation in determining image classification is not consistent with previous results on the salience of symmetries. It is well established that reflection is more salient in dot arrays or geometrical forms than rotation (e.g., [7]), and the same difference is seen in the perceived complexity of one-dimensional band patterns ([19]). However, we found that the self-similarity of (which contains only a rotation) is greater than that of (which contains only a reflection). Furthermore, images from these two groups were very frequently classified together (see Figure 7). Treating the results more globally, we have already noted above the negative correlation between similarity of images and difference between them in number of rotation axes, and the absence of a correlation in the case of similarity axes.
The effect of reflection and rotation symmetries on the appearance of the images that we used therefore cannot be predicted from their salience in simpler patterns, and we hypothesise instead that they are based on the distinct types of large-scale motifs characteristic of groups with different numbers of rotational symmetry axes. Those with none (, , , ) have the appearance of fine meshes or grids; those with one (, , , ) of more conspicuous grids, striations or zigzags; those with two (, , ) of larger, more conspicuous geometrical forms arranged in square arrays; those with three (, , ) of similar geometrical forms but in triangular arrays; and those with six (, ) of arrays of conspicuously large circular or hexagonal forms. Varying the number of reflection axes does not have equally consistent effects on large-scale structure.
Another feature of our results is more consistent with previous data on salience of symmetries. Wenderoth et al. [26] varied the number of reflection symmetry axes in a pattern, and found that symmetry in patterns with four axes was detected more quickly and accurately than in ones with two or three axes, which in turn gave superior performance to patterns with a single axis. Although, as noted above, we find an effect of number of rotation axes, our results are consistent with the more general hypothesis that perceived similarity of patterns, like their salience, is influenced by the number of symmetry axes present. It is interesting to note in this respect that if the total numbers of rotation and reflection axes in our images are considered, the five groups that contain six in all (i.e., , , , and ) form a tightly interconnected subset in Figure 7.
The experiment reported here is the first to investigate the effect of symmetry properties on the perceived appearance of patterns constructed from repeated patches of random dots, using all the 17 wallpaper groups that define possible symmetries in two dimensional patterns. We have shown that images with the same symmetry properties are classified together as similar more often than would be expected by chance, and therefore that these properties have an effect on the appearance of images. We have also shown that the number of axes of rotational symmetry has a significant effect on the classification of images, but the number of reflection or glide axes does not. At this stage, it is not possible to conclude to what extent the goodness, or salience, of the different symmetries in images like these influences their perceptual classification. Further experiments that controlled the presentation time of images could resolve this question by restricting decisions to the most salient symmetries present. It will also be interesting to explore the contribution of texton similarity and scale to the perceptual classification of symmetrical patterns.
References and Notes
- Abas, S.J.; Salman, A.S. Symmetries of Islamic Geometrical Patterns; World Scientific Publishing Company: Singapore, 1994. [Google Scholar]
- Rnning, F. Geometry and Islamic Patterns. Available online: http://people.exeter.ac.uk/PErnest/ pome24/index.htm (accessed on 23 May 2011).
- Tyler, C.W. The human expression of symmetry: Art and neuroscience. Available online: http://www.ski.org/CWTyler_lab/CWTyler/Art%20Investigations/Symmetry/Symmetry.html (accessed on 23 May 2011).
- Grnbaum, B.; Grnbaum, Z.; Shephard, G.C. Symmetry in moorish and other ornaments. Comput. Math. Appl. 1986, 12, 641–653. [Google Scholar] [CrossRef]
- Grnbaum, B. What symmetry groups are present in the Alhambra? Not. AMS 2010, 53, 670–673. [Google Scholar]
- Bruce, V.; Morgan, M. Violations of symmetry and repetition in visual patterns. Perception 1975, 4, 239–249. [Google Scholar]
- Palmer, S.; Hemenway, K. Orientation and symmetry: Effects of multiple, rotational and near symmetries. J. Exp. Psychol. Hum. Percept. Perform. 1978, 4, 691–702. [Google Scholar]
- Van der Helm, P.; Leeuwenberg, E. Goodness of visual regularities: A nontransformational approach. Psychol. Rev. 1996, 103, 429–456. [Google Scholar]
- Treder, M.S. Behind the looking-glass: A review on human symmetry perception. Symmetry 2010, 1, 1510–1543. [Google Scholar]
- Scognamillo, R.; Rhodes, G.; Morrone, C.; Burr, D. A feature-based model of symmetry detection. Proc. Biol. Sci. 2003, 270, 1727–1733. [Google Scholar]
- Dry, M.J. Using relational structure to detect symmetry: A Voronoi tessellation based model of symmetry perception. Acta Psychol. 2007, 128, 75–90. [Google Scholar] [CrossRef] [PubMed]
- Poirier, F.J.A.M.; Wilson, H.R. A biologically plausible model of human shape symmetry perception. J. Vis. 2010, 10, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Fairchild, M.D. Color Appearance Models, 2nd ed.; Wiley-IS&T: Chichester, UK, 2005. [Google Scholar]
- Rao, A.; Lohse, G. Towards a texture naming system: Identifying relevant dimensions of texture. Vis. Res. 1996, 36, 1649–1669. [Google Scholar] [PubMed]
- Heaps, C.; Handel, S. Similarity and features of natural textures. J. Exp. Psychol: Hum. Percept. Perform. 1999, 25, 299–320. [Google Scholar] [CrossRef]
- Padilla, S.; Drbohlav, O.; Green, P.; Spence, A.; Chantler, M. Perceived roughness of 1/fβ surfaces. Vis. Res. 2008, 48, 1791–1797. [Google Scholar] [CrossRef] [PubMed]
- Emrith, K.; Chantler, M.; Green, P.; Maloney, L.; Clarke, A. Measuring perceived differences in surface texture due to changes in higher order statistics. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2010, 27, 1232–1244. [Google Scholar]
- Jacobsen, T.; Höfel, L. Descriptive and evaluative judgment processes: Behavioral and electrophysiological indices of processing symmetry and aesthetics. Cogn. Affect. Behav. Neurosci. 2003, 3, 289–299. [Google Scholar] [CrossRef] [PubMed]
- Strother, L.; Kubovy, M. Perceived complexity and the grouping effect in band patterns. Acta Psychol. 2003, 114, 229–244. [Google Scholar] [CrossRef]
- Liu, Y.; Collins, R.T.; Tsin, Y. A computational model for periodic pattern perception based on frieze and wallpaper groups. IEEE Trans. Pattern Anal. Mach. Int. 2004, 26, 354–371. [Google Scholar]
- Chetverikov, D. Pattern orientation and texture symmetry. Lect. Notes Comput. Sci. 1995, 970, 222–229. [Google Scholar]
- Park, H.; Martin, G.R.; Bhalerao, A.H. Structural Texture Segmentation using Affine Symmetry. In Proceedings of the International Conference on Image Processing, San Antonio, TX, USA, 16 September–19 October 2011; pp. II-49–II-52. [Google Scholar]
- Zwillinger, D. CRC Standard Mathematical Tables and Formulae, 31st ed.; Chapman and Hall, CRC: Boca Raton, FL, USA, 2002. [Google Scholar]
- We can also recommend the wikipedia page (http://en.wikipedia.org/wiki/Wallpaper_group) as an excellent resource for examples and an accessible introduction as to why there are only 17 unique wallpaper groups.
- Schattschneider, D. The plane symmetry groups: Their recognition and notation. Am. Math. Mon. 1978, 85, 439–450. [Google Scholar] [CrossRef]
- Wenderoth, P.; Welsh, S. Effects of pattern orientation and number of symmetry axes on the detection of mirror symmetry in dot and solid patterns. Perception 1998, 27, 965–976. [Google Scholar] [CrossRef] [PubMed]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/.).