Visual Discrimination of the 17 Plane Symmetry Groups

Abstract

Within most of the 17 plane symmetry groups, individual symmetry operations act in multiple, nonequivalent ways. This, and the fact that many groups can be realized on the basis of different unit cells and generating regions, poses difficulties for visual discrimination and identification. Because of inherent confounds, only few of the groups can be studied by traditional experimental methodology. The use of an oddity paradigm and specific tiling patterns that camouflage groups in complex textures are recommended as partial remedy to this impasse. In order to prepare readers for an appreciation of the aforementioned issues and to provide a rationale for their investigation, the reporting of experiments and the discussion of methodological problems is preceded by a brief overview of the role which symmetry has played in the visual arts.

1. Symmetry in the Visual Arts

Symmetry seems ubiquitous in nature as well as in human artifacts [1]. It has also played an important role in the visual arts. Early examples are pottery ornaments, and friezes, from Ancient Egypt or even prehistoric times [2,3,4]. Although a comprehensive overview is not easily obtained, it appears that the earliest designs were dominated by simple repetitions (translations) and reflections. During antiquity and the Gothic period, rotations and glide reflections seem to have become more popular [2]. Symmetric mosaics that extend across whole walls or even whole buildings were created by the Moores and other Islamic cultures [5]. Since no relevant documents have ever been found, it seems that craftsmen realized their ideas without any mathematical theory [6].

This changed during the Renaissance. Although no sophisticated theory was developed, symmetry was regarded as an ideal to which architecture and design had to conform [7]. In order to depict existing buildings and objects or to illustrate those yet to be made such that they appear real, Alberti [8] devised a technique to construct a squares grid on canvas the way it appears to a beholder—thereby establishing the principles of linear perspective [9,10]. In so doing, Alberti not only used a highly symmetric model case, but he also related symmetry to tilings. This connection was certainly noted before, as testified by the existence of olden, non-square pavements [5,11]. Although symmetry has been a theme in many subsequent arts traditions [12], it was only with newer developments that it figured more prominently—again closely related to the topic of tessellation. The Austrian painter and artisan Koloman Moser (1868–1918), member of the so-called Vienna Secession, produced a number of plane-filling designs. Such designs, albeit in modified form (e.g., stretched or deformed) also dominate in OpArt, especially in the work of Victor Vasarely (1908–1997). The emphasis, however, now is on ambiguity and illusion. Vitz and Glimcher [13,14] noted that these developments went hand-in-hand with, and may partly even have been influenced by, trends in modern vision science [15,16]. A direct intrusion of mathematical thinking into the visual arts took many different routes. A very recent example is represented by Heinz-Otto Peitgen and his collaborators’ illustrations of recursive functions (or “fractals” [17]), another one, by the Austrian physicist and novelist Herbert Franke’s (born 1927) “computer art” (which focuses on continuous functions). In either type of pictures, higher-order symmetries are present, but a deepened mathematical understanding or artistic appreciation of symmetry has not been the driving force behind this work.

Interest in the mathematical analysis of symmetry was spawned by crystallographers [18]. It was found (among many other things which seem to be of greater concern to crystallography) that there are seven distinct possibilities to combine the different plane symmetry operations in friezes [19], and seventeen to create larger-scale designs that extend in two directions, covering the whole Euclidean plane [20]. In modern mathematics, these combinatorial singularities are now understood as algebraic groups [21]. It was the Dutch graphic craftsman M.C. Escher (1898–1972) who seized upon the idea to systematically exploit the aforementioned possibilities for visual art [22,23]. Escher, on a visit to Granada, Spain, had been impressed by the Moorish ornaments, but found them “lifeless” [22] (p. 24). Hence, he decided to replace geometric forms by images of (mainly) animals, people, and mythical creatures. These, in turn, were not only arranged to represent certain symmetries, but also in such a way as to gaplessly tile the picture plane. Indeed, for some time at least, this was Escher’s main interest [24], and, given the much greater (in fact infinite) number of possibilities, he devised his own systematization to derive new variants [25].

Escher’s status as an artist is sometimes disputed [26], but can be defended on the grounds of his integration of highly symmetric tessellations into pictorial narrations. For example, in one of his best-known prints, Dag en nacht (Day and Night), a flock of (antisymmetric) birds merge with the fields of a typical landscape from the Netherlands, as seen during daylight and in the night [22] (p. 273). This kind of “metamorphosis” was also used by Escher for his huge murals [22] (pp. 271, 280–281, 326–327) and by others who followed in Escher’s footsteps, like the Japanese graphic artist Makoto Nakamura [27,28]. More importantly perhaps, Escher also went beyond simple applications of geometry in his extensive use of color, introducing additional layers of symmetry, the mathematics of which still poses serious challenges [29,30]. Finally, it should be noted that Escher’s work comprises much more than the symmetry and tessellation pictures which I focused upon here (the major part of Escher’s oeuvre is now available via internet at http://mcescher.com).

The preceding observations suggest, or so I think, two empirical questions. If early artisans did not implement mathematical knowledge, how did they arrive at representations of almost all symmetry groups for both friezes and the plane? Several authors have suggested that craftsmen, possibly because of availability, used a limited set of “building blocks” (mosaic tiles or motifs) which they arranged in different ways [6,31], but this can hardly be the whole story. The second question, with which I shall be concerned in the remainder of this paper, is this: once representatives of different symmetry groups (or different representatives of the same group) have been produced, do they appeal differently to beholders? One condition for this to happen seems to be that the respective designs can be discriminated in the first place. I shall disregard friezes, and deal with the plane symmetry groups only.

2. The 17 Plane Symmetry Groups

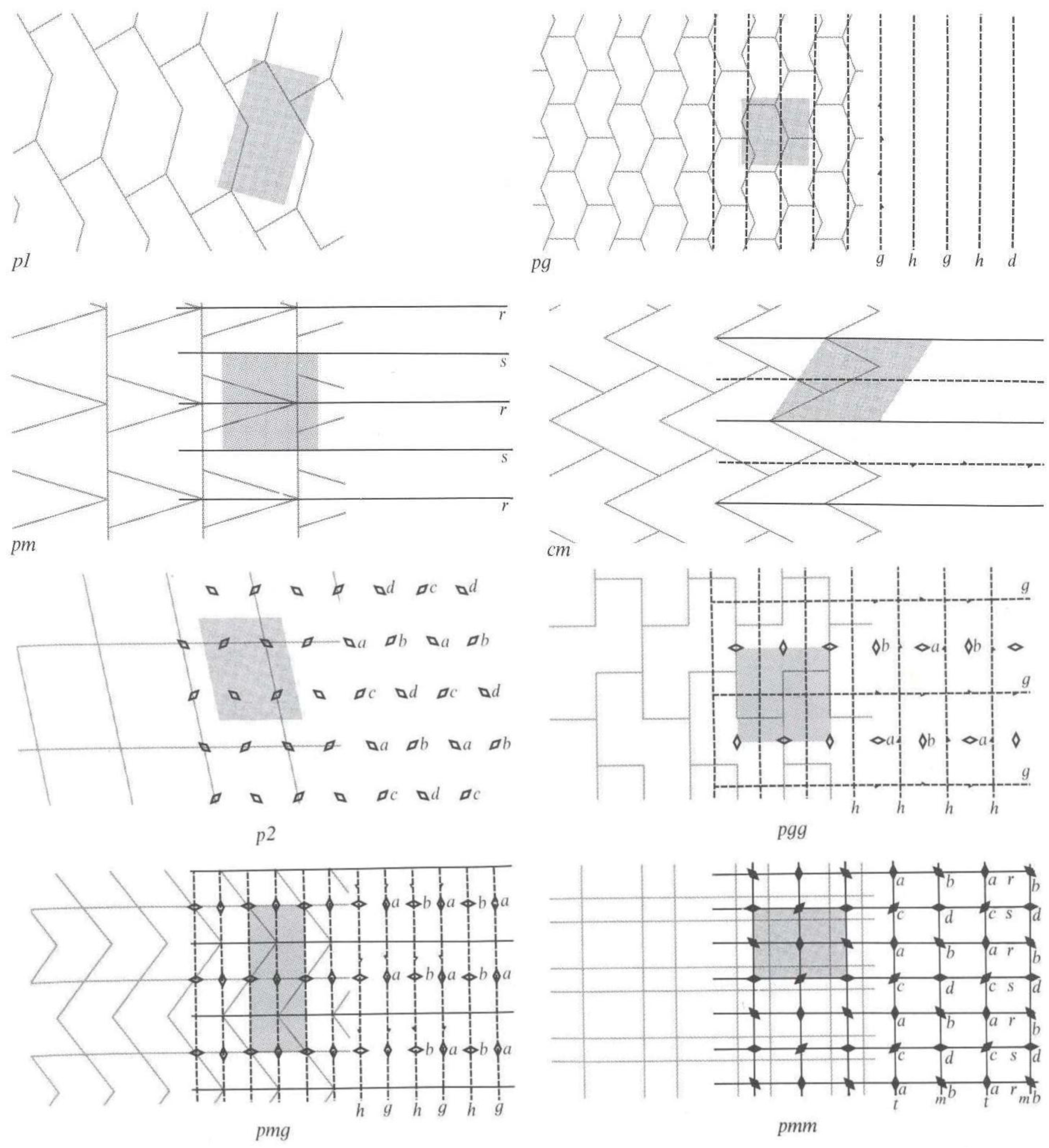
Although the 17 plane symmetry groups have been treated in many geometry textbooks [21,32] and have even been popularized for recreational mathematics [33], as well as the graphic arts [34], ignorance of the groups’ exact description still prevails. Grünbaum and Shephard [35] is one of the few sources which I am aware of that points to the nonequivalence of some of the symmetry operations in several of the groups. This complication is easily appreciated in some of the simplest groups which—besides translations—contain only one additional type of symmetry operation (Figure 1). For example, in the case of pm, depending on which class of reflection axes is chosen to mirror the exemplifying tiling of triangles and trapezes onto itself, different parts of the tiles (or, more precisely, different sets of points of the two half-planes that are defined by the axes) are mapped onto corresponding ones.

In fact, matters are even worse. Often, the relations between symmetry groups, translating unit cells, and generating regions (i.e., those parts of unit cells that actually “produce” the symmetry groups) are equivocal.

Table 1. The 17 plane symmetry groups and the 5 types of unit cells (together with their respective symmetry groups) that can be used to realize the groups. The + sign indicates possible constructions. Grey shaded fields denote combinations that—with certain reservations—can be studied by means of traditional experimental methodology.

Unit cell Group	Parallelogram p2	Rectangle pmm	Square p4m	Rhomb cmm	2 equilateral triangles p6m
p1	+	+	+	+	+
pm		+	+
pg		+	+
cm			+	+	+
p2	+	+	+	+	+
pmm		+	+
pmg		+	+
pgg		+	+
cmm			+	+	+
p4			+
p4m			+
p4g			+
p3					+
p3m1					+
p31m					+
p6					+
p6m					+

summarizes information from several sources, including my own observations regarding Escher-type tilings, created by using minimum numbers of indentations of tiles’ edges [22] (p. 142, for the logic of this procedure). Apparently, many groups can be synthesized on the basis of different unit cells, and for two groups at least (p2 and p6), different generating regions can be used to actually materialize the group [32] (pp. 92–107), [33] (p. 447), [35] (pp. 40–42). Hence, unit cells and generating regions do not always provide reliable cues to discriminate between or identify the plane symmetry groups.

Table 1 suggests that eight of the 17 plane symmetry groups can be studied by means of traditional experimental methodology. Before I demonstrate how this can be achieved, I shall briefly explain my understanding of the notion of discrimination as used in the title of this paper.

3. Discrimination versus Identification

In their operational definition of perception, Garner, Hake, and Eriksen [36,37,38] (for historical perspectives), [39] (for modern perspectives) proposed to distinguish detection, discrimination, and identification. Macmillan and Creelman [40] suggested further subdividing the third category (which they call classification) into categorization (with the number of response alternatives being smaller than the number of stimuli) and identification (with the numbers of response alternatives and stimuli being equal). Although the concepts as listed may appear self-explanatory, closer inspection of experimental paradigms and real-world tasks reveals some ambiguity. For example, from a signal detection point of view [41]—although it may sound paradoxical—detection is actually discrimination between signal and noise [42]. On the other hand, considering that, in the prototypical signal detection experiment, the number of response alternatives (yes, no) equals the number of stimulus variants (signal, noise), detection turns out to qualify as identification. Conversely, in the vernacular, the discrimination between object and background in camouflage breaking would normally be regarded as detection [43]. In this latter case at least, the notion of detection connotes a temporal delay, or period of search (see Section 3.5).

Going back to experimental paradigms, a common response measure for discrimination is the categorization of stimuli into same versus different. Importantly, for this task, observers are not expected to be able to verbally justify their choices [40] (pp. 213–214). This contrasts sharply with the common-sense understanding of identification. With regard to the topic of symmetry, instructions for experimental subjects would either ask for a definite naming of symmetry operations or groups, or else avoid mentioning the word symmetry at all. In my research, I preferred to pursue the second strategy.

4. Experiments

To study visual discriminability of selected plane symmetry groups, I performed two experiments, the details of which have been reported elsewhere [44]. For present purposes, I will briefly describe the rationale and the main results of these experiments, focusing on methodological and technical issues that are only briefly dealt with in the preceding publication.

4.1. Experimental Paradigm

An oddity procedure was used [40] (pp. 235–238). Sets of 4 pictures were shown, and subjects had to sort “the odd one” out. The idea behind this paradigm as applied to my topic is that representatives of different symmetry groups will be easier to discriminate than those of the same group. Observers were told that they would see “textures” in the sense of Gibson [45], and that oddity was defined by the “internal structure” of these. Observers were expressly discouraged to use color or lightness as clues to targets.

4.2. Observers

A total of 81 psychology undergraduates participated, 43 for Experiment 1, and 38 for Experiment 2. Four students took part in both experiments. Participants were naive with regard to the aims of the study. Upon debriefing, all subjects declared that they had heard about the notion of symmetry before, but none was acquainted with the concepts of isometry or symmetry group. All noted that there had been some kind of repetition in the stimuli, but nobody was able to precisely describe the symmetries that were presented.

4.3. Stimuli and Procedure

If the plane symmetry groups are illustrated by tilings (Figure 1) or discrete patterns (e.g., copies of flags or commas, as used by Grünbaum et al. [6] and Stevens [46], respectively), discrimination is trivially easy. I therefore concealed symmetry groups in natural textures. In the “camouflage technique”, transparent generating regions of symmetry groups are electronically created, overlaid onto digitized pictures, cut out, and retiled to produce various specimens of the respective groups. Mathematically, the resulting pictures are tiling patterns [35] (pp. 250–252). Examples can be read off Figure 2 and Figure 3 below.

For Experiment 1, different textures were used per stimulus set, for Experiment 2, the same textures were used. Experiment 1 comprised pairwise comparisons between p1 and p2, pm and pg, with groups interchanging their roles as targets versus distractors. Experiment 2 used pm stimuli only for catch trials (which are trials in which there is no target). Stimulus sets were shown for 6 s, and then code numbers for the individual pictures appeared on the screen. Subjects responded by typing the number of the picture they had chosen as presumptive target on a conventional computer keyboard. 0.5 s later, the next trial started. In Experiment 2, a fifth response alternative (in addition to the four pictures shown in every stimulus set) was granted, so that observers had a chance to correctly respond to catch trials. Experiments were controlled by Presentation software of Neurobehavioral Systems, Inc. (Albany, CA, USA).

4.4. Results

Data from nine participants (three from Experiment 1, six from Experiment 2) had to be discarded because numbers of correct responses lay below chance level. Responses of the other subjects were pooled per experiment and transformed to the signal-detection sensitivity measure d’ [40], (Table A5.5). Performance was similar for the target trials of both experiments (d’_{Exp. 1} = 1.27; d’_{Exp. 2_target} = 1.09), but was much worse for the catch trials of Experiment 2 (d’_{Exp. 2_catch} = 0.63). Effects concerning individual symmetry groups were tested via z-transformed binomial coefficients [47]. While the discrimination between p1 and p2 was always unproblematic, only in Experiment 1 could pg as a target reliably be discriminated from p1. pm catch trials were generally responded to incorrectly, and in Experiment 1, there was a trend for pm to go unnoticed in the neighbourhood of p1 distractors, whereas p1 targets were never missed between pm distractors.

4.5. Discussion

The reported experimental findings suggest that, in extended textures, rotational symmetries are easier to detect than mirror or glide reflections. This may have to do with the minimum area of texture one has to survey in order to identify instantiations of the different symmetry operations [44] (p. 1718). A main issue for the construction of suitable stimuli, therefore, is the presence of specific, object-like motifs or larger-scale structures which support or distract from the detection of critical features. For example, the blobs (parallelograms) apparent in the target of Figure 2a, might be used to infer the absence of mirror reflections in this picture. Conversely, the apparent vertical fault lines in the distractor at the bottom right of the same figure may appear as axes of mirror reflection (which they are not).

Given that the participants of my experiments were unable to precisely describe the symmetries of the stimuli they saw, a more holistic processing of information also has to be considered. For example, the target in Figure 2c might be chosen because of its “wavy” appearance, without noticing the glide reflections it contains (actually, much to my surprise, the target was missed by most observers). Yet, distributed local motifs may also play a role. The small white patches in both the target and one distractor in Figure 2d emphasize the translation vectors which are present in all plane designs, and hence may have made it difficult to decide on the target (in this case, only one quarter of observers correctly hit the target, whereas one third took the whole set to be a catch trial).

In an oddity task, similarities between specimens may seem helpful but are also likely to be puzzling. This can be seen in Figure 3a. The pictures at top right and bottom left both exhibit the presently mentioned wavy appearance and hence hardly qualify as targets. However, the other two pictures in this set also appear fairly similar to one another and so do not stand out as potential targets either. Observers are now forced to scrutinize all pictures again for mutual commonalities. Empirically, only four of my subjects arrived at the correct answer. Eventually, the stimulus set shown in Figure 3b is a truly difficult one. The target at top right and the distractor at bottom left appear quite similar, and, with regard to lightness distribution, the distractor at bottom right seems comparable to both. Yet, the picture top right is pg, whereas all others are p1. Two thirds of observers, seemingly ignoring instructions, chose the picture top left (the darkest one) as target.

Evidence from discrimination experiments is typically of the negative kind. If observers did not succeed in discriminating stimuli of which the experimenter knows that they differ in just one aspect, that aspect must have gone unnoticed. Unfortunately, in the case of the 17 plane symmetry groups, there is one confound that can hardly ever be eliminated: within almost all groups, symmetry operations are tied to specific generating regions (cf. Section 2). It is therefore difficult to know whether observers base their decisions about targets and distractors on the operations as such or on the implied structure of repetitiveness. For example, two of the distractors in Figure 2b (the ones on the right side) exhibit the parallelogram-type structure mentioned earlier, whereas the remaining distractor displays a snake-like motif which perhaps more convincingly conveys the rotational symmetry that characterizes p2.

Much more needs to be done before we understand how plane symmetry groups are discriminated or identified. Within the paradigm that I described here, variation of the unit cell and its size and orientation are the logical next steps. Beyond this, identification studies also appear both feasible and meaningful. Observers can be trained to understand the plane symmetry operations and then asked to report on their presence or absence in a yes-no procedure as alluded to in Section 2. The camouflage stimuli used for discrimination should also prove useful for that kind of task.

5. Conclusions and Outlook

All the 17 plane symmetry groups differ with regard to more than one property, and thus—strictly speaking—defy empirical study by means of traditional experimental methodology. However, focusing on the presence of individual symmetry operations, and utilizing stimuli that render these operations less obvious than they usually are in discrete patterns or outline tilings, may make some comparisons telling (the grey shaded cells in Table 1). In two experiments with camouflage-type stimuli, I compared symmetry groups p1, p2, pm, and pg, and observed surprisingly poor discrimination of mirror and glide reflection, whereas rotation at π was easily detected [44]. These findings are at odds with what is usually seen with delimited figures which may exemplify the cyclic or dihedral symmetry groups [48,49]. Future work along the lines that I described earlier [44] and more succinctly in the present paper may look at p1 versus p3 (added rotation) and p2 versus p4 (added four-fold rotation), pmm (added mirror reflection), and pgg (added glide reflection). Other tractable questions concern the discriminability of unit cells and the detectability of generating regions. To a certain degree, then, the plane symmetry groups are amenable to empirical, experimental study. Finding ways to fruitfully investigate visual discrimination and identification of the more complex groups remains a challenge for the future.