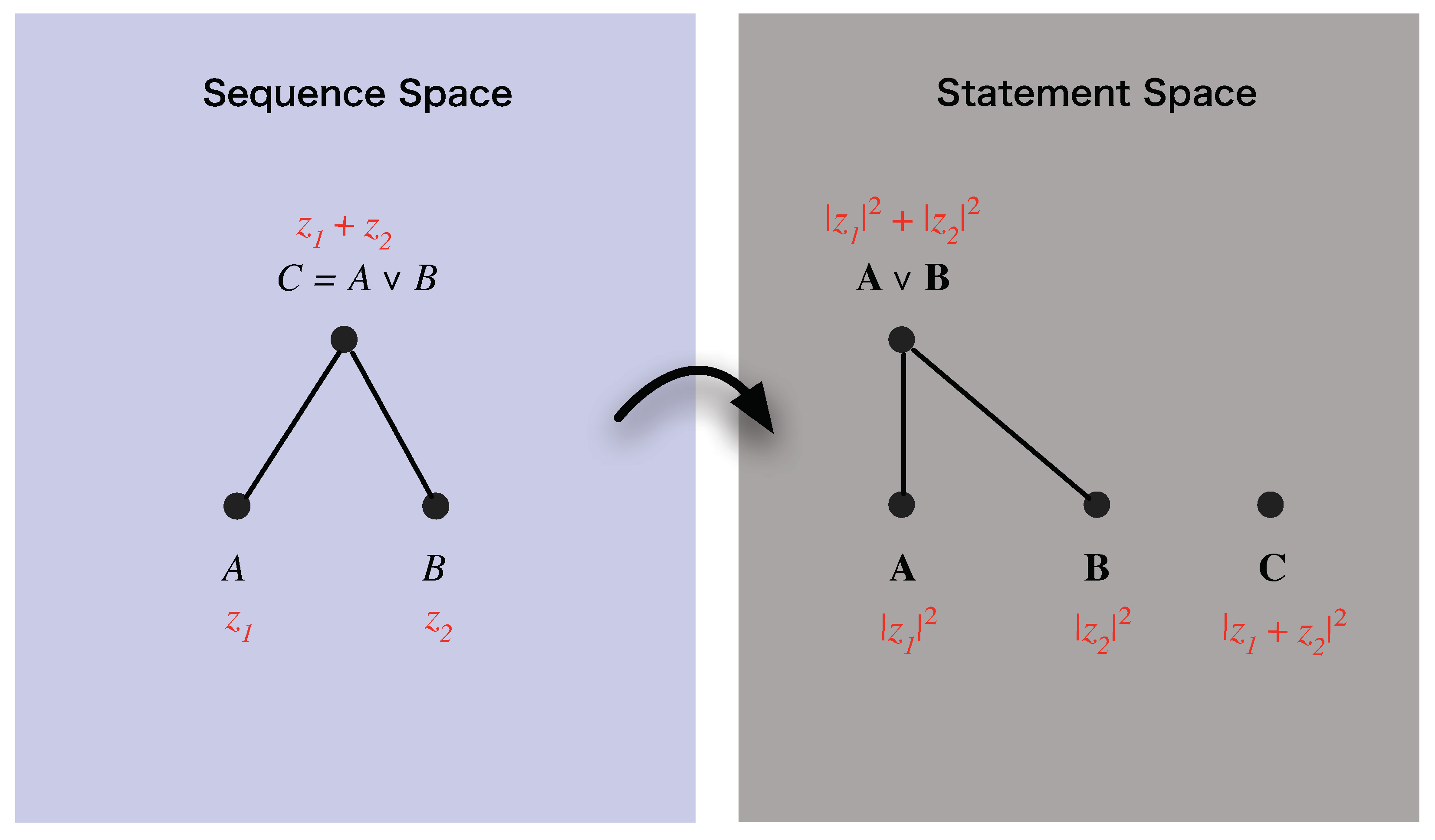
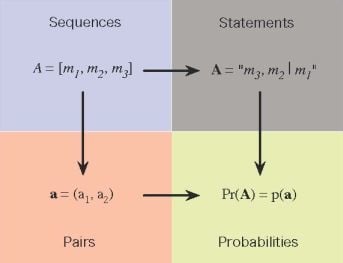
1. Introduction
Quantum theory is an extraordinarily successful theory which, since its creation in the mid-1920s, has provided us with a quantitatively precise understanding of a vast and an ever-growing range of physical phenomena. In essence, quantum theory is a probabilistic calculus that yields a list of the probabilities of the possible outcomes of a measurement performed on a physical system prepared in some specified manner. For example, in Schroedinger’s wave equation for a system of N particles, the quantum state, , of the system determines the probability, , that a measurement of the positions of the particles will localize them within the volume of configuration space located around . More generally, in the abstract quantum formalism articulated by von Neumann, the state of a system is given by a (possibly infinite dimensional) complex vector, , while the probability that a particular measurement yields outcome i when performed on the system is given by (known as the Born rule), where is the vector that corresponds to the ith outcome of the measurement.
The probabilistic character of quantum theory naturally raises the question: What is the relationship of quantum theory—of the quantum probabilistic calculus—to probability theory itself? Is quantum theory consistent with probability theory? Is it some kind of extension of probability theory, and, if so, what is the nature and conceptual foundation of that extension?
A significant source of difficulty in clearly answering these questions is that, apart from the notion of probability that they both utilize, probability theory and the standard von Neumann formulation of quantum theory share little in the way of language, conceptual foundations or mathematical structure. In 1948, this gap was narrowed by Feynman, who provided an alternative formulation of the standard quantum formalism [
1]. Feynman’s formulation strips away much of the elaborate mathematical machinery of the standard von Neumann quantum formalism, leaving behind essentially a single key idea: To each
path that a system can take classically from some initial event,
, to some final event,
, is associated a complex number, or
amplitude. Each such
event is to be understood as being the outcome of a measurement performed on the system. Feynman’s rules can then be stated as follows:
- (a)
Amplitude Sum Rule: If a system classically can take possible paths from to , but the experimental apparatus does not permit one to determine which path was taken, then the total amplitude, z, for the transition from to is given by the sum of the amplitudes, , associated with these paths, so that ;
- (b)
Amplitude Product Rule: If the transition from to takes place via intermediate event , the total amplitude, u, is given by the product of the amplitudes, and , for the transitions and , respectively, so that ; and
- (c)
Probability-Amplitude Rule: The probability, , of the transition from to is equal to the modulus-squared of the total amplitude, z, for the transition, so that .
Although these rules apply to measurements performed upon an abstract quantum system, a helpful concrete picture to have in mind when interpreting these rules is that of a particle moving in space-time from some initial point, (corresponding to ), to some final point, (corresponding to ). The upshot of these rules is that, if a particle classically has, say, two available paths from to , but the experimental apparatus used by the experimenter does not actually establish that the particle took one path or the other, one is not permitted to compute the transition probability, , by simply summing the transition probabilities along each of these two paths. Rather, one is required to sum the amplitudes associated with these two paths, and then compute the transition probability by taking the modulus-squared of the resultant amplitude. As a result, the quantum transition probability , is not in general the sum of the two respective transition probabilities, but can take values less than or greater than this value, a fact often summarized by saying that it is as if the paths can “interfere” constructively or destructively with one another.
As one can see from these rules, there is a close formal parallel between Feynman’s rules and the rules of probability theory. In probability theory, the probability of the joint proposition given proposition is given by the sum rule in the case where and are mutually exclusive propositions, while the probability of the proposition for any , given proposition is given by the product rule . Formally, these rules are closely paralleled by Feynman’s amplitude sum and product rules, respectively.
However, although Feynman’s formulation narrows the gulf, it does not close it. Feynman’s rules are a curious admixture of the language of physics on the one hand and the event language of probability theory on the other. In particular, while the rules speak of initial and final events (language appropriate to Kolmogorov’s probability theory), the notion of a classical path available to a system is a physical one and presupposes the framework of classical physics. Moreover, the manner in which Feynman’s rules (particularly the amplitude sum rule) are stated suggest that probability theory is inapplicable in certain situations, and that, in those situations, one should instead use Feynman’s rules. On this view, probability theory carries the imprint of the assumptions embodied in classical physics, rendering it inapplicable when one is dealing with quantum phenomena. Indeed, this view is not uncommon, and is bolstered by such commonly-used phrases as “(classical) paths can interfere constructively or destructively with one another”, which we mentioned above, or Feynman’s evocative image that it is as if the particle sniffs out all of the classically-available paths.
In this paper, we seek to close the gulf between probability theory and quantum theory, and thereby to precisely establish their relationship. For example, we show that the apparent inapplicability of probability theory to quantum systems is due to the failure to identify assumptions external to probability theory which are rooted in classical physics, and we prove that Feynman’s rules are compatible with probability theory by explicitly deriving Feynman’s rules on the assumption that probability theory is generally valid.
Our approach is inspired by Cox’s pioneering derivation of probability theory [
2,
3]. The first modern formulation of probability theory was due to Kolmogorov in 1933 [
4]. In this formulation based on set theory, propositions are represented by sets, and probabilities by measures on sets. The key components of Kolmogorov’s formulation are what we recognize as the sum and product rules of probability theory stated above, which, at the time of Kolmogorov’s formulation, were regarded as ultimately justified by recourse to the frequency interpretation of probability. However, in 1946, Cox showed that it was possible to
derive these rules from much more primitive ideas, and to understand probability in a more general way. As a result of Cox’s development, the probability calculus can be regarded a
systematic generalization of the Boolean logic of propositions. In a nutshell, his line of thinking runs as follows.
In Boolean logic, existing logical propositions (well-formed statements which are objectively true or false) can be used to generate new logical propositions by using the unary negation (or complementation) operator and the binary operators AND and OR [
5]. The logic is solely concerned with propositions that are true or false, and formalizes the process of
deductive reasoning. Cox showed that it was possible to systematically generalize Boole’s logic by quantifying over the space of propositions in such a way as to remain faithful to the symmetries of the logic, thereby formalizing the process of
inductive reasoning (that is, reasoning on the basis of incomplete information). In particular, to each pair,
, of propositions, he associates a real number,
, which is interpreted as quantifying the
degree to which an agent believes proposition
is true given that the agent believes proposition
is true. Cox then requires that the quantification be consistent with the symmetries of the Boolean logic. For example, due to the
associativity of the logical AND operator ∧, for any propositions
and
, one has that
, which leads to the constraint
. These constraints on
p yield a set of functional equations whose solution yields the standard sum and product rules of probability theory. Thus, Cox showed that probability theory can be understood as a calculus that systematically generalizes the Boolean logic of propositions, and that probability could be interpreted as an agent’s degree of belief in a proposition on some given evidence. Very importantly, this view of probability recognizes that, from the outset, all probability statements are
conditional in nature—one always speaks of the probability of a proposition
given some other proposition—which greatly encourages explicit statement of the assumptions that, in application of Kolmogorov’s formulation, are oftentimes left implicit.
Apart from the importance of Cox’s work in establishing a new mathematical and conceptual foundation for probability theory, his work also offered a
methodological innovation, namely to show how one can systematically generalize a
logic to a
calculus in a manner that respects the symmetries that characterize the logic. In recent years, Cox’s example has been expanded into a general methodology [
6] that has been used to yield insights not only into existing areas such as measure theory [
7] but also to aid in the construction of new calculi, such as a calculus of questions [
7,
8]. It is this methodology which we employ here to derive Feynman’s rules of quantum theory.
In the following, we proceed in three stages. First, defining probability as a real-valued quantification of the degree to which one logical proposition implies another, we show how probability theory can be derived as the unique calculus for manipulating these probabilities which is consistent with the underlying Boolean logic of propositions. Our presentation is based on the work of Cox [
2,
3], but reflects the substantial conceptual and mathematical refinement due to Knuth [
8,
9] and Knuth and Skilling [
10]. We thereby establish that probability theory is free from physical assumptions that would be deemed objectionable from the standpoint of quantum theory.
Second, we analyze the double-slit interference experiment using probability theory. We show that the naive application of probability theory to the situation tacitly introduces an assumption rooted in classical physics. However, if the situation is analyzed carefully, taking due account of the conditional nature of probability assignments, the classical assumption is clearly visible. We show that, if this classical assumption is not made, probability theory is no longer able to provide predictions that conflict with Feynman’s rules.
Third, we derive Feynman’s rules of quantum theory in a manner closely analogous to our derivation of probability theory. The derivation we describe is based on that presented in [
11], but offers an alternative line of argument which has the benefit of allowing us to much more clearly exhibit the relationship of Feynman’s rules to the rules of probability theory. The derivation has four main phases:
Operational Framework: First, we establish a fully operational framework in which to describe measurements performed upon physical systems. The framework allows the results of an experiment to be described in purely operational terms by simply stating which sequence of measurements was performed and what were their results. In particular, any metaphysical speculations or physical pictures about how a system behaves between measurements (such as imagining “classical paths” of a “particle” between initial and final position measurements as envisaged in Feynman’s rules) is eschewed.
Experimental Logic: Second, we identify an experimental logic in which parallel and series operators can be used to combine together sequences of measurement outcomes obtained in experiments. These measurement sequences list the outcomes obtained when a sequence of measurements are performed on a physical system. The action of applying the logical parallel and series operators allows us to formally relate the results of different experiments. The logic itself is characterized by five symmetries that are induced by the operational definition of these operators.
Process Calculus: Third, we
represent these measurement sequences with pairs of real numbers, this choice of representation being inspired by the principle of complementarity articulated by Bohr [
12]. This representation induces a
pair-valued calculus characterized by a set of functional equations, which are then solved to yield the possible forms of the two
pair operators which correspond to the parallel and series sequence operators.
Connection with Probability Theory: Fourth, and finally, we associate a logical proposition with each measurement sequence, and postulate that the pair associated with each sequence determines the probability of this proposition. We further require that (a) the calculus be consistent with probability theory when applied to series-combined sequences, and (b) when applied to parallel-combined sequences, the maximum and minimum values of the probabilistic predictions of the calculus are placed symmetrically about what one would predict using probability theory on the assumption that these sequences are probabilistically independent (an assumption which follows from classical physics). The resulting calculus—which we refer to as the process calculus—coincides with Feynman’s rules of quantum theory.
Our derivation explicitly demonstrates that Feynman’s rules are fully compatible with probability theory. In particular, a vital part of our derivation involves requiring that the process calculus agrees with probability theory wherever probability theory is able to yield predictions. We are thereby able to see that the role of the process calculus is to allow us to interrelate the probabilities associated with different experiments in certain situations when probability theory is by itself unable to provide any interrelation. However, the process calculus cannot be viewed as a generalization of probability theory as the former is specialized to the particular purpose of relating together the results of experiments on physical systems, and it thus concerned with particular kinds of propositions, while the latter is concerned with logical propositions in general.
The remainder of this paper is organized as follows. First, in
Section 2, we give an overview of the derivation of probability theory. Then, in
Section 3, we analyze the double-slit experiment using probability theory and Feynman’s rules. In
Section 4, we present the derivation of Feynman’s rules. Finally, in
Section 5, we summarize the main findings, and, in
Section 6, conclude with a summary of the key points.
2. Symmetries in Probability Theory
In this section, we review how probability theory arises as a quantification of implication amongst logical propositions constrained by the symmetries of Boolean algebra. These symmetries are outlined in
Table 1.
While the first derivation relying on symmetries was originally performed by Cox [
2,
3], the derivation we present follows Knuth [
9] and Knuth and Skilling [
10], which relies on the more general class of distributive algebras (all the operations in
Table 1 except those involving the unary complementation operation) and more closely mirrors the steps involved in the present derivation of Feynman’s rules. These symmetries associated with the logical AND and OR operations are augmented with the symmetries associated with joining independent spaces of statements and the symmetries associated with combining inferences to obtain a probability calculus. This is accomplished by quantifying the
degree to which one logical proposition implies another by introducing a function called a
bivaluation that takes a pair of logical propositions to a real number (scalar). A scalar representation suffices since the aim is to rank the propositions based on a single ordering relation: implication. These symmetries lead to constraint equations in the bivaluation assignments, which are the sum and product rules of probability theory.
We begin by considering two mutually exclusive propositions and such that , where ⊥ represents the logical absurdity, which is always false. We also consider a third proposition, , such that and . The degree of implication is introduced by defining a bivaluation, , that takes two propositions to a real number. For example, the quantity represents the degree to which the proposition implies the proposition . Furthermore, the bivaluation encodes the rank of the statements so that whenever and , we have that .
We now consider the composite proposition
and the degree to which it is implied by
,
. For this calculus to encode the underlying algebra, the degree
must be a function of the degrees
and
, so that
where ⊕ is a binary operator to be determined.
Consider another logical proposition
where
,
,
, and form the element
. We can use associativity of ∨ to write this element two ways
Applying Equation (
1), we obtain
Applying Equation (
1) again to the arguments
and
above, we get
Defining
,
, and
, the above expression can be written as the functional equation
known as the
Associativity Equation [
13], whose general solution [
13] is
where
f is an arbitrary invertible function. This means that there exists a function
that re-maps
u and
v to a representation in which
Writing this in terms of the original expressions, and defining
we have
We can consider more general propositions
and
formed from mutually disjoint propositions
,
and
by
and
. Since
and
are disjoint
Similarly, since
and
are disjoint
Solving both equations for
, we find
Noting that
and
, and recalling that
, we have
which is the familiar
sum rule, or inclusion-exclusion relation
It should be noted that this result is symmetric with respect to interchange of the logical AND and OR operation. The operations are dual to one another and associativity of one operation guarantees associativity of the other. The result is that the symmetry of associativity of both the logical OR and logical AND operations results in a constraint equation for the bivaluation, which is the sum rule of probability theory. More generally, the sum rule ensures the symmetry of associativity of the binary operations of the distributive algebra [
7].
Another important symmetry represents the fact that one should be able to append statements that have absolutely nothing to do with the problem at hand without affecting one’s inferences. For example, the inferential relationship between the statement “it is cloudy” and the statement “it is raining” cannot be affected if we append the fact that “eggplants are purple” to each. More specifically, the degree to which the statement C = “it is cloudy” implies the statement R = “it is raining”, , should be equal to the degree to which the statement (C, E) = “it is cloudy, and eggplants are purple” implies the statement (R, E) = “it is raining, and eggplants are purple”, denoted .
Consider the direct (Cartesian) product of two conceptually independent spaces of logical propositions. The direct product is associative since
which allows us to drop the internal parentheses and write
. Furthermore, it is distributive over logical OR
Given bivaluations
and
defined in the two independent spaces, we aim to define the bivaluation
in the joint space. These bivaluations must be consistent with the symmetries associated with combining the two spaces above. In addition, the bivaluations defined on the joint space must obey associativity of the direct product, which as we saw above requires that the bivaluations must be additive
where
g is some invertible function.
In the case where
and
are mutually exclusive, the joint propositions
and
are also mutually exclusive, and we can write the bivaluation quantifying the degree to which the joint proposition
implies the joint proposition
as
Additivity requires that
Writing
and writing
, we have the
product equation
which encodes the symmetry that the direct product is distributive over the logical OR. Solving this functional equation one finds that
g is the logarithm function [
10], so that
where
C is an arbitrary positive constant, which can be set equal to unity without loss of generality. This results in the
direct product ruleLast, we consider the symmetry involved in chaining our inferences together. We consider three logical statements where
and
, so that by transitivity
. This symmetry can be viewed in terms of the logical AND operation, or dually the logical OR operation, since
implies that
and
as listed in
Table 1. Transitivity of implication can be viewed as associativity of the logical AND when applied to the implicate since
which, in the case where
and
, can be simplified to
which implies that
. The transitivity implies that, when
, the bivaluation
must be a function of
and
.
Since this functional relationship holds in general, it must hold in special cases. We consider a special case that completely constrains this relationship, which therefore results in the general solution. Consider the following relations obtained by applying the direct product rule
and
Setting
,
,
so that
and substituting Equation (
24) and Equation (
25) into Equation (
26) we find
This is the
chain product rule.
This can be extended to accommodate arbitrary statements
,
, and
. Consider the following application of the sum rule where the implicate is
Since
, we have that
, which implies that
Setting
,
in Equation (
27) and applying the identity above, we have the general form of the
product rule for probability,
The result of the considerations above is that the symmetries of Boolean algebra place constraints on bivaluation assignments used to quantify degrees of implication among logical statements. These constraints take the form of constraint equations, which are the familiar sum and product rules of probability theory
The remainder of this section focuses on demonstrating how the rules above result in bivaluations that agree with the standard definitions and results for probability measures, such as in Kolmogorov [
4]. Specifically, we will use the sum and product rules to derive the range of values that the bivaluations may take, and show that, in the extreme cases of falsity and truth, the bivaluations take values of zero and unity, respectively; and in general range from zero to unity. We will also show that the definition of a bivaluation leads directly to the standard definition of conditional probability. These results are derived below in a sequence that lends itself to an efficient derivation, but will be summarized at the end of the section in a logically-unified fashion.
The falsity, or absurdity, ⊥, is defined by taking the logical conjunction (AND) of two mutually exclusive (disjoint) statements
. As such, it is always false. Previously, we found that for any two disjoint statements,
. But the sum rule above applies to all logical statements, so we can write
so that, for all
Of particular note is the fact that
.
All statements, excluding the bottom, imply themselves with certainty. To see this, set
in the product rule
so that
which implies that either
or that
. We first consider the possibility that
and consider the special case of the degree to which the truism implies itself,
. As described above, the bivaluation is meant to encode the rank of the statements so that whenever
and
we have that
. If we let
and
, we have that
, which implies that
. Therefore, it must be that the solution to Equation (
36) is
. This numerically encodes the fact that all non-absurd statements imply themselves with certainty. This particular value of unity is determined by our choice of setting the arbitrary constant
in Equation (
19), which, as we will show, defines the scale for the maximum value that can be assigned to the bivaluation.
The result above suggests that for all statements
we should have that
. This can be shown by noting that
when
. This enables one to write the product rule
as
which implies that
whenever
and
. Since, the truism, ⊤, which is the top element of the lattice, trivially satisfies
for all
, we have that
for all
.
We have examined the extreme cases, and have seen that, for all
,
and
, while
whenever
. We now consider the intermediate cases. By considering non-disjoint
and
so that
, Boolean logic implies that
. In the case where
does not imply
so that
, the fact that bivaluations rank the statements implies that
which can be simplified to
We can apply the product rule to
and write
Since
, we have that
. Dividing through by
, and recognizing that
indicating the normalized range of values over which the bivaluation
is defined.
The definition of bivaluation suggests that the
is to be identified with the conditional probability of
given
. We now show that this is indeed the case. We consider the product rule
for the case where
. Recalling that
, we can divide by
and solve for
to obtain
which is Kolmogorov’s definition of conditional probability, arrived at here from an entirely different perspective. As a final check, by considering the case where
, we have that
, which, by Equation (
43), implies that
whenever
.
In summary, we have shown that bivaluations fall within the following range
where, in the extreme cases of truth and falsity, we have that, for all
In general, for
, we have shown that bivaluations representing degrees of implication obey [
14]
These results for the values of the bivaluation
, together with the sum and product rules above, encompass standard probability theory [
2,
3,
4]. The theory describes how to reason consistently in the sense of agreement with Boolean logic.
We observe that the constraint equations do not totally constrain the bivaluation (probability) assignments. In particular, consider the set of atomic propositions, , namely those propositions which cannot be obtained via the union of other propositions, and write the truism as . Then the N probabilities are freely assignable up to the normalization condition . This means that there is freedom for the probability assignments to be problem-dependent. We will see that, in quantum theory, the set of constraints on the quantification of logical statements identified above are coupled to a set of constraints governing the quantification of measurement sequences, so that the probabilities of statements about a quantum system will depend on the quantum amplitudes.
3. Feynman’s Rules of Quantum Theory
The first general quantum theories of matter were formulated in 1925–1926 by Schroedinger [
15] and Heisenberg [
16]. From these specific theories, the general-purpose quantum formalism—which provides a general framework for building quantum theories—was shortly thereafter abstracted by Dirac [
17] and put in precise mathematical form by von Neumann [
18]. As mentioned earlier, in 1948, Feynman abstracted a set of rules (Feynman’s rules) from the von Neumann formalism [
1] which do away with most of the elaborate mathematical machinery of the standard abstract quantum formalism, and which can be put in close formal correspondence with sum and product rules of probability theory. Furthermore, the formal similarity of Feynman’s rules to the rules of probability theory suggests that it might be possible to
derive Feynman’s rules in a manner analogous to that used to derive probability theory described above. We shall indeed show this to be the case.
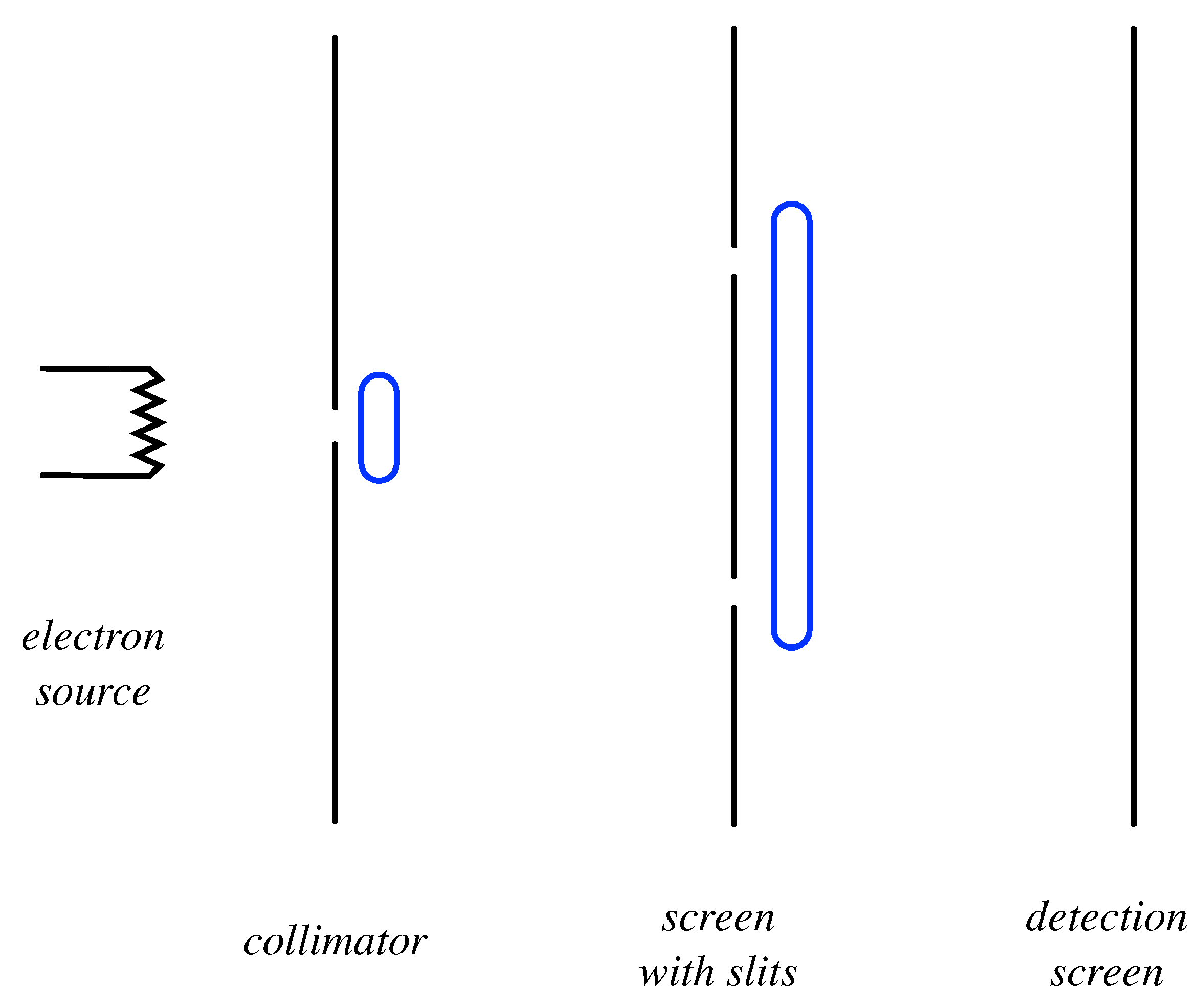
In this section, we shall analyze the double-slit experiment (see
Figure 1) using probability theory and Feynman’s rules.
On the left, a heated electrical filament,
A, emits electrons (all assumed to have the same energy), that pass through a wire-loop detector which registers the time of their emission. These electrons then impinge on screen
B in which there are two slits,
and
. Some of the electrons will subsequently emerge, pass through a wire-loop detector which registers their time of emergence, and finally reach screen
C, which is covered by a grid of highly-sensitive detectors, each of which is capable of detecting an individual electron [
19]. When the experiment is run, if the temperature of the electrical element is reduced sufficiently, one finds that one and only one of the screen detectors fires within the resolution time of the detectors [
20]. For the purposes of visualization, let us suppose that the outputs of the detectors is wired into a grid of light-emitting diodes (LEDs) on the backside of
C. So, watching the experiment, one sees a sequence of flashes, each emanating from a particular cell in the LED grid. After the accumulation of many such flashes, one builds up an
intensity pattern over the screen, which allows us to estimate the probability that a given electron will strike a particular detector on the screen on a given run of the experiment.
Note that it is the atomicity of these detections—only one detector fires at a particular time—that leads us to visualize electrons as entities that fly through space in highly-localized bundles of energy. However, this model extrapolates too far from the observed facts, and leads to manifestly incorrect predictions. To see this, let us compute the probability that, in a given run of the experiment, a detection is obtained at some given location on
C at time
and passes
B at time
given that an electron is emitted from the filament,
A, at time
. We shall suppose that screen
B is sufficiently large that these holes provide the only avenue through which the electrons can reach
C. According to probability theory
where we have defined the propositions
A = “Electron is emitted from A at time t1”
B = “Electron passes through the union of the space occupied by slits B1 and B2 at time t2”
C = “Electron is detected at given cell at C at time t3”
Note that we are inferring the truth of proposition
from the truth of
and
, which one might legitimately question if one wishes to avoid interpolating beyond the observed data. However, if we wish, we could employ a detector (consisting of an induction loop, as shown in the figure) which can register the passage of an electron through the slits, without localizing its passage through one slit or the other. In that case, one would find that this detector fires whenever
and
are both true, thereby providing empirical justification for Equation (
50).
Suppose, now, we admit the classical model of electrons as
highly localized entities. Then, in the above experiment, given detection at
C and emission at
A, one would infer that the electron must have travelled through
B via either slit
or
. That is, one would infer the statement
where
Under this assumption, Equation (
50) becomes
where the sum rule of probability theory, Equation (
31), has been used to arrive at the second line.
Now, Equation (
52) asserts a relationship that can readily be tested. If slit
is closed and the experiment is run, the only electrons that strike
C must pass through slit
[
21]. On the assumption that probability
is unaffected by the closure of slit
, which assumption follows naturally from the classical model of the electron, the probability
can be estimated. Similarly, if slit
is closed but
left open, one can estimate
. One then finds
experimentally that Equation (
52) does
not hold true. The conclusion seems inescapable: the model of electrons as highly localized entities must be false [
22].
The intensity pattern over screen
C obtained when both slits are open in fact resembles the pattern that would be expected if classical waves (such as water waves or electromagnetic waves) were being emitted from the electrical filament. In particular, one observes constructive and destructive interference, the hallmark of wave phenomena. Indeed, the intensity pattern can be
quantitatively reasonably well described using a classical wave model [
23]. Yet, this model manifestly conflicts with the atomicity of the detections at
C. Thus, we find ourselves in a somewhat perplexing situation where we require both the classical particle model and the classical wave model to account for the observations, but where each appears to be in conflict with the other, a situation known as the “wave-particle duality” of the electron.
The failure of Equation (
51) naturally raises the question: how can the probability
be related to the probabilities
and
? From the experimental findings mentioned above, it can be seen that, although
is not
determined by
and
, it is not
independent of them either. So, presumably there is a looser relation between these three probabilities, involving additional degrees of freedom. But, if so, what is that relationship?
According to Feynman’s rules, the probability
is equal to
, where
z is a complex number, referred to as the
amplitude, associated with the process leading from the detection at
A at time
via detection at
B at time
to the detection at
C at time
. This amplitude is, in turn, the sum of the amplitudes
and
, where
(
) is the amplitude associated with the process leading from the detection at
A at time
to detection at
C at time
via slit
at time
. Thus, in place of Equation (
52), one has the
amplitude sum rule
while the relationship between the amplitude,
u, associated with a process and its probability,
p, is given by the
amplitude-probability rule as
, so that
As a consequence of these relations, in place of Equation (
52), one obtains
where, for brevity, we have written
and
. Hence, as anticipated, there does exist a non-trivial relationship between the three probabilities, but this relationship involves an additional degree of freedom,
.
In summary, we see that the conflict of predictions is not between probability theory and Feynman’s rules per se, but rather between (a) the union of probability theory and an assumption whose origin lies in classical physics and (b) Feynman’s rules. The conflict disappears once the classical assumption is dropped.
We conclude by noting that, in addition to the two Feynman rules listed above (the amplitude sum rule and the amplitude-probability rule), there is also a third rule, the
amplitude product rule, which states that, if a process (with amplitude
u) can be broken into two sub-processes (with amplitudes
and
) concatenated in series, then
For example, the process leading from the detection at
A at time
to the detection at
C at time
via
at time
can be broken into (i) the detection at
A at time
to
at time
, and (ii)
at time
to the detection at
C at time
, so that
, where
and
are the amplitudes of the sub-processes.
We note that, in this example, the amplitude product rule implies that
In contrast, the application of the product rule of probability theory, Equation (
32), implies that
which is the same provided that
, which is true provided that the second sub-process is Markov (probabilistically independent) with respect to the first, which is indeed experimentally valid. Hence, there is a close formal relationship between Feynman’s amplitude sum and product rules on the one hand, and the sum and product rules of probability theory on the other.
4. Derivation of Feynman’s Rules
As we have seen above, Feynman’s rules express the content of the quantum formalism with a minimum of formal means, and does so in a manner which establishes a close formal parallel to the rules of probability theory. The latter observation raises the question of whether Feynman’s rules may be derivable in a manner analogous to that described in
Section 2, namely by quantifying over a suitably-defined logic. In this section, we shall outline such a derivation.
4.1. Operational Experimental Framework
We begin by establishing a fully operational framework for describing experimental set-ups consisting of sequences of measurements and interactions on a physical system. The motivation for such a framework is twofold. First, as described above, the application of Feynman’s rules to an experiment involving electrons requires that one considers the various
classical paths that an electron (modeled as a particle) could take from some initial point to some final point in spacetime. To appeal to a classical model in the statement of rules for a theory that is inconsistent with that same classical model can (and indeed does) lead to confusion. Hence, it is highly desirable to formulate a way to describe experiments which is sufficiently precise as to obviate the need for such an appeal. Second, although the primitive terms “measurement”, “outcome”, and “interaction” may seem very simple and transparent, it turns out that they require very careful formal specification in order that they can be consistently used in a derivation of Feynman’s rules. The experimental framework provides such a specification. The experimental framework is described in [
11], to which the reader is referred for full details. Below, for completeness, we shall recount the main points.
The key primitives of an experimental set-up are as follows. A source is a black box which issues physical systems which behave identically as far as a set of given measurements and interactions are concerned. Measurements are black boxes which take a physical system from the source as input, yield one of a finite number of possible repeatable outcomes, and then output the physical system. A repeatable outcome is a macroscopically stable output (such as the illumination of an LED) of the measurement device which is such that, if the output is obtained when a measurement is performed on a system, then the same output is again obtained with certainty if the measurement is immediately repeated on the system. We refer to measurements all of whose outcomes are repeatable as repeatable measurements. Finally, an interaction is anything which happens to a system in between measurements which is itself not a measurement, but which non-trivially influences the outcome probabilities of subsequent measurements.
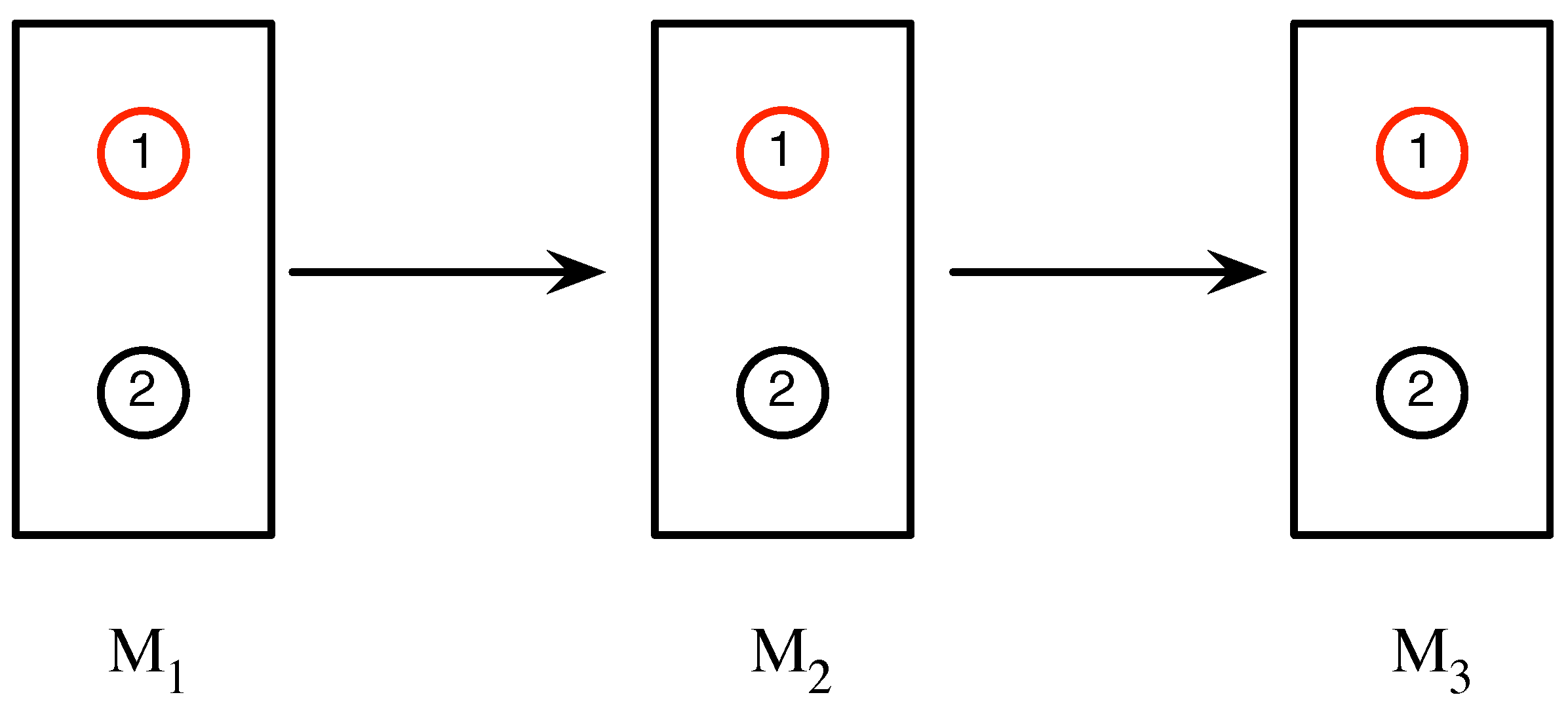
An experimental set-up is defined by specifying a source, a sequence of measurements, and the interactions occur that during the experiment. In a run of an experiment, a physical system from the source passes through a sequence of measurements
,
, which respectively yield outcomes
at times
,
, .... These outcomes are summarized in the
measurement sequence . For notational brevity, the measurements that yield these outcomes, and the times at which these outcomes occur, are left implicit. In between these measurements, the system may undergo interactions with the environment. For example, as illustrated in
Figure 2, in particular run of an experiment involving a sequence of three measurements, each of whose outcomes are labeled 1 and 2, the sequence
is obtained.
In this case, the system may, for instance, be a silver atom, upon which Stern-Gerlach measurements (which, in this case, would each have two possible outcomes) are performed.
Over many runs of the experiment, the experimenter will observe the frequencies of the various possible measurement sequences, from which one can (using Bayes’ rule) estimate the probability associated with each sequence. We define the probability
associated with sequence
as the probability of obtaining outcomes
conditional upon obtaining
The conditionalization on outcome
ensures that
is independent of the history of the system prior to the first measurement, and so is fully under experimental control.
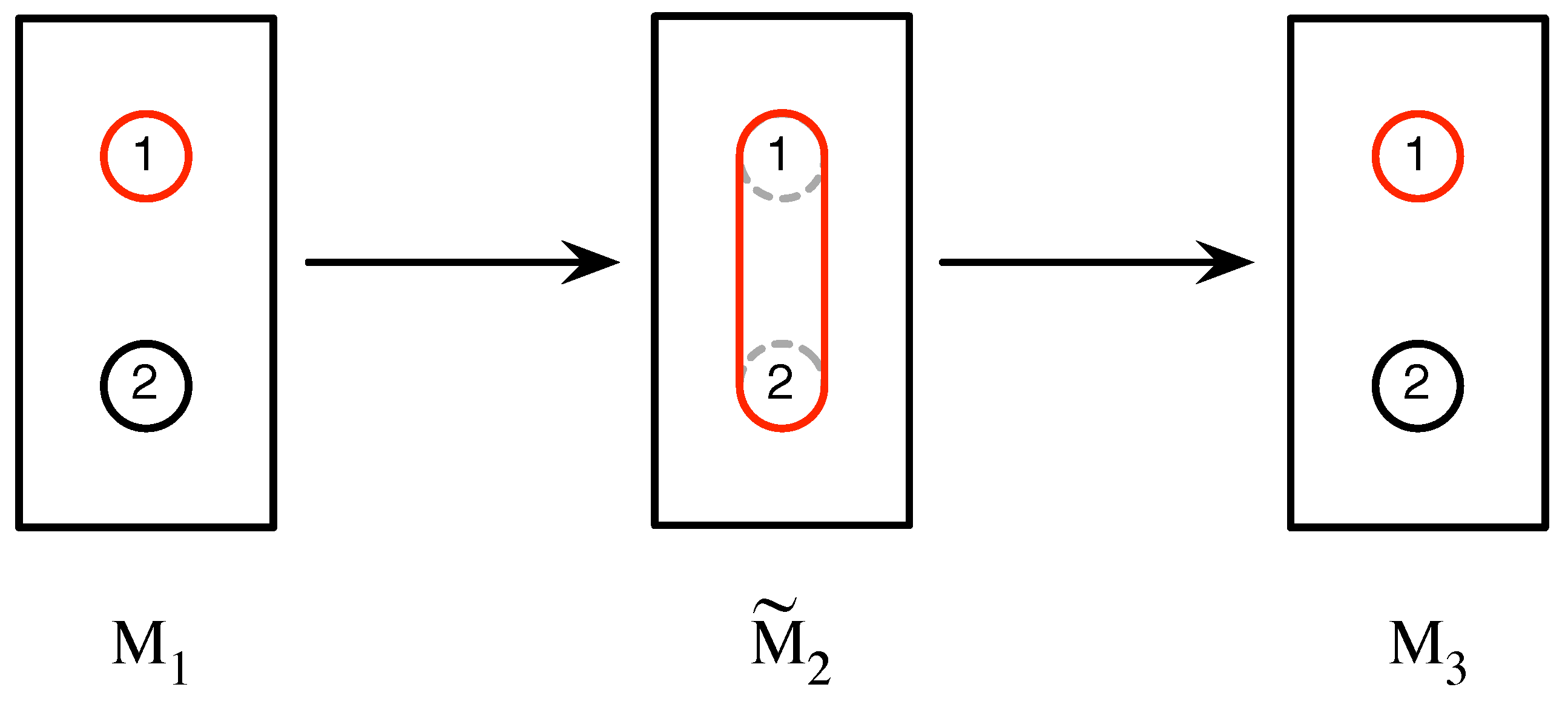
A particular outcome of a measurement is either
atomic or
coarse-grained. An atomic outcome cannot be more finely divided in the sense that the detector whose output corresponds to the outcome cannot be sub-divided into smaller detectors whose outputs correspond to two or more outcomes. A coarse-grained outcome is one that does not differentiate between two or more outcomes. For example, in the experiment in
Figure 3, the second measurement,
, has a single outcome which is a coarse-graining of the outcomes labeled 1 and 2 of measurement
. Accordingly, the outcome of
is labeled
, and we apply this notational convention to coarse-grained outcomes generally. The measurement sequence obtained in this case is
.
In general, if all of the possible outcomes of a measurement are atomic, we shall call the measurement itself atomic. Otherwise, we shall refer to it as a coarse-grained measurement, and sometimes symbolize this as if we wish to indicate that it is obtained by coarse-graining over some of the outcomes of the atomic measurement .
It is important that all of the measurements, , , ...that are employed in an experimental set-up come from the same measurement set, , or are coarsened versions of measurements in this set. The set consists only of atomic, repeatable measurements, and satisfies the closure condition that, if any pair of measurements, , are selected from , then, if an experiment is performed where is used to prepare a system (namely, selecting those systems that yield a particular outcome of ) and measurement is performed immediately afterwards, then the outcome probabilities of are independent of interactions with the system prior to . Interactions between measurements are likewise selected from a set, , of possible interactions, which are such that they preserve closure when performed between any pair of measurements from . These rather intricate requirements are necessary to ensure that the behavior of the system under study is independent of the history of the system prior to the start of the experiment, and that all of the measurements performed on the system are probing the same aspect of the system. We shall restrict consideration throughout to sequences whose initial and final outcomes are atomic.
4.2. Sequence Combination Operators
We wish to develop a calculus—which we shall refer to henceforth as the
process calculus—that is capable of establishing a relation between the probabilities observed in experimental set-ups such as those in
Figure 2 and
Figure 3. For example, in a run of the first experiment, one might observe the sequences
or
, while, in a run of the second experiment, one might observe
. The calculus should provide a relationship between the probabilities
,
and
associated with these sequences.
As the discussion of the double-slit experiment above makes clear, probability theory cannot by itself establish a relationship between these probabilities unless an additional assumption drawn from classical physics is made. That is, if one assumes that, in
Figure 3, when the large detector of
fires, the system
in fact went via the top or bottom of the detector (that is, via outcome 1 or 2)
even though it was not measured doing so, one is led by a simple application of probability theory to the relationship
, which is in manifest conflict with experimental data. If, however, we refrain from making this classical assumption, probability theory provides no relationship between
,
and
whatsoever. The calculus we seek to develop is designed to fill this void.
Recognizing that the probabilities associated with sequences A, B and C cannot be simply related, we seek a deeper theoretical description of the sequences where the description of C is determined by the descriptions of A and B, and where the description of each sequence yields the probability associated with that sequence. That is, we seek to introduce a level of theoretical description which is one level lower (more fundamental) than the probability-level of description.
To carry out this program, we begin by formalizing the relationship between
A,
B and
C by introducing the
sequence parallel composition operator, ∨, so that we write
. Formally, if two sequences can be obtained from the same experimental set-up, agree in the first and last outcomes, but differ in precisely one outcome, then they can be combined in parallel. That is, if we have sequences
and
obtained from the same experimental set-up which differ only in the
ith outcome (
), but neither the first nor the last, then
where
symbolizes a coarse-grained outcome.
In order to reflect the idea of series concatenation of experimental set-ups, we also introduce a
series composition operator, symbolized as ·. For example, the sequence
can be viewed as the series composition of the shorter sequences
and
, so that
More generally, if two sequences are obtained in two different experimental set-ups that immediately follow one another in time, and the sequences are such that the last measurement and outcome of one sequence are the same as the first measurement and outcome of the other sequence, then they can be combined together in series.
From these definitions, it follows that the two binary operators have the following five symmetries:
namely commutativity and associativity of ∨ (Equations (
62) and (
63)), associativity of · (Equation (
64)), and right- and left- distributivity of · over ∨ (Equations (
65) and (
66)).
4.3. Pair Representation of Sequences
We now introduce the desired theoretical level of description of the sequences. In particular, we represent each sequence,
A, with a
real number pair [
24],
, and require that this representation is consistent with the five symmetries identified above. For example, if pairs
,
represent the sequences
A,
B, respectively, then the pair
that represents
must be determined by
,
through the relation
where ⊕ is a pair-valued binary operator, assumed continuous, to be determined. Similarly, if the sequences
and
C are related by
, then the pair
that represents
C must be determined by
through the relation
where ⊙ is another pair-valued binary operator, assumed continuous, also to be determined.
From these definitions of ⊕ and ⊙, the five symmetries of the sequence combination operators immediately imply that
In [
11], we show that these symmetry conditions impose strong restrictions on the possible form of the operators ⊕ and ⊙. In particular, commutativity and associativity of ⊕, subject to some minor auxiliary mathematical conditions, imply that, without loss of generality, one can take
which we refer to as the
sum rule. The distributivity conditions (
S4) and (
S5) then imply that
has a bilinear multiplicative form
where the
are real-valued quantities to be determined. Finally, the associativity of ⊙ implies that
has one of five possible standard forms, namely
and
We recognize possibility (
C1) as complex multiplication, while (
C2) and indeed also (
C3) are variations thereof known respectively as dual numbers and split-complex numbers. Finally, the last two possibilities (
N1 and
N2) are non-commutative multiplication rules.
4.4. Probabilities, and the Probability Product Equation
We defined the probability
associated with sequence
in Equation (
59) as
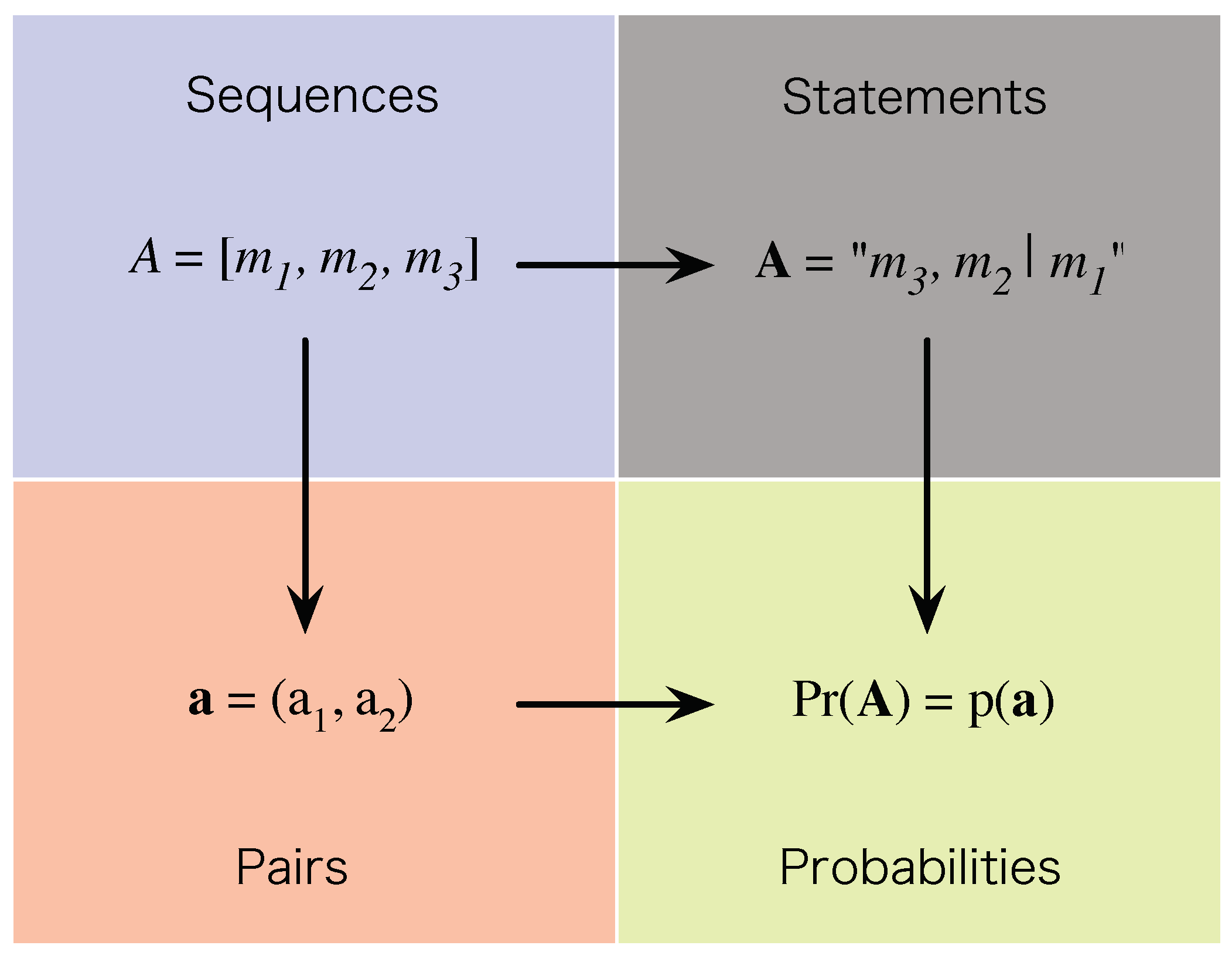
. We now create a link between the theoretical representation,
, of a sequence,
A, and the probability,
, associated with the sequence by requiring that the former determine the latter, so that
where
is a continuous real-valued function that depends non-trivially on both real components of its argument. The overall structure that this link establishes is shown in
Figure 4.
Now, once a link between pairs and probabilities has been postulated, the process calculus provides the means to relate the probabilities associated with different sequences. In certain cases, such as for the sequences
, and
mentioned in
Section 4.2 above, probability theory alone can establish no relation, which is precisely the void the process calculus is designed to fill. However, there are situations where both the process calculus
and probability theory can be applied, and in these circumstances they must agree, on pain of the process calculus being inconsistent with probability theory. This consistency requirement sharply delimits the form that the function
can take.
To exhibit this consistency requirement, consider the two sequences
and
of atomic outcomes, with the sequences represented by pairs
and
. Since outcome
is the same in each,
is given by
, represented by the pair
. The probability,
, associated with sequence
C is given by
which, by the product rule of probability theory, can be rewritten as
Since
is atomic, measurement
(with outcome
) establishes closure with respect to
(with outcome
). Therefore, the probability of outcome
is independent of
, and the above equation simplifies to
Since
,
, and
, the consistency of the process calculus with probability theory requires that, for any
,
, the function
must satisfy the equation
As shown in [
11], if one solves for the function
that satisfies this equation in each of the five forms of ⊙ given above, one obtains
Case
C1:
;
Case
C2:
;
Case
C3:
;
Case
N1:
;
Case
N2:
;
with real constants.
We now note that, while in the three commutative forms (
C1), (
C2) and (
C3), the function
depends upon
both components of its pair argument, in the two non-commutative forms (
N1) and (
N2), it depends only on the first component of its argument. Consequently, in the latter two cases, the process calculus reduces to a scalar calculus insofar as predictions as concerned.
To see this, consider case (
N1): pairs
and
can be combined using ⊕ and ⊙ to yield
and
, respectively. The associated probabilities are
,
,
and
, all of which are independent of the second components of pairs
and
. Hence, the second component of each pair can be dropped without in any way affecting the probabilistic predictions made by the calculus. Hence, the calculi in cases (
N1) and (
N2) are effectively scalar calculi, contrary to our design desideratum. Accordingly, we reject these two cases. Of the five possible forms of ⊙, we are therefore left with three: (
C1), (
C2) and (
C3).
In Reference [
11], additional arguments were mounted which eliminated cases (
C2) and (
C3), and picked out case (
C1) with
. In the remainder of this paper, we shall present a novel line of argument which leads to the same conclusion.
4.5. Pair Symmetry
When representing a sequence with a pair, we did not distinguish the role played by each component of pair. That is to say, of the resulting process calculi consistent with the constraints imposed thus far, there should be at least one whose predictions are invariant under the operation which swaps the components of every pair used to represent a sequence. This
pair symmetry requirement implies that
must be invariant under this swap operation, namely that, for any
,
In case (
C1),
, which already satisfies this symmetry for any
. However, in case (
C2),
, which is not symmetric under the swap operation for any
,
apart from the trivial
. Therefore, case (
C2) must be eliminated. Finally, in case (
C3),
, which satisfies this symmetry provided that
.
In summary, after having imposed the pair symmetry condition, we are left with the case (
C1) and case (
C3) with
.
4.6. Independent Parallel Processes
Consider an experimental set-up consisting of three measurements, and performed in succession. On one run, this generates sequence and, on another run, sequence , with . Then consider a second set-up, identical to the first except that the intermediate measurement coarsens outcomes and of , and suppose that this generates the sequence . If sequences A and B are represented by pairs , respectively, then sequence C is represented by the pair .
Now, as we have discussed above in the context of the double-slit experiment, if one were to assume according to classical physics that, in the second experiment, the system went through either the portion of the large detector corresponding to outcome
or through the portion corresponding to outcome
even though neither was explicitly measured, it would follow that
Using the sum rule of probability theory, the right hand side can be written as
Thus, in the special case where the classical assumption is valid—that is to say, the two processes represented by sequences
A and
B are independent (do not interfere)—it follows that
It seems very reasonable to require that the pair-calculus that we are developing should include the possibility of independent (non-interfering) processes as a special case. Accordingly, we shall require that the pair-calculus satisfy the:
Additivity Condition: For any given probabilities and for which , there exist pairs and satisfying such that Equation (
76)
(which we shall henceforth refer to as the additivity equation
) holds true whenever . We shall now investigate the constraints that this condition imposes in cases (
C1) and (
C3).
4.7. Case (C1), with
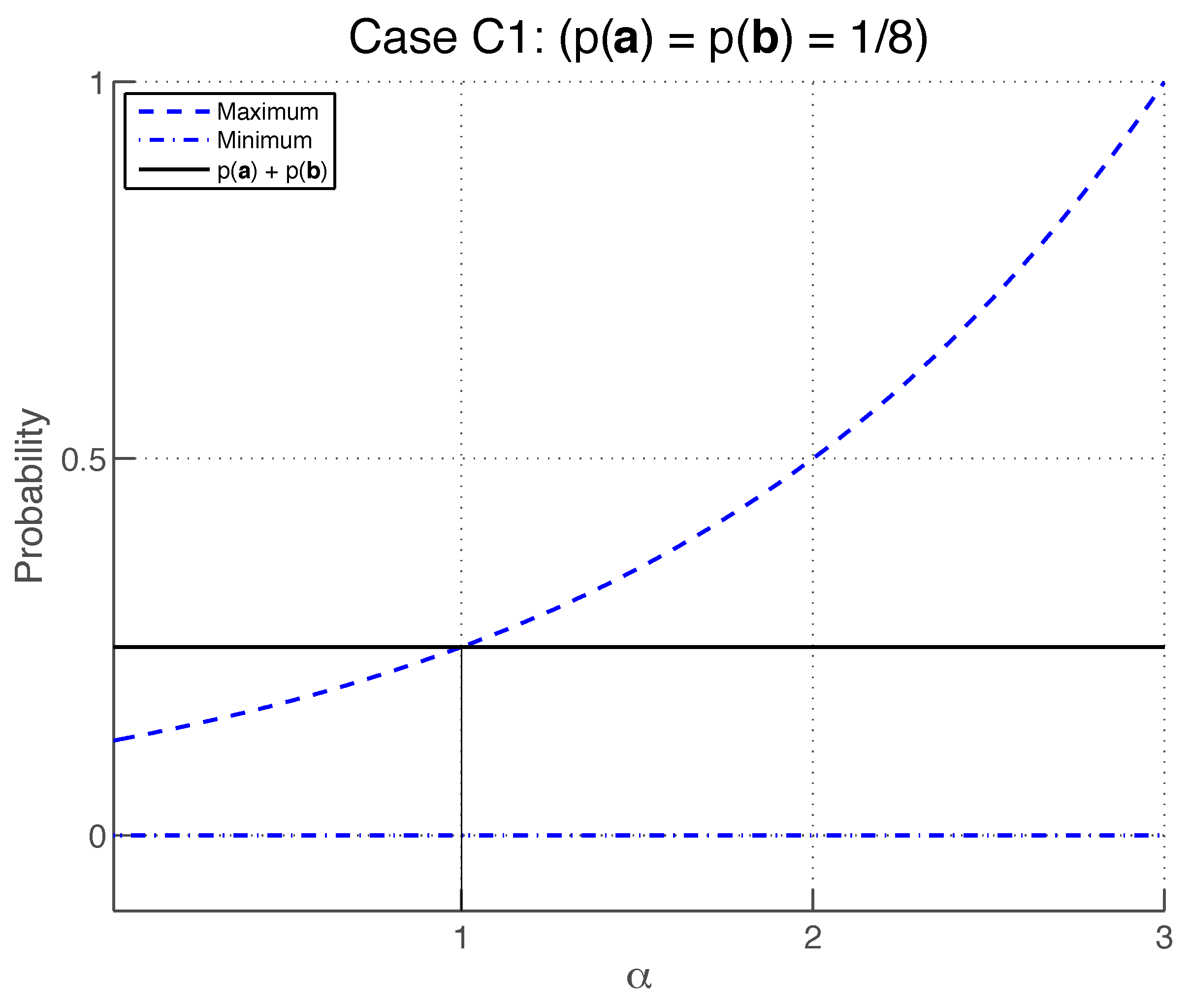
Setting
and
, the additivity Equation (
76) becomes
where
. By the additivity condition, for any
for which
, there must exist some value of
which satisfies this equation. Since
so that (as illustrated in
Figure 5) a value of
can be found that satisfies Equation (
77) provided that
The inequality
is satisfied provided that
, which also satisfies
.
Therefore, the additivity condition is satisfied by case (
C1) for any
.
Case (
C3), with
In this case, the additivity Equation (
76) reads
Parameterizing
,
as
where
are real non-zero parameters, we obtain
where
. Extremising with respect to
, one finds that
with the lower and upper limits obtained, respectively, when
and
(see
Figure 6).
The inequality
is satisfied by any
. Therefore, the additivity condition is satisfied by case (
C3) for any
.
4.8. Symmetric Bias
Although the additivity condition imposes constraints on the value of
in cases (
C1) and (
C3), it is by itself insufficient to pick out either of these cases and to pick out a unique value of
. In this section, we strengthen the additivity condition in such a way that uniquely picks out case (
C1) with
.
Consider again the three sequences
A,
B and
of
Section 4.6. In general, for fixed values of
and
, it will not be true that
. Instead, the possible values of
will span a range whose endpoints will (in general) be a function of
and
.
Now, in general, the maximum and minimum values of
will
not be symmetrically placed about
. However, it seems natural to suppose that the process calculus should allow two processes to interfere constructively and destructively to an equal degree. That is, if we define the
biases
where the maximizations and minimizations are constrained by given values of
and
, it seems natural to suppose that
. Accordingly, we now require that the process calculus satisfy the:
Symmetric Bias Condition [25]: For any given probabilities and for which , there exist pairs and satisfying such that holds true whenever . We shall now investigate the constraints that this condition imposes in cases (
C1) and (
C3).
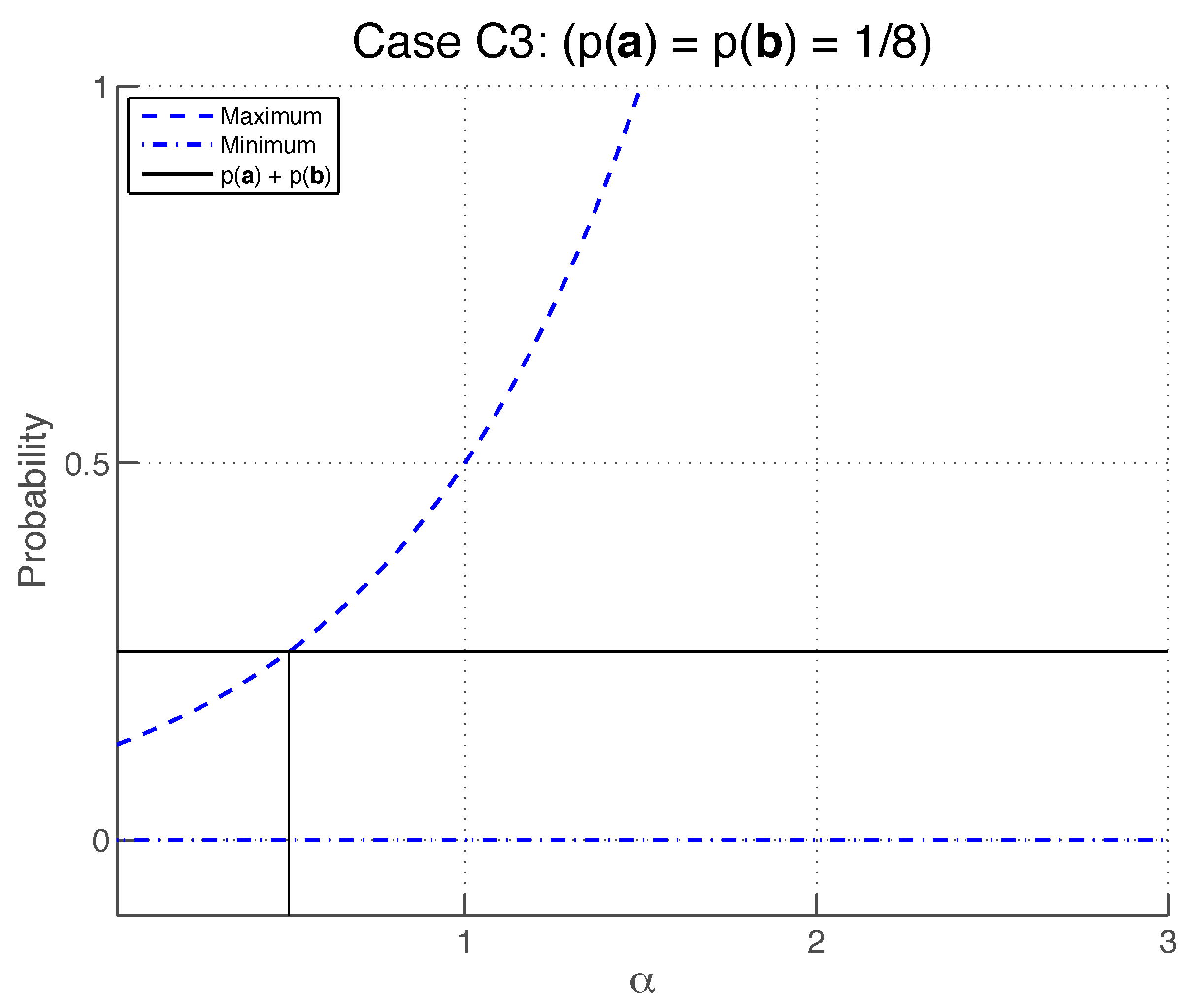
Case (
C1), with
If we rewrite Equation (
79) in terms of
and
, we obtain
from which the biases are
Let us consider two special cases. For
, one finds
and
, so that although no constructive interference is possible, destructive interference is always possible, which is a highly asymmetric situation. In contrast, for
, one finds that
, which means that one has complete symmetry between constructive and destructive interference, so that the symmetric bias condition is satisfied. We now show that
is the
only value of
that satisfies this condition.
The symmetric bias condition requires that
for any given
provided that
and
(see
Figure 7). This must hold in the special case where
, in which case, since
and, to second order in
The symmetric bias condition
then implies that
which must hold for any ratio
, which implies that
. More generally, when
, Equations (
88) and (
89) imply that
.
Therefore, the symmetric bias condition is satisfied by case (
C1) only if
.
Case (
C3), with
From Equation (
84), the biases are
The symmetric bias condition requires that
for any
,
provided that
and
. In particular, if
, it follows from
that
which implies
. With this setting, using Equations (
94) and (
95),
becomes
which, as illustrated in
Figure 8, cannot hold for all
. Therefore, the symmetric bias condition cannot be satisfied by case (
C3) for any value of
.
6. Conclusions
In this paper, we have shown that, by harnessing the symmetries in an experimental logic, and requiring correspondence to probability theory, it is possible to derive the core of the quantum formalism. The key physical inputs in the derivation are the pair-valued representation of the experimental logic, which is inspired by the principle of complementarity, and the symmetric bias condition, which ensures that the predictions of the process calculus are (in some precise sense) symmetrically placed around the predictions that arise from the application of probability theory on the assumption that two processes combined in parallel are probabilistically independent.
Hence, by explicit derivation, we have shown that Feynman’s rules can be understood as a probabilistic calculus whose predictions coincide with probability theory whenever probability theory is applicable, but which also yields predictions in certain situations where probability theory alone yields no predictions.
As we mentioned in the Introduction, the view is sometimes expressed that Feynman’s rules are inconsistent with probability theory. This misconception, which is unfortunately fairly widespread, stems from the failure to appreciate the fundamental origins of the probability calculus, and a failure to distinguish between
probability theory on the one hand, and an
assumption that has its roots in classical physics on the other. As we have shown, probability theory is a precise and controlled generalization of the process of deductive reasoning embodied in Boolean logic, and is not dependent upon assumptions peculiar to classical physics. Furthermore, as we have illustrated in our discussion of the double-slit experiment (
Section 3), this classical assumption amounts to assuming that a system (such as an electron) travels through a screen via one of two slits
even though it was not measured doing so. By deriving Feynman’s rules while making use of probability theory in its unmodified form, we have explicitly demonstrated that it is this classical assumption which is at fault,
not probability theory.
It is interesting to note that, from a conceptual standpoint, the above-mentioned classical assumption is highly speculative in that it asks us to believe something about what happened without the benefit of having made a measurement to verify that it is actually the case. That we are usually willing to grant this assumption is, as humans, the result of our long training with macroscopic objects in everyday life, and is, as physicists, the result of our long habituation to the assumptions embodied in the framework of classical physics. If one, however, exercises metaphysical caution and refrains from making this assumption, one opens up the possibility of a richer predictive theory. In this sense, quantum theory arises when we stay closer to the actual observed phenomena; when we are more wary about accepting statements that are not based on empirical data. In that sense, classical physics is more metaphysically speculative (and correspondingly less well grounded in empirical data) than quantum physics.
Another view that is sometimes expressed is that quantum theory is incompatible with Boolean logic. In this view, which can be traced to Birkhoff and von Neumann [
26], the distributive law of Boolean logic fails when one is dealing with certain propositions concerning the properties of quantum systems, and Boolean logic must accordingly be replaced by a so-called quantum logic that is abstracted from the quantum formalism. However, this cannot be the case: as we have demonstrated here, Feynman’s rules are entirely compatible with Boolean logic. Indeed, our derivation of Feynman’s rules
depends upon the validity of the latter—in particular, to each sequence of experiment outcomes is associated a logical proposition that is subject to the usual rules of Boolean logic (as well as the rules of probability theory, which we have shown are a systematic generalization of the Boolean logic). We suspect that this erroneous view arises from a failure similar to that mentioned above in connection with the supposed incompatibility of probability theory and quantum theory, namely a failure to distinguish between Boolean logic on the one hand, and additional assumptions rooted in a particular view of physical reality on the other. Indeed, a significant number of workers in the quantum logic area share the view that quantum logic is not to be regarded as a modification of Boolean logic, but rather is to be regarded as an operational (or experimental) logic rather like the experimental logic we describe above (see [
27], for example). It would be interesting to make a comparison of the quantum logic and our experimental logic. It would also be instructive to explicitly pinpoint the misconception that underpins the view that quantum theory is incompatible with Boolean logic. We hope to return to both of these tasks in subsequent papers.
Although our paper has been primarily concerned with delineating the relationship between probability theory and quantum theory, the results presented here have much broader implications. First, our derivation of Feynman’s rules does not employ most of the fundamental notions (such as space, mass, energy and momentum) of classical physics. A large part of the input to the derivation is the experimental logic and the consistency conditions emanating from probability theory, and the only other significant input which could be regarded as
physical is the
pair-valued representation of sequences. These observations suggest that the quantum formalism is logically prior to most of the concepts we ordinarily regard as fundamental to our description of the physical world, in turn suggesting that the quantum formalism is much closer in its nature to probability theory than was ever previously suspected. Not only do these observations have important implications for the further development of physics (as we elaborate in [
11]), but they also suggest that is may be possible to develop a clearer understanding of the meaning of the recent application of the quantum formalism in areas outside physics such as in artificial intelligence, cognition, and psychology (for example, [
28,
29]).
Second, the methodology we have employed appears to have many possible applications. As we have illustrated, the key idea behind the methodology is to start with a logic which captures the relationships between entities of interest (be they logical propositions, measurement sequences, or something else) and then to derive a
calculus by
suitable quantification of this logic. As we have seen, the derivation of quantum theory involves the crucial further step of
connecting the pair calculus together with the probability calculus, and then using conditions expressed in terms of the latter to constrain the former. The methodology has the great benefit of being transparent and highly systematic. Its efficacy in deriving quantum theory raises the question of whether the same methodology can be applied to better understand other existing physical theories or even to derive new ones. In this connection, one of us is currently exploring whether the application of this methodology to quantify causal sets of events can aid the understanding of space-time structure as an emergent phenomenon [
30]. The efficacy of the methodology also raises the question of whether it can be used to derive calculi in other areas of science. This indeed appears to be the case: as mentioned in the Introduction, we have already used this methodology to derive the axioms of measure theory [
7] and to develop a new calculus of questions [
7,
8]. However, we suspect that this work merely scratches the surface of what is possible.