Abstract
Much is already known about single mirror symmetry, but multiple mirror symmetry is still understood poorly. In particular, perceptually, multiple symmetry does not seem to behave as suggested by the number of symmetry axes alone. Here, theoretical ideas on single symmetry perception and their extensions to multiple symmetry are discussed alongside empirical findings on multiple symmetry perception. The evidence suggests that, apart from the number of axes, also their relative orientation is perceptually relevant. This, in turn, suggests that perception is responsible for the preponderance of 3-fold and 5-fold symmetries in flowers as well as for their absence in decorative art.
1. Introduction
Mirror symmetry (henceforth, symmetry) is abundant in the world and seems relevant in many domains [1,2,3,4]. In most domains, symmetry research focuses on the role of symmetry. In biology, for instance, humans and various other species have been found to prefer more symmetrical shapes over less symmetrical ones in mating and pollinating behavior [5,6,7,8,9,10,11]. Symmetry is also a much investigated topic in perception research, where two categories of research can be distinguished. First, analogous to other domains, research that focuses on the role of symmetry in perception. For instance, in human perception research, symmetry has been found to play a relevant role in issues such as object recognition [12,13], figure-ground segregation [14,15,16], and amodal completion [17,18]. Second, research that focuses on how, and how well, symmetry in itself is perceived (for reviews, see [19,20,21,22]).
This article starts from the latter category of symmetry research. This research showed that symmetry is one of the visual regularities, that is, one of the regularities the visual systems of humans and many other species are sensitive to [23,24,25]. For instance, even if a pattern is far from perfectly symmetrical, humans are well able to detect the presence of symmetry [23,26]. Not surprising therefore, symmetry detection is believed to be an integral part of the perceptual process that is applied to every input.
In this article, I focus on multiple symmetry perception and its potential influence on nature and art. Multiple symmetrical patterns are patterns with two or more global symmetry axes. Patterns with one or more symmetry axes are also called cases of n-fold symmetry (), and patterns with many symmetry axes are also called cases of radial symmetry. Because a multiple symmetry is a composition of single symmetries, perception thereof obviously leans upon the above-mentioned sensitivity to single symmetry. However, the question is whether, perceptually, multiple symmetry behaves as the sum of the constituent single symmetries—does it behave as might be expected on the basis of the number of symmetry axes alone? I argue it does not, and I also argue that this perceptual factor has influenced the distribution of multiple symmetries in the world. Thereby, it also sheds new light on the evolutionary question of whether the sensitivity of visual systems to symmetry is cause or consequence of the abundance and role of symmetry in the world. I begin by specifying the latter question in more detail.
2. Evolutionary Considerations
The high perceptual sensitivity to symmetry has been proposed to have evolved because symmetry is a useful cue in object recognition [20]. An argument, sketched in Figure 1, could be that it is useful because many relevant objects exhibit symmetry, which in turn may have been caused by the symmetry preference in mating and pollinating behavior (and probably also in other behavior). This symmetry preference, in turn, may have evolved because the degree of shape symmetry is a marker of an organism’s quality [27]. That is, natural growth processes tend to produce shapes that are basically symmetrical but also exhibit fluctuating amounts of asymmetry, and a higher amount of asymmetry may indicate a lesser genetic quality or a lesser ability to cope with environmental stress.
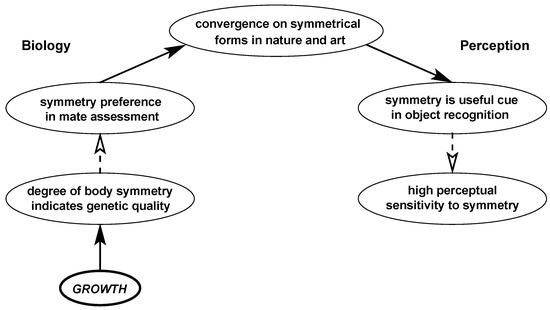
Figure 1.
Evolutionary factors relevant to a high perceptual sensitivity to symmetry. The dashed arrows do not indicate direct causation—they merely indicate that their starting terms provide survival value to their end terms which must have been caused by something else.
This argument, however, ignores that the symmetry preference already requires a high perceptual sensitivity to symmetry. Therefore, Figure 2 provides an alternative argument, which does not deny the evolutionary relevance of the just-mentioned factors, but which proposes clearer causal relationships. This argument starts from growth as a fundamental natural force towards order, which forms a balance against the also-natural force towards chaos [28]. By this, I do not mean that growth should be considered to be distinct from other physical or biochemical processes (a quite common idea in the 19th century). Instead, I simply mean that natural growth processes are responsible for virtually all symmetrical shapes in nature, be they crystals or living organisms. As I argue later in this article, growth may also reflect the way in which visual systems build structured mental representations. This suggests not only that fluctuating asymmetry may indeed be a marker of quality, but independently thereof, also that the natural principle of growth gave rise to visual systems that are pre-eminently suited to process symmetry.
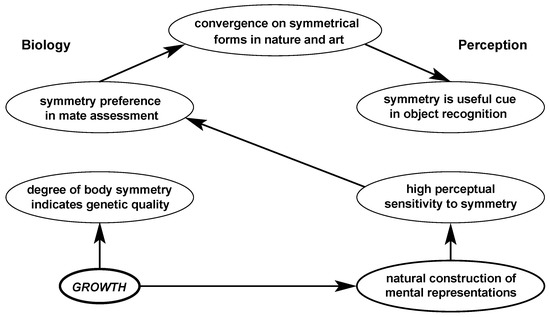
Figure 2.
Natural selection mechanism, according to which a high perceptual sensitivity to symmetry is not the consequence but the cause of the symmetry preference in mate assessment. The separate functionalities of symmetry regarding genetic quality and object recognition then are factors favourable towards the survival of such a visual system.
The latter then may have triggered the symmetry preference in mating and pollinating behavior [6,29], which provided such visual systems with evolutionary survival value because fluctuating asymmetry indicates quality. The symmetry preference, by the way, is obviously not the only factor in mating and pollinating behavior, but the idea is that it co-evolved together with other factors. Also in other behavioral domains, this symmetry preference may have exerted selection pressure on symmetrical features, thus boosting the occurrence of symmetrical shapes [1]—providing such visual systems with further survival value because, thereby, symmetry reinforced itself as a useful cue in object recognition.
Notice that the argument in Figure 2 specifies rather than challenges the argument in Figure 1. It also suggests, however, that the sensitivity of visual systems to symmetry is not so much a passive consequence of the abundance of symmetry in the world but, rather, a factor that actively influences the occurrence of symmetry in the world. In this article, I explore if this might explain a remarkable peculiarity in the distribution of multiple symmetries in nature and art.
3. Multiple Symmetry in Nature and Art
Multiple symmetry occurs in the animal kingdom (think of starfish) and in crystals, and also prominently in flowers and human designs. Remarkably, in both flowers and human designs, 3-fold and 5-fold symmetries seem to have a special status. Next, I discuss this first for flowers and then for human designs.
3.1. Flowers
In plants, the family of monocotyledons (with one seed-leaf) usually produces 2-fold and 3-fold symmetrical flowers, and the family of dicotyledons (with two seed-leafs) usually produces 4-fold and 5-fold symmetrical flowers (Figure 3). The distribution within each family, however, is skewed. Based on a count in Heywood’s Flowering Plants of the World [30], I estimate that 80% of the monocotyledons produce 3-fold symmetrical flowers, and that 70% of the dicotyledons produce 5-fold symmetrical flowers. It has been proposed that the preponderance of 3-fold and 5-fold symmetrical flowers is related to the fact that 3 and 5 are among the Fibonacci numbers (which are defined by , , and for ). Such numbers of petals might indeed allow for efficient petal packing in spiral flowers, but their status in whorled flowers is less clear [31]. As indicated next, timelines allow for an alternative, perceptual, explanation.
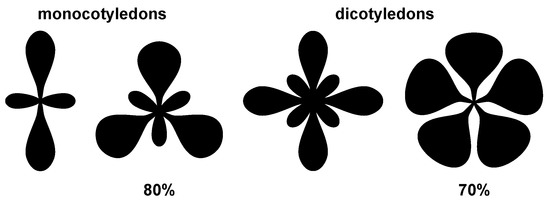
Figure 3.
In the plant family of monocotyledons, 80% of the mostly 2-fold and 3-fold symmetrical flowers is 3-fold symmetrical, and in the plant family of dicotyledons, 70% of the mostly 4-fold and 5-fold symmetrical flowers is 5-fold symmetrical.
Insect vision evolved about 400 million years ago whereas flowering plants evolved only about 125 million years ago [30]. Hence, the preponderance of 3-fold and 5-fold symmetrical flowers might well find its origin in the insect’s perceptual sensitivity to symmetry [32,33]. For instance, Horridge found that the honeybee (Apis mellifera) is sensitive to angles of 60° [34]. These are also the angles between the symmetry axes in 3-fold symmetry, which suggests that the preponderance of 3-fold symmetrical flowers in monocotyledons might be a consequence of this perceptual sensitivity. That is, due to this perceptual sensitivity, pollinators might be attracted more to 3-fold symmetrical flowers than to 2-fold symmetrical flowers, so that the former would have a procreation advantage over the latter.
3.2. Human Designs
Throughout recorded and unrecorded human history, symmetry seems to have fascinated people [1,2,4,35]. Already 400,000 years ago, it was a factor in the design of stone tools [36]. Also in human designs, 3-fold and 5-fold symmetries seem to have a special status: they do occur in mystical art but not in decorative art. For instance, Hardonk created a database of 800 decorative bands (40 bands for each of 20 extinct and present-day cultures from all over the world) [37]. A decorative band consists of a repetition of a motif, and about 600 of these 800 bands contain motifs with 1–8 symmetry axes. As a rule, motifs with more symmetry axes occur less often, but motifs with 3 or 5 symmetry axes escape this rule and are virtually absent (Figure 4). The latter motifs might be harder to produce, but this can hardly be the reason considering that they do occur in mystical art.
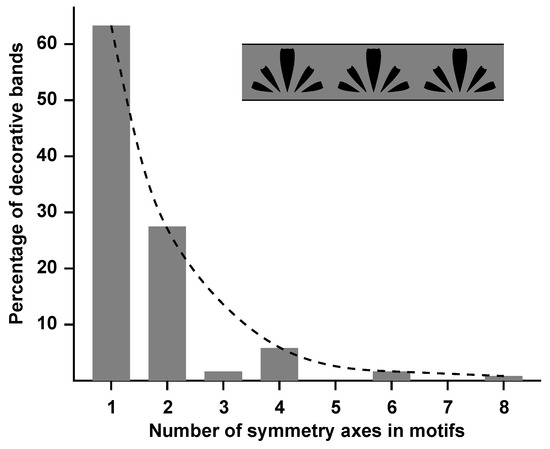
Figure 4.
Decorative bands. The inset shows a decorative band consisting of a repetition of a 1-fold symmetrical motif. The histogram covers about 600 decorative bands containing motifs with 1–8 symmetry axes [37]. The dashed line indicates the rule—with notable exceptions—that motifs with more symmetry axes occur less often.
In mystical art, 3-fold and 5-fold symmetrical motifs—such as the triqueta and the pentagram (Figure 5)—have often been used to symbolize supernatural powers [38], and nowadays, such motifs are widely used in the emblems of police forces, armies, national flags, car brands, sports clubs, and so on. The pentagram is probably the all-time favorite, with a history of over 5000 years [39]. In ancient Greece, its alleged supernatural status led to the definition of the golden ratio as the ratio 1.618 in which each intersection of edges in a pentagram sections these edges (this ratio was believed to have aesthetical value, but see [40]). Furthermore, in ancient Mesopotamia, the pentagram symbolized imperial power; among Druids and Celts, it symbolized divine power; in medieval England, it was associated with knightly virtues; and in India, it features in Tantric art.

Figure 5.
Motifs used often in mystical art to symbolize supernatural powers; (a) The 3-fold symmetrical triqueta; (b) The 5-fold symmetrical pentagram.
Just as flowers, human designs do not seem to have intrinsic properties that could evoke the special status of 3-fold and 5-fold symmetries, which, also this time, might well have been caused by properties intrinsic to visual systems. To explore this, I turn to research on human symmetry perception.
4. Models of Human Symmetry Perception
The human perceptual process organizes visual input. To this end, it constructs mental representations of inputs, exploiting input features it is sensitive to. Symmetry and repetition are such features, and commonly accepted is that representations capture the structural relationships between two symmetry halves or repeats. In the next subsections, however, I discuss three models of human symmetry perception, which propose different specifications of these structural relationships, thereby implying different stances regarding multiple symmetry perception.
4.1. The Transformational Approach
The traditionally considered approach to visual regularity is the transformational approach which, in perception research, has been promoted most prominently by Garner [41] and Palmer [42]. It holds that visual regularities are configurations characterized by invariance under motion, that is, configurations which, if present in an object, yield image invariance under rigid rotations and translations of the object (Figure 6a). According to this approach, repetition qualifies as visual regularity because, at least when looked at through a restricting aperture, it remains invariant under translations (i.e., shifts along the longitudinal axis) the size of one or more repeats. Furthermore, single symmetry qualifies as visual regularity because it remains invariant under a 180° 3-D rotation about its symmetry axis. Notice that these invariance transformations establish identity relationships between repeats and between symmetry halves, independently of the number of elements in each of them (Figure 6a). Both repetition and symmetry are therefore said to have a transformational block structure.

Figure 6.
Proposed perceptual structures of symmetry and repetition (see text for details); (a) The transformational approach specifies visual regularities by invariance under rotations and translations, implying a block structure for both symmetry and repetition; (b) The bootstrap model starts from shared properties of virtual lines between corresponding elements, implying a point structure for both symmetry and repetition; (c) The holographic approach specifies these regularities by invariance under growth (i.e., under expansion by symmetry pairs or repeats), implying a point structure for symmetry and a block structure for repetition.
By the same token, n-fold symmetry with qualifies as visual regularity because it remains invariant under n such 3-D rotations plus n 2-D rotations of degrees in the picture plane. Notice that this characterizes an n-fold symmetry as one regularity rather than as a composition of n single symmetries. Notice further that the number of invariance transformations increases monotonically with the number of symmetry axes, and that the figural goodness of multiple symmetry (i.e., its salience, or its detectability) is known to increase also with the number of symmetry axes—at least, if one compares 1-fold, 2-fold, and 4-fold symmetries [43,44,45]. Hence, a common-sense transformational quantification of the goodness of n-fold symmetries could be given by the formula , which also incorporates a plausible ceiling effect (Figure 7). In any case, the foregoing shows the transformational approach does not assign a special perceptual status to 3-fold and 5-fold symmetries, so that it cannot explain a special status in nature and art by their alleged perceptual status.
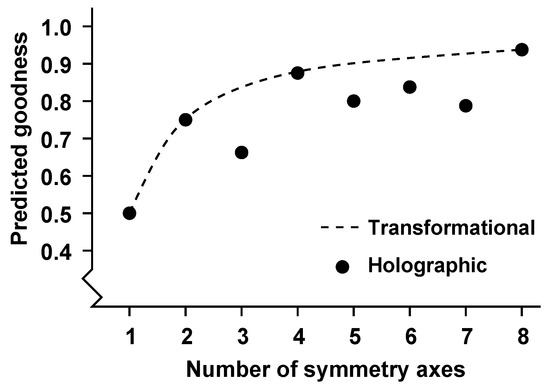
Figure 7.
Predicted goodness (i.e., salience, or detectability) of n-fold symmetries with . The dashed line indicates the predictions by the transformational approach; the dots indicate the predictions by the holographic approach.
However, does it properly specify their perceptual status? It is true that the transformational approach has proved to be suited for a formal classification of already-perceived objects such as crystals and regular tilings [3,46]. Besides, a transformationally invariant object yields the same retinal image from different viewpoints, which is functional in that recognition can occur fairly independently of viewpoint [29]—think, for instance, of a honeybee approaching a flower with one of the shapes in Figure 3. Yet, it does not seem suited to account for how such objects are perceived preceding recognition. For instance, it neither accounts for the detectability of perturbed symmetry nor for the fact that symmetry is better detectable than repetition [21]. Hence, the transformational approach does not seem eligible to assess if the special status of 3-fold and 5-fold symmetries in nature and art is due to their perceptual status.
4.2. The Bootstrap Model
The bootstrap model by Wagemans and co-workers builds on Jenkins’ proposal to specify visual regularities by shared properties of virtual lines between corresponding pattern points [45,47]. For instance, virtual lines between corresponding points in a repetition are parallel and of the same length, and virtual lines between corresponding points in a symmetry are parallel and midpoint colinear (Figure 6b). Wagemans noted that a pair of such virtual lines forms a parallelogram in repetition and a symmetrical trapezoid in symmetry (Figure 8a), and he provided empirical evidence that also these correlation quadrangles are perceptually relevant [48]. Subsequently, he proposed that these correlation quadrangles are the structural anchors from which regularity detection propagates [45,48]. In symmetry, for instance, the symmetry axis of a trapezoid indicates the direction in which the detection process may propagate by searching for additional virtual lines between corresponding points.
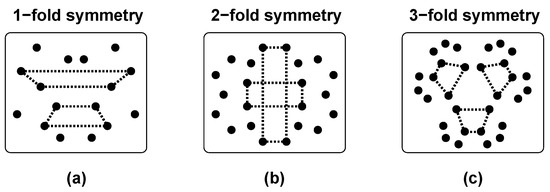
Figure 8.
Symmetry detection according to the bootstrap model; (a) In 1-fold symmetry, virtual lines between corresponding elements form correlation trapezoids, which serve as anchors for the detection process; (b) In 2-fold symmetry, some of these trapezoids are rectangles, which are proposed to boost the detection process; (c) In 3-fold symmetry, rectangles do not occur, so that the detection process can only start from trapezoids.
I think that, regarding regularity detection, this idea is a plausible starting point which deserves further elaboration [49]. It also gives rise to an interesting stance regarding multiple symmetry. In 2-fold and 4-fold symmetry, for instance, some of the correlation trapezoids are rectangles, that is, they exhibit extra structure (Figure 8b). Whereas proper trapezoids (with one symmetry axis) indicate one propagation direction, rectangles (with two symmetry axes) indicate two propagation directions, and Wagemans proposed that this boosts detection [45]. This would explain why 2-fold symmetry is so much better detectable than 1-fold symmetry, and notably, it also predicts that 3-fold symmetry is an odd one out. Wagemans did not mention the latter, but notice that 3-fold symmetry does not contain correlation rectangles (Figure 8c), so that it cannot benefit from their boosting effect.
Hence, the bootstrap model suggests that 3-fold (and, likewise, 5-fold) symmetries have a special perceptual status, which might explain their special status in nature and art. To this end, however, it must be established if correlation rectangles indeed have the alleged boosting effect. Treder, van der Vloed, and van der Helm [50] investigate this by means of equally noisy 2-fold symmetries with and without correlation rectangles (Figure 9). Participants’ performance on discrimination from random patterns showed no difference between these conditions, however. This casts severe doubts on the alleged boosting effect of correlation rectangles over correlation trapezoids. This does not affect the plausibility of correlation trapezoids as detection anchors (see also [49,51,52]). It does suggest, however, that the lack of correlation rectangles in 3-fold and 5-fold symmetries is not perceptually relevant, so that it also cannot be a perceptual factor that might explain their special status in nature and art.
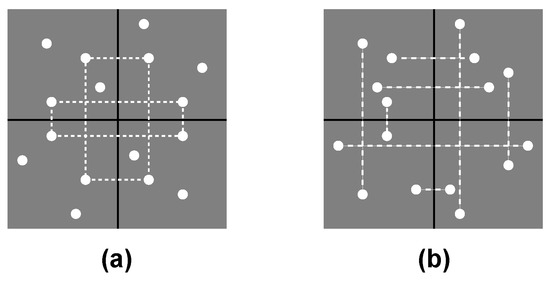
Figure 9.
Schematic overview of Treder et al.’s [50] experimental conditions involving equally noisy 2-fold symmetries with and without correlation rectangles (the actual stimuli contained dots only; here, in both cases, correlation trapezoids are present but not highlighted); (a) Fifty percent of the elements are noise about both axes, and the other 50% are symmetrical about both axes, so that there are both correlation trapezoids and correlation rectangles; (b) Fifty percent of the elements are symmetrical about one axis but noise about the other axis, and vice versa for the other 50%, so that there are trapezoids but no rectangles.
4.3. The Holographic Approach
The holographic approach [21,53] holds that visual regularities are configural properties characterized by invariance under growth (Figure 6c). For instance, a repetition remains a repetition after expansion by one or more repeats, and a symmetry remains a symmetry after expansion by one or more pairs of symmetrically positioned identical elements (just as bodies preserve their symmetrical shape while growing). Formally, such a regularity is called a holographic regularity, referring to the fact that it is a structure with substructures that all reflect the same kind of regularity [53]. This implies that, in a similar fashion as the bootstrap model does, the representation of its structure can be build easily from its substructures [49]. Furthermore, the holographic approach models the detectability of a regularity in a stimulus by the weight of evidence for this regularity in the stimulus [21]. This is explicated next.
In the holographic approach, amounts of regularity are quantified by the number of nonredundant identity relationships between stimulus parts (E) that give rise to a regularity. Applied to repetition, this implies that E equals the number of repeats minus one, independently of the number of elements in each repeat—repetition is therefore said to have a holographic block structure. Furthermore, applied to symmetry, it implies that E equals the number of symmetrically positioned pairs of identical elements—symmetry is therefore said to have a holographic point structure. The detectability of a regularity in a stimulus then is quantified by the weight of evidence (W) for this regularity, where with N the total number of elements in the stimulus.
This approach appeared to provide a fairly comprehensive account of the detectability of single and combined regularities, whether or not perturbed by noise. For instance, qualitatively, the formal notion of holographic regularity seems to supply a perceptually relevant border between visual and nonvisual regularities [54], and also the holographic difference in structure between symmetry (point structure) and repetition (block structure) seems perceptually relevant [55]. Furthermore, the quantitative model accounts for various perceptual differences between symmetry and repetition, including the fact that symmetry is better detectable than repetition, and it accounts for the detectability of symmetry in the presence of noise (for more details, see [21,26,49,51,56,57]).
Furthermore, the holographic approach builds on the idea that regularities allow for efficient stimulus representations [58,59,60,61,62,63]. For instance, to represent a symmetrical object, the visual system may exploit the object’s symmetry to reduce the information needed to represent it, that is, it may represent the object by only the information in one symmetry half. Further regularity in this symmetry half then can be exploited to further reduce this information. This implies the following for multiple symmetry.
To represent a 2-fold symmetrical object, first, one global symmetry can be exploited to reduce information, and then, the local symmetry in the remaining symmetry half can be exploited to further reduce information (Figure 10a). In terms of the model , a 1-fold symmetry on N elements contains symmetry pairs, so that it has a weight of evidence of , and by the foregoing, a 2-fold symmetry has a weight of evidence of because the second symmetry adds nonredundant identity relationships.

Figure 10.
Representational information reduction by exploiting symmetry; (a) In 2-fold symmetry, one global symmetry can be exploited to represent the pattern by the information in one symmetry half, after which the remaining local symmetry can be exploited to further reduce information; (b) In 3-fold symmetry, after exploiting a global symmetry, only one of the remaining local symmetries can be exploited to further reduce information; (c) A 3-fold symmetry can be represented more efficiently by a repetition of three local symmetries.
To represent a 3-fold symmetrical object, first, again one global symmetry can be exploited to reduce information, but then, only one of the two local symmetries in the remaining symmetry half can be exploited to further reduce information (Figure 10b). This implies that a 3-fold symmetry has a weight of evidence of only because the second symmetry adds only nonredundant identity relationships (by the way, unlike in case of 2-fold symmetry, representing a 3-fold symmetry by a repetition of three local symmetries—see Figure 10c—yields more information reduction, but also notice that this repetition has a lower weight of evidence; I return to this later on in this article).
Extending the foregoing to n-fold symmetry with yields the weights of evidence depicted in Figure 7. This figure shows that the holographic and transformational approaches predict the same if n is a power of 2, but not for other values of n. In other words, the holographic approach assigns a special perceptual status to, among others, 3-fold and 5-fold symmetries—which might explain their special status in nature and art. As argued, the holographic approach is perceptually valid insofar as single regularities are concerned, but what about its predictions regarding multiple symmetry perception?
5. Multiple Symmetry Perception
Compared to single symmetry, multiple symmetry has been less investigated, but the available empirical evidence is fairly consistent. As mentioned, as a rule, the detectability of multiple symmetry was found to increase with the number of symmetry axes—at least, if one compares 1-fold, 2-fold, and 4-fold symmetries [43,44,45]. Furthermore, to test the holographic approach, Nucci and Wagemans considered eight different combinations of global and local symmetries (Figure 11), and they asked participants to discriminate these from random patterns [64]. The holographic weights of evidence for these combinations ranged from for a local symmetry flanked by noise, to for a 2-fold symmetry with additional local symmetries, and they reported a correlation of between participants’ performance and W values. To the second combination in Figure 11, they assigned , but considering the task, this must be yielding a corrected correlation of (without this second combination, the correlation would be ).
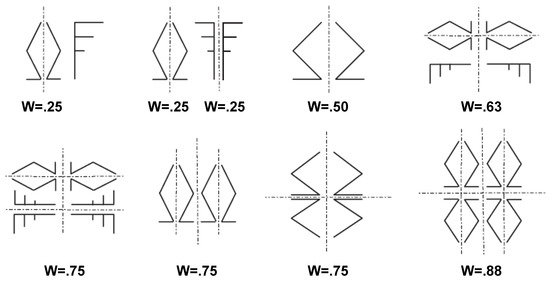
Figure 11.
Schematic overview of Nucci and Wagemans’ [64] experimental conditions combining global and local symmetries (the actual stimuli were dot stimuli), and the associated holographic weights of evidence (W) for the regularities. In the second condition, each of the two flanking local symmetries has , which does not sum to : they constitute noise to one another, so that considering the task, this condition hardly differs from the first condition with one local symmetry flanked by noise.
Notice that these studies did not consider 3-fold symmetry. To my knowledge, Hamada and Ishihara were the first to test 3-fold symmetry [65]. Their data suggest that, perceptually, 3-fold symmetry behaves like a repetition of three local symmetries. This agrees with the earlier-mentioned idea that this representation yields maximum information reduction (Figure 10c). It also suggests that 3-fold symmetry does not behave as might be expected on the basis of the number of global symmetry axes alone.
To investigate this further, Wenderoth and Welsh compared the transformational and holographic predictions for n-fold symmetries with [66]. They asked participants to discriminate such stimuli from random patterns, and not surprising, they found that performance for 2-fold and 3-fold symmetries was better than that for 1-fold symmetries and worse than that for 4-fold symmetries. They also found, however, that performance for 3-fold symmetry did not differ significantly from that for 2-fold symmetry and in fact tended to be worse. This finding goes against the transformational approach and tends to support the holographic approach: It confirms that the difference between 2-fold and 3-fold symmetries is indeed not as might be expected on the basis of the number of symmetry axes alone.
In this respect, two remarks are in order. First, van der Vloed also considered n-fold symmetries with , and he found that detectability increases linearly with n [67]. Considering that there must be a ceiling effect, such a linear increase is implausible, and on methodological grounds, he also argued that findings on multiple symmetry might be task dependent. Second, Wenderoth and Welsh’s [66] finding would be in line also with the bootstrap model—at least, if correlation rectangles would have had the proposed boosting effect over correlation trapezoids [45]. However, as mentioned, Treder et al. found no differential effect of correlation rectangles at all [50].
Treder et al. went on to investigate what other factor might affect multiple symmetry perception, and they focused on the relative orientation of symmetry axes [50]. In the holographic approach, this factor is relevant in that it determines which additional regularity in a global symmetry can be exploited to reduce the information needed to represent it (see Figure 10). Furthermore, symmetry axes seem to form subjective contours which are processed in a similar orientation-dependent way as luminance contours are, so that, for instance, symmetry axes in dot patterns elicit tilt aftereffects comparable to those of luminance contours [68,69,70,71,72,73,74]. This too suggests that relative orientation is a relevant factor.
In perfect multiple symmetry, the number of symmetry axes dictates the relative orientation of the axes. For instance, perfect 2-fold and 4-fold symmetries have orthogonal axes, whereas perfect 3-fold and 5-fold symmetries only have nonorthogonal axes. To decouple these two factors, Treder et al. constructed 2-fold symmetries by superimposing two perfect 1-fold symmetries [50]. This enables the construction of equally noisy 2-fold symmetries without correlation rectangles, and here more important, with varying relative orientations of the two axes (Figure 12). In particular, Treder et al. considered orthogonal axes with 90° relative orientation, and nonorthogonal axes with 45/135° relative orientation (i.e., one angle is 45° and the other angle is 135°). To control for known effects of absolute orientation, they positioned the stimuli such that the axes were at the roughly equisalient absolute orientations of +22.5° and −22.5° with respect to the vertical and the horizontal.

Figure 12.
Examples of Treder et al.’s [50] equally noisy 2-fold symmetrical stimuli, constructed by superimposing two perfect 1-fold symmetries in different relative orientations (absolute orientations are given in the insets); (a) Two superimposed dot patterns; (b) Two superimposed Gaussian noise patterns, filtered in the spatial frequency (SF) domain to a 1-octave low-SF band and a 1-octave high-SF band, respectively, with one octave in between (in the insets, thick lines refer to the low-SF band and thin lines to the high-SF band).
In one experiment, they superimposed two symmetrical dot patterns, and in another experiment, two symmetrical Gausian noise patterns restricted each to a different spatial frequency band. They asked participants to discriminate such stimuli from random stimuli, and for both stimulus types, they found that performance for such a 2-fold symmetry was better than that for either 1-fold symmetry alone. More importantly, for the 2-fold symmetries, they found that performance was better for orthogonal axes than for nonorthogonal axes. This suggests that the single symmetries in a multiple symmetry engage in an interaction which depends on their relative orientation. This is consistent with the holographic approach and suggests that 3-fold and 5-fold symmetries indeed have a special perceptual status—not because they lack correlation rectangles, but because of the nonorthogonal relative orientations of their axes.
6. Discussion and Conclusions
In this article, I argued that the traditionally considered transformational approach to visual regularity may be suited for object recognition but not for object perception, so that it does not seem eligible to assess if the special status of 3-fold and 5-fold symmetries in nature and art is due to their perceptual status. I argued further that the bootstrap model implies a special perceptual status for 3-fold and 5-fold symmetries, which, however, relies on a non-established role of correlation rectangles. The holographic approach also implies a special perceptual status for 3-fold and 5-fold symmetries, which, this time, relies on an established role of the relative orientation of symmetry axes.
More specifically, Treder et al.’s [50] finding suggests that, perceptually, a multiple symmetry is not processed as one regularity, but as consisting of separate single symmetries which, after having been detected, engage in an orientation-dependent interaction. This is a fine example of the more general Gestalt motto that “the whole is something else than the sum of its parts” [75]. The foregoing brings me to make the following case for the influence of perception on the world.
Natural growth processes are the primary cause of the occurrence of symmetrical shapes in nature [28]. Symmetrically shaped organisms, however, tend to arrange their environment such that it is also symmetrical [1], and this proliferation of symmetry requires perception. A tendency to produce simple symmetrical environments may arise because simple environments are more easily produced, but probably also because they can be represented perceptually by means of less information, which facilitates subsequent usage. The tendency to produce simple symmetrical environments can be observed in bird nests, for instance, and also in man-made environments like cities—whose arrangement is generally much simpler than that of natural environments like jungles. In fact, the complexity of jungles might be the reason that their inhabitants rely on smell and sound rather than on vision [76].
The latter indicates that perception is not the only factor that shapes the world, but the foregoing suggests it is yet a substantial factor. It not only seems to assert the role of symmetry in the world but it also seems to boost the occurrence of symmetry. The causal reason for this might well be that, as argued in the holographic approach, growth also reflects the way in which the human visual system builds structured mental representations—this makes it pre-eminently suited to process single symmetries. As argued, it also implies a perceptual differentiation between multiple symmetries, which shows undeniable parallels with their distribution in flowers and human designs. That is, as predicted by the holographic approach, 3-fold and 5-fold symmetries have a special perceptual status, which runs parallel to their preponderance in flowers as well as to their occurrence in mystical art but not in decorative art.
Of course, due to differences in visual systems, insect vision and human vision cannot simply be lumped together. Furthermore, one can of course only speculate that the special status of 3-fold and 5-fold symmetries in nature and art is indeed due to their special perceptual status. However, to conclude, the influence of the latter on the former might also be understood as follows.
As argued, 2-fold and 4-fold symmetrical stimuli yield unambiguous stable percepts which capture all regularity in such stimuli. In contrast, 3-fold and 5-fold symmetrical stimuli yield unstable ambiguous percepts. That is, as illustrated in Figure 10b,c, they can be organized as a salient global symmetry with additional regularity that cannot be captured completely, or as a more efficient but less salient repetition of local symmetries. In other words, they can be said to contain hidden order, that is, more order than can be captured in one stable percept. It is known that such hidden order creates a perceptual tension between roughly equally strong and therefore competing percepts, which may trigger one’s curiosity, interest, and aesthetical feelings, for instance [77,78]. Though still cautious because of differences in visual systems, I suspect that 3-fold and 5-fold symmetrical flowers have a procreation advantage over others, precisely because this perceptually hidden order attracts more pollinators. Furthermore, I suspect that, again because of this perceptually hidden order, throughout history humans have felt that 3-fold and 5-fold symmetrical motifs are more appropriate for mystical art than for decorative art.
References
- Allen, G. The origin of the sense of symmetry. Mind 1879, 4, 301–316. [Google Scholar] [CrossRef]
- Hargittai, I. Symmetry: Unifying Human Understanding; Pergamon: New York, NY, USA, 1986. [Google Scholar]
- Shubnikov, A.V.; Koptsik, V.A. Symmetry in Science and Art; Plenum: New York, NY, USA, 1974. [Google Scholar]
- Weyl, H. Symmetry; Princeton University Press: Princeton, NJ, USA, 1952. [Google Scholar]
- Grammer, K.; Thornhill, R. Human (Homo sapiens) facial attractiveness and sexual selection: The role of symmetry and averageness. J. Comp. Psychol. 1994, 108, 233–242. [Google Scholar] [CrossRef] [PubMed]
- Johnstone, R.A. Female preferences for symmetrical males as a by-product of selection for mate recognition. Nature 1994, 372, 172–175. [Google Scholar] [CrossRef] [PubMed]
- Møller, A.P. Female swallow preference for symmetrical male sexual ornaments. Nature 1992, 357, 238–240. [Google Scholar] [CrossRef] [PubMed]
- Møller, A.P. Bumblebee preference for symmetrical flowers. Proc. Natl. Acad. Sci. USA 1995, 92, 2288–2292. [Google Scholar] [CrossRef] [PubMed]
- Swaddle, J.; Cuthill, I.C. Preference for symmetric males by female zebra finches. Nature 1993, 367, 165–166. [Google Scholar] [CrossRef]
- Thornhill, R.; Gangestad, S.W. Human fluctuating asymmetry and sexual behavior. Psychol. Sci. 1994, 5, 297–302. [Google Scholar] [CrossRef]
- Watson, P.J.; Thornhill, R. Fluctuating asymmetry and sexual selection. Trend. in Ecol. Evolut. 1994, 9, 21–25. [Google Scholar] [CrossRef]
- Pashler, H. Coordinate frame for symmetry detection and object recognition. J. Exp. Psychol. Hum. Percept. Perform. 1990, 16, 150–163. [Google Scholar] [CrossRef]
- Vetter, T.; Poggio, T. Symmetric 3D objects are an easy case for 2D object recognition. Spatial Vision 1994, 8, 443–453. [Google Scholar]
- Driver, J.; Baylis, G.C.; Rafal, R.D. Preserved figure-ground segregation and symmetry perception in visual neglect. Nature 1992, 360, 73–75. [Google Scholar] [CrossRef] [PubMed]
- Leeuwenberg, E.L.J.; Buffart, H.F.J.M. The perception of foreground and background as derived from structural information theory. Acta Psychol. 1984, 55, 249–272. [Google Scholar] [CrossRef]
- Machilsen, B.; Pauwels, M.; Wagemans, J. The role of vertical mirror symmetry in visual shape detection. J. Vision 2009, 9, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Kanizsa, G. Seeing and thinking. Acta Psychol. 1985, 59, 23–33. [Google Scholar] [CrossRef]
- van Lier, R.J.; van der Helm, P.A.; Leeuwenberg, E.L.J. Competing global and local completions in visual occlusion. J. Exp. Psychol. Hum. Percept. Perform. 1995, 21, 571–583. [Google Scholar] [CrossRef] [PubMed]
- Treder, M.S. Behind the looking-glass: A review on human symmetry perception. Symmetry 2010, 2, 1510–1543. [Google Scholar] [CrossRef]
- Tyler, C.W. Human Symmetry Perception and Its Computational Analysis; Tyler, C.W., Ed.; VSP: Zeist, The Netherlands, 1996; pp. 3–22. [Google Scholar]
- van der Helm, P.A.; Leeuwenberg, E.L.J. Goodness of visual regularities: A nontransformational approach. Psychol. Rev. 1996, 103, 429–456. [Google Scholar] [CrossRef]
- Wagemans, J. Characteristics and models of human symmetry detection. Trends Cogn. Sci. 1997, 1, 346–352. [Google Scholar] [CrossRef]
- Barlow, H.B.; Reeves, B.C. The versatility and absolute efficiency of detecting mirror symmetry in random dot displays. Vision Res. 1979, 19, 783–793. [Google Scholar] [CrossRef]
- Giurfa, M.; Eichmann, B.; Menzel, R. Symmetry perception in an insect. Nature 1996, 382, 458–461. [Google Scholar] [CrossRef]
- Horridge, G.A. The honeybee (Apis mellifera) detects bilateral symmetry and discriminates its axis. J. Insect Physiol. 1996, 42, 755–764. [Google Scholar] [CrossRef]
- van der Helm, P.A. Weber-Fechner behaviour in symmetry perception? Atten. Percept. Psychophys. 2010, 72, 1854–1864. [Google Scholar] [CrossRef] [PubMed]
- Møller, A.P. Fluctuating asymmetry in male sexual ornaments may reliably reveal male quality. Anim. Behav. 1990, 40, 1185–1187. [Google Scholar] [CrossRef]
- Thompson, D.W. On Growth and Form; University Press: Cambridge, UK, 1942; (Original work published 1917). [Google Scholar]
- Enquist, M.; Arak, A. Symmetry, beauty and evolution. Nature 1994, 372, 169–172. [Google Scholar] [CrossRef] [PubMed]
- Heywood, V.H. Flowering Plants of the World; Batsford: London, UK, 1993. [Google Scholar]
- Endress, P.K. Floral phyllotaxis and floral evolution. Bot. Jahrb. 1987, 108, 417–438. [Google Scholar]
- Giurfa, M.; Dafni, A.; Neal, P.R. Floral symmetry and its role in plant-pollinator systems. Int. J. Plant Sci. 1999, 160, S41–S50. [Google Scholar] [CrossRef] [PubMed]
- Neal, P.R.; Dafni, A.; Giurfa, M. Floral symmetry and its role in plant-pollinator systems: Terminology, Distribution, and Hypotheses. Annu. Rev. Ecol. Syst. 1998, 29, 345–373. [Google Scholar] [CrossRef]
- Horridge, G.A. Visual discrimination of radial cues by the honeybee (Apis mellifera). J. Insect Physiol. 2000, 46, 629–645. [Google Scholar] [CrossRef]
- Washburn, D.K.; Crowe, D.W. Symmetries of Culture: Theory and Practice of Plane Pattern Analysis; University of Washington Press: Seattle, WA, USA, 1988. [Google Scholar]
- Wynn, T. Archaeology and cognitive evolution. Behav. Brain Sci. 2002, 25, 389–402, 432–438. [Google Scholar] [CrossRef]
- Hardonk, M. Cross-cultural Universals of Aesthetic Appreciation in Decorative Band Patterns. Ph.D. Thesis, Radboud University, Nijmegen, The Netherlands, 1999. [Google Scholar]
- Forstner, D. Die Welt der Symbole; Tyriola Verlag: Innsbruck, 1961. [Google Scholar]
- Labat, R. Manuel D’épigraphie Akkadienne: Signes, Syllabaire, Idéogrammes, 6th ed.; Imprimerie Nationale: Paris, France, 1988. [Google Scholar]
- Boselie, F. The golden section and the shape of objects. Empir. Stud. Arts. 1997, 15, 131–141. [Google Scholar] [CrossRef]
- Garner, W.R. The Processing of Information and Structure; Erlbaum: Potomac, MD, USA, 1974. [Google Scholar]
- Palmer, S.E. Human and Machine Vision; Beck, J., Hope, B., Rosenfeld, A., Eds.; Academic Press: New York, NY, USA, 1983; pp. 269–339. [Google Scholar]
- Palmer, S.E.; Hemenway, K. Orientation and symmetry: Effects of multiple, rotational, and near symmetries. J. Exp. Psychol. Hum. Percept. Perform. 1978, 4, 691–702. [Google Scholar] [CrossRef] [PubMed]
- Royer, F.L. Detection of symmetry. J. Exp. Psychol. Hum. Percept. Perform. 1981, 7, 1186–1210. [Google Scholar] [CrossRef] [PubMed]
- Wagemans, J.; van Gool, L.; Swinnen, V.; van Horebeek, J. Higher-order structure in regularity detection. Vision Res. 1993, 33, 1067–1088. [Google Scholar] [CrossRef]
- Viola, C.M. Grundzüge der Kristallographie; W. Engelman: Leipzig, Germany, 1904. [Google Scholar]
- Jenkins, B. Component processes in the perception of bilaterally symmetric dot textures. Percept. Psychophys. 1983, 34, 433–440. [Google Scholar] [CrossRef] [PubMed]
- Wagemans, J.; van Gool, L.; d’Ydewalle, G. Detection of symmetry in tachistoscopically presented dot patterns: Effects of multiple axes and skewing. Percept. Psychophys. 1991, 50, 413–427. [Google Scholar] [CrossRef] [PubMed]
- van der Helm, P.A.; Leeuwenberg, E.L.J. A better approach to goodness: Reply to Wagemans (1999). Psychol. Rev. 1999, 106, 622–630. [Google Scholar] [CrossRef]
- Treder, M.S.; van der Vloed, G.; van der Helm, P.A. Interactions between constituent single symmetries in multiple symmetry. Atten. Percept. Psychophys. 2011. In Press. [Google Scholar] [CrossRef]
- van der Helm, P.A.; Leeuwenberg, E.L.J. Holographic goodness is not that bad: Reply to Olivers, Chater, and Watson (2004). Psychol. Rev. 2004, 111, 261–273. [Google Scholar] [CrossRef]
- van der Vloed, G.; Csathó, Á.; van der Helm, P.A. Symmetry and repetition in perspective. Acta Psychol. 2005, 120, 74–92. [Google Scholar] [CrossRef]
- van der Helm, P.A.; Leeuwenberg, E.L.J. Accessibility, a criterion for regularity and hierarchy in visual pattern codes. J. Math. Psychol. 1991, 35, 151–213. [Google Scholar] [CrossRef]
- van der Helm, P.A.; Treder, M.S. Detection of (anti)symmetry and (anti)repetition: Perceptual mechanisms versus cognitive strategies. Vision Res. 2009, 49, 2754–2763. [Google Scholar] [CrossRef] [PubMed]
- Treder, M.S.; van der Helm, P.A. Symmetry versus repetition in cyclopean vision: A microgenetic analysis. Vision Res. 2007, 47, 2956–2967. [Google Scholar] [CrossRef] [PubMed]
- Csathó, Á.; van der Vloed, G.; van der Helm, P.A. Blobs strengthen repetition but weaken symmetry. Vision Res. 2003, 43, 993–1007. [Google Scholar] [CrossRef]
- Csathó, Á.; van der Vloed, G.; van der Helm, P.A. The force of symmetry revisited: Symmetry-to-noise ratios regulate (a)symmetry effects. Acta Psychol. 2004, 117, 233–250. [Google Scholar] [CrossRef] [PubMed]
- Attneave, F. Some informational aspects of visual perception. Psychol. Rev. 1954, 61, 183–193. [Google Scholar] [CrossRef] [PubMed]
- Attneave, F. Symmetry, information, and memory for patterns. Am. J. Psychol. 1955, 68, 209–222. [Google Scholar] [CrossRef] [PubMed]
- Barlow, H.B. Current Problems in Animal Behaviour; Thorpe, W.H., Zangwill, O.L., Eds.; Cambridge University Press: Cambridge, UK, 1961; pp. 331–360. [Google Scholar]
- Barlow, H. The exploitation of regularities in the environment by the brain. Behav. Brain. Sci. 2001, 24, 602–607, 652–671. [Google Scholar] [CrossRef]
- Leeuwenberg, E.L.J. Quantitative specification of information in sequential patterns. Psychol. Rev. 1969, 76, 216–220. [Google Scholar] [CrossRef]
- Leeuwenberg, E.L.J. A perceptual coding language for visual and auditory patterns. Amer. J. Psychol. 1971, 84, 307–349. [Google Scholar] [CrossRef]
- Nucci, M.; Wagemans, J. Goodness of regularity in dot patterns: global symmetry, local symmetry, and their interactions. Perception 2007, 36, 1305–1319. [Google Scholar] [CrossRef]
- Hamada, J.; Ishihara, T. Complexity and goodness of dot patterns varying in symmetry. Psychol. Res. 1988, 50, 155–161. [Google Scholar] [CrossRef] [PubMed]
- Wenderoth, P.; Welsh, S. Effects of pattern orientation and number of symmetry axes on the detection of mirror symmetry in dot and solid patterns. Perception 1998, 27, 965–976. [Google Scholar] [CrossRef] [PubMed]
- van der Vloed, G. The Structure of Visual Regularities. Ph.D. Thesis, Radboud University, Nijmegen, The Netherlands, 2005. [Google Scholar]
- Beh, H.C.; Latimer, C.R. Symmetry detection and orientation perception: Electrocortical responses to stimuli with real and implicit axes of orientation. Aust. J. Psychol. 1997, 49, 128–133. [Google Scholar] [CrossRef]
- Gurnsey, R.; Herbert, A.M.; Kenemy, J. Bilateral symmetry embedded in noise is detected accurately only at fixation. Vision Res. 1998, 38, 3795–3803. [Google Scholar] [CrossRef]
- Lee, T.S.; Mumford, D.; Romero, R.; Lamme, V.A.F. The role of the primary visual cortex in higher level vision. Vision Res. 1998, 38, 2429–2454. [Google Scholar] [CrossRef]
- Sally, S.; Gurnsey, R. Symmetry detection across the visual field. Spatial Vision 2001, 14, 217–234. [Google Scholar] [PubMed]
- Joung, W.; Latimer, C. Tilt aftereffects generated by symmetrical dot patterns with two or four axes of symmetry. Spatial Vision 2003, 16, 155–182. [Google Scholar] [CrossRef]
- Joung, W.; van der Zwan, R.; Latimer, C.R. Tilt aftereffects generated by bilaterally symmetrical patterns. Spatial Vision 2000, 13, 107–128. [Google Scholar]
- van der Zwan, R.; Leo, E.; Joung, W.; Latimer, C.; Wenderoth, P. Evidence that both area V1 and extrastriate visual cortex contribute to symmetry perception. Curr. Biol. 1998, 8, 889–892. [Google Scholar] [CrossRef]
- Koffka, K. Principles of Gestalt Psychology; Routledge & Kegan Paul: London, UK, 1935. [Google Scholar]
- van der Helm, P.A. Simplicity versus likelihood in visual perception: From surprisals to precisals. Psychol. Bull. 2000, 126, 770–800. [Google Scholar] [CrossRef]
- Birkhoff, G.D. Aesthetic Measure; Harvard University Press: Cambridge, MA, UK, 1933. [Google Scholar]
- Boselie, F.; Leeuwenberg, E.L.J. Birkhoff revisited: Beauty as a function of effect and means. Amer. J. Psychol. 1985, 98, 1–39. [Google Scholar] [CrossRef] [PubMed]
© 2011 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/.)