Abstract
In this paper, we study the dynamical mass generation in the Abelian Higgs model in dimensions. Instead of adopting the approximations in [Jiang H et al., J. Phys. A 41 2008 255402.], we numerically solve the coupled Dyson–Schwinger Equations (DSEs) for the fermion and gauge boson propagators using a specific truncation for the fermion-photon vertex ansatz and compare our results with the corresponding ones in the above mentioned paper. It is found that the results quoted in the above paper remain qualitatively unaffected by refining the truncation scheme of the DSEs, although there exist large quantitative differences between the results presented in the above paper and ours. In addition, our numerical results show that the critical number of fermion flavor decreases steeply with the the gauge boson mass (or the ratio of the Higgs mass to the gauge boson mass , ) increasing. It is thus easier to generate a finite fermion mass by the mechanism of DCSB for a small ratio r for a given .
1. Introduction
Quantum electrodynamics in 2+1 dimensions (QED3) has been extensively studied for over twenty years. It has many features similar to quantum chromodynamics (QCD), such as spontaneous chiral symmetry breaking in the massless fermion limit and confinement [,,,,,,,,,,,,]. Moreover, it is super-renormalizable, so it does not suffer from the ultraviolet divergence which are present in QED4. Due to these reasons it can serve as a toy model of QCD. In parallel with its relevance as a tool to gain insight into the aspects of QCD, QED3 is also found to be equivalent to the low-energy effective theories of strongly correlated electronic systems. Recently, QED3 has been studied in high Tc cuprate superconductors [,,,,,,,,,], quantum Heinsenberg antiferromagnets [], and fractional quantum Hall effect []. In particular, some authors have made progress in studying the property of graphene based on QED3 [,,].
Dynamical chiral symmetry breaking (DCSB) occurs when the massless fermion acquires a nonzero mass through non-perturbative effects at low energy, but the Lagrangian keeps chiral symmetry when the fermion mass is neglected. In a four-fermion interaction model [] Nambu and Jona-Lasinio first adopted the mechanism of DCSB to generate a nonzero mass for the fermion without using the Yukawa type coupling . In 1988, Appelquist et al. [] studied DCSB in massless QED3 with N fermion flavors by solving the DSE for fermion self-energy in the lowest-order of expansion and found DCSB occurs when N is less than a critical number . Later Nash showed that the critical number of fermion flavor still exists by considering higher order corrections and he obtained []. In 1995, Maris solved the coupled DSEs with a set of simplified vertex functions and obtained the critical number of fermion flavor = 3.3 [,]. Soon after that, Fisher et al. [] self-consistently solved a set of coupled DSE and obtained by using more sophisticated vertex ansatz which satisfies the Ward–Takahashi identity. Here it should be noted that all the above results hold under the condition that the gauge boson is massless. Once a finite gauge boson mass is generated by Anderson–Higgs mechanism, it weakens the strength of interaction and affects DCSB. QED3 with Abelian Higgs model has been widely studied as the effective theory of the high Tc superconductors [,]. Recently, Liu et al. [,,] studied the DSEs for the fermion self-energy in Landau gauge in QED3 with Abelian Higgs model and found that DCSB occurs only when the gauge boson mass is smaller than a critical value. However, we note that in [,,], the authors used the so-called nonlocal gauge function approach to solve the nonlinear DSE where the wave function renormalization and the vertex correction are simply absent (in connection to the use of the nonlocal gauge in QED3, one can see, e.g., []). Because of its importance, this problem deserves further study. In this paper, instead of adopting the approximations in [,,], we numerically solve the coupled DSE for the fermion and gauge boson propagators of QED3 with Abelian Higgs model using a specific truncation for the fermion-photon vertex ansatz for a range of finite gauge boson mass.
2. Results and Discussions
In Euclidean space, the total Lagrangian of QED3 with N massless fermion flavors and N scalar boson flavors is = + [,], where
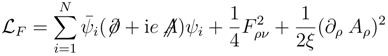 Here contains the coupling between massless Dirac fermions and the gauge field. In Abelian Higggs model is added to describe the additional interaction between the complex scalar fields and the gauge field, which will change the gauge boson propagator. The spinor represents the fermion field, the matrices obey the Clifford algebra, and are the flavor indices. For physical reasons, the number of flavors of fermion or scalar boson N equals to 2, and is the gauge parameter. The bare propagator and the full fermion propagator is , where is the wave-function renormalization and is the fermion self-energy function. The full fermion propagator satisfies the DSE
where . In QED3 with Abelian Higgs model the gauge field couples to both the fermion field and the scalar boson field. is the total vacuum polarization tensor and the full inverse gauge boson propagator is
where is the free inverse gauge boson propagator. The gauge boson propagator in Landau gauge is
where and are the polarization function from the fermion part and the boson part, respectively.
Here contains the coupling between massless Dirac fermions and the gauge field. In Abelian Higggs model is added to describe the additional interaction between the complex scalar fields and the gauge field, which will change the gauge boson propagator. The spinor represents the fermion field, the matrices obey the Clifford algebra, and are the flavor indices. For physical reasons, the number of flavors of fermion or scalar boson N equals to 2, and is the gauge parameter. The bare propagator and the full fermion propagator is , where is the wave-function renormalization and is the fermion self-energy function. The full fermion propagator satisfies the DSE
where . In QED3 with Abelian Higgs model the gauge field couples to both the fermion field and the scalar boson field. is the total vacuum polarization tensor and the full inverse gauge boson propagator is
where is the free inverse gauge boson propagator. The gauge boson propagator in Landau gauge is
where and are the polarization function from the fermion part and the boson part, respectively.
Next we decompose the scalar field as follows:
For , in Anderson–Higgs model the nonzero vacuum expectation value . In fact, a nonzero induces the spontaneous breaking of gauge symmetry and the gauge boson acquires a nonzero mass via the Anderson–Higgs mechanism. However, the finite gauge boson mass will suppress the occurrence of DCSB. Now the boson Lagrangian can be written in the form:
The mass of gauge boson is and . ¿From these two mass scales we obtain the Ginzburg–Landau parameter . In high temperature superconductors r is generally about 100 []. The one-loop vacuum polarization has been calculated by evaluating four Feynman diagrams [,] and the result is
where .
In order to obtain a closed system of coupled DSEs which can be solved by iteration method, one should specify the fermion-photon vertex function. In the literature, there are several attempts to determine the form of the fermion-photon vertex [,,,,,,,,,,], for instance, the Ball–Chiu (BC) [] and Curtis–Pennington (CP) vertex []. In this paper we shall follow [] to choose the vertex ansatz (the BC1 vertex). This choice has the advantage that the equations are simplified significantly and it already contains all qualitative features of the solution employing the CP/BC vertex in the infrared region, as was demonstrated by the numerical calculations given in []. Based on the above discussion, we obtain the coupled DSEs with gauge boson mass and Higgs mass [,]:
It is well known that one can obtain two types of solution by iterating the above coupled DSEs, the Nambu solution and the Wigner solution. If Equations (10′12) has a nontrivial solution, i.e., the Nambu solution, then the fermions can acquire a nonzero mass by DCSB. In DCSB phase (, the fermion mass function ) the attractive force between a pair of fermion and anti-fermion becomes weak with increasing.
Here it is interesting to look at the quantitative impact of refining the truncation scheme used in this paper. In order to show a comparison of our result with that of the bare vertex approximation, in Figure 1, taking the case as an example, we draw the curves of the mass function versus for and for both the bare vertex and the BC1 vertex ansatz. It can be seen that for both the bare vertex and the BC1 vertex ansatz, the mass function almost remains constant for small , and decreases monotonously with increasing after reaches a certain value. In the whole range of , the mass function obtained using the BC1 vertex is much larger than that obtained using the bare vertex. This shows that the dressing effect of the fermion-photon vertex is very important in the study of dynamical mass generation in the Abelian Higgs Model in dimensions. In addition, due to the fact that increasing gauge boson mass weakens the attractive force between a pair of fermion and antifermion, the larger infrared value of the mass function for the case of BC1 ansatz implies that the critical gauge boson mass for the case of BC1 ansatz should be larger that the one for the case of bare vertex.
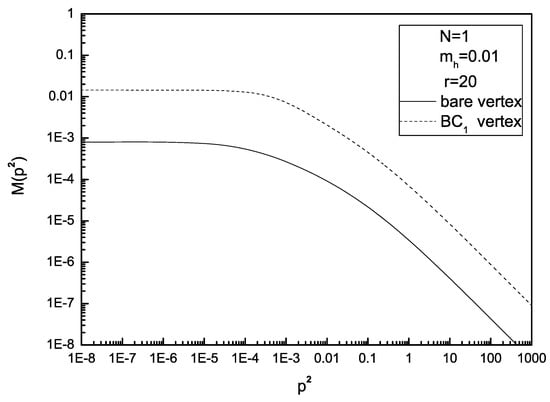
Figure 1.
The mass function versus at and for case calculated using both the bare vertex and the BC1 vertex ansatz.
In Figure 2, the variation of on for several values of the ratio r is shown. From the obtained numerical results one finds that DCSB is completely suppressed when exceeds a critical value for a fixed number of fermion flavor N (here the mass terms are scaled by ). From Figure 2 one finds that decreases monotonically with the gauge boson mass increasing for fixed value of r and it decreases monotonically with the Ginzburg–Landau parameter r increasing for fixed value of . It can be seen that the corresponding critical number of fermion flavor is about 2.4 when the gauge boson mass tends to zero. So the originally massless fermion acquires a dynamical mass (the physical number of fermion flavor ). But in Figure 2 the curve is steeper and for the same value of and r, is much larger than the value of []. In fact, for and , we find that the critical gauge boson mass is too small and DCSB can be hardly observed when we numerically solve the coupled DSEs by means of iteration method using the bare vertex ansatz. Here we note that QED3 theory (and its generalization to the Abelian Higgs model) with is employed as an effective continuum theory for the 2D quantum antiferromagnetic (Neel) ordering corresponding to dynamical fermion mass generation [,,,]. So a reliable value of the critical number of fermion flavors is important for the study of dynamical fermion mass generation and chiral symmetry breaking.
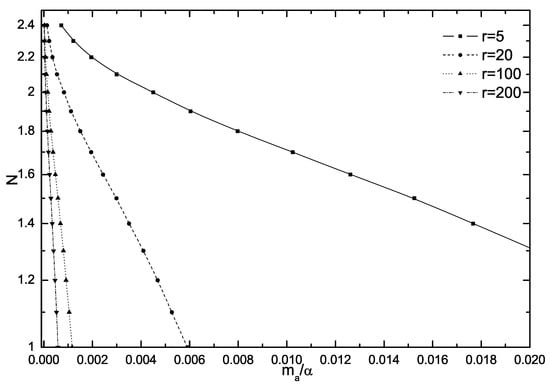
Figure 2.
Dependence of the number of fermion flavor on for several values of the ratio .
3. Conclusions
In this paper, the DSE for the fermion self-energy in QED3 with Abelian Higgs model is studied. We numerically solve the coupled DSEs by means of iteration method using the BC1 vertex ansatz and compare our result with that obtained using the bare vertex. It is found that the mass function obtained using the BC1 vertex ansatz is much larger than the one obtained using the bare vertex. This shows that the dressing effect of the fermion-photon vertex is very important in the study of dynamical mass generation in the Abelian Higgs model in dimensions. It is also found that the gauge boson mass suppresses the critical number of fermion flavor for a fixed ratio . When exceeds a critical value , DCSB will be completely suppressed. One the other hand, the gauge boson mass is reduced rapidly as r increases. These results imply that for a fixed value of , the smaller is the ratio r, the easier is it to generate a finite fermion mass by the mechanism of DCSB. The above results qualitatively accord with the conclusion of Liu et al. []. Finally, we note that the BC1 vertex ansatz employed in our calculation does not satisfy the Ward–Takahashi identity when the dynamical mass function is present in the fermion propagator. In a more reliable calculation the CP [] vertex should be employed. This work will be done in the future.
Acknowledgments
We are grateful to G.Z. Liu for helpful discussions. This work was supported in part by the National Natural Science Foundation of China (under Grant Nos 10775069 and 10935001) and the Research Fund for the Doctoral Program of Higher Education (under Grant No 200802840009).
References
- Cornwall, J.M. Confinement and chiral-symmetry breakdown: estimates of Fπ and of effective quark masses. Phys.Rev. D 1980, 22, 1452–1468. [Google Scholar] [CrossRef]
- Pisarski, R.D. Chiral-symmetry breaking in three-dimensional electrodynamics. Phys. Rev. D 1984, 29, 2423–2426. [Google Scholar] [CrossRef]
- Appelquist, T.W.; Bowick, M.; Karabali, D; Wijewardhana, L.C.R. Spontaneous chiral-symmetry breaking in three-dimensional QED. Phys. Rev. D 1986, 33, 3704–3713. [Google Scholar] [CrossRef]
- Appelquist, T.; Nash, D.; Wijewardhana, L.C.R. Critical behavior in (2+1)-dimensional QED. Phys. Rev. Lett. 1988, 60, 2575–2578. [Google Scholar] [CrossRef] [PubMed]
- Nash, D. Higher-order corrections in (2+1)-dimensional QED. Phys. Rev. Lett. 1989, 62, 3024–3026. [Google Scholar] [CrossRef] [PubMed]
- Burden, C.J.; Roberts, C.D. Light-cone regular vertex in three-dimensional quenched QED. Phys. Rev. D 1991, 44, 540–550. [Google Scholar] [CrossRef]
- Maris, P. Confinement and complex singularities in three-dimensional QED. Phys. Rev. D 1995, 52, 6087–6097. [Google Scholar] [CrossRef]
- Maris, P. Influence of the full vertex and vacuum polarization on the fermion propagator in (2+1)-dimensional QED. Phys. Rev. D 1996, 54, 4049–4058. [Google Scholar] [CrossRef]
- Kondo, K.-I.; Maris, P. Spontaneous chiral-symmetry breaking in three-dimensional QED with a Chern-Simons term. Phys. Rev. D 1995, 52, 1212–1233. [Google Scholar] [CrossRef]
- Burden, C.J.; Praschifka, J.; Roberts, C.D. Photon polarization tensor and gauge dependence in three-dimensional quantum electrodynamics. Phys. Rev. D 1992, 46, 2695–2702. [Google Scholar] [CrossRef]
- Grignani, G.; Semenoff, G.; Sodano, P. Confinement-deconfinement transition in three-dimensional QED. Phys. Rev. D 1996, 53, 7157–7161. [Google Scholar] [CrossRef]
- Bashir, A.; Raya, A.; Cloët, I.C.; Roberts, C.D. Confinement and dynamical chiral symmetry breaking in QED3. Phys. Rev. C 2008, 78, 055201–055207. [Google Scholar]
- Bashir, A.; Raya, A.; Sanchez-Madrigal, S.; Roberts, C.D. Gauge invariance of a critical number of flavours in QED3. Few Body Syst 2009, 46, 229–237. [Google Scholar] [CrossRef]
- Wen, X.G.; Zee, A. Neutral superfluid modes and magnetic monopoles in multilayered quantum Hall systems. Phys. Rev. Lett. 1992, 69, 1811–1814. [Google Scholar] [CrossRef] [PubMed]
- Rantner, W.; Wen, X.G. Electron spectral function and algebraic spin liquid for the normal state of underdoped high Tc superconductors. Phys. Rev. Lett. 2001, 86, 3871–3874. [Google Scholar] [CrossRef] [PubMed]
- Lee, P.A.; Wen, X.G. Theory of underdoped cuprates. Phys. Rev. Lett. 1996, 76, 503–506. [Google Scholar]
- Lee, P.A.; Nagaosa, N.; Wen, X.G. Doping a mott insulator: physics of high-temperature superconductivity. Rev. Mod. Phys. 2006, 78, 17–85. [Google Scholar] [CrossRef]
- Kim, D.H.; Lee, P.A.; Wen, X.G. Massless Dirac fermions, gauge fields, and underdoped cuprates. Phys. Rev. Lett. 1997, 79, 2109–2112. [Google Scholar] [CrossRef]
- Kim, D.H.; Lee, P.A. Theory of spin excitations in undoped and underdoped cuprates. Ann. Phys. 1999, 272, 130–164. [Google Scholar] [CrossRef]
- Franz, M.; Tesaanovic, Z. Algebraic Fermi liquid from phase fluctuations: topological fermions, vortex Berryons, and QED3 theory of cuprate superconductors. Phys. Rev. Lett. 2001, 87, 257003–257006. [Google Scholar] [CrossRef]
- Herbut, I.F. Antiferromagnetism from phase disordering of a d-wave superconductor. Phys. Rev. Lett. 2002, 88, 047006–047009. [Google Scholar] [CrossRef] [PubMed]
- Herbut, I.F. QED3 theory of underdoped high-temperature superconductors. Phys. Rev. B 2002, 66, 094504–094522. [Google Scholar] [CrossRef]
- Herbut, I.F. Effective theory of high-temperature superconductors. Phys. Rev. Lett. 2005, 94, 237001–237004. [Google Scholar] [CrossRef] [PubMed]
- Marston, J.B. Instantons and massless fermions in (2+1)-dimensional lattice QED and antiferromagnets. Phys. Rev. Lett. 1990, 64, 1166–1169. [Google Scholar] [CrossRef] [PubMed]
- Hermele, B.I.; Lee, P.A.; Read, N. Theory of the half-filled Landau level. Phys. Rev. B 1993, 47, 7312–7343. [Google Scholar]
- Gusynin, V.P.; Sharapov, S.G. Unconventional integer quantum Hall effect in graphene. Phys. Rev. Lett. 2005, 95, 146801–146804. [Google Scholar] [CrossRef]
- Gusynin, V.P.; Sharapov, S.G.; Carbotte, J.P. Unusual microwave response of Dirac quasiparticles in graphene. Phys. Rev. Lett. 2006, 96, 256802–256805. [Google Scholar] [CrossRef]
- Durt, J.E.; Lahde, T.A. Lattice field theory simulations of graphene. Phys. Rev. B 2009, 79, 165425–165438. [Google Scholar]
- Nambu, Y.; Lasinio, G.J. Dynamical model of elementary particles based on an analogy with superconductivity. I. Phys. Rev. 1961, 122, 345–358. [Google Scholar] [CrossRef]
- Fisher, C.S.; Alkofer, R.; Dahm, T.; Maris, P. Dynamical chiral symmetry breaking in unquenched QED3. Phys. Rev. D 2004, 70, 073007-1-19. [Google Scholar] [CrossRef]
- Liu, G.Z.; Cheng, G. Effect of gauge boson mass on chiral symmetry breaking in three-dimensional QED. Phys. Rev. D 2003, 67, 065010-1-11. [Google Scholar] [CrossRef]
- Liu, G.Z.; Jiang, H.; Li, W.; Cheng, G. Quantum electrodynamics in three dimensions: dynamical chiral symmetry breaking, confinement, and disorder effects. Phys. Rev. B 2009, 79, 014507-1-5. [Google Scholar] [CrossRef]
- Jiang, H.; Liu, G.Z.; Cheng, G. Chiral symmetry breaking in three-dimensional QED with Abelian Higgs model. J. Phys. A 2008, 41, 255402–255410. [Google Scholar] [CrossRef]
- Gusynin, V.; Hams, A.; Reenders, M. Nonperturbative infrared dynamics of three-dimensional QED with a four-fermion interaction. Phys. Rev. D 2001, 63, 045025-1-19. [Google Scholar] [CrossRef]
- Kleinert, H.; Nogueira, F.S. Charged fixed point found in superconductor below T(c). Nucl. Phys. B 2003, 651, 361–386. [Google Scholar] [CrossRef]
- Kizilersü, A.; Pennington, M. Building the full fermion-photon vertex of QED by imposing multiplicative renormalizability of the Schwinger-Dyson equations for the fermion and photon propagators. Phys. Rev. D 2009, 79, 125020-1-25. [Google Scholar]
- Bashir, A.; Raya, A. Constructing the fermion-boson vertex in three-dimensional QED. Phys. Rev. D 2001, 64, 105001-1-10. [Google Scholar] [CrossRef]
- Bashir, A.; Huet, A.; Raya, A. Gauge dependence of mass and condensate in chirally asymmetric phase of quenched three-dimensional QED. Phys. Rev. D 2002, 66, 025029-1-8. [Google Scholar] [CrossRef]
- Curtis, D.C.; Peninington, M.R. Truncating the Schwinger-Dyson equations: How multiplicative renormalizability and the Ward identity restrict the three-point vertex in QED. Phys. Rev. D 1990, 42, 4165–4169. [Google Scholar] [CrossRef]
- King, J.E. Transverse vertex and gauge technique in quantum electrodynamics. Phys. Rev. D 1982, 27, 1821–1829. [Google Scholar] [CrossRef]
- Kizilersü, A.; Reenders, M.; Pennington, M.R. One-loop QED vertex in any covariant gauge: Its complete analytic form. Phys. Rev. D 1995, 52, 1242–1259. [Google Scholar]
- Burden, C.J.; Tjiang, P.C. Deconstructing the vertex Ansatz in three-dimensional quantum electrodynamics. Phys. Rev. D 1998, 58, 085019-1-8. [Google Scholar] [CrossRef]
- Bashir, A.; Kizilersü, A.; Peninington, M.R. Does the weak coupling limit of the Burden-Tjiang deconstruction of the massless quenched three-dimensional QED vertex agree with perturbation theory? Phys. Rev. D 2000, 62, 085002-1-8. [Google Scholar] [CrossRef]
- Bashir, A.; Peninington, M.R. Gauge-independent chiral symmetry breaking in quenched QED. Phys. Rev. D 1994, 50, 7679–7689. [Google Scholar] [CrossRef]
- Ball, J.S.; Chiu, T.W. Analytic properties of the vertex function in gauge theories. Phys. Rev. D 1980, 22, 2542–2549. [Google Scholar] [CrossRef]
- Kondo, K.; Nakatani, H. Strong coupling unquenched QED.2. Prog. Theor. Phys. 1992, 87, 193–206. [Google Scholar] [CrossRef]
- Feng, H.T.; Sun, W.M.; Hu, F.; Zong, H.S. The influence of the gauge boson mass on the critical number of the fermion flavors in QED(3). Int. J. Mod. Phys. A 2005, 20, 2753–2762. [Google Scholar] [CrossRef]
- Feng, H.T.; Sun, W.M.; He, D.K.; Zong, H.S. Influence of finite chemical potential on the fermion chiral condensate in QED3. Phys. Lett. B 2008, 661, 57–65. [Google Scholar] [CrossRef]
- Marston, J.; Affleck, I. Large-n limit of the Hubbard-Heisenberg model. Phys. Rev. B 1989, 39, 11538–11558. [Google Scholar] [CrossRef]
- Ioffe, L.B.; Larkin, A.I. Gapless fermions and gauge fields in dielectrics. Phys. Rev. B 1989, 39, 8988–8999. [Google Scholar] [CrossRef]
- Marston, J.B. Instantons and massless fermions in (2+1)-dimensional lattice QED and antiferromagnets. Phys. Rev. Lett. 1990, 64, 1166–1169. [Google Scholar] [CrossRef] [PubMed]
- Laughlin, R.B.; Zou, Z. Properties of the chiral-spin-liquid state. Phys. Rev. B 1990, 41, 664–687. [Google Scholar] [CrossRef]
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license http://creativecommons.org/licenses/by/3.0/.