Abstract
The essay is dedicated to the relation of symmetry and asymmetry-chirality in Nature. The Introduction defines symmetry and its impact on basic definitions in science and human activities. The following section Chirality of molecules reveals breifly development of notion of chirality and its significance in living organisms and science. Homochirality is a characteristic hallmark of life and its significance is presented in the section Homochirality of Life. Proteins, important constituents of living cells performing versatile functions are chiral macromolecules composed of l-amino acids. In particular, the protein assemblies are of a great importance in functions of a cell. Therefore, they have attracted researches to examine them from different points of view. Among proteins of known three-dimensional structures about 50–80% of them exist as homomeric protein complexes. Protein monomers lack any intrinsic, underlying symmetry, i.e. enantiomorphic protein molecules involve left-handed amino acids but their asymmetry does not appear to extend to the level of quaternary structures (homomeric complexes) as observed by Chothia in 1991. In the section Homomeric assemblies we performed our analysis of very special cases of homomers revealing non-crystallographic symmetry in crystals. Homochiral proteins can crystallize only in enantiomorphic space groups. Among 230 existing space groups 65 are enantiomorphic containing limited symmetry elements that are rotation and screw-rotation axes. Any axis of rotation symmetry of a crystal lattice must be two-fold, three-fold, four-fold, or six-fold. Five-fold, seven-fold, and higher-fold rotation symmetry axes are incompatible with the symmetry under spatial displacement of the three-dimensional crystal lattice.
1. Symmetry
Symmetry is one of the most powerful concepts in science and can be used to describe animate and inanimate objects of nature and man-made ‘products’. Symmetry and complexity determine the essence of nonlinear science that can describe the expansion of the Universe, the evolution of life and even the globalisation of human economies and societies []. As Mainzer described in his book-triad [,,] symmetry and complexity are fundamental principles in science of 21st century connecting natural, cognitive, and social sciences, mathematics, humanities, and philosophy. Symmetry was primarily related to simplicity of order, beauty and harmony. However, the Universe is far from being static, balanced and neatly ordered. The symmetry breaking leads to new orders and structures, and transitions from unstable to balanced states involving processes of self-assembling governed by the laws of nonlinear dynamics.
At the same time symmetry is multi-cultural phenomenon. Symmetry is visually appealing to the human eye provoking the aesthetic pleasure. It can be found in pictures, drawings, sculptures, architecture (Figure 1, Figure 2 and Figure 3), music, textile (Figure 4) and pottery decoration, and many other human-made objects. Symmetry and chirality have been recognized in Nature since the prehistoric times (Figure 5).

Figure 1.
St. Jacob cathedral in Šibenik on the Adriatic coast (Croatia) from 16th century (under protection of UNESCO). Bilateral symmetry is by far the most common form of symmetry in architecture. The rose-window is of the 20-fold symmetry.

Figure 2.
Taj Mahal in Agra, India built in marble from 1634 to 1656. The reflection in water multiplies the high symmetry of mausoleum. http://www.nomadicmatt.com/travel-blogs/ten-historical-sites.

Figure 3.
The Sheikh Lotfollah Mosque in Isfahan, Iran (under protection of UNESCO) built in the Safavid era (1615–1618); http://www.interiordesignandremodeling.net/interior_design_remodeling_mosque_Iran.htm. The interior hallway leading to the entrance of the mosque is shown. The mosaic tile-work, calligraphy and the architecture are spectacular. Lord G.G. Byron, the English poet admired the mosque: “I have never encountered splendour of this kind before.”
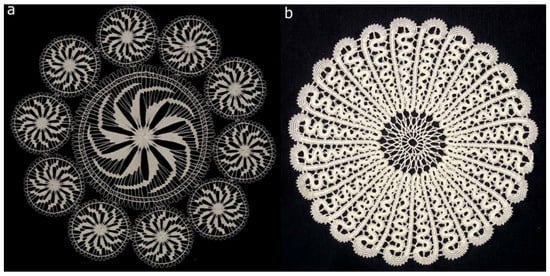
Figure 4.
Very old and fine techniques of lace making are under the UNESCO protection (as cultural heritage) including two selected examples from Croatia. a) The tenfold rotation symmetry visible in very fine, hand-made lace of centennial plant fibres originates from Benedictine monastery in Hvar, island Hvar. b) The lace with symbolic name “Sun” exhibits the 24-fold symmetry and originates from Lepoglava, a small town in the north-west part of Croatia. The lace tradition originates from Pauline monastery established in 15th century. (Courtesy of Ms Jasna Mokos, Photo-documentation Centre of Etnographic Museum, Zagreb, Croatia).

Figure 5.
The famous two cats of Wadi Matkhendoush, engraved prehistoric drawing from Libya. http://www.temehu.com/sahara-prehistoric-rock-art.htm/.
Through history symmetry elements were used to illustrate the essence of life in philosophical context and to describe myths. Different symmetries in the religious symbols such as Christian, Jewish, Hindu, Islamic, Buddhist, Shinto, Sikh, Raha’i and Jain, have been used over centuries. The development of human society directed artists to use symmetry for decoration purposes or to frame an aesthetic value of the artistic object and sometimes to send a particular message to an observer.
The symmetry of an object is defined in terms of transformations that bring the object into its initial form; it means that the object is unchanged or invariant upon transformation. Generally, such transformations can be operated by rotation, inversion, and reflection (mirror plane) (Figure 6).
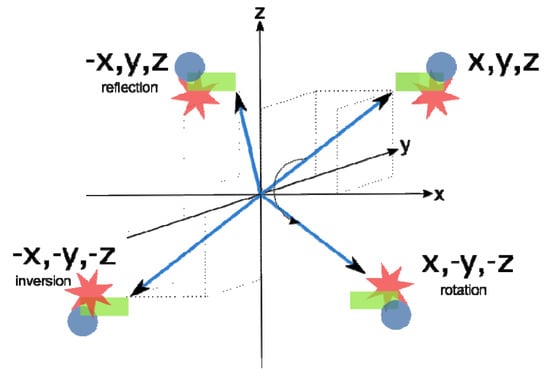
Figure 6.
The operations of symmetry: rotation, inversion, and reflection (mirror plane).
Mathematical description of symmetry operations is provided by the group theory which in chemistry leads to point groups describing the internal molecular symmetry and space groups in crystallography. The symmetries of natural minerals in Figure 7, Figure 8a and 8b and synthetic crystals are classified into seven different classes with fourteen different three-dimensional lattice-types, named as Bravais’s lattices. The set of symmetry elements which forms a point group describes the symmetry of the crystal as a whole and may be recognised from the external shape of the crystal; there are such 32 point groups.

Figure 7.
Crystal of quartz from Busovača, Bosnia and Herzegovina (courtesy of Prof. Dr. Galiba Sijarić, Sarajevo).
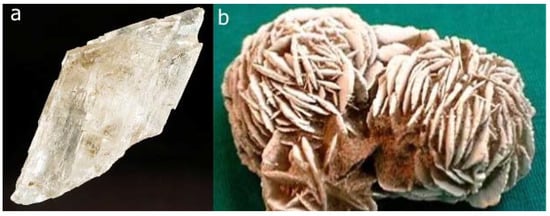
Figure 8.
a) Crystal of gypsum from Debar, Macedonia. b) Rosette of gypsum crystals from Morocco named ‘Desert Rose’ (or sand rose) (courtesy of Prof. Dr. Galiba Sijarić, Sarajevo). An Arabian legend claims that Allah blesses the person who finds a Desert Rose with a good luck.
However, internal symmetry of crystals at atomic level which describes the atom arrangements in the Bravais crystal lattice, in addition to operations of the first order symmetry elements (inversion, rotation and mirror plane), involves also translation symmetry. Their combinations define 230 space groups which describe the symmetry of arrangements within the crystals which are either enantiomorphic or non-enantiomorphic space groups. The enatiomorphic space groups comprise 65 possibilities and chiral molecules can crystallise in the space groups that do not involve mirror-reflection and inversion operations.
“Science is our view of Nature through symmetry spectacles and we understand Nature in language of symmetry” was summarised by J. Rosen []. This concise definition points out the role of symmetry in description of physical phenomena and their mathematical formulation. The basic laws of classical physics defining Nature’s phenomena in all parts of Universe at any time are always the same and thus they are symmetrical. However, the systems created in accord to these laws are subjected to changes, and generally not symmetrical. To understand relation of symmetry and asymmetry in the simplest way one can follow transformations and see what changes and what remains the same. In the classical physics approach mirror symmetry (Figure 6) is conserved in the strong and electromagnetic interactions whereas quantum physics considers the parity violation of the weak force, distinguishing left from right at subatomic level []. The experiment of β-decay of 60Co performed by Lee and Yang in 1956 [] revealed deviation from the parity law of weak interactions which govern the decay. Physics of elementary particles based on quantum mechanics defines spins and helicity recognizing chirality at a subatomic level. The projection of a spin onto the direction of particle motion defines its helicity (chirality). Thus, the spin of the particle can be used to define a handedness (chirality) for that particle. In most circumstances, two-left handed fermions interact more strongly than right-handed or opposite-handed fermions. Fine energy differences between photon induced transitions between atomic states offered an additional evidence of parity violation. Such experiments are very delicate and reflect the strange preference for left-handedness of the Universe. The ‘Standard Model’ involved explanation of parity violation at subatomic level and earned the Nobel prize to Glashow, Salam and Weinberg in 1979 “for their contributions to the theory of the unified weak and electromagnetic interaction between elementary particles, including inter alla the prediction of the weak neutral current.”
On the other hand, perception of symmetry can be perceived by human mind or vision where intrinsic asymmetry exists. Thus, approximate symmetry is a softening of the dichotomy between symmetry and asymmetry. In addition to exact mathematical definition there are different effects that affect approximate symmetry as illustrated by two selected examples (Figure 9a and b).

Figure 9.
Two, among different, types of asymmetry are shown: a) the leaning tower in Pisa; b) an approximate bilateral symmetry (from http://hs.houstonisd.org).
The concept used matters in recognising symmetry (vs. asymmetry) of the objects and phenomena but also the scale of magnification used by an observer. Concepts can be modified or changed by time as our knowledge expands using more technologically improved experimental techniques. For quite a long time bilateral symmetry was assigned to animal and human (Vitruvian man) bodies and number of plants, and high morphological symmetry to bacteria such as E. coli and B. subtillis. Now, the violation of bilateral symmetry in lower and evolutionary higher organisms is obvious [,,]. Phyllotaxis (originally from Greek means arrangement of leaves) explains and mathematically describes by Fibonacci series the asymmetry in flower petals, seed heads, pine cones, leaf arrangements, vegetable and fruits (Figures 10 a, b, and c). The evidences of chirality in distant past of Earth are fossils and ammonites (Figure 11).

Figure 10.
Illustrations of helical symmetry in plants: a) in sunflower, b) pine cone (http://www.math.smith.edu) and c) flower of plant banksia, native to Australia (http://www.flickr.com/photos).

Figure 11.
Chirality of an ammonite from epoch Lias, period Jurassic, Mesozoic era found in Zalomka, near Gacko, Bosnia and Herzegovina (courtesy of Prof. Dr. Galiba Sijarić, Sarajevo).
Symmetry breaking is unavoidable when dynamical concept of cell functioning is applied. Polar distribution of internal and external products of a cell mechanism is an asymmetrical process (polarity of a cell) []. Asymmetrical cell divisions in plants is influenced by cooperative function of intrinsic (developmental) and extrinsic (ecological) factors as exemplified in embryogenesis, formation of stomata, and ground tissue formation on model plant Arabidopsis thaliana []. The common bilateral symmetry of flowers can disappear by evolution in order to make pollination by insects more efficient. From the present knowledge it is clear that just genes alone do not influence asymmetry but their role is highly dominant []. However, the mechanisms for symmetry breaking (left-right asymmetry) in plants and animals remain to be discovered [,]. By all means left-right asymmetry originates in a single cell starting at an embryo level. Disorders in asymmetry of living species, such as reversed body asymmetry-named situs inversus, are of outmost importance for human health. Totally reversed human body asymmetry, situs inversus, is not a problem by itself but becomes a problem when organs are symmetrical. For example, heart composed of two left halves, body with two left lungs, two left kidneys are lethal for human beings []. To link asymmetry at subcellular and higher levels up to the level of the whole organism, will be the way to understand the life mechanisms and their dynamics.
On the other hand, proteins that are chiral molecules, representing asymmetry, can be assembled into homomeric, symmetric structures. However, the asymmetry imposed by the limitation of l-amino acids does not appear to extend to the level of quaternary structures (homomeric complexes) as observed by Chothia []. Among proteins oligomeric form is preferred over the monomeric one where the homomeric assemblies are much more represented. One can propose different reasons to support formation of symmetric homomers. According to Baker et al. [] in favour of symmetric structures are energetically favourable interactions (tested on dimers). Plaxco and Gross [] found their approach also valid for larger scale multimers. In spite of important role of homomers in biology, only anecdotal knowledge on their principle of evolution and assembly exists. However, an application of electrospray-ionization mass spectrometry, that allows study of protein assembling, together with 3D-structures of proteins, and bioinformatics can predict evolutionary routes leading to protein oligomers [].
2. Chirality (Left-Right Asymmetry) of Molecules
The abundance of literature devoted to discovery of molecular chirality is proportional to its importance in life and its origin, and many fields of chemistry [,,,]. However, one among the numerous published articles On wine, chirality and crystallography written by Z.S. Derewenda [] offers a special ‘flavour’. The article was dedicated to the 160th anniversary of Pasteur’s discovery and 60th years of International Union of Crystallography and the scientific journal Acta Crystallographica.
The first physical phenomenon related to chirality – optical activity- was discovered by J.B. Biot in 1815 []; when a beam of plane-polarised light passes through a solution of optically active compound, the plane of polarization is rotated levorotatory or dextrorotatory. By convention, rotation to the left is given a minus (−) sign, and the rotation to the right is given a plus (+) sign. From the time of Biot’s discovery there were no significant contributions until 1848 when L. Pasteur [] studied the crystals of tartrates isolated from wine lees. He observed a spontaneous resolution of that two crystal forms which were mirror images. Pasteur managed to separate ‘left-handed’ crystals from ‘right-handed’ ones by hand (Figure 12) and characterized them as ‘dissymmetric’.
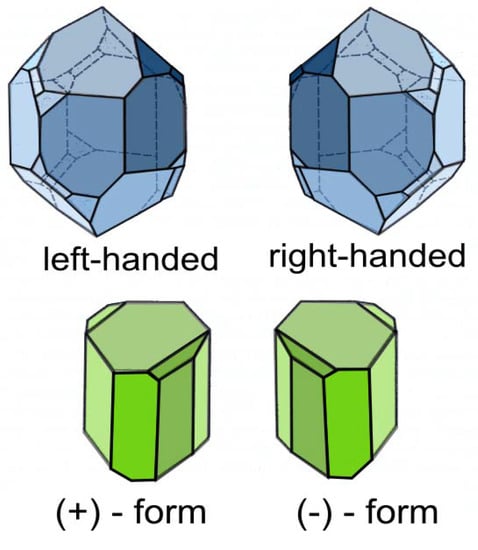
Figure 12.
The enantiomorphous crystals of a) quartz and b) sodium ammonium tartrate.
Pasteur detected that crystals of each separated piles had been optically active and their specific rotations were equal in amount but opposite in sign whereas the original sample having a mixture of right and left in equal proportions (racemate with ratio 50:50) was optically inactive. Pasteur’s method of enantiomer separations from a racemic mixture using crystallization has been in use nowadays. Briefly, Pasteur discovered enantiomers. The term chirality (in Greek means hand; Figures 13 a) and b) has been saved from the past to the present days. It originates from Lord Kelvin in 1884 [].
Figure 13.
a) A sketch by Leonardo da Vinci dated about 1474; b) Drawing hands by M.C. Escher, 1948.
Pasteur’s explanation of the phenomenon was as bright as its discovery. The explanation for this phenomenon was based on molecules as stated by him. “There is no doubt that in the dextro tartaric acid exists an asymmetric arrangement having a non-superimposable image. It is no less certain that the levo acid possesses precisely the inverse asymmetric arrangement.” At the time of Pasteur’s discovery neither tetrahedral carbon atom arrangement nor Kekulé’s theory were known. A tetrahedral model of carbon atom proposed simultaneously by J. H. van’t Hoff [] and J.A. Le Bel in 1874 [] added a new value to Pasteur’s discovery and offered an explanation of chirality by introducing ‘asymmetrically’ substituted carbon atom. That model is the most general type of chirality whereas topological and conformational chiralities are more complex. A tetrahedral concept of a carbon atom invented by van’t Hoff and Le Bel was used by E. Fischer to recognise the optical isomers and conformational differences which helped him to resolve stereochemistry of carbohydrates []. He was able to establish relative configurations of each studied carbohydrate using glyceraldehyde as a standard. Almost six decades passed before the absolute configuration of glyceraldehyde was confirmed to be correct by M. J. Bijvoet’s determination of an absolute configuration by use of anomalous dispersion of X-rays. He determined the absolute configuration of rubidium sodium tartrate and other salts of tartaric acid []. These days anomalous dispersion is widely used for determination of phases of structure factors in X-ray structure analysis of proteins. After the experimental evidences resolved the problem of the absolute configuration of the chiral molecule Prelog, Cahn and Ingold had worked out nomenclature to unambiguously define the absolute configuration []. The previously used notations of D and L were replaced by R and S (originating from Latin words rectus and sinister).
Pasteur’s discovery initiated a novel approach in correlating properties of molecules and their symmetries. From d- and l-tartaric acid enantiomers he prepared diastereomers with l-cinchonine. The solubility of enantiomers of tartaric acid are identical whereas of their salts with l-cinchonine are different. The resolution of enantiomers through their conversion into diasteromeric salts or covalent diasteromeric derivatives is nowadays a common procedure. Fischer found the reactions of diasteromers mediated by natural chiral catalysts (enzymes) to be particularly selective. On his experience of enzymatic reactions Fischer introduced ‘key and lock’ hypothesis [] that explains the molecular recognition processes and became the mostly used paradigm. The recognition of ‘proper’ enantiomer in life processes is of utmost importance. Therefore, the enantiomericaly pure drugs must be used, only. The enantiomers can have physically and biologically different properties; one enantiomer can be drug whereas the other one can be harmful (medical accidents caused by thalidomide). There is an imperative for synthetic chemists to produce homochiral drug. Enzymatically driven syntheses are widely in use for stereoselective reactions. However, asymmetric synthesis should be mentioned too; chiral catalyst transforms an achiral substrate into a homochiral product. An efficient example dates back to 70-ties of last century in Monsanto where W. Knowlles and co-workers used rhodium complex with a chiral phosphine ligand which catalysed a selective H2 –addition to prochiral substrate where a chiral centre with high enantioselectivity was generated. This procedure was commercialised in synthesis of l-dopamine, an anti-Parkinsonic drug. Recent years a significant progress has been made on use of asymmetric synthesis even on large scale stereoselective processes []. Under nanoscience umbrella there is a large number of variations in preparations that can generate the chiral-assemblies from achiral molecules. However, many cooperative phenomena influencing supramolecular processes have not been completely understood, yet. Very interesting phenomena are transfer, expression and amplification of chirality at surfaces but their mechanism has not been not known, yet [].
The importance of chirality in various fields of chemistry, material science, and life sciences motivated The Italian Chemical Society to introduce the Chirality Medal (Figure 14) to honour internationally recognized scientists who have made a distinguished contribution to all aspects of chirality. The medal has been awarded annually since 1991. In 2010 the Chirality Medal will be awarded to Prof. Kenji Mori for his seminal contributions to the importance of chirality of pheromones in signalling processes.

Figure 14.
Chirality Medal has been awarded annually since 1991 to recognize seminal contributions to the research on chirality.
3. Homochirality of Life
Homochirality is a characteristic hallmark of life. The presence of l-amino acids and d-carbohydrates in almost all known living beings was firmly documented and there is no dilemma on that. However, what is the reason for homochiral preference in life has been an open question over a century [,,,]. To discuss all possible explanations would be out of the focus of this paper. There is one more reason for not going into the long lasting debate. On February 2, 2010 Science Daily announced the very attractive news, that theory of primordial soup origin of life is rejected. Instead of the commonly accepted ‘soup theory’ an alternative view that life arose from gases such as hydrogen, carbon dioxide, nitrogen and hydrogen sulphide and energy for syntheses came from deep-sea hydrothermal vent having tiny compartments or pores. The theory has been supported by a series of experiments performed by G. Wächtershäuser []. In view of this theory it might be that a role of chiral mineral layers of earth core would be revisited.
Although the basic building blocks of proteins are homochiral (l-amino acids), representing a symmetry break (lack of bilateral symmetry), they undergo a special order. Thus, l-amino acids form the right α-helices and β-sheets with right-handed twist. In spite of protein complex structures, there are principles which govern conformations, packing, and topologies in their asymmetrical tertiary structures. The structural elements, responsible for protein fold were used for classification; quite a number of databases and servers are available to classify each particular protein. However, limitations imposed by l-amino acids asymmetry do not extend to the quaternary structure of protein []. Protein assembling usually generates symmetrical structures in accord with rotation symmetries although there are some exceptions. The homomeric assembling can occur as a process of agglomeration under influence of the surrounding media (during crystallization) on a particular protein or can be an intrinsic property of a given protein adjusted for its cell function during evolution [,,,]. Very interesting analysis of homomeric structures that allowed authors [] to propose routes of homomer evolution was published; the results obtained suggested that evolutionary route of a homomer can be predicted from its interface sizes, only. However, it is very important that heteromeric and homomeric protein assemblies are involved in functioning of a cell [,,,]. Significantly improved analytical techniques based on mass spectrometry and proteomics together with genetic experiments will offer more evidence on the process of protein assembly. The energy evaluation of different ways of assembling also gives an insight into the formation of homomers []. The classification of protein assemblies provided by Levy, Pereira-Leal, Chothia, and Teichmann at http://www.3Dcomplex.org [] enables an overview of protein oligomers whereas their structural symmetry and functions were discussed in the review by Goodsell and Olson []. We would like to pay attention to homomers revealing primarily non-crystallographic symmetry (NCS) in crystals and to discuss them in view of symmetry–asymmetry relationship.
4. Homomeric Assemblies
The three-dimensional structures of proteins provided by X-ray structure analysis (stored in Protein Data Bank, PDB) []) offer an abundance of detailed information revealing the nature of protein homomeric and heteromeric complexes (assemblies). Vast majority of the structures deposited in the PDB originates from X-ray crystallography (86.3 % out of more than 63200 deposited by the mid February 2010). However, the inference of the number of monomers associated into a multimeric protein from crystal structure is not always straightforward as already discussed by Thornton et al. []. One of the approaches to address this question is PISA at web (http://www.ebi.ac.uk/msd-srv/prot_int/pistart.html) []. Krissinel and Henrick considered all the possible combinations of protein subunits (protein chains) in the crystal structure without any previous knowledge on their multimeric state. The authors compared thermodynamical values of dissociation energy calculated for all possible assemblies to select the most probable biological unit; the approach used is 80–90% effective []. According to PISA web service (based on data from PDB) (Figure 15) homomeric dimers outnumber the heteromers by more than four times. A high number of dimeric homomers can be explained by a presence of the crystallographic twofold axes in many of enantiomorphic space groups but also an appearance of non-crystallographic twofold axes. There are also enzymes that are active in dimeric form, only. This reason can be valid for some trimeric, tetrameric, and hexameric homomers whereas for higher oligomers it would be less reasonable to expect them as a prerequisite for catalytic activity. However, one should not neglect a possibility that tetrameric and hexameric homomers can include the catalytic dimers. This possibility leaves an open question if the high symmetry of homomeric enzyme will be preserved on substrate or inhibitor binding. Very interesting algorithm for determination of the oligomeric number for symmetrical homomer is based on search of symmetry configuration space using NMR restrains and van der Waals packing. This approach was tested on a number of homomeric assemblies ranging from dimers to heptamers [].
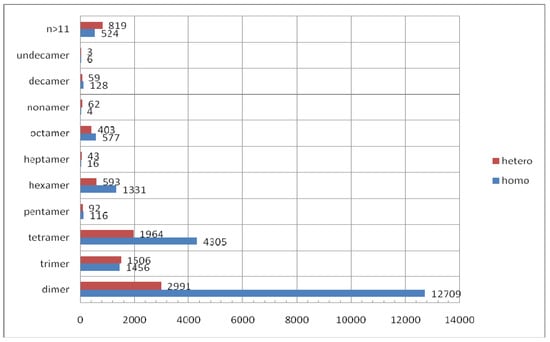
Figure 15.
The distribution of oligomers in the PDB as assigned by the PISA web service. Distributions of homomers and heteromers with respect to their oligomeric numbers are shown.
4.1 Homomers Generated by Non-Crystallographic Symmetry
In the focus of our analysis are homomeric assemblies generated predominantly by operations of non-crystallographic symmetries (NCS). A large portion of oligomeric proteins forms highly symmetrical assemblies. As the proteins are composed of amino acids that are chiral molecules, the symmetry operations cannot include symmetry elements that invert chirality. This leaves only rotations as possible symmetry elements. In the crystalline state, we can distinguish two kinds of symmetry: symmetry of the space group that is valid throughout the crystal and a local symmetry (also called non-crystallographic symmetry, NCS) which is valid only in a limited parts of the unit cell. NCS operates between similar subunits of the asymmetric unit in the unit cell. (As NCS relates similar structural units its operation is an approximate symmetry element. Therefore, the operation that is not compatible with the periodicity of a crystal pattern, the term NCS, commonly used in biological crystallography is not welcomed in fundamental crystallography.) In the case of space group symmetry the periodicity of the unit cell greatly reduces the possible rotational symmetry to 2, 3, 4 and 6-fold symmetry axis, whereas in the local symmetry these rotations are, in principle, allowed to be of any order. For example, it is possible for a protein to be arranged into a homomer with any n-fold rotational non-crystallographic symmetry in the space group P 1 which has no rotational symmetry at all. In such case NCS can be even higher order rotation symmetry although applying only locally.
The strict operations of the space group symmetry, in fact, introduce an inconvenience for someone trying to determine the native multimeric state of the protein from its crystal structure. An asymmetric unit of the crystal structure not necessarily represents the protein native multimeric state. If only a part of a protein comprises the asymmetric unit then exact crystallographic symmetry operations relates remaining parts of the protein. On the opposite, it is possible that more than one homomer comprises the asymmetric unit of the crystal. Therefore, several ways of determining the native multimeric state of the protein have been proposed [,,,]. The presence of the NCS in the protein crystals somewhat alleviates the situation. The NCS operations are separated from the symmetry operations of the space group and operate locally. Therefore it is a good chance that the homomer generated by NCS is indeed a native form of assembly. If the symmetry of the homomer is compatible with some crystallographic symmetry then it is likely that the protein will crystallize in the space group of that symmetry (e.g. homomer having a two-fold axis is likely to crystallize in a space group having the two-fold axis like P 2, C 2, P 2 2 2 etc.). On the contrary, if the homomer reveals NCS (such as n-fold rotations where n is a prime number larger or equal to 5) it is possible that at least one homomer occupies the asymmetric unit of the unit cell and its symmetry is NCS. The homomer with the prime number of monomers (i.e. 5, 7, 11, 13) cannot be divided into smaller assemblies related by any symmetry. This phenomenon can be interpreted by the mathematical theorem postulating that every group of prime order is cyclic. In another words, it means that homomer consisting of prime number of monomers must be arranged into a ring revealing n-fold symmetry axis. Such homomers are illustrated and discussed in the following section.
4.2 Homomers with Prime Number of Subunits
A prime number of subunits can form a symmetrical assembly only through single rotation axis. In general, it is valid for all prime numbers including 2 and 3; thus, homo-dimers and homo-trimers related by twofold and threefold axis are possible. These two symmetry operations are allowed by the space group symmetry operations although they can operate locally but only through NCS, running in directions that are not allowed by the space group. The fivefold rotation axis is the lowest order that cannot be part of crystal symmetry. Thus, for the pentameric homomer at least one pentamer will crystallise in the asymmetric unit. Moreover, the only possible symmetry of this assembly is the fivefold rotation axis, i.e. point group 5. In order to verify this principle the PDB was searched for all the structures which have exactly five subunits in the biological homomeric assembly. Unfortunately, in PDB the view of the plot of an assembly is not always along the highest symmetry axis. Therefore, it is not straightforward to find the homomer of desired rotational symmetry. For such homomers the assemblies were manually oriented by the “View in JMOL” link [].
The homomers with prime number of subunits display the inevitable circular symmetry (Figure 16). The number of available structures decreases for higher oligonumbers; only, the single structure comprising a homomer with 13 subunits is found in PDB. The number of homomers with prime number of subunits is suppressed with respect to the other homomers (Figure 15). This is undeniably influenced by the existence of single possible mode of assembling.
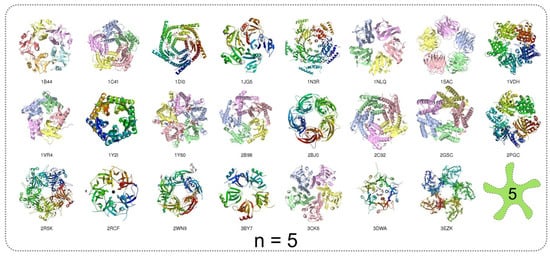
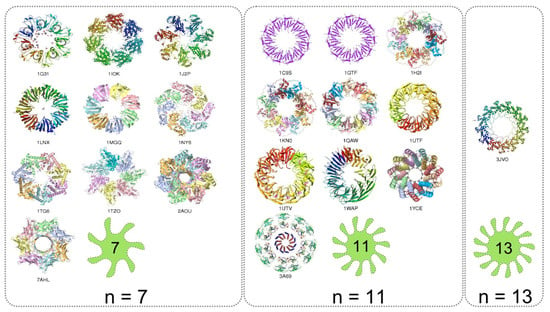
Figure 16.
Examples of homomeric structures with prime number of subunits ranging from n = 5 to n = 13; the ring skeletons of n-fold rotational symmetry characterise these homomeric structures. The light-green icon denotes the order of rotational symmetry. PDB code for each homomer in the gallery is provided.
4.3 Symmetry of Homomers with Non-Prime Number of Subunits
The analysis of protein homomers with non-prime number of subunits reveals increased number of possible arrangements upon assembling than those with prime number of subunits (Figure 15). This is reflected in the number of point group symmetries of the homomers. Some of the possible symmetries for different oligomeric numbers n are illustrated (Figure 17). For any given n two different types of symmetries are possible: a) the symmetries with a single rotational axis and b) symmetries with more rotational axes (Figure 17 and Figure 18). In the first case the axis of symmetry can be of order n or of any divisor of n. The point group symmetry is then a simple n-fold rotation. However, in majority of homomers with non-prime number of subunits the point groups including more symmetry axes prevail; various combinations of rotation axes offer more possibilities for assembling. Combinations for n = 8 are exemplified; some homomers show either the eightfold or fourfold symmetry axis, whereas majority of homomers reveal the 422 point group symmetry, which involves a fourfold axis and twofold axes perpendicular to it (Figure 18). Analogously, it is valid for monomers with n = 10, 12, 14. This preference towards the point groups with more than one axis of symmetry could be viewed as possibility to maximize the number of contacts between subunits. The assemblies generated by operations with more symmetry axes can maximize the number of contacts between neighbouring subunits that contribute to a more stable homomer. In the assembly revealing 422 point group symmetry each subunit is surrounded by three subunits whereas in the assembly of point group 8 each subunit is surrounded by two neighbours. There is a very small number of nonamers (Figure 15). Namely, 9 is an odd number and the twofold symmetry cannot be present in homomers having 9 subunits. Although number 9 is not a prime and therefore nonameric homomers are not constrained to have circular symmetry, the impossibility of assembling via twofold axis greatly reduces the number of possible symmetries (Figure 15).
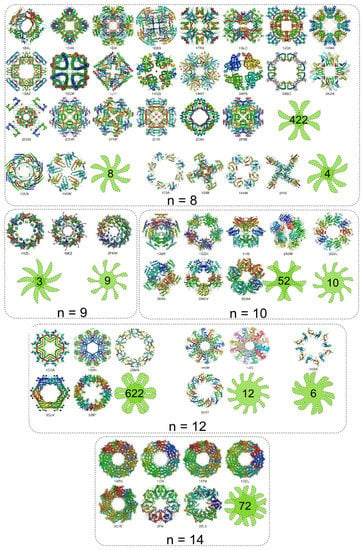
Figure 17.
Examples of homomers with the number of subunits ranging from 8 to 14 and their possible symmetries are shown. The light-green icons illustrate the point group symmetry of the homomers. PDB code for each homomer in the gallery is provided.
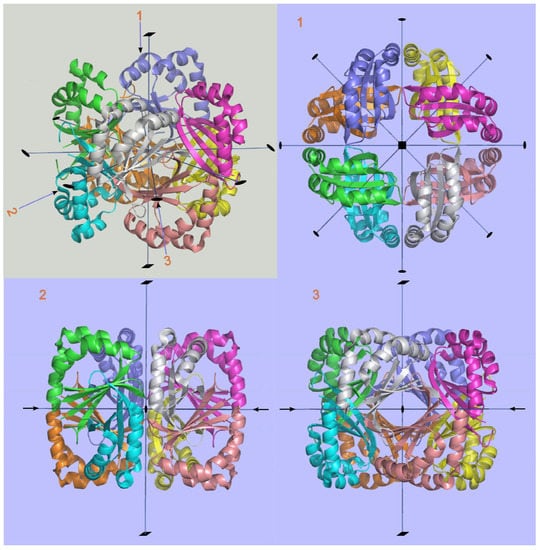
Figure 18.
The 422 point group symmetry generating an octameric homomer of the protein Atu4242 from Agrobacterium tumefaciens (2AP6). In the figure with grey background general view of the homomer is depicted where the digits in red correspond to three different orientations of the octamer (shown in figures with the light-blue background). Three different views along the principle axes of symmetry: view 1 along the fourfold axis and views 2 and 3 along two different twofold axes.
4.4 Crystallographer’s View of Two Homomers from Evolutionary Distant Organisms that Conserved Protein Fold and Symmetry of Homomers
The conservation of a particular symmetry of protein assembly during evolution may indicate the importance of that symmetry for a function of the protein. The crystal structure of the proteolytic component of the caseinolytic Clp protease (ClpP) from E. coli [] and the homologous hydrolytic enzyme from human mitochondria (hClpP) [] were selected as crystallographically and evolutionary interesting examples. In E. coli this enzyme can account for more than 80% of total protein degradation (together with another enzyme, Lon) []. The similarity of the fold of two proteins is expressed in terms of root-mean-square deviation (RMSD) of their equivalent atom positions. The protein fold and symmetry of homomeric assemblies of these two enzymes show a high degree of similarity (Figure 19) although they originate from two evolutionary distant organisms. Their structural similarity suggests that their biological function has been preserved over evolutionary time.
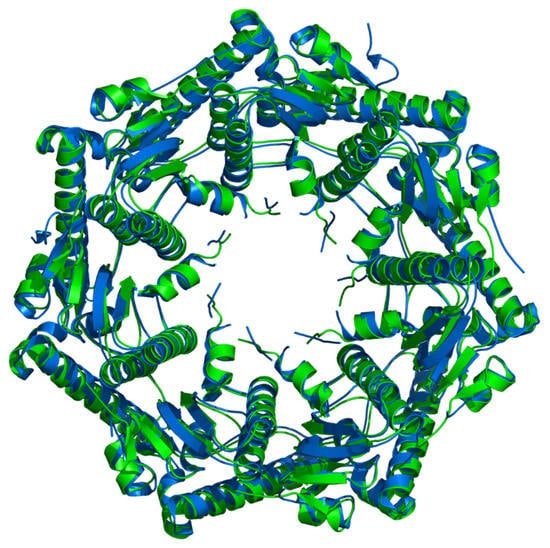
Figure 19.
The overlap of 3D-structures of enzyme from E. coli (1TYF, in green) and human (1TG6, in blue) proteolytic component of the caseinolytic Clp protease. Two enzymes from evolutionary distant organisms show a remarkable structural similarity (RMSD is 0.93 Å).
It is very interesting to analyse the crystal packing of these two enzymes with very similar 3D-homomeric architecture. The active form of E. coli enzyme is composed of two heptamers which are joined together to form cylinder and their sevenfold axes of symmetry coincide. There is a twofold axis running perpendicular to the sevenfold axis. In the structure of E. coli protease (1TYF) this very twofold axis is non-crystallographic symmetry element (the asymmetric unit is tetradecamer), whereas in the structure of human enzyme (1TG6) operates the crystallographic twofold rotation (the strict symmetry) parallel to the crystallographic b axis (i.e. the heptamer forms the asymmetric unit of the crystal). The crystal packing of these two enzymes illustrates that homomers of similar architecture are embedded differently in the unit cells of their crystals (Figure 20).
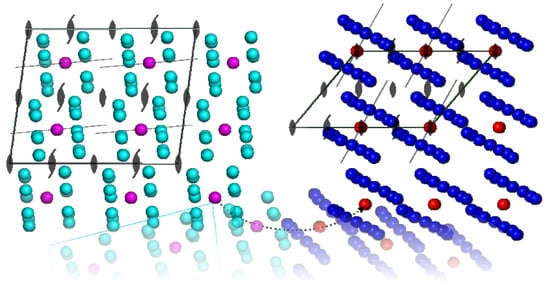
Figure 20.
View down the crystallographic b axis in the structures of E. coli (1TYF, cyan) and human (1TG6, blue) proteolytic component of the caseinolytic Clp protease. Each monomer (subunit) is represented by a sphere and centres of proteins are coloured magenta and red, respectively. The approximate sevenfold symmetry axes are shown by thin lines. The transformation of the unit cell of 1TYF (shown schematically by dotted line) to 1TG6 by the rotation reveals that approximate twofold NCS turns to the strict twofold axis of the space group C 2 (both structures crystallized in the space group C2). The distances between the centres of homomers remain almost constant whereas the volume of the unit cell is reduced by 1/2. In both structures the sevenfold axes are only slightly tilted with respect to the crystallographic axes.
5. Conclusions
General concept of symmetry is briefly described. Symmetry-asymetry (chirality) relationship in chemistry is discussed. Historical evolution of the notion of chirality is briefly described. An implication of chirality in life, mainly through asymmetry of protein structures, is shown. Life and its processes can be considered in view of symmetry-asymmetry relationship. This approach is highly demanding and at the present state of knowledge no one can derive a general theory. However, we decided to show an impact of non-crystallographic symmetry on protein homomers at qualitative level.
Protein – protein interactions, initiated on complementarity principle, are starting points for assembling processes. Protein complexes generated by assembling are important for cell self-organisation and life. Although Nature has been creating such systems over million years scientists are at the beginning to learn the Nature’s secrets. However, tendency towards assembling of proteins into heteromeric and homomeric oligomers has been known for a few decades. The asymmetry of protein molecules has not been extended to their oligomeric state as demonstrated by Chothia in 1991 []; homomers reveal symmetry that can be in accord with the space group operations but it can also involve approximate rotation operations (non-crystallographic symmetry). The protein units can be either all α-helices or all β-sheets, and mixed α/β proteins but none of these structures are preferred for assembly.
The significantly lower number of homomeric structures with prime number of subunits could be partly due to a limitation mode for assembling allowed only by the cyclic group symmetry. This is a direct implication of mathematical theorem and it is not restricted to homomer assemblies. It implies that the formation of various symmetrical homomers is influenced not only by various factors of biological nature but also by the available symmetry configuration space.
Acknowledgements
This work was supported by the Ministry of Science, Education and Sports of the Republic of Croatia grant No. 098-1191344-2943.
References and Notes
- Mainzer, K. Symmetry and Complexity: The Spirit and Beauty of Nonlinear Science; World Scientific: Singapore, 2005. [Google Scholar]
- Mainzer, K. Symmetries of Nature: A Handbook of philosophy of Nature and Science; de Gruyter: Berlin, Germany, 1988. [Google Scholar]
- Mainzer, K. Thinking in Complexity: The Complex Dynamics of Matter, Mind and Mankind, 4th ed.; Springer: Berlin, Germany, 2004. [Google Scholar]
- Rosen, J. Symmetry Rules: How Science and Nature are Founded on Symmetry; Springer: Berlin, Germany, 2008. [Google Scholar]
- Janoschek, R. Chirality from Weak Bosons to the α-Helix; Springer: Berlin, Germany, 1991. [Google Scholar]
- Lee, T.; Yang, C. Question of parity conservation in weak interactions. Phys. Rev. 1956, 104, 254–258. [Google Scholar] [CrossRef]
- Liu, S.V. Intrinsic Asymmetry underneath Apparent Symmetry. Pionieer 2006, 1, 29–30. [Google Scholar]
- Perticka, J.J.; van Norman, J.M.; Benfey, P.N. Symmetry Breaking in Plants: Molecular Mechanisms Regulating Asymmetric Cell Divisions in Arabidopsis. Cold Spring Harb. Perspect. Biol. 2009, 1, a000497. [Google Scholar]
- Wood, W.B. Left-right asymmetry in animal development. Annu. Rev. Cell Dev. Biol. 1997, 13, 53–82. [Google Scholar] [CrossRef] [PubMed]
- Hudson, A. Development of symmetry in plants. Annu. Rev. Plant Mol. Biol. 2000, 51, 349–370. [Google Scholar] [CrossRef] [PubMed]
- Kuroda, R.; Endo, B.; Abe, M.; Shimizu, M. Chiral blastomer arrangement dictates zygotic left-right asymmetry pathway in snails. Nature 2009, 462, 790–794. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.L. Broken symmetry. Sci. News 2009, 176, 26. [Google Scholar]
- Chothia, C. Asymmetry in protein structures. In Biological Asymmetry and Handness; Bock, G.R., Marsh., J., Eds.; Wiley & Sons: New York, USA, 1991; Ciba Foundation Symposium 162; pp. 36–57. [Google Scholar]
- Andre, I.; Strauss, C.E.M.; Kaplan, D.B.; Bradley, P.; Baker, D. Emergence of symmetry in homooligomeric biological assemblies. Proc. Natl. Acad. Sci. USA 2008, 105, 16148–16152. [Google Scholar] [CrossRef] [PubMed]
- Plaxco, K.W.; Gross, M. Protein Complexes: The Evolution of Symmetry. Curr. Biol. 2008, 19, R25–R26. [Google Scholar] [CrossRef] [PubMed]
- Levy, E.D.; Boeri Erba, E.; Robinson, C.V.; Teichmann, S.A. Assembly reflects evolution of protein complexes. Nature 2008, 453, 1262–1265. [Google Scholar] [CrossRef]
- Molčanov, K.; Kojić-Prodić, B. Chirality-Forthcoming 160th Anniversary of Pasteur’s Discovery. Kem. Ind. 2007, 56, 275–292. [Google Scholar]
- Lough, W.J.L.; Wainer, I.W. Chirality in Natural and Applied Science; Blackwell Science Ltd.: Oxford, UK, 2002. [Google Scholar]
- Prelog, V. Chirality in Chemistry, Nobel lecture, December 12, 1975, reprinted in Croat. Chem. Acta 2006, 79, XLIX-LVII.
- Derewenda, Z.S. On wine, chirality and crystallography. Acta Cryst. 2008, A64, 246–258. [Google Scholar] [CrossRef] [PubMed]
- Biot, J.B. Phénomènes de polarisation successive, observés dans des fluides homogènes. Bull. Soc. Philomath. 1815, 190–192. [Google Scholar]
- Pasteur, L. Mémoire sur la relation qui peut exister entre la forme crystalline et la composition chimique, et sur la cause de la polarization rotatoire. Compt. Rend. Acad. Sci. 1848, 26, 33–38. [Google Scholar]
- Kelvin, L. Baltimore Lectures. Clay: London, UK, 1904; pp. 618–619. [Google Scholar]
- van’t Hoff, J.H. Arch. Neeland. Sci. Exact. Nat. 1874, 9, 445–454.
- Le Bel, J.A. Sur les relations qui existent entre molecules. Bull. Soc. Chim. 1874, 22, 337–347. [Google Scholar]
- Fischer, E. Über die Configuration des Traubenzuckers und seiner Isomeren I und Über die Configuration des Traubenzuckers und seiner Isomeren II. Ber. Dtsch. Chem. Ges. 1891, 24, 1836–1845, 2683–2687. [Google Scholar] [CrossRef]
- Bijvoet, J.M.; Peerdeman, A.F.; Bommel, A.J. Determination of the absolute configuration of optically active compounds by means of X-rays. Nature 1951, 168, 271–271. [Google Scholar] [CrossRef]
- Cahn, R.S.; Ingold, C.K.; Prelog, V. The specification of asymmetric configuration in organic chemistry. Experientia 1956, 12, 81–94. [Google Scholar] [CrossRef]
- Fischer, E. Einfluss der Configuration auf die Wirkung der Enzyme. Ber. Dtsch. Chem. Ges. 1894, 27, 2985–2993. [Google Scholar] [CrossRef]
- Federsel, H.J. Asymmetry on a large scale: the road map to stereoselective processes. Nat. Rev. Drug Discov. 2005, 4, 685–697. [Google Scholar] [CrossRef]
- Ernst, K.-H. Aspects of molecular chirality at metal surfaces. Z. Phys. Chem. 2009, 223, 37–51. [Google Scholar] [CrossRef]
- Mason, S.F. Origin of biomolecular handedness. Nature 1984, 311, 19–23. [Google Scholar] [CrossRef] [PubMed]
- Mason, S.F. Origin of biomolecular chirality. Nature 1985, 314, 400–401. [Google Scholar] [CrossRef]
- Bada, J.L. Origins of homochirality. Nature 1995, 374, 594–595. [Google Scholar] [CrossRef] [PubMed]
- Siegel, J.S. Single-handed cooperation. Nature 2001, 409, 777–778. [Google Scholar] [CrossRef]
- Wächtershäuser, G. Origin of life: Life as we do not know it. Science 2000, 289, 1307–1308. [Google Scholar] [CrossRef]
- Goodsell, D.S.; Olson, A.J. Structural Symmetry and Protein Function. Annu. Rev. Biophys. Biomol. Struct. 2000, 29, 105–153. [Google Scholar] [CrossRef]
- Nobeli, I.; Fiavia, A.D.; Thornton, J.M. Protein promiscuity and its implications for biotechnology. Nat. Biotechn. 2009, 27, 157–167. [Google Scholar] [CrossRef]
- Koike, R.; Kidera, A.; Ota, M. Alteration of oligomeric state and domain architecture is essential for functional transformation between transferase and hydrolase with the same scaffold. Protein Sci. 2009, 18, 2060–2066. [Google Scholar] [CrossRef] [PubMed]
- Jones, S.; Thornton, J.M. Principles of protein-protein interactions. Proc. Natl. Acad. Sci. USA 1996, 93, 13–20. [Google Scholar] [CrossRef] [PubMed]
- Rohl, C.A.; Strauss, C.E.; Misura, K.M.; Baker, D. Protein structure prediction using Rosetta. Methods Enzymol. 2004, 383, 66–93. [Google Scholar] [PubMed]
- Levy, E.D.; Pereira-Leal, J.B.; Chothia, C.; Teichmann, S.A. 3D Complex: A Structural Classification of Protein Complexes. PLoS Comput. Biol. 2006, 2, 1395–1406. [Google Scholar] [CrossRef]
- Berman, H.M.; Henrick, K.; Nakamura, H. Announcing the worldwide Protein Data Bank. Nat. Struct. Biol. 2003, 10, 980–980. [Google Scholar] [CrossRef] [PubMed]
- Ponstingl, H.; Kabirb, T.; Thornton, J.M. Automatic inference of protein quaternary structure from crystals. J. Appl. Cryst. 2003, 36, 1116–1122. [Google Scholar] [CrossRef]
- Krissinel, E.; Henrick, K. Inference of Macromolecular Assemblies from Crystalline State. J. Mol. Biol. 2007, 372, 774–797. [Google Scholar] [CrossRef] [PubMed]
- Potluri, S.; Yan, A.K.; Chou, J.J.; Donald, B.R.; Bailey-Kelogg, C. Structure determination of symmetric homo-oligomers by a complete search of symmetry configuration space, using NMR restrains and van der Waals packing. Proteins 2006, 65, 203–219. [Google Scholar] [CrossRef]
- Ponstingl, H.; Henrick, K.; Thornton, J.M. Discriminating Between Homodimeric and Monomeric Proteins in the Crystalline State. PROTEIN-Struct. Funct. Genet. 2000, 41, 47–57. [Google Scholar] [CrossRef]
- Jmol: an open-source Java viewer for chemical structures in 3D. http://www.jmol.org/.
- Wang, J.; Hartling, J.A.; Flanagan, J.M. The structure of ClpP at 2.3 A resolution suggests a model for ATP-dependent proteolysis. Cell 1997, 91, 447–456. [Google Scholar] [CrossRef]
- Kang, S.G.; Maurizi, M.R.; Thompson, M.; Mueser, T.; Ahvazi, B. Crystallography and mutagenesis point to an essential role for the N-terminus of human mitochondrial ClpP. J. Struct. Biol. 2004, 148, 338–352. [Google Scholar] [CrossRef] [PubMed]
- Maurizi, M.R. Proteases and protein degradation in Escherichia coli. Experientia 1992, 48, 178–201. [Google Scholar] [CrossRef] [PubMed]
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).