Bayesian and Classical Inferences of Two-Weighted Exponential Distribution and Its Applications to HIV Survival Data

Abstract

The paper presents a statistical model based on the two-weighted exponential distribution (TWED) to examine censored Human Immunodeficiency Virus (HIV) survival information. Identifying HIV as a disability, the study endorses an inclusive and sustainable health policy framework through some predictive findings. The TWED provides an accurate representation of the inherent hazard patterns and also improves the modelling of survival data. The parameter estimation is achieved in both a classical maximum likelihood estimation (MLE) and a Bayesian approach. Bayesian inference can be carried out under general entropy loss conditions and the symmetric squared error loss function through the Markov Chain Monte Carlo (MCMC) method. Based on the symmetric properties of the inverse of the Fisher information matrix, the asymptotic confidence intervals (ACLs) for the MLEs are constructed. Moreover, two-sided symmetric credible intervals (CRIs) of Bayesian estimates are also constructed based on the MCMC results that are based on symmetric normal proposals. The simulation studies are very important for indicating the correctness and probability of a statistical estimator. Implementing the model on actual HIV data illustrates its usefulness. Altogether, the paper supports the idea that statistics play an essential role in promoting disability-friendly and sustainable research in the field of public health in general.

1. Introduction

HIV is a major public health problem around the world impacting millions of people. In addition to medical implications, HIV has social and legal implications. Most countries, such as the United States and the United Kingdom, have included HIV as a disability under the laws against discrimination due to the long-term effects of the virus on health and involvement in society. According to the Americans with Disabilities Act (ADA), people with HIV are considered to be covered by all the discrimination protections, notwithstanding the presence of symptoms. For more details, refer to the U.S. Department of Justice [1]. Statistical modelling can be used to analyse survival patterns, estimate life expectancy, and assess risk factors of death in HIV-positive individuals. Furthermore, evidence-based policy, resource allocation, and observance of legal and ethical provisions stipulated by international frameworks may be affected by disability data, especially those informed as a result of high-end statistical techniques; see Mitra et al. [2]. Recently published research indicates the iterative exploration of new statistical instruments, namely, survival models and Bayesian models, to comprehensively overcome the challenges of censored statistics, time-to-event results, and inaccuracy in the real-life datasets related to disability; see Groce [3] and Lee and Wang [4].

We point out that the TWED is a generalization of the traditional exponential distribution, as presented by Gupta and Kundu [5] and generalised by Shakhatreh [6], which can be used to represent non-constant hazard rates. Our contribution will involve developing Bayesian inference techniques for the TWED and comparing the outcomes of classical methods with those of the Bayesian method. Shakhatreh [6] previously determined the MLEs of the TWED; we extend this to obtain the Bayesian estimates corresponding to a loss function of both symmetric squared error and general entropy using a Metropolis-within-Gibbs sampler. An extensive simulation study, along with an application on real data, is also provided to illustrate the power of the Bayesian approach in terms of interval estimation and performance of censored data. Moreover, we quote the results of Shakhatreh [6] on the TWED better fitting an HIV survival dataset than alternative distributions to justify focusing on the TWED in the analysis of such data.

This paper has been framed to give a clear statistical model of the survival of HIV-infected patients using the two-weighted exponential distribution (TWED). In Section 2, the model formulation and theoretical basis of the TWED, a flexible distribution with two extra shape parameters, are presented. The flexibility enables the TWED to capture the differences in the hazard behaviours and adapt to different censoring structures regularly observed in survival data. Section 3 obtains the MLEs of the model parameters and suggests their confidence intervals with asymptotic and bootstrap methods. In Section 4, the Bayesian estimation technique is presented, and the Markov Chain Monte Carlo (MCMC) method is used with both symmetric squared error loss (SEL) and general entropy loss (GEL) functions. A simulation study of the performance of the suggested estimators with different sample sizes was conducted as outlined in Section 5. Section 6 describes our use of the model on a real dataset of HIV patient survival times and compares and contrasts the results of classical and Bayesian inference. Lastly, Section 7 presents the major findings and future recommendations.

2. Model Description

This section presents the TWED as a model for survival data subject to right-censoring. The section shows how the distribution can adapt to different hazard rates and includes a model based on proportional hazard, which is the basis for the next estimation method. Consider an experiment setup with n units, each of which has a lifetime represented by the notation $X_1,X_2,\dots ,X_n$. With cumulative distribution function (CDF), $F_X\left(x\right)$, and probability density function (PDF), $f_X\left(x\right)$, these lifetimes are defined as independent and identically distributed (iid) random variables. Furthermore, the iid random censoring times for these units are represented by the additional sequences $T_1,T_2,\dots ,T_n$ defined by CDF $F_T\left(t\right)$ and PDF $f_T\left(t\right).$ We can observe iid random pairs $(Y_1,D_1),\dots ,(Y_n,D_n)$ where $Y_i=min(X_i,T_i),i=1,\dots ,n$ assuming mutual independence between $X_i$ and $T_i.$ Furthermore, we define $D_i$, described by the CDF $F_T\left(t\right),$ as

$$D_i=\left\{\begin{array}{c}1\\ 0\end{array}\right.\begin{array}{c}\mathrm{if}{X}_i⩽T_i,\\ \mathrm{if}{X}_i>T_i,\end{array}\begin{array}{c}\mathrm{censored}\mathrm{case}\\ \mathrm{non-censored}\mathrm{case}.\end{array}$$

It becomes apparent that the joint PDF of $Y_i$ and $D_i$ is

$$f_{Y,D}(y,d)={\left\{f_X\left(y\right)(1-F_T\left(y\right))\right\}}^d{\left\{f_T\left(y\right)(1-F_X\left(y\right))\right\}}^{1-d},y⩾0,d=0,1.$$

(1)

Additionally, the random variable X and T adhere to the proportional hazards model, governed by the proportionality constant $\beta >0,$ given by

$$(1-F_T\left(t\right))={(1-F_X\left(t\right))}^{\beta }.$$

(2)

For more details on the proportional hazards model, see Danish et al. [7]. From Equations (1) and (2) we obtain the joint density joint of Y and D

$$f_{Y,D}(y,d)=f_X\left(y\right){\left\{1-F_X\left(y\right)\right\}}^{\beta }{\beta }^{1-d},y⩾0,d=0,1.$$

(3)

Gupta and Kundu [5] proposed the weighted exponential distribution, which has been used to describe the classical exponential model as an attempt at generalization to capture non-constant hazard rates. Extending the model on their foundation, Shakhatreh [6] further generalized the model by introducing yet another parameter to make it even more flexible in fitting lifetime data. Shakhatreh [6] determined key statistical features of the TWED, like the moments and quantiles. Shakhatreh [6] obtained only the maximum likelihood estimates, showing that the model works better with censored survival data. The PDF of the TWED $(\lambda ,{\alpha }_1,{\alpha }_2)$ is given as follows:

$$f_X\left(x;\lambda ,{\alpha }_1,{\alpha }_2\right)=\lambda K\left({\alpha }_1,{\alpha }_2\right)\left(1-e^{-{\alpha }_1\lambda x}\right)\left(1-e^{-{\alpha }_2\lambda x}\right)e^{-\lambda x},x>0,\lambda ,{\alpha }_1,{\alpha }_2>0,$$

(4)

where $K\left({\alpha }_1,{\alpha }_2\right)={\displaystyle \frac{({\alpha }_1+1)({\alpha }_2+1)({\alpha }_1+{\alpha }_2+1)}{{\alpha }_1{\alpha }_2({\alpha }_1+{\alpha }_2+2)}}.$

The survival and hazard functions for the TWED are given, respectively, as

$$S(x;\lambda ,{\alpha }_1,{\alpha }_2)=K\left({\alpha }_1,{\alpha }_2\right)\left({\displaystyle \frac{e^{-\lambda ({\alpha }_1+{\alpha }_2)x}}{{\alpha }_1+{\alpha }_2+1}}-{\displaystyle \frac{e^{-{\alpha }_1\lambda x}}{{\alpha }_1+1}}-{\displaystyle \frac{e^{-{\alpha }_2\lambda x}}{{\alpha }_2+1}}+1\right)e^{-\lambda x},$$

(5)

and

$$h(x;\lambda ,{\alpha }_1,{\alpha }_2)={\displaystyle \frac{\lambda \left(1-e^{-{\alpha }_1\lambda x}\right)\left(1-e^{-{\alpha }_2\lambda x}\right)}{1+{\displaystyle \frac{e^{-\lambda x({\alpha }_1+{\alpha }_2)}}{{\alpha }_1+{\alpha }_2+1}}-{\displaystyle \frac{e^{-{\alpha }_1\lambda x}}{{\alpha }_1+1}}-{\displaystyle \frac{e^{-{\alpha }_2\lambda x}}{{\alpha }_2+1}}}}.$$

(6)

From Equations (4) and (5), the density function in Equation (3) appears as follows:

$$\begin{array}{c}{f}_{Y,D}(y,d;\lambda ,{\alpha }_1,{\alpha }_2)=\lambda {\left[K({\alpha }_1,{\alpha }_2)\right]}^{\beta +1}{\beta }^{1-d}\left(1-e^{-{\alpha }_1\lambda y}\right)\left(1-e^{-{\alpha }_2\lambda y}\right)e^{-\lambda (\beta +1)y}\hfill \\ \times {\left({\displaystyle \frac{e^{-\lambda ({\alpha }_1+{\alpha }_2)y}}{{\alpha }_1+{\alpha }_2+1}}-{\displaystyle \frac{e^{-{\alpha }_1\lambda y}}{{\alpha }_1+1}}-{\displaystyle \frac{e^{-{\alpha }_2\lambda y}}{{\alpha }_2+1}}+1\right)}^{\beta },y>0,d=0,1.\end{array}$$

To conclude, the TWED offers a general model that is generative with a wide range of modelling characteristics of hazard rate behaviour. Its shape and hazard functions vary in a meaningful way as the parameters are varied, as shown in Figure 1 and Figure 2; therefore, it is suitable for the analysis of survival data, especially in situations where some censored data are used.

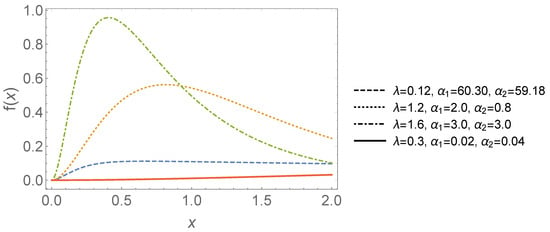
Figure 1. PDF of the TWED (inspired from Shakhatreh [6]).

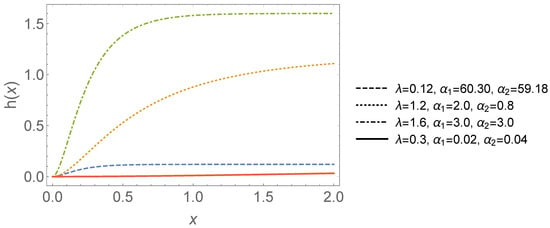
Figure 2. The hazard function of the TWED (inspired from Shakhatreh [6]).

3. Maximum Likelihood Estimation

This section gives an outline of MLE when fitting the TWED model. It obtains the log-likelihood function with right-censorship, and it estimates the parameters numerically. Based on the model observations, $(y_1,d_1),(y_2,d_2),\dots ,(y_n,d_n),$ deciphered in Section 2, and referring to Equation (3), the likelihood function can be written as follows:

$$\begin{array}{ccc}\hfill L(\mathbf{\Theta }|\mathrm{data})& =& {\lambda }^n{\left[K({\alpha }_1,{\alpha }_2)\right]}^{n(\beta +1)}{\beta }^{\left(n-{\displaystyle \sum _{i=1}^n}{d}_i\right)}exp\left[\begin{array}{c}-\lambda (\beta +1){\displaystyle \sum _{i=1}^n}{y}_i\end{array}\right]\times \hfill \\ & & {\displaystyle \prod _{i=1}^n}\left[\begin{array}{c}\left(1-e^{-{\alpha }_1\lambda y_i}\right)\end{array}\right]\times {\displaystyle \prod _{i=1}^n}\left[\begin{array}{c}\left(1-e^{-{\alpha }_2\lambda y_i}\right)\end{array}\right]\times \hfill \\ & & {\displaystyle \prod _{i=1}^n}{\left[\begin{array}{c}{\displaystyle \frac{e^{-\lambda ({\alpha }_1+{\alpha }_2)y_i}}{{\alpha }_1+{\alpha }_2+1}}-{\displaystyle \frac{e^{-{\alpha }_1\lambda y_i}}{{\alpha }_1+1}}-{\displaystyle \frac{e^{-{\alpha }_2\lambda y_i}}{{\alpha }_2+1}}+1\end{array}\right]}^{\beta },\hfill \end{array}$$

(7)

where $\mathbf{\Theta }=(\lambda ,{\alpha }_1,{\alpha }_2,\beta ).$ The likelihood function is the basis of inferences, and it varies based on the nature of observed datasets, whether these data are complete or right-censored; see Casella and Berger [8]. Taking the logarithm of Equation (7), we have

$$\begin{array}{ccc}\hfill l(\mathbf{\Theta }|\mathrm{data})& =& nln\lambda +n(\beta +1)lnK({\alpha }_1,{\alpha }_2)+(n-{\displaystyle \sum _{i=1}^n}{d}_i)ln\beta .-\lambda (\beta +1)\left({\displaystyle \sum _{i=1}^n}{y}_i\right)+\hfill \\ & & {\displaystyle \sum _{i=1}^n}ln\left(1-e^{-{\alpha }_1\lambda y_i}\right)+{\displaystyle \sum _{i=1}^n}ln\left(1-e^{-{\alpha }_2\lambda y_i}\right)+\hfill \\ & & \beta {\displaystyle \sum _{i=1}^n}ln\left[\begin{array}{c}{\displaystyle \frac{e^{-\lambda ({\alpha }_1+{\alpha }_2)y_i}}{{\alpha }_1+{\alpha }_2+1}}-{\displaystyle \frac{e^{-{\alpha }_1\lambda y_i}}{{\alpha }_1+1}}-{\displaystyle \frac{e^{-{\alpha }_2\lambda y_i}}{{\alpha }_2+1}}+1\end{array}\right].\hfill \end{array}$$

(8)

Equating each of the first partial derivatives of Equation (8) to zero with respect to the involved parameters results in the following:

$$\begin{array}{c}{\displaystyle \frac{\mathsf{\partial }l(\mathbf{\Theta }|\mathrm{data})}{\mathsf{\partial }\lambda }}=\beta {\displaystyle \sum _{i=1}^n}\left[{\displaystyle \frac{{\displaystyle \frac{{\alpha }_1{y}_i\left(-e^{-\lambda ({\alpha }_1+{\alpha }_2)y_i}\right)-{\alpha }_2{y}_i{e}^{-\lambda ({\alpha }_1+{\alpha }_2)y_i}}{{\alpha }_1+{\alpha }_2+1}+\frac{{\alpha }_1{y}_i{e}^{-{\alpha }_1\lambda y_i}}{{\alpha }_1+1}+\frac{{\alpha }_2{y}_i{e}^{-{\alpha }_2\lambda y_i}}{{\alpha }_2+1}}}{{\displaystyle \frac{e^{-\lambda ({\alpha }_1+{\alpha }_2)y_i}}{{\alpha }_1+{\alpha }_2+1}-\frac{e^{-{\alpha }_1\lambda y_i}}{{\alpha }_1+1}-\frac{e^{-{\alpha }_2\lambda y_i}}{{\alpha }_2+1}+1}}}\right]\\ +{\displaystyle \sum _{i=1}^n}{\displaystyle \frac{{\alpha }_1{y}_i{e}^{-{\alpha }_1\lambda y_i}}{1-e^{-{\alpha }_1\lambda y_i}}}+{\displaystyle \sum _{i=1}^n}{\displaystyle \frac{{\alpha }_2{y}_i{e}^{-{\alpha }_2\lambda y_i}}{1-e^{-{\alpha }_2\lambda y_i}}}-(\beta +1){\displaystyle \sum _{i=1}^n}{y}_i+{\displaystyle \frac{n}{\lambda }}=0,\end{array}$$

(9)

$$\begin{array}{c}{\displaystyle \frac{\mathsf{\partial }l(\mathbf{\Theta }|\mathrm{data})}{\mathsf{\partial }{\alpha }_1}}=\beta {\displaystyle \sum _{i=1}^n}\left[{\displaystyle \frac{-\frac{\lambda y_i{e}^{-\lambda ({\alpha }_1+{\alpha }_2)y_i}}{{\alpha }_1+{\alpha }_2+1}-\frac{e^{-\lambda ({\alpha }_1+{\alpha }_2)y_i}}{{({\alpha }_1+{\alpha }_2+1)}^2}+\frac{\lambda y_i{e}^{-{\alpha }_1\lambda y_i}}{{\alpha }_1+1}+\frac{e^{-{\alpha }_1\lambda y_i}}{{({\alpha }_1+1)}^2}}{\frac{e^{-\lambda ({\alpha }_1+{\alpha }_2)y_i}}{{\alpha }_1+{\alpha }_2+1}-\frac{e^{-{\alpha }_1\lambda y_i}}{{\alpha }_1+1}-\frac{e^{-{\alpha }_2\lambda y_i}}{{\alpha }_2+1}+1}}\right]\\ +{\displaystyle \sum _{i=1}^n}\left[{\displaystyle \frac{\lambda y_i{e}^{-{\alpha }_1\lambda y_i}}{1-e^{-{\alpha }_1\lambda y_i}}}\right]+{\displaystyle \frac{n({\alpha }_2+1)(1-\beta )(2{\alpha }_1+{\alpha }_2+2)}{{\alpha }_1({\alpha }_1+1)({\alpha }_1+{\alpha }_2+1)({\alpha }_1+{\alpha }_2+2)}}=0,\end{array}$$

(10)

$$\begin{array}{c}{\displaystyle \frac{\mathsf{\partial }l(\mathbf{\Theta }|\mathrm{data})}{\mathsf{\partial }{\alpha }_2}}=\beta {\displaystyle \sum _{i=1}^n}{\displaystyle \frac{-{\displaystyle \frac{\lambda y_i{e}^{-\lambda ({\alpha }_1+{\alpha }_2)y_i}}{{\alpha }_1+{\alpha }_2+1}}-{\displaystyle \frac{e^{-\lambda ({\alpha }_1+{\alpha }_2)y_i}}{{({\alpha }_1+{\alpha }_2+1)}^2}}+{\displaystyle \frac{\lambda y_i{e}^{-{\alpha }_2\lambda y_i}}{{\alpha }_2+1}}+{\displaystyle \frac{e^{-{\alpha }_2\lambda y_i}}{{({\alpha }_2+1)}^2}}}{{\displaystyle \frac{e^{-\lambda ({\alpha }_1+{\alpha }_2)y_i}}{{\alpha }_1+{\alpha }_2+1}}-{\displaystyle \frac{e^{-{\alpha }_1\lambda y_i}}{{\alpha }_1+1}}-{\displaystyle \frac{e^{-{\alpha }_2\lambda y_i}}{{\alpha }_2+1}}+1}}\\ +{\displaystyle \sum _{i=1}^n}\left[{\displaystyle \frac{\lambda y_i{e}^{-{\alpha }_2\lambda y_i}}{1-e^{-{\alpha }_2\lambda y_i}}}\right]+{\displaystyle \frac{({\alpha }_1+1)(1-\beta )n({\alpha }_1+2{\alpha }_2+2)}{{\alpha }_2({\alpha }_2+1)({\alpha }_1+{\alpha }_2+1)({\alpha }_1+{\alpha }_2+2)}}=0,\end{array}$$

(11)

and

$$\begin{array}{c}{\displaystyle \frac{\mathsf{\partial }l(\mathbf{\Theta }|\mathrm{data})}{\mathsf{\partial }\beta }}={\displaystyle \frac{n-{\sum }_{i=1}^n{d}_i}{\beta }}+{\displaystyle \sum _{i=1}^n}log\left({\displaystyle \frac{e^{-\lambda ({\alpha }_1+{\alpha }_2)y_i}}{{\alpha }_1+{\alpha }_2+1}}-{\displaystyle \frac{e^{-{\alpha }_1\lambda y_i}}{{\alpha }_1+1}}-{\displaystyle \frac{e^{-{\alpha }_2\lambda y_i}}{{\alpha }_2+1}}+1\right)\\ -\lambda \left({\displaystyle \sum _{i=1}^n}{y}_i\right)+nlog\left({\displaystyle \frac{({\alpha }_1+1)({\alpha }_2+1)({\alpha }_1+{\alpha }_2+1)}{{\alpha }_1{\alpha }_2({\alpha }_1+{\alpha }_2+2)}}\right)=0.\end{array}$$

(12)

Since Equations (9)–(12) cannot be solved analytically, the Newton–Raphson iteration approach is one of the appropriate numerical techniques that may be used to obtain the estimates. Wolfram Mathematica Version 12 has been used, through some commands, to deploy the Newton–Raphson iteration; for more details, see Mohammad et al. [9].

3.1. Approximate Confidence Interval

The asymptotic normality of the maximum likelihood estimates is applied asymptotically to determine approximate confidence intervals for TWED parameters, where approximate variances are produced based on the inverse of the observed result of a Fisher information matrix. The delta method is used to estimate these variances in the case of survival and hazard functions so that the construction of confidence intervals is practical, on a case-by-case basis, as a function of the estimated parameters; for more details see Greene [10].

The ACIs of the TWED parameters at a confidence level $\left(1-\gamma \right)\%$, $\gamma \in \left(0,1\right)$ can be given as follows:

$$\widehat{\lambda }\pm Z_{{\displaystyle \frac{\gamma }{2}}}\sqrt{\widehat{Var}\left(\widehat{\lambda }\right)},{\widehat{\alpha }}_1\pm Z_{{\displaystyle \frac{\gamma }{2}}}\sqrt{\widehat{Var}\left({\widehat{\alpha }}_1\right)}\mathrm{and}{\widehat{\alpha }}_2\pm Z_{{\displaystyle \frac{\gamma }{2}}}\sqrt{\widehat{Var}\left({\widehat{\alpha }}_2\right)},$$

while the ACI of the proportionality hazard constant $\beta ,$ is given by

$$\widehat{\beta }\pm Z_{{\displaystyle \frac{\gamma }{2}}}\sqrt{\widehat{Var}\left(\widehat{\beta }\right).}$$

The variance quantities of the MLEs $\widehat{\lambda },{\widehat{\alpha }}_1,{\widehat{\alpha }}_2$, and $\widehat{\beta }$ are estimated from the inverse of the Fisher information matrix.

Referring to the delta method approach, the variance of $\widehat{S}\left(t\right)$ and $\widehat{h}\left(t\right)$ can be approximated, respectively, by

$${\widehat{\sigma }}_{\widehat{S}\left(t\right)}^2={\left[\nabla \widehat{S}\left(t\right)\right]}^T\left[\widehat{V}\right]\left[\nabla \widehat{S}\left(t\right)\right]\mathrm{and}{\widehat{\sigma }}_{\widehat{h}\left(t\right)}^2={\left[\nabla \widehat{h}\left(t\right)\right]}^T\left[\widehat{V}\right]\left[\nabla \widehat{h}\left(t\right)\right],$$

(13)

where $\widehat{V}$ represents the inverse of the Fisher information matrix, which is a symmetric squared matrix, while $\nabla \widehat{S}\left(t\right)={\left(\begin{array}{c}{\displaystyle \frac{\mathsf{\partial }S}{\mathsf{\partial }\lambda }}\\ {\displaystyle \frac{\mathsf{\partial }S}{\mathsf{\partial }{\alpha }_1}}\\ {\displaystyle \frac{\mathsf{\partial }S}{\mathsf{\partial }{\alpha }_2}}\end{array}\right)}_{(\lambda ,{\alpha }_1,{\alpha }_2)=\left(\widehat{\lambda },{\widehat{\alpha }}_1,{\widehat{\alpha }}_2\right)}$ and $\nabla \widehat{h}\left(t\right)={\left(\begin{array}{c}{\displaystyle \frac{\mathsf{\partial }h}{\mathsf{\partial }\lambda }}\\ {\displaystyle \frac{\mathsf{\partial }h}{\mathsf{\partial }{\alpha }_1}}\\ {\displaystyle \frac{\mathsf{\partial }h}{\mathsf{\partial }{\alpha }_2}}\end{array}\right)}_{(\lambda ,{\alpha }_1,{\alpha }_2)=\left(\widehat{\lambda },{\widehat{\alpha }}_1,{\widehat{\alpha }}_2\right)}$ are the gradients of $\widehat{S}\left(t\right)$ and $\widehat{h}\left(t\right)$, respectively, with respect to $\lambda ,{\alpha }_1$ and ${\alpha }_2.$

For computational purposes, the survival and hazard functions may be written as functions in TWED parameters and the proportionality hazard constant $\beta ,$ but keep in mind that

$${\displaystyle \frac{\mathsf{\partial }S}{\mathsf{\partial }\beta }=\frac{\mathsf{\partial }h}{\mathsf{\partial }\beta }=0,}$$

which is to justify the algebraic operations when multiplying matrices; refer to Equation (13) as the square matrix $\widehat{V}$ is from the rank $4\times 4.$

3.2. Bootstrap Confidence Intervals

In this subsection, confidence intervals are proposed based on the parametric bootstrap methods where the parametric model for the data is known, $f_{Y,D}(y,d)$, where bootstrap data are sampled from $f_{Y,D}(y,d;\widehat{\lambda },{\widehat{\alpha }}_1,{\widehat{\alpha }}_2,\widehat{\beta }),$ where $\left(\widehat{\lambda },{\widehat{\alpha }}_1,{\widehat{\alpha }}_2,\widehat{\beta }\right)$ are the MLEs obtained from the original data. For the resampling process, a Wolfram Mathematica command, “RandomChoice”, is used to generate 1000 bootstrap samples based on the principle of drawing with replacement. For an explanation of how the “RandomChoice” command works, see the following URL: https://reference.wolfram.com/language/ref/RandomChoice.html, accessed on 20 July 2025. Recently, many papers have dealt with bootstrap methods based on the idea of Efron [11], such as Qin et al. [12] and Al Luhayb et al. [13]. After the bootstrap samples are generated based on the MLEs and the inference approaches have been applied to these samples, the results that represent the bootstrap estimates, say $({\widehat{\lambda }}^{*},{\widehat{\alpha }}_1^{*},{\widehat{\alpha }}_2^{*},{\widehat{\beta }}^{*},{\widehat{S}}^{*}\left(t\right),{\widehat{h}}^{*}\left(t\right))\equiv ({\widehat{\Omega }}_1^{*},{\widehat{\Omega }}_2^{*},{\widehat{\Omega }}_3^{*},{\widehat{\Omega }}_4^{*},{\widehat{\Omega }}_5^{*},{\widehat{\Omega }}_6^{*})$, are sorted, and the confidence intervals for the parameters, survival, and hazard functions are constructed in the following manner to obtain the percentile bootstrap (Boot-P) confidence intervals: let $\Phi \left(z\right)=P({\widehat{\Omega }}_k^{*}\le z)$ be the cumulative distribution function of ${\widehat{\Omega }}_k^{*},$$k=1,2,\dots ,6.$ Define ${\widehat{\Omega }}_{kBoot}^{*}={\Phi }^{-1}\left(z\right)$ for given z. The approximate bootstrap-p $100(1-\gamma )\%$ confidence interval of ${\widehat{\Omega }}_k^{*}$ is given by

$$\left[\begin{array}{ccc}{\widehat{\Omega }}_{kBoot}^{*}\left({\displaystyle \frac{\gamma }{2}}\right)& ,& {\widehat{\Omega }}_{kBoot}^{*}(1-{\displaystyle \frac{\gamma }{2}})\end{array}\right].$$

4. Bayesian Estimation

This section introduces Bayesian estimation of the TWED model with the MCMC method with the loss functions of the squared error and general entropy. The Bayesian method makes use of prior knowledge, and it is applicable in censored survival data with flexible inference and credible intervals due to uncertainty regarding parameters.

It is assumed that the prior knowledge about the parameters $\lambda ,{\alpha }_1,{\alpha }_2,$ and $\beta$ is represented by the informative gamma priors as follows:

$$\left\{\begin{array}{c}{\pi }_1\left(\lambda \right)={\displaystyle \frac{b_1^{a_1}}{\Gamma \left(a_1\right)}}{\lambda }^{a_1-1}exp\left\{-b_1\lambda \right\},a_1,b_1,\lambda >0,\\ {\pi }_2\left({\alpha }_1\right)={\displaystyle \frac{b_2^{a_2}}{\Gamma \left(a_2\right)}}{\alpha }_1^{a_2-1}exp\left\{-b_2{\alpha }_1\right\},a_2,b_2,{\alpha }_1>0,\\ {\pi }_3\left({\alpha }_2\right)={\displaystyle \frac{b_3^{a_3}}{\Gamma \left(a_3\right)}}{\alpha }_2^{a_3-1}exp\left\{-b_3{\alpha }_2\right\},a_3,b_3,{\alpha }_2>0,\\ {\pi }_4\left(\beta \right)={\displaystyle \frac{b_4^{a_4}}{\Gamma \left(a_4\right)}}{\beta }^{a_4-1}exp\left\{-b_4\beta \right\},a_4,b_4,\beta >0.\end{array}\right.$$

(14)

The joint prior density function can be written as follows:

$$\pi (\mathbf{\Theta })\propto {\lambda }^{a_1-1}{\alpha }_1^{a_2-1}{\alpha }_2^{a_3-1}{\beta }^{a_4-1}exp\left\{\begin{array}{c}-\left(b_1\lambda +b_2{\alpha }_1+b_3{\alpha }_2+b_4\beta \right)\end{array}\right\}.$$

The expressions in Equations (7) and (14) are combined to obtain the joint posterior of $\lambda ,{\alpha }_1,{\alpha }_2$ and $\beta$ as follows:

$$\begin{array}{ccc}\hfill \pi (\mathbf{\Theta }|y,d)& =& {\lambda }^{n+a_1-1}{\alpha }_1^{a_2-1}{\alpha }_2^{a_3-1}{\beta }^{a_4-1}{\left[K({\alpha }_1,{\alpha }_2)\right]}^{n(\beta +1)}\hfill \\ & \times & {\beta }^{\left(n-{\displaystyle \sum _{i=1}^n}{d}_i\right)}exp\left[\begin{array}{c}-\left(b_1\lambda +b_2{\alpha }_1+b_3{\alpha }_2+b_4\beta +\lambda (\beta +1){\displaystyle \sum _{i=1}^n}{y}_i\right)\end{array}\right]\hfill \\ & \times & {\displaystyle \prod _{i=1}^n}\left[\begin{array}{c}\left(1-e^{-{\alpha }_1\lambda y_i}\right)\end{array}\right]{\displaystyle \prod _{i=1}^n}\left[\begin{array}{c}\left(1-e^{-{\alpha }_2\lambda y_i}\right)\end{array}\right]\hfill \\ & \times & {\displaystyle \prod _{i=1}^n}{\left[\begin{array}{c}{\displaystyle \frac{e^{-\lambda ({\alpha }_1+{\alpha }_2)y_i}}{{\alpha }_1+{\alpha }_2+1}}-{\displaystyle \frac{e^{-{\alpha }_1\lambda y_i}}{{\alpha }_1+1}}-{\displaystyle \frac{e^{-{\alpha }_2\lambda y_i}}{{\alpha }_2+1}}+1\end{array}\right]}^{\beta }.\hfill \end{array}$$

(15)

The Bayesian estimates of any function of the parameters, say ${\rm Y}(\mathbf{\Theta })$, under the squared error loss (SEL) function are

$$\begin{array}{ccc}\hfill {\widehat{{\rm Y}}}_{SEL}(\mathbf{\Theta })& =& E({\rm Y}(\mathbf{\Theta }\left)\right)\hfill \\ & =& {\displaystyle \frac{{\int }_{\mathbf{\Theta }}{\rm Y}(\mathbf{\Theta })L(\mathbf{\Theta }|\mathrm{data})\times \pi \left(\mathbf{\Theta }\right)d\mathbf{\Theta }}{{\int }_{\mathbf{\Theta }}L(\mathbf{\Theta }|\mathrm{data})\times \pi \left(\mathbf{\Theta }\right)d\mathbf{\Theta }}}.\hfill \end{array}$$

(16)

The general entropy loss (GEL) function, which was proposed by Calarbria and Pulcini [14], is another loss function that can be applied. The following represents this loss function, which is a generalization of the entropy loss function:

$$L(\Phi ,\widehat{\Phi })\propto \left[\left({\displaystyle \frac{\widehat{\Phi }}{\Phi }}\right)-qln\left({\displaystyle \frac{\widehat{\Phi }}{\Phi }}\right)-1\right];q\ne 0.$$

where $\widehat{\Phi }$ is the decision rule which estimate $\Phi .$ Under the GEL function the Bayes estimate of the parameter, $\theta ,$ is given as follows:

$$\widehat{\Phi }={\left(E\left[{\Phi }^{-q}(\mathbf{\Theta })\right]\right)}^{-{\displaystyle \frac{1}{q}}}.$$

It is noted that when q is equal to $-1$, the Bayes estimators of the GEL function are reduced to those of the SEL function.

The Bayes estimates for a function $\Phi (\mathbf{\Theta }),$ employing the GEL function, can be represented as

$$\widehat{\Phi }(\mathbf{\Theta })={\left({\displaystyle \frac{{\int }_{\mathbf{\Theta }}{\Phi }^{-q}(\mathbf{\Theta })L(\mathbf{\Theta }|\mathrm{data})\times \pi \left(\mathbf{\Theta }\right)d\mathbf{\Theta }}{{\int }_{\mathbf{\Theta }}L(\mathbf{\Theta }|\mathrm{data})\times \pi \left(\mathbf{\Theta }\right)d\mathbf{\Theta }}}\right)}^{-{\displaystyle \frac{1}{q}}}.$$

(17)

The ratio of two integrals presented by Equations (16) and (17) cannot be provided in the form of a closed expression. Thus, Gibbs sampling and more generally the Metropolis–Hastings (M-H) algorithm within-Gibbs samplers are regarded as an important subclass of Markov chain Monte Carlo (MCMC) approaches. The Metropolis algorithm was first formulated by Metropolis et al. [15], and Hastings [16] later generalised the Metropolis algorithm. The complexity of Bayesian computations, in this case, can be addressed by implementing a coded software package to execute the Metropolis–Hastings (M-H) algorithm to guarantee a convergence behaviour of the estimates. In this study the “Metropolis–Hastings” coded package in Wolfram Mathematica was used: https://resources.wolframcloud.com/FunctionRepository/resources/MetropolisHastingsSequence/, accessed on 1 November 2025. The application of the MCMC method requires the conditional posterior distributions of the unknown parameters $\lambda ,{\alpha }_1,{\alpha }_2,\beta$ to be defined as follows:

Based on Equation (15), we get

$$\begin{array}{ccc}\hfill {\pi }_1\left(\lambda \right|{\alpha }_1,{\alpha }_2,\beta ;\mathrm{data})& \propto & {\lambda }^{n+a_1-1}exp\left[\begin{array}{c}-\lambda \left(b_1+(\beta +1){\displaystyle \sum _{i=1}^n}{y}_i\right)\end{array}\right]\hfill \\ & \times & {\displaystyle \prod _{i=1}^n}\left[\begin{array}{c}\left(1-e^{-{\alpha }_1\lambda y_i}\right)\end{array}\right]\times {\displaystyle \prod _{i=1}^n}\left[\begin{array}{c}\left(1-e^{-{\alpha }_2\lambda y_i}\right)\end{array}\right]\hfill \\ & \times & {\displaystyle \prod _{i=1}^n}{\left[\begin{array}{c}{\displaystyle \frac{e^{-\lambda ({\alpha }_1+{\alpha }_2)y_i}}{{\alpha }_1+{\alpha }_2+1}}-{\displaystyle \frac{e^{-{\alpha }_1\lambda y_i}}{{\alpha }_1+1}}-{\displaystyle \frac{e^{-{\alpha }_2\lambda y_i}}{{\alpha }_2+1}}+1\end{array}\right]}^{\beta }.\hfill \end{array}$$

(18)

$$\begin{array}{ccc}\hfill {\pi }_2\left({\alpha }_1\right|\lambda ,{\alpha }_2,\beta ;\mathrm{data})& \propto & {\alpha }_1^{a_2-1}{\left[{\displaystyle \frac{\left({\alpha }_1+1\right)\left({\alpha }_1+{\alpha }_2+1\right)}{{\alpha }_1\left({\alpha }_1+{\alpha }_2+2\right)}}\right]}^{n(\beta +1)}{e}^{-b_2{\alpha }_1}\hfill \\ & \times & {\displaystyle \prod _{i=1}^n}\left[\begin{array}{c}\left(1-e^{-{\alpha }_1\lambda y_i}\right)\end{array}\right]\hfill \\ & \times & {\displaystyle \prod _{i=1}^n}{\left[\begin{array}{c}{\displaystyle \frac{e^{-\lambda ({\alpha }_1+{\alpha }_2)y_i}}{{\alpha }_1+{\alpha }_2+1}}-{\displaystyle \frac{e^{-{\alpha }_1\lambda y_i}}{{\alpha }_1+1}}-{\displaystyle \frac{e^{-{\alpha }_2\lambda y_i}}{{\alpha }_2+1}}+1\end{array}\right]}^{\beta }.\hfill \end{array}$$

(19)

$$\begin{array}{ccc}\hfill {\pi }_3\left({\alpha }_2\right|\lambda ,{\alpha }_1,\beta ;\mathrm{data})& \propto & {\alpha }_2^{a_{3-1}}{\left[{\displaystyle \frac{\left({\alpha }_2+1\right)\left({\alpha }_1+{\alpha }_2+1\right)}{{\alpha }_2\left({\alpha }_1+{\alpha }_2+2\right)}}\right]}^{n(\beta +1)}{e}^{-b_3{\alpha }_2}\hfill \\ & \times & {\displaystyle \prod _{i=1}^n}\left[\begin{array}{c}\left(1-e^{-{\alpha }_2\lambda y_i}\right)\end{array}\right]\hfill \\ & \times & {\displaystyle \prod _{i=1}^n}{\left[\begin{array}{c}{\displaystyle \frac{e^{-\lambda ({\alpha }_1+{\alpha }_2)y_i}}{{\alpha }_1+{\alpha }_2+1}}-{\displaystyle \frac{e^{-{\alpha }_1\lambda y_i}}{{\alpha }_1+1}}-{\displaystyle \frac{e^{-{\alpha }_2\lambda y_i}}{{\alpha }_2+1}}+1\end{array}\right]}^{\beta }.\hfill \end{array}$$

(20)

$${\pi }_4\left(\beta \right|\lambda ,{\alpha }_1,{\alpha }_{2}data)\equiv Gamma\left(n-{\displaystyle \sum _{i=1}^n}{d}_i+a_4,\Omega \right),$$

(21)

where $\Omega =b_4-n$$lnK\left({\alpha }_1,{\alpha }_2\right)+\lambda {\displaystyle \sum _{i=1}^n}{y}_i-{\displaystyle \sum _{i=1}^n}ln\left[\begin{array}{c}1-{\displaystyle \frac{e^{-\lambda {\alpha }_1{y}_i}}{{\alpha }_1+1}}-{\displaystyle \frac{e^{-\lambda {\alpha }_2{y}_i}}{{\alpha }_2+1}}+{\displaystyle \frac{e^{-\lambda ({\alpha }_1+{\alpha }_2)y_i}}{{\alpha }_1+{\alpha }_2+1}}\end{array}\right].$ The derivation of conditional posteriors from the joint posterior distribution (15) is a common strategy in the literature to obtain the Bayesian estimates of the parameters; see, for example, Casella and Berger [8].

Since the conditional posteriors of $\lambda ,{\alpha }_1$ and ${\alpha }_2$ are unknown distributions, the MCMC approach based on Metropolis-within-Gibbs samplers is used as follows:

1. Start with ${\lambda }^{\left(o\right)},{\alpha }_1^{\left(o\right)},{\alpha }_2^{\left(o\right)},$ and ${\beta }^{\left(o\right)}$.

2. Let $j=1$.

3. Generate ${\beta }^{\left(j\right)}$ from

$$Gamma\left(n-{\displaystyle \sum _{i=1}^n}{d}_i+a_4,\Omega \right).$$

4. Using the following M-H algorithm, generate ${\lambda }^{\left(j\right)},{\alpha }_1^{\left(j\right)}$ and ${\alpha }_2^{\left(j\right)}$ from (18)–(20) with normal suggested distribution (symmetric proposals) $N({\lambda }^{\left(j-1\right)},Var\left(\lambda \right))$, $N({\alpha }_1^{(j-1)},Var\left({\alpha }_1\right))$ and $N({\alpha }_2^{\left(j-1\right)},Var\left({\alpha }_2\right))$, where $Var\left(\lambda \right)$, $Var\left({\alpha }_1\right))$, and $Var\left({\alpha }_2\right))$, respectively, can be obtained from the main diagonal in the inverse fisher information matrix.

(i) Generate a proposal ${\lambda }^{*}$ from $N({\lambda }^{\left(j-1\right)},Var\left(\lambda \right)),{\alpha }_1^{*}$ from $N({\alpha }_1^{\left(j-1\right)},Var\left({\alpha }_1\right))$ and ${\alpha }_2^{*}$ from $N({\alpha }_2^{\left(j-1\right)},Var\left({\alpha }_2\right)).$

(ii) Evaluate the acceptance probabilities

$$\begin{array}{ccc}\hfill {\rho }_{\lambda }& =& min\left[1,{\displaystyle \frac{{\pi }_1^{*}\left({\lambda }^{*}\left|{\alpha }_1^{(j-1)},{\alpha }_2^{(j-1)},{\beta }^{\left(j\right)};\mathrm{data}\right.\right)}{{\pi }_1^{*}\left({\lambda }^{(j-1)}\left|{\alpha }_1^{(j-1)},{\alpha }_2^{(j-1)},{\beta }^{\left(j\right)};\mathrm{data}\right.\right)}}\right],\hfill \\ \hfill {\rho }_{{\alpha }_1}& =& min\left[1,{\displaystyle \frac{{\pi }_2^{*}\left({\alpha }_1^{*}\left|{\lambda }^{\left(j\right)},{\alpha }_2^{(j-1)},{\beta }^{\left(j\right)};\mathrm{data}\right.\right)}{{\pi }_2^{*}\left({\alpha }_1^{(j-1)}\left|{\lambda }^{\left(j\right)},{\alpha }_2^{(j-1)},{\beta }^{\left(j\right)};\mathrm{data}\right.\right)}}\right],\hfill \\ \hfill {\rho }_{{\alpha }_2}& =& min\left[1,{\displaystyle \frac{{\pi }_3^{*}\left({\alpha }_2^{*}\left|{\lambda }^{\left(j\right)},{\alpha }_1^{\left(j\right)},{\beta }^{\left(j\right)};\mathrm{data}\right.\right)}{{\pi }_3^{*}\left({\alpha }_2^{(j-1)}\left|{\lambda }^{\left(j\right)},{\alpha }_1^{\left(j\right)},{\beta }^{\left(j\right)};\mathrm{data}\right.\right)}}\right].\hfill \end{array}$$

5. Compute ${\lambda }^{\left(j\right)},{\alpha }_1^{\left(j\right)}$ and ${\alpha }_2^{\left(j\right)}.$

6. Evaluate the reliability and hazard functions as follows:

$$\left\{\begin{array}{c}{S}^{\left(j\right)}\left(t\right)=K\left({\alpha }_1^{\left(j\right)},{\alpha }_2^{\left(j\right)}\right)\left({\displaystyle \frac{e^{-{\lambda }^{\left(j\right)}({\alpha }_1^{\left(j\right)}+{\alpha }_2^{\left(j\right)})t}}{{\alpha }_1^{\left(j\right)}+{\alpha }_2^{\left(j\right)}+1}}-{\displaystyle \frac{e^{-{\alpha }_1^{\left(j\right)}{\lambda }^{\left(j\right)}t}}{{\alpha }_1^{\left(j\right)}+1}}-{\displaystyle \frac{e^{-{\alpha }_2^{\left(j\right)}{\lambda }^{\left(j\right)}t}}{{\alpha }_2^{\left(j\right)}+1}}+1\right)e^{-{\lambda }^{\left(j\right)}t},t⩾0\\ \\ h^{\left(j\right)}\left(t\right)={\displaystyle \frac{{\lambda }^{\left(j\right)}\left(1-e^{-{\alpha }_1^{\left(j\right)}{\lambda }^{\left(j\right)}t}\right)\left(1-e^{-{\alpha }_2^{\left(j\right)}{\lambda }^{\left(j\right)}t}\right)}{1+{\displaystyle \frac{e^{-{\lambda }^{\left(j\right)}({\alpha }_1^{\left(j\right)}+{\alpha }_2^{\left(j\right)})t}}{{\alpha }_1^{\left(j\right)}+{\alpha }_2^{\left(j\right)}+1}}-{\displaystyle \frac{e^{-{\alpha }_1^{\left(j\right)}{\lambda }^{\left(j\right)}t}}{{\alpha }_1^{\left(j\right)}+1}}-{\displaystyle \frac{e^{-{\alpha }_2^{\left(j\right)}{\lambda }^{\left(j\right)}t}}{{\alpha }_2^{\left(j\right)}+1}}}},t⩾0.\end{array}.\right.$$

7. Let $j=j+1$.

8. Repeat Steps (4–6) 1000 times.

9. To guarantee the convergence to remove the influence of the selection of initial values, the first M simulated varieties are ignored. Then the selected samples are ${\lambda }^{\left(j\right)},{\alpha }_1^{\left(j\right)},{\alpha }_2^{\left(j\right)},$ and ${\beta }^{\left(j\right)},j=M+1,\dots ,L,$ for sufficiently large L, which forms an approximate posterior sample which can be used to obtain the Bayes MCMC point estimates of ${\lambda }^{\left(j\right)},{\alpha }_1^{\left(j\right)},{\alpha }_2^{\left(j\right)},$ and ${\beta }^{\left(j\right)}$ based on SEL, respectively:

$$\left.\begin{array}{c}{\widehat{\lambda }}_{B-SEL}={\displaystyle \frac{1}{L-M}}{\displaystyle \sum _{j=M+1}^L}{\lambda }^{\left(j\right)},{\widehat{{\alpha }_1}}_{MCMC}={\displaystyle \frac{1}{L-M}}{\displaystyle \sum _{j=M+1}^L}{\alpha }_1^{\left(j\right)},\\ {\widehat{{\alpha }_2}}_{MCMC}={\displaystyle \frac{1}{L-M}}{\displaystyle \sum _{j=M+1}^L}{\alpha }_2^{\left(j\right)},{\widehat{\beta }}_{MCMC}={\displaystyle \frac{1}{L-M}}{\displaystyle \sum _{j=M+1}^L}{\beta }^{\left(j\right)},\\ {\widehat{S}}_{MCMC}\left(t\right)={\displaystyle \frac{1}{L-M}}{\displaystyle \sum _{j=M+1}^L}{S}^{\left(j\right)}\left(t\right),{\widehat{h}}_{MCMC}\left(t\right)={\displaystyle \frac{1}{L-M}}{\displaystyle \sum _{j=M+1}^L}{h}^{\left(j\right)}\left(t\right).\end{array}\right\}$$

10. Now, the Bayes estimates of $\lambda ,{\alpha }_1,{\alpha }_2$ and $\beta$ under the GEL function using MCMC method are, respectively, obtained as

$$\begin{array}{c}{\widehat{\lambda }}_{MCMC}={\left[{\displaystyle \frac{1}{L-M}}{\displaystyle \sum _{j=M+1}^L}{\left({\lambda }^{\left(j\right)}\right)}^{-q}\right]}^{-{\displaystyle \frac{1}{q}}},{\widehat{{\alpha }_1}}_{MCMC}={\left[{\displaystyle \frac{1}{L-M}}{\displaystyle \sum _{j=M+1}^L}{\left({\alpha }_1^{\left(j\right)}\right)}^{-q}\right]}^{-{\displaystyle \frac{1}{q}}},\\ {\widehat{{\alpha }_2}}_{MCMC}={\left[{\displaystyle \frac{1}{L-M}}{\displaystyle \sum _{j=M+1}^L}{\left({\alpha }_2^{\left(j\right)}\right)}^{-q}\right]}^{-{\displaystyle \frac{1}{q}}},{\widehat{\beta }}_{MCMC}={\left[{\displaystyle \frac{1}{L-M}}{\displaystyle \sum _{j=M+1}^L}{\left({\beta }^{\left(j\right)}\right)}^{-q}\right]}^{-{\displaystyle \frac{1}{q}}},\\ {\widehat{S}}_{MCMC}\left(t\right)={\left[{\displaystyle \frac{1}{L-M}}{\displaystyle \sum _{j=M+1}^L}{\left(S^{\left(j\right)}\left(t\right)\right)}^{-q}\right]}^{-{\displaystyle \frac{1}{q}}},{\widehat{h}}_{MCMC}\left(t\right)={\left[{\displaystyle \frac{1}{L-M}}{\displaystyle \sum _{j=M+1}^L}{\left(h^{\left(j\right)}\left(t\right)\right)}^{-q}\right]}^{-{\displaystyle \frac{1}{q}}}.\end{array}$$

11. To compute the credible intervals of $\lambda ,{\alpha }_1,{\alpha }_2,\beta ,$$S\left(t\right)$ and $h\left(t\right),$ order ${\lambda }^{\left(i\right)},{\alpha }_1^{\left(i\right)},{\alpha }_2^{\left(i\right)},{\beta }^{\left(i\right)},$$S^{\left(i\right)}\left(t\right)$, and $h^{\left(i\right)}\left(t\right),$$i=1,2,\dots ,N.$ Then the $100(1-\gamma )\%$ credible intervals of $\psi =(\lambda ,{\alpha }_1,{\alpha }_2,\beta ,S\left(t\right),h\left(t\right))$ are given by

$$\left[\begin{array}{ccc}{\Psi }_{\left(N\gamma /2\right)}& ,& {\Psi }_{\left(N\left(1-\gamma /2\right)\right)}\end{array}\right].$$

5. Simulation Study

In general, simulation studies can play a strong role in interpreting, confirming, and comparing procedures of statistical inference when theory or real data is insufficient. A simulation study was performed to assess the performance of the proposed estimators developed in Section 3 and Section 4. Six sample sizes ($n=20,$ 40, $60,$ 80, 100, and 120) were considered, and all calculations were implemented using Wolfram Mathematica version 12. The command that was adopted for the generation of samples is “ProbabilityDistribution”. An explanation of this command can be obtained through the following URL: https://reference.wolfram.com/language/ref/ProbabilityDistribution.html, accessed on 20 November 2025. Parameters values that were used for generating the simulated samples were chosen as follows: $(\lambda ,{\alpha }_1,{\alpha }_1,\beta )=(0.12,60.30,59.18,1.2)$. The Bayesian estimates were computed based on the MCMC method hyperparameters under the SEL and GEL functions as $q=1$ for the case of the GEL function. The hyperparameters $(a_1,b_1,a_2,b_2,a_3,b_3,a_4,b_4)$ for Gamma priors were all selected equally to be $0.02,$ which expresses weakly knowledgeable priors. The survival and hazard functions were estimated at $t=2.$ The comparison of the estimates was performed using their mean square error (MSE) and bias using 12,000 simulated samples. The coverage probability (CP) and average length of confidence intervals (ALCI) were also considered in the comparison between the simulated samples.

Tracing plots of the posterior samples of the parameters calculated based on the Metropolis–Hastings algorithm are shown in Figure 3, Figure 4, Figure 5 and Figure 6. These plots depict well-mixed chains with stable fluctuations and no visible trends, indicating satisfactory convergence, which indicates that the Bayesian estimates provided were valid.

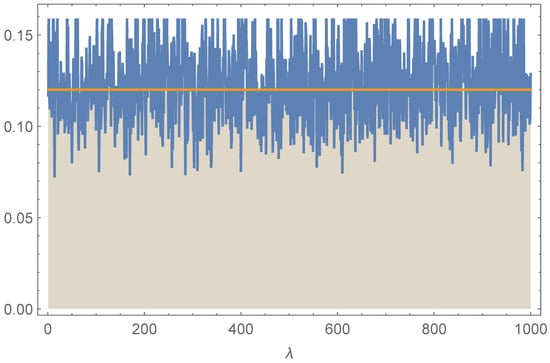
Figure 3. Tracing plots for the parameter $\lambda$.

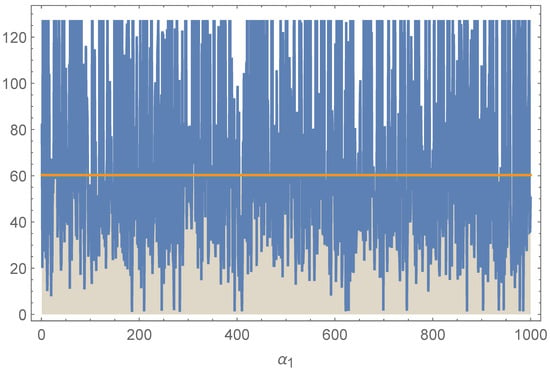
Figure 4. Tracing plots for the parameter ${\alpha }_1$.

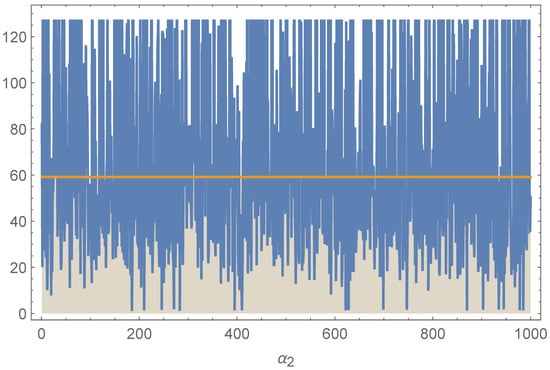
Figure 5. Tracing plots for the parameter ${\alpha }_2$.

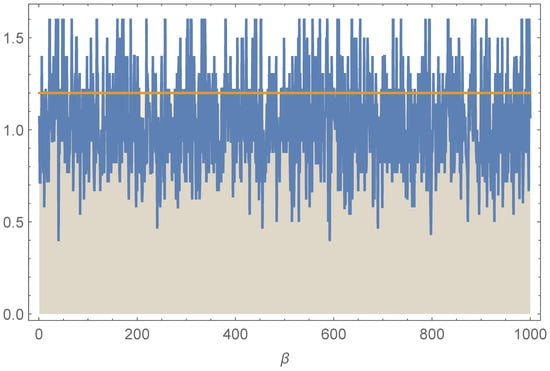
Figure 6. Tracing plots for the parameter $\beta$.

Further, the simulation results are tabulated in Table 1, Table 2, Table 3, Table 4, Table 5, Table 6 and Table 7, providing a comprehensive comparison across different methods as follows:

Table 1. Estimates for the parameter $\lambda$.

		MLE	MCMC
n			SEL	GEL
20	$\begin{array}{c}\mathrm{Bias}\\ \mathrm{MSE}\end{array}$	$\begin{array}{c}0.0209\\ 0.0787\end{array}$	$\begin{array}{c}0.0369\\ 0.0909\end{array}$	$\begin{array}{c}0.0289\\ 0.0690\end{array}$
40	$\begin{array}{c}\mathrm{Bias}\\ \mathrm{MSE}\end{array}$	$\begin{array}{c}0.0105\\ 0.0529\end{array}$	$\begin{array}{c}0.0630\\ 0.1283\end{array}$	$\begin{array}{c}0.0515\\ 0.1121\end{array}$
60	$\begin{array}{c}\mathrm{Bias}\\ \mathrm{MSE}\end{array}$	$\begin{array}{c}0.0047\\ 0.0326\end{array}$	$\begin{array}{c}0.1266\\ 0.1948\end{array}$	$\begin{array}{c}0.1052\\ 0.1713\end{array}$
80	$\begin{array}{c}\mathrm{Bias}\\ \mathrm{MSE}\end{array}$	$\begin{array}{c}0.0094\\ 0.0497\end{array}$	$\begin{array}{c}0.1486\\ 0.2346\end{array}$	$\begin{array}{c}0.1247\\ 0.2102\end{array}$
100	$\begin{array}{c}\mathrm{Bias}\\ \mathrm{MSE}\end{array}$	$\begin{array}{c}0.0085\\ 0.0524\end{array}$	$\begin{array}{c}0.1385\\ 0.2123\end{array}$	$\begin{array}{c}0.1140\\ 0.1876\end{array}$
120	$\begin{array}{c}\mathrm{Bias}\\ \mathrm{MSE}\end{array}$	$\begin{array}{c}0.0098\\ 0.0444\end{array}$	$\begin{array}{c}0.1299\\ 0.2054\end{array}$	$\begin{array}{c}0.1115\\ 0.1866\end{array}$

Table 2. Estimates for the parameter ${\alpha }_1$.

		MLE	MCMC
n			SEL	GEL
20	$\begin{array}{c}\mathrm{Bias}\\ \mathrm{MSE}\end{array}$	$\begin{array}{c}37.4065\\ 221.066\end{array}$	$\begin{array}{c}-0.019\\ 0.3879\end{array}$	$\begin{array}{c}-0.020\\ 0.3881\end{array}$
40	$\begin{array}{c}\mathrm{Bias}\\ \mathrm{MSE}\end{array}$	$\begin{array}{c}36.3892\\ 140.290\end{array}$	$\begin{array}{c}0.0220\\ 0.5350\end{array}$	$\begin{array}{c}0.0212\\ 0.5350\end{array}$
60	$\begin{array}{c}\mathrm{Bias}\\ \mathrm{MSE}\end{array}$	$\begin{array}{c}31.8405\\ 101.607\end{array}$	$\begin{array}{c}-0.022\\ 0.7941\end{array}$	$\begin{array}{c}-0.024\\ 0.7939\end{array}$
80	$\begin{array}{c}\mathrm{Bias}\\ \mathrm{MSE}\end{array}$	$\begin{array}{c}36.5644\\ 115.978\end{array}$	$\begin{array}{c}-0.005\\ 0.8626\end{array}$	$\begin{array}{c}-0.007\\ 0.8630\end{array}$
100	$\begin{array}{c}\mathrm{Bias}\\ \mathrm{MSE}\end{array}$	$\begin{array}{c}24.9429\\ 100.150\end{array}$	$\begin{array}{c}0.0095\\ 0.8017\end{array}$	$\begin{array}{c}0.0074\\ 0.8021\end{array}$
120	$\begin{array}{c}\mathrm{Bias}\\ \mathrm{MSE}\end{array}$	$\begin{array}{c}26.9121\\ 113.573\end{array}$	$\begin{array}{c}0.0297\\ 0.8860\end{array}$	$\begin{array}{c}0.0280\\ 0.8859\end{array}$

Table 3. Estimates for the parameter ${\alpha }_2$.

		MLE	MCMC
n			SEL	GEL
20	$\begin{array}{c}\mathrm{Bias}\\ \mathrm{MSE}\end{array}$	$\begin{array}{c}38.5265\\ 221.259\end{array}$	$\begin{array}{c}-0.001\\ 0.4659\end{array}$	$\begin{array}{c}-0.002\\ 0.4655\end{array}$
40	$\begin{array}{c}\mathrm{Bias}\\ \mathrm{MSE}\end{array}$	$\begin{array}{c}37.5092\\ 140.585\end{array}$	$\begin{array}{c}0.0278\\ 0.5298\end{array}$	$\begin{array}{c}0.0268\\ 0.5302\end{array}$
60	$\begin{array}{c}\mathrm{Bias}\\ \mathrm{MSE}\end{array}$	$\begin{array}{c}32.9605\\ 101.964\end{array}$	$\begin{array}{c}0.0140\\ 0.7949\end{array}$	$\begin{array}{c}0.0118\\ 0.7955\end{array}$
80	$\begin{array}{c}\mathrm{Bias}\\ \mathrm{MSE}\end{array}$	$\begin{array}{c}37.6844\\ 116.336\end{array}$	$\begin{array}{c}0.0431\\ 0.7727\end{array}$	$\begin{array}{c}0.0415\\ 0.7726\end{array}$
100	$\begin{array}{c}\mathrm{Bias}\\ \mathrm{MSE}\end{array}$	$\begin{array}{c}26.0629\\ 100.435\end{array}$	$\begin{array}{c}-0.023\\ 0.6967\end{array}$	$\begin{array}{c}-0.025\\ 0.6966\end{array}$
120	$\begin{array}{c}\mathrm{Bias}\\ \mathrm{MSE}\end{array}$	$\begin{array}{c}28.0321\\ 113.844\end{array}$	$\begin{array}{c}0.0787\\ 0.7876\end{array}$	$\begin{array}{c}0.0771\\ 0.7876\end{array}$

Table 4. Estimates for the parameter $\beta$.

		MLE	MCMC
n			SEL	GEL
20	$\begin{array}{c}\mathrm{Bias}\\ \mathrm{MSE}\end{array}$	$\begin{array}{c}-0.030\\ 0.8137\end{array}$	$\begin{array}{c}-0.108\\ 0.2803\end{array}$	$\begin{array}{c}-0.133\\ 0.3210\end{array}$
40	$\begin{array}{c}\mathrm{Bias}\\ \mathrm{MSE}\end{array}$	$\begin{array}{c}-0.201\\ 0.4878\end{array}$	$\begin{array}{c}-0.160\\ 0.3760\end{array}$	$\begin{array}{c}-0.195\\ 0.4220\end{array}$
60	$\begin{array}{c}\mathrm{Bias}\\ \mathrm{MSE}\end{array}$	$\begin{array}{c}-0.171\\ 0.3668\end{array}$	$\begin{array}{c}-0.180\\ 0.4529\end{array}$	$\begin{array}{c}-0.245\\ 0.5114\end{array}$
80	$\begin{array}{c}\mathrm{Bias}\\ \mathrm{MSE}\end{array}$	$\begin{array}{c}-0.216\\ 0.4583\end{array}$	$\begin{array}{c}-0.255\\ 0.4906\end{array}$	$\begin{array}{c}-0.312\\ 0.5436\end{array}$
100	$\begin{array}{c}\mathrm{Bias}\\ \mathrm{MSE}\end{array}$	$\begin{array}{c}-0.191\\ 0.4269\end{array}$	$\begin{array}{c}-0.167\\ 0.4008\end{array}$	$\begin{array}{c}-0.249\\ 0.4871\end{array}$
120	$\begin{array}{c}\mathrm{Bias}\\ \mathrm{MSE}\end{array}$	$\begin{array}{c}-0.212\\ 0.4486\end{array}$	$\begin{array}{c}-0.217\\ 0.4792\end{array}$	$\begin{array}{c}-0.267\\ 0.5204\end{array}$

Table 5. ALCIs and CPs for the parameters $\lambda$ and ${\alpha }_1$.

		$\mathit{\lambda }$				${\mathit{\alpha }}_1$
		Non-Bayesian		Bayesian		Non-Bayesian		Bayesian
n		90%	95%	90%	95%	90%	95%	90%	95%
20	$\begin{array}{c}\mathrm{ALCI}\\ \mathrm{CP}\end{array}$	$\begin{array}{c}3.3257\\ 0.9124\end{array}$	$\begin{array}{c}5.8786\\ 0.9433\end{array}$	$\begin{array}{c}0.0389\\ 0.8660\end{array}$	$\begin{array}{c}0.0389\\ 0.8660\end{array}$	$\begin{array}{c}718.72\\ 0.7938\end{array}$	$\begin{array}{c}852.19\\ 0.8505\end{array}$	$\begin{array}{c}0.2141\\ 0.8814\end{array}$	$\begin{array}{c}0.2141\\ 0.8814\end{array}$
40	$\begin{array}{c}\mathrm{ALCI}\\ \mathrm{CP}\end{array}$	$\begin{array}{c}2.5764\\ 0.9381\end{array}$	$\begin{array}{c}3.0699\\ 0.9639\end{array}$	$\begin{array}{c}0.0604\\ 0.7732\end{array}$	$\begin{array}{c}0.0604\\ 0.7732\end{array}$	$\begin{array}{c}648.55\\ 0.8711\end{array}$	$\begin{array}{c}772.79\\ 0.9175\end{array}$	$\begin{array}{c}0.2731\\ 0.7784\end{array}$	$\begin{array}{c}0.2731\\ 0.7784\end{array}$
60	$\begin{array}{c}\mathrm{ALCI}\\ \mathrm{CP}\end{array}$	$\begin{array}{c}0.4853\\ 0.9124\end{array}$	$\begin{array}{c}0.5782\\ 0.9588\end{array}$	$\begin{array}{c}0.1172\\ 0.6289\end{array}$	$\begin{array}{c}0.1172\\ 0.6289\end{array}$	$\begin{array}{c}552.26\\ 0.8918\end{array}$	$\begin{array}{c}658.06\\ 0.9072\end{array}$	$\begin{array}{c}0.4798\\ 0.6546\end{array}$	$\begin{array}{c}0.4798\\ 0.6546\end{array}$
80	$\begin{array}{c}\mathrm{ALCI}\\ \mathrm{CP}\end{array}$	$\begin{array}{c}1.4151\\ 0.9286\end{array}$	$\begin{array}{c}1.6862\\ 0.9847\end{array}$	$\begin{array}{c}0.1165\\ 0.602\end{array}$	$\begin{array}{c}0.1165\\ 0.602\end{array}$	$\begin{array}{c}616.42\\ 0.9133\end{array}$	$\begin{array}{c}734.51\\ 0.9184\end{array}$	$\begin{array}{c}0.4596\\ 0.6327\end{array}$	$\begin{array}{c}0.4596\\ 0.6327\end{array}$
100	$\begin{array}{c}\mathrm{ALCI}\\ \mathrm{CP}\end{array}$	$\begin{array}{c}2.2594\\ 0.8838\end{array}$	$\begin{array}{c}2.6922\\ 0.9293\end{array}$	$\begin{array}{c}0.1169\\ 0.6313\end{array}$	$\begin{array}{c}0.1169\\ 0.6313\end{array}$	$\begin{array}{c}605.16\\ 0.8838\end{array}$	$\begin{array}{c}721.09\\ 0.8990\end{array}$	$\begin{array}{c}0.4446\\ 0.6667\end{array}$	$\begin{array}{c}0.4446\\ 0.6667\end{array}$
120	$\begin{array}{c}\mathrm{ALCI}\\ \mathrm{CP}\end{array}$	$\begin{array}{c}1.1164\\ 0.8835\end{array}$	$\begin{array}{c}1.3303\\ 0.9272\end{array}$	$\begin{array}{c}0.0996\\ 0.6214\end{array}$	$\begin{array}{c}0.0996\\ 0.6214\end{array}$	$\begin{array}{c}636.14\\ 0.8883\end{array}$	$\begin{array}{c}758.01\\ 0.9029\end{array}$	$\begin{array}{c}0.4523\\ 0.6505\end{array}$	$\begin{array}{c}0.4523\\ 0.6505\end{array}$

Table 6. ALCIs and CPs for the parameters ${\alpha }_2$ and $\beta$.

		${\mathit{\alpha }}_2$				$\mathit{\beta }$
		Non-Bayesian		Bayesian		Non-Bayesian		Bayesian
n		90%	95%	90%	95%	90%	95%	90%	95%
20	$\begin{array}{c}\mathrm{ALCI}\\ \mathrm{CP}\end{array}$	$\begin{array}{c}818.72\\ 0.7990\end{array}$	$\begin{array}{c}752.19\\ 0.8608\end{array}$	$\begin{array}{c}0.2346\\ 0.8660\end{array}$	$\begin{array}{c}0.2346\\ 0.8660\end{array}$	$\begin{array}{c}42.169\\ 0.8093\end{array}$	$\begin{array}{c}85.800\\ 0.9021\end{array}$	$\begin{array}{c}0.1444\\ 0.8814\end{array}$	$\begin{array}{c}0.1444\\ 0.8814\end{array}$
40	$\begin{array}{c}\mathrm{ALCI}\\ \mathrm{CP}\end{array}$	$\begin{array}{c}648.55\\ 0.8866\end{array}$	$\begin{array}{c}772.79\\ 0.9175\end{array}$	$\begin{array}{c}0.2924\\ 0.7784\end{array}$	$\begin{array}{c}0.2924\\ 0.7784\end{array}$	$\begin{array}{c}10.448\\ 0.8247\end{array}$	$\begin{array}{c}52.500\\ 0.8763\end{array}$	$\begin{array}{c}0.1811\\ 0.7732\end{array}$	$\begin{array}{c}0.1811\\ 0.7732\end{array}$
60	$\begin{array}{c}\mathrm{ALCI}\\ \mathrm{CP}\end{array}$	$\begin{array}{c}552.26\\ 0.8918\end{array}$	$\begin{array}{c}658.06\\ 0.9124\end{array}$	$\begin{array}{c}0.5096\\ 0.6804\end{array}$	$\begin{array}{c}0.5096\\ 0.6804\end{array}$	$\begin{array}{c}2.9072\\ 0.7629\end{array}$	$\begin{array}{c}4.1100\\ 0.8299\end{array}$	$\begin{array}{c}0.3183\\ 0.6804\end{array}$	$\begin{array}{c}0.3183\\ 0.6804\end{array}$
80	$\begin{array}{c}\mathrm{ALCI}\\ \mathrm{CP}\end{array}$	$\begin{array}{c}616.42\\ 0.9133\end{array}$	$\begin{array}{c}734.51\\ 0.9184\end{array}$	$\begin{array}{c}0.4155\\ 0.6582\end{array}$	$\begin{array}{c}0.4155\\ 0.6582\end{array}$	$\begin{array}{c}7.6507\\ 0.7449\end{array}$	$\begin{array}{c}7.9170\\ 0.8469\end{array}$	$\begin{array}{c}0.3040\\ 0.6429\end{array}$	$\begin{array}{c}0.3040\\ 0.6429\end{array}$
100	$\begin{array}{c}\mathrm{ALCI}\\ \mathrm{CP}\end{array}$	$\begin{array}{c}605.16\\ 0.8939\end{array}$	$\begin{array}{c}721.09\\ 0.8990\end{array}$	$\begin{array}{c}0.4222\\ 0.6566\end{array}$	$\begin{array}{c}0.4222\\ 0.6566\end{array}$	$\begin{array}{c}8.4138\\ 0.7727\end{array}$	$\begin{array}{c}5.2500\\ 0.8384\end{array}$	$\begin{array}{c}0.3251\\ 0.6818\end{array}$	$\begin{array}{c}0.3251\\ 0.6818\end{array}$
120	$\begin{array}{c}\mathrm{ALCI}\\ \mathrm{CP}\end{array}$	$\begin{array}{c}636.14\\ 0.8932\end{array}$	$\begin{array}{c}758.01\\ 0.9078\end{array}$	$\begin{array}{c}0.4534\\ 0.6650\end{array}$	$\begin{array}{c}0.4534\\ 0.6650\end{array}$	$\begin{array}{c}6.2389\\ 0.7087\end{array}$	$\begin{array}{c}5.8190\\ 0.8301\end{array}$	$\begin{array}{c}0.3200\\ 0.6796\end{array}$	$\begin{array}{c}0.3200\\ 0.6796\end{array}$

Table 7. ALCIs and CPs for the functions $S\left(t\right)$ and $h\left(t\right)$ at $t=2$.

		$\mathit{S}\left(\mathit{t}\right)$				$\mathit{h}\left(\mathit{t}\right)$
		Non-Bayesian		Bayesian		Non-Bayesian		Bayesian
n		90%	95%	90%	95%	90%	95%	90%	95%
20	$\begin{array}{c}\mathrm{ALCI}\\ \mathrm{CP}\end{array}$	$\begin{array}{c}2.7388\\ 0.8454\end{array}$	$\begin{array}{c}3.3708\\ 0.8918\end{array}$	$\begin{array}{c}0.0472\\ 0.8660\end{array}$	$\begin{array}{c}0.0472\\ 0.8660\end{array}$	$\begin{array}{c}2.6059\\ 0.8969\end{array}$	$\begin{array}{c}3.5956\\ 0.9278\end{array}$	$\begin{array}{c}0.0389\\ 0.8660\end{array}$	$\begin{array}{c}0.0389\\ 0.8660\end{array}$
40	$\begin{array}{c}\mathrm{ALCI}\\ \mathrm{CP}\end{array}$	$\begin{array}{c}2.6880\\ 0.9124\end{array}$	$\begin{array}{c}3.2030\\ 0.9588\end{array}$	$\begin{array}{c}0.0726\\ 0.7732\end{array}$	$\begin{array}{c}0.0726\\ 0.7732\end{array}$	$\begin{array}{c}2.9310\\ 0.9330\end{array}$	$\begin{array}{c}3.4925\\ 0.9639\end{array}$	$\begin{array}{c}0.0604\\ 0.7732\end{array}$	$\begin{array}{c}0.0604\\ 0.7732\end{array}$
60	$\begin{array}{c}\mathrm{ALCI}\\ \mathrm{CP}\end{array}$	$\begin{array}{c}0.5361\\ 0.9072\end{array}$	$\begin{array}{c}0.6388\\ 0.9691\end{array}$	$\begin{array}{c}0.1239\\ 0.6289\end{array}$	$\begin{array}{c}0.1239\\ 0.6289\end{array}$	$\begin{array}{c}0.5395\\ 0.9124\end{array}$	$\begin{array}{c}0.6429\\ 0.9588\end{array}$	$\begin{array}{c}0.1172\\ 0.6289\end{array}$	$\begin{array}{c}0.1172\\ 0.6289\end{array}$
80	$\begin{array}{c}\mathrm{ALCI}\\ \mathrm{CP}\end{array}$	$\begin{array}{c}1.4409\\ 0.9235\end{array}$	$\begin{array}{c}1.7170\\ 0.9286\end{array}$	$\begin{array}{c}0.1206\\ 0.6020\end{array}$	$\begin{array}{c}0.1206\\ 0.6020\end{array}$	$\begin{array}{c}1.5588\\ 0.9286\end{array}$	$\begin{array}{c}1.8574\\ 0.9847\end{array}$	$\begin{array}{c}0.1165\\ 0.6020\end{array}$	$\begin{array}{c}0.1165\\ 0.6020\end{array}$
100	$\begin{array}{c}\mathrm{ALCI}\\ \mathrm{CP}\end{array}$	$\begin{array}{c}2.3495\\ 0.8535\end{array}$	$\begin{array}{c}2.7997\\ 0.9343\end{array}$	$\begin{array}{c}0.1208\\ 0.6313\end{array}$	$\begin{array}{c}0.1208\\ 0.6313\end{array}$	$\begin{array}{c}2.5883\\ 0.8838\end{array}$	$\begin{array}{c}3.0842\\ 0.9293\end{array}$	$\begin{array}{c}0.1169\\ 0.6313\end{array}$	$\begin{array}{c}0.1169\\ 0.6313\end{array}$
120	$\begin{array}{c}\mathrm{ALCI}\\ \mathrm{CP}\end{array}$	$\begin{array}{c}1.1569\\ 0.8932\end{array}$	$\begin{array}{c}1.3785\\ 0.9369\end{array}$	$\begin{array}{c}0.1092\\ 0.6214\end{array}$	$\begin{array}{c}0.1092\\ 0.6214\end{array}$	$\begin{array}{c}1.2279\\ 0.8786\end{array}$	$\begin{array}{c}1.4631\\ 0.9223\end{array}$	$\begin{array}{c}0.0996\\ 0.6214\end{array}$	$\begin{array}{c}0.0996\\ 0.6214\end{array}$

• Table 1: Across all sample sizes, MLE of $\lambda$ performs better, having less bias and less MSE than both Bayesian SEL and GEL. The Bayesian SEL and GEL estimators, on the contrary, have greater bias and MSE. Generally, it is evident that MLE is better at estimating the parameter $\lambda .$
• Table 2: MLE yields very large bias and MSE for ${\alpha }_1$, especially at smaller sample sizes, whereas SEL and GEL deliver much lower bias with far better accuracy. Consequently, as n increases, Bayesian estimates remain steady and continue to outperform MLE, highlighting their robustness.
• Table 3: The estimation of ${\alpha }_2$ again shows extremely high bias and MSE with MLE; however, Bayesian SEL and GEL consistently provide low bias and strong accuracy. As a result, performance becomes particularly stable for n ≥ 80, with both Bayesian methods producing almost identical outcomes.
• Table 4: Although all methods exhibit negative bias when estimating $\beta$, they remain close in overall performance, and MSE decreases steadily with larger n. Therefore, estimator stability improves for all approaches, and no major differences emerge among the three methods.
• Table 5: Bayesian intervals for $\lambda$ and ${\alpha }_1$ are much shorter than non-Bayesian ACIs, yet their coverage probabilities remain relatively stable across sample sizes. Nevertheless, the non-Bayesian ACIs achieve slightly higher coverage but only at the expense of extremely wide intervals, especially for ${\alpha }_1$.
• Table 6: For ${\alpha }_2$, non-Bayesian ACIs are extremely wide, while Bayesian intervals are far more practical and precise, leading to acceptable, though slightly lower, coverage due to their tightness. Similarly, $\beta$ intervals benefit from increased precision in Bayesian estimation, particularly at larger sample sizes.
• Table 7: Bayesian intervals for $S\left(2\right)$ and $h\left(2\right)$ remain consistently shorter than their MLE-based counterparts, while coverage probabilities stay stable across all n. Hence, Bayesian methods provide clearly more precise functional estimates, especially once n reaches 80 or higher.

According to the results of the simulation, MLE is not always better than Bayesian estimation in small samples, particularly when its bias and MSE values are large (${\alpha }_1$ and ${\alpha }_2$). Bayesian SEL and GEL do not change with n and are obviously better with larger sample sizes, especially above $n=80$. These gains are particularly pronounced in interval estimation and the estimation of such functionals as the survival and hazard functions, where Bayesian techniques provide more accurate inferences as the sample size increases. This simulation further enables the Bayesian approaches to have more power to be used in the real data context, as discussed in the next section on the HIV survival dataset.

6. Data Analysis

In this section, a real-data application is presented to demonstrate the practicality of the proposed methods. Survival times (in months) of 100 HIV-infected patients were analysed, as reported by Hosmer and Lemeshow [17], with right-censored observations indicated by a plus sign.

Observed HIV dataset

5

$6+$

8

3

22

$1+$

7

9

3

12

$2+$

12

1

15

34

1

4

$19+$

$2+$

6

$60+$

$7+$

$60+$

11

$2+$

5

$4+$

$1+$

13

$3+$

$2+$

$1+$

30

$7+$

$4+$

$8+$

$2+$

$9+$

36

$3+$

$9+$

$3+$

35

$8+$

$1+$

$5+$

11

$56+$

$2+$

$3+$

15

$1+$

10

$1+$

$3+$

$2+$

32

$3+$

$10+$

11

$3+$

$7+$

$5+$

31

$5+$

58

$1+$

$2+$

1

$3+$

43

$1+$

14

$4+$

54

$1+$

$1+$

$8+$

$5+$

$1+$

$1+$

$2+$

$7+$

$1+$

10

$24+$

$7+$

$12+$

$4+$

57

$3+$

$5+$

$7+$

$6+$

$1+$

2

10

$3+$

53

$12+$

Shakhatreh [6] showed that the TWED is a well-fitted distribution to the HIV data and compared the TWED with other alternatives like generalised Weibull, weighted exponential, Weibull, and log logistic distributions. The comparison showed that the TWED was superior in fitting the data through the Akaike information criterion (AIC).

The important statistics of the HIV survival data are provided in Table 8, which shows a high right skewness ($2.06$) and much variability. Mean survival is $11.36$ months but with a median survival of a mere five months, implying that the majority of patients have short survival periods, with some of them having far longer survival periods. The dispersion index (D $=20.56$ as D is the ratio of the variance to the average) shows the presence of over-dispersion since the value is considerably above 1. This implies that the variability in survival distribution is higher than it would be under a regular exponential model, where the risk is constant.

Table 8. Summary statistics for HIV data.

Min.	Max.	Median	Mean	Variance	D	Skewness
1	60	5	$11.36$	$233.59$	$20.56$	$2.06$

These observations can be supported by Figure 7 with the major concentration in the histogram of the patients with low survival times, and the data is skewed, with the boxplot showing extreme survival times. The combination of the numerical and graphical evidence supports the necessity of a flexible surviving distribution, such as the TWED, that fits such heterogeneity and skewed behaviour in the data.

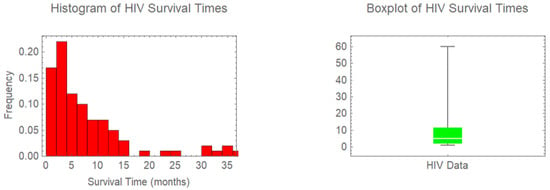
Figure 7. Histogram and boxplot of HIV data.

Both classical (MLE) and Bayesian (SEL and GEL) methods were used with the the same dataset, which makes it possible to directly compare the obtained point estimates, confidence intervals, and predictive functions, including survival and hazard rates. This empirical framework explains and complements the results of the simulation in Section 5.

In Table 9, point estimates are given in the MLE and Bayesian approaches of $(\lambda ,{\alpha }_1,{\alpha }_2,\beta )$ under SEL and GEL functions. The findings demonstrate that there is a strong association in all the techniques and little variation. Specifically, the $\lambda$ estimates are almost equal (about $0.0577$), and the same could be said about $\beta$ (it varies around 0.582–0.587). This strengthens the validity of both Bayesian and classical methods.

Table 9. Different point estimates for $(\lambda ,{\alpha }_1,{\alpha }_2,\beta )$.

Parameters	$\mathit{MLE}$	$\mathit{MCMC}\mathbf{-}\mathit{SEL}$	$\mathit{MCMC}\mathbf{-}\mathit{GEL}$
$\lambda$	$0.0575863$	$0.0577271$	$0.0577266$
${\alpha }_1$	$60.95800$	$60.099300$	$60.086400$
${\alpha }_2$	$60.95800$	$63.321000$	$63.313000$
$\beta$	$0.587390$	$0.5827630$	$0.5827580$

As illustrated in Figure 8, the PDF curves using MLE, SEL, and GEL estimations are almost the same, with slight distinctions only in the early parts of the distribution. This tight fit indicates the strength of the TWED fit and proves that both the Bayesian and classical analysis methodologies provide consistent inferences to the HIV survival data.

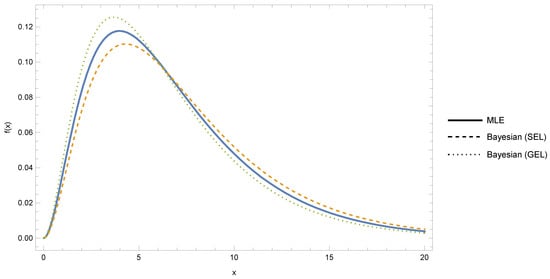
Figure 8. PDF based on MLE, SEL, and GEL estimates of the TWED parameters.

Table 10 provides $95\%$ confidence intervals and their length. The Bayesian yield results in much narrower intervals than the non-Bayesian (bootstrap) method. As an example, the credible interval of the $\lambda$ is much smaller (length $\approx 0.00055$) than the bootstrap interval (length $\approx 0.04377$). This finding indicates that Bayesian methods yield interval estimates that are narrower, and it confirms the trend seen in the simulation study.

Table 10. The 95% confidence intervals for $(\lambda ,{\alpha }_1,{\alpha }_1,\beta )$.

	ACI	Length	Bootstrap	Length	CRI	Length
$\lambda$	$0.04326,0.07190$	$0.02862$	$0.04061,0.08438$	$0.04377$	$0.05735,0.05790$	$0.00055$
${\alpha }_1$	$-15.469,137.385$	$152.854$	$35.3586,93.6671$	$58.3085$	$58.5735,61.8349$	$3.26143$
${\alpha }_2$	$-15.469,137.385$	$152.854$	$35.3586,93.6671$	$58.3085$	$62.3287,64.3229$	$1.99424$
$\beta$	$0.34894,0.82584$	$0.47691$	$0.36998,0.85196$	$0.48198$	$0.58053,0.58638$	$0.00586$
$S\left(2\right)$	$0.88825,0.93822$	$0.04997$	$0.87919,0.93824$	$0.05904$	$0.91231,0.91334$	$0.00103$
$h\left(2\right)$	$0.04325,0.07172$	$0.02847$	$0.04045,0.08382$	$0.04337$	$0.05726,0.05781$	$0.00056$

The results focus on the significance of early intervention and lifelong care, and a conjoint impression of risk and survival during early HIV progression is presented in terms of the probability of $S\left(2\right)$ and $h\left(2\right)$. At two months, the probability of survival $S\left(2\right)$ in HIV patients will be about $0.913$, which translates to the fact that more than $91\%$ of the HIV patients will survive until after the two months. The hazard rate $h\left(2\right)$ is approximated to be $0.0575$, which implies that if a patient survives to two months, that person will have a risk of dying of $5.75\%$ at that instance. Bayesian techniques, particularly in GEL, give very precise approximations; this kind of statistical accuracy increases the confidence of clinical expectations and planning.

7. Conclusions

The TWED is explored in this paper in terms of its role as a strong model for analysing censored data of HIV survival. Using the classical and the Bayesian approaches of estimation, the TWED is demonstrated to capture a large array of hazard behaviour, providing relevant information on patient survival. Bayesian estimation was more accurate, and narrower credible intervals were obtained, especially when using the general entropy Loss. As shown in Section 6, the model gave consistent survival probabilities and hazard rates, thus indicating its practical applicability. The above observations justify the importance of high-tech statistical methods in the study of disability-related healthcare and long-term care planning. In the future, the associations of the survival risk factors might be further clarified in the context of a regression-based TWED model including covariates. The robustness of the model could further be tested through comparative studies with alternative distributions. The simulation study was performed on large sample sizes $(n=80,100,120)$ to demonstrate the dependence of the performance of the estimators on the amount of data. These findings prove that Bayesian estimators (symmetric SEL and GEL) converge to MLE, yielding smaller intervals with confident coverage. Figure 1 and Figure 2 graphically show the influence of the parameters of the simulation on the PDF and hazard functions. It is also shown in Figure 4 that the fitted curves of the PDF of estimates of MLE, symmetric SEL, and GEL are almost identical to the HIV data, which indicates the consistency of these estimation methods and the stability of the TWED model in real data.