Early-Stage Prediction of Steel Weight in Industrial Buildings Using Neural Networks

Abstract

In industrial building projects, steel is the main material used to create sturdy structures that have large open spaces without many columns in the center of the building. To estimate the cost of constructing a building before it enters the detailed design stage, engineers and stakeholders must have the right tools and guidelines. Steel is an important construction material used at high volumes in industrial buildings, and it plays a significant role in determining the total cost of a project. This study develops and evaluates an artificial neural network (ANN) model based on multilayer perceptron (MLP) to predict the weight of steel structures in industrial buildings. The data collected include actual projects from 180 industrial building projects, using parameters that influence the weight of steel. The findings show that the ANN method can accurately estimate the weight of steel at an early stage in the building project, even before the detailed design phase. It was found that ANN has the ability to predict the weight of steel for industrial buildings with an excellent degree of accuracy, with a coefficient of correlation (R²) of 94.85% and prediction accuracy (PA) of 94.23%. This indicates that the relationship between the independent and dependent variables of the developed models is good and the predicted values from the forecast model fit with the real-life data.

1. Introduction

Steel structures have long been a popular choice for symmetrical industrial buildings due to their durability, strength, and cost-effectiveness. Such structures allow for the efficient use of open space, which is required by most industrial buildings, making steel ideal for use in the construction of warehouses, factories, and other industrial facilities [1,2]. In addition, steel structures can easily be customized and adapted to meet the specific needs of a project, allowing for efficient construction and flexibility in terms of design. With advancements in technology and construction techniques, steel structures continue to be a reliable and versatile option for industrial buildings [1]. Steel structures also offer sustainability benefits, as they are often made from recycled materials and can be recycled at the end of their lifespan. This makes them a more environmentally friendly option compared to traditional building materials. Additionally, steel structures can be erected quickly, reducing construction time and costs [3]. Overall, the versatility, durability, and sustainability of steel structures mean that they are a top choice for industrial buildings in today’s market.

Many researchers have applied the neural network approach in various fields of engineering prediction and optimization. However, research on the use of neural networks to predict the weight of steel in the construction world is still very limited.

In this study, we developed an ANN model to predict the weight of steel in industrial building projects at the conceptual stage, depending on historical data, of projects implemented in Indonesia between 2010 and 2024 to help users predict the weight of steel at the early stage of the construction of industrial buildings with a high level of accuracy.

The choice of an artificial neural network (ANN) utilizing a multilayer perceptron (MLP) architecture was driven by its established capability to represent intricate, nonlinear correlations among design parameters. Unlike dimensionality reduction methods such as principal component analysis (PCA) or t-distributed stochastic neighbor embedding (t-SNE), which focus on feature extraction or visualization, an artificial neural network (ANN) offers a direct predictive mapping from input to output. While PCA can reduce input dimensionality, our dataset consists of only seven important characteristics, making dimensionality reduction unnecessary. Furthermore, an artificial neural network can intrinsically obtain relevant feature combinations through its hidden layers. Future research may involve integrating PCA or t-SNE with an ANN as a preprocessing technique to improve training efficiency, especially with the availability of larger datasets containing additional parameters.

2. Applications of Artificial Neural Networks in Weight Prediction

In 1943, McCulloch and Pitts created the first artificial neural network paradigm for programming [4]. McCulloch’s and Pitts’s network constitutes the foundational model for all those developed thereafter. In 1960, with the McCulloch–Pitts neuron model, Rosenblatt [5] developed a direct representation of real neurons, termed the perceptron. Rosenblatt’s perceptron comprises responsive units and is linked to single-layer neurons introduced by McCulloch and Pitts. ANN has been applied in various fields of structural engineering. These applications include studies on the evaluation of beam damage location [6], the influence of various design parameters on the seismic performance [7], the evaluation of the capacity and strength of structural components [8,9,10], the study of the inelastic distortional buckling capacity of CFS elements [11], the prediction of the moment–rotation behavior of semi-rigid composite joints [12], the assessment of the bond strength between steel and concrete in reinforced concrete [13], material behavior modeling [14], concrete corrosion in sewer systems [15], and moment-resisting frame structures [16]. This variety of examples shows that the application of the ANN method is not limited to a particular field; rather, this method can be used in various fields of structural engineering.

At the conceptual stage, predicting the weight of a steel structure is a crucial element of an industrial building project. An early, accurate estimation of the cost of the project helps to support stakeholders in the decision-making process [17,18,19], allowing them to choose adequate alternatives and avoid misjudging solutions. In industrial building projects, various parameters influence the steel weight per unit area of a structure, such as the span, length, height, rafter pitch, structure type, and type of roof. Moreover, the accuracy of predicting the weight of a steel structure is a key factor in the success of a construction project, also affecting the stakeholders’ decision-making process [20]. However, it is difficult to quickly and accurately predict the weight of a steel structure at the conceptual stage because the drawings and documentation are generally incomplete. For this reason, AI techniques have been developed to accurately estimate the weight of steel with the limited project information available at the early stages.

Our previous research, entitled “Prediction of steel structure weight can be achieved using artificial neural network (ANN)” [16], showed that an ANN can accurately predict the weight of steel structures, which can be crucial for estimating building costs and construction time, and ensuring that the project runs well and in a sustainable way. While many studies have investigated the application of artificial neural networks (ANNs) in structural engineering, research especially aimed at the early-stage prediction of steel weight for industrial structures is still few. This research utilized ANN on a constrained dataset with few parameters, primarily concentrating on building height and span. This study fills this research gap by employing a much bigger dataset of 180 finished buildings that includes seven important design factors: span, eaves height, building length, bay spacing, rafter pitch, structural type, and roof type. The suggested model seeks to facilitate conceptual design decisions by providing rapid and precise steel weight estimations. Recent machine learning applications in construction [21] show that AI-based methods could accurately learn nonlinear relationships between design parameters.

3. Methods

3.1. Neural Network Models

New approaches based on computer systems theory that simulate the learning effects of the human brain, such as artificial neural networks (ANNs), have grown in popularity. The ANN is an artificial intelligence technique that takes a computational approach inspired by the way the human brain processes information; it studies how to make computers solve problems by learning from a set of data [22,23]. Figure 1 shows a biological neuron in comparison to an artificial neural network.

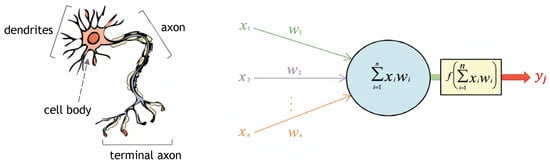
Figure 1. A biological neuron in comparison to an artificial neural network [24].

ANNs operate differently to computer programs that necessitate explicit and precise instructions. Artificial neural networks possess the capacity to learn from a multitude of defined examples, akin to human learning [24]. Artificial neural networks (ANNs), commonly referred to as neural networks, provide a system and methodology for computational machine learning aimed at representing knowledge and subsequently utilizing the acquired knowledge to forecast the output response of a complex system. This system comprises numerous process units termed “neurons”, which are combined to solve problems together and transmit information through synapses, as shown in Figure 2. In this network, if a neuron is damaged, other neurons can compensate for its absence. This network is like a biological cell that can learn and adapt based on collective input. Learning in this system occurs in an adaptive way, namely by using examples. The weights of synapses are changed in terms of new entries, and the system will generate the correct response by ignoring the incorrect entries. Learning inside this system occurs adaptively; utilizing data examples, synaptic weights are adjusted with the introduction of fresh data, enabling the system to produce accurate replies while disregarding erroneous inputs.

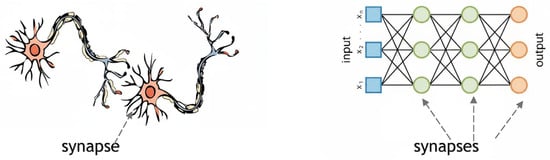
Figure 2. A biological synapse and ANN synapses [24].

The artificial neuron receives input impulses and produces output signals. All data from the surrounding environment or an output from other neurons can be used as an input signal. A model of an artificial neuron is shown in Figure 3.

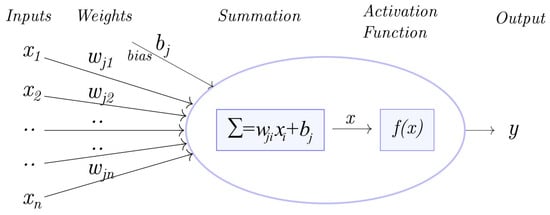
Figure 3. Model of artificial neuron.

3.2. Architecture of Neural Network

A neural network is composed of numerous mutually connected neurons grouped in layers. The complexity of the network is determined by the number of layers. Between the input (first) and the output (last) layer, a network can have one or several hidden layers (Figure 4). The function of the input layer is to receive data from the environment. The data are processed in the hidden layers and sent to the output layer.

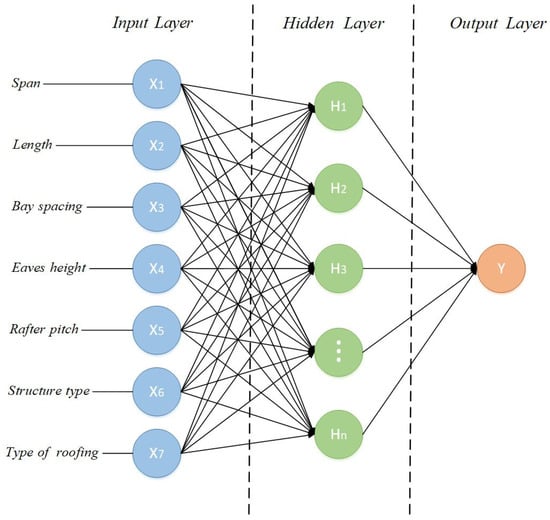
Figure 4. Model artificial neural network.

The final outputs from the network are the neuron activations from the last layer, which constitute the solution to the analyzed problem. The input data can have any form or type. The fundamental principle is that for each piece of data, we must have only one input value. Depending on the problem’s type, the network can have one or few outputs.

3.3. Weight Coefficients

Weight coefficients are fundamental components of all neural networks. They express the relative importance of each neuron’s input and determine the input’s ability to stimulate the neurons [25,26,27,28].

Every input neuron has its own weight coefficient. We compute the input signal from each neuron by multiplying the weight coefficients with the input signals and summing the results. The input data are marked as x_i, and the appropriate weight coefficients are marked as w_ij, as shown in Figure 4. Neurons register the summed input impulse, which is equal to the sum of all inputs, as shown in Equation (1).

$$\sum =w_{ij}{x}_i+b$$

(1)

The main purpose of the activation function is to determine whether the result from the summation inputs from Equation (2) can generate an output. This function is related to the neurons from the hidden layers. Almost every nonlinear function can be used as an activation function, but a common practice is to use the sigmoid function (log sigmoid and hyperbolic tangent), as demonstrated with Equation (2).

$$f(x)={\displaystyle \frac{1}{1+e^{-x}}}$$

(2)

A crucial property of neural networks is their capacity to modify weights based on historical input, which is the network’s learning process.

3.4. Neural Network Training Process

Artificial neural networks possess several fundamental characteristics, notably their learning ability, which aligns them with real-world processes and human cognition, alongside their capacity to identify connections within chaotic and incomprehensible data and their generalization ability. Therefore, network parameters such as number of hidden layers, number of hidden nodes, transfer functions, and learning rules were trained multiple times to produce the best weights for the model.

The training process of neural networks involves the periodic transmission of data through the network and the comparison of the received input values with the anticipated ones. If a discrepancy exists between those values, an adjustment of the weight coefficient (change in the neuron connections) must be implemented. This procedure is reiterated several times until the network responds as desired, or until all weight coefficients from the training data are fully adjusted. When the network produces accurate outputs for the entirety of the training data, it can be classified as a trained network. After the training process, the network should be able to generate outputs for new input data that are different from the training ones [29,30,31].

The learning and training processes within neural networks are crucial to ensuring their effectiveness in addressing engineering prediction challenges.

4. Methodology

This study employs a case study approach using an earned value dataset comprising 180 historical cases of industrial building projects from engineering institutions, contractors, and consultants in Indonesia. Multiple models are built and trained with different structures using the ANN model created in Python 3.8.0. To assure reproducibility, we established a fixed random seed to guarantee deterministic outcomes. Input parameters were standardized by min-max scaling to the range [0, 1]. The model was executed in Python 3.8.0 utilizing TensorFlow 2.0, trained for 200 epochs with a batch size of 32, a learning rate of 0.001, and the Adam optimizer (β1 = 0.9, β2 = 0.999). The data was arbitrarily allocated to 85% for training and 15% for testing. The average performance indicators (R², MSE, MAPE, PA) were documented after each experiment was conducted three times.

4.1. Data Collection

The data collection method used in this study is based on direct and indirect historical data. Table A1 in the Appendix A shows 180 industrial building constructions collected between 2010 and 2024 from engineering institutions, consultants, and contractors in Indonesia. Furthermore, the data are analyzed, in addition to the information on the type of structure and the weight per square meter obtained by forecasting techniques such as regression modeling and neural networks used as tools for prediction and optimization in various fields of project management knowledge. Thus, this study is based on the scientific foundations set by previous studies; we also use historical data analysis as a methodological basis. In addition, the use of historical data helps us to identify relationships between the main factors that influence the value parameters obtained from public building projects to make estimates for new projects used for validation purposes. A total of 180 industrial building projects were included in the dataset, which is statistically adequate for training a supervised learning model with seven input parameters. The number of samples should be at least 10–20 times the number of model parameters, the sample size in this study exceeds the recommended minimum. Data quality was ensured by cleaning for outliers and missing values: projects with incomplete geometric data, inconsistent unit usage, or extreme steel weights outside three standard deviations from the mean were excluded. The final dataset represents a balanced distribution of portal frame and portal truss structures and different roofing types. All data were validated through cross-checking with engineering consultants and project records.

In the questionnaire, the respondents were expected to provide the following details: information regarding the significant influence of industrial building information (see Figure 5), such as span, length, bay spacing, height, rafter pitch, structure type, and type of roof, on the steel weight per unit area of the building. Structure type, such as a portal frame or portal truss, is illustrated in Figure 6.

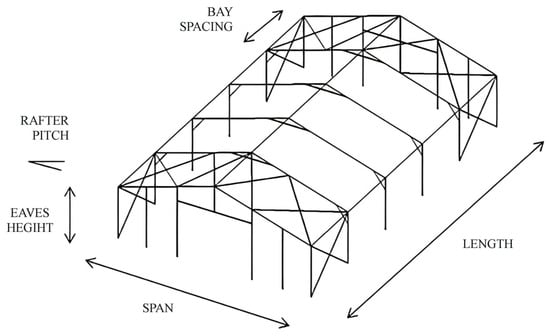
Figure 5. Geometry of symmetrical portal frames.

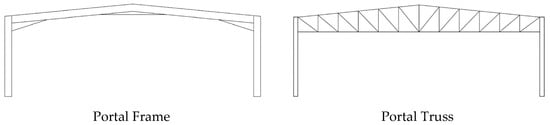
Figure 6. Structure Type.

The total weight of the structure includes the weight of the beams, columns, connections, base plates, etc. At the end, by dividing the total weight value by the building’s covered area, the weight of steel structures per unit area of the building was calculated and implemented.

Considering the importance of accuracy in the implementation of the network, 15% of the designed data were assigned to testing to ensure that the program would not face any problems in the processing of the final response. The range of variations in the input parameters for AAN is summarized in Table 1. Network training was performed after the division of the database.

Table 1. Design parameters.

Design Parameter	Definition	Range
X1	Span	8–45 m
X2	Length	36–96 m
X3	Bay spacing	4–8 m
X4	Eaves height	5–8 m
X5	Rafter pitch	10–15°
X6	Structure Type	Portal frame (1), portal truss (2)
X7	Type of Roofing	Metal sheet (1), Upvc sheet (2) Metal sheet, solar panel (3) Upvc sheet, solar panel (4)

4.2. Performance Evaluation

Four methods were used to evaluate the performance: mean squared error (MSE), mean absolute percent error (MAPE), coefficient of determination (R²), and prediction accuracy (PA). MSE, MAPE, R², and PA can be calculated by Equations (3)–(6).

$$MSE={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n(O_i-P_i}{)}^2$$

(3)

$$MAPE={\displaystyle \frac{{\displaystyle \sum _{i=1}^n\left|\frac{O_i-P_i}{O_i}\right|}}{n}}\times 100\%$$

(4)

$$R^2=1-{\displaystyle \frac{{\displaystyle \sum _{i=1}^n{(O_i-P_i)}^2}}{{\displaystyle \sum _{i=1}^n(O_i-}\overline{O}{)}^2}}$$

(5)

PA = 100 − MAPE

(6)

where O_i represents the original data or the observed/actual data, P_i represents the predicted data or modeled data, Ō represents the mean of the observed data, n represents the total number of data in each stage of the training and test trials, and PA represents the prediction accuracy. The ANN was implemented in Python 3.8.0 (TensorFlow) using a multilayer perceptron (MLP) architecture. The hidden layer employed the ReLU activation function, while the output layer used a linear activation function. For model validation, the dataset was randomly divided into 85% training data and 15% testing data, ensuring unbiased evaluation in each run.

5. Results and Discussion

Model validation is a very important step in the steel weight prediction model to test its accuracy; this includes testing and evaluating the developed model with some validation or test data. The validation data are taken randomly from the dataset and should not enter into model development. This study used 30 datasets to check the accuracy of the model. We also evaluated the validity of the derived equation of the model. Regression plot of predicted vs. actual steel weight displayed in Figure 7 and ANN training vs. validation loss displayed in Figure 8.

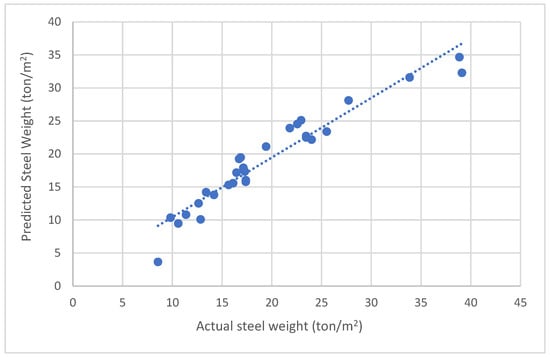
Figure 7. Regression plot of predicted vs. actual steel weight.

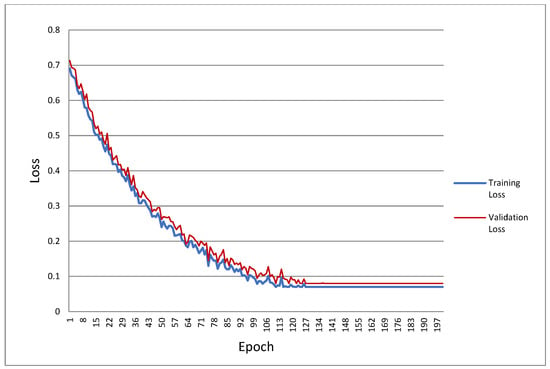
Figure 8. Training vs. validation loss.

Table 2 shows the results of the validation process. It shows test data for actual steel weight and ANN model prediction. The developed model (7-8-1) predicts an accuracy (PA) of more than 94.23%. Therefore, the performance of the developed model was considered to be more than satisfactory.

Table 2. Actual steel weight and ANN model prediction.

No.	Actual Steel (ton/m2)	ANN Model (7-4-1)	Prediction Accuracy (%)	ANN Model (7-6-1)	Prediction Accuracy (%)	ANN Model (7-8-1)	Prediction Accuracy (%)	ANN Model (7-10-1)	Prediction Accuracy (%)
1	23.45	21.40	91.27	22.40	95.53	22.70	96.81	22.80	4.47
2	22.94	22.80	99.40	25.70	89.25	25.10	91.39	25.10	10.75
3	16.87	19.30	87.39	18.90	89.24	18.70	90.19	18.50	10.76
4	13.39	15.30	87.54	13.60	98.49	13.60	98.49	13.60	1.51
5	16.70	20.50	81.47	17.10	97.67	17.30	96.54	17.70	2.33
6	17.14	18.60	92.14	17.10	99.78	17.00	99.19	16.90	0.22
7	24.00	21.90	91.26	21.10	87.93	21.60	90.01	21.40	12.07
8	16.10	16.30	98.77	14.10	87.58	14.30	88.82	14.20	12.42
9	27.71	25.90	93.45	28.40	97.58	28.00	98.98	28.00	2.42
10	14.18	16.00	88.59	14.10	99.47	13.90	98.06	14.00	0.53
11	11.37	14.30	79.48	12.10	93.93	11.10	97.67	11.70	6.07
12	9.81	14.50	67.66	11.30	86.81	10.70	91.68	11.40	13.19
13	27.71	25.90	93.45	28.40	97.58	28.00	98.98	28.00	2.42
14	10.60	13.50	78.48	11.00	96.32	10.80	98.10	12.00	3.68
15	33.84	28.20	83.33	32.60	96.33	32.60	96.33	32.60	3.67
16	16.45	16.40	99.71	16.00	97.28	16.50	99.68	16.40	2.72
17	19.42	19.90	97.56	21.40	90.72	21.60	89.88	21.70	9.28
18	22.56	24.70	91.34	23.30	96.83	23.70	95.20	23.00	3.17
19	38.85	29.10	74.90	34.40	88.54	34.50	88.79	34.70	11.46
20	17.28	16.50	95.50	17.20	99.55	17.50	98.73	17.60	0.45
21	12.84	14.10	91.06	11.80	91.91	11.60	90.35	12.20	8.09
22	25.52	23.20	90.92	23.60	92.49	23.40	91.71	24.00	7.51
23	23.45	20.90	89.14	22.80	97.24	23.40	99.80	23.80	2.76
24	21.80	22.20	98.19	22.60	96.45	23.20	93.96	24.70	3.55
25	15.66	16.80	93.19	15.20	97.09	15.30	97.73	15.10	2.91
26	17.37	15.80	90.94	15.20	87.49	15.80	90.94	15.40	12.51
27	39.10	27.90	71.35	32.10	82.09	32.10	82.09	31.90	17.91
28	17.37	16.10	92.67	14.60	84.03	15.00	86.34	14.70	15.97
29	8.55	12.30	69.54	9.50	90.04	9.10	94.00	9.80	9.96
30	12.63	15.00	84.21	12.20	96.59	12.20	96.59	12.80	3.41
			88.13%		93.39%		94.23%		93.37%

From the regression value of 0.9485 found by ANN (7-8-1), outlined in Table 3, it can be seen that the predicted values from the testing data in the ANN model are very close to the target value. A network with eight neurons in the hidden layer has the smallest error, so this type of network is chosen as the best for predicting the steel weight per square meter. The performance results are collected in Table 3 and displayed in Figure 9, showing that the prediction accuracy of the chosen ANN model (7-8-1) is 94.23%.

Table 3. Neural network testing result.

	ANN	ANN	ANN	ANN	ANN	ANN	ANN
	(7-4-1)	(7-5-1)	(7-6-1)	(7-7-1)	(7-8-1)	(7-9-1)	(7-10-1)
R2	0.9051	0.9121	0.9426	0.9448	0.9485	0.9421	0.9409
MSE	12.676	9.206	4.132	4.168	3.717	3.913	4.147
MAPE	13.710	10.744	6.859	6.352	5.933	6.813	6.990
Prediction Accuracy	88.13%	90.23%	93.39%	93.85%	94.23%	93.52%	93.36%

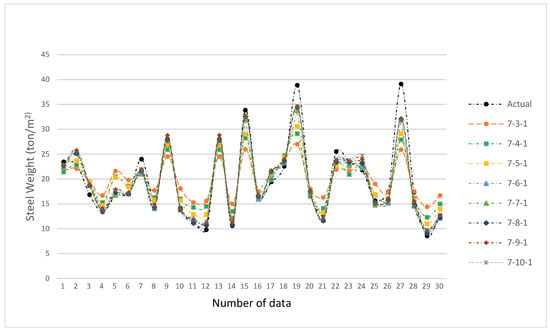
Figure 9. Comparison of ANN prediction with actual steel weight.

Table 4 shows ANOVA results for design parameters, indicate that span and eaves height are the two most influential predictors of steel weight (p < 0.01), followed by length and bay spacing (p < 0.05). Rafter pitch shows a weaker but still meaningful effect (p ≈ 0.07), while categorical variables (structure type and roof type) are significant at p < 0.10 when encoded as one-hot vectors. This finding emphasizes the importance of span optimization at the early design stage, as it has the greatest impact on steel consumption and overall structural efficiency.

Table 4. ANOVA Results for Design Parameters.

No.	Factor	F	p-Value
1.	Span	24.8	0.000
2.	Eaves Height	19.7	0.000
3.	Length	7.6	0.008
4.	Bay Spacing	5.4	0.022
5.	Rafter Pitch	3.3	0.072
6.	Structure Type	2.9	0.089
7.	Roof Type	2.4	0.12

A sensitivity study based on perturbation analysis of normalized inputs corroborates the ANOVA findings: span exhibits the largest marginal effect, and then eaves height, length, and bay spacing, displayed in Figure 10. This alignment between statistical and sensitivity perspectives helps explain the high predictive performance of the 7-8-1 MLP.

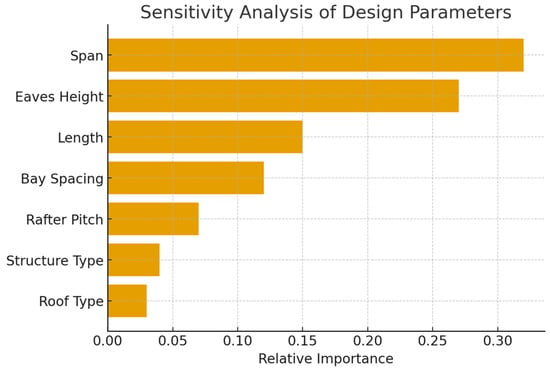
Figure 10. Sensitivity analysis of design parameters.

6. Conclusions

In this study, we aimed to develop an ANN model for predicting the preliminary design phase structural steel weight of industrial building projects in Indonesia. This model helps to assist the stakeholders involved in industrial building projects, such as owners, consultants, and contractors, with obtaining structural steel weights during the preliminary design phase before moving on to the main design phase.

The model that provided the most accurate results was the supervised learning artificial neural network multilayer perceptron (MLP) model with a backpropagation algorithm. This model was structured with one input layer that included seven input neurons, one hidden layer that contained eight hidden neurons, and one output neuron that represented the predicted steel weight, activation function, and backpropagation algorithm.

The accuracy performance of the adopted model was recorded at 94.234%; the model performed well, and no significant difference was discerned between the estimated output and the actual steel weight. This model is capable of providing excellent estimates and predictions of structural steel weight at a project’s early stage.

There are two potential developments that will be considered in future research. Combining optimization techniques such as genetic algorithms or particle swarm optimization could improve predictive accuracy, convergence rate, and model generalization. Furthermore, expanding the existing project dataset to include a broader and more diverse sample from different geographies and construction types could improve model generalization. This improvement would be more adaptable and broadly applicable to predicting steel weight in construction projects while simultaneously improving predictive accuracy.