Abstract
Collective intelligence systems have demonstrated considerable potential in dynamic adversarial environments due to their distributed, self-organizing, and highly robust characteristics. The crux of an efficacious defense lies in establishing a dynamically adjustable, non-uniform defense structure through the differentiation of internal member roles. The proposed model is a heterogeneous-swarm adaptive-defense model based on symmetry breaking and skin effect. The model draws from symmetry theory, incorporating the skin effect of conductor currents and the hierarchical structural characteristics of biological groups, such as starlings. The construction of a radially symmetric dynamic hierarchical swarm structure is achieved by assigning different types of individuals with distinct safety radius preferences. Secondly, the principle of symmetry breaking is employed to establish a phase transition mechanism from radial symmetry to directed defense, thereby achieving an adaptive barrier formation algorithm. This algorithm enables the defensive group to assess threat characteristics and dynamically adjust defense resource deployment. The simulation results obtained from this study validate the phase transition process from continuous rotational symmetry to directed defense. This process demonstrates the barrier formation mechanism and ensures the safety and integrity of the core units within the group.
1. Introduction
Collective systems, which demonstrate intricate collective behavior through local interactions among a substantial number of relatively elementary individuals, have been the subject of considerable interest in interdisciplinary research for some time. The phenomenon of self-organization and emergence [1,2] is at the core of their appeal. In this process, simple rules governing interactions between individuals can spontaneously generate macroscopic ordered structures and functions, thus circumventing the necessity of global control or predefined blueprints. The modeling of collective systems is imperative for comprehending their fundamental mechanisms and for the subsequent design of application systems. In preliminary studies, Reynolds’ [3] Boids model effectively replicated the flight behavior of bird flocks by employing three fundamental rules: separation, alignment, and aggregation. That model established the theoretical foundation for collective system modeling, with subsequent studies building upon and refining it [4]. Vicsek [5,6] and others proposed models focusing on the alignment and phase transition phenomena of self-driven particles under noise influence. This transition from a disordered state to a collective alignment state can be conceptualized as a phase transition in a non-equilibrium system, which can be interpreted as spontaneous symmetry breaking [7]. Jadbabaie [8] and others explained the behavior observed in the Vicsek model and found that moving autonomous agents could achieve coordination through nearest-neighbor rules without centralized coordination. Additionally, they proposed the seminal leader–follower protocol [9], which provides a theoretical analysis of alignment and consensus issues in the context of changing network topologies. The emergent behavior exhibited by these models bears a striking resemblance to that observed in other self-organizing systems within the fields of physics and mathematics. To illustrate, within the Kuramoto model, which consists of coupled oscillators, the occurrence of symmetry and symmetry-breaking phenomena can also be observed. Synchronized oscillator clusters have been observed to exhibit one of three distinct states: consensus, polarization, or fragmentation. These states bear a striking resemblance to the formation process of opinion clusters in sociophysical models, such as equality (symmetry) and majority (symmetry breaking) [10]. Its symmetry breaking is a spontaneous mode formation in phase space based on the relative phase relations between oscillators. In the model proposed by Couzin et al. [11], individuals attempt to maintain the minimum distance from other individuals (regional repulsion). In the absence of avoidance behaviors, these individuals tend to be attracted to and align with others, a phenomenon known as regional attraction and regional orientation. It was demonstrated that heterogeneous stratification could emerge spontaneously through differences in individual interaction regions. However, this stratification was essentially a mechanical spatial ordering based on individual parameter differences and lacked explicit functional role assignment. Subsequently, Olfati-Saber [12,13] and others advanced a rigorous mathematical framework, proposing swarm algorithms that encompassed leader following, obstacle avoidance, and formation control. They explored the role of collective potential energy in shaping group behavior and analyzed its convergence and stability. While that rigorous framework supported a synergistic response by the group, this usually implied a holistic maneuver by the entire formation. Lennard-Jones [14] addressed the problem of molecular fields using the state equation of gases, demonstrating that many gases could be explained by assuming that both the repulsive and attractive components of molecular fields followed a power-law relationship with distance. These classical models established a substantial foundation for subsequent studies of more complex behaviors. Recent studies have focused on mechanisms generating layered structures through drift–diffusion interactions. For instance, Auricchio et al. [15] proposed a nonlocal Fokker–Planck-type model employing nonlocal, discontinuous drift while maintaining constant diffusion. That model explicitly computed quasi-steady-state distributions, proving the existence, uniqueness, and positivity of global solutions while providing precise convergence rates and numerical validation. Another study [16] investigates a class of Fokker–Planck models featuring linear drift and time-dependent diffusion coefficients. It demonstrates the emergence of layered structures through drift–diffusion interactions, providing asymptotic analysis and numerical results.
In the domain of swarm intelligence applications, swarm-based offensive and defensive strategies have emerged as a prominent research focus. Researchers are dedicated to exploring how groups can effectively collaborate, protect themselves, or safeguard critical assets when facing hostile targets or complex threats. A comprehensive exploration of cooperative defense strategies, pursuit–evasion game models, and group-versus-group combat algorithms has been conducted. In their seminal work, Ran et al. [17] advanced a decentralized multi-agent coordination design method based on bee swarm intelligence. This pioneering approach facilitated autonomous collaboration among drone swarms in electronic defense scenarios. Chipade et al. [18] proposed a multi-modal solution to defend a circular protection zone against widespread attacks from a group of risk-taking and risk-averse attackers. Shahid et al. [19] explored the offensive and defensive decision-making issues between drone swarms when attacking aircraft carriers in open seas. In their seminal work, Zhang et al. [20] advanced a multi-agent, multi-level distributed defense system design for the collaborative defense tasks of multiple unmanned surface vessels. Alqudsi et al. [21] have highlighted recent advancements in the coordinated control of swarm flying robots, noting that distributed systems can rapidly respond to environmental changes through local advantages, a characteristic that is particularly important in large-scale swarm systems. Furthermore, to address the decision-making challenges inherent in swarm-based conflicts, researchers have developed novel algorithmic frameworks to address complex decision-making problems in offensive–defensive scenarios [22]. The implementation of these defensive strategies is contingent upon the formation and maintenance of specific functional formations in space, with symmetry playing a pivotal role in this process [23]. For instance, formations surrounding high-value assets inherently manifest circular symmetry [24]. In recent years, research in the field of engineering has yielded the development of distributed algorithms capable of achieving symmetrical pattern formation without the necessity of a global planner. A two-stage paradigm, designated SymSwarm, facilitates the formation of a symmetrical formation around a central point within a specified area by a swarm of mobile robots through distributed communication. This method exhibits resilience to the presence of obstacles in the environment [25]. This engineering implementation is not merely theoretical; rather, it reflects evolutionary selection in nature. The V-shaped symmetrical formation formed by flocks of geese during flight is an efficient pattern that emerges when individuals follow local rules under the constraint of a limited field of view [26]. Consequently, the construction of symmetrical formations in engineering systems can be regarded as an effective design principle that draws inspiration from biological principles to achieve robustness.
In group-based adversarial scenarios, individual heterogeneity is a critical factor that cannot be overlooked. Heterogeneous groups, composed of individuals with differing abilities, resources, roles, or behavioral preferences, often exhibit greater adaptability and task performance capabilities than homogeneous groups [27]. Gao et al. [28] contemplated heterogeneous teams with numerical and resilience advantages (e.g., differing individual health points) in UGV cluster conflicts and formulated corresponding conflict algorithms using MARL. Zhen et al. [29] developed a collaborative target allocation algorithm for heterogeneous UAV clusters in task allocation, with the objective of optimizing multiple metrics, including flight distance, time, target survival rate, and load balancing. Xue et al. [30] designed a smooth, bounded mixed potential energy function with uncertain parameters to study the effects of individual and group differences (such as sensing radius, force, obstacle avoidance, and tracking capabilities) on swarm and obstacle avoidance movements. They also explored the potential of “highly influential” mutants as leaders. Wei [31] took into consideration the differences in social distances between individuals, divided the group into multiple sub-groups, and designed a multi-virtual leader swarm algorithm to address collision and obstacle avoidance problems from a differential game theory perspective. Heterogeneous drone swarms exhibit distinctive advantages in leader–follower formations, wherein leader drones can land and traverse complex terrain while concurrently functioning as both aerial and ground robots [32]. In heterogeneous target capture tasks, homogeneous robot swarms exhibit robust, flexible, and scalable performance through adaptive density interaction mechanisms [33]. Heterogeneous swarms demonstrate distinct advantages in defense applications due to their capacity to more effectively adapt to complex tasks and environments. Kaminka et al. [34] demonstrated through a generalized fully cooperative game model that heterogeneous foraging groups could achieve better performance through adaptive role differentiation. Furthermore, in the context of resource allocation problems, such as spectrum sharing, heterogeneous multi-agent deep reinforcement learning algorithms have demonstrated potential in addressing complex group coordination issues [35]. These studies provide important theoretical foundations for designing more flexible and efficient heterogeneous group defense systems.
Another concept closely related to group defense is risk perception and spatial positioning. The “Selfish Herd Theory” in ecology, proposed by W. D. Hamilton in 1971 [36], suggests that individuals within a group tend to minimize their own risk of predation by moving to safer locations, such as the center of the group. This results in a higher exposure to threats for individuals on the periphery [37]. This self-organizing process, driven by individual risk-avoidance behavior, gives rise to efficient collective defense structures in nature. To illustrate, in flocks of starlings, bird density in the peripheral regions is often greater than in the central regions, forming a structure with a dense outer layer and a relatively loose inner layer [38]. As indicated by the extant literature, birds located at the periphery of a group demonstrate heightened vigilance and tend to reposition themselves to reduce risk [39]. This structural element not only facilitates coordination among individuals but, more crucially, enables rapid internal information transmission, manifesting wave propagation phenomena [40]. Consequently, the group can respond promptly and consistently to external stimuli (e.g., predators). The transmission of information in an efficient manner, coupled with a hierarchical structure, offers significant insights that are instrumental in the design of robust group defense systems. In recent years, there has been notable progress in the field of research on the subject of selfish herd theory. Yang et al. [41] found that the physical performance of individuals in crowded selfish herds affects their adaptability, and group movement becomes the ultimate effect of crowded selfish herds. This theoretical development provides a novel framework for understanding the intricate relationship between individual behavior and collective emergence within a group. Intriguingly, this biological defense mechanism finds a compelling analogy in physics, specifically the skin effect [42,43,44,45]. This effect describes the phenomenon in which high-frequency alternating current primarily flows along the surface of a conductor, resulting in a reduction in current density in the core region of the conductor. This core region is, to a certain degree, “protected” from the impact of external strong currents. Whether it is the layered structure of starlings or the skin effect in conductors, their essence is to achieve effective protection of the interior by forming a heterogeneous structure where the outer layer bears the pressure and the core is protected. These phenomena are not merely simple analogies but can be unified under the physical realization of symmetry breaking. These phenomena exemplify a fundamental engineering principle: the exploitation of symmetry breaking. Systems have been observed to spontaneously transition from a high-symmetry state to a low-symmetry yet functionally superior structure under the influence of external pressure or internal heterogeneity [46]. In recent years, this principle has been explicitly applied to the domain of engineering design. In the domain of soft robotics, for instance, researchers have employed the buckling of actuators under pressure (a manifestation of symmetry breaking) to achieve complex hand manipulation with minimal control inputs [47]. In this context, symmetry breaking is no longer regarded as a defect to be corrected; rather, it is recognized as a fundamental characteristic that can be harnessed and utilized.
Despite the substantial advancements in the field of group systems modeling, existing research exhibits notable deficiencies in the design of defense mechanisms. A significant number of models prioritize homogeneous groups or heterogeneous groups with predefined roles, while comparatively less attention is devoted to spontaneous functional differentiation driven by differences in individual intrinsic attributes. Moreover, traditional aggregation models based on simple attraction–repulsion rules, while capable of forming groups, often have defense formations that are easily breached when faced with organized invasions. Recent research has further underscored the significance of enhancing the operational resilience of group systems, particularly in dynamic environments where systems necessitate greater adaptability and robustness [48]. The objective of this paper is to draw inspiration from the behaviors of biological groups and the physical skin effect, in conjunction with symmetry theory, to propose a heterogeneous group defense model based on symmetry-breaking mechanisms. This model utilizes individuals’ risk aversion levels or safety needs (parameterized by the safety radius d) as the fundamental source of heterogeneity, thereby driving the spontaneous formation of a layered defense system that protects the core region under symmetry constraints. In the event of a threat, the system undergoes a transition from a radially symmetric state to a directional defense state. This design offers a novel modeling approach for heterogeneous group defense and aligns with ecological principles, such as the “selfish herd theory,” in terms of outcomes. Specifically, the core region becomes safer due to the “buffer” provided by the outer layers. The primary contributions of this paper are as follows.
- (1)
- A theoretical framework for fast, controllable, and radially symmetric spontaneous hierarchical defense structures with a clear functional division of labor in heterogeneous groups using explicit radial forces inspired by a form of physical skinning effect;
- (2)
- A threat response model based on symmetry-breaking mechanisms is proposed, enabling an intelligent transition from passive sensing to active countermeasures.
- (3)
- A dynamic adaptive barrier defense strategy is developed, enabling the group to perceive and analyze threat characteristics and to dynamically adjust the scale, position, and intensity of the defense barrier accordingly.
- (4)
- The efficacy of the proposed method is systematically substantiated through a series of simulation experiments. These experiments demonstrate the method’s capacity to form stable structures and achieve intelligent defense. Consequently, these experiments reveal the emergent defense mechanisms underlying the model.
2. System Model
2.1. Classic Clustering Model
In the classic Olfati-Saber swarm model [12], each individual (referred to as an -agent) is described by its position and velocity . Its dynamical equations can typically be expressed as:
where is the control input for agent i. In discrete-time simulations, the velocity and position at the next time step are typically updated by calculating the resultant force. The goal of -agents is to form a desired configuration called an -lattice, where each agent maintains an ideal distance d from its neighbors.
The control input consists of three components and can be expressed as:
The initial term is founded on gradient-based attraction–repulsion forces. denotes the set of neighbors within the perception range r of individual i. The linear constant from to is represented by . The potential energy function is represented by . The phenomenon of attraction or repulsion is determined by the relationship between the distance between individuals and the expected safe distance. The specific form of is , where , and a, b, c are tuning parameters. Together, these form the pair potential function , which has a minimum value at the desired distance . The second term is known as the velocity consensus term. In this context, denotes an element of the adjacency matrix, thereby representing the connection strength between individuals i and j. The third term constitutes the navigation feedback term. This term is provided by virtual -agents (representing the group goal) that guide the entire group towards the goal and help maintain the group’s overall cohesion, thus avoiding fragmentation.
The interaction term founded on the potential function is a specific instance of what is broadly termed an aggregation potential in the collective behavior literature. This concept, which models social interactions through attraction and repulsion forces, is fundamental to many models of self-organization. While the Olfati-Saber framework explicitly builds the control law around such a potential, the related Cucker–Smale model, which focuses primarily on velocity alignment, is often extended with similar potential-based terms to ensure collision avoidance and formation cohesion. The heterogeneous-group adaptive-defense model based on symmetry breaking and skin effect proposed in this paper is based on the interaction framework of the classic model. The introduction of symmetry constraints, individual heterogeneity, and specific hierarchical driving mechanisms enables the exploration of a self-organizing approach to forming a heterogeneous group structure with specific defensive functions (core area protection).
2.2. System Dynamics and Overall Control Framework
Each individual in the group is modeled as an autonomous decision-making entity. The state of each individual i is described in a two-dimensional plane by its position vector, denoted , and its velocity vector, denoted . The motion of the agents follows Newton’s second law, with their acceleration determined by the net force acting on them and their mass :
The update of an individual’s position and velocity as a function of time t can be expressed as:
Among them, is the simulation time step. The resultant force constitutes the fundamental element of the entire model. It is a comprehensive control input composed of multiple mechanical component vectors with clear physical or sociological significance. The overarching objective of this design is to ensure the maintenance of structural integrity, the establishment of a unified goal orientation, the facilitation of dynamic adaptation, and the implementation of effective countermeasures against external threats within the group, all of which are to be executed in a coordinated manner.
From a more fundamental level, the dynamics of this swarm system are constrained by a universal physical law common to electromagnetism—the local conservation law. In electromagnetism, the local conservation of charge is described by the current continuity equation, , which indicates that any change in charge density must be accompanied by a flow of charge. Likewise, since the total number of individuals in this model is conserved (individuals are neither created nor destroyed), their number density, , and particle flux, , must also strictly adhere to the same continuity equation: . This shared, fundamental conservation law provides a solid theoretical basis for situating the problem of swarm dynamics within a field-theory-like physical framework. The local interaction forces in the model (such as ) are the microscopic mechanisms that drive the particle flux, . These micro-dynamics ultimately work in concert at the macroscopic level to maintain a stable swarm structure that satisfies the constraints of the continuity equation.
The complete mathematical expression for the combined force is as follows:
Among these, denotes the intra-group interaction force, responsible for maintaining the basic cohesion of the group and the safe distance between individuals. is the virtual leader interaction force, providing the group with a global goal orientation, regulated by the weighting coefficient . The function is responsible for the activation of the skin effect indicator, which is set to 1 in the model. This constant force maintains the radially symmetric hierarchical structure. denotes the radial force of the skin effect, and signifies the corresponding velocity-damping force. The function serves as the indicator for the activation of the defense barrier. The value of is 1 when individual i is designated as a barrier unit, and 0 in all other cases. is the tangential force exerted by the barrier individual, and is the repulsive force exerted by the barrier individual toward threats.
Subsequent sections provide detailed mathematical definitions for each component in the formula.
2.3. Defensive Structure Design Based on the Principle of Symmetry
The efficiency of the group defense system is fundamentally derived from the synergistic integration of its inherent symmetrical design and dynamic symmetry-breaking mechanism. The symmetrical design of this model is reflected in three aspects:
The initial concept is geometric symmetry, wherein the defense group assumes a radially symmetrical multilayer ring structure, with a virtual leader positioned at the center of symmetry. The position vector of each individual i relative to the center of the group can be expressed as:
Among these, represents the geometric center of the group (virtual leader position), denotes the distance from an individual to the center, and signifies the azimuth angle. The radially symmetric design guarantees the equitable allocation of defensive resources, thereby establishing a foundational framework for subsequent adaptive modifications.
The second is interactive symmetry, where the potential energy function between individuals exhibits distance symmetry, i.e., , ensuring the balance between action and reaction forces. Furthermore, the information propagation mechanism exhibits isotropy in the initial state, satisfying the following condition:
The third is dynamical symmetry. In the absence of external threats, the Hamiltonian of the system exhibits rotational invariance, signifying that the energy of the system remains constant under rotation at any angle. In the event of a perceived threat, the system initiates a spontaneous symmetry-breaking process. The introduction of the threat direction vector disrupts the initial radial symmetry, thereby inducing the formation of a directional barrier:
Among them, denotes the defense strength distribution in the direction, signifies the threat direction angle, and represents the symmetry-breaking strength parameter.
2.4. Radial Symmetry’s Spontaneous Layering Mechanism Driven by Skin Effect
The present study draws inspiration from the collective defensive wisdom exhibited by flocks of starlings in biological systems when facing external threats, specifically the formation of a dynamic protective structure characterized by a tightly packed outer layer and a loosely structured core [38]. Although empirical studies indicate that natural flocks of starlings typically exhibit anisotropic rather than perfectly symmetrical structures, they consistently demonstrate this hierarchical principle of protecting the core. From a modeling perspective, this biological layering principle is translated into an idealized, radially symmetric, multi-ring system where each annular layer distributes around a common symmetry center (a virtual leader). This symmetric configuration serves as a theoretical baseline, enabling clear analysis of the system’s transition to directional, asymmetric defense—symmetry breaking—upon detecting threats. Therefore, we propose a model based on symmetry theory with skinning effects, whose core mechanisms are rooted in intrinsic heterogeneity and symmetry constraints within the group and driven by local interaction rules. The model’s symmetry design ensures that, in the equilibrium state, individuals with the same safety radius are statistically uniformly distributed on a circular ring centered at the virtual leader with a radius of , satisfying the statistical symmetry of radial distribution. To replicate this characteristic in the model and establish a rigorous theoretical foundation for the skin effect analogy, we first elucidate, from the level of the mathematical structure of the dynamical equations, the profound similarity it shares with the group-layering phenomenon in our model. In physics, the skin effect originates from the diffusion process of the electromagnetic field in a conductor. Its steady-state current density distribution, , satisfies a Helmholtz equation, which can be formally written as and its solution in cylindrical coordinates is described by Bessel functions. Similarly, in our group model, the spatio-temporal evolution of individual density, , follows a Fokker–Planck-type equation (also known as a drift–diffusion equation): . Under steady-state conditions (), this equation describes the balance between the random motion of individuals (the diffusion term, ) and the deterministic motion driven by internal interaction forces (the drift term, ). The governing equations of the two systems share a core mathematical structure: a Laplacian operator (representing a tendency to “diffuse” or “spread out”) is counteracted by a term related to the function itself (representing a tendency to “converge” or “decay”). Both ultimately lead to a non-uniform steady-state distribution with a gradient that decreases from the system boundary inward. It is noteworthy that the driving force for the skin effect is a continuous, externally oscillating electromagnetic field, whereas in our model, the formation of the initial layered structure is driven by internal rules, namely, the heterogeneity of individual safety radii and the radial forces designed to maintain the layered structure.
Specifically, the heterogeneity of the model is reflected by assigning different safety radii to individuals of different types (or populations, k). Conceptually, the safety radius, , delineates not only an individual’s demand for personal safety space but is further abstracted as a quantitative representation of an individual’s risk aversion level or the role they assume within the group. Therefore, we establish three categories of individuals, whose respective safety radius values dictate their behavioral inclinations and ultimate spatial arrangements. It is hypothesized that individuals with larger safety radii are more risk-averse and thus tend to seek protection within the group, ultimately forming the protected core layer. Conversely, individuals with smaller safety radii exhibit higher risk tolerance, naturally distributing themselves at the group’s periphery to undertake critical surveillance and frontline defense tasks. This predefined heterogeneity, based on the safety radius, serves as the key intrinsic driving force behind the spontaneous formation of a radially symmetric hierarchical structure within the group.
In order to transform this intrinsic heterogeneity into an ordered macrostructure, it is necessary to define the interaction rules between individuals. Each individual in the system (of type k) possesses a finite perception range () for detecting neighboring individuals and the local environment, and has communication capabilities within a certain range to share critical information. The fundamental principle of this interaction framework is an enhanced skin-effect potential function, designated as . The primary function of this mechanism is to generate precise attraction and repulsion gradients, which are based on the relative relationship between each individual’s current position and its ideal “comfort zone.” The latter is defined by its exclusive safety radius, , and perception radius, . The potential function is expressed as follows:
Among them, a and b are the repulsive and attractive coefficient, respectively, and is a skin factor used to regulate the decay characteristics of the repulsive force within the safety radius . When the distance between individuals () is less than their safety radius (), an exponentially enhanced repulsive force is generated as the distance decreases. When , an attractive force is generated, the magnitude of which increases with distance. The design of the short-range repulsion component of this potential function is functionally inspired by the skin effect in electromagnetism. In the skin effect, current density decays exponentially and rapidly from the conductor’s surface inward, forming a distinct “skin depth,” . Similarly, in our model, when the distance between agents, , is less than their safety radius, , we generate a repulsive force using an exponential potential function, . This design ensures that the repulsive force intensifies sharply as the agents penetrate deeper into each other’s safety zones, thereby creating a “hard-core,” impenetrable repulsive region around each individual. This functional design allows the outer-layer individuals to form a robust defensive boundary, providing effective protection for the inner-layer individuals. This is analogous to the macroscopic effect in the skin effect, where the external current “shields” the internal region.
As demonstrated in the preceding potential energy function, the movement state of an individual is determined by two core forces. The first of these is the internal interaction force, . This force is derived from a bespoke aggregation potential designed to generate the desired skin effect, and it is responsible for maintaining the cohesion and internal structure of the group. The expression under consideration is inspired by the classic model of Olfati-Saber et al., combining a gradient-based term with a velocity alignment term. For individual i belonging to category k and individual j belonging to category l, the interaction force is given by the following equation:
The first term is based on gradient-based attraction–repulsion forces, while the second term represents velocity alignment. The interaction parameters and are employed to regulate the coupling strength between individuals of different categories. is an element of the adjacency matrix, regulating the strength of velocity alignment.
The second is the virtual leader interaction force , which provides the group with a global goal orientation. The aforementioned force functions as a guide, directing individual i toward a virtual leader (position , velocity ). The expression for this force is as follows:
Among these, and are gain coefficients that control the convergence speed, used to regulate the rate at which individuals converge towards the leader state. The synergistic combination of these two forces collectively drives the group to exhibit the expected self-organized hierarchical structure and goal-oriented behavior.
In order to guide individuals with different safety radii to their respective target layers with the greatest possible precision, the model introduces a radial force related to the skin effect. The objective of this force is to propel the kth individual i (located at with the group center at ) to its target ring radius (e.g., inner layer , middle layer , outer layer ). The term is employed to denote the distance difference between an individual and its ideal ring, and is used to denote the radial unit vector pointing from the group center to the individual. The skin effect force is defined in segments based on the relationship between and the predefined layer width :
In this model, is the fundamental magnitude of the skin effect, and is the ideal width of each layer. When an individual is outside the target ring band (), it experiences a strong attraction towards the center of the group that is proportional to the deviation distance. When an individual is within the target ring band (), it experiences a strong repulsive force directed away from the group center, proportional to the deviation distance. When an individual is within the target ring band (), a smaller corrective force is experienced, aimed at precisely adjusting their position and maintaining it within the ring. The magnitude of this force is directly proportional to the radial distance (), and its direction causes the individual to move towards the center of the ring. The coefficient a is utilized for more precise adjustments within this region. In our simulation, its value was set to 0.8 to ensure smooth and stable fine-tuning. This design ensures that individuals can be effectively guided and maintained at their expected levels, thereby forming a stable, radially symmetrical layered structure.
In Figure 1, the mechanism of radially symmetric spontaneous layering driven by the skin effect, as defined by Formula (13), is intuitively demonstrated. The figure comprises three distinct types of individuals: inner-layer individuals (green triangle i, target radius ), middle-layer individuals (blue triangle j, target radius ), and outer-layer individuals (orange triangle m, target radius ). It is evident that outer-layer individual and middle-layer individual are both located outside their respective target rings (orange and blue dashed rings), consequently rendering them susceptible to a strong attractive force towards the center, which effectively pulls them back into the target region. The outer-layer individual has drifted to the inner side of its target ring, resulting in subjection to a strong repulsive force away from the center, thereby pushing it towards the outer layer. The outer-layer individual , the middle-layer individual , and the inner-layer individual are all located inside their respective target rings but are not precisely on the target radius. The particles are subjected to a smaller corrective force, which exerts a precise pulling or pushing force on them, thereby adjusting their position to their respective target radii (illustrated as the solid orange, blue, and green rings in the figure). This process enables fine-tuning of their positions.
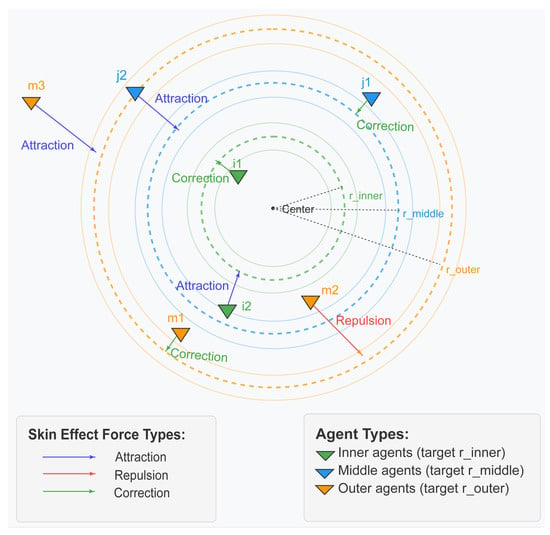
Figure 1.
Schematic diagram of skin effect force.
Furthermore, in order to mitigate fluctuations in individuals during the process of approaching the target level and enhance system stability, a damping term is incorporated, which is associated with the current speed of the individual.
In this context, denotes the current velocity of individual i. The damping coefficient, , is dynamically adjusted to apply appropriate damping according to the degree of deviation of individual i from the target level:
In this system, denotes the base damping coefficient, the purpose of which is to ensure that, even within the target layer, there is minimal damping. , on the other hand, is the adaptive damping gain factor, the function of which is to adjust the sensitivity of damping to radial position deviation . If an individual is far from its target level ( is large), there is an increase in , which provides stronger damping and results in the rapid stabilization of movement. Conversely, when an individual is close to or at the target level ( is small), decreases, thereby allowing for more precise position adjustments.
This additional driving force, based on individual type and predefined target level, constitutes the core mathematical mechanism for achieving and maintaining skin-effect-driven spontaneous hierarchical structures. This enables the group to spontaneously emerge into ordered, specific protective group morphologies through local rules and individual heterogeneity alone.
While the layered structure of the defense swarm is fundamentally determined by the heterogeneity of the safety radius parameter , the stability of the skin effect also depends on the overall population density. Specifically, the radial stratification remains present across different densities, but its effectiveness varies with the number of individuals. At low densities, the outer layer becomes sparse, resulting in a weaker shielding capability and less efficient information transmission. At moderate densities, the outer layer forms a compact barrier that maximizes the protective function of the skin effect. At excessively high densities, however, the structure may become overly compressed, reducing the mobility of inner individuals and limiting adaptive responses. These findings indicate that the skin effect emerges from the interplay between intrinsic heterogeneity (safety radius differences) and extrinsic factors such as group density, consistent with observations in the D’Orsogna–Bertozzi model [49], where collective phenomena are density-dependent.
2.5. Threat Response Model for Symmetry-Breaking Mechanisms
The fundamental defensive mechanism of this model is a closed-loop control process that encompasses threat detection, online analysis, parameter tuning, and dynamic countermeasures. The process of barrier formation can be conceptualized as a phase transition from radial symmetry to directional symmetry. The detection of threats initiates a process of symmetry breaking, leading to a transition in the system’s rotational symmetry from continuous to directional, with the directional symmetry being relative to the threat’s direction.
The starting point for defensive responses is threat detection and group information propagation. The detection capability of individual i of class k toward threat individual j is contingent on the Euclidean distance between them. In instances where this distance is found to be less than the specific threat perception radius, denoted by for the designated class of individuals, that is to say, , the threat is detected. To ensure the timeliness of early warning, individuals located on the outer layer of the defense group are typically assigned a larger threat perception radius, denoted by . This enables them to detect potential threats earlier and from a greater distance.
The perception of a threat by any individual is the catalyst for the rapid dissemination of information within the group, thereby triggering a collective response. To establish a framework for the analysis, it is necessary to define a binary information state, , for each individual i. In order to indicate that the individual is aware of the threat at time t, it is necessary to set . The propagation of information is governed by the following iterative rules:
Among these, represents the set of neighbors of individual i at time t, while is the communication perception radius of individual i’s category for peers. Initially, the state of individuals directly satisfying the detection conditions is updated to 1, and this information is then propagated through the adjacent individual network in successive rounds via the aforementioned logical OR operation. The overall threat perception level, denoted by , is defined as the proportion of individuals who have detected threats out of the total number. This suggests that if an individual perceives a threat itself, or if any of its neighbors perceive a threat, it will also perceive the threat at the next time step. The purpose of this mechanism is to simulate the rapid, hierarchical transmission of threat information within the group, thereby ensuring that relevant individuals (especially outer-layer individuals responsible for forming barriers) can promptly detect dangers and take action.
Following the dissemination of information, the group transitions to the online analysis and quantification phase of threat characteristics, thereby transforming passive perception into structured macro-level insights. The system’s initial function is to identify the unique set of threat individuals, denoted by , observed by all alerted defensive individuals at time t. It then calculates three key features based on this information. The first of these is the number of perceived threats:
Next is the perceived center of gravity, which provides macro-level positional information for the threat group:
Finally, there is perceived compactness , which measures the degree of threat concentration:
Specifically, and denote the mean and standard deviation of the distance between the threat and its center of gravity, respectively. It is evident that the smaller the coefficient of variation (), the more concentrated the threat distribution and the higher the compactness. is a quantity saturation threshold employed to adjust the weight of the perceived quantity on the compactness calculation.
Subsequently, the model transitions to the dynamic tuning phase of adaptive defense parameters, whereby abstract threat characteristics are mapped to specific control parameters. First, the number of threats and compactness are combined into a comprehensive threat intensity index :
Among these, denotes the base weight, and is the compactness weight. The impact of the number of perceptions is standardized using the baseline . This metric is then utilized to linearly adjust three core adaptive defense parameters. These parameters consist of a base value and a gain term related to threat intensity. The first is the repulsion scaling factor, denoted by , which is determined by the base value, denoted by , and the gain factor, denoted by . The gain factor regulates the adversarial strength of the defense barrier:
The second is the barrier individual proportion , which is determined by the base proportion and the gain factor . It determines the scale of the outer defense force’s mobilization:
The third is the barrier strength factor , which is determined by the base value and the gain factor . It has been demonstrated that this process regulates the magnitude of the tangential force during barrier formation:
The series of deterministic processes, from analysis to parameter tuning, constitutes the core of the model’s interpretability.
In conclusion, the group implements dynamic barrier formation and counteraction control laws based on the tuned parameters. In the event of the overall threat perception ratio exceeding the activation threshold , the system intelligently selects a proportion of individuals from the already alerted outer layer individuals as barrier units. These individuals are selected based on their alignment with the perceived threat . The designated barrier units to which this pertains will be subject to additional control forces. One such force is the barrier tangential force , which drives individuals to efficiently converge along the outer edge of the group, with its direction determined by the threat’s orientation.
The second is the repulsive force . To avoid expelling the individual who poses a threat to an unacceptable degree and thereby disrupting the formation’s stability, the magnitude of the force is calculated using a sophisticated function that comprehensively considers the minimum distance , the mass ratio between the two parties, and an adaptive scaling factor.
In this study, and are defined as the base and maximum repulsive forces, respectively. An equal and opposite force acts simultaneously on the corresponding threat individual. is an exponential decay function, where is the minimum distance to a threat agent. This ensures the force smoothly diminishes as the distance increases. is a mass ratio factor that modulates the force based on the relative masses of the defending and threatening agents, ensuring conservation of momentum. An equal and opposite force acts simultaneously on the corresponding threat individual, adhering to Newton’s third law.
It should be noted that this paper constructs a stable hierarchical defense structure and verifies its protective effect on the core only within the model framework, interaction rules, parameter ranges, and boundary conditions established by this research institute. Different model forms can also produce hierarchical or multi-peak steady-state distributions under suitable conditions, and the quality of the structure depends on specific objectives and constraints.
3. Simulation Experiments and Analysis of Results
The objective of this section is to validate the effectiveness of the proposed heterogeneous-group adaptive-defense model based on symmetry breaking and skin effect. To this end, a series of simulation experiments were designed and conducted to analyze the model’s radial symmetry self-organizing layering capability, symmetry-breaking threat response mechanism, and dynamic barrier defense efficacy. The simulation environment was developed on the MATLAB R2016b platform, which offers a user-friendly programming environment and visualization tools for modeling and simulating multi-agent systems. The configuration of the simulation’s fundamental parameters exerts a substantial influence on the model’s operational dynamics and the ensuing outcomes. Table 1 presents a comprehensive list of the primary simulation parameters employed in this study.

Table 1.
Main simulation parameters.
The simulation environment was set in a two-dimensional plane, comprising a defensive group constructed using this model and an adversarial group using a traditional attraction–repulsion model as the threat group. The defensive group consisted of 126 individuals, with clear heterogeneity within it, specifically divided into three functional categories: the population under consideration was comprised of 12 individuals occupying the inner core (safety radius ), 52 individuals occupying the middle layer (), and 62 individuals occupying the outer layer (). For visual representation, the three categories of individuals are represented by triangles in shades of red, ranging from dark to light. The opposing threat group consisted of 126 homogeneous individuals, uniformly represented by blue triangles. The connecting lines drawn between any two individuals in the figure indicate that they are within each other’s communication perception radius and can exchange information effectively. In the initial stage, the virtual leaders of the defense and threat groups (denoted by red and blue “o” symbols, respectively) were positioned on the left and right sides, ensuring sufficient safety distance between them to complete initial internal aggregation and stabilization. Consequently, the threat group, under the guidance of its virtual leader, initiated an attack on the defense group, simulating an invasion process.
Simulation 1: Validation of Radial Symmetry Self-Organization and Layering Capabilities Driven by the Skin Effect. This simulation verified if a defensive group could spontaneously form a predefined, stable, radially symmetric, multilayer structure based solely on internal rules, without external interference. Figure 2 shows the group evolution process, demonstrating the establishment of an ordered, symmetrical structure from a disordered state:

Figure 2.
Radial symmetry spontaneous layering process driven by the skin effect.
Figure 2a: Initial random state (step = 0). The system is in its lowest symmetry state. Individuals are randomly distributed, and there is no obvious geometric symmetry;
Figure 2b: Symmetry emergence stage (step = 30). Under the strong influence of virtual leader interaction forces, the system begins to converge toward a radially symmetric state. Individuals cluster around the center and establish an initial centrally symmetric geometric structure;
Figure 2c: Symmetry refinement stage (step = 60). At this point, skin effect and damping forces begin to dominate. Individuals of different types move toward their respective target ring layers based on their heterogeneity parameters (safety radius: ), and the system’s radial symmetry gradually refines;
Figure 2d: Stable radial-symmetry layered structure (step = 100). After sufficient self-organization evolution, the system converges to a macroscopically ordered, structurally stable, three-layer, radial-symmetry structure. The individuals in the inner, middle, and outer layers, respectively, aggregate near the predefined target radii , , , and their radial density distributions are highly consistent with the theoretical design.
This result strongly confirms that the model can achieve robust, spontaneous, radial-symmetry stratification through individual heterogeneity (i.e., different safety radii, ) and local interaction rules. This lays the structural foundation for subsequent defensive functions.
To address the model’s sensitivity to parameter variations and ensure reproducibility, we conducted systematic robustness tests on two critical parameters: safety radius () and skin force scale (). We evaluated model performance using two metrics: the Layering Quality Index (LQI), representing the proportion of agents correctly positioned within their target layer bands (), and the Convergence Time (CT), denoting the number of iterations required to achieve LQI .
As shown in Figure 3a, the model exhibits asymmetric robustness: for , the LQI stays above 0.94 with accelerated convergence (42–80 iterations); for , we observe gradual performance degradation (LQI , CT ); and for , there is a partial structural collapse (LQI ), indicating the upper robustness boundary. This asymmetry aligns with biological defense principles—tighter formations enhance collective protection, while excessive dispersion compromises structural integrity.
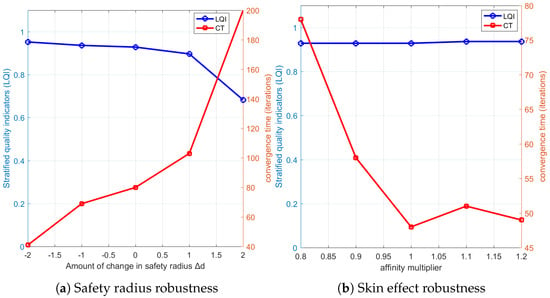
Figure 3.
Chart of parameter robustness analysis results.
Figure 3b demonstrates remarkable stability across : the LQI remains stable (0.94–0.95) throughout the range; the CT varies smoothly (48–78 iterations) without anomalies; the consistent performance confirms that skin force primarily affects convergence dynamics rather than final structure quality.
The analysis reveals a robust operational range for , ; an optimal performance zone for with baseline ; and a critical threshold for , which risks structural instability.
Simulation 2: A thorough examination of the failure process of the threat response in traditional aggregation models is imperative to ensure the efficacy of these models. The objective of this simulation was to examine the dynamic process of heterogeneous groups defending against invasive threats in the absence of skin effect and adaptive barrier logic, relying exclusively on fundamental attraction–repulsion rules. Table 2 lists the primary simulation parameters for defending against groups using the traditional clustering model. The parameters for the adversarial threat group model were identical to those used in subsequent simulations 3 and 5.

Table 2.
Simulation parameters for traditional aggregation model defense against groups.
The simulation results are displayed in Figure 4. Figure 4a: Initial Aggregation Stage (Step = 100). In the early stages of the simulation, the defensive group and the threat group each follow their internal attraction–repulsion rules to self-organize and aggregate within their predefined initial regions, forming relatively stable initial cluster structures. However, due to the absence of radial symmetry constraints, individual distributions exhibit unevenness.

Figure 4.
Schematic diagram of the threat response process in the traditional aggregation model.
Figure 4b: Initial Invasion Stage (Step = 150). If the threat group instigates an incursion against the defense group, the defense group manifests evident deficiencies. The absence of effective long-range perception and coordination mechanisms leads to a limitation in the capacity of defense individuals to respond to threats. Specifically, they are only able to respond with localized repulsion reactions to threat targets within their perception range. This limitation precludes the possibility of coordinating a unified response to the threat.
Figure 4c: Formation, Penetration, and Structural Collapse Stage (Step = 180). As the threat continues to advance, the structural weaknesses of the defensive formation become evident. The threat group employs a wedge-shaped breakthrough strategy, leveraging the outer weak areas with larger intervals between defensive individuals, also known as formation gaps. Concurrently, the defensive group’s original aggregated structure is gradually eroded and dismantled through sustained local pushing, destroying its overall integrity.
Figure 4d: Defense Collapse and Core Exposure Stage (Step = 200). In the event of a successful penetration of the outer defense, the core individuals inside are directly exposed to the threat due to the loss of outer protection. At this juncture, the defensive structure rapidly disintegrates, connections among individuals become ineffective, and the group is unable to maintain any viable defensive formation.
Simulation 3: The process of adaptive barrier defense is driven by symmetry breaking. In order to provide a comprehensive demonstration and analysis of the adaptive capabilities of the model in response to threats, a key simulation was conducted. The results of that simulation revealed a complete defense chain, ranging from macro behavior to micro decision-making. As illustrated in Figure 5, the simulation demonstrated the complete process of symmetry breaking and functional emergence from a macro perspective.
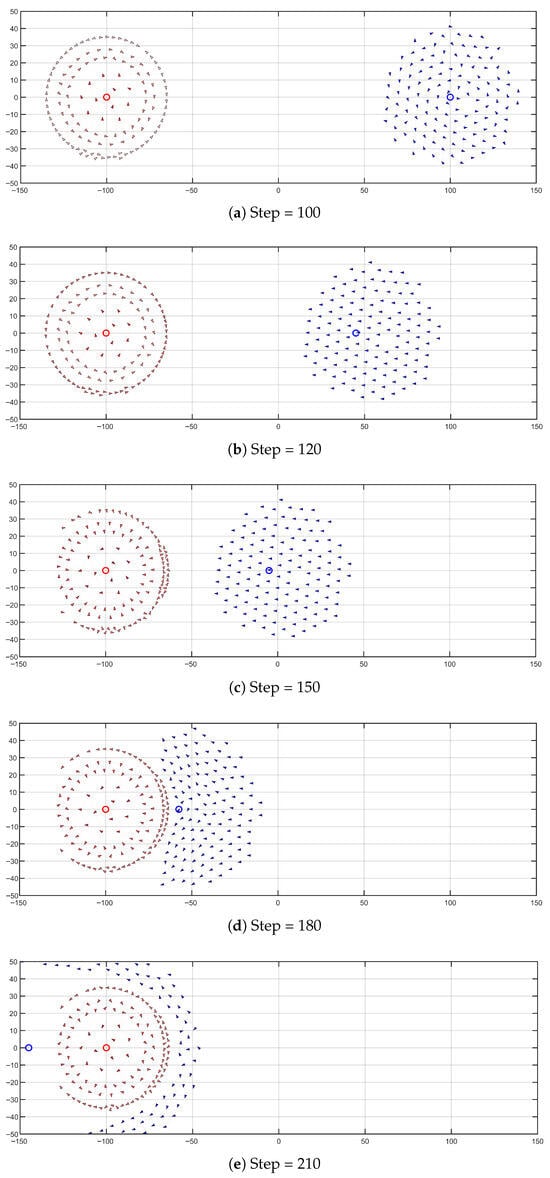
Figure 5.
Schematic diagram of the adaptive barrier defense process driven by symmetry breaking.
Figure 5a illustrates a symmetrical equilibrium state (step = 100). The defense and threat groups complete their internal self-organization at their predefined positions. The defense system has been configured into a stable, radially symmetric, three-layer, hierarchical structure that satisfies continuous rotational symmetry, with defense strength uniformly distributed in all directions.
Figure 5b presents a detailed analysis of the symmetry-breaking trigger (step = 120). As the threat group approaches, it enters the perception range of the outer layer of the defense group. The alarm information (illustrated in a deep red) rapidly saturates and propagates within the defense network. The rapid propagation of threat perception information disrupts the rotational symmetry of the system, thereby introducing a specific spatial directionality (threat direction ), marking the onset of spontaneous symmetry breaking.
Figure 5c shows the ordered symmetry breaking (step = 150). Upon the attainment of the barrier formation threshold by the perception ratio, individuals residing within the outer layer who have discerned the imminent threat undergo activation as barrier individuals. In the presence of tangential forces and radial skin forces, the subjects exhibit rapid movement and aggregation toward the periphery of the group, aligning with the direction of the threatening group’s approach. This results in the formation of an arc-shaped, locally high-density defensive barrier. The system transitions from symmetry to directional symmetry about the threat direction axis.
Figure 5d presents a detailed examination of the symmetry-breaking steady state (step = 180). When the vanguard of the threat group comes sufficiently close to the defensive barrier, strong repulsive forces arise between barrier individuals and threat individuals. It is evident that the barrier’s robust nature, in conjunction with the threat group’s aggregation characteristics, renders it impenetrable to a frontal assault. The system establishes a stable asymmetric defensive structure along the threat direction, achieving a phase transition from passive radial symmetry to active directed defense.
Figure 5e: threat bypass, core protected (step = 210). The asymmetric structure, consequent to symmetry breaking, effectively realizes the anticipated defensive function. The obstructed threat group is compelled to modify its overall movement trajectory, diverting and bypassing the defensive barrier from its flanks. During the confrontation process, the inner and middle core structures of the defensive side remain virtually undisturbed, thereby achieving the primary objective of protecting the core.
To address the need for objective measurement of the model’s effectiveness, we introduce four quantitative metrics to evaluate the adaptive barrier defense mechanism. The defense success rate (DSR) is the proportion of simulation steps where the threat group is successfully prevented from entering the core defense area, defined as , where is the number of steps without core intrusion, and is the total simulation steps. The core area intrusion probability (CAIP) represents the probability of threat agents penetrating the innermost defense layer, calculated as , where counts the steps with at least one threat agent within the core radius. The defense resource utilization rate (DRUR) is the ratio of actively defending agents to total defense agents, expressed as , where represents agents that have perceived threats and positioned themselves within of the threat direction. The threat detour time (TDT) denotes the average time interval between forced path changes of the threat group, computed as , where is the angular change in threat velocity at step i, and I is an indicator function.
Figure 6 presents the temporal evolution of these four metrics during the adaptive barrier defense process. The results demonstrate exceptional defensive performance.

Figure 6.
Quantitative evaluation metrics for adaptive barrier defense.
Figure 6a shows that the defense success rate stays at 100% throughout the simulation. Figure 6b illustrates the core area intrusion probability remains at 0%. Figure 6c shows that the defense resource utilization has three distinct phases: dormant (0–50 s), activation (50–100 s), and stabilization (100–200 s). In Figure 6d, the threat detour time increases progressively, indicating growing barrier effectiveness. The DSR (100%) and zero CAIP throughout the simulation validate the model’s core objective of protecting the innermost layer. These metrics confirm that no threat agent successfully penetrated the core defense zone, demonstrating the robustness of the adaptive barrier mechanism. The progressive increase in TDT from 0 to 20 steps reveals another critical aspect of the defense strategy. As the barrier solidifies and adapts to threat movements, it forces the attacking group to change direction more frequently, effectively increasing the “cost” of attempting penetration. This metric quantifies the barrier’s deterrent effect beyond simple blocking. Notably, the DRUR stabilization at 55% rather than 100% reflects an important design principle: efficient defense does not require total mobilization. The model achieves complete protection (DSR = 100%) while utilizing only essential resources, demonstrating both effectiveness and efficiency. This partial activation strategy maintains reserve capacity for potential multi-directional threats while minimizing energy expenditure. These quantitative results provide objective evidence that the proposed symmetry-breaking mechanism successfully transforms a passive, symmetric structure into an active, adaptive defense system.
In order to gain a more profound understanding of the underlying mechanisms driving the aforementioned macro-level behaviors, a quantitative analysis of the key adaptive parameters in the simulation process was conducted. As demonstrated in Figure 7, this analysis meticulously delineated a causal sequence of “perception-decision-action”:

Figure 7.
Quantitative analysis of adaptive defense mechanisms. (a) Dynamic curve chart of real-time perception of threat quantity. (b) Dynamic curve chart of real-time assessment of threat compactness. (c) Dynamic diagram of adaptive gain factor for repulsive force intensity. (d) Dynamic deployment quantity curve of active barrier units.
Figure 7a shows that the number of threats perceived by the defense cluster increases as engagement distance decreases. In Figure 7b, the perceived compactness of the threat cluster remains consistently high, indicating a concentrated attack formation. Collectively, these two metrics form the defensive party’s quantitative assessment of the current threat landscape. Figure 7c shows the adaptive repulsive force scaling factor—a key defense decision parameter—exhibiting a positive correlation with perceived threat intensity. The repulsion scaling factor grows linearly. This indicates the physical resistance strength of the defensive barrier dynamically intensifies according to threat severity. Figure 7d represents the number of barrier factors deployed for defensive actions, rapidly scaling to the necessary level determined by the adaptive barrier ratio. This demonstrates that the scale of defensive resource allocation is precisely regulated based on threat levels.
This simulation demonstrates the macro-level effectiveness of the defense model and reveals the underlying logic of its adaptive capabilities. This phenomenon elucidates a lucid and explicable decision-making process, whereby a more substantial threat (i.e., a greater number of concentrated forces) invariably precipitates a more robust defense response (i.e., augmented repulsive force and more substantial barriers), thereby ensuring the efficient utilization of resources and the maximization of defense efficacy.
Simulation 4: Symmetry quantification analysis verification. To quantitatively verify the symmetry characteristics of the model, we introduced an improved radial distribution symmetry index . This index was defined as the weighted sum of the radial symmetry index and the angular symmetry index :
where and are the weighting coefficients for radial and angular symmetry, respectively, satisfying . The radial symmetry was calculated based on the coefficient of variation of the radial distance, defined as:
where is a positive sensitivity factor used to adjust the extent to which the exponential function responds to the dispersion of the radial distribution.
The angular symmetry was calculated based on the variance of angular intervals:
The simulation results are illustrated in Figure 8, with the four subfigures demonstrating various aspects of the symmetry analysis.

Figure 8.
Symmetry quantification analysis. (a) Dynamic evolution of radial symmetry in defensive groups. (b) Radial and angular symmetry decomposition. (c) Relationship between symmetry breaking and threat perception. (d) Comparison of symmetry statistics at different stages.
Figure 8a illustrates the dynamic evolution of the radial symmetry of the defensive group. The figure illustrates the temporal evolution of the comprehensive symmetry index of the defensive group. The red solid line signifies the gradual increase in the comprehensive symmetry index from an initial low level to a high symmetry state. This increase is followed by a decline at a specific time point, after which the index remains at a relatively stable level. The black dashed line functions as a baseline symmetry reference line, thereby establishing a standard for comparison. The regions demarcated by dense orange circles correspond to symmetry-breaking phases, which are concentrated during the period when the system perceives threats and begins to respond.
Figure 8b presents a decomposition of radial and angular symmetry. This figure separately displays the contributions of radial symmetry and angular symmetry, thereby revealing the fundamental mechanisms underlying barrier formation. The blue solid line (radial symmetry) remains at a high and relatively stable level throughout the process, indicating that the integrity of the layered structure is maintained. The green solid line (angular symmetry) rapidly rises from a low level to a high symmetry state, then undergoes a significant decline at a critical time point and remains at a markedly reduced level. The red dashed line (combined symmetry) reflects the weighted combined effect of the two. This finding indicates a substantial decline in angular symmetry, while radial symmetry maintains stability or exhibits a modest increase, thereby substantiating the theoretical prediction that barrier formation predominantly occurs through the modulation of angular distribution, while preserving the integrity of the layered structure.
Figure 8c displays the relationship between symmetry breaking and threat perception. This figure substantiates the causal relationship between symmetry breaking and threat perception. The red line (left axis) indicates the trajectory of changes in the symmetry index, while the blue line (right axis) displays the abrupt transition in the proportion of threat perception, jumping suddenly from the zero baseline to a state close to full value. The findings demonstrate a complete synchronization between symmetry breaking and threat perception, thereby substantiating the causal relationship “threat perception → symmetry breaking” and validating the sensitivity and immediacy of the system’s response.
Figure 8d presents a comparison of symmetry statistics at different stages. This figure provides a quantitative comparison of the symmetry characteristics between the normal stage and the breaking stage. In the normal stage, all three symmetry indices (radial, angular, and comprehensive) remain at elevated levels and are closely aligned. In the breaking stage, radial symmetry remains at a high level, angular symmetry significantly decreases, and comprehensive symmetry lies between the two.
The present study employed a symmetry quantification analysis to successfully verify the phase transition process of the system from continuous rotational symmetry to directional defense. The substantial decline in angular symmetry, concomitant with the consistent preservation of radial symmetry, mirrors the theoretically postulated barrier formation mechanism. This mechanism posits that the system can attain directional defense functionality by modulating the uniformity of angular distribution while preserving the integrity of its fundamental layered structure. This finding not only substantiates the viability of symmetry theory in the context of collective defense but also unveils the underlying mathematical principles that underpin efficient defense systems.
Simulation 5: A thorough examination of the adaptive barrier defense process in response to alterations in threat groups was conducted. The objective of that simulation was to verify the core adaptive capability of the proposed model more intuitively. Specifically, the simulation assessed whether the defense barrier could track and respond to dynamic changes in threat vectors in real time. The ensuing discussion focuses on the simulation process and its subsequent outcomes, as illustrated in Figure 9:

Figure 9.
Schematic diagram of the adaptive barrier defense process for changing the direction of threat groups.
Figure 9a illustrates a symmetrical equilibrium state (step = 100). The defense side has formed a stable, radially symmetrical layered structure, and the threat side has begun to move toward it.
Figure 9b illustrates the process of symmetry breaking and barrier pre-formation (step = 130). Upon entering the perception range of outer-layer individuals, threat information disseminates rapidly within the group (individuals perceiving the threat darken in color). Individuals in the outer layer initiate tangential maneuvers in the direction of the perceived threat, leading to local symmetry breaking in the angle of the barrier formation along the initial threat direction.
Figure 9c shows the threat turn and barrier repositioning (step = 160). The threat group has undergone a substantial shift in its operational trajectory, guided under the direction of its virtual leader. In response, the individuals forming the defensive barrier reposition themselves almost simultaneously, ensuring that the geometric center and orientation of the entire barrier remain aligned with the latest threat direction.
Figure 9d displays the new directional symmetry state (step = 180). In the event that the threat group, having altered its trajectory, initiates another offensive, the barrier, which has been repositioned, comes into direct contact with it. The system effectively establishes a stable directional defensive structure in the new threat direction. The robust, regulated repulsive forces among individuals are once again in effect, effectively impeding the threat’s penetration.
Figure 9e shows successful defense (step = 210). Confronted with this formidable obstacle, the insurgent group is compelled to divide its forces and undertake an attempt to circumvent the defensive line from the flanks. During that process, the defensive barrier demonstrates significant elasticity and morphological adaptability, continuously dynamically fine-tuning its shape and position in response to the threat’s movement, consistently blocking the threat outside the core area, and completing the defensive task. The system’s efficacy is confirmed by the robust performance of its symmetric dynamic regulation.
As demonstrated by simulation 5, the model possesses the capability of achieving self-organizing layering stably. Furthermore, the model was shown to possess the capability of dynamically adjusting the deployment of defense resources in response to real-time threat information when faced with an intrusion. This results in the formation of an accurate and effective defense barrier that effectively prevents penetration of the core area and maintains the integrity of its structure.
4. Conclusions
The present paper put forth and substantiated a heterogeneous-group adaptive-defense model grounded in symmetry breaking and the skin effect. The model transformed concepts from symmetry theory, physics, and biology into a set of computable and interpretable group control laws, providing a new theoretical framework and implementation path for designing advanced defense systems with bio-inspired characteristics.
The model’s effectiveness is contingent upon the synergistic interaction of two key mechanisms. Firstly, a symmetry-driven heterogeneous-induced spontaneous layering was observed. The model’s efficacy was demonstrated by its successful conversion of microscopic individual attributes, abstractly represented as risk preferences, into macroscopic, stable, multilayered spatial structures under radial symmetry constraints. This conversion process results in the formation of an initial defense layout that exhibits external rigidity and internal stability. Secondly, adaptive dynamic barrier formation was driven by symmetry breaking. In the event of a threat, the system undergoes a transition from rotational symmetry to a directional defense state, oriented toward the threat direction via the symmetry-breaking mechanism. Individuals in the outer layer make adaptive adjustments to the scale and intensity of the barrier based on real-time assessments of the number and density of threat groups. These individuals actively converge toward the direction of the threat to form a high-density dynamic defense barrier. The radial symmetry design ensures the balanced distribution of defensive resources and the system’s intrinsic stability; the symmetry-breaking mechanism enables intelligent transition from passive defense to active confrontation. Simulation experiments demonstrated that the proposed model endowed the defensive group with the ability to generate dynamic defensive barriers. These barriers were designed to ensure the safety of the core units within the group by effectively shielding the core area and repelling external threats. In comparison with conventional aggregation models, this model, through its inherent adaptive layering and barrier strategies, can intelligently deploy defensive resources precisely to the most critical interfaces, thereby significantly enhancing the system’s defensive robustness and structural resilience.
While the efficacy of the model was validated by this study, there is considerable scope for enhancement and expansion. Subsequent research endeavors will center on the incorporation of more realistic complexity, such as threat perception models that account for line-of-sight obstruction and perceptual uncertainty, as well as decision-making mechanisms capable of handling multi-source, fuzzy information fusion. In terms of the model’s application scope, expanding the model from a two-dimensional plane to a three-dimensional space and studying its adaptability in complex environments with obstacles is key to enhancing its practical value. Furthermore, it is imperative to take into account the practical constraints inherent to networked systems, including communication delays, bandwidth limitations, and incomplete information, to successfully translate the model from theoretical frameworks to practical applications. Additionally, the exploration of symmetry principles in other collective behaviors, such as foraging, migration, and rescue, has the potential to unveil novel theoretical frameworks for collective intelligence research.
Author Contributions
Conceptualization, Y.M. and X.-B.C.; methodology, Y.M.; software, Y.M.; validation, Y.M., X.-B.C., and M.L.; formal analysis, Y.M. and P.Y.; investigation, Y.M. and M.L.; resources, Y.M. and P.Y.; writing—original draft preparation, Y.M.; writing—review and editing, Y.M.; visualization, Y.M.; supervision, X.-B.C. and M.L.; project administration, X.-B.C. and P.Y.; funding acquisition, X.-B.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China under Grant 71571091 and Grant 71771112.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Vicsek, T.; Zafeiris, A. Collective motion. Phys. Rep. 2012, 517, 71–140. [Google Scholar] [CrossRef]
- Sumpter, D.J.T. Collective animal behavior. In Collective Animal Behavior; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Reynolds, C.W. Flocks, herds, and schools: A distributed behavioral model. Comput. Graph. 1987, 21, 25–34. [Google Scholar] [CrossRef]
- Cucker, F.; Smale, S. Emergent behavior in flocks. IEEE Trans. Autom. Control 2007, 52, 852–862. [Google Scholar] [CrossRef]
- Vicsek, T.; Czirók, A.; Ben-Jacob, E.; Cohen, I.; Shochet, O. Novel type of phase transition in a system of self-driven particles. Phys. Rev. Lett. 1995, 75, 1226–1229. [Google Scholar] [CrossRef] [PubMed]
- Helbing, D.; Farkas, I.; Vicsek, T. Simulating dynamical features of escape panic. Nature 2000, 407, 487–490. [Google Scholar] [CrossRef]
- Kikuchi, Y.; Iwamoto, M. Intermediate Interaction Strategies for Collective Behavior. arXiv 2025, arXiv:2507.09457. [Google Scholar] [CrossRef]
- Jadbabaie, A.; Lin, J.; Morse, A.S. Coordination of groups of mobile autonomous agents using nearest neighbor rules. IEEE Trans. Autom. Control 2003, 48, 988–1001. [Google Scholar] [CrossRef]
- Tahbaz-Salehi, A.; Jadbabaie, A. A necessary and sufficient condition for consensus over random networks. IEEE Trans. Autom. Control 2008, 53, 791–795. [Google Scholar] [CrossRef]
- Ren, Q.; Long, Q.; Zhao, J. Symmetry and symmetry breaking in a Kuramoto model induced on a Möbius strip. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2013, 87, 022811. [Google Scholar] [CrossRef] [PubMed]
- Couzin, I.D.; Krause, J.; James, R.; Ruxton, G.D.; Franks, N.R. Collective memory and spatial sorting in animal groups. J. Theor. Biol. 2002, 218, 1–11. [Google Scholar] [CrossRef]
- Olfati-Saber, R. Flocking for multi-agent dynamic systems: Algorithms and theory. IEEE Trans. Autom. Control 2006, 51, 401–420. [Google Scholar] [CrossRef]
- Olfati-Saber, R.; Murray, R.M. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Autom. Control 2004, 49, 1520–1533. [Google Scholar] [CrossRef]
- Jones, J.E. On the determination of molecular fields.—II. From the equation of state of a gas. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1924, 106, 463–477. [Google Scholar]
- Auricchio, F.; Carraturo, M.; Toscani, G.; Zanella, M. Impact of interaction forces in first order many-agent systems for swarm manufacturing. arXiv 2023, arXiv:2307.04264. [Google Scholar] [CrossRef]
- Auricchio, F.; Toscani, G.; Zanella, M. Fokker-Planck modeling of many-agent systems in swarm manufacturing: Asymptotic analysis and numerical results. arXiv 2022, arXiv:2205.09996. [Google Scholar] [CrossRef]
- Ran, W.; Nantogma, S.; Zhang, S.; Xu, Y. Bio-inspired UAV swarm operation approach towards decentralized aerial electronic defense. Appl. Soft Comput. 2025, 177, 113136. [Google Scholar] [CrossRef]
- Chipade, V.S.; Panagou, D. Aerial swarm defense using interception and herding strategies. IEEE Trans. Robot. 2023, 39, 3821–3837. [Google Scholar] [CrossRef]
- Shahid, S.; Zhen, Z.; Javaid, U.; Wen, L. Offense-defense distributed decision making for swarm vs. swarm confrontation while attacking the aircraft carriers. Drones 2022, 6, 271. [Google Scholar] [CrossRef]
- Zhang, S.; Ran, W.; Liu, G.; Li, Y.; Xu, Y. A multi-agent-based defense system design for multiple unmanned surface vehicles. Electronics 2022, 11, 2797. [Google Scholar] [CrossRef]
- Alqudsi, Y.; Makaraci, M. Exploring advancements and emerging trends in robotic swarm coordination and control of swarm flying robots: A review. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2025, 239, 180–204. [Google Scholar] [CrossRef]
- Wang, L.; Qiu, T.; Pu, Z.; Yi, J.; Zhu, J.; Zhao, Y. A Decision-Making Method for Swarm Agents in Attack-Defense Confrontation. IFAC-PapersOnLine 2023, 56, 7858–7864. [Google Scholar] [CrossRef]
- Martius, G.; Der, R.; Ay, N. Information driven self-organization of complex robotic behaviors. PLoS ONE 2013, 8, e63400. [Google Scholar] [CrossRef] [PubMed]
- Kuang, M.; Yan, W.; Wang, Q.; Zheng, Y. Self-Organizing Coverage Method of Swarm Robots Based on Dynamic Virtual Force. Symmetry 2025, 17, 1202. [Google Scholar] [CrossRef]
- Istiak, M.A.; Ullah, M.S.; Ashraf, Z.B.; Sarker, S.C.; Chowdhury, M.M.; Ahbab, S.S. SymSwarm: A Two-Staged Decentralized Symmetrical Pattern Formation Paradigm for a Swarm of Mobile Robots. Arab. J. Sci. Eng. 2023, 48, 15509–15526. [Google Scholar] [CrossRef]
- Yang, J.; Wang, X.; Bauer, P. V-shaped formation control for robotic swarms constrained by field of view. Appl. Sci. 2018, 8, 2120. [Google Scholar] [CrossRef]
- Ye, D.; Zhang, M.; Vasilakos, A.V. A Survey of Self-Organization Mechanisms in Multiagent Systems. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 441–461. [Google Scholar] [CrossRef]
- Gao, H.; Zhao, C.; Yu, X.; Ren, S.; Cai, H. Swarm Confrontation Algorithm for UGV Swarm with Quantity Advantage by a Novel MSRM-MAPOCA Training Method. Actuators 2025, 14, 15. [Google Scholar] [CrossRef]
- Zhen, Z.; Wen, L.; Wang, B.; Hu, Z.; Zhang, D. Improved contract network protocol algorithm based cooperative target allocation of heterogeneous UAV swarm. Aerosp. Sci. Technol. 2021, 119, 107054. [Google Scholar] [CrossRef]
- Xue, Y.; Xu, S.; Chen, X.B. The influence of intra-group differences on the flocking and obstacle avoidance movement of multiagent systems. ISA Trans. 2023, 138, 106–119. [Google Scholar] [CrossRef]
- Wei, H.; Chen, X.B. Flocking for multiple subgroups of multi-agents with different social distancing. IEEE Access 2020, 8, 164705–164716. [Google Scholar] [CrossRef]
- Darush, Z.; Martynov, M.; Fedoseev, A.; Shcherbak, A.; Tsetserukou, D. SwarmGear: Heterogeneous Swarm of Drones with Morphogenetic Leader Drone and Virtual Impedance Links for Multi-Agent Inspection. In Proceedings of the 2023 International Conference on Unmanned Aircraft Systems (ICUAS), Warsaw, Poland, 6–9 June 2023; pp. 557–563. [Google Scholar]
- Zhang, S.; Lei, X.; Peng, X.; Pan, J. Heterogeneous Targets Trapping With Swarm Robots by Using Adaptive Density-Based Interaction. IEEE Trans. Robot. 2024, 40, 2729–2748. [Google Scholar] [CrossRef]
- Kaminka, G.A.; Douchan, Y. Heterogeneous foraging swarms can be better. Front. Robot. AI 2025, 11, 1426282. [Google Scholar] [CrossRef]
- Liao, X.; Wang, Y.; Han, Y.; Li, Y.; Lin, C.; Zhu, X. Heterogeneous Multi-Agent Deep Reinforcement Learning for Cluster-Based Spectrum Sharing in UAV Swarms. Drones 2025, 9, 377. [Google Scholar] [CrossRef]
- Hamilton, W.D. Geometry for the selfish herd. J. Theor. Biol. 1971, 31, 295–311. [Google Scholar] [CrossRef]
- Morrell, L.J.; Ruxton, G.D.; James, R. Spatial positioning in the selfish herd. Behav. Ecol. 2011, 22, 16–22. [Google Scholar] [CrossRef]
- Ballerini, M.; Cabibbo, N.; Candelier, R.; Cavagna, A.; Cisbani, E.; Giardina, I.; Orl, I.A.; Parisi, G.; Procaccini, A.; Viale, M.; et al. Empirical investigation of starling flocks: A benchmark study in collective animal behaviour. Anim. Behav. 2008, 76, 201–215. [Google Scholar] [CrossRef]
- Attanasi, A.; Cavagna, A.; Del Castello, L.; Giardina, I.; Jelic, A.; Melillo, S.; Parisi, L.; Pohl, O.; Shen, E.; Viale, M. Emergence of collective changes in travel direction of starling flocks from individual birds’ fluctuations. J. R. Soc. Interface 2015, 12, 20150319. [Google Scholar] [CrossRef]
- Procaccini, A.; Orlandi, A.; Cavagna, A.; Giardina, I.; Zoratto, F.; Santucci, D.; Chiarotti, F.; Hemelrijk, C.K.; Alleva, E.; Parisi, G. Propagating waves in starling, Sturnus vulgaris, flocks under predation. Anim. Behav. 2011, 82, 759–765. [Google Scholar] [CrossRef]
- Yang, W.C.; Schmickl, T. Collective motion as an ultimate effect in crowded selfish herds. Sci. Rep. 2019, 9, 6618. [Google Scholar] [CrossRef]
- Liu, C.H.; Zhang, K.; Yang, Z.; Chen, S. Helical damping and dynamical critical skin effect in open quantum systems. Phys. Rev. Res. 2020, 2, 043167. [Google Scholar] [CrossRef]
- Mattis, D.C.; Bardeen, J. Theory of the anomalous skin effect in normal and superconducting metals. Phys. Rev. 1958, 111, 412. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, T.; Lu, M.H.; Chen, Y.F. A review on non-Hermitian skin effect. Adv. Phys. X 2022, 7, 2109431. [Google Scholar] [CrossRef]
- Yang, F.; Jiang, Q.D.; Bergholtz, E.J. Liouvillian skin effect in an exactly solvable model. Phys. Rev. Res. 2022, 4, 023160. [Google Scholar] [CrossRef]
- Yuan, Y.; Fan, Z.; Zhu, X.; Ma, L.; Ouyang, J.; Bao, W.; Wang, J.; Wang, Z. SUNDER: Self-organized grouping and entrapping method for swarms in multitarget environments. Def. Technol. 2023, 26, 68–83. [Google Scholar] [CrossRef]
- Hashem, R.; Howison, T.; Stilli, A.; Stoyanov, D.; Xu, W.; Iida, F. Harnessing Symmetry Breaking in Soft Robotics: A Novel Approach for Underactuated Fingers. In Proceedings of the 2024 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Abu Dhabi, United Arab Emirates, 14–18 October 2024; pp. 241–246. [Google Scholar]
- Phadke, A.; Medrano, F.A. Increasing operational resiliency of UAV swarms: An agent-focused search and rescue framework. Aerosp. Res. Commun. 2024, 1, 12420. [Google Scholar] [CrossRef]
- D’Orsogna, M.R.; Chuang, Y.L.; Bertozzi, A.L.; Chayes, L.S. Self-propelled particles with soft-core interactions: Patterns, stability, and collapse. Phys. Rev. Lett. 2006, 96, 12420104302. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).