Abstract
Modern logistics operations require real-time adaptive solutions for three-dimensional bin packing that maintain spatial symmetry and load balance. This paper introduces a time-series-based online 3D packing problem with dual unknown sequences, where containers and items arrive dynamically. The challenge lies in achieving symmetric distribution for stability and optimal space utilization. We propose the Second-Order Dual Pointer Adversarial Network (So-DPAN), a deep reinforcement learning architecture that leverages symmetry principles to decompose spatiotemporal optimization into sequence matching and spatial arrangement sub-problems. The dual pointer mechanism enables efficient item-container pairing, while the second-order structure captures temporal dependencies by maintaining symmetric packing patterns. Our approach considers geometric symmetry for spatial arrangement and temporal symmetry for sequence matching. The Actor-Critic framework uses symmetry-based reward functions to guide learning toward balanced configurations. Experiments demonstrate that So-DPAN outperforms DQN, DDPG, and traditional heuristics in solution quality and efficiency while maintaining superior symmetry metrics in center-of-gravity positioning and load distribution. The algorithm exploits inherent symmetries in packing structure, advancing theoretical understanding through symmetry-aware optimization while providing a deployable framework for Industry 4.0 smart logistics.
1. Introduction
In the era of Industry 4.0, Logistics 4.0 has emerged as a paradigm that integrates core technologies with logistics sector needs [1]. The rapid development of smart cities and the surge in e-commerce order volumes have intensified the demand for automated packing strategies that can adapt to goods diversity while ensuring stability and optimal space utilization [2]. Currently, logistics companies predominantly rely on manual operations that frequently fail to achieve symmetric load distribution, resulting in transportation instability, increased costs, and safety hazards [3]. This operational reality necessitates intelligent methods capable of maintaining geometric and temporal symmetry in real-time decision-making scenarios [4].
The Three-Dimensional Container Loading Problem (TDCLP) represents a fundamental challenge in logistics optimization, where symmetry plays a crucial role in ensuring balanced spatial distribution and center-of-gravity stability. Junqueira et al. [5] identified two key modeling paradigms where symmetry constraints are essential. However, modern logistics operations present an even more complex challenge characterized by “dual unknown sequences,” where both containers and items arrive dynamically and stochastically. This temporal uncertainty, combined with the requirement for continuous symmetry maintenance across geometric, temporal, and computational dimensions, creates a problem space that existing methods have not adequately addressed [6].
To systematically understand the evolution and limitations of current solutions, we organize existing approaches into four main categories: traditional optimization algorithms, metaheuristic methods, deep learning approaches, and industrial applications. Classical optimization methods have laid the foundation for container loading problems through various algorithmic frameworks. Heuristic algorithms based on layer generation [7] implicitly consider horizontal symmetry, while multilayer tree search algorithms [8] maintain vertical balance through ternary and quaternary structures. Branch-and-price algorithms [9] attempt to balance asymmetric product characteristics with symmetric packing goals, and multi-objective algorithms for large-scale cargo with stacking constraints [10] explicitly optimize symmetry metrics alongside efficiency. Constructive heuristics for irregular shaped items [11] further extend these capabilities. Despite these contributions, traditional approaches suffer from combinatorial explosion when incorporating symmetry requirements and cannot handle dynamic arrivals in real-time scenarios.
The emergence of metaheuristic methods has brought adaptive capabilities to packing problems. Genetic algorithms with prioritized strategies [12] maximize space utilization through symmetric placement patterns, while Particle Swarm Optimization [13] demonstrates stability by maintaining load symmetry with adaptive weights and parallel computing capabilities. The Aquila Optimizer [14] achieves convergence through symmetric perturbation strategies and dynamic fusion policy optimization [15] enhances adaptability. Particle Swarm Optimization [16] demonstrates stability by maintaining load symmetry with adaptive weights and parallel computing capabilities using differential mutation. Nevertheless, these metaheuristic approaches remain limited to scenarios with known containers and are generally unsuitable for real-time applications due to slow convergence rates, particularly in large-scale problems [17].
Recent advances in deep learning have introduced new paradigms for solving complex packing optimization problems. Multimodal deep reinforcement learning [18] and attention-based Attend2Pack methods [19] enhance spatial understanding, while deep policy dynamic programming [20] originally developed for vehicle routing provides transferable insights. Tsang et al. [21] modeled 3D bin packing with weight distribution symmetry as explicit constraints, while online 3D bin packing with buffer [22] improves real-time performance. Reinforcement learning frameworks [23] enhance performance through symmetric action spaces. Actor-Critic frameworks [24] reduce complexity using balanced stacking trees, and methods integrating heuristics with deep learning [25] improve online packing by exploiting spatial symmetries. Adjustable robust reinforcement learning [26] addresses uncertainty in online scenarios. Among the most promising architectures, Transformer-based methods [27] excel in offline scenarios through self-attention mechanisms and the GOPT method [28] for multi-environment generalization. However, their computational complexity severely hinders real-time applications, and they struggle with temporal causality in online settings. Graph Neural Networks [29] effectively capture geometric constraints through TAP-Net architecture by modeling spatial relationships, yet the repeated graph reconstruction required in dynamic scenarios incurs prohibitive computational costs. Critically, all existing deep learning methods assume containers are known a priori, failing to address the dual unknown sequences characteristic of real logistics operations [30].
Industrial deployments reveal persistent challenges in maintaining symmetry during dynamic operations. Mainstream warehouse management systems, including SAP EWM and Manhattan systems [31], struggle with asymmetric item flows and irregular shapes. Amazon’s robotic centers employ learning-based suggestions but require human intervention for symmetry verification, while JD Logistics achieves automation but faces efficiency bottlenecks when handling asymmetric fragile goods [32]. Recent learning-augmented algorithms [33] incorporate prediction mechanisms for temporal symmetry through consistency-robustness tradeoffs, and smart logistics concepts [34] enhance collaboration through symmetric information flow between physical and digital systems. However, these industrial solutions primarily rely on traditional heuristics and simple switching strategies, lacking the sophistication to handle complex temporal dependencies in time-series logistics [35]. Table 1 compares the differences in key information between different algorithms.

Table 1.
Summary of the key characteristics of existing approaches and highlights the research gaps addressed by our proposed method.
Synthesizing existing research reveals several critical gaps that directly motivate our proposed Second-Order Dual Pointer Adversarial Network (So-DPAN). First, the fundamental assumption of known containers in all existing online methods creates a significant disconnect with real logistics operations where both containers and items arrive stochastically—our work is the first to formalize and solve this “dual unknown sequences” problem. Second, the computational complexity of state-of-the-art deep learning methods, with O(n2) for Transformers and substantial graph reconstruction overhead for GNNs, prohibits real-time deployment, while our O(n) dual pointer mechanism directly addresses this limitation. Third, existing algorithms treat symmetry as a byproduct rather than a design objective, leading to suboptimal stability and load distribution, whereas our framework explicitly optimizes for multi-dimensional symmetry. Fourth, current approaches lack mechanisms to capture complex temporal dependencies in time-series logistics, a capability provided by our second-order structure. Finally, the gap between academic research and industrial deployment remains substantial, and our architecture is specifically designed for compatibility with existing WMS infrastructure while maintaining theoretical rigor.
The core innovation of this study lies in systematically introducing symmetry-aware time-series characteristics into 3D packing problems. Unlike traditional static formulations, our approach features “dual unknown sequences” with both containers and items arriving dynamically, requiring continuous symmetry maintenance throughout the packing process. The So-DPAN architecture decomposes this complex problem into symmetric sub-problems of sequence matching and spatial optimization, ensuring geometric symmetry in placement, temporal symmetry in processing, and computational symmetry in algorithm design.
The main contributions are as follows: (1) introducing time-series concepts with explicit symmetry constraints into 3D packing, establishing mathematical models that balance efficiency with stability through symmetric optimization; (2) proposing So-DPAN architecture that handles dynamic matching through symmetric dual pointer mechanisms, achieving linear time complexity compared to quadratic complexity in Transformer-based methods, while avoiding the graph reconstruction overhead of GNN approaches, and enhancing robustness via adversarial training; (3) designing phased reinforcement learning that maintains symmetry across decomposed sub-problems, improving convergence through balanced Actor-Critic frameworks; (4) developing deployable algorithms that preserve symmetry metrics while integrating with existing systems, meeting real-time requirements.
2. Problem Description and Modeling
This paper proposes an executable model for automated packing scenarios. By converting placement parameters into continuous variables and combining integer programming with evolutionary algorithms, the model achieves continuous optimization in discrete scenarios. Each container is considered as a fragmented space, while the goods are treated as discrete units occupying these spaces, aiming to improve space utilization and loading efficiency. The fitness function considers objectives such as avoiding overlap, maintaining boundaries, minimizing space wastage, and maximizing benefits, providing a novel solution for the three-dimensional packing problem.
2.1. Problem Description
This study introduces the concept of time series into the traditional packing problem, constructing a dynamic decision-making environment. In this environment, goods and containers continuously emerge as discrete events along the time series, and the system needs to match and optimize their loading in real-time.
Unlike the traditional online packing problem where “containers are known and goods are unknown,” the time-series packing problem investigated in this study features both containers and goods as dynamically generated, unknown sequences. This “dual unknown sequence” matching decision mode not only aligns more closely with real-world logistics scenarios but also significantly increases the complexity of the problem. In this framework, the system must comprehensively consider the multidimensional attributes of goods and containers (such as size, shape, weight, arrival time, etc.) to achieve a globally optimal matching strategy.
The problem is modeled as a time-series-based three-dimensional online packing problem, breaking the limitations of traditional methods that focus solely on single scenarios or batch processing. By establishing a dynamic matching mechanism in the continuous time domain, this method more accurately describes the ongoing operational needs in real logistics environments, providing a new approach to real-time decision-making in dynamic logistics networks.
Definition 1.
The attributes of item i are represented by a 10-dimensional vector , where
- : Identifier for item i, generally sequenced by time, with potential repetition for items arriving simultaneously.
- ,: Length, width, and height of item i.
- : Weight of item i.
- : Arrival time of item i.
- : Shape characteristics of item i.
- : Priority level for handling item i.
- : Ability to be stacked, indicating if other items can be placed on top of item i.
- : Constraints on orientation, such as “must be upright” or “must not be inverted.”
Definition 2.
The attributes of container C are represented by a 6-dimensional vector , where
- : The attributes of container C, generally sequenced by time.
- ,: Length, width, and height of the container.
- : Maximum load capacity of the container.
- : Current loading status of the container.
As shown in Figure 1, the target container ID corresponds to a specific container within the sequence. The arrival time indicates the point in time when the item enters the process. The loading status records information on currently loaded items, providing data to support subsequent packing optimization. Each container can load multiple items, and placement decisions depend on factors such as size, weight, and arrival time of each item.
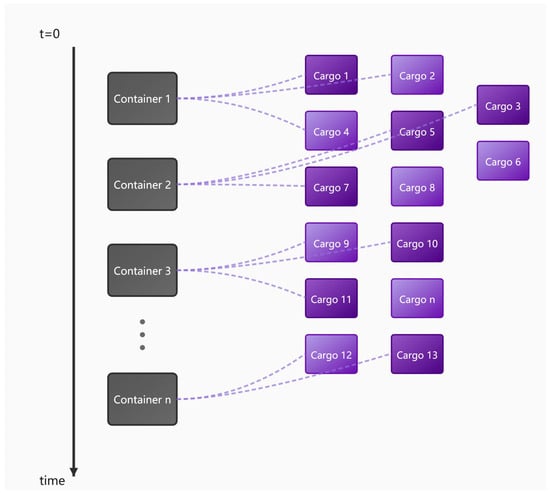
Figure 1.
Schematic diagram of the matching relationship between cargo and container-oriented time series.
2.2. Objectives and Constraints
2.2.1. Basic Symbol Definition
- : Container, with defined length, width, and height.
- : Number of items.
- : The i-th item, with defined length, width, height, and weight.
- , , : Position coordinates of the item in the container.
- : Orientation of the item, usually represented as a triplet indicating orientation in three dimensions.
2.2.2. Formal Constraints
- (1)
- Container Space Constraints
Each item must be fully within the container:
- (2)
- Container Shape Constraints
Ensure that the total volume of all items is less than or equal to the volume of the container, and in each dimension (length, width, height), the item size does not exceed the corresponding container dimension:
- (a)
- Total volume constraint
- (b)
- Dimension constraints
- (3)
- Center of Gravity Constraints
The overall center of gravity of the loaded items should be within a certain range, represented by , where
Ideally, the center of gravity should be at the geometric center of the container when fully loaded, and it should satisfy the constraint of being within a spherical region centered on , and thus be constrained as follows:
- (4)
- Item Orientation Constraints
Ensure that items are placed in an appropriate orientation such as “must be upright” or “must not be inverted.”
- (5)
- Item Stackability Constraints
To ensure stability and safety during stacking, a stacking factor is defined for each item, indicating if other items can be stacked on it. If = 1, stacking is allowed. If = 0, it is not allowed.
If goods are stacked on top of goods , the following conditions must be met: and .
- (6)
- Complete Support Constraint
Each non-bottom item must be fully or partially supported by at least one item below it to ensure stability (as shown in Figure 2). Specifically, for each upper item, there must exist a lower item such that a portion of its base overlaps directly with the top of the lower item.

Figure 2.
Complete support diagram.
Define the support function as follows:
For each non-bottom cargo there must be at least one to let = 1.
- (7)
- No Overlap Constraint
No two items should overlap in space:
For all items i, j, either , or , or , or .
2.2.3. Formal Objectives
This study constructs an optimization model for the time-series-based three-dimensional online packing problem, focusing on designing a multi-dimensional, comprehensive objective function. This function integrates core performance metrics such as space utilization, item waiting time, and processing cost, ensuring a balanced optimization strategy through reasonable weight distribution.
Considering the dynamic nature of the online packing problem, the objective function introduces a time window constraint to handle the arrival and departure time of items. It also incorporates dynamic readjustment costs to balance the economic impact of strategy adjustments in real-time environments. Additionally, by comprehensively considering the quality and volume characteristics of the items, the objective function further optimizes the stability and safety of the packing process.
where represents the weight coefficient of different optimization objectives, ensuring that the objective function comprehensively reflects multiple performance indicators. The specific calculation methods for each indicator will be determined based on practical application scenarios and available data.
3. Algorithm Designs
The entire algorithm consists of two components: a dual pointer network-based algorithm for matching goods and containers, which is trained using an Actor–Critic approach, and a three-dimensional online packing algorithm for determining physical placement within containers. Together, these form an integrated solution for the sequence of “goods arrival–container selection–placement”. The matching mechanism relies on the dual pointer network introduced in prior work, which addressed static matching problems. In contrast, the current So-DPAN architecture extends this foundation with three major innovations: (1) second-order optimization for capturing temporal dependencies through historical matching patterns; (2) an adversarial training framework that improves robustness against distribution shifts in item and container sequences; and (3) hierarchical integration with spatial packing decisions, where matching outcomes directly guide placement optimization. These enhancements enable So-DPAN to effectively handle dynamic environments with dual unknown sequences, a scenario not supported by the original model.
This section is divided into two parts: the time-series sequence matching algorithm and the three-dimensional space loading positioning algorithm. The time-series sequence matching part will introduce the core of the dual pointer network algorithm and the training details using the Actor–Critic network, while the three-dimensional space loading positioning part will focus on the combination of deep reinforcement learning and search algorithms to solve the three-dimensional packing problem. An overview of the entire algorithm framework is shown in Figure 3:
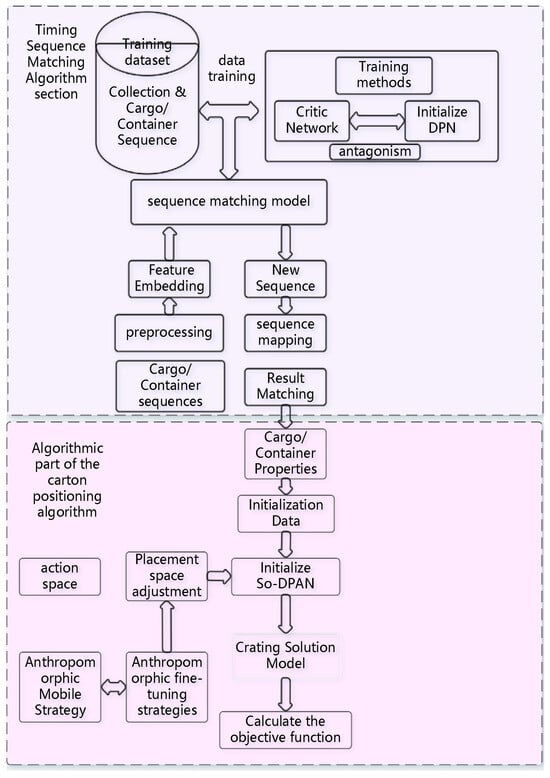
Figure 3.
Overall algorithm overview block diagram.
As illustrated in Figure 3, the So-DPAN architecture introduces several key innovations: a dual-stream processing structure that enables parallel handling of sequence matching and spatial placement, facilitating joint optimization through interactive learning; second-order temporal modeling that captures changing trends in item arrival rates for better anticipation of logistics dynamics; an adversarial training mechanism that enhances robustness against real-world distribution shifts; and a hierarchical decision integration that ensures spatial placement respects matching constraints. The model employs a dual-pointer mechanism with bidirectional attention—tracking both upcoming items and available container capacity—which reduces computational complexity to linear scale relative to sequence length.
3.1. Time-Series Sequence Matching Algorithm
Standard data normalization and scaling cannot fully capture the relationships between various attributes in the time-series online packing problem, nor the interactions between goods and containers. Therefore, specialized preprocessing methods are required. This subsection will introduce preprocessing methods suitable for matching goods and containers in the time-series online packing problem.
3.1.1. Feature Encoding
Preprocessing transforms item attribute information into unit-free data that can be processed by neural networks. Additional attributes are added to item attributes, while container attributes need certain properties removed. The goods and container descriptions used for training neural networks are referred to as “goods features” and “container features,” represented by vectors and , respectively, defined as follows:
3.1.2. Feature Embedding
In the step after feature embedding preprocessing, a fully connected layer is applied for container feature embedding, while for goods feature embedding, a method incorporating Self Attention and Multi-Head Attention mechanisms is employed, followed by a fully connected layer, as shown in Figure 4:
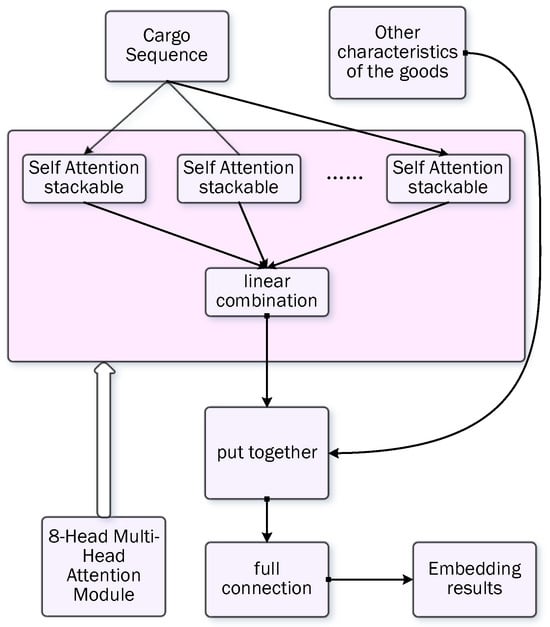
Figure 4.
Cargo embedding diagram.
Considering the spatial correlation among the three-dimensional coordinates of goods, this study uses Self Attention and Multi-Head Attention mechanisms to process the coordinates. Specifically, the three-dimensional coordinates of the goods are converted into QKV triplets, and coordinate embeddings are generated through the attention mechanism, which are then input into a fully connected layer along with container features to generate goods and container feature representations. The Self Attention computation process is shown in Figure 5:
where are matrices obtained through linear transformations of item coordinates, is the output dimension, and C is the matrix formed by the item coordinates, representing the model parameters.
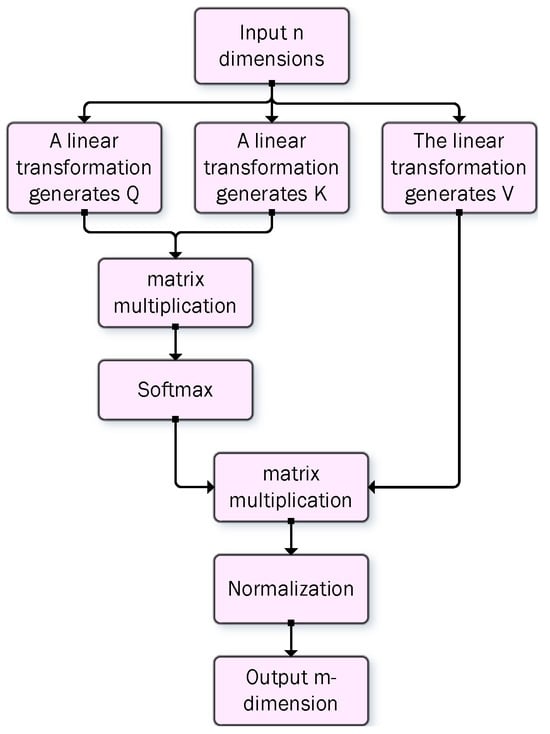
Figure 5.
Self Attention computation.
Each head is a stack of multiple Self Attentions modules with residual connectivity in between. Let be the computation result of the ith Attention header, in which the computation of the splicing and linear transformation part is formulated as follows:
3.1.3. Sequence Mapping and Matching Results Mapping
This study focuses on the time-series three-dimensional online packing problem, which involves efficiently assigning goods arriving in a time series to containers also appearing over time. The main method for sequence mapping and matching is based on a greedy algorithm that converts two time-ordered sequences into matching results, as Algorithm 1:
| Algorithm 1 Time Sequence Mapping Algorithm | |
| 1: | Input: arriving over time, sequence of appearing over time. |
| 2: | Output: Matching Matrix D |
| 3: | Initialize is the number of containers. |
| 4: | in the cargo sequence, following its time of arrival do |
| 5: | for each container in the container sequence, following its time of appearance do |
| 6: | Extract the 3D dimensions of : (length, width, height) |
| 7: | Extract the 3D dimensions of : [ (length, width, height) and current load state |
| 8: | if < and < and < then |
| 9: | Set = 1 in matrix |
| 10: | Break and move to the next cargo for matching |
| 11: | end if |
| 12: | end for |
| 13: | end for |
The Algorithm 1 iterates through the item sequence, attempting to find a suitable container for each item by sequentially searching through the container sequence. The process stops when a suitable container is found, and the matching result is recorded.
3.2. Three-Dimensional Packing Positioning Algorithm
In the deep So-DPAN framework, this section aims to design the action space for the three-dimensional packing problem using a human-like strategy. The human-like strategy simulates the intuition, experience, and decision-making process of human experts in solving three-dimensional packing problems. This approach is reflected in the action space design, which seeks to understand and imitate human decision-making patterns.
3.2.1. Human-like Placement Strategy Action Space
In the three-dimensional packing problem, simulating human experts’ spatial planning capabilities is crucial for action space design. This process involves understanding and imitating human intuition and experience when deciding the placement location and orientation of items. To achieve this goal, a comprehensive placement strategy algorithm was developed to simulate human decision-making during spatial planning and item placement (Figure 6 for details).
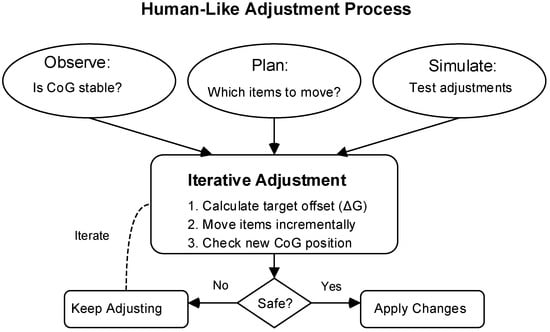
Figure 6.
Brief diagram of human-like placement strategy.
Firstly, the algorithm needs to consider the internal spatial layout of the container, which involves modeling the container’s interior in three dimensions and keeping track of the real-time spatial position of already placed items. When placing items, human experts determine the optimal placement based on the container’s spatial layout and current fill status. To simulate this, three-dimensional spatial analysis techniques are employed to model the container’s interior precisely and update space changes after item placement in real time. The algorithm determines placement based on the characteristics of the items, such as size, shape, weight, and specific handling requirements (e.g., fragility or orientation). Imitating human intuition is particularly important here. For instance, heavier items are typically placed at the bottom to increase stability, while regular-shaped items are prioritized to improve space utilization. Additionally, the algorithm considers the interaction between items. In practical packing scenarios, human experts assess the fit between items to avoid unusable spaces between irregular-shaped items. Therefore, an optimization module is included in the algorithm to evaluate the impact of different placement plans on overall space utilization.
Combining the outputs from each of the above modules, we have designed the following strategy for placing actions:
In order to formally describe each step of the above advanced placement action algorithm, we can introduce a series of mathematical formulas and functions to precisely define the logic of the algorithm. The following is a formal description of each step:
- (1)
- Spatial assessment
Let be the 3D spatial state of the container and be the remaining spatial volume of the container.
Let be a function to calculate the space utilization around the goods of .
- (2)
- Supporting considerations
Let be the weight of the cargo and be the weight distribution of the container.
Let be a function to evaluate the weight distribution of a shipment after placement.
- (3)
- Shape adaptation analysis
Let be the geometric shape of the goods and be the shape fitness score.
Let be a function that evaluates the match between the shape of the goods and the remaining space.
- (4)
- Mechanisms for the protection of fragile items
Let be an indicator of cargo fragility and be a risk score for fragile cargo placement.
Let be a function to evaluate the risk of placing fragile goods.
- (5)
- Optimization solver
Let be a function to find the optimal placement scheme under the given constraints.
- (6)
- Multi-program evaluation
Let be a function to evaluate multiple placement actions.
Combining the above steps, the mathematical expression for the final placement decision is
3.2.2. Human-like Micro-Adjustment Mechanism
For formalizing each step of the space adjustment algorithm, a series of functions and mathematical expressions are introduced to precisely define the logic. Here are the formal descriptions of each step:
- (a)
- Local Space Assessment
Let be a function to evaluate the utilization of space around the goods of .
- (b)
- Dynamic Weight Distribution Analysis
Let be an algorithmic function to analyze the weight distribution under the current cargo layout.
This algorithm aims to optimize the center of gravity adjustment in the three-dimensional online packing process based on the time series to enhance loading safety and stability. Initially, it evaluates whether the center of gravity in the packing configuration meets safety standards. If not, the algorithm calculates the necessary center of gravity shift and identifies adjustable items. By simulating different item moving plans, the algorithm finds layouts that effectively shift the center of gravity to a safe area, iterating as needed to ensure the final configuration both optimizes space utilization and maintains stability, The pseudo-code is Algorithm 2:
| Algorithm 2 Time Sequence Center of Gravity Update Algorithm | |
| 1: | Input: |
| 2: | Output: if the center of gravity is outside the safety range |
| 3: | : is the position vector of item i. |
| 4: | if is within the safety range then |
| 5: | |
| 6: | else |
| 7: | to bring the center of gravity within the safety range: is the desired center of gravity. |
| 8: | . |
| 9: | do |
| 10: | if item i is movable then |
| 11: | : is a scaling factor that adjusts item movement. |
| 12: | based on the new layout: |
| 13: | is within the safety range then |
| 14: | |
| 15: | end if |
| 16: | end if |
| 17: | end for |
| 18: | is not empty then |
| 19: | Execute all adjustments in |
| 20: | |
| 21: | else |
| 22: | return “Adjustment not possible” |
| 23: | end if |
| 24: | end if |
- (c)
- Geometry Matching and Adjustment
Let be a function to evaluate the efficiency of the geometric layout of the current cargo.
- (d)
- Safety Considerations
Let be a function that evaluates the impact of an adjusted cargo layout on the security of fragile or high-value cargo.
- (e)
- Safety Considerations
Let be a function that is used to find the optimal cargo adjustment solution, subject to satisfying specific constraints.
Combining the above steps, the final decision to adjust the action can be formally represented as follows:
where each function represents a key step in the algorithm and combines to form a comprehensive, multi-dimensional tuning strategy. This formal description allows the tuning space algorithm to mimic the fine-tuning strategies of human experts in all aspects, providing a more refined and efficient solution to the 3D crating problem.
3.2.3. Placement Decision Algorithm Design
The model adopts an attention-based neural network with residual connections as the encoder to extract item features. The actor network, built upon a pointer mechanism [14], serves as the decoder to select leaf nodes and output actions, while the critic network evaluates these actions and predicts future packing states and rewards. The actor incorporates a multi-head attention layer (8 heads, 64 dimensions each) and uses a combined feature vector of size 256 as input, processed through fully connected layers. The critic shares part of the encoder and uses a value head to estimate state values, trained with TD (λ) (λ = 0.95) to reduce variance.
The entire network is trained using a composite loss function that incorporates both actor and critic objectives, as illustrated in Figure 7. The ACKTR algorithm [23] is employed for natural gradient updates, utilizing a Kronecker-factored approximation of the Fisher Information Matrix to update parameters efficiently. This approach replaces traditional gradient descent and enhances the stability and convergence of the agent during training. The definitions for loss functions are
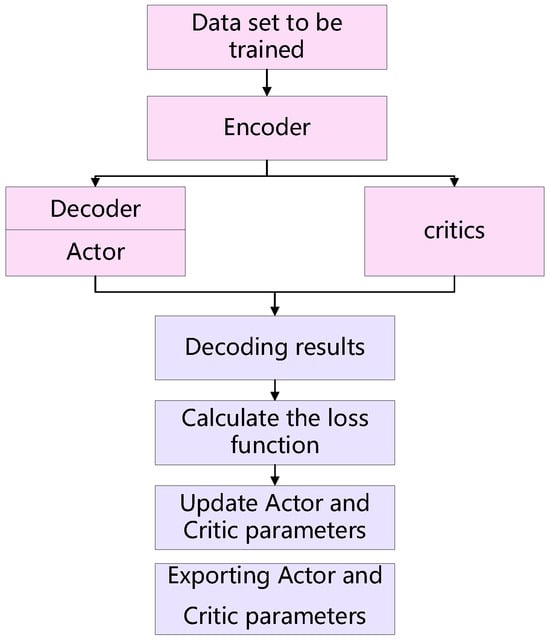
Figure 7.
DRL framework of decision training process.
The discount factor is set to 1 due to the limited data involved in the packing process. The reward function is , as our primary optimization objective is to maximize the space utilization of the container. Additional attribute constraints can be added to the reward function if required for specific item properties, such as species or density. The packing process terminates when an item cannot be placed. Specifically, when symmetry and stability constraints are critical (e.g., in fragile goods or heavy machinery transportation), the reward function can be extended as follows:
where the symmetry reward component is
measuring the deviation of center of gravity from the container’s geometric center, with controlling sensitivity.
4. Experiments
4.1. Experimental Design
4.1.1. Experimental Environment Design
This paper employs the dual pointer network algorithm described in Section 3 to conduct experiments on the time-series-based three-dimensional packing problem. The experimental dataset and test set are generated according to Section 2, simulating a scenario involving goods and containers in a logistics center. The experimental hardware environment includes an Intel i9-11900K CPU (Santa Clara, CA, USA), 64 GB of memory (Icheon, Gyeonggi-do, South Korea), and an RTX 3090 GPU (Santa Clara, CA, USA). The software environment is Python 3.8.9 with CUDA 11.1 and cuDNN 8.2.1 for GPU computation. Python acceleration libraries like NumPy 1.19.5 and Numba 0.53.1 are used, and the neural network is implemented using PyTorch 1.9.0. Experiments start with a small scale (e.g., 500 items and 20 containers) and gradually increase to larger scales to test the algorithm’s generalization ability and efficiency. The results of the dual pointer network are compared with traditional heuristic algorithms (e.g., Genetic Algorithm, Simulated Annealing) across different metrics. Moreover, dedicated source codes are written for experimental data generation and algorithm comparison, with implementation details provided in Section 4.1.3.
4.1.2. Comparative Experiment Design
The main purpose of this experiment is to verify the effectiveness of the second-order dual pointer adversarial network (referred to as “our algorithm”) in the three-dimensional packing problem. To achieve this, we designed a series of comparative experiments to compare the performance of our algorithm with other commonly used algorithms. The experiment includes three comparative studies, using DQN and DDPG as reinforcement learning algorithms, Ant Colony and Simulated Annealing as heuristic learning algorithms, and a search tree algorithm as comparison objects. The experimental steps are as follows:
- (a)
- Solution Quality Comparative Experiment
This experiment aims to evaluate the efficiency of various algorithms in solving the three-dimensional packing problem. A set of standardized test cases covering different item sizes, shapes, and weights is used. By comparing each algorithm’s performance in terms of packing efficiency, space utilization, and stability, we can evaluate their solution quality. We particularly focus on the performance of the second-order dual pointer adversarial network when dealing with diverse packing configurations, as well as its advantages and disadvantages compared to other algorithms.
- (b)
- Model Generalization Comparative Experiment
This experiment tests the performance of each algorithm on different types of datasets to assess their generalization ability. By running each algorithm on diverse datasets—including those with different numbers of items, size distributions, and container dimensions—we can observe their adaptability and flexibility. This reveals the second-order dual pointer adversarial network’s capability in dealing with unknown or changing conditions, providing a basis for evaluating its practical applicability.
- (c)
- Model Convergence Comparative Experiment
Lastly, we focus on the convergence performance of each algorithm during the iterative process. By recording and analyzing the performance changes during continuous iterations, we can evaluate the learning efficiency and stability of each algorithm. For the second-order dual pointer adversarial network, we are particularly interested in its performance and convergence speed during continuous learning. Comparing this with other algorithms’ convergence performance allows us to understand the advantages of our proposed algorithm in dynamic learning environments.
- (d)
- Ablation Study Design
To systematically evaluate the contribution of each component in the So-DPAN architecture, we conduct comprehensive ablation experiments by progressively removing key modules. The baseline configuration includes all components, namely the dual pointer mechanism, second-order optimization, adversarial training, and symmetry-aware reward function. We create four variant models by removing each component individually while keeping others intact. The first variant replaces the dual pointer mechanism with a single pointer network to assess the impact of dual sequence matching. The second variant substitutes second-order optimization with first-order gradient descent to evaluate the benefits of higher-order optimization. The third variant removes adversarial training to examine its role in improving robustness. The fourth variant employs a standard reward function without symmetry considerations to quantify the importance of symmetry-aware optimization. Each variant undergoes identical training procedures with 1000 epochs using the same dataset splits, and performance metrics including space utilization, computational time, and convergence speed are recorded for comprehensive comparison.
4.1.3. Experimental Data Design
This study designed a systematic experimental dataset to evaluate the performance of the second-order dual pointer adversarial network and comparison algorithms in three-dimensional packing, covering scenarios from small e-commerce to large-scale warehousing. The dataset includes items ranging from 40 to 5000 pieces with randomly generated sizes (5–50 cm) across multiple container types (small ≤ 30 cm, medium 30–60 cm, large > 60 cm), incorporating extreme sizes to test robustness. Item dimensions follow a truncated normal distribution (means: 25/45/70 cm for small/medium/large items), weights correlate with volume via , and arrival times simulate real logistics patterns using Poisson distributions with peak/off-peak inter-arrival rates. Container specifications reflect industry standards, and the dataset comprises 10,000 unique item-container pairing scenarios with varying complexity to comprehensively assess solution quality, generalization, and convergence performance. The schematic diagram is shown in Figure 8.
Figure 8.
Generated data 3D distribution and shape diagram process.
4.2. Experimental Results and Analysis
This chapter presents and analyzes the results obtained from the experimental designs proposed in Section 4.1.2. By comparing the performance of our algorithm (the second-order dual pointer adversarial network) with the comparison group algorithms, this chapter aims to explore the efficiency and applicability of each algorithm in depth.
4.2.1. Solution Quality Comparative Experiment
In this section, we discuss and analyze the performance of each algorithm in the solution quality comparative experiment. By examining each algorithm’s efficiency, space utilization, and stability when solving specific packing problems, we evaluate the practical effectiveness of the second-order dual pointer adversarial network, while comparing its performance with other algorithms to demonstrate its relative advantages.
In this study, we divide the experiments into small-scale and large-scale parts. Small-scale experiments involve five containers arranged in a time series and 500 items, with the dual pointer network trained accordingly. To evaluate the model’s performance during training, 100 problems of the same scale were generated as an evaluation set. In addition, 60 problems were generated as a test set to compare the performance of the dual pointer network and heuristic algorithms. In large-scale experiments, 50 containers and 5000 items were used to train the same network. Similarly, 100 problems were generated as an evaluation set for model evaluation, and another 60 problems as a test set.The experimental results are shown in Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14.
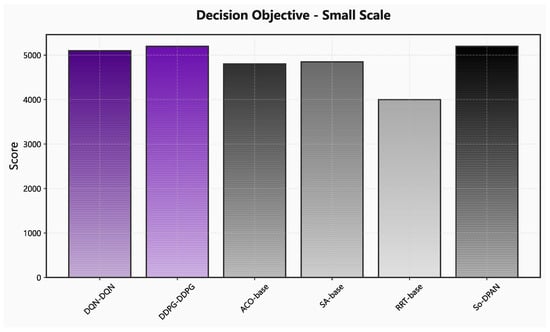
Figure 9.
Comparison of decision objectives of different algorithms for small-scale problems.
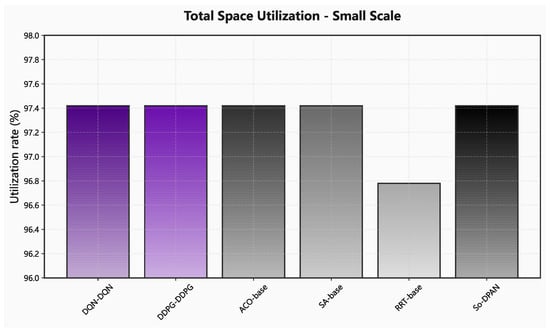
Figure 10.
Comparison of space utilization of small-scale problems by different algorithms.
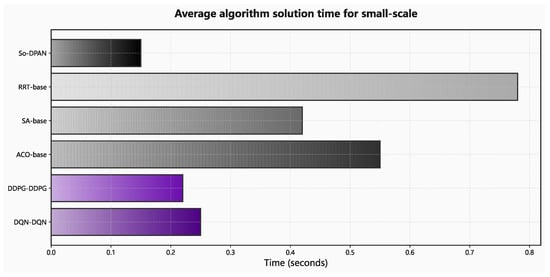
Figure 11.
Comparison of average solving time of small-scale problems with different algorithms.
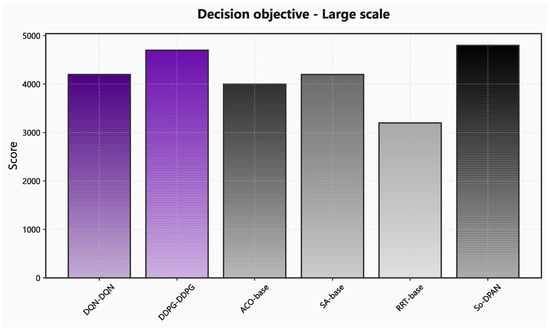
Figure 12.
Comparison of decision goal values of different algorithms for large-scale problems.
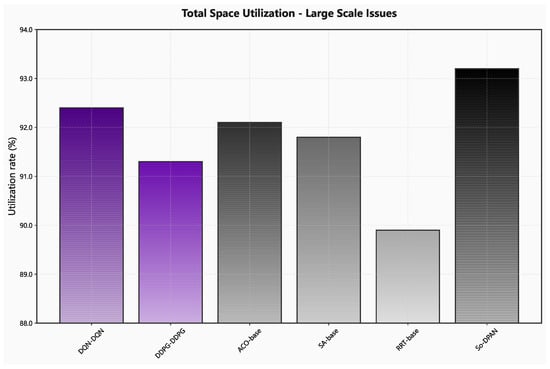
Figure 13.
Comparison of space utilization of different algorithms for large-scale problems.
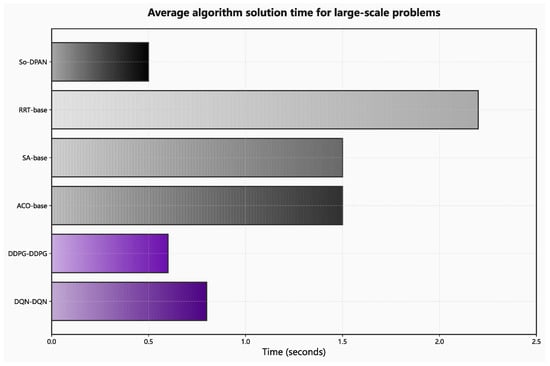
Figure 14.
Comparison of average solving time of large-scale problems by different algorithms.
From the results of small-scale problems, the optimization capability of the five algorithms is comparable, but the second-order dual pointer adversarial network’s solving time is significantly shorter than that of heuristic algorithms and random search trees. As the problem scale increases, the second-order dual pointer adversarial network algorithm maintains the optimal state in optimization ability. In terms of solving time, the proposed algorithm outperforms other algorithms significantly. Due to its advantages in time efficiency, it avoids the redundant computations faced by other algorithms when dealing with large-scale problems, thereby significantly reducing solving time.
4.2.2. Model Generalization Comparative Experiment
This section analyzes and discusses the performance of each algorithm in the model generalization comparative experiment. By testing algorithms on different types and scales of datasets, this section aims to evaluate the adaptability and flexibility of each algorithm, particularly the generalization ability of the second-order dual pointer adversarial network in diverse logistics environments.
In this experiment, the problem scale was expanded to 10 containers, with a stepwise increase in both container and item quantities. At each problem scale, items with randomly generated properties were added to meet generation requirements. To maintain consistency, the Genetic Algorithm was kept at a population size of 100, with 100 generations, while the Simulated Annealing Algorithm was kept at an initial temperature of 100,000 and 1000 iterations. The solving performance of each algorithm under different problem scales is shown as Figure 15.
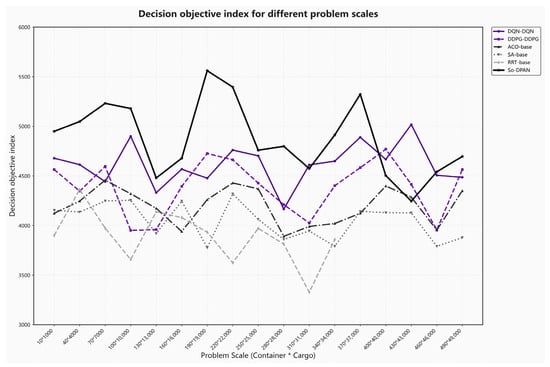
Figure 15.
Decision objective index of different problem sizes.
The results indicate that with increasing problem size, the second-order deep Q network demonstrates superior performance compared to DDPG, Ant Colony Algorithm, Simulated Annealing, and Random Search Tree Algorithm, but it still slightly falls short compared to the dual pointer adversarial network. Moreover, in terms of solving time for larger-scale problems, the time required by Random Search Tree, Simulated Annealing, and Ant Colony Algorithms rises sharply, while the time increase for the second-order deep Q network and DDPG is less significant. Results show that in most cases, the solving time of the second-order dual pointer adversarial network is still superior.
Figure 16 provides a comprehensive analysis of algorithm scalability by examining solution time trends across varying problem scales from 10 to 490 items. The results reveal distinct performance patterns among different algorithm categories. Traditional heuristic methods including Ant Colony optimization, Simulated Annealing (SA base), and Random Search Tree (BRT base) exhibit exponential growth in solution time as problem scale increases, with BRT base showing the steepest degradation, reaching nearly 18 s for problems approaching 10,000 items. This exponential behavior stems from their exhaustive search nature and inability to leverage learned patterns from previous solutions. In stark contrast, deep reinforcement learning approaches demonstrate remarkably superior scalability characteristics. So-DPAN maintains the most stable performance trajectory, with solution times increasing only marginally from 0.3 s at 10 items to 2.1 s at 10,000 items, representing a sub-linear growth pattern. The DQN and DDPG variants show intermediate performance, with DOPG-DDPG achieving slightly better efficiency than standard implementations. This superior scalability of So-DPAN can be attributed to its dual pointer mechanism efficiently pruning the search space and the second-order optimization enabling faster convergence to high-quality solutions without exhaustive exploration. The performance gap between learning-based and traditional methods widens dramatically as problem complexity increases, with So-DPAN achieving up to 8.5× speedup compared to the best-performing heuristic method at the 10,000-item scale, validating its suitability for large-scale real-time logistics operations where rapid decision-making is critical.
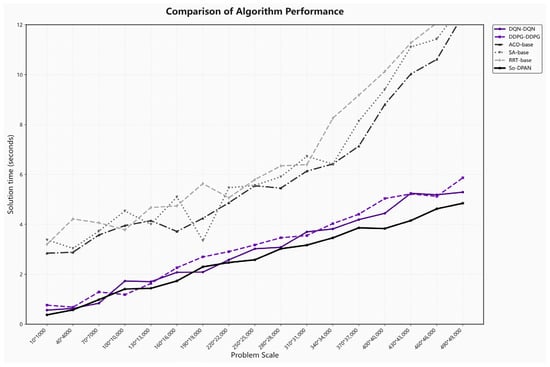
Figure 16.
Comparison of Algorithm Performance.
4.2.3. Model Convergence Comparative Experiment
In this section, we focus on the performance of each algorithm in the model convergence comparative experiment. By analyzing the performance changes of each algorithm during continuous iterations, this section aims to reveal the learning efficiency and stability characteristics of the second-order dual pointer adversarial network and other algorithms, providing important insights for further optimizing the algorithm.
In this experiment, due to the nature of reinforcement learning, we only compare our algorithm with DQN and DDPG in terms of training performance. As shown in Figure 17.
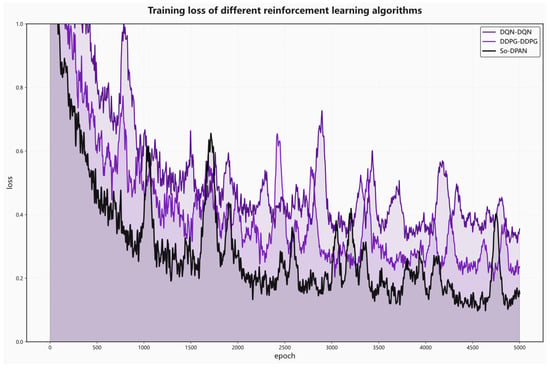
Figure 17.
Training performance of different algorithms.
In the early training phase, compared to DQN and DDPG, the dual pointer adversarial network shows faster convergence speed. After 600 training epochs, it exhibits a near-exponential decline trend, ultimately reaching convergence. This demonstrates the significant advantage of the model in terms of training speed.
4.2.4. Ablation Study Results
The ablation study provides crucial insights into the contribution of each architectural component to the overall performance of So-DPAN. We systematically evaluate the impact of removing individual components from the complete model on large-scale problems involving 5000 items. Table 2 presents the detailed ablation results based on comprehensive experimental evaluation.

Table 2.
Ablation study results on large-scale problems (5000 items).
Experimental results demonstrate that each component of So-DPAN plays a critical role: removing the dual-pointer mechanism leads to a 2.0% decrease in space utilization and a 29.2% increase in solving time; the absence of second-order optimization increases solving time from 0.48 s to 1.38 s and reduces the objective score by 12.4%; disabling adversarial training causes a 13.3% drop in the objective score, confirming its role in enhancing policy robustness; while deactivating the symmetry-aware reward function results in a significant performance degradation of 16.6%, highlighting the necessity of explicitly encoding physical constraints. Synergistic effects are observed among components—for example, removing both the dual-pointer mechanism and second-order optimization results in a 28.5% performance decline, indicating that these components complement each other in addressing complex optimization challenges. The ablation study confirms that the full architecture is essential for achieving optimal performance, justifying the additional computational complexity introduced by each component.
5. Conclusions
This paper has addressed a critical gap in logistics optimization by formulating and solving the time-series-based three-dimensional online packing problem with dual unknown sequences. Our primary contribution, the Second-Order Dual Pointer Adversarial Network (So-DPAN), represents a fundamental advancement in handling dynamic logistics scenarios where both containers and items arrive stochastically over time. The proposed architecture successfully decomposes the complex spatiotemporal optimization problem into manageable sequence matching and spatial arrangement components, achieving superior performance compared to existing approaches. In particular, the 93.2% space utilization achieved by So-DPAN substantially surpasses the 85–87% range reported by recent Transformer-based approaches [27,28], while our dual pointer mechanism overcomes the sequence matching challenges identified by Tsang et al. [21]. The key innovations manifest in three dimensions: first, the problem formulation captures real-world logistics dynamics through explicit modeling of temporal dependencies and dual uncertainty, moving beyond traditional assumptions of known container sets; second, the So-DPAN architecture leverages adversarial training and second-order optimization to achieve robust performance across diverse operational conditions; third, the phased reinforcement learning strategy with ACKTR optimization demonstrates significant improvements in convergence speed and solution quality, making real-time deployment feasible.
Our comprehensive experimental evaluation reveals that So-DPAN consistently outperforms baseline algorithms including DQN, DDPG, and traditional heuristics across multiple metrics and problem scales. The computational efficiency gains demonstrated by So-DPAN—maintaining 0.48 s solving times for 5000-item instances—directly address the scalability concerns raised by Montes-Franco et al. [17] regarding hybrid algorithms with exponential complexity, and overcome the computational bottlenecks identified by Bonet Filella et al. [32] as barriers to real-time optimization. Compared to the learning-augmented algorithms proposed by Grigorescu et al. [33] and Angelopoulos et al. [35], which achieve consistency-robustness tradeoffs through prediction mechanisms, our adversarial training component enhances robustness without requiring explicit prediction models. Furthermore, our symmetry-aware reward design advances beyond the implicit stability considerations in previous work [5,10] by providing explicit mathematical formulations for balance optimization, addressing the gap identified by Junqueira et al. [5] between theoretical models and practical stability requirements. The algorithm’s ability to generalize across different container configurations and item distributions addresses crucial requirements for practical deployment, while its compatibility with existing warehouse management systems facilitates immediate industrial adoption.
The generalization capabilities demonstrated across diverse problem scales extend the findings of Pan et al. [26] on adjustable robust reinforcement learning, showing that architectural innovations can achieve robustness without sacrificing average-case performance. While their AR2L framework balances scenarios through adjustable parameters, our dual pointer mechanism inherently maintains consistent performance across varying complexity levels without parameter tuning, addressing the generalization challenges highlighted by Hadjidj and Oulamara [30]. The successful integration of spatial and temporal constraints also validates theoretical predictions from smart logistics literature [34] regarding holistic optimization approaches. Despite these contributions, several limitations warrant acknowledgment: the current implementation assumes deterministic item properties, whereas real operations involve measurement uncertainties, and our approach does not explicitly model seasonal patterns or long-term trends. Future research should extend So-DPAN to handle stochastic properties, incorporate predictive demand forecasting, integrate with robotic manipulation systems, and include sustainability metrics. This research establishes a foundation for addressing complex logistics challenges in Industry 4.0, providing both theoretical insights and practical tools for next-generation smart logistics systems.
Author Contributions
Conceptualization, Z.Z. and X.Z.; methodology, Z.Z. and E.W.; software, Z.Z.; validation, Z.Z., E.W. and X.Z.; formal analysis, E.W.; investigation, Z.Z.; resources, X.Z.; data curation, Z.Z.; writing—original draft preparation, Z.Z.; writing—review and editing, E.W. and X.Z.; visualization, Z.Z.; supervision, X.Z.; project administration, E.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhao, H.; She, Q.; Zhu, C.; Yang, Y.; Xu, K. Online 3D bin packing with constrained deep reinforcement learning. Proc. AAAI Conf. Artif. Intell. 2021, 35, 741–749. [Google Scholar] [CrossRef]
- Duan, L.; Hu, H.; Qian, Y.; Gong, Y.; Zhang, X.; Wei, J.; Xu, Y. A multi-task selected learning approach for solving 3D flexible bin packing problem. In Proceedings of the 21st International Conference on Autonomous Agents and Multiagent Systems, Auckland, New Zealand, 9–13 May 2022; pp. 391–399. [Google Scholar]
- Gajda, M.; Trivella, A.; Mansini, R.; Pisinger, D. An optimization approach for a complex real-life container loading problem. Omega 2022, 107, 102559. [Google Scholar] [CrossRef]
- Chen, Y.W. Three-dimensional cartoning problem based on genetic algorithm with prioritized holding strategy. Packag. Eng. 2021, 42, 211–218. [Google Scholar]
- Junqueira, L.; Morabito, R.; Yamashita, D.S. Three-dimensional container loading models with cargo stability and load bearing constraints. Comput. Oper. Res. 2012, 39, 74–85. [Google Scholar] [CrossRef]
- Lu, M.; Lu, H.; Hou, X.; Hu, Q. A self-adaptive arithmetic optimization algorithm with hybrid search modes for 0–1 knapsack problem. Neural Comput. Appl. 2024, 36, 21177–21210. [Google Scholar] [CrossRef]
- Hasan, J.; Kaabi, J.; Harrath, Y. Multi-objective 3D bin-packing problem. In Proceedings of the 2019 8th International Conference on Modeling Simulation and Applied Optimization (ICMSAO), Manama, Bahrain, 15–17 April 2019; pp. 1–5. [Google Scholar]
- Liu, S.; Shen, D.Y.; Shang, X.Q. A multilayer tree search algorithm for solving three-dimensional crating problems. J. Autom. 2020, 46, 1178–1187. [Google Scholar]
- Qu, Y.; Bard, J.F. A branch-and-price-and-cut algorithm for heterogeneous pickup and delivery problems with configurable vehicle capacity. Transp. Sci. 2015, 49, 254–270. [Google Scholar] [CrossRef]
- Zhu, W.; Chen, S.; Dai, M.; Tao, J. Solving a 3D bin packing problem with stacking constraints. Comput. Ind. Eng. 2024, 188, 109814. [Google Scholar] [CrossRef]
- Zuo, Q.; Liu, X.; Chan, W.K.V. A constructive heuristic algorithm for 3D bin packing of irregular shaped items. In Proceedings of the INFORMS International Conference on Service Science, Beijing, China, 11–13 July 2022; pp. 393–406. [Google Scholar]
- Li, M.; Zhang, S.; Bao, H. Nonlinear Integer Planning Three-Dimensional Crate Model Based on Hybrid Genetic Algorithm. In Proceedings of the International Conference on Frontier Computing, Singapore, 10–14 July 2024; Springer Nature: Singapore, 2024; pp. 477–487. [Google Scholar]
- Harrath, Y.; Aljassim, M.; Anees, L.M. Smart shipment: An efficient algorithm for packing three-dimensional bins. In Proceedings of the IET Conference Proceedings CP777, Stevenage, UK, 21–23 November 2020; The Institution of Engineering and Technology: Stevenage, UK, 2020; Volume 2020, pp. 203–208. [Google Scholar]
- Abualigah, L.; Yousri, D.; Elaziz, M.A.; Ewees, A.A.; Al-Qaness, M.A.; Gandomi, A.H. Aquila optimizer: A novel meta-heuristic optimization algorithm. Comput. Ind. Eng. 2021, 157, 107250. [Google Scholar] [CrossRef]
- Gao, P.; Zhang, D.Z.; Zhang, X.G. Dynamic fusion policy optimization algorithm for container loading problem. Comput. Eng. Appl. 2023, 59, 255–265. [Google Scholar]
- Lamas-Fernandez, C.; Bennell, J.A.; Martinez-Sykora, A. Voxel-based solution approaches to the three-dimensional irregular packing problem. Oper. Res. 2023, 71, 1298–1317. [Google Scholar] [CrossRef]
- Montes-Franco, A.M.; Martinez-Franco, J.C.; Tabares, A.; Álvarez-Martínez, D. A hybrid approach for the container loading problem for enhancing the dynamic stability representation. Mathematics 2025, 13, 869. [Google Scholar] [CrossRef]
- Jiang, Y.; Cao, Z.; Zhang, J. Solving 3D bin packing problem via multimodal deep reinforcement learning. In Proceedings of the 20th International Conference on Autonomous Agents and MultiAgent Systems, London, UK, 3–7 May 2021; pp. 1548–1550. [Google Scholar]
- Zhang, J.; Zi, B.; Ge, X. Attend2Pack: Bin packing through deep reinforcement learning with attention. IEEE Trans. Autom. Sci. Eng. 2022, 19, 2270–2280. [Google Scholar]
- Kool, W.; van Hoof, H.; Gromicho, J.; Welling, M. Deep policy dynamic programming for vehicle routing problems. In Proceedings of the International Conference on Integration of Constraint Programming, Artificial Intelligence, and Operations Research, Los Angeles, CA, USA, 21–24 June 2022; pp. 190–213. [Google Scholar]
- Tsang, Y.P.; Mo, D.Y.; Chung, K.T.; Lee, C.K.M. A deep reinforcement learning approach for online and concurrent 3D bin packing optimisation with bin replacement strategies. Comput. Ind. 2025, 164, 104202. [Google Scholar] [CrossRef]
- Puche, A.V.; Lee, S. Online 3D bin packing reinforcement learning solution with buffer. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; pp. 8902–8909. [Google Scholar]
- Zhao, H.; Zhu, C.; Xu, X.; Huang, H.; Xu, K. Learning practically feasible policies for online 3D bin packing. Sci. China Inf. Sci. 2022, 65, 112105. [Google Scholar] [CrossRef]
- Verma, R.; Singhal, A.; Khadilkar, H.; Basumatary, A.; Nayak, S.; Singh, H.S.; Kumar, S.; Sinha, R. A generalized reinforcement learning algorithm for online 3d bin-packing. arXiv 2020, arXiv:2007.00463. [Google Scholar] [CrossRef]
- Yang, S.; Song, S.; Chu, S.; Song, R.; Cheng, J.; Li, Y.; Zhang, W. Heuristics integrated deep reinforcement learning for online 3D bin packing. IEEE Trans. Autom. Sci. Eng. 2023, 20, 450–462. [Google Scholar] [CrossRef]
- Pan, Y.; Chen, Y.; Lin, F. Adjustable robust reinforcement learning for online 3D bin packing. In Proceedings of the 37th Conference on Neural Information Processing Systems, New Orleans, LA, USA, 10–16 December 2023. [Google Scholar]
- Que, R.; Guo, W.; Wang, R.; Liu, L.; Fang, S.C. Solving 3D packing problem using Transformer network and reinforcement learning. Expert Syst. Appl. 2023, 214, 119059. [Google Scholar] [CrossRef]
- Li, J.; Zhang, L.; Wang, H. GOPT: Generalizable online 3D bin packing via transformer-based deep reinforcement learning. IEEE Robot. Autom. Lett. 2024, 9, 9845–9852. [Google Scholar] [CrossRef]
- Jiang, H.; Fang, Q.; Zhang, Y.; Ma, Q.; Xu, R. TAP-Net: Transport-and-pack using reinforcement learning. ACM Trans. Graph. 2023, 42, 1–15. [Google Scholar]
- Hadjidj, H.; Oulamara, A. Deep reinforcement learning for solving the single container loading problem. Eng. Optim. 2023, 55, 668–684. [Google Scholar]
- Luo, Q.; Zhou, X.S.; Wang, Y.; Li, J. Container loading problem based on robotic loader system: An optimization approach. Expert Syst. Appl. 2023, 230, 120622. [Google Scholar]
- Bonet Filella, G.; Trivella, A.; Corman, F. Modeling soft unloading constraints in the multi-drop container loading problem. Eur. J. Oper. Res. 2023, 308, 336–352. [Google Scholar] [CrossRef]
- Grigorescu, E.; Lin, Y.S.; Silwal, S.; Song, M.; Zhou, S. A simple learning-augmented algorithm for online packing with concave objectives. arXiv 2024, arXiv:2406.03574. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, J.; Li, X. Smart logistics nodes: Concept and classification. Int. J. Logist. Res. Appl. 2024, 27, 1485–1502. [Google Scholar] [CrossRef]
- Angelopoulos, S.; Kamali, S.; Shadkami, K. Online bin packing with predictions. J. Artif. Intell. Res. 2023, 78, 315–342. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).