On the Conformable Triple Laplace–Sumudu Transform and Two-Dimensional Fractional Partial Differential Equations

Abstract

In this work, we introduce the conformabletriple Laplace–Sumudu transform (CTLST), a novel integral transform designed to solve both linear and nonlinear conformable FPDEs. This new approach builds on the recent development of the triple Laplace–Sumudu transform and incorporates the conformable derivative to extend its applicability to fractional models. We first present the foundational definitions and key properties of the CTLST, followed by its application to a variety of two- and three-dimensional conformable FPDEs. The effectiveness of the proposed method is demonstrated through several examples, where exact and approximate solutions are derived, illustrative 3D plots are presented, and symmetry analysis is employed to verify the obtained results. The CTLST provides a promising analytical tool for tackling complex conformable FPDEs in mathematical physics and engineering.

1. Introduction

Fractional partial differential equations (FPDEs) have become a central topic of research in mathematics and applied sciences due to their ability to model complex systems with memory and hereditary properties [1]. Their applications span a broad range of fields, including fluid mechanics, physics, biology, chemistry, economics, electromagnetic theory, and signal processing [2].

Solution methods play a vital role in the analysis and classification of differential equations. Integral transforms such as the Laplace, Fourier, Mellin, Hankel, and Sumudu transforms are among the most powerful tools for solving both ordinary and partial differential equations [3,4,5]. However, when solutions are not expressible in Taylor series form or the Laplace transform becomes difficult to compute, alternative approaches are needed.

In response to such challenges, the conformable fractional derivative (CFD) was introduced as a more accessible form of fractional calculus [6]. Defined using a limit-based approach, the CFD has attracted attention for its simplicity and effectiveness in modeling and analysis across numerous disciplines [7].

The Laplace transform remains widely used for solving fractional differential equations (FDEs), including both exact and approximate solutions [8,9]. To further extend its applicability, the single conformable Laplace transform (SCLT) was introduced in [10] as a natural adaptation of the classical Laplace transform to conformable derivatives.

Subsequent advancements include numerical methods for time–space FPDEs involving the spectral fractional Laplacian [11], and the introduction of the conformable double Laplace transform (CDLT) for solving more complex fractional models [12]. In parallel, the double Sumudu and Laplace–Sumudu transforms have been successfully applied to wave equations and other partial differential equations [13,14,15,16].

More recently, the combination of conformable transforms with decomposition methods has been employed to solve nonlinear FPDEs [17,18], and the triple Laplace–Sumudu transform was introduced in [19] to handle heat and wave equations with boundary conditions. Another significant approach is Lie symmetry analysis, which is used to investigate the invariance properties of nonlinear FPDEs involving conformable fractional derivatives in both time and space. This technique has been applied to generalized forms of classical equations such as the Korteweg–de Vries, Burgers, and modified Burgers equations [20].

In this paper, we build upon these developments and introduce the CTLST, a new analytical tool designed to solve both linear and nonlinear conformable FPDEs. We present the foundational definitions of the conformable Laplace transform, the conformable Sumudu transform, and the proposed CTLST. We then establish the core properties of the CTLST and apply it to a range of fractional partial differential equations. Illustrative examples and 3D plots are included to demonstrate the effectiveness of the method.

2. Terminology and Properties

In this section, we review the definitions of key integral transforms used in this work, including the conformable Laplace transform, the conformable Sumudu transform, and the conformable double Laplace transform. We then introduce the CTLST, which plays a central role in our proposed methodology.

Before proceeding with these definitions, we recall the concept of a function of exponential order. A function $g\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }}\right)$ is said to be of exponential order i with respect to ${\displaystyle \frac{p^{\mu }}{\mu }}$, and of order j with respect to ${\displaystyle \frac{q^{\eta }}{\eta }}$, if there exists a constant $M>0$ such that for all $p>S_1$ and $q>S_2$, the inequality

$$\left|g\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }}\right)\right|<M{e}^{i{\displaystyle \frac{p^{\mu }}{\mu }}+j{\displaystyle \frac{q^{\eta }}{\eta }}}$$

holds [21].

Definition 1

(Definition 4 [22]). Let f be a continuous function on $[0,\infty )$. The conformable Sumudu transform (CST) of $f\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)$ is defined as

$$S_r^{\delta }\left[f\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]={\displaystyle \frac{1}{\phi }}{\int }_0^{\infty }{e}^{-{\displaystyle \frac{1}{\phi }}{\displaystyle \frac{r^{\delta }}{\delta }}}f\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)d^{\delta }r=F\left(\phi \right),$$

(1)

where $d^{\delta }r=r^{\delta -1}dr$, $0<\delta \le 1$, and $\phi \in \mathbb{C}$.

Definition 2.

Let g:$[0,\infty )\to \mathbb{R}$ be a real-valued function. The conformable Laplace transform (CLT) of $g\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)$ is given by

$$L_p^{\mu }\left[g\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)\right]={\int }_0^{\infty }{e}^{-{\theta }_1\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)}g\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)dp=G\left({\theta }_1\right)$$

(2)

for all values of ${\theta }_1\in \mathbb{C}$, provided the integral exists.

Definition 3

(Definition 5 [21]). Let $g\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }}\right)$ be a piecewise continuous function on $[0,\infty )\times [0,\infty )$ and of exponential order. The CDLT is defined as

$$L_p^{\mu }{L}_q^{\eta }\left[g\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }}\right)\right]={\int }_0^{\infty }{\int }_0^{\infty }{e}^{-{\theta }_1\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)-{\theta }_2\left({\displaystyle \frac{q^{\eta }}{\eta }}\right)}g\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }}\right)dpdq=G({\theta }_1,{\theta }_2),$$

(3)

where $0<\mu ,\eta \le 1$ and ${\theta }_1,{\theta }_2\in \mathbb{C}$.

We now introduce the definition of the conformable triple Laplace–Sumudu transform (CTLST), along with its inverse.

Definition 4.

Let $\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)$ be a piecewise continuous function of exponential order. The conformable triple Laplace–Sumudu transform (CTLST), denoted by $L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }$, is defined as

$$\begin{array}{cc}\hfill L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]& ={\displaystyle \frac{1}{\phi }}{\int }_0^{\infty }{\int }_0^{\infty }{\int }_0^{\infty }{e}^{-{\theta }_1\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)-{\theta }_2\left({\displaystyle \frac{q^{\eta }}{\eta }}\right)-{\displaystyle \frac{1}{\phi }}\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}\hfill \\ \hfill & \times \mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)dpdqdr\hfill \\ \hfill & =\mathsf{\Phi }({\theta }_1,{\theta }_2,\phi ),\hfill \end{array}$$

(4)

where ${\displaystyle \frac{p^{\mu }}{\mu }}>0$, ${\displaystyle \frac{q^{\eta }}{\eta }}>0$, ${\displaystyle \frac{r^{\delta }}{\delta }}>0$, ${\theta }_1,{\theta }_2,\phi \in \mathbb{C}$, and $\mu ,\eta ,\delta \in (0,1]$.

Definition 5.

The inverse conformable triple Laplace–Sumudu transform (ICTLST), denoted by $L_p^{-1}{L}_q^{-1}{S}_r^{-1}$, of a function $\mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)$ is defined by

$$\begin{array}{cc}\hfill L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[\mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)\right]& =\left[{\displaystyle \frac{1}{2\pi i}}{\int }_{{\epsilon }_2-i\infty }^{{\epsilon }_1+i\infty }{e}^{-{\theta }_1\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)}d{\theta }_1\right]\times \left[{\displaystyle \frac{1}{2\pi i}}{\int }_{{\epsilon }_2-i\infty }^{{\epsilon }_1+i\infty }{e}^{-{\theta }_2\left({\displaystyle \frac{q^{\eta }}{\eta }}\right)}d{\theta }_2\right]\hfill \\ \hfill & \times \left[{\displaystyle \frac{1}{2\pi i}}{\displaystyle \frac{1}{\phi }}{\int }_{{\epsilon }_2-i\infty }^{{\epsilon }_1+i\infty }{e}^{-{\displaystyle \frac{1}{\phi }}\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}d\phi \right]=\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right).\hfill \end{array}$$

(5)

Now, we give the definitions of the conformable partial fractional derivatives and apply the CTLST to the partial derivatives of the function $\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right).$ Also, we establish several key operational properties of the transform.

Definition 6.

Let $\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)$:${\mathbb{R}}^{+}\times {\mathbb{R}}^{+}\times {\mathbb{R}}^{+}\to \mathbb{R}$ be a function. Then the conformable partial fractional derivatives of the order $\mu ,\eta$, and δ of the function Φ are defined by

$$\begin{array}{ccc}\hfill {\displaystyle \frac{{\partial }^{\mu }\mathsf{\Phi }\left(\frac{p^{\mu }}{\mu },\frac{q^{\eta }}{\eta },\frac{r^{\delta }}{\delta }\right)}{\partial p^{\mu }}}& =& \underset{\nu \to 0}{lim}{\displaystyle \frac{\mathsf{\Phi }\left(\frac{p^{\mu }}{\mu }+\nu p^{1-\mu },\frac{q^{\eta }}{\eta },\frac{r^{\delta }}{\delta }\right)-\mathsf{\Phi }\left(\frac{p^{\mu }}{\mu },\frac{q^{\eta }}{\eta },\frac{r^{\delta }}{\delta }\right)}{\nu }},\hfill \\ \hfill {\displaystyle \frac{{\partial }^{\eta }\mathsf{\Phi }\left(\frac{p^{\mu }}{\mu },\frac{q^{\eta }}{\eta },\frac{r^{\delta }}{\delta }\right)}{\partial q^{\eta }}}& =& \underset{\kappa \to 0}{lim}{\displaystyle \frac{\mathsf{\Phi }\left(\frac{p^{\mu }}{\mu },\frac{q^{\eta }}{\eta }+\kappa q^{1-\eta },\frac{r^{\delta }}{\delta }\right)-\mathsf{\Phi }\left(\frac{p^{\mu }}{\mu },\frac{q^{\eta }}{\eta },\frac{r^{\delta }}{\delta }\right)}{\kappa }},\hfill \\ \hfill {\displaystyle \frac{{\partial }^{\delta }\mathsf{\Phi }\left(\frac{p^{\mu }}{\mu },\frac{q^{\eta }}{\eta },\frac{r^{\delta }}{\delta }\right)}{\partial r^{\delta }}}& =& \underset{\sigma \to 0}{lim}{\displaystyle \frac{\mathsf{\Phi }\left(\frac{p^{\mu }}{\mu },\frac{q^{\eta }}{\eta },\frac{r^{\delta }}{\delta }+\sigma r^{1-\delta }\right)-\mathsf{\Phi }\left(\frac{p^{\mu }}{\mu },\frac{q^{\eta }}{\eta },\frac{r^{\delta }}{\delta }\right)}{\sigma }},\hfill \end{array}$$

where $0<\mu ,\eta ,\delta \le 1,$ and ${\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}>0$

Theorem 1.

Let $\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)$ be a differentiable function at ${\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}>0.$ Then

$$\begin{array}{ccc}\hfill {\displaystyle \frac{{\partial }^{\mu }}{\partial p^{\mu }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)& =& p^{-\mu +1}{\displaystyle \frac{\partial \mathsf{\Phi }\left(\frac{p^{\mu }}{\mu },\frac{q^{\eta }}{\eta },\frac{r^{\delta }}{\delta }\right)}{\partial p}},\hfill \\ \hfill {\displaystyle \frac{{\partial }^{\eta }}{\partial q^{\eta }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)& =& q^{-\eta +1}{\displaystyle \frac{\partial \mathsf{\Phi }\left(\frac{p^{\mu }}{\mu },\frac{q^{\eta }}{\eta },\frac{r^{\delta }}{\delta }\right)}{\partial q}},\hfill \\ \hfill {\displaystyle \frac{{\partial }^{\delta }}{\partial r^{\delta }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)& =& r^{-\delta +1}{\displaystyle \frac{\partial \mathsf{\Phi }\left(\frac{p^{\mu }}{\mu },\frac{q^{\eta }}{\eta },\frac{r^{\delta }}{\delta }\right)}{\partial r}}.\hfill \end{array}$$

Definition 6 and Theorem 1 are extensions of Definition 2 and Theorem 1 in [23]. For further details, the reader is referred to [24].

Theorem 2.

Let

$$L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]=\mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)$$

for $0<\mu ,\eta ,\delta \le 1.$ Then the CTLST of the functions ${\displaystyle \frac{{\partial }^{\mu }\mathsf{\Phi }}{\partial p^{\mu }}},{\displaystyle \frac{{\partial }^{\eta }\mathsf{\Phi }}{\partial q^{\eta }}},{\displaystyle \frac{{\partial }^{\delta }\mathsf{\Phi }}{\partial r^{\delta }}},{\displaystyle \frac{{\partial }^{2\mu }\mathsf{\Phi }}{\partial p^{2\mu }}},{\displaystyle \frac{{\partial }^{2\eta }\mathsf{\Phi }}{\partial q^{2\eta }}}$, and ${\displaystyle \frac{{\partial }^{2\delta }\mathsf{\Phi }}{\partial r^{2\delta }}}$ are given by the following identities:

$$L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[{\displaystyle \frac{{\partial }^{\mu }}{\partial p^{\mu }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]={\theta }_1\mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)-L_q^{\eta }{S}_r^{\delta }\left[\mathsf{\Phi }\left(0,{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right],$$

(6)

$$L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[{\displaystyle \frac{{\partial }^{\eta }}{\partial q^{\eta }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]={\theta }_2\mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)-L_p^{\mu }{S}_r^{\delta }\left[\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},0,{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right],$$

(7)

$$L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[{\displaystyle \frac{{\partial }^{\delta }}{\partial r^{\delta }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]={\displaystyle \frac{1}{\phi }}\mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)-{\displaystyle \frac{1}{\phi }}{L}_p^{\mu }{L}_q^{\eta }\left[\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},0\right)\right],$$

(8)

$$\begin{array}{cc}\hfill L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[{\displaystyle \frac{{\partial }^{2\mu }}{\partial p^{2\mu }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]& ={\theta }_1^2\mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)-{\theta }_1{L}_q^{\eta }{S}_r^{\delta }\left[\mathsf{\Phi }\left(0,{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]\hfill \\ \hfill & -L_q^{\eta }{S}_r^{\delta }\left[\mathsf{\Phi }\left(0,{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right],\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[{\displaystyle \frac{{\partial }^{2\eta }}{\partial q^{2\eta }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]& ={\theta }_2^2\mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)-{\theta }_2{L}_p^{\mu }{S}_r^{\delta }\left[\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},0,{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]\hfill \\ \hfill & -L_p^{\mu }{S}_r^{\delta }\left[\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},0,{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right],\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[{\displaystyle \frac{{\partial }^{2\delta }}{\partial r^{2\delta }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]& ={\displaystyle \frac{1}{{\phi }^2}}\mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)-{\displaystyle \frac{1}{{\phi }^2}}{L}_p^{\mu }{L}_q^{\eta }\left[\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},0\right)\right]\hfill \\ \hfill & -{\displaystyle \frac{1}{\phi }}{L}_p^{\mu }{L}_q^{\eta }\left[\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},0\right)\right].\hfill \end{array}$$

(11)

Proof. 

The proof is an extension of Theorem 1 in [21]. Here, we prove (6) and (9), and leave the remaining identities to the reader. Starting from the definition of the CTLST, we have

$$\begin{array}{cc}\hfill L_p^{\mu }& L_q^{\eta }{S}_r^{\delta }\left[{\displaystyle \frac{{\partial }^{\mu }}{\partial p^{\mu }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]\hfill \\ & ={\displaystyle \frac{1}{\phi }}{\int }_0^{\infty }{\int }_0^{\infty }{\int }_0^{\infty }{e}^{-{\theta }_1\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)-{\theta }_2\left({\displaystyle \frac{q^{\eta }}{\eta }}\right)-{\displaystyle \frac{1}{\phi }}\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}\left[{\displaystyle \frac{{\partial }^{\mu }}{\partial p^{\mu }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]dpdqdr\hfill \\ \hfill & ={\int }_0^{\infty }{e}^{-{\theta }_2\left({\displaystyle \frac{q^{\eta }}{\eta }}\right)}dq\times {\displaystyle \frac{1}{\phi }}{\int }_0^{\infty }{e}^{-{\displaystyle \frac{1}{\phi }}\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}dr\left[{\int }_0^{\infty }{e}^{-{\theta }_1\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)}{\displaystyle \frac{{\partial }^{\mu }}{\partial p^{\mu }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)dp\right].\hfill \end{array}$$

To evaluate the inner integral, we use integration by parts, with the assumptions $u=e^{-{\theta }_1\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)}$ and $dv={\displaystyle \frac{{\partial }^{\mu }\mathsf{\Phi }}{\partial p^{\mu }}}\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)dp$. Thus,

$$\begin{array}{cc}\hfill L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[{\displaystyle \frac{{\partial }^{\mu }\mathsf{\Phi }}{\partial p^{\mu }}}\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]& ={\int }_0^{\infty }{e}^{-{\theta }_2\left({\displaystyle \frac{q^{\eta }}{\eta }}\right)}dq\times {\displaystyle \frac{1}{\phi }}{\int }_0^{\infty }{e}^{-{\displaystyle \frac{1}{\phi }}\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}dr\hfill \\ \hfill & \times \left(-{\theta }_1\mathsf{\Phi }\left(0,{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)+{\theta }_1^2{\int }_0^{\infty }\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)dp\right)\hfill \\ \hfill & ={\theta }_1\mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)-L_q^{\eta }{S}_r^{\delta }\left[\mathsf{\Phi }\left(0,{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right].\hfill \end{array}$$

To prove (9), we apply the same technique recursively:

$$\begin{array}{cc}\hfill L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[{\displaystyle \frac{{\partial }^{2\mu }}{\partial p^{2\mu }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]& =L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[{\displaystyle \frac{{\partial }^{\mu }}{\partial p^{\mu }}}\left({\displaystyle \frac{{\partial }^{\mu }}{\partial p^{\mu }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right)\right]\hfill \\ \hfill & ={\theta }_1{L}_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[{\displaystyle \frac{{\partial }^{\mu }}{\partial p^{\mu }}}\left(\mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)\right)\right]\hfill \\ \hfill & -{\theta }_1{L}_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[L_q^{\eta }{S}_r^{\delta }\left[\mathsf{\Phi }\left(0,{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]\right]\hfill \\ \hfill & ={\theta }_1^2\mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)-{\theta }_1{L}_q^{\eta }{S}_r^{\delta }\left[\mathsf{\Phi }\left(0,{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]\hfill \\ \hfill & -L_q^{\eta }{S}_r^{\delta }\left[\mathsf{\Phi }\left(0,{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right].\hfill \end{array}$$

□

Theorem 3.

Let $\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right),$ where $\mu ,\eta ,\delta \in (0,1],$ be a real-valued piecewise continuous function and of exponential order. If $L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]=\mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)$ and $m\in {\mathbb{Z}}^{+},$ then the CTLST of conformable partial derivatives of the order $\mu m,\eta m$, and $\delta m$ is given by

$$\begin{array}{cc}\hfill L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }& \left[{\displaystyle \frac{{\partial }^{\mu m}}{\partial p^{\mu m}}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]\hfill \\ & ={\theta }_1^m\mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)-\sum _{k=0}^{m-1}{\theta }_1^{m-1-k}{L}_q^{\eta }{S}_r^{\delta }\left[{\displaystyle \frac{{\partial }^k}{\partial p^k}}\mathsf{\Phi }\left(0,{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right],\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[{\displaystyle \frac{{\partial }^{\eta m}}{\partial q^{\eta m}}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]=& {\theta }_2^m\mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)\hfill \\ & -\sum _{k=0}^{m-1}{\theta }_2^{m-1-k}{L}_p^{\mu }{S}_r^{\delta }\left[{\displaystyle \frac{{\partial }^k}{\partial q^k}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},0,{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right],\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[{\displaystyle \frac{{\partial }^{\delta m}}{\partial r^{\delta m}}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]=& {\displaystyle \frac{1}{{\phi }^m}}\mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)\hfill \\ & -\sum _{k=0}^{m-1}{\phi }^{-m+k}{L}_p^{\mu }{L}_q^{\eta }\left[{\displaystyle \frac{{\partial }^k}{\partial r^k}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},0\right)\right].\hfill \end{array}$$

(14)

Proof. 

The proof is a generalization of the proof of Theorem 2 and the proofs of Theorem 1 in [19] and Theorem 1 in [21]. □

Theorem 4.

Let Φ and Θ be piecewise continuous functions on the interval $[0,\infty )\times [0,\infty )\times [0,\infty )$ and of exponential order. If

$$L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]=\mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)$$

and

$$L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[\mathsf{\Theta }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]=\mathsf{\Theta }\left({\theta }_1,{\theta }_2,\phi \right),$$

where $\mu ,\eta ,\delta \in (0,1],$ and $a_1$ and $a_2$ are constants, then the CTLST of the following functions is

• $$\begin{array}{cc}\hfill L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[a_1\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)+a_2\mathsf{\Theta }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]=& a_1{L}_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]\hfill \\ & +a_2{L}_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[\mathsf{\Theta }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right],\hfill \end{array}$$
• $L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[\zeta \right]={\displaystyle \frac{\zeta }{{\theta }_1{\theta }_2}}$, where ζ is constant,
• $L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[{\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)}^k{\left({\displaystyle \frac{q^{\eta }}{\eta }}\right)}^m{\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}^n\right]={\displaystyle \frac{{\phi }^{n}k!m!n!}{{\theta }_1^{k+1}{\theta }_2^{m+1}}}$, where $k,m,n$ are positive integers,
• $L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[e^{b_1{\displaystyle \frac{p^{\mu }}{\mu }}+b_2{\displaystyle \frac{q^{\eta }}{\eta }}+b_3{\displaystyle \frac{r^{\delta }}{\delta }}}\right]={\displaystyle \frac{1}{({\theta }_1-b_1)({\theta }_2-b_2)(\phi -b_3)}},$
• $L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[e^{i\left(b_1{\displaystyle \frac{p^{\mu }}{\mu }}+b_2{\displaystyle \frac{q^{\eta }}{\eta }}+b_3{\displaystyle \frac{r^{\delta }}{\delta }}\right)}\right]$
  $={\displaystyle \frac{{\theta }_1{\theta }_2-{\theta }_1\phi b_2{b}_3-{\theta }_2\phi b_1{b}_3-b_1{b}_2+i\left({\theta }_1{\theta }_2\phi b_3+{\theta }_1{b}_2+{\theta }_1{b}_1-\phi b_1{b}_2{b}_3\right)}{({\theta }_1^2+b_1^2)({\theta }_2^2+b_2^2)(1+{\phi }^2{b}_3^2)}},$
• $L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[sin\left(b_1{\displaystyle \frac{p^{\mu }}{\mu }}+b_2{\displaystyle \frac{q^{\eta }}{\eta }}+b_3{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]={\displaystyle \frac{{\theta }_1{\theta }_2\phi b_3+{\theta }_1{b}_2+{\theta }_2{b}_1-\phi b_3{b}_2{b}_1}{({\theta }_1^2+b_1^2)({\theta }_2^2+b_2)(1+{\phi }^2{b}_3^2)}},$
• $L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[cos\left(b_1{\displaystyle \frac{p^{\mu }}{\mu }}+b_2{\displaystyle \frac{q^{\eta }}{\eta }}+b_3{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]={\displaystyle \frac{{\theta }_1{\theta }_2+{\theta }_1\phi b_2{b}_3+{\theta }_2\phi b_1{b}_3+b_1{b}_2}{({\theta }_1^2-b_1^2)({\theta }_2^2-b_2)(1-{\phi }^2{b}_3^2)}},$
• $L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[sinh\left(b_1{\displaystyle \frac{p^{\mu }}{\mu }}+b_2{\displaystyle \frac{q^{\eta }}{\eta }}+b_3{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]={\displaystyle \frac{{\theta }_1{\theta }_2\phi b_3+{\theta }_1{b}_2+{\theta }_2{b}_1+\phi b_3{b}_2{b}_1}{({\theta }_1^2-b_1^2)({\theta }_2^2-b_2)(1-{\phi }^2{b}_3^2)}},$
• $L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[cosh\left(b_1{\displaystyle \frac{p^{\mu }}{\mu }}+b_2{\displaystyle \frac{q^{\eta }}{\eta }}+b_3{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]={\displaystyle \frac{{\theta }_1{\theta }_2+{\theta }_1\phi b_2{b}_3+{\theta }_2\phi b_1{b}_3+b_1{b}_2}{({\theta }_1^2-b_1^2)({\theta }_2^2-b_2)(1-{\phi }^2{b}_3^2)}}.$

Proof. 

From the definition of the CTLST, the proof of the first point is clear. For the proof of $2,$

$$\begin{array}{ccc}\hfill L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[\zeta \right]& =& {\displaystyle \frac{1}{\phi }}{\int }_0^{\infty }{\int }_0^{\infty }{\int }_0^{\infty }\zeta e^{-{\theta }_1\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)-{\theta }_2\left({\displaystyle \frac{q^{\eta }}{\eta }}\right)-{\displaystyle \frac{1}{\phi }}\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}dpdqdr\hfill \\ & =& \left({\int }_0^{\infty }{e}^{-{\theta }_1\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)}dp\right)\left({\int }_0^{\infty }{e}^{-{\theta }_2{\displaystyle \frac{q^{\eta }}{\eta }}}dq\right)\left({\displaystyle \frac{\zeta }{\phi }}{\int }_0^{\infty }{e}^{-{\displaystyle \frac{1}{\phi }}{\displaystyle \frac{r^{\delta }}{\delta }}}dr\right)\hfill \\ & =& {\displaystyle \frac{\zeta }{{\theta }_1{\theta }_2}}.\hfill \end{array}$$

When the CTLST is applied on $\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)={\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)}^k{\left({\displaystyle \frac{q^{\eta }}{\eta }}\right)}^m{\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}^n,$ it gives the following:

$$\begin{array}{cc}\hfill L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }& \left[{\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)}^k{\left({\displaystyle \frac{q^{\eta }}{\eta }}\right)}^m{\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}^n\right]\hfill \\ & ={\displaystyle \frac{1}{\phi }}{\int }_0^{\infty }{\int }_0^{\infty }{\int }_0^{\infty }{e}^{-{\theta }_1\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)-{\theta }_2{\displaystyle \frac{q^{\eta }}{\eta }}-{\displaystyle \frac{1}{\phi }}{\displaystyle \frac{r^{\delta }}{\delta }}}\times \left[{\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)}^k{\left({\displaystyle \frac{q^{\eta }}{\eta }}\right)}^m{\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}^n\right]dpdqdr\hfill \\ & =\left({\int }_0^{\infty }{e}^{-{\theta }_1\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)}{\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)}^{k}dp\right)\times \left({\int }_0^{\infty }{e}^{-{\theta }_2\left({\displaystyle \frac{q^{\eta }}{\eta }}\right)}{\left({\displaystyle \frac{q^{\eta }}{\eta }}\right)}^{m}dq\right)\hfill \\ & \times \left({\displaystyle \frac{1}{\phi }}{\int }_0^{\infty }{e}^{-{\displaystyle \frac{1}{\phi }}\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}{\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}^{n}dr\right)\hfill \\ & ={\displaystyle \frac{{\phi }^{n}k!m!n!}{{\theta }_1^{k+1}{\theta }_2^{m+1}}},\hfill \end{array}$$

which is the proof of $3.$ Also, when $\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)=e^{b_1{\displaystyle \frac{p^{\mu }}{\mu }}+b_2{\displaystyle \frac{q^{\eta }}{\eta }}+b_3{\displaystyle \frac{r^{\delta }}{\delta }}},$ we get the following:

$$\begin{array}{cc}\hfill L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }& \left[e^{b_1{\displaystyle \frac{p^{\mu }}{\mu }}+b_2{\displaystyle \frac{q^{\eta }}{\eta }}+b_3{\displaystyle \frac{r^{\delta }}{\delta }}}\right]\hfill \\ & ={\displaystyle \frac{1}{\phi }}{\int }_0^{\infty }{\int }_0^{\infty }{\int }_0^{\infty }{e}^{-{\theta }_1{\displaystyle \frac{p^{\mu }}{\mu }}-{\theta }_2{\displaystyle \frac{q^{\eta }}{\eta }}-{\displaystyle \frac{1}{\phi }}{\displaystyle \frac{r^{\delta }}{\delta }}}\times \left[e^{b_1{\displaystyle \frac{p^{\mu }}{\mu }}+b_2{\displaystyle \frac{q^{\eta }}{\eta }}+b_3{\displaystyle \frac{r^{\delta }}{\delta }}}\right]dpdqdr\hfill \\ \hfill & =\left({\int }_0^{\infty }{e}^{(-{\theta }_1+b_1){\displaystyle \frac{p^{\mu }}{\mu }}}dp\right)\left({\int }_0^{\infty }{e}^{(-{\theta }_2+b_2){\displaystyle \frac{q^{\eta }}{\eta }}}dq\right)\times \left({\displaystyle \frac{1}{\phi }}{\int }_0^{\infty }{e}^{(-{\displaystyle \frac{1}{\phi }}+b_3){\displaystyle \frac{r^{\delta }}{\delta }}}dr\right)\hfill \\ \hfill & =\left({\displaystyle \frac{1}{{\theta }_1-b_1}}\right)\left({\displaystyle \frac{1}{{\theta }_2-b_2}}\right)\left({\displaystyle \frac{1}{1-\phi b_3}}\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{\left({\theta }_1-b_1\right)\left({\theta }_2-b_2\right)\left(1-\phi b_3\right)}}.\hfill \end{array}$$

By the same way of proving 3 and $4,$ we can prove $5,6,$ and $7,$; we leave these for the reader.

For $8,$ we apply the CTLST on

$$\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)=sinh\left(b_1{\displaystyle \frac{p^{\mu }}{\mu }}+b_2{\displaystyle \frac{q^{\eta }}{\eta }}+b_3{\displaystyle \frac{r^{\delta }}{\delta }}\right)={\displaystyle \frac{e^{\left(b_1\frac{p^{\mu }}{\mu }+b_2\frac{q^{\eta }}{\eta }+b_3\frac{r^{\delta }}{\delta }\right)}-e^{-\left(b_1\frac{p^{\mu }}{\mu }+b_2\frac{q^{\eta }}{\eta }+b_3\frac{r^{\delta }}{\delta }\right)}}{2}},$$

so we get

$$\begin{array}{cc}\hfill L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }& \left[sinh\left(b_1{\displaystyle \frac{p^{\mu }}{\mu }}+b_2{\displaystyle \frac{q^{\eta }}{\eta }}+b_3{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]\hfill \\ \hfill & ={\displaystyle \frac{1}{2\phi }}\left[{\int }_0^{\infty }{\int }_0^{\infty }{\int }_0^{\infty }{e}^{\left(-{\theta }_1+b_1\right){\displaystyle \frac{p^{\mu }}{\mu }}+\left(-{\theta }_2+b_2\right){\displaystyle \frac{q^{\eta }}{\eta }}+\left(-{\displaystyle \frac{1}{\phi }}+b_3\right){\displaystyle \frac{r^{\delta }}{\delta }}}dpdqdr\right.\hfill \\ \hfill & \left.-{\int }_0^{\infty }{\int }_0^{\infty }{\int }_0^{\infty }{e}^{\left(-{\theta }_1-b_1\right){\displaystyle \frac{p^{\mu }}{\mu }}+\left(-{\theta }_2-b_2\right){\displaystyle \frac{q^{\eta }}{\eta }}+\left(-{\displaystyle \frac{1}{\phi }}-b_3\right){\displaystyle \frac{r^{\delta }}{\delta }}}dpdqdr\right]\hfill \\ \hfill & ={\displaystyle \frac{{\theta }_1{b}_2+{\theta }_2{b}_1+{\theta }_1{\theta }_2\phi b_3+b_1{b}_2{b}_3\phi }{\left({\theta }_1^2-b_1^2\right)\left({\theta }_2^2-b_2^2\right)\left(1-{\phi }^2{b}_3^2\right)}}.\hfill \end{array}$$

By the same method, we can prove $9.$ □

3. Solving Two-Dimensional Fractional Partial Differential Equations Using the CTLST

In this section, we demonstrate the effectiveness of the triple Laplace–Sumudu transform (CTLST) technique for solving a class of two-dimensional time-fractional partial differential equations. This approach integrates the Laplace and Sumudu transforms into a triple structure tailored to fractional differential operators in multiple variables, offering a systematic way to handle linear and nonlinear terms within a unified transform domain.

We consider the following nonlinear time-fractional partial differential equation, as studied in [25]:

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\partial }^{k\delta }}{\partial r^{k\delta }}}\left[\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]& +\mathbf{R}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)+\mathbf{N}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)=f\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right),\hfill \end{array}$$

(15)

subject to the initial condition

$${\displaystyle \frac{{\partial }^{k\delta -1}}{\partial r^{k\delta -1}}}\left[\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},0\right)\right]=f_{k\delta -1}\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},0\right),$$

(16)

where $m-1<\delta \le m$, $\mathbf{R}$ is a linear differential operator, $\mathbf{N}$ is a nonlinear operator, f is a source term, and $k=1,2,3,\dots$.

Step 1: Apply the CTLST to both sides of Equation (15). This results in the transformed form

$$\begin{array}{c}{L}_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[{\displaystyle \frac{{\partial }^{k\delta }}{\partial r^{k\delta }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]+L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[\mathbf{R}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]\hfill \\ +L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[\mathbf{N}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]=L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[f\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right].\hfill \end{array}$$

(17)

Step 2: By applying the operational rules of the CTLST, we obtain

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{{\phi }^{\delta }}}\mathsf{\Phi }({\theta }_1,{\theta }_2,\phi )& -\sum _{k=0}^{m-1}{\displaystyle \frac{1}{{\phi }^{\delta -k}}}{L}_p^{\mu }{L}_q^{\eta }\left[{\displaystyle \frac{{\partial }^{k\delta }}{\partial r^{k\delta }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},0\right)\right]+L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[\mathbf{R}\mathsf{\Phi }\right]\hfill \\ & +L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[\mathbf{N}\mathsf{\Phi }\right]=L_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[f\right].\hfill \end{array}$$

(18)

Step 3: Substituting the initial condition (16) into (18) leads to

$$\begin{array}{cc}\hfill \mathsf{\Phi }({\theta }_1,{\theta }_2,\phi )& =F({\theta }_1,{\theta }_2,\phi )+{\phi }^{\delta }\sum _{k=0}^{m-1}{\displaystyle \frac{1}{{\phi }^{\delta -k}}}{L}_p^{\mu }{L}_q^{\eta }\left[{\displaystyle \frac{{\partial }^{k\delta }}{\partial r^{k\delta }}}\mathsf{\Phi }\left(·,·,0\right)\right]\hfill \\ \hfill & -{\phi }^{\delta }{L}_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[\mathbf{R}\mathsf{\Phi }\right]-{\phi }^{\delta }{L}_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[\mathbf{N}\mathsf{\Phi }\right].\hfill \end{array}$$

(19)

Step 4: Applying the inverse CTLST to (19), we obtain

$$\begin{array}{cc}\hfill L_p^{-1}& L_q^{-1}{S}_r^{-1}\left[\mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)\right]\hfill \\ & =\mathsf{\Psi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)+L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[{\phi }^{\delta }\sum _{k=0}^{m-1}{\displaystyle \frac{1}{{\phi }^{\delta -k}}}{L}_p^{\mu }{L}_q^{\eta }\left[{\displaystyle \frac{{\partial }^{k\delta }}{\partial r^{k\delta }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},0\right)\right]\right]\hfill \\ \hfill & -L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[{\phi }^2{L}_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[\mathbf{R}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]\right]\hfill \\ & -L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[{\phi }^2{L}_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[\mathbf{N}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]\right].\hfill \end{array}$$

(20)

Assume that the solution $\mathsf{\Phi }$ can be expressed as a series:

$$\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)=\sum _{k=0}^{\infty }{\mathsf{\Phi }}_k\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right).$$

(21)

Then the nonlinear term $\mathbf{N}\mathsf{\Phi }$ can be decomposed as

$$\mathbf{N}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)=\sum _{k=0}^{\infty }{G}_k,$$

(22)

where $G_k$ are the Adomian polynomials given by

$$\begin{array}{ccc}\hfill G_0& =& {\displaystyle \frac{1}{0!}}{\displaystyle \frac{d^0}{d{\lambda }^0}}{\left[N\left(\sum _{k=0}^0{\lambda }^k{\mathsf{\Phi }}_k\right)\right]}_{\lambda =0}=N\left({\mathsf{\Phi }}_0\right),\hfill \\ \hfill G_1& =& {\displaystyle \frac{1}{1!}}{\displaystyle \frac{d^1}{d{\lambda }^1}}{\left[N\left(\sum _{k=0}^1{\lambda }^k{\mathsf{\Phi }}_k\right)\right]}_{\lambda =0}={\mathsf{\Phi }}_1{N}^{\prime }\left({\mathsf{\Phi }}_0\right),\hfill \\ \hfill G_2& =& {\displaystyle \frac{1}{2!}}{\displaystyle \frac{d^2}{d{\lambda }^2}}{\left[N\left(\sum _{k=0}^2{\lambda }^k{\mathsf{\Phi }}_k\right)\right]}_{\lambda =0}={\mathsf{\Phi }}_2{N}^{\prime }\left({\mathsf{\Phi }}_0\right)+{\displaystyle \frac{{\mathsf{\Phi }}_1^2}{2!}}{N}^{″}\left({\mathsf{\Phi }}_0\right),\hfill \\ & & ⋮\hfill \end{array}$$

Substituting (21) and (22) into (20) gives

$$\begin{array}{cc}\hfill \sum _{k=0}^{\infty }{\mathsf{\Phi }}_k\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)=& \mathsf{\Psi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\hfill \\ & +L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[{\phi }^{\delta }\sum _{k=0}^{m-1}{\displaystyle \frac{1}{{\phi }^{\delta -k}}}{L}_p^{\mu }{L}_q^{\eta }\left[{\displaystyle \frac{{\partial }^{k\delta }}{\partial r^{k\delta }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},0\right)\right]\right]\hfill \\ \hfill & -L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[{\phi }^2{L}_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[\mathbf{R}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]\right]\hfill \\ & -L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[{\phi }^2{L}_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[\mathbf{N}\sum _{k=0}^{\infty }{G}_k\right]\right].\hfill \end{array}$$

(23)

The recursive relations are then given by

$${\mathsf{\Phi }}_0\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)=F\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right),$$

and for $k\ge 0$,

$$\begin{array}{cc}\hfill {\mathsf{\Phi }}_{k+1}\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)=& L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[L_p^{\mu }{L}_q^{\eta }\left[\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},0\right)\right]\right]\hfill \\ \hfill & +L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[{\phi }^{\delta }\sum _{k=0}^{m-1}{\displaystyle \frac{1}{{\phi }^{\delta -k}}}{L}_p^{\mu }{L}_q^{\eta }\left[{\displaystyle \frac{{\partial }^{k\delta }}{\partial r^{k\delta }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},0\right)\right]\right]\hfill \\ & -L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[{\phi }^2{L}_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[\mathbf{R}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]\right]\hfill \\ & -L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[{\phi }^2{L}_p^{\mu }{L}_q^{\eta }{S}_r^{\delta }\left[\mathbf{N}\sum _{k=0}^{\infty }{G}_k\right]\right].\hfill \end{array}$$

(24)

Finally, the approximate solution of (15) is given by the infinite series

$$\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)=\sum _{k=0}^{\infty }{\mathsf{\Phi }}_k\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)={\mathsf{\Phi }}_0+{\mathsf{\Phi }}_1+{\mathsf{\Phi }}_2+{\mathsf{\Phi }}_3+\dots .$$

This method efficiently constructs a series solution for the given FPDE, capturing both linear and nonlinear behaviors across multiple fractional dimensions through an integrated transform-decomposition framework.

4. Illustrative Examples

In this section, we apply the CTLST to solve linear and nonlinear fractional partial differential equations. The first example is taken from [26], and the equation is a Poisson partial differential equation. The second example is conformable Laplace partial differential equation [26], and the third example is a conformable nonlinear wave equation [27].

Example 1.

We consider the following Poisson partial differential equation:

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\partial }^{2\delta }}{\partial r^{2\delta }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)+{\displaystyle \frac{{\partial }^{2\mu }}{\partial p^{2\mu }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)& +{\displaystyle \frac{{\partial }^{2\eta }}{\partial q^{2\eta }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\hfill \\ & =2sin\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)cos\left({\displaystyle \frac{q^{\eta }}{\eta }}\right)sinh\left(2{\displaystyle \frac{r^{\delta }}{\delta }}\right),\hfill \end{array}$$

(25)

with the initial and boundary conditions

$$\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},0\right)=0,{\displaystyle \frac{{\partial }^{\delta }\mathsf{\Phi }\left(\frac{p^{\mu }}{\mu },\frac{q^{\eta }}{\eta },0\right)}{\partial r^{\delta }}}=2sin\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)cos\left({\displaystyle \frac{q^{\eta }}{\eta }}\right),$$

(26)

$$\mathsf{\Phi }\left(0,{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)=0,{\displaystyle \frac{{\partial }^{\mu }\mathsf{\Phi }\left(0,\frac{q^{\eta }}{\eta },\frac{r^{\delta }}{\delta }\right)}{\partial p^{\mu }}}=cos\left({\displaystyle \frac{q^{\eta }}{\eta }}\right)sinh\left(2{\displaystyle \frac{r^{\delta }}{\delta }}\right),$$

(27)

$$\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},0,{\displaystyle \frac{r^{\delta }}{\delta }}\right)=sin\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)sinh\left(2{\displaystyle \frac{r^{\delta }}{\delta }}\right),{\displaystyle \frac{{\partial }^{\delta }\mathsf{\Phi }\left(\frac{p^{\mu }}{\mu },0,\frac{r^{\delta }}{\delta }\right)}{\partial q^{\delta }}}=0.$$

(28)

First step: Applying the CTLST on both sides of (25) gives the following:

$$\begin{array}{cc}\hfill L_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }& \left[{\displaystyle \frac{{\partial }^{2\delta }}{\partial r^{2\delta }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]+L_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left[{\displaystyle \frac{{\partial }^{2\mu }}{\partial p^{2\mu }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]\hfill \\ & +L_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left[{\displaystyle \frac{{\partial }^{2\eta }}{\partial q^{2\eta }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]\hfill \\ \hfill & =2L_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left[sin\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)cos\left({\displaystyle \frac{q^{\eta }}{\eta }}\right)sinh\left(2{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right].\hfill \end{array}$$

(29)

Second step: From the derivative properties of the CTLST, we find that

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{{\phi }^2}}\mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)-{\displaystyle \frac{1}{{\phi }^2}}{L}_p^{\mu }{L}_q^{\eta }\left[\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},0\right)\right]-{\displaystyle \frac{1}{\phi }}{L}_p^{\mu }{L}_q^{\eta }\left[{\displaystyle \frac{\partial }{\partial r}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},0\right)\right]\hfill \\ & +{\theta }_1^2\mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)-{\theta }_1{L}_q^{\eta }{S}_r^{\phi }\left[\mathsf{\Phi }\left(0,{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]-L_q^{\eta }{S}_r^{\phi }\left[{\displaystyle \frac{\partial }{\partial p}}\mathsf{\Phi }\left(0,{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]\hfill \\ & +{\theta }_2^2\mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)-{\theta }_2{L}_p^{\mu }{S}_r^{\phi }\left[\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},0,{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]\hfill \\ & -L_p^{\mu }{S}_r^{\phi }\left[{\displaystyle \frac{\partial }{\partial q}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},0,{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]={\displaystyle \frac{4{\theta }_2\phi }{\left(1+{\theta }_1^2\right)\left(1+{\theta }_2^2\right)\left(1-4{\phi }^2\right)}}.\hfill \end{array}$$

(30)

When we apply the CTLST on the initial and boundary conditions, we get following:

$$L_p^{\mu }{L}_q^{\eta }\left[\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},0\right)\right]=0,$$

(31)

$$\begin{array}{cc}\hfill L_p^{\mu }{L}_q^{\eta }\left[{\displaystyle \frac{\partial }{\partial r}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},0\right)\right]& =L_p^{\mu }{L}_q^{\eta }\left[2sin\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)cos\left({\displaystyle \frac{q^{\eta }}{\eta }}\right)\right]={\displaystyle \frac{2{\theta }_2}{\left(1+{\theta }_1^2\right)\left(1+{\theta }_2^2\right)}},\hfill \end{array}$$

(32)

$$L_q^{\eta }{S}_r^{\phi }\left[\mathsf{\Phi }\left(0,{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]=0,$$

(33)

$$\begin{array}{cc}\hfill L_q^{\eta }{S}_r^{\phi }\left[{\displaystyle \frac{\partial }{\partial p}}\mathsf{\Phi }\left(0,{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]=& L_q^{\eta }{S}_r^{\phi }\left[cos\left({\displaystyle \frac{q^{\eta }}{\eta }}\right)sinh\left(2{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]={\displaystyle \frac{2{\theta }_2\phi }{\left(1+{\theta }_2^2\right)\left(1-4{\phi }^2\right)}},\hfill \end{array}$$

(34)

$$L_p^{\mu }{S}_r^{\phi }\left[\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},0,{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]=L_p^{\mu }{S}_r^{\phi }\left[sin\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)sinh\left(2{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]={\displaystyle \frac{2\phi }{\left(1+{\theta }_1^2\right)\left(1-4{\phi }^2\right)}}$$

(35)

$$\begin{array}{c}\hfill L_p^{\mu }{S}_r^{\phi }\left[{\displaystyle \frac{{\partial }^{\delta }}{\partial q^{\delta }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},0,{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]=0.\end{array}$$

(36)

By substituting (31), (32), (33), (34), (35), and (36) into (30), we get

$$\begin{array}{cc}\hfill \left[{\displaystyle \frac{1}{{\phi }^2}}+{\theta }_1^2+{\theta }_2^2\right]\mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)& ={\displaystyle \frac{2{\theta }_2}{\phi \left(1+{\theta }_1^2\right)\left(1+{\theta }_2^2\right)}}+{\displaystyle \frac{2{\theta }_2\phi }{\left(1+{\theta }_2^2\right)\left(1-4{\phi }^2\right)}}\hfill \\ \hfill & +{\displaystyle \frac{2{\theta }_2\phi }{\left(1+{\theta }_1^2\right)\left(1-4{\phi }^2\right)}}+{\displaystyle \frac{4{\theta }_2\phi }{\left(1+{\theta }_1^2\right)\left(1+{\theta }_2^2\right)\left(1-4{\phi }^2\right)}},\hfill \end{array}$$

(37)

by arranging the above equation, we find

$$\left[{\displaystyle \frac{1+{\phi }^2{\theta }_1^2+{\phi }^2{\theta }_2^2}{{\phi }^2}}\right]\mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)={\displaystyle \frac{2{\theta }_2\left(1+{\phi }^2{\theta }_1^2+{\phi }^2{\theta }_2^2\right)}{\phi \left(1+{\theta }_1^2\right)\left(1+{\theta }_2^2\right)\left(1-4{\phi }^2\right)}},$$

(38)

and so

$$\mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)={\displaystyle \frac{2\phi {\theta }_2}{\left(1+{\theta }_1^2\right)\left(1+{\theta }_2^2\right)\left(1-4{\phi }^2\right)}}.$$

(39)

Third step: In this step, we apply the inverse of the CTLST to (39):

$$L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[\mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)\right]=L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[{\displaystyle \frac{2\phi {\theta }_2}{\left(1+{\theta }_1^2\right)\left(1+{\theta }_2^2\right)\left(1-4{\phi }^2\right)}}\right],$$

(40)

and from Theorem (4), the inverse of the CTLST in (40) becomes

$$\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)=sin\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)cos\left({\displaystyle \frac{q^{\eta }}{\eta }}\right)sinh\left(2{\displaystyle \frac{r^{\delta }}{\delta }}\right).$$

(41)

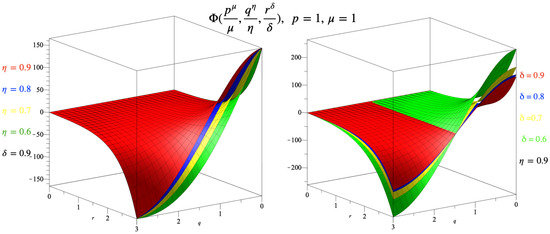
Figure 1 illustrates the 3D plots of the approximation solutions of $\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)$ at $p=1,$ $\mu =1$, and different values of δ and η. The exact solution of (25) is when $\mu =\eta =\delta =1$ in (41), and it is

$$\mathsf{\Phi }\left(p,q,r\right)=sin\left(p\right)cos\left(q\right)sinh\left(2r\right).$$

Figure 1. The 3D plots of the approximation solutions of $\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)$ in Example 1.

Example 2.

Consider the following conformable Laplace partial differential equation, Example 4 in [26]:

$${\displaystyle \frac{{\partial }^{2\delta }}{\partial r^{2\delta }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)+{\displaystyle \frac{{\partial }^{2\mu }}{\partial p^{2\mu }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)+{\displaystyle \frac{{\partial }^{2\eta }}{\partial q^{2\eta }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)=0,$$

(42)

subject to the initial and boundary conditions

$$\begin{array}{ccc}\hfill \mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},0\right)& =& 0,{\displaystyle \frac{{\partial }^{\delta }\mathsf{\Phi }\left(\frac{p^{\mu }}{\mu },\frac{q^{\eta }}{\eta },0\right)}{\partial r^{\delta }}}=\sqrt{2}sin\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)sin\left({\displaystyle \frac{q^{\eta }}{\eta }}\right),\hfill \end{array}$$

(43)

$$\begin{array}{ccc}\hfill \mathsf{\Phi }\left(0,{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)& =& 0,{\displaystyle \frac{{\partial }^{\mu }\mathsf{\Phi }\left(0,\frac{q^{\eta }}{\eta },\frac{r^{\delta }}{\delta }\right)}{\partial p^{\mu }}}=sin\left({\displaystyle \frac{q^{\eta }}{\eta }}\right)sinh\left(\sqrt{2}{\displaystyle \frac{r^{\delta }}{\delta }}\right),\hfill \end{array}$$

(44)

$$\begin{array}{ccc}\hfill \mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},0,{\displaystyle \frac{r^{\delta }}{\delta }}\right)& =& 0,{\displaystyle \frac{{\partial }^{\delta }\mathsf{\Phi }\left(\frac{p^{\mu }}{\mu },0,\frac{r^{\delta }}{\delta }\right)}{\partial q^{\delta }}}=sin\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)sinh\left(\sqrt{2}{\displaystyle \frac{r^{\delta }}{\delta }}\right).\hfill \end{array}$$

(45)

First step: Applying the CTLST on both sides of (42) leads to

$$\begin{array}{cc}\hfill L_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left[{\displaystyle \frac{{\partial }^{2\delta }}{\partial r^{2\delta }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]=& -L_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left[{\displaystyle \frac{{\partial }^{2\mu }}{\partial p^{2\mu }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]\hfill \\ & -L_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left[{\displaystyle \frac{{\partial }^{2\eta }}{\partial q^{2\eta }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right].\hfill \end{array}$$

(46)

Second step: By applying the properties of the CTLST, Theorem $,$ we find that

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{{\phi }^2}}& \mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)-{\displaystyle \frac{1}{{\phi }^2}}{L}_p^{\mu }{L}_q^{\eta }\left[\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},0\right)\right]-{\displaystyle \frac{1}{\phi }}{L}_p^{\mu }{L}_q^{\eta }\left[{\displaystyle \frac{\partial }{\partial r}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},0\right)\right]\hfill \\ & =-\left[{\theta }_1^2\mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)-{\theta }_1{L}_q^{\eta }{S}_r^{\phi }\left[\mathsf{\Phi }\left(0,{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]-L_q^{\eta }{S}_r^{\phi }\left[{\displaystyle \frac{\partial }{\partial p}}\mathsf{\Phi }\left(0,{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]\right]\hfill \\ & -\left[{\theta }_2^2\mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)-{\theta }_2{L}_p^{\mu }{S}_r^{\phi }\left[\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},0,{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]-L_p^{\mu }{S}_r^{\phi }\left[{\displaystyle \frac{\partial }{\partial q}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},0,{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]\right].\hfill \end{array}$$

(47)

Applying the transform on the initial and boundary conditions leads to

$$L_p^{\mu }{L}_q^{\eta }\left[\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},0\right)\right]=0,$$

(48)

$$\begin{array}{cc}\hfill L_p^{\mu }{L}_q^{\eta }\left[{\displaystyle \frac{\partial }{\partial r}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},0\right)\right]& =L_p^{\mu }{L}_q^{\eta }\left[\sqrt{2}sin\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)sin\left({\displaystyle \frac{q^{\eta }}{\eta }}\right)\right]={\displaystyle \frac{\sqrt{2}\phi }{\left(1+{\theta }_1^2\right)\left(1+{\theta }_2^2\right)}}\hfill \end{array}$$

(49)

$$L_q^{\eta }{S}_r^{\phi }\left[\mathsf{\Phi }\left(0,{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]=0,$$

(50)

$$\begin{array}{cc}\hfill L_q^{\eta }{S}_r^{\phi }\left[{\displaystyle \frac{{\partial }^{\mu }}{\partial p^{\mu }}}\mathsf{\Phi }\left(0,{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]& =L_q^{\eta }{S}_r^{\phi }\left[sin\left({\displaystyle \frac{q^{\eta }}{\eta }}\right)sinh\left(\sqrt{2}{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]={\displaystyle \frac{\sqrt{2}\phi }{\left(1+{\theta }_2^2\right)\left(1-2{\phi }^2\right)}},\hfill \end{array}$$

(51)

$$\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},0,{\displaystyle \frac{r^{\delta }}{\delta }}\right)=0,$$

(52)

$$\begin{array}{cc}\hfill L_p^{\mu }{S}_r^{\phi }\left[{\displaystyle \frac{{\partial }^{\delta }}{\partial q^{\delta }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},0,{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]& =L_p^{\mu }{S}_r^{\phi }\left[sin\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)sinh\left(\sqrt{2}{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]={\displaystyle \frac{\sqrt{2}\phi }{\left(1+{\theta }_1^2\right)\left(1-2{\phi }^2\right)}}.\hfill \end{array}$$

(53)

After substituting (48), (49), (50), (51), (52), and (53) into (47), we get

$$\begin{array}{ccc}\hfill \left[{\displaystyle \frac{1}{{\phi }^2}}+{\theta }_1^2+{\theta }_2^2\right]\mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)& =& {\displaystyle \frac{\sqrt{2}}{\phi \left(1+{\theta }_1^2\right)\left(1+{\theta }_2^2\right)}}+{\displaystyle \frac{\sqrt{2}\phi }{\left(1+{\theta }_2^2\right)\left(1-2{\phi }^2\right)}}\hfill \\ & & +{\displaystyle \frac{\sqrt{2}\phi }{\left(1+{\theta }_1^2\right)\left(1-2{\phi }^2\right)}},\hfill \end{array}$$

(54)

By rearranging the above equation, we have

$$\left[{\displaystyle \frac{1+{\phi }^2{\theta }_1^2+{\phi }^2{\theta }_2^2}{{\phi }^2}}\right]\mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)={\displaystyle \frac{\sqrt{2}\left(1+{\phi }^2{\theta }_1^2+{\phi }^2{\theta }_2^2\right)}{\phi \left(1+{\theta }_1^2\right)\left(1+{\theta }_2^2\right)\left(1-2{\phi }^2\right)}},$$

(55)

and simplifying Equation (55) leads to

$$\mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)={\displaystyle \frac{\sqrt{2}\phi }{\left(1+{\theta }_1^2\right)\left(1+{\theta }_2^2\right)\left(1-2{\phi }^2\right)}}.$$

(56)

Third step: Applying the inverse of the CTLST of (56) gives

$$L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[\mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)\right]=L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[{\displaystyle \frac{\sqrt{2}\phi }{\left(1+{\theta }_1^2\right)\left(1+{\theta }_2^2\right)\left(1-2{\phi }^2\right)}}\right],$$

(57)

and hence the conformable solution becomes

$$\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)=sin\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)sin\left({\displaystyle \frac{q^{\eta }}{\eta }}\right)sinh\left(\sqrt{2}{\displaystyle \frac{r^{\delta }}{\delta }}\right).$$

(58)

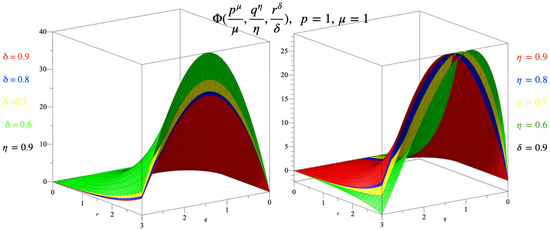
Figure 2 presents the 3D surface plots of the approximate solutions of $\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)$ evaluated at $p=1$ and $\mu =1$, while varying the values of δ and η. The exact solution of (42) is given by

$$\mathsf{\Phi }\left(p,q,r\right)=sin\left(p\right)cos\left(q\right)sinh\left(\sqrt{2}r\right),$$

when $\mu =\eta =\delta =1$ in (58).

Figure 2. The 3D plots of the approximation solutions of $\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)$ in Example 2.

Example 3.

Consider the following two-dimensional conformable nonlinear wave equation, Example 7 in [27]:

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\partial }^{2\delta }}{\partial r^{2\delta }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)=& {\displaystyle \frac{{\partial }^{\mu +\eta }}{\partial p^{\mu }\partial q^{\eta }}}\left({\displaystyle \frac{{\partial }^{2\delta }}{\partial p^{2\delta }}}\mathsf{\Phi }{\displaystyle \frac{{\partial }^{2\eta }}{\partial q^{2\eta }}}\mathsf{\Phi }\right)\hfill \\ & -{\displaystyle \frac{{\partial }^{\mu +\eta }}{\partial p^{\mu }\partial q^{\eta }}}\left({\displaystyle \frac{{\partial }^{\delta }}{\partial p^{\delta }}}\mathsf{\Phi }{\displaystyle \frac{{\partial }^{\eta }}{\partial q^{\eta }}}\mathsf{\Phi }\right)-\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right),\hfill \end{array}$$

(59)

with the initial condition

$$\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},0\right)=e^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}},{\displaystyle \frac{{\partial }^{\delta }}{\partial r^{\delta }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},0\right)=e^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}.$$

(60)

To find solutions for the equation, we implement the following steps:

First step: Apply the CTLST on both sides of (59), so we get

$$\begin{array}{cc}\hfill L_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left[{\displaystyle \frac{{\partial }^{2\delta }}{\partial r^{2\delta }}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]=& L_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left[{\displaystyle \frac{{\partial }^{\mu +\eta }}{\partial p^{\mu }\partial q^{\eta }}}\left({\displaystyle \frac{{\partial }^{2\delta }}{\partial p^{2\delta }}}\mathsf{\Phi }{\displaystyle \frac{{\partial }^{2\eta }}{\partial q^{2\eta }}}\mathsf{\Phi }\right)\right]\hfill \\ & -L_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left[{\displaystyle \frac{{\partial }^{\mu +\eta }}{\partial p^{\mu }\partial q^{\eta }}}\left({\displaystyle \frac{{\partial }^{\delta }}{\partial p^{\delta }}}\mathsf{\Phi }{\displaystyle \frac{{\partial }^{\eta }}{\partial q^{\eta }}}\mathsf{\Phi }\right)\right]\hfill \\ & -L_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left[\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right].\hfill \end{array}$$

(61)

Second step: By using the partial derivatives properties of the CTLST, we find

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{{\phi }^2}}& \mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)-{\displaystyle \frac{1}{{\phi }^2}}{L}_p^{\mu }{L}_q^{\eta }\left[\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},0\right)\right]-{\displaystyle \frac{1}{\phi }}{L}_p^{\mu }{L}_q^{\eta }\left[{\displaystyle \frac{\partial }{\partial r}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},0\right)\right]\hfill \\ & =L_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left[{\displaystyle \frac{{\partial }^{\mu +\eta }}{\partial p^{\mu }\partial q^{\eta }}}\left({\displaystyle \frac{{\partial }^{2\delta }}{\partial p^{2\delta }}}\mathsf{\Phi }{\displaystyle \frac{{\partial }^{2\eta }}{\partial q^{2\eta }}}\mathsf{\Phi }\right)\right]-L_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left[{\displaystyle \frac{{\partial }^{\mu +\eta }}{\partial p^{\mu }\partial q^{\eta }}}\left({\displaystyle \frac{{\partial }^{\delta }}{\partial p^{\delta }}}\mathsf{\Phi }{\displaystyle \frac{{\partial }^{\eta }}{\partial q^{\eta }}}\mathsf{\Phi }\right)\right]\hfill \\ & -L_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left[\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right].\hfill \end{array}$$

(62)

By applying the transform to the initial conditions, we get

$$\begin{array}{ccc}\hfill L_p^{\mu }{L}_q^{\eta }\left[\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},0\right)\right]& =& L_p^{\mu }{L}_q^{\eta }\left[e^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}\right]={\displaystyle \frac{1}{\left(1-{\theta }_1\right)\left(1-{\theta }_2\right)}},\hfill \end{array}$$

(63)

$$\begin{array}{ccc}\hfill L_p^{\mu }{L}_q^{\eta }\left[{\displaystyle \frac{\partial }{\partial r}}\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},0\right)\right]& =& L_p^{\mu }{L}_q^{\eta }\left[e^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}\right]={\displaystyle \frac{1}{\left(1-{\theta }_1\right)\left(1-{\theta }_2\right)}}.\hfill \end{array}$$

(64)

After substituting (63) and (64) into (62), we obtain

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{{\phi }^2}}\mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)-& {\displaystyle \frac{1}{{\phi }^2}}\left[{\displaystyle \frac{1}{\left(1-{\theta }_1\right)\left(1-{\theta }_2\right)}}\right]-{\displaystyle \frac{1}{\phi }}\left[{\displaystyle \frac{1}{\left(1-{\theta }_1\right)\left(1-{\theta }_2\right)}}\right]\hfill \\ \hfill & =L_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left[{\displaystyle \frac{{\partial }^{\mu +\eta }}{\partial p^{\mu }\partial q^{\eta }}}\left({\displaystyle \frac{{\partial }^{2\delta }}{\partial p^{2\delta }}}\mathsf{\Phi }{\displaystyle \frac{{\partial }^{2\eta }}{\partial q^{2\eta }}}\mathsf{\Phi }\right)\right]\hfill \\ & -L_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left[{\displaystyle \frac{{\partial }^{\mu +\eta }}{\partial p^{\mu }\partial q^{\eta }}}\left({\displaystyle \frac{{\partial }^{\delta }}{\partial p^{\delta }}}\mathsf{\Phi }{\displaystyle \frac{{\partial }^{\eta }}{\partial q^{\eta }}}\mathsf{\Phi }\right)\right]-L_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left[\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right].\hfill \end{array}$$

(65)

By arranging the terms of (65), the function becomes

$$\begin{array}{ccc}\hfill \mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)& =& {\displaystyle \frac{1}{\left(1-{\theta }_1\right)\left(1-{\theta }_2\right)}}+{\displaystyle \frac{\phi }{\left(1-{\theta }_1\right)\left(1-{\theta }_2\right)}}\hfill \\ & & +{\phi }^2{L}_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left[{\displaystyle \frac{{\partial }^{\mu +\eta }}{\partial p^{\mu }\partial q^{\eta }}}\left({\displaystyle \frac{{\partial }^{2\delta }}{\partial p^{2\delta }}}\mathsf{\Phi }{\displaystyle \frac{{\partial }^{2\eta }}{\partial q^{2\eta }}}\mathsf{\Phi }\right)\right]\hfill \\ & & -{\phi }^2{L}_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left[{\displaystyle \frac{{\partial }^{\mu +\eta }}{\partial p^{\mu }\partial q^{\eta }}}\left({\displaystyle \frac{{\partial }^{\delta }}{\partial p^{\delta }}}\mathsf{\Phi }{\displaystyle \frac{{\partial }^{\eta }}{\partial q^{\eta }}}\mathsf{\Phi }\right)\right]\hfill \\ & & -{\phi }^2{L}_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left[\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right].\hfill \end{array}$$

(66)

Third step: Apply the inverse of the CTLST to (66) to get the following function:

$$\begin{array}{cc}\hfill L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[\mathsf{\Phi }\left({\theta }_1,{\theta }_2,\phi \right)\right]& =L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[{\displaystyle \frac{1}{\left(1-{\theta }_1\right)\left(1-{\theta }_2\right)}}+{\displaystyle \frac{\phi }{\left(1-{\theta }_1\right)\left(1-{\theta }_2\right)}}\right]\hfill \\ \hfill & +L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[{\phi }^2{L}_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left[{\displaystyle \frac{{\partial }^{\mu +\eta }}{\partial p^{\mu }\partial q^{\eta }}}\left({\displaystyle \frac{{\partial }^{2\delta }}{\partial p^{2\delta }}}\mathsf{\Phi }{\displaystyle \frac{{\partial }^{2\eta }}{\partial q^{2\eta }}}\mathsf{\Phi }\right)\right]\right]\hfill \\ & -L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[{\phi }^2{L}_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left[{\displaystyle \frac{{\partial }^{\mu +\eta }}{\partial p^{\mu }\partial q^{\eta }}}\left({\displaystyle \frac{{\partial }^{\delta }}{\partial p^{\delta }}}\mathsf{\Phi }{\displaystyle \frac{{\partial }^{\eta }}{\partial q^{\eta }}}\mathsf{\Phi }\right)\right]\right]\hfill \\ \hfill & -L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[{\phi }^2{L}_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left[\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]\right].\hfill \end{array}$$

(67)

From Theorem 4, we find that

$$\begin{array}{cc}\hfill \mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)=& e^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}+{\displaystyle \frac{r^{\delta }}{\delta }}{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}\hfill \\ & +L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[{\phi }^2{L}_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left[{\displaystyle \frac{{\partial }^{\mu +\eta }}{\partial p^{\mu }\partial q^{\eta }}}\left({\displaystyle \frac{{\partial }^{2\delta }}{\partial p^{2\delta }}}\mathsf{\Phi }{\displaystyle \frac{{\partial }^{2\eta }}{\partial q^{2\eta }}}\mathsf{\Phi }\right)\right]\right]\hfill \\ \hfill & -L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[{\phi }^2{L}_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left[{\displaystyle \frac{{\partial }^{\mu +\eta }}{\partial p^{\mu }\partial q^{\eta }}}\left({\displaystyle \frac{{\partial }^{\delta }}{\partial p^{\delta }}}\mathsf{\Phi }{\displaystyle \frac{{\partial }^{\eta }}{\partial q^{\eta }}}\mathsf{\Phi }\right)\right]\right]\hfill \\ & -L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[{\phi }^2{L}_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left[\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\right]\right].\hfill \end{array}$$

(68)

Suppose that

$$\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)=\sum _{k=0}^{\infty }{\mathsf{\Phi }}_k\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right).$$

(69)

When we apply the fractional derivatives, which are in (59) on (69), we get

$${\displaystyle \frac{{\partial }^{2\delta }\mathsf{\Phi }}{\partial p^{2\delta }}}{\displaystyle \frac{{\partial }^{2\eta }\mathsf{\Phi }}{\partial q^{2\eta }}}=\sum _{k=0}^{\infty }{G}_k,{\displaystyle \frac{{\partial }^{\delta }\mathsf{\Phi }}{\partial p^{\delta }}}{\displaystyle \frac{{\partial }^{\eta }\mathsf{\Phi }}{\partial q^{\eta }}}=\sum _{k=0}^{\infty }{B}_k,$$

(70)

where $G_k$ and $B_k$ are called Adomian polynomials, which can be calculated as follows:

$$G_k={\displaystyle \frac{1}{k!}}{\displaystyle \frac{\partial }{\partial {\lambda }^k}}{\left[\sum _{i=0}^{\infty }{\lambda }^i{\mathsf{\Phi }}_i\right]}_{\lambda =0},k=0,1,2,\dots$$

(71)

and

$$B_k={\displaystyle \frac{1}{k!}}{\displaystyle \frac{\partial }{\partial {\lambda }^k}}{\left[\sum _{i=0}^{\infty }{\lambda }^i{\mathsf{\Phi }}_i\right]}_{\lambda =0},k=0,1,2,\dots ,$$

(72)

where

$$\begin{array}{ccc}\hfill G_0& =& {\left({\mathsf{\Phi }}_0\right)}_{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{p^{\mu }}{\mu }}}{\left({\mathsf{\Phi }}_0\right)}_{{\displaystyle \frac{q^{\eta }}{\eta }}{\displaystyle \frac{q^{\eta }}{\eta }}},\hfill \\ \hfill G_1& =& {\left({\mathsf{\Phi }}_0\right)}_{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{p^{\mu }}{\mu }}}{\left({\mathsf{\Phi }}_1\right)}_{{\displaystyle \frac{q^{\eta }}{\eta }}{\displaystyle \frac{q^{\eta }}{\eta }}}+{\left({\mathsf{\Phi }}_1\right)}_{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{p^{\mu }}{\mu }}}{\left({\mathsf{\Phi }}_0\right)}_{{\displaystyle \frac{q^{\eta }}{\eta }}{\displaystyle \frac{q^{\eta }}{\eta }}},\hfill \\ \hfill G_2& =& {\left({\mathsf{\Phi }}_0\right)}_{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{p^{\mu }}{\mu }}}{\left({\mathsf{\Phi }}_2\right)}_{{\displaystyle \frac{q^{\eta }}{\eta }}{\displaystyle \frac{q^{\eta }}{\eta }}}+{\left({\mathsf{\Phi }}_1\right)}_{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{p^{\mu }}{\mu }}}{\left({\mathsf{\Phi }}_1\right)}_{{\displaystyle \frac{q^{\eta }}{\eta }}{\displaystyle \frac{q^{\eta }}{\eta }}}+{\left({\mathsf{\Phi }}_2\right)}_{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{p^{\mu }}{\mu }}}{\left({\mathsf{\Phi }}_0\right)}_{{\displaystyle \frac{q^{\eta }}{\eta }}{\displaystyle \frac{q^{\eta }}{\eta }}},\hfill \\ & & ⋮\hfill \end{array}$$

(73)

and

$$\begin{array}{ccc}\hfill B_0& =& {\left({\mathsf{\Phi }}_0\right)}_{{\displaystyle \frac{p^{\mu }}{\mu }}}{\left({\mathsf{\Phi }}_0\right)}_{{\displaystyle \frac{q^{\eta }}{\eta }}},\hfill \\ \hfill B_1& =& {\left({\mathsf{\Phi }}_0\right)}_{{\displaystyle \frac{p^{\mu }}{\mu }}}{\left({\mathsf{\Phi }}_1\right)}_{{\displaystyle \frac{q^{\eta }}{\eta }}}+{\left({\mathsf{\Phi }}_1\right)}_{{\displaystyle \frac{p^{\mu }}{\mu }}}{\left({\mathsf{\Phi }}_0\right)}_{{\displaystyle \frac{q^{\eta }}{\eta }}},\hfill \\ \hfill B_2& =& {\left({\mathsf{\Phi }}_0\right)}_{{\displaystyle \frac{p^{\mu }}{\mu }}}{\left({\mathsf{\Phi }}_2\right)}_{{\displaystyle \frac{q^{\eta }}{\eta }}}+{\left({\mathsf{\Phi }}_1\right)}_{{\displaystyle \frac{p^{\mu }}{\mu }}}{\left({\mathsf{\Phi }}_1\right)}_{{\displaystyle \frac{q^{\eta }}{\eta }}}+{\left({\mathsf{\Phi }}_2\right)}_{{\displaystyle \frac{p^{\mu }}{\mu }}}{\left({\mathsf{\Phi }}_0\right)}_{{\displaystyle \frac{q^{\eta }}{\eta }}},\hfill \\ & & ⋮\hfill \end{array}$$

(74)

After substituting (69) and (70) into (68), one can get

$$\begin{array}{ccc}\hfill \sum _{k=0}^{\infty }{\mathsf{\Phi }}_k\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)& =& e^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}+{\displaystyle \frac{r^{\delta }}{\delta }}{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}+L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[{\phi }^2\left(L_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left(\sum _{k=0}^{\infty }{G}_k\right)\right)\right]\hfill \\ & & -L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[{\phi }^2\left(L_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left(\sum _{k=0}^{\infty }{B}_k\right)\right)\right]\hfill \\ & & -L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[{\phi }^2\left(L_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left[\sum _{k=0}^{\infty }{\mathsf{\Phi }}_k\right]\right)\right].\hfill \end{array}$$

(75)

The recursive relations are

$${\mathsf{\Phi }}_0\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)=e^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}+{\displaystyle \frac{r^{\delta }}{\delta }}{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}},$$

$$\begin{array}{ccc}\hfill {\mathsf{\Phi }}_{k+1}\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)& =& L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[{\phi }^2\left(L_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left(G_0\right)\right)\right]\hfill \\ & & -L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[{\phi }^2{L}_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left(B_0\right)\right]\hfill \\ & & -L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[{\phi }^2\left(L_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left({\mathsf{\Phi }}_0\right)\right)\right].\hfill \end{array}$$

(76)

When $k=0,$ then

$$\begin{array}{cc}\hfill & {\mathsf{\Phi }}_1\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\hfill \\ & =L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[{\phi }^2\left(\begin{array}{c}{L}_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }{\left({\left({\mathsf{\Phi }}_0\right)}_{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{p^{\mu }}{\mu }}}{\left({\mathsf{\Phi }}_0\right)}_{{\displaystyle \frac{q^{\eta }}{\eta }}{\displaystyle \frac{q^{\eta }}{\eta }}}\right)}_{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}\\ -{\left({\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}\left({\left({\mathsf{\Phi }}_0\right)}_{{\displaystyle \frac{p^{\mu }}{\mu }}}{\left({\mathsf{\Phi }}_0\right)}_{{\displaystyle \frac{q^{\eta }}{\eta }}}\right)\right)}_{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}-{\mathsf{\Phi }}_0\end{array}\right)\right]\hfill \\ \hfill & =L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[{\phi }^2\left[L_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }{\left[\begin{array}{c}\left({\left({\displaystyle \frac{q^{\eta }}{\eta }}\right)}^2{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}+{\left({\displaystyle \frac{q^{\eta }}{\eta }}\right)}^2{\displaystyle \frac{r^{\delta }}{\delta }}{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}\right)\\ \left(\left({\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)}^2{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}+{\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)}^2{\displaystyle \frac{r^{\delta }}{\delta }}{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}\right)\right)\end{array}\right]}_{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}\right]\right]\hfill \\ \hfill & -L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[{\phi }^2\left[L_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left[{\left({\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}\left(\begin{array}{c}\left({\displaystyle \frac{q^{\eta }}{\eta }}{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}+{\displaystyle \frac{q^{\eta }}{\eta }}{\displaystyle \frac{r^{\delta }}{\delta }}{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}\right)\\ \left({\displaystyle \frac{p^{\mu }}{\mu }}{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}+{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{r^{\delta }}{\delta }}{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}\right)\end{array}\right)\right)}_{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}\right]\right]\right]\hfill \\ \hfill & -L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[{\phi }^2\left(L_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left(e^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}+{\displaystyle \frac{r^{\delta }}{\delta }}{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}\right)\right)\right],\hfill \\ \hfill & =L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[{\phi }^2\left[L_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left(0-\left(e^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}+{\displaystyle \frac{r^{\delta }}{\delta }}{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}\right)\right)\right]\right]\hfill \\ \hfill & =L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[{\phi }^2\left[L_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left(e^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}+{\displaystyle \frac{r^{\delta }}{\delta }}{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}\right)\right]\right]\hfill \\ \hfill & =-L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[{\displaystyle \frac{{\phi }^2}{\left(1-{\theta }_1\right)\left(1-{\theta }_2\right)}}+{\displaystyle \frac{{\phi }^3}{\left(1-{\theta }_1\right)\left(1-{\theta }_2\right)}}\right],\hfill \end{array}$$

and so

$${\mathsf{\Phi }}_1\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)=-\left({\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}^2{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}+{\displaystyle \frac{1}{6}}{\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}^3{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}\right).$$

At $k=1,$ we get

$$\begin{array}{c}{\mathsf{\Phi }}_2\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\hfill \\ =L_p^{-1}{L}_q^{-1}{S}_r^{-1}\hfill \\ \left[{\phi }^2\left(\begin{array}{c}{L}_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }{\left({\left({\mathsf{\Phi }}_0\right)}_{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{p^{\mu }}{\mu }}}{\left({\mathsf{\Phi }}_1\right)}_{{\displaystyle \frac{q^{\eta }}{\eta }}{\displaystyle \frac{q^{\eta }}{\eta }}}+{\left({\mathsf{\Phi }}_1\right)}_{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{p^{\mu }}{\mu }}}{\left({\mathsf{\Phi }}_0\right)}_{{\displaystyle \frac{q^{\eta }}{\eta }}{\displaystyle \frac{q^{\eta }}{\eta }}}\right)}_{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}\\ -{\left({\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}\left({\left({\mathsf{\Phi }}_0\right)}_{{\displaystyle \frac{p^{\mu }}{\mu }}}{\left({\mathsf{\Phi }}_1\right)}_{{\displaystyle \frac{q^{\eta }}{\eta }}}+{\left({\mathsf{\Phi }}_1\right)}_{{\displaystyle \frac{p^{\mu }}{\mu }}}{\left({\mathsf{\Phi }}_0\right)}_{{\displaystyle \frac{q^{\eta }}{\eta }}}\right)\right)}_{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}-{\mathsf{\Phi }}_1\end{array}\right)\right]\hfill \\ =L_p^{-1}{L}_q^{-1}{S}_r^{-1}\hfill \\ \left[{\phi }^2\left[L_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }{\left[\begin{array}{c}\left({\left({\displaystyle \frac{q^{\eta }}{\eta }}\right)}^2{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}+{\left({\displaystyle \frac{q^{\eta }}{\eta }}\right)}^2\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)e^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}\right)\\ \left({\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)}^2{\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}^2{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}+{\displaystyle \frac{1}{6}}{\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)}^2{\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}^3{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}\right)\\ +\left({\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{q^{\eta }}{\eta }}\right)}^2{\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}^2{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}+{\displaystyle \frac{1}{6}}{\left({\displaystyle \frac{q^{\eta }}{\eta }}\right)}^2{\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}^3{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}\right)\\ +\left({\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)}^2{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}+{\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)}^2\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)e^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}\right)\end{array}\right]}_{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}\right]\right]\hfill \\ -L_p^{-1}{L}_q^{-1}{S}_r^{-1}\hfill \\ \left[{\phi }^2\left[L_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }{\left[{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}\left[\begin{array}{c}\left(\left({\displaystyle \frac{q^{\eta }}{\eta }}\right)e^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}+\left({\displaystyle \frac{q^{\eta }}{\eta }}\right)\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)e^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}\right)\\ \left({\displaystyle \frac{1}{2}}\left({\displaystyle \frac{p^{\mu }}{\mu }}\right){\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}^2{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}+{\displaystyle \frac{1}{6}}\left({\displaystyle \frac{p^{\mu }}{\mu }}\right){\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}^3{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}\right)\\ +\left({\displaystyle \frac{1}{2}}\left({\displaystyle \frac{q^{\eta }}{\eta }}\right){\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}^2{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}+{\displaystyle \frac{1}{6}}\left({\displaystyle \frac{q^{\eta }}{\eta }}\right){\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}^3{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}\right)\\ \left(\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)e^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}+\left({\displaystyle \frac{p^{\mu }}{\mu }}\right)\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)e^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}\right)\end{array}\right]\right]}_{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}\right]\right]\hfill \\ -L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[{\phi }^2\left[L_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }\left[\left({\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}^2{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}+{\displaystyle \frac{1}{6}}{\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}^3{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}\right)\right]\right]\right]\hfill \\ =L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left({\displaystyle \frac{{\phi }^4}{\left(1-{\theta }_1\right)\left(1-{\theta }_2\right)}}+{\displaystyle \frac{{\phi }^5}{\left(1-{\theta }_1\right)\left(1-{\theta }_2\right)}}\right)\hfill \\ ={\displaystyle \frac{1}{24}}{\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}^4{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}+{\displaystyle \frac{1}{120}}{\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}^5{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}.\hfill \end{array}$$

We continue in this manner to obtain

$$\begin{array}{ccc}& & {\mathsf{\Phi }}_3\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)\hfill \\ & & =L_p^{-1}{L}_q^{-1}{S}_r^{-1}\left[{\phi }^2\left(\begin{array}{c}{L}_p^{\mu }{L}_q^{\eta }{S}_r^{\phi }{\left(\begin{array}{c}{\left({\mathsf{\Phi }}_0\right)}_{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{p^{\mu }}{\mu }}}{\left({\mathsf{\Phi }}_2\right)}_{{\displaystyle \frac{q^{\eta }}{\eta }}{\displaystyle \frac{q^{\eta }}{\eta }}}+{\left({\mathsf{\Phi }}_1\right)}_{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{p^{\mu }}{\mu }}}\\ {\left({\mathsf{\Phi }}_1\right)}_{{\displaystyle \frac{q^{\eta }}{\eta }}{\displaystyle \frac{q^{\eta }}{\eta }}}+{\left({\mathsf{\Phi }}_2\right)}_{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{p^{\mu }}{\mu }}}{\left({\mathsf{\Phi }}_0\right)}_{{\displaystyle \frac{q^{\eta }}{\eta }}{\displaystyle \frac{q^{\eta }}{\eta }}}\end{array}\right)}_{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}\\ -{\left({\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}\left(\begin{array}{c}{\left({\mathsf{\Phi }}_0\right)}_{{\displaystyle \frac{p^{\mu }}{\mu }}}{\left({\mathsf{\Phi }}_2\right)}_{{\displaystyle \frac{q^{\eta }}{\eta }}}+{\left({\mathsf{\Phi }}_1\right)}_{{\displaystyle \frac{p^{\mu }}{\mu }}}\\ {\left({\mathsf{\Phi }}_1\right)}_{{\displaystyle \frac{q^{\eta }}{\eta }}}+{\left({\mathsf{\Phi }}_2\right)}_{{\displaystyle \frac{p^{\mu }}{\mu }}}{\left({\mathsf{\Phi }}_0\right)}_{{\displaystyle \frac{q^{\eta }}{\eta }}}\end{array}\right)\right)}_{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}-{\mathsf{\Phi }}_2\end{array}\right)\right]\hfill \\ & & =-\left({\displaystyle \frac{1}{720}}{\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}^6{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}+{\displaystyle \frac{1}{5040}}{\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}^7{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}\right).\hfill \\ & & ⋮\hfill \end{array}$$

Therefore, the approximate solution of (59) is

$$\begin{array}{cc}\hfill \mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)& =\sum _{k=0}^{\infty }{\mathsf{\Phi }}_k\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)={\mathsf{\Phi }}_0+{\mathsf{\Phi }}_1+{\mathsf{\Phi }}_2+{\mathsf{\Phi }}_3+{\mathsf{\Phi }}_4+\dots \hfill \\ \hfill & =\left(e^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}+\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)e^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}\right)-\left({\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}^2{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}+{\displaystyle \frac{1}{6}}{\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}^3{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}\right)\hfill \\ \hfill & +\left({\displaystyle \frac{1}{24}}{\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}^4{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}+{\displaystyle \frac{1}{120}}{\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}^5{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}\right)\hfill \\ & -\left({\displaystyle \frac{1}{720}}{\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}^6{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}+{\displaystyle \frac{1}{5040}}{\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}^7{e}^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}\right)+\dots \hfill \\ \hfill & =e^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}\left[1-{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}^2+{\displaystyle \frac{1}{24}}{\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}^4-{\displaystyle \frac{1}{720}}{\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}^6+\dots \right]\hfill \\ & +e^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}\left[\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)-{\displaystyle \frac{1}{6}}{\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}^3+{\displaystyle \frac{1}{120}}{\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}^5-{\displaystyle \frac{1}{5040}}{\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)}^7+\dots \right]\hfill \\ \hfill & =e^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}sin\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)+e^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}cos\left({\displaystyle \frac{r^{\delta }}{\delta }}\right).\hfill \end{array}$$

Hence, the solution of (59) is

$$\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)=e^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}sin\left({\displaystyle \frac{r^{\delta }}{\delta }}\right)+e^{{\displaystyle \frac{p^{\mu }}{\mu }}{\displaystyle \frac{q^{\eta }}{\eta }}}cos\left({\displaystyle \frac{r^{\delta }}{\delta }}\right).$$

(77)

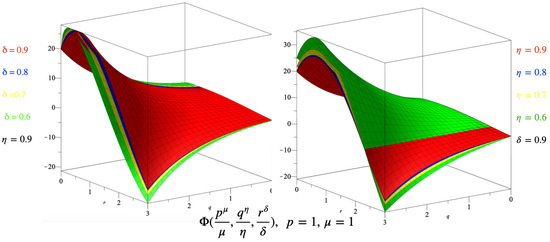
Figure 3 displays the three-dimensional plots of the approximate solutions of $\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)$ for fixed values $p=1$ and $\mu =1$, with various choices of δ and η. The exact solution of (59) is

$$\mathsf{\Phi }\left(p,q,r\right)=e^{pq}sin\left(r\right)+e^{pq}cos\left(r\right).$$

when $\mu =\eta =\delta =1$ in (77).

Figure 3. The 3D plots of the approximate solutions of $\mathsf{\Phi }\left({\displaystyle \frac{p^{\mu }}{\mu }},{\displaystyle \frac{q^{\eta }}{\eta }},{\displaystyle \frac{r^{\delta }}{\delta }}\right)$ in Example 3.

5. Conclusions

In this paper, we introduce the conformable triple Laplace–Sumudu transform and apply it to both linear and nonlinear conformable fractional partial differential equations. The effectiveness of the CTLST is demonstrated through illustrative examples, including the wave and Poisson equations. The results highlight the simplicity and efficiency of the proposed method in handling various types of fractional partial differential equations. Future research will focus on extending this approach to three-dimensional conformable fractional partial differential equations.