On the Conformable Triple Laplace–Sumudu Transform and Two-Dimensional Fractional Partial Differential Equations
Abstract
1. Introduction
2. Terminology and Properties
- , where ζ is constant,
- , where are positive integers,
3. Solving Two-Dimensional Fractional Partial Differential Equations Using the CTLST
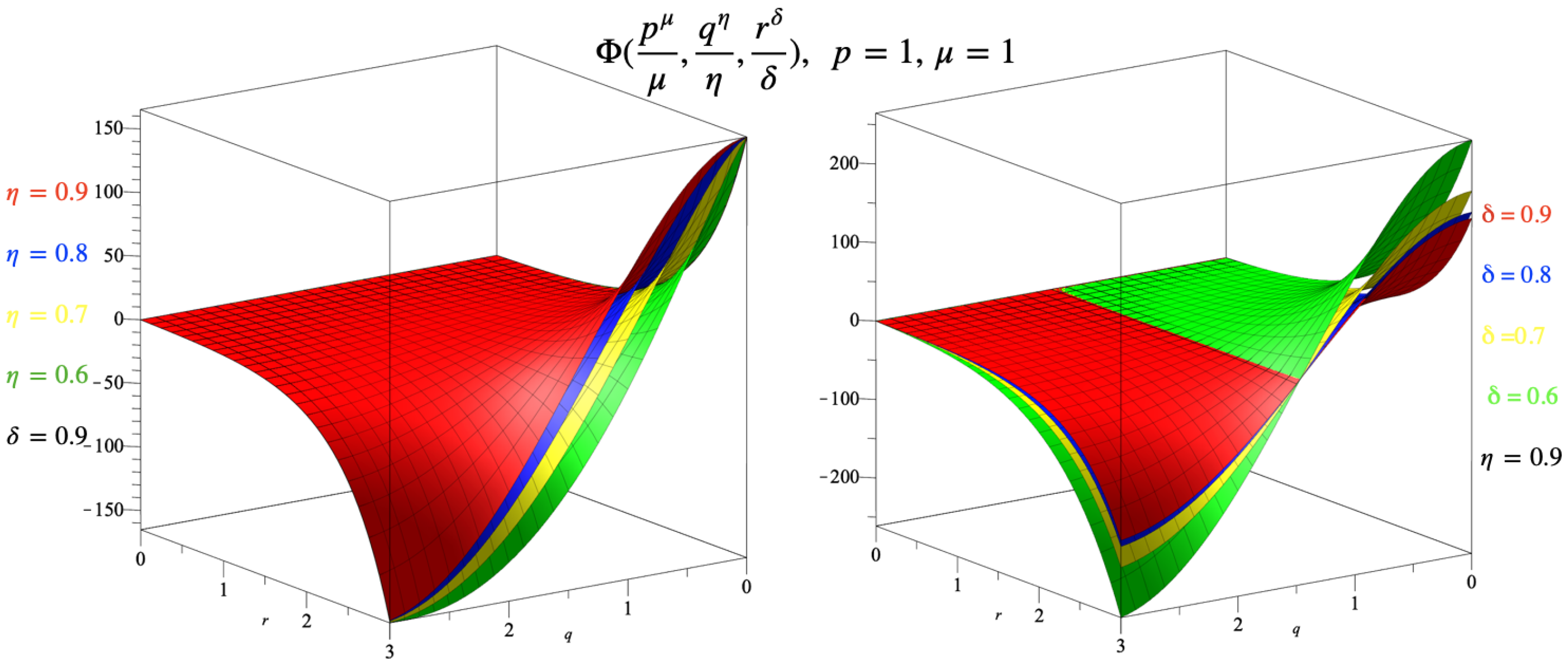
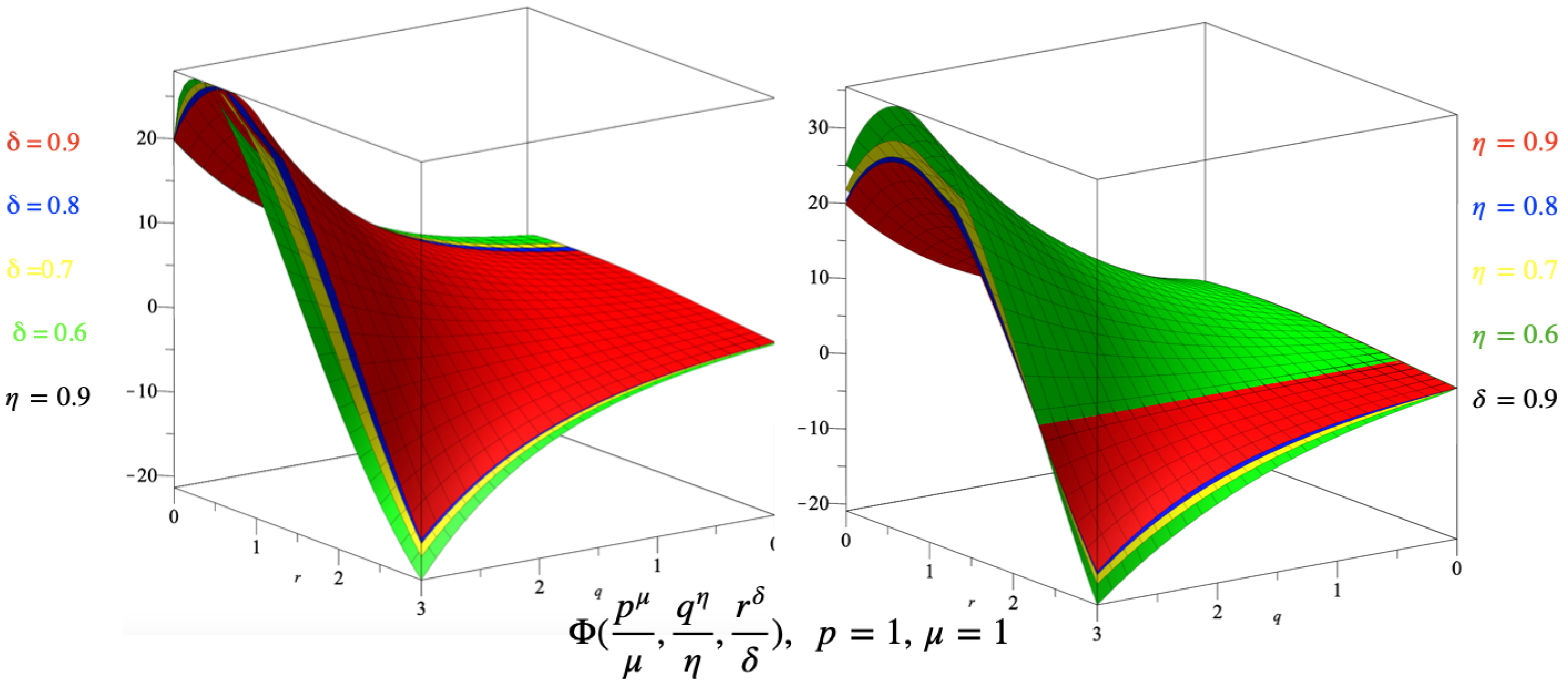
4. Illustrative Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nieto, J.; Rodríguez-López, R. Fractional Differential Equations: Theory, Methods and Applications; MDPI: Basel, Switzerland, 2019. [Google Scholar]
- Chakraverty, S.; Mahato, N.; Karunakar, P.; Rao, T. Advanced Numerical and Semi-Analytical Methods for Differential Equations; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Kilbas, A.; Srivastava, H.; Trujillo, J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Schiff, J. The Laplace Transform: Theory and Applications; Springer Science & Business Media: New York, NY, USA, 1999. [Google Scholar]
- Rezaei, H.; Jung, S.; Rassias, T. Laplace transform and Hyers–Ulam stability of linear differential equations. J. Math. Anal. Appl. 2013, 403, 244–251. [Google Scholar] [CrossRef]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Thabet, H.; Kendre, S. Analytical solutions for conformable space-time fractional partial differential equations via fractional differential transform. Chaos Solitons Fractals 2018, 109, 238–245. [Google Scholar] [CrossRef]
- Alfaqeih, S.; Kayijuka, I. Solving system of conformable fractional differential equations by conformable double Laplace decomposition method. J. Partial Differ. Equ. 2020, 33, 275–290. [Google Scholar] [CrossRef]
- Kilicman, A.; Gadain, H. An application of double Laplace transform and double Sumudu transform. Lobachevskii J. Math. 2009, 30, 214–223. [Google Scholar] [CrossRef]
- Abdeljawad, T. On conformable fractional calculus. J. Comput. Appl. Math. 2015, 279, 57–66. [Google Scholar] [CrossRef]
- Difonzo, F.; Garrappa, R. A numerical procedure for fractional-time-space differential equations with the spectral fractional Laplacian. In Proceedings of the INdAM workshop on Fractional Differential Equations: Modeling, Discretization, and Numerical Solvers, Roma, Italy, 12–14 July 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 29–51. [Google Scholar]
- Özkan, O.; Kurt, A. On conformable double Laplace transform. Opt. Quantum Electron. 2018, 50, 103. [Google Scholar] [CrossRef]
- Kılıçman, A.; Gadain, H. On the applications of Laplace and Sumudu transforms. J. Frankl. Inst. 2010, 347, 848–862. [Google Scholar] [CrossRef]
- Weerakoon, S. Application of Sumudu transform to partial differential equations. Int. J. Math. Educ. Sci. Technol. 1994, 25, 277–283. [Google Scholar] [CrossRef]
- Ziane, D.; Baleanu, D.; Belghaba, K.; Cherif, M. Local fractional Sumudu decomposition method for linear partial differential equations with local fractional derivative. J. King Saud Univ.-Sci. 2019, 31, 83–88. [Google Scholar] [CrossRef]
- Elzaki, T.; Ahmed, S.; Areshi, M.; Chamekh, M. Fractional partial differential equations and novel double integral transform. J. King Saud Univ.-Sci. 2022, 34, 101832. [Google Scholar] [CrossRef]
- Ahmed, S.; Saadeh, R.; Qazza, A.; Elzaki, T. Modified conformable double Laplace–Sumudu approach with applications. Heliyon 2023, 9, e15891. [Google Scholar] [CrossRef] [PubMed]
- Watugala, G. Sumudu transform: A new integral transform to solve differential equations and control engineering problems. Integr. Educ. 1993, 24, 35–43. [Google Scholar] [CrossRef]
- Wang, C.; Xu, T. Triple Mixed Integral Transformation and Applications for Initial-Boundary Value Problems. J. Nonlinear Math. Phys. 2024, 31, 39. [Google Scholar] [CrossRef]
- Tayyan, B.; Sakka, A. Lie symmetry analysis of some conformable fractional partial differential equations. Arab. J. Math. 2020, 9, 201–212. [Google Scholar] [CrossRef]
- Eltayeb, H.; Bachar, I.; Kılıçman, A. On conformable double laplace transform and one dimensional fractional coupled burgers’ equation. Symmetry 2019, 11, 417. [Google Scholar] [CrossRef]
- Hamza, A.; Mohamed, M.; Abd Elmohmoud, E.; Magzoub, M. Conformable Sumudu Transform of Space-Time Fractional Telegraph Equation. In Abstract and Applied Analysis; Wiley Online Library: Hoboken, NJ, USA, 2021; Volume 2021, p. 6682994. [Google Scholar]
- Ahmed, S.; Qazza, A.; Saadeh, R.; Elzaki, T. Conformable double laplace–sumudu iterative method. Symmetry 2022, 15, 78. [Google Scholar] [CrossRef]
- Bhanotar, S.; Belgacem, F. Theory and applications of distinctive conformable triple Laplace and Sumudu transforms decomposition methods. J. Partial Differ. Equ. 2021, 35, 49–77. [Google Scholar] [CrossRef]
- Baleanu, D.; Jassim, H. Exact solution of two-dimensional fractional partial differential equations. Fractal Fract. 2020, 4, 21. [Google Scholar] [CrossRef]
- Saadah, R.; Amleh, M.; Qazza, A.; Al-Omari, S.; Akdemir, A. Results Involving Partial Differential Equations and Their Solution by Certain Integral Transform. CMES-Comput. Model. Eng. Sci. 2024, 140, 1594–1616. [Google Scholar] [CrossRef]
- Khan, H.; Shah, R.; Kumam, P.; Arif, M. Analytical solutions of fractional-order heat and wave equations by the natural transform decomposition method. Entropy 2019, 21, 597. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aldossari, S.; GadAllah, M.R. On the Conformable Triple Laplace–Sumudu Transform and Two-Dimensional Fractional Partial Differential Equations. Symmetry 2025, 17, 1543. https://doi.org/10.3390/sym17091543
Aldossari S, GadAllah MR. On the Conformable Triple Laplace–Sumudu Transform and Two-Dimensional Fractional Partial Differential Equations. Symmetry. 2025; 17(9):1543. https://doi.org/10.3390/sym17091543
Chicago/Turabian StyleAldossari, Shayea, and Musa Rahamh GadAllah. 2025. "On the Conformable Triple Laplace–Sumudu Transform and Two-Dimensional Fractional Partial Differential Equations" Symmetry 17, no. 9: 1543. https://doi.org/10.3390/sym17091543
APA StyleAldossari, S., & GadAllah, M. R. (2025). On the Conformable Triple Laplace–Sumudu Transform and Two-Dimensional Fractional Partial Differential Equations. Symmetry, 17(9), 1543. https://doi.org/10.3390/sym17091543








