Broken Mirrors: Multiple Circular Polarization and Inversion in the Ground and Photoexcited States of Mirror-Symmetric Helical Poly(di-iso-alkylsilane)s in Achiral Molecular Solvents
Abstract
1. Introduction
2. Materials and Methods
3. Results
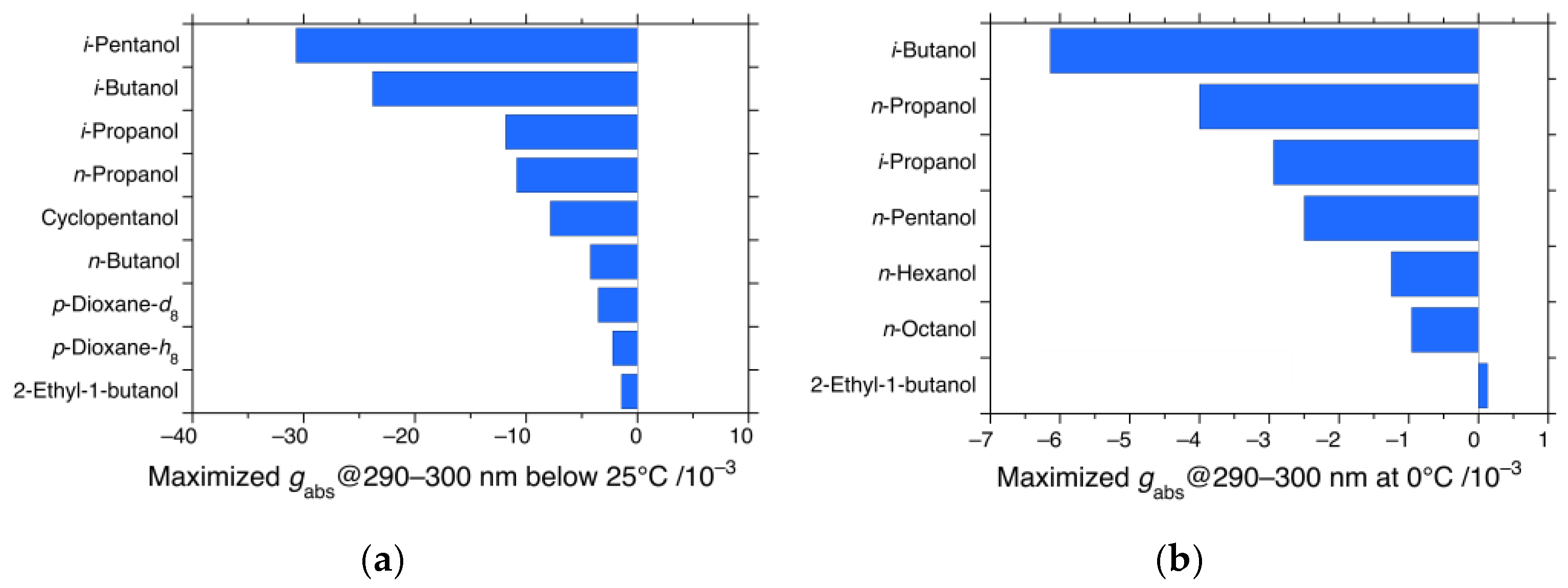
3.1. Solvent-Dependent CD, UV, CPL and PL Spectral Characteristics of iBS
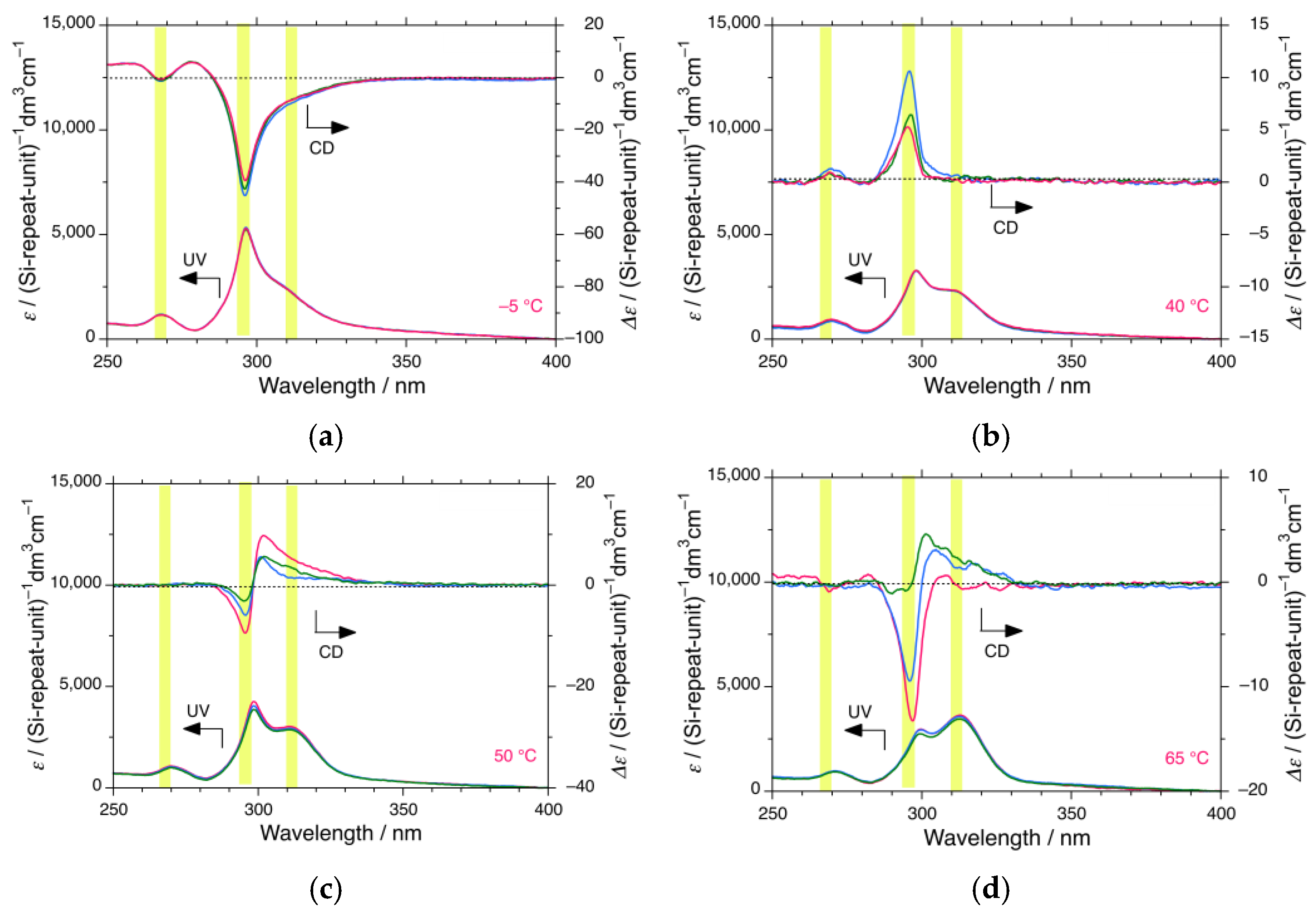
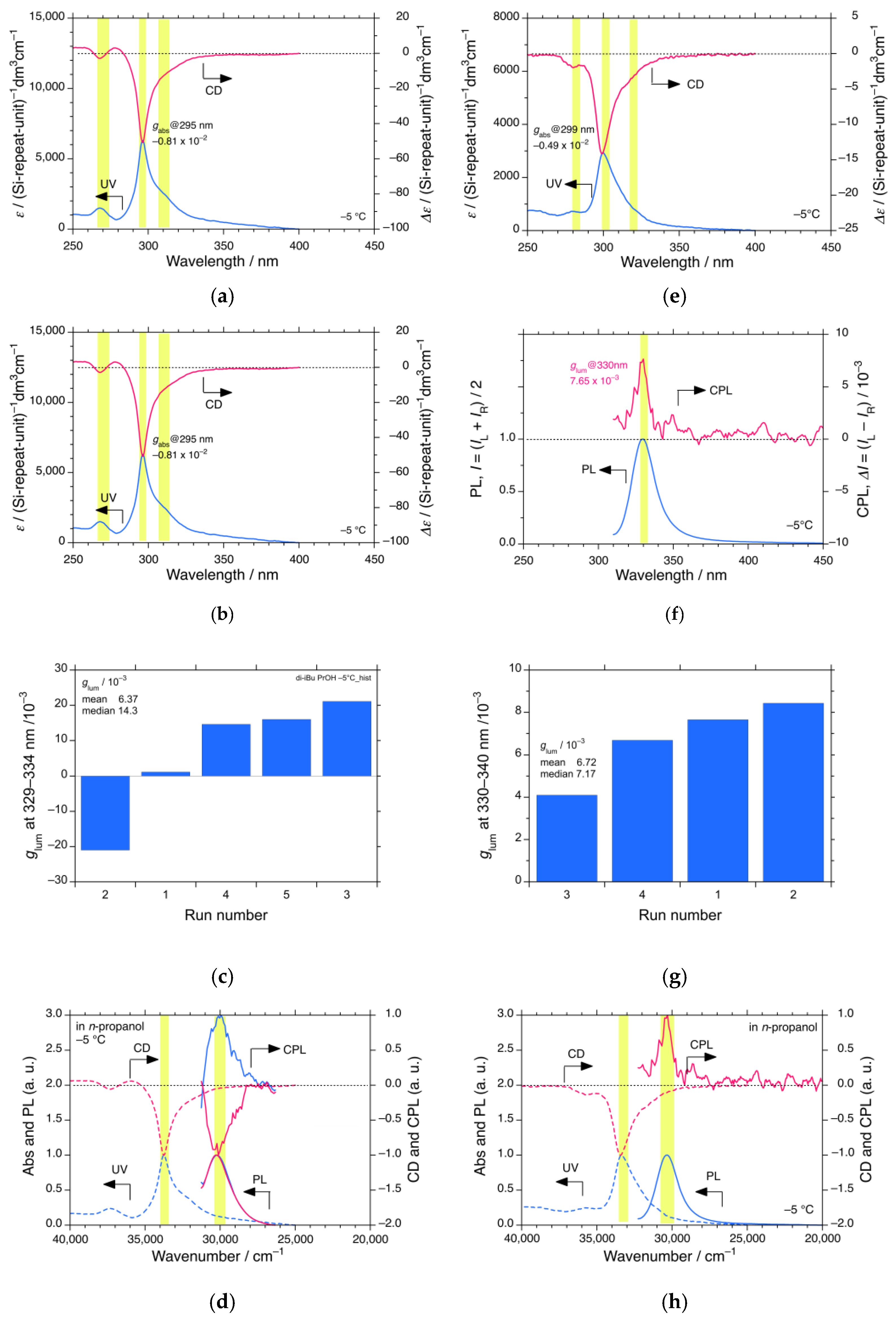
3.1.1. iBS in n-Propanol
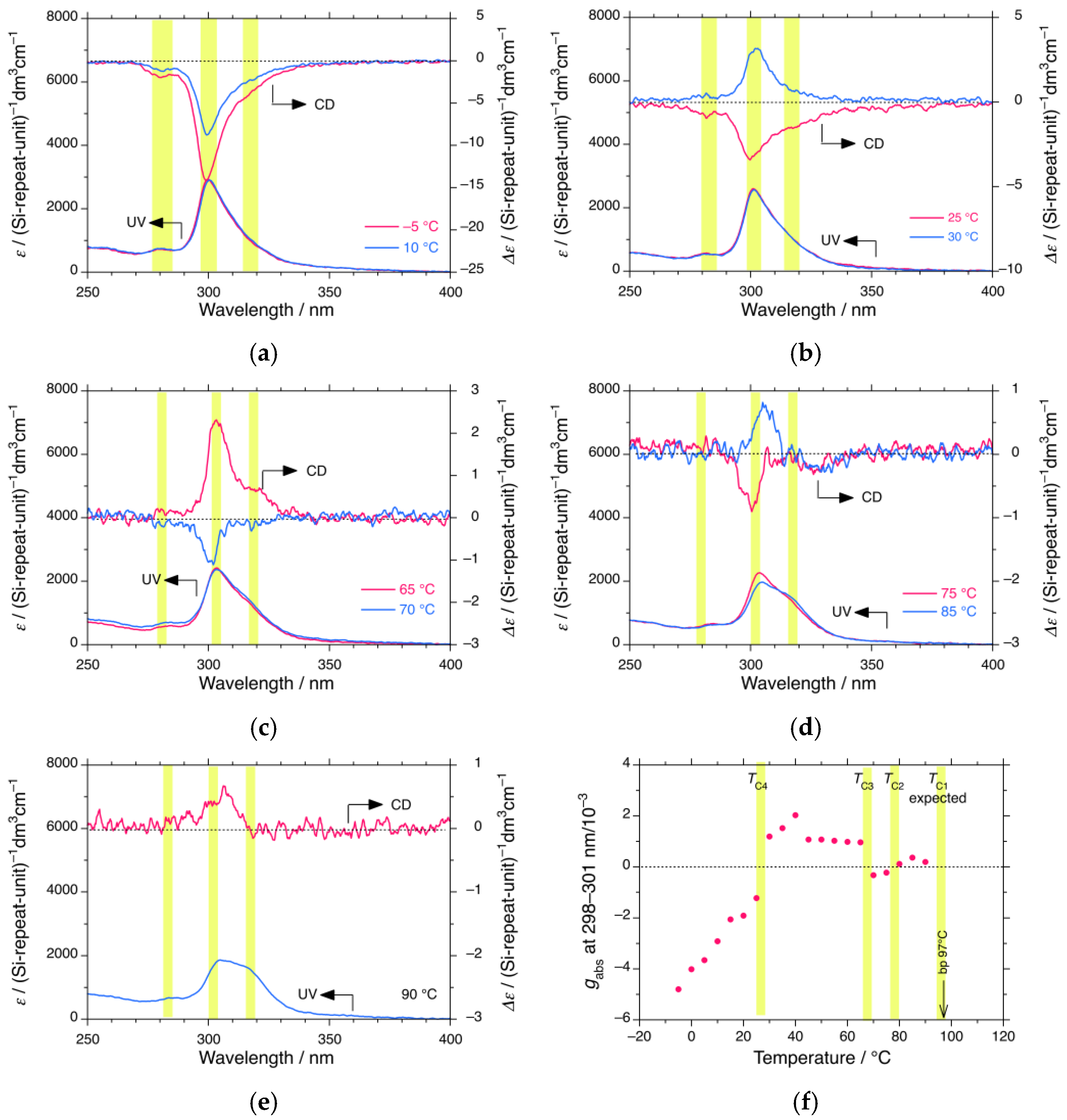
3.1.2. iBS in i-Propanol
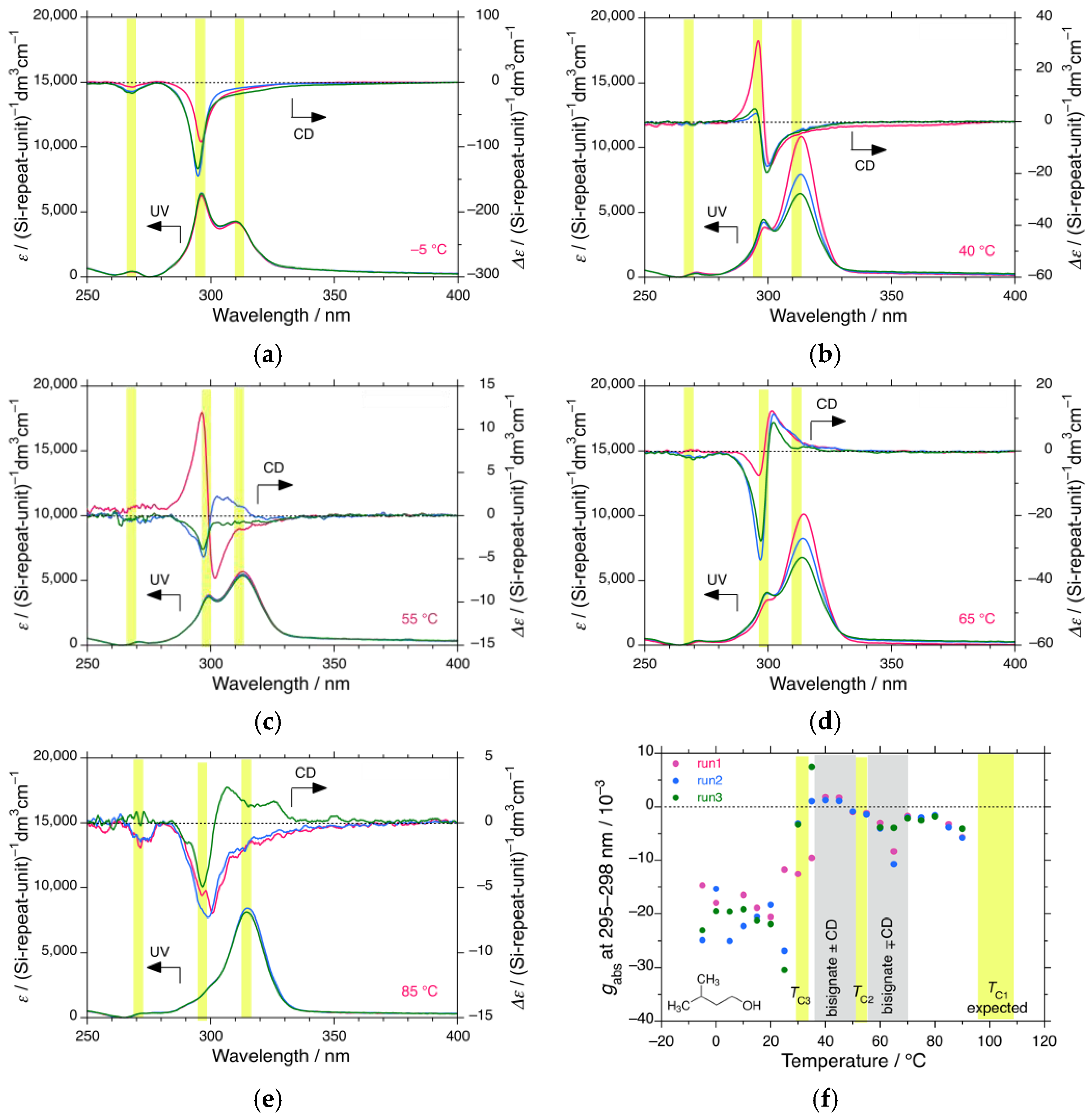
3.1.3. iBS in i-Butanol
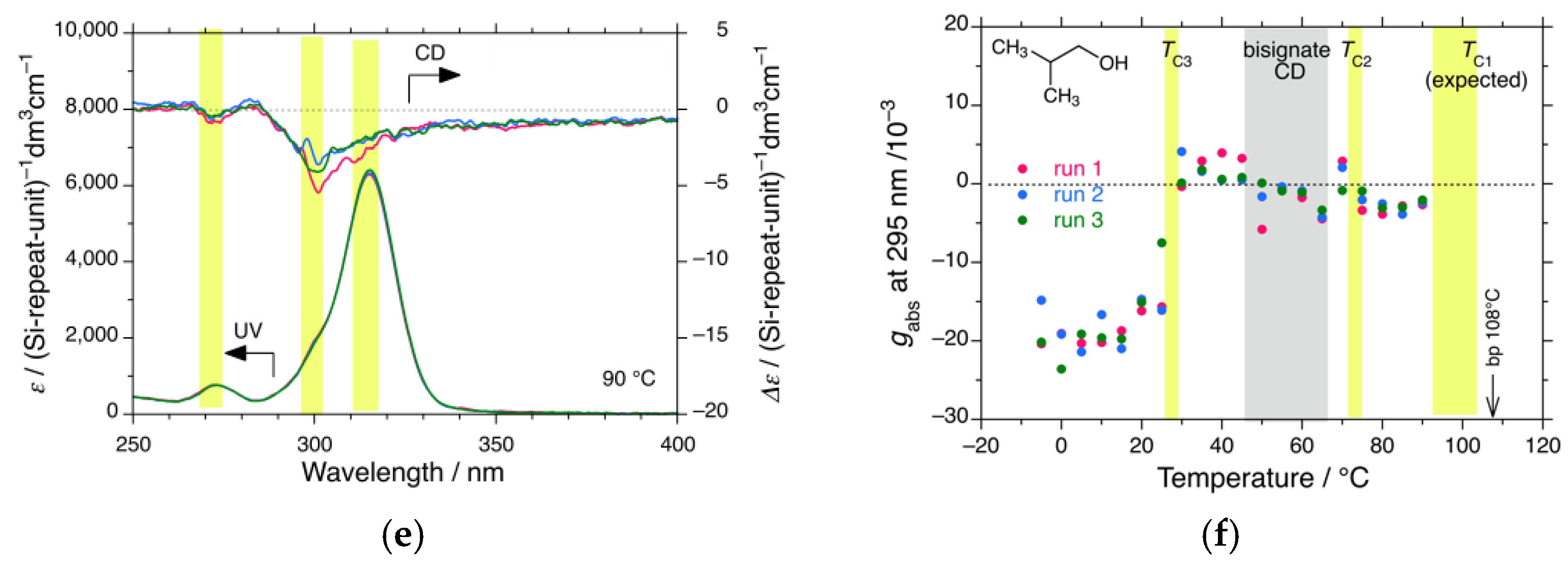
3.1.4. iBS in i-Pentanol
3.1.5. iBS in n-Butanol, 2-Ethyl-1-butanol, and Cyclopentanol
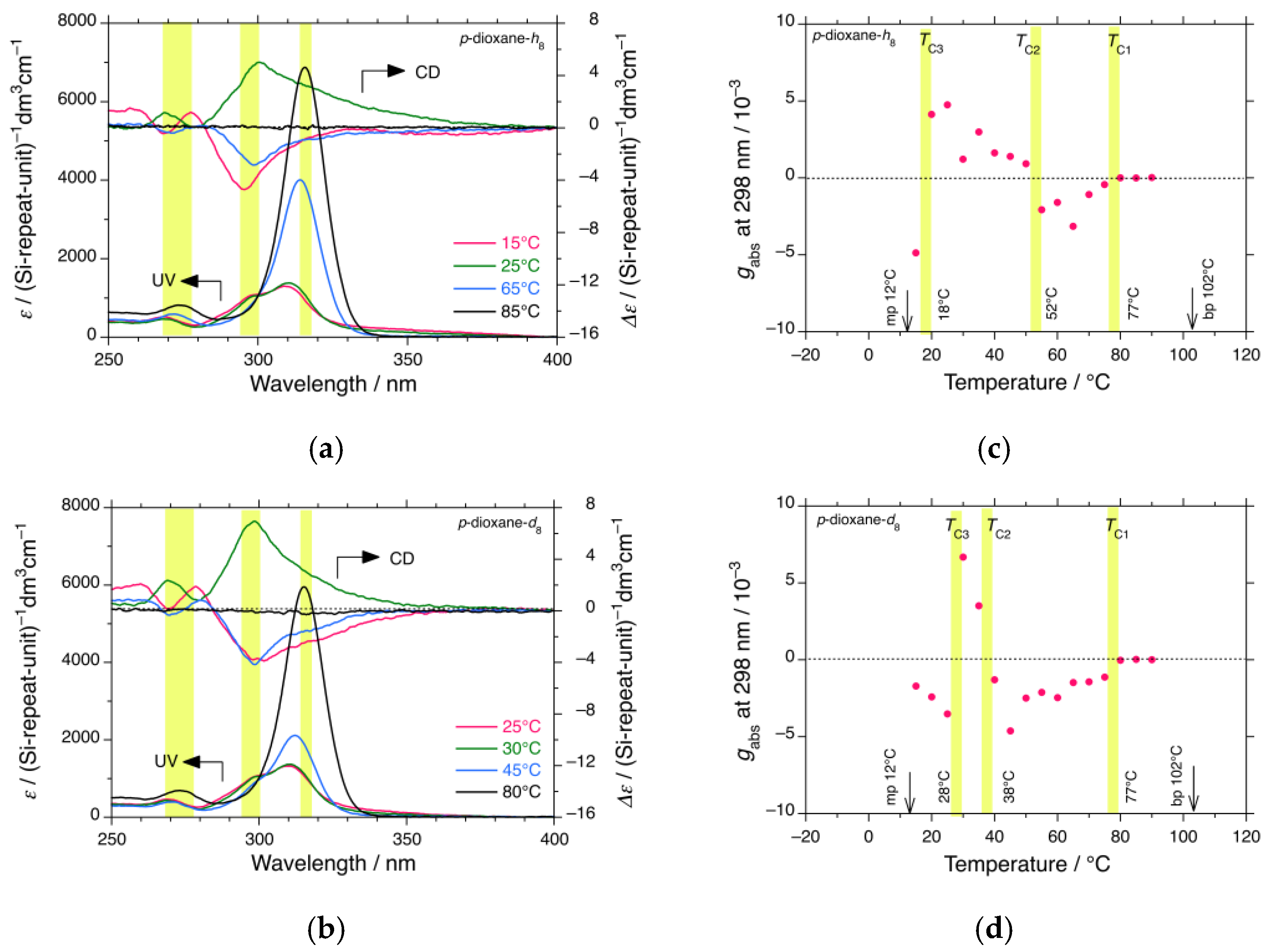
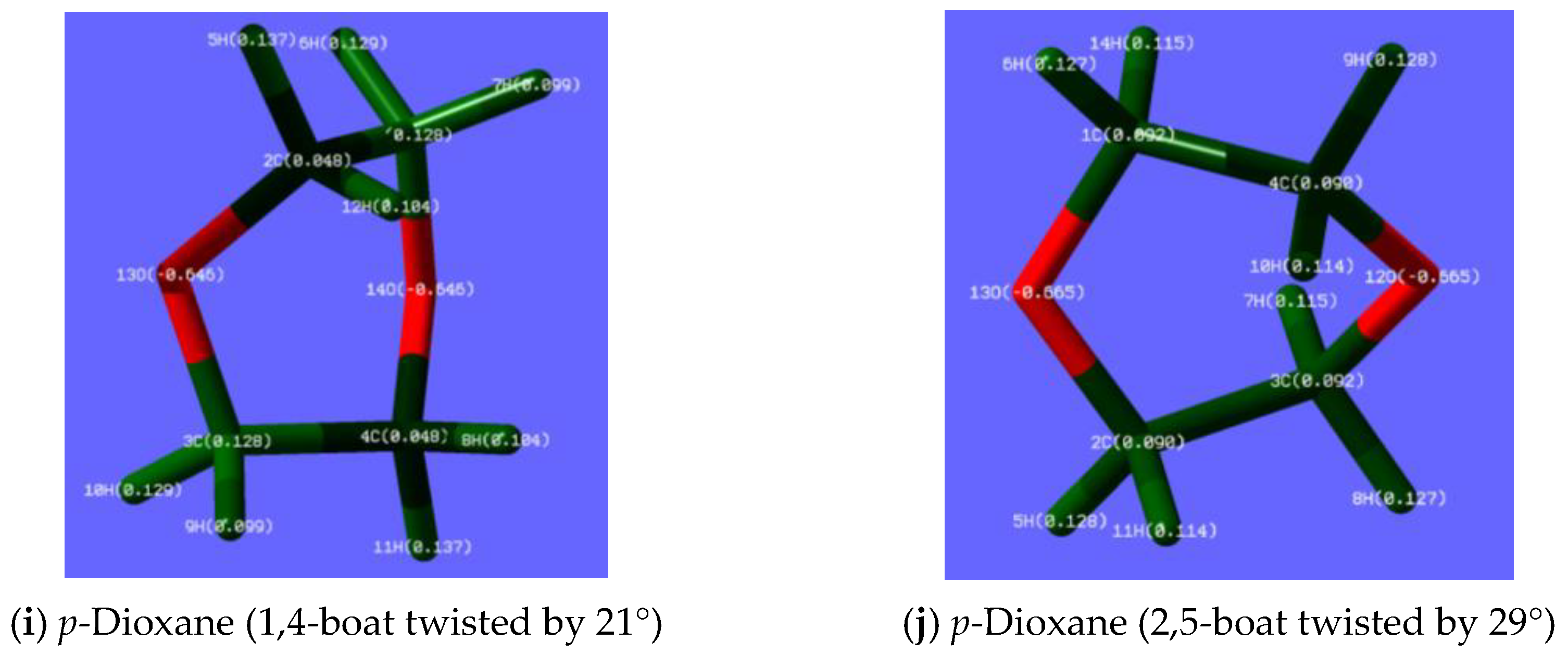
3.1.6. iBS in p-Dioxane-h8 and p-Dioxane-d8—Less-Obvious H/D Isotope Effect
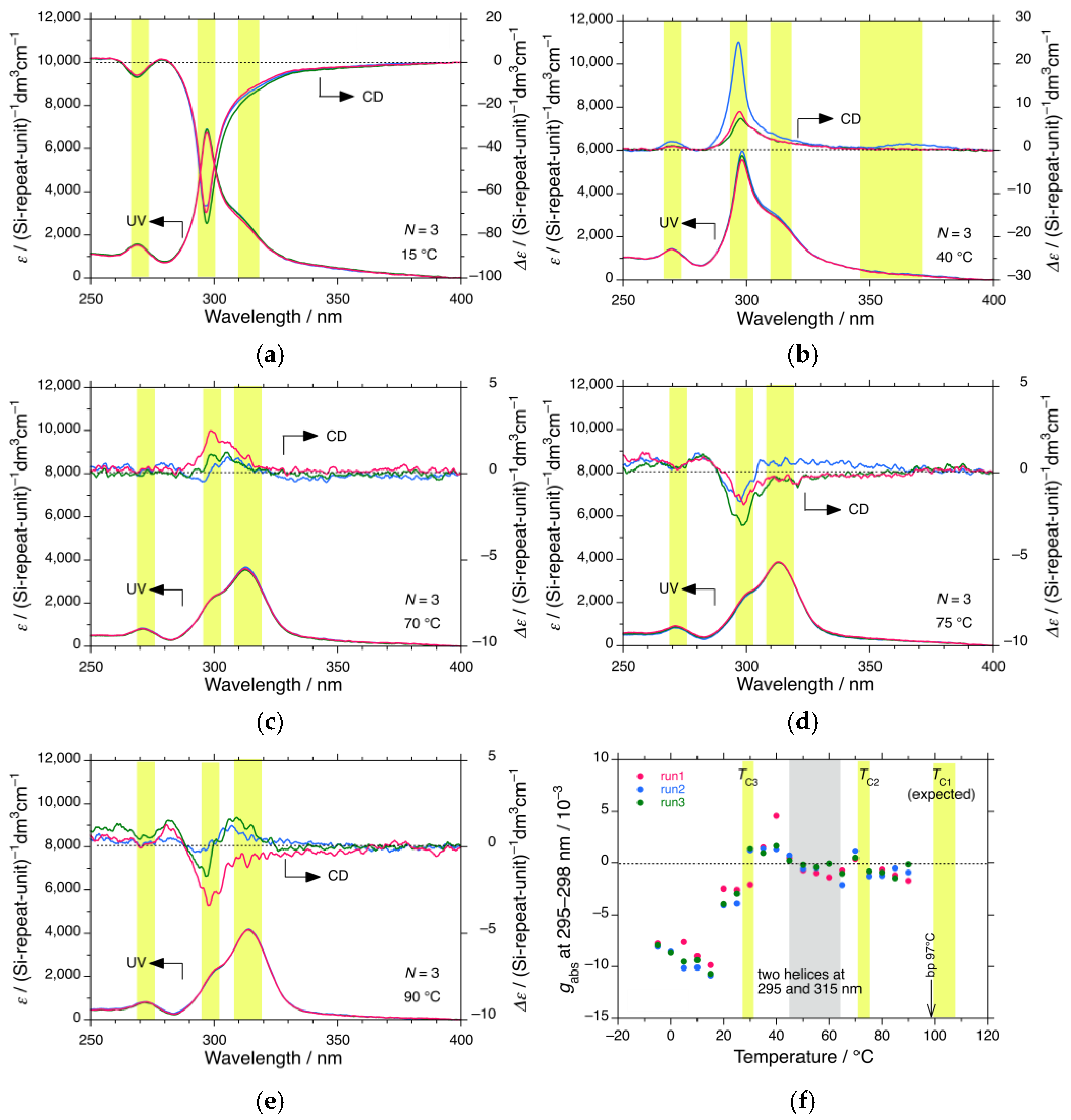
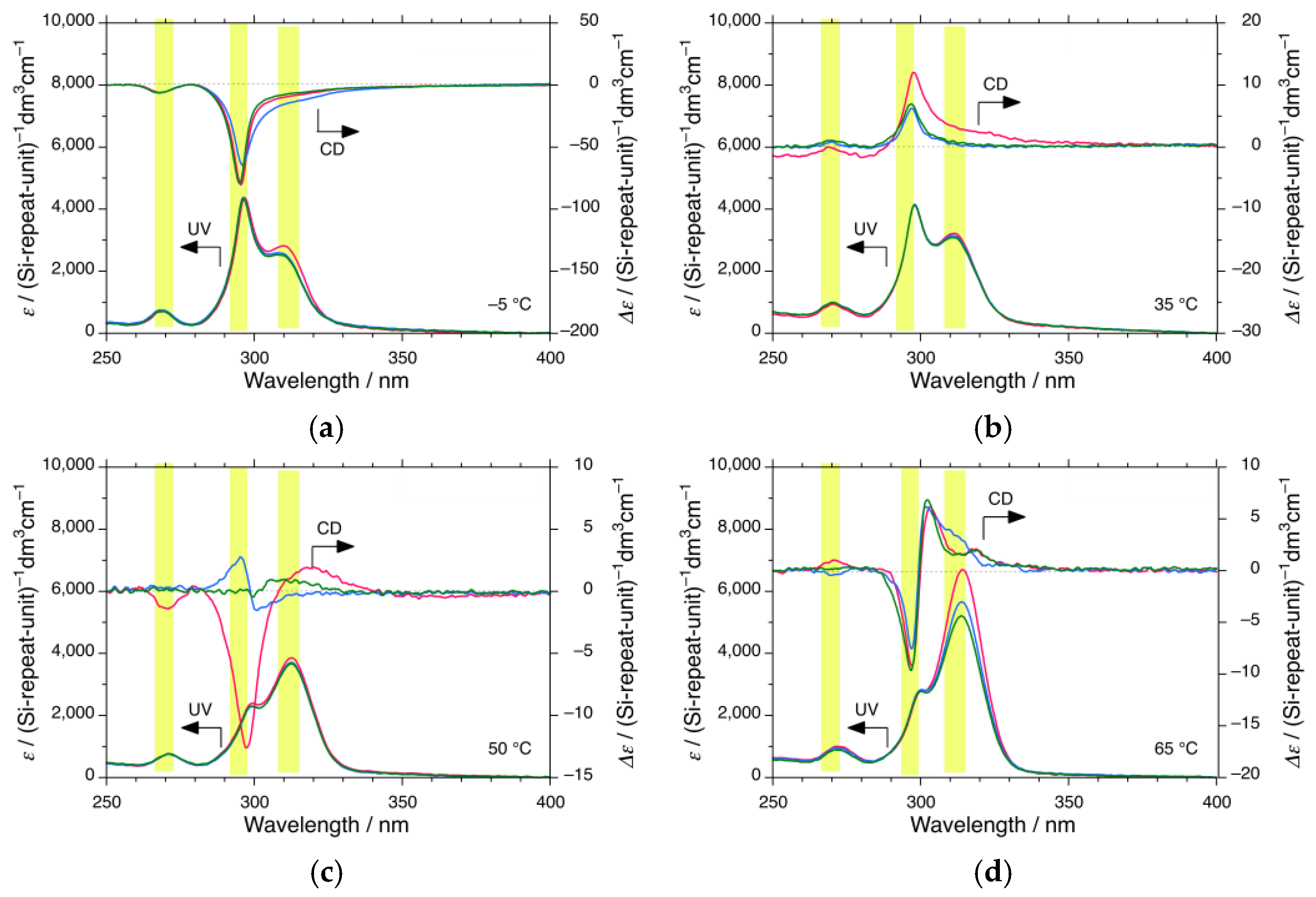
3.2. CD, UV, CPL, and PL Spectral Characteristics of iPS and iHS
3.2.1. iPS in n-Propanol
3.2.2. iPS in n-Pentanol, n-Hexanol, and n-Octanol, and iHS in n-Octanol
3.2.3. iPS in i-Propanol, i-Butanol, and 2-Ethyl-1-butanol
3.3. Solvent Effects in CD and UV Characteristics of iBS and iPS
3.4. CPL and CD Polarization and Inversion of iBS and iPS in n-Propanol at −5 °C
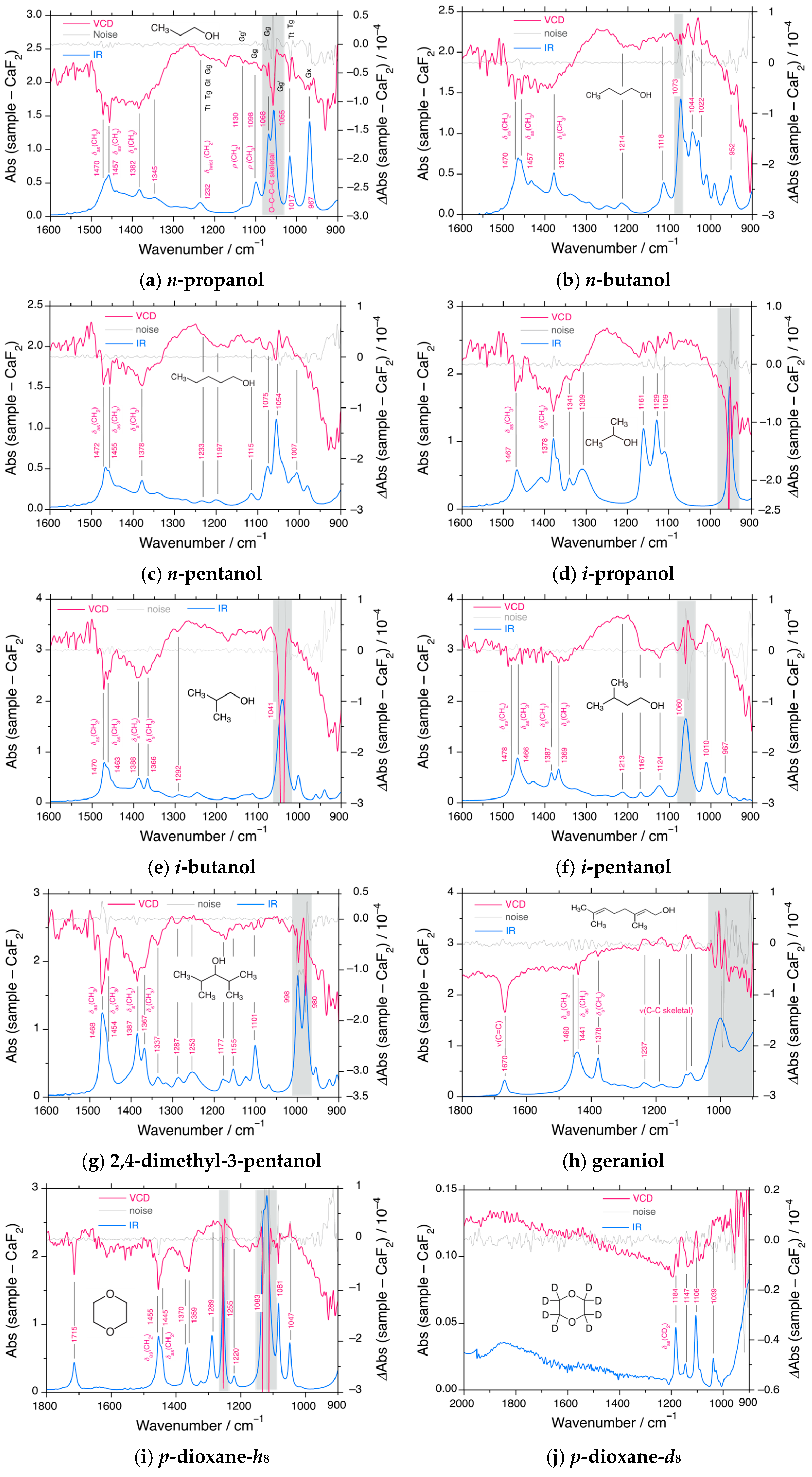
3.5. VCD and IR Spectral Characteristics of Achiral Alkanols and Alkyl Ethers
4. Discussion
4.1. Helix–Helix Transition Temperatures of Mirror-Symmetric Polysilanes in Achiral Solvents
4.2. Rotamers in Alkanols, Alkyl Ethers, and Trisilane Derivatives
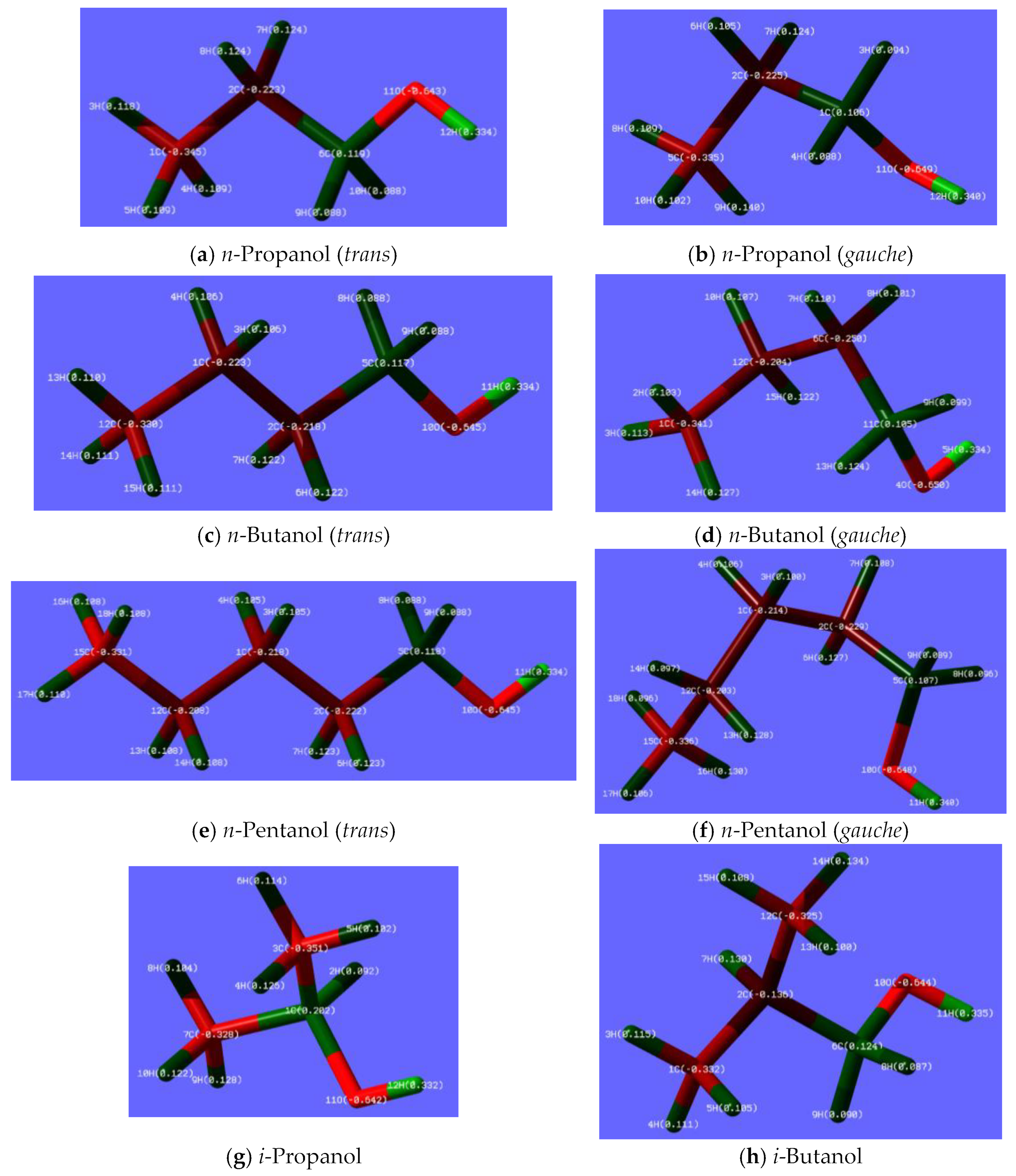
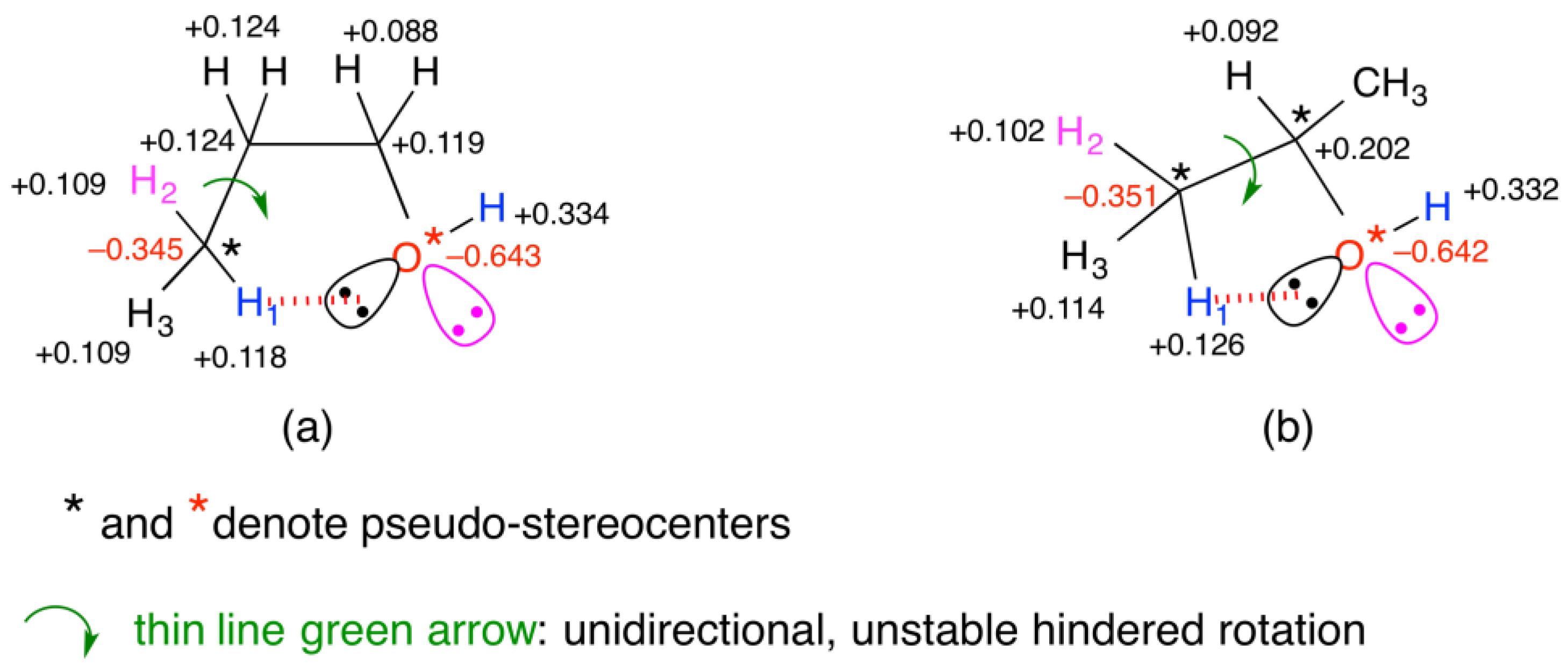
4.2.1. Mulliken Charges and Electroweak Charges
4.2.2. Inequality of the Two Lone Pairs at Oxygen Atom in Alkanols and Alkyl Ethers
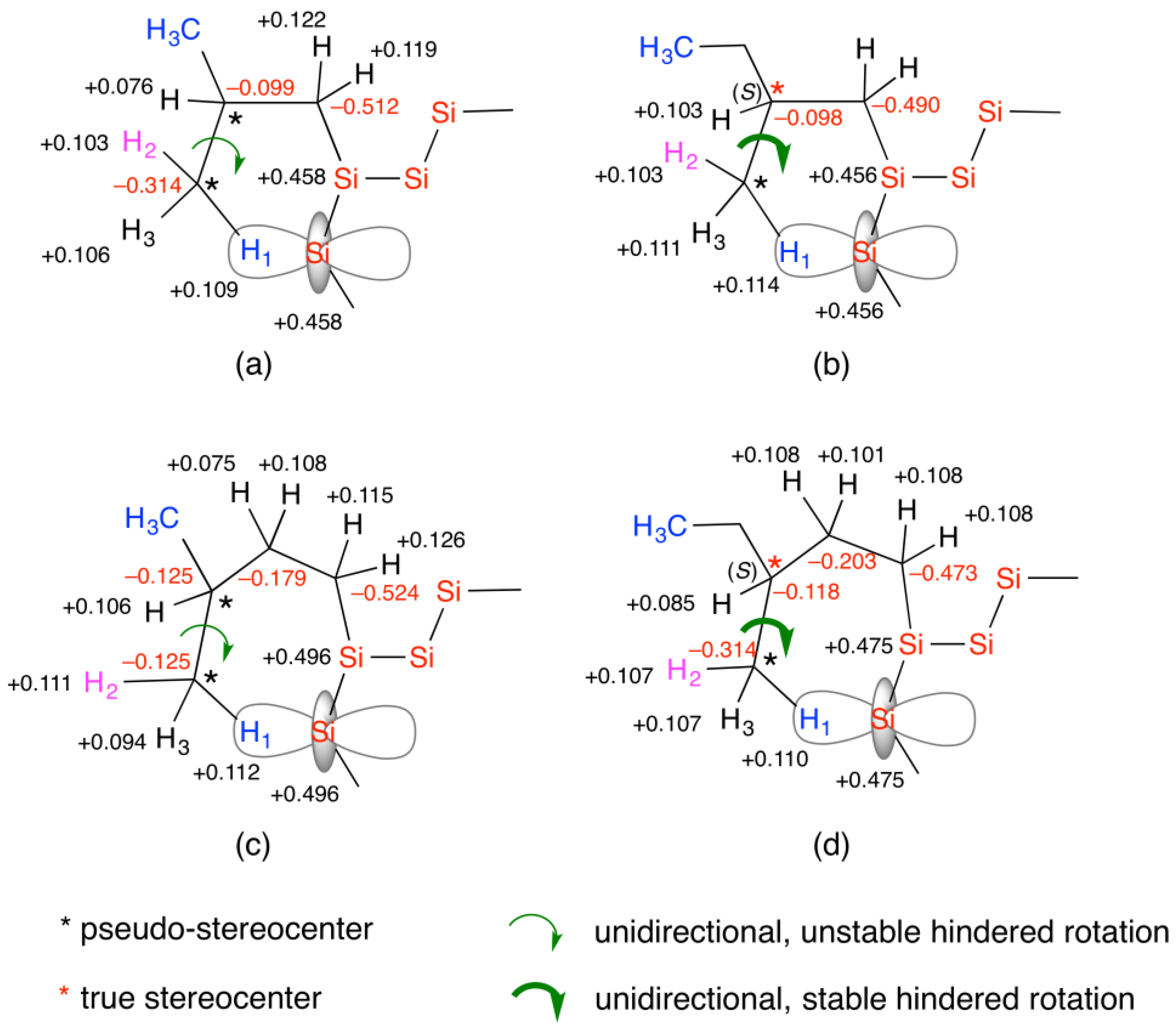
4.2.3. VCD and IR Spectra of Trisilanes Carrying Achiral and (S)-Chiral Substituents
4.2.4. Scenarios of CD Polarization in iBS, iPS, and nBS with Alkanols and Alkyl Ethers
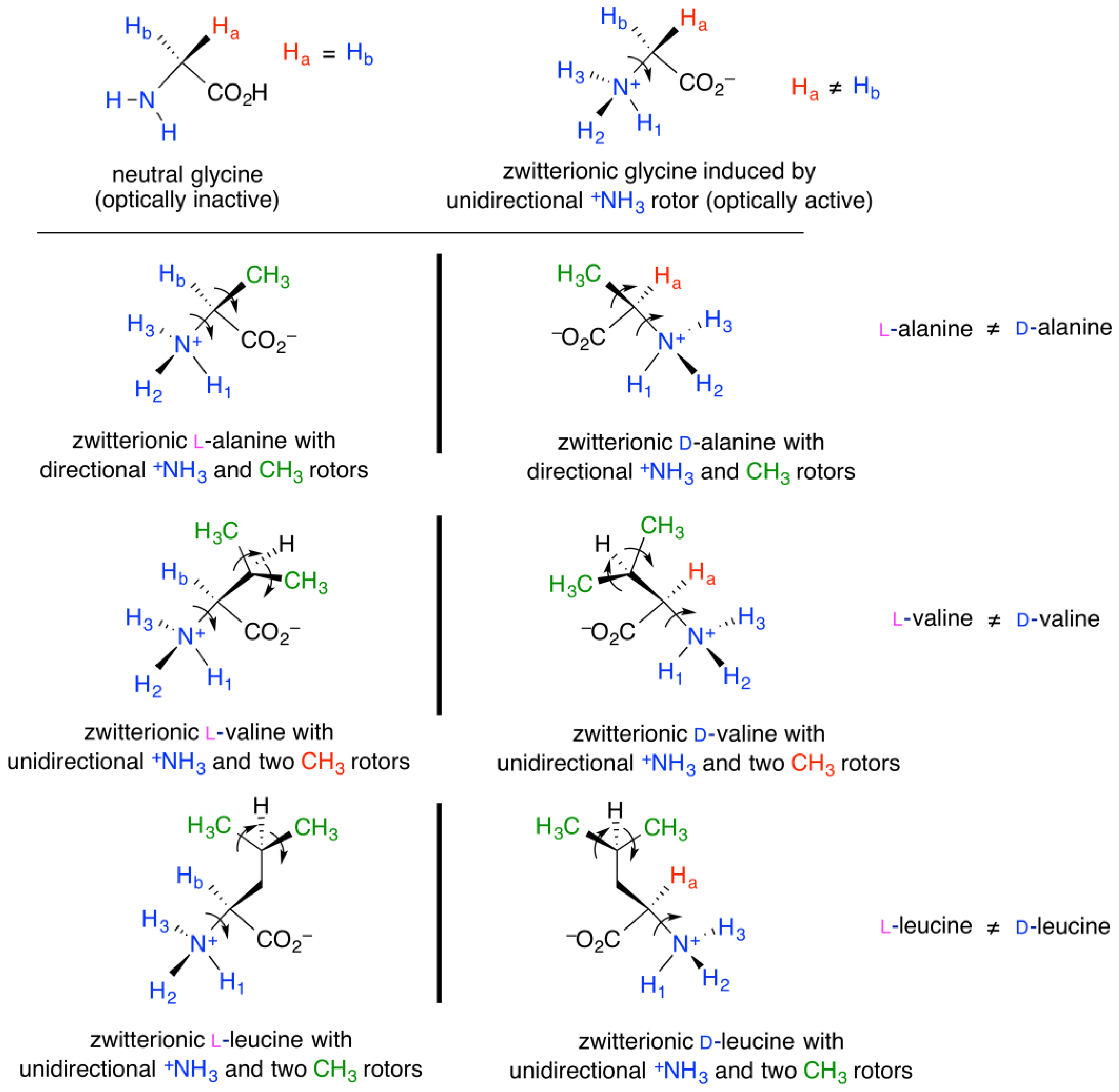
5. Perspective—Possible Origin of Biomolecular Handedness
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Einstein, A. The Ultimate Quotable Einstein; Calaprice, A., Ed.; Princeton University Press: Princeton, NJ, USA, 2010; pp. 397, 475, ISBN-13 978-0-691-13817-6. [Google Scholar]
- Myneni, K. Symmetry Destroyed: The Failure of Parity, History of Science: Parity Violation. 1984. Available online: https://ccreweb.org/documents/parity/parity.html (accessed on 1 August 2025).
- Gardner, M. The New Ambidextrous Universe: Symmetry and Asymmetry from Mirror Reflections to Superstrings, 3rd rev. ed.; Dover: Mineola, NY, USA, 2005; ISBN-13 978-0486442440. [Google Scholar]
- Brading, K.; Castellani, E.; Teh, N. Symmetry and symmetry breaking. In Stanford Encyclopedia of Philosophy; Metaphysics Research Lab, Stanford University: Stanford, CA, USA, 2023; pp. 1–53. Available online: https://plato.stanford.edu/entries/symmetry-breaking/ (accessed on 1 August 2025).
- Lee, T.D.; Yang, C.N. Question of parity violation in weak interactions. Phys. Rev. 1956, 104, 254–258. [Google Scholar] [CrossRef]
- Wu, C.S.; Ambler, E.; Hayward, R.W.; Hoppes, D.D.; Hudson, R.P. Experimental test of parity conservation in beta decay. Phys. Rev. 1957, 105, 1413–1415. [Google Scholar] [CrossRef]
- Ambler, E.; Hayward, R.W.; Hoppes, D.D.; Hudson, R.P.; Wu, C.S. Further experiments on β decay of polarized nuclei. Phys. Rev. 1957, 106, 1361–1363. [Google Scholar] [CrossRef]
- Garwin, R.L.; Lederman, L.M.; Weinrich, M. Observations of the failure of conservation of parity and charge conjugation in meson decays: The magnetic moment of the free muon. Phys. Rev. 1957, 105, 1415–1417. [Google Scholar] [CrossRef]
- Schopper, H. Circular polarization of γ-rays: Further proof for parity failure in β decay. Phil. Mag. 1957, 2, 710–713. [Google Scholar] [CrossRef]
- Rodberg, L.S.; Weisskopf, V.F. Fall of parity—Recent discoveries related to symmetry of laws of nature. Science 1957, 125, 627–632. [Google Scholar] [CrossRef] [PubMed]
- Christenson, J.H.; Cronin, J.W.; Fitch, V.L.; Turlay, R. Evidence for the 2π decay of the K20 meson. Phys. Rev. Lett. 1964, 13, 138–140. [Google Scholar] [CrossRef]
- Abe, K.; Abe, R.; Adachi, I.; Ahn, B.S.; Aihara, H.; Akatsu, M.; Alimonti, G.; Asai, K.; Asai, M.; Asano, Y.; et al. Observation of large CP violation in the neutral B meson system. Phys. Rev. Lett. 2001, 87, 091802. [Google Scholar] [CrossRef]
- Aubert, B.; Boutigny, D.; Gaillard, J.-M.; Hicheur, A.; Karyotakis, Y.; Lees, J.P.; Robbe, P.; Tisserand, V.; Palano, A.; Chen, G.P.; et al. Observation of CP violation in the B0 meson system. Phys. Rev. Lett. 2001, 87, 091801. [Google Scholar] [CrossRef]
- LHCb Collaboration. Observation of charge–parity symmetry breaking in baryon decays. Nature 2025, 643, 1223–1228. [Google Scholar] [CrossRef]
- Baryon. Available online: https://en.wikipedia.org/wiki/Baryon (accessed on 1 August 2025).
- Michel, F.C. Parity nonconservation in nuclei. Phys. Rev. 1964, 133, B329–B349. [Google Scholar] [CrossRef]
- Stodolsky, L. Neutron optics and weak currents. Phys. Lett. B 1974, 50, 352–356. [Google Scholar] [CrossRef]
- Bouchiat, M.A.; Bouchiat, C. Weak neutral currents in atomic physics. Phys. Lett. B 1974, 48, 111–114. [Google Scholar] [CrossRef]
- Bouchiat, M.A.; Bouchiat, C.I. Parity violation induced by weak neutral currents in atomic physics. J. Phys. 1974, 35, 899–927. [Google Scholar] [CrossRef]
- Fortson, E.N.; Wilets, L. Parity nonconservation in atoms: Status of theory and experiment. Adv. Atom. Mol. Phys. 1980, 16, 319–373. [Google Scholar] [CrossRef]
- Fortson, E.N.; Lewis, L.L. Atomic parity nonconservation experiments. Phys. Rep. 1984, 113, 289–344. [Google Scholar] [CrossRef]
- Bouchiat, M.A.; Guena, J.; Hunter, L.; Pottier, L. Observation of a parity violation in cesium. Phys. Lett. B 1982, 117, 358–364. [Google Scholar] [CrossRef]
- Bouchiat, M.-A.; Bouchiat, C. Parity violation in atoms. Rep. Prog. Phys. 1997, 60, 1351–1396. [Google Scholar] [CrossRef]
- Forte, M.; Heckle, B.R.; Ramsey, N.F.; Green, K.; Ramsey, G.L.; Byrne, J.; Pendlebury, J.M. First measurement of parity-nonconserving neutron-spin rotation: The tin isotopes. Phys. Rev. Lett. 1980, 45, 2088–2091. [Google Scholar] [CrossRef]
- Alfimenkov, V.P.; Borzakov, S.B.; Van Thuan, V.; Mareev, Y.D.; Pikelner, L.B.; Khrykin, A.S.; Sharapov, E. Parity nonconservation in neutron resonances. Nucl. Phys. A 1983, 398, 93–106. [Google Scholar] [CrossRef]
- Mitchell, G.E.; Bowman, J.D.; Weidenmüller, H.A. Parity violation in the compound nucleus. Rev. Mod. Phys. 1999, 71, 445–457. [Google Scholar] [CrossRef]
- Smith, D.A.; Bowman, D.; Crawford, B.E.; Grossmann, C.A.; Haseyama, T.; Johnson, M.B.; Masaike, A.; Matsuda, Y.; Mitchell, G.E.; Nazarenko, V.A.; et al. Parity violation in neutron resonances of 117Sn. Phys. Rev. C 2001, 64, 015502. [Google Scholar] [CrossRef]
- Quack, M. On biomolecular homochirality as a quasi-fossil of the evolution of life. Adv. Chem. Phys. 2014, 157, 249–291. [Google Scholar] [CrossRef]
- Eliel, E.L.; Wilen, S.H.; Mander, L.N. Stereochemistry of Organic Compounds; Wiley-Interscience: New York, NY, USA, 1994; ISBN 978-0471016700. [Google Scholar]
- Mislow, K. Introduction to Stereochemistry; Dover: Mineola, NY, USA, 2003; ISBN 978-0486425306. [Google Scholar]
- Anslyn, E.V.; Dougherty, D.A. Chapter 6: Stereochemistry. In Modern Physical Organic Chemistry; University Science Books: Sausalito, CA, USA, 2004; pp. 297–351. ISBN 978-1-891389-31-3. [Google Scholar]
- Vollhardt, P.; Schore, N.E. Chapter 5: Stereoisomers. In Organic Chemistry: Structure and Function, 7th ed.; W.H. Freeman: New York, NY, USA, 2015; pp. 167–210, ISBN-13: 978-1-4641-2027-5. [Google Scholar]
- Berova, N.; Polavarapu, P.; Nakanishi, K.; Woody, R.W. Comprehensive Chiroptical Spectroscopy, Volume 1: Instrumentation, Methodologies, and Theoretical Simulations; Wiley: Hoboken, NJ, USA, 2012; ISBN 978-1118012932. [Google Scholar]
- Berova, N.; Polavarapu, P.; Nakanishi, K.; Woody, R.W. Comprehensive Chiroptical Spectroscopy, Volume 2: Applications in Stereochemical Analysis of Synthetic Compounds, Natural Products, and Biomolecules; Wiley: Hoboken, NJ, USA, 2012; ISBN 978-1118012925. [Google Scholar]
- Zhang, X.; Xu, Y.; Valenzuela, C.; Zhang, X.; Wang, L.; Feng, W.; Li, Q. Liquid crystal-templated chiral nanomaterials: From chiral plasmonics to circularly polarized luminescence. Light Sci. Appl. 2022, 1, 223. [Google Scholar] [CrossRef] [PubMed]
- Yamagata, Y. A hypothesis for the asymmetric appearance of biomolecules on Earth. J. Theor. Biol. 1966, 11, 495–498. [Google Scholar] [CrossRef]
- Rein, D.W. Some remarks on parity violating effects of intramolecular interactions. J. Mol. Evol. 1974, 4, 15–22. [Google Scholar] [CrossRef]
- Letokhov, V.S. On difference of energy levels of left and right molecules due to weak interactions. Phys. Lett. A 1975, 53, 275–276. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B.; Saakyan, D.B.; Sobel’man, I.I. Energy difference between right–hand and left-hand molecules, due to parity nonconservation in weak interactions of electrons with nuclei. Sov. Phys. JETP Lett. 1977, 25, 94–97. Available online: http://jetpletters.ru/ps/1388/article_21066.pdf (accessed on 1 August 2025).
- Keszthelyi, L. Origin of the asymmetry of biomolecules and weak interaction. Orig. Life 1977, 8, 299–340. [Google Scholar] [CrossRef]
- Harris, R.A.; Stodolsky, L. Quantum beats in optical activity and weak interactions. Phys. Lett. B 1978, 78, 313–317. [Google Scholar] [CrossRef]
- Hegstrom, R.A.; Rein, D.W.; Sandars, P.G.H. Calculation of the parity nonconverging energy difference between mirror-image molecules. J. Chem. Phys. 1980, 73, 2329–2341. [Google Scholar] [CrossRef]
- Mason, S.F.; Tranter, G.E. The parity-violating energy difference between enantiomeric molecules. Mol. Phys. 1984, 53, 1091–1111. [Google Scholar] [CrossRef]
- Wiesenfeld, L. Effect of atomic number on parity-violating energy differences between enantiomers. Mol. Phys. 1988, 64, 739–745. [Google Scholar] [CrossRef]
- Avetisov, V.A.; Goldanskii, V.I.; Kuz’min, V.V. Handedness, origin of life and evolution. Phys. Today 1991, 44, 33–41. [Google Scholar] [CrossRef]
- Salam, A. The role of chirality in the origin of life. J. Mol. Evol. 1991, 33, 105–113. [Google Scholar] [CrossRef]
- Janoschek, R. Chapter 2: Theories on the origin of biomolecular homochirality. In Chirality: From Weak Bosons to the α–Helix; Janoschek, R., Ed.; Springer: Berlin/Heidelberg, Germany, 1991; pp. 18–33. ISBN 978-3642765711. [Google Scholar] [CrossRef]
- Laerdahl, J.K.; Wesendrup, R.; Schwerdtfeger, P. D- or L-alanine: That is the question. ChemPhysChem 2000, 1, 60–62. [Google Scholar] [CrossRef] [PubMed]
- Tranter, G.E.; MacDermott, A.J. Parity-violating energy differences between chiral conformations of tetrahydrofuran, a model system for sugars. Chem. Phys. Lett. 1986, 130, 120–122. [Google Scholar] [CrossRef]
- Zanasi, R.; Lazzeretti, P. On the stabilization of natural L-enantiomers of α-amino acids via parity-violating effects. Chem. Phys. Lett. 1998, 286, 240–242. [Google Scholar] [CrossRef]
- Wagnière, G.H. On Chirality and the Universal Asymmetry: Reflections on Image and Mirror Image; Wiley-VCH: Weinheim, Germany, 2007; ISBN 978-3906390383. [Google Scholar]
- Guijarro, A.; Yus, M. The Origin of Chirality in the Molecules of Life: A Revision from Awareness to the Current Theories and Perspectives of this Unsolved Problem; RSC: Cambridge, UK, 2008; ISBN 978-0854041565. [Google Scholar]
- Bargueño, P.; Gonzalo, I.; de Tudela, R.P. Detection of parity violation in chiral molecules by external tuning of electroweak optical activity. Phys. Rev. A 2009, 80, 012110. [Google Scholar] [CrossRef]
- Macdermott, A.J. Chiroptical signatures of life and fundamental physics. Chirality 2012, 24, 764–769. [Google Scholar] [CrossRef]
- Quack, M.; Seyfang, M.G.; Wichmann, G. Perspectives on parity violation in chiral molecules: Theory, spectroscopic experiment and biomolecular homochirality. Chem. Sci. 2022, 13, 10598–10643. [Google Scholar] [CrossRef]
- Sallembien, Q.; Bouteiller, L.; Crassous, J.; Raynal, M. Possible chemical and physical scenarios towards biological homochirality. Chem. Soc. Rev. 2022, 51, 3436–3476. [Google Scholar] [CrossRef] [PubMed]
- Fiechter, M.R.; Haase, P.A.B.; Saleh, N.; Soulard, P.; Tremblay, B.; Havenith, R.W.A.; Timmermans, R.G.E.; Schwerdtfeger, P.; Crassous, J.; Darquié, B.; et al. Toward detection of the molecular parity violation in chiral Ru(acac)3 and Os(acac)3. J. Phys. Chem. Lett. 2022, 13, 10011–10017. [Google Scholar] [CrossRef] [PubMed]
- Fujiki, M.; Mori, T.; Koe, J.R.; Abdellatif, M.M. Nuclear-spin-dependent chirogenesis: Hidden symmetry breaking of poly(di-n-butylsilane) in n-alkanes. Symmetry 2025, 17, 433. [Google Scholar] [CrossRef]
- Sushkov, O.P.; Flambaum, V.V.; Khriplovich, I.B. Possibility of investigating P- and T-odd nuclear forces in atomic and molecular experiments. Sov. Phys. JETP 1984, 60, 873–883. Available online: http://www.jetp.ras.ru/cgi-bin/dn/e_060_05_0873.pdf (accessed on 1 August 2025).
- Barra, A.L.; Robert, J.B.; Wiesenfeld, L. Possible observation of parity nonconservation by high-resolution NMR. Europhys. Lett. 1988, 5, 217–222. [Google Scholar] [CrossRef]
- Khriplovich, I.B.; Pospelov, M.E. Anapole moment of a chiral molecule. Z. Phys. 1990, 17, 81–84. [Google Scholar] [CrossRef]
- Laerdahl, J.K.; Schwerdtfeger, P. Fully relativistic ab initio calculations of the energies of chiral molecules including parity-violating weak interactions. Phys. Rev. A 1999, 60, 4439–4453. [Google Scholar] [CrossRef]
- DeMille, D.; Cahn, S.B.; Murphree, D.; Rahmlow, D.A.; Kozlov, M.G. Using molecules to measure nuclear spin-dependent parity violation. Phys. Rev. Lett. 2008, 100, 023003. [Google Scholar] [CrossRef]
- Fabian, H.; Berger, R.; Stohner, J. Investigation of parity violation in nuclear spin-rotation interaction of fluorooxirane. Mol. Phys. 2013, 111, 2345–2362. [Google Scholar] [CrossRef]
- Eills, J.; Blanchard, J.W.; Bougas, L.; Kozlov, M.G.; Pines, A.; Budker, D. Measuring molecular parity nonconservation using nuclear-magnetic-resonance spectroscopy. Phys. Rev. A 2017, 96, 042119. [Google Scholar] [CrossRef]
- Kipping, F.S.; Pope, W.J. LXIIL—Enantiomorphism. J. Chem. Soc. Trans. 1898, 73, 606–617. [Google Scholar] [CrossRef]
- Challenger, F.; Kipping, F.S. LII.—Organic derivatives of silicon. Part XIII. Optically active compounds containing one asymmetric silicon group. J. Chem. Soc. Trans. 1910, 97, 755–773. [Google Scholar] [CrossRef]
- Kipping, F.S. CCCVIII.—Organic derivatives of silicon. Part XXX. Complex silicohydrocarbons [SiPh2]n. J. Chem. Soc. Trans. 1924, 125, 2291–2297. [Google Scholar] [CrossRef]
- Garay, A.S.; Keszthelyi, L.; Demeter, I.; Hraskó, P. Differences in the annihilation of positrons in optical isomers. Chem. Phys. Lett. 1973, 23, 549–552. [Google Scholar] [CrossRef]
- Thiemann, W.; Darge, W. Experimental attempts for the study of the origin of optical activity on earth. Orig. Life 1974, 5, 263–283. [Google Scholar] [CrossRef]
- Szabó-Nagy, A.; Keszthelyi, L. Demonstration of the parity-violating energy difference between enantiomers. Proc. Natl. Acad. Sci. USA 1999, 96, 4252–4255. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Yi, F.; Ni, Y.; Zhao, Z.; Jin, X.; Tang, Y. Parity violation of electroweak force in phase transitions of single crystals of D-and L-alanine and valine. J. Biol. Phys. 2000, 26, 51–65. [Google Scholar] [CrossRef] [PubMed]
- Mahurin, S.; McGinnis, M.; Bogard, J.S.; Hulett, L.D.; Pagni, R.M.; Compton, R.N. Effect of beta radiation on the crystallization of sodium chlorate from water: A new type of asymmetric synthesis. Chirality 2001, 13, 636–640. [Google Scholar] [CrossRef] [PubMed]
- Vallazza, M.; Perbandt, M.; Klussmann, S.; Rypniewski, W.; Einspahr, H.M.; Erdmann, V.A.; Betzel, C. First look at RNA in L-configuration. Acta Cryst. D 2004, 60, 1–7. [Google Scholar] [CrossRef]
- Shinitzky, M. Space asymmetry as a possible global feature. Chirality 2013, 25, 308–311. [Google Scholar] [CrossRef]
- Belo, E.A.; Pereira, J.E.; Freire, P.T.; Argyriou, D.N.; Eckert, J.; Bordallo, H.N. Hydrogen bonds in crystalline D-alanine: Diffraction and spectroscopic evidence for differences between enantiomers. IUCrJ 2018, 5, 6–12. [Google Scholar] [CrossRef] [PubMed]
- Kozlova, S.; Ryzhikov, M.; Pishchur, D.; Mirzaeva, I. Overview of low-temperature heat capacity data for Zn2(C8H4O4)2C6H12N2 and the Salam hypothesis. Symmetry 2019, 11, 657. [Google Scholar] [CrossRef]
- Kiliszek, A.; Błaszczyk, L.; Bejger, M.; Rypniewski, W. Broken symmetry between RNA enantiomers in a crystal lattice. Nucleic Acids Res. 2021, 49, 12535–12539. [Google Scholar] [CrossRef] [PubMed]
- Shinitzky, M.; Haimovitz, R. Chiral surfaces in micelles of enantiomeric N-palmitoyl- and N-stearoylserine. J. Am. Chem. Soc. 1993, 115, 12545–12549. [Google Scholar] [CrossRef]
- Kodona, E.K.; Alexopoulos, C.; Panou-Pomonis, E.; Pomonis, P.J. Chirality and helix stability of polyglutamic acid enantiomers. J. Colloid Interface Sci. 2008, 319, 72–80. [Google Scholar] [CrossRef]
- Fujiki, M.; Suzuki, N.; Taguchi, M.; Zhang, W.; Abdellatif, M.M.; Nomura, K. Chiral optofluidics: Gigantic circularly polarized light enhancement of all-trans-poly(9,9-di-n-octylfluorene-2,7-vinylene) during mirror-symmetry-breaking aggregation by optically tuning fluidic media. RSC Adv. 2012, 2, 6663–6671. [Google Scholar] [CrossRef]
- Fujiki, M.; Yoshida, K.; Suzuki, N.; Zhang, J.; Zhang, W.; Zhu, X. Mirror symmetry breaking and restoration within μm-sized polymer particles in optofluidic media by pumping circularly polarised light. RSC Adv. 2013, 3, 5213–5219. [Google Scholar] [CrossRef]
- Dubey, M.; Kumar, A.; Dhavale, V.M.; Kurungot, S.; Pandey, D.S. Can enantiomer ligands produce structurally distinct homochiral MOFs? CrystEngComm 2015, 17, 8202–8206. [Google Scholar] [CrossRef]
- Fujiki, M.; Yoshida, K.; Suzuki, N.; Rahim, N.A.A.; Abd, J.J. Tempo-spatial chirogenesis. Limonene-induced mirror symmetry breaking of Si–Si bond polymers during aggregation in chiral fluidic media. J. Photochem. Photobiol. A Chem. 2016, 331, 120–129. [Google Scholar] [CrossRef]
- Fujiki, M.; Okazaki, S.; Rahim, N.A.A.; Yamada, T.; Nomura, K. Synchronization in non-mirror-symmetrical chirogenesis: Non-helical π–conjugated polymers with helical polysilane copolymers in co-colloids. Symmetry 2021, 13, 594. [Google Scholar] [CrossRef]
- Fujiki, M. Experimental tests of parity violation at helical polysilylene level. Macromol. Rapid Commun. 2001, 22, 669–674. [Google Scholar] [CrossRef]
- Scolnik, Y.; Portnaya, I.; Cogan, U.; Tal, S.; Haimovitz, R.; Fridkin, M.; Elitzur, A.C.; Deamer, D.W.; Shinitzky, M. Subtle differences in structural transitions between poly-L- and poly-D-amino acids of equal length in water. Phys. Chem. Chem. Phys. 2006, 8, 333–339. [Google Scholar] [CrossRef]
- Fujiki, M. Mirror symmetry breaking in helical polysilanes: Preference between left and right of chemical and physical origin. Symmetry 2010, 2, 1625–1652. [Google Scholar] [CrossRef]
- Teramae, H.; Takeda, K. Ab initio studies on silicon compounds. 2. On the gauche structure of the parent polysilane. J. Am. Chem. Soc. 1989, 111, 1281–1285. [Google Scholar] [CrossRef]
- Tachibana, H.; Matsumoto, M.; Tokura, Y.; Moritomo, Y.; Yamaguchi, A.; Koshihara, S.; Miller, R.D.; Abe, S. Spectra of one-dimensional excitons in polysilanes with various backbone conformations. Phys. Rev. B 1993, 47, 4363–4371. [Google Scholar] [CrossRef] [PubMed]
- Fujiki, M. Effect of main chain length in the exciton spectra of helical-rod polysilanes as a model of a 5 Å wide quantum wire. Appl. Phys. Lett. 1994, 65, 3251–3253. [Google Scholar] [CrossRef]
- Fujiki, M. Optically active polysilylenes: State-of-the-art chiroptical polymers. Macromol. Rapid Commun. 2001, 22, 539–563. [Google Scholar] [CrossRef]
- Fujiki, M. Mirror symmetry breaking of silicon polymers—From weak bosons to artificial helix. Chem. Rec. 2009, 9, 271–298. [Google Scholar] [CrossRef]
- Sullivan, R.; Pyda, M.; Pak, J.; Wunderlich, B.; Thompson, J.R.; Pagni, R.; Barnes, C.; Schwerdtfeger, P.; Compton, R. Search for electroweak interactions in amino acid crystals. II. The Salam hypothesis. J. Phys. Chem. A 2003, 107, 6674–6680. [Google Scholar] [CrossRef]
- Bürgia, H.-B.; Macchi, P. Comments on ‘Hydrogen bonds in crystalline D-alanine: Diffraction and spectroscopic evidence for differences between enantiomers’. IUCrJ 2018, 5, 654–657. [Google Scholar] [CrossRef]
- Fujiki, M.; Koe, J.R.; Mori, T.; Kimura, Y. Questions of mirror symmetry at the photoexcited and ground states of non-rigid luminophores raised by circularly polarized luminescence and circular dichroism spectroscopy: Part 1. Oligofluorenes, oligophenylenes, binaphthyls and fused aromatics. Molecules 2018, 23, 2606. [Google Scholar] [CrossRef] [PubMed]
- Fujiki, M.; Koe, J.R.; Amazumi, S. Questions of mirror symmetry at the photoexcited and ground states of non-rigid luminophores raised by circularly polarized luminescence and circular dichroism spectroscopy. Part 2: Perylenes, BODIPYs, molecular scintillators, coumarins, rhodamine B, and DCM. Symmetry 2019, 11, 363. [Google Scholar] [CrossRef]
- Puneet, P.; Singh, S.; Fujiki, M.; Nandan, B. Handed mirror symmetry breaking at the photo-excited state of π-conjugated rotamers in solutions. Symmetry 2021, 13, 272. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian09 (Rev.D.01); Gaussian, Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Ohno, O.; Kaizu, Y.; Kobayashi, H. J-aggregate formation of a water-soluble porphyrin in acidic aqueous media. J. Chem. Phys. 1993, 99, 4128–4139. [Google Scholar] [CrossRef]
- Ribó, J.M.; Crusats, J.; Sagués, F.; Claret, J.; Rubires, R. Chiral sign induction by vortices during the formation of mesophases in stirred solutions. Science 2001, 292, 2063–2066. [Google Scholar] [CrossRef]
- Okano, K.; Taguchi, M.; Fujiki, M.; Yamashita, T. Circularly polarized luminescence of rhodamine B in a supramolecular chiral medium formed by a vortex flow. Angew. Chem. Int. Ed. 2011, 50, 12474–12477. [Google Scholar] [CrossRef]
- Tang, X.; Ji, X.; Li, Y.; Li, B.; Yang, Y. Achiral polydialkylsilane aggregates that record stirring direction. Chem. Asian J. 2016, 11, 852–857. [Google Scholar] [CrossRef]
- Sun, J.; Li, Y.; Yan, F.; Liu, C.; Sang, Y.; Tian, F.; Feng, Q.; Duan, P.; Zhang, L.; Shi, X.; et al. Control over the emerging chirality in supramolecular gels and solutions by chiral microvortices in milliseconds. Nat. Commun. 2018, 9, 2599. [Google Scholar] [CrossRef]
- Lin-Vien, D.; Colthup, N.B.; Fateley, W.G.; Grasselli, J.G. Chapter 2: Alkanes. In The Handbook of Infrared and Raman Characteristic Frequencies of Organic Molecules; Elsevier: Amsterdam, The Netherlands, 1991; ISBN 978-0124511606. [Google Scholar]
- Socrates, G. Chapter 2: Alkane Group Residue: C–H Group. In Infrared and Raman Characteristic Group Frequencies: Tables and Charts, 3rd ed.; Wiley: Chichester, UK, 2001; ISBN 978-0470093078. [Google Scholar]
- Wada, R.; Kato, M. A Raman spectroscopic study of the conformations of 1,4-dioxane in the pure liquid, methanol, and aqueous solution. Chem. Phys. Lett. 2015, 641, 74–79. [Google Scholar] [CrossRef]
- Takahashi, O.; Kohno, Y.; Nishio, M. Relevance of weak hydrogen bonds in the conformation of organic compounds and bioconjugates: Evidence from recent experimental data and high-level ab initio MO calculations. Chem. Rev. 2010, 110, 6049–6076. [Google Scholar] [CrossRef] [PubMed]
- Desiraju, G.R.; Steiner, T. The Weak Hydrogen Bond in Structural Chemistry and Biology; Oxford Science Press: New York, NY, USA, 1999; ISBN-13 978-0198502524. [Google Scholar]
- Lewis, G.N. The atom and the molecule. J. Am. Chem. Soc. 1916, 38, 762–785. [Google Scholar] [CrossRef]
- Fujiki, M.; Jalilah, A.J.; Koe, J.R.; Nomura, K.; Suzuki, N.; Rahim, N.A.A.; Zhang, W. Chapter 17: Ultraweak intermolecular interactions in chirogenesis from noncharged CPL-/CD-silent molecules, oligomers, and polymers endowed with noncharged chiral terpenes, mono-/polysaccharides, and helical polysilanes. In Chiral Luminescence: From Molecules to Materials and Devices; Akagi, K., Ed.; Wiley-VCH: Weinheim, Germany, 2024; pp. 381–415. ISBN 978-3527351800. [Google Scholar] [CrossRef]
- Coussan, S.; Bouteiller, Y.; Perchard, J.P.; Zheng, W.Q. Rotational isomerism of ethanol and matrix isolation infrared spectroscopy. J. Phys. Chem. A 1998, 102, 5789–5793. [Google Scholar] [CrossRef]
- Chen, L.; Zhu, W.; Lin, K.; Hu, N.; Yu, Y.; Zhou, X.; Yuan, L.-F.; Hu, S.-M.; Luo, Y. Identification of alcohol conformers by Raman spectra in the C−H stretching region. J. Phys. Chem. A 2015, 119, 3209–3217. [Google Scholar] [CrossRef]
- Balanay, M.P.; Kim, D.H.; Haiyan Fan, H. Revisiting the formation of cyclic clusters in liquid ethanol. J. Chem. Phys. 2016, 144, 154302. [Google Scholar] [CrossRef]
- Doroshenko, I.; Onuk, M.; Meyliev, L.; Kuyliev, B. Conformational composition of propanol in gaseous state and in matrix isolation. Mol. Cryst. Liq. Cryst. 2022, 747, 81–90. [Google Scholar] [CrossRef]
- Michniewicz, N.; Muszyński, A.S.; Wrzeszcz, W.; Czarnecki, M.A.; Golec, B.; Hawranek, J.P.; Mielke, Z. Vibrational spectra of liquid 1-propanol. J. Mol. Structr. 2008, 887, 180–186. [Google Scholar] [CrossRef]
- Dobrowolski, J.C.; Ostrowski, S.; Kołos, R.; Jamróz, M.H. Ar-matrix IR spectra of 2-propanol and its OD, D7 and D8 isotopologues. Vib. Spectrosc. 2008, 48, 82–91. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, Y.; Hu, N.; Lin, K.; Zhou, X.; Liu, S. Overlapping spectral features and new assignment of 2-propanol in the C–H stretching region. J. Raman Spectrosc. 2014, 45, 259–265. [Google Scholar] [CrossRef]
- Salah, M.; Marakchi, K.; Komiha, N.; Senent, M.L. Theoretical Spectroscopic Study of Isopropyl Alcohol (CH3-CHOH-CH3). Astrophys. J. 2024, 963, 143. [Google Scholar] [CrossRef]
- Czarnecki, M.A.; Wojtków, D.; Haufa, K. Rotational isomerism of butanols: Infrared, near-infrared and DFT study. Chem. Phys. Lett. 2006, 431, 294–299. [Google Scholar] [CrossRef]
- Malherbe, F.E.; Bernstein, H.J. The infrared and Raman spectra of p-dioxane. J. Am. Chem. Soc. 1952, 74, 4438–4440. [Google Scholar] [CrossRef]
- Freeman, F.; Kasner, M.L.; Hehre, W.J. An ab initio theory and density functional theory (DFT) study of conformers of tetrahydro-2H-pyran. J. Phys. Chem. A 2001, 105, 10123–10132. [Google Scholar] [CrossRef]
- Luger, P.; Buschmann, J. Twist conformation of tetrahydrofuran in the crystal. Angew. Chem. Int. Ed. Engl. 1983, 22, 410. [Google Scholar] [CrossRef]
- Johansson, P.; Grondin, J.; Lassègues, J.-C. Structural and vibrational properties of diglyme and longer glymes. J. Phys. Chem. A 2010, 114, 10700–10705. [Google Scholar] [CrossRef]
- Gámez, F.; Martínez-Haya, B.; Blanco, S.; López, J.C.; Alonso, J.L. High-resolution rotational spectroscopy of a cyclic ether. J. Phys. Chem. Lett. 2012, 3, 482–485. [Google Scholar] [CrossRef]
- Marzec, K.M.; Reva, I.; Fausto, R.; Malek, K.; Proniewicz, M. Conformational space and photochemistry of α-terpinene. J. Phys. Chem. A 2010, 114, 5526–5536. [Google Scholar] [CrossRef]
- Tranter, G.E. Parity-violating energy differences and the origin of biomolecular homochirality. J. Theor. Biol. 1986, 119, 467–479. [Google Scholar] [CrossRef]
- Hegstrom, R.A.; Kondepudi, D.K. The handedness of the universe. Sci. Am. 1990, 262, 108–115. [Google Scholar] [CrossRef]
- Ikehara, K. Possible steps to the emergence of life: The [GADV]-protein world hypothesis. Chem. Rec. 2005, 5, 107–108. [Google Scholar] [CrossRef]
- Minami, Y.; Komatsu, E. New extraction of the cosmic birefringence from the Planck 2018 polarization data. Phys. Rev. Lett. 2020, 125, 221301. [Google Scholar] [CrossRef]
- Fujiki, M. Chapter 1: Chirogenesis in parity violation and weak forces. In Chirogenesis in Chemical Science; Borovkov, V., Aav, R., Eds.; World Scientific: Singapore, 2023; pp. 1–68. ISBN 978-9811259210. [Google Scholar] [CrossRef]
- Shamir, L. The distribution of galaxy rotation in JWST advanced deep extragalactic survey. Mon. Not. R. Astron. Soc. 2025, 538, 76–91. [Google Scholar] [CrossRef]
- Savukov, I.M.; Lee, S.-K.; Romalis, M.V. Optical detection of liquid-state NMR. Nature 2006, 442, 1021–1024. [Google Scholar] [CrossRef] [PubMed]
- Koralewski, M.; Baranowski, M.; Ryzner, A. Probing physical invariance between enantiomers: The magnetooptical and refractive properties of the simplest chiral amino acid—Alanine. J. Mol. Liq. 2021, 339, 117279. [Google Scholar] [CrossRef]
- Poggiali, G.; Fornaro, T.; Potenti, S.; Corazzi, M.A.; Brucato, J.R. Ultraviolet photoprocessing of glycine adsorbed on various space-relevant minerals. Astron. Space Sci. 2020, 7, 18. [Google Scholar] [CrossRef]
- Prager, M.; Heidemann, A. Rotational tunneling and neutron spectroscopy: A compilation. Chem. Rev. 1997, 97, 2933–2966. [Google Scholar] [CrossRef]
- Jensen, J.H.; Gordon, M.S. On the number of water molecules necessary to stabilize the glycine zwitterion. J. Am. Chem. Soc. 1995, 117, 8159–8170. [Google Scholar] [CrossRef]
- de Tudela, R.P.; Marx, D. Water-induced zwitterionization of glycine: Stabilization mechanism and spectral signatures. J. Phys. Chem. Lett. 2016, 7, 5137–5142. [Google Scholar] [CrossRef]
- Tripathi, R.; Caballero, L.D.; de Tudela, R.P.; Hölzl, C.; Marx, D. Unveiling zwitterionization of glycine in the microhydration limit. ACS Omega 2021, 6, 12676–12683. [Google Scholar] [CrossRef]
- Kikuchi, O.; Watanabe, T.; Ogawa, Y.; Takase, H.; Takahashi, O. Ab initio MO and Monte Carlo simulation study on the conformation of L-alanine zwitterion in aqueous solution. J. Phys. Org. Chem. 1997, 10, 145–151. [Google Scholar] [CrossRef]
- MacDermott, A.J.; Fu, T.; Hyde, G.O.; Nakatsuka, R.; Coleman, A.P. Electroweak parity-violating energy shifts of amino acids: The “conformation problem”. Orig. Life Evol. Biosph. 2009, 39, 407–437. [Google Scholar] [CrossRef] [PubMed]
- Bonner, W.A. The origin and amplification of biomolecular chirality. Orig. Life Evol. Biosph. 1991, 21, 59–111. [Google Scholar] [CrossRef] [PubMed]
- Cronin, J.R.; Pizzarello, S. Enantiomeric excesses in meteoritic amino acids. Science 1997, 275, 951–955. [Google Scholar] [CrossRef] [PubMed]
- Meinert, C.; Garcia, A.D.; Topin, J.; Jones, N.C.; Diekmann, M.; Berger, R.; Nahon, L.; Hoffmann, S.; Meierhenrich, U.J. Amino acid gas phase circular dichroism and implications for the origin of biomolecular asymmetry. Nat. Commun. 2022, 13, 502. [Google Scholar] [CrossRef]
- Kobayashi, M.; Takahashi, J.-I.; Ota, H.; Matsuo, K.; Ibrahim, M.I.; Minato, T.; Fujimori, G.; Katoh, M.; Kobayashi, K.; Kebukawa, Y.; et al. Emergence of optical activity and surface morphology changes in racemic amino acid films under circularly polarized Lyman-α light irradiation. Chirality 2024, 36, e70004. [Google Scholar] [CrossRef]
- Famiano, M.; Boyd, R.; Kajino, T.; Onaka, T.; Mo, Y. Astrophysical sites that can produce enantiomeric amino acids. Symmetry 2019, 11, 23. [Google Scholar] [CrossRef]
- Enoto, T.; Wada, Y.; Furuta, Y.; Nakazawa, K.; Yuasa, T.; Okuda, K.; Makishima, K.; Sato, M.; Sato, Y.; Nakano, T.; et al. Photonuclear reactions triggered by lightning discharge. Nature 2017, 551, 481–484. [Google Scholar] [CrossRef]
- Ozturk, S.F.; Liu, Z.; Sutherland, J.D.; Sasselov, D.D. Origin of biological homochirality by crystallization of an RNA precursor on a magnetic surface. Sci. Adv. 2023, 9, eadg8274. [Google Scholar] [CrossRef]
- Bloom, B.P.; Paltiel, Y.; Naaman, R.; Waldeck, D.H. Chiral induced spin selectivity. Chem. Rev. 2024, 124, 1950–1991. [Google Scholar] [CrossRef]
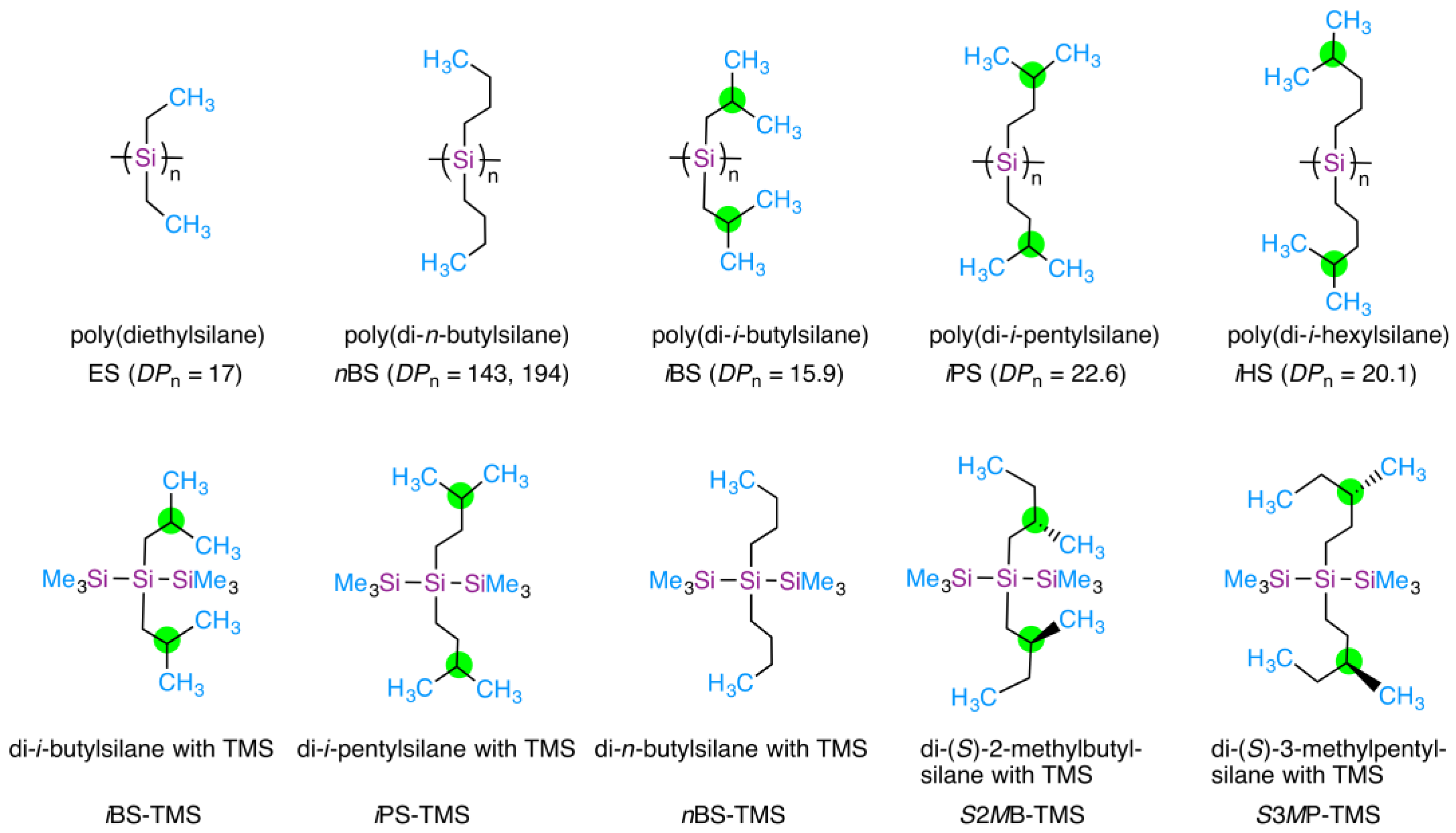





| Polymers (Side Chain Type) | Solvents | TC1/°C | TC2/°C | TC3/°C | TC4/°C | Numbers of CH3 Rotors | |
|---|---|---|---|---|---|---|---|
| as Repeating Unit | as Solvent | ||||||
| iBS (β-branched) | n-propanol | >97 * | 72 | 29 | <–20 * | 4 | 1 |
| i-propanol | >83 * | 60 | 32 | 4 | 2 | ||
| i-butanol | >100 * | 72 | 28 | 4 | 2 | ||
| i-pentanol | >100 * | 55 | 25 | 4 | 2 | ||
| p-dioxane-h8 | 77 | 52 | 18 | 4 | 0 | ||
| p-dioxane-d8 | 77 | 38 | 28 | <10 * | 4 | 0 | |
| iPS (γ-branched) | n-propanol | >97 * | 80 | 67 | 27 | 4 | 1 |
| n-pentanol | ~10 * | 4 | 1 | ||||
| n-hexanol | ~10 * | 4 | 1 | ||||
| n-octanol | ~20 * | 4 | 1 | ||||
| i-propanol | ~20 * | 4 | 2 | ||||
| i-butanol | ~20 * | 4 | 2 | ||||
| iHS (δ-branched) | n-octanol | ~20 * | 4 | 1 | |||
| nBS ** (non-branched) | n-undecane | 40 | 2 | 2 | |||
| n-dodecane | 105 | 28 | 2 | 2 | |||
| n-dodecane-d26 | 42 | 25 | 2 | 2 | |||
| n-tridecane | 105 | 28 | 2 | 2 | |||
| n-tetradecane | 95 * | 28 | 2 | 2 | |||
| ES ** (non-branched) | n-propanol | 30 | <–10* | 2 | 1 | ||
| Systems | T > TC1 1–3 | TC1 > T > TC2 1–3 | TC2 > T > TC3 1–3 | TC3 > T > TC4 1–3 | T < TC4 1–3 |
|---|---|---|---|---|---|
| iBS, n-propanol | (⟲+⟳) + (⟳+⟲) = 0 | (⟲+⟳) + (⟲+⟲) = –2 | (⟲+⟳) + (⟳+⟳) = +2 | (⟲+⟲) + (⟲+⟲) = –4 | (⟳+⟳) + (⟳+⟳) = +4 |
| iBS, i-propanol | (⟲+⟳) + (⟳+⟲) = 0 | (⟲+⟳) + (⟲+⟲) = –2 | (⟲+⟳) + (⟳+⟳) = +2 | (⟲+⟲) + (⟲+⟲) = –4 | Possibly = +4 |
| iBS, p-dioxane-d8 | (⟲+⟳) + (⟳+⟲) = 0 | (⟲+⟳) + (⟲+⟲) = –2 | (⟲+⟳) + (⟳+⟳) = +2 | (⟲+⟲) + (⟲+⟲) = –4 | Possibly = +4 |
| iPS, n-propanol | (⟲+⟳) + (⟳+⟲) = 0 | (⟳+⟳) + (⟳+⟲) = +2 | (⟲+⟲) + (⟳+⟲) = –2 | (⟳+⟳) + ⟳+⟳) = +4 | (⟲+⟲) + (⟲+⟲) = –4 |
| Systems | T > TC1 | TC1 > T > TC2 | T < TC2 | ||
| nBS, n-dodecane-h26 | ⟲+⟳ = 0 | ⟲+⟲ = –2 | ⟳+⟳ = +2 | ||
| nBS, n-dodecane-h26 with THF | Possibly = 0 | ⟳+⟳ = +2 | ⟲+⟲ = –2 | ||
| nBS, n-dodecane-d26 | ⟲+⟳ = 0 | ⟲+⟲ = –2 | ⟳+⟳ = +2 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fujiki, M.; Mori, T.; Koe, J.R.; Abdellatif, M.M. Broken Mirrors: Multiple Circular Polarization and Inversion in the Ground and Photoexcited States of Mirror-Symmetric Helical Poly(di-iso-alkylsilane)s in Achiral Molecular Solvents. Symmetry 2025, 17, 1544. https://doi.org/10.3390/sym17091544
Fujiki M, Mori T, Koe JR, Abdellatif MM. Broken Mirrors: Multiple Circular Polarization and Inversion in the Ground and Photoexcited States of Mirror-Symmetric Helical Poly(di-iso-alkylsilane)s in Achiral Molecular Solvents. Symmetry. 2025; 17(9):1544. https://doi.org/10.3390/sym17091544
Chicago/Turabian StyleFujiki, Michiya, Takashi Mori, Julian R. Koe, and Mohamed Mehawed Abdellatif. 2025. "Broken Mirrors: Multiple Circular Polarization and Inversion in the Ground and Photoexcited States of Mirror-Symmetric Helical Poly(di-iso-alkylsilane)s in Achiral Molecular Solvents" Symmetry 17, no. 9: 1544. https://doi.org/10.3390/sym17091544
APA StyleFujiki, M., Mori, T., Koe, J. R., & Abdellatif, M. M. (2025). Broken Mirrors: Multiple Circular Polarization and Inversion in the Ground and Photoexcited States of Mirror-Symmetric Helical Poly(di-iso-alkylsilane)s in Achiral Molecular Solvents. Symmetry, 17(9), 1544. https://doi.org/10.3390/sym17091544








