Abstract
This study presents a cohesive physical model that predicts lava flow morphology by establishing a quantitative link between a lava’s yield strength and its geometric complexity, measured by a prefractal dimension. The model is founded on the principle of symmetry, where the potential for fracturing and complexity peaks at an intermediate yield strength. This peak in complexity, observed with a predicted prefractal dimension (Dpf) of 1.15 for terrestrial ‘a’ā-like lava, arises from a critical state where a balance between gravitational driving forces and internal resistance allows for the formation of intricate margins. The model demonstrates that as lavas deviate from this optimal strength, becoming either too fluid (pāhoehoe, Dpf = 1.05) or too rigid (rhyolite, Dpf = 1.07), their morphology becomes progressively simpler, representing a symmetrical decline in complexity. Our approach also incorporates the overriding influence of topographic confinement and the temporal evolution of complexity as the lava cools. Validated against terrestrial lavas and successfully applied to lower-gravity environments, the model predicts a reduction in complexity for similar flows on Mars (Dpf = 1.13) and the Moon (Dpf = 1.09), providing a tool for interpreting volcanic processes grounded in the fundamental principles of symmetry and complexity.
1. Introduction
Complex flow patterns are omnipresent in natural systems [1]. These patterns often arise from the fundamental principles of complexity theory, where intricate, emergent structures are generated from a few simple rules [2,3,4]. A key concept is the role of symmetry and symmetry-breaking, where the most complex and interesting patterns in many physical systems appear not at the extremes of a parameter range, but at a critical intermediate state where competing forces are balanced. In geology, complex patterns serve as a physical record of the dynamic processes that shape a planet’s surface, offering crucial insights into its history [5,6,7]. Among the most important examples are lava flows, whose final morphology provides a real link to the complex interplay between the intrinsic properties of magma and the external forces it encounters during emplacement [8,9]. Researchers have sought to decipher this relationship, aiming to develop models that can predict a flow’s final form from a set of initial conditions [10,11].
The foundation of this effort lies in understanding lava rheology, particularly the concept of yield strength, i.e., the internal resistance that must be overcome for the lava to deform and flow [12,13]. Early studies established a clear link between a lava’s yield strength and its classification, with low-strength magmas forming the smooth, ropy surfaces of pāhoehoe and high-strength magmas forming the rough, clinkery crust of ‘a’ā or blocky flows [14,15]. However, simply classifying flows proved insufficient for capturing the full variety of their geometric diversity. A more quantitative approach was needed to describe the intricate and often irregular margins of lava flows.
A significant advancement came with the application of fractal geometry, which provided a mathematical framework for quantifying the complexity of these irregular shapes [1,2,16,17]. This method allowed researchers to move beyond qualitative descriptions and assign a numerical value, the prefractal dimension, to a flow’s complexity [1,2,18,19]. Groundbreaking work in this area revealed a non-monotonic relationship between a lava’s yield strength and its prefractal dimension, suggesting that complexity does not increase indefinitely with internal strength [20]. Instead, it peaks at an intermediate yield strength, characteristic of ‘a’ā lava, and diminishes for lavas that are either weaker or stronger. This observation points to a deeper, more fundamental principle: the role of symmetry in the emergence of complex geological structures [5]. In many physical systems, the most complex patterns arise not at the extremes, but from a critical state of broken symmetry where competing forces are perfectly balanced [2,3,21]. In the context of lava flows, this peak complexity can be viewed as a state where the driving gravitational forces and the lava’s internal resistance to fracturing are in optimal opposition. The simpler morphologies of pāhoehoe and rhyolite then represent a symmetrical decline from this peak, where one force tremendously dominates the other.
While intrinsic properties are fundamental, the external environment, particularly topography, can exert a dominant control on a flow’s final morphology. Studies have shown that even lavas with a high intrinsic potential for complexity can be forced into simple, linear forms when confined by a channel or valley [22,23,24]. This highlights the need for any comprehensive model to account for both the lava’s internal nature and the landscape through which it travels. Despite the progress in understanding these individual components, a unified model that synthesizes them into a single, predictive framework has remained unavailable.
Therefore, the goal of this study is to develop and validate a cohesive physical model that predicts the geometric complexity of a lava flow by integrating its intrinsic rheological properties with the extrinsic influence of its environment. Building upon the foundational principles of symmetry and complexity, this work aims to create a comprehensive framework that can trace the evolution of a lava flow from its initial state to its final, solidified form. By doing so, we seek to provide a robust tool for interpreting volcanic processes on Earth and other planetary bodies.
2. Materials and Methods
Modeling lava flow is complicated by its composite nature, a molten interior covered by a rigid or semi-rigid crust. The style of flow advancement, whether as a cohesive unit or through a series of smaller breakouts, is largely determined by the mechanical properties of this crust. A critical parameter governing this behavior is the lava’s yield strength, which is the stress required to initiate flow or fracture the crust.
Observational data suggests that the tendency for a flow to advance via crustal fracturing is maximized at an intermediate, or “peak,” yield strength. Low-strength lavas (e.g., pāhoehoe) are too fluid to form a strong, brittle crust, while high-strength lavas (e.g., some andesites) are too rigid to break apart easily, tending to move as a single, thick mass. Consequently, intermediate-strength lavas (e.g., ‘a’ā) have a crust that is strong enough to be brittle but weak enough to be consistently fractured by the pressure of the molten interior, promoting advance through breakouts. This relationship, where breakout activity peaks at a specific yield strength, can be effectively described by a Gaussian function [25]. Because yield strength in lavas spans several orders of magnitude, it is best analyzed on a logarithmic scale. In this context, the yield strength (τy) represents the strength of the solidified or semi-solid crust. The Gaussian term models the efficiency of crustal fracturing: when the lava’s yield strength is close to the optimal peak strength (τpeak), the crust breaks apart easily, leading to a smaller effective flow thickness (heff) as the flow advances through breakouts. Conversely, when τy is very high or very low, the crust either resists fracture or is too weak to form a brittle structure, respectively, resulting in an effective thickness closer to the bulk thickness. This leads to the following approach for a normalized effective flow thickness
where heff is the effective flow thickness, h is the bulk thickness, τy is the lava’s yield strength, τpeak is the peak yield strength at which fracturing is most pronounced, h*min is the minimum heff/h observed in nature, and σ is parameter that controls how broadly the fracturing behavior extends across the range of yield strengths.
Equation (1) quantifies the characteristic thickness of the active flow margin as a function of the lava’s yield strength relative to the peak strength for fracturing. To standardize this model, we must identify a lava type that best embodies the physical process of efficient crustal fracturing. Pāhoehoe lava (yield strength ~102 Pa [14]) is too fluid, forming a skin that stretches and inflates. Rhyolite lava (yield strength ~105 Pa [15]) is so rigid that it resists internal deformation and moves as a coherent block. In contrast, ‘a’ā lava (yield strength ≈ 103 Pa [14]) is strong enough to form a brittle crust but weak enough for the molten core to consistently break it apart. It is just right because it maximizes the creation of a fragmented, rubbly flow front where the advancing lobes are much thinner than the flow’s core. Therefore, ‘a’ā lava provides the core observational data to define the model parameters for Equation (1): τpeak = 103 Pa, h*min = 0.25 and σ = 0.75. Notice that the h*min represents the physical limit of crustal collapse efficiency. An analogy can be found in the study of granular materials, such as packed beds. When uniform spheres are randomly packed, they achieve a maximum packing density that leaves a minimum void fraction of approximately 0.26. By analogy, h*min can be viewed as the minimum possible height ratio (heff/h) for the fractured crust, representing a state of maximum collapse where further compaction is physically resisted, similar to a densely packed rubble pile.
For the lava to flow, the shear stress at some point within the flow must exceed the yield stress. The gravitational component of shear stress acting on a fluid layer of density ρ and height h on a slope with angle α is
Since the shear stress is maximum at the base of the flow, the condition for the entire flow to move is that the shear stress at the base must be greater than or equal to the yield stress. So, this condition can be written as a dimensionless number by dividing the driving stress by the resisting yield stress
where Npf,eff represents the ratio between the gravitational pressure pushing the lava forward and the lava’s internal strength resisting its flow. This is a generalized form of fracturing number [26] and replaces the very often unmeasurable internal viscous stress with the overall gravitational driving stress, which is the definitive cause of the flow. Npf,eff can be considered a control variable because it quantifies the behavior of the system, i.e., it limits the fate of the lava’s surface. If the stress imposed by the flowing lava is less than the strength of the crust, Npf,eff < 1: the crust is strong enough to resist breaking and can deform in a ductile manner, resulting in the smooth that characterizes the pāhoehoe lava. On the other hand, if the stress from the underlying flow exceeds the crust’s strength, causing it to fracture and break apart, Npf,eff > 1. This is characteristic of surfaces of ‘a’ā lava flows.
We propose that the intrinsic complexity defined by the corresponding prefractal dimension is a non-monotonic, log-normal function of Npf,eff, peaking at moderate strength and decreasing at high strength due to channelization
where Dint is the intrinsic prefractal dimension, Dmax is the prefractal dimension that correspond to the peak complexity, Dmin is the basal prefractal dimension for near-stationary flow, and σ is a coefficient that controls the width or spread of the peak (i.e., the standard deviation of ln(Npf,eff) and 2σ2 is related to the variance of the log-normal distribution). Similarly to Equation (1), the term represents the probability density function of a log-normal distribution, normalized to have a peak value of 1, and the corresponding exponential term acts as a weighting factor that determines the contribution of the complexity range Dmax − Dmin to the final intrinsic prefractal dimension. So, the prefractal dimension is not simply monotonic with fracturing number Npf,eff, but it can reach a maximum at a critical value (Npf,crit) and decreases on either side.
Consider that the yield strength governs the characteristic size of the structural elements that make up the lava flow. So, this directly influences the flow’s geometric complexity, which is measured by the prefractal dimension. For low-yield-strength lavas (e.g., pāhoehoe lava), maximum complexity (Dmax) means a low-strength crust that is easily deformed that allow to form numerous small, intricate, and overlapping lobes. In addition, minimum complexity (Dmin) means that lava flow can form simple, channelized paths. For high-yield-strength lavas (e.g., rhyolite lava), low maximum complexity (Dmax) means that a high-strength crust that strongly resists deformation cannot breach to form small lobes, and stress builds up until the crust fails to create big, blocky structures. The flow advances as a more unified front because it lacks the ability to create fine details. Consequently, the resistance to forming complex shapes lowers the maximum possible complexity (Dmax). It is important to note that very strong lavas are characterized by almost non-distinction between the simplest and most complex possible shapes. So, lava flow is always blocky and simple, and the values of the prefractal Dmax and Dmin converge.
The relationship between a lava’s internal resistance (and yield strength) and its resulting morphology is logarithmic, and it was found that Dmax and Dmin have a linear dependence of the logarithmic yield strength [10,20]; i.e., for each increase in yield strength, the prefractal dimension decreases by a constant amount [10,20]
To illustrate this sensitivity, the dependence of maximum complexity on yield strength is shown in Table 1. This shows a linear relationship with the logarithm of the yield strength, where Dmax decreases as the lava becomes more rigid. For each order of magnitude increase in yield strength, the maximum potential complexity decreases by 0.03.

Table 1.
Sensitivity of maximum complexity (Dmax) to yield strength (τy).
The negative sign in Equations (5) and (6) captures the fact that higher yield strength inhibits complexity (i.e., as lava becomes stiffer, it resists breaking into the small-scale instabilities and branches that create a complex margin).
Lava flow’s complexity does not just depend on its yield strength but also depends on the landscape it flows through. Topography strongly controls lava flow morphology, often overriding its intrinsic properties [22]. So, topography can override the lava’s natural tendency to form complex shapes. To account for topography, we introduce the confinement index [23]
where w is the width of the lava flow and wchan is the width of the channel or valley confining it, and it ranges from 0 (unconfined) to 1 (perfectly confined).
Bruno et al. [20] suggest that lava flows have an intrinsic complexity based on their properties, which is then simplified by channels. Assuming a linear interpolation to create a smooth transition between two states (Dint and Dchan) based on the confinement index, the prefractal dimension is calculated as
where Dchan is the prefractal dimension of a perfectly straight, confining channel or valley. Studies [17,19] suggest that real-world quasi-linear features including natural channels have minor sinuosity and present a prefractal dimension slightly greater than 1.0, ranging from 1.01 to 1.03. So, we assume that Dchan = 1.02 is for the geometry of a lava flow through a completely straightened, confining channel.
The previously developed approaches are static, calculating a final complexity without accounting for temporal evolution. However, lava flow is a dynamic process where properties change over time. Specifically, lava’s yield strength is not constant; it increases as the lava cools and crystallizes, which raises its internal resistance. This evolution of yield strength can be described by an Arrhenius-type equation and can be written as [12,26]
where τ0 is the initial yield strength, T0 is the initial absolute temperature, Ea is the activation energy for viscous flow, and R is the universal gas constant.
Since the variation in yield strength is a result of changes in lava temperature (Equation (9)), an equation for the lava’s temperature evolution is also required. Heat loss from a very hot body, such as a lava flow, is dominated by thermal radiation to its cooler surroundings. The rate at which the lava’s temperature changes is directly proportional to this net energy loss and can be written based on the Stefan–Boltzmann law
where γ is the Stefan–Boltzmann constant, ϵ is the lava’s emissivity, ρ is density of the lava, clava is the lava’s capacity to store heat, h is the bulk thickness of lava flow, and t the time.
The time variation of complexity Dpf,t is then calculated using Equation (8).
3. Results and Discussion
To understand the interplay between intrinsic lava properties and external environmental factors of our model, we performed a sensitivity analysis. We systematically varied key parameters such as slope and flow thickness, for an unconfined ‘a’ā lava flow (τy = 103 Pa, Cc = 0), which represents the peak intrinsic complexity in our model. All calculations assume a standard basaltic lava density of 2650 kg/m3 [12], and other parameters used in this analysis are shown in Table 2.

Table 2.
Value of the parameters used in the calculations.
Figure 1 reveals that the fracturing number (Npf,eff), and consequently the flow’s intrinsic complexity (Dpf), is sensitive to the topographic slope. On a small 1° slope, the fracturing number is low, but as the slope increases, the fracturing number rises, indicating that the gravitational driving forces are increasing. The complexity (Dpf) is a non-monotonic function of this stress: it begins high (Dpf = 1.14), peaks at a slope of approximately 2° with a maximum complexity of Dpf = 1.15, and then decreases as the slope continues to rise. For instance, at a slope of 8°, the complexity is reduced to approximately Dpf = 1.09. This demonstrates a key feature of our approach: while a certain level of stress is required to initiate fracturing, excessive stress may lead to more efficient, channelized flow paths within the breakout lobes, thereby reducing the overall geometric complexity of the margin.
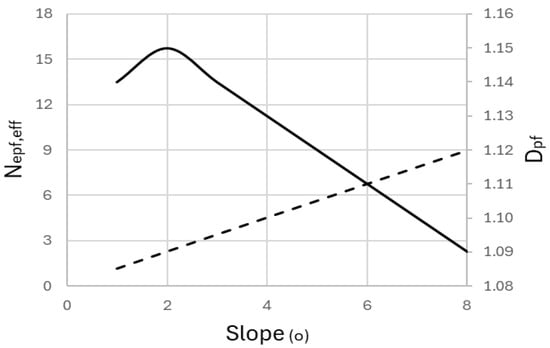
Figure 1.
The effect of topographic slope on flow complexity. The solid line represents the prefractal dimension (Dpf), and the dashed line indicates the fracturing number (Npf,eff). The simulation assumes the following parameters τy = 103 Pa, h = 10 m, Cc = 0 and g = 9.8 m/s2.
Figure 2 shows how flow thickness influences complexity for a flow on a 2° slope. For a thin flow of 5 m, the fracturing number is relatively low, leading to a high complexity of Dpf = 1.14. As the flow thickness increases towards 10 m, the fracturing number increases, and the system reaches its peak complexity with a prefractal dimension of Dpf = 1.15. As the flow continues to thicken to 20 m, the fracturing number continues to rise, pushing the system past its peak complexity, with the prefractal dimension slightly decreasing to Dpf = 1.145. This means that for a given lava type, thicker and more rapidly advancing flows are not necessarily more morphologically complex; their immense driving force can lead to simpler, more direct flow paths.
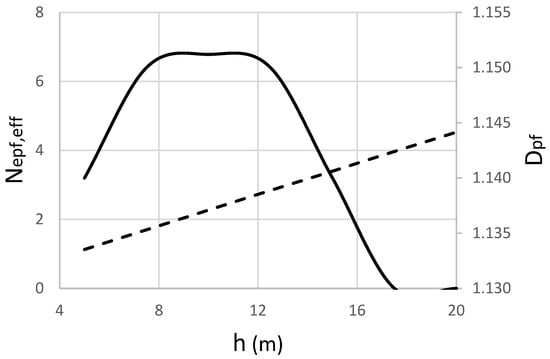
Figure 2.
The effect of lava flow thickness on complexity. The solid line shows the prefractal dimension (Dpf) and the dashed line shows the fracturing number (Npf,eff) versus the flow’s bulk thickness (h): τy = 103 Pa, α = 2°, Cc = 0 and g = 9.8 m/s2.
The influence of yield strength on complexity is depicted in Figure 3. This figure shows a curve that begins at a low complexity for fluid-like pāhoehoe lava (τy∼102 Pa), rises to a distinct peak in the intermediate-strength range characteristic of ‘a’a lava (τy∼103 Pa), and then declines again for high-strength rhyolitic lavas (τy∼105 Pa). This figure shows that the most complex flow margins are formed at an optimal yield strength, where the crust is strong enough to be brittle but weak enough to be consistently fractured by the molten interior.
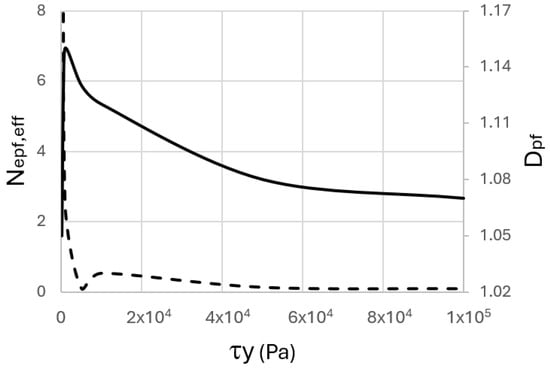
Figure 3.
The relationship between yield strength and flow complexity. The solid line shows the prefractal dimension (Dpf) and the dashed line the fracturing number (Npf,eff): h = 10 m, α = 2°, Cc = 0.
To solve the differential equation for temperature evolution (Equation (10)), specific initial and boundary conditions must be defined. The initial condition is the lava’s eruption temperature, T0. For the simulations in this study, a typical basaltic eruption temperature of T0 = 1423 K is used. The primary boundary condition is the temperature of the surrounding environment to which the lava radiates heat, Tatm. A standard ambient temperature of Tatm = 293 K is assumed. The initial yield strength is calculated based on the initial temperature.
Figure 4a,b show the evolution of a lava’s temperature, yield strength, and the prefractal dimension over 20 h. The simulation depicts a scenario consistent with the transition from a more fluid state to a rigid one. Initially, the lava flow has a low complexity (Dpf = 1.04). As the lava begins to cool, its yield strength increases, approaching the optimal value for fracturing. Consequently, after approximately two hours of cooling, the flow’s complexity peaks at Dpf = 1.15. At this point, the lava’s crust is strong enough to be brittle but weak enough to be consistently fractured, maximizing its geometric complexity. Beyond this peak, as the lava continues to cool and solidify, its yield strength becomes too high for efficient fracturing, and its ability to form fine-scale features diminishes, causing the complexity to drop steadily. The initial rise to peak complexity can be seen as a representation of the pahoehoe-to-‘a’a transition. The steady decrease in complexity after the peak demonstrates the principle that as lava becomes stiffer, its ability to form complex features diminishes, which agrees with [20].
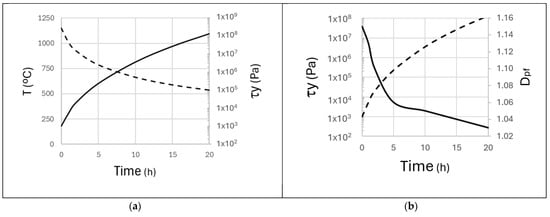
Figure 4.
Temporal evolution of an unconfined lava flow. (a) Change in lava properties over time, showing the dashed line the temperature (T,) and the solid lines yield strength (τy). (b) Evolution of flow complexity, where the solid line is the prefractal dimension (Dpf) and the dashed line is the yield strength (τy): h = 10 m; α = 2°; Cc = 0; T0 = 1423 K (typical eruption temperature for basaltic lava); Tatm = 293 K; Ea = 300 kJ/mol; clava = 1300 J/kg K; ε = 0.95.
To assess the predictive capacity of the model, its performance was evaluated against four distinct lava types (two basaltic and two non-basaltic) under two contrasting environmental scenarios: an unconfined, gentle slope and a confined, steep slope. The results are depicted in Table 3 and Table 4.

Table 3.
Comparison of predicted and observed complexity for different lava types in an unconfined setting. Predictions were calculated assuming h = 10 m, α = 2° and Cc = 0.

Table 4.
Influence of topographic confinement on the complexity of different lava types. Predictions were calculated for α = 10° and Cc = 0.85 (i.e., a high degree of confinement where the flow occupies 15% of the channel width).
Table 3 shows the model’s good agreement in capturing how a lava’s inherent properties influence its geometric complexity for unconfined flows. Regarding low- and high- yield-strength lavas, such as pāhoehoe lava, it results in a low complexity (Dpf = 1.05) due to the fact that it is too fluid to form a strong crust capable of significant fracturing. Similarly, rhyolite lava, with its extremely high yield strength, also has a relatively low complexity (Dpf = 1.07) because it resists breaking and moves as a more unified, blocky mass. Regarding intermediate-strength lavas, ‘a’a (Dpf = 1.15) and andesite (Dpf = 1.12) lavas show the highest complexities. This is because their yield strength is in the optimal range to form a brittle crust that the molten interior can consistently fracture, which creates a fragmented flow front with a high degree of geometric complexity.
The geometry complexity for flows influenced by topography (confined flows) is analyzed based on Table 4. For every lava type, the calculated complexity is significantly lower in the confined scenario than in the unconfined one. For example, the complexity of ‘a’a lava drops from 1.15 to 1.04, and pāhoehoe lava drops from 1.05 to 1.03. This illustrates a key principle that topography can override a lava’s intrinsic tendency to form complex shapes. As confinement increases, the final prefractal dimension is pushed toward the dimension of the confining channel (Dchan = 1.02). This aligns with field observations where flows that might otherwise be complex are forced into simpler, quasi-linear forms by the surrounding landscape.
Basaltic lava, which is the most common on Earth, is a key feature of the volcanic history of Moon and Mars. While ‘a’ā-like flows exist on both the Moon and Mars, their appearance and scale differ from those on Earth [6,7]. To test the model’s applicability beyond Earth, the prefractal dimension for basaltic lava flows on Mars and the Moon is calculated and the results compared with observational data in the literature [18,20]. The results are depicted at Table 5.

Table 5.
Effect of gravity on the complexity of an ‘a’ā-type lava flow on Earth, Mars, and the Moon. Predictions for each planetary body were calculated for an unconfined setting (Cc = 0), and h = 10 m and α = 2°.
Table 5 shows that for lava with similar characteristics, gravity has a direct impact on complexity: Earth (Dpf = 1.15), Mars (Dpf = 1.13), and the Moon (Dpf = 1.09). This trend directly correlates with the gravitational acceleration of each body, which agrees with the study of Wilson and Head [6]. The fracturing number quantifies the ratio of gravitational driving forces to the lava’s internal strength. On Earth, higher gravity results in a higher fracturing number (Npf,eff = 2.27), meaning the driving forces can efficiently overcome the lava’s resistance, leading to significant crustal breaking and high complexity. On Mars and the Moon, the lower gravity reduces the fracturing number to 0.86 and 0.37, respectively. With weaker driving forces, the lava is less able to fracture its crust, resulting in simpler flow margins and a lower prefractal dimension. ‘A’a lava on Earth exists in such a way that its yield strength is perfectly suited to form a brittle crust that is consistently broken by the flow’s pressure, maximizing complexity.
Model Applications and Limitations
The predictive capacity of the model presented here lends itself to several applications in volcanology. As demonstrated in the validation tables, its primary use is to infer the rheological properties and emplacement dynamics of lava flows from their final morphology. This is particularly valuable when direct sampling is impossible. By analyzing the complexity of lava flows on Mars and the Moon, we can better constrain the eruption conditions and composition of ancient lavas. Furthermore, the model could be extended for volcanic hazard assessment.
However, the model is based on several simplifying assumptions that constitute its limitations: (a) The model is a 1D representation of an inherently 3D process. It calculates a single complexity value and does not simulate the spatial path of the flow. (b) The model assumes uniform thermal and physical properties (e.g., density, emissivity) throughout the lava flow at any given time. (c) The temporal evolution component assumes heat loss is dominated by thermal radiation. It neglects other mechanisms such as convection to the atmosphere, conduction to the ground, and heat generated by latent heat of crystallization.
4. Conclusions
This study has developed and validated a predictive model for the geometric complexity of lava flows, unifying their intrinsic rheological properties with extrinsic environmental forces. Our approach shows that the morphology of a lava flow is not arbitrary but is governed by a predictable interplay between the lava’s internal strength and the external stresses it endures.
The basis of our model is the principle that a lava’s potential for fracturing diminishes symmetrically from an optimal yield strength. This leads to a non-monotonic relationship between a lava’s internal resistance and its resulting complexity. It is shown that the most intricate flow margins do not arise from the most fluid or the most viscous lavas, but from those at the peak of this symmetrical curve. It is in this critical, ‘a’a lava-like state that the crust is perfectly balanced: strong enough to fracture, yet weak enough to be consistently broken by the molten interior. The simpler, less complex morphologies of pāhoehoe and rhyolite lavas represent the symmetrical decline from this peak. Furthermore, the model accounts for the influence of the surrounding landscape by incorporating a confinement index, which quantifies how topography can override a lava’s inherent tendencies.
The critical contributions and key findings of this work can be summarized as follows:
- -
- Presents a unified physical model linking lava rheology (yield strength) and environmental factors (topography; gravity) to geometric complexity (prefractal dimension).
- -
- Demonstrates that complexity follows a symmetrical, non-monotonic relationship with yield strength, peaking for intermediate-strength lavas like ‘a’ā.
- -
- Successfully validates the model against a range of terrestrial and planetary (Mars; Moon) lava flows, confirming the critical role of gravity in influencing morphology.
- -
- Includes a dynamic component to model the temporal evolution of complexity as the lava cools and solidifies, linking initial fluid states to final solidified forms.
Funding
The author gratefully acknowledges the financial support provided to the Institute of Earth Sciences through the multi-annual funding agreement with the Foundation for Science and Technology of Portugal (FCT), under project UID/04683.
Data Availability Statement
The data supporting the conclusions of this article will be made available by the author on request.
Conflicts of Interest
The author declares no conflicts of interest.
List of Symbols
| Cc | Confinement index (0 (unconfined) to 1 (perfectly confined)) |
| Clava | Specific heat capacity of lava |
| Dchan | Prefractal dimension of a perfectly straight, confining channel |
| Dint | Intrinsic prefractal dimension of a lava flow based on its properties |
| Dmax | Maximum prefractal dimension, corresponding to peak complexity |
| Dmin | Basal prefractal dimension for a near-stationary flow. |
| Dpf | Final prefractal dimension of a lava flow, accounting for all factors |
| Ea | Activation energy for viscous flow in lava |
| g | Gravitational acceleration. |
| h | Bulk thickness of the lava flow. |
| heff | Effective thickness of the active flow margin |
| h*min | Minimum possible ratio of effective thickness to bulk thickness (0.25) |
| Npf,crit | Critical fracturing number at which the highest complexity occurs |
| Npf,eff | Fracturing number |
| R | Universal gas constant (8.314 J/(mol·K)) |
| Tatm | Absolute temperature of the surrounding atmosphere. |
| Tt | Absolute temperature of the lava at a given time |
| T0 | Initial absolute temperature of the lava |
| w | Width of the lava flow. |
| wchan | Width of the confining channel or valley |
| Greek Symbols | |
| α | Slope angle of the terrain. |
| γ | Stefan–Boltzmann constant for thermal radiation. |
| ε | Emissivity of the lava |
| Density of the lava | |
| σ | Parameter controlling the spread of fracturing behavior across yield strengths (0.75) |
| τbase,eff | Shear stress at the base of the flow caused by gravity. |
| τpeak | Peak yield strength where fracturing and complexity are most pronounced (103 Pa) |
| τy | Yield strength of the lava, its internal resistance to flow |
| τy,T | Yield strength of the lava as it changes with temperature |
| τ0 | Initial yield strength of the lava |
References
- Miguel, A.F.; Lorente, S. Dendritic flow networks: The link between patterns and design with purpose in biosystems. Res. Biomed. Eng. 2025, 41, 19. [Google Scholar] [CrossRef]
- Miguel, A.F. Low dissipative configuration in flow networks subject to constraints. Phys. D 2024, 467, 134269. [Google Scholar] [CrossRef]
- Krakauer, D.C. Symmetry–simplicity, broken symmetry–complexity. Interface Focus 2023, 13, 20220075. [Google Scholar] [CrossRef] [PubMed]
- Pepe, V.; Miguel, A.F.; Zinani, F.; Rocha, L.A.O. New insights into creeping fluid flow through dendritic networks: A constructal view. Int. Comm. Heat Mass Transf. 2023, 139, 106409. [Google Scholar] [CrossRef]
- Reston, T.J. The structure, evolution and symmetry of the magma-poor rifted margins of the North and Central Atlantic: A synthesis. Tectonophysics 2009, 468, 6–27. [Google Scholar] [CrossRef]
- Wilson, L.; Head, J.W. A comparison of volcanic eruption processes on Earth, Moon, Mars, Io and Venus. Nature 1983, 302, 663–669. [Google Scholar] [CrossRef]
- Keszthelyi, L.; Jaeger, W.; McEwen, A.; Tornabene, L.; Beyer, R.A.; Dundas, C.; Milazzo, M. High Resolution Imaging Science Experiment (HiRISE) images of volcanic terrains from the first 6 months of the Mars Reconnaissance Orbiter Primary Science Phase. J. Geophys. Res. Planets. 2008, 113, E4. [Google Scholar] [CrossRef]
- Walker, G.P.L. Lengths of lava flows. Phil. Trans. R. Soc. Lond. A 1973, 274, 107–118. [Google Scholar]
- Hulme, G. The interpretation of lava flow morphology. Geophys. J. R. Astron. Soc. 1974, 39, 361–383. [Google Scholar] [CrossRef]
- Griffiths, R.W. The dynamics of lava flows. Annu. Rev. Fluid Mech. 2000, 32, 477–518. [Google Scholar] [CrossRef]
- Gonnermann, H.M.; Manga, M. The fluid mechanics inside a volcano. Annu. Rev. Fluid Mech. 2007, 39, 321–356. [Google Scholar] [CrossRef]
- McBirney, A.R.; Murase, T. Rheological properties of magmas. Annu. Rev. Earth Planet. Sci. 1984, 12, 337–357. [Google Scholar] [CrossRef]
- Giordano, D.; Russell, J.K.; Dingwell, D.B. Viscosity of magmatic liquids: A model. Earth Planet. Sci. Lett. 2008, 271, 123–134. [Google Scholar] [CrossRef]
- Rowland, S.K.; Walker, G.P.L. Pāhoehoe and ‘a’a in Hawai’i: Volumetric flow rate controls the lava structure. Bull. Volcanol. 1990, 52, 615–628. [Google Scholar] [CrossRef]
- Fink, J.H.; Griffiths, R.W. Morphology, eruption rates, and rheology of lava domes—Insights from laboratory models. J. Volcanol. Geotherm. Res. 1998, 103, 527–545. [Google Scholar] [CrossRef]
- Gaonac’h, H.; Lovejoy, S.; Stix, J. Scale invariance of basaltic lava flows and their fractal dimensions. Geophys. Res. Lett. 1992, 19, 785–788. [Google Scholar] [CrossRef]
- Tarboton, D.G.; Bras, R.L.; Rodriguez-Iturbe, I. The fractal nature of river networks. Water Resour. Res. 1988, 24, 1317–1322. [Google Scholar] [CrossRef]
- Schaefer, E.I.; Hamilton, C.W.; Neish, C.D.; Sori, M.M.; Bramson, A.M.; Beard, S.P. Reexamining the potential to classify lava flows from the fractality of their margins. J. Geophys. Res. Solid Earth 2021, 126, e2020JB020949. [Google Scholar] [CrossRef]
- Andrle, R. The west coast of Britain: Statistical self-similarity vs. characteristic scales in the landscape. Earth Surf. Process. Landf. 1996, 21, 955–962. [Google Scholar] [CrossRef]
- Bruno, B.C.; Rowland, S.K.; Taylor, G.J. Quantifying the effect of rheology on lava-flow margins using fractal geometry. Bull. Volcanol. 1994, 56, 193–206. [Google Scholar] [CrossRef]
- Pepe, V.; Miguel, A.F.; Zinani, F.; Rocha, L.A.O. Fluid flow in isomeric constructal networks of tubes. J. Porous Media 2024, 27, 1–18. [Google Scholar] [CrossRef]
- Gregg, T.K.P.; Fink, J.H. A laboratory investigation into the effects of slope on lava flow morphology. J. Volcanol. Geotherm. Res. 2000, 96, 145–159. [Google Scholar] [CrossRef]
- Scaini, C.; Felpeto, A.; Martí, J.; Carniel, R. A GIS-based methodology for the estimation of potential volcanic damage and its application to Tenerife Island, Spain. J. Volcanol. Geotherm. Res. 2014, 278–279, 40–58. [Google Scholar] [CrossRef]
- Aufaristama, M.; Höskuldsson, Á.; Ulfarsson, M.O.; Jónsdóttir, I.; Thordarson, T. Lava flow roughness on the 2014–2015 lava flow-field at Holuhraun, Iceland, derived from airborne LiDAR and photogrammetry. Geosciences 2020, 10, 125. [Google Scholar] [CrossRef]
- Kueppers, U.; Scheu, B.; Dingwell, D.B. Fragmentation efficiency of explosive volcanic eruptions: A study of experimentally produced pyroclasts. J. Volcanol. Geotherm. Res. 2006, 153, 125–135. [Google Scholar] [CrossRef]
- Kilburn, C.R.J. Multiscale fracturing as a key to forecasting volcanic eruptions. J. Volcanol. Geotherm. Res. 2003, 125, 271–289. [Google Scholar] [CrossRef]
- Miller, S.A.; Crown, D.A.; Berman, D.C. Fractal dimensions of terrestrial and planetary lava flows: The influence of pre-flow topography on flow margins. In Proceedings of the 56th Lunar and Planetary Science Conference, The Woodlands, TX, USA, 10–14 March 2025; p. 1468. [Google Scholar]
- Fink, J.H. Surface folding and viscosity of rhyolite flows. Geology 1980, 8, 250–254. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).