A Modified Collocation Technique for Addressing the Time-Fractional FitzHugh–Nagumo Differential Equation with Shifted Legendre Polynomials

Abstract

This study is devoted to solving the nonlinear inhomogeneous time-fractional FitzHugh–Nagumo differential problem ($\mathsf{TFFNDP}$) using the spectral modified collocation method. The proposed algorithm uses non-symmetric polynomials, namely shifted Legendre polynomials ($\mathsf{SLPs}$), which are orthogonal. The orthogonality property of $\mathsf{SLPs}$ and certain relations facilitate the acquisition of accurate spectral approximations. Comprehensive convergence and error studies are conducted to validate the accuracy of the suggested shifted Legendre expansion. Several numerical examples are presented to demonstrate the method’s effectiveness and accuracy. The proposed scheme is benchmarked against known analytical solutions and compared with other algorithms to ensure the applicability and efficiency of the proposed algorithm.

1. Introduction

Spectral methods are important numerical approaches employed to solve all types of differential equations [1,2,3]. The philosophy behind applying these methods is based on the assumption that the numerical solutions are represented in terms of suitable special functions that are often special polynomials. Unlike other numerical techniques, these methods present several advantages; see [4,5]. Also, these methods produce accurate approximations that converge rapidly. There are three primary spectral approaches. Each method has different advantages and applications. The selection of basis functions in the tau and collocation methods is less restrictive than that in the Galerkin approach; see [6,7,8]. References [9,10,11,12] demonstrate that the Galerkin and Petrov–Galerkin approaches are effective for various problems. For more studies, see [13,14,15,16,17,18].

In many fields, such as physics, engineering, and mathematics, orthogonal polynomials [19,20] are crucial. These polynomials can be classified as either symmetric or non-symmetric. These polynomials have some properties that make them more important in many situations. Applications of particular polynomials have been demonstrated in several publications; see [21,22,23]. In particular, $\mathsf{SLPs}$ are essential in various disciplines, including control theory, signal processing, and cryptography, due to their distinctive characteristics. These polynomials are used more frequently in numerical analyses and approximation theory. The authors of [24] employed $\mathsf{SLPs}$ in a numerical method to address fractional-order multi-point boundary value problems. Also, the authors of [25] employed the differential quadrature approach utilizing $\mathsf{SLPs}$ and generalized Laguerre polynomials to solve the Benjamin–Bona–Mahony equation.

The FitzHugh–Nagumo equation system was derived by both FitzHugh [26] and Nagumo et al. [27]. Its simplicity and ability to capture key dynamics make it a valuable tool in studying nonlinear dynamical systems and analyzing biological phenomena related to excitation and signal propagation. The $\mathsf{TFFNDP}$, which combines diffusion and nonlinearity, has attracted the interest of many scientists in the fields of nuclear reactor theory, neurophysiology, branching Brownian motion, flame propagation, and logistic population growth [28]. The purpose of this study is to accurately solve the following nonlinear inhomogeneous $\mathsf{TFFNDP}$:

$$D_t^{\alpha }u=u_{\eta \eta }+u(u-\epsilon )(1-u)+f(\eta ,t),0<\alpha \le 1,$$

(1)

constrained with

$$\begin{array}{cc}\hfill & u(\eta ,0)=u_0\left(\xi \right),0<\eta \le 1,\hfill \end{array}$$

(2)

$$\begin{array}{c}\hfill u(0,t)=u_1\left(t\right),u(1,t)=u_2\left(t\right),0<t\le 1,\end{array}$$

(3)

where u is a function of both $\eta$ and t, i.e., $u=u(\eta ,t)$; $f(\eta ,t)$ is the source function; and $\epsilon$ is a real number. Various numerical and analytical approaches have been used to solve the $\mathsf{TFFNDP}$. For example, a Petrov–Galerkin finite element technique was applied to solving a space $\mathsf{TFFNDP}$ in [29]. A collocation method was developed in [30] to treat the $\mathsf{TFFNDP}$ using a kind of Chebyshev polynomial. The authors in [31] offered a spectral technique for finding solutions to the $\mathsf{TFFNDP}$ using shifted Lucas polynomials. Although this method demonstrated good accuracy, it required more terms in the retained modes compared to the presented method. The authors in [32] presented a numerical technique using approximations of radial basis functions to solve this problem. Finally, the authors of [33] applied the fractional reduced differential transform method to this problem. The disadvantage of the methods presented in [32,33] is that they offer a lower accuracy compared to that of the proposed method.

The following points are the main contributions and novelties of this work:

• Presenting two sets of basis functions in terms of $\mathsf{SLPs}$;
• Deriving some new identities is crucial for efficient computation of the collocation matrices;
• Using the collocation method to treat the $\mathsf{TFFNDP}$;
• Offering a thorough examination of the convergence and error, tailored to the suggested basis functions;
• Investigating our numerical algorithm by presenting some supporting numerical examples;
• We expect that the scheme utilized could be used to solve other problems [34] using the collocation method.

Also, some advantages of this work are

• Choosing the suggested basis functions results in faster convergence and improved stability;
• The procedure needs fewer computations to reach the desired precision.

This paper is structured as follows: Section 2 presents the main concepts and essential formulas. Section 3 introduces a collocation spectral method for the nonlinear inhomogeneous $\mathsf{TFFNDP}$. A study on the convergence of the shifted Legendre expansion is presented in Section 4. Five examples are presented in Section 5. The conclusions are presented in Section 6.

2. Essential Principles and Formulas

This section presents some fundamentals of fractional calculus related to Caputo’s fractional derivative (FD). Furthermore, we will introduce key principles and significant formulas for the $\mathsf{SLPs}$, which will be crucial for subsequent discussions.

2.1. A Review of Caputo’s FD

Definition 1. 

Caputo’s FD is defined as [35]

$${\displaystyle D_{\zeta }^{\alpha }\psi \left(\zeta \right)=\frac{1}{\Gamma (\mathsf{\ell }-\alpha )}{\int }_0^{\zeta }{(\zeta -t)}^{\mathsf{\ell }-\alpha -1}{\psi }^{\left(r\right)}\left(t\right)dt,\alpha >0,\zeta >0,\mathsf{\ell }-1⩽\alpha <\mathsf{\ell },\mathsf{\ell }\in \mathbb{N}.}$$

(4)

In addition, we have

$$\begin{array}{cc}\hfill D_{\zeta }^{\alpha }{\zeta }^{\tau }& =\left\{\begin{array}{cc}0,\hfill & \mathrm{if}\tau \in {\mathbb{N}}_{0}and\tau <\lceil \alpha \rceil ,\hfill \\ {\displaystyle \frac{\tau !}{\Gamma (\tau +1-\alpha )}}{\zeta }^{\tau -\alpha },\hfill & \mathrm{if}\tau \in {\mathbb{N}}_{0}and\tau \ge \lceil \alpha \rceil ,\hfill \end{array}\right.\hfill \end{array}$$

(5)

where $\lceil \alpha \rceil$ denotes the ceiling function, ${\mathbb{N}}_0=\{0,1,2,\dots \}$, and $\mathbb{N}=\{1,2,\dots \}$.

2.2. A Basic Overview of Legendre Polynomials and Their Shifted Equivalents

The Legendre polynomial of degree s, ${\mathrm{L}}_s^{(-1,1)}\left(\eta \right)$, can be defined in numerous forms over the range $[-1, 1]$, including using the following recurrence relation [36,37]:

$$\left\{\begin{array}{cc}\hfill & {\mathrm{L}}_0^{(-1,1)}\left(\eta \right)=1,{\mathrm{L}}_1^{(-1,1)}\left(\eta \right)=\eta ,\hfill \\ \hfill & (s+1){\mathrm{L}}_{s+1}^{(-1,1)}\left(\eta \right)=(2s+1)\eta {\mathrm{L}}_s^{(-1,1)}\left(\eta \right)-s{\mathrm{L}}_{s-1}^{(-1,1)}\left(\eta \right).\hfill \end{array}\right.$$

(6)

A significant characteristic of the Legendre polynomials is their orthogonality on the interval $[-1, 1]$ regarding the ${\mathrm{L}}^2$ inner product:

$${\int }_{-1}^1{\mathrm{L}}_m^{(-1,1)}\left(\eta \right){\mathrm{L}}_s^{(-1,1)}\left(\eta \right)d\eta ={\displaystyle \frac{2}{2s+1}}{\delta }_{ms},$$

where ${\delta }_{mn}$ is the renowned Kronecker delta function.

• The $\mathsf{SLPs}$${\mathrm{L}}_m^{(a,b)}\left(\eta \right)$ are defined on $[a,b]$:

$${\mathrm{L}}_m^{(a,b)}\left(\eta \right)=L_m^{(-1,1)}\left(\eta \right)\left({\displaystyle \frac{2\eta -b-a}{b-a}}\right),$$

and they are orthogonal on $[a, b]$ in the following manner:

$${\int }_a^b{\mathrm{L}}_m^{(a,b)}\left(\eta \right){\mathrm{L}}_s^{(a,b)}\left(\eta \right)d\eta ={\displaystyle \frac{b-a}{2s+1}}{\delta }_{ms}.$$

(7)

The power form of ${\mathrm{L}}_i^{(0,1)}\left(\eta \right)$ is

$${\displaystyle {\mathrm{L}}_i^{(0,1)}\left(\eta \right)=\sum _{m=0}^i\frac{{(-1)}^{i+m}(i+m)!}{(i-m)!\left(m\right){!}^2}{\eta }^m,}$$

(8)

and its inversion formula is

$${\eta }^i=\sum _{m=0}^r{\displaystyle \frac{{(-1)}^{2m}(2m+1)\Gamma {(r+1)}^2}{\Gamma (-m+r+1)\Gamma (m+r+2)}}{\mathrm{L}}_m^{(0,1)}\left(\eta \right).$$

(9)

Theorem 1 

([36]). Assume ${\varphi }_i\left(\eta \right)=(\eta -a)(\eta -b){\mathrm{L}}_i^{(a,b)}\left(\eta \right)$. Then, for all $i\ge 1$, the following holds:

$$D{\varphi }_i\left(\eta \right)={\displaystyle \frac{2}{b-a}}\sum _{\begin{array}{c}j=0\\ (i+j)odd\end{array}}^{i-1}(2j+1)(1+2{\mathcal{H}}_i-2{\mathcal{H}}_j){\varphi }_j\left(\eta \right)-{\delta }_i\left(\eta \right),$$

where ${\delta }_i\left(\eta \right)$ is provided by

$${\delta }_i\left(\eta \right)=\left\{\begin{array}{cc}a+b-2\eta ,\hfill & ifi\mathit{even},\hfill \\ a-b,\hfill & ifi\mathit{odd},\hfill \end{array}\right.$$

and ${\mathcal{H}}_m$ is the mth harmonic number, defined as

$${\mathcal{H}}_m=\sum _{n=1}^m{\displaystyle \frac{1}{n}}.$$

(10)

2.3. Trial Functions

We choose the trial functions to be

$$\begin{array}{cc}& {\theta }_i\left(\eta \right)=\eta (1-\eta ){\mathrm{L}}_i^{(0,1)}\left(\eta \right),\hfill \\ & {\vartheta }_j\left(t\right)=t{\mathrm{L}}_j^{(0,1)}\left(t\right).\hfill \end{array}$$

(11)

Based on the orthogonality relation in (7), we acquire the following relations:

$${\int }_0^1{\theta }_m\left(\eta \right){\theta }_s\left(\eta \right){\omega }_1\left(\eta \right)d\eta ={\displaystyle \frac{1}{2s+1}}{\delta }_{ms},$$

(12)

and

$${\int }_0^1{\vartheta }_m\left(t\right){\vartheta }_s\left(t\right){\omega }_2\left(t\right)dt={\displaystyle \frac{1}{2s+1}}{\delta }_{ms}.$$

(13)

where ${\omega }_1\left(\eta \right)={\displaystyle \frac{1}{{\eta }^2{(1-\eta )}^2}}$ and ${\omega }_2\left(t\right)={\displaystyle \frac{1}{t^2}}$.

Corollary 1. 

For $i\ge 1$, one has

$${\displaystyle \frac{d{\theta }_i\left(\eta \right)}{d\eta }}=2\sum _{\begin{array}{c}j=0\\ (i+j)\mathit{odd}\end{array}}^{i-1}(2j+1)(1+2{\mathcal{H}}_i-2{\mathcal{H}}_j){\theta }_j\left(\eta \right)+{\mu }_i\left(\eta \right),$$

(14)

where

$${\mu }_i\left(\eta \right)=\left\{\begin{array}{cc}1-2\eta ,\hfill & \mathit{if}i\mathit{even},\hfill \\ -1,\hfill & \mathit{if}i\mathit{odd},\hfill \end{array}\right.$$

(15)

Proof. 

The proof of this corollary can be readily derived by substituting $a=0$ and $b=1$ into Theorem 1. □

Remark 1. 

The first and second derivatives of the vector $\mathit{\theta }\left(\eta \right)$ are provided by

$$\begin{array}{cc}\hfill & {\displaystyle \frac{d\mathit{\theta }\left(\eta \right)}{d\eta }}=\mathit{A}\mathit{\theta }\left(\eta \right)+\mathit{\mu },\hfill \end{array}$$

(16)

$$\begin{array}{cc}& {\displaystyle \frac{d^2\mathit{\theta }\left(\eta \right)}{d{\eta }^2}}={\mathit{A}}^2\mathit{\theta }\left(\eta \right)+\mathit{A}\mathit{\mu }+{\mathit{\mu }}^{\prime },\hfill \end{array}$$

(17)

where $\mathit{A}={\left(a_{ij}\right)}_{0\le i,j\le \mathcal{K}}$ is a matrix of order ${(\mathcal{K}+1)}^2$, whose nonzero elements can be expressly specified as

$$a_{ij}=\left\{\begin{array}{cc}2(2j+1)(1+2{\mathcal{H}}_i-2{\mathcal{H}}_j),\hfill & (i+j)\mathit{odd},i>j,\hfill \\ 0,\hfill & \mathit{otherwise},\hfill \end{array}\right.$$

(18)

and also

$$\mathit{\mu }={\left({\mu }_0,{\mu }_1,\dots ,{\mu }_{\mathcal{K}}\right)}^T,$$

(19)

and

$${\mathit{\mu }}^{\prime }={\left({\mu }_0^{\prime },{\mu }_1^{\prime },\dots ,{\mu }_{\mathcal{K}}^{\prime }\right)}^T,{\mu }_i^{\prime }=\left\{\begin{array}{cc}-2,\hfill & i\mathit{even},\hfill \\ 0,\hfill & i\mathit{odd}.\hfill \end{array}\right.$$

(20)

For example, the matrices $\mathit{A},\mathit{\mu },$ and ${\mathit{\mu }}^{\prime }$ take the following form for $\mathcal{K}=6$ as

$$\mathit{A}=\left(\begin{array}{ccccccc}0& 0& 0& 0& 0& 0& 0\\ 6& 0& 0& 0& 0& 0& 0\\ 0& 12& 0& 0& 0& 0& 0\\ {\displaystyle \frac{28}{3}}& 0& {\displaystyle \frac{50}{3}}& 0& 0& 0& 0\\ 0& 19& 0& 21& 0& 0& 0\\ {\displaystyle \frac{167}{15}}& 0& {\displaystyle \frac{77}{3}}& 0& {\displaystyle \frac{126}{5}}& 0& 0\\ 0& {\displaystyle \frac{117}{5}}& 0& {\displaystyle \frac{469}{15}}& 0& {\displaystyle \frac{88}{3}}& 0\end{array}\right),$$

(21)

and

$$\mathit{\mu }=\left(\begin{array}{c}1-2\eta \\ -1\\ 1-2\eta \\ -1\\ 1-2\eta \\ -1\\ 1-2\eta \end{array}\right),{\mathit{\mu }}^{\prime }=\left(\begin{array}{c}-2\\ 0\\ -2\\ 0\\ -2\\ 0\\ -2\end{array}\right).$$

(22)

Theorem 2. 

The subsequent formula is valid for $\alpha \in (0,1)$:

$$D_t^{\alpha }{\vartheta }_s\left(t\right)\simeq \sum _{\mathsf{\ell }=0}^{\mathcal{K}}{\mathcal{Q}}_{\mathsf{\ell },s}{\vartheta }_n\left(t\right)+{\lambda }_s\left(t\right),$$

(23)

where

$${\mathcal{Q}}_{\mathsf{\ell },s}=\sum _{\tau =0}^{s+1}{\displaystyle \frac{(\tau +2)(2\mathsf{\ell }+1){(-1)}^{s+\tau +2\mathsf{\ell }+1}(s+\tau +1)!\Gamma (\tau -\alpha +2)}{(-\alpha +\tau +2)(\tau +1)!\Gamma (s-\tau )\Gamma (\tau -\mathsf{\ell }-\alpha +2)\Gamma (\tau +\mathsf{\ell }-\alpha +3)}},$$

(24)

and

$${\lambda }_s\left(t\right)={\displaystyle \frac{{(-1)}^s}{\Gamma (2-\alpha )}}{t}^{1-\alpha }.$$

(25)

Proof. 

Based on (8), along with the definition of ${\vartheta }_j\left(t\right)$, one obtains

$${\displaystyle {\vartheta }_j\left(t\right)=\sum _{\tau =0}^j\frac{{(-1)}^{j+\tau }(j+\tau )!}{{(\tau !)}^2(j-\tau )!}{t}^{\tau +1},}$$

(26)

Using Caputo’s FD from (5) and the last relation, we can write

$$\begin{array}{cc}\hfill D_t^{\alpha }{\vartheta }_j\left(t\right)& =\sum _{\tau =0}^j{\displaystyle \frac{\left((\tau +1)!{(-1)}^{j+\tau }(j+\tau )!\right)}{{(\tau !)}^2(j-\tau )!(-\alpha +\tau +1)!}}{t}^{-\alpha +\tau +1}\hfill \\ & =\sum _{\tau =1}^j{\displaystyle \frac{\left((\tau +1)!{(-1)}^{j+\tau }(j+\tau )!\right)}{{(\tau !)}^2(j-\tau )!(-\alpha +\tau +1)!}}{t}^{-\alpha +\tau +1}+{\displaystyle \frac{{(-1)}^j{t}^{1-\alpha }}{\Gamma (2-\alpha )}}.\hfill \end{array}$$

(27)

Now, based on the inversion formula of $L_m^{(0,1)}\left(\eta \right)$ defined in (9) and for a sufficiently large positive number $\mathcal{K}$, we can approximate $t^{-\alpha +\tau +1}$ in the form

$$t^{-\alpha +\tau +1}\simeq \sum _{m=0}^{\mathcal{K}}{\displaystyle \frac{{(-1)}^{2m}(2m+1){((\tau -\alpha )!)}^2}{\Gamma (\tau -m-\alpha +1)\Gamma (\tau +m-\alpha +2)}}{\vartheta }_m\left(t\right).$$

(28)

Inserting the previous relation into (27) leads to the following approximation:

$$\begin{array}{cc}\hfill D_t^{\alpha }{\vartheta }_j\left(t\right)& =\sum _{\tau =1}^j{\displaystyle \frac{(\tau +1)!{(-1)}^{j+\tau }(j+\tau )!}{{(\tau !)}^2(j-\tau )!(-\alpha +\tau +1)!}}\sum _{m=0}^{\mathcal{K}}{\displaystyle \frac{{(-1)}^{2m}(2m+1){((\tau -\alpha )!)}^2}{\Gamma (\tau -m-\alpha +1)\Gamma (\tau +m-\alpha +2)}}{\vartheta }_m\left(t\right)\hfill \\ & +{\displaystyle \frac{{(-1)}^j{t}^{1-\alpha }}{\Gamma (2-\alpha )}}.\hfill \end{array}$$

(29)

The previous equation can be reformulated by rearranging the elements as

$$D_t^{\alpha }{\vartheta }_s\left(t\right)\simeq \sum _{\mathsf{\ell }=0}^{\mathcal{K}}{\mathcal{Q}}_{\mathsf{\ell },s}{\vartheta }_n\left(t\right)+{\lambda }_s\left(t\right),$$

(30)

where

$${\mathcal{Q}}_{\mathsf{\ell },s}=\sum _{\tau =0}^{s+1}{\displaystyle \frac{(\tau +2)(2\mathsf{\ell }+1){(-1)}^{s+\tau +2\mathsf{\ell }+1}(s+\tau +1)!\Gamma (\tau -\alpha +2)}{(-\alpha +\tau +2)(\tau +1)!\Gamma (s-\tau )\Gamma (\tau -\mathsf{\ell }-\alpha +2)\Gamma (\tau +\mathsf{\ell }-\alpha +3)}},$$

(31)

and

$${\lambda }_s\left(t\right)={\displaystyle \frac{{(-1)}^s}{\Gamma (2-\alpha )}}{t}^{1-\alpha }.$$

(32)

This concludes the proof of the theorem. □

Remark 2. 

The fractional derivative of the vector $\mathit{\vartheta }\left(t\right)$ is given by

$$D_t^{\alpha }\mathit{\vartheta }\left(t\right)\simeq \mathit{B}\mathit{\vartheta }\left(t\right)+\mathit{\lambda },$$

(33)

where $\mathit{B}={\left(Q_{m,j}\right)}_{0\le m,j\le \mathcal{K}}$ is a matrix of order ${(\mathcal{K}+1)}^2$ whose nonzero elements are given in (24), and

$$\mathit{\lambda }={\left({\lambda }_0,{\lambda }_1,\dots ,{\lambda }_{\mathcal{K}}\right)}^T.$$

(34)

For example, the matrices $\mathit{B}$ and $\mathit{\lambda }$ take the following form for $\mathcal{K}=6$ at $\alpha =0.5$ as

$$\mathit{B}=\left(\begin{array}{ccccccc}0& 0& 0& 0& 0& 0& 0\\ {\displaystyle \frac{32}{9\sqrt{\pi }}}& {\displaystyle \frac{32}{15\sqrt{\pi }}}& -{\displaystyle \frac{32}{63\sqrt{\pi }}}& {\displaystyle \frac{32}{135\sqrt{\pi }}}& -{\displaystyle \frac{32}{231\sqrt{\pi }}}& {\displaystyle \frac{32}{351\sqrt{\pi }}}& -{\displaystyle \frac{32}{495\sqrt{\pi }}}\\ -{\displaystyle \frac{224}{75\sqrt{\pi }}}& {\displaystyle \frac{608}{175\sqrt{\pi }}}& {\displaystyle \frac{352}{105\sqrt{\pi }}}& -{\displaystyle \frac{2336}{2475\sqrt{\pi }}}& {\displaystyle \frac{12128}{25025\sqrt{\pi }}}& -{\displaystyle \frac{6176}{20475\sqrt{\pi }}}& {\displaystyle \frac{2912}{14025\sqrt{\pi }}}\\ {\displaystyle \frac{2816}{735\sqrt{\pi }}}& -{\displaystyle \frac{256}{147\sqrt{\pi }}}& {\displaystyle \frac{5888}{1617\sqrt{\pi }}}& {\displaystyle \frac{38656}{9009\sqrt{\pi }}}& -{\displaystyle \frac{46336}{35035\sqrt{\pi }}}& {\displaystyle \frac{350464}{487305\sqrt{\pi }}}& -{\displaystyle \frac{81152}{174097\sqrt{\pi }}}\\ -{\displaystyle \frac{9728}{2835\sqrt{\pi }}}& {\displaystyle \frac{37888}{10395\sqrt{\pi }}}& -{\displaystyle \frac{77824}{81081\sqrt{\pi }}}& {\displaystyle \frac{223744}{57915\sqrt{\pi }}}& {\displaystyle \frac{353792}{69615\sqrt{\pi }}}& -{\displaystyle \frac{19757056}{11904165\sqrt{\pi }}}& {\displaystyle \frac{859136}{915705\sqrt{\pi }}}\\ {\displaystyle \frac{148448}{38115\sqrt{\pi }}}& -{\displaystyle \frac{426784}{165165\sqrt{\pi }}}& {\displaystyle \frac{354272}{99099\sqrt{\pi }}}& -{\displaystyle \frac{475808}{1203345\sqrt{\pi }}}& {\displaystyle \frac{72847392}{17782765\sqrt{\pi }}}& {\displaystyle \frac{84086176}{14549535\sqrt{\pi }}}& -{\displaystyle \frac{32737184}{16656255\sqrt{\pi }}}\\ -{\displaystyle \frac{2111264}{585585\sqrt{\pi }}}& {\displaystyle \frac{730976}{195195\sqrt{\pi }}}& -{\displaystyle \frac{3917728}{1990989\sqrt{\pi }}}& {\displaystyle \frac{96387488}{27020565\sqrt{\pi }}}& {\displaystyle \frac{983968}{21015995\sqrt{\pi }}}& {\displaystyle \frac{1711517152}{395482815\sqrt{\pi }}}& {\displaystyle \frac{10724589152}{1673196525\sqrt{\pi }}}\end{array}\right),$$

(35)

and

$$\mathit{\lambda }=\left(\begin{array}{c}{\displaystyle \frac{2\sqrt{t}}{\sqrt{\pi }}}\\ -{\displaystyle \frac{2\sqrt{t}}{\sqrt{\pi }}}\\ {\displaystyle \frac{2\sqrt{t}}{\sqrt{\pi }}}\\ -{\displaystyle \frac{2\sqrt{t}}{\sqrt{\pi }}}\\ {\displaystyle \frac{2\sqrt{t}}{\sqrt{\pi }}}\\ -{\displaystyle \frac{2\sqrt{t}}{\sqrt{\pi }}}\\ {\displaystyle \frac{2\sqrt{t}}{\sqrt{\pi }}}\end{array}\right).$$

(36)

3. The Collocation Method for the Nonlinear Inhomogeneous Time-Fractional FitzHugh–Nagumo Differential Problem

This part analyzes a numerical algorithm for solving the nonlinear inhomogeneous equation $\mathsf{TFFNDP}$ (1) subject to conditions (2) and (3).

To proceed with the proposed collocation technique, we define the following transformation:

$$\psi (\eta ,t):=u(\eta ,t)+\widehat{u}(\eta ,t),$$

(37)

where

$$\begin{array}{cc}\hfill \widehat{u}(\eta ,t)=& -\left(\right(1-\eta \left)u\right(0,t)+\eta u(1,t)+((\eta -1)u(0,0)-\eta u(1,0)+u(\eta ,0)\left)\right).\hfill \end{array}$$

(38)

Then, Equation (37) converts the nonlinear inhomogeneous $\mathsf{TFFNDP}$ (1) governed by (2) and (3) into the adapted equation that follows:

$$D_t^{\alpha }\psi ={\psi }_{\eta \eta }+\psi (\psi -\epsilon )(1-\psi )+g(\eta ,t),0<\alpha \le 1,$$

(39)

subject to homogeneous initial and boundary conditions (HIBCs)

$$\begin{array}{cc}& \psi (\eta ,0)=0,0<\eta \le 1,\hfill \\ & \psi (0,t)=\psi (1,t)=0,0<t\le 1,\hfill \end{array}$$

(40)

where

$$g(\eta ,t)=f(\eta ,t)+D_t^{\alpha }\widehat{u}-{\widehat{u}}_{\eta \eta }-\widehat{u}(\widehat{u}-\epsilon )(1-\widehat{u}).$$

(41)

Thus, we can solve the modified Equation (39) governed by (40) instead of solving (1) governed by (2) and (3).

Remark 3. 

Using a modified collocation method with the HIBCs leads to fewer computations to achieve the desired precision, better numerical stability, and fewer computations to achieve the desired accuracy.

Now, assume the following space functions:

$$\begin{array}{cc}\hfill & L_{\omega (\eta ,t)}^2(\Omega )=\mathrm{span}\{{\theta }_i\left(\eta \right){\vartheta }_j\left(t\right):i,j=0,1,\dots ,\infty \}\hfill \end{array}$$

(42)

$$\begin{array}{cc}& {\Delta }_{\omega (\eta ,t)}(\Omega )=\mathrm{span}\{\psi \in L_{\omega (\eta ,t)}^2(\Omega ):\psi (\eta ,0)=\psi (0,t)=\psi (1,t)=0\},\hfill \end{array}$$

(43)

where $\omega (\eta ,t)={\omega }_1\left(\eta \right){\omega }_2\left(t\right)$, and $\Omega =(0,1)\times (0,1).$ Then, any $\psi \in {\Delta }_{\omega (\eta ,t)}(\Omega )$ can be approximated as

$$\psi \approx {\psi }^{\mathcal{K}}=\sum _{i=0}^{\mathcal{K}}\sum _{j=0}^{\mathcal{K}}{c}_{ij}{\theta }_i\left(\eta \right){\vartheta }_j\left(t\right)={\left(\mathit{\theta }\left(\eta \right)\right)}^T\mathit{C}\mathit{\vartheta }\left(t\right),$$

(44)

where $\mathit{\theta }\left(\eta \right)={[{\theta }_0\left(\eta \right),{\theta }_1\left(\eta \right),\dots ,{\theta }_{\mathcal{K}}\left(\eta \right)]}^T,\mathit{\vartheta }\left(t\right)={[{\vartheta }_0\left(t\right),{\vartheta }_1\left(t\right),\dots ,{\vartheta }_{\mathcal{K}}\left(t\right)]}^T,$ and $\mathit{C}={\left(c_{ij}\right)}_{0\le i,j\le \mathcal{K}}$ is the unknown matrix whose order is ${(\mathcal{K}+1)}^2$.

• The residual $\mathsf{R}(\eta ,t)$ of Equation (39) is expressed as

$$\mathsf{R}(\eta ,t)=D_t^{\alpha }{\psi }^{\mathcal{K}}-{\psi }_{\eta \eta }^{\mathcal{K}}-{\psi }^{\mathcal{K}}({\psi }^{\mathcal{K}}-\epsilon )(1-{\psi }^{\mathcal{K}})-g(\eta ,t).$$

(45)

Utilizing Remarks 1 and 2 alongside the expansion (44), we can express $\mathsf{R}(\eta ,t)$, as defined in (45), in the subsequent matrix form:

$$\begin{array}{cc}\hfill \mathsf{R}(\eta ,t)& ={\left(\mathit{\theta }\left(\eta \right)\right)}^T\mathit{C}\left(\mathit{B}\mathit{\vartheta }\left(t\right)+\mathit{\lambda }\right)-{\left({\mathit{A}}^2\mathit{\theta }\left(\eta \right)+\mathit{A}\mathit{\mu }+{\mathit{\mu }}^{\prime }\right)}^T\mathit{C}\mathit{\vartheta }\left(t\right)\hfill \\ & -{\left(\mathit{\theta }\left(\eta \right)\right)}^T\mathit{C}\mathit{\vartheta }\left(t\right)\left({\left(\mathit{\theta }\left(\eta \right)\right)}^T\mathit{C}\mathit{\vartheta }\left(t\right)-\epsilon \right)\left(1-{\left(\mathit{\theta }\left(\eta \right)\right)}^T\mathit{C}\mathit{\vartheta }\left(t\right)\right)-g(\eta ,t)\hfill \end{array}$$

(46)

The application of the spectral collocation method at certain collocation points $({\eta }_i,t_j)$ produces

$$\mathsf{R}({\eta }_i,t_j)=0,i,j=2,3,\dots ,\mathcal{K}+2,$$

(47)

where $\{({\eta }_i,t_j):i,j=2,3,\dots ,\mathcal{K}+2\}$ are the roots of $({\theta }_{\mathcal{K}+2}\left(\eta \right),{\vartheta }_{\mathcal{K}+2}\left(t\right))$. We may employ Newton’s iterative method to numerically address the nonlinear system of Equation (47), which has a dimension of ${(\mathcal{K}+1)}^2$ in the unknowns $c_{ij}$.

Remark 4. 

The term $g(\eta ,t)$, which may include Caputo’s FD, is treated as known and evaluated at collocation points $({\eta }_i,t_j)$ using its analytical form; fractional derivatives are computed numerically using Mathematica before substituting it into the nonlinear system.

4. The Error Analysis

This section focuses on the error analysis of the double expansion utilized for approximation.

Lemma 1. 

The following inequalities are satisfied in the interval $[0, 1]$:

$$\begin{array}{cc}\hfill & |{\theta }_i\left(\eta \right)|<{\displaystyle \frac{1}{4}},\forall i\ge 0,\hfill \end{array}$$

(48)

$$\begin{array}{cc}& |{\vartheta }_i\left(t\right)|\le 1,\forall i\ge 0.\hfill \end{array}$$

(49)

Proof. 

To prove the first part, Equation (11) enables one to write

$$\begin{array}{cc}\hfill |{\theta }_i\left(\eta \right)|& =|\eta (1-\eta ){\mathrm{L}}_i^{(0,1)}\left(\eta \right)|\hfill \\ & \le {\displaystyle \frac{1}{4}}\left|{\mathrm{L}}_i^{(0,1)}\left(\eta \right)\right|,\hfill \end{array}$$

(50)

Using the following inequality [38]

$$|{\mathrm{L}}_i^{(0,1)}\left(\eta \right)|\le 1,\forall i\ge 0,$$

(51)

the first part can be obtained.

• To prove the second part, Equation (11) along with the previous inequality enable us to write

$$\begin{array}{cc}\hfill |{\vartheta }_i\left(t\right)|& =|t{\mathrm{L}}_i^{(0,1)}\left(t\right)|\hfill \\ & \le 1,\hfill \end{array}$$

(52)

this completes the proof of the theorem. □

Theorem 3. 

Assume that the expansion $\psi ={\sum }_{i=0}^{\infty }{\sum }_{j=0}^{\infty }{c}_{ij}{\theta }_i\left(\eta \right){\vartheta }_j\left(t\right)$ is satisfied by a function $\psi =\eta t(1-\eta )g_1\left(\eta \right)g_1\left(\eta \right)g_2\left(t\right)\in {\Delta }_{\omega (\eta ,t)}(\Omega ),$ with $g_1\left(\eta \right)$ and $g_2\left(t\right)$ having bounded fourth-order derivatives. After this, the series in (44) converges to ψ. Additionally, the following inequality is satisfied by the following bound on the expansion coefficients in (44).

$$|c_{ij}|\lesssim {\displaystyle \frac{1}{i^3{j}^3}},\forall i,j\ge 4,$$

(53)

where $r_1\lesssim r_2$ indicates that $r_1\le n{r}_2.$ for a constant n.

Proof. 

In light of the orthogonality of ${\theta }_i\left(\eta \right)$ and ${\vartheta }_j\left(t\right)$, it is possible to obtain the following:

$${\displaystyle c_{ij}=(2i+1)(2j+1){\int }_0^1{\int }_0^1\psi {\theta }_i\left(\eta \right){\vartheta }_j\left(t\right)\omega \left(\eta \right)d\eta dt.}$$

(54)

The last equation can be rewritten after using the assumption $\psi =\eta t(1-\eta )g_1\left(\eta \right)g_2\left(t\right),$ as

$${\displaystyle c_{ij}=(2i+1)(2j+1){\int }_0^1{\int }_0^1{g}_1\left(\eta \right)g_2\left(t\right)L_i^{(0,1)}\left(\eta \right)L_j^{(0,1)}\left(t\right)d\eta dt.}$$

(55)

which can be rewritten as

$$c_{ij}={\Lambda }_1\times {\Lambda }_2,$$

(56)

where

$${\displaystyle {\Lambda }_1=(2i+1){\int }_0^1{g}_1\left(\eta \right)L_i^{(0,1)}\left(\eta \right)d\eta ,}$$

(57)

and

$${\displaystyle {\Lambda }_2=(2j+1){\int }_0^1{g}_2\left(t\right)L_j^{(0,1)}\left(t\right)dt.}$$

(58)

Integrating by parts ${\Lambda }_1$ and ${\Lambda }_2$ four times, we obtain

$$\begin{array}{cc}\hfill & {\Lambda }_1=(2i+1){\int }_0^1{g}_1^{\left(4\right)}\left(\eta \right)I_1^{\left(4\right)}\left(\eta \right)d\eta ,\hfill \end{array}$$

(59)

$$\begin{array}{cc}& {\Lambda }_2=(2j+1){\int }_0^1{g}_2^{\left(4\right)}\left(t\right)I_2^{\left(4\right)}\left(t\right)dt,\hfill \end{array}$$

(60)

where

$$I_1^{\left(4\right)}\left(\eta \right)={\displaystyle \frac{1}{2^8}}\sum _{m=0}^4\left({\displaystyle \genfrac{}{}{0pt}{}{4}{m}}\right){(-1)}^m{\displaystyle \frac{(i-2m+\frac{9}{2})\Gamma (i-m+\frac{1}{2})}{\Gamma (i-m+\frac{11}{2})}}{L}_{i+4-2m}^{(0,1)}\left(\eta \right),$$

(61)

and

$$I_2^{\left(4\right)}\left(t\right)={\displaystyle \frac{1}{2^8}}\sum _{m=0}^4\left({\displaystyle \genfrac{}{}{0pt}{}{4}{m}}\right){(-1)}^m{\displaystyle \frac{(i-2m+\frac{9}{2})\Gamma (i-m+\frac{1}{2})}{\Gamma (i-m+\frac{11}{2})}}{L}_{i+4-2m}^{(0,1)}\left(t\right).$$

(62)

Now, imitating similar steps to those in Theorem 4 in Ref. [37], we acquire the desired estimation

$$|c_{ij}|\lesssim {\displaystyle \frac{1}{i^3{j}^3}},\forall i,j\ge 4.$$

(63)

□

Remark 5. 

If we follow the same principles as those for Theorem 3, we will have the following inequalities:

$$|c_{0j}|\lesssim {\displaystyle \frac{1}{j^3}},|c_{1j}|\lesssim {\displaystyle \frac{1}{j^3}},|c_{2j}|\lesssim {\displaystyle \frac{1}{j^3}},\left|c_{3j}\right|\lesssim {\displaystyle \frac{1}{j^3}},\forall j>3,$$

(64)

and

$$|c_{i0}|\lesssim {\displaystyle \frac{1}{i^3}},|c_{i1}|\lesssim {\displaystyle \frac{1}{i^3}},|c_{i2}|\lesssim {\displaystyle \frac{1}{i^3}},\left|c_{i3}\right|\lesssim {\displaystyle \frac{1}{i^3}},\forall i>3.$$

(65)

Theorem 4. 

The truncation error can be approximated as

$$|\psi -{\psi }^{\mathcal{K}}|\lesssim {\displaystyle \frac{1}{{\mathcal{K}}^2}}.$$

(66)

Proof. 

First, we can write

$$\begin{array}{cc}\hfill |\psi -{\psi }^{\mathcal{K}}|& \le \left|\sum _{j=\mathcal{K}+1}^{\infty }(c_{0j}{\theta }_0\left(\eta \right)+c_{1j}{\theta }_1\left(\eta \right)+c_{2j}{\theta }_2\left(\eta \right)+c_{3j}{\theta }_3\left(\eta \right)){\vartheta }_j\left(t\right)\right|\hfill \\ & +\left|\sum _{i=\mathcal{K}+1}^{\infty }(c_{i0}{\vartheta }_0\left(t\right)+c_{i1}{\vartheta }_1\left(t\right)+c_{i2}{\vartheta }_2\left(t\right)+c_{i3}{\vartheta }_3\left(t\right)){\theta }_i\left(\eta \right)\right|\hfill \\ & +\left|\sum _{i=4}^{\mathcal{K}}\sum _{j=\mathcal{K}+1}^{\infty }{c}_{ij}{\theta }_i\left(\xi \right){\vartheta }_j\left(t\right)\right|+\left|\sum _{i=\mathcal{K}+1}^{\infty }\sum _{j=4}^{\infty }{c}_{ij}{\theta }_i\left(\xi \right){\vartheta }_j\left(t\right)\right|.\hfill \end{array}$$

(67)

With the aid of Lemma 1; Theorem 3; and Equations (64) and (65), the last equation becomes

$$\begin{array}{cc}\hfill |\psi -{\psi }^{\mathcal{K}}|\lesssim & \sum _{i=\mathcal{K}+1}^{\infty }\sum _{j=4}^{\infty }{\displaystyle \frac{1}{i^3{j}^3}}+\sum _{j=\mathcal{K}+1}^{\infty }{\displaystyle \frac{1}{j^3}}\hfill \\ & +\sum _{i=4}^{\mathcal{K}}\sum _{j=\mathcal{K}+1}^{\infty }{\displaystyle \frac{1}{i^3{j}^3}}+\sum _{i=\mathcal{K}+1}^{\infty }{\displaystyle \frac{1}{i^3}}.\hfill \\ \end{array}$$

(68)

Now, noting the inequality

$${\displaystyle \frac{1}{i^3}}<{\displaystyle \frac{1}{i(i^2-1)}},\forall i>1,$$

we acquire

$$\begin{array}{cc}& \sum _{i=\mathcal{K}+1}^{\infty }{\displaystyle \frac{1}{i\left(i^2-1\right)}}={\displaystyle \frac{1}{2{\mathcal{K}}^2+2\mathcal{K}}}<{\displaystyle \frac{1}{{\mathcal{K}}^2}},\forall \mathcal{K}>0,\hfill \\ & \sum _{i=4}^{\mathcal{K}}{\displaystyle \frac{1}{i\left(i^2-1\right)}}={\displaystyle \frac{(\mathcal{K}-3)(\mathcal{K}+4)}{24\mathcal{K}(\mathcal{K}+1)}}<{\displaystyle \frac{1}{24}},\forall \mathcal{K}>0,\hfill \\ & \sum _{i=4}^{\infty }{\displaystyle \frac{1}{i\left(i^2-1\right)}}={\displaystyle \frac{1}{24}}.\hfill \end{array}$$

(69)

Inserting Equation (69) into Equation (68), we obtain

$$|\psi -{\psi }^{\mathcal{K}}|\lesssim {\displaystyle \frac{1}{{\mathcal{K}}^2}}.$$

□

Theorem 5 (Stability).

Under the assumptions of Theorem 3, we have

$$\left|{\psi }^{\mathcal{K}+1}-{\psi }^{\mathcal{K}}\right|\lesssim {\displaystyle \frac{1}{{\mathcal{K}}^2}}.$$

(70)

Proof. 

Applying the following inequality and Theorem 4 yields the desired result

$$\begin{array}{cc}\hfill \left|{\psi }^{\mathcal{K}+1}-{\psi }^{\mathcal{K}}\right|& \le \left|\psi -{\psi }^{\mathcal{K}}\right|+\left|\psi -{\psi }^{\mathcal{K}+1}\right|\hfill \\ & \lesssim {\displaystyle \frac{1}{{\mathcal{K}}^2}}.\hfill \end{array}$$

(71)

This concludes the proof of this theorem. □

5. Illustrative Examples

In this section, we present some numerical examples to demonstrate the accuracy and efficiency of the suggested numerical algorithm by using the absolute error ($\mathsf{AE}$) and the $L^{\infty }$ error

$$\begin{array}{cc}\hfill & \mathsf{AE}=\left|u_{exact}-u_{approximate}\right|,\hfill \end{array}$$

(72)

$$\begin{array}{cc}& L^{\infty }error=\underset{(\eta ,t)\in \Omega }{max}\left|\mathsf{AE}\right|.\hfill \end{array}$$

(73)

All codes were written and debugged using Mathematica 11 on an HP Z420 Workstation, with an Intel(R) Xeon(R) CPU E5-1620 processor, v2, 3.70 GHz; 16 GB of RAM, DDR3; and 512 GB of storage.

Example 1 

([32,33]). Consider the $\mathsf{TFFNDP}$

$$D_t^{\alpha }u=u_{\eta \eta }+u(u-\epsilon )(1-u)+f(\eta ,t),0<\alpha \le 1,$$

(74)

constrained with

$$\begin{array}{cc}& u(\eta ,0)={\displaystyle \frac{1}{2}}tanh\left({\displaystyle \frac{\eta }{2\sqrt{2}}}\right)+{\displaystyle \frac{1}{2}},0<\eta \le 1,\hfill \\ & u(0,t)={\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}tanh\left({\displaystyle \frac{t}{4}}\right),u(1,t)={\displaystyle \frac{1}{2}}tanh\left({\displaystyle \frac{1}{4}}\left(\sqrt{2}-t\right)\right)+{\displaystyle \frac{1}{2}},0<t\le 1,\hfill \end{array}$$

(75)

where $f(\eta ,t)$ is selected such that the exact solution of this problem is $u={\displaystyle \frac{1}{2}}tanh\left({\displaystyle \frac{1}{4}}\left(\sqrt{2}\eta -t\right)\right)+{\displaystyle \frac{1}{2}}$.

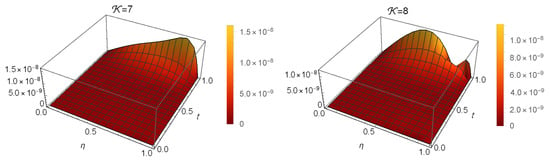
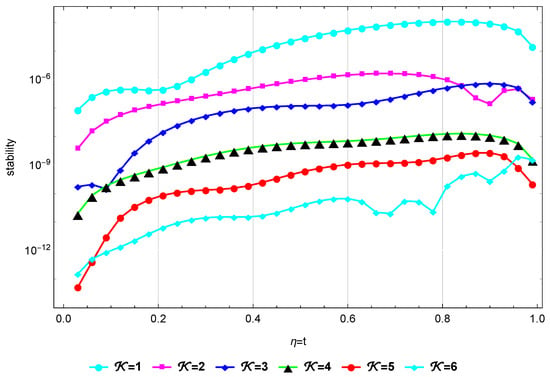
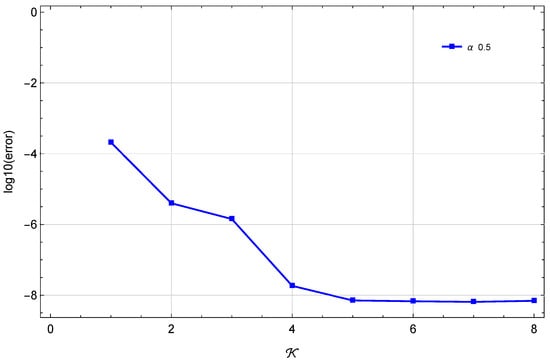
At $\epsilon =1$, the $L^{\infty }$ error at various α values is compared between our technique at $\mathcal{K}=7$ and the method described in [32] in Table 1. The absolute errors ($\mathsf{AE}$s) at $\alpha =0.65$ and $\epsilon =0.1$ are depicted in Figure 1. Table 2 presents a comparison of the $\mathsf{AE}s$ between our method and method in [33] at $\alpha =1$ and $\epsilon =1$. The $\mathsf{AE}s$ are presented in Table 3 at varying values of ε when $\alpha =0.65$ and $\mathcal{K}=7$. Figure 2 illustrates the stability $|{\psi }^{\mathcal{K}+1}-{\psi }^{\mathcal{K}}|$ at $\eta =t$ and $\alpha =0.5$. Finally, Figure 3 illustrates the Log10(maximum $\mathsf{AE}$) at different values of $\mathcal{K}$ when $\alpha =0.5$ and $\epsilon =1$. The results of this method are exceedingly near to the precise solution, as evidenced by these findings.

Table 1. $L^{\infty }$ errors of Example 1.

t	Method in [32]				Presented Technique at $\mathcal{K}=7$
	$\alpha =0.25$	$\alpha =0.5$	$\alpha =0.75$	$\alpha =1$	$\alpha =0.25$	$\alpha =0.5$	$\alpha =0.75$	$\alpha =1$
$0.2$	$6.166\times {10}^{-4}$	$3.14\times {10}^{-4}$	$1.28\times {10}^{-4}$	$3.64\times {10}^{-5}$	$2.41\times {10}^{-10}$	$3.23047\times {10}^{-10}$	$3.98\times {10}^{-10}$	$4.66\times {10}^{-10}$
$0.4$	$2.99\times {10}^{-4}$	$2.30\times {10}^{-4}$	$1.41\times {10}^{-4}$	$1.57\times {10}^{-4}$	$2.071\times {10}^{-10}$	$1.87\times {10}^{-10}$	$1.52\times {10}^{-10}$	$1.41\times {10}^{-10}$
$0.6$	$4.323\times {10}^{-5}$	$7.29\times {10}^{-5}$	$5.034\times {10}^{-5}$	$1.59\times {10}^{-4}$	$1.57\times {10}^{-10}$	$1.49\times {10}^{-10}$	$1.58\times {10}^{-10}$	$2.72\times {10}^{-10}$
$0.8$	$9.45\times {10}^{-5}$	$1.61\times {10}^{-5}$	$4.743\times {10}^{-5}$	$6.20\times {10}^{-5}$	$6.03\times {10}^{-10}$	$1.11\times {10}^{-9}$	$1.81\times {10}^{-9}$	$2.64\times {10}^{-9}$
1	$7.90\times {10}^{-6}$	$8.04\times {10}^{-6}$	$2.664\times {10}^{-6}$	$6.82\times {10}^{-6}$	$5.76\times {10}^{-9}$	$1.07\times {10}^{-8}$	$1.92\times {10}^{-8}$	$3.35\times {10}^{-8}$

Figure 1. The $\mathsf{AE}$ of Example 1 at $\alpha =0.65$ and $\epsilon =0.1.$.

Table 2. Comparison of $\mathsf{AE}s$ for Example 1 at $\alpha =1$.

$\mathit{\eta }$	t	Method in [33]	Proposed Method at $\mathcal{K}=7$
0.1	0.2	$5.26\times {10}^{-8}$	$8.90\times {10}^{-11}$
	0.4	$5.11\times {10}^{-7}$	$2.47\times {10}^{-11}$
	0.6	$9.06\times {10}^{-7}$	$4.48\times {10}^{-11}$
	0.8	$2.40\times {10}^{-6}$	$5.87\times {10}^{-10}$
0.3	0.2	$1.95\times {10}^{-7}$	$2.61\times {10}^{-10}$
	0.4	$2.80\times {10}^{-6}$	$7.71\times {10}^{-11}$
	0.6	$1.26\times {10}^{-5}$	$1.43\times {10}^{-10}$
	0.8	$3.45\times {10}^{-5}$	$1.65\times {10}^{-9}$
0.5	0.2	$3.21\times {10}^{-7}$	$4.02\times {10}^{-10}$
	0.4	$4.86\times {10}^{-6}$	$1.30\times {10}^{-10}$
	0.6	$2.32\times {10}^{-5}$	$2.49\times {10}^{-10}$
	0.8	$6.86\times {10}^{-5}$	$2.41\times {10}^{-9}$
0.7	0.2	$4.22\times {10}^{-7}$	$4.66\times {10}^{-10}$
	0.4	$6.54\times {10}^{-6}$	$1.14\times {10}^{-10}$
	0.6	$3.20\times {10}^{-5}$	$2.27\times {10}^{-10}$
	0.8	$9.72\times {10}^{-5}$	$2.64\times {10}^{-9}$
0.9	0.2	$4.9\times {10}^{-7}$	$3.70\times {10}^{-10}$
	0.4	$7.72\times {10}^{-6}$	$1.20\times {10}^{-10}$
	0.6	$3.83\times {10}^{-5}$	$1.78\times {10}^{-10}$
	0.8	$1.18\times {10}^{-4}$	$1.67\times {10}^{-9}$

Table 3. The $\mathsf{AE}$ of Example 1 at $\alpha =0.65$.

$\mathit{\eta }=\mathit{t}$	$\mathit{\epsilon }=0.3$	CPU Time	$\mathit{\epsilon }=0.6$	CPU Time	$\mathit{\epsilon }=0.9$	CPU Time
0.1	$4.97520\times {10}^{-11}$		$4.79537\times {10}^{-11}$		$4.62389\times {10}^{-11}$
0.2	$9.34854\times {10}^{-11}$		$8.96371\times {10}^{-11}$		$8.60031\times {10}^{-11}$
0.3	$1.09946\times {10}^{-10}$		$1.0548\times {10}^{-10}$		$1.01279\times {10}^{-10}$
0.4	$1.21079\times {10}^{-10}$		$1.16213\times {10}^{-10}$		$1.1163\times {10}^{-10}$
0.5	$8.43561\times {10}^{-11}$	24.875	$8.06663\times {10}^{-11}$	25.827	$7.72103\times {10}^{-11}$	26.189
0.6	$1.26159\times {10}^{-11}$		$1.32163\times {10}^{-11}$		$1.37233\times {10}^{-11}$
0.7	$4.20313\times {10}^{-10}$		$4.14684\times {10}^{-10}$		$4.09208\times {10}^{-10}$
0.8	$1.26053\times {10}^{-9}$		$1.24131\times {10}^{-9}$		$1.22274\times {10}^{-9}$
0.9	$1.71685\times {10}^{-9}$		$1.68629\times {10}^{-9}$		$1.65686\times {10}^{-9}$

Figure 2. Stability $|{\psi }^{\mathcal{K}+1}-{\psi }^{\mathcal{K}}|$ at $\eta =t$ for Example 1.

Figure 3. The Log10(maximum $\mathsf{AE}$) at $\alpha =0.5$ of Example 1.

Example 2 

([31,32,33]). Consider the $\mathsf{TFFNDP}$

$$D_t^{\alpha }u=u_{\eta \eta }+u(u-\epsilon )(1-u)+f(\eta ,t),0<\alpha \le 1,$$

(76)

constrained with

$$\begin{array}{cc}& u(\eta ,0)={\displaystyle \frac{1}{e^{-\frac{\eta }{\sqrt{2}}}+1}},0<\eta \le 1,\hfill \\ & u(0,t)={\displaystyle \frac{1}{e^{\left(\sqrt{2}+\frac{1}{\sqrt{2}}\right)t}+1}},u(1,t)={\displaystyle \frac{1}{e^{\left(\sqrt{2}+\frac{1}{\sqrt{2}}\right)t-\frac{1}{\sqrt{2}}}+1}},0<t\le 1,\hfill \end{array}$$

(77)

where $f(\eta ,t)$ is selected such that the exact solution of (76) is $u={\displaystyle \frac{1}{1+e^{\left(\frac{1}{\sqrt{2}}-\sqrt{2}\epsilon \right)t-\frac{\eta }{\sqrt{2}}}}}$.

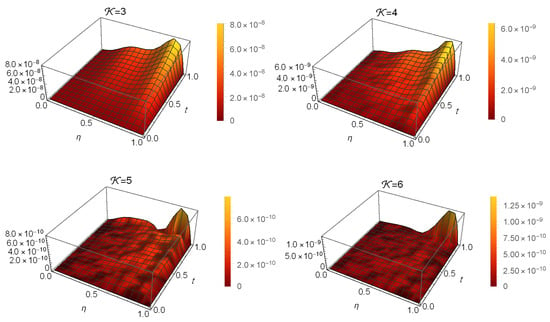
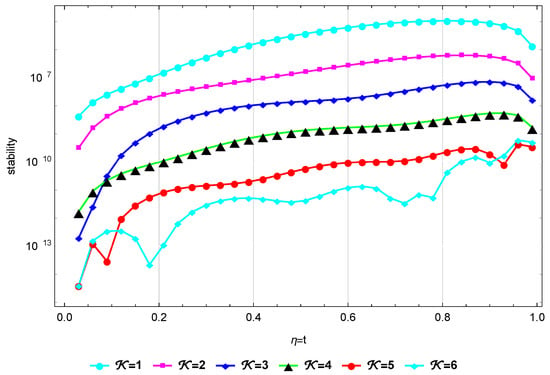
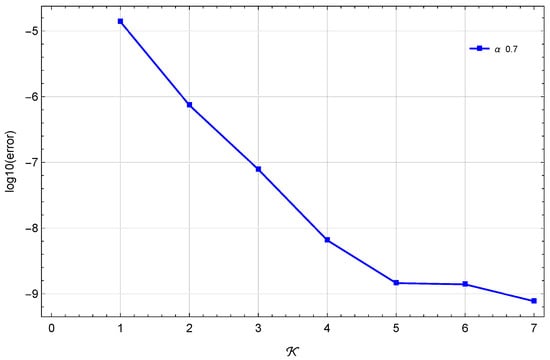
In Table 4 and Table 5, we compare the $\mathsf{AE}s$ of our technique at $\mathcal{K}=11$ with those in [32,33] at different α and ε values. Table 6 also shows how the proposed technique and the method in [32] compare in terms of the $L^{\infty }$ error at different α values. When $\alpha =0.7$ and $\epsilon =0.45$, Figure 4 illustrates the $\mathsf{AE}$ at different values of $\mathcal{K}$. Figure 5 illustrates the stability $|{\psi }^{\mathcal{K}+1}-{\psi }^{\mathcal{K}}|$ at $\eta =t$ and $\alpha =0.7$. Finally, Figure 6 illustrates the Log10(maximum $\mathsf{AE}$) at different values of $\mathcal{K}$ when $\alpha =0.7$ and $\epsilon =1$. These findings show that this method’s results are quite near to the exact solution.

Table 4. Comparison of $\mathsf{AE}$s of Example 2 at $\alpha =1,\epsilon =-1$.

$(\mathit{\eta },\mathit{t})$	Method in [33]	Method in [32]	Method in [31]	Proposed Method at $\mathcal{K}=11$	Our CPU Time
(0.001, 0.001)	$1.5\times {10}^{-3}$	$1.0\times {10}^{-9}$	$4.1\times {10}^{-10}$	$2.4\times {10}^{-13}$	33.891
(0.002, 0.002)	$3.0\times {10}^{-3}$	$8.7\times {10}^{-11}$	$5.2\times {10}^{-10}$	$3.1\times {10}^{-14}$
(0.003, 0.003)	$4.5\times {10}^{-3}$	$1.3\times {10}^{-9}$	$5.5\times {10}^{-10}$	$2.9\times {10}^{-12}$
(0.004, 0.004)	$6.0\times {10}^{-3}$	$3.3\times {10}^{-9}$	$5.3\times {10}^{-10}$	$1.0\times {10}^{-11}$
(0.005, 0.005)	$7.5\times {10}^{-3}$	$4.5\times {10}^{-9}$	$4.9\times {10}^{-10}$	$2.5\times {10}^{-11}$
(0.006, 0.006)	$9.1\times {10}^{-3}$	$5.8\times {10}^{-9}$	$4.4\times {10}^{-10}$	$4.5\times {10}^{-11}$
(0.007, 0.007)	$1.0\times {10}^{-2}$	$1.1\times {10}^{-8}$	$3.9\times {10}^{-10}$	$7.1\times {10}^{-11}$
(0.008, 0.008)	$1.2\times {10}^{-2}$	$1.2\times {10}^{-8}$	$3.4\times {10}^{-10}$	$1.0\times {10}^{-10}$
(0.009, 0.009)	$1.3\times {10}^{-2}$	$6.5\times {10}^{-9}$	$3.0\times {10}^{-10}$	$1.3\times {10}^{-10}$
(0.01, 0.01)	$1.5\times {10}^{-2}$	$1.4\times {10}^{-9}$	$2.7\times {10}^{-10}$	$1.5\times {10}^{-10}$

Table 5. Comparison of $\mathsf{AE}$s of Example 2 at $\alpha =0.5,\epsilon =0.45$.

$(\mathit{\eta },\mathit{t})$	Method in [33]	Method in [32]	Method in [31]	Proposed Method at $\mathcal{K}=7$	Our CPU Time
(0.001, 0.001)	$2.8\times {10}^{-2}$	$8.7\times {10}^{-10}$	$5.7\times {10}^{-13}$	$1.0\times {10}^{-13}$	37.139
(0.002, 0.002)	$4.1\times {10}^{-2}$	$4.3\times {10}^{-10}$	$7.6\times {10}^{-13}$	$4.1\times {10}^{-13}$
(0.003, 0.003)	$5.3\times {10}^{-2}$	$1.4\times {10}^{-8}$	$1.2\times {10}^{-12}$	$9.0\times {10}^{-13}$
(0.004, 0.004)	$6.2\times {10}^{-2}$	$6.6\times {10}^{-8}$	$1.8\times {10}^{-12}$	$1.5\times {10}^{-12}$
(0.005, 0.005)	$6.9\times {10}^{-2}$	$1.8\times {10}^{-9}$	$2.6\times {10}^{-12}$	$2.3\times {10}^{-12}$
(0.006, 0.006)	$8.0\times {10}^{-2}$	$4.1\times {10}^{-9}$	$3.6\times {10}^{-12}$	$3.2\times {10}^{-12}$
(0.007, 0.007)	$8.7\times {10}^{-2}$	$2.0\times {10}^{-9}$	$4.6\times {10}^{-12}$	$4.2\times {10}^{-12}$
(0.008, 0.008)	$9.4\times {10}^{-2}$	$3.5\times {10}^{-10}$	$5.8\times {10}^{-12}$	$5.3\times {10}^{-12}$
(0.009, 0.009)	$1.0\times {10}^{-2}$	$7.4\times {10}^{-10}$	$7.1\times {10}^{-12}$	$6.5\times {10}^{-12}$
(0.01, 0.01)	$1.1\times {10}^{-2}$	$1.0\times {10}^{-9}$	$8.4\times {10}^{-12}$	$7.7\times {10}^{-12}$

Table 6. $L^{\infty }$ errors of Example 2.

t	Method in [32]		Proposed Method
	$\alpha =1,\epsilon =-1$	$\alpha =0.5,\epsilon =0.45$	$\alpha =1,\epsilon =-1,\mathcal{K}=11$	$\alpha =0.5,\epsilon =0.45,\mathcal{K}=7$
$0.02$	$2.00\times {10}^{-8}$	$6.58\times {10}^{-10}$	$3.10\times {10}^{-9}$	$3.23\times {10}^{-11}$
$0.04$	$1.23\times {10}^{-8}$	$4.18\times {10}^{-10}$	$2.31\times {10}^{-9}$	$5.12\times {10}^{-11}$
$0.06$	$9.86\times {10}^{-8}$	$4.33\times {10}^{-10}$	$1.66\times {10}^{-9}$	$6.26\times {10}^{-11}$
$0.08$	$2.40\times {10}^{-9}$	$5.09\times {10}^{-10}$	$1.31\times {10}^{-9}$	$7.00\times {10}^{-11}$
$0.11$	$1.26\times {10}^{-9}$	$2.45\times {10}^{-10}$	$9.66\times {10}^{-10}$	$7.60\times {10}^{-11}$

Figure 4. The $\mathsf{AE}$ of Example 2 at $\alpha =0.7,\epsilon =0.45$.

Figure 5. Stability $|{\psi }^{\mathcal{K}+1}-{\psi }^{\mathcal{K}}|$ at $\eta =t$ for Example 2.

Figure 6. The Log10(maximum $\mathsf{AEs}$) at $\alpha =0.7$ of Example 2.

Example 3 

([32]). Consider the $\mathsf{TFFNDP}$

$$D_t^{\alpha }u=u_{\eta \eta }+u(u-\epsilon )(1-u)+f(\eta ,t),0<\alpha \le 1,$$

(78)

constrained with

$$\begin{array}{cc}& u(\xi ,0)={\displaystyle \frac{1}{2}}tanh\left({\displaystyle \frac{\eta }{2\sqrt{2}}}\right)+{\displaystyle \frac{1}{2}},0<\eta \le 1,\hfill \\ & u(0,t)={\displaystyle \frac{1}{2}}tanh\left({\displaystyle \frac{t}{4}}\right)+{\displaystyle \frac{1}{2}},u(1,t)={\displaystyle \frac{1}{2}}tanh\left({\displaystyle \frac{1}{4}}\left(t+\sqrt{2}\right)\right)+{\displaystyle \frac{1}{2}},0<t\le 1,\hfill \end{array}$$

(79)

where $f(\eta ,t)$ is selected such that the exact solution of this problem is $u={\displaystyle \frac{1}{2}}tanh\left({\displaystyle \frac{1}{4}}\left(t+\sqrt{2}\eta \right)\right)+{\displaystyle \frac{1}{2}}$.

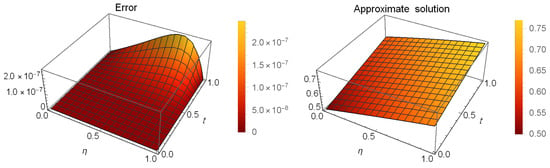
Table 7 compares the $L^{\infty }$ error for our technique at $\mathcal{K}=7$ with that of [32] at different α values when $\epsilon =0$. Figure 7 shows the $\mathsf{AE}$ (left) and estimated solution ($\mathsf{AS}$) (right) at $\alpha =0.3,\epsilon =0.5$ for $\mathcal{K}=7$. Table 8 shows the $\mathsf{AE}$ at $\alpha =0.8$ and different values of ε at $\mathcal{K}=7$. Table 9 presents the $\mathsf{AE}$ at different values of α and ϵ when $\mathcal{K}=7$.

Table 7. $L^{\infty }$ errors of Example 3.

t	Method in [32]				Proposed Technique at $\mathcal{K}=7$
	$\alpha ={\displaystyle \frac{25}{100}}$	$\alpha ={\displaystyle \frac{5}{10}}$	$\alpha ={\displaystyle \frac{75}{100}}$	$\alpha =1$	$\alpha ={\displaystyle \frac{25}{100}}$	$\alpha ={\displaystyle \frac{5}{10}}$	$\alpha ={\displaystyle \frac{75}{100}}$	$\alpha =1$
$0.2$	$9.50\times {10}^{-4}$	$6.34\times {10}^{-4}$	$2.56\times {10}^{-4}$	$8.71\times {10}^{-6}$	$1.56\times {10}^{-9}$	$2.61\times {10}^{-9}$	$4.20\times {10}^{-9}$	$6.468\times {10}^{-9}$
$0.4$	$7.42\times {10}^{-4}$	$7.79\times {10}^{-4}$	$4.51\times {10}^{-4}$	$3.39\times {10}^{-5}$	$7.31\times {10}^{-9}$	$1.14\times {10}^{-8}$	$1.73\times {10}^{-8}$	$2.55\times {10}^{-8}$
$0.6$	$5.77\times {10}^{-4}$	$5.47\times {10}^{-4}$	$4.56\times {10}^{-4}$	$6.51\times {10}^{-5}$	$2.66\times {10}^{-8}$	$4.04\times {10}^{-8}$	$5.97\times {10}^{-8}$	$8.58\times {10}^{-8}$
$0.8$	$3.26\times {10}^{-4}$	$6.66\times {10}^{-5}$	$1.64\times {10}^{-4}$	$2.61\times {10}^{-4}$	$8.37\times {10}^{-8}$	$1.23\times {10}^{-7}$	$1.78\times {10}^{-7}$	$2.51\times {10}^{-7}$
1	$1.17\times {10}^{-6}$	$3.61\times {10}^{-6}$	$4.25\times {10}^{-6}$	$3.06\times {10}^{-6}$	$2.34\times {10}^{-7}$	$3.34\times {10}^{-7}$	$4.70\times {10}^{-7}$	$6.55\times {10}^{-7}$

Figure 7. The $\mathsf{AE}$ (left) and $\mathsf{AS}$ (right) of Example 3 at $\alpha =0.3,\epsilon =0.5$, when $\mathcal{K}=7$.

Table 8. The $\mathsf{AE}$ of Example 3 at $\alpha =0.8$.

$\mathit{\eta }=\mathit{t}$	$\mathit{\epsilon }=0.3$	CPU Time	$\mathit{\epsilon }=0.6$	CPU Time	$\mathit{\epsilon }=0.9$	CPU Time
0.1	$1.33026\times {10}^{-10}$		$1.29237\times {10}^{-10}$		$1.25581\times {10}^{-10}$
0.2	$7.95432\times {10}^{-10}$		$7.7033\times {10}^{-10}$		$7.46275\times {10}^{-10}$
0.3	$2.78714\times {10}^{-9}$		$2.70253\times {10}^{-9}$		$2.62156\times {10}^{-9}$
0.4	$8.16272\times {10}^{-9}$		$7.938\times {10}^{-9}$		$7.72269\times {10}^{-9}$
0.5	$2.12029\times {10}^{-8}$	83.03	$2.06932\times {10}^{-8}$	90.893	$2.0204\times {10}^{-8}$	84.86
0.6	$5.00448\times {10}^{-8}$		$4.90351\times {10}^{-8}$		$4.80639\times {10}^{-8}$
0.7	$1.05611\times {10}^{-7}$		$1.03882\times {10}^{-7}$		$1.02214\times {10}^{-7}$
0.8	$1.88777\times {10}^{-7}$		$1.86351\times {10}^{-7}$		$1.84007\times {10}^{-7}$
0.9	$2.41631\times {10}^{-7}$		$2.39296\times {10}^{-7}$		$2.37035\times {10}^{-7}$

Table 9. The $\mathsf{AE}$ of Example 3 at $\mathcal{K}=7$.

$\mathit{\eta }=\mathit{t}$	$\mathit{\alpha }=0.01,\mathit{\epsilon }=0.01$	CPU Time	$\mathit{\alpha }=0.02,\mathit{\epsilon }=0.02$	CPU Time	$\mathit{\alpha }=0.03,\mathit{\epsilon }=0.001$	CPU Time
0.1	$3.67187\times {10}^{-11}$		$3.75785\times {10}^{-11}$		$3.86181\times {10}^{-11}$
0.2	$2.34813\times {10}^{-11}$		$2.39402\times {10}^{-10}$		$2.45066\times {10}^{-10}$
0.3	$8.62635\times {10}^{-10}$		$8.78073\times {10}^{-10}$		$8.97186\times {10}^{-10}$
0.4	$2.52802\times {10}^{-9}$		$2.57116\times {10}^{-9}$		$2.62409\times {10}^{-9}$
0.5	$6.49957\times {10}^{-9}$	26.094	$6.60822\times {10}^{-9}$	25.968	$6.73914\times {10}^{-9}$	26.047
0.6	$1.5112\times {10}^{-8}$		$1.53617\times {10}^{-8}$		$1.56557\times {10}^{-8}$
0.7	$3.16022\times {10}^{-8}$		$3.21185\times {10}^{-8}$		$3.27112\times {10}^{-8}$
0.8	$5.66429\times {10}^{-8}$		$5.75556\times {10}^{-8}$		$5.85777\times {10}^{-8}$
0.9	$7.33268\times {10}^{-8}$		$7.44858\times {10}^{-8}$		$7.57545\times {10}^{-8}$

Example 4. 

Consider the $\mathsf{TFFNDP}$

$$D_t^{\alpha }u=u_{\eta \eta }+u(u-\epsilon )(1-u)+t^2\left(1-t^2\right){\eta }^2\left(1-{\eta }^2\right),0<\alpha \le 1,$$

(80)

constrained with

$$\begin{array}{cc}& u(\xi ,0)=0,0<\eta \le 1,\hfill \\ & u(0,t)=u(1,t)=0,0<t\le 1,\hfill \end{array}$$

(81)

Since the exact solution is not available, let us define the following absolute residual error norm:

$$ARE=\underset{(\eta ,t)\in (0,1)\times (0,1)}{max}\left|D_t^{\alpha }{u}^{\mathcal{K}}-u_{\eta \eta }-u^{\mathcal{K}}(u^{\mathcal{K}}-\epsilon )(1-u^{\mathcal{K}})-t^2\left(1-t^2\right){\eta }^2\left(1-{\eta }^2\right)\right|.$$

(82)

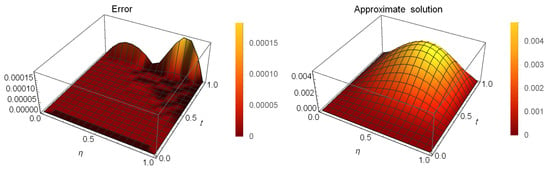
and apply the presented method at $\alpha =0.9$ and $ϵ=0.01$ at different values of $\eta =t$ to obtain Table 10, which illustrates the ARE at various values of $\mathcal{K}$. Figure 8 illustrates the ARE and the approximate solution at $\alpha =0.9,ϵ=0.01$, and $\mathcal{K}=14$.

Table 10. The ARE for Example 4 at $\alpha =0.9$ and $ϵ=0.01$.

$\mathit{\eta }=\mathit{t}$	$\mathcal{K}=7$	$\mathcal{K}=9$	$\mathcal{K}=11$	$\mathcal{K}=14$
0.1	$3.58511\times {10}^{-7}$	$5.8678\times {10}^{-7}$	$1.09412\times {10}^{-8}$	$7.62746\times {10}^{-8}$
0.2	$1.30324\times {10}^{-7}$	$8.73372\times {10}^{-7}$	$3.20856\times {10}^{-7}$	$4.43158\times {10}^{-8}$
0.3	$1.98591\times {10}^{-8}$	$9.20873\times {10}^{-7}$	$3.31491\times {10}^{-7}$	$1.11666\times {10}^{-7}$
0.4	$1.98839\times {10}^{-6}$	$2.48025\times {10}^{-7}$	$1.3223\times {10}^{-7}$	$9.93006\times {10}^{-8}$
0.5	$7.45931\times {10}^{-7}$	$5.6552\times {10}^{-6}$	$1.9082\times {10}^{-7}$	$2.12828\times {10}^{-8}$
0.6	$1.09483\times {10}^{-5}$	$2.21417\times {10}^{-6}$	$3.76167\times {10}^{-7}$	$1.56756\times {10}^{-7}$
0.7	$1.35793\times {10}^{-5}$	$6.06985\times {10}^{-6}$	$1.45322\times {10}^{-6}$	$4.49382\times {10}^{-7}$
0.8	$4.74879\times {10}^{-6}$	$9.235\times {10}^{-6}$	$2.70249\times {10}^{-6}$	$4.10856\times {10}^{-7}$
0.9	$2.6111\times {10}^{-5}$	$1.55784\times {10}^{-5}$	$2.41674\times {10}^{-7}$	$1.93747\times {10}^{-6}$

Figure 8. The ARE and the approximate solution of Example 4 at $\alpha =0.9,ϵ=0.01$, and $\mathcal{K}=14$.

Remark 6. 

The approximate solution at $\alpha =0.9$, $ϵ=0.01$, and $\mathcal{K}=3$ is

$$\begin{array}{cc}& u^3(\eta ,t)=\eta t\left(-0.00169533{\eta }^4+0.00332928{\eta }^3-0.000865217{\eta }^2+0.0000997735\eta \right.\hfill \\ & +\left(-0.0929458{\eta }^4+0.161879{\eta }^3-0.00258051{\eta }^2+0.00255686\eta -0.0689095\right)t^3\hfill \\ & +\left(0.0423435{\eta }^4-0.0335923{\eta }^3-0.0669551{\eta }^2-0.000925701\eta +0.0591296\right)t^2\hfill \\ & \left.+\left(0.0560843{\eta }^4-0.134855{\eta }^3+0.0647677{\eta }^2-0.00181725\eta +0.0158202\right)t-0.000868501\right).\hfill \end{array}$$

(83)

Example 5. 

Consider the $\mathsf{TFFNDP}$

$$D_t^{\alpha }u=u_{\eta \eta }+u(u-\epsilon )(1-u)+f(\eta ,t),0<\alpha \le 1,$$

(84)

constrained with

$$\begin{array}{cc}& u(\eta ,0)=0,0<\eta \le 1,\hfill \\ & u(0,t)=t^{5\alpha },u(1,t)={\displaystyle \frac{t^{5\alpha }}{e}},0<t\le 1,\hfill \end{array}$$

(85)

where $f(\eta ,t)$ is selected such that the exact solution of this problem is $u=e^{-{\eta }^2}{t}^{5\alpha }$ at $\epsilon =1$.

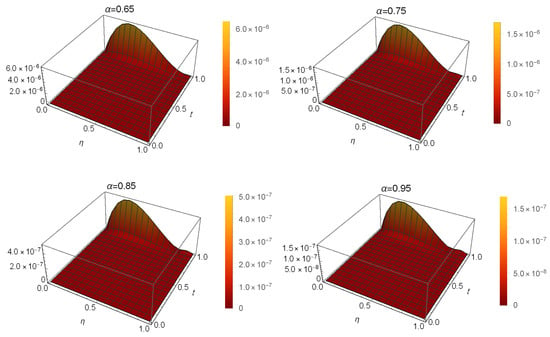
Table 11 presents the $\mathsf{AE}$ at $\alpha =0.5$ and $\mathcal{K}=9$. In addition, Figure 9 illustrates the $\mathsf{AE}$ at different values of α when $\mathcal{K}=9$.

Table 11. The $\mathsf{AE}$ for Example 5 at $\alpha =0.5$ and $\mathcal{K}=9$.

$\mathit{\eta }$	$\mathit{t}=0.2$	$\mathit{t}=0.4$	$\mathit{t}=0.6$	$\mathit{t}=0.8$
0.1	$1.67673\times {10}^{-7}$	$1.44428\times {10}^{-7}$	$2.92782\times {10}^{-7}$	$6.62384\times {10}^{-7}$
0.2	$2.72581\times {10}^{-7}$	$2.26141\times {10}^{-7}$	$4.74903\times {10}^{-7}$	$1.03788\times {10}^{-6}$
0.3	$3.21423\times {10}^{-7}$	$2.56773\times {10}^{-7}$	$5.58722\times {10}^{-7}$	$1.17977\times {10}^{-6}$
0.4	$3.23482\times {10}^{-7}$	$2.48188\times {10}^{-7}$	$5.60807\times {10}^{-7}$	$1.14174\times {10}^{-6}$
0.5	$2.89911\times {10}^{-7}$	$2.12231\times {10}^{-7}$	$5.01144\times {10}^{-7}$	$9.7832\times {10}^{-7}$
0.6	$2.32888\times {10}^{-7}$	$1.60574\times {10}^{-7}$	$4.01155\times {10}^{-7}$	$7.42428\times {10}^{-7}$
0.7	$1.64676\times {10}^{-7}$	$1.04229\times {10}^{-7}$	$2.82315\times {10}^{-6}$	$4.84053\times {10}^{-7}$
0.8	$9.67461\times {10}^{-8}$	$5.30397\times {10}^{-8}$	$1.65031\times {10}^{-6}$	$2.49294\times {10}^{-7}$
0.9	$3.91504\times {10}^{-8}$	$1.5833\times {10}^{-8}$	$6.63186\times {10}^{-8}$	$7.69010\times {10}^{-8}$

Figure 9. The $\mathsf{AE}$ of Example 5 at different values of $\alpha$.

Remark 7. 

The source term $f(\eta ,t)$ that contains Caputo’s FD of the exact solution u for Examples 1, 2, 3, and 5 is evaluated numerically using Mathematica 11.

6. Concluding Remarks

This paper presents and analyzes an accurate solver employing a modified collocation technique for solving the nonlinear inhomogeneous $\mathsf{TFFNDP}$. Specific theoretical findings related to $\mathsf{SLPs}$ were significant in applying our numerical methods to resolve this problem. We designed the proposed numerical method by using the integer derivatives and fractional operational matrices of $\mathsf{SLPs}$. Numerous numerical findings and comparisons were presented to validate the proposed methodology. As expected future work, we think that the presented approach could be extended to treating other fractional-order PDE models [39,40].