Abstract
In this paper, a hierarchical optimization framework combining Bayesian and pseudospectral approaches is developed to solve the challenging problem of hybrid trajectory planning for energy-augmented hypersonic skip–glide vehicles that have plane symmetry. Traditional trajectory optimization methods usually deal with discrete energy injection timing and continuous flight control variables separately, yielding suboptimal solutions. To achieve global optimality, this proposed framework optimizes the discrete and continuous variables simultaneously, conducting Bayesian optimization for discrete global search and hp-adaptive pseudospectral algorithm for local continuous optimization. A rigorous dynamic model, considering Earth’s oblateness, rotation, aerodynamic interactions, and thrust dynamics, is established to ensure high-fidelity trajectory simulation. Numerical simulation through three representative tests indicates significant improvements: The hp-adaptive pseudospectral method achieves over 20% higher computational efficiency and accuracy compared to standard pseudospectral methods. Bayesian optimization demonstrates rapid global convergence within 22 iterations, achieving the optimal single augmentation timing that enhances flight range by up to 55.08%. Further, comprehensive joint optimization with double energy augmentation yields an additional 7.5% range extension compared to randomly selected augmentation timings. The results verify that the proposed hierarchical framework substantially improves the planned trajectory performance and adaptability to the skip–glide trajectories with hybrid maneuver.
1. Introduction
Hypersonic waveriders with plane symmetry, offering possible auxiliary maneuvers, is a crucial direction for future aerospace development. In response to evolving demands on control flexibility for complex environment, recently, hypersonic skip–glide vehicles with midcourse energy augmentation have been proposed, aiming to extend flight range, enhance maneuverability, and mitigate aerodynamic heating. A conceptual illustration of the energy-augmented skip–glide trajectory is shown in Figure 1.
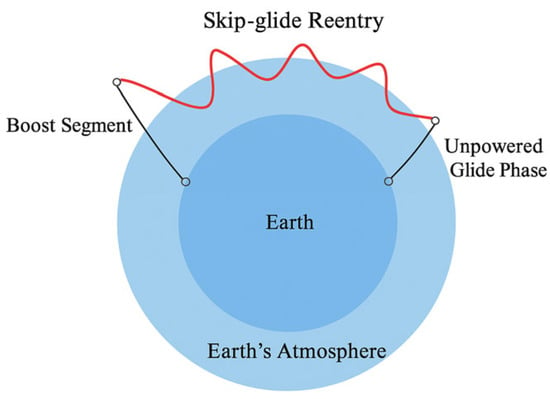
Figure 1.
Conceptual diagram of the energy-augmented skip–glide trajectory.
For planning the skip–glide trajectory problem, conventional methods primarily adjust the angle of attack and the bank angle. However, energy-augmented skip–glide trajectory involves a more complex optimization space, including introduction of propulsion characteristics, energy injection time, and allocation strategy, which challenges traditional continuous optimization methods.
Presently, studies on energy-augmented skip–glide vehicles remain limited. Chai et al. [1] analyzed multiple energy injection strategies, highlighting the trade-off between range extension and thermal load increasement. Feng et al. [2] derived analytical solutions for Sanger-type trajectories, optimizing attack angles and propulsion ignition time to balance range and fuel efficiency. Also, our previous work established an analytical model linking energy injection parameters to reachable range and proposed the concept of a multi-constrained skip–glide corridor to guide the energy augmentation timing [3].
For a corresponding trajectory optimization problem, Zhao et al. [4] employed an indirect method and a conjugate gradient algorithm to optimize multi-ignition trajectories, achieving reduced skip amplitude but prolonged thermal exposure. Huang [5] utilized a segmented dynamic Gaussian pseudospectral method to address discontinuous dynamics under pulsed propulsion, thereby enhancing computational efficiency. Song et al. [6] combined an improved adaptive particle swarm algorithm with segmented pseudospectral methods for system-level optimization, though they did not address energy augmentation timing. Yong et al. [7] proposed a globally optimized energy-augmented trajectory using sequence-segmented Gaussian pseudospectral optimization, which improved flight performance but lacked a specified timing strategy.
Clearly, existing studies demonstrate the potential value of energy-augmented skip–glide trajectories and reveal challenges in joint optimization with both discrete and continuous variables. A key variable is energy augmentation timing, which should be addressed reasonably.
To bridge this gap, the present study proposes a nested hybrid optimization framework that integrates Bayesian optimization with an adaptive pseudospectral method. This approach enables the joint optimization of discrete energy augmentation parameters and continuous trajectory control parameters, combining the advantages of the global search efficiency of Bayesian optimization with the local precision of pseudospectral techniques.
The rest of this paper is organized as follows. Section 2 and Section 3 formulate the maneuvering reentry model and the hybrid trajectory planning problem, respectively. Section 4 describes the hybrid optimization architecture and algorithms in detail. Section 5 shows three test cases to verify the proposed method. Finally, Section 6 summarizes the paper.
2. Energy-Augmented Skip–Glide Model During Reentry Phase
To model the skip–glide reentry trajectory of a plane-symmetric hypersonic vehicle, the Earth is approximated as a rotating oblate spheroid, and the vehicle is assumed to fly under zero sideslip conditions. A geocentric polar coordinate system is established with the Earth’s center as the origin. The position state vector is composed of the geocentric radius , longitude , and latitude , while the velocity state vector consists of forward velocity , flight path angle , and heading angle .
The flight dynamics of a hypersonic reentry phase are significantly affected by factors involved in Earth’s rotation, particularly the Coriolis force and centrifugal forces. Accordingly, the dynamic equations employed in this study account for these effects, expressed as follows [8]:
In the equations, denotes the angle of attack, and is the bank angle. The aerodynamic forces acting on the vehicle include lift and drag , defined respectively as follows:
where is the atmospheric density, is the aerodynamic reference area, and , are the lift and drag coefficients, respectively. Given the oblateness perturbation of the Earth, gravitational acceleration is modeled as a combination of geocentric gravitational force and meridional gravitational components . The energy augmentation thrust is denoted as . Due to the non-zero angle of attack, the thrust vector is decomposed into components aligned with aerodynamic force directions as follows:
The aerodynamic characteristics adopted in this study are based on the published HGV configuration “CAV-H”, with lift and drag coefficients fitted as functions of angle of attack and the Mach number [9], as follows:
where, , , , , and are the fitting coefficients of or . The atmospheric density profiles follow the Standard Atmosphere (USSA-1976) model [10].
3. Hybrid Planning of Energy-Augmented Skip–Glide Trajectory
For long-range reentry flight, hypersonic vehicles often employ skip–glide trajectories to balance range, maneuverability, and thermal protection. To further enhance endurance and energy efficiency, in this study, we introduce an auxiliary maneuver for energy augmentation, wherein propulsive energy is injected during the glide phase to elevate the overall energy of the vehicle, enabling a higher-dimensional design space for trajectory planning.
The planning of energy-augmented skip–glide trajectories inherently exhibits a hybrid structure, involving both continuous and discrete control variables. Conventional glide trajectory planning optimizes only continuous inner variables, such as angle of attack and bank angle, while determination of the energy injection timing constitutes a discrete decision, rendering the trajectory planning a hybrid optimal control problem.
To address this challenge, we decompose the planning process into two subproblems: (1) continuous optimization of the inner control variables for the glide trajectory and (2) discrete optimization of the outer control variables for energy injection timing. The continuous component refines control inputs under specified constraints to achieve optimal free-flying trajectories, whereas the discrete component employs intelligent search algorithms, such as Bayesian optimization, to determine the optimal injection moments that maximize augmentation benefits.
Under this framework, the trajectory optimization must simultaneously satisfy the equations of motion, boundary conditions, control/state constraints, and multiple performance objectives (including maximum range, minimum thermal load, and dynamic pressure limits). Clearly, the coupling between the energy augmentation maneuver and the subsequent flight dynamics significantly increases the nonlinearity of system control, the characteristics of tight constraints, and the complexity arising from multivariable coupling.
3.1. Control Variables
Generally, the equations of skip–glide reentry dynamics, as shown in Equation (1), can be represented by a piecewise-affine model, expressed as follows:
where denotes the state vector, represents the control vector, is the energy augmentation thrust, and and denote the initiation time and duration of the energy injection, respectively.
In this study, we consider the bank angle as a control variable of the unpowered (free flying) phase, whereas the timing of energy injection is considered a control variable of the powered (energy-augmented) phase. Typically, we define the angle of attack using a piecewise function [11] as follows:
where and denote the initial velocity and final velocity, respectively; is the maximum of the angle of attack; is the angle corresponding to the maximum lift-to-drag ratio; and are threshold velocities that are adjustable during optimization iteration.
3.2. Physical Constraints
The trajectory planning needs to ensure the output path satisfies all relevant physical and operational constraints. Typically, the main path constraints include the maximum heat flux , maximum dynamic pressure , maximum overload , and the stability condition for steady glide. Their corresponding mathematical formulations are expressed as follows [12]:
where is an empirical coefficient used in the heat flux constraint [13], defined by
where denotes the nose-tip radius of curvature of the vehicle, is the atmospheric density at sea level, and represents the first cosmic speed.
In addition to process constraints, terminal constraints on the initial and final states of the vehicle (including velocity, position, and other flight parameters) should also be imposed to ensure accuracy in the target arrival state (if needed) and adaptability to variable missions.
Control constraints are also enforced to regulate the magnitude and rate of control inputs, preserving vehicle responsiveness and stability. Excessive control inputs may lead to over-actuation and instability, while insufficient inputs can cause late maneuvering. In this study, constraints on the magnitude of the bank angle with rate are imposed to ensure smooth trajectory adjustments.
3.3. Objective Function
From the energy point of view, energy augmentation may lead to variations in relevant properties, such as flight range, maneuverability, or terminal velocity. The objective is to maximize flight range, and the objective function can be formally expressed as follows:
where denotes the continuous control input, which is the bank angle when is taken as Equation (6), during the unpowered phase, and represents the discrete energy augmentation timing during the powered phase. is the flight range defined as the great-circle distance between the initial and terminal positions of the vehicle, which can be calculated using the Haversine formula [14]:
where and are latitudes of the start and endpoints with longitudes and . denotes the radius of the Earth.
3.4. Planning Problem Statement
The trajectory planning problem can be stated as follows. Given the initial state and the dynamic model in Equation (1), the objective is to determine the best continuous trajectory control inputs (angle of attack and bank angle) and the best discrete energy augmentation decision (injection timing, duration, and thrust times) by maximizing in Equations (9) and (10), subject to the aforementioned constraints on flight state, control limits, and environmental conditions as specified in Equation (7), thereby maximizing the flight range.
The planning problem is characterized by a multi-phase, multi-constraint, hybrid continuous–discrete structure, thereby rendering it a hybrid optimal control problem. Solving such a problem necessitates an integrated optimization strategy, which can optimize continuous trajectory efficiently while searching for the discrete energy augmentation scheme smartly. Considering the advantages of pseudospectral planning for continuous system and Bayesian decision for discontinuous event-triggered system, we propose a hierarchical framework in the following section.
4. Hierarchical Bayesian–Pseudospectral Optimization Framework
To address hybrid trajectory optimization for energy-augmented skip–glide vehicles, we integrate the Bayesian optimization with the hp-adaptive pseudospectral method that we previously developed [15] to form a hybrid optimization approach named the Hierarchical Bayesian–Pseudospectral Optimization (HBPO) framework. This framework ensures both the accuracy of local optimization and the efficiency of global search, providing a globally optimal glide trajectory under conditions of energy augmentation. We built this structure because traditional pseudospectral methods are used primarily for continuous variable problems, and they struggle to handle discrete decision tasks like event-triggered energy injections. On the other hand, discrete optimization techniques, such as particle swarm optimization and genetic algorithms, focus on global search but often lack the precision and stability for continuous trajectory optimization. Thus, a cooperative structure that unifies discrete and continuous optimization with refined searching capabilities is essential for solving the hybrid planning problem inherent in advanced reentry trajectories.
The flowchart of the HBPO method is illustrated in Figure 2. As shown in the figure, the hierarchical framework decomposes the reentry trajectory into powered and unpowered segments, each optimized using appropriate planning strategies. In the powered segment, energy injection timing, treated as a discrete variable, is determined globally by Bayesian optimization within the discrete parameter space. Based on this, the powered trajectory segment is constructed via direct numerical integration using a Runge–Kutta scheme. For the unpowered segment of the skip–glide trajectory, the hp-adaptive pseudospectral method is employed to optimize the inner motional states, obtaining accurate nominal solutions within the continuous domain.
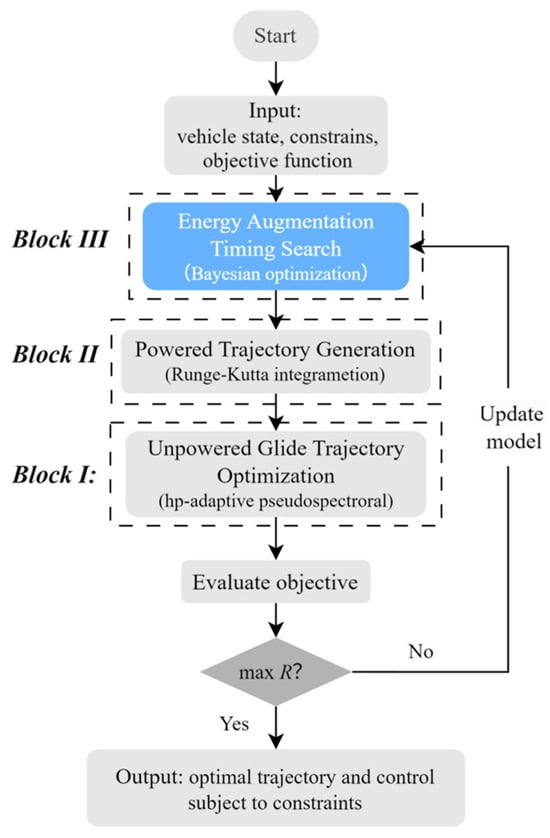
Figure 2.
The flowchart of the HBPO method.
4.1. Block I: Unpowered Glide Trajectory Optimization (hp-Adaptive Pseudospectral Method)
For the unpowered glide phase, the hp-adaptive pseudospectral method is employed aiming to achieve high-precision approximation of trajectory control variables. Essentially, the optimal control problem is transcribed into a nonlinear programming (NLP) problem through polynomial interpolation and adaptive node adjustment, thereby improving solution accuracy and convergence stability.
Considering Equation (1), we approximate the state variables over collocation points by a normalized interval via the Lagrange polynomial interpolation as follows:
where denotes the Lagrange basis polynomials, , representing the interpolation nodes corresponding to the collocation points. The state vector represents the state variables of the unpowered glide dynamics. The constraints from the system dynamics are imposed as residuals at the pseudospectral collocation points , where, expressed as follows:
where represents the equations of system dynamics stated in Equation (1).
Applying the hp-adaptive pseudospectral method given in [2], we can achieve the unpowered trajectory states with optimized flight control inputs. The hp-adaptive method autonomously adjusts both the polynomial degree and the segment partitioning based on local error estimates, enabling better nonlinear adaptability and robustness compared to the standard pseudospectral method. It is suitable for complex skip–glide trajectories characterized by sharp thermal and attitude variations.
4.2. Block II: Powered Trajectory Generation (The Runge–Kutta Integration)
As for the powered segment of the glide trajectory, it corresponds to a short thrust-driven phase, where the control inputs are deemed known and only require numerical calculation of the trajectory states.
The state propagation is performed using the classical fourth-order Runge–Kutta (RK4) algorithm [16] as follows:
where denotes the intermediate slope evaluations at each sub-step. The RK4 algorithm can generate simple but accurate results with good responsiveness to transient dynamics, making it suitable for providing consistent state sequences, which may serve as initial conditions for subsequent trajectory segments.
4.3. Block III: Energy Augmentation Timing Search (Bayesian Optimization)
Energy augmentation parameters (referring to injection timing assuming known thrust magnitude and duration) exhibit noticeable nonlinearity effects on trajectory performance. To enable efficient global searching over these parameters with limited cost of computational complexity, we introduce Bayesian optimization into the above two blocks.
The performance objective (maximum range), i.e., Equation (9), is denoted as , where represents the timing of energy augmentation. It is assumed that the objective function follows a Gaussian process (GP) surrogate model [17], expressed as follows:
where is the predicted mean, and is the radial basis function (RBF) kernel [18]. Also, we use an expected improvement (EI) acquisition function to update the candidate vector of [19], expressed as follows:
where is the expected objective value. and , respectively, denote the probability density of the standard normal distribution and the cumulative distribution function.
Based on Equations (9) and (15), the Bayesian optimization block may maximize by evaluating and updating τ iteratively, gradually approximating the global optimum. The candidate is updated by following the gradient of until is sufficiently small. By using this iterative approach, the block can obtain efficient convergence with light computational load, which is necessary for solving decision problems with high evaluation cost but low-dimensional decision space.
Performing Block III, Block II, and Block I in sequence, as shown in Figure 2, we establish the proposed hybrid HBPO method, capable of implementing trajectory planning for an energy-augmented skip–glide vehicle in its reentry phase. It is noticeable that the calculations of the three blocks are coupled, integrating the HBPO method into a multi-layer structure with inner and outer optimization loops.
4.4. Computational Complexity
The computational complexity of the HBPO method can be estimated as follows. The inner-layer pseudospectral method has a time cost of approximately per trajectory evaluation due to the highly efficient hp-adaptive mechanism, where denotes the number of collocation points. The outer-layer Bayesian optimization contains a Gaussian process surrogate model with each iteration costing . Considering the neglectable linear time cost of RK4 and trajectory evaluations, the total time complexity of the HBPO framework can be written as . With a similar structure, the space complexity of the method is governed by , which remains tractable for the problem scales considered in this study.
5. Numerical Simulation and Discussion
To verify the HBPO method, we designed three representative test cases within the same scenario. Test I and Test II demonstrate the performance of the inner-layer pseudospectral trajectory optimizer and the outer-layer Bayesian global search module, respectively. In the two tests, only the relevant layer works. Test III illustrates the effectiveness of the overall HBPO method under various conditions, showing the joint optimization results for cases with single and double energy augmentation.
In the simulation tests, an aerospace vehicle flies at hypersonic speed during its reentry phase along a skip–glide trajectory. The vehicle has auxiliary maneuver capability through an energy augmentation thruster. During reentry flight, the lift and drag coefficients are parameterized as functions of flight conditions. The fitted functions for the aerodynamic coefficients are expressed as follows:
Physical parameters of the hypersonic vehicle in the scenario are summarized in Table 1.

Table 1.
Physical parameters of the hypersonic vehicle.
5.1. Test I: Performance of the Pseudospectral Trajectory Optimizer
Firstly, we illustrate the trajectory accuracy and constraint-handling capability of the inner hp-adaptive pseudospectral method. In Test I, trajectory optimization is performed under standard conditions without energy augmentation. Continuous control variables are used to plan the trajectory, subject to the endpoint and boundary constraints listed in Table 2.

Table 2.
Endpoint constraints and boundary values of state variables.
Both the standard pseudospectral method (fixed collocation) and the hp-adaptive pseudospectral method (adaptive collocation) were simulated for performance comparison. The standard method uses 10 mesh intervals with 8 points per interval, whereas the adaptive method adjusts the number of collocation points between 4 and 12 based on local error estimates. The results are shown in Figure 3.
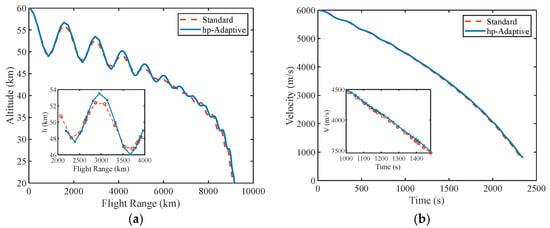

Figure 3.
The trajectory planning parameters using the inner-layer pseudospectral optimization: (a) range–altitude curve; (b) time-variant velocity; (c) time-variant flight path angle; (d) time-variant heading angle; (e) time-variant bank angle; (f) time-variant angle of attack.
From Figure 3, we observe that the hp-adaptive pseudospectral method obtains a smoother trajectory, with improved local resolution in high-curvature regions and better planning accuracy than the standard pseudospectral method. Also, the hp-adaptive pseudospectral method improves computational efficiency by reducing the total number of collocation points needed to achieve the same error tolerance, especially in problems exhibiting strong local nonlinearities. This results in smaller NLP dimensions and shorter solver time. In our tests, as shown in Table 3, the adaptive method achieved better accuracy with approximately 20–30% fewer nodes and 20% lower computational cost.

Table 3.
Point and interval usage of different pseudospectral methods.
5.2. Test II: Performance of the Bayesian Global Search Module
The objective of Test II is to verify the global search capability of Bayesian optimization in finding the optimal timing of energy augmentation by assessing its sample efficiency and convergence performance under a high-cost objective function setting.
In this test, energy augmentation is assumed to occur freely along the entire trajectory. The objective function in Equation (14), which maximizes flight range, is applied based on the trajectory of Equation (1) generated numerically through our developed Simulink-based system model [20], without incorporating pseudospectral trajectory optimization.
In the Bayesian optimization module, we use a Gaussian process with a squared exponential RBF kernel as the surrogate model. The EI acquisition function (15) uses the exploration parameter ξ = 0.01. The algorithm is initialized with 5 Latin hypercube samples and allowed to run up to 30 iterations. The Kernel hyperparameters are automatically optimized by marginal likelihood. The optimization domain for the augmentation timing is set between 100 s and 2000 s. The process is terminated when either the expected improvement falls below 10−3 or the iteration limit is reached.
The experimental data and the results of the optimization process are summarized in Table 4 and Figure 4.

Table 4.
Iterative results of flight range varying with timepoints of energy augmentation.
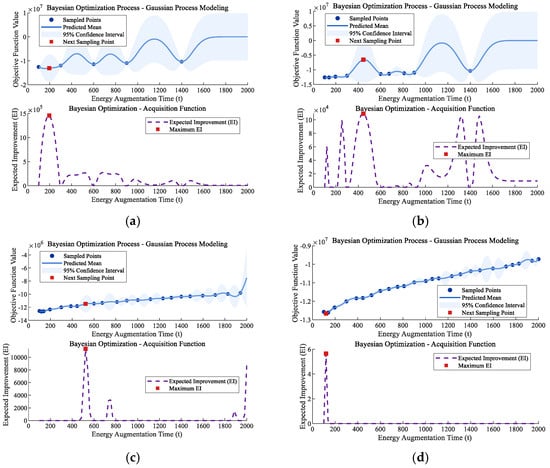
Figure 4.
The trajectory planning parameters using the outer-layer Bayesian optimization. The iterative results of the objective function and the expected improvement at (a) the 1st iteration; (b) the 5th iteration; (c) the 17th iteration; and (d) the 22nd iteration.
The results in Figure 4 show that the Bayesian optimization mechanism quickly explores the augmentation window, achieving full coverage by the 17th iteration and converging by the 22nd iteration. The optimal augmentation timing is found at 119.19 s, corresponding to a maximum flight range of 12,659,583.42 m (shown in Table 4), with a total computation time of 12.38 s.
We can infer from the results that the Bayesian optimization module has sound global search capability and high sampling efficiency in high-cost evaluation but low-dimensional decision problems, making it suitable as an outer layer in the hierarchical framework of hybrid trajectory optimization.
In addition to the fast convergence observed in our test case, the choice of Bayesian optimization is also supported by existing comparative studies. For example, in [21], BO achieved comparable optimization accuracy with 4% computation time required by genetic algorithms (GAs) in a similar low-dimensional decision problem. This further justifies the use of BO as the outer-layer optimizer in the HBPO framework, particularly for cases like trajectory evaluations with high computational costs.
5.3. Test III: Performance of the HBPO Method
Test III is conducted to assess the trajectory planning results using the proposed HBPO method, for which we considered scenarios with single and double energy augmentation and evaluated the impact of energy augmentation on flight range under multiple physical constraints.
Following skip–glide corridor of the vehicle [3], shown as the surrounded zone in Figure 5, and applying the physical constraints expressed in Equation (7), we select the candidate energy augmentation points along the reference trajectory obtained from the inner hp-adaptive pseudospectral method. In the test case, five feasible time windows are determined according to the height–velocity (H–V) envelope of the vehicle, as shown in Figure 5, within the skip–glide corridor that indicates boundary constraints on the energy augmentation timing. Within each window, the Bayesian optimization module is applied to search for the optimal augmentation timing, initialized with 4 random samples and capped at 30 iterations.
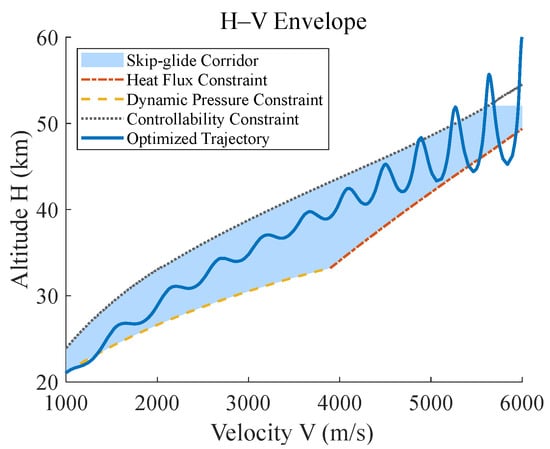
Figure 5.
The skip–glide corridor and the H–V envelope.
The results in Table 5 show that under single energy augmentation, the maximum flight range occurs at 78.80 s, with a range of 14,160.02 km, representing an increment of 55.08% compared to the maximum range of 9134 km achieved by standard pseudospectral optimization without energy augmentation.

Table 5.
Optimal points and corresponding ranges in different intervals.
For the optimal trajectory result with single energy augmentation at 78.80 s, the range–altitude profile and the H–V envelop are shown in Figure 6. The figure illustrates that the optimal trajectory reaches the maximum range compared with that of energy augmentation at other random times, satisfying physical constraints simultaneously with enhanced controllability and reduced boundary crossing.
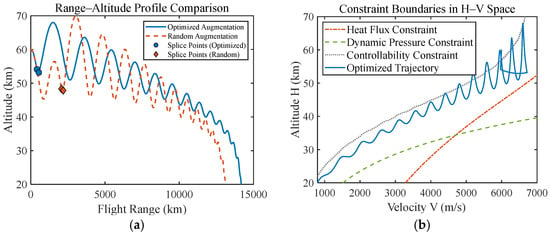
Figure 6.
The optimal trajectory result with single energy augmentation using the HBPO method: (a) range–altitude curve; (b) H-V envelope.
We further consider the case of double energy augmentation. Two search windows with a time span of [50, 1000] seconds and [1000, 2000] seconds are selected. We assume that there is a minimum interval of 1000 s between the two energy augmentation events [7]. By applying the HBPO method, simulation results show that algorithm convergence is achieved after 14 iterations, identifying the optimal augmentation timing at 50.00 s and 1062.16 s. The objective function values at each sampling point during the entire optimization process are presented in Figure 7, clearly showing the decision space and the globally optimal decision time of double energy augmentation.
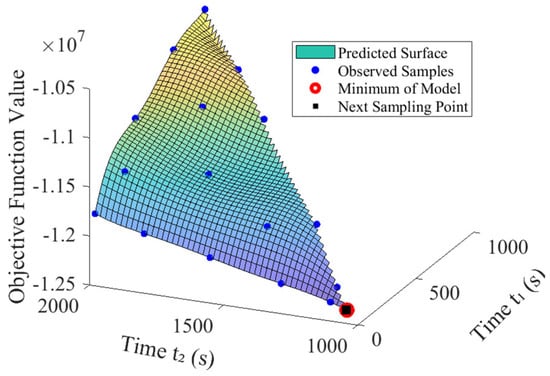
Figure 7.
Objective function values varying with time of double energy augmentation.
For the optimal trajectory with double energy augmentation at 50.00 s and 1062.16 s, the range–altitude and velocity–time profiles are shown in Figure 8, where we randomly take another double augmentation case ( = 321.43 s and = 1693.77 s) to evaluate the performance of the optimal trajectory. The result in the figure shows that the optimized trajectory achieves an increment of 7.5% in flight range and 2.5% in flight time relative to the compared random augmentation case.
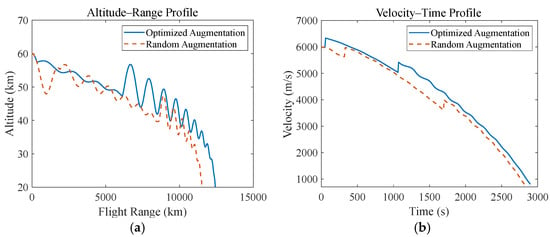
Figure 8.
The optimal trajectory result with double energy augmentation using the HBPO method: (a) range–altitude curve; (b) H–V envelope.
From the results of the three tests, we can conclude that the effectiveness of the proposed HBPO framework for hybrid trajectory planning is verified. Its multi-layer optimization structure offers advantage over single-layered pseudospectral methods, achieving better flight performance and adaptability to the skip–glide trajectories of reentry vehicles with hybrid maneuver.
Moreover, in the design of our comparison tests, environmental and aerodynamic parameters (such as atmospheric density, lift-to-drag ratio, and vehicle mass) were kept constant to ensure fair comparison across optimization method; moderate variations in these parameters (e.g., ±5% changes in air density or aerodynamic coefficients) appeared during early-stage testing, showing limited impact on the optimal energy injection timing and overall trajectory quality. It indicates that the HBPO framework also demonstrates performance robustness within reasonable uncertainty bounds.
6. Conclusions
For the problem of energy-augmented hypersonic skip–glide trajectory optimization, we proposed the HBPO framework in this paper. It provides a hierarchical hybrid planning method by cooperatively integrating Bayesian optimization with the hp-adaptive pseudospectral algorithm, demonstrating the following positive characteristics.
- The developed framework addresses discrete decision variables of energy injection timing and continuous control variables of reentry flight together, overcoming limitations of traditional approaches that typically separate these two optimization domains.
- Numerical results indicate that the inner-layer hp-adaptive pseudospectral approach provides more than 20% improvement in computational efficiency and trajectory accuracy compared to conventional pseudospectral methods. Its adaptive capability ensures high accuracy in high-curvature trajectory segments and robust constraint handling.
- The outer-layer Bayesian optimization module converges quickly within very few iterations (less than 30) to find the optimal augmentation strategy that can greatly enhance mission performance. In a typical case, single energy augmentation can increase flight range by up to 55.08%, demonstrating its high sampling efficiency and global search capability.
- Joint optimization tests further confirm the effectiveness of the proposed strategy. Specifically, double energy augmentation optimization achieves additional 7.5% increment in flight range compared to the randomly timed augmentation cases, underlining the importance of reasonable and intelligent timing selection.
Overall, the proposed HBPO framework offers a new solution to the midcourse energy injection timing problem in skip–glide vehicles, which is a topic rarely addressed in previous research. By combining Bayesian optimization with an hp-adaptive pseudospectral method, it efficiently handles discrete timing decisions and continuous trajectory planning in a unified way. Future studies may extend the method to real-time trajectory reconfiguration, game planning, intelligent guidance, and control by providing predicted nominal trajectories for aerospace vehicles operating in complex environments.
Author Contributions
Conceptualization, Y.L.; methodology, L.W., Y.L. and X.W.; software, L.W.; validation, L.W. and G.Z.; formal analysis, L.W.; investigation, L.W.; resources, Y.L.; data curation, G.Z. and X.W.; writing—original draft preparation, L.W.; writing—review and editing, Y.L.; supervision, Y.L. and X.W.; funding acquisition, Y.L. and X.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Sichuan Province of China, grant number 2024NSFSC0181; Natural Science Foundation of Shanghai Municipality of China, grant number 24R1437300; Aeronautical Science Foundation of China, grant number 201901080001.
Data Availability Statement
The data presented in this study are available on request from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| HBPO | Hierarchical Bayesian–Pseudospectral Optimization |
| NLP | Nonlinear Programming |
| GP | Gaussian Process |
| RBF | Radial Basis Function |
| EI | Expected Improvement |
| H-V | Height–Velocity |
References
- Chai, K.; Zhang, K.; Wang, J.; Yang, L. Analysis of energy supply strategy for hypersonic skip-glide trajectory. Tactical Missile Technol. 2020, 41, 23–29+58. [Google Scholar] [CrossRef]
- Feng, X.; Lv, Y.; Gao, Y.; Li, Y. Adaptive Radau pseudo-spectral optimization for descending trajectory of a hypersonic cruise vehicle. Aerosp. Syst. 2020, 3, 275–286. [Google Scholar] [CrossRef]
- Wang, L.; Li, Y.; Yong, E.; Li, G. Performance boundary analysis and multi-constrained design for jumping-glide trajectory with maneuver assistance. Flight Dyn. 2025, 43, 57–63. [Google Scholar] [CrossRef]
- Zhao, J.; Gu, L.; Gong, C. Design and optimization of hypersonic skip-glide trajectory. J. Solid Rocket. Technol. 2009, 32, 123–126. [Google Scholar]
- Huang, R. Research on Parameter/Trajectory Optimization and on-Board Guidance for Boost Complement Glide Vehicle. Ph.D. Dissertation, Harbin Institute of Technology, Harbin, China, December 2016. [Google Scholar]
- Song, M.; Guo, J.; Li, J.; Tang, S. Comprehensive optimization design of parameters and trajectory for complement glide vehicle. Flight Dyn. 2023, 41, 59–66. [Google Scholar] [CrossRef]
- Yong, E.; Wei, T.; Liu, S.; Chen, Q.; Yu, J. A trajectory optimization method for boost-energy supplementing skip gliding motion based on pseudospectral method. J. Astronaut. 2024, 45, 893–902. [Google Scholar]
- Li, Y.; Wang, L.; Tang, J.; Li, G. Energy-based range augmentation analysis for maneuver-assisted jumping-glide trajectory design. In Advances in Guidance, Navigation and Control; Yan, L., Duan, H., Deng, Y., Eds.; Springer Nature: Singapore, 2024; Volume 7, pp. 437–448. [Google Scholar] [CrossRef]
- Zou, Y. Study of Deorbit and Reentry Trajectory Design and Guidance Methods for Lifting Body Spacecraft. Ph.D. Dissertation, National University of Defense Technology, Changsha, China, November 2014. [Google Scholar]
- NOAA; NASA; USAF. U.S. Standard Atmosphere, 1976; U.S. Goverment Printing Office: Washington, DC, USA, 1976. Available online: https://ntrs.nasa.gov/citations/19770009539 (accessed on 8 August 2013).
- Yong, E.; Zhao, T.; Cui, W.; Liu, T. A full-phase dynamic motion model of boost–glide vehicle. Mech. Eng. 2022, 44, 1297–1302. [Google Scholar] [CrossRef]
- Li, Z. Penetration of Hypersonic Gliding Aircraft: Trajectory Planning and Guidance Method. Ph.D. Dissertation, National University of Defense Technology, Changsha, China, October 2019. [Google Scholar]
- Mehta, P.; Minisci, E.; Vasile, M.; Walker, A.C.; Brown, M. An open source hypersonic aerodynamic and aerothermodynamic modelling tool. In Proceedings of the 8th European Symposium on Aerothermodynamics for Space Vehicles, Lisbon, Portugal, 2–6 March 2015. [Google Scholar]
- Setiawan, E.; Setia Budi, A.; Syauqy, D. Design of flight safe system for quadcopter based on data-driven regression and Haversine distance calculation. In Proceedings of the 6th International Conference on Sustainable Information Engineering and Technology, Malang, Indonesia, 13–14 September 2021. [Google Scholar]
- Feng, Y.; Wang, R.; Mei, Y.; Sun, H.; Wu, L. Reentry trajectory planning for range-extended hypersonic vehicles with boosters. J. Beijing Univ. Aeronaut. Astronaut. 2020, 46, 1503–1513. [Google Scholar] [CrossRef]
- Carpenter, M.H.; Kennedy, C.A.; Bijl, H.; Viken, S.A.; Vatsa, V.N. Fourth-order Runge-Kutta schemes for fluid mechanics applications. J. Sci. Comput. 2005, 25, 157–194. [Google Scholar] [CrossRef]
- Kim, H.C.; Ghahramani, Z. Bayesian Gaussian process classification with the EM-EP algorithm. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1948–1959. [Google Scholar] [CrossRef] [PubMed]
- Ring, M.; Eskofier, B.M. An approximation of the Gaussian RBF kernel for efficient classification with SVMs. Pattern Recognit. Lett. 2016, 84, 107–113. [Google Scholar] [CrossRef]
- Guo, Z.; Ong, Y.S.; Liu, H. Calibrated and recalibrated expected improvements for Bayesian optimization. Struct. Multidiscip. Optim. 2021, 64, 3549–3567. [Google Scholar] [CrossRef]
- Feng, X. Research on Trajectory Optimization of Hypersonic Vehicle Based on Adaptive Pseudo-Spectral Method. Master’s Thesis, University of Electronic Science and Technology of China, Chengdu, China, June 2021. [Google Scholar]
- Ye, Y.; Shen, H.; Liu, Y.; Gao, Z.; Kong, X.; Chen, J. Integrated design of hypersonic aircraft wing layout and mission trajectory. J. Beijing Univ. Aeronaut. Astronaut. 2024, 50, 1–17. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).